Scaling the Dynamic Buckling Behavior of a Box Girder Based on the Finite Similitude Approach
Abstract
1. Introduction
2. Finite Similitude Theory
2.1. Transport Equations
2.2. Derivation of Similar Equations
2.3. Scaling of the Constitutive Equations
2.4. Practical Constraints
3. Similarity Criteria for the Box Girder Based on Finite Similitude Theory
3.1. Scaling Criteria for Static Ultimate Strength of Box Girders
- (1)
- Determine the geometric dimensions lps, material properties (density ρps, material yield stress σyps), and boundary conditions of the full-scale model of the box girder;
- (2)
- Determine the geometric scale factor β, material properties (density ρts, material yield stress σyts), and boundary conditions of the box girder trial model;
- (3)
- The geometric dimensions lts and density scale factor αρ of the trial model are determined by similarity criteria Π1 and Π2, respectively;
- (4)
- The time scale factor h is calculated by the similarity criterion Π3;
- (5)
- The bending moment M and the corresponding rotation angle θ of the full-scale model and the trial model of the box girder are obtained through experimental or finite element calculation, and the predicted bending moment Mps and angle θps relative to the full-scale model are calculated using the similarity criteria Π4 and Π5.
3.2. Scaling Criteria for Dynamic Responses of Box Girders
- (1)
- Determine the geometric dimensions lps, material properties (density ρps, material yield stress σyps), initial conditions (initial peak bending moment Mdps, bending moment action time history Tdps), and boundary conditions of the full-scale model of the box girder;
- (2)
- Determine the geometric scale factor (β), material properties (density ρts, material yield stress σyts), initial conditions (initial peak load Mdts, load action time history Tdts), and boundary conditions of the box girder trial model;
- (3)
- The geometric dimensions (lts) and density scale factor (αρ) of the trial model are determined using similarity criteria Π1 and Π2, respectively;
- (4)
- The time scale factor h is calculated by the similarity criterion Π3;
- (5)
- Obtain the displacement angle (θ) and its temporal evolution (time history, t) for both the full-scale and trial models of the box girder through experimental or finite element calculations, and calculate the predicted displacement angle (θps) and the change in the angle over time relative to the full-scale model using similarity criteria Π4 and Π5.
3.3. Correction of the Nonlinear Response Scaling Criterion of Box Girder
- (1)
- Determine the geometric dimensions lps, material properties (density ρps, constitutive relationship, such as the C-S equation), initial conditions (initial peak bending moment load Mdps, initial load action time history Tdps), and boundary conditions of the full-scale model of the box girder;
- (2)
- Determine the geometric scale factor β, the material properties (density ρts, constitutive relationship C-S equation), and boundary conditions of the box girder trial model;
- (3)
- The geometric dimensions lts and density scale factor αρ of the trial model are determined by similarity criteria Π1 and Π2, respectively;
- (4)
- Determine the average dynamic stress between the full-scale model of the box girder and the materials of each trial model, calculate the velocity ratio βv using the similarity criterion Π3, and further obtain the time scale factor h through the similarity criterion Π4;
- (5)
- Calculate the time history Tts and initial peak bending moment load Mdts of the box girder trial model by combining the scale factors Π5 and Π6, respectively;
- (6)
- The displacement angle θ of the full-scale model of the box girder and the trial model are obtained by experiment or finite element calculation, and the predicted displacement angle θps and displacement-time change history relative to the full-scale model are calculated using the similarity criteria Π5 and Π7.
4. Numerical Analyses
4.1. Finite Element (FE) Model of Box Girder Specimen
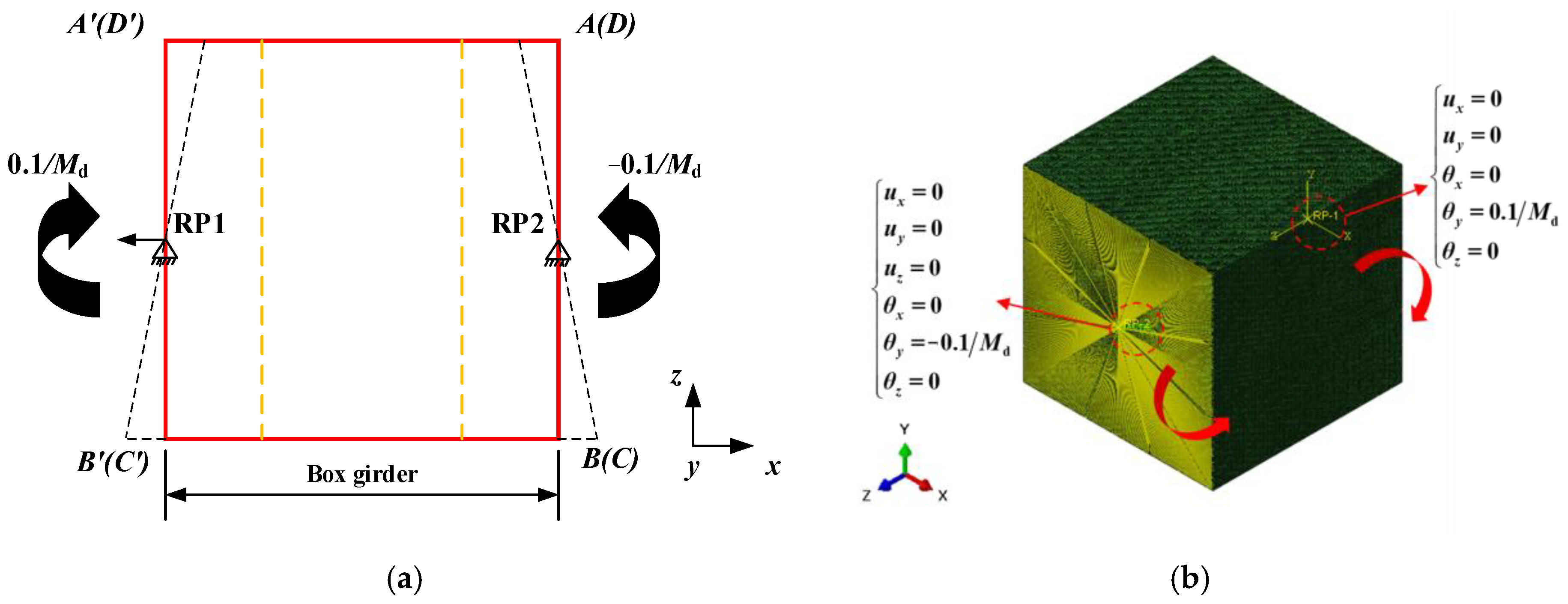
4.2. Boundary and Loading Conditions
4.2.1. Static Load Setting
4.2.2. Dynamic Load Setting
4.3. Design Results of Small-Scale Box Girder Model
4.3.1. Detailed Information
4.3.2. Modified Scaling Factors
4.4. Mesh Convergence Analysis
5. Similarity Validation of Quasi-Static Cases
5.1. Ultimate Strength
5.2. Buckling Failure Mode
6. Similarity Validation of Dynamic Cases
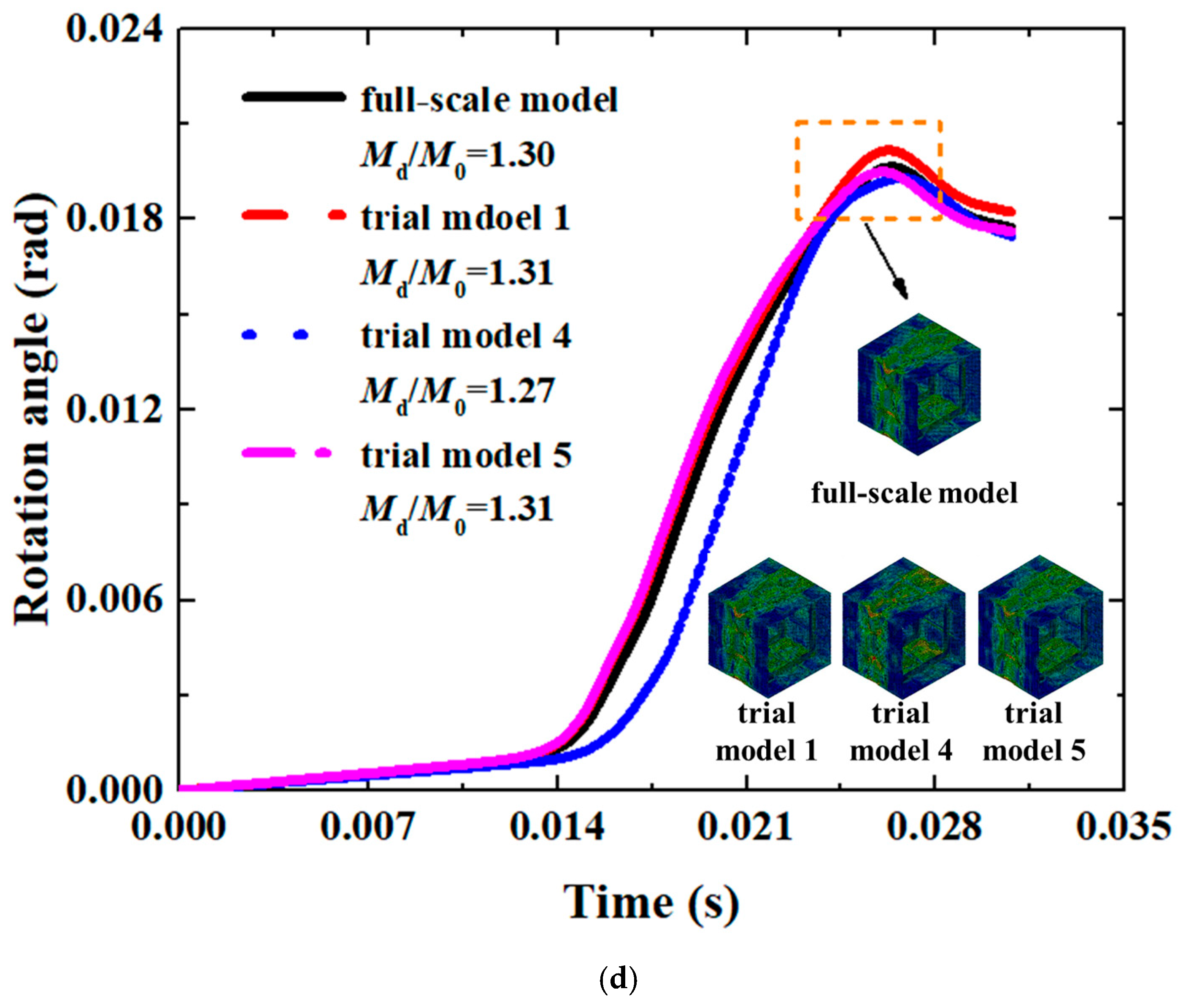
6.1. Dynamic Critical Buckling Load
6.2. Correction of Dynamic Critical Buckling Load
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sugimura, T.; Nozaki, M.; Suzuki, T. Destructive experiment of ship hull model under longitudinal bending. J. Zosen Kiokai 2009, 1966, 209–220. [Google Scholar] [CrossRef]
- Dow, R.S. Testing and Analysis of a 1/3-Scale Welded Steel Frigate Model. In Proceedings of the International Conference on Advances in Marine Structures-2, Dunfermline, UK, 21–24 May 1991. [Google Scholar]
- Dowling, P.J. The effect of shear lag on the ultimate strength of box girders. In Proceedings of the International Congress on Steel Plated Structures, London, UK, 20–21 July 1976; pp. 108–147. [Google Scholar]
- Reckling, K.A. Behaviour of box girders under bending and shear. In Proceedings of the 7th International Ship and Offshore Structures Congress (ISSC), Paris, France, 20–24 August 1979. [Google Scholar]
- Ostapenko, A. Strength of Ship Hull Girders under Moment, Shear and Torque. In Proceedings of the SSC-SNAME Symposium on Extreme Loads Response, Arlington, TX, USA, 19–20 October 1981; pp. 149–166. [Google Scholar]
- Xu, X.D.; Cui, W.C.; Leng, J.X. Experimental and theoretical study on the ultimate bearing capacity of box girder. Ship Mech. 2000, 5, 36–43. [Google Scholar]
- Sun, H.H.; Soares, C.G. An experimental study of ultimate torsional strength of a ship-type hull girder with a large deck opening. Mar. Struct. 2003, 16, 51–67. [Google Scholar] [CrossRef]
- Yang, P. Research on Ultimate Strength and Damage Residual Strength of Hull Structure. Ph.D. Thesis, Wuhan University of Technology, Wuhan, China, 2005. [Google Scholar]
- Liu, B. Research on the Ultimate Strength of Small Waterplane Area Catamaran. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2009. [Google Scholar]
- Liu, W.Q. Research on the Ultimate Strength of High-Speed Trimaran. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2011. [Google Scholar]
- Yuan, T. Nonlinear Similarity Criterion and Experimental Study on Ultimate Strength of Axially Compressed Stiffened Plate. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2019. [Google Scholar]
- Li, J.; Zhang, R.; Jin, L.; Lan, D.; Du, X. Scaling laws of low-velocity impact response for RC beams: Impact force and reaction force. Int. J. Impact Eng. 2024, 186, 104887. [Google Scholar] [CrossRef]
- Huang, X.; Feng, Y.; Wang, M.; Qiu, X. The dominating dimensionless numbers of an elastic-plastic thin plate under dynamic loading. J. Mech. Phys. Solids 2024, 186, 105593. [Google Scholar] [CrossRef]
- Cheng, Y.Q.; Liu, K.; Wang, Z.L. Scaling behaviour of corrugated sandwich panels under impact load. J. Sandw. Struct. Mater. 2023, 25, 846–865. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.; Wang, Z.; Yang, N. Compensation model for truncated ogive projectiles penetrating ship stiffened plates made from different materials. Ocean Eng. 2023, 286, 115604. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Yao, X.; Yang, N. Material similarity law of blunt projectiles penetrating scaled steel target plates. Int. J. Impact Eng. 2023, 178, 104603. [Google Scholar] [CrossRef]
- Ma, H.; Kawamura, Y.; Okada, T.; Wang, D.; Hayakawa, G. An improved scaled model design method for box girders under hogging moment considering the ultimate bending moment and collapse modes. Mar. Struct. 2024, 98, 103660. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, L.; Okada, T.; Kawamura, Y.; Wang, D.; Sun, S.; Liu, N.; Li, C. Experimental and numerical study on a universal distorted model design strategy for the box girder with the double bottom under the bending moment considering the ultimate strength and buckling collapse modes, Part 1: Scaling strategy. Ocean Eng. 2025, 338, 121878. [Google Scholar] [CrossRef]
- Oshiro, R.E.; Calle, M.A.; Mazzariol, L.M.; Alves, M. Experimental Study of Collision in Scaled Naval Structures. Int. J. Impact Eng. 2017, 110, 149–161. [Google Scholar] [CrossRef]
- Mazzariol, L.M.; Oshiro, R.E.; Alves, M. A Method to Represent Impacted Structures Using Scaled Models Made of Different Materials. Int. J. Impact Eng. 2016, 90, 81–94. [Google Scholar] [CrossRef]
- Davey, K.; Sadeghi, H.; Darvizeh, R.; Golbaf, A.; Darvizeh, A. A Finite Similitude Approach to Scaled Impact Mechanics. Int. J. Impact Eng. 2020, 148, 103744. [Google Scholar] [CrossRef]
- Sadeghi, H.; Davey, K.; Darvizeh, R.; Darvizeh, A. Scaled Models for Failure under Impact Loading. Int. J. Impact Eng. 2019, 129, 36–56. [Google Scholar] [CrossRef]
- Davey, K.; Darvizeh, R.; Zhang, J. Finite Similitude in Fracture Mechanics. Eng. Fract. Mech. 2021, 245, 107573. [Google Scholar] [CrossRef]
- Davey, K.; Darvizeh, R.; Al-Tamimi, A. Scaled metal forming experiments: A transport equation approach. Int. J. Solids Struct. 2017, 125, 184–205. [Google Scholar] [CrossRef]
- Davey, K.; Darvizeh, R.; Al-Tamimi, A. Finite Similitude in Metal Forming. In Proceedings of the 12th International Conference on Numerical Methods in Industrial Forming Processes, Troyes, France, 4–7 July 2016; Volume 80, p. 01005. [Google Scholar]
- Raul, O.C.; Teresa, A.R.; Keith, D. Scaling in biomechanical experimentation: A finite similitude approach. J. R. Soc. Interface 2018, 15, 20180254. [Google Scholar] [CrossRef]
- Darvizeh, R.; Davey, K. A transport approach for analysis of shock waves in cellular materials. Int. J. Impact Eng. 2015, 82, 59–73. [Google Scholar] [CrossRef]
- Sadeghi, H.; Davey, K.; Darvizeh, R.; Rajabiehfard, R.; Darvizeh, A. An Investigation into Finite Similitude for High-Rate Loading Processes: Advantages in Comparison to Dimensional Analysis and its Practical Implementation. Int. J. Impact Eng. 2020, 140, 103554. [Google Scholar] [CrossRef]
- Zhang, J.; Davey, K.; Darvizeh, R.; Sadeghi, H. A two-experiment approach to physical modelling: Damage and failure under high-rate loading. Thin-Walled Struct. 2022, 179, 109589. [Google Scholar] [CrossRef]
- Ochoa-Cabrero, R.; Alonso-Rasgado, T.; Davey, K. A Two-Experiment Approach to Scaling in Biomechanics. J. Biomech. Eng. 2022, 144, 081004. [Google Scholar] [CrossRef]
- Davey, K.; Zhang, J.; Darvizeh, R. Fracture mechanics: A two-experiment theory. Eng. Fract. Mech. 2022, 271, 108618. [Google Scholar] [CrossRef]
- Al-Tamimi, A. Scaling of bi-material sandwich panels subjected to impact loadings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 5443–5459. [Google Scholar] [CrossRef]
- Davey, K.; Darvizeh, R.; Akhigbe-Midu, O.; Sadeghi, H. Scaled cohesive zone models for fatigue crack propagation. Int. J. Solids Struct. 2022, 256, 111956. [Google Scholar] [CrossRef]
- Davey, K.; Sadeghi, H.; Darvizeh, R. The theory of scaled electromagnetism. Proc. R. Soc. A 2022, 478, 20210950. [Google Scholar] [CrossRef]
- Davey, K.; Darvizeh, R.; Atar, M. A first order finite similitude approach to scaled aseismic structures. Eng. Struct. 2021, 231, 111739. [Google Scholar] [CrossRef]
- Xie, R.Z.; Zhong, W.Z.; Huang, X.C. Model Experiment and Numerical Simulation of Drop Impact of Packaging Composite Structure. In Proceedings of the 11th National Academic Conference on Impact Dynamics, Xian, China, 14–17 August 2013. [Google Scholar]
- Yang, X.; Ma, J.; Sun, Y.; Yang, J. An Internally Nested Circular-Elliptical Tube System for Energy Absorption. Thin-Walled Struct. 2019, 139, 281–293. [Google Scholar] [CrossRef]
- Karagiozova, D.; Alves, M.; Jones, N. Inertia Effects in Axisymetrically Deformed Cylindrical Shells under Axial Impact. Int. J. Impact Eng. 2000, 24, 1083–1115. [Google Scholar] [CrossRef]
- Krzysztof, W. TB11 Test for Short W-Beam Road Barrier. In Proceedings of the 11th European LS-DYNA Conference, Salzburg, Austria, 9–11 May 2017. [Google Scholar]
- Tsuda, T.; Ohnishi, Y.; Ohtagaki, R.; Cho, K.; Fujimoto, T. Three-Point Bending Crack Propagation Analysis of Beam Subjected to Eccentric Impact Loading by X-FEM. In Proceedings of the 10th European LS-DYNA Conference, Wurzburg, Germany, 15–17 September 2015. [Google Scholar]

















| Symbol | Meanings |
|---|---|
| D* | Differential |
| t | Time |
| Ω | Control Volume |
| ps | Physical Space |
| ts | Trial Space |
| ρ | Density |
| Ψ | Physical Quantity |
| V | Unit Volume |
| v | Velocity |
| n | Unit Normal Of The Boundary Γ Of The Control Volume Ω |
| Γ | The Boundary For Ω |
| J | Flux |
| b | Source Term |
| αρ | Density Scaling Factor |
| β | Scaling Ratio |
| h | Time Scaling Factor |
| σy/σstat | Static Yield Strength |
| αv | Velocity Scaling Factor |
| αu | Displacement Scaling Factor |
| u | Displacement |
| l | Scale |
| σi | Unit Stress |
| Fi | Unit Force |
| Ai | Unit Area |
| F | Force |
| M | Bending Moment |
| L | Arm Of Force |
| θ | Angle Of Rotation |
| R | Radius Of Corner |
| Average Stress | |
| ε | Strain |
| D | Coefficient In C—S Constitutive Equation |
| q | Coefficient In C—S Constitutive Equation |
| βv | Velocity Modifying Factor |
| ζ | Ratio Of Average Dynamic Yield Strength |
| M0 | Initial Bending Moment Load |
| T0 | Initial Loading Time |
| hmod | Modified Time Scaling Factor |
| M0mod | Modified Bending Moment Load |
| T0mod | Modified Loading Time |
| NO (Material) | Geometry Properties | Material Properties | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scale Ratio | Plate | Stiffener | Plate and Stiffener | ||||||||||
| β | a | b | t | hs | ts | hw | tw | ρ (10−9) (T/mm3) | μ | E (GPa) | σy (MPa) | σy/E (10−3) | |
| Full-scale model (Q235 [36]) | 1 | 600 | 400 | 5 | 60 | 4 | 120 | 8 | 7.85 | 0.3 | 206 | 235 | 1.14 |
| Trial model 1 (Q235) | 2 | 300 | 200 | 2.5 | 30 | 2 | 60 | 4 | 7.85 | 0.3 | 206 | 235 | 1.14 |
| Trial model 2 (Q345 [37]) | 2 | 300 | 200 | 2.5 | 30 | 2 | 60 | 4 | 7.85 | 0.3 | 206 | 345 | 1.68 |
| Trial model 3 (Al [38]) | 2 | 300 | 200 | 2.5 | 30 | 2 | 60 | 4 | 2.69 | 0.33 | 72 | 295 | 4.07 |
| Trial model 4 (S235 [39]) | 2 | 300 | 200 | 2.5 | 30 | 2 | 60 | 4 | 7.80 | 0.3 | 210 | 240 | 1.14 |
| Trial model 5 (20 steel [36]) | 2 | 300 | 200 | 2.5 | 30 | 2 | 60 | 4 | 7.85 | 0.29 | 211 | 245 | 1.16 |
| Location | Translation | Rotational | ||||
|---|---|---|---|---|---|---|
| ux | uy | uz | θx | θy | θz | |
| RP1 | fix | fix | - | fix | 0.1/Md | fix |
| RP2 | fix | fix | fix | fix | −0.1/Md | fix |
| M0 | T0 | |
|---|---|---|
| Full-scale model | 1.87 × 109 | 7.71 × 10−3 |
| Trial model 1 | 2.34 × 108 | 3.85 × 10−3 |
| Trial model 4 | 2.39 × 108 | 3.80 × 10−3 |
| Trial model 5 | 2.41 × 108 | 3.82 × 10−3 |
| Q235-Q235 | 2 | 0.125 | 2.000 | 0.125 | 0.063 |
| Q235-Q345 | 2 | 0.125 | 2.423 | 0.151 | 0.063 |
| Q235-Al | 2 | 0.043 | 3.832 | 0.082 | 0.021 |
| Q235-S235 | 2 | 0.124 | 2.028 | 0.126 | 0.062 |
| Q235-20 steel | 2 | 0.125 | 2.042 | 0.128 | 0.063 |
| D (s−1) | q | |
|---|---|---|
| Full-scale model | 40.4 | 5 |
| Trial model 1 | 40.4 | 5 |
| Trial model 2 | 40.4 | 5 |
| Trial model 3 | 12,880 | 4 |
| Trial model 4 | 4000 | 5 |
| Trial model 5 | 40.4 | 5 |
| Q235-Q235 | 2 | 1.03 | 0.125 | 2.06 |
| Q235-S235 | 2 | 0.90 | 0.124 | 1.80 |
| Q235-20 steel | 2 | 1.05 | 0.125 | 2.10 |
| M0 | M0mod | T0 | T0mod | |
|---|---|---|---|---|
| Full-scale model | 1.87 × 109 | 1.87 × 109 | 7.71 × 10−3 | 7.71 × 10−3 |
| Trial model 1 | 2.34 × 108 | 2.48 × 108 | 3.85 × 10−3 | 3.74 × 10−3 |
| Trial model 4 | 2.39 × 108 | 1.88 × 108 | 3.80 × 10−3 | 3.28 × 10−3 |
| Trial model 5 | 2.41 × 108 | 2.58 × 108 | 3.82 × 10−3 | 3.67 × 10−3 |
| Mtsmax | Mpsmax | Error | θts | θps | Error | |
|---|---|---|---|---|---|---|
| Full-scale model | —— | 1.87 × 109 | —— | —— | 9.50 × 10−4 | —— |
| Trial model 1 | 2.34 × 108 | 1.87 × 109 | 0.00% | 9.50 × 10−4 | 9.50 × 10−4 | 0.00% |
| Trial model 2 | 3.05 × 108 | 1.66 × 109 | −11.11% | 1.25 × 10−3 | 1.25 × 10−3 | −31.55% |
| Trial model 3 | 2.18 × 108 | 1.39 × 109 | −25.57% | 2.88 × 10−3 | 2.88 × 10−3 | 203.30% |
| Trial model 4 | 2.39 × 108 | 1.87 × 109 | 0.02% | 9.50 × 10−4 | 9.50 × 10−4 | 0.05% |
| Trial model 5 | 2.41 × 108 | 1.85 × 109 | −1.07% | 9.63 × 10−4 | 9.63 × 10−4 | 1.42% |
| Dynamic Buckling Critical Load | ||||||||
|---|---|---|---|---|---|---|---|---|
| Td = T0 | Error | Td = 1.33T0 | Error | Td = 2T0 | Error | Td = 4T0 | Error | |
| Full-scale model | 1.90 | \ | 1.70 | \ | 1.51 | \ | 1.30 | \ |
| Trial model 1 | 1.95 | −2.63% | 1.74 | −2.35% | 1.55 | −2.65% | 1.34 | −3.08% |
| Trial model 4 | 1.65 | 13.16% | 1.49 | 12.35% | 1.34 | 11.26% | 1.19 | 8.46% |
| Trial model 5 | 1.95 | −2.63% | 1.75 | −2.94% | 1.56 | −3.31% | 1.35 | −3.85% |
| Dynamic Buckling Critical Load | ||||||||
|---|---|---|---|---|---|---|---|---|
| Td = T0 | Error | Td = 1.33T0 | Error | Td = 2T0 | Error | Td = 4T0 | Error | |
| Full-scale model | 1.90 | \ | 1.70 | \ | 1.51 | \ | 1.30 | \ |
| trial model 1 | 1.92 | −1.05% | 1.71 | −0.59% | 1.53 | −1.32% | 1.31 | −0.77% |
| trial model 4 | 1.77 | 6.84% | 1.59 | 6.47% | 1.43 | 5.30% | 1.27 | 2.31% |
| trial model 5 | 1.91 | −0.53% | 1.71 | −0.59% | 1.52 | −0.66% | 1.31 | −0.77% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Wang, Z.; Kong, X.; Zhou, H.; Zheng, C.; Wu, W. Scaling the Dynamic Buckling Behavior of a Box Girder Based on the Finite Similitude Approach. J. Mar. Sci. Eng. 2025, 13, 1496. https://doi.org/10.3390/jmse13081496
Xu C, Wang Z, Kong X, Zhou H, Zheng C, Wu W. Scaling the Dynamic Buckling Behavior of a Box Girder Based on the Finite Similitude Approach. Journal of Marine Science and Engineering. 2025; 13(8):1496. https://doi.org/10.3390/jmse13081496
Chicago/Turabian StyleXu, Chongxi, Zhuo Wang, Xiangshao Kong, Hu Zhou, Cheng Zheng, and Weiguo Wu. 2025. "Scaling the Dynamic Buckling Behavior of a Box Girder Based on the Finite Similitude Approach" Journal of Marine Science and Engineering 13, no. 8: 1496. https://doi.org/10.3390/jmse13081496
APA StyleXu, C., Wang, Z., Kong, X., Zhou, H., Zheng, C., & Wu, W. (2025). Scaling the Dynamic Buckling Behavior of a Box Girder Based on the Finite Similitude Approach. Journal of Marine Science and Engineering, 13(8), 1496. https://doi.org/10.3390/jmse13081496







