Comparative Study of Local Stress Approaches for Fatigue Strength Assessment of Longitudinal Web Connections
Abstract
1. Introduction
2. Local Stress Approach
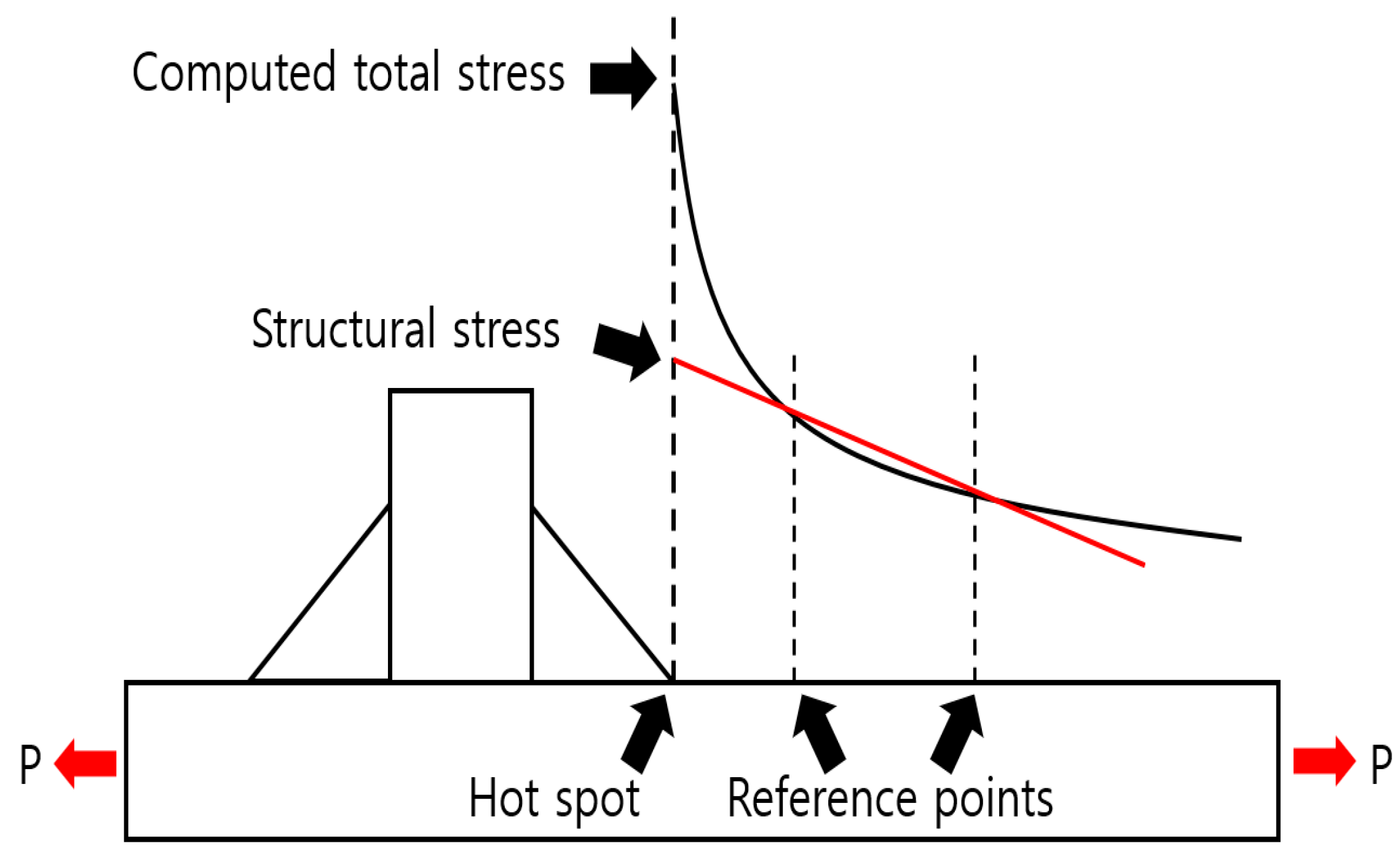
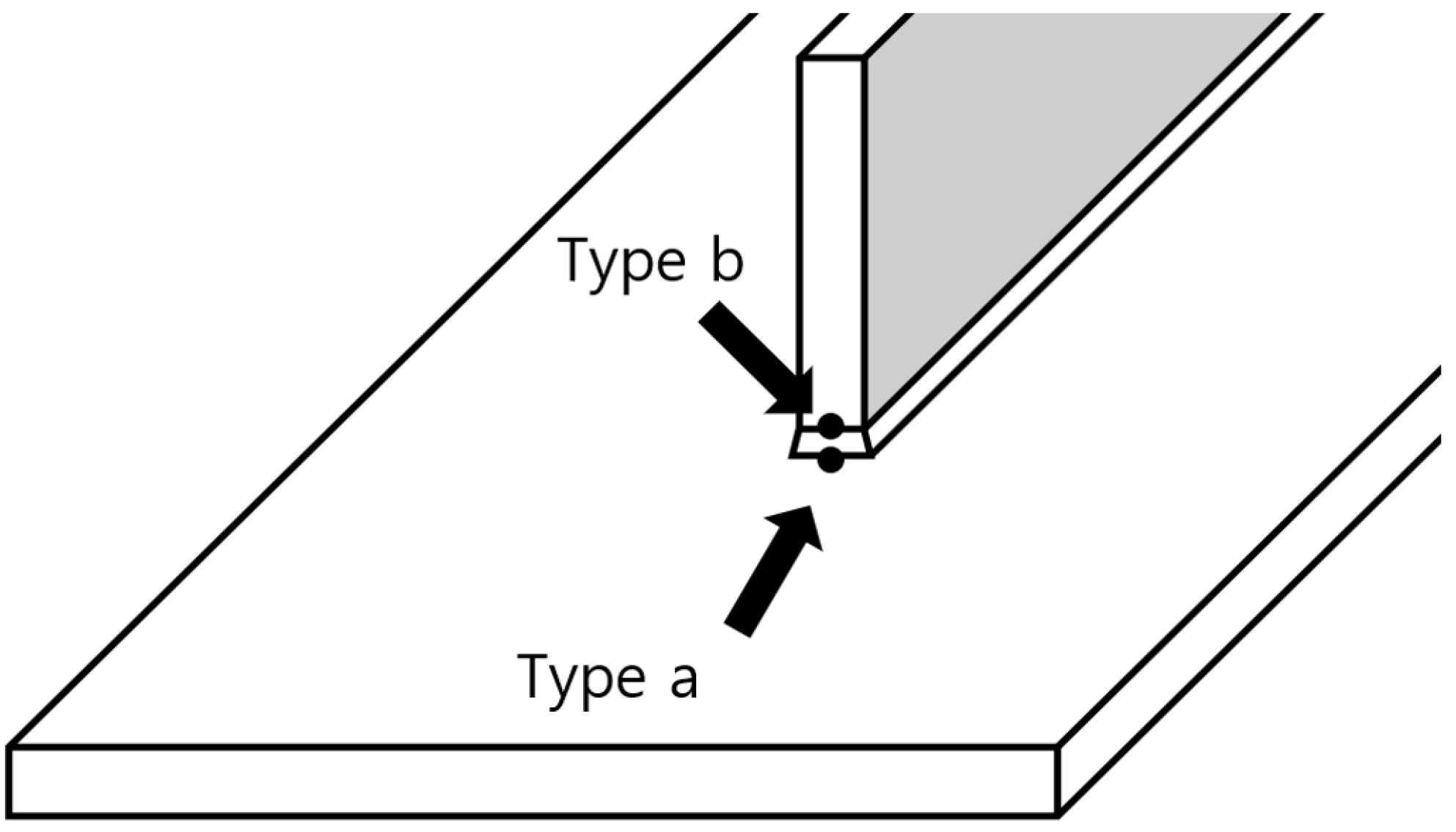
2.1. Hot Spot Stress Approach
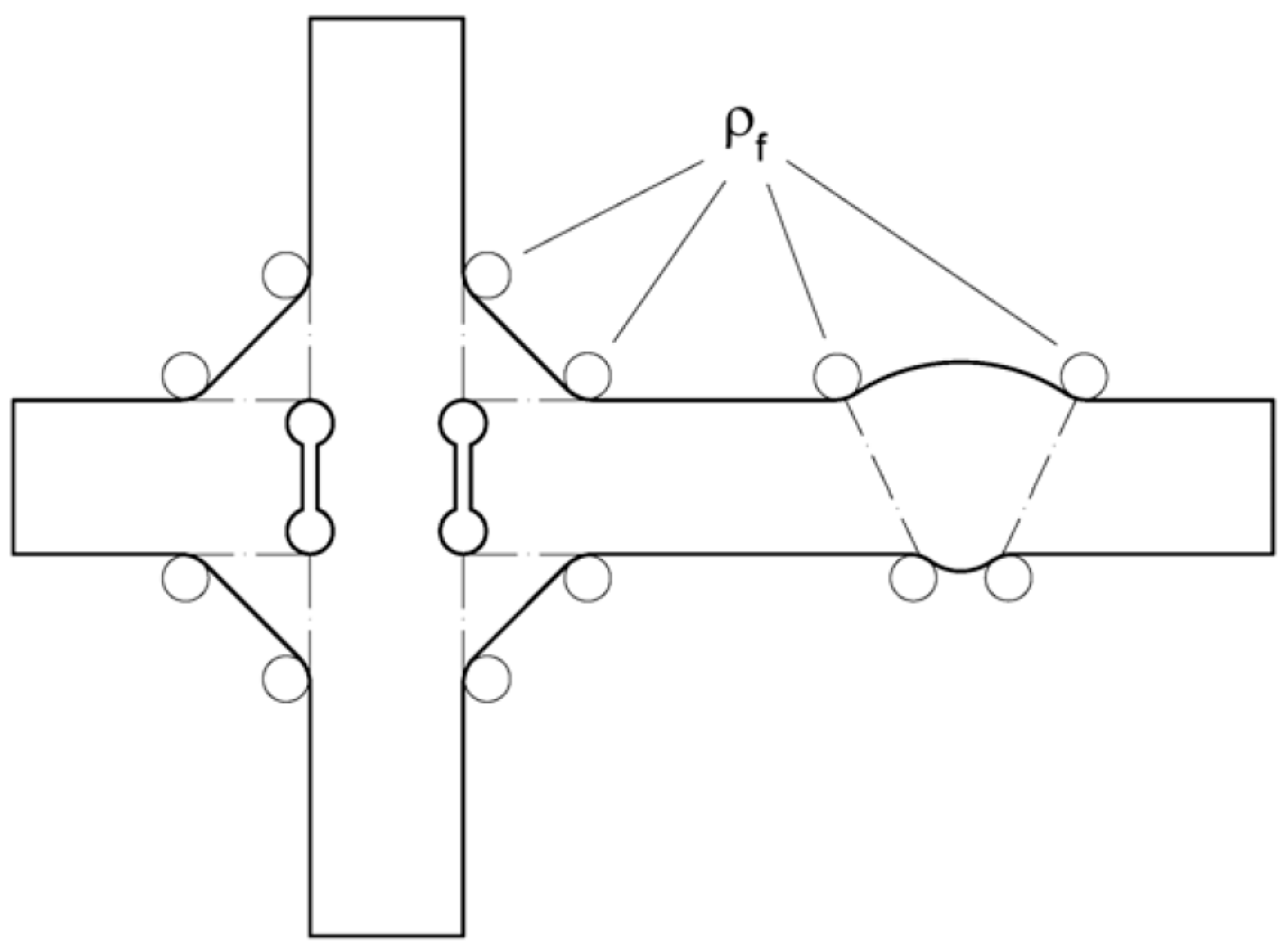
2.2. Effective Notch Stress Approach
2.3. Notch Stress Intensity Factor Approach
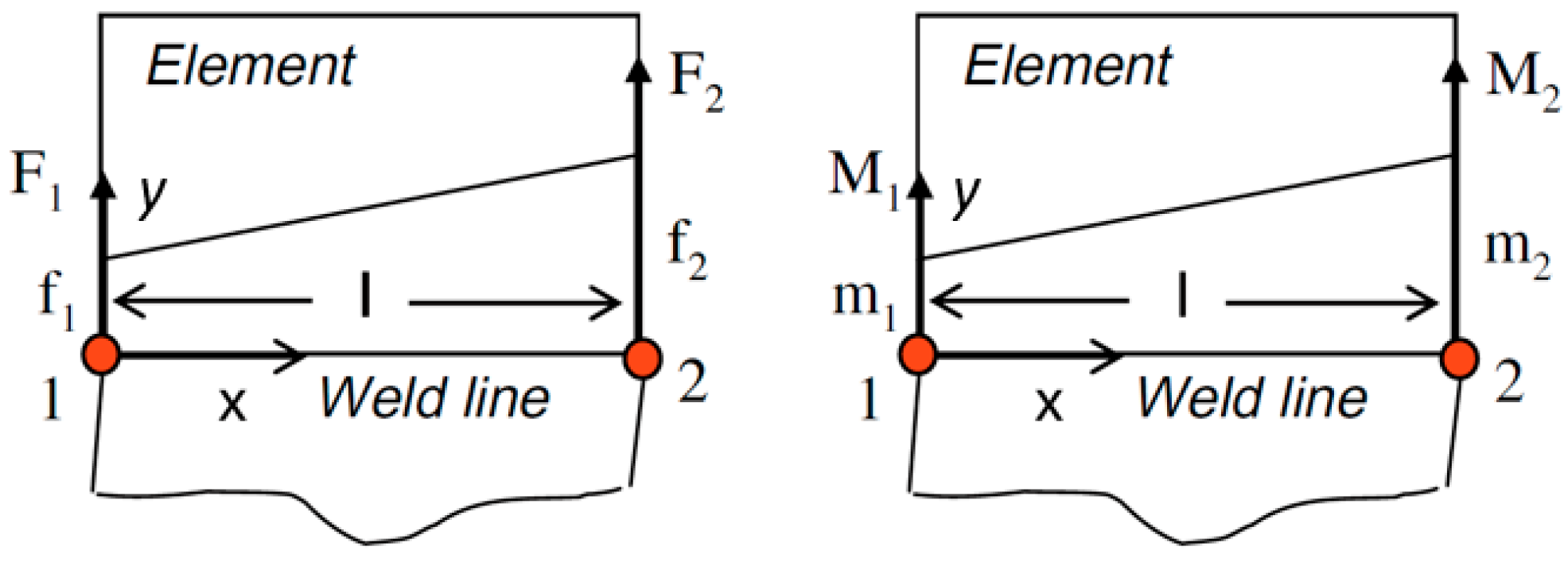
2.4. Structural Stress Approach
3. Longi-Web Connection
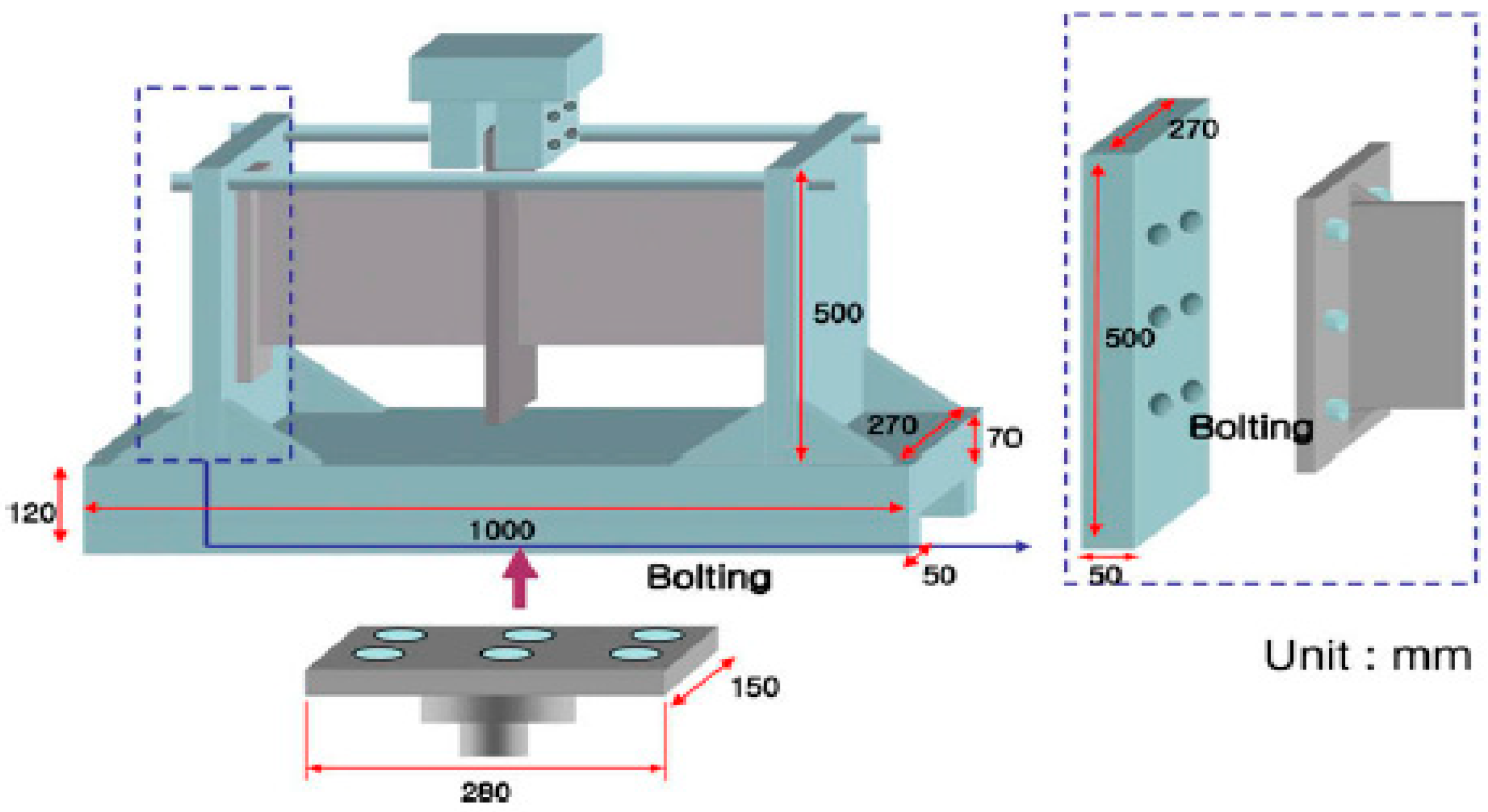
3.1. Experiments
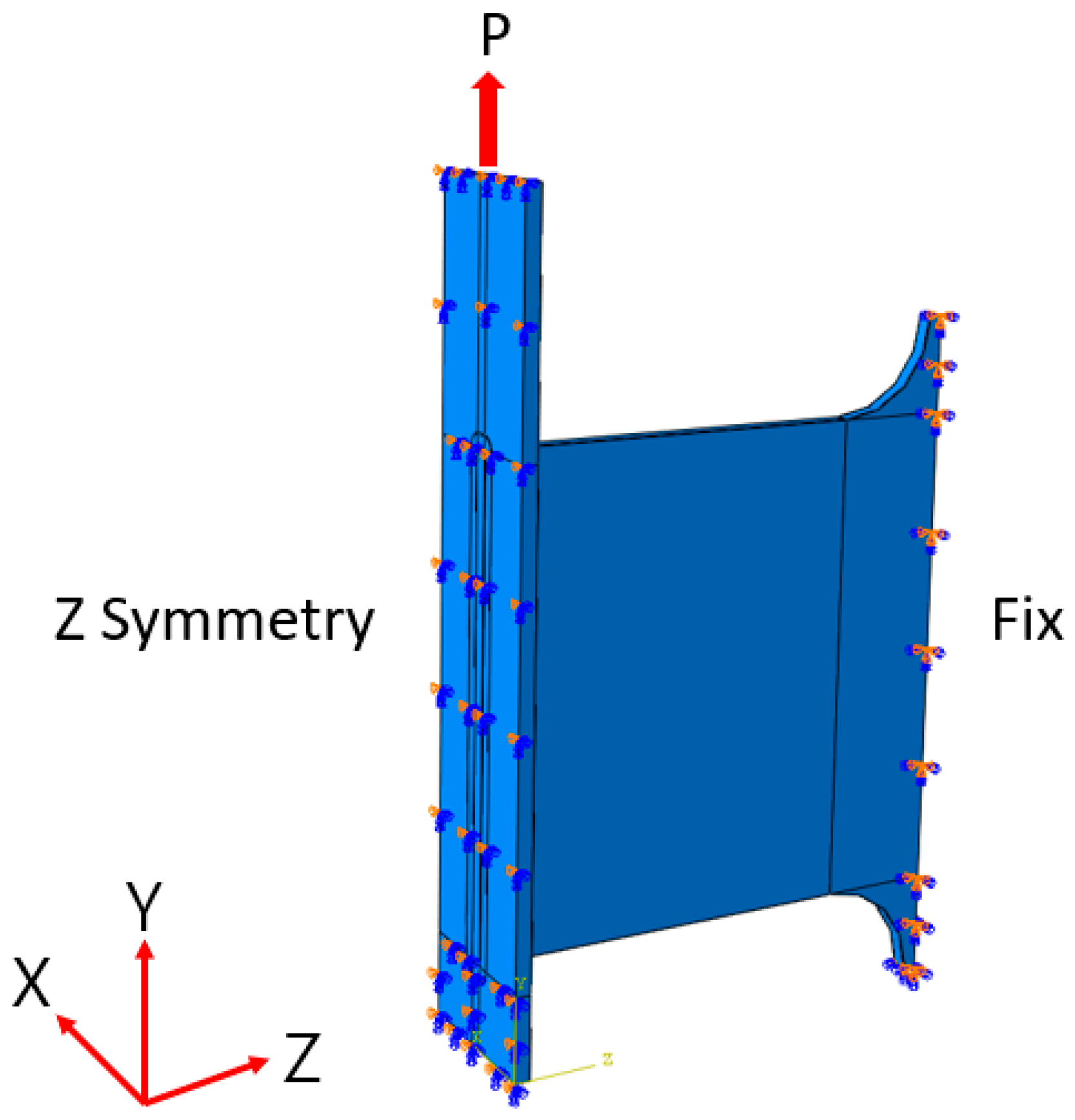
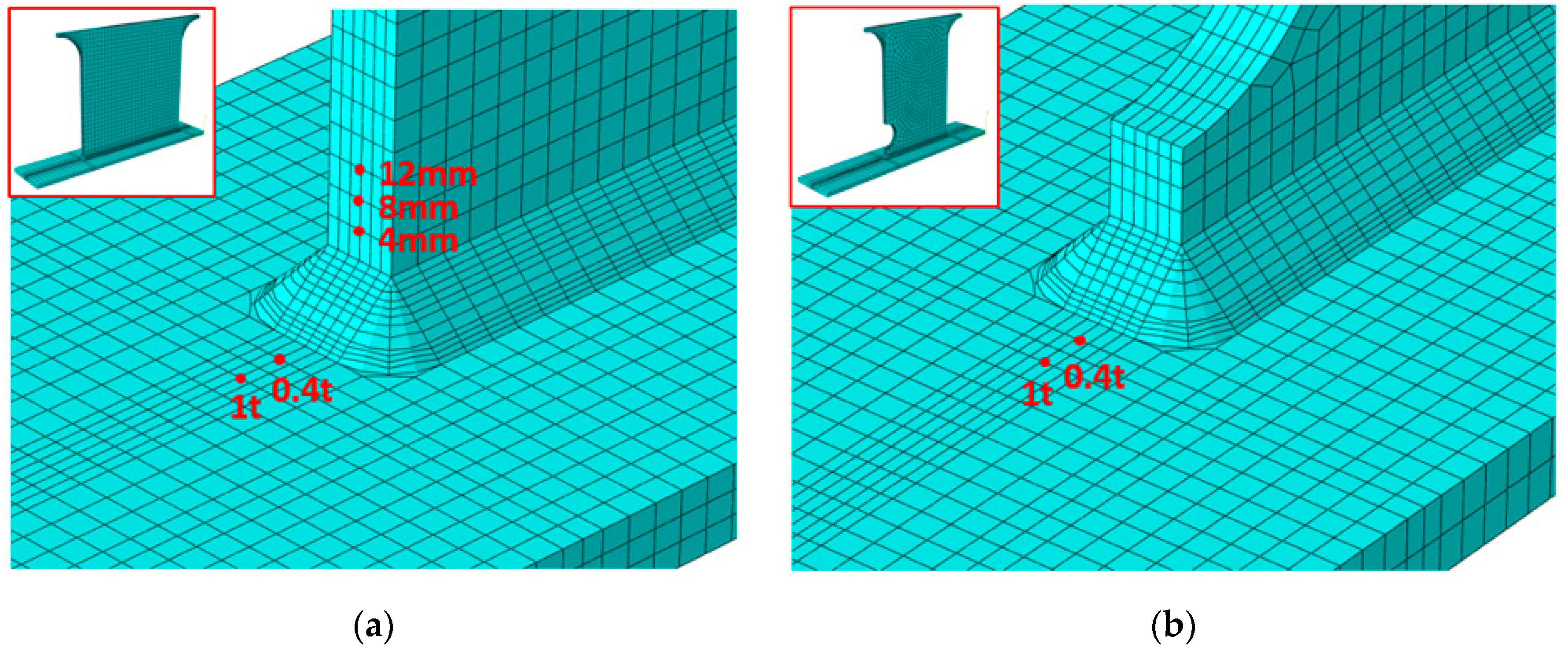
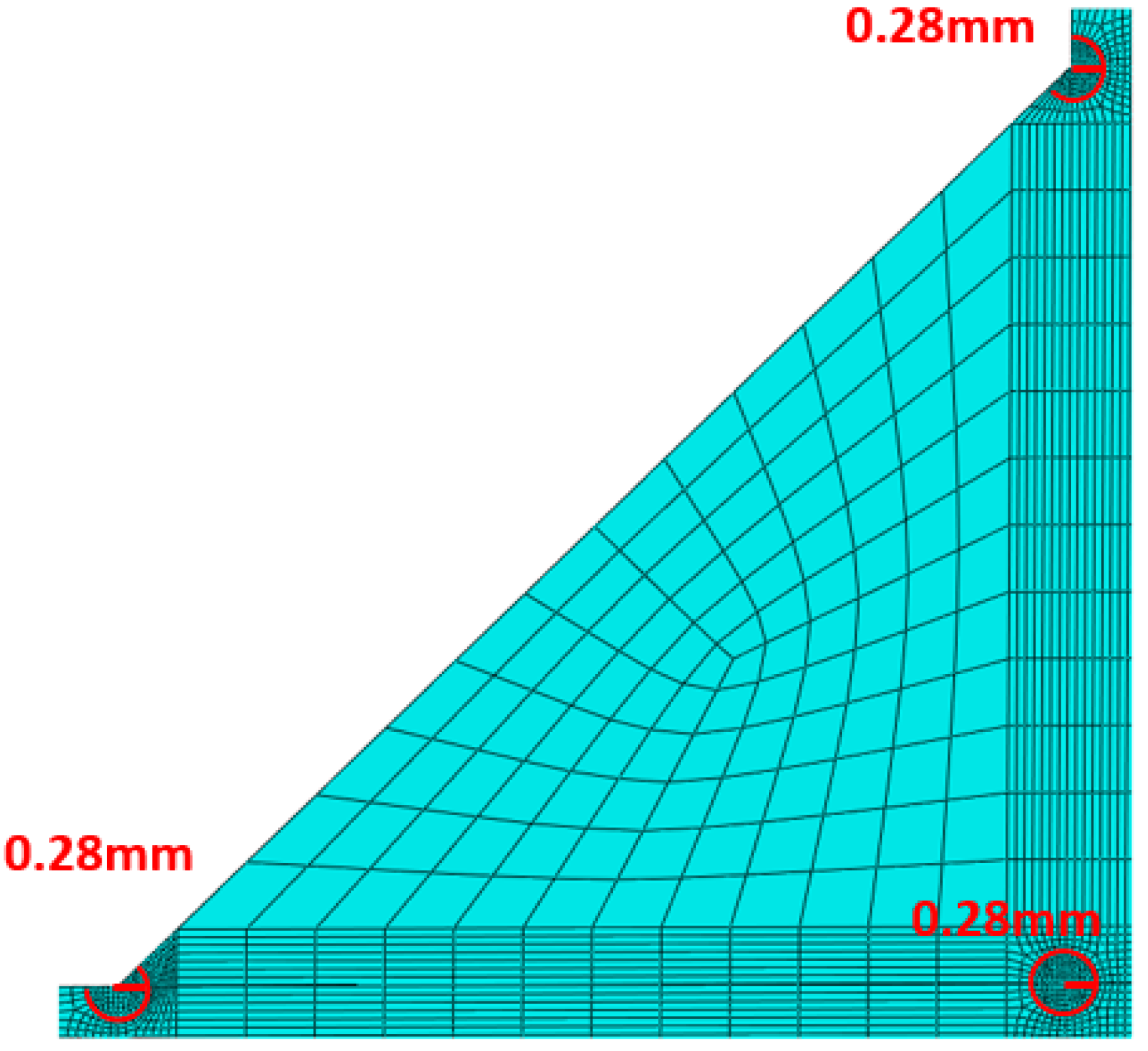
3.2. Finite Element Model
4. Results
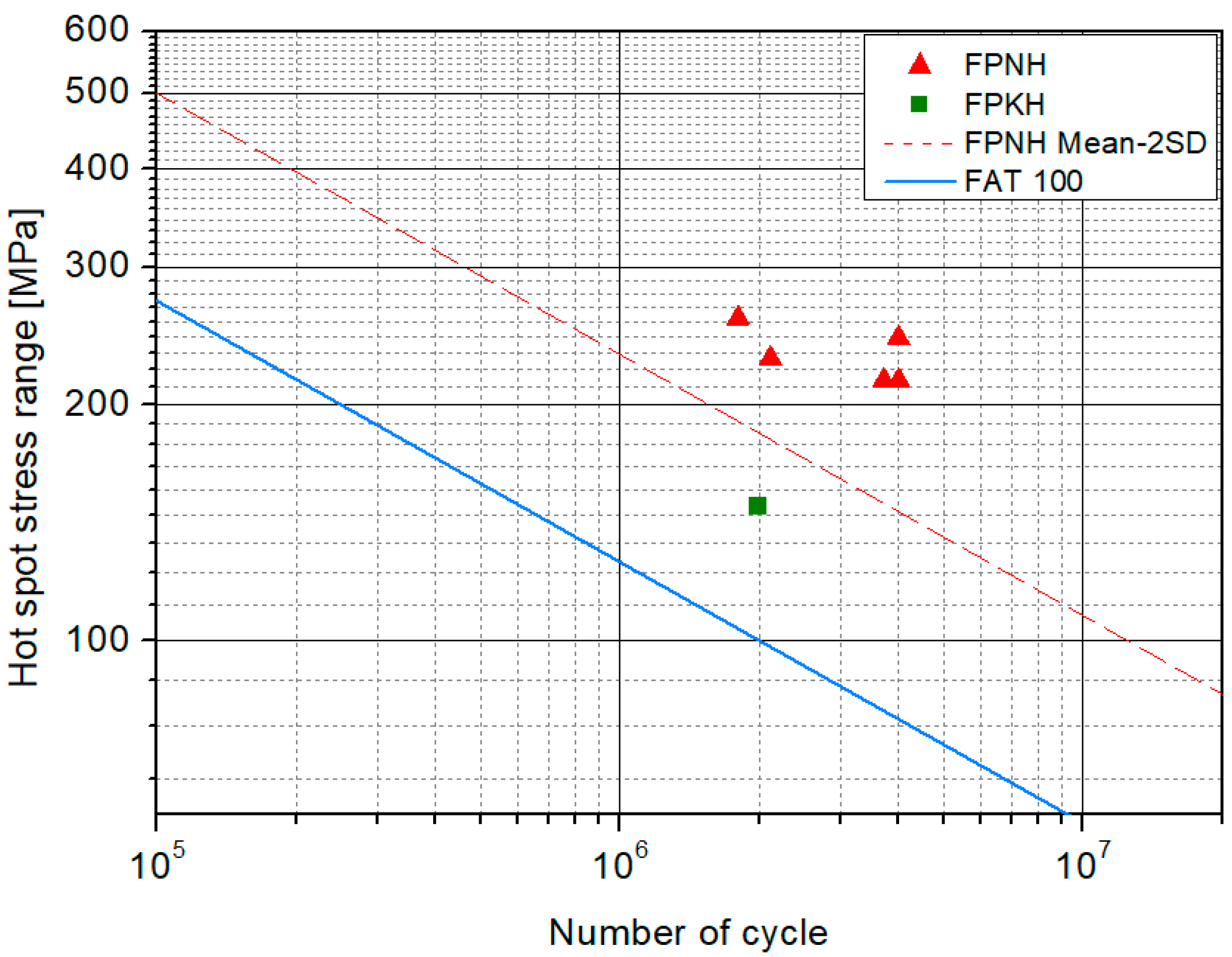
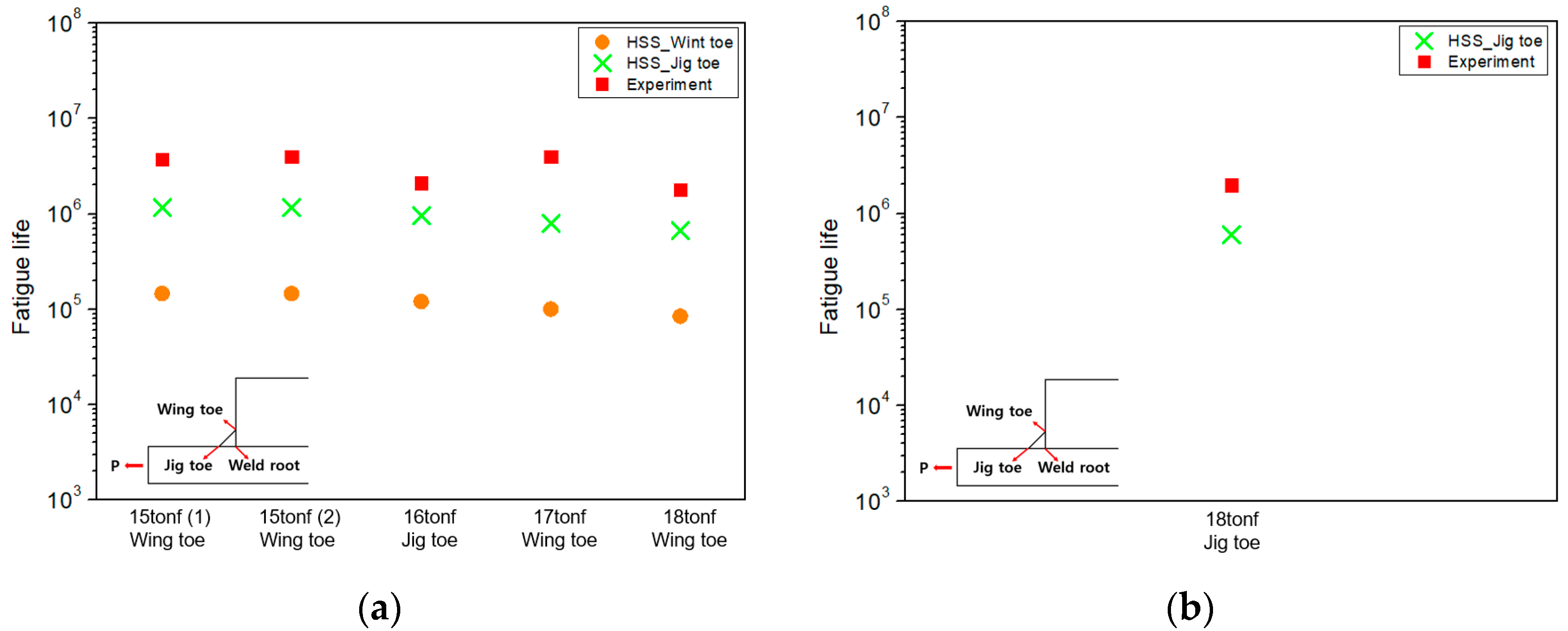
4.1. Hot Spot Stress Results
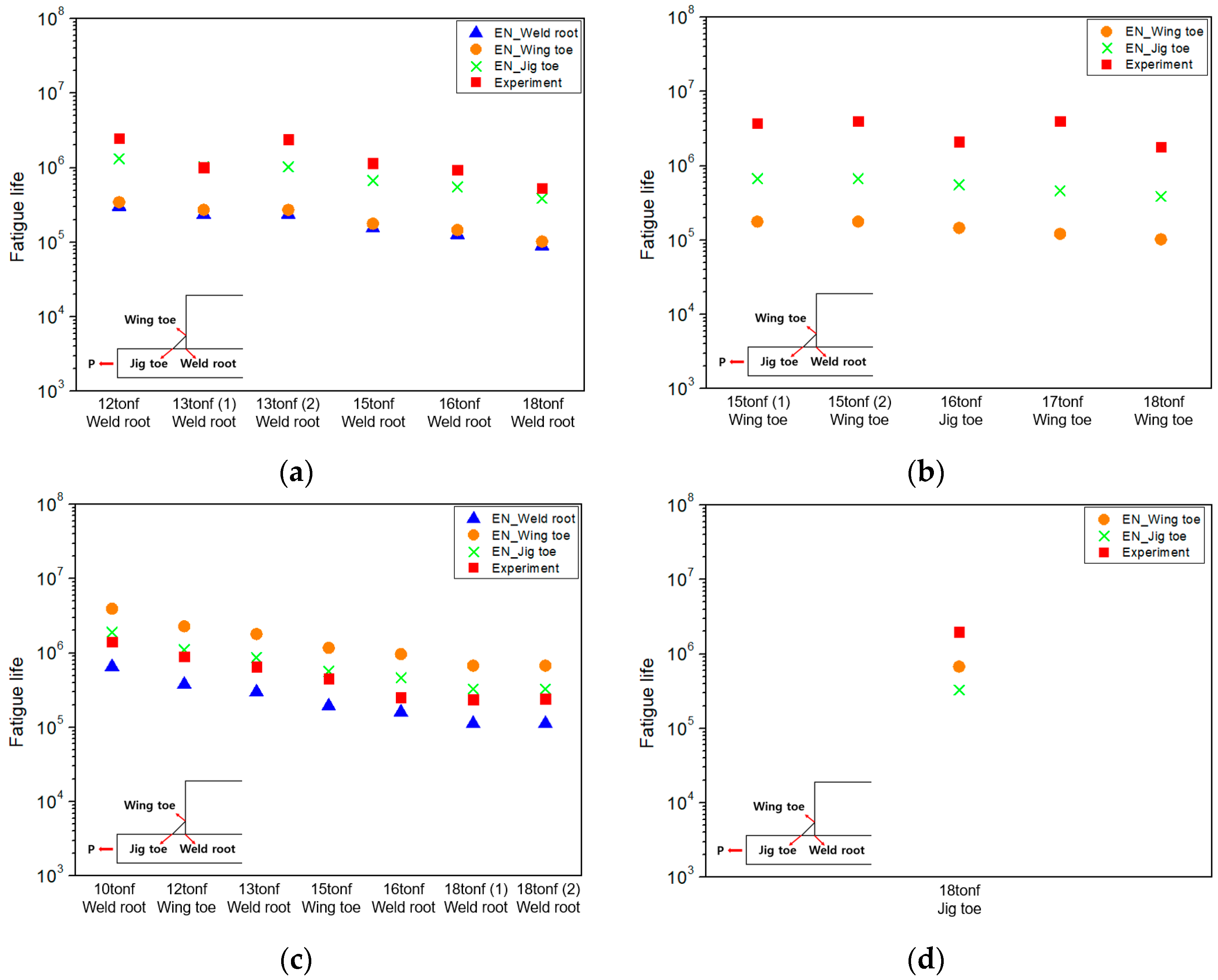
4.2. Effective Notch Stress Results
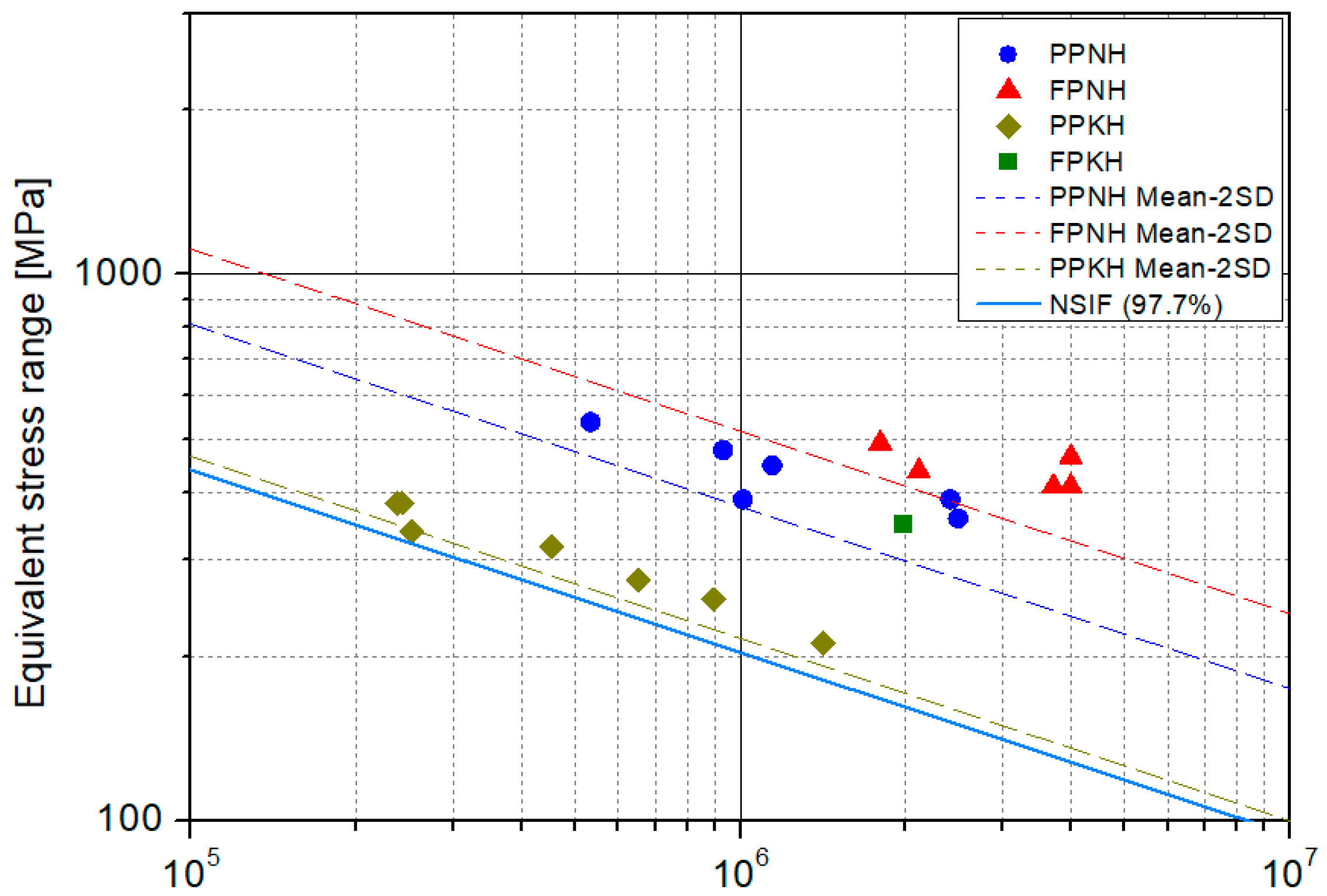
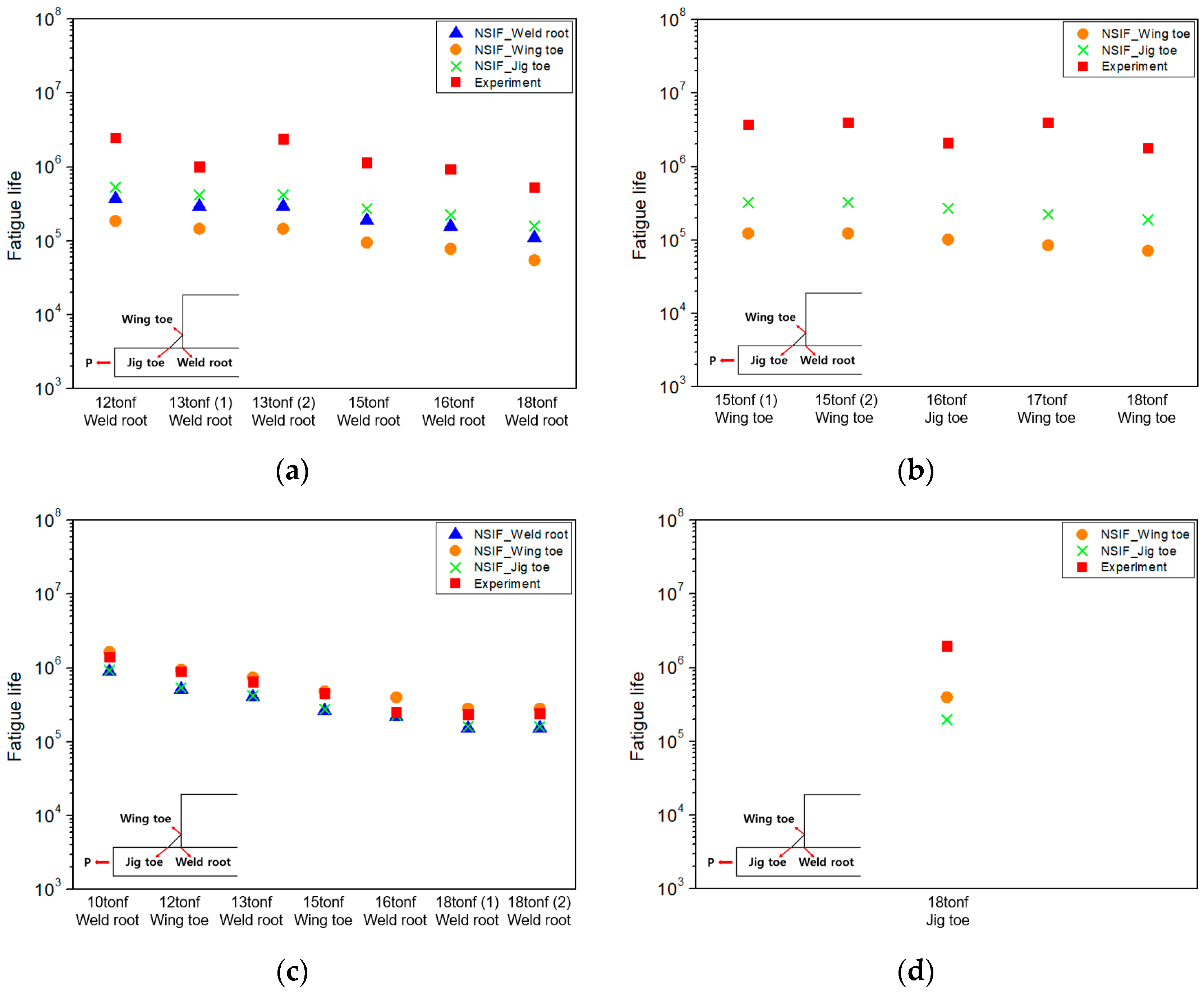
4.3. Notch Stress Intensity Factor Results
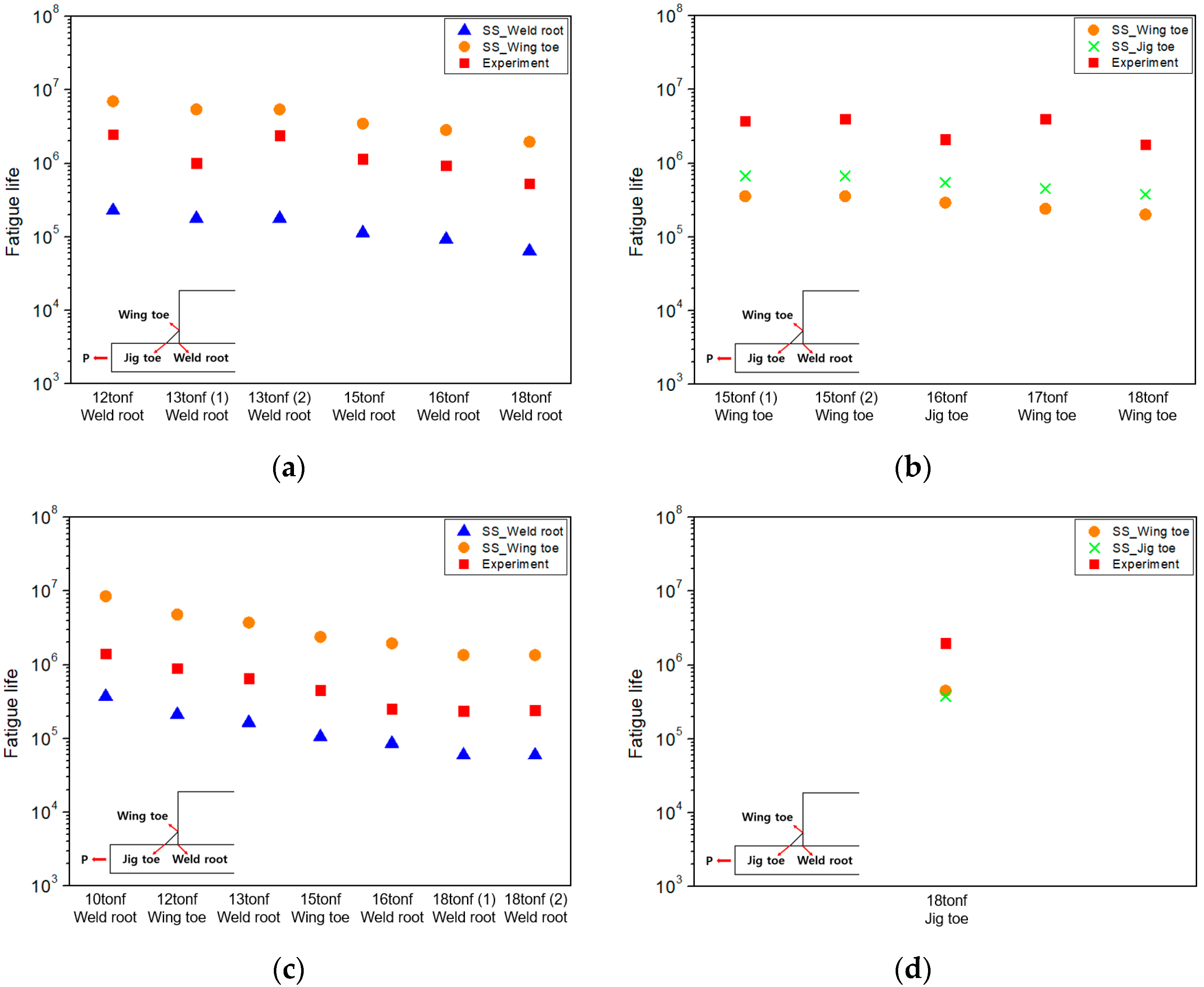
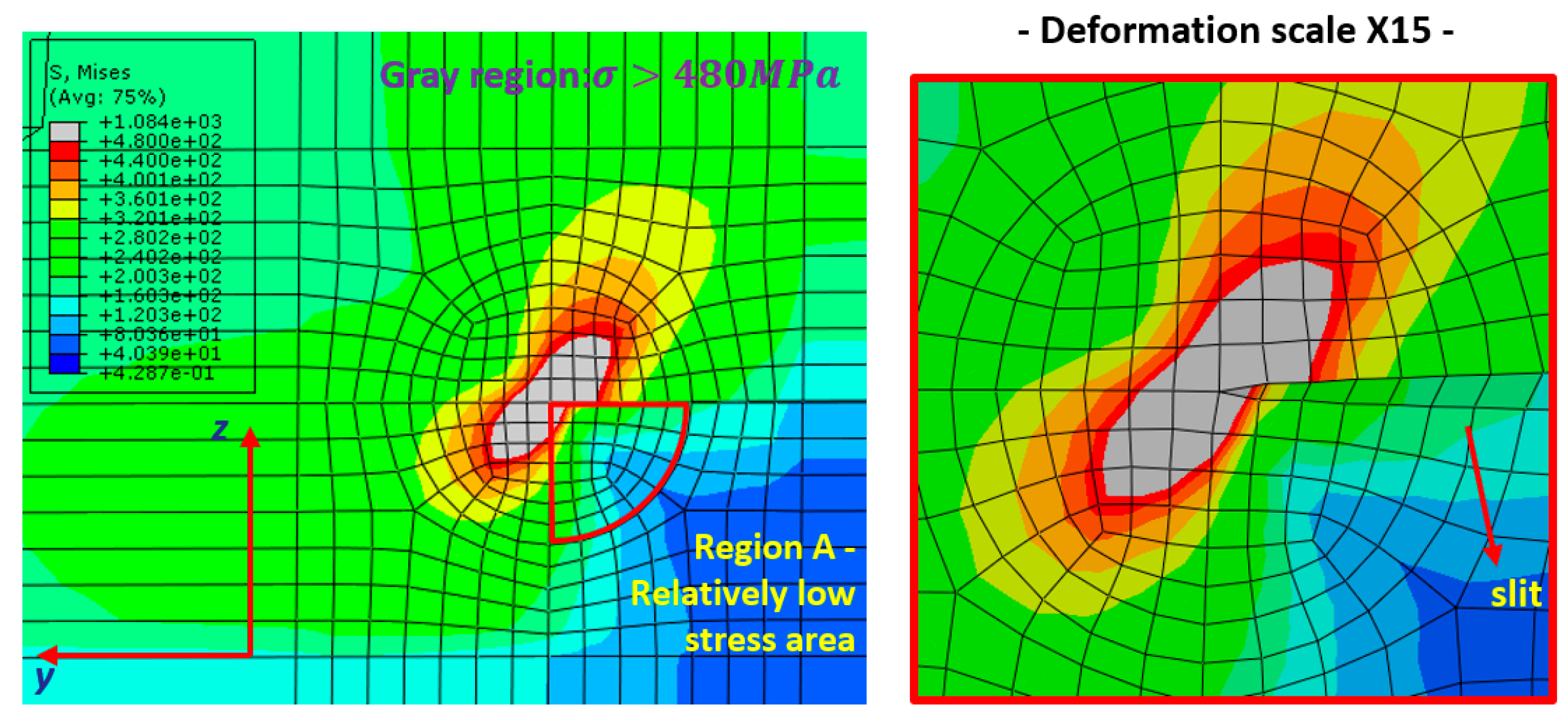
4.4. Structural Stress Results
5. Discussion
6. Conclusions
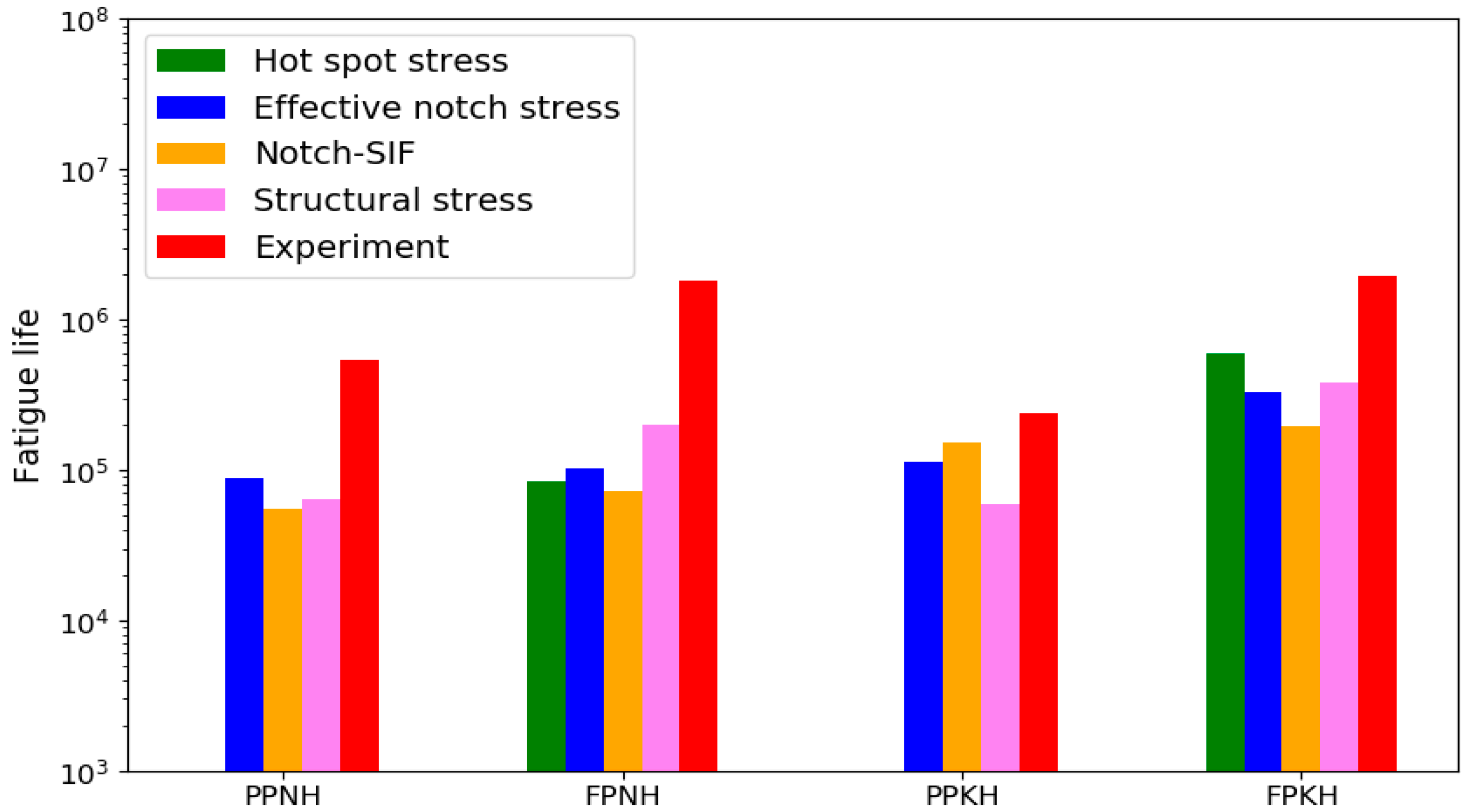
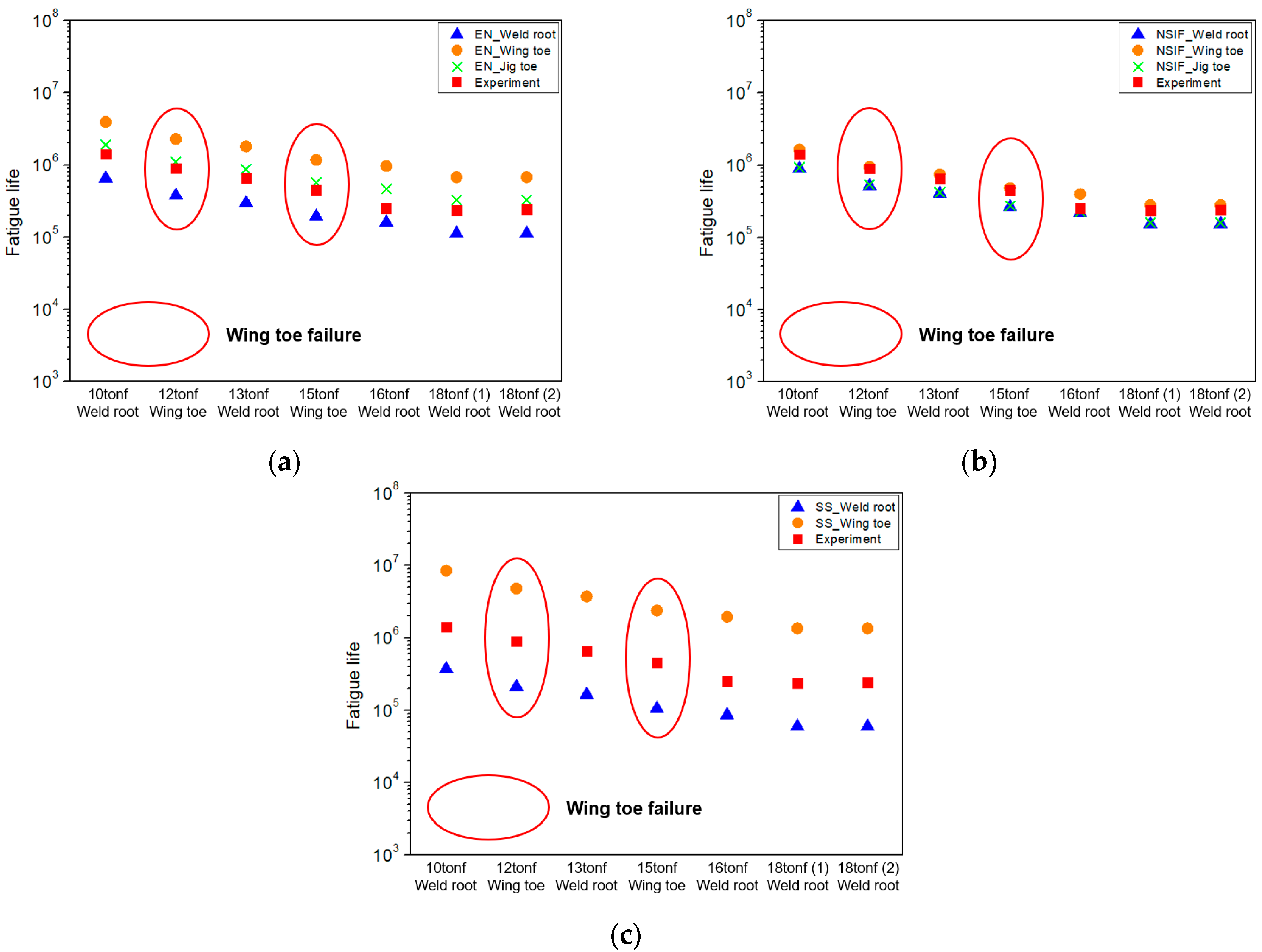
- In all cases, the predicted fatigue life was lower than the experimental results. This indicates that local stress approaches provide a conservative result.
- The hot spot stress approach offers the advantage of relatively simple application and is suitable for estimating fatigue at weld toes. However, it has the limitation that it cannot be used to assess the fatigue strength of the weld root, which is critical for structural integrity but cannot be visually inspected. This limitation highlights the need for further studies focusing on root-side fatigue evaluation.
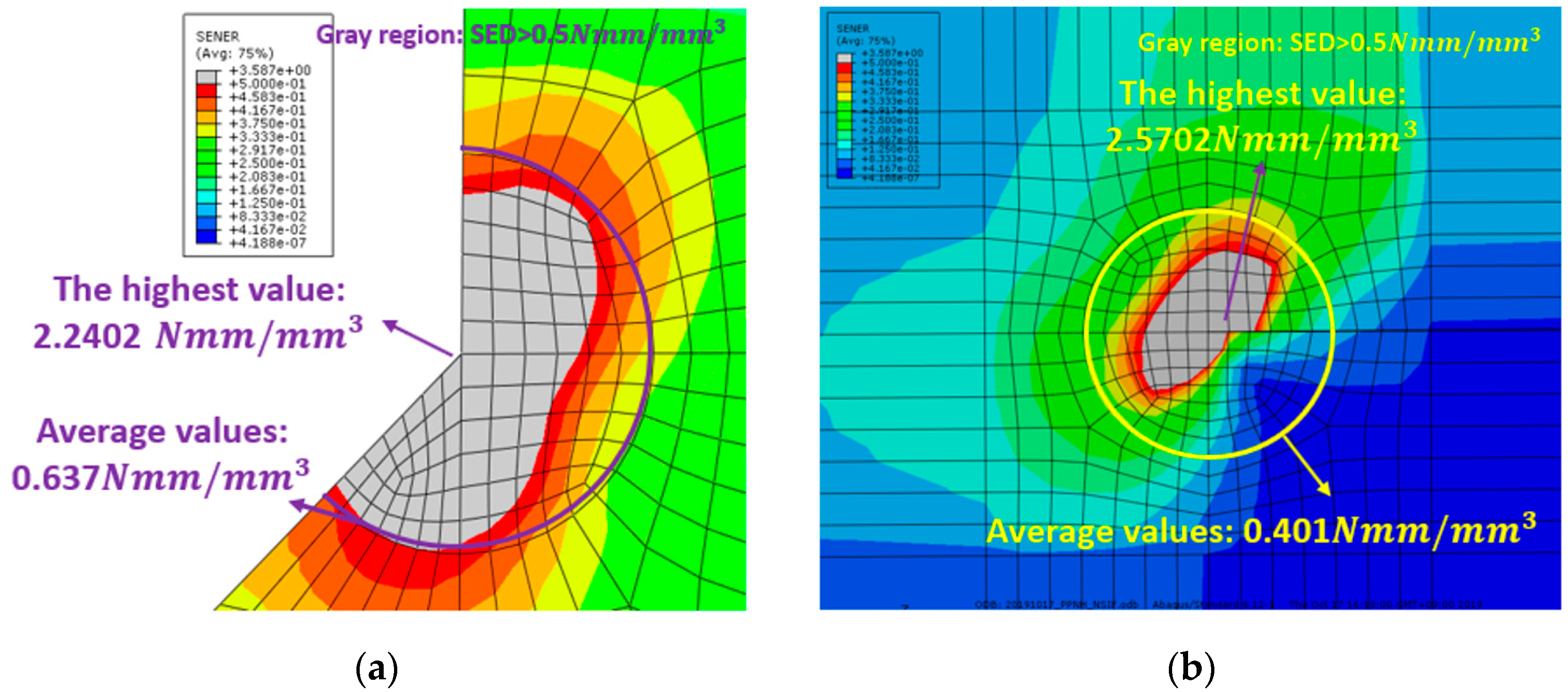
- The effective notch stress approach and the structural stress approach accurately predicted the primary failure locations observed in the experiments. However, in the PPKH model, failure also occurred at the wing toe under certain conditions. Nevertheless, the predicted fatigue life at that wing toe were all longer than the experimental results, and thus failure at the wing toe could not be predicted.
- Among the methods, only the notch stress intensity factor approach was able to predict failure at the wing toe in the PPKH model. The predicted fatigue life at this location was close to the experimental results, suggesting that this method is more suitable for assessing complex weld details despite potentially higher computational effort.
- Although the notch stress intensity factor approach demonstrates the highest predictive accuracy for the PPKH model, fatigue assessment requires a balance between accuracy, computational efficiency, and practical applicability. In cases where fatigue failure occurs exclusively at the weld toe, such as full penetration conditions, the hot spot stress approach offers an efficient and practical solution. However, when fatigue failure can occur at both the weld toe and weld root, such as partial penetration conditions, the effective notch stress approach provides the most balanced selection. Although it did not capture the exceptional wing toe failure observed in the PPKH model, it successfully predicted the primary failure locations and showed good agreement with the experimental fatigue life, making it a reliable and efficient method for fatigue assessment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silva, C.A.; Suarez, B.J.C.; Herreros, S.M.A. Effect of local cut-out on fatigue strength assessment in ship structures. Int. J. Naval Arch. Ocean Eng. 2023, 15, 100508. [Google Scholar] [CrossRef]
- Ahola, A.; Lipiainen, K.; Lindroos, J.; Koskimaki, M.; Laukia, K.; Bjork, T. On the Fatigue Strength of Welded High-Strength Steel Joints in the As-Welded, Post-Weld-Treated and Repaired Conditions in a Typical Ship Structural Detail. J. Mar. Sci. Eng. 2023, 11, 644. [Google Scholar] [CrossRef]
- Parunov, J.; Corak, M.; Gilja, I. Calculated and prescribed stress concentration factors of ship side longitudinal connections. Eng. Struct. 2013, 52, 629–641. [Google Scholar] [CrossRef]
- Fajri, A.; Prabowo, A.R.; Muhayat, N. Assessment of ship structure under fatigue loading: FE benchmarking and extended performance analysis. Curved Later. Struct. 2022, 9, 163–186. [Google Scholar] [CrossRef]
- Fricek, W.; Remes, H.; Feltz, O.; Lillemae, I.; Tchuindjang, D.; Reinert, T.; Nevierov, A.; Sishermann, W.; Brinkmann, M.; Kontkanen, T.; et al. Fatigue strength of laser-welded thin-plate ship structures based on nominal and structural hot-spot stress approach. Ships Offshore Struct. 2015, 10, 39–44. [Google Scholar]
- Braun, M.; Milakovic, A.S.; Renken, F.; Fricke, W.; Ehlers, S. Application of local approaches to the assessment of fatigue test results obtained for welded joints at sub-zero temperatures. Int. J. Fatigue 2020, 138, 105672. [Google Scholar] [CrossRef]
- Kodvanj, J.; Garbatov, Y.; Guedes, S.C.; Parunov, J. Numerical Analysis of Stress Concentration in Non-uniformly Corroded Small-Scale Specimens. J. Mar. Sci. Appl. 2020, 20, 1–9. [Google Scholar] [CrossRef]
- Fricke, W. IIW guideline for the assessment of weld root fatigue. Weld. World 2013, 57, 753–791. [Google Scholar] [CrossRef]
- Fricke, W. Fatigue and Fracture of Ship Structures. In Encyclopedia of Maritime and Offshore Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Dong, Y.; Garbatov, Y.; Guedes, S.C. Recent Developments in Fatigue Assessment of Ships and Offshores Structures. J. Mar. Sci. Appl. 2022, 21, 3–25. [Google Scholar] [CrossRef]
- Niemi, E.; Fricke, W.; Maddox, J.S. The Structural Hot-Spot Stress Approach to Fatigue. In Structural Hot-Spot Stress Approach to Fatigue Analysis of Welded Components, 2nd ed.; IIW International Institute of Welding, ZI Paris Nord II; Springer Nature Singapore Pte Ltd.: Singapore, 2018; pp. 5–12. [Google Scholar]
- Hobbacher, A. Fatigue actions. In Recommendations for Fatigue Design of Welded Joints and Components; International Institute of Welding: Paris, France, 2008. [Google Scholar]
- Lazzarin, P.; Berto, F.; Gomez, F.J.; Zappalorto, M. Some advantages derived from the use of the strain energy density over a control volume in fatigue strength assessments of welded joints. Int. J. Fatigue 2007, 30, 1345–1357. [Google Scholar] [CrossRef]
- Fischer, C.; Feltz, O.; Fricke, W.; Lazzarin, P. Application of the notch stress intensity and crack propagation approaches to weld toe and root fatigue. Weld. World 2011, 55, 30–39. [Google Scholar] [CrossRef]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, S.M.; Kim, Y.N.; Kim, S.G.; Lee, K.E.; Kim, G.R. A comparative study for the fatigue assessment of a ship structure by use of hot spot stress and structural stress approaches. Ocean Eng. 2009, 36, 1067–1072. [Google Scholar] [CrossRef]
- Kim, M.H.; Kang, S.W.; Kim, J.H.; Kim, K.S.; Kang, J.K.; Heo, J.H. An experimental study on the fatigue strength assessment of longi-web connections in ship structures using structural stress. Int. J. Fatigue 2010, 32, 318–329. [Google Scholar] [CrossRef]







| Penetration | Keyhole | Expected Failure Location | |
|---|---|---|---|
| PPNH (Partial Penetration without Keyhole) | Partial | ✕ | Weld root |
| FPNH (Full Penetration without Keyhole) | Full | ✕ | Wing toe |
| PPKH (Partial Penetration with Keyhole) | Partial | ⃝ | Weld root |
| FPKH (Full Penetration with Keyhole) | Full | ⃝ | Jig toe |
| Hot Spot Stress | Effective Notch Stress | Structural Stress | Notch-SIF | |
|---|---|---|---|---|
| PPNH | - | 0.167 | 0.120 | 0.103 |
| FPNH | 0.047 | 0.057 | 0.112 | 0.040 |
| PPKH | - | 0.47 | 0.25 | 0.65 |
| FPKH | 0.31 | 0.166 | 0.192 | 0.099 |
| Main Failure Location by Experiment | Estimated Failure Location | ||||
|---|---|---|---|---|---|
| Hot Spot Stress | Effective Notch Stress | Structural Stress | Notch-SIF | ||
| PPNH | Weld root | - | Weld root | Wing toe | Weld root |
| FPNH | Wing toe | Wing toe | Wing toe | Wing toe | Wing toe |
| PPKH | Weld root | - | Weld root | Weld root | Weld root |
| FPKH | Jig toe | Jig toe | Jig toe | Jig toe | Jig toe |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.H.; Lee, J.S.; Kim, M.H. Comparative Study of Local Stress Approaches for Fatigue Strength Assessment of Longitudinal Web Connections. J. Mar. Sci. Eng. 2025, 13, 1491. https://doi.org/10.3390/jmse13081491
Kim JH, Lee JS, Kim MH. Comparative Study of Local Stress Approaches for Fatigue Strength Assessment of Longitudinal Web Connections. Journal of Marine Science and Engineering. 2025; 13(8):1491. https://doi.org/10.3390/jmse13081491
Chicago/Turabian StyleKim, Ji Hoon, Jae Sung Lee, and Myung Hyun Kim. 2025. "Comparative Study of Local Stress Approaches for Fatigue Strength Assessment of Longitudinal Web Connections" Journal of Marine Science and Engineering 13, no. 8: 1491. https://doi.org/10.3390/jmse13081491
APA StyleKim, J. H., Lee, J. S., & Kim, M. H. (2025). Comparative Study of Local Stress Approaches for Fatigue Strength Assessment of Longitudinal Web Connections. Journal of Marine Science and Engineering, 13(8), 1491. https://doi.org/10.3390/jmse13081491





