A Preliminary Assessment of Offshore Winds at the Potential Organized Development Areas of the Greek Seas Using CERRA Dataset
Abstract
1. Introduction
- The evaluation of CERRA wind speed and direction data for the Greek Seas is based on in situ wind measurements.
- The detailed characterization of the wind climate and the assessment of wind power density at the OWFODA, including long-term trends and extreme value analysis of wind speed. Long-term trends should be taken into account in the feasibility study of an OWF, while extreme wind speed is a critical design parameter for offshore wind turbines.
- The preliminary evaluation of the offshore wind energy production at the OWFODA at the annual, monthly, and daily time scales. Monthly scale reveals the seasonality characteristics of the produced energy, while the daily and hourly time scales will greatly facilitate the efficient design and management of the energy transmission network.
- Finally, the identification of synergies and complementarities between the OWFODA is of utmost importance as it regards the coordination of the electric power transmission and distribution system.
2. Wind Data Sources
2.1. In Situ Wind Data
2.2. CERRA Reanalysis System
- The great lengths of the relevant time series, without gaps, allow for the estimation of interannual variability, long-term/climatic trends, etc.
- The spatial coverage extends to remote and offshore locations.
- Reanalysis data are usually provided for free.
- The assimilation of additional observations, available from the observing system, throughout the reanalysis period in order to represent the atmospheric conditions more accurately. These observations are obtained from ECMWF’s Meteorological Archival and Retrieval System (MARS) and European Centre File Storage system and include conventional (e.g., synoptic surface observations, drifting buoys, ships) and other observations, such as scatterometer and radiance observations. In this respect, let it be noted that the buoy measurements used in this work for the evaluation of the CERRA data have not been used in the assimilation procedure [22]. See also El-Said et al. [23] where a detailed description of the CERRA assimilation procedure is provided.
- A coupling between the Ensemble Data Assimilation system with the CERRA system to estimate the background error covariance matrix (B-Matrix) with flow-dependency updates to sufficiently represent errors when changes in weather regime are detected [23].
3. Methodology and Theoretical Background
3.1. Information on the OWFODA
- Crete1 and Crete2 (800 MW),
- Rhodes (300 MW–550 MW),
- Gyaros and Donousa (200 MW–450 MW),
- Ag. Apostoli and Chios (300 MW), and
- Diapontia and Patras (450 MW).


3.2. Statistical Analysis of Wind Speed and Wind Power Density
3.3. Offshore Wind Turbine and Annual Energy Production
3.4. The IEA 15-MW Offshore Wind Turbine
3.5. Collocation of Datasets in Space and Time
4. Evaluation of the CERRA Wind Dataset
4.1. Evaluation of Wind Speed
4.2. Evaluation of Wind Direction
5. Offshore Wind Speed Assessment
5.1. Annual Time Scale
5.2. Seasonal Time Scale
5.3. n-Year Return Levels (Design Values)
6. Offshore Wind Speed Characteristics and Wind Power Density in the OWFODA
6.1. Statistics of the 3-Hour Wind Speed
6.2. Statistics of the Annual Wind Speed
6.3. Statistics of Extreme Wind Speeds and Trends
6.3.1. Long-Term Trends of Wind Speed
6.3.2. Wind Speed Extremes
6.4. Wind Power Density at the OWFODA
- For Eolmed, the annual mean wind speed at 150 m asl is 9.02 m/s and the corresponding wind power density is 877.78 W/m2. Based on the results presented in Table A2 and Table A6, it can be concluded that Eolmed exhibits higher wind speed and wind power density than the Greek OWFODA, except for O3 (Crete1). Specifically, O3 exhibits a mean annual wind speed of 9.12 m/s and a wind power density of 908.60 W/m2. Moreover, the summer means for O3 are 10.946 m/s and 1389.31 W/m2 compared to 7.87 m/s and 603.75 W/m2 for Eolmed. The effect of the Etesian winds in the area of Crete1 is evident.
7. Offshore Wind Energy Production
7.1. Number of Wind Turbines and Capacity
- CDS_3: This setting refers to a capacity density of 3.0 MW/km2 that is almost corresponding to the capacity density of the Pilot1 area. Specifically, assuming that the Pilot1 will have a capacity of 600 MW and taking into consideration that it has a total surface of 219.28 km2 and that the IEA 15-MW offshore wind turbines will be used, this is translated to the installation of 40 wind turbines (e.g., 14 wind turbines for the Pilot1A and 26 wind turbines for the Pilot1B). Therefore, the capacity density of the Pilot1 is 2.74 MW/km2;
- CDS_5: This setting refers to a capacity density of 5.0 MW/km2;
- CDS_7: This setting refers to a capacity density of 7.0 MW/km2.
7.2. Annual Wind Energy Production
7.3. Monthly Wind Energy Production
7.4. Daily Energy Production
7.5. Hourly Energy Production
8. Correlation, Synergies, and Complementarity of Wind Energy
- At all the examined time scales, there is a rather high degree of synergy for most of the OWFODA, while for the hourly and monthly scales, there is no complementarity present.
- For all time scales, GyarosA,B,C and Donousa2 seem to play a crucial role in this framework since they exhibit increased synergy with most of the OWFODA in the Aegean Sea.
- Diapontia exhibits very low synergy and complementarity with respect to the rest of OWFODA at all time scales. Nevertheless, at the annual scale, it exhibits some signs of (reduced) complementarity with some of the rest areas.
- Correlation coefficients above 0.7 are encountered for Ag. Apostoli-GyarosA,B,C (at lag 1), Crete1-Donousa2 (at lag −1), Donousa2-GyarosA,B (at lag −1), and Pilot1A-Pilot1B (at lag 0).
- Correlation coefficients above 0.6 are encountered for Crete1-Crete2A, Crete2B (at lag −1), and Donousa2-GyarosC (at lag −1).
- Fair correlation values are encountered at different lags (which are always less than 2 in the absolute sense).
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEP | Annual energy production |
| asl | Above sea level |
| CERRA | Copernicus European Regional Reanalysis |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| FB | Fixed-bottom wind turbines |
| FL | Floating wind turbines |
| GEV | Generalized extreme value distribution |
| HEREMA | Hellenic Hydrocarbons & Energy Resources Management Company SA |
| MET | Norwegian Meteorological Institute |
| MK | Mann–Kendall |
| NDP—OWF | National Offshore Wind Farms Development Programme |
| NECP | National Energy and Climate Plan |
| NREL | National Renewable Energy Laboratory |
| NWP | Numerical weather prediction |
| OWF | Offshore wind farm(s) |
| OWFODA | Offshore wind farm organized development areas |
| SEIA | Strategic Environmental Impact Assessment |
| SSF—RES | Special Spatial Framework for Renewable Energy Sources |
| WPD | Wind power density |
Appendix A. Calculation of the Centroid of a Non-Intersecting Polygon
Appendix B
Appendix B.1. Wind Speed and Wind Power Density Statistics in the Greek Seas
| Polygon | Parameter | ||||||
|---|---|---|---|---|---|---|---|
m/s | m/s | m/s | m/s | % | m/s | m/s | |
| O1 | 7.58 | 7.48 | 4.06 | 29.61 | 53.60 | 14.38 | 17.42 |
| O2 | 7.89 | 7.56 | 4.21 | 29.52 | 53.32 | 15.30 | 19.38 |
| O3 | 9.12 | 8.83 | 5.04 | 29.03 | 55.21 | 17.56 | 19.86 |
| O4 | 7.82 | 7.93 | 3.89 | 25.96 | 49.75 | 13.88 | 16.20 |
| O5 | 8.01 | 8.16 | 3.86 | 26.01 | 48.15 | 14.01 | 16.59 |
| O6 | 6.60 | 5.94 | 4.09 | 29.30 | 62.03 | 14.07 | 17.39 |
| O7 | 8.84 | 8.94 | 4.16 | 28.79 | 47.09 | 15.44 | 17.93 |
| O8 | 6.00 | 5.31 | 4.12 | 30.18 | 68.66 | 13.54 | 18.28 |
| O9 | 8.32 | 8.09 | 4.58 | 28.63 | 55.08 | 15.81 | 18.21 |
| O10 | 8.36 | 8.13 | 4.65 | 29.54 | 55.64 | 16.05 | 18.65 |
| O11 | 8.49 | 8.06 | 4.85 | 28.65 | 57.15 | 16.76 | 19.28 |
| O12 | 6.17 | 5.69 | 3.73 | 28.55 | 60.39 | 12.88 | 17.20 |
| O13 | 6.97 | 6.59 | 4.06 | 28.59 | 58.26 | 14.16 | 18.64 |
| O14 | 8.28 | 8.24 | 3.90 | 29.61 | 47.08 | 14.82 | 17.60 |
| Polygon | Parameter | |||||||
|---|---|---|---|---|---|---|---|---|
m/s | m/s | m/s | m/s | % | % | m/s | m/s | |
| O1 | 7.58 | 7.68 | 0.33 | 8.16 | 53.39 | 4.35 | 8.00 | 8.16 |
| O2 | 7.89 | 7.89 | 0.24 | 8.37 | 53.19 | 3.01 | 8.28 | 8.37 |
| O3 | 9.12 | 9.13 | 0.40 | 9.96 | 55.04 | 4.39 | 9.85 | 9.96 |
| O4 | 7.82 | 7.79 | 0.32 | 8.64 | 49.62 | 4.13 | 8.37 | 8.64 |
| O5 | 8.01 | 8.00 | 0.32 | 8.87 | 48.02 | 3.99 | 8.54 | 8.87 |
| O6 | 6.60 | 6.59 | 0.29 | 7.25 | 61.92 | 4.40 | 7.07 | 7.25 |
| O7 | 8.84 | 8.87 | 0.37 | 9.82 | 46.94 | 4.21 | 9.33 | 9.82 |
| O8 | 6.00 | 5.96 | 0.31 | 6.74 | 68.41 | 5.15 | 6.57 | 6.74 |
| O9 | 8.32 | 8.37 | 0.41 | 9.00 | 54.90 | 4.91 | 8.93 | 9.00 |
| O10 | 8.36 | 8.43 | 0.42 | 9.08 | 55.44 | 5.06 | 9.00 | 9.08 |
| O11 | 8.49 | 8.58 | 0.44 | 9.27 | 56.93 | 5.19 | 9.15 | 9.27 |
| O12 | 6.17 | 6.16 | 0.25 | 6.66 | 60.25 | 4.02 | 6.63 | 6.66 |
| O13 | 6.97 | 7.00 | 0.27 | 7.53 | 58.12 | 3.86 | 7.44 | 7.53 |
| O14 | 8.28 | 8.30 | 0.37 | 9.20 | 46.91 | 4.42 | 8.92 | 9.20 |
| Polygon | Parameter | |||||
|---|---|---|---|---|---|---|
m/s/y | -Value | m/s/y | -Value | m/s/y | -Value | |
| O1 | −0.004 | 0.505 | −0.012 | 0.215 | −0.014 | 0.376 |
| O2 | −0.001 | 0.902 | 0.016 | 0.048 | 0.036 | 0.048 |
| O3 | −0.011 | 0.051 | −0.022 | 0.016 | −0.019 | 0.028 |
| O4 | −0.003 | 0.505 | −0.006 | 0.334 | 0.000 | 0.967 |
| O5 | −0.004 | 0.391 | −0.006 | 0.470 | 0.003 | 0.775 |
| O6 | 0.005 | 0.294 | 0.012 | 0.178 | 0.014 | 0.307 |
| O7 | −0.004 | 0.540 | −0.004 | 0.614 | 0.003 | 0.754 |
| O8 | −0.007 | 0.138 | −0.030 | 0.037 | −0.007 | 0.924 |
| O9 | −0.002 | 0.634 | −0.006 | 0.438 | 0.003 | 0.859 |
| O10 | −0.003 | 0.673 | −0.010 | 0.307 | −0.003 | 0.634 |
| O11 | −0.006 | 0.247 | −0.015 | 0.215 | −0.002 | 0.859 |
| O12 | 0.004 | 0.307 | 0.004 | 0.754 | 0.021 | 0.186 |
| O13 | 0.002 | 0.796 | −0.003 | 0.838 | 0.013 | 0.470 |
| O14 | −0.018 | 0.002 | −0.027 | 0.001 | 0.000 | 0.946 |
| Parameters and 95% Confidence Intervals | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Polygon | |||||||||
| O1 | −0.149 | −0.345 | 0.047 | 2.155 | 1.677 | 2.770 | 21.780 | 21.003 | 22.556 |
| O2 | −0.285 | −0.512 | −0.059 | 2.093 | 1.619 | 2.705 | 24.253 | 23.494 | 25.012 |
| O3 | −0.087 | −0.331 | 0.157 | 1.453 | 1.116 | 1.891 | 23.721 | 23.186 | 24.257 |
| O4 | −0.230 | −0.415 | −0.045 | 1.890 | 1.483 | 2.407 | 20.673 | 19.998 | 21.348 |
| O5 | −0.274 | −0.481 | −0.066 | 2.014 | 1.571 | 2.582 | 21.100 | 20.376 | 21.825 |
| O6 | −0.095 | −0.291 | 0.100 | 1.571 | 1.220 | 2.023 | 22.629 | 22.061 | 23.196 |
| O7 | −0.176 | −0.333 | −0.019 | 1.778 | 1.403 | 2.253 | 22.455 | 21.825 | 23.085 |
| O8 | 0.102 | −0.250 | 0.454 | 1.989 | 1.465 | 2.700 | 23.397 | 22.619 | 24.174 |
| O9 | −0.015 | −0.242 | 0.212 | 1.544 | 1.189 | 2.006 | 22.194 | 21.630 | 22.758 |
| O10 | 0.036 | −0.175 | 0.248 | 1.415 | 1.090 | 1.837 | 22.288 | 21.777 | 22.800 |
| O11 | 0.031 | −0.297 | 0.359 | 1.521 | 1.134 | 2.042 | 22.767 | 22.178 | 23.355 |
| O12 | −0.211 | −0.438 | 0.017 | 1.974 | 1.521 | 2.562 | 22.559 | 21.839 | 23.279 |
| O13 | −0.244 | −0.427 | −0.062 | 1.745 | 1.365 | 2.229 | 23.490 | 22.867 | 24.113 |
| O14 | −0.077 | −0.309 | 0.155 | 2.004 | 1.547 | 2.594 | 22.131 | 21.399 | 22.863 |
| Polygon | Design Values and 95% Confidence Intervals | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| O1 | 26.954 | 25.439 | 28.468 | 27.510 | 25.773 | 29.248 | 28.159 | 26.096 | 30.222 |
| O2 | 28.444 | 27.430 | 29.458 | 28.794 | 28.008 | 31.217 | 29.177 | 27.854 | 30.500 |
| O3 | 27.525 | 26.213 | 28.837 | 27.982 | 26.409 | 29.554 | 28.530 | 26.574 | 30.485 |
| O4 | 24.741 | 23.704 | 25.778 | 25.118 | 23.961 | 26.276 | 25.542 | 24.208 | 26.876 |
| O5 | 25.195 | 24.200 | 26.191 | 25.545 | 24.433 | 26.657 | 25.930 | 24.646 | 27.214 |
| O6 | 26.693 | 25.402 | 27.983 | 27.174 | 25.670 | 28.678 | 27.749 | 25.932 | 29.565 |
| O7 | 26.569 | 25.472 | 27.667 | 26.990 | 25.767 | 28.214 | 27.476 | 26.071 | 28.881 |
| O8 | 30.296 | 26.751 | 33.841 | 31.435 | 26.796 | 36.073 | 32.927 | 26.588 | 39.267 |
| O9 | 26.679 | 24.986 | 28.373 | 27.289 | 25.234 | 29.343 | 28.045 | 25.455 | 30.635 |
| O10 | 26.725 | 24.952 | 28.498 | 27.383 | 25.215 | 29.551 | 28.218 | 25.461 | 30.976 |
| O11 | 27.501 | 25.361 | 29.64 | 28.196 | 25.464 | 30.928 | 29.078 | 25.444 | 32.712 |
| O12 | 26.919 | 25.728 | 28.109 | 27.338 | 25.975 | 28.7 | 27.812 | 26.195 | 29.429 |
| O13 | 27.175 | 26.273 | 28.077 | 27.508 | 26.511 | 28.505 | 27.879 | 26.741 | 29.016 |
| O14 | 27.451 | 25.597 | 29.304 | 28.100 | 25.883 | 30.317 | 28.884 | 26.134 | 31.634 |
| Polygon | Parameter | ||||
|---|---|---|---|---|---|
| , W/m2 | , W/m2 | , W/m2 | % | ||
| O1 | 509.75 | 522.36 | 61.31 | 136.03 | 12.03 |
| O2 | 584.26 | 578.75 | 58.07 | 151.90 | 9.94 |
| O3 | 908.60 | 918.99 | 102.60 | 126.12 | 11.29 |
| O4 | 513.21 | 511.48 | 50.35 | 117.40 | 9.81 |
| O5 | 536.56 | 537.21 | 51.14 | 116.51 | 9.53 |
| O6 | 408.14 | 402.51 | 43.43 | 168.18 | 10.64 |
| O7 | 708.16 | 712.73 | 69.35 | 114.27 | 9.79 |
| O8 | 359.56 | 348.26 | 53.62 | 208.20 | 14.91 |
| O9 | 688.13 | 701.69 | 78.44 | 126.57 | 11.40 |
| O10 | 706.45 | 723.48 | 84.34 | 128.40 | 11.94 |
| O11 | 765.16 | 773.10 | 96.54 | 132.81 | 12.62 |
| O12 | 328.03 | 323.31 | 36.01 | 188.80 | 10.98 |
| O13 | 448.99 | 452.65 | 49.25 | 172.57 | 10.97 |
| O14 | 588.56 | 594.78 | 64.68 | 124.02 | 10.99 |
Appendix B.2. Correlation Coefficient at the OWFODA
| Polygon Name (Short Names) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | O9 | O10 | O11 | O12 | O13 | O14 | |
| O1 | 1.000 | |||||||||||||
| O2 | 0.581 | 1.000 | ||||||||||||
| O3 | 0.350 | 0.398 | 1.000 | |||||||||||
| O4 | 0.371 | 0.347 | 0.659 | 1.000 | ||||||||||
| O5 | 0.368 | 0.356 | 0.647 | 0.971 | 1.000 | |||||||||
| O6 | 0.019 | 0.108 | −0.051 | −0.028 | −0.012 | 1.000 | ||||||||
| O7 | 0.489 | 0.560 | 0.706 | 0.651 | 0.628 | −0.012 | 1.000 | |||||||
| O8 | 0.352 | 0.239 | 0.087 | 0.044 | 0.032 | 0.050 | 0.158 | 1.000 | ||||||
| O9 | 0.769 | 0.626 | 0.521 | 0.498 | 0.485 | −0.014 | 0.689 | 0.328 | 1.000 | |||||
| O10 | 0.776 | 0.613 | 0.518 | 0.500 | 0.486 | −0.015 | 0.691 | 0.323 | 0.987 | 1.000 | ||||
| O11 | 0.763 | 0.608 | 0.488 | 0.454 | 0.440 | −0.021 | 0.637 | 0.373 | 0.958 | 0.946 | 1.000 | |||
| O12 | 0.456 | 0.371 | 0.131 | 0.097 | 0.111 | 0.044 | 0.207 | 0.389 | 0.390 | 0.391 | 0.399 | 1.000 | ||
| O13 | 0.514 | 0.409 | 0.134 | 0.094 | 0.108 | 0.050 | 0.222 | 0.383 | 0.429 | 0.430 | 0.436 | 0.888 | 1.000 | |
| O14 | 0.118 | 0.204 | 0.528 | 0.504 | 0.508 | 0.025 | 0.510 | −0.040 | 0.230 | 0.234 | 0.203 | 0.018 | −0.010 | 1.000 |
References
- Soukissian, T.; Sotiriou, M.-A. Long-Term Variability of Wind Speed and Direction in the Mediterranean Basin. Wind 2022, 2, 513–534. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Karathanasi, F.E.; Axaopoulos, P.; Voukouvalas, E.; Kotroni, V. Offshore wind climate analysis and variability in the Mediterranean Sea. Int. J. Climatol. 2018, 38, 384–402. [Google Scholar] [CrossRef]
- Kardakaris, K.; Boufidi, I.; Soukissian, T. Offshore Wind and Wave Energy Complementarity in the Greek Seas Based on ERA5 Data. Atmosphere 2021, 12, 1360. [Google Scholar] [CrossRef]
- Alpert, P.; Osetinsky-Tzidaki, I.; Ziv, B.; Shafir, H. A new seasons definition based on classified daily synoptic systems: An example for the Eastern Mediterranean. Int. J. Climatol.—INT J. Clim. 2004, 24, 1013–1021. [Google Scholar] [CrossRef]
- Poupkou, A.; Zanis, P.; Nastos, P.; Papanastasiou, D.; Melas, D.; Tourpali, K.; Zerefos, C. Present climate trend analysis of the Etesian winds in the Aegean Sea. Theor. Appl. Climatol. 2011, 106, 459–472. [Google Scholar] [CrossRef]
- Stefatos, A.; Karathanasi, F.; Dimou, E.; Loukaidi, V.; Pashalinos, I.; Spinos, S.; Ninou, E.; Patra, S. National Development Program of Offshore Wind Farms; HEREMA: Athens, Greece, 2023. (In Greek) [Google Scholar]
- Soukissian, T.; Papadopoulos, A.; Skrimizeas, P.; Karathanasi, F.; Axaopoulos, P.; Avgoustoglou, E.; Kyriakidou, H.; Tsalis, C.; Voudouri, A.; Gofa, F.; et al. Assessment of offshore wind power potential in the Aegean and Ionian Seas based on high-resolution hindcast model results. Aims Energy 2017, 5, 268–289. [Google Scholar] [CrossRef]
- Wind Europe. Wind Energy in Europe: 2023 Statistics and the Outlook for 2024–2030; Wind Europe: Bilbao, Spain, 2024; p. 56. Available online: https://windeurope.org/intelligence-platform/product/wind-energy-in-europe-2023-statistics-and-the-outlook-for-2024-2030/ (accessed on 17 January 2025).
- Soukissian, T.H.; Chronis, G.T.; Nittis, K.; Diamanti, C. Advancement of Operational Oceanography in Greece: The Case of the Poseidon System. J. Atmos. Ocean. Sci. 2002, 8, 93–107. [Google Scholar] [CrossRef]
- Soukissian, T.; Chronis, G. Poseidon: A marine environmental monitoring, forecasting and information system for the Greek seas. Mediterr. Mar. Sci. 2000, 1, 71–78. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Karathanasi, F.E.; Zaragkas, D.K. Exploiting offshore wind and solar resources in the Mediterranean using ERA5 reanalysis data. Energ. Convers. Manag. 2021, 237, 114092. [Google Scholar] [CrossRef]
- Medina-Lopez, E.; McMillan, D.; Lazic, J.; Hart, E.; Zen, S.; Angeloudis, A.; Bannon, E.; Browell, J.; Dorling, S.; Dorrell, R.M.; et al. Satellite data for the offshore renewable energy sector: Synergies and innovation opportunities. Remote Sens. Environ. 2021, 264, 112588. [Google Scholar] [CrossRef]
- Soukissian, T.; Karathanasi, F.; Axaopoulos, P. Satellite-Based Offshore Wind Resource Assessment in the Mediterranean Sea. IEEE J. Ocean. Eng. 2017, 42, 73–86. [Google Scholar] [CrossRef]
- Li, X.; Mitsopoulos, P.; Yin, Y.; Peña, M. SARAL-AltiKa Wind and Significant Wave Height for Offshore Wind Energy Applications in the New England Region. Remote Sens. 2021, 13, 57. [Google Scholar] [CrossRef]
- Ahsbahs, T.; Badger, M.; Volker, P.; Hansen, K.S.; Hasager, C.B. Applications of satellite winds for the offshore wind farm site Anholt. Wind Energy Sci. 2018, 3, 573–588. [Google Scholar] [CrossRef]
- de Baar, J.; Nhat Luu, L.; van der Schrier, G.; van den Besselaar, E.; Garcia-Marti, I. Recent improvements in the E-OBS gridded data set for daily mean wind speed over Europe in the period 1980–2021. In Proceedings of the EMS Annual Meeting 2022, Bonn, Germany, 5–9 September 2022. [Google Scholar]
- Zhang, H.; Jeffrey, S.; Carter, J. Improved quality gridded surface wind speed datasets for Australia. Meteorol. Atmos. Phys. 2022, 134, 85. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Voukouvalas, E.; Annunziato, A.; Giardino, A.; Feyen, L. Projections of extreme storm surge levels along Europe. Clim. Dynam 2016, 47, 3171–3190. [Google Scholar] [CrossRef]
- Schimanke, S.; Ridal, M.; Le Moigne, P.; Berggren, L.; Undén, P.; Randriamampianina, R.; Andrea, U.; Bazile, E.; Bertelsen, A.; Brousseau, P.; et al. CERRA Sub-Daily Regional Reanalysis Data for Europe on Single Levels from 1984 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Bonn, Germany, 2021; Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-cerra-single-levels?tab=overview (accessed on 13 August 2023).
- Galanaki, E.; Giannaros, C.; Agathangelidis, I.; Cartalis, C.; Kotroni, V.; Lagouvardos, K.; Matzarakis, A. Validating the Copernicus European Regional Reanalysis (CERRA) Dataset for Human-Biometeorological Applications. Environ. Sci. Proc. 2023, 26, 111. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Randriamampianina, R. The Impact of Assimilating Satellite Radiance Observations in the Copernicus European Regional Reanalysis (CERRA). Remote Sens. 2021, 13, 426. [Google Scholar] [CrossRef]
- El-Said, A.; Brousseau, P.; Ridal, M.; Randriamampianina, R. Towards Full Flow-Dependence: New Temporally Varying EDA Quotient Functionality to Estimate Background Errors in CERRA. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002637. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information. 2022: ETOPO 2022 15 Arc-Second Global Relief Model. 2022. Available online: https://doi.org/10.25921/fd45-gt74 (accessed on 13 January 2025).
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology; Raj, B., Koerts, J., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Peng, H.; Wang, S.; Wang, X. Consistency and asymptotic distribution of the Theil–Sen estimator. J. Stat. Plan. Infer. 2008, 138, 1836–1850. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Tsalis, C. The effect of the generalized extreme value distribution parameter estimation methods in extreme wind speed prediction. Nat. Hazards 2015, 78, 1777–1809. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Tsalis, C. Effects of parameter estimation method and sample size in metocean design conditions. Ocean Eng. 2018, 169, 19–37. [Google Scholar] [CrossRef]
- Ahmed, A.S. Wind energy as a potential generation source at Ras Benas, Egypt. Renew. Sustain. Energy Rev. 2010, 14, 2167–2173. [Google Scholar] [CrossRef]
- Irwanto, M.; Gomesh, N.; Mamat, M.R.; Yusoff, Y.M. Assessment of wind power generation potential in Perlis, Malaysia. Renew. Sustain. Energy Rev. 2014, 38, 296–308. [Google Scholar] [CrossRef]
- Koçak, K. Practical ways of evaluating wind speed persistence. Energy 2008, 33, 65–70. [Google Scholar] [CrossRef]
- Shirvaikar, V.V. Persistence of wind direction. Atmos. Environ. (1967) 1972, 6, 889–898. [Google Scholar] [CrossRef]
- Poje, D. Wind persistence at the Adriatic. Hrvat. Meteorološki Časopis 1990, 25, 49–60. Available online: https://hrcak.srce.hr/69066 (accessed on 23 June 2025).
- Astariz, S.; Perez-Collazo, C.; Abanades, J.; Iglesias, G. Co-located wave-wind farms: Economic assessment as a function of layout. Renew. Energ. 2015, 83, 837–849. [Google Scholar] [CrossRef]
- Gao, Q.; Hayward, J.A.; Sergiienko, N.; Khan, S.S.; Hemer, M.; Ertugrul, N.; Ding, B. Detailed mapping of technical capacities and economics potential of offshore wind energy: A case study in South-eastern Australia. Renew. Sustain. Energy Rev. 2024, 189, 113872. [Google Scholar] [CrossRef]
- Benini, G.; Cattani, G. Measuring the long run technical efficiency of offshore wind farms. Appl. Energ. 2022, 308, 118218. [Google Scholar] [CrossRef]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind; National Renewable Energy Laboratory: Golden, CO, USA, 2020; p. 54. [Google Scholar]
- Mortensen, N.G.; Landberg, L.; Troen, I.; Petersen, E.L. Wind Analysis and Application Program (WAsP)–User’s Guide (Tech. Rep. I-666(EN)); Risø National Laboratory: Roskilde, Denmark, 1993. [Google Scholar]
- Fernandes, I.G.; Pimenta, F.M.; Saavedra, O.R.; Silva, A.R. Offshore Validation of ERA5 Reanalysis with Hub Height Wind Observations of Brazil. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Lima, Peru, 15–17 September 2021; pp. 1–5. [Google Scholar]
- Kim, Y.-H.; Lim, H.-C. Effect of island topography and surface roughness on the estimation of annual energy production of offshore wind farms. Renew. Energ. 2017, 103, 106–114. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. Roy. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly Data on Single Levels from 1979 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://doi.org/10.24381/cds.adbb2d47 (accessed on 13 May 2025).
- Martinez, A.; Iglesias, G. Techno-economic assessment of potential zones for offshore wind energy: A methodology. Sci. Total Environ. 2024, 909, 168585. [Google Scholar] [CrossRef] [PubMed]
- Zhai, R.; Huang, C.; Yang, W.; Tang, L.; Zhang, W. Applicability evaluation of ERA5 wind and wave reanalysis data in the South China Sea. J. Oceanol. Limnol. 2023, 41, 495–517. [Google Scholar] [CrossRef]
- Sifnioti, D.E.; Soukisian, T.S.; Poulos, S.E.; Nastos, P.T.; Hatzaki, M. Evaluation of in-situ wind speed and wave height measurements against reanalysis data for the Greek Seas. Mediterr. Mar. Sci. 2018, 18, 486–503. [Google Scholar] [CrossRef][Green Version]
- Ji, W.; Li, R.; Xue, W.; Cao, Z.; Yang, H.; Ning, Q.; Hu, X.; Liao, G. Evaluation of ERA5 wind parameter with in-situ data offshore China. PLoS ONE 2025, 20, e0317751. [Google Scholar] [CrossRef]
- Soukissian, T.H. Probabilistic modeling of directional and linear characteristics of wind and sea states. Ocean. Eng. 2014, 91, 91–110. [Google Scholar] [CrossRef]
- Vagenas, C.; Anagnostopoulou, C.; Tolika, K. Climatic Study of the Marine Surface Wind Field over the Greek Seas with the Use of a High Resolution RCM Focusing on Extreme Winds. Climate 2017, 5, 29. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Prospathopoulos, A.; Korres, G.; Papadopoulos, A.; Hatzinaki, M.; Kambouridou, M. A New Wind and Wave Atlas of the Hellenic Seas. In Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; pp. 791–799. [Google Scholar]
- Wang, J.; Qin, S.; Jin, S.; Wu, J. Estimation methods review and analysis of offshore extreme wind speeds and wind energy resources. Renew. Sustain. Energy Rev. 2015, 42, 26–42. [Google Scholar] [CrossRef]
- Cheynet, E.; Li, L.; Jiang, Z. Metocean Conditions at Two Norwegian Sites for Development of Offshore Wind Farms. 2023. Available online: https://doi.org/10.2139/ssrn.4408728 (accessed on 5 March 2025).
- Mulas-Hernando, D.; Musial, W.; Duffy, P.; Shields, M. Capacity Density Considerations for Offshore Wind Plants in the United States (Report no. NREL/TP-5000-86933); National Renewable Energy Laboratory: Golden, CO, USA, 2023. Available online: https://www.nrel.gov/docs/fy24osti/86933.pdf (accessed on 5 March 2025).
- Borrmann, R.; Rehfeldt, K.; Wallasch, A.-K.; Lüers, S. Capacity Densities of European Offshore Wind Farms (Report of the Project Interreg Baltic Sea Region—Project Baltic LINes); Deutsche WindGuard: Varel, Germany, 2018; Available online: https://vasab.org/wp-content/uploads/2018/06/BalticLINes_CapacityDensityStudy_June2018-1.pdf (accessed on 13 January 2025).
- Faraggiana, E.; Ghigo, A.; Sirigu, M.; Petracca, E.; Giorgi, G.; Mattiazzo, G.; Bracco, G. Optimal floating offshore wind farms for Mediterranean islands. Renew. Energ. 2024, 221, 119785. [Google Scholar] [CrossRef]
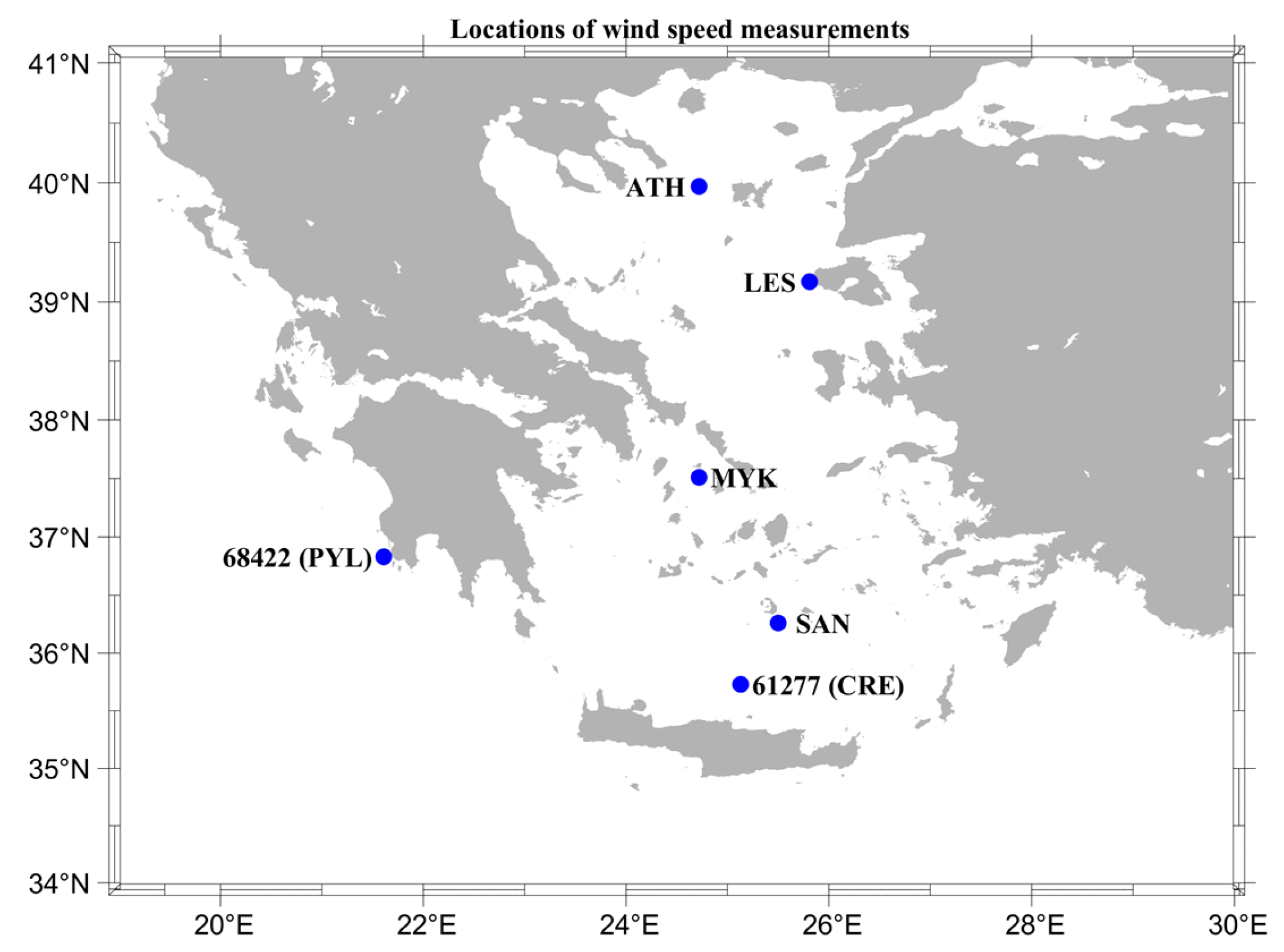









| Buoy Name/Code | Latitude–Longitude | Overlapping Time Periods | Sample Size |
|---|---|---|---|
| 68422 (PYL) | [36.83° N, 21.61° E] | 2007–2020 | 24,445 |
| 61277 (CRE) | [35.73° N, 25.13° E] | 2007–2020 | 24,741 |
| ATH (Athos) | [39.97° N, 24.72° E] | 2000–2015 | 31,849 |
| LES (Lesvos) | [39.17° N, 25.81° E] | 2000–2012 | 27,418 |
| MΥΚ (Mykonos) | [37.51° N, 25.46° E] | 2000–2012 | 27,209 |
| SAN (Santorini) | [36.26° N, 25.50° E] | 2000–2012 | 30,831 |
| Full OWFODA Name | Short Name |
|---|---|
| Ag. Apostoli | O1 |
| Chios | O2 |
| Crete1 | O3 |
| Crete2A | O4 |
| Crete2B | O5 |
| Diapontia | O6 |
| Donousa2 | O7 |
| Patras | O8 |
| GyarosA | O9 |
| GyarosB | O10 |
| GyarosC | O11 |
| Pilot1A | O12 |
| Pilot1B | O13 |
| Rhodes | O14 |
| Parameter | Value |
|---|---|
| 15 MW | |
| 332 W/m2 | |
| 3 m/s | |
| 10.59 m/s | |
| 25 m/s | |
| 240 | |
| 150 m | |
| 3 |
| Buoy Name | (m/s) | (m/s) | (m/s) | (%) | |
|---|---|---|---|---|---|
| PYL | −0.108 | 1.373 | 1.843 | 8.921 | 0.824 |
| CRE | 0.122 | 1.319 | 1.821 | 8.699 | 0.824 |
| ATH | 0.463 | 1.494 | 1.951 | 9.338 | 0.880 |
| LES | −0.506 | 1.553 | 2.163 | 8.820 | 0.840 |
| MΥΚ | 0.456 | 1.803 | 2.381 | 7.968 | 0.788 |
| SAN | 0.176 | 1.515 | 1.986 | 9.347 | 0.813 |
| Buoy Name | (m/s) | (m/s) | (m/s) | (%) | |
|---|---|---|---|---|---|
| PYL | −0.476 | 1.634 | 2.136 | 10.339 | 0.768 |
| CRE | 0.236 | 1.333 | 1.813 | 8.660 | 0.824 |
| ATH | −0.484 | 1.573 | 2.180 | 8.888 | 0.833 |
| LES | 0.951 | 2.005 | 2.545 | 8.516 | 0.782 |
| MΥΚ | 0.132 | 1.575 | 2.049 | 9.807 | 0.857 |
| SAN | −0.575 | 1.621 | 2.120 | 9.976 | 0.800 |
| Buoy Name | |||
|---|---|---|---|
| PYL | −3.226 | 45.240 | 0.655 |
| CRE | −5.684 | 43.576 | 0.758 |
| ATH | −8.547 | 37.859 | 0.730 |
| LES | −5.433 | 61.468 | 0.399 |
| MΥΚ | −4.847 | 41.307 | 0.723 |
| SAN | −6.911 | 39.327 | 0.772 |
| Settings | ||||||||
|---|---|---|---|---|---|---|---|---|
| CDS_3 | CDS_5 | CDS_7 | CDS_3 | CDS_5 | CDS_7 | |||
| Polygon | Surface [km2] | Foundation | No. of Wind Turbines | Capacity (MW) | ||||
| O1 | 133.9 | FL | 26 | 44 | 62 | 402 | 670 | 937 |
| O2 | 65.54 | FL | 13 | 21 | 24 | 197 | 328 | 360 |
| O3 | 118.0 | FL | 23 | 39 | 55 | 354 | 590 | 826 |
| O4 | 40.06 | FL | 8 | 13 | 14 | 120 | 200 | 220 |
| O5 | 187.26 | FL | 37 | 62 | 87 | 562 | 936 | 1311 |
| O6 | 54.34 | FB | 10 | 18 | 19 | 163 | 272 | 299 |
| O7 | 65.03 | FL | 13 | 21 | 30 | 195 | 325 | 455 |
| O8 | 138.83 | FB | 27 | 46 | 50 | 416 | 694 | 764 |
| O9 | 43.44 | FL | 8 | 14 | 20 | 130 | 217 | 304 |
| O10 | 14.90 | FL | 2 | 4 | 5 | 45 | 75 | 82 |
| O11 | 41.41 | FL | 8 | 13 | 19 | 124 | 207 | 290 |
| O12 | 77.39 | FB | 14 | 14 | 14 | 210 | 210 | 210 |
| O13 | 141.89 | FB | 26 | 26 | 26 | 390 | 390 | 390 |
| O14 | 74.86 | FL | 14 | 24 | 27 | 225 | 374 | 412 |
| Total | 1196.85 | 229 | 365 | 452 | 3131 | 5488 | 6860 | |
| Polygon | AEP (GWh) | ||
|---|---|---|---|
| Settings | |||
| CDS_3 | CDS_5 | CDS_7 | |
| O1 | 1260.70 | 2133.49 | 3006.29 |
| O2 | 645.48 | 1042.70 | 1191.65 |
| O3 | 1384.36 | 2347.39 | 3310.43 |
| O4 | 418.02 | 679.28 | 731.53 |
| O5 | 1999.71 | 3350.86 | 4702.01 |
| O6 | 377.27 | 679.09 | 716.81 |
| O7 | 797.95 | 1288.99 | 1841.41 |
| O8 | 867.69 | 1478.29 | 1606.83 |
| O9 | 441.25 | 772.18 | 1103.12 |
| O10 | 110.73 | 221.45 | 276.82 |
| O11 | 441.04 | 716.69 | 1047.46 |
| O12 | 452.41 | 452.41 | 452.41 |
| O13 | 1058.54 | 1058.54 | 1058.54 |
| O14 | 773.79 | 1326.50 | 1492.31 |
| Total | 11,028.93 | 17,547.86 | 22,537.64 |
| Polygon | GWh/km2 | GWh/Num. of Turbines | ||
|---|---|---|---|---|
| Settings | ||||
| CDS_3 | CDS_5 | CDS_7 | For all CDS | |
| O1 | 9.42 | 15.93 | 22.45 | 48.49 |
| O2 | 9.85 | 15.91 | 18.18 | 49.65 |
| O3 | 11.73 | 19.89 | 28.05 | 60.19 |
| O4 | 10.43 | 16.96 | 18.26 | 52.25 |
| O5 | 10.68 | 17.89 | 25.11 | 54.05 |
| O6 | 6.94 | 12.50 | 13.19 | 37.73 |
| O7 | 12.27 | 19.82 | 28.32 | 61.38 |
| O8 | 6.25 | 10.65 | 11.57 | 32.14 |
| O9 | 10.16 | 17.78 | 25.40 | 55.16 |
| O10 | 7.43 | 14.86 | 18.57 | 55.36 |
| O11 | 10.65 | 17.31 | 25.29 | 55.13 |
| O12 | 5.85 | 5.85 | 5.85 | 32.32 |
| O13 | 7.46 | 7.46 | 7.46 | 40.71 |
| O14 | 10.34 | 17.72 | 19.93 | 55.27 |
| Overall | 9.21 | 14.66 | 18.83 | |
| Polygon | Months | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| O1 | 197 | 180 | 180 | 146 | 140 | 144 | 212 | 232 | 163 | 182 | 167 | 192 |
| O2 | 100 | 96 | 97 | 76 | 65 | 68 | 102 | 102 | 72 | 78 | 84 | 101 |
| O3 | 199 | 180 | 176 | 154 | 148 | 186 | 277 | 271 | 205 | 188 | 172 | 193 |
| O4 | 49 | 47 | 49 | 48 | 49 | 65 | 93 | 91 | 57 | 44 | 40 | 46 |
| O5 | 248 | 239 | 247 | 236 | 247 | 326 | 451 | 437 | 272 | 209 | 203 | 236 |
| O6 | 65 | 64 | 62 | 55 | 48 | 51 | 61 | 51 | 43 | 49 | 65 | 65 |
| O7 | 103 | 99 | 98 | 86 | 88 | 106 | 161 | 157 | 109 | 95 | 87 | 100 |
| O8 | 162 | 143 | 143 | 121 | 100 | 78 | 75 | 86 | 97 | 150 | 160 | 163 |
| O9 | 68 | 63 | 62 | 50 | 47 | 52 | 84 | 88 | 63 | 66 | 62 | 67 |
| O10 | 20 | 18 | 18 | 14 | 14 | 15 | 24 | 26 | 18 | 19 | 18 | 19 |
| O11 | 64 | 59 | 58 | 46 | 44 | 47 | 75 | 79 | 58 | 63 | 59 | 64 |
| O12 | 49 | 45 | 45 | 31 | 27 | 20 | 30 | 37 | 32 | 41 | 44 | 51 |
| O13 | 116 | 103 | 103 | 73 | 63 | 48 | 70 | 87 | 75 | 99 | 103 | 120 |
| O14 | 106 | 103 | 103 | 93 | 98 | 129 | 170 | 153 | 115 | 80 | 79 | 97 |
| TOTAL | 1546 | 1439 | 1441 | 1229 | 1178 | 1335 | 1885 | 1897 | 1379 | 1363 | 1343 | 1514 |
| Polygon | Parameter | ||
|---|---|---|---|
MWh | MWh | % | |
| O1 | 5841.19 | 4466.18 | 76.46 |
| O2 | 2854.75 | 2070.58 | 72.53 |
| O3 | 6426.81 | 4315.44 | 67.15 |
| O4 | 1859.77 | 1369.11 | 73.62 |
| O5 | 9174.15 | 6428.38 | 70.07 |
| O6 | 1859.24 | 1639.75 | 88.19 |
| O7 | 3529.06 | 2266.24 | 64.22 |
| O8 | 4047.33 | 4101.49 | 101.34 |
| O9 | 2114.13 | 1571.60 | 74.34 |
| O10 | 606.30 | 450.48 | 74.30 |
| O11 | 1962.18 | 1447.54 | 73.77 |
| O12 | 1238.64 | 1238.66 | 100.00 |
| O13 | 2898.12 | 2548.92 | 87.95 |
| O14 | 3631.75 | 2482.43 | 68.35 |
| Polygon Name | Parameter | |||||
|---|---|---|---|---|---|---|
| (%) | (%) | MWh | MWh | % | (Hours in UTC) | |
| O1 | 43.35 | 76.9 | 243.38 | 220.32 | 90.52 | 12:00–15:00 |
| O2 | 44.39 | 79.9 | 118.95 | 104.79 | 88.09 | 18:00–21:00 |
| O3 | 53.81 | 80.1 | 267.78 | 209.85 | 78.37 | 03:00–06:00 |
| O4 | 46.71 | 79.4 | 77.49 | 65.60 | 84.66 | 12:00–15:00 |
| O5 | 48.32 | 81.2 | 382.26 | 311.56 | 81.51 | 12:00–15:00 |
| O6 | 33.73 | 67.5 | 77.47 | 86.73 | 111.96 | 18:00–21:00 |
| O7 | 54.87 | 85.1 | 147.04 | 107.82 | 73.33 | 15:00–18:00 |
| O8 | 28.73 | 60.5 | 168.64 | 208.08 | 123.39 | 15:00–18:00 |
| O9 | 49.31 | 77.9 | 88.09 | 74.97 | 85.10 | 15:00–18:00 |
| O10 | 49.49 | 77.7 | 25.26 | 21.45 | 84.90 | 15:00–18:00 |
| O11 | 49.29 | 77.7 | 81.76 | 69.99 | 85.61 | 15:00–18:00 |
| O12 | 28.89 | 66.3 | 51.61 | 60.71 | 117.64 | 21:00–00:00 |
| O13 | 36.40 | 71.7 | 120.76 | 123.96 | 102.66 | 03:00–06:00 |
| O14 | 49.41 | 84.4 | 151.32 | 119.23 | 78.79 | 15:00–18:00 |
| Polygon | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | O9 | O10 | O11 | O12 | O13 | O14 | |
| O1 | 1 | |||||||||||||
| O2 | 0.753 | 1 | ||||||||||||
| O3 | 0.684 | 0.595 | 1 | |||||||||||
| O4 | 0.560 | 0.430 | 0.854 | 1 | ||||||||||
| O5 | 0.545 | 0.443 | 0.836 | 0.994 | 1 | |||||||||
| O6 | −0.108 | 0.231 | −0.143 | −0.146 | −0.103 | 1 | ||||||||
| O7 | 0.720 | 0.615 | 0.923 | 0.898 | 0.884 | −0.139 | 1 | |||||||
| O8 | 0.272 | 0.251 | −0.109 | −0.358 | −0.372 | 0.054 | −0.161 | 1 | ||||||
| O9 | 0.926 | 0.736 | 0.813 | 0.677 | 0.653 | −0.134 | 0.848 | 0.202 | 1 | |||||
| O10 | 0.924 | 0.718 | 0.816 | 0.685 | 0.660 | −0.148 | 0.854 | 0.189 | 0.998 | 1 | ||||
| O11 | 0.923 | 0.725 | 0.778 | 0.612 | 0.585 | −0.149 | 0.798 | 0.288 | 0.989 | 0.986 | 1 | |||
| O12 | 0.538 | 0.558 | 0.099 | −0.127 | −0.126 | 0.175 | 0.091 | 0.679 | 0.449 | 0.437 | 0.499 | 1 | ||
| O13 | 0.564 | 0.584 | 0.100 | −0.143 | −0.141 | 0.182 | 0.090 | 0.691 | 0.464 | 0.451 | 0.514 | 0.978 | 1 | |
| O14 | 0.296 | 0.319 | 0.735 | 0.811 | 0.825 | 0.020 | 0.755 | −0.392 | 0.416 | 0.424 | 0.353 | −0.195 | −0.219 | 1 |
| Polygon | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | O9 | O10 | O11 | O12 | O13 | O14 | |
| O1 | 1 | |||||||||||||
| O2 | 0.613 | 1 | ||||||||||||
| O3 | 0.668 | 0.660 | 1 | |||||||||||
| O4 | 0.596 | 0.641 | 0.818 | 1 | ||||||||||
| O5 | 0.537 | 0.626 | 0.796 | 0.990 | 1 | |||||||||
| O6 | −0.330 | 0.015 | −0.073 | 0.047 | 0.106 | 1 | ||||||||
| O7 | 0.720 | 0.773 | 0.897 | 0.764 | 0.736 | −0.104 | 1 | |||||||
| O8 | 0.346 | 0.349 | 0.259 | 0.047 | 0.021 | −0.355 | 0.344 | 1 | ||||||
| O9 | 0.896 | 0.698 | 0.826 | 0.711 | 0.657 | −0.324 | 0.881 | 0.391 | 1 | |||||
| O10 | 0.903 | 0.683 | 0.814 | 0.697 | 0.642 | −0.334 | 0.877 | 0.407 | 0.998 | 1 | ||||
| O11 | 0.884 | 0.689 | 0.816 | 0.680 | 0.623 | −0.363 | 0.867 | 0.463 | 0.990 | 0.988 | 1 | |||
| O12 | 0.468 | 0.383 | 0.270 | 0.199 | 0.173 | −0.032 | 0.431 | 0.454 | 0.453 | 0.474 | 0.452 | 1 | ||
| O13 | 0.575 | 0.427 | 0.350 | 0.297 | 0.262 | −0.168 | 0.513 | 0.478 | 0.573 | 0.596 | 0.574 | 0.948 | 1 | |
| O14 | 0.144 | 0.401 | 0.578 | 0.553 | 0.583 | 0.254 | 0.497 | 0.164 | 0.279 | 0.281 | 0.305 | 0.079 | 0.122 | 1 |
| Polygon | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| O1 | O2 | O3 | O4 | O5 | O6 | O7 | O8 | O9 | O10 | O11 | O12 | O13 | O14 | |
| O1 | 1 | |||||||||||||
| O2 | 0.592 (1) | 1 | ||||||||||||
| O3 | 0.425 (4) | 0.440 (2) | 1 | |||||||||||
| O4 | 0.413 (4) | 0.379 (3) | 0.664 (−1) | 1 | ||||||||||
| O5 | 0.399 (3) | 0.382 (3) | 0.648 (−1) | 0.971 (0) | 1 | |||||||||
| O6 | 0.095 (−4) | 0.187 (−8) | 0.063 (−9) | 0.061 (−7) | 0.076 (−7) | 1 | ||||||||
| O7 | 0.525 (2) | 0.562 (1) | 0.723 (−1) | 0.651 (0) | 0.628 (0) | 0.083 (8) | 1 | |||||||
| O8 | 0.352 (0) | 0.242 (−1) | 0.144 (−4) | 0.094 (−4) | 0.087 (−4) | 0.055 (−81) | 0.187 (−3) | 1 | ||||||
| O9 | 0.775 (1) | 0.626 (0) | 0.558 (−2) | 0.518 (−2) | 0.501 (−2) | 0.079 (6) | 0.702 (−1) | 0.337 (1) | 1 | |||||
| O10 | 0.780 (1) | 0.613 (0) | 0.555 (−2) | 0.518 (−2) | 0.500 (−2) | 0.075 (5) | 0.703 (−1) | 0.331 (1) | 0.987 (0) | 1 | ||||
| O11 | 0.767 (1) | 0.608 (0) | 0.530 (−3) | 0.476 (−2) | 0.458 (−2) | 0.076 (6) | 0.653 (−1) | 0.378 (1) | 0.958 (0) | 0.946 (0) | 1 | |||
| O12 | 0.472 (−2) | 0.371 (0) | 0.147 (−3) | 0.140 (−6) | 0.141 (−4) | 0.088 (4) | 0.227 (−3) | 0.389 (0) | 0.410 (−2) | 0.411 (−2) | 0.418 (−2) | 1 | ||
| O13 | 0.532 (−2) | 0.409 (0) | 0.176 (−7) | 0.158 (−6) | 0.155 (−6) | 0.106 (4) | 0.261 (−4) | 0.390 (−2) | 0.459 (−2) | 0.461 (−2) | 0.467 (−2) | 0.888 (0) | 1 | |
| O14 | 0.184 (5) | 0.217 (3) | 0.537 (1) | 0.519 (1) | 0.523 (1) | 0.119 (8) | 0.526 (1) | 0.049 (906) | 0.275 (3) | 0.280 (3) | 0.247 (3) | 0.054 (7) | 0.061 (7) | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soukissian, T.; Koutri, N.-E.; Karathanasi, F.; Kardakaris, K.; Stefatos, A. A Preliminary Assessment of Offshore Winds at the Potential Organized Development Areas of the Greek Seas Using CERRA Dataset. J. Mar. Sci. Eng. 2025, 13, 1486. https://doi.org/10.3390/jmse13081486
Soukissian T, Koutri N-E, Karathanasi F, Kardakaris K, Stefatos A. A Preliminary Assessment of Offshore Winds at the Potential Organized Development Areas of the Greek Seas Using CERRA Dataset. Journal of Marine Science and Engineering. 2025; 13(8):1486. https://doi.org/10.3390/jmse13081486
Chicago/Turabian StyleSoukissian, Takvor, Natalia-Elona Koutri, Flora Karathanasi, Kimon Kardakaris, and Aristofanis Stefatos. 2025. "A Preliminary Assessment of Offshore Winds at the Potential Organized Development Areas of the Greek Seas Using CERRA Dataset" Journal of Marine Science and Engineering 13, no. 8: 1486. https://doi.org/10.3390/jmse13081486
APA StyleSoukissian, T., Koutri, N.-E., Karathanasi, F., Kardakaris, K., & Stefatos, A. (2025). A Preliminary Assessment of Offshore Winds at the Potential Organized Development Areas of the Greek Seas Using CERRA Dataset. Journal of Marine Science and Engineering, 13(8), 1486. https://doi.org/10.3390/jmse13081486







