Abstract
The maritime sector is undergoing rapid transformation, driven by increasingly stringent international regulations targeting air pollution. While newly built vessels integrate advanced technologies for compliance, the global fleet averages 21.8 years of age and must meet emission requirements through retrofitting or operational changes. This study evaluates, at environmental and economic levels, two key sulphur abatement strategies for a 1998-built cruise vessel nearing the end of its service life: (i) the installation of open-loop scrubbers with fuel enhancement devices, and (ii) a switch to marine diesel oil as main fuel. The analysis was based on real operational data from a cruise vessel. For the environmental assessment, a Tier III hybrid emissions model was used. The results show that scrubbers reduce SOx emissions by approximately 97% but increase fuel consumption by 3.6%, raising both CO2 and NOx emissions, while particulate matter decreases by only 6.7%. In contrast, switching to MDO achieves over 99% SOx reduction, an 89% drop in particulate matter, and a nearly 5% reduction in CO2 emissions. At an economic level, it was found that, despite a CAPEX of nearly USD 1.9 million, scrubber installation provides an average annual net saving exceeding USD 8.2 million. From the deterministic and probabilistic analyses performed, including Monte Carlo simulations under various fuel price correlation scenarios, scrubber installation consistently shows high profitability, with NPVs surpassing USD 70 million and payback periods under four months.
1. Introduction
Global energy demand continues to rise at an accelerating pace. Between 2013 and 2023, the average annual growth rate was approximately 1.3%; however, this figure surged to 2.2% in 2024 alone [1]. To meet this escalating demand, fossil fuels, namely coal, oil, and natural gas, remain the dominant energy sources, with projections from the International Energy Agency (IEA) indicating that their peak usage will not occur before 2030 [2]. This persistent reliance on fossil fuels plays a critical role in two pressing global challenges: the intensification of climate change and the deterioration of public health [3,4].
It is well established, both in the scientific community and among public and private stakeholders, that emissions resulting from the combustion of fossil fuels are directly linked to global warming. This is primarily due to the high carbon content of these fuels, which leads to significant carbon dioxide (CO2) emissions during combustion [5]. This process adds an excess amount of CO2 to the levels naturally present in the atmosphere. Similar patterns are observed with other well-known greenhouse gases, such as methane (CH4) and nitrous oxide (N2O) [6].
The impact of methane in climate change is a result of two distinct processes. In one hand, methane can be released directly into the atmosphere in its pure form from fossil sources, having a Global Warming Potential (GWP) of 29.8 over a 100-year time horizon [3]. On the other hand, the combustion of methane decreases its GWP, since the process converts it into carbon dioxide (2.75 g of CO2 per gram of CH4) and water. However, the combustion of methane can also result in the release of unburned methane to the atmosphere when an incomplete combustion of methane–air mixture happens, a phenomenon known as methane slip. In modern engines, methane slip can account for up to 6% of the total fuel consumed [7,8]. Such levels of unburned methane contribute significantly to global warming and may offset the environmental benefits gained by avoiding the use of more carbon-intensive fossil fuels.
In the case of N2O, it contributes only a small fraction to total greenhouse gas emissions by volume, but its impact on global warming is disproportionately large due to its GWP, which is 273 times greater than that of CO2 over a 100-year timescale [3]. This high GWP, combined with an atmospheric lifetime of approximately 116 ± 9 years, makes N2O a significant contributor to climate change. Emissions of N2O are projected to continue increasing in the coming years. While agriculture remains the primary source of these emissions, industrial sectors also play a notable role in their release [9].
Nitrogen oxides, primarily nitric oxide (NO) and nitrogen dioxide (NO2), are not considered strong greenhouse gases themselves. However, they contribute indirectly to climate change and have a significant public health impact. Although NOx lacks the radiative forcing strength of gases like CO2 or CH4, it plays an important role in the formation of tropospheric ozone, a potent greenhouse gas, particularly relevant in sectors such as aviation [10]. Additionally, NOx emissions extend the atmospheric lifetime of methane, further amplifying its climate impact. From a health perspective, NO2 is of particular concern due to its association with respiratory problems. It exacerbates conditions such as asthma and bronchitis, impairs lung function in children, and is linked to increased mortality rates [11].
In addition to nitrogen oxides, the combustion of fossil fuels poses further public health risks. These fuels often contain sulphur, which leads to the emission of sulphur oxides (SOx) during combustion. These compounds are not only harmful on their own but also contribute to the formation of particulate matter (PM), posing serious risks to respiratory and cardiovascular health [12,13].
1.1. Pollutant Emissions from Maritime Sector
The maritime industry is not exempt from the challenges posed by emissions, both in terms of their contribution to global warming and their impact on public health. As a sector responsible for transporting approximately 80% of goods involved in global world trade, it is particularly sensitive to these issues [14]. This sensitivity arises from the sector’s dependence on fossil fuels for propulsion combined with its high operational mobility, as vessels are capable of global voyages within days, yet often operate with outdated technologies, reflected by the average age of merchant vessel fleets being 21.8 years [15].
Traditionally, merchant vessels have relied on heavy fuel oil (HFO) for their main propulsion needs, using lighter marine diesel oil (MDO) in a marginal role, accounting for approximately 6% of total fuel consumption [16,17]. These vessels, which were predominantly designed to operate on high-sulphur fossil fuels, are associated with the emission of substantial quantities of pollutants, particularly SO2, NOx, and particulate matter. The International Maritime Organization (IMO), recognizing the environmental and health challenges posed by maritime emissions, began developing a regulatory framework to mitigate these impacts. Initial efforts focused on public health, with the adoption in 1997 of the Technical Code on Control of Emission of Nitrogen Oxides from Marine Diesel Engines. This Code was revised in 2008 and further amended during the 83rd session of the Marine Environment Protection Committee (MEPC 83). The latest amendments, which permit the use of multiple operational profiles for marine diesel engines, aim to improve emission control under varying engine loads. This will enable ships to optimize fuel consumption according to their specific operational profiles, thereby enhancing energy efficiency while ensuring compliance with NOx emission limits [18].
Regarding SOx emissions, IMO recognized that these emissions are directly dependent on the sulphur content of fuels. Consequently, regulating fuel sulphur content would effectively reduce SOx emissions from the maritime sector. In line with this, the IMO implemented a global sulphur cap of 4.5% in 2008, which was subsequently lowered to 3.5% in 2012 [19]. Most recently, the IMO 2020 regulation further reduced the cap to the current limit of 0.5% for all seagoing vessels worldwide, with an even stricter limit of 0.1% enforced within designated Sulphur Emission Control Areas (SECAs) [20]. This reduction has significant public health benefits; however, some unintended consequences emerged in the early years of the sulphur cap. Sulphur oxides contribute to negative radiative forcing through aerosol formation, which has a cooling effect on the climate. Thus, reducing SOx emissions may have diminished this cooling influence, with complex implications for global temperature trends [21,22].
Although the IMO initially focused on mitigating air pollutants with direct impacts on human health, such as NOx, SOx, and particulate matter, its current agenda has expanded to include the reduction in greenhouse gas (GHG) emissions from the maritime sector. To address this broader challenge, the IMO has established a comprehensive regulatory framework aimed at abating air pollution generated by international shipping. Regarding climate change mitigation, one of the IMO’s key milestones is the 2023 IMO GHG Strategy, which sets a target of reaching net-zero GHG emissions from international shipping by or around 2050, with interim checkpoints in 2030 and 2040 [23].
Building upon the existing NOx Technical Code and the IMO 2020 sulphur cap, the addition of the 2023 IMO GHG Strategy requires shipowners to comply with SOx and NOx limits while simultaneously reducing greenhouse gas emissions. Although new vessels will be designed with these regulations in mind, a critical question remains: How can aged vessels comply with these increasingly stringent requirements and remain profitable?
1.2. Exhaust Gas Cleaning Systems
For compliance with the NOx Technical Code, shipowners typically employ Selective Catalytic Reduction (SCR). Additionally, other measures such as Fuel Water Emulsification (FEW), Direct Water Injection (DWI), and Exhaust Gas Recirculation (EGR) can also be implemented [24]. These alternatives help to mitigate the need for installing dedicated NOx exhaust gas cleaning systems on the engine funnel, thereby reducing the backpressure generated by such systems [25].
Following the implementation of the IMO 2020 regulation, shipowners faced the decision of either switching to low-sulphur fuels or adopting alternative compliance strategies. The installation of exhaust gas cleaning systems, commonly referred to as scrubbers, has become one of the preferred solutions within the maritime industry. Scrubbers enable vessels already in service to meet SOx emission limits without switching to low-sulphur fuels, primarily for economic reasons. Notably, within five years of installation, more than 95% of ships equipped with the most common scrubber systems achieve cost break-even [26]. While exhaust gas cleaning systems provide a convenient pathway to continue using low-cost residual fuels, concerns remain regarding the emission of other pollutants, such as CO2, NOx, and PM. This is in part motivated by the fact that the scrubber increases backpressure in the engine funnel, which raises the fuel consumption of the engines [25]. This raises critical questions about whether scrubbers effectively improve air quality and public health, while also contributing to the broader objective of maritime decarbonization [27,28]. Several studies have assessed the impact of scrubber installation on SOx and PM emissions in merchant vessels. In 2013, Caiazzo et al. demonstrated that the use of an open-loop scrubber in a marine diesel engine operating on HFO led to a reduction in SO2 emissions of approximately 93% [29]. This effectiveness was further validated by Fridell and Salo in 2016, who reported a reduction of about 99% in SO2 emissions using a similar open-loop system [30]. Winnes et al. carried out a more comprehensive assessment in 2020 by studying a RoPax ferry equipped with a four-stroke engine and a scrubber, reporting a 99% reduction in SO2 emissions but only a 40% reduction in PM emissions [31]. Yang et al. highlighted limitations in PM removal, showing that not all particulate matter is captured by the scrubber. The study, conducted on a container ship, confirmed a reduction of more than 95% in SOx emissions, but only around 10% in PM emissions, underscoring the variable effectiveness of scrubbers in addressing different pollutant types [32]. However, research addressing their effects on NOx and CO2 emissions remains limited.
In addition to the potential increase in other air pollutant emissions, the use of scrubbers on ships to reduce SOx emissions has raised environmental concerns due to the discharge of large volumes of polluted acidic washwater into the sea [26]. In 2023, the International Council on Clean Transportation reported the identification of up to 93 bans and restrictions related to scrubber washwater discharges [33]. These include outright prohibitions on any discharge of washwater or bleed-off from scrubbers, as well as conditional allowances based on specific criteria, with most restrictions targeting open-loop scrubbers. More recently, in June 2025, OSPAR, the cooperative mechanism involving 15 governments and the European Union to protect the marine environment of the North-East Atlantic, expressed serious concerns over hazardous discharges from ship scrubbers, particularly in coastal areas. During its Ministerial Meeting held in Vigo, OSPAR agreed to implement a phased ban on scrubber discharges in internal waters and port zones across the North-East Atlantic region [34]. Discharges from open-loop scrubbers will be prohibited in internal waters and port areas across the North-East Atlantic starting in July 2027, while discharges from closed-loop scrubbers will be banned by January 2029.
From an economic standpoint, open-loop scrubbers offer several advantages, including lower capital and operational expenditures (CAPEX and OPEX, respectively). By contrast, closed-loop systems retain the effluent onboard, and their operation is limited by the vessel’s waste storage capacity. This constraint may compel shipowners to schedule additional port calls for effluent discharge, thereby incurring further operational costs. For this reason, closed-loop systems demand more onboard space and entail higher CAPEX and OPEX [35]. Hybrid scrubbers aim to mitigate the disadvantages of both configurations, offering greater operational flexibility, albeit with comparatively higher installation and operating costs [36].
Owners of older vessels must make strategic decisions to meet International Maritime Organization emission reduction targets without compromising economic viability. The initial focus of IMO regulations was the reduction of SOx emissions, prompting many shipowners to retrofit their fleets with scrubbers. As the IMO now intensifies efforts to reduce GHG emissions, it is essential to assess whether scrubbers contribute meaningfully to GHG mitigation or if a transition to alternative fuels, such as low-sulphur marine diesel oil, is required. Although significant research has addressed SOx abatement technologies, there remains a lack of comprehensive studies comparing the environmental and economic impacts of using MDO versus open-loop scrubbers, particularly for aging vessels. This study addresses this gap by presenting a novel comparative analysis of these two strategies on a case study vessel built in 1998, evaluating their effectiveness in reducing SOx and other harmful emissions, as well as their economic implications. The rest of the paper is structured as follows: Section 2 presents the case study vessel and outlines the methodology used for the environmental and economic assessments. Section 3 discusses the results obtained from both the use of MDO and the scrubber installation scenarios. Finally, Section 4 summarizes the main conclusions of the study.
2. Materials and Methods
This paper presents a case study of a cruise vessel that initially operated using MDO and later retrofitted scrubbers in all its engines to comply with IMO SOx emission regulations, enabling continued operation on the more economic HFO. The vessel’s specifications are detailed in Table 1.

Table 1.
Particulars of case study vessel.
The case study vessel was built in 1998 and typically operates between ports in the southern United States, primarily Miami, and various destinations throughout the Caribbean Sea. This operational profile is particularly relevant, as Miami lies within the North American Emission Control Area (ECA) designated by IMO. ECAs enforce stricter SOX emission limits than the global standard, reducing the permissible sulphur content in marine fuels from 0.5% to 0.1%. The data for the environmental and economic assessments were collected from the ship’s electronic logbook, during the month of April 2024. Although the vessel is aging, company officials intend to keep it in operation for an additional ten years. This projected service lifetime has therefore been adopted as the time horizon for the economic modelling.
2.1. Environmental Assessment
Currently, the assessment of pollutant emissions from marine vessels can be performed by using three different methods: bottom-up, top-down, or a combination of both [37,38]. These methods are outlined in the Emission Inventory Guidebook 2023, published by the European Environment Agency (EEA), more specifically in Chapter 1.A.3.d Navigation (shipping) [39]. The guidebook, first published in 1996, included a chapter on estimating emissions from navigation starting in 2009. Since then, it has been continuously updated and adopted by numerous scientists, also being referenced in the Fourth IMO Greenhouse Gas Study [16,39]. In the literature, these approaches are often referred to as Tier I, Tier II, and Tier III, differing in the emission assessment process and the geographic characterization of the ship [40].
The complete “bottom-up” method assesses emissions from an individual ship by considering its characteristics, such as type, construction date, cargo, engine power, and fuel consumption under specific load conditions. With this method, it is possible to estimate the near-instantaneous emission production of a vessel, helping to identify the main contributors to the emissions, offering a clear understanding of their impact. Since the method is data intensive, it is also expensive and time consuming [37,38].
The “top-down” method takes a broader perspective based on the highly aggregated information of a given shipping activity, relying on generalized factors such as fuel use statistics and engine types across ships to estimate emissions, as there is no information regarding specific circumstance or specific shipping activities. The advantage of the top-down approach, since it requires a small quantity of data, is that it is less expensive and less time consuming than the bottom-up approach [37,38].
The present study uses a hybrid method, which is a combination between the bottom-up and the top-down approaches, known also as the Tier III ship movement method. This hybrid method is generally recommended when detailed data on ship operations and technical characteristics (e.g., size, engine technology, installed power, fuel consumption, and operating hours in different activities) are available, as considered in the presented case study. This enables the estimation of emissions during open-sea navigation, port approach maneuvers, and docking [39]. Compared to Tier I or Tier II, this methodology ensures higher resolution and reliability in emission assessments and is aligned with international standards.
For commercial vessels, Tier III methodology calculates the emissions based on the engine’s installed capacity and fuel consumption. Emissions for a trip are determined by summing the emissions from each segment of the journey [39].
Based on the data of fuel consumption in the three different navigation phases, cruise, dock, and maneuvering, the emissions can be calculated using specific fuel emission factors for each phase. In this sense, the pollutant emission calculation can be performed based on Equation (2) [39,40].
where represents the emissions during a complete journey (tons); FC is the fuel consumption (tons); EF is the emission factor (kg/ton); is the pollutant type (NOx, SOx, CO2, PM); is the fuel type (HFO, MDO/MGO); is the engine type (low, medium, and high speed); and is the different phases of the journey (cruise, dock, and maneuvering).
For each level and emission calculation algorithm, it is necessary to use specific emission factors. While Tier I and II methodologies use tabulated emission factors, the more complex methodology, Tier III, adopted in the present study, requires the calculation of specific emission factors based on the present case load-dependent emission factors. It is important to note that variations in emission factor calculations can lead to discrepancies of up to 30% in total emissions [16].
The pollutant emissions () were determined using two primary methods. The energy-based approach estimates emissions based on engine power output (), applying an energy-based emission factor () in grams per kilowatt-hour (g/kWh) [16].
In the present study was obtained from the data collected on the ship.
This method is used for pollutants such as NOx, CH4, CO, N2O, PM, and Non-Methane Volatile Organic Compounds (NMVOCs).
The fuel-based approach calculates emissions by multiplying hourly fuel consumption () by a fuel-based emission factor (), expressed in grams of air pollutant per gram of fuel (g/g); it is used for CO2 and SOx emissions.
where
The baseline specific fuel consumption for main engines, auxiliary engines, and boilers represents the minimum specific fuel consumption along the load curve, indicating the point of maximum fuel efficiency for the engine [41]. In Table 2, the baseline SFC values used in this study are depicted.

Table 2.
Specific fuel consumption [16].
The methodologies and formulas used in this study were initially introduced in the IMO Third Greenhouse Gas Study [42] and later refined in the Fourth IMO Greenhouse Gas Study [16]. This revision integrated findings from literature reviews, engine manufacturers, research institutions, academic studies, and classification societies, providing a more accurate and up-to-date framework for emission calculations.
2.1.1. Carbon Dioxide
Based on the IMO proposals in document MEPC.1/Circ.684, Table 3 represents CO2 emission factors for HFO and MDO.

Table 3.
Emission factors for HFO and MDO [43].
The carbon dioxide emissions from the case study cruise vessel were calculated using Equations (4) and (5), which determine the vessel’s total fuel consumption and the corresponding CO2 emissions.
2.1.2. Nitrogen Oxides
Nitrogen oxide emissions result from the high combustion temperatures in the engines, which cause the oxidation of nitrogen present in the intake air as well as nitrogen particles in the fuel. The NOx emission factor depends on the engine rate speed and the ship’s Tier (i.e., the year when the engine was manufactured). In the present study, NOx emission factors were based on the engine rotational speed, as referred to in Annex VI of IMO MARPOL Regulation 13. Table 4 presents the IMO regulatory limits for NOx emissions, which vary according to the engine’s rated speed.

Table 4.
IMO Tier limits for NOx emissions as a function of engine rated speed [44].
is the engine rate speed, which for the Wärtsilä Sulzer ZA40S diesel generators installed in the ship assessed, the alternators have a frequency of 60 Hz and 12 poles, which correspond to an engine rate speed of 514 rpm. Applying the Tier I coefficient for this engine category, the NOx emission limit for the case study vessel engines is calculated to be 12.91 gNOx/kWh.
2.1.3. Sulphur Oxides
Sulphur oxide emissions depend on the sulphur content of the fuel used. In this sense, the SOx emission factor (g SOx/g of fuel) is calculated as follows [16]:
where it is considered that 97.753% of the fuel sulphur content is converted to SOx (with the remainder converted to sulphate/sulfite aerosol and classified as part of the particulate matter). The number “2” reflects the ratio of the molecular weight of SO2 to sulphur, since the majority of SOx is released as SO2. The term represents the sulphur content of the fuel assessed. In the present study the sulphur content of HFO is considered to be 3.5% and for MDO, it is 0.1% [45].
2.1.4. Particulate Matter
The emission factors for particulate matter are influenced by the sulphur content of the fuel. Table 5 presents the equations used to calculate the PM for engines running on heavy fuel oil or marine diesel oil [16].

Table 5.
Particulate matter emission equations [16].
The number 7 in the equations represents the molecular weight ratio between the sulphate of the particles and sulphur, while the value 0.02247 reflects the proportion of sulphur in the fuel that is converted to PM sulphate. Again, the term represents the sulphur content of the fuel assessed.
In this study, the Tier III methodology was applied in the following stages:
- Onboard data collection: Engine particulars, power output, load profiles, NOx Tier classification, and fuel consumption for each phase (cruise, maneuvering, docking) were obtained from ship logs and manufacturer datasheets.
- Determination of SFC of engines based on IMO baseline values corresponding to the engines type and rating.
- Calculation of fuel and energy-based emission factors and pollutant emissions:
- Total trip emissions were calculated by summing the three phase emissions: cruise, maneuvering, and docking.
2.2. Economic Assessment
While environmental considerations may justify the investment in the long term, shipowners, operating within the constraints of commercial viability, prioritize profitability and financial sustainability. Consequently, for a greener solution to be adopted within the sector, it must also demonstrate economic feasibility. In the case of scrubbers, their installation involves a substantial retrofit, which requires modifications such as cutting funnel bulkheads and integrating the scrubber units into the exhaust systems of each engine. This results in a significant initial capital investment. In addition to capital expenditure, there are also ongoing operational expenditures related to system operation and maintenance. Table 6 summarizes the estimated CAPEX and OPEX associated with scrubber installation in US dollars (USD) (data provided by the shipowner).

Table 6.
Capital and operational expenditures of scrubbers.
When deciding whether to switch from HFO to MDO to comply with IMO SOx regulations or to install scrubbers, shipowners must carefully evaluate the primary cost driver: fuel expenditure. Although the CAPEX for scrubber installation approaches USD 2 million, and the associated annual OPEX for scrubber operation and maintenance exceeds USD 108,000, these costs represent only a small fraction of the vessel’s yearly fuel expenses. Based on the fuel consumption data, and assuming average fuel prices of USD 547 per ton for HFO and USD 885 per ton for MDO, the annual fuel costs are estimated at USD 18,394,500.68 for HFO and USD 26,612,116.38 for MDO [46]. Consequently, the annual differential in fuel costs between operating on MDO versus HFO is USD 8,217,615.69.
Both HFO and MDO are fossil fuels and thus correlated to some extent, but their prices have historically exhibited significant volatility and variable spreads, especially during periods of uncertainty or the introduction of stringent regulations. A notable example is the implementation of the IMO 2020 regulation, which increased the demand for MDO and led to a relative drop in the demand for HFO. Given the substantial impact of fuel prices on the total cost of each compliance strategy and considering that this is a long-term decision intended to span the remaining service life of the vessel, projected at ten years, the decision must be carefully weighed and supported by reliable data.
In this case, the economic assessment is based on the Net Present Value (NPV), to evaluate the long-term economic feasibility, and the Return on Investment (ROI), to measure the profitability of installing scrubbers, as compared to the alternative compliance strategy of switching from HFO to MDO. Additionally, the Internal Rate of Return (IRR) and the Discounted Payback Period (DPP) were calculated to provide a more comprehensive understanding of the investment’s performance.
NPV is calculated using Equation (7):
where represents the net cash inflow or outflow at time, is the discount rate, set at 10% in this analysis, and is the time period, which in this case is set to 10 years, corresponding to the expected remaining operational life of the vessel.
The ROI is obtained using Equation (8):
where FVI represents the Final Value of the Investment, obtained by adding the initial CAPEX of the scrubber system to the accumulated net cash flows over the evaluation period, while IVI denotes the Initial Value of the Investment, corresponding to the upfront capital expenditure required for the installation of the scrubbers. The difference between FVI and IVI yields the net cash flows generated by the investment. The denominator of the ROI expression is the Initial Value of the Investment, which represents the total capital initially committed.
The IRR is obtained by setting NPV equal to zero, while DPP is calculated using the previously mentioned discount rate of 10% over a 10-year evaluation period.
While the calculation of NPV and the other aforementioned key economic indicators at a specific point in time, such as when data was collected onboard the case study vessel, may be sufficient to support preliminary decision-making, the significant influence of fuel prices, coupled with the high volatility of fossil fuel markets, requires a more comprehensive assessment. This is especially relevant when considering a long-term investment such as scrubber installation, expected to last for a ten-year period.
To address this, the present study conducted a deterministic grid sweep sensitivity analysis, which involved systematically evaluating combinations of HFO and MDO prices within the historical ranges shown in Table 7 [46]. This analysis aimed to assess the economic viability of scrubber installation under different fuel price scenarios by calculating the Net Present Value (NPV) for each price pair. For the scrubber installation to be considered economically viable, the NPV must remain positive. Otherwise, from both economic and environmental perspectives, switching to cleaner MDO fuel is preferred. This method allows for a robust understanding of how fluctuations in fuel prices impact investment decisions over the scrubber’s expected lifetime.

Table 7.
Price range of HFO and MGO in period of 2021–2025 (extracted from [46]).
To assess the long-term economic performance of installing scrubbers versus switching to MDO, and given the potential variability in fuel prices over the vessel’s remaining ten-year operational life and consequently in the price spread between HFO and MDO fuels, a risk-based economic assessment was conducted using a Monte Carlo simulation framework. This approach allows for the evaluation of investment feasibility across a wide range of plausible future fuel price scenarios. Fuel price uncertainty was modelled using 100,000 Monte Carlo iterations, based on historical price ranges of HFO and MDO presented in Table 7. To account for the interdependence between HFO and MDO prices under different market conditions, it was essential to incorporate statistical correlation between fuel types. For this purpose, a Gaussian copula, a statistical tool that models the joint behaviour of correlated variables by separately capturing their individual marginal distributions and their dependence structure (correlation), was employed to accurately represent the joint price dynamics of HFO and MDO. This approach enables the preservation of each fuel’s distinct historical price distribution while realistically simulating their correlated movements under varying market conditions [47]. This method enables the generation of correlated random samples while maintaining the marginal distributions of HFO and MDO prices. This process involved the following steps:
- Sampling from a bivariate standard normal distribution with a specified Pearson correlation coefficient ().
- Transforming each marginal using the standard normal cumulative distribution function (CDF) to obtain uniform variables.
- Mapping the uniform variables to the historical price ranges of HFO and MDO using the inverse CDF of each fuel’s empirical distribution.
The CDF plays a relevant role in the Gaussian copula framework by enabling the transformation of each variable’s historical price data into uniform variables on the interval (0,1). For a given random variable , the CDF is defined as follows:
This represents the probability that takes a value less than or equal to . This transformation facilitates the modelling of dependence separately from the marginal distributions. After introducing the desired correlation structure in the transformed space, the inverse CDF is applied to map the correlated uniform variables back to their original price distributions, preserving their historical characteristics while reflecting their joint behaviour.
According to the analysis of fuel prices for the 2021–2025 period, the Pearson correlation coefficient between HFO and MDO prices was found to be approximately ( with a p-value < 0.01. This result suggests a statistically significant, yet weak, negative correlation between the two fuels, indicating that when the price of one tends to increase, the other tends to decrease slightly. Despite its low magnitude, this inverse relationship may reflect underlying regulatory or market-driven dynamics affecting fuel demand. In addition to this observed correlation, two alternative scenarios were also modelled to capture more extreme but plausible market behaviours:
- A negative correlation (: This negative correlation reflects regulatory situations, such as IMO 2020 sulphur restrictions, where the demand shifts from HFO to MDO. When one price goes up, the other tends to go down, increasing their price spread.
- A moderately positive correlation (: This positive correlation represents normal market conditions where fuel prices generally move together because they share common cost drivers like crude oil prices.
For each iteration, the correlated pair of HFO and MDO prices was used to compute the annual fuel cost differential between the two compliance options. This differential, adjusted for the fixed annual OPEX and amortized CAPEX of the scrubber system, was treated as a constant net cash flow over the vessel’s remaining 10-year operational life. The resulting cash flows were discounted at a rate of 10% and integrated into the Net Present Value (NPV) model, as defined in Equation (8). This probabilistic framework provides a robust basis for investment appraisal by incorporating both fuel price volatility and the statistical dependence between HFO and MDO prices under varying regulatory and market conditions [48,49].
To provide a clearer overview of the entire process, Figure 1 presents a flowchart outlining the methodology followed in this study.
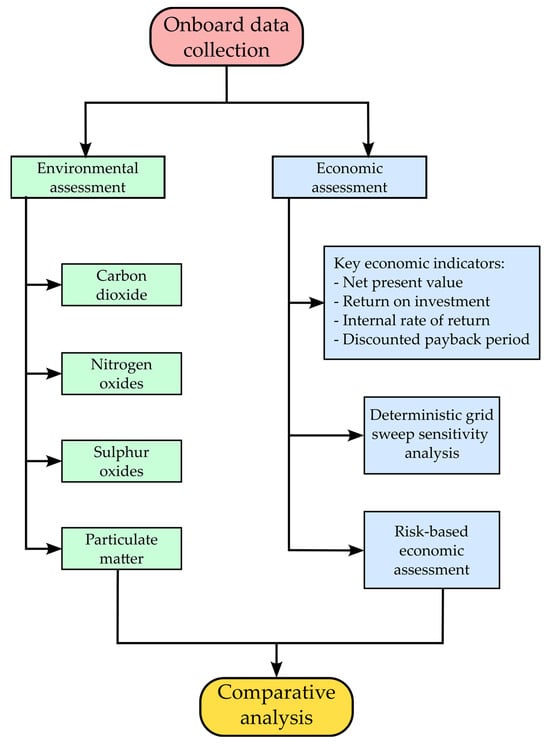
Figure 1.
A flowchart of the methodological approach adopted in this study.
3. Results and Discussion
The results, in line with the methodology, are divided into two parts: an environmental and an economic assessment. Together, these analyses provide a comprehensive basis for decision-making, enabling shipowners to identify the most suitable emission reduction strategy from both environmental and economic standpoints, while ensuring compliance with IMO regulations on air pollution.
3.1. Environmental Assessment
To conduct this analysis, energy consumption data for a one-month period of the studied vessel’s voyage was gathered. It was verified that the ship typically operates on routes between the United States and the eastern Caribbean countries. Using real-time voyage data collected during April 2024, it was verified that the vessel spent 71% of its time in transit, 24% docked or at anchor, and 5% performing port maneuvers. Fuel consumption calculation was based on the respective baseline specific fuel consumption (see Table 2).
Since no consumption data was available before the installation of the exhaust gas cleaning systems, there was a need to estimate this consumption. This fuel consumption was performed based on the specific characteristics of the vessel, which has diesel–electric propulsion, a given electrical energy need, and a specific fuel oil consumption.
Beyond the installation of scrubbers, the vessel is also equipped with fuel improvement devices (FIDs). These systems are designed to reduce the formation of nitrogen oxides and particulate matter by promoting fuel emulsification with small amounts of water or additives. The emulsification process leads to lower peak combustion temperatures, thereby mitigating thermal NOx formation. Additionally, the built-in homogenizer enhances fuel atomization and uniformity, reducing sludge accumulation and promoting more efficient and complete combustion. As a result, soot and PM emissions are also reduced [50,51].
Table 8 presents the energy consumption associated with the three operational scenarios: (i) the use of HFO without scrubbers or FID, (ii) the use of HFO with scrubbers and FID, and (iii) the use of MDO.

Table 8.
Vessel energy consumption by fuel type.
The results indicate that the installation of scrubbers leads to an increase in energy consumption of approximately 3.52% from the baseline, primarily due to the additional power demand of the pumps and treatment systems. Conversely, switching from using HFO and scrubbers to MDO results in an estimated 7.31% reduction in energy consumption, owing to the superior combustion characteristics of distillate fuels. Taken together, these effects account for a total difference of 10.83% in energy efficiency between the HFO–scrubber configuration and the direct use of MDO. Although slightly lower, these figures are consistent with the findings of Karatuğ et al., who reported a fuel consumption increase ranging from 11% to 17% when scrubbers are employed [28].
Based on the methodology for emission calculation referred to in the previous section, and on the energy consumption estimations, pollutant emissions were calculated for the three considered scenarios. The results are depicted on Table 9.

Table 9.
Emissions by fuel (ton/month).
The results reveal that the installation of scrubbers in combination with FID has led to a substantial reduction in SOx emissions, decreasing from 185.01 to 5.75 ton/month, equivalent to an approximate 96.89% reduction. In terms of PM emissions, a moderate decline was observed, from 22.23 to 20.73 ton/month, representing a reduction of about 6.71%. Similar emission abatement efficiencies were reported by Yang et al., who documented a 97% reduction in SOx and a 10% decrease in PM2.5 concentrations following scrubber implementation [32].
However, the calculations performed show that the installation of scrubbers has a negative impact on carbon dioxide and nitrogen oxide emissions. The emission of CO2 increased from 8419.3 ton/month to 8726.5 ton/month, which represents an increase of 3.52%, similar to previous studies [32]. Regarding NOx emissions, the increase was from 170.30 to 176.52 ton/month, representing a 3.65% increase. These adverse outcomes are consistent with the findings of Yang et al., who reported a 4.35% increase in NOx emissions [32]. This rise is directly associated with the higher consumption of HFO, as vessels equipped with scrubbers are not obligated to switch to MDO when approaching coastal areas. Consequently, these ships tend to operate on HFO more frequently, contributing to elevated NOx emissions.
It can be concluded that scrubbers are suitable to meet sulphur emission regulations but not to fulfil the IMO’s decarbonization strategy due to the increase in fuel consumption. In this sense, and considering the substantial investments already made by shipowners with the installation of scrubbers, there is a need to integrate additional technologies to reduce greenhouse gas emissions.
The results from the scenario of using MDO instead of HFO show positive impacts in CO2, SOx, and PM emissions. When comparing both scenarios, the use of MDO as a substitute for HFO results in a reduction of SOx emissions of more than 99% and of about 89% for PM. When comparing the MDO scenario with the HFO + scrubbers + FID scenario, it is interesting to verify that the use of MDO has lower emissions for both SOx (more than 91% of reduction) and PM (about 88%).
Regarding the impact of the consumption of MDO on CO2 emissions, it can be verified that it is also positive when compared with the other two scenarios assessed. For the HFO scenario, a reduction of 5% is reached and when compared with the scrubber scenario, the reduction is about 8%.
Regarding NOx, the International Maritime Organization’s MARPOL Annex VI establishes global NOx emission limits (Tiers I and II), while the more stringent Tier III standards only apply within designated NOx Emission Control Areas (NECAs). In parallel, SOx regulations have also evolved, with stricter fuel sulphur limits of 0.1% in SOx Emission Control Areas (SECAs), compared to the global cap of 0.5% [52]. While exhaust gas cleaning systems, such as the scrubbers analyzed in this study, are effective in reducing SOx emissions, they do not mitigate NOx. Therefore, additional NOx reduction strategies are required to ensure compliance, particularly in Tier III Emission Control Areas. These include primary measures such as Exhaust Gas Recirculation (EGR), water-based techniques like Direct Water Injection (DWI) and fuel–water emulsions (FWE), as well as post-combustion technologies such as the Selective Catalytic Reduction (SCR). Among these, SCR is the most mature and widely implemented option, capable of achieving up to 90% NOx reduction under appropriate conditions and enabling compliance with IMO Tier III standards [24].
However, care must be taken when integrating multiple exhaust gas treatment technologies, such as SCR units, scrubbers, and exhaust gas boilers, into the engine funnel. The combined presence of these systems can significantly increase backpressure, potentially forcing the engine to work harder to be able to expel the exhaust gases [25]. This may lead to higher fuel consumption, offsetting some of the environmental gains and becoming counterproductive from an energy efficiency perspective. In the case of NOx, implementing DWI or FWE techniques may be a viable solution to improve its reduction while managing flow-related constraints [53]. The EGR option, on the other hand, is less favourable for marine applications due to maintenance challenges caused by fouling from exhaust gases [54]. With regard to SOx control, one effective alternative to scrubber installation is the use of sulphur-free fuels, such as MDO, which inherently comply with SECA fuel sulphur requirements and avoid the space and operational complexity of additional equipment.
3.2. Economic Assessment
Following the environmental assessment, where it was demonstrated that using MDO leads to significantly lower particulate matter emissions compared to the continued use of HFO with scrubbers, given that scrubbers are largely ineffective in removing PM, the focus of the economic analysis shifts toward evaluating the viability of adopting MDO as the main fuel. The financial indicators presented in this section are therefore interpreted with the premise that MDO is the environmentally preferred option, and economic success is understood as achieving comparable or superior financial performance without installing scrubbers.
Initially, a set of standalone economic indicators, including Net Present Value, Return on Investment, Internal Rate of Return, and Discounted Payback Period, were calculated to assess the project’s financial feasibility, using the prevailing prices of HFO and MDO at the time the data were collected. These economic indicators are depicted in Table 10.

Table 10.
Economic indicators related to installation of scrubbers and use of HFO.
As a result of the IMO 2020 regulation on SOx emissions, the global merchant fleet is now required to either switch to low-sulphur fuels or install exhaust gas cleaning systems to continue operating on cheaper residual fuels [55]. For the case study vessel, the installation of the scrubber system involved a CAPEX of just under USD 1.9 million. Considering the annual fuel cost differential between operating on MDO and HFO, calculated at USD 8,217,615.69 based on prevailing market prices at the time of data collection, both the initial CAPEX and the associated annual OPEX of the scrubber system are relatively minor compared to the potential cost savings. Table 10 summarizes the economic performance of scrubber installation over a projected ten-year operational period. The NPV is markedly positive, primarily due to the significant annual savings achieved by continuing to use HFO in combination with scrubbers rather than switching to MDO. The ROI over ten years reaches 4239%, while the IRR is calculated at 434%, both of which confirm the high profitability of the investment. Additionally, the DPP is just 3.1 months, underscoring the rapid recovery of the initial investment under the current assumptions.
It is important to highlight that the profitability of scrubber installation is highly sensitive to the price differential between HFO and MDO, which has historically exhibited significant volatility due to their independent market dynamics [56]. Consequently, relying on fixed price assumptions would be insufficient to capture the range of possible economic outcomes over the vessel’s projected operational lifespan. To address this, a sensitivity analysis was carried out using a deterministic grid sweep approach. This analysis aims to evaluate the robustness of the investment decision and determine under which market conditions the use of MDO might become more economically viable than continuing to operate on HFO with scrubbers. The results of this analysis are presented in Figure 2.
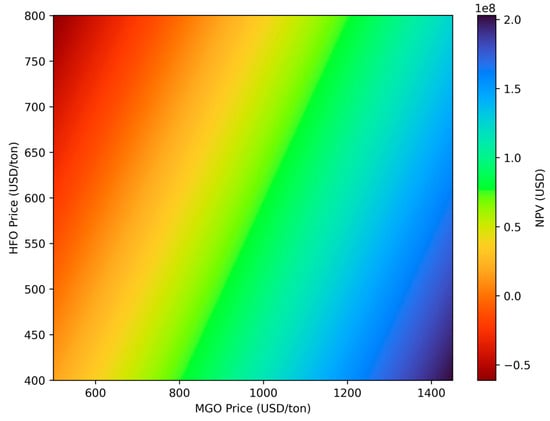
Figure 2.
Grid sweep sensitivity analysis of HFO and MGO prices on NPV of scrubber installation.
The deterministic grid sweep analysis explored a range of HFO and MDO price combinations based on the ranges presented in Table 7. As shown in Figure 2, scrubber installation remains economically viable across the majority of scenarios. The only circumstances under which MDO emerges as the more favourable option occur when the price differential between MDO and HFO narrows substantially, or in the unlikely event that HFO becomes more expensive than MDO. Although MDO offers a marginal energy efficiency advantage, due to its slightly higher lower heating value, as indicated in Table 8, this is generally insufficient to counterbalance the substantial cost savings enabled by using HFO in combination with scrubbers. The capital and operating costs associated with the scrubber system, while not negligible, are relatively minor compared to the potential fuel cost savings over the vessel’s remaining lifetime. Overall, the grid sweep analysis underscores the robustness of the investment decision in favour of scrubber installation across a broad spectrum of plausible market conditions, while also delineating the narrow set of fuel price scenarios under which switching to MDO may be justified from a financial standpoint. Zhu et al. similarly observed that fuel switching to MDO was economically feasible only when the HFO–MDO price differential surpassed USD 56 per ton [55].
Following the recommendation of Sheng et al. to exercise caution when interpreting the influence of fuel price differentials on scrubber adoption trends, a probabilistic analysis was conducted to complement the deterministic assessment of the HFO–MDO price spread [56]. This analysis employed the Monte Carlo method to account for price volatility and uncertainty. This approach aims to evaluate the likelihood of economic viability when choosing to operate with MDO instead of installing scrubbers and continuing to use HFO, accounting for market uncertainty. The correlation derived from 2021–2025 fuel price data was first analyzed, followed by the exploration of two additional correlation scenarios to capture alternative and more extreme market behaviours. Figure 3 presents the results based on the correlation obtained from actual fuel price data. Figure 4 illustrates the scenario, assuming a moderately positive correlation between HFO and MDO prices, while Figure 5 displays the outcome of the third scenario, which considers a negative correlation between the two fuel types.
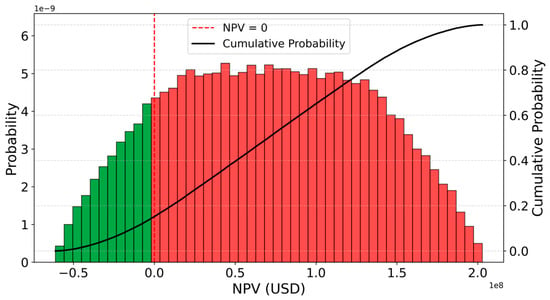
Figure 3.
Results of Monte Carlo simulation for NPV of scrubber installation .
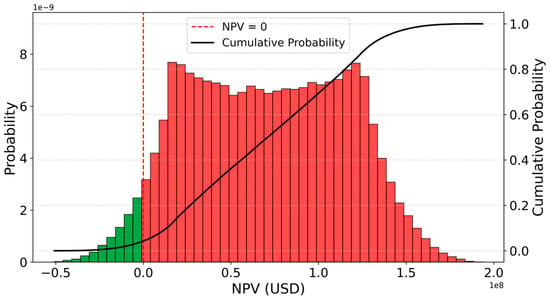
Figure 4.
Results of Monte Carlo simulation for NPV of scrubber installation .
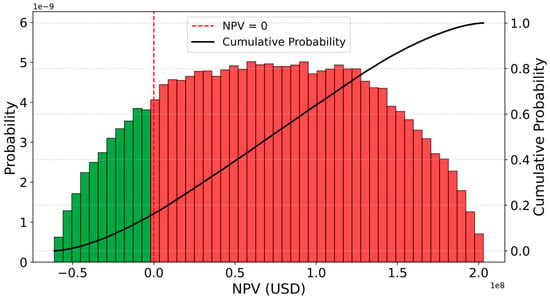
Figure 5.
Results of Monte Carlo simulation for NPV of scrubber installation .
The histograms display the probability density of NPV outcomes across the simulated range. The height of each bar represents the likelihood that the NPV falls within the corresponding interval. Taller bars indicate a higher probability density, meaning that a larger number of simulations yielded NPVs in that range. In the first scenario, Figure 3 , bars corresponding to negative NPVs (displayed in green and associated with the strategy of switching to MDO) reach a maximum probability density of just over 4. In contrast, positive NPVs (shown in red and corresponding to the installation of scrubbers and continued use of HFO) peak near 5. Under these conditions, the probability of obtaining a positive NPV, indicating that scrubber installation is economically advantageous, is 84.87%. Conversely, the likelihood of achieving economic success by switching to MDO is only 4.3%. The average NPV is approximately USD 70,962,358, further supporting the financial viability of the scrubber-based compliance strategy under the assumed market conditions.
Figure 4 illustrates the distribution of NPV outcomes obtained from the Monte Carlo simulation under the assumption of a moderate positive correlation between HFO and MDO prices, aiming to reflect the fact that both fuels are derived from crude oil and share similar refining and distribution pathways. The red-shaded area denotes scenarios where the installation of scrubbers and continued use of HFO yields a positive NPV, while the green area indicates conditions under which switching to the less pollutant MDO becomes economically advantageous. In this second scenario, the green bars are relatively low, peaking at around 2.2, while the red bars exceed 7.5, indicating a much stronger concentration of positive NPV outcomes. Under this scenario, the probability of obtaining a positive NPV, indicating that scrubber installation is more economically favourable, is 95.7%. This leaves only a 4.3% probability of economic success when switching to MDO. The average NPV is USD 70,683,731, further substantiating the financial robustness of the scrubber-based compliance strategy within the defined market conditions.
Figure 5 presents the distribution of NPV results under a negative correlation between HFO and MDO prices, as modelled through Monte Carlo simulation. This scenario reflects a market condition in which the prices of the two fuels are not closely aligned and may diverge, for instance, if regulatory shifts or fuel switching trends create independent price dynamics. In the figure, the green-shaded area highlights scenarios in which switching to MDO yields a positive economic outcome, with a probability density peaking just below 4. In contrast, the red-shaded area represents cases where continuing to use HFO with a scrubber proves more financially advantageous, with the probability density exceeding 5. Under this correlation, the probability of achieving a positive NPV from scrubber installation is 83.65%, with an average NPV of USD 70,820,100. Conversely, the probability of an economically favourable outcome when switching to MDO is 16.35%. Although this represents a reduction in the certainty of scrubber profitability compared to the positively correlated case, the installation of scrubbers remains the preferred option in the vast majority of market scenarios.
The cumulative probability curves in Figure 4 and Figure 5 provide additional insights into the risk profile associated with choosing MDO over the installation of scrubbers. These curves represent the probability that the NPV will fall below a given threshold, thereby offering a clear view of the economic risk distribution under each correlation scenario. In the positively correlated case, Figure 4, the cumulative distribution increases more gradually, with a relatively low probability of negative NPV outcomes. This reflects a high confidence level in achieving positive returns from scrubber installation. In contrast, the negatively correlated scenario, Figure 5, exhibits a noticeably steeper cumulative curve around the NPV = 0 threshold. This inflection reflects an increased likelihood of borderline or negative economic returns, implying that the relative advantage of scrubbers weakens under such market dynamics. The results align with previous studies, indicating that while scrubbers generally remain the more profitable option, the probability of favourable outcomes when switching to MDO rises in scenarios characterized by negatively correlated fuel prices [57].
The long-term abatement of air pollution in maritime transport will require a transition to alternative fuels. LNG remains a widely used option due to its technological maturity and reduced emissions, although concerns about methane slip persist. Renewable methanol is a promising alternative but is currently limited by availability and the need for engine modifications. Hydrogen and ammonia offer near-zero-emission potential, yet they face significant challenges related to storage, safety, and high production costs. Nuclear propulsion has also attracted renewed interest, but regulatory, safety, and societal concerns remain substantial. A combination of these fuels, supported by robust regulatory frameworks and technological advancements, is likely to define the future marine fuel mix and reduce the need for exhaust gas treatment systems.
4. Conclusions
The world is facing record-high temperatures and increasingly extreme weather events. Stakeholders, from all sectors, believe that these phenomena are related to the increase in greenhouse gas emissions. As international maritime transport accounts for 3% of global CO2 emissions, the International Maritime Organization has set ambitious targets to reduce air pollution by at least 70%, striving for 80%, by 2040 and achieve net-zero GHG emissions by or around 2050. To meet these goals, the industry will need to make a transition to low-carbon and carbon-neutral fuels and to improve energy efficiency. New and ordered vessels are, already, being built based on these new IMO targets. The main problem is related with the fleet already in service, where shipowners need to make difficult decisions, namely, renew the fleet, retrofit the existing ships, switch to alternative fuels, or pay penalties such as EU ETS allowances or IMO Remedial Units.
Addressing the current gap in the literature concerning the environmental and economic comparison of low-sulphur MDO versus open-loop scrubbers, this study evaluates three operational scenarios applied to a 1998-built cruise ship: (i) HFO as baseline; (ii) HFO combined with an open-loop scrubber equipped with FID; and (iii) MDO use.
The environmental assessment results reveal that scrubber installation reduces SOx emissions by approximately 97% (from 185.01 to 5.75 tons/month) and particulate matter by around 7%, from 22.23 to 20.72 tons/month. However, scrubbers increase CO2 and NOx emissions by approximately 3.52% and 3.65%, respectively, due to higher fuel consumption. In contrast, MDO usage lowers SOx and PM emissions more effectively than scrubbers and reduces CO2 emissions by about 7.3% compared to baseline, with no significant change in NOx emissions. The findings from this case study corroborate previous works confirming the trade-offs associated with scrubber technology.
As previously noted, environmental assessments alone are insufficient for shipowners to make informed decisions regarding the adoption of emission reduction technologies. Economic considerations are also essential to ensure business profitability. In this context, the present study includes an economic assessment comparing the financial performance of installing exhaust gas cleaning systems with switching to marine diesel oil. Based on the prevailing prices of HFO and MDO at the time of data collection, key economic indicators were calculated: Net Present Value, Return on Investment, Internal Rate of Return, and Discounted Payback Period.
The results indicate that, under the considered price conditions, the installation of scrubbers represents a more economically favourable option than switching to MDO. However, given the volatility of fuel prices influenced by market dynamics and regulatory factors, a probabilistic Monte Carlo analysis and a deterministic grid sweep were conducted. These analyses considered the actual correlation derived from market data spanning 2021 to 2025, as well as hypothetical scenarios involving both positive and negative correlations between HFO and MDO prices. The results indicate that fuel costs dominate economic feasibility, and the expected HFO–MDO price spread disfavors switching to MDO under current market conditions.
This integrated decision-making framework demonstrates that while switching to MDO offers superior environmental performance, scrubber installation currently represents a more viable economic pathway for shipowners. Nonetheless, the increasing regulatory restrictions on open-loop scrubbers, particularly the forthcoming bans on discharge, limit their long-term applicability. Hence, future regulatory policies should support and incentivize a global transition toward low-emission or carbon-neutral fuels.
Future research should enhance decision-support tools by incorporating real-world operational data and extending comparative analyses to include a broader range of technical options, such as alternative fuels and energy efficiency technologies. This will better equip shipowners with comprehensive, context-specific guidance for sustainable fleet management.
Author Contributions
Conceptualization, L.B.; methodology, S.P. and L.A.D.-S.; software, L.A.D.-S.; formal analysis, S.P.; resources, L.B.; writing—original draft preparation, S.P. and L.A.D.-S.; writing—review and editing, L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the author.
Acknowledgments
The authors gratefully acknowledge the financial support provided by the University of Oviedo and Banco Santander. The research stay of L.A. Díaz-Secades at the Escola Superior Náutica Infante D. Henrique (ENIDH) in Portugal was funded by Banco Santander through the “Ayudas Económicas de Movilidad de Excelencia para Docentes e Investigadores de la Universidad de Oviedo, 2025” program. The article was based on the MSc on Marine Engineering thesis of Juliana Almeida at ENIDH named “Steering toward a sustainable future: a comparative technical-economic review of maritime shipowner options” (in Portuguese).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CAPEX | Capital Expenditure |
| CDF | Cumulative Distribution Function |
| DPP | Discounted Payback Period |
| DWI | Direct Water Injection |
| ECA | Emission Control Area |
| EGR | Exhaust Gas Recirculation |
| EU ETS | European Union Emissions Trading System |
| EEA | European Environment Agency |
| FID | Fuel Improvement Devices |
| FVI | Final Value of the Investment |
| FWE | Fuel–Water Emulsions |
| GWP | Greenhouse Warming Potential |
| HFO | Heavy Fuel Oil |
| IMO | International Maritime Organization |
| IRR | Internal Rate of Return |
| IVI | Initial Value of Investment |
| MDO | Marine Diesel Oil |
| NECA | NOx Emission Control Areas |
| NMVOC | Non-Methane Volatile Organic Compounds |
| NPV | Net Present Value |
| OPEX | Operational Expenditure |
| PM | Particulate Matter |
| ROI | Return on Investment |
| SCR | Selective Catalytic Reduction |
| SECA | Sulphur Emission Control Areas |
| SFC | Specific Fuel Consumption |
| UNFCC | United Nations Framework Convention on Climate Change |
References
- Global Energy Review 2025; International Energy Agency (IEA): Paris, France, 2025.
- World Energy Outlook 2024; International Energy Agency (IEA): Paris, France, 2024.
- IPCC Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Khalaf, E.M.; Mohammadi, M.J.; Sulistiyani, S.; Ramírez-Coronel, A.A.; Kiani, F.; Jalil, A.T.; Almulla, A.F.; Asban, P.; Farhadi, M.; Derikondi, M. Effects of Sulfur Dioxide Inhalation on Human Health: A Review. Rev. Environ. Health 2024, 39, 331–337. [Google Scholar] [CrossRef]
- Supran, G.; Rahmstorf, S.; Oreskes, N. Assessing ExxonMobil’s Global Warming Projections. Science 2023, 379. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.W.; Peters, G.P.; Gasser, T.; Andrew, R.M.; Schwingshackl, C.; Gütschow, J.; Houghton, R.A.; Friedlingstein, P.; Pongratz, J.; Le Quéré, C. National Contributions to Climate Change Due to Historical Emissions of Carbon Dioxide, Methane, and Nitrous Oxide since 1850. Sci. Data 2023, 10, 155. [Google Scholar] [CrossRef]
- Comer, B.; Beecken, J.; Vermeulen, R.; Sturrup, E.; Paschinger, P.; Osipova, L.; Gore, K.; Delahaye, A.; Verhagen, V.; Knudsen, B.; et al. Fugitive and Unburned Methane Emissions from Ships (FUMES): Characterizing Methane Emissions from LNG-Fueled Ships Using Drones, Helicopters, and on-Board Measurements; ICCT: Bellagio, Italy, 2024. [Google Scholar]
- Álvarez, A.N.F.; Díaz-Secades, L.A. Enhancing Energy Efficiency in High-Speed Craft: A Trigeneration Energy Recovery System for LNG-Fuelled Vessels in the Mediterranean Sea. Polish Marit. Res. 2025, 32, 94–105. [Google Scholar] [CrossRef]
- Tian, H.; Xu, R.; Canadell, J.G.; Thompson, R.L.; Winiwarter, W.; Suntharalingam, P.; Davidson, E.A.; Ciais, P.; Jackson, R.B.; Janssens-Maenhout, G.; et al. A Comprehensive Quantification of Global Nitrous Oxide Sources and Sinks. Nature 2020, 586, 248–256. [Google Scholar] [CrossRef]
- Eastham, S.D.; Chossière, G.P.; Speth, R.L.; Jacob, D.J.; Barrett, S.R.H. Global Impacts of Aviation on Air Quality Evaluated at High Resolution. Atmos. Chem. Phys. 2024, 24, 2687–2703. [Google Scholar] [CrossRef]
- Liu, Z.; Rieder, H.E.; Schmidt, C.; Mayer, M.; Guo, Y.; Winiwarter, W.; Zhang, L. Optimal Reactive Nitrogen Control Pathways Identified for Cost-Effective PM2.5 Mitigation in Europe. Nat. Commun. 2023, 14, 4246. [Google Scholar] [CrossRef]
- Clappier, A.; Thunis, P.; Beekmann, M.; Putaud, J.P.; de Meij, A. Impact of SOx, NOx and NH3 Emission Reductions on PM2.5 Concentrations across Europe: Hints for Future Measure Development. Environ. Int. 2021, 156, 106699. [Google Scholar] [CrossRef]
- Khaniabadi, Y.O.; Polosa, R.; Chuturkova, R.Z.; Daryanoosh, M.; Goudarzi, G.; Borgini, A.; Tittarelli, A.; Basiri, H.; Armin, H.; Nourmoradi, H.; et al. Human Health Risk Assessment Due to Ambient PM10 and SO2 by an Air Quality Modeling Technique. Process Saf. Environ. Prot. 2017, 111, 346–354. [Google Scholar] [CrossRef]
- The Role of Shipbuilding in Maritime Decarbonisation; OECD Publishing: Paris, France, 2025; ISBN 9789264319424.
- Review of Maritime Transport 2024; UNCTAD: Geneva, Switzerland, 2024; ISBN 978-92-1-003206-3.
- International Maritime Organization (IMO). Fourth IMO Greenhouse Gas Study. Int. Marit. Organ. 2021, 951–952. [Google Scholar]
- Díaz-Secades, L.A. Enhancement of Maritime Sector Decarbonization through the Integration of Fishing Vessels into IMO Energy Efficiency Measures. J. Mar. Sci. Eng. 2024, 12, 663. [Google Scholar] [CrossRef]
- Marine IMO Marine Environment Protection Committee (MEPC 83): Summary Report; Lloyd’s Register: London, UK, 2025.
- Resolution MEPC. 176(58) Revised MARPOL Annex VI; International Maritime Organization (IMO): London, UK, 2010; Volume 9, pp. 76–99.
- Resolution MEPC. 328 (76) Amendments to the Annex of the Protocol of 1997–2021 Revised MARPOL Annex VI; International Maritime Organization (IMO): London, UK, 2021; Volume 148, pp. 148–162.
- Fuglestvedt, J.; Berntsen, T.; Eyring, V.; Isaksen, I.; Lee, D.S.; Sausen, R. Shipping Emissions: From Cooling to Warming of Climate—And Reducing Impacts on Health. Environ. Sci. Technol. 2009, 43, 9057–9062. [Google Scholar] [CrossRef]
- Yuan, T.; Song, H.; Oreopoulos, L.; Wood, R.; Bian, H.; Breen, K.; Chin, M.; Yu, H.; Barahona, D.; Meyer, K.; et al. Abrupt Reduction in Shipping Emission as an Inadvertent Geoengineering Termination Shock Produces Substantial Radiative Warming. Commun. Earth Environ. 2024, 5, 281. [Google Scholar] [CrossRef]
- Cret, L.; Baudry, M.; Lantz, F. How to Implement the 2023 IMO GHG Strategy? Insights on the Importance of Combining Policy Instruments and on the Role of Uncertainty. Mar. Policy 2024, 169, 106332. [Google Scholar] [CrossRef]
- Zannis, T.C.; Katsanis, J.S.; Christopoulos, G.P.; Yfantis, E.A.; Papagiannakis, R.G.; Pariotis, E.G.; Rakopoulos, D.C.; Rakopoulos, C.D.; Vallis, A.G. Marine Exhaust Gas Treatment Systems for Compliance with the IMO 2020 Global Sulfur Cap and Tier III NOx Limits: A Review. Energies 2022, 15, 3638. [Google Scholar] [CrossRef]
- Baldasso, E.; Mondejar, M.E.; Andreasen, J.G.; Rønnenfelt, K.A.T.; Nielsen, B.Ø.; Haglind, F. Design of Organic Rankine Cycle Power Systems for Maritime Applications Accounting for Engine Backpressure Effects. Appl. Therm. Eng. 2020, 178, 115527. [Google Scholar] [CrossRef]
- Lunde Hermansson, A.; Hassellöv, I.-M.; Grönholm, T.; Jalkanen, J.-P.; Fridell, E.; Parsmo, R.; Hassellöv, J.; Ytreberg, E. Strong Economic Incentives of Ship Scrubbers Promoting Pollution. Nat. Sustain. 2024, 7, 812–822. [Google Scholar] [CrossRef]
- Bendl, J.; Saraji-Bozorgzad, M.R.; Käfer, U.; Padoan, S.; Mudan, A.; Etzien, U.; Giocastro, B.; Schade, J.; Jeong, S.; Kuhn, E.; et al. How Do Different Marine Engine Fuels and Wet Scrubbing Affect Gaseous Air Pollutants and Ozone Formation Potential from Ship Emissions? Environ. Res. 2024, 260, 119609. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Arslanoğlu, Y.; Guedes Soares, C. Feasibility Analysis of the Effects of Scrubber Installation on Ships. J. Mar. Sci. Eng. 2022, 10, 1838. [Google Scholar] [CrossRef]
- Caiazzo, G.; Langella, G.; Miccio, F.; Scala, F. An Experimental Investigation on Seawater SO2 Scrubbing for Marine Application. Environ. Prog. Sustain. Energy 2013, 32, 1179–1186. [Google Scholar] [CrossRef]
- Fridell, E.; Salo, K. Measurements of Abatement of Particles and Exhaust Gases in a Marine Gas Scrubber. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 230, 154–162. [Google Scholar] [CrossRef]
- Winnes, H.; Fridell, E.; Moldanová, J. Effects of Marine Exhaust Gas Scrubbers on Gas and Particle Emissions. J. Mar. Sci. Eng. 2020, 8, 299. [Google Scholar] [CrossRef]
- Yang, J.; Tang, T.; Jiang, Y.; Karavalakis, G.; Durbin, T.D.; Wayne Miller, J.; Cocker, D.R.; Johnson, K.C. Controlling Emissions from an Ocean-Going Container Vessel with a Wet Scrubber System. Fuel 2021, 304, 121323. [Google Scholar] [CrossRef]
- Osipova, L.; Georgeff, E.; Comer, B. Global Scrubber Washwater Discharges Under IMO’s 2020 Fuel Sulfur Limit; ICCT: Washington, DC, USA, 2021. [Google Scholar]
- OSPAR Ministers Meet in Vigo to Take Concrete Measures to Enhance Protection of the North-East Atlantic Ocean. Available online: https://www.ospar.org/news/ministers-meet-in-vigo-to-take-concrete-measures-to-enhance-protection-of-the-north-east-atlantic-ocean (accessed on 22 July 2025).
- den Boer, E.; Hoen, M. Scrubbers—An Economic and Ecological Assessment; IVL Swedish Environmental Research Institute Ltd.: Stockholm, Sweden, 2015. [Google Scholar]
- Jee, J. Hybrid Multi-Criteria Decision-Making for Marine SOx Scrubber Systems. J. Mar. Sci. Eng. 2022, 10, 1599. [Google Scholar] [CrossRef]
- Toscano, D.; Murena, F.; Quaranta, F.; Mocerino, L. Assessment of the Impact of Ship Emissions on Air Quality Based on a Complete Annual Emission Inventory Using AIS Data for the Port of Naples. Ocean Eng. 2021, 232, 109166. [Google Scholar] [CrossRef]
- Topic, T.; Murphy, A.J.; Pazouki, K.; Norman, R. Assessment of Ship Emissions in Coastal Waters Using Spatial Projections of Ship Tracks, Ship Voyage and Engine Specification Data. Clean. Eng. Technol. 2021, 2, 100089. [Google Scholar] [CrossRef]
- Air Pollutant Emission Inventory Guidebook 2023; European Environment Agency (EEA): Copenhagen, Denmaek, 2023.
- Trozzi, C. Emission Estimate Methodology for Maritime Navigation. In Proceedings of the 9th International Emissions Inventory Conference, San Antonio, TX, USA, 27–30 September 2010. [Google Scholar]
- Cooper, D.; Gustafsson, T. Methodology for Calculating Emissions from Ships: 2. Emission Factors for 2004 Reporting; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 2004. [Google Scholar]
- Smith, T.W.P.; Jalkanen, J.P.; Anderson, B.A.; Corbett, J.J.; Faber, J.; Hanayama, S.; O’Keeffe, E.; Parker, S.; Johansson, L.; Aldous, L.; et al. Third IMO GHG Study 2014; International Maritime Organization: London, UK, 2015. [Google Scholar]
- MEPC.1/Circ.684; International Maritime Organization (IMO): London, UK, 2009.
- International Maritime Organization (IMO). Nitrogen Oxides (NOx)—Regulation 13. Available online: https://www.imo.org/en/OurWork/Environment/Pages/Nitrogen-oxides-(NOx)-–-Regulation-13.aspx (accessed on 3 January 2022).
- MARPOL Annex VI, Regulation 14; International Maritime Organization (IMO): London, UK, 2020.
- Ship&Bunker Global 20 Ports Average Bunker Prices—Ship & Bunker. Available online: https://shipandbunker.com/prices/av/global/av-g20-global-20-ports-average (accessed on 28 June 2025).
- Hawas, F.; Cifuentes, A. Valuation of Projects with Minimum Revenue Guarantees: A Gaussian Copula–Based Simulation Approach. Eng. Econ. 2017, 62, 90–102. [Google Scholar] [CrossRef]
- Han, T.-C.; Wang, C.-M. Shipping Bunker Cost Risk Assessment and Management during the Coronavirus Oil Shock. Sustainability 2021, 13, 4998. [Google Scholar] [CrossRef]
- Hofstadler, C.; Kummer, M. The Fundamentals of Monte Carlo Simulations; Springer: Berlin/Heidelberg, Germany, 2021; pp. 155–212. [Google Scholar]
- Hasannuddin, A.K.; Yahya, W.J.; Sarah, S.; Ithnin, A.M.; Syahrullail, S.; Sugeng, D.A.; Razak, I.F.A.; Abd Fatah, A.Y.; Aqma, W.S.; Rahman, A.H.A.; et al. Performance, Emissions and Carbon Deposit Characteristics of Diesel Engine Operating on Emulsion Fuel. Energy 2018, 142, 496–506. [Google Scholar] [CrossRef]
- Iakovenko, A.; Dunin, A.; Dushkin, P.; Savastenko, E.; Shatrov, M. The Influence of Mass Composition of Water-Fuel Emulsion on Ecological Characteristics of a Diesel Engine. Energies 2019, 12, 2689. [Google Scholar] [CrossRef]
- Contini, D.; Merico, E. Recent Advances in Studying Air Quality and Health Effects of Shipping Emissions. Atmosphere 2021, 12, 92. [Google Scholar] [CrossRef]
- Ni, P.; Wang, X.; Li, H. A Review on Regulations, Current Status, Effects and Reduction Strategies of Emissions for Marine Diesel Engines. Fuel 2020, 279, 118477. [Google Scholar] [CrossRef]
- Díaz-Rodríguez, S.; Suárez, E.; Concheiro, M.; Paz-Penín, C. Experimental Study of the Ozone as an Anti-Fouling System in an Exhaust Gas Heat Exchanger. Appl. Therm. Eng. 2025, 273, 126538. [Google Scholar] [CrossRef]
- Zhu, M.; Li, K.X.; Lin, K.-C.; Shi, W.; Yang, J. How Can Shipowners Comply with the 2020 Global Sulphur Limit Economically? Transp. Res. Part D Transp. Environ. 2020, 79, 102234. [Google Scholar] [CrossRef]
- Sheng, D.; Jiang, J.; Wang, H.; Tan, Z.; Wang, Y. Optimal Compliance Choices for Ocean Carriers under the Sulphur Regulation. Transp. Res. Part D Transp. Environ. 2023, 116, 103639. [Google Scholar] [CrossRef]
- Zis, T.P.V.; Cullinane, K.; Ricci, S. Economic and Environmental Impacts of Scrubbers Investments in Shipping: A Multi-Sectoral Analysis. Marit. Policy Manag. 2022, 49, 1097–1115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).