Research on the Influence of Hydrofoil Propulsive Parameters on Propulsion Efficiency

Abstract

Oscillating hydrofoils can be used to simplify the study of the swinging caudal fin propulsive mode of fish, where the motion parameters have a direct impact on the hydrodynamic performance and propulsive efficiency. In this study, numerical calculations were carried out on two-dimensional hydrofoils for sinusoidal and non-sinusoidal heave oscillation, and the numerical results of sinusoidal hydrofoils were compared with the experimental values, which were in good agreement. An analysis of how different motion parameters of the sinusoidal hydrofoil affect the hydrodynamic performance was conducted, and the recommended operating condition range was given in combination with the flow field analysis. A unique non-sinusoidal curve was defined, which can enable the motion to enter the crest and trough earlier or later. The parameters for controlling the degree of non-sinusoidal were also defined. A detailed discussion was carried out on how the non-sinusoidal parameters affect the hydrodynamic performance and the change in the flow field. The corresponding recommended working conditions and application scope were given. Further studies can reveal the propulsive mechanism of the swinging caudal fin and provide a reference for the engineering and design of the next generation of bionic fish.

1. Introduction

With the continuous depletion of non-renewable resources on land, exploration and development costs have risen rapidly. Consequently, the ocean has emerged as the next major frontier for resource extraction. However, the harsh deep-sea environment renders manned submersibles prohibitively expensive and bulky. Many countries and organizations have therefore shifted their focus towards marine resource exploration utilizing Unmanned Underwater Vehicles (UUVs). Currently, most UUVs employ propeller-based propulsion, which is often accompanied by significant noise and cavitation bubbles, adversely impacting marine ecosystems and the vehicles themselves. Furthermore, high energy consumption restricts the development of untethered UUVs. Bionic propulsion offers a promising solution to these challenges. Aquatic organisms like fish, having evolved over hundreds of millions of years, exhibit swimming characteristics such as high speed, maneuverability, and low noise [1], making them an ideal model for underwater vehicles. Consequently, bio-inspired robotic fish have become a major research focus in underwater vehicle technology in recent years.

Research on the propulsive mechanism of oscillating caudal fins remains ongoing. Given the similarity between the crescent-shaped caudal fin profile and an airfoil, early researchers simplified it as a hydrofoil for study. Lighthill (1971) [2] proposed the “Large-Amplitude Elongated Body Theory” (LAEBT) to model and analyze the swimming of slender-bodied trevallies. Wu (1961) [3] approximated the fish body as an elastic thin plate, developed the two-dimensional waving plate theory, and used it to study undulatory and variable-speed motions. Cheng et al. (1991) [4] further extended this to three-dimensional waving plate theory. By comparing three distinct swimming modes, they explored optimal fish locomotion strategies. They also enhanced the theory by incorporating boundary layer treatments, enabling the analysis of large-amplitude fish movements. However, the aforementioned theoretical models are only applicable to specific scenarios, and a comprehensive understanding of fish swimming mechanics is still lacking.

Fish swimming generates a unique wake characterized by a reverse Kármán vortex street, a crucial mechanism for thrust generation. The Strouhal number (St) is the key parameter characterizing these wake structures. The existence of the reverse Kármán vortex street was initially theorized by Lighthill (1975) [5] and Videler (1993) [6]. Subsequently, Müller et al. (1997) [7] and Lauder et al. (2002) [8] experimentally visualized this wake structure behind swimming fish using Digital Particle Image Velocimetry (DPIV). The wake exhibits a distinct flow pattern downstream of the trailing edge, consisting of staggered arrays of discrete vortices. Earlier experiments by Triantafyllou et al. (1991) [9] and Koochesfahani (1989) [10] demonstrated vortex flow patterns and the emergence of jet profiles in the wake, highlighting distinct features of different propulsive modes, such as high-efficiency or high-thrust modes. Lai et al. (1999) [11] visually demonstrated the transition of the wake vortex pattern from drag-producing to thrust-producing regimes by increasing the oscillation amplitude or frequency of a hydrofoil. Through numerical and experimental studies, Andersen et al. (2017) [12] compared wake structures between pure heave and pure pitch motions. They found that the drag-to-thrust transition occurred within a specific parameter region characterized by a wake forming two vortex pairs per oscillation cycle. This contrasts sharply with the transition typically observed in the classical reverse Kármán vortex street. Gupta et al. (2021) [13] discovered that the drag-to-thrust transition is consistent with that found for a wide variety of fish and birds in nature, and studied how a wide range of St (0~1.4) and Reynolds numbers (Re) affect the propulsion performance.

In recent years, Computational Fluid Dynamics (CFD)-based numerical simulation methods have gained significant prominence. Liu H. et al. (1996) [14] developed a novel CFD modeling approach using an artificial pseudo-compressibility finite volume method to investigate the undulatory propulsion and hydrodynamic performance of tadpoles, discussing their thrust generation mechanism. Sandberg et al. (1999) [15] employed an innovative unstructured grid discretization technique combined with finite element numerical analysis to compute and study the hydrodynamic performance of crescent-shaped tail fins and oscillating hydrofoils. Zhang et al. (2006) [16] performed numerical simulations of two-dimensional rigid and flexible hydrofoils, comparing the results with experimental data and finding good agreement. Yang (2009) [17] conducted numerical simulations on both two-dimensional and three-dimensional hydrofoils and oscillating caudal fins using a Reynolds-Averaged Navier–Stokes (RANS) solver and dynamic mesh techniques, providing an in-depth analysis of the influence of motion parameters on hydrodynamic performance. Gupta et al. (2023) [18] researched the influence of the curvature, shape and thickness of the hydrofoil on the propulsion performance, they also delved into the relationship between flow separation and the parameters of the hydrofoil as well as its impact on the thrust. All the above studies were limited to sinusoidal motion. At the same time, many scholars (Kaya and Tuncer 2007 [19], Boudis et al., 2019 [20], Li et al., 2022 [21]) have also conducted in-depth research on the non-sinusoidal motion of hydrofoils and have adopted various non-sinusoidal motions. They found that the non-sinusoidal motion always improved the thrust force but decreased, the maximum propulsive efficiency.

In summary, the propulsive performance and mechanisms of hydrofoils remain a central research focus within the field, serving as a fundamental approach to understanding fish swimming mechanics. Despite years of development, related research remains incomplete, presenting substantial opportunities for further investigation. This study establishes a two-dimensional numerical model of a rigid oscillating hydrofoil. The motion of the 2D hydrofoil is simulated by the open-source CFD tool OpenFOAM, and the technique of dynamic fluid–body interaction is applied to simulate the translation and rotation of the hydrofoil. In this study, computed results are compared with tank test results for verification and validation. Then, sinusoidal and non-sinusoidal hydrofoil motions and their parameters are defined. The influence of various motion parameters on hydrodynamic performance is analyzed in detail. Concurrently, flow field variations are meticulously examined, leading to the proposal of recommended ranges for stable operating parameters, and the effect of the propulsive parameters and the corresponding vortex generation on the efficiency of the hydrofoil is analyzed.

2. Principles and Methods

2.1. Numerical Methods

The governing equations for the unsteady incompressible flow around the hydrofoil are the continuity equation and Navier–Stokes equations. By combining these two equations and performing the Reynolds average method, the RANS equations are obtained, defined as:

$$\left\{\begin{array}{l}\nabla \cdot \overline{u}=0\\ {\displaystyle \frac{\partial \overline{u}}{\partial t}}+\nabla ·(\overline{uu}+\overline{u^{\prime }{u}^{\prime }})=\overline{f}-{\displaystyle \frac{\nabla \overline{p}}{\rho }}+\nabla \cdot (\nu \overline{u})\end{array}\right.$$

(1)

where the motion speed $\mathbf{u}=\overline{\mathbf{u}}+{\mathbf{u}}^{\prime }$, $\overline{\mathbf{u}}$ is the time-averaged velocity, ${\mathbf{u}}^{\prime }$ is the velocity fluctuation value, $f$ is the additional mass force, $p$ is the pressure, $\rho$ is density, and $\upsilon$ is the fluid viscosity.

The RANS equations are very complex and generally cannot be solved directly. In this paper, the $SSTk-\omega$ turbulence model is adopted to assist the closed equation, and its transport equation is:

$$\left\{\begin{array}{l}{\displaystyle \frac{\partial }{\partial t}}(\rho k)+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho k{u}_i\right)={\displaystyle \frac{\partial }{\partial x_j}}\left({\Gamma }_k{\displaystyle \frac{\partial k}{\partial x_j}}\right)+{\tilde{G}}_k-Y_k+S_k\\ {\displaystyle \frac{\partial }{\partial t}}(\rho \omega )+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho \omega u_i\right)={\displaystyle \frac{\partial }{\partial x_j}}\left({\Gamma }_{\omega }{\displaystyle \frac{\partial \omega }{\partial x_j}}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }\end{array}\right.$$

(2)

where the effective diffusion rates ${\Gamma }_k=\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_k}}$ and ${\Gamma }_{\omega }=\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\omega }}}$; the turbulent generation term ${\tilde{G}}_k=min(G_k,10\rho {\beta }^{\ast }k\omega )$, $G_{\omega }={\displaystyle \frac{\alpha }{v_t}}{G}_k$; the turbulence dissipation terms $Y_k=\rho {\beta }^{\ast }k\omega$ and $Y_{\omega }=\rho {\beta }_i{\omega }^2$; and the cross-diffusion term $D_{\omega }=2\left(1-F_1\right)\rho {\sigma }_{\omega ,2}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_j}}{\displaystyle \frac{\partial \omega }{\partial x_j}}$.

2.2. Computational Model and Meshing

Figure 1 provides a schematic diagram of the computational domain and boundary conditions for the oscillating hydrofoil. The square region represents the background domain, corresponding to the water pool. The upper, lower, and left boundaries are designated as velocity inlets, while the right boundary is set as a pressure outlet. The hydrofoil surface is defined as a wall boundary. A circular region encompassing the hydrofoil constitutes the overset mesh domain. The interface between the background domain and the overset domain is defined as the overset boundary, where an overset mesh interface is created. In the two-dimensional mesh, this boundary is treated as a line. The heave and pitch motions of the physical hydrofoil are simulated by applying translation and rotation to the entire overset region.

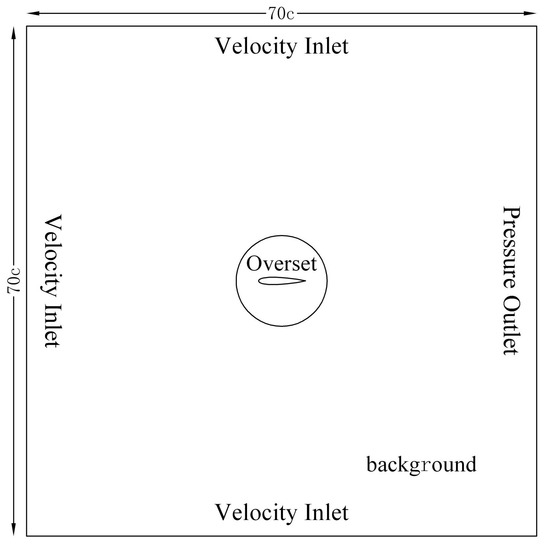
Figure 1. Diagram of computational domain and boundary conditions.

The standard airfoil NACA 0015 was selected, and a two-dimensional grid was drawn and calculated. Firstly, the pre-process utility snappyHexMesh of OpenFOAM was used to conduct three-dimensional division of all areas. Prism layers were employed to refine the mesh near the hydrofoil surface. Then, the three-dimensional mesh was converted into a two-dimensional computational grid. The airfoil chord length is $c = 0.06 \mathrm{m}$. The overset region is circular, centered at $0.5c$ with a radius of $1c$. Figure 2 illustrates the actual overset mesh configuration implemented in the software.

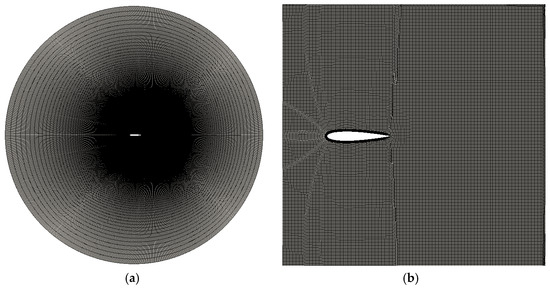
Figure 2. Grid division situation. (a) Overall computational domain. (b) Details of the hydrofoil surface and overset grids.

2.3. Hydrofoil Motion Model

The coordinate axes and the motion trajectory within one period of the sinusoidal hydrofoil are shown in Figure 3a, where $U_{\infty }$ is both the free stream velocity and is equivalent to the forward velocity of the hydrofoil. Assuming that the heave and pitch motions of the hydrofoil are both simple harmonic motions with the same frequency and constant, the heave position $y\left(t\right)$ and the pitch angle $\theta \left(t\right)$ are defined as follows:

$$y(t)=y_0\cdot \sin (2\pi ft)$$

(3)

$$\theta (t)={\theta }_0\cdot \sin (2\pi ft+\varphi )$$

(4)

where $y_0$ and ${\theta }_0$ represent the heave and pitch amplitudes, respectively. The pitch axis is at the front 1/3 of the hydrofoil, $\varphi$ is the phase offset between the heave and pitch motions, and $f$ is the motion frequency, corresponding to the period $T=1/f$.

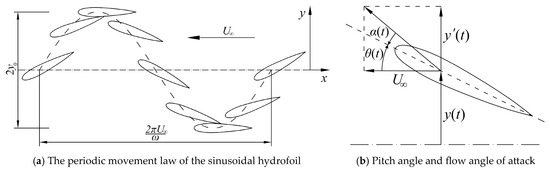
Figure 3. Rigid sinusoidal oscillation hydrofoil motion model.

In hydrofoil research, the Strouhal number $St$ and effective angle of attack (AoA) $\alpha \left(t\right)$ are commonly used to reflect the hydrodynamic conditions. $St$ is the ratio of the local inertial force to the convective inertial force, and it is generally regarded as the dimensionless frequency of the hydrofoil. In this paper, it is expressed as:

$$St={\displaystyle \frac{fA}{U_{\infty }}}$$

(5)

where $A$ is the wake width, and its size is generally approximately twice the amplitude of the heave motion $y_0$.

As shown in Figure 3b, the effective AoA is defined as the angle between the instantaneous relative flow velocity of the hydrofoil and the chord line:

$$\alpha \left(t\right)=\theta \left(t\right)-\arctan \left({\displaystyle \frac{y^{\prime }(t)}{U_{\infty }}}\right)$$

(6)

The amplitude of AoA (${\alpha }_{max}$) is usually used as the kinematic parameter. In this paper, the selected ${\alpha }_{max}$ is numerically approximated by changing ${\theta }_0$, and the calculated ${\theta }_0$ has 7 significant digits. Hover et al. (2004) [22] provided a detailed definition of this.

Because the non-sinusoidal heave hydrofoil is easier to implement in engineering, considering the calculation time, this paper only conducts a calculation and analysis of the non-sinusoidal heave hydrofoil. The non-sinusoidal heave curve used in this paper can make the heave motion enter the peaks or troughs earlier or later. This may enable the hydrofoil to generate the leading-edge vortex earlier during the pitch motion and interact with the trailing edge vortex after shedding to reduce the influence of wake drag. In order to make the motion smoother, the heave velocity equation will be changed to indirectly alter the heave motion. The definition within a single period is as follows:

$$y^{\prime }(t)=\left\{\begin{array}{ll}2\pi f{y}_0\sin \left(2\pi f_{1}t\right)& \left(0\le t\le {\displaystyle \frac{T}{4}}+{T^{\prime }}_m\right)\\ 2\pi f{y}_0\sin \left(2\pi f_2(t-2{T^{\prime }}_m)\right)& \left({\displaystyle \frac{T}{4}}+{T^{\prime }}_m<t\le {\displaystyle \frac{T}{2}}\right)\\ -2\pi f{y}_0\sin \left(2\pi f_1(t-{\displaystyle \frac{T}{2}})\right)& \left({\displaystyle \frac{T}{2}}<t\le {\displaystyle \frac{3}{2}}T+{T^{\prime }}_m\right)\\ -2\pi f{y}_0\sin \left(2\pi f_2(t-{\displaystyle \frac{T}{2}}-2{T^{\prime }}_m)\right)& \left({\displaystyle \frac{3}{2}}T+{T^{\prime }}_m<t\le T\right)\end{array}\right.$$

(7)

where $f$, $y_0$, and $T$ are the frequencies, heave amplitudes, and periods of the corresponding sinusoidal $y\left(t\right)$ curves, $f_1$ and $f_2$ are the frequencies of the curves on the left and right sides of the peak and trough of the $y^{\prime }\left(t\right)$ curve, respectively, defined as:

$$f_1={\displaystyle \frac{1}{4(T/4+{T^{\prime }}_m)}}\hspace{1em}\hspace{1em}\hspace{1em}{f}_2={\displaystyle \frac{1}{4(T/4-{T^{\prime }}_m)}}$$

(8)

where $T_m$ and ${T^{\prime }}_m$ are the crest offset values of the $y\left(t\right)$ and $y^{\prime }\left(t\right)$ curves, respectively, and ${T^{\prime }}_m$ is determined by the following formula:

$$\begin{array}{l}g(x)=\left({\displaystyle \frac{1}{4f}}-2x\right)-\arccos \left({\displaystyle \frac{4fx}{1-4fx}}\right)\cdot \left({\displaystyle \frac{1}{2\pi f}}-{\displaystyle \frac{2x}{\pi }}\right)\\ T_m=t_m\cdot {\displaystyle \frac{T}{4}}=\left\{\begin{array}{ll}g({T^{\prime }}_m)\hfill & \left({T^{\prime }}_m\le 0\right)\hfill \\ -g(-{T^{\prime }}_m)\hfill & \left({T^{\prime }}_m>0\right)\hfill \end{array}\right.\end{array}$$

(9)

Figure 4 shows the $y\left(t\right)$ and $y^{\prime }\left(t\right)$ curves within a single period of the non-sinusoidal heave motion. The practical meanings of the parameters $T_m$ and ${T^{\prime }}_m$ are marked, and the right deviation relative to the sinusoidal curve peak is taken as positive. The peak offset rate $t_m$ is defined as a calculation parameter, which is the dimensionless form of $T_m$ and is used to control the non-sinusoidal degree of the curve, characterizing the degree of advance or delay in the amplitude of the heave motion.

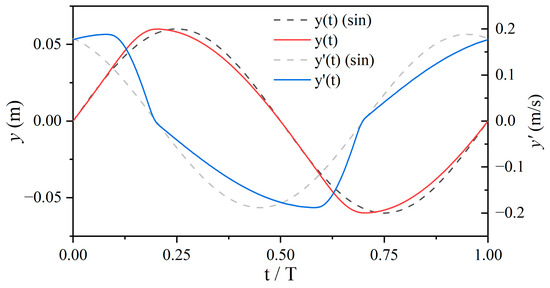
Figure 4. The $y\left(t\right)$ and $y^{\prime }\left(t\right)$ curves of the non-sinusoidal hydrofoil.

It should be noted that there are many other non-sinusoidal motion forms within the field. Choosing $t_m$ allows for a more intuitive control over the non-sinusoidal degree, and the results are easier to quantitatively analyze. It is also convenient to calculate the coordinates for controlling the servo motor to achieve non-sinusoidal motion in practical applications.

2.4. Hydrodynamic Calculation

The definitions of the transient thrust coefficient $C_x$, lift coefficient $C_y$ and moment coefficient $C_z$ are:

$$C_x(t)={\displaystyle \frac{F_x(t)}{0.5\rho cs{U}_{\infty }^2}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{C}_y(t)={\displaystyle \frac{F_y(t)}{0.5\rho cs{U}_{\infty }^2}},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{C}_z(t)={\displaystyle \frac{M_z(t)}{0.5\rho cs{U}_{\infty }^3}}$$

(10)

where $F_x\left(t\right)$ and $F_y\left(t\right)$ are the instantaneous thrust and lift force, respectively, $M_z\left(t\right)$ is the moment around the rotation axis, $c$ is the chord length, and $s$ is the span. In this paper, the two-dimensional hydrofoil is taken as $s=1$, and $\rho$ is the density of water.

The cycle-averaged thrust coefficient $C_T$, the cycle-averaged lift coefficient $C_L$, and the cycle-averaged moment coefficient $C_M$ are:

$$C_T={\displaystyle {\int }_0^T}{C}_x(t)dt/T,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{C}_L={\displaystyle {\int }_0^T}{C}_y(t)dt/T,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{C}_M={\displaystyle {\int }_0^T}{C}_z(t)dt/T$$

(11)

The cycle-averaged input power $P_{in}$ and the cycle-averaged input power coefficient $C_P$ are:

$$P_{\mathrm{in}}={\displaystyle \frac{1}{T}}\left({\displaystyle {\int }_0^T}{F}_y(t)y^{\prime }(t)+{\displaystyle {\int }_0^T}{M}_z(t){\theta }^{\prime }(t)dt\right)$$

(12)

$$C_P={\displaystyle \frac{P_{\mathrm{in}}}{0.5\rho cs{U}_{\infty }^3}}$$

(13)

The cycle-averaged thrust $\overline{F_x}$ is:

$$\overline{F_x}={\displaystyle \frac{1}{T}}{\displaystyle {\int }_0^T}{F}_x(t)dt={\displaystyle \frac{1}{2}}\rho cs{U}_{\infty }^2{C}_T$$

(14)

The propulsive efficiency $\eta$ of the hydrofoil is the ratio of output power to input power, and is expressed as:

$$\eta ={\displaystyle \frac{C_T}{C_P}}$$

(15)

2.5. Model Verification

Based on the above numerical model, the standard airfoil NACA 0015 was selected for convergence verification. The calculation parameters were selected as follows: $c=0.06 \mathrm{m}$, $y_0=c$, $\phi =\pi /2$, ${\alpha }_{max}=20°$, $St=0.3$, $U_{\infty }=0.2 \mathrm{m}/\mathrm{s}$, $Re=1.4\times {10}^4$. Figure 5 shows the transient thrust coefficient $C_x$ of different grid sizes and time steps in a period. It can be seen that the data consistency is good, but data offset will occur when the grid size or time step is too large. To reduce the computing time, a grid size of 0.0021 m and a time step of 0.002 s were finally selected.

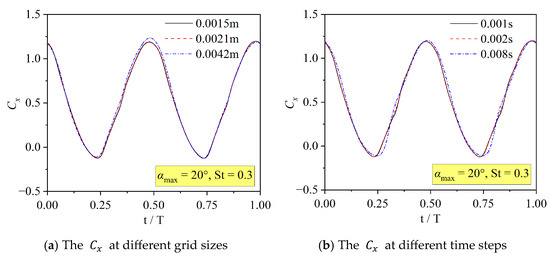
Figure 5. Verification of grid size and time step.

Figure 6 and Figure 7 present the calculation results of the transient thrust $F_x$ and lift $F_y$ under different ${\alpha }_{max}$ and $St$ values. Compared with the experimental values from Harbin Engineering University [23], it can be seen that the numerical results are in good agreement with the experimental values. Although there is a difference in the dynamic range, the slope changes in the curves are relatively close, which can be considered to indicate the reliability of the results of this model.

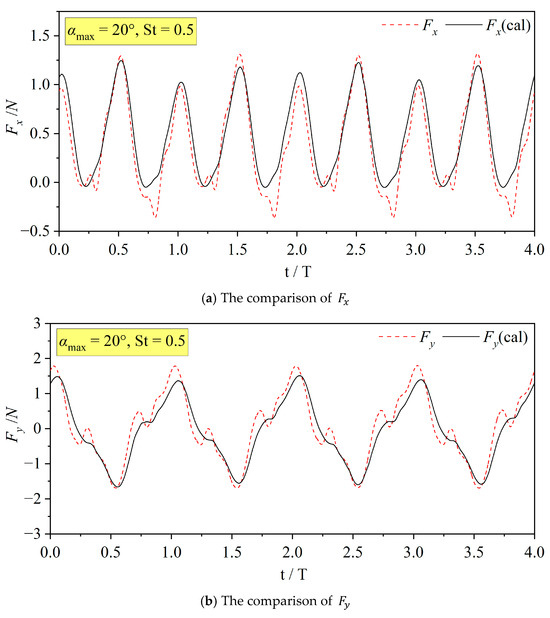
Figure 6. The experimental and calculated values of $F_x$ and $F_y$ at ${\alpha }_{max}=20°$ and $St=0.5$.

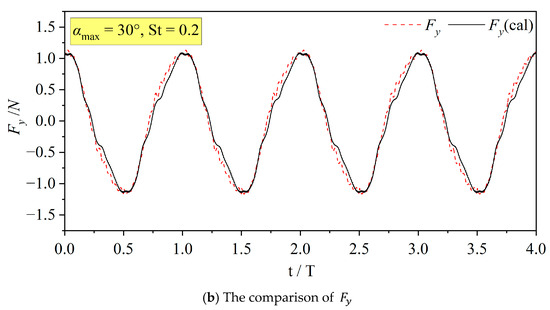
Figure 7. The calculated and experimental values of $F_x$ and $F_y$ at ${\alpha }_{max}=30°$ and $St=0.2$.

3. Effect of Propulsive Parameters on Propulsive Performance

3.1. Propulsive Performance of Sinusoidal Hydrofoil

The calculation parameters are based on the compound motion of the NACA 0015 hydrofoil performing both heave and pitch simultaneously. The basic parameters are $c = 0.06 \mathrm{m}$, $y_0=c$, $U_{\infty }=0.24 \mathrm{m}/\mathrm{s}$, ${Re=1.6 \times 10}^4$, $\varphi = \pi /2$. Table 1 shows the range of kinematic parameters. According to the study of Read et al. (2003) [24], when the phase offset $\varphi = \pi /2$, the hydrofoil can achieve a good average thrust and propulsive efficiency over a wide frequency range. Therefore, to save computing time, $\varphi$ is taken as π/2 in this paper.

Table 1. Kinematic parameters of sinusoidal hydrofoil.

αmax	St
10°	0.2	0.25	0.3	0.4
15°	0.2	0.3	0.4	0.5	0.6
20°	0.2	0.3	0.4	0.5	0.6	0.7	0.8
25°	0.2	0.3	0.4	0.5	0.6	0.7	0.8
30°	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
35°		0.3	0.4	0.5	0.6	0.7	0.8	0.9

Figure 8, Figure 9 and Figure 10 present the transient thrust coefficient $C_x$, lift coefficient $C_y$, and moment coefficient $C_z$ corresponding to one period of the hydrofoil when ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, 20°, 30°$. Under the same ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, the dynamic ranges of $C_x$, $C_y$, and $C_z$ increase with the increase in $St$, and the slope change in the curve increases significantly. Meanwhile, from the comparison of Figure 9 and Figure 10, the amplitude of the curve is not greatly affected by ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Due to the symmetry of the oscillation, the amplitudes of $C_y$ and $C_z$ in the positive and negative directions are approximately equal with the increase in $St$. Therefore, the values of cycle-averaged $C_y$ and $C_z$ are approximately equal to zero. However, the oscillation is not symmetrical in the $x$ direction. While the amplitude of $C_x$ increases with the increase in St, the cycle-averaged $C_x$ ($C_T$), also increases rapidly, which can be seen in Figure 11.

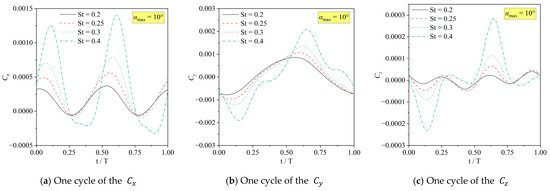
Figure 8. The $C_x$, $C_y$, and $C_z$ of the sinusoidal hydrofoil at ${\alpha }_{max}=10°$.

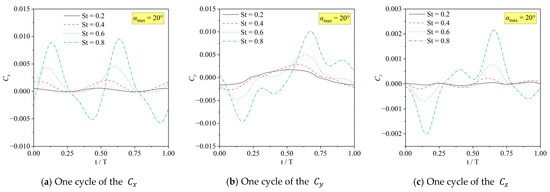
Figure 9. The $C_x$, $C_y$, and $C_z$ of the sinusoidal hydrofoil at ${\alpha }_{max}=20°$.

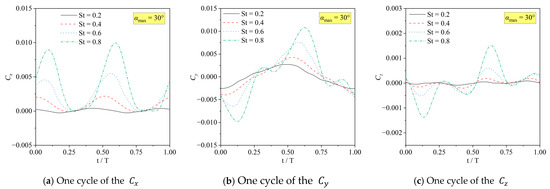
Figure 10. The $C_x$, $C_y$, and $C_z$ of the sinusoidal hydrofoil at ${\alpha }_{max}=30°$.

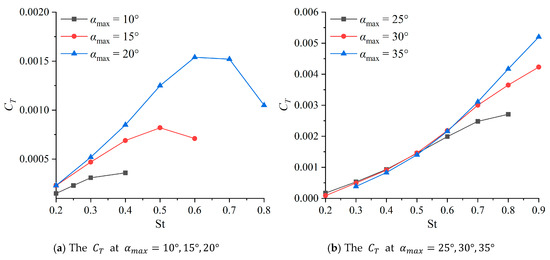
Figure 11. The $C_T$ of the sinusoidal hydrofoil with different $St$.

Figure 11, Figure 12 and Figure 13 present the variations in the cycle-averaged thrust coefficient $C_T$, cycle-averaged input power coefficient $C_P$, and propulsive efficiency $\eta$ with the Strouhal number $St$, respectively.

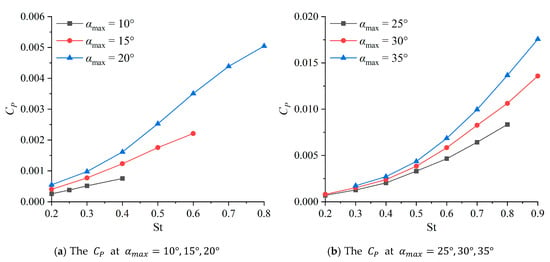
Figure 12. The $C_P$ of the sinusoidal hydrofoil with different $St$.

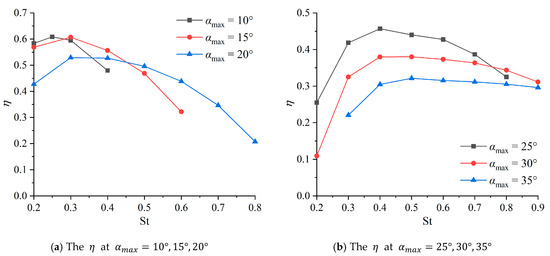
Figure 13. The $\eta$ of the sinusoidal hydrofoil with different $St$.

Figure 11 reveals that for each ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, $C_T$ rapidly decreases after reaching its peak value. This trend is more pronounced for ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°,15°$. Increasing ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ results in a steeper slope of the $C_T-St$ curve. Concurrently, both the peak $C_T$ and its corresponding critical $St$ increase. Under the investigated kinematic parameters, the location of the absolute maximum $C_T$ peak remains undetermined. While it is plausible that this maximum occurs at higher ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $St$ values, achieving such conditions is challenging in practical engineering applications, thus limiting their practical significance.

As shown in Figure 12, for a fixed ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, each $C_P-St$ curve exhibits a monotonic increase. Furthermore, the slope of the $C_P-St$ curve increases with ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Most of the $C_P$ curves are concave upward, indicating that $C_P$ generally increases rapidly with an increase in either ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ or $St$.

Figure 13 demonstrates that at $St$ values exceeding a critical threshold, the $\eta$ for each ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ decreases rapidly with increasing $St$. The peak $\eta$ remains nearly constant as ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increases from 10° to 15°, but subsequently decreases with further increases in ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Additionally, the critical $St$ value corresponding to the peak $\eta$ increases with ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Beyond this peak, a region of gradual $\eta$ decline with increasing $St$ is observed, as is clearly visible in Figure 13b. The width of this gradual descent region expands with increasing ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$; for ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=35°$, it extends beyond the maximum $St$ investigated in this study. Across all computed conditions, the peak $\eta$ ranges from 32% to 61%, with corresponding critical $St$ values ranging from 0.25 to 0.5.

Based on the above analysis, it can be seen that as ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increases, the critical $St$ at which the propulsive performance begins to decline will also increase accordingly. This indicates that ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ can change the $St$ value range at which the hydrofoil’s propulsive performance begins to deteriorate. Moreover, the effect of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ on the propulsive performance is also reflected in the fact that as ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increases, most of $C_T$ show an upward trend, while the peak $\eta$ undergoes a process of first increasing and then decreasing.

Figure 14 presents the effects of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ on the propulsive performance under different $St$ conditions. It can be seen that as $St$ increases, the influence amplitude of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ on $C_T$ is also greater. However, for $\eta$, the smaller $St$ is, the greater the influence amplitude of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ on $\eta$.

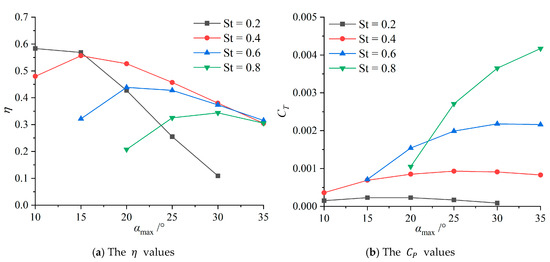
Figure 14. The $\eta$ and $C_P$ of the sinusoidal hydrofoil with different ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$.

Based on the above analysis, for sinusoidal hydrofoil, a stable operating range with $\eta$ greater than 50% can be obtained, that is, ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°~20°$, and $St=0.25~0.4$. This range can provide data reference for the development and design of fish-like robots.

3.2. Vorticity Field of Sinusoidal Hydrofoil

The analysis of the vorticity field can enable a more in-depth exploration of the reasons for the changes in propulsive performance. This section selects the three conditions of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°, St=0.3$, ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°, St=0.6$, and ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=25°, St=0.3$ in the sinusoidal hydrofoil mentioned above for comparative analysis. When ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.3$, it belongs to the situation where the propulsive efficiency $\eta$ is quite high under the same ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ where the critical St value lies. When ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.6$, the situation belongs to a far more critical St, and the propulsive performance decreases significantly. Through a comparison with the previous condition, the influence of $St$ on the propulsive performance under the same ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ can be obtained. When ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=25°$ and $St=0.3$, the situation closest to the critical $St$ is also selected. By comparing it with the first condition, the influence of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ on the propulsive performance when $St$ remains unchanged can be obtained.

Figure 15 presents the transient effective AoA $\alpha \left(t\right)$ of the three conditions in one cycle, and their changes will be analyzed in combination with the vorticity field analysis. Figure 16, Figure 17 and Figure 18 present the vorticity fields in one cycle under the three conditions. It can be seen from Figure 1 that, when ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.3$, the attached vortices that have just detached from the hydrofoil surface will be disturbed by the next vortex, resulting in the truncation of its tail and the formation of two vortices in the same direction, and the vortex formed by the truncated tail will be larger. This vortex structure occurs because, when the pitch amplitude is reached, $\alpha \left(t\right)$ has decreased and entered a local flat or low point, which will cause subsequent vortices to fall off prematurely. Overall, the reverse Kármán vortex street situation is maintained, with the red counterclockwise vortex and the blue clockwise vortex each remaining above and below the horizontal center line. Larger vortices are distributed on the outside of the flow field, while smaller vortices are concentrated near the midline. The vortex structure of this type of reverse Kármán vortex street can generate a significant backward jet, effectively increasing the $C_T$ value, so $\eta$ remains at a relatively high level.

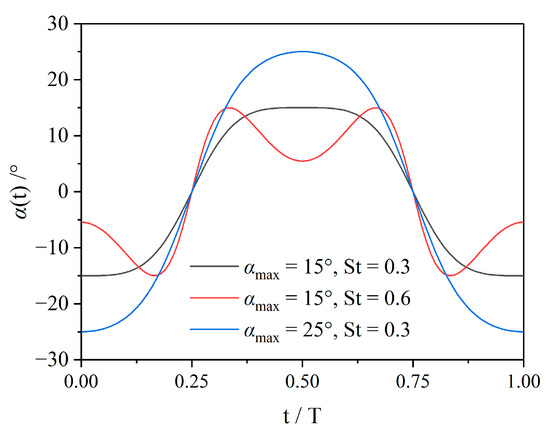
Figure 15. The $\alpha \left(t\right)$ of the sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°,25°$ and $St=0.3,0.6$.

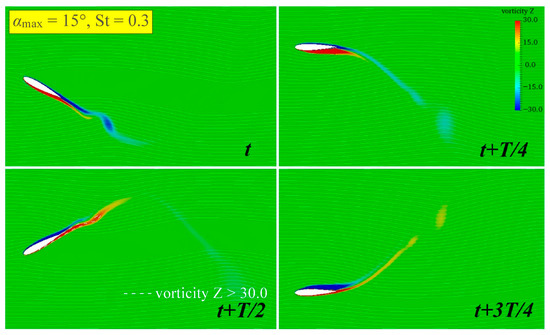
Figure 16. The vorticity field of sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.3$.

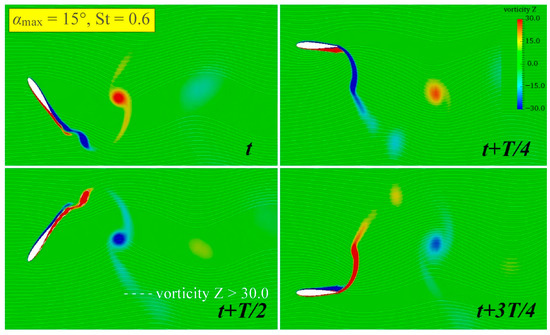
Figure 17. The vorticity field of sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.6$.

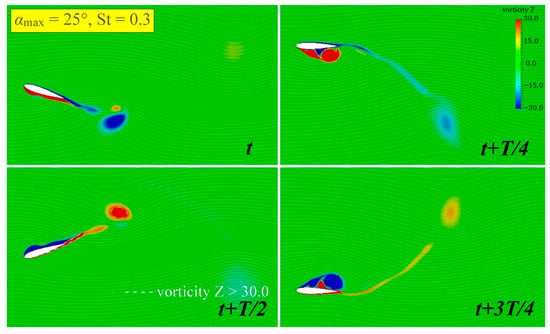
Figure 18. The vorticity field of sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=25°$ and $St=0.3$.

When ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.6$, the $\alpha \left(t\right)$ curve becomes quite undulating, with obvious local troughs and increased slope changes. This leads to a rapid rate of change in the corresponding effective AoA before and after the shedding of the attached vortex, resulting in the tail vortex presenting a unique S-shaped structure with a large vortex core, and the vortex core area (vorticity Z > 30.0) increases by 78%. As shown in Figure 17, the vortices are linearly arranged horizontally to form a single row of vortex streets. The jet induced by it mainly flows laterally, and the backward component is significantly weakened. This means that when $St$ is too high, although the vortex energy also increases, it will cause the attached vortices to fall off prematurely, forming this unfavorable single-column vortex street flow field form. This flow field will lead to the rapid dissipation of vortex energy, resulting in a significant decrease in $C_T$ and $\eta$.

When ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=25°$ and $St=0.3$, the $\alpha \left(t\right)$ curve is quite smooth. Compared with the same $St$ but ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$, the vortex core area increases by 75% at this time, as shown in Figure 18. When the attached vortices fall off (t + T/4, t + 3T/4), it can be seen that the attached vortices on the same side are also mixed with those on the opposite side, which may lead to an actual reduction in the expected vortex energy. This might be because although the $\alpha \left(t\right)$ curve seems smoother in Figure 15, due to the larger ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, the slope of the $\alpha \left(t\right)$ curve is larger when the amplitude of heave occurs (t + T/4, t + 3T/4). This means that when ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increases, this rapid change in $\alpha \left(t\right)$ may lead to instability in the flow field when the attached vortices fall off, mixing in vortices in the opposite direction and causing unnecessary energy loss, resulting in the actual $\eta$ being lower than the low ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ situation. Overall, similar to the condition of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$ and $St=0.3$, the flow field presents a symmetrically distributed reverse Kármán vortex street form, but the vortex intensity is significantly enhanced. Corresponding to this working condition, the $C_T$ of the hydrofoil is relatively large, and $\eta$ is also in a relatively high state.

From the above comparative analysis, it can be seen that the variation in the local rate of $\alpha \left(t\right)$ directly affects the shedding mechanism of the attached vortex and the evolution of the tail vortex configuration. Especially under the condition of a high $St$ number, the rapid and drastic change in the $\alpha \left(t\right)$ curve is the key factor causing deterioration in the hydrodynamic performance, providing a theoretical basis for optimizing the propulsive performance of sinusoidal hydrofoil.

3.3. Propulsive Performance of Non-Sinusoidal Hydrofoil

In order to reduce the calculation time and verify the conjecture of improving the propulsive efficiency, ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$ and $St=0.2$ were used for the verification of the peak offset rate $t_m$. Other parameters were the same as those of sinusoidal hydrofoil. Figure 19 shows the calculation results. The comparison term $t_m=0$ is the same as the sinusoidal motion. It is observed that when $t_m>0$, it will only cause a decrease in $\eta$. However, when $t_m<0$, $\eta$ rises first and then decreases. It can be inferred that when $t_m<0$, there exists an optimal $\eta$ and it is higher than that during sinusoidal motion, and the corresponding $t_m$ should be within the range of $-0.2\sim 0$.

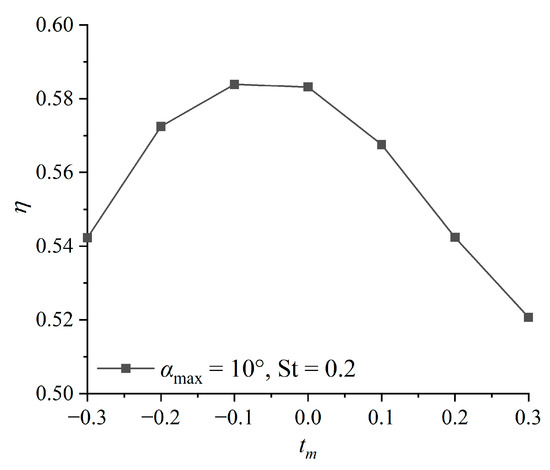
Figure 19. The $\eta$ of non-sinusoidal hydrofoil with different $t_m$ at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$ and $St=0.2$.

Table 2 shows all selected kinematic parameters. ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $St$ are selected from the parameters that achieve stable and high efficiency in the sinusoidal hydrofoil calculation. $t_m$ fully covers the parts that may optimize $\eta$ in the verification calculation.

Table 2. Kinematic parameters of non-sinusoidal hydrofoil.

Kinematic Parameters
αmax	St	tm
10	0.2~0.35	−0.25~0
15, 20	0.25~0.35	−0.2~0

Figure 20, Figure 21 and Figure 22 present the propulsive efficiency $\eta$ and the cycle-averaged thrust coefficient $C_T$ with the peak offset rate $t_m$ under different ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $St$ conditions.

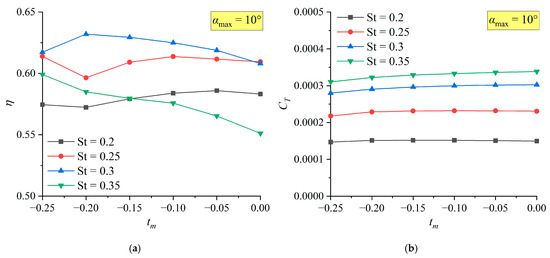
Figure 20. The $\eta$ and $C_T$ of non-sinusoidal hydrofoil with different $t_m$ at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°.$ (a) The $\eta$ values. (b) The $C_T$ values.

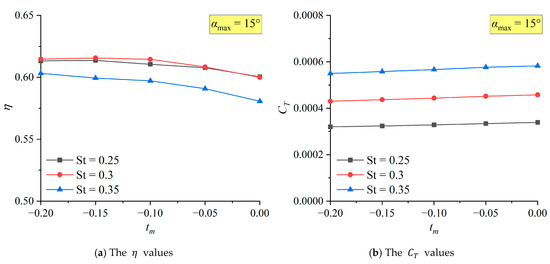
Figure 21. The $\eta$ and $C_T$ of non-sinusoidal hydrofoil with different $t_m$ at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=15°$.

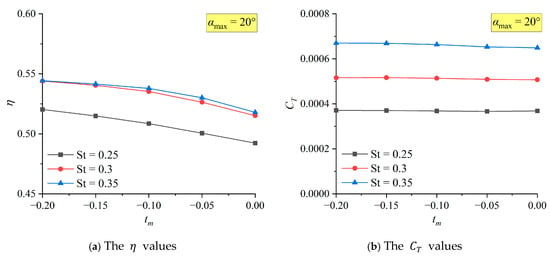
Figure 22. The $\eta$ and $C_T$ of non-sinusoidal hydrofoil with different $t_m$ at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=20°$.

It can be seen from the trend in the $C_T$ curve that the change in $t_m$ has little influence on $C_T$. In most cases, $C_T$ will slightly decrease with the decrease in $t_m$, but Figure 22b indicates that it may slightly increase at a high ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$. Under the same ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, the degree to which $C_T$ is affected by $t_m$ also increases with the increase in $St$. When $t_m$ remains constant, the trend of variation in $C_T$ with ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $St$ is basically the same as that in the sinusoidal state.

The variation in the propulsive efficiency $\eta$ with $t_m$ is rather complex. However, it can be generally judged that under the same ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, as $t_m$ decreases, $\eta$ shows a trend of first increasing and then decreasing. When $t_m$ is too small, the $\eta -t_m$ curve shows rather abnormal fluctuations. The $\eta$ at $St=0.25, 0.35$ in Figure 20a both increase significantly when $t_m = -0.25$. In the $t_m$ verification, $\eta$ should obviously decrease after $t_m<-0.2$, which means that these are abnormal situations. A possible mechanism will be discussed in detail below.

It can be clearly seen from Figure 21a that there is a gentle zone when $\eta$ improves to its optimal value as $t_m$ decreases, and its range shifts to the left as ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ increases. In Figure 22a, it is speculated that the gentle zone has exceeded the specified $t_m$ range. This indicates that the method of improving $\eta$ through $t_m$ is more obvious for low ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ hydrofoil, but more stable for high ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$ hydrofoil but with relatively limited effect.

Although η increases, the corresponding $C_T$ is affected to a very small extent. This reflects that $t_m$ has a greater influence on $C_P$ of the hydrofoil, and demonstrates that $t_m$ actually achieves the effect of improving $\eta$ by reducing $C_P$ and maintaining the stability of $C_T$. The stability of $C_T$ can maintain the speed of the hydrofoil, improve the energy utilization rate, and is more meaningful in practical engineering optimization.

Under all the calculated conditions, the maximum efficiency occurs when ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, $St=0.3$, and $t_m=-0.2$. For the cases where ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°\sim 20°$ and $St$ is low, taking $t_m=-0.1\sim -0.05$ appropriately can improve $\eta$ very well. This range can provide a reference for bionic underwater robots to further improve the propulsive efficiency.

Regarding the abnormal increase in $\eta$ at $t_m=-0.25$, since $\eta =C_T/C_P$, and $C_T$ changes very little in Figure 20b, it can be determined that the abnormality originates from $C_P$. Figure 23 shows the $C_P-t_m$ curves at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$. It can be seen that the two $C_P-t_m$ curves of $St=0.25, 0.35$ both abnormally decrease when $t_m=-0.25$, which also corresponds to the abnormal increase in $\eta$ in Figure 20a.

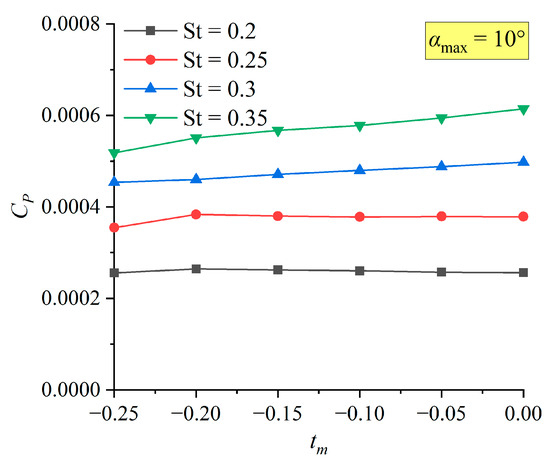
Figure 23. The $C_P$ of non-sinusoidal hydrofoil with different $t_m$ at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$.

Because $C_P$ is the dimensionless coefficient of the cycle-averaged input power $P_{\mathrm{i}\mathrm{n}}$, it is necessary to analyze the $F_y\left(t\right)y^{\prime }\left(t\right)$, and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ that make up $P_{\mathrm{i}\mathrm{n}}$ to identify the underlying causes. Take two sets of typical parameters: ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, $St=0.25, 0.35$. Figure 24 and Figure 25, respectively, show the $F_y\left(t\right)y^{\prime }\left(t\right)$ and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ curves within a single period. It can be seen that with the decrease in $t_m$, the amplitudes increase significantly, and the slope changes more sharply. The negative extremum increases at a greater rate with the decrease in $t_m$ than the positive extremum does, which leads to the abnormal decrease in $P_{\mathrm{i}\mathrm{n}}$ and $C_P$.

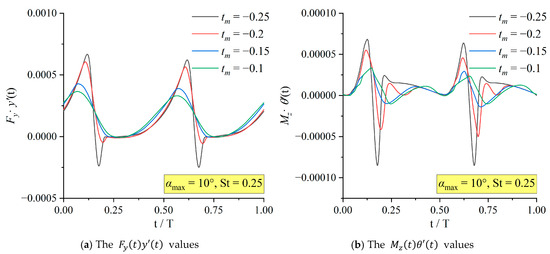
Figure 24. The $F_y\left(t\right)y^{\prime }\left(t\right)$ and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, $St=0.25$.

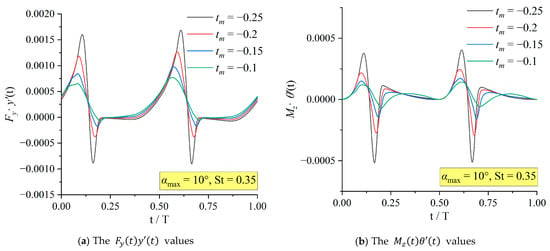
Figure 25. The $F_y\left(t\right)y^{\prime }\left(t\right)$ and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, $St=0.35$.

It can also be seen from the figure that the extreme value mutation segments of the $F_y\left(t\right)y^{\prime }\left(t\right)$ and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ curves all occur at the same time. The extreme value mutation segments of different $St$ also occur at the same time in the corresponding period. By comparing the time axes, it can be determined that within one cycle, the two sudden change segments occur when the amplitudes of the heave motion $y\left(t\right)$ are present. This indicates that the root causes of the problems in the two conditions are the same. In the following analysis of flow field changes, the changes in vortex structure at corresponding times will be analyzed to explore the root cause of the true anomaly $\eta$ problem.

3.4. Vorticity Field of Non-Sinusoidal Hydrofoil

Figure 26 shows the effective AoA $\alpha \left(t\right)$ of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.3$ within one period, which will be analyzed in combination with the vorticity field analysis.

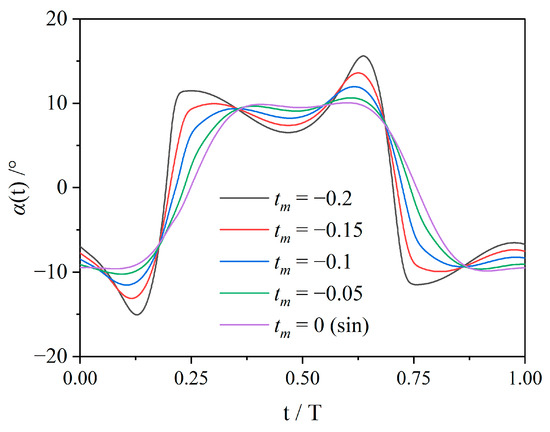
Figure 26. The $\alpha \left(t\right)$ of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$ and $St=0.3$.

It can clearly be seen that although both are ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, with the decrease in $t_m$, the actual amplitude of AoA has gradually exceeded ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, and the amplitude can reach more than 15°. In the analysis of the sinusoidal hydrofoil in Figure 14a, it has been concluded that when $St$ remains unchanged, $\eta$ will first increase and then gradually decrease with the increase in ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, and ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.3$ is exactly in the ascending section. The effect of reducing $t_m$ to improve $\eta$ is likely to come partly from this. Therefore, it may be necessary to further optimize the non-sinusoidal curve in the future to eliminate the influence of ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$.

As $t_m$ decreases, the $\alpha \left(t\right)$ curve becomes more undulating, with the peaks and troughs being further apart and changing rapidly. Meanwhile, the trend in the $\alpha \left(t\right)$ curve moving to the left can be observed in the positive and negative transition sections. This is the same as the trend in the peaks and troughs of the $y^{\prime }\left(t\right)$ curve moving to the left represented by the decrease in $t_m$. This indicates that $t_m$ also causes the $\alpha \left(t\right)$ to enter and exit the gentle zone in advance.

The reasons why $t_m$ affects the hydrodynamic performance can be more clearly identified through the analysis of the details of the vorticity field. In this section, the non-sinusoidal hydrofoil with ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$ will be divided into two groups for vorticity field analysis. In the first group, $St=0.3$, $t_m=0,-0.2$; compare $t_m=-0.2$ with $t_m=0$ to explore the mechanism by which $t_m$ improves $\eta$. The second group takes $St=0.25$, $t_m=0,-0.2,-0.25$; compare and analyze the reasons why a too small $t_m$ will reduce $\eta$ when $t_m=-0.2$ and $0$. Since the root causes of the problems in the conditions corresponding to the two abnormal $\eta$ are the same, one of the cases, $St=0.25$ and $t_m=-0.25$, was used to analyze the vorticity field and compared with $t_m=0$ and $-0.2$, attempting to analyze the reasons behind the abnormal $\eta$.

Figure 27 shows the structure of the oscillating hydrofoil tail vortex with ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°$, $St=0.3$, and $t_m=0$. It is known from Figure 26 that the rate of change in its $\alpha \left(t\right)$ curve is relatively smooth. Therefore, after the attached vortex falls off, no clear vortex core will be formed. It mainly exists in a slanting and slender linear form, simultaneously spanning the upper and lower sides of the center line. Overall, a very clear reverse Kármán vortex street pattern has not been formed. Although the propulsive efficiency $\eta$ is relatively high and the possible cavitation effect is reduced, it can only move at a low speed as a result.

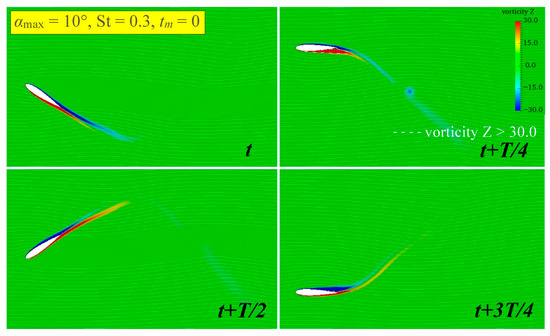
Figure 27. The vorticity field of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.3, t_m=0$.

When $t_m$ decreases, as the $\alpha \left(t\right)$ curve becomes more fluctuating, one cycle will release a pair of vortices at each of the two pitch amplitudes, and one of them presents an S-shaped strip, as shown in Figure 28. All vortex pairs occur on the same side of the horizontal centerline, and the red clockwise vortex is on top and the blue clockwise vortex is at the bottom, forming the reverse Kármán vortex street form. The overall vortex core area (vorticity Z > 30.0) increases by 25%, but the improvement is limited. Although in one cycle, the non-sinusoidal hydrofoil generates four vortices while the sinusoidal hydrofoil only has two, in the vortex pair, one vortex core is obvious and one S-shaped rapidly dissipates. This uneven vortex energy may cause the jet of the reverse Kármán vortex street to have more lateral components. Therefore, compared with increasing $C_T$, $t_m$ has a more obvious influence on $C_P$. This might also be the mechanism of $t_m$ optimizing $\eta$.

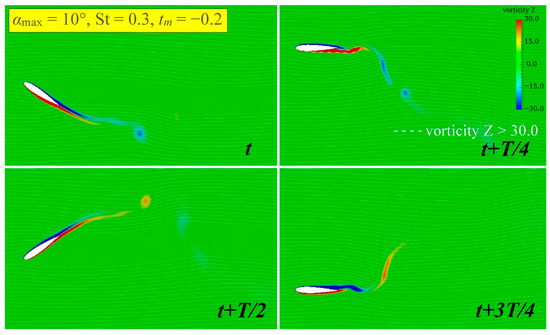
Figure 28. The vorticity field of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.3, t_m=-0.2$.

When $t_m$ is too low, by comparing Figure 29 with Figure 30, it can be found that the energy of the S-shaped strip-shaped vortices becomes less and dissipates rapidly. As a result, when the other vortex in the vortex pair is formed, it has almost disappeared and cannot form an effective reverse Kármán vortex street form, thereby leading to the ineffective dissipation of more vortex energy. It is speculated that when $t_m$ is too low, the hydrofoil prematurely enters the heave amplitude, the S-shaped vortex falls off prematurely, and is in the slow frequency and low power state under the low $St$ operating condition. When the S-shaped vortex is formed, the effective energy is insufficient, which further leads to the deterioration of the propulsive performance when $t_m$ is too low.

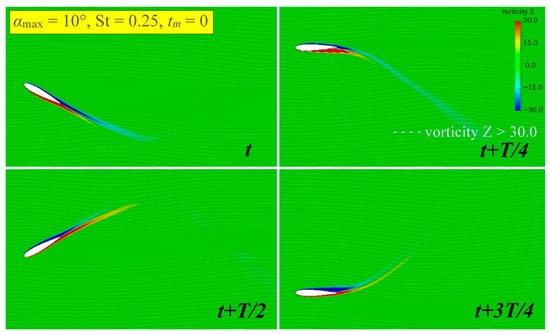
Figure 29. The vorticity field of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.25, t_m=0$.

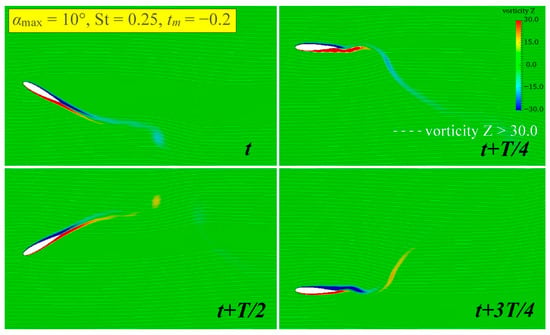
Figure 30. The vorticity field of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.25, t_m=-0.2$.

For the abnormal $\eta$ condition at $t_m=-0.25$, it can be seen from Figure 31 that as $t_m$ decreases, when the attached vortices of the pitch amplitude fall off, its lateral direction becomes increasingly lateral and has completely exceeded the thickness of the hydrofoil. This phenomenon occurs because when $t_m$ is too small and the heave motion reaches the amplitude, the hydrofoil still maintains a considerable pitch angle, and the attached vortices have not yet fallen off. However, at this time, the heave amplitude of the hydrofoil has begun to decrease, resulting in the attached vortices still maintaining lateral inertia and being thrown towards the outside of the hydrofoil, and then detaching to form vortices.

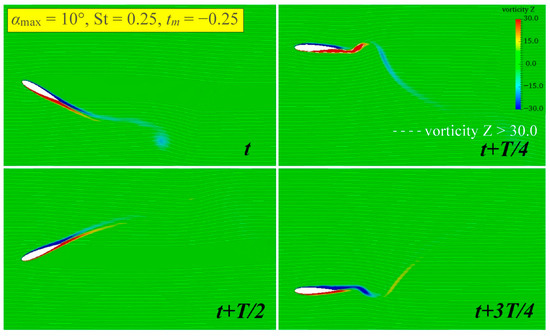
Figure 31. The vorticity field of non-sinusoidal hydrofoil at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°, St=0.25, t_m=-0.25$.

When $t_m$ decreases to −0.25, although the process in which this attached vortex is forcibly flung away can increase the vortex intensity to a certain extent (the vortex core area increases by 26%), there is also a considerable lateral reaction force on the hydrofoil itself when it detaches. Furthermore, as shown in Figure 24, when the hydrofoil reaches the heave amplitude, the $F_y\left(t\right)y^{\prime }\left(t\right)$ and $M_z\left(t\right){\theta }^{\prime }\left(t\right)$ curves enter the state of extremely high negative extreme values. The above might be the important factors that cause abnormal $C_P$ and $\eta$ when $t_m$ is too low.

4. Conclusions

This study employed computational fluid dynamics (CFD) to investigate the hydrodynamic performance of hydrofoils undergoing sinusoidal and non-sinusoidal heaving oscillations. A two-dimensional numerical model was established, enabling systematic analysis and comparative evaluation of propulsive performance across various sinusoidal and non-sinusoidal motion parameters.

The principal work and conclusions are summarized as follows:

• Regarding the hydrodynamic performance of sinusoidal hydrofoil, the analysis revealed that the cycle-averaged input power coefficient ($C_P$) increases rapidly with either an increasing maximum angle of attack (${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$) or Strouhal number ($St$). Both the cycle-averaged thrust coefficient ($C_T$) and propulsive efficiency ($\eta$) exhibit a critical $St$ value beyond which they decline; this critical St increases and its corresponding range widens with higher αmaxαmax. The stable operating regime achieving $\eta >50\%$ is identified as ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°~20°$ and $St=0.25~0.4$.
• For the analysis of the sinusoidal hydrofoil vorticity field, the hydrofoil tail vortex effectively forms reverse Kármán vortex streets, generating forward thrust. An excessively high $St$ promotes single-row vortex streets, reducing thrust. At high ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}$, adverse vortices may mix with shedding attached vortices, degrading hydrodynamic performance. The local rate of change in the transient effective angle of attack curve directly governs attached vortex shedding dynamics and wake evolution.
• For the non-sinusoidal heave hydrofoil, when using the peak offset rate ($t_m$) as the non-sinusoidal parameter, efficiency improvements ($\eta$) were observed only for $t_m<0$. While $t_m$ minimally affects $C_T$, it significantly enhances $\eta$, indicating improved energy utilization. An optimal efficiency for hydrofoils at ${\alpha }_{\mathrm{m}\mathrm{a}\mathrm{x}}=10°~20°$ and low St (0.2~0.25) is achieved with $t_m=-0.1~-0.05$, maintaining cruising speed.
• Further analysis of the vorticity field reveals that non-sinusoidal motion increases the number of vortices shed per cycle from two to four, maintaining dual reverse Kármán vortex pairs and thereby improving $\eta$. Thrust gains remain limited due to energy imbalance within vortex pairs. An excessively low $t_m$ ($<-0.15$) causes premature attached vortex shedding and rapid dissipation, severely reducing $\eta$. The anomalous $\eta$ at $t_m=-0.25$ may stem from lateral kinetic energy in the attached vortices exerting reaction forces during premature detachment.