Distributed Robust Predefined-Time Sliding Mode Control for AUV-USV Heterogeneous Multi-Agent Systems Based on Memory Event-Triggered Mechanism Under Input Saturation
Abstract
1. Introduction
- A distributed PTSO for each follower is designed to estimate the state information of the virtual leader accurately, and the observer does not need to count on the global information of the heterogeneous system. Rapid convergence can be achieved within a predefined time, thus improving the fast response of the system.
- A PTADS is developed to alleviate the influence caused by actuator input saturation and ensure that the heterogeneous multi-agent system is predefined-time stable.
- Different from the existing event-triggered mechanism [35], a memory event-triggered mechanism is proposed to better adapt to environmental changes according to historical data information, which can dramatically reduce the communication frequency and economize the communication resources.
- A DRPSC strategy is constructed to improve the robustness and control precision in the presence of external disturbances and model uncertainty. Moreover, the heterogeneous underactuated AUV-USV system is guaranteed to be predefined-time stable.
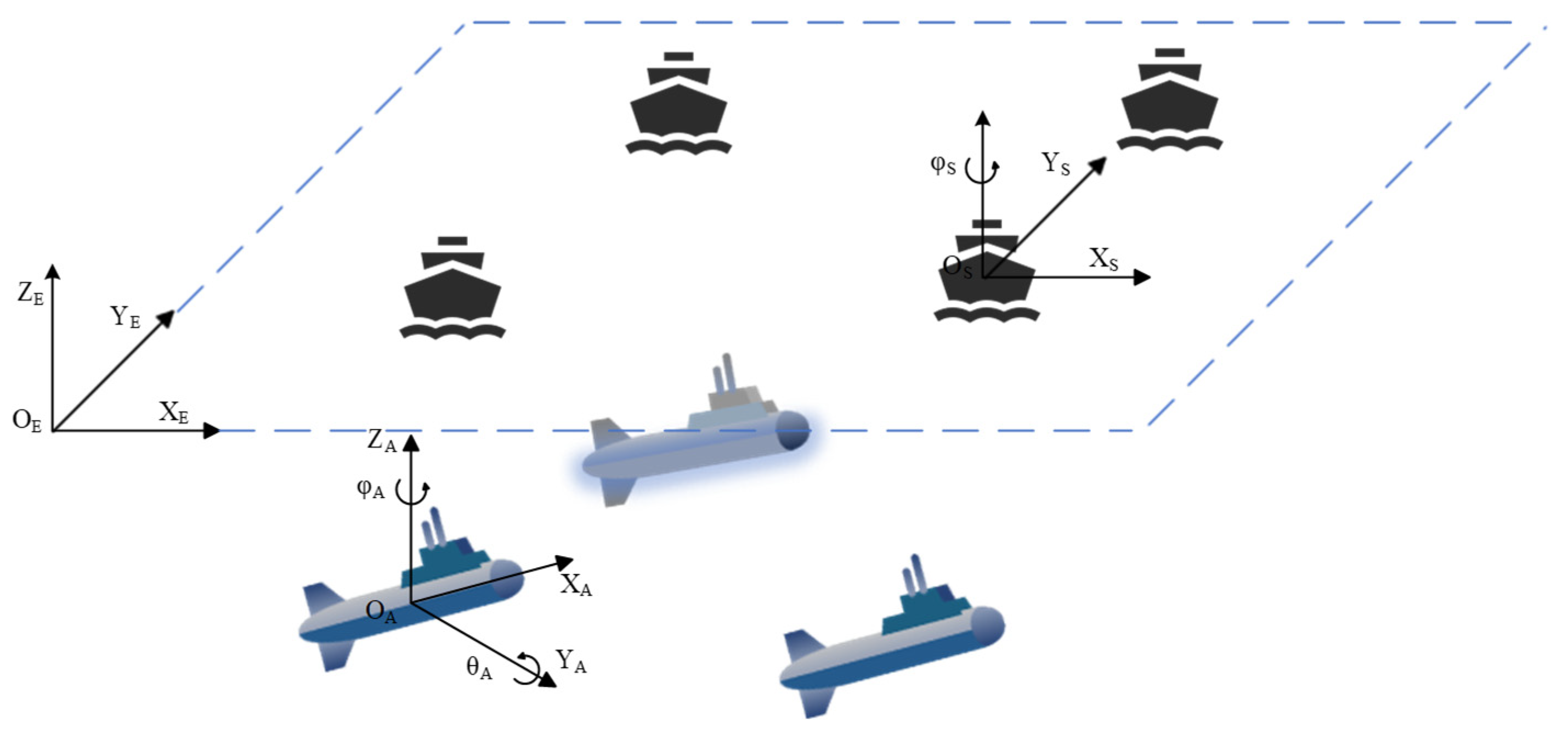
2. Preliminaries and Problem Statement
2.1. Symbolic Declaration
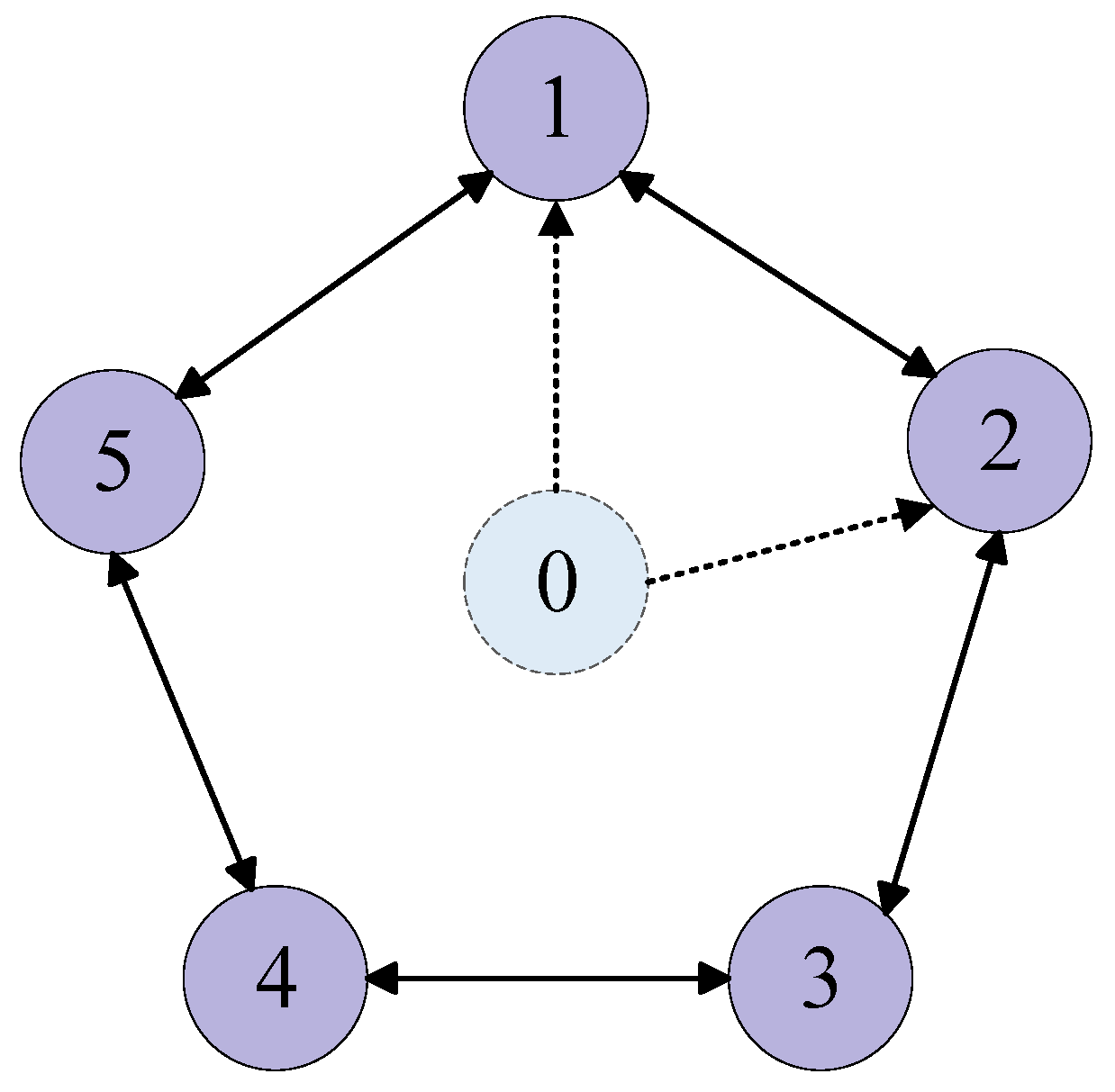
2.2. Graph Theory
2.3. Relevant Lemmas
2.4. Problem Formulation
- In the underactuated AUV-USV system, all the error signals are bounded, the tracking error is limited to a certain small range near zero, and the system reaches stability at a predefined time.
- The underactuated AUV-USV system can complete the predetermined formation pattern within the predefined time and maintain the formation during subsequent control.
- The effects of actuator input saturation, external environment disturbances, and model uncertainty in the underactuated AUV-USV system are eliminated.
- The designed memory event-triggered mechanism does not exhibit “Zeno” behavior.
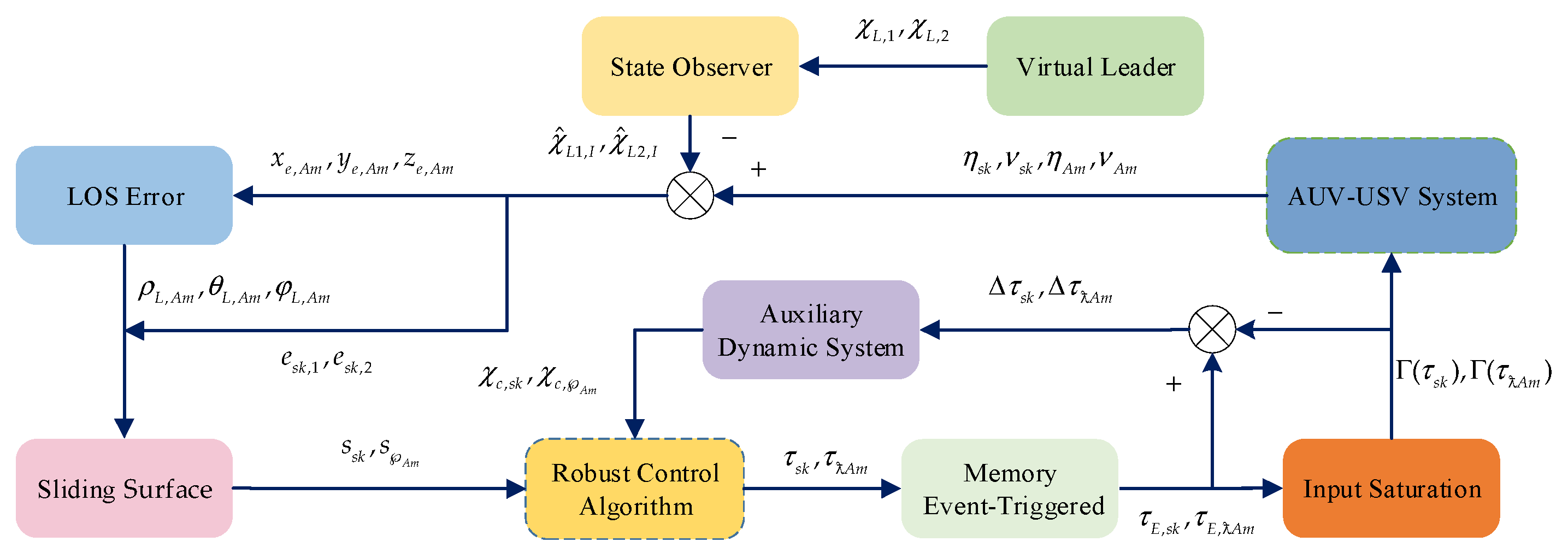
3. Main Results
3.1. Distributed Predefined-Time State Observer
3.2. Distributed Robust Predefined-Time Sliding Mode Control
3.2.1. Predefined-Time Sliding Surface
3.2.2. Predefined-Time Auxiliary Dynamic System and Predefined-Time H∞ Control
- is positive definite in .
- .
| Algorithm 1 The distributed robust predefined-time sliding mode control algorithm. |
| Step I: Initialization: Define the state space model of the AUV-USV heterogeneous multi-agent system, (9) and (14). |
| Step II: Define the formation tracking error, (28) and (29), and perform LOS error conversion for the five-degree-of-freedom underdriven AUV (31). |
| Step III: Design a distributed predefined-time state observer, (19), to obtain the state information of the virtual leader. |
| Step IV: Define the predefined-time sliding surface, (35). |
| Step V: Design a predefined-time auxiliary dynamic system to solve the problem of actuator input saturation, (38), combined with H∞ control for the system and lumped uncertainty disturbance. |
| Step VI: Design the final controller, (45). |
| Step VII: Design the memory event-triggered mechanism, (46) and (47). |
| Stop Algorithm |
3.2.3. Memory Event-Triggered Mechanism
4. Stability Analysis
- and
- 2.
- and
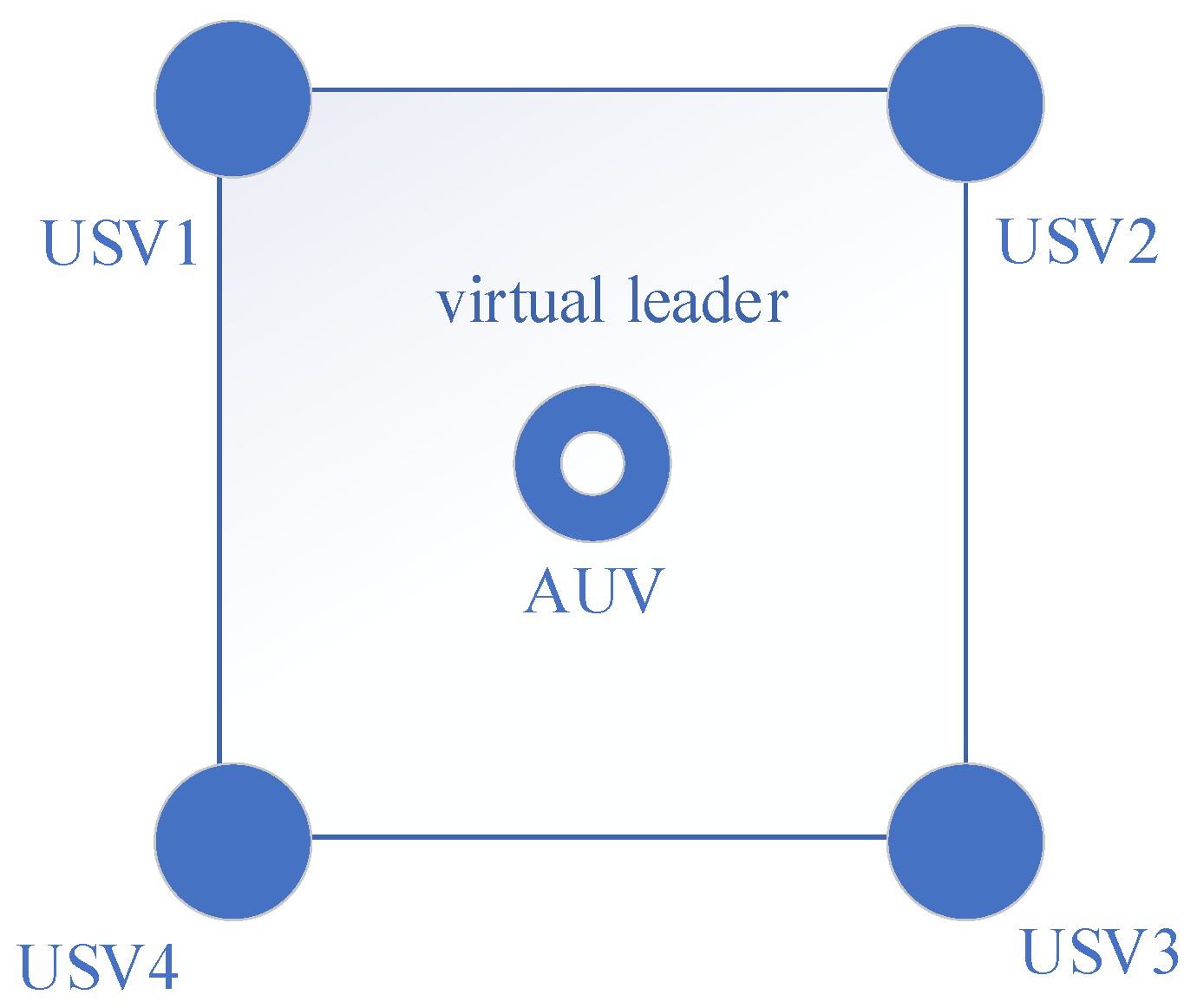
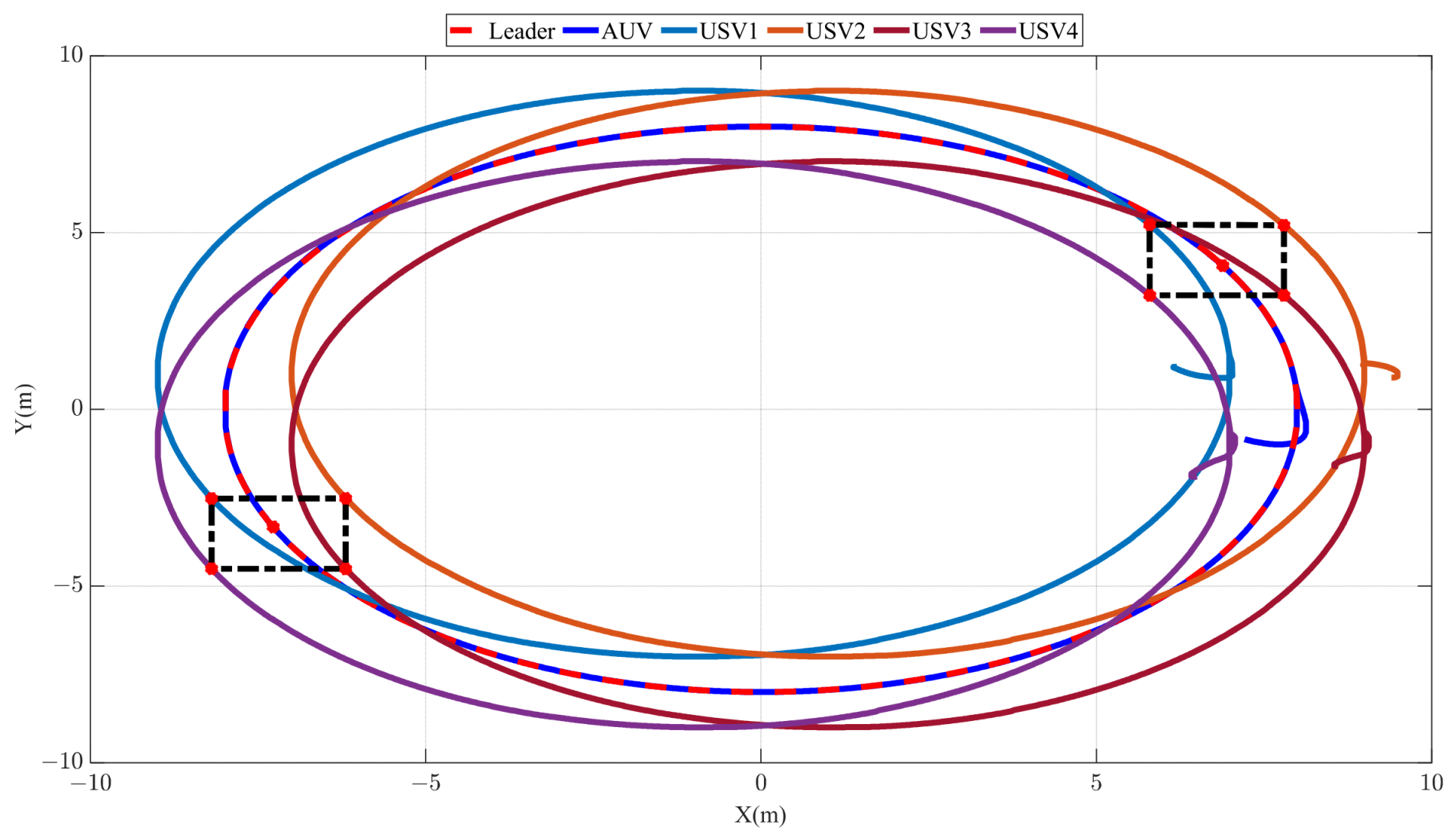
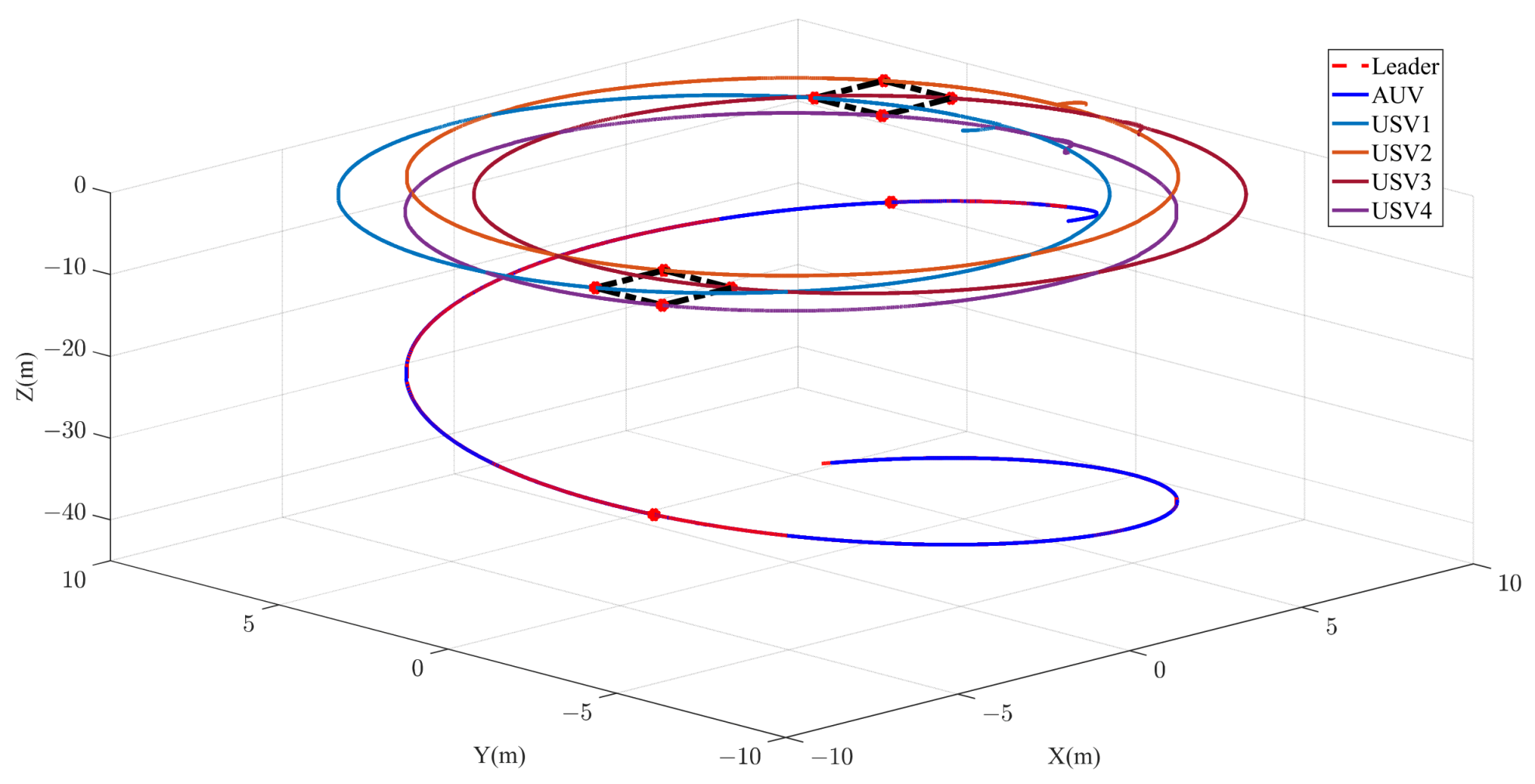
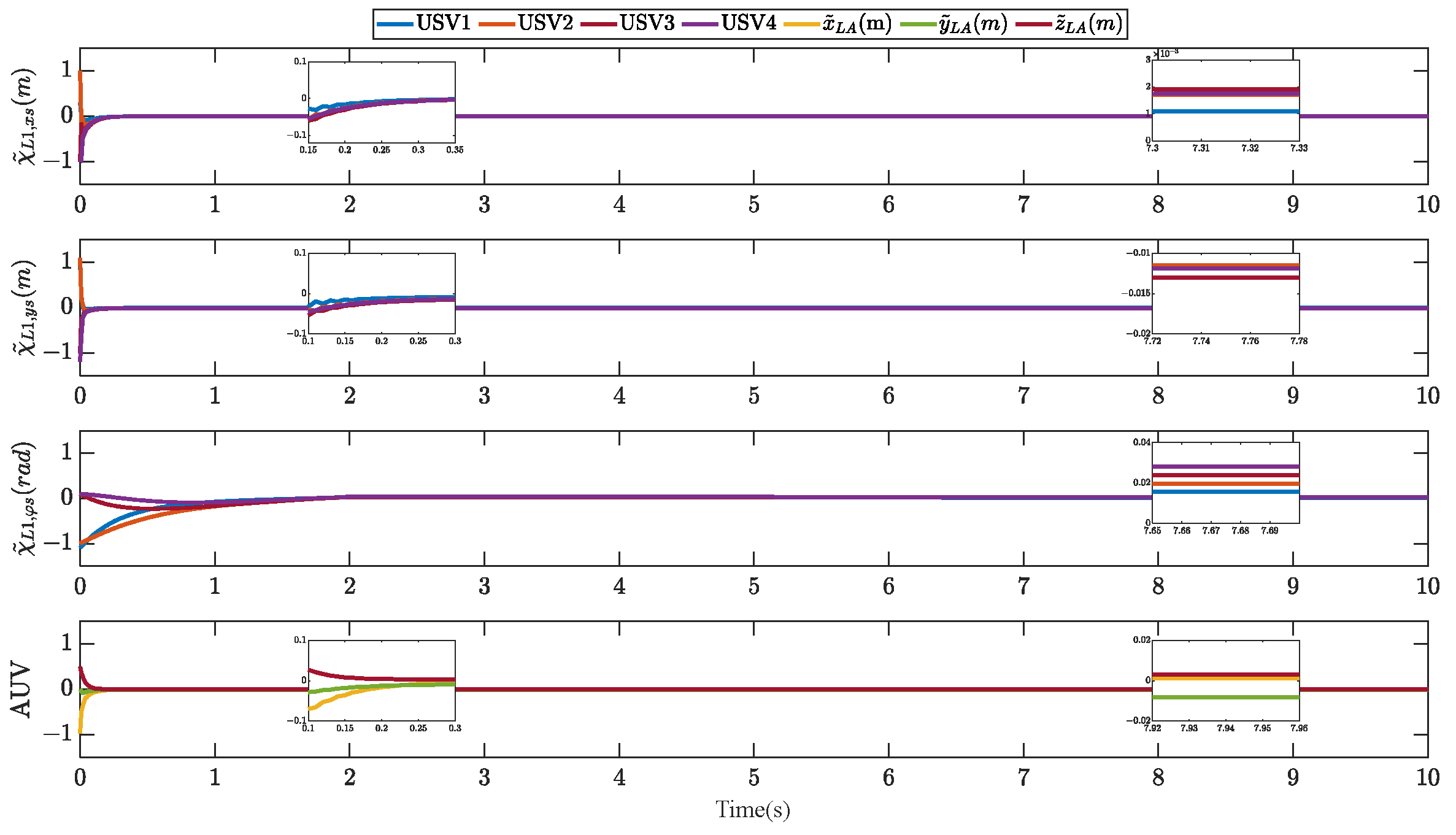
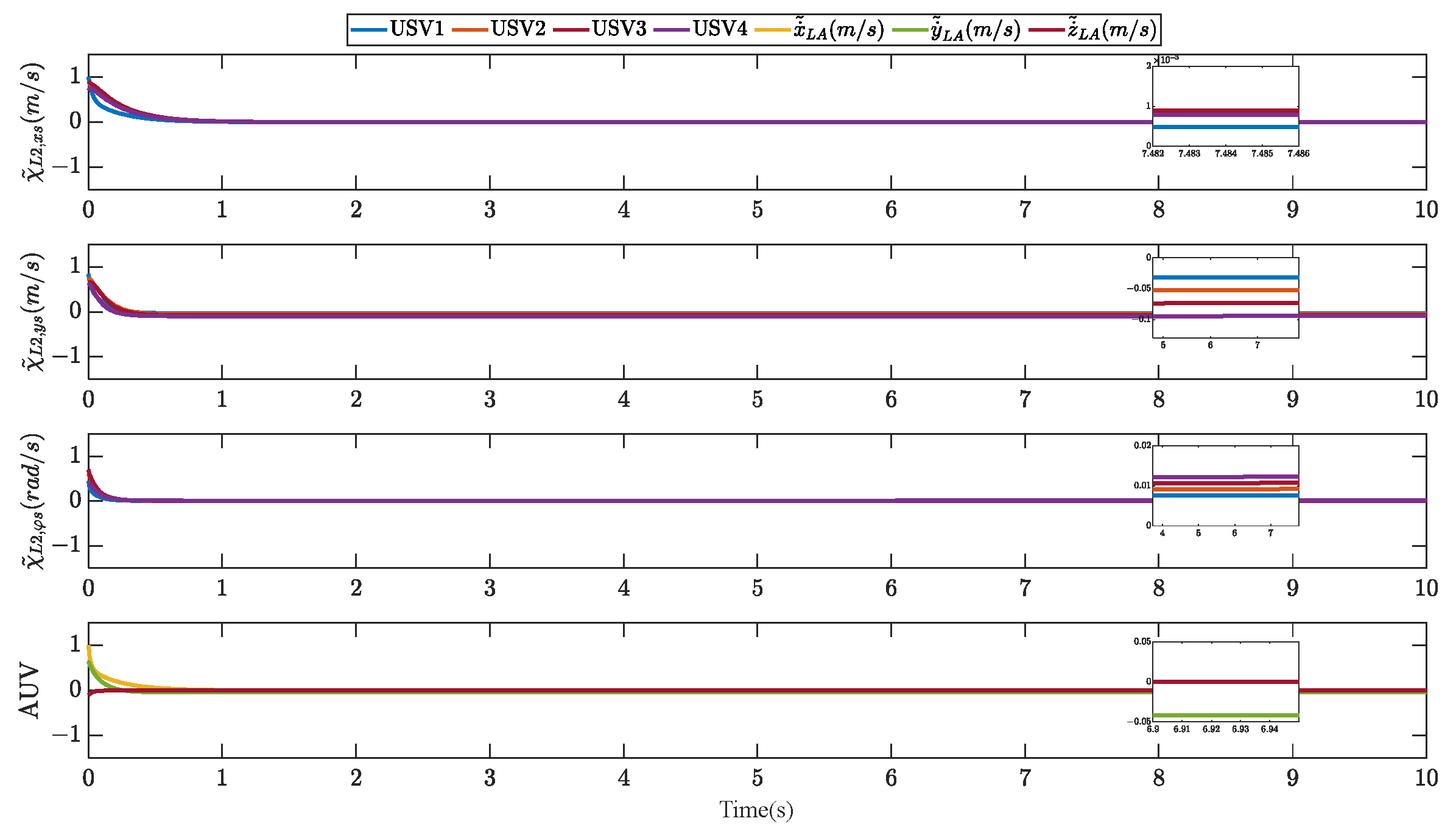
5. Simulations
5.1. In Advance Simulation Preparation
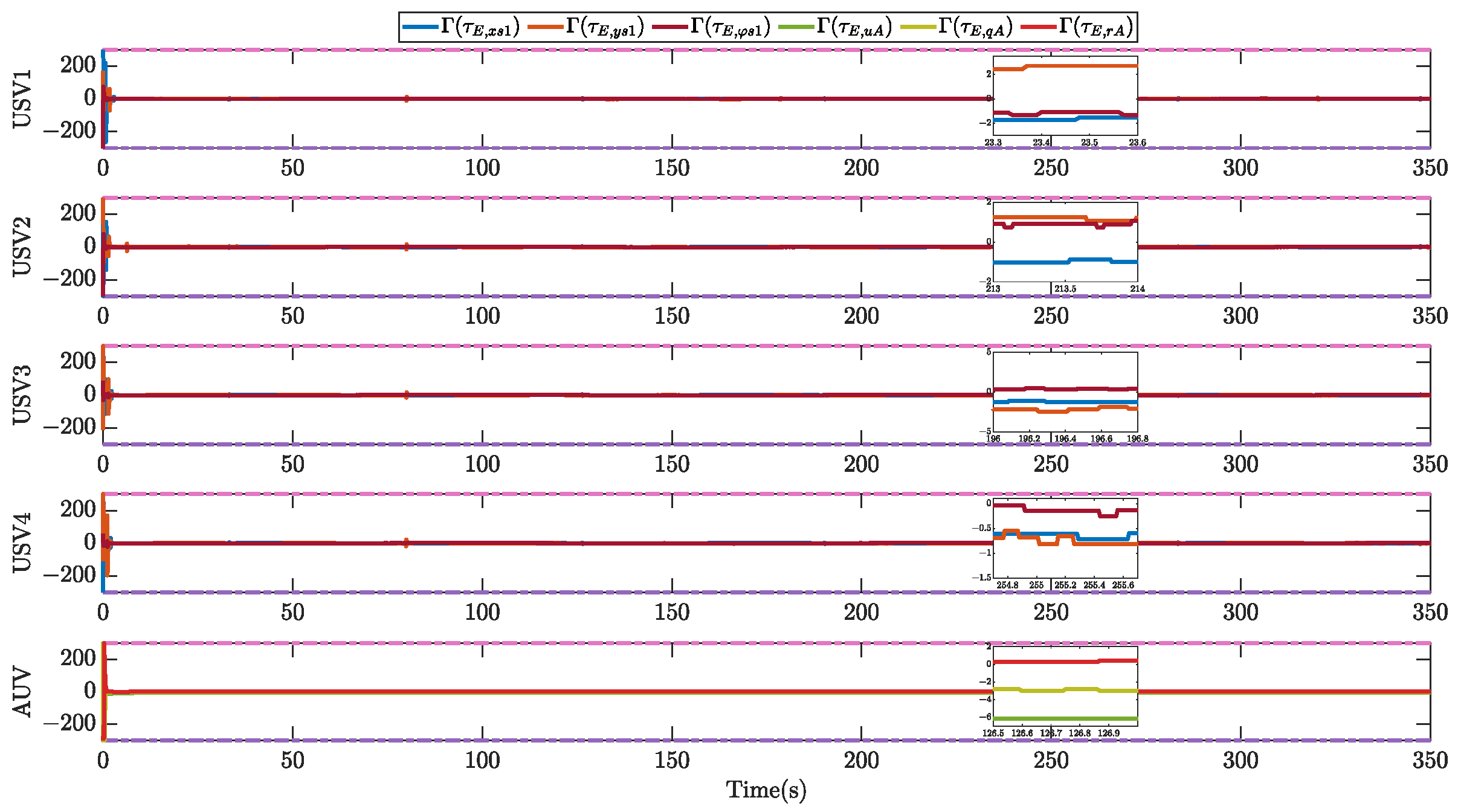
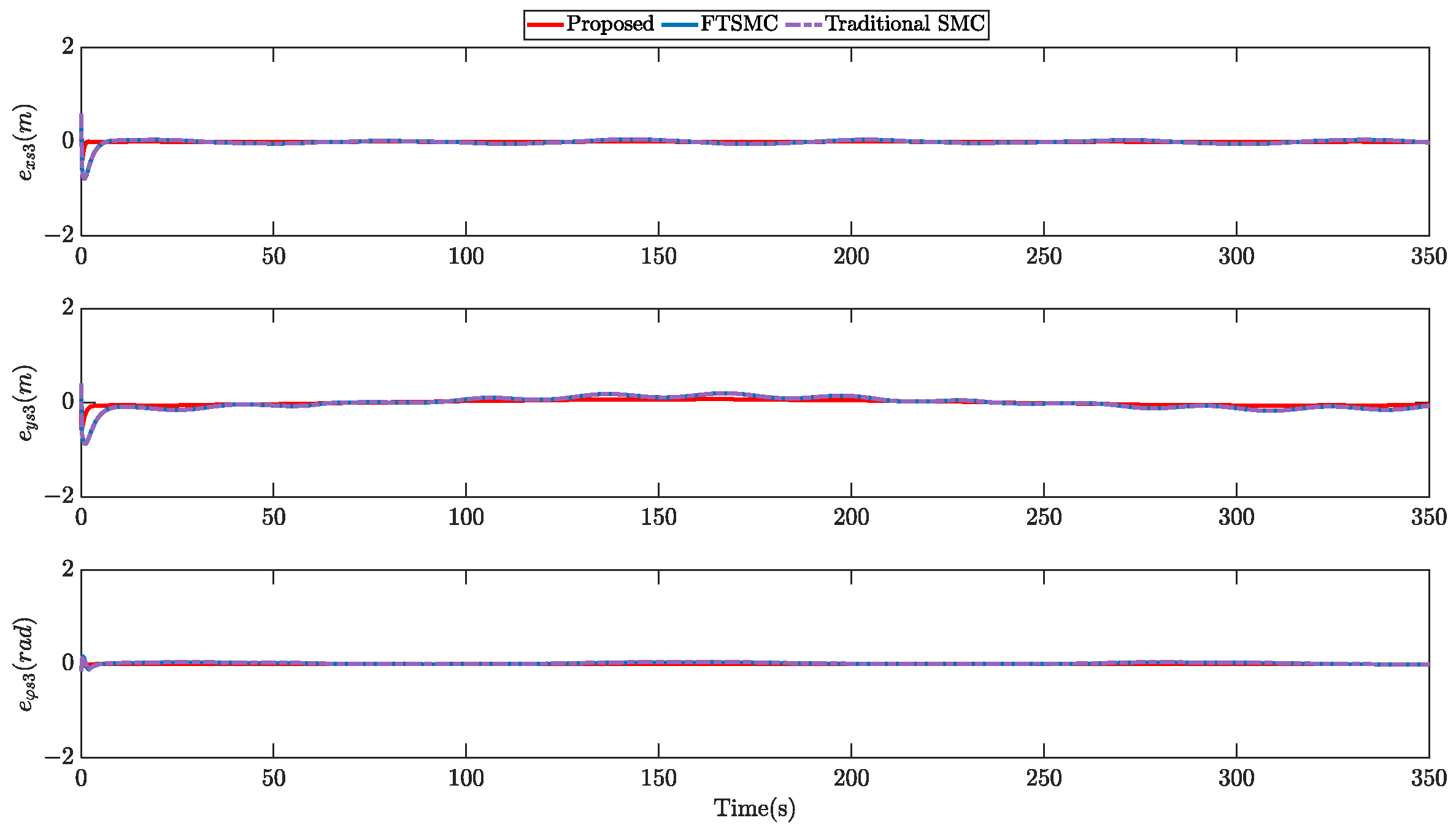
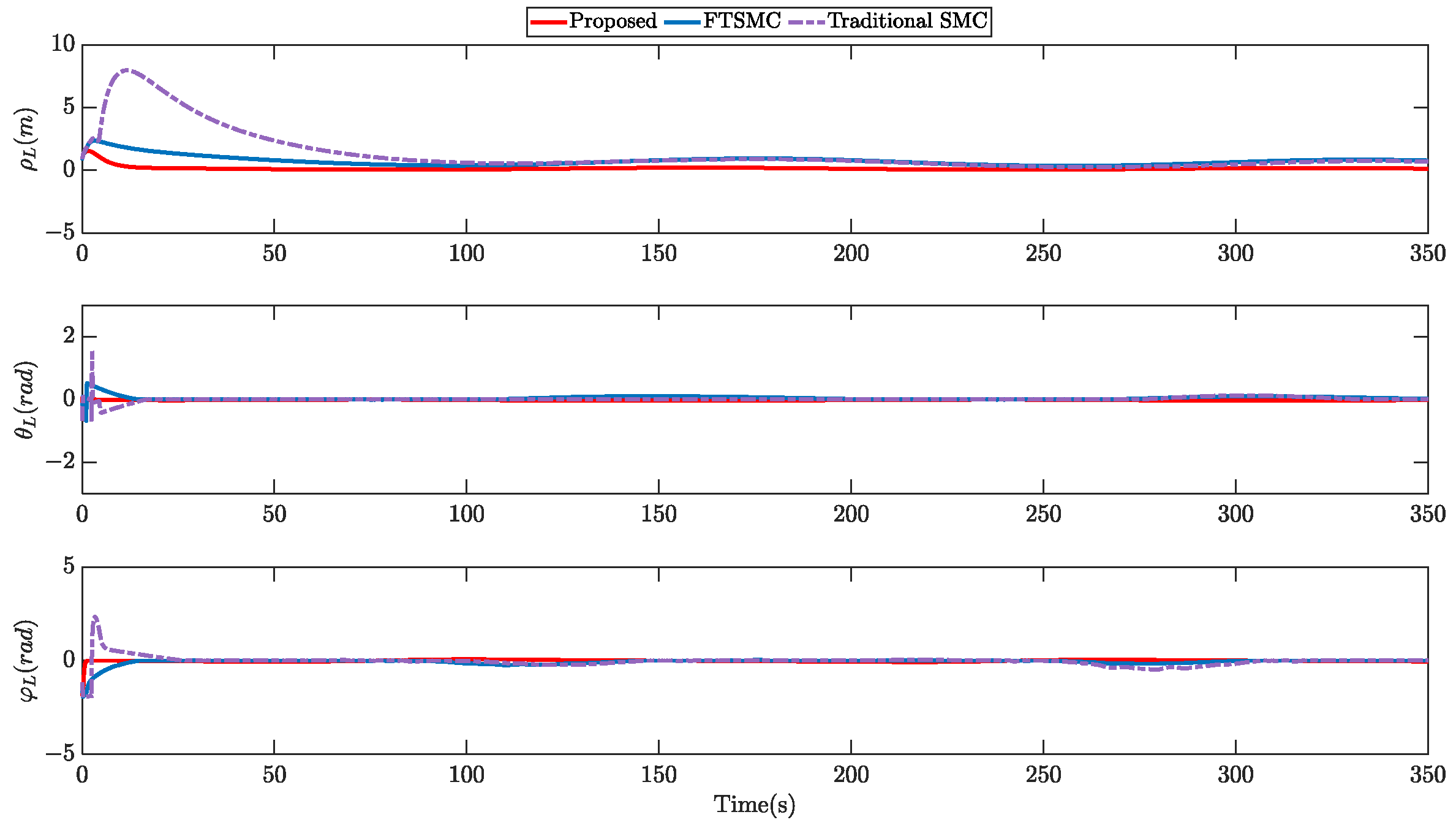
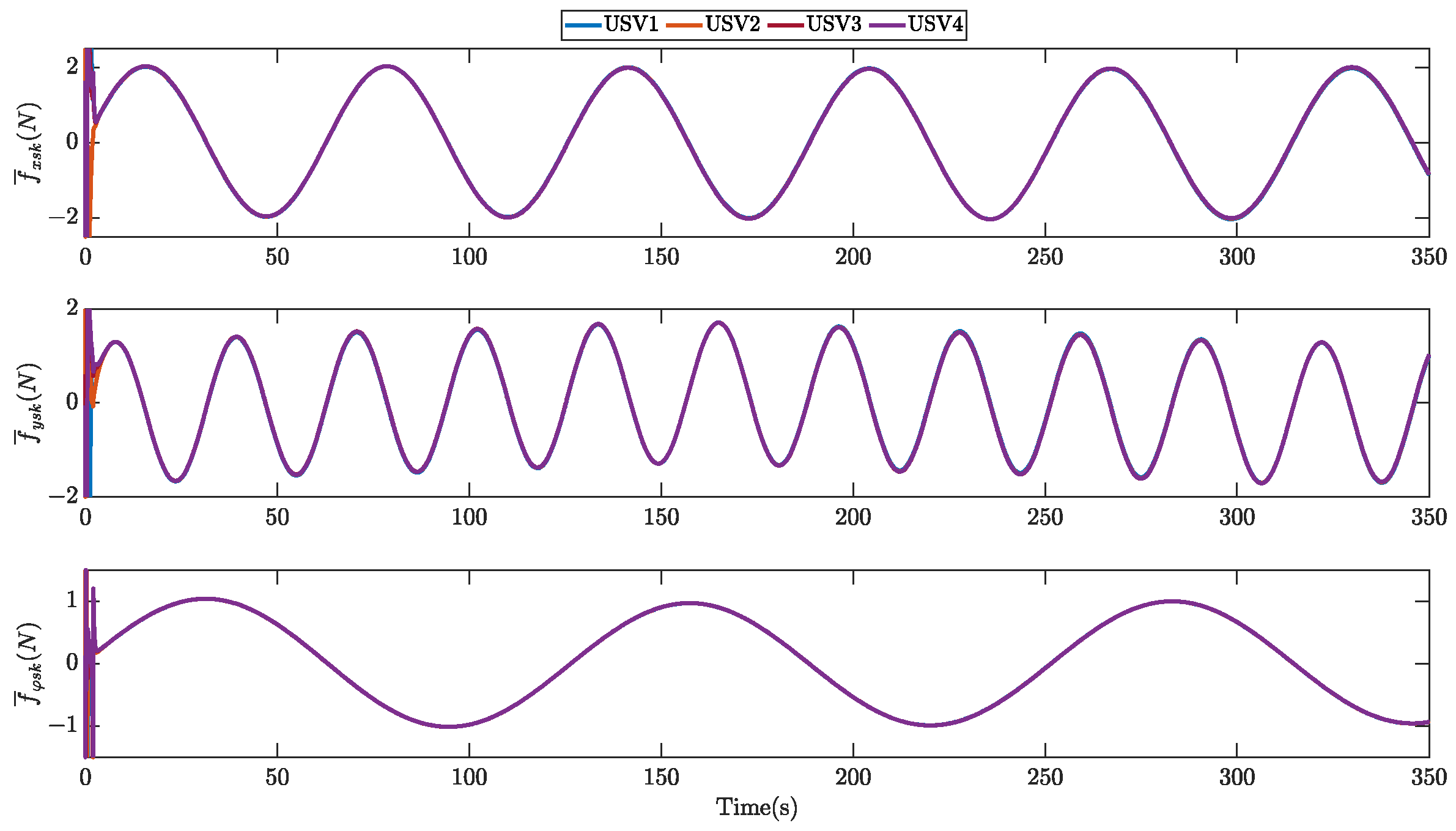
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.; Wang, W.; Bi, W.; Huang, Z. A path planning method based on deep reinforcement learning for AUV in complex marine environment. Ocean Eng. 2024, 313, 119354. [Google Scholar] [CrossRef]
- Sun, B.; Niu, N. Multi-AUVs cooperative path planning in 3D underwater terrain and vortex environments based on improved multi-objective particle swarm optimization algorithm. Ocean Eng. 2024, 311, 118944. [Google Scholar] [CrossRef]
- Liu, J.; Yu, F.; He, B.; Soares, C.G. A review of underwater docking and charging technology for autonomous vehicles. Ocean Eng. 2024, 297, 117154. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y. Joint-optimized coverage path planning framework for USV-assisted offshore bathymetric mapping: From theory to practice. Knowl. Based Syst. 2024, 304, 112449. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Shen, Y.; Dai, N.; He, B. Multi-AUV cooperative control and autonomous obstacle avoidance study. Ocean Eng. 2024, 304, 117634. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Zhang, G.; Chen, T. IROA-based LDPC-Lévy method for target search of multi AUV–USV system in unknown 3D environment. Ocean Eng. 2023, 286, 115648. [Google Scholar] [CrossRef]
- Peng, H.; Hu, J.-S. Traction/Braking Force Distribution for Optimal Longitudinal Motion During Curve Following. Veh. Syst. Dyn. 1996, 26, 301–320. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. Experimental verification using a driving simulator of the effect of simultaneous optimal distribution of tyre forces for active vehicle handling control. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2005, 219, 135–149. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Liu, Y. Event based practical fixed-time consensus control for heterogeneous nonlinear multiagent systems. Inf. Sci. 2023, 650, 119397. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, K. Backstepping-based adaptive control of underactuated AUV subject to unknown dynamics and zero tracking errors. Ocean Eng. 2024, 302, 117640. [Google Scholar] [CrossRef]
- Xu, H.; Fossen, T.I.; Guedes Soares, C. Uniformly semiglobally exponential stability of vector field guidance law and autopilot for path-following. Eur. J. Control 2020, 53, 88–97. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, J.; Shang, Y.; Zhang, Y.; Zhang, L.; Chen, W. Predefined-time global recursive sliding mode control for trajectory tracking of unmanned surface vehicles with disturbances uncertainties. Ocean Eng. 2024, 313, 119408. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Qin, X. Adaptive sliding mode control using a novel fully feedback recurrent neural network for quad-rotor UAVs. Neurocomputing 2024, 610, 128592. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Global robust adaptive path following of underactuated ships. Automatica 2006, 42, 1713–1722. [Google Scholar] [CrossRef]
- Yu, X.; Lin, W. Non-identifier based adaptive control of a chain of integrators and perturbations with unknown delays and parameters. Automatica 2025, 171, 111969. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H. Lyapunov-based model predictive control for trajectory tracking of hovercraft with actuator constraints and external disturbances. Ocean Eng. 2024, 310, 118631. [Google Scholar] [CrossRef]
- Moudoud, B.; Aissaoui, H. Fixed-time adaptive sliding mode-based trajectory tracking control for Wheeled Mobile Robot: Theoretical development and real-time implementation. e-Prime Adv. Electr. Eng. Electron. Energy 2024, 10, 100830. [Google Scholar] [CrossRef]
- Moudoud, B.; El Adraoui, I.; Aissaoui, H.; Bahani, A. Fault-Tolerant Control for Wheeled Mobile Robot via Finite-Time Adaptive Sliding Mode. In Proceedings of the 2024 4th International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), FEZ, Morocco, 16–17 May 2024; pp. 1–5. [Google Scholar]
- Wang, X.; Li, F.; Lee, S.; Shen, H. Event-triggered sliding mode control for interval type-2 fuzzy interconnected systems under Markov-model-based hybrid cyberattacks. Inf. Sci. 2025, 719, 122467. [Google Scholar] [CrossRef]
- Sahu, B.K.; Subudhi, B. Flocking Control of Multiple AUVs Based on Fuzzy Potential Functions. IEEE Trans. Fuzzy Syst. 2018, 26, 2539–2551. [Google Scholar] [CrossRef]
- Min, H.; Shi, S.; Gu, J.; Duan, N. Further results on fixed-time control for nonlinear systems with asymmetric output constraints. Automatica 2025, 171, 111933. [Google Scholar] [CrossRef]
- Jin, X.; Dong, J. Predefined time fuzzy adaptive control for stochastic nonlinear systems with limited time interval output constraints. Inf. Sci. 2025, 689, 121506. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, K.; Ni, J. Predefined-time adaptive learning control of nonlinear strict-feedback systems via dynamic regressor extension and mixing. ISA Trans. 2025. [Google Scholar] [CrossRef]
- Wang, H.; Shi, S.; Zhen, Z. Flexible performance-based predefined-time tracking control for unmanned helicopter with irregular constraints. Aerosp. Sci. Technol. 2025, 164, 110445. [Google Scholar] [CrossRef]
- Guo, G.; Xiao, S.; Chen, F.; Hou, Z.; Tan, H. Dynamic event-triggered predefined-time adaptive attitude fault-tolerant control for uncertain unmanned aerial vehicles with disturbances and actuator faults. Aerosp. Sci. Technol. 2025, 165, 110481. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, X.; Tian, X.; Mai, Q.; Sun, N. Predefined-time prescribed performance second-order sliding mode path following control for underactuated marine surface vehicles using self-structuring NN. Ocean Eng. 2024, 309, 118333. [Google Scholar] [CrossRef]
- Inoue, D.; Ito, Y.; Kashiwabara, T.; Saito, N.; Yoshida, H. Partially Centralized Model-Predictive Mean Field Games for controlling multi-agent systems. IFAC J. Syst. Control 2023, 24, 100217. [Google Scholar] [CrossRef]
- Chen, X.; Hao, F. Event-triggered consensus control of second-order multi-agent systems. Asian J. Control 2015, 17, 592–603. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S. Distributed Kalman Filtering and Control Through Embedded Average Consensus Information Fusion. IEEE Trans. Autom. Control 2019, 64, 4396–4403. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S.; Gupta, V.; Huang, Y.F. On Stability and Convergence of Distributed Filters. IEEE SIGNAL Process. Lett. 2021, 28, 494–498. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, L.; Zhang, G.; Wang, C.; Chai, Y.; Mao, Z. Research on 3D trajectory tracking of underactuated AUV under strong disturbance environment. Comput. Electr. Eng. 2023, 111, 108924. [Google Scholar] [CrossRef]
- Liu, H.; Feng, Z.; Tian, X.; Mai, Q. Adaptive predefined-time specific performance control for underactuated multi-AUVs: An edge computing-based optimized RL method. Ocean Eng. 2025, 318, 120048. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y. Leader-following control of high-order multi-agent systems under directed graphs: Pre-specified finite time approach. Automatica 2018, 87, 113–120. [Google Scholar] [CrossRef]
- Duan, Q.-S.; Tang, Z.; Ding, D. Distributed adaptive optimal secondary control for AC islanded microgrid under multiple event-triggered mechanisms. ISA Trans. 2025, 163, 65–75. [Google Scholar] [CrossRef]
- You, X.; Shi, M.; Guo, B.; Zhu, Y.; Lai, W.; Dian, S.; Liu, K. Event-triggered adaptive fuzzy tracking control for a class of fractional-order uncertain nonlinear systems with external disturbance. Chaos Solitons Fractals 2022, 161, 112393. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, G.; Huang, C.; Zhang, W. Memory-based event-triggered path-following control for a USV in the presence of DoS attack. Ocean Eng. 2024, 310, 118627. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L. Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica 2012, 48, 1432–1439. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-time sliding mode formation control of AUVs based on a disturbance observer. IEEE/CAA J. Autom. Sin. 2020, 7, 539–545. [Google Scholar] [CrossRef]
- González-Prieto, J.A. Practical fixed-time non-singular sliding mode control of second order nonlinear dynamic systems with chattering and overshooting avoidance. Eur. J. Control 2024, 80, 101114. [Google Scholar] [CrossRef]
- Ding, T.-F.; Ge, M.-F.; Xiong, C.; Liu, Z.-W.; Ling, G. Prescribed-time formation tracking of second-order multi-agent networks with directed graphs. Automatica 2023, 152, 110997. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.L.P. Reduced-Order Observer-Based Dynamic Event-Triggered Adaptive NN Control for Stochastic Nonlinear Systems Subject to Unknown Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1678–1690. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Dai, Y.; Yang, C.; Yu, S.; Mao, Y.; Zhao, Y. Finite-Time Trajectory Tracking for Marine Vessel by Nonsingular Backstepping Controller With Unknown External Disturbance. IEEE Access 2019, 7, 165897–165907. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Design for Underactuated and Nonlinear Marine Systems. In Control of Ships and Underwater Vehicles; Springer Nature: London, UK, 2009. [Google Scholar]
- Sui, B.; Zhang, J.; Liu, Z.; Wei, J. Distributed prescribed-time cooperative formation tracking control of networked unmanned surface vessels under directed graph. Ocean Eng. 2024, 305, 117993. [Google Scholar] [CrossRef]
- Liu, H.; Tian, X.; Wang, G.; Zhang, T. Robust H∞ finite-time stability control of a class of nonlinear systems. Appl. Math. Model. 2016, 40, 5111–5122. [Google Scholar] [CrossRef]
- El Khazane, J.; Tissir, E.H. Achievement of MPPT by finite time convergence sliding mode control for photovoltaic pumping system. Sol. Energy 2018, 166, 13–20. [Google Scholar] [CrossRef]
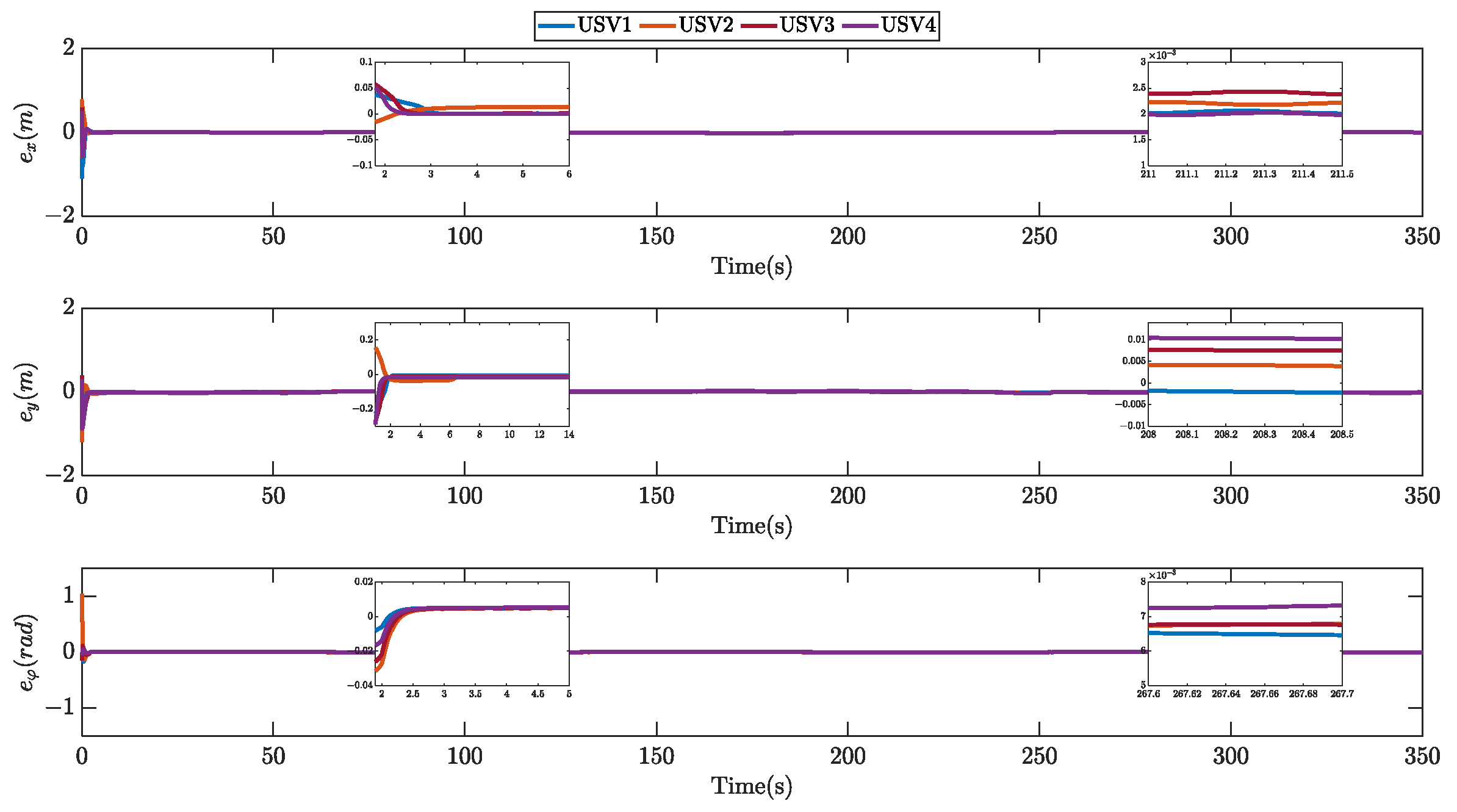
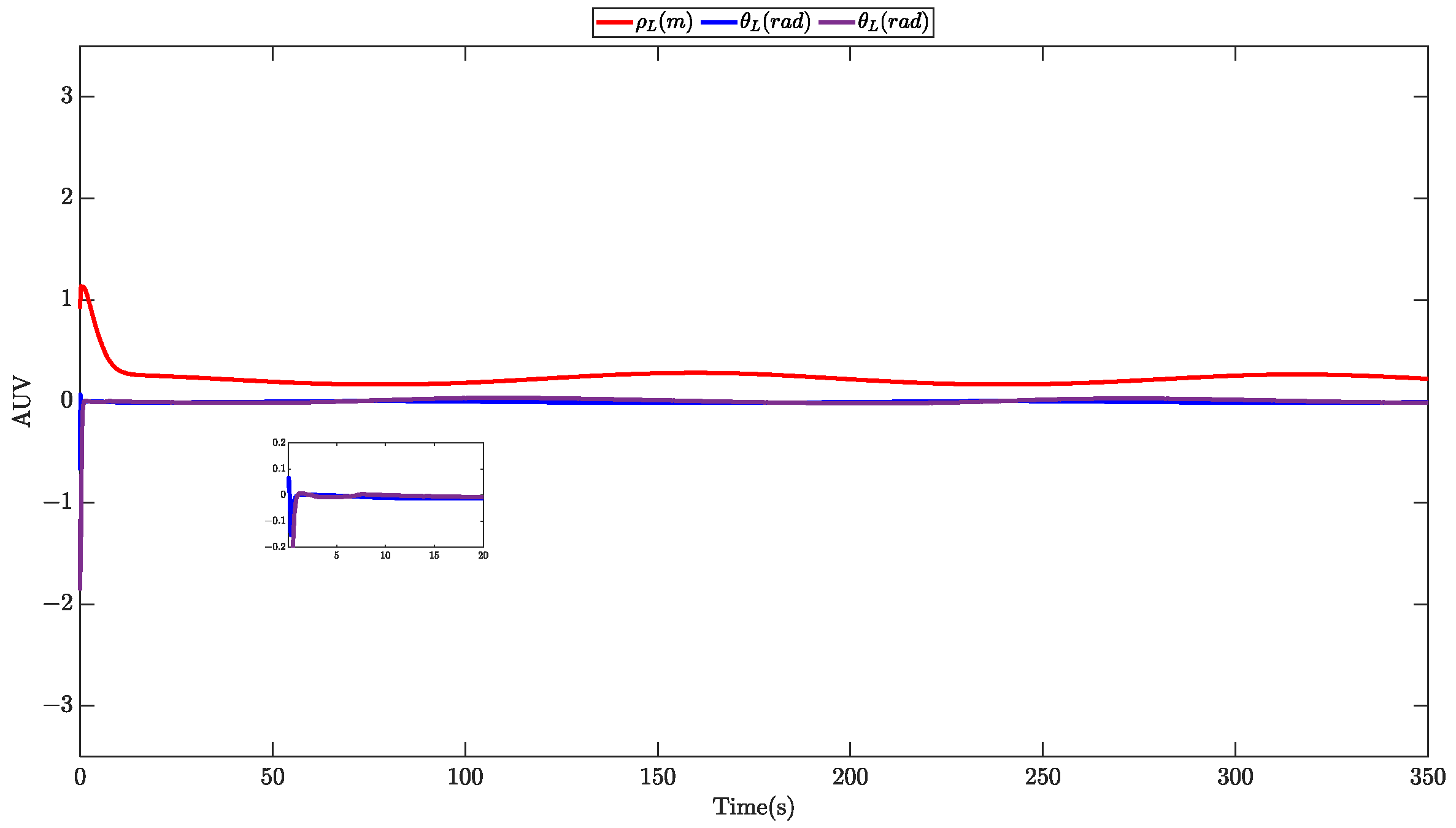



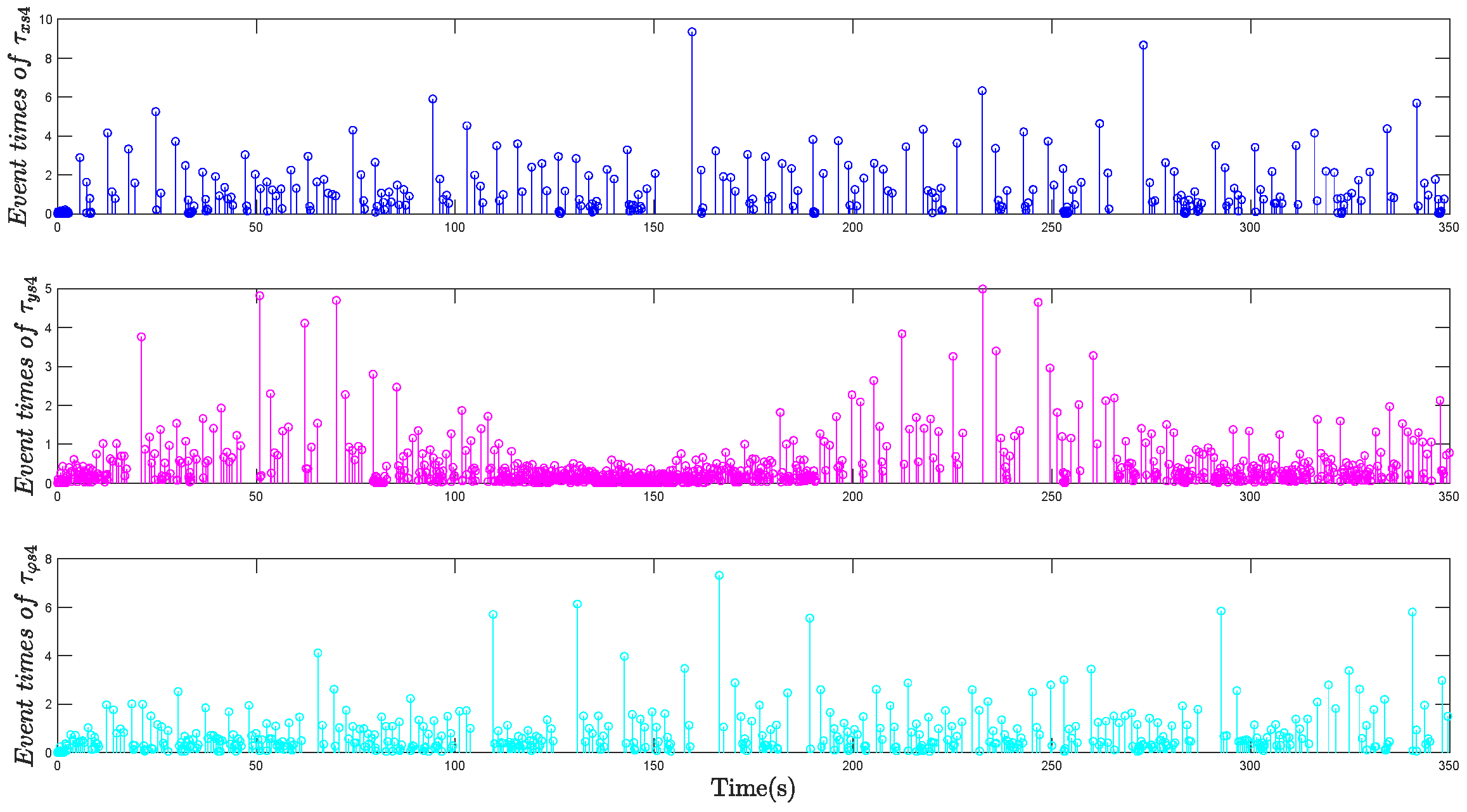
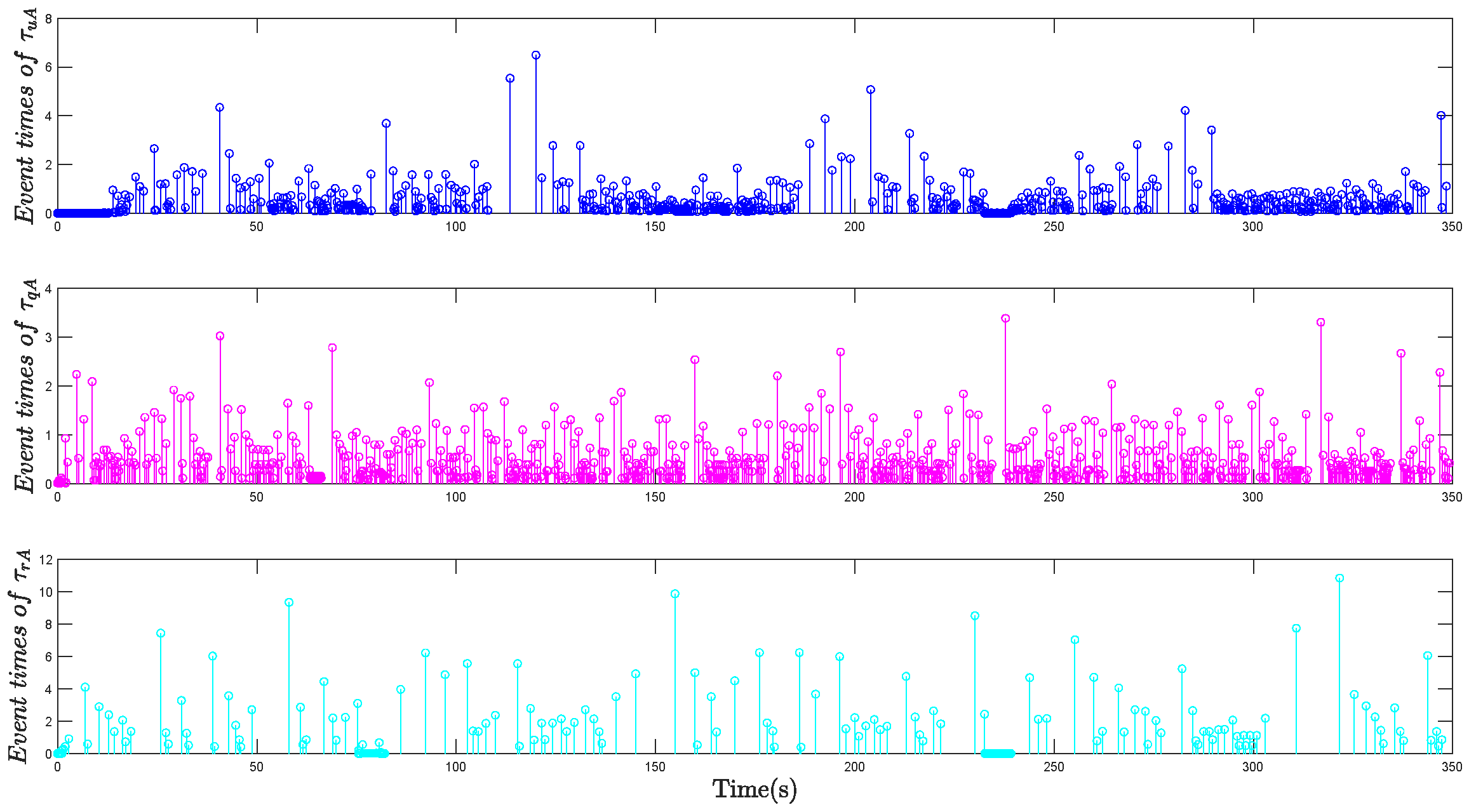





| Symbol | Value | Symbol | Value |
|---|---|---|---|
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| DRPSC/FTSMC/Traditional SMC | |||||
|---|---|---|---|---|---|
| Convergence Time (s) | SD of Control Inputs (N) | RMSE of Tracking Errors | |||
| Normal Disturbance (m) | Large Disturbance (m) | ||||
| USV1 | x | 5/15/15 | 6.6720/18.0863/18.3247 | 0.0321/0.0716/0.0712 | 0.0370/0.1060/0.1007 |
| y | 5/15/15 | 3.4357/13.2030/13.3310 | 0.0242/0.0302/0.0296 | 0.0276/0.0571/0.0510 | |
| 3/6/7 | 3.5073/14.9712/14.8417 | 0.0191/0.0217/0.0215 | 0.0212/0.0234/0.0235 | ||
| USV2 | x | 5/15/15 | 5.7180/18.2679/18.4101 | 0.0225/0.0339/0.0339 | 0.0292/0.0448/0.0484 |
| y | 5/15/15 | 2.8891/12.6037/12.6430 | 0.0356/0.0221/0.0218 | 0.0379/0.0388/0.0417 | |
| 3/6/7 | 3.2316/14.3522/14.4568 | 0.0187/0.0261/0.0260 | 0.0208/0.0278/0.0293 | ||
| USV3 | x | 5/10/10 | 6.0189/13.3098/8.6996 | 0.0150/0.0440/0.0435 | 0.0240/0.0751/0.0746 |
| y | 5/15/15 | 5.0535/11.2161/12.0689 | 0.0543/0.0549/0.0543 | 0.0557/0.0867/0.0865 | |
| 3/6/7 | 1.1838/20.4412/22.9665 | 0.0059/0.0095/0.0098 | 0.0109/0.0133/0.0183 | ||
| USV4 | x | 5/15/15 | 6.3733/6.8035/6.8977 | 0.0188/0.0500/0.0496 | 0.0266/0.0816/0.0834 |
| y | 5/15/15 | 5.9358/14.2980/14.3725 | 0.0723/0.0757/0.0751 | 0.0733/0.1121/0.1140 | |
| 3/6/7 | 0.8599/21.6587/21.8173 | 0.0066/0.0076/0.0076 | 0.0113/0.0146/0.0219 | ||
| AUV | 15/40/80 | 5.3334/17.7609/18.4482 | 0.2255/1.1604/2.0929 | 0.2350/0.8690/2.2084 | |
| 5/15/18 | 13.3637/18.5128/43.6015 | 0.0261/0.0773/0.0676 | 0.0304/0.1930/0.1234 | ||
| 3/15/30 | 10.7234/12.3839/10.7510 | 0.0684/0.1479/0.2786 | 0.0685/0.1545/0.4719 | ||
| DRPSC | FTSMC | Traditional SMC | ||||
|---|---|---|---|---|---|---|
| Trigger Times | Percentage | Trigger Times | Percentage | Trigger Times | Percentage | |
| 411 | 1.17% | 3193 | 9.12% | 3475 | 9.93% | |
| 1152 | 3.29% | 10719 | 30.62% | 10879 | 31.08% | |
| 495 | 1.41% | 6620 | 18.91% | 7412 | 21.18% | |
| 336 | 0.96% | 3161 | 9.03% | 3215 | 9.19% | |
| 674 | 1.93% | 11040 | 31.54% | 11085 | 31.67% | |
| 523 | 1.49% | 6159 | 17.60% | 6144 | 17.55% | |
| 369 | 1.05% | 3196 | 9.13% | 3211 | 9.17% | |
| 574 | 1.64% | 11249 | 32.14% | 11197 | 31.99% | |
| 543 | 1.55% | 6248 | 17.85% | 6446 | 18.42% | |
| 395 | 1.13% | 3056 | 8.73% | 3067 | 8.76% | |
| 1266 | 3.62% | 11195 | 31.98% | 11305 | 32.30% | |
| 497 | 1.42% | 8445 | 24.13% | 8205 | 23.44% | |
| 2449 | 7.00% | 3962 | 11.32% | 6730 | 19.23% | |
| 736 | 2.10% | 6609 | 18.88% | 9775 | 27.93% | |
| 1210 | 3.46% | 6788 | 19.39% | 6837 | 19.53% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Li, L.; Tian, X.; Mai, Q. Distributed Robust Predefined-Time Sliding Mode Control for AUV-USV Heterogeneous Multi-Agent Systems Based on Memory Event-Triggered Mechanism Under Input Saturation. J. Mar. Sci. Eng. 2025, 13, 1428. https://doi.org/10.3390/jmse13081428
Liu H, Li L, Tian X, Mai Q. Distributed Robust Predefined-Time Sliding Mode Control for AUV-USV Heterogeneous Multi-Agent Systems Based on Memory Event-Triggered Mechanism Under Input Saturation. Journal of Marine Science and Engineering. 2025; 13(8):1428. https://doi.org/10.3390/jmse13081428
Chicago/Turabian StyleLiu, Haitao, Luchuan Li, Xuehong Tian, and Qingqun Mai. 2025. "Distributed Robust Predefined-Time Sliding Mode Control for AUV-USV Heterogeneous Multi-Agent Systems Based on Memory Event-Triggered Mechanism Under Input Saturation" Journal of Marine Science and Engineering 13, no. 8: 1428. https://doi.org/10.3390/jmse13081428
APA StyleLiu, H., Li, L., Tian, X., & Mai, Q. (2025). Distributed Robust Predefined-Time Sliding Mode Control for AUV-USV Heterogeneous Multi-Agent Systems Based on Memory Event-Triggered Mechanism Under Input Saturation. Journal of Marine Science and Engineering, 13(8), 1428. https://doi.org/10.3390/jmse13081428






