Nonparametric Prediction of Ship Maneuvering Motions Based on Interpretable NbeatsX Deep Learning Method
Abstract
1. Introduction
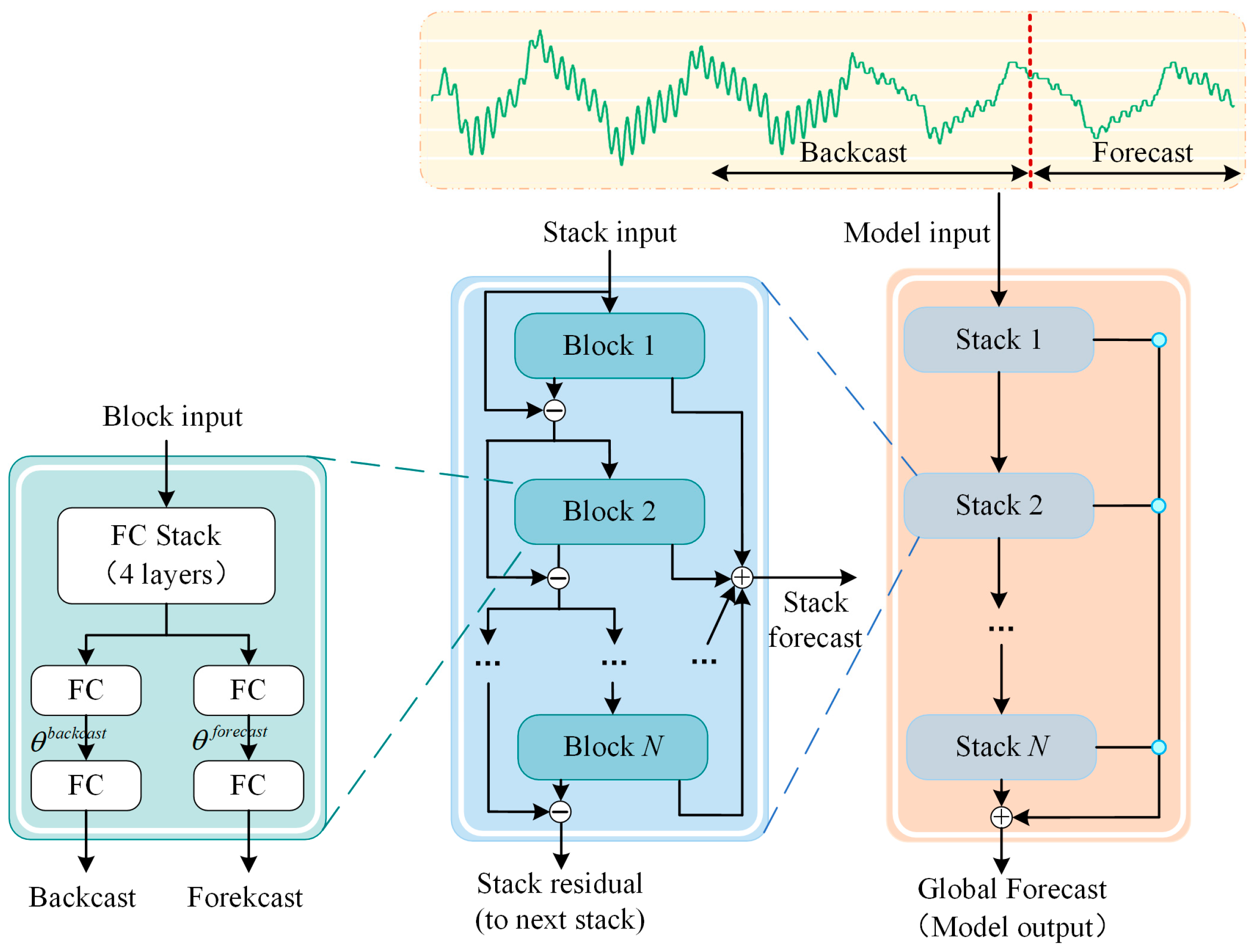
- Simple, general, and expressive model architecture: The architecture comprises a novel backbone built exclusively from fully connected layers, organized into block and stack modules. Block layers employ residual connections to iteratively backcast input signals, while stack layers aggregate multi-horizon forecasts and backcasts, enabling efficient time series feature learning without recurrent or convolutional operations.
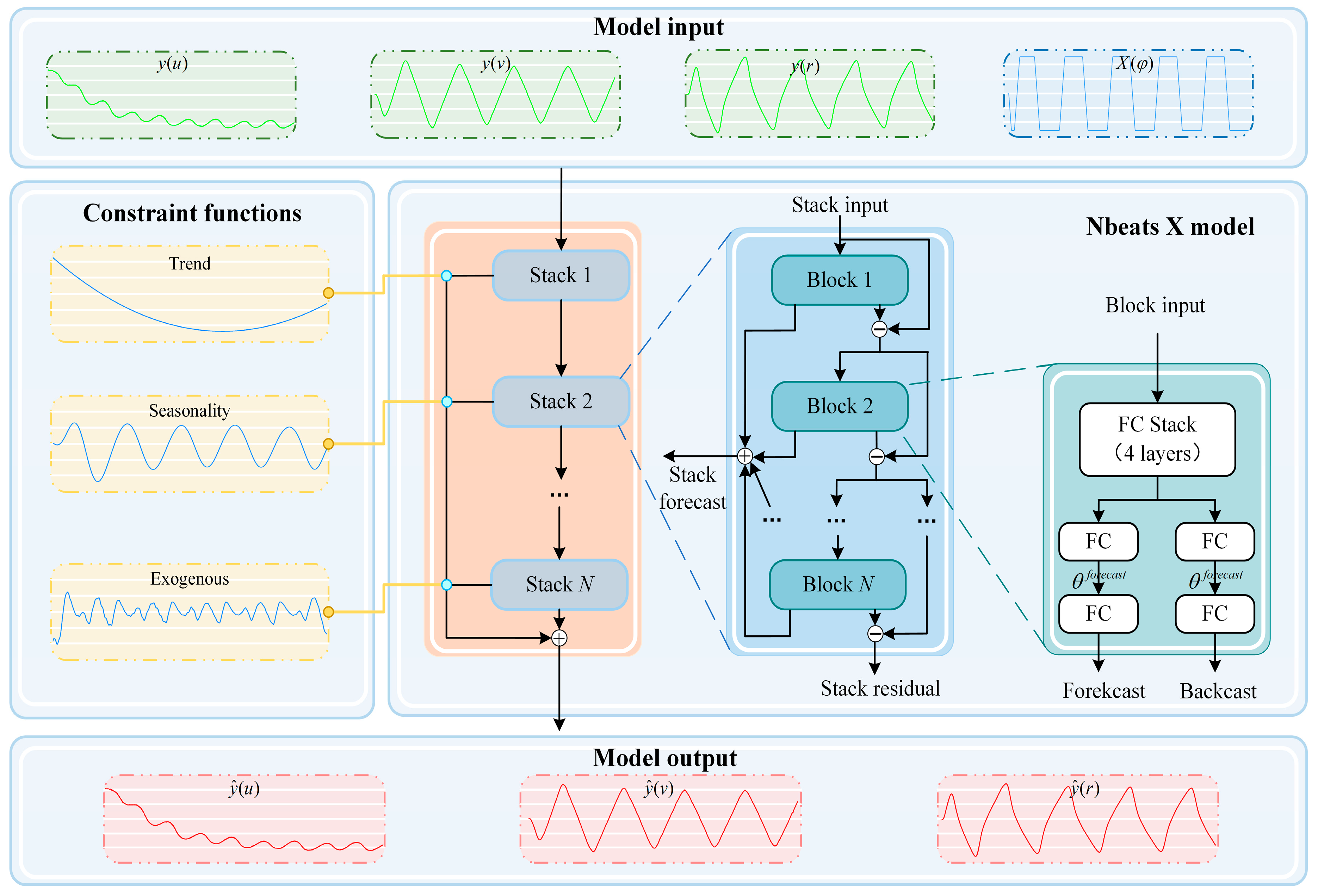
- Interpretable time series signal decomposition: Based on the stack structure of the NbeatsX model, through the establishment of flexible prediction modules with stack restrictions, it is feasible to select classic time series feature functions such as trend, seasonality, and expansion factor functions to jointly construct precise and interpretable prediction outcomes.
- Results and discussion based on the KVLCC2 dataset: The model’s prediction accuracy is validated using KVLCC2 ship model data obtained from SIMMAN workshop benchmark test cases. A dedicated interpretability module then decomposes each prediction into trend, seasonal, and exogenous contributions, providing clear and actionable insights into the model’s decision process.
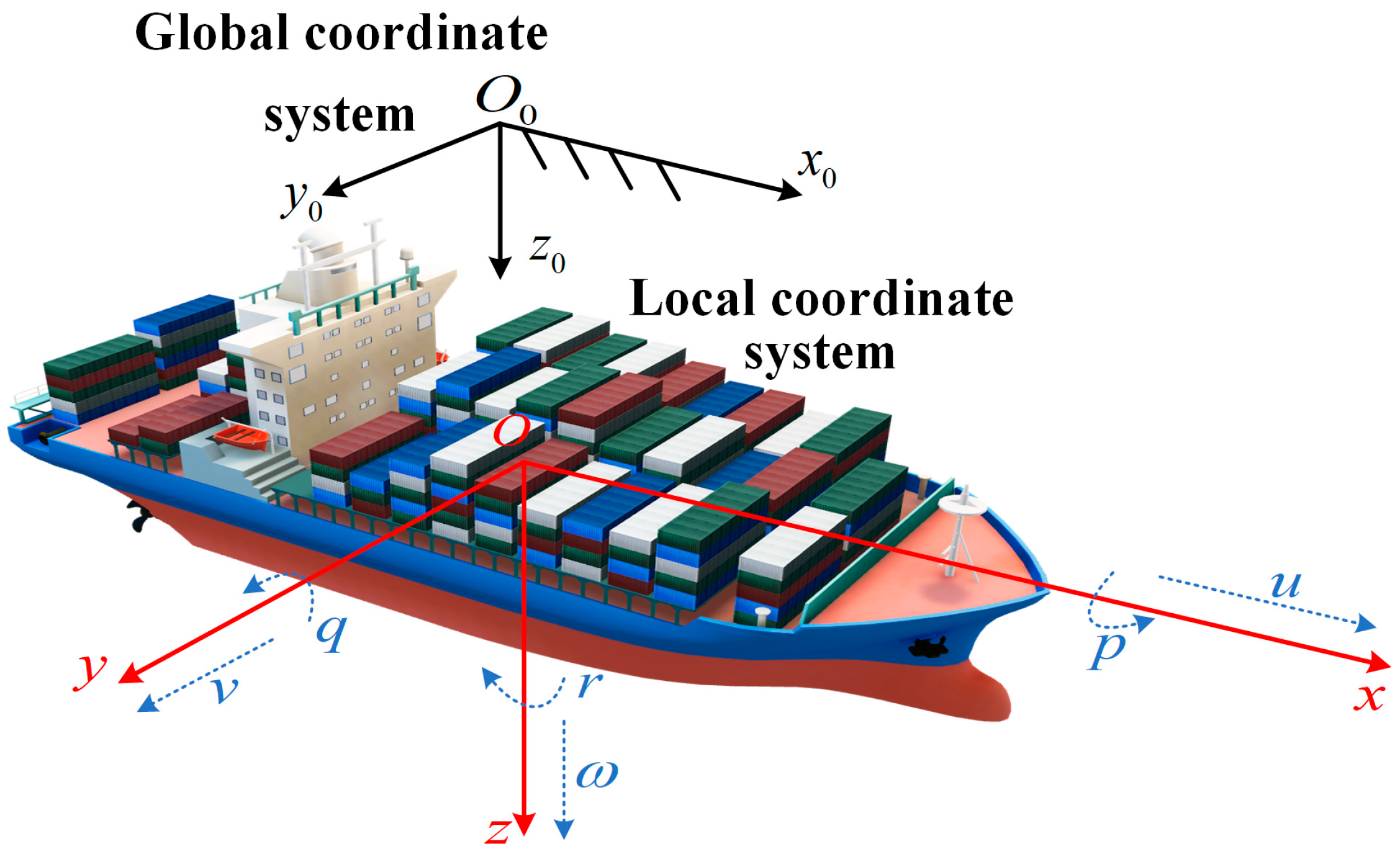
2. Nonparametric Ship Maneuvering Model
3. Proposed Method
3.1. Input Matrix Based on Spatiotemporal Features
3.2. Interpretable Configuration
| Algorithm 1: Using the interpretable module for predicting ship maneuvering motion. |
| Input: Dataset// Ship maneuvering motion dataset ; b, f, epochs // b for external feature sequences length, f for target feature sequence length , // The basic parameter vector of the calculated trend , // The basic parameter vector of the calculated seasonality , // The basic parameter vector of the calculated exogenous t = shape ()[0], s = shape ()[0], e = shape ()[0]; while epoch < epochs do index = [random(0 – len(Dataset), b)] x = Dataset[index]; //using index as a pointer y = Dataset[index + f][−f]; forecast = x, residuals = x; while i < number of blocks do if block == T then = FCNN(residuals);// expansion coefficient block_forecast = [: t] * ; block_backcast = [t :] * ; if block == S then = FCNN(residuals); block_forecast = [: s] * ; block_backcast = [s :] * ; if block == E then theta = FCNN(residuals); block_forecast = [: e] * ; block_backcast = [e :] * ; residuals = (residuals –block_backcast); = residuals + block_forecast; // the prediction results i++; Get cost function of (, y); epoch++; |
3.3. Nonparametric Prediction Method Based on Nbeatsx
4. Results and Discussion
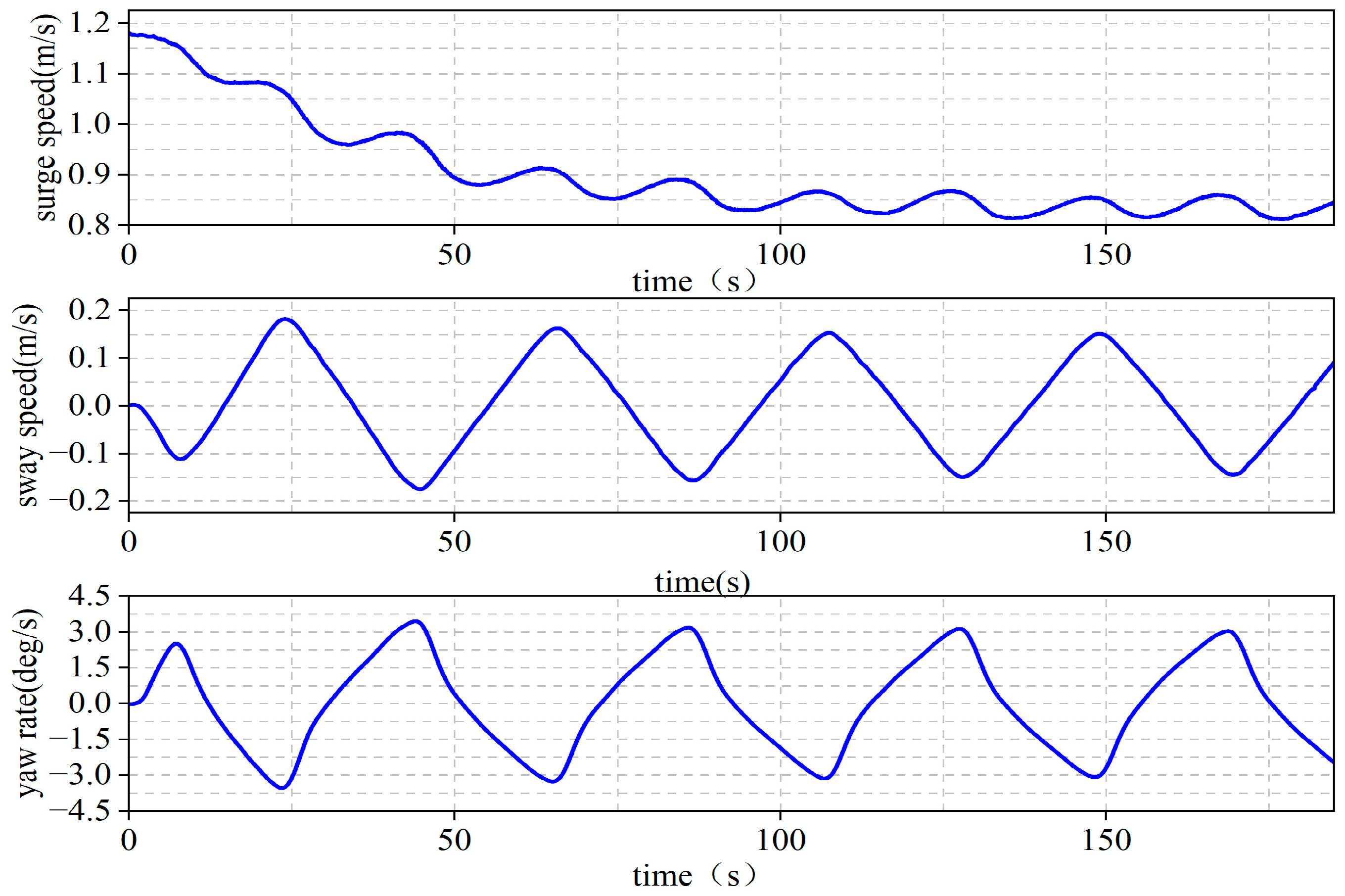
4.1. Data Description and Preparation
4.2. Prediction Results and Discussion
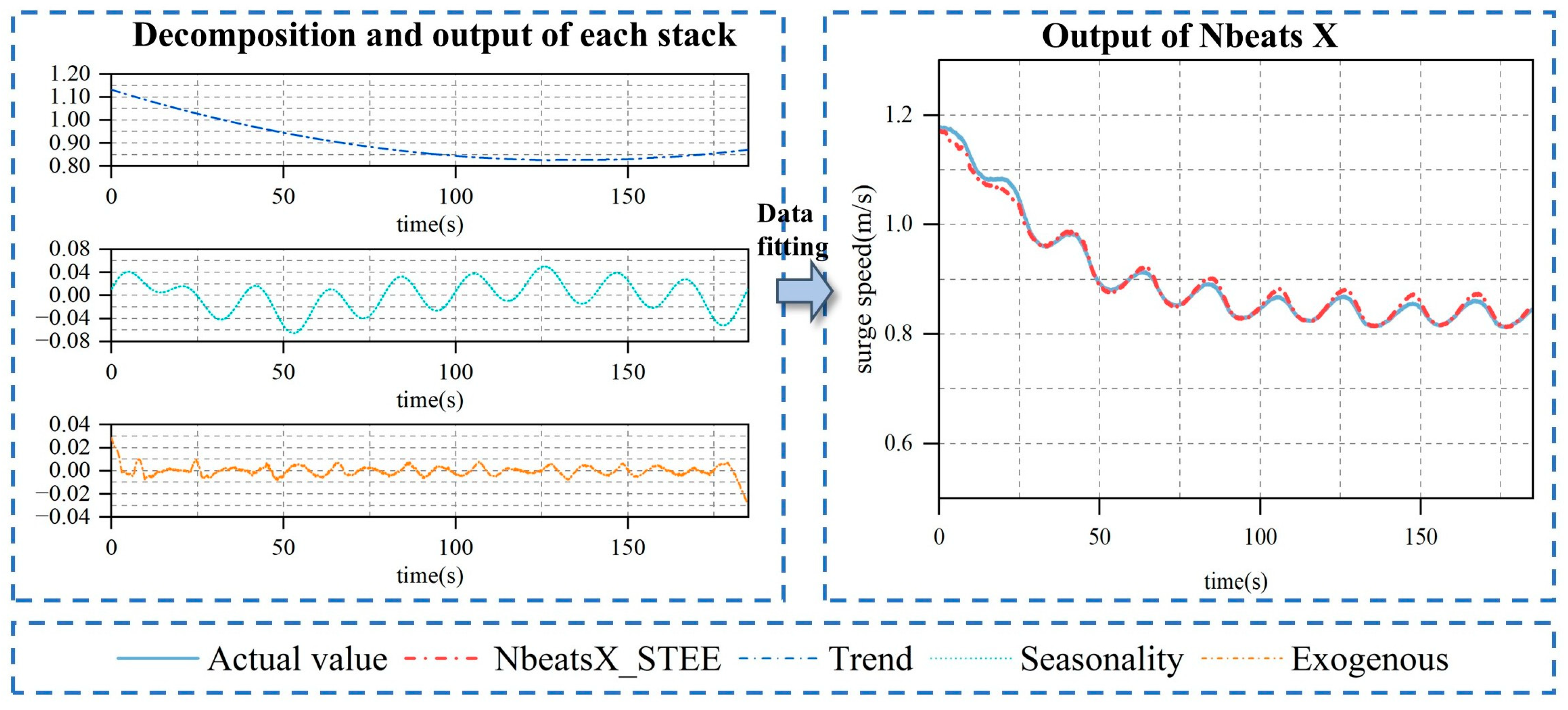
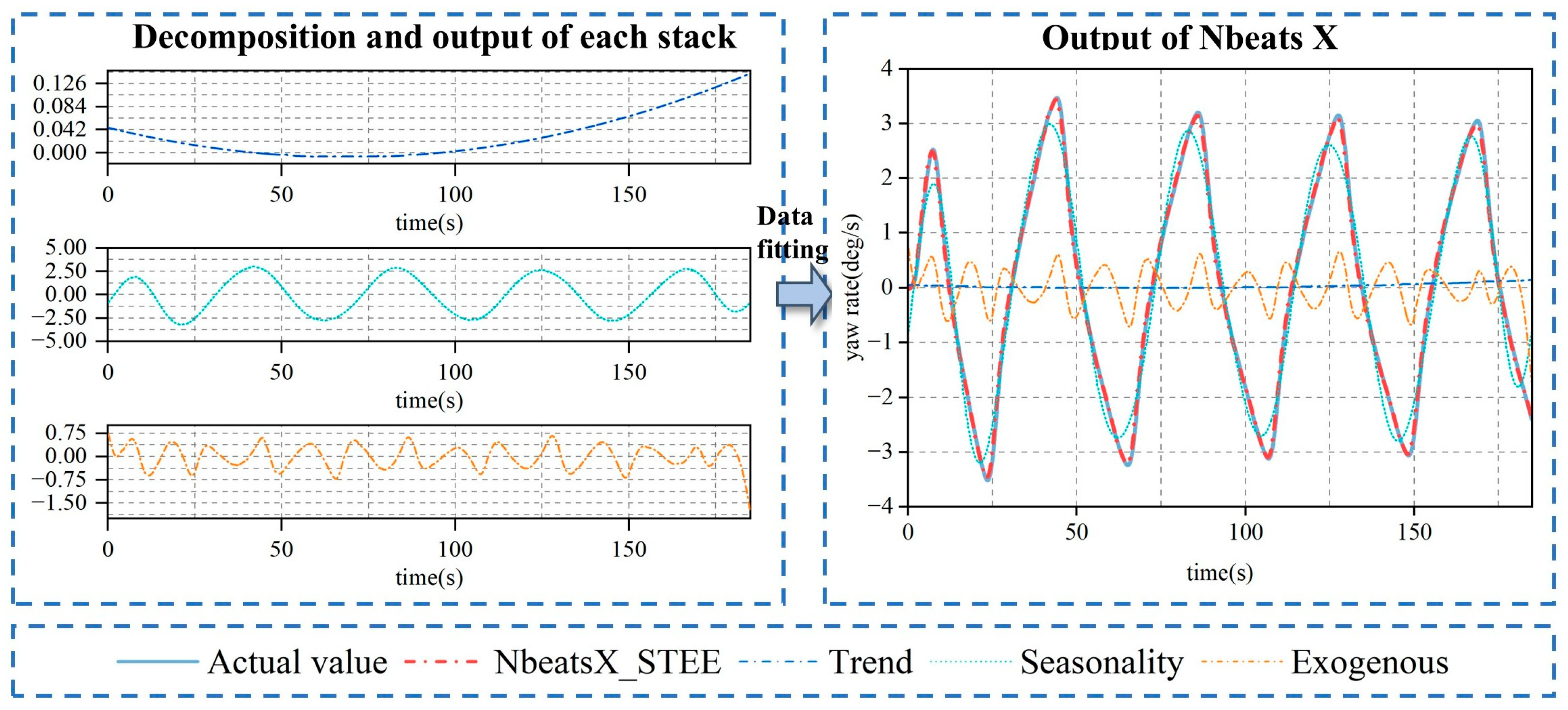
- Engineering perspective: From an engineering perspective, NbeatsX conducts decomposition processing based on the prescribed basis functions and subsequently integrates the decomposed data to form the final prediction outcome. This implies the addition of “constraints” to the deep learning model, for instance, the necessity to employ polynomial functions for fitting. Moreover, these constraints are typically interpretable (e.g., periodic and polynomial functions).
- Clearer understanding of ship motion patterns: NbeatsX offers a transparent and streamlined architecture. Its stack modules, each configured with trend, seasonal, or exogenous basis functions, enable the model to isolate and examine specific motion characteristics. For instance, fitting the seasonal stack reveals the cyclic behavior of ship maneuvers, while the trend stack exposes longer-term tendencies across different degrees of freedom.
- Interface for advanced ship maneuvering motion research: The stack structure of the NbeatsX model provides an interface for more specialized research in ship maneuvering motion. For instance, setting specific computational formulas as the general function constraints in the exogenous factors stack could help analyze unobserved variables or random noise, revealing information the model might have overlooked.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IMO. Regulatory Scoping Exercise for the Use of Maritime Autonomous Surface Ships (MASS). MSC 99th Session. In Report of the Working Group; IMO: London, UK, 2018. [Google Scholar]
- Kaidi, S.; Lefrançois, E.; Smaoui, H. Numerical Modelling of the Muddy Layer Effect on Ship’s Resistance and Squat. Ocean Eng. 2020, 199, 106939. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, Z.; Zhao, C.; Chen, X. Deterministic ship roll forecasting model based on multi-objective data fusion and multi-layer error correction. Appl. Soft Comput. 2023, 132, 109915. [Google Scholar] [CrossRef]
- Perera, L.P.; Oliveira, P.; Guedes Soares, C. Dynamic Parameter Estimation of a Nonlinear Vessel Steering Model for Ocean Navigation. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 31 October 2011; ASME: New York, NY, USA, 2011; pp. 881–888. [Google Scholar]
- Yu, Y.; Hao, H.; Wang, Z.; Peng, Y.; Xie, S. Online prediction of ship maneuvering motions based on adaptive weighted ensemble learning under dynamic changes. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2341922. [Google Scholar] [CrossRef]
- Luo, W.L.; Zou, Z.J. Parametric Identification of Ship Maneuvering Models by Using Support Vector Machines. Ship Res. 2009, 53, 19–30. [Google Scholar] [CrossRef]
- Jian, C.; Jiayuan, Z.; Feng, X.; Jianchuan, Y.; Zaojian, Z.; Hao, Y.; Tao, X.; Luchun, Y. Parametric estimation of ship maneuvering motion with integral sample structure for identification. Appl. Ocean Res. 2015, 52, 212–221. [Google Scholar] [CrossRef]
- Zhang, X.G.; Zou, Z.J. Black-Box Modeling of Ship Manoeuvring Motion Based on Feed-Forward Neural Network with Chebyshev Orthogonal Basis Function. J. Mar. Sci. Technol. 2013, 18, 42–49. [Google Scholar] [CrossRef]
- Xu, W.Z.; Maki, K.J.; Silva, K.M. A Data-Driven Model for Nonlinear Marine Dynamics. Ocean Eng. 2021, 236, 109469. [Google Scholar] [CrossRef]
- Silva, K.M.; Maki, K.J. Data-Driven System Identification of 6-DoF Ship Motion in Waves with Neural Networks. Appl. Ocean Res. 2022, 125, 103222. [Google Scholar] [CrossRef]
- Mei, B.; Sun, L.; Shi, G. White-Black-Box Hybrid Model Identification Based on RM-RF for Ship Maneuvering. IEEE Access 2019, 7, 57691–57705. [Google Scholar] [CrossRef]
- Skulstad, R.; Li, G.; Fossen, T.I.; Vik, B.; Zhang, H. A Hybrid Approach to Motion Prediction for Ship Docking—Integraton of a Neural Network Model into the Ship Dynamic Model. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the Difficulty of Training Recurrent Neural Networks. In Proceedings of the 30th International Conference on Machine Learning (ICML’13). Proc. Mach. Learn. Res. 2013, 28, 1310–1318. [Google Scholar]
- Mangkunegara, I.S.; Purwono, P.; Ma’arif, A.; Basil, N.; Marhoon, H.M.; Sharkawy, A.-N. Transformer Models in Deep Learning: Foundations, Advances, Challenges and Future Directions. Bul. Ilm. Sarj. Tek. Elektro 2025, 7, 231–241. [Google Scholar]
- Zhang, T.; Zheng, X.Q.; Liu, M.X. Multiscale Attention-Based LSTM for Ship Motion Prediction. Ocean Eng. 2021, 230, 109066. [Google Scholar] [CrossRef]
- Wang, N.; Kong, X.; Ren, B.; Hao, L.; Han, B. SeaBil: Self-Attention-Weighted Ultrashort-Term Deep Learning Prediction of Ship Maneuvering Motion. Ocean Eng. 2023, 287, 115890. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.P.; Soares, C.G. Maritime Traffic Probabilistic Prediction Based on Ship Motion Pattern Extraction. Reliab. Eng. Syst. Saf. 2022, 217, 108061. [Google Scholar] [CrossRef]
- Majidiyan, H.; Enshaei, H.; Howe, D.; Gubesch, E. A Concise Account for Challenges of Machine Learning in Seakeeping. Procedia Comput. Sci. 2025, 253, 2849–2858. [Google Scholar] [CrossRef]
- Wang, H.; Yan, R.; Wang, S.; Zhen, L. Innovative Approaches to Addressing the Tradeoff between Interpretability and Accuracy in Ship Fuel Consumption Prediction. Transp. Res. Part C 2023, 157, 104361. [Google Scholar] [CrossRef]
- Davies, A.; Veličković, P.; Buesing, L.; Blackwell, S.; Zheng, D.; Tomašev, N.; Tanburn, R.; Battaglia, P.; Blundell, C.; Juhász, A.; et al. Advancing Mathematics by Guiding Human Intuition with AI. Nature 2021, 600, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Wang, Z.H.; Zou, Z.J. Black-box modeling of ship maneuvering motion based on multi-output nu-support vector regression with random excitation signal. Ocean Eng. 2022, 257, 111279. [Google Scholar] [CrossRef]
- Zhou, X.; Zou, L.; Ouyang, Z.L.; Liu, S.Y.; Zou, Z.J. Nonparametric Modeling of Ship Maneuvering Motions in Calm Water and Regular Waves Based on R-LSTM Hybrid Method. Ocean Eng. 2023, 285, 115259. [Google Scholar] [CrossRef]
- Ouyang, Z.-L.; Liu, S.-Y.; Zou, Z.-J. Nonparametric Modeling of Ship Maneuvering Motion in Waves Based on Gaussian Process Regression. Ocean Eng. 2022, 264, 112100. [Google Scholar] [CrossRef]
- Wang, X.; Li, C.; Yi, C.; Xu, X.; Wang, J.; Zhang, Y. EcoForecast: An Interpretable Data-Driven Approach for Short-Term Macroeconomic Forecasting Using N-BEATS Neural Network. Eng. Appl. Artif. Intell. 2022, 114, 105072. [Google Scholar] [CrossRef]
- Souto, H.G.; Moradi, A. Introducing NBEATSx to Realized Volatility Forecasting. Expert Syst. Appl. 2024, 242, 122802. [Google Scholar] [CrossRef]
- Zhu, B.; Li, X.; Wang, Y.; Xu, Q. Text-based corn futures price forecasting using improved neural basis expansion analysis with exogenous variables. Int. J. Forecast. 2024, 43, 2042–2063. [Google Scholar]
- Lin, Y.; Chen, J.; Zhang, L. Agricultural yield forecasting using NBEATSx with satellite-derived exogenous inputs. Field Crops Res. 2025, 292, 108774. [Google Scholar]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar]
- Olivares, K.G.; Challu, C.; Marcjasz, G.; Weron, R.; Dubrawski, A. Neural Basis Expansion Analysis with Exogenous Variables: Forecasting Electricity Prices with NBEATSx. Int. J. Forecast 2023, 39, 884–900. [Google Scholar] [CrossRef]
- Salim, M.; Rauf, H.T.; Mushtaq, M. DRCNN: Decomposing Residual Convolutional Neural Networks for Time-Series Trend Extraction. Sci. Rep. 2023, 13, 15901. [Google Scholar]
- Hao, J.; Liu, F. Improving Long-Term Multivariate Time Series Forecasting with a Seasonal-Trend Decomposition-Based 2-Dimensional Temporal Convolution Dense Network. Sci. Rep. 2024, 14, 1689. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Wang, C.; Lin, H.; Zhang, H. CWGWO-N-BEATSx: An Improved Time Series Prediction Method With Multiple External Variables for Situation Prediction. IEEE Internet Things J. 2025, 99, 1-1. [Google Scholar] [CrossRef]
- Ouyang, Z.L.; Chen, G.; Zou, Z.J. Identification Modeling of Ship Maneuvering Motion Based on Local Gaussian Process Regression. Ocean Eng. 2023, 267, 113251. [Google Scholar] [CrossRef]
- Chen, G.; Wang, W.; Xue, Y. Identification of Ship Dynamics Model Based on Sparse Gaussian Process Regression with Similarity. Symmetry 2021, 13, 1956. [Google Scholar] [CrossRef]
- Zhou, X.; He, H.-W.; Zou, L.; Wu, Z.-X.; Zou, Z.-J. Real-Time Prediction of Full-Scale Ship Maneuvering Motions at Sea under Random Rudder Actions Based on BiLSTM-SAT Hybrid Method. Ocean Eng. 2024, 314, 119664. [Google Scholar] [CrossRef]
- Chen, L.J.; Yang, P.Y.; Li, S.G.; Liu, K.Z.; Wang, K.; Zhou, X.W. Online Modeling and Prediction of Maritime Autonomous Surface Ship Maneuvering Motion under Ocean Waves. Ocean Eng. 2023, 276, 114183. [Google Scholar] [CrossRef]
- Jiang, L.; Shang, X.; Jin, B.; Zhang, Z.; Zhang, W. Black-Box Modeling of Ship Maneuvering Motion Using Multi-Output Least-Squares Support Vector Regression Based on Optimal Mixed Kernel Function. Ocean Eng. 2024, 293, 116663. [Google Scholar] [CrossRef]
- Zhong, X.; Gallagher, B.; Liu, S.; Kailkhura, B.; Hiszpanski, A.; Han, T.Y.J. Explainable Machine Learning in Materials Science. npj Comput. Mater. 2022, 8, 204. [Google Scholar] [CrossRef]



| Parameter | Setting |
|---|---|
| OS | Windows 11 |
| CPU | Intel Core i7-10700 |
| GPU | NVIDIA GeForce RTX3060 |
| Programming language | Python 3.8 |
| Framework | Pytorch 1.6.0 + CUDA 11.0 |
| Parameters | Model (1/45.7) | Full Scale |
|---|---|---|
| Length between perpendiculars (Lpp/m) | 7.00 | 320.0 |
| Beam of the ship (B/m) | 1.27 | 58.0 |
| Ship draft (d/m) | 0.46 | 20.8 |
| Displacement (∇/m3) | 3.27 | 312,600 |
| Ship block coefficient (Cb) | 0.810 | 0.810 |
| Propeller diameter (DP/m) | 0.216 | 9.86 |
| Rudder height (HR/m) | 0.345 | 15.80 |
| Rudder area (AR/m2) | 0.539 | 112.5 |
| NRMSE | SMAPE | R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| u (m/s) | v (m/s) | r (deg/s) | u | v | r | u | v | r | |
| LS-SVM | 0.04218 | 0.03947 | 0.03375 | 25.56% | 30.42% | 21.91% | 95.60% | 95.51% | 98.62% |
| LSTM | 0.05925 | 0.04293 | 0.03489 | 28.56% | 35.39% | 26.06% | 93.74% | 92.69% | 97.53% |
| LSTM-Attn | 0.03303 | 0.04713 | 0.03592 | 23.81% | 24.05% | 27.98% | 98.53% | 94.60% | 98.44% |
| NbeatsX | 0.04088 | 0.03437 | 0.02005 | 30.80% | 11.01% | 7.25% | 95.26% | 96.60% | 99.51% |
| NRMSE | SMAPE | R2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| u (m/s) | v (m/s) | r (deg/s) | u | v | r | u | v | r | |
| NbeatsX | 0.04088 | 0.03437 | 0.02005 | 30.80% | 11.01% | 7.25% | 95.26% | 96.60% | 99.51% |
| NbeatsX_TES | 0.03887 | 0.01615 | 0.05083 | 32.28% | 6.46% | 12.69% | 95.93% | 99.69% | 99.56% |
| NbeatsX_TSE | 0.03591 | 0.01578 | 0.04786 | 33.39% | 6.39% | 11.40% | 95.47% | 99.70% | 99.40% |
| NbeatsX_STE | 0.03441 | 0.01311 | 0.04795 | 31.27% | 5.44% | 8.24% | 96.57% | 99.79% | 99.45% |
| NbeatsX_STEE | 0.02721 | 0.01661 | 0.03824 | 20.71% | 6.40% | 7.66% | 99.60% | 99.67% | 99.65% |
| Models | Time Consumption (s) | ||
|---|---|---|---|
| Training Time | Prediction Time | Total Time | |
| LS-SVM | 325.993 | 0.176 | 326.069 |
| LSTM | 354.721 | 0.249 | 354.870 |
| LSTM-Attn | 408.194 | 0.251 | 408.345 |
| NbeatsX | 348.973 | 0.229 | 349.102 |
| NbeatsX_TES | 349.123 | 0.233 | 349.256 |
| NbeatsX_TSE | 349.272 | 0.237 | 349.409 |
| NbeatsX_STE | 350.422 | 0.241 | 350.563 |
| NbeatsX_STEE | 350.571 | 0.242 | 350.713 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Zhou, X.; Liu, K.; Zhou, Y.; Tian, H. Nonparametric Prediction of Ship Maneuvering Motions Based on Interpretable NbeatsX Deep Learning Method. J. Mar. Sci. Eng. 2025, 13, 1417. https://doi.org/10.3390/jmse13081417
Chen L, Zhou X, Liu K, Zhou Y, Tian H. Nonparametric Prediction of Ship Maneuvering Motions Based on Interpretable NbeatsX Deep Learning Method. Journal of Marine Science and Engineering. 2025; 13(8):1417. https://doi.org/10.3390/jmse13081417
Chicago/Turabian StyleChen, Lijia, Xinwei Zhou, Kezhong Liu, Yang Zhou, and Hewei Tian. 2025. "Nonparametric Prediction of Ship Maneuvering Motions Based on Interpretable NbeatsX Deep Learning Method" Journal of Marine Science and Engineering 13, no. 8: 1417. https://doi.org/10.3390/jmse13081417
APA StyleChen, L., Zhou, X., Liu, K., Zhou, Y., & Tian, H. (2025). Nonparametric Prediction of Ship Maneuvering Motions Based on Interpretable NbeatsX Deep Learning Method. Journal of Marine Science and Engineering, 13(8), 1417. https://doi.org/10.3390/jmse13081417






