COLREGs-Compliant Distributed Stochastic Search Algorithm for Multi-Ship Collision Avoidance
Abstract
1. Introduction
1.1. Research Background
1.2. Summary and Analysis of Related Research
1.3. The Motivation for the Study
- A quantitative modeling framework for COLREGs is proposed, encompassing encounter situation identification, collision risk assessment, and phase division of the collision-avoidance process. This framework establishes precise mapping between regulatory provisions and the collision-avoidance behaviors of autonomous ship agents, thereby enhancing their comprehension of navigational rules while improving the interpretability and compliance of their decision-making processes;
- A comprehensive collision avoidance cost function integrating multiple factors is constructed, considering collision risk, COLREGs compliance, and navigation efficiency. A dynamic weight-adjustment mechanism based on relative distance is introduced to more accurately reflect the varying threat levels posed by each encountered vessel in a multi-ship environment, providing a unified and regulation-aware evaluation criterion for distributed optimization;
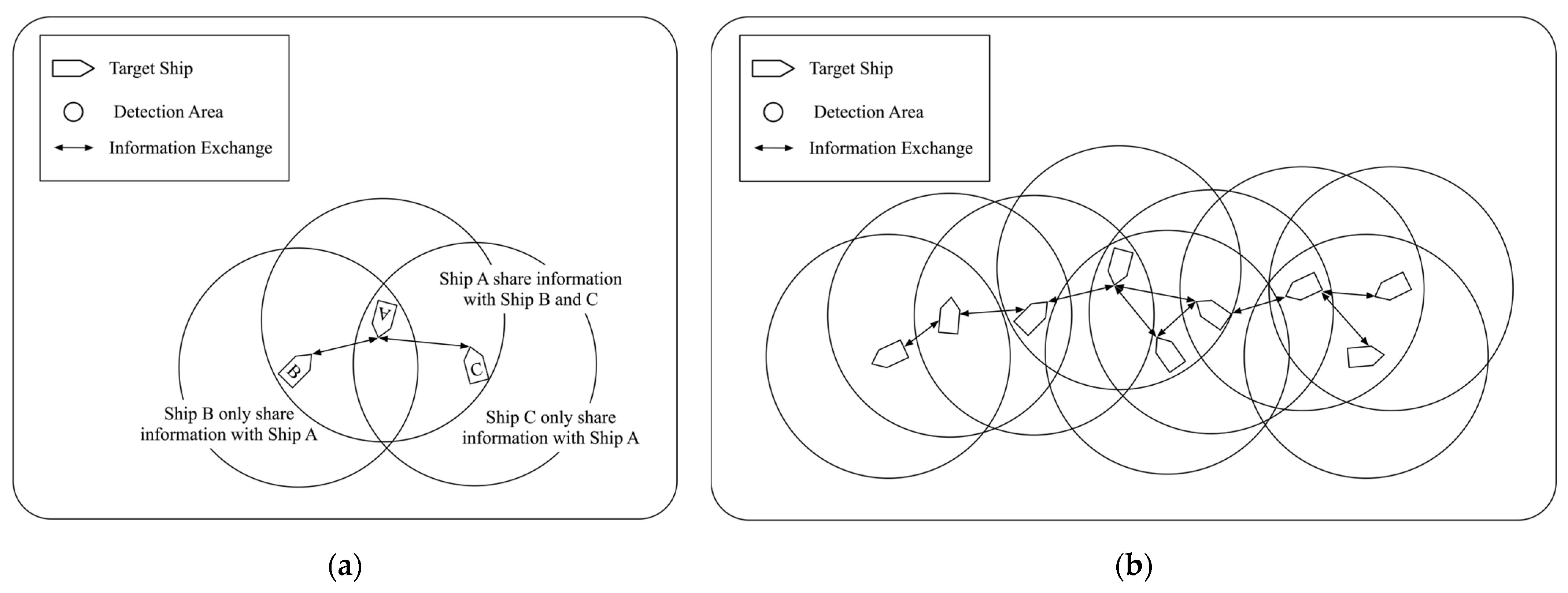
- A distributed multi-ship cooperative collision-avoidance decision-making framework is developed under a decentralized communication structure. Ship agents cooperate through local information exchange and probabilistic strategy updates. This method has the ability to escape local optima, effectively reduces communication frequency, and is suitable for intelligent cooperative navigation in large-scale autonomous ship systems.
2. Quantitative Analysis of COLREGs
- All ships are assumed to navigate in open waters under calm sea conditions and good visibility. The navigational environment excludes fixed obstacles such as islands, buoys, and other stationary obstructions, focusing solely on interactions with surrounding dynamic target ships;
- All ships are equipped with Automatic Identification System (AIS) transceivers that enable real-time transmission and reception of both static and dynamic navigational data. AIS also allows each vessel to broadcast its navigational intent, thereby facilitating information interoperability and sharing among ships.
- What type of encounter situation (e.g., head-on, crossing, overtaking) and what is the current stage (e.g., close-quarter situation, imminent danger, etc.) that exists between the own ship and the target ship?
- After identifying their respective roles as either the give-way vessel or the stand-on vessel, what collision-avoidance actions should be taken to comply with the relevant avoidance requirements specified in the COLREGs?
2.1. Ship Encounter Situation
2.1.1. Ship Encounter Situation Identification
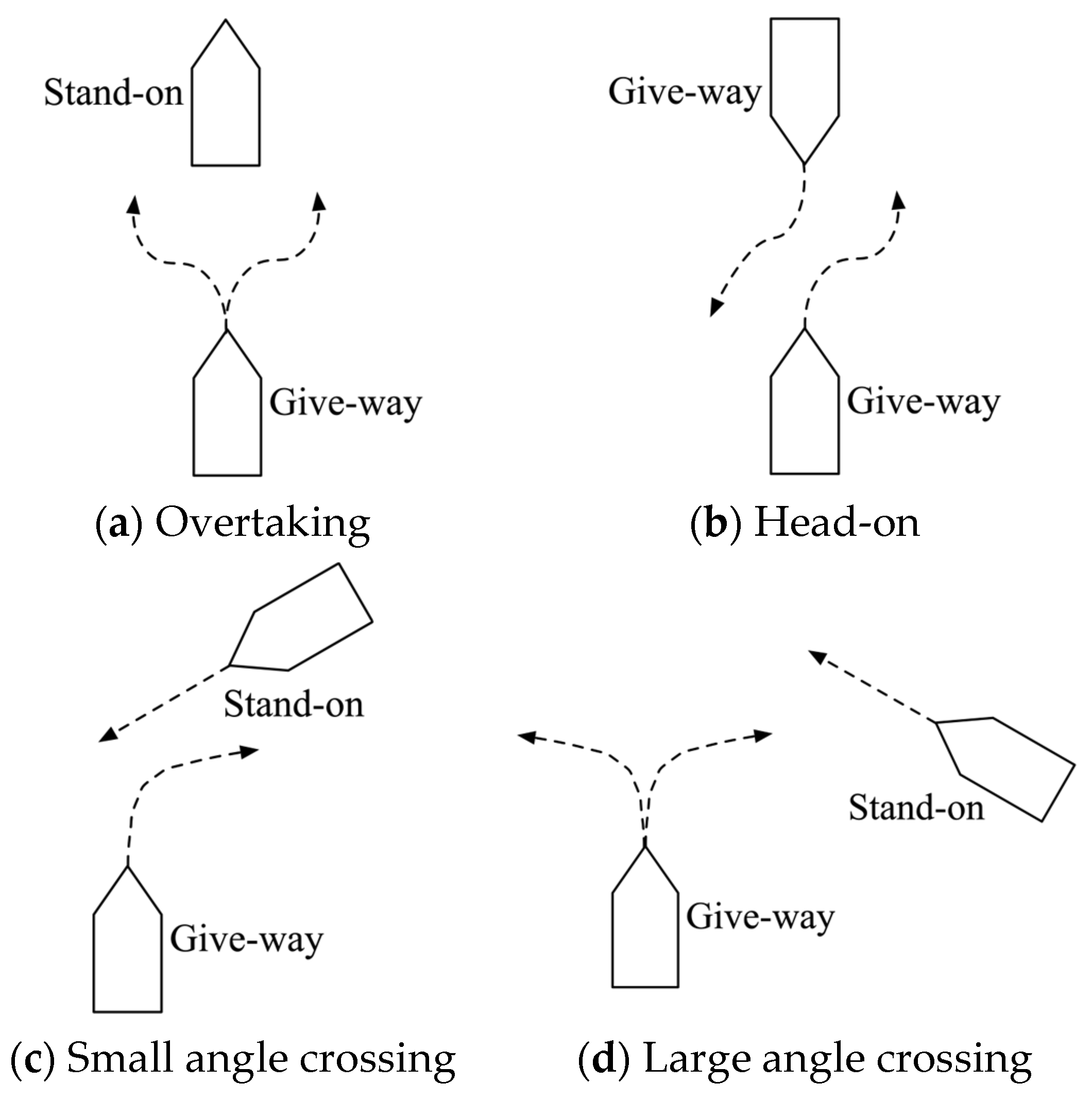
2.1.2. Collision-Avoidance Responsibilities Under Different Encounter Situations
2.2. Collision Risk Assessment Method
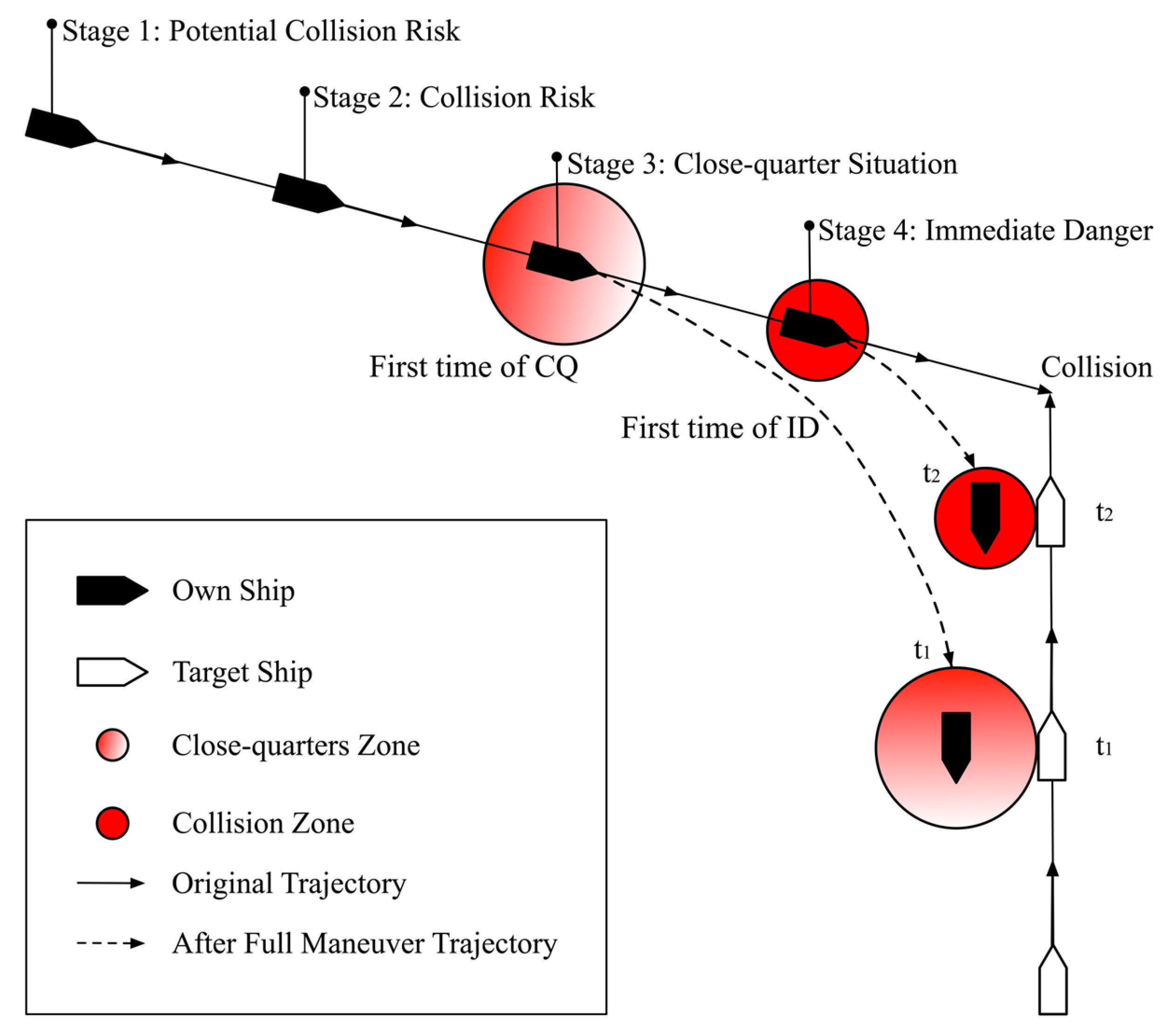
2.3. Collision-Avoidance Stage Model
2.3.1. Quantitative Analysis of Collision-Avoidance Stage
- Stage I: Free Action Stage
- Stage II: Collision Risk Stage
- Stage III: Close-quarters Situation Stage
- Stage IV: Immediate Danger Stage
2.3.2. Collision-Avoidance Actions at Different Stages
- Give-way ship actions in head-on, overtaking, and crossing situations.
- 2.
- Stand-on ship actions.
3. Ship Collision-Avoidance Decision-Making Model Based on Distributed Stochastic Search Algorithm
3.1. Distributed Ship Collision-Avoidance Framework
3.2. Cost and Improvement Function Design
3.2.1. Navigational Safety Cost
3.2.2. COLREGs Compliance Cost
3.2.3. Navigational Efficiency Cost
3.2.4. Total Cost and Improvement Function
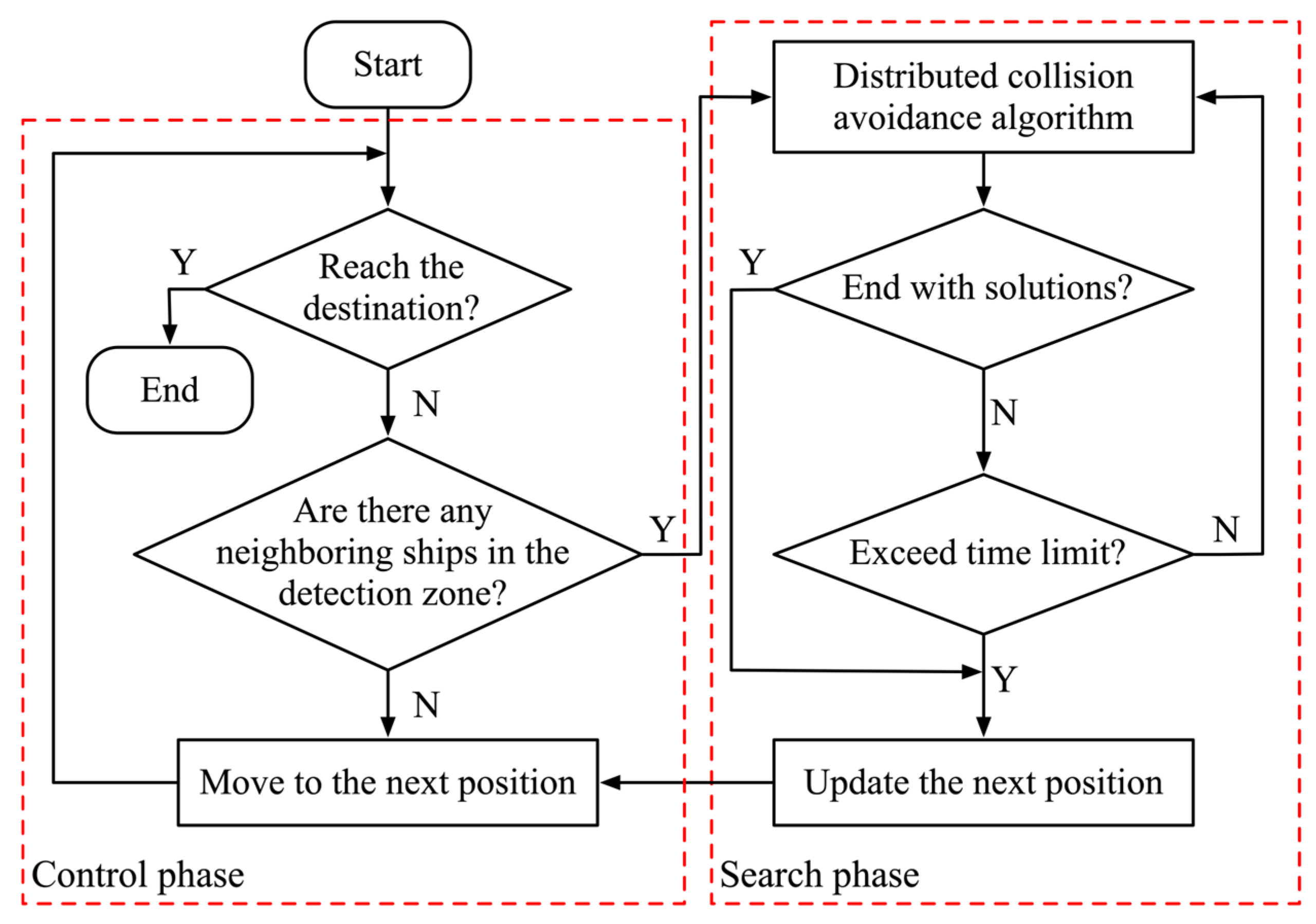
3.3. Ship Collision-Avoidance Algorithm Based on Distributed Stochastic Search
3.3.1. Distributed Stochastic Search
3.3.2. Distributed Ship Collision-Avoidance Decision-Making Under COLREGs
4. Simulation Experiment and Result Analysis
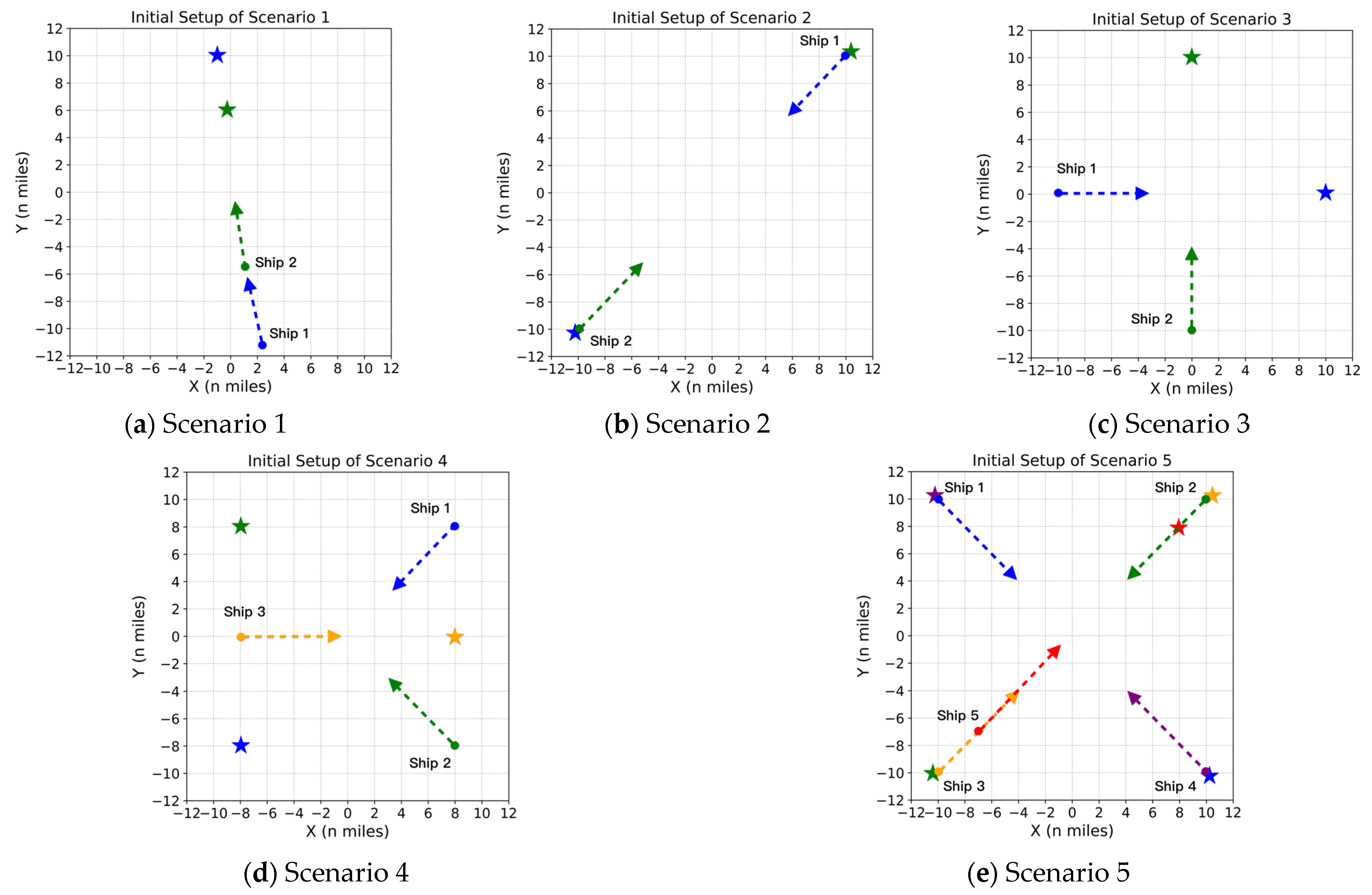
4.1. Simulation Scenario Setup
4.2. Experimental Results of Two-Ship Encounter Situations
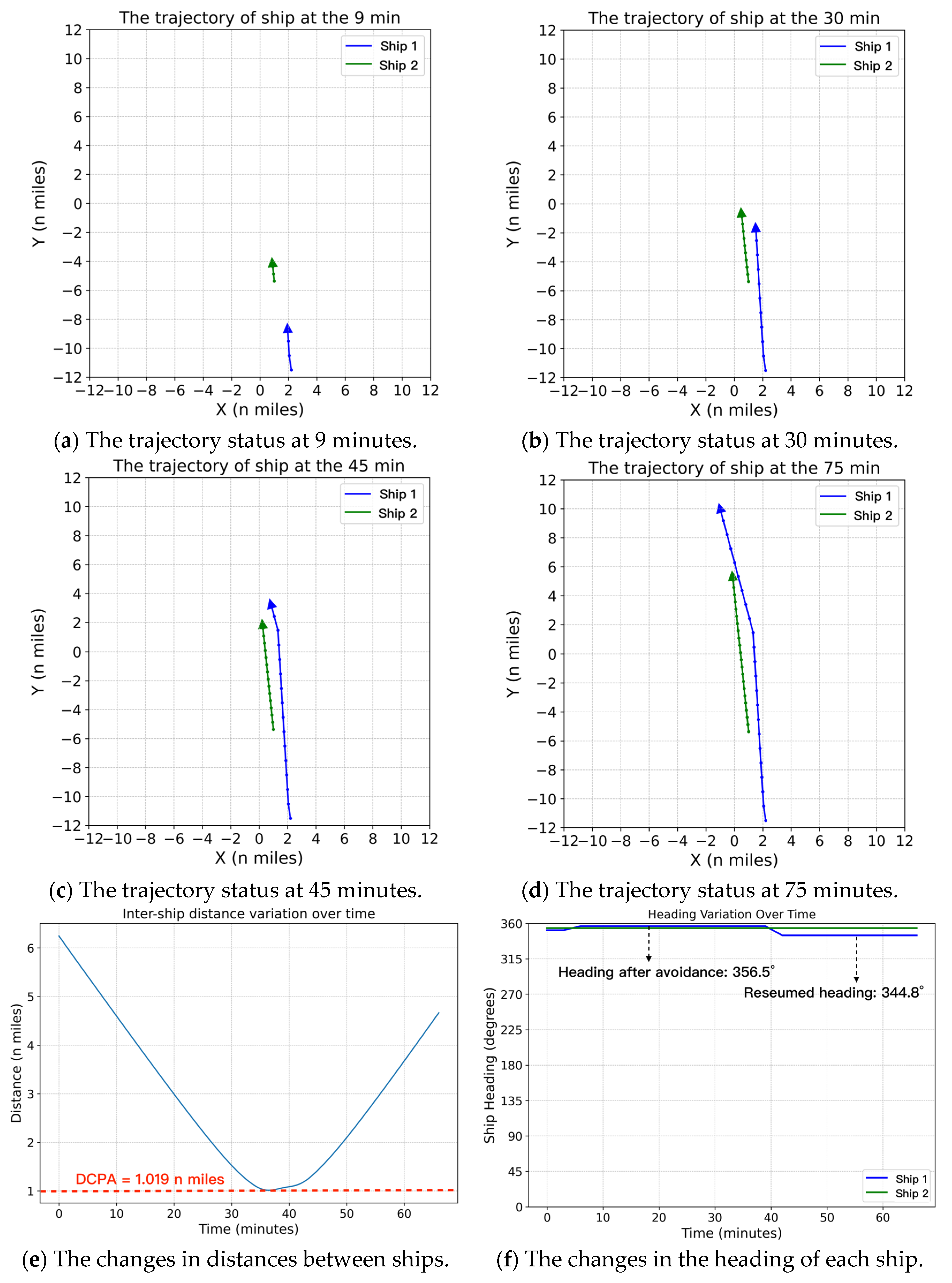
4.2.1. Simulation Scenario 1
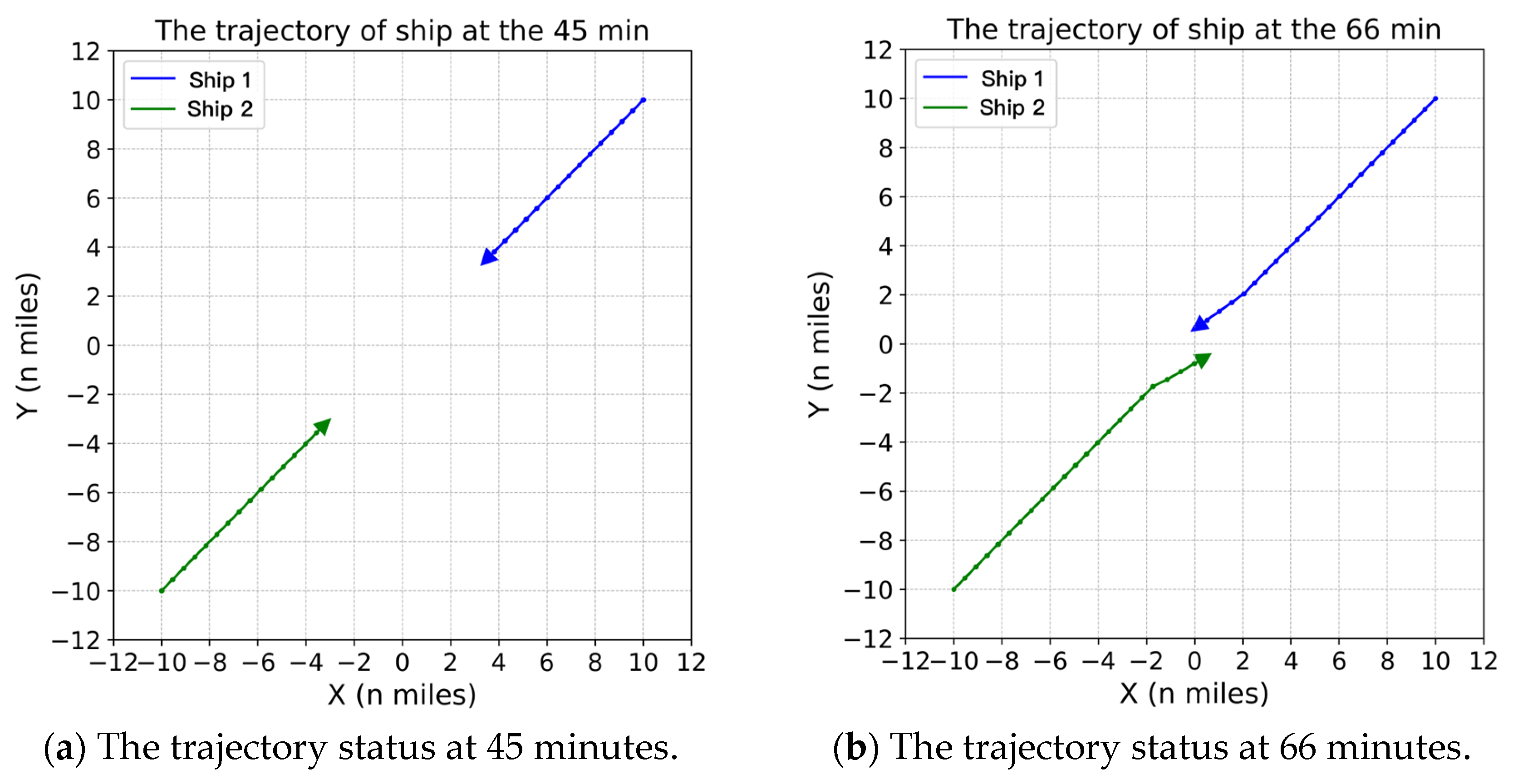
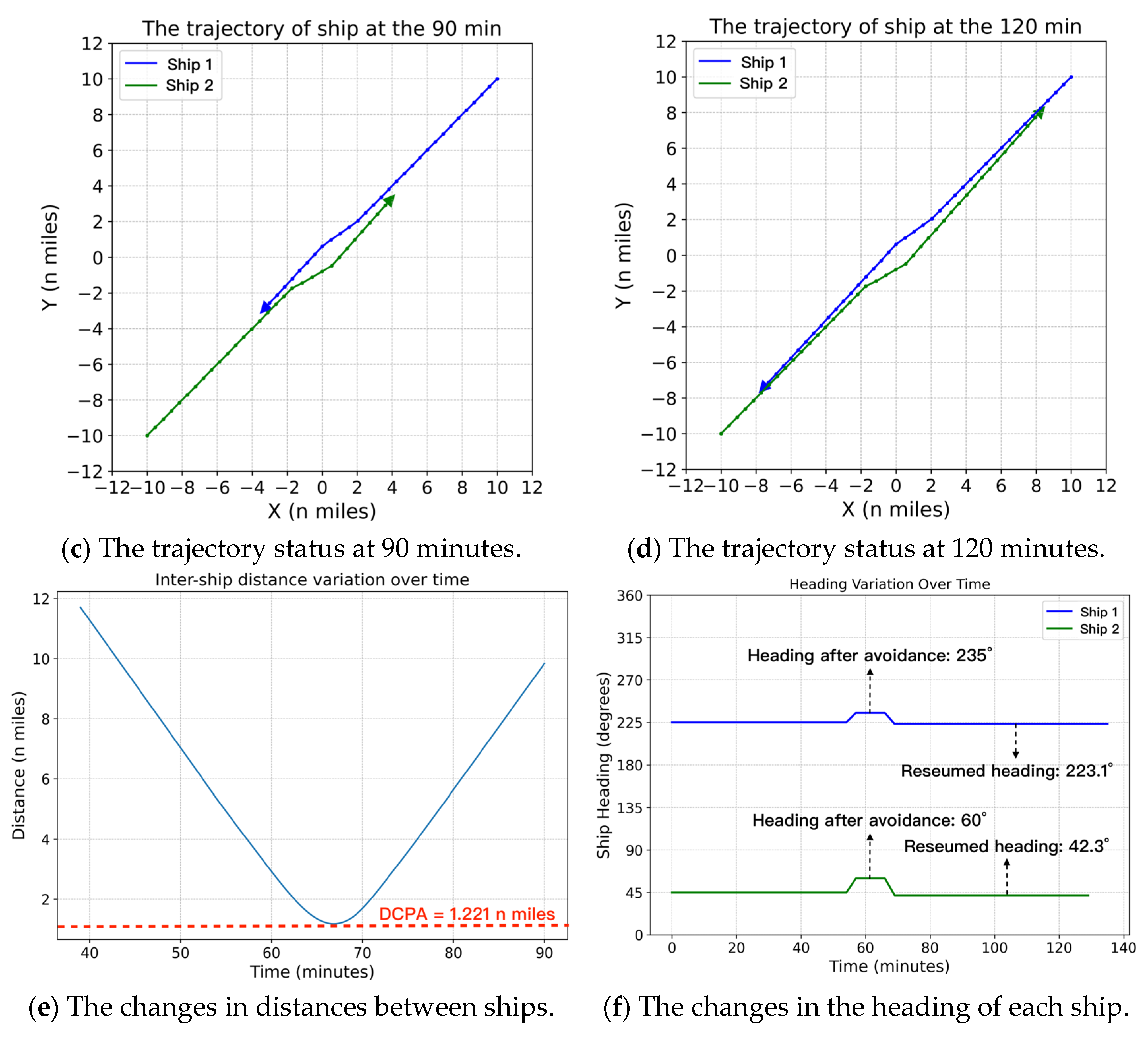
4.2.2. Simulation Scenario 2
4.2.3. Simulation Scenario 3
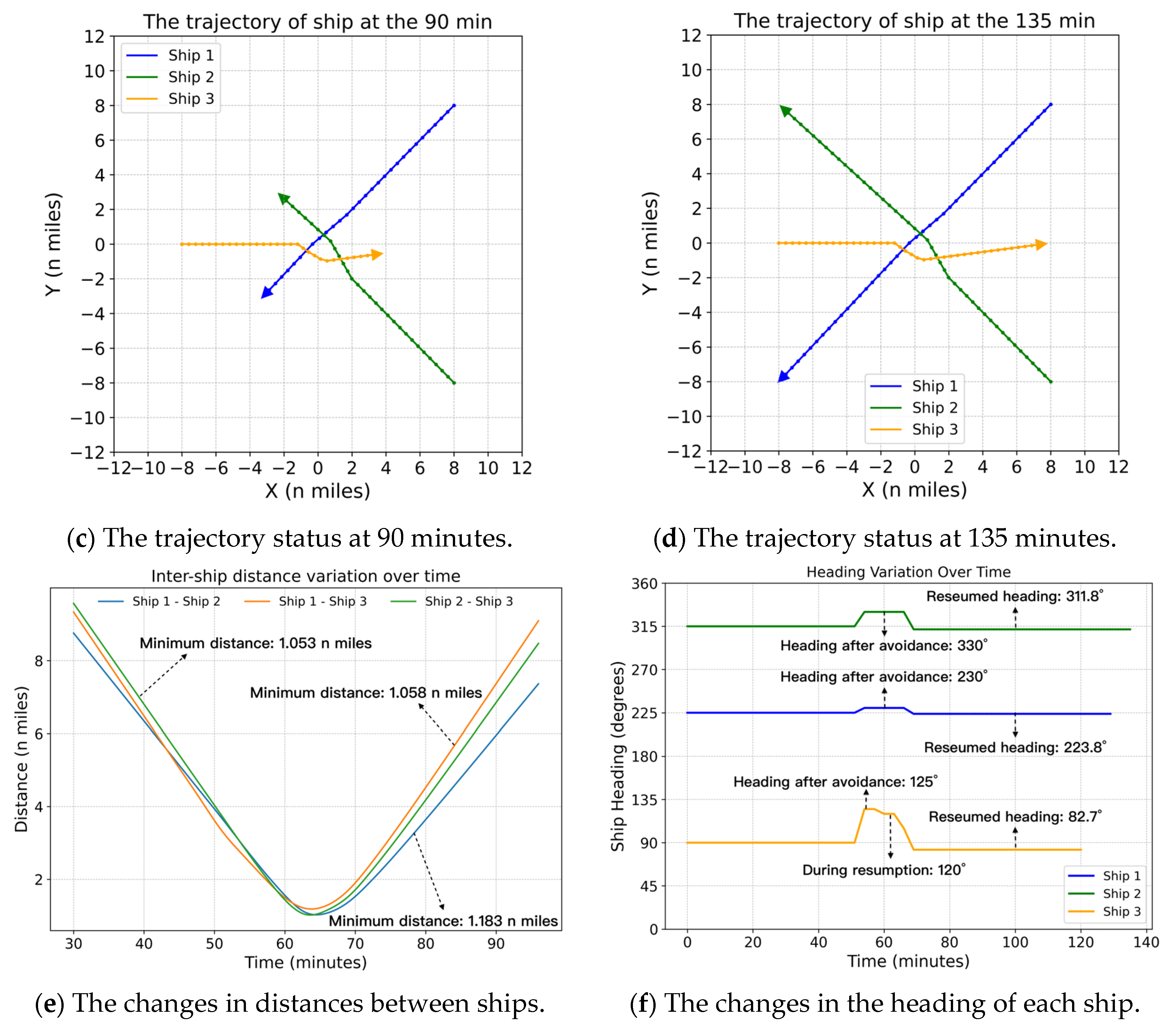
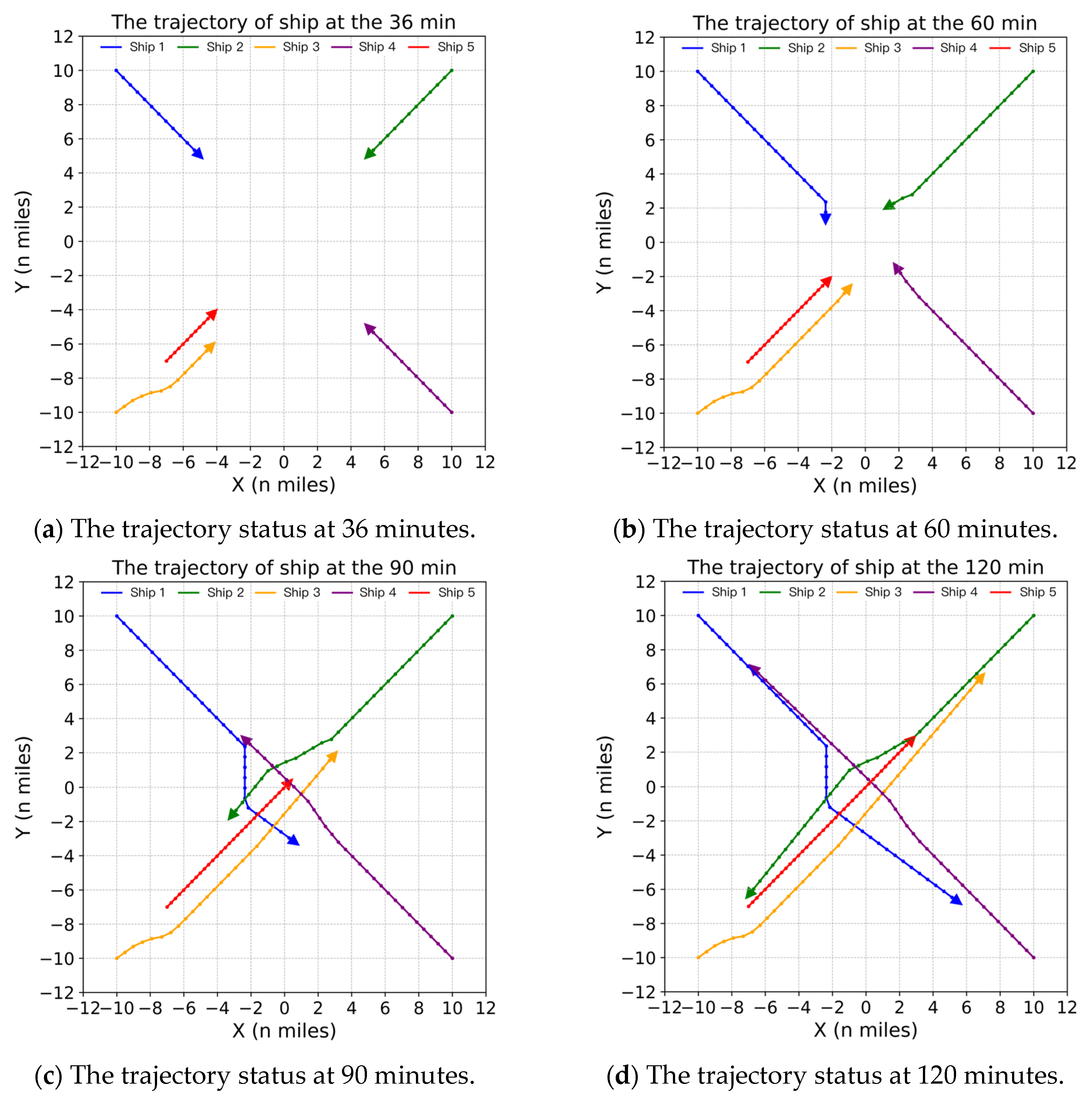
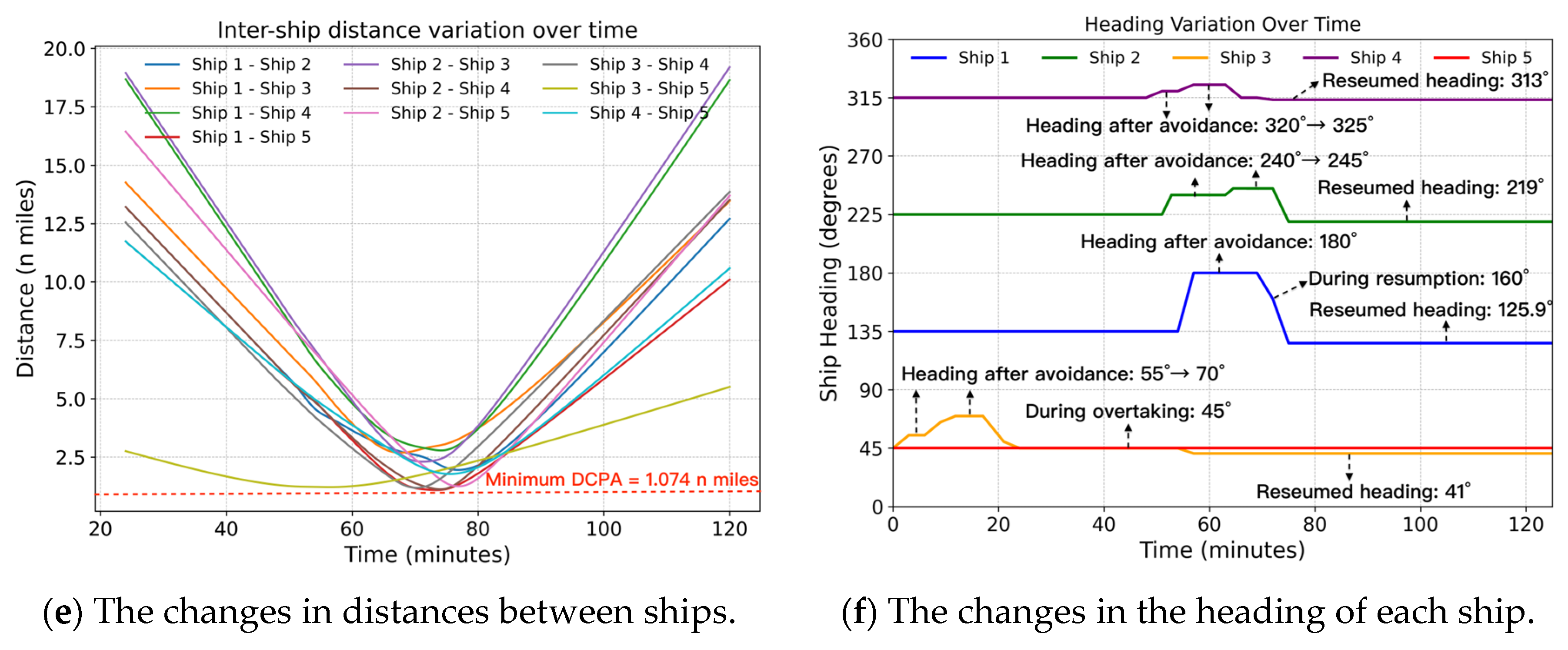
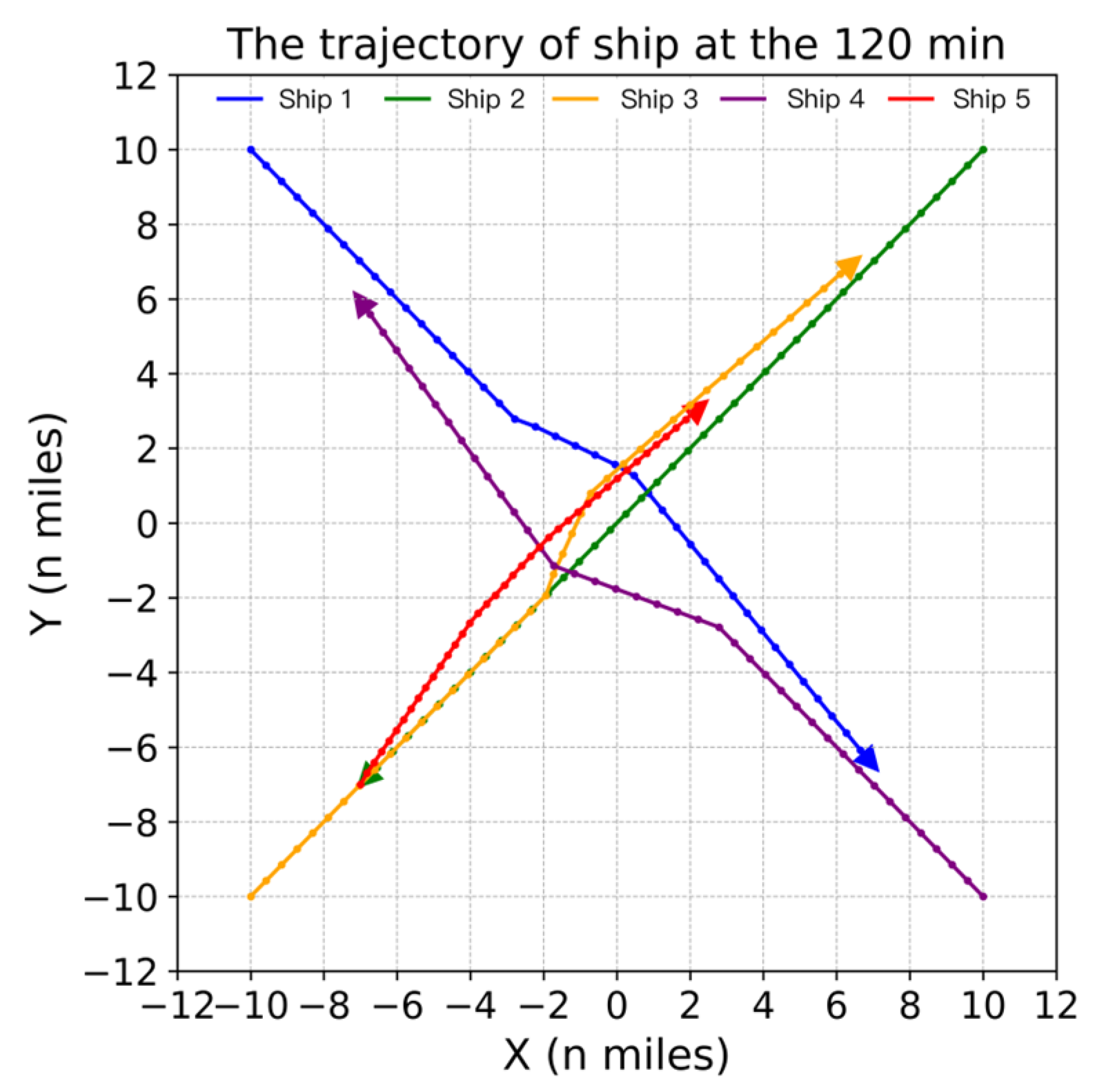
4.3. Experimental Results of Multi-Ship Encounter Situations
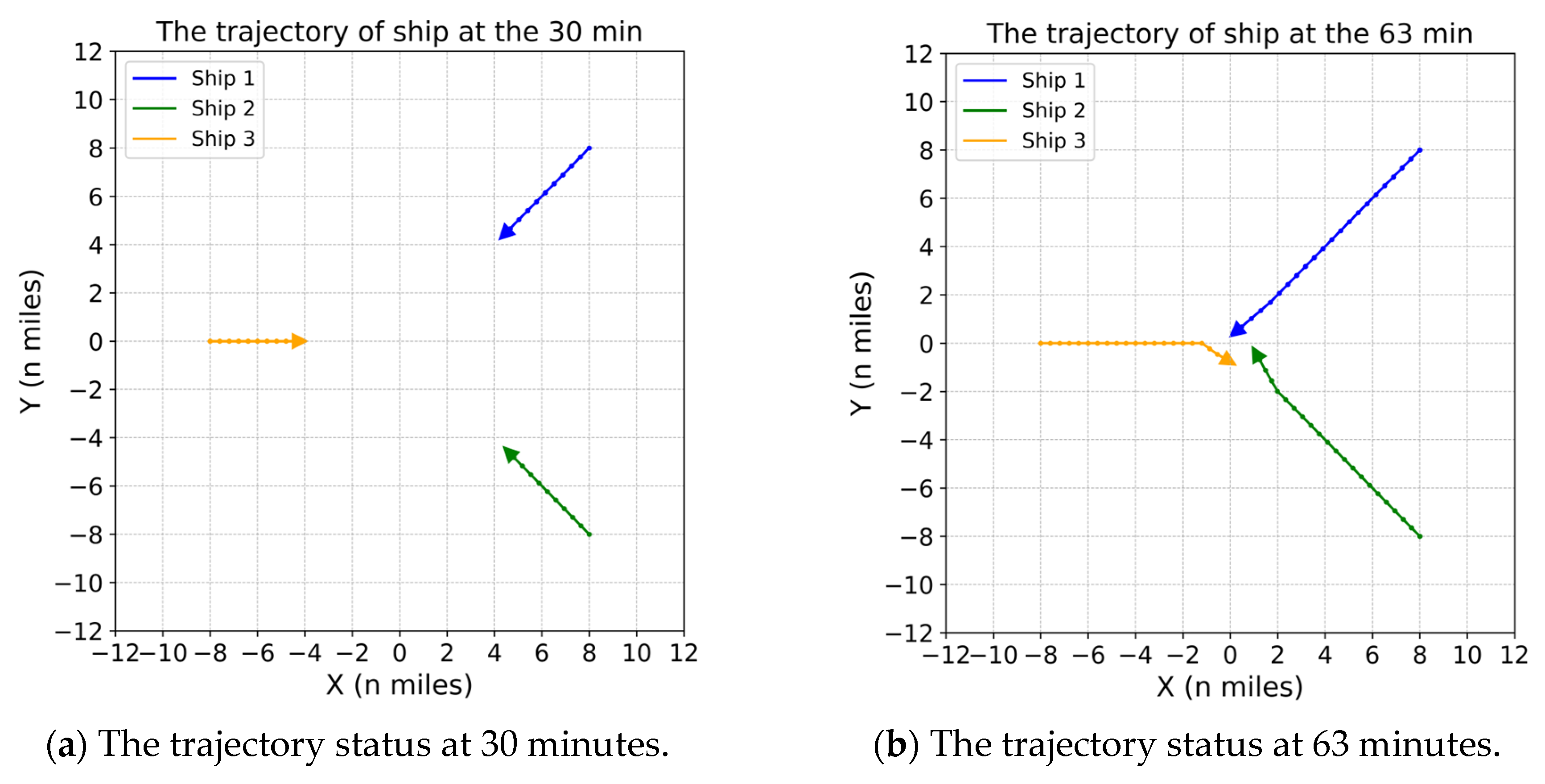
4.3.1. Simulation Scenario 4
4.3.2. Simulation Scenario 5
4.4. Result Discussion and Comparative Analysis
4.4.1. Navigation Safety
4.4.2. COLREGs Compliance
4.4.3. Navigation Efficiency
4.4.4. Computational Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
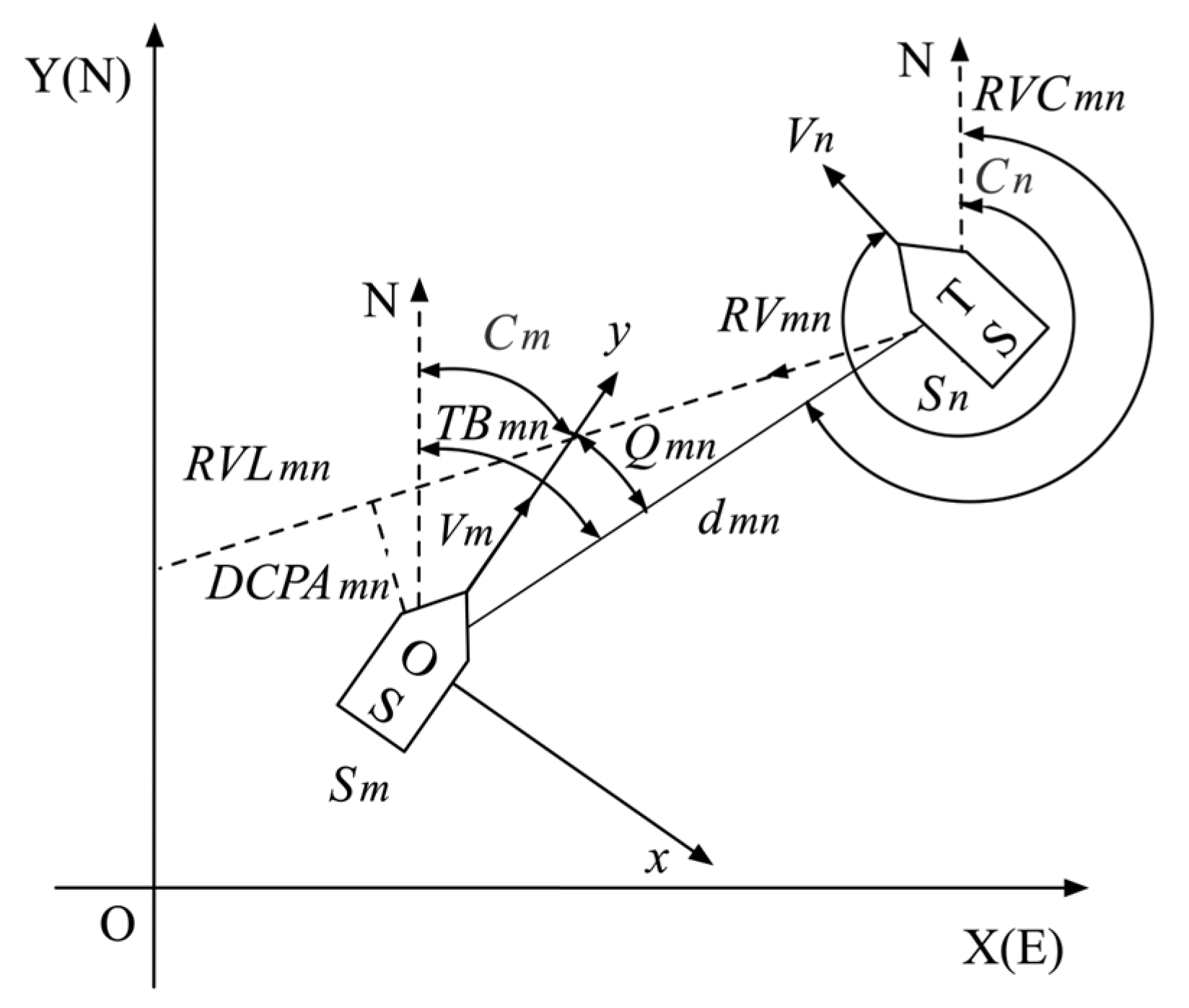
| Parameters | Meanings |
|---|---|
| Sm, Sn | Ship m (OS: Own ship), Ship n (TS: Target ship) |
| Cm, Cn | Ship course of Sm, Sn |
| Vm, Vn | Ship speed of Sm, Sn |
| TBmn | True bearing of Sn to Sm, the angle from OY to relative bearing |
| Qmn | Relative bearing of Sn to Sm, the angle from oy to bearing line |
| Dmn | Distance between Sm and Sn |
| RVmn | Relative velocity of Sm to Sn |
| RVLmn | Relative velocity line of Sm to Sn |
| RVCmn | Relative velocity course of Sm to Sn, the angle from OY to RVLmn |
| DCPAmn | Distance at the closest point of approach of Sm and Sn |
| TCPAmn | Time to closest point of approach of Sm and Sn |
| Own Ship Passes Astern of the Target Ship | Own Ship Passes Ahead of the Target Ship |
|---|---|
References
- United Nations Conference on Trade and Development (UNCTAD). Review of Maritime Transport 2024; United Nations: Geneva, Switzerland, 2024; Available online: https://unctad.org/webflyer/review-maritime-transport-2024 (accessed on 10 June 2025).
- Allianz Global Corporate & Specialty. Safety and Shipping Review 2025. Allianz SE, 2025. Available online: https://commercial.allianz.com/news-and-insights/reports/shipping-safety.html (accessed on 10 June 2025).
- Madsen, A.N.; Kim, T.E. A state-of-the-art review of AI decision transparency for autonomous shipping. J. Int. Marit. Saf. Environ. Aff. Shipp. 2024, 8, 2336751. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Negenborn, R.R. Distributed coordination for collision avoidance of multiple ships considering ship maneuverability. Ocean Eng. 2019, 181, 212–226. [Google Scholar] [CrossRef]
- Kim, J.K.; Park, D.J. Understanding of sailing rule based on COLREGs: Comparison of navigator survey and automated collision-avoidance algorithm. Mar. Policy 2024, 159, 105894. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, L.; Chen, P.; Negenborn, R.R.; van Gelder, P.H.A.J.M. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Akdağ, M.; Solnør, P.; Johansen, T.A. Collaborative collision avoidance for maritime autonomous surface ships: A review. Ocean Eng. 2022, 250, 110920. [Google Scholar] [CrossRef]
- Zhu, Q.; Xi, Y.; Weng, J.; Han, B.; Hu, S.; Ge, Y.-E. Intelligent ship collision avoidance in maritime field: A bibliometric and systematic review. Expert Syst. Appl. 2024, 252, 124148. [Google Scholar] [CrossRef]
- Chang, C.-H.; Wijeratne, I.B.; Kontovas, C.; Yang, Z. COLREG and MASS: Analytical review to identify research trends and gaps in the Development of Autonomous Collision Avoidance. Ocean Eng. 2024, 302, 117652. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Li, L. A collision avoidance decision-making system for autonomous ship based on modified velocity obstacle method. Ocean Eng. 2020, 215, 107910. [Google Scholar] [CrossRef]
- Wei, G.; Kuo, W. COLREGs-compliant multi-ship collision avoidance based on multi-agent reinforcement learning technique. J. Mar. Sci. Eng. 2022, 10, 1431. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Lyu, H.; Yin, Y. COLREGS-constrained real-time path planning for autonomous ships using modified artificial potential fields. J. Navig. 2018, 72, 588–608. [Google Scholar] [CrossRef]
- Xie, S.; Garofano, V.; Chu, X.; Negenborn, R.R. Model predictive ship collision avoidance based on Q-learning beetle swarm antenna search and neural networks. Ocean Eng. 2019, 193, 106609. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, W. Concise deep reinforcement learning obstacle avoidance for underactuated unmanned marine vessels. Neurocomputing 2018, 272, 63–73. [Google Scholar] [CrossRef]
- Shen, H.; Hashimoto, H.; Matsuda, A.; Taniguchi, Y.; Terada, D.; Guo, C. Automatic collision avoidance of multiple ships based on deep Q-learning. Appl. Ocean Res. 2019, 86, 268–288. [Google Scholar] [CrossRef]
- Gao, M.; Kang, Z.; Zhang, A.; Liu, J.; Zhao, F. MASS autonomous navigation system based on AIS big data with dueling deep Q networks prioritized replay reinforcement learning. Ocean Eng. 2022, 249, 110834. [Google Scholar] [CrossRef]
- Liu, H.; Deng, R.; Zhang, L. The application research for ship collision avoidance with hybrid optimization algorithm. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 760–767. [Google Scholar]
- Li, S.; Liu, J.; Negenborn, R.R.; Ma, F. Optimizing the joint collision avoidance operations of multiple ships from an overall perspective. Ocean Eng. 2019, 191, 106511. [Google Scholar] [CrossRef]
- Dong, H.; Zhen, R.; Gu, Q.; Lin, Z.; Chen, J.; Yan, K.; Chen, B. A novel collaborative collision avoidance decision method for multi-ship encounters in complex waterways. Ocean Eng. 2024, 313, 119512. [Google Scholar] [CrossRef]
- Hirayama, K.; Yokoo, M. Distributed partial constraint satisfaction problem. In Proceedings of the 3rd International Conference on Principles and Practice of Constraint Programming, Linz, Austria, 29 October–1 November 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 222–236. [Google Scholar]
- Petcu, A.; Faltings, B. A Scalable Method for Multiagent Constraint Optimization. In Proceedings of the 19th International Joint Conference on Artificial Intelligence (IJCAI-2005), Edinburgh, Scotland, 30 July–5 August 2005; pp. 266–271. [Google Scholar]
- Gershman, A.; Meisels, A.; Zivan, R. Asynchronous Forward Bounding for Distributed COPs. J. Artif. Intell. Res. 2009, 34, 61–88. [Google Scholar] [CrossRef]
- Kim, D.; Hirayama, K.; Okimoto, T. Ship Collision Avoidance by Distributed Tabu Search. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2015, 9, 23–29. [Google Scholar] [CrossRef]
- Kim, D.G.; Hirayama, K.; Park, G.K. Collision Avoidance in Multiple-Ship Situations by Distributed Local Search. J. Adv. Comput. Intell. Intell. Inform. 2014, 18, 839–848. [Google Scholar] [CrossRef]
- Zhen, R.; Shi, Z.; Gu, Q.; Yang, S. A novel deterministic search-based algorithm for multi-ship collaborative collision avoidance decision-making. Ocean Eng. 2024, 292, 116524. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, G.; Xing, Z.; Wittenburg, L. Distributed stochastic search and distributed breakout: Properties, comparison and applications to constraint optimization problems in sensor networks. Artif. Intell. 2005, 161, 55–87. [Google Scholar] [CrossRef]
- Kim, D.; Hirayama, K.; Okimoto, T. Distributed Stochastic Search Algorithm for Multi-ship Encounter Situations. J. Navig. 2017, 70, 699–718. [Google Scholar] [CrossRef]
- Hirayama, K.; Miyake, R.; Shiota, T.; Okimoto, T. DSSA+: Distributed Collision Avoidance Algorithm in an Environment where Both Course and Speed Changes are Allowed. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 117–124. [Google Scholar] [CrossRef]
- Zheng, H.; Negenborn, R.R.; Lodewijks, G. Fast ADMM for Distributed Model Predictive Control of Cooperative Waterborne AGVs. IEEE Trans. Control Syst. Technol. 2016, 25, 1406–1413. [Google Scholar] [CrossRef]
- Tran, H.A.; Johansen, T.A.; Negenborn, R.R. Parallel distributed collision avoidance with intention consensus based on ADMM. IFAC-PapersOnLine 2024, 58, 302–309. [Google Scholar] [CrossRef]
- Gleeson, J.; Dunbabin, M.; Ford, J.J. COLREG Scenario classification and Compliance Evaluation with temporal and multi-vessel awareness for collision avoidance systems. Ocean Eng. 2024, 313, 119552. [Google Scholar] [CrossRef]
- Liang, Z.; Li, F.; Zhou, S. An Improved NSGA-II Algorithm for MASS Autonomous Collision Avoidance under COLREGs. J. Mar. Sci. Eng. 2024, 12, 1224. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, C.; Wang, N. Mult objective optimization based vessel collision avoidance strategy optimization. Math. Probl. Eng. 2014, 2014, 914689. [Google Scholar] [CrossRef]
- He, Y.; Jin, Y.; Huang, L.; Xiong, Y.; Chen, P.; Mou, J. Quantitative analysis of COLREG rules and seamanship for autonomous collision avoidance at open sea. Ocean Eng. 2017, 140, 281–291. [Google Scholar] [CrossRef]
- Cockcroft, A.N.; Lameijer, J.N.F. A Guide to the Collision Avoidance Rules: International Regulations for Preventing Collisions at Sea (the Seventh Version); Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Liu, J.; Zhang, J.; Yan, X.; Soares, C.G. Multi-ship collision avoidance decision-making and coordination mechanism in Mixed Navigation Scenarios. Ocean Eng. 2022, 257. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, D.; Yan, X.; Haugen, S.; Soares, C.G. A distributed anti-collision decision support formulation in multi-ship encounter situations under COLREGs. Ocean Eng. 2015, 105, 336–348. [Google Scholar] [CrossRef]
- Goodwin, E.M. A statistical study of ship domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Wang, T.; Yan, X.P.; Wang, Y.; Wu, Q. Ship domain model for multi-ship collision avoidance decision-making with COLREGs based on artificial potential field. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2017, 11, 85–92. [Google Scholar] [CrossRef]
- Wu, X.; Liu, K.; Zhang, J.; Yuan, Z.; Liu, J.; Yu, Q.; Chen, X. An Optimized Collision Avoidance Decision-Making System for Autonomous Ships under Human-Machine Cooperation Situations. J. Adv. Transp. 2021, 2021, 7537825. [Google Scholar] [CrossRef]
- Zhong, J.D. Analysis of the risk of collision, close quarters situation and immediate danger. J. Shanghai Marit. Univ. 1999, 2, 76–80. [Google Scholar]
- Hu, Y.; Zhang, A.; Tian, W.; Zhang, J.; Hou, Z. Multi-ship collision avoidance decision-making based on collision risk index. J. Mar. Sci. Eng. 2020, 8, 640. [Google Scholar] [CrossRef]
- Johansen, T.A.; Perez, T.; Cristofaro, A. Ship collision avoidance and COLREGS compliance using simulation-based control behavior selection with predictive hazard assessment. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3407–3422. [Google Scholar] [CrossRef]





| Type | Reference | Technique | Multi-Ship Encounter | Computational Overhead | COLREGs Compliance |
|---|---|---|---|---|---|
| Single-ship Strategies Method | [10,11] | Velocity obstacle method | No | Low | Partially |
| [12,13] | Artificial potential field method | No | Low | No | |
| [14] | Model predictive | No | High | Yes | |
| [15,16] | DRL in continuous action space | No | High | No | |
| [17] | AIS historical data mining | No | High | Partially | |
| Centralized Coordination Method | [18] | Hybrid swarm method | Yes | High | No |
| [19] | Receding horizon optimization | Yes | High | Yes | |
| [20] | Multi-objective evolutionary method | Yes | High | No | |
| Distributed Coordination Method | [24] | Distributed tabu search algorithm | Yes | Low | No |
| [25,26] | Distributed local search algorithm | Yes | Low | No | |
| [28,29] | Distributed stochastic search algorithm | Yes | Low | No | |
| [30,31] | Alternating direction method of multipliers | Yes | High | Partially | |
| This study | DSA-based considering the COLREGs | Yes | Low | Yes |
| Decision-Making Algorithm Module | The Relevant Provisions Supporting the Quantification Method of Rules |
|---|---|
| Situation awareness | Part B: Rule 5, 7 |
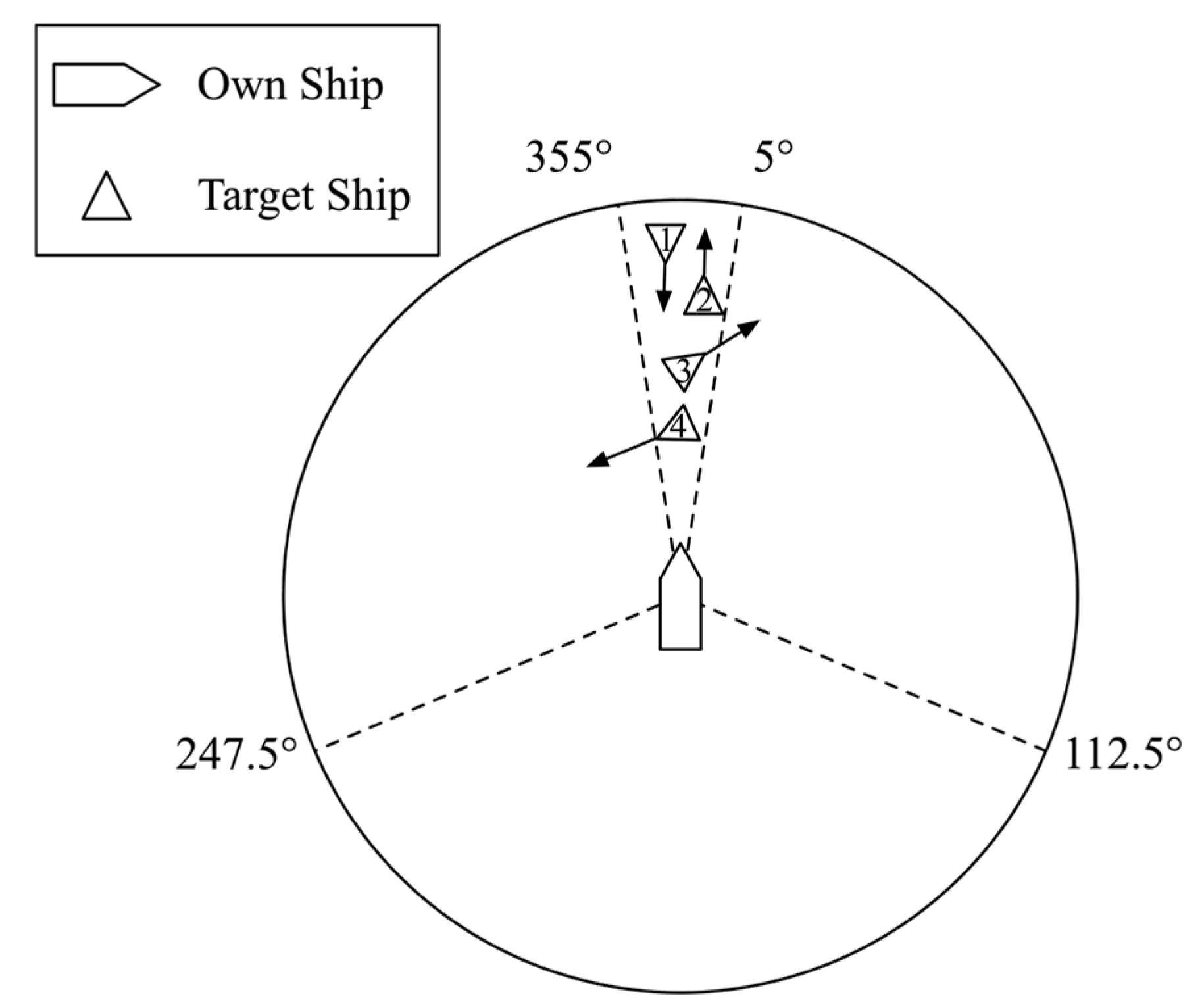
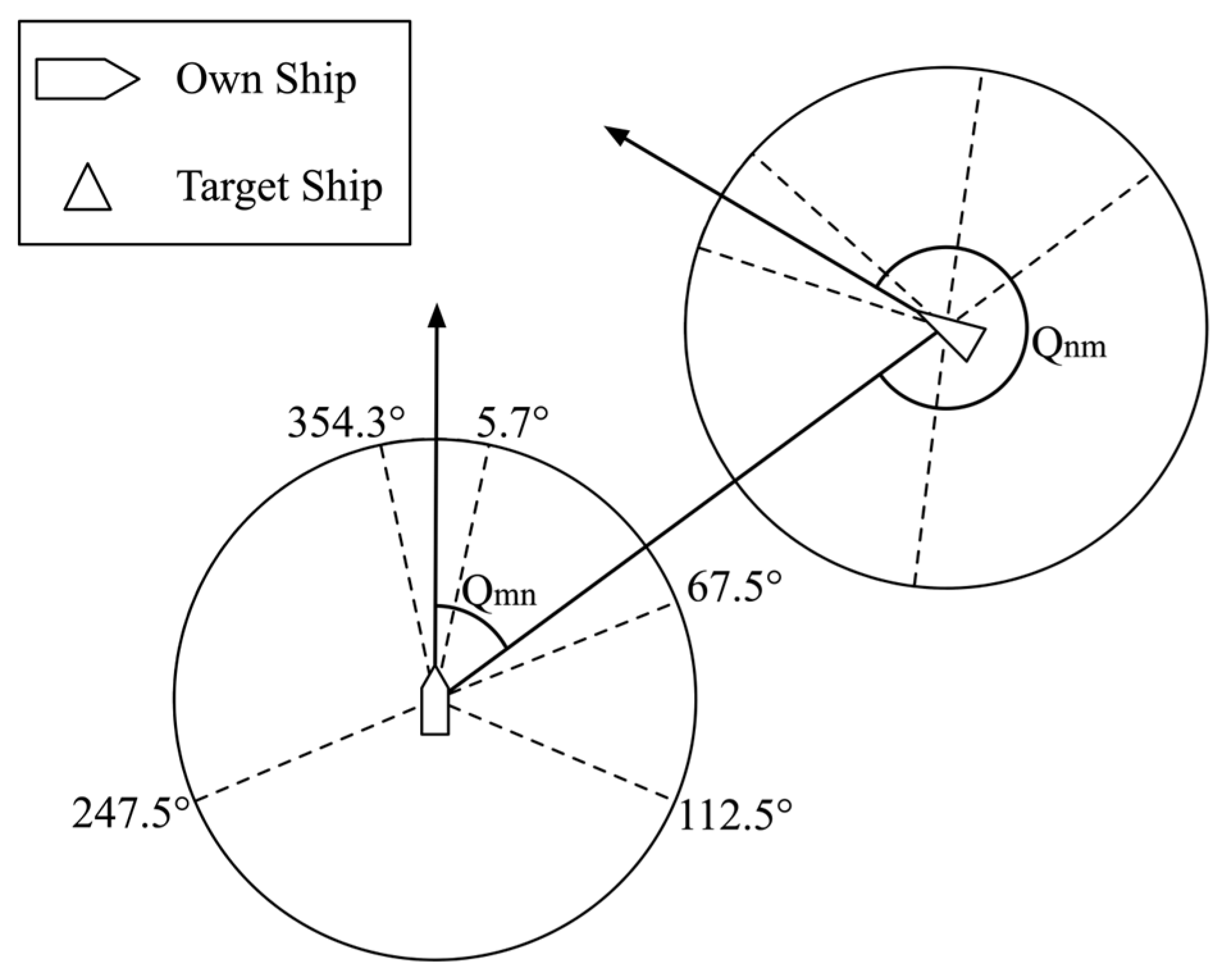
| Encounter situation identification | Part B: Rule 7, 13, 14, 15; Part C: Rule 21, 22 |
| Role recognition and responsibility assessment | Part B: Rule 2, 8, 16, 17 |
| Collision avoidance action generation | Part B: Rule 2, 8, 13, 14, 15, 16, 17 |
| Encounter Situation | Limitations | |||
|---|---|---|---|---|
| PCR exists and TCPA > 0 | Head-on | , ; , ; , | ||
| Overtaking | Give-way | , | ||
| Stand-on | , | |||
| Crossing | Small-angle | Give-way | , | |
| Stand-on | , | |||
| Large-angle | Give-way | , | ||
| Stand-on | , | |||
| No PCR or TCPA ≤ 0 | ||||
| Analysis of Collision Risk | Limitations | Explain |
|---|---|---|
| Safe Ship | or | Not posing any threat or having already passed safely. |
| Potential Collision Risk Ship | , , | Vessels with PCR present but not yet in the collision avoidance action area. |
| Collision Risk Ship | , , | An actual collision threat exists, and immediate collision avoidance action is required. |
| Stage Classification | Explain | Action Limitations | |
|---|---|---|---|
| Stage I | Only PCR exists | Give-way ship | Free to take any available action. |
| Stand-on ship | |||
| Stage II | CR exists, * | Give-way ship | Collision-avoidance actions guided by the rules in Section 2.1.2. |
| Stand-on ship | |||
| Stage III | CR exists, | Give-way ship | In an emergency, the vessel should take the most effective action under Rule 2, even if it temporarily deviates from other rules. |
| Stand-on ship | |||
| Stage IV | CR exists, | Give-way ship | |
| Stand-on ship | |||
| Encounter Situation | Explain | Rule Violation Cost Matrix * | |
|---|---|---|---|
| Head-on | Give-way ship | [1 1 0] | |
| Overtaking | Give-way ship | [0 1 0] | |
| Stand-on ship | [1 0 1] | ||
| Crossing | Small angle crossing | Give-way ship | [1 1 0] |
| Stand-on ship | [1 0 1] | ||
| Large angle crossing | Give-way ship | [0 1 0] | |
| Stand-on ship | [1 0 1] | ||
| Scenario | Ship ID | Initial Position | Destination | Course (°) | Speed (Knots) | Relationship with Collision Risk |
|---|---|---|---|---|---|---|
| 1 | Ship 1 | (2.2, −11.5) | (−1, 10) | 351.5 | 20 | Ship 2 |
| Ship 2 | (1, −5.37) | (−0.2, 6) | 354 | 10 | Ship 1 | |
| 2 | Ship 1 | (10, 10) | (−10, 10) | 225 | 12.5 | Ship 2 |
| Ship 2 | (−10, −10) | (10, 10) | 45 | 13 | Ship 1 | |
| 3 | Ship 1 | (−10, 0) | (10, 0) | 90 | 12 | Ship 2 |
| Ship 2 | (0, −10) | (0, 10) | 0 | 12 | Ship 1 | |
| 4 | Ship 1 | (8, 8) | (−8, −8) | 225 | 10.5 | Ship 2, Ship 3 |
| Ship 2 | (8, −8) | (−8, 8) | 315 | 10 | Ship 1, Ship 2 | |
| Ship 3 | (−8, 0) | (8, 0) | 90 | 8 | Ship1, Ship 2 | |
| 5 | Ship 1 | (−10, 10) | (10, −10) | 135 | 12 | Ship 2, Ship 3, Ship4 |
| Ship 2 | (10, 10) | (−10, −10) | 225 | 12 | Ship1, Ship 3, Ship 4, Ship5 | |
| Ship 3 | (−10, −10) | (10, 10) | 45 | 12 | Ship 1, Ship 2, Ship 4, Ship 5 | |
| Ship 4 | (10, −10) | (−10, 10) | 315 | 12 | Ship1, Ship 2, Ship 3 | |
| Ship 5 | (−7, −7) | (8, 8) | 45 | 7 | Ship 2, Ship 3 |
| Ship ID | Ship 1 | Ship 2 |
|---|---|---|
| Ship 1 | — | 0.011 n miles |
| Ship 2 | 0.011 n miles | — |
| Ship ID | Ship 1 | Ship 2 |
|---|---|---|
| Ship 1 | — | 0 n miles |
| Ship 2 | 0 n miles | — |
| Ship ID | Ship 1 | Ship 2 |
|---|---|---|
| Ship 1 | — | 0 n miles |
| Ship 2 | 0 n miles | — |
| Ship ID | Ship 1 | Ship 2 | Ship 3 |
|---|---|---|---|
| Ship 1 | — | 0.488 n miles | 0.336 n miles |
| Ship 2 | 0.488 n miles | — | 0.558 n miles |
| Ship 3 | 0.336 n miles | 0.558 n miles | — |
| Ship ID | Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 |
|---|---|---|---|---|---|
| Ship 1 | — | 0 n miles | 0 n miles | 0 n miles | 1.425 n miles |
| Ship 2 | 0 n miles | — | 0 n miles | 0 n miles | 0 n miles |
| Ship 3 | 0 n miles | 0 n miles | — | 0 n miles | 0 n miles |
| Ship 4 | 0 n miles | 0 n miles | 0 n miles | — | 1.425 n miles |
| Ship 5 | 1.425 n miles | 0 n miles | 0 n miles | 1.425 n miles | — |
| Ship ID | Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 |
|---|---|---|---|---|---|
| Ship 1 | — | 1.051 n miles | 1.576 n miles | 2.954 n miles | 2.888 n miles |
| Ship 2 | 1.051 n miles | — | 1.120 n miles | 1.114 n miles | 1.091 n miles |
| Ship 3 | 1.576 n miles | 1.120 n miles | — | 1.851 n miles | 0.977 n miles |
| Ship 4 | 2.954 n miles | 1.114 n miles | 1.851 n miles | — | 0.996 n miles |
| Ship 5 | 2.888 n miles | 1.091 n miles | 0.977 n miles | 0.996 n miles | — |
| Ship ID | Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 |
|---|---|---|---|---|---|
| Ship 1 | — | 2.027 n miles | 2.660 n miles | 2.723 n miles | 1.107 n miles |
| Ship 2 | 2.027 n miles | — | 2.396 n miles | 1.074 n miles | 1.330 n miles |
| Ship 3 | 2.660 n miles | 2.396 n miles | — | 1.225 n miles | 1.203 n miles |
| Ship 4 | 2.723 n miles | 1.074 n miles | 1.225 n miles | — | 1.707 n miles |
| Ship 5 | 1.107 n miles | 1.330 n miles | 1.203 n miles | 1.707 n miles | — |
| No. | Compliance | No. | Compliance | No. | Compliance | No. | Compliance |
|---|---|---|---|---|---|---|---|
| No. 1 | N | No. 5 | N | No. 9 | N | No. 13 | Y |
| No. 2 | N | No. 6 | N | No. 10 | Y | No. 14 | N |
| No. 3 | N | No. 7 | N | No. 11 | N | No. 15 | N |
| No. 4 | N | No. 8 | Y | No. 12 | N | No. 16 | N |
| No. | Compliance | No. | Compliance | No. | Compliance | No. | Compliance |
|---|---|---|---|---|---|---|---|
| No. 1 | N | No. 5 | N | No. 9 | N | No. 13 | Y |
| No. 2 | Y | No. 6 | Y | No. 10 | Y | No. 14 | N |
| No. 3 | Y | No. 7 | Y | No. 11 | Y | No. 15 | N |
| No. 4 | Y | No. 8 | Y | No. 12 | Y | No. 16 | Y |
| Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 | Total | |
|---|---|---|---|---|---|---|
| Deviation distance | 0.372 n miles | 0 n miles | 0.314 n miles | 0.598 n miles | 0.136 n miles | 1.420 n miles |
| Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 | Total | |
|---|---|---|---|---|---|---|
| Deviation distance | 1.024 n miles | 0.306 n miles | 0.312 n miles | 0.021 n miles | 0 n miles | 1.663 n miles |
| Safety | Number of Unreasonable Violations of COLREGs | Total Yaw Distance | Computational Cost (per Time Step) | |||
|---|---|---|---|---|---|---|
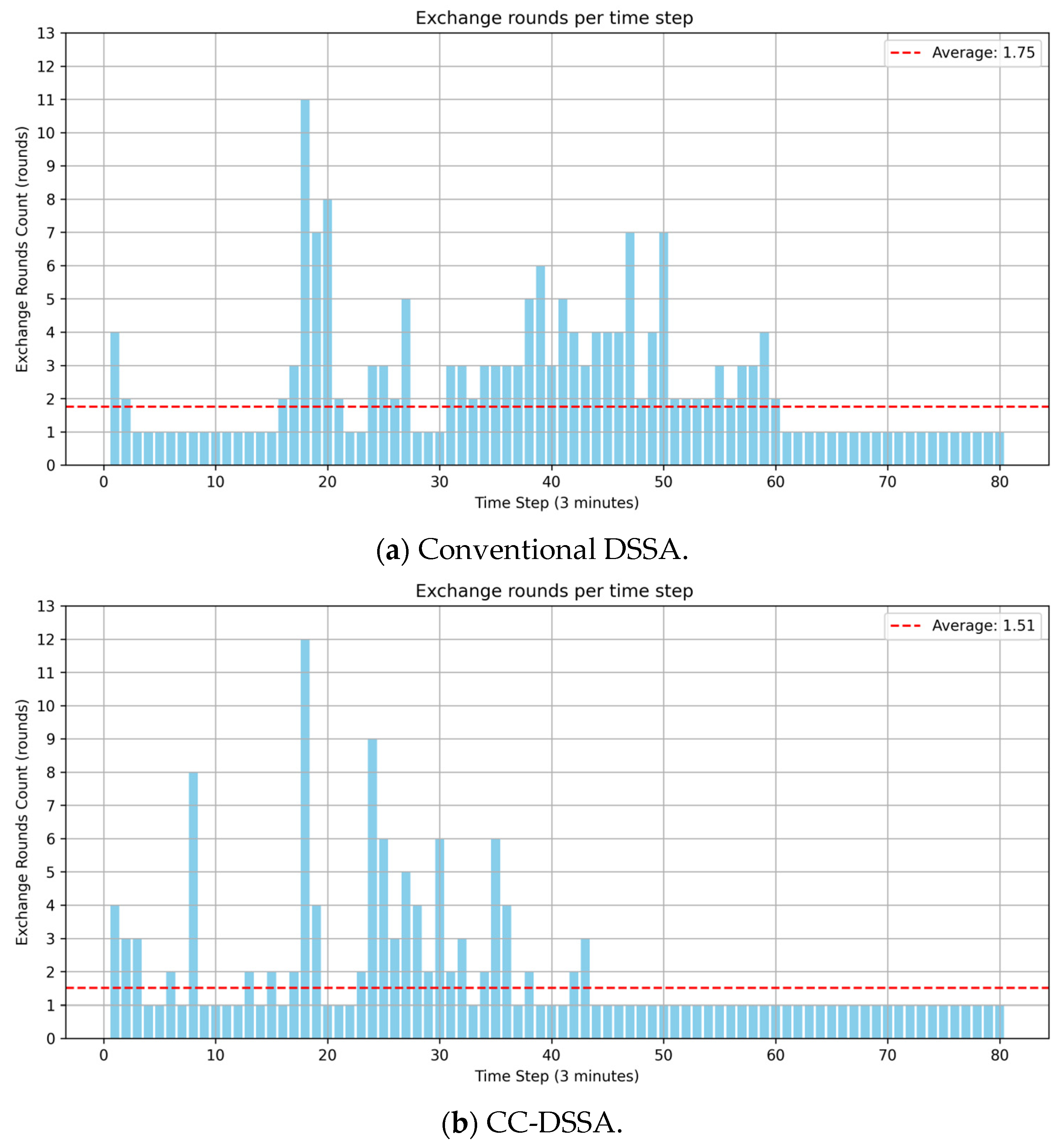
| Collision Count | Occurrences of DCPA Below SDA Threshold | Average Decision-Making Time | Average Exchange Rounds Count | |||
| DSSA | 0 | 2 | 13 | 1.420 n miles | 0.062 s | 1.750 rounds |
| CC-DSSA | 0 | 0 | 0 | 1.663 n miles | 0.068 s | 1.510 rounds |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Koue, J.; Okimoto, T.; Hirayama, K. COLREGs-Compliant Distributed Stochastic Search Algorithm for Multi-Ship Collision Avoidance. J. Mar. Sci. Eng. 2025, 13, 1402. https://doi.org/10.3390/jmse13081402
Zhang B, Koue J, Okimoto T, Hirayama K. COLREGs-Compliant Distributed Stochastic Search Algorithm for Multi-Ship Collision Avoidance. Journal of Marine Science and Engineering. 2025; 13(8):1402. https://doi.org/10.3390/jmse13081402
Chicago/Turabian StyleZhang, Bohan, Jinichi Koue, Tenda Okimoto, and Katsutoshi Hirayama. 2025. "COLREGs-Compliant Distributed Stochastic Search Algorithm for Multi-Ship Collision Avoidance" Journal of Marine Science and Engineering 13, no. 8: 1402. https://doi.org/10.3390/jmse13081402
APA StyleZhang, B., Koue, J., Okimoto, T., & Hirayama, K. (2025). COLREGs-Compliant Distributed Stochastic Search Algorithm for Multi-Ship Collision Avoidance. Journal of Marine Science and Engineering, 13(8), 1402. https://doi.org/10.3390/jmse13081402










