Power Assessment and Performance Comparison of Wind Turbines Driven by Multivariate Environmental Factors
Abstract
1. Introduction
- A hybrid data cleaning approach is developed based on the bidirectional quartile method, with the incorporation of power curtailment detection. This method improves the identification of outliers in typical data distribution areas.
- Taking into account the differences between maximum power point tracking (MPPT) and constant power control approaches for variable-speed, variable-pitch wind turbines, the rated wind speed is used as the segmentation reference value to construct multivariable environmental factor samples for training a segmented LSTM model. The sample features are constructed without involving turbine-specific parameters (such as rotor speed, pitch angle, etc.), enabling the samples to serve as a unified input for comparing the power output of different turbines.
- By applying the proposed method to a full year of SCADA data, a comparative analysis of the power generation performance of three 5.5 MW offshore wind turbines is conducted. Furthermore, the results are compared with their annual power output, fault occurrences, and total maintenance time, thereby enriching the perspective on turbine performance assessment.
2. Methods
2.1. Data Cleaning
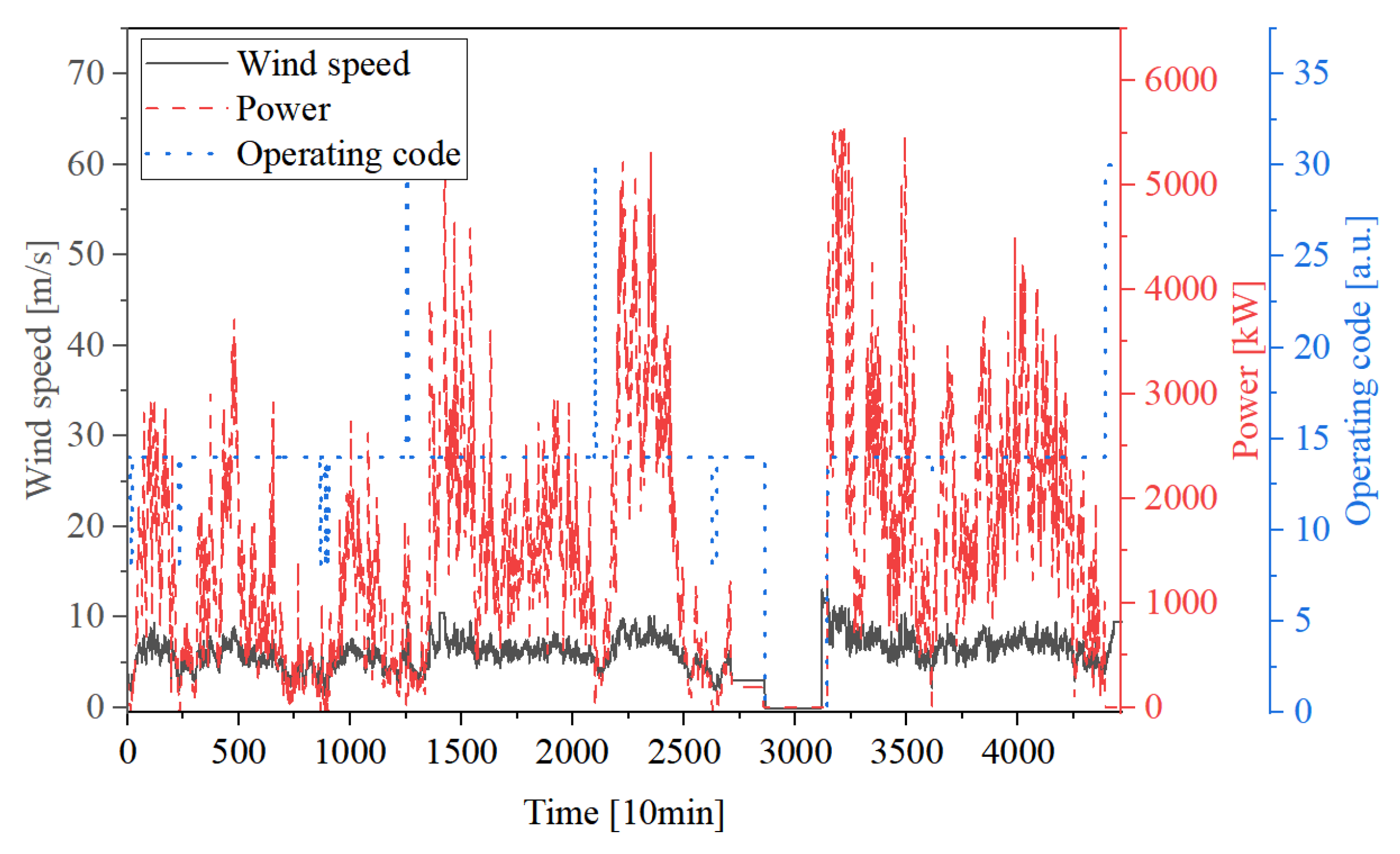
2.1.1. Power Curtailment Detection Algorithm
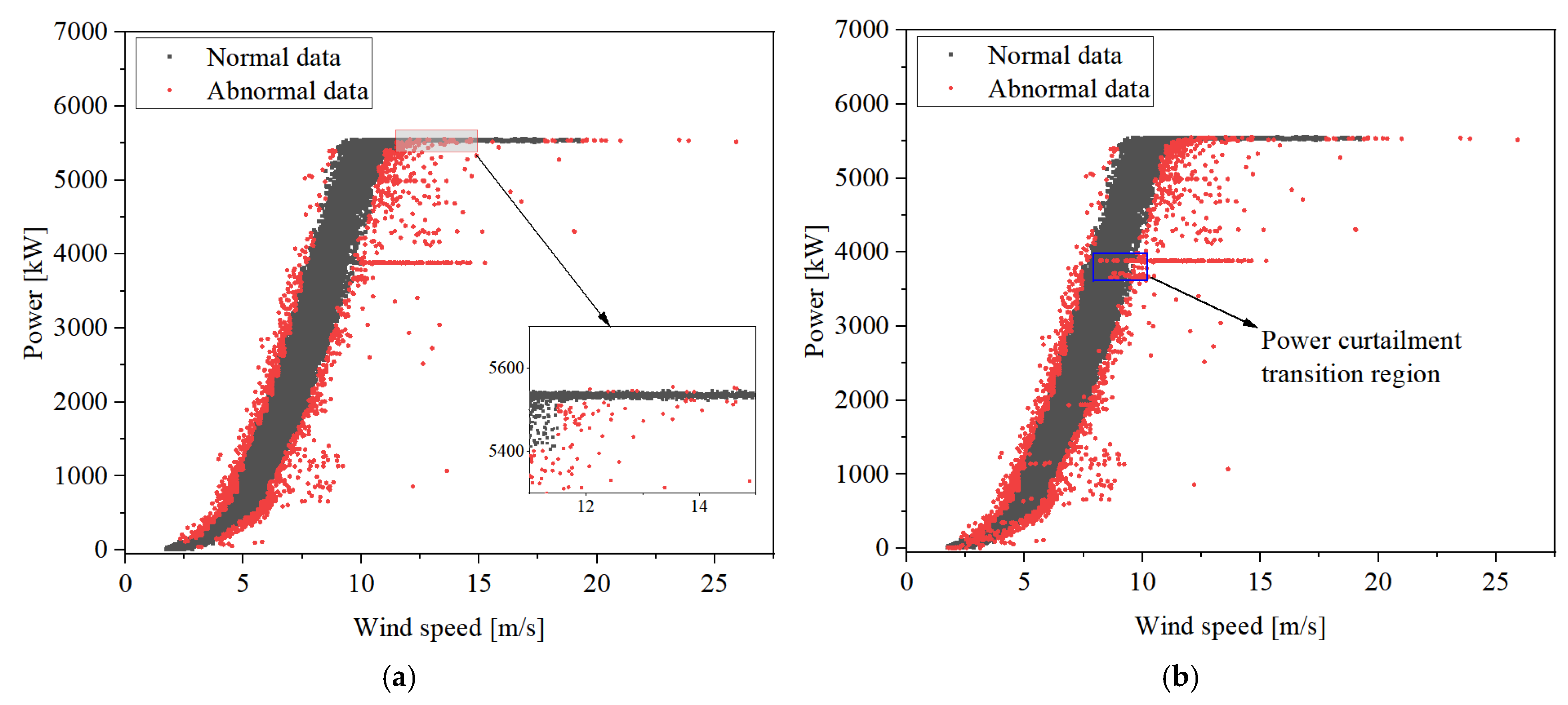
2.1.2. Bidirectional Quartile Method
2.2. Data Classification
2.3. Machine Learning
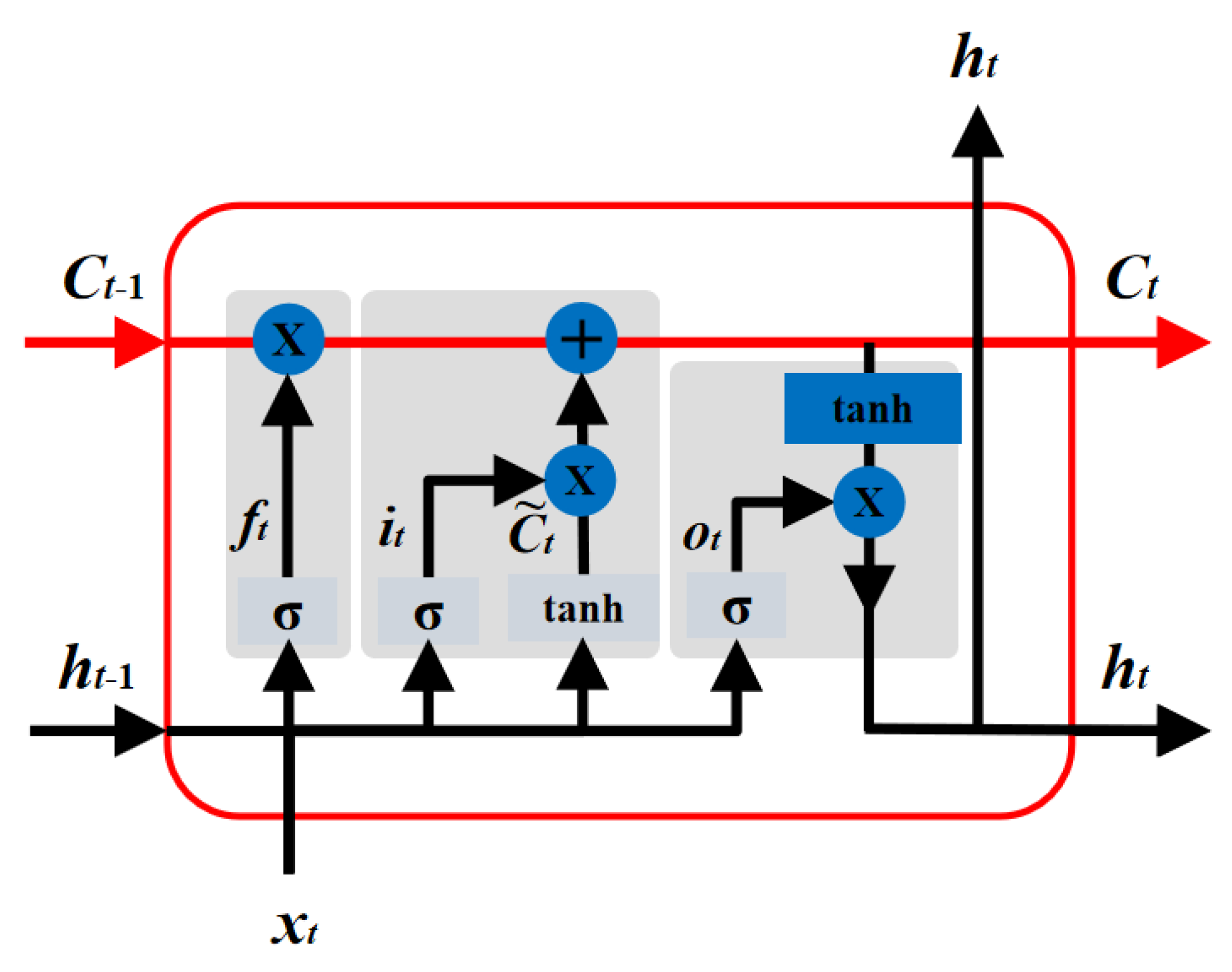
2.3.1. LSTM Unit
2.3.2. Evaluation Metrics
2.4. Selection of Multivariable Environmental Factors
2.5. Power Assessment Model Framework
3. Results and Discussion
3.1. Wind Turbine Data Cleaning Results
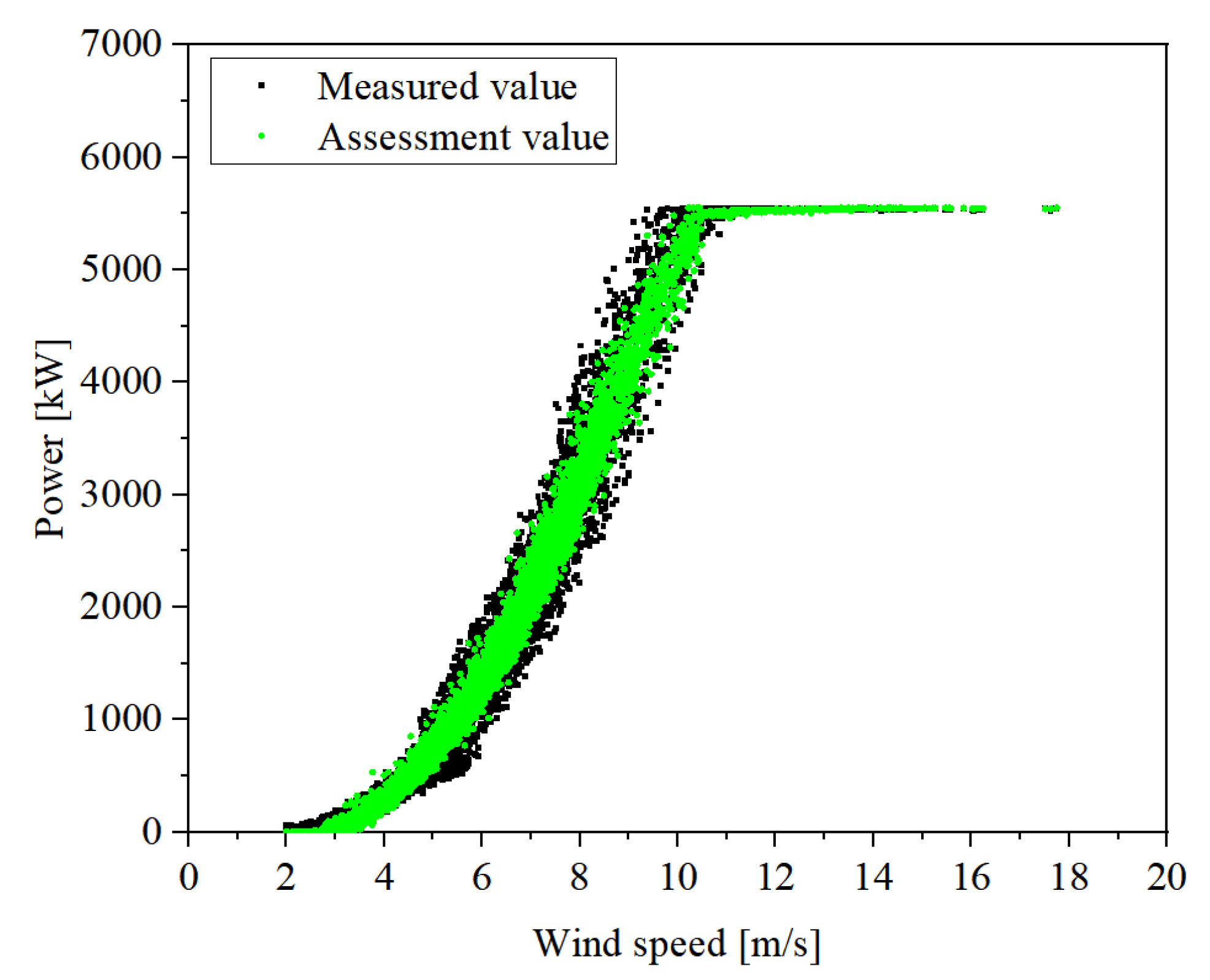
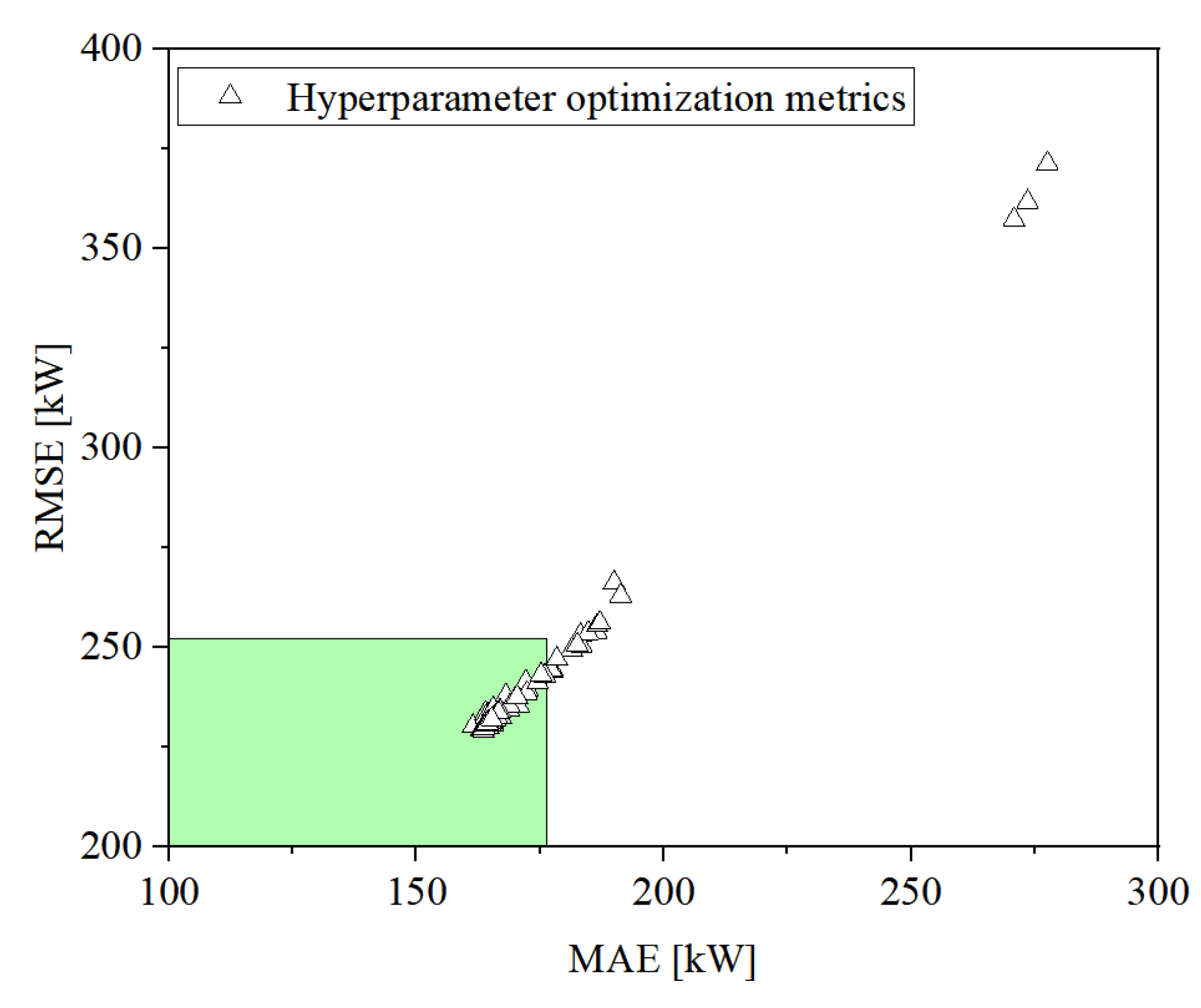
3.2. Proposed Model Training
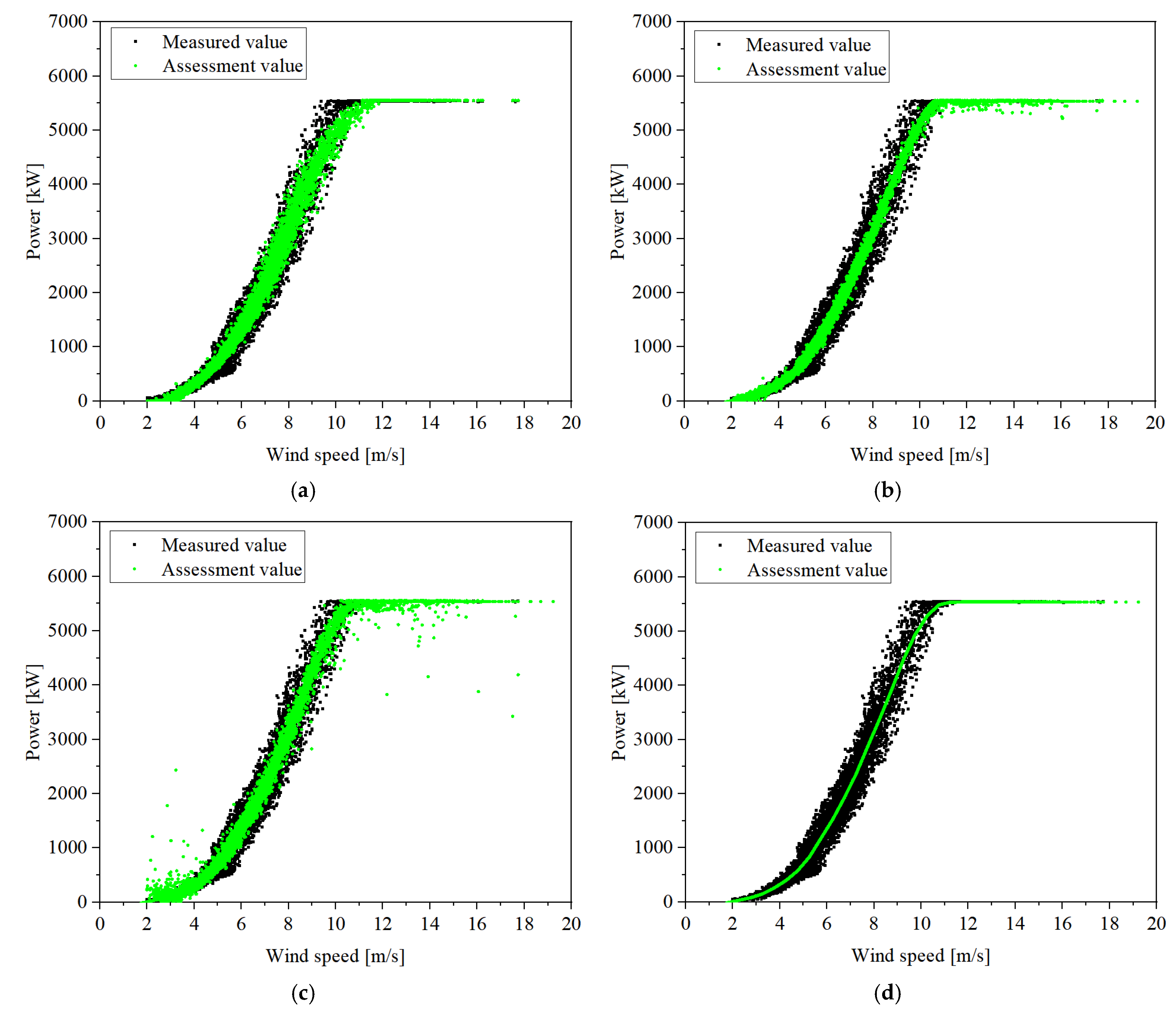
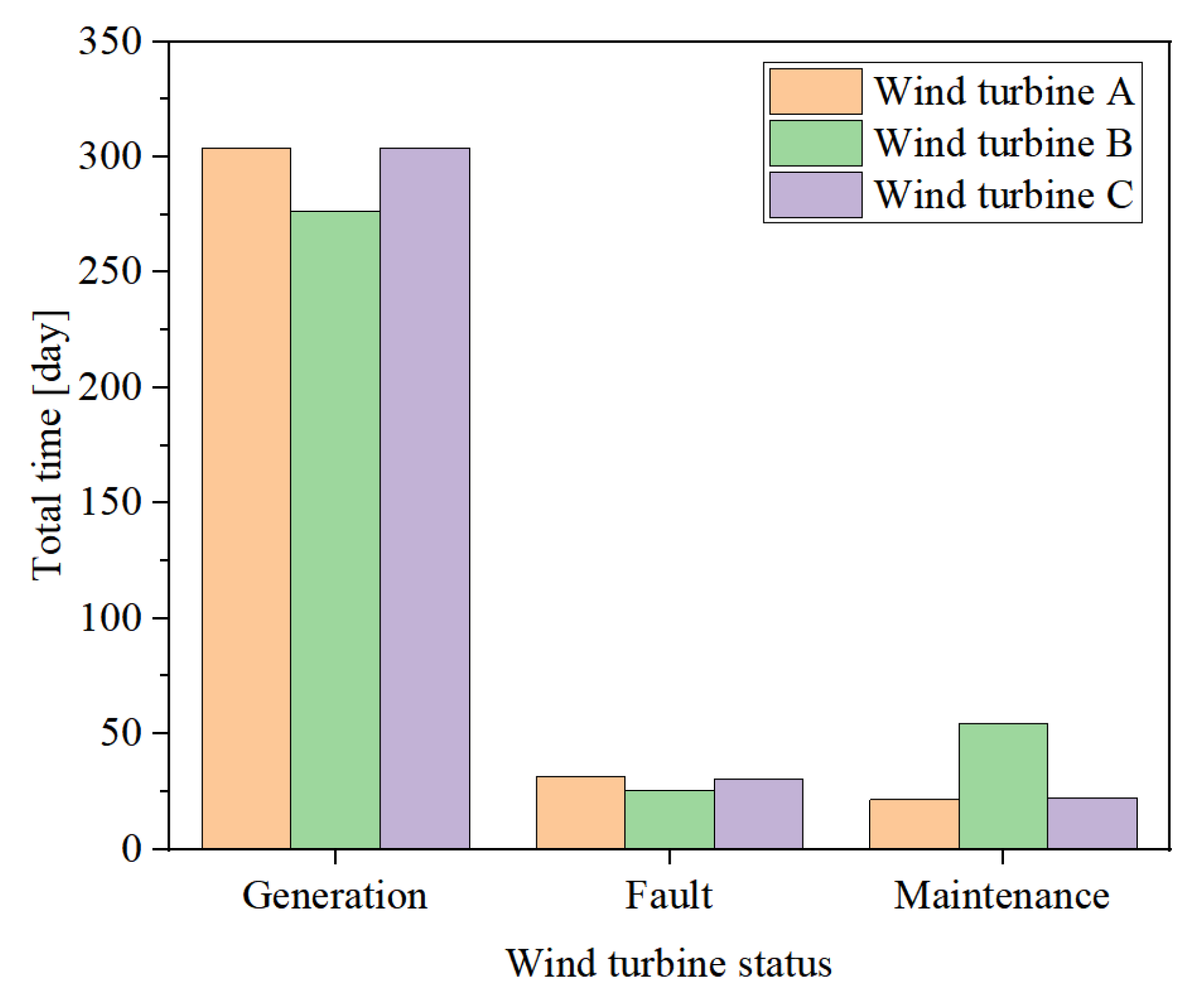
3.3. Performance Comparison of Wind Turbines
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | |
| BPNN | Backpropagation neural network |
| CFD | Computational fluid dynamics |
| GRU | Gated recurrent unit |
| HAWTs | Horizontal-axis wind turbines |
| IEA | International Energy Agency |
| IQR | Interquartile range |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MPPT | Maximum power point tracking |
| NMAPE | Normalized mean absolute percentage error |
| RMSE | Root mean square error |
| SCADA | Supervisory control and data acquisition |
| SVM | Support vector machines |
| TI | Turbulence intensity |
| VAWTs | Vertical-axis wind turbines |
| WDC | Wind direction cosine |
| WDS | Wind direction sine |
| WTPC | Wind turbine power curve |
| Symbols and terms | |
| A | The rotor swept area |
| Cp | The wind energy utilization coefficient at the hub height wind speed |
| The cell states at time step t | |
| The candidate cell state at time step t | |
| The forget gate at time step t | |
| The hidden states at time step t | |
| The input gate at time step t | |
| The output gate at time step t | |
| The standard deviation of the power within the window | |
| The sigmoid function | |
| Dynamic threshold determined through statistical analysis of historical data | |
| Proportional coefficient | |
| Air density | |
| Pt | The power at time t |
| Prated | The rated power of the turbine |
| Estimated value of power | |
| Actual target value of power | |
| Mean of target values | |
| Maximum of target values | |
| R2 | Coefficient of determination |
| tanh(·) | The hyperbolic tangent function |
| VH | The wind speed at the hub height |
| The input data vector at time step t | |
References
- Wang, J.Z.; Wang, Y.; Jiang, P. The study and application of a novel hybrid forecasting model–A case study of wind speed forecasting in China. Appl. Energy 2015, 143, 472–488. [Google Scholar] [CrossRef]
- Shao, H.; Henriques, R.; Morais, H.; Tedeschi, E. Power quality monitoring in electric grid integrating offshore wind energy: A review. Renew. Sustain. Energy Rev. 2024, 191, 114094. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Lian, J. Review of integrated installation technologies for offshore wind turbines: Current progress and future development trends. Energy Convers. Manag. 2022, 255, 115319. [Google Scholar] [CrossRef]
- Kassa, B.Y.; Baheta, A.T.; Beyene, A. Current trends and innovations in enhancing the aerodynamic performance of small-scale, horizontal axis wind turbines: A review. ASME Open J. Eng. 2024, 3, 031001. [Google Scholar] [CrossRef]
- Ghafoorian, F.; Wan, H.; Chegini, S. A systematic analysis of a small-scale HAWT configuration and aerodynamic performance optimization through kriging, factorial, and RSM methods. J. Appl. Comput. Mech. 2024, 11, 887–903. [Google Scholar]
- Farajyar, S.; Ghafoorian, F.; Mehrpooya, M.; Asadbeigi, M. CFD investigation and optimization on the aerodynamic performance of a Savonius vertical axis wind turbine and its installation in a hybrid power supply system: A case study in Iran. Sustainability 2023, 15, 5318. [Google Scholar] [CrossRef]
- Enevoldsen, P.; Valentine, S.V. Do onshore and offshore wind farm development patterns differ? Energy Sustain. Dev. 2016, 35, 41–51. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, H.; Liu, Y.; Han, S.; Li, L. Uncertainty estimation for wind energy conversion by probabilistic wind turbine power curve modelling. Appl. Energy 2019, 239, 1356–1370. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. A global wind farm potential index to increase energy yields and accessibility. Energy 2021, 231, 120923. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Development of onshore wind turbine fleet counteracts climate change-induced reduction in global capacity factor. Nat. Energy 2022, 7, 608–619. [Google Scholar] [CrossRef]
- Lee, G.; Ding, Y.; Genton, M.G.; Xie, L. Power curve estimation with multivariate environmental factors for inland and offshore wind farms. J. Am. Stat. Assoc. 2015, 110, 56–67. [Google Scholar] [CrossRef]
- Cascianelli, S.; Astolfi, D.; Castellani, F.; Cucchiara, R.; Fravolini, M.L. Wind turbine power curve monitoring based on environmental and operational data. IEEE Trans. Ind. Inform. 2021, 18, 5209–5218. [Google Scholar] [CrossRef]
- Janssens, O.; Noppe, N.; Devriendt, C.; de Walle, V.; Hoecke, V. Data-driven multivariate power curve modeling of offshore wind turbines. Eng. Appl. Artif. Intell. 2016, 55, 331–338. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Besseau, R.; Jansen, M.; Staffell, I.; Troccoli, A.; Dubus, L.; Schmidt, J.; Gruber, K.; Simões, S.G.; Heier, S. A parametric model for wind turbine power curves incorporating environmental conditions. Renew. Energy 2020, 157, 754–768. [Google Scholar] [CrossRef]
- Astolfi, D.; Castellani, F.; Lombardi, A.; Terzi, L. Multivariate SCADA data analysis methods for real-world wind turbine power curve monitoring. Energies 2021, 14, 1105. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D. Wind turbine power curve modeling and monitoring with Gaussian process and SPRT. IEEE Trans. Sustain. Energy 2018, 11, 107–115. [Google Scholar] [CrossRef]
- IEC 61400-12-1:2017; Wind energy generation systems – Part 12-1: Power performance measurements of electricity producing wind turbines. International Electrotechnical Commission: Geneva, Switzerland, 2017.
- Mushtaq, K.; Zou, R.; Waris, A.; Yang, K.; Wang, J.; Iqbal, J.; Jameel, M. Multivariate wind power curve modeling using multivariate adaptive regression splines and regression trees. PLoS ONE 2023, 18, e0290316. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhou, B.; Zhu, D.; Zou, M.; Luo, H. Pre-Filtering SCADA data for enhanced machine learning-based multivariate power estimation in wind turbines. J. Mar. Sci. Eng. 2025, 13, 410. [Google Scholar] [CrossRef]
- Qiao, Y.; Han, S.; Zhang, Y.; Liu, Y.; Yan, J. A multivariable wind turbine power curve modeling method considering segment control differences and short-time self-dependence. Renew. Energy 2024, 222, 119894. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D. Comparative assessments of binned and support vector regression-based blade pitch curve of a wind turbine for the purpose of condition monitoring. Int. J. Energy Environ. Eng. 2019, 10, 181–188. [Google Scholar] [CrossRef]
- Karamichailidou, D.; Kaloutsa, V.; Alexandridis, A. Wind turbine power curve modeling using radial basis function neural networks and tabu search. Renew. Energy 2021, 163, 2137–2152. [Google Scholar] [CrossRef]
- Tao, T.; Liu, Y.; Qiao, Y.; Gao, L.; Lu, J.; Zhang, C.; Wang, Y. Wind turbine blade icing diagnosis using hybrid features and Stacked-XGBoost algorithm. Renew. Energy 2021, 180, 1004–1013. [Google Scholar] [CrossRef]
- Meng, A.; Chen, S.; Ou, Z.; Ding, W.; Zhou, H.; Fan, J.; Yin, H. A hybrid deep learning architecture for wind power prediction based on bi-attention mechanism and crisscross optimization. Energy 2022, 238, 121795. [Google Scholar] [CrossRef]



| Parameters | Value | Units |
|---|---|---|
| Rated power | 5.5 | MW |
| Rotor diameter | 155 | m |
| Hub height | 100 | m |
| Cut-in wind speed | 3 | m/s |
| Rated wind speed | 10.1 | m/s |
| Cut-out wind speed | 25 | m/s |
| Blade tip speed | 97.34 | m/s |
| Gear transmission ratio | 1:23.187 | |
| Blade pitch range | 0 to 91 | ° |
| Model | MAE (kW) | RMSE (kW) | R2 | NMAPE (%) |
|---|---|---|---|---|
| Proposed | 159.7231 | 222.3996 | 0.9793 | 2.8796 |
| LSTM | 161.4178 | 230.1190 | 0.9778 | 2.9101 |
| BPNN | 177.5985 | 251.0999 | 0.9736 | 3.2018 |
| SVM | 188.1254 | 266.4495 | 0.9703 | 3.3916 |
| Bins method | 176.2705 | 252.0215 | 0.9733 | 3.1758 |
| Wind Turbine | Total Power Generation (MWh) | Max. Normalization |
|---|---|---|
| A | 1029.0538 | 1.0000 |
| B | 881.3843 | 0.8565 |
| C | 943.7895 | 0.9171 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhou, B.; Zhu, D.; Zou, M.; Rao, Z.; Luo, H.; Ji, W. Power Assessment and Performance Comparison of Wind Turbines Driven by Multivariate Environmental Factors. J. Mar. Sci. Eng. 2025, 13, 1377. https://doi.org/10.3390/jmse13071377
Wang B, Zhou B, Zhu D, Zou M, Rao Z, Luo H, Ji W. Power Assessment and Performance Comparison of Wind Turbines Driven by Multivariate Environmental Factors. Journal of Marine Science and Engineering. 2025; 13(7):1377. https://doi.org/10.3390/jmse13071377
Chicago/Turabian StyleWang, Bubin, Bin Zhou, Denghao Zhu, Mingheng Zou, Zhao Rao, Haoxuan Luo, and Weihao Ji. 2025. "Power Assessment and Performance Comparison of Wind Turbines Driven by Multivariate Environmental Factors" Journal of Marine Science and Engineering 13, no. 7: 1377. https://doi.org/10.3390/jmse13071377
APA StyleWang, B., Zhou, B., Zhu, D., Zou, M., Rao, Z., Luo, H., & Ji, W. (2025). Power Assessment and Performance Comparison of Wind Turbines Driven by Multivariate Environmental Factors. Journal of Marine Science and Engineering, 13(7), 1377. https://doi.org/10.3390/jmse13071377









