Wake Characteristics and Thermal Properties of Underwater Vehicle Based on DDES Numerical Simulation
Abstract
1. Introduction
2. Numerical Theoretical Model
2.1. Control Equation
2.1.1. Equation of Continuity
2.1.2. Momentum Conservation Equation
2.1.3. Energy Conservation Equation
2.2. Turbulence Solving Method
3. Calculation Model and Numerical Verification
3.1. SUBOFF Computational Model
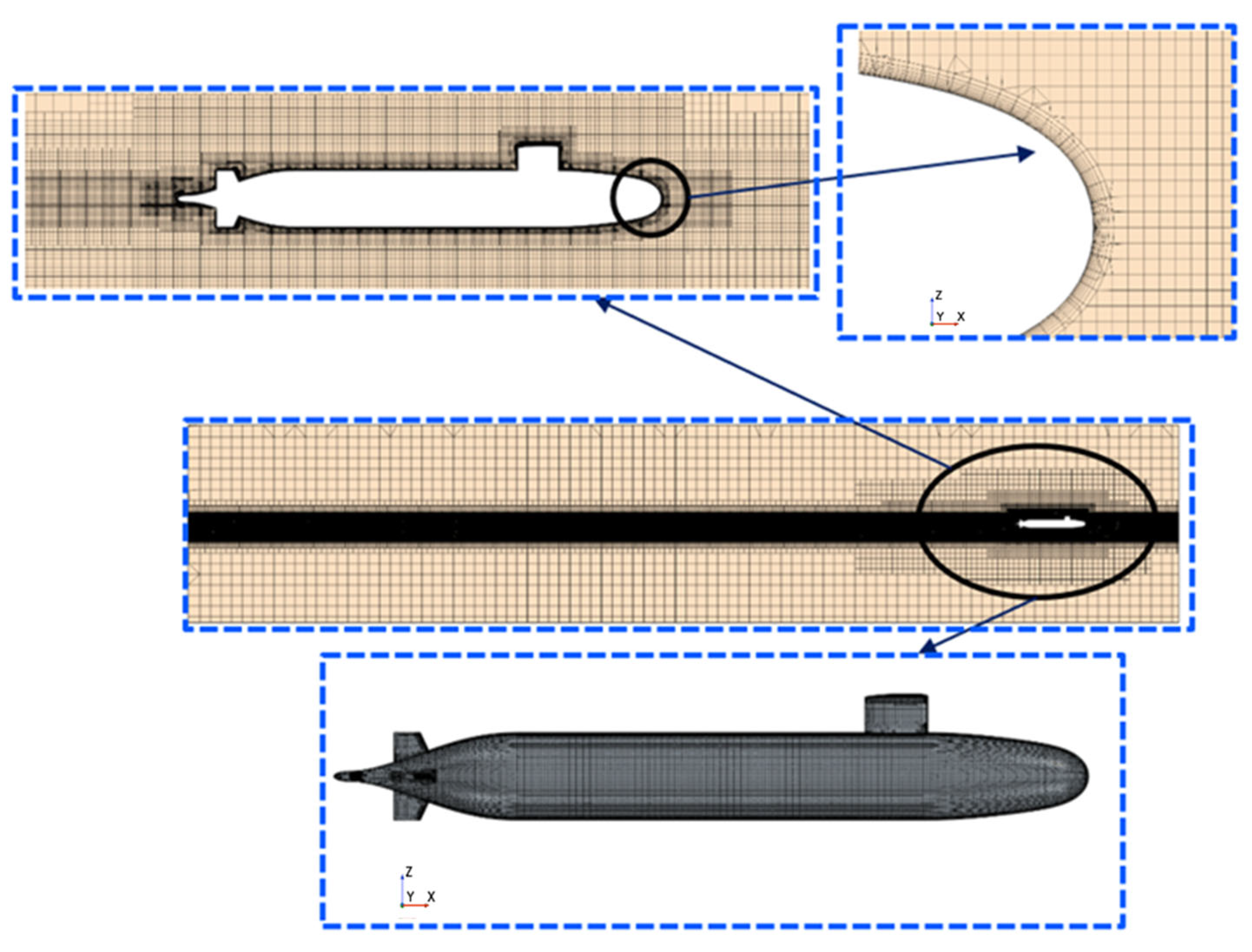
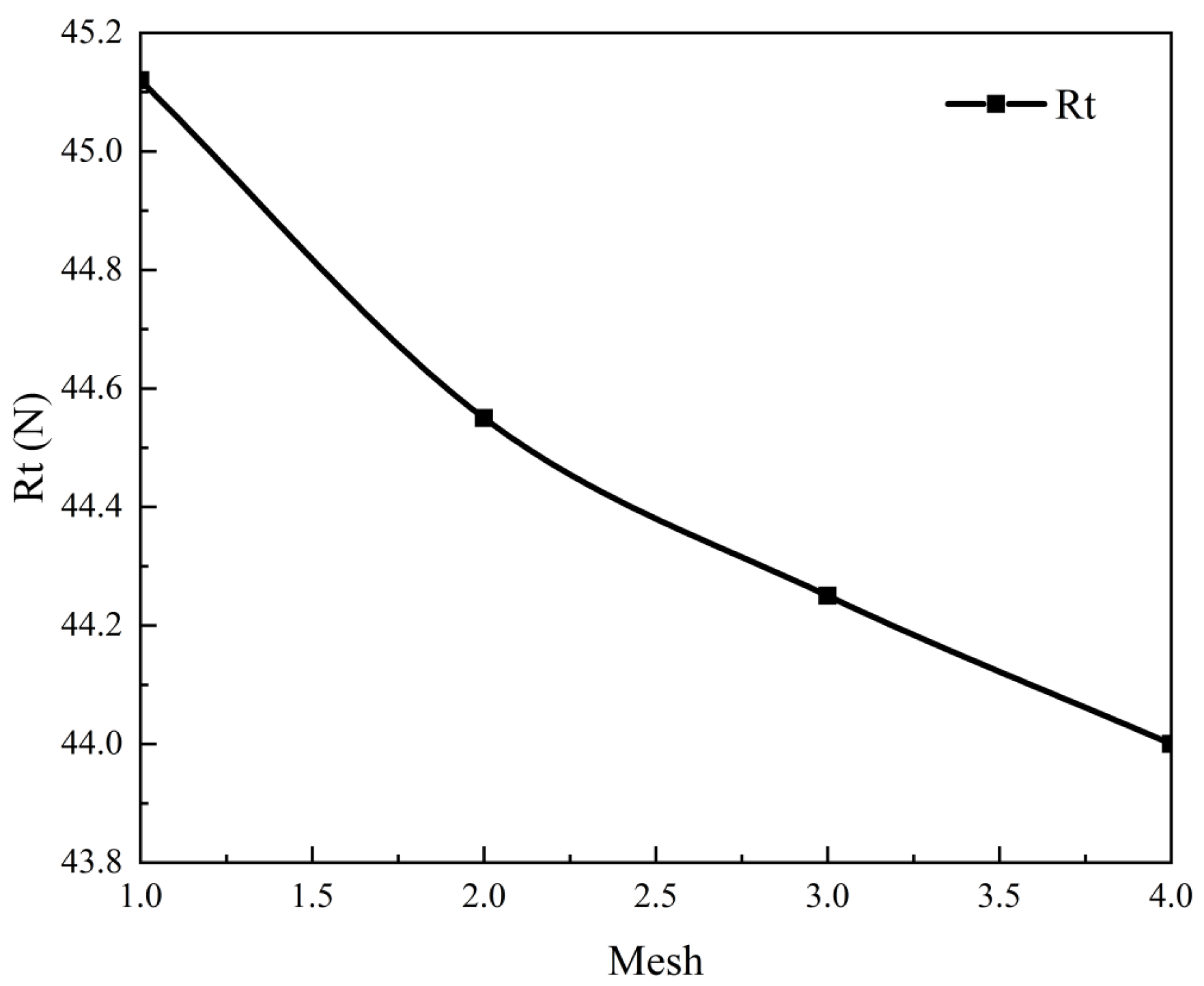
3.2. Calculation Domain and Grid Independence Verification
3.3. Numerical Verification
4. Underwater Vehicle Wake Characteristics and Wake Thermal Characteristics
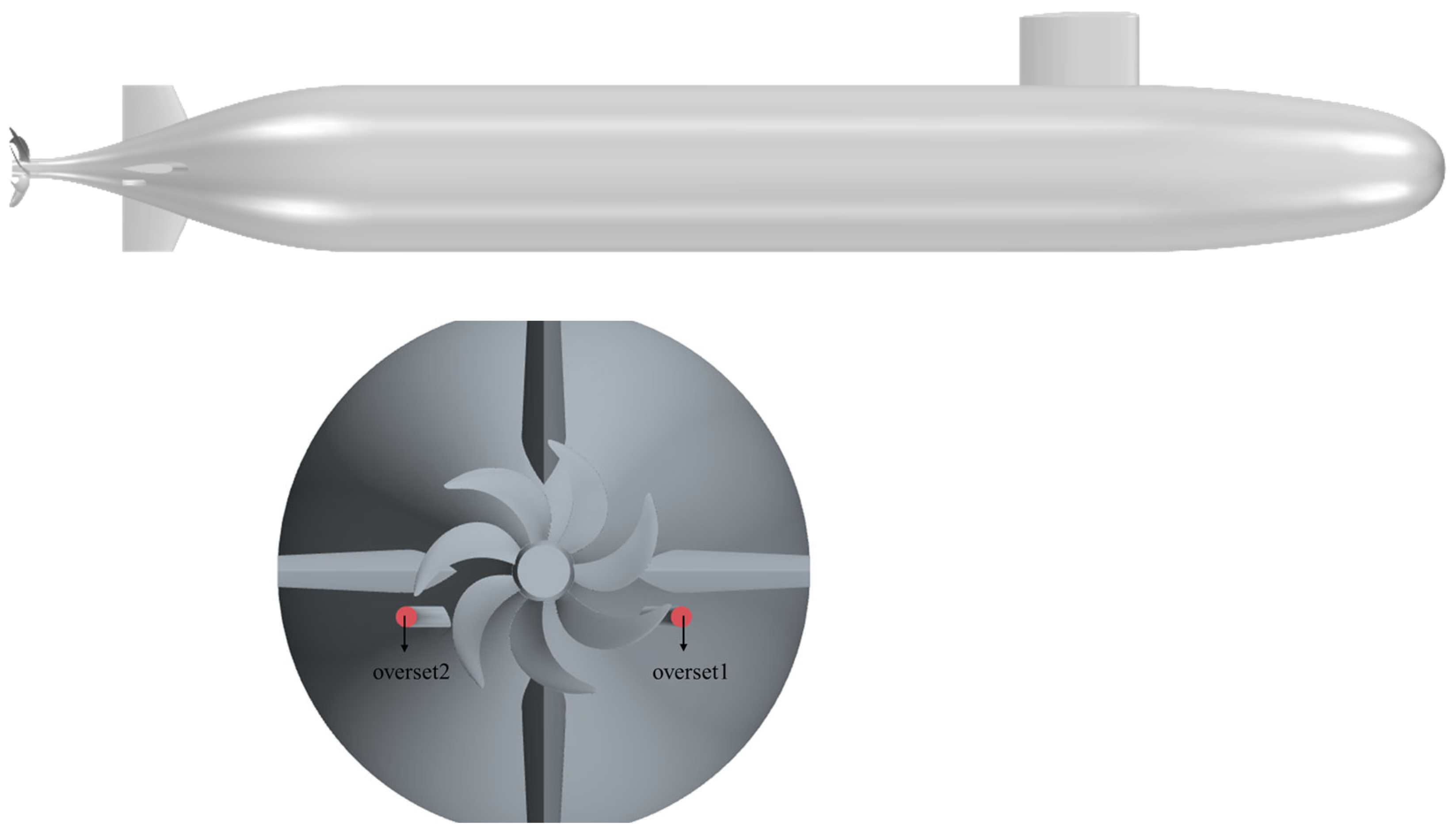
4.1. SUBOFF Model and Meshing
4.2. Numerical Model and Calculation Condition
4.3. Results and Analysis
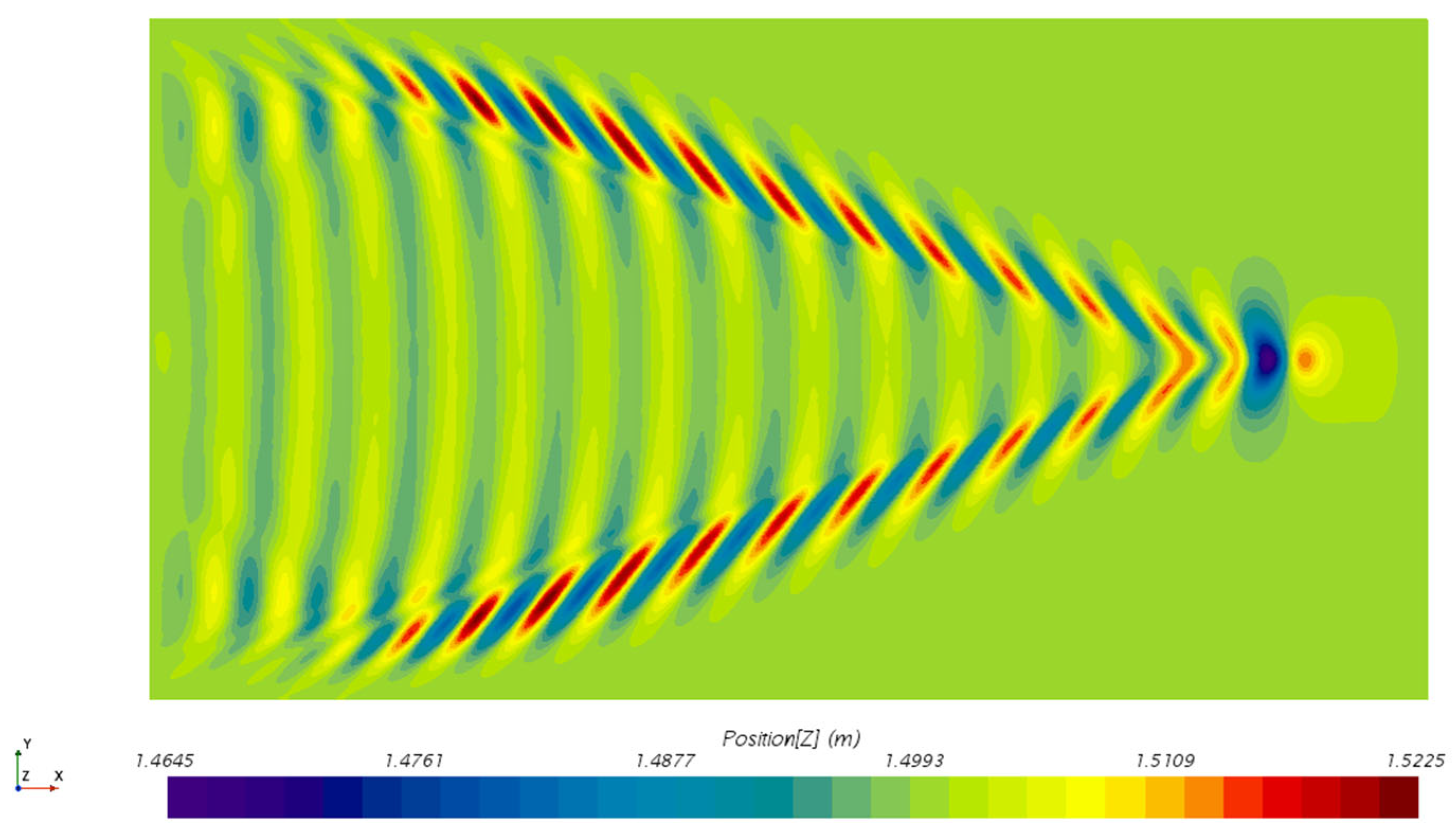
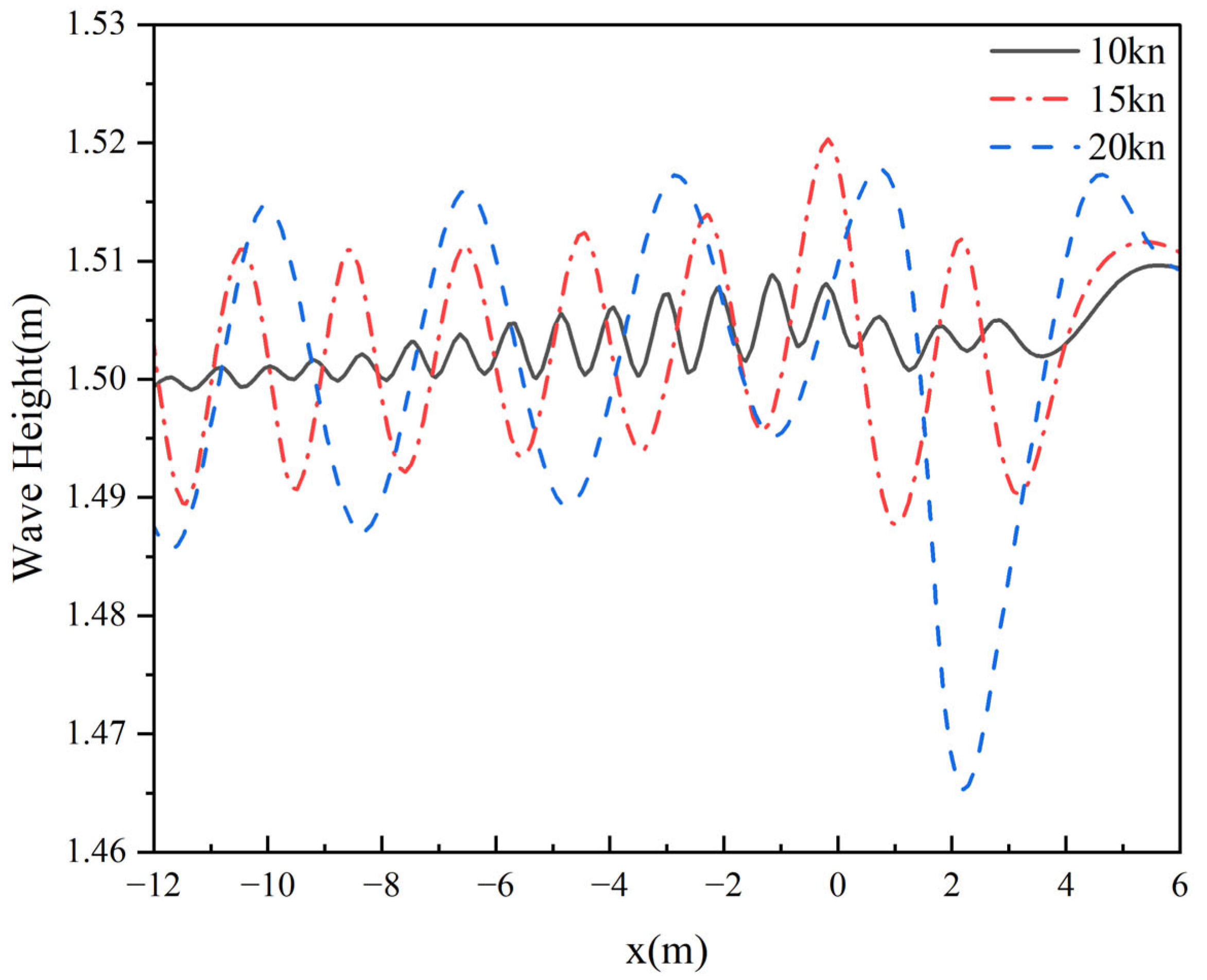
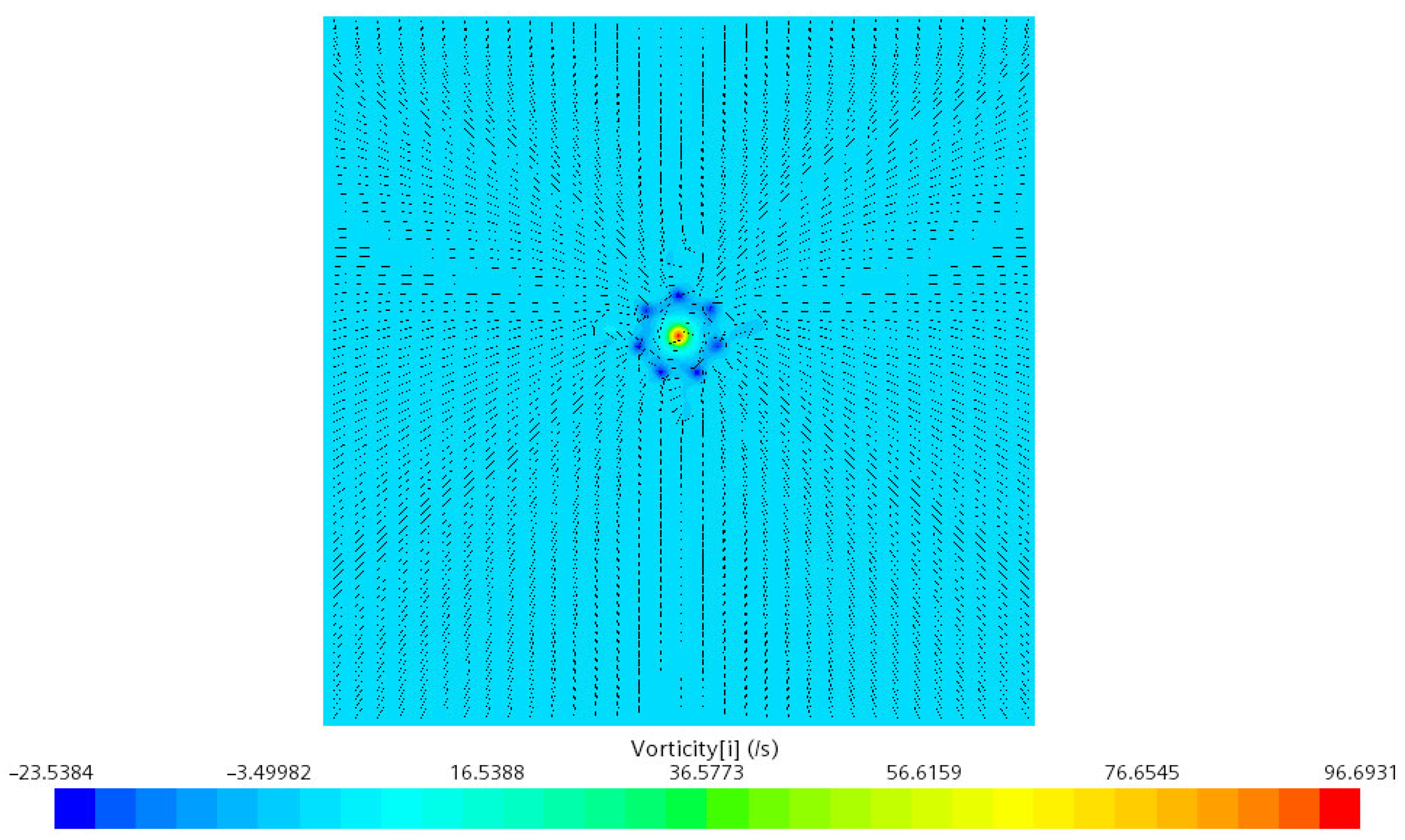
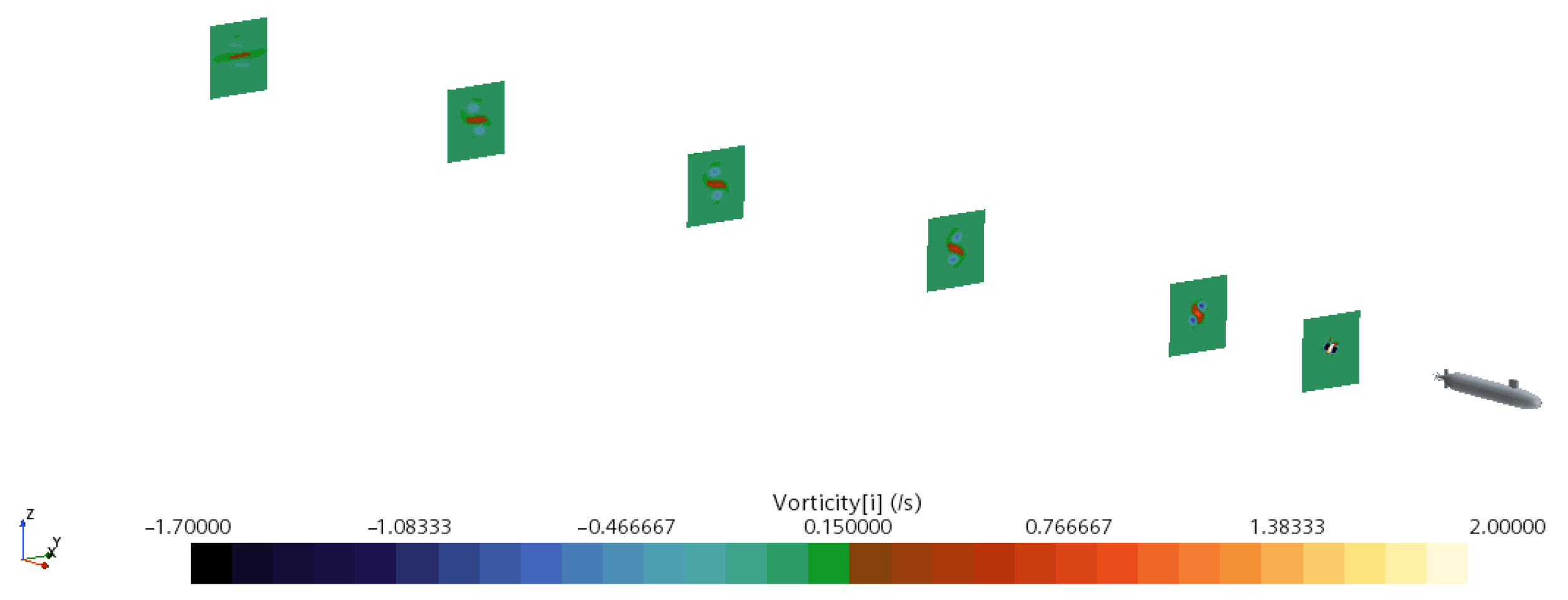
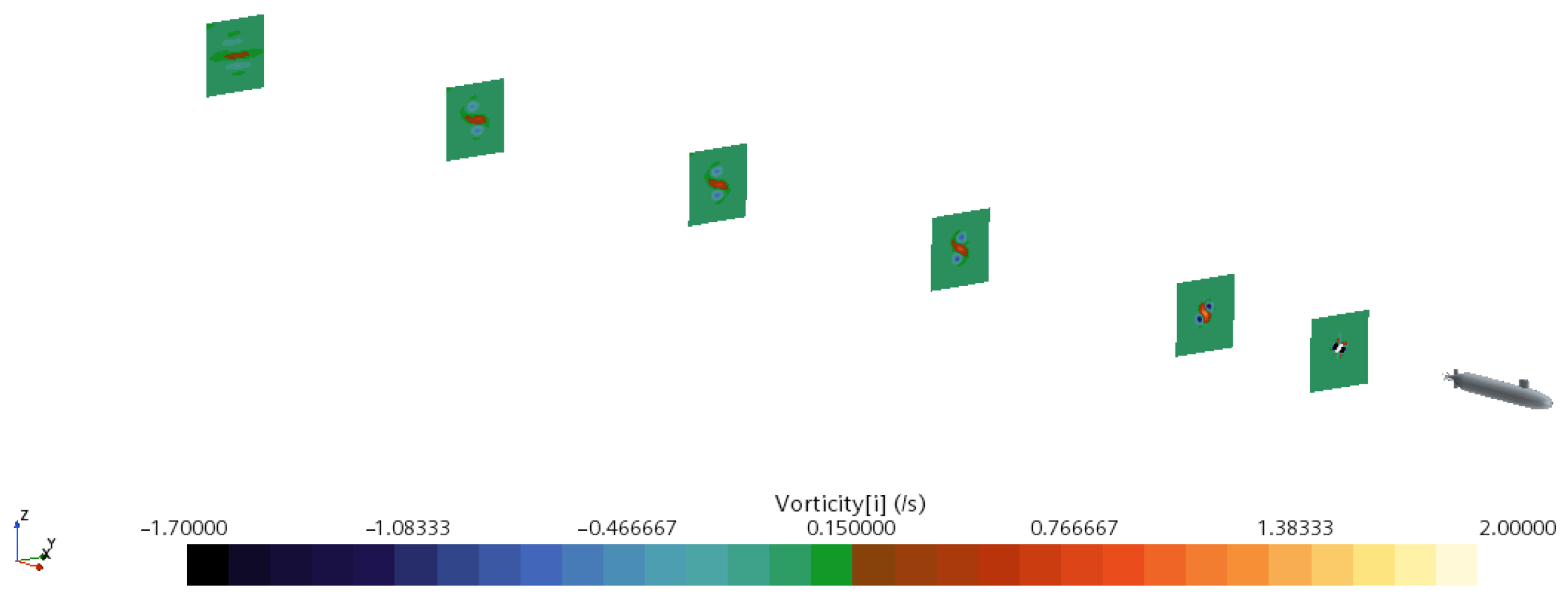
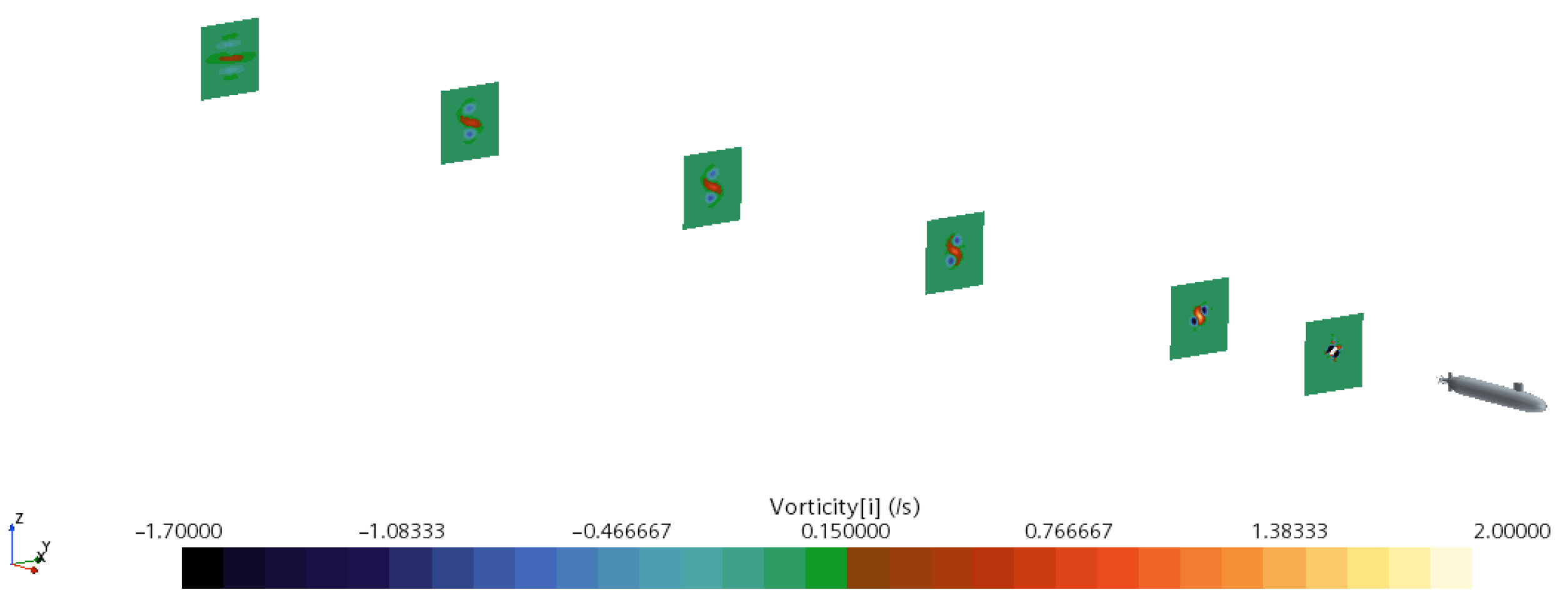
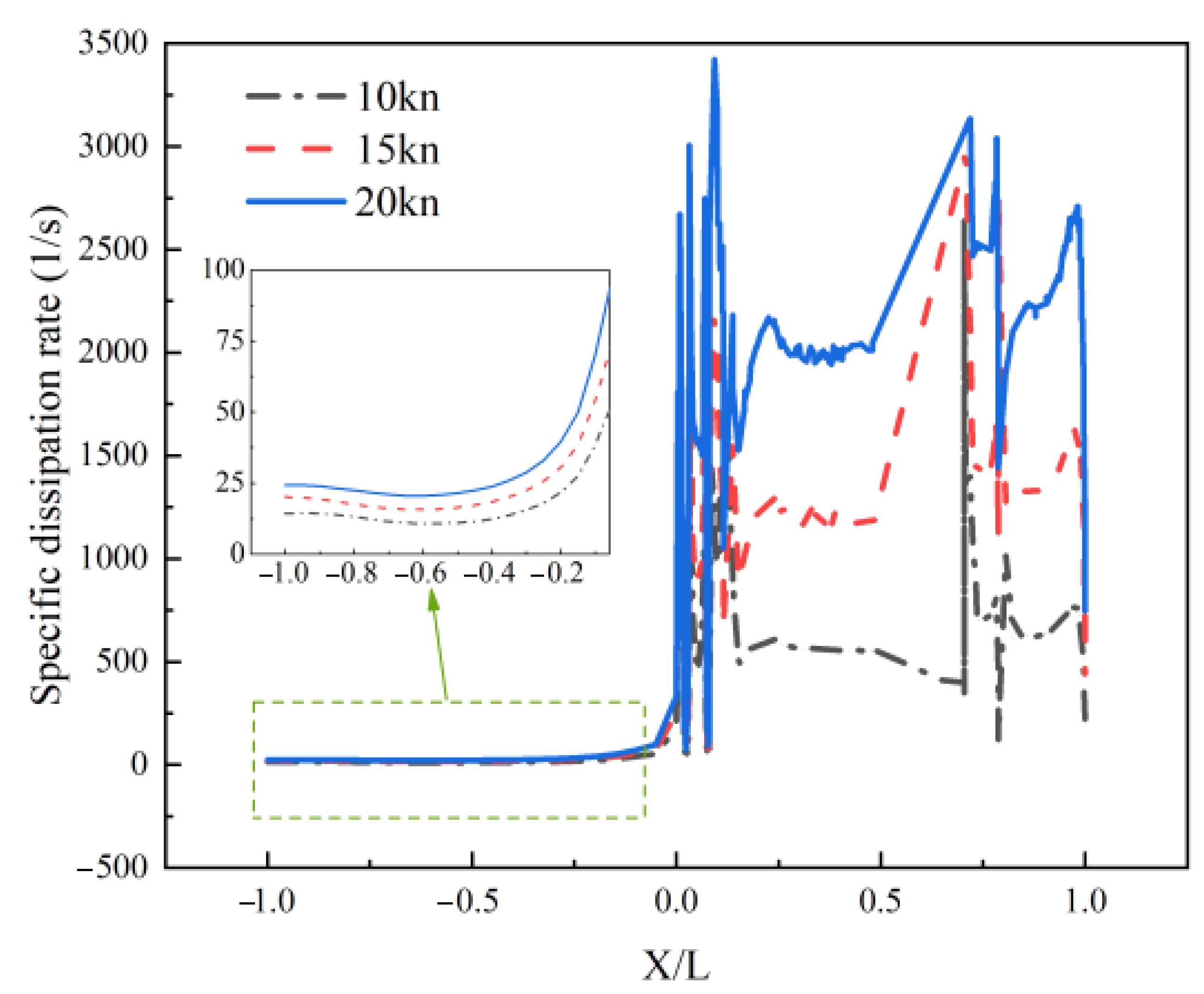
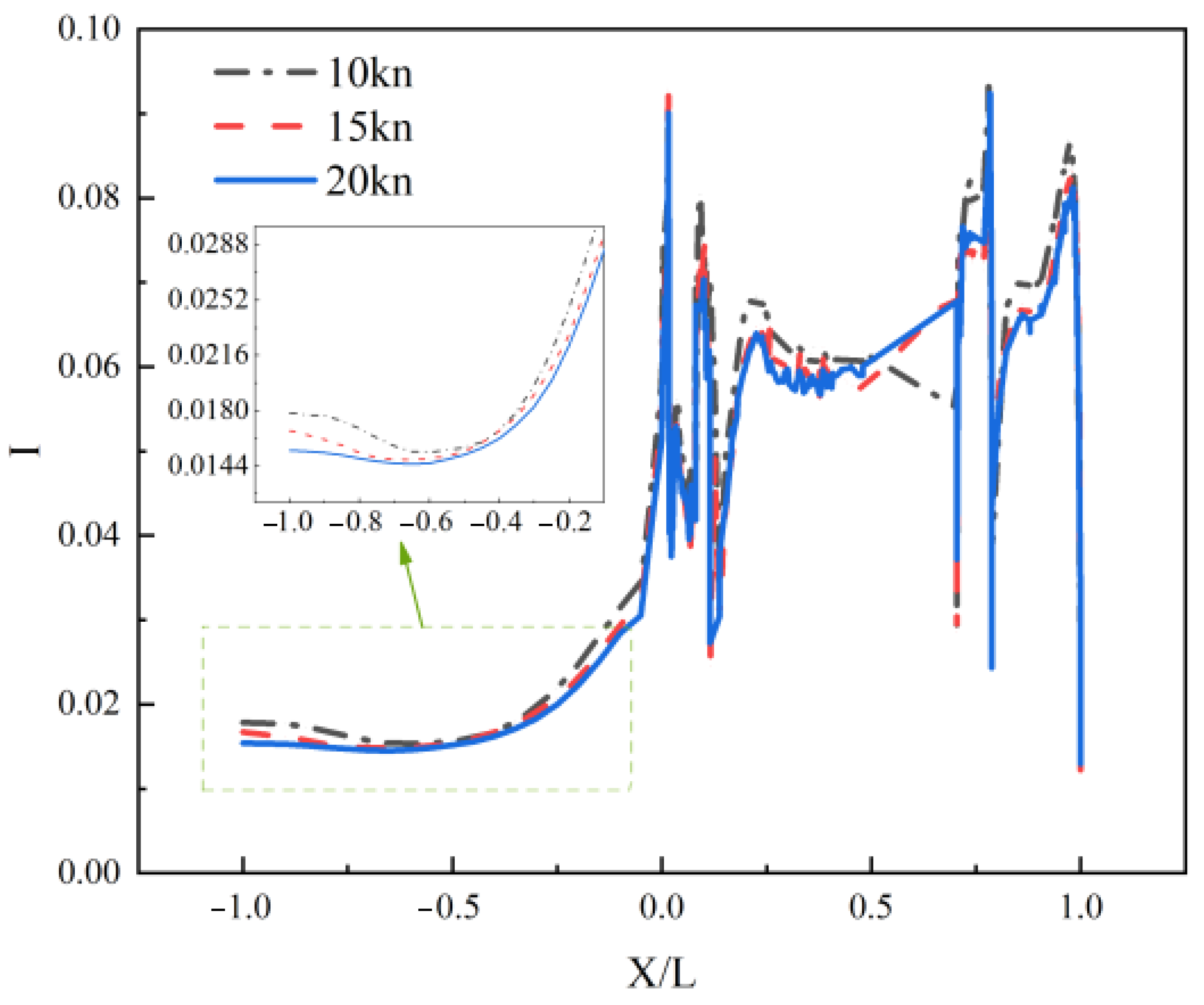
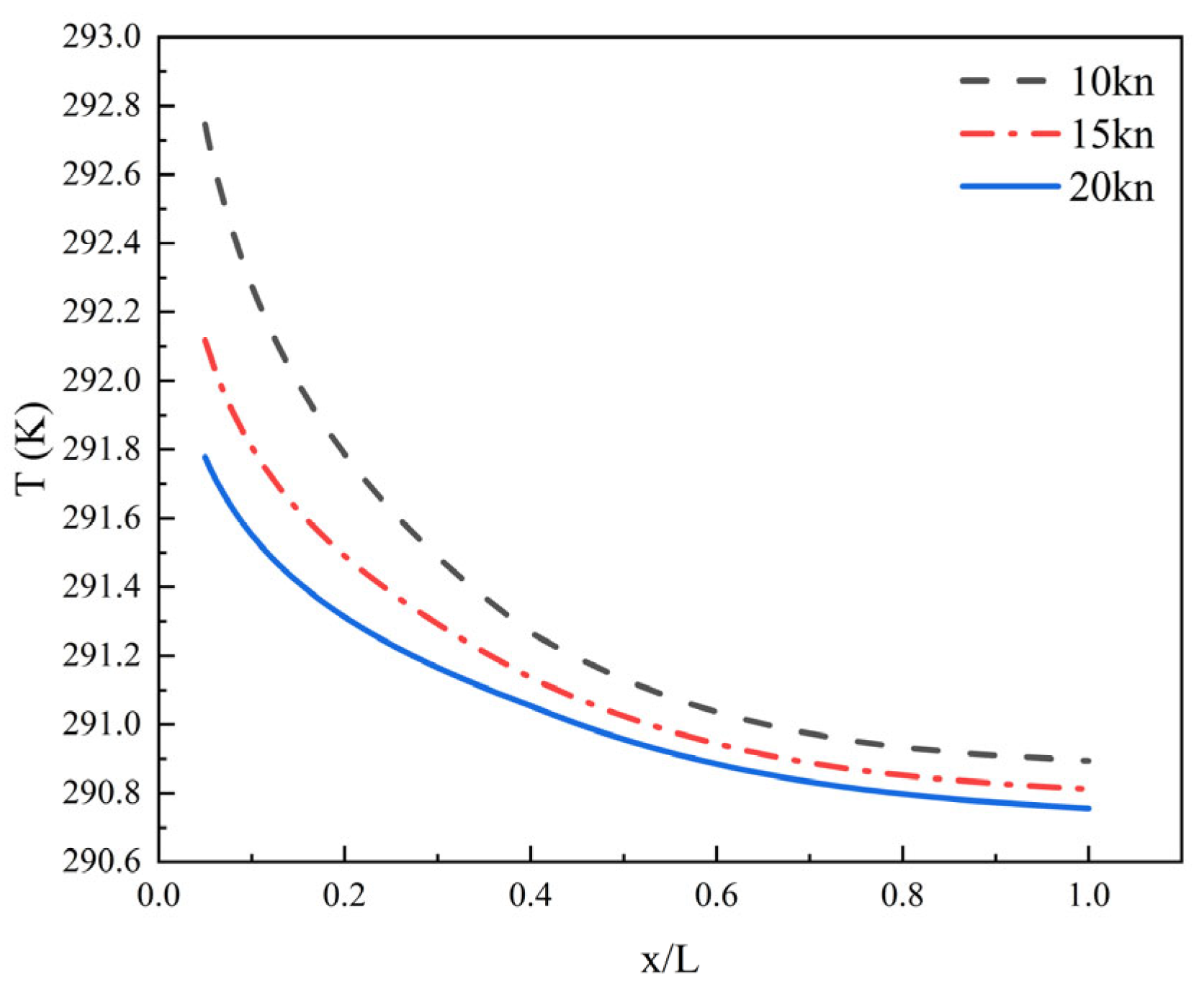
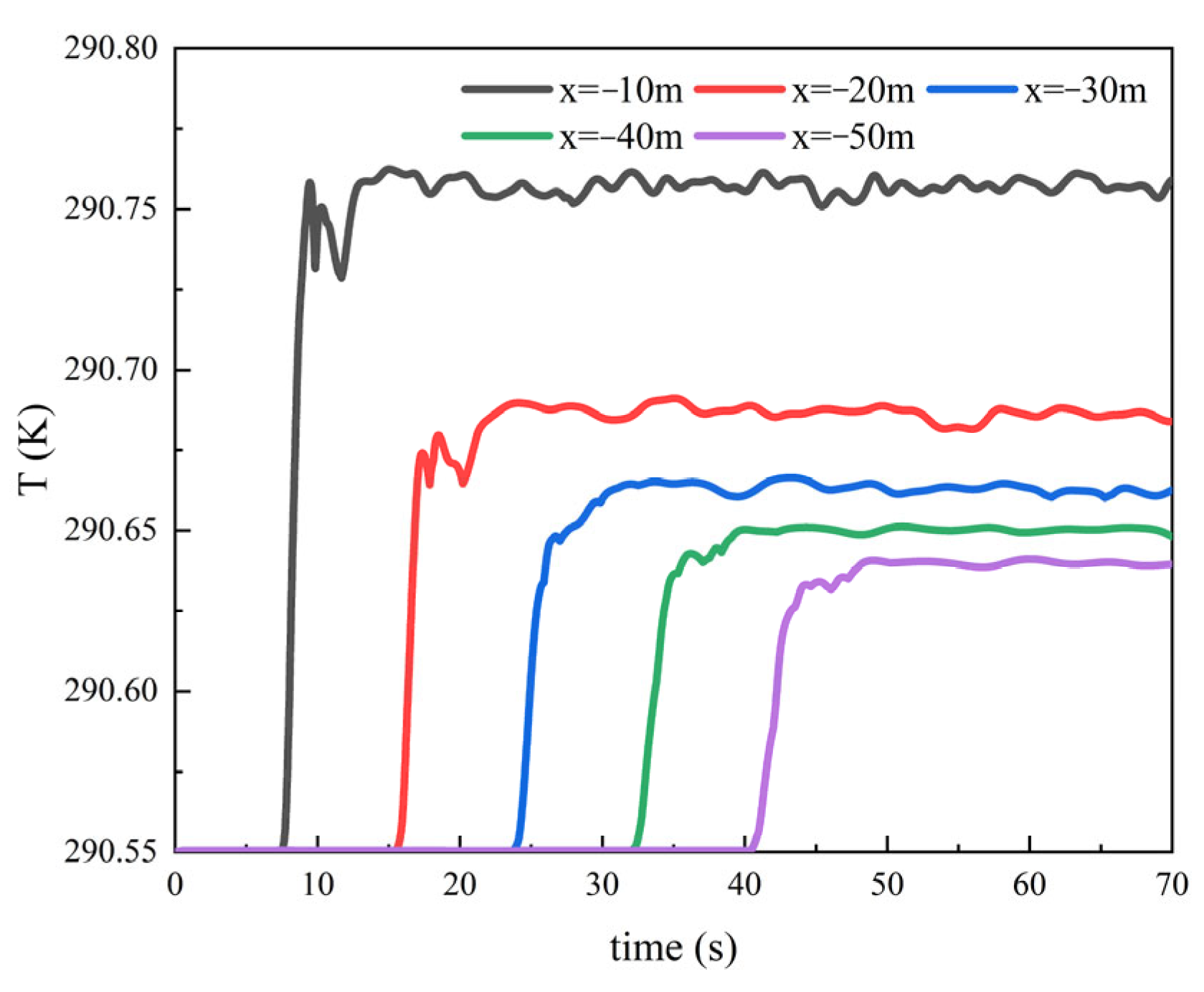
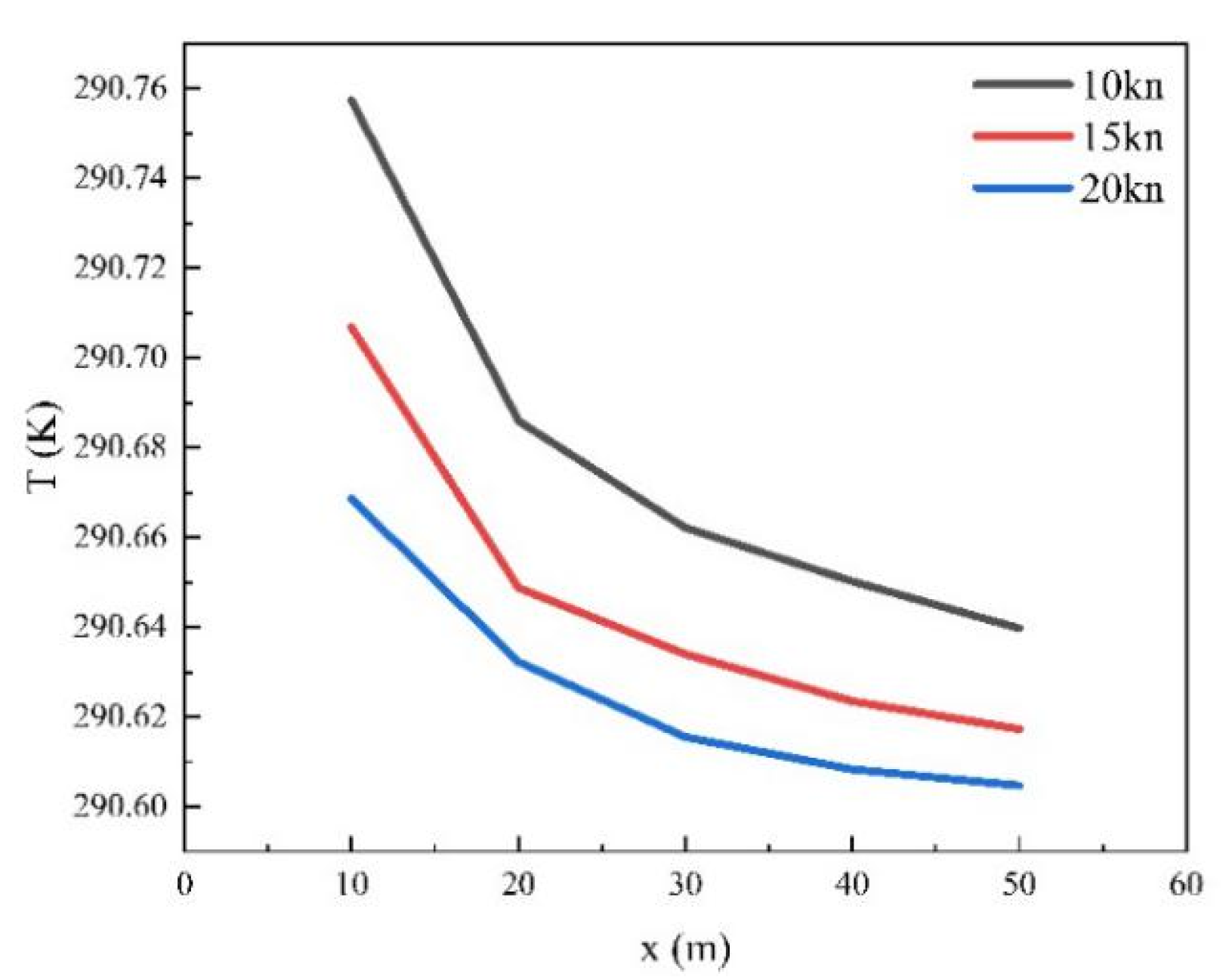
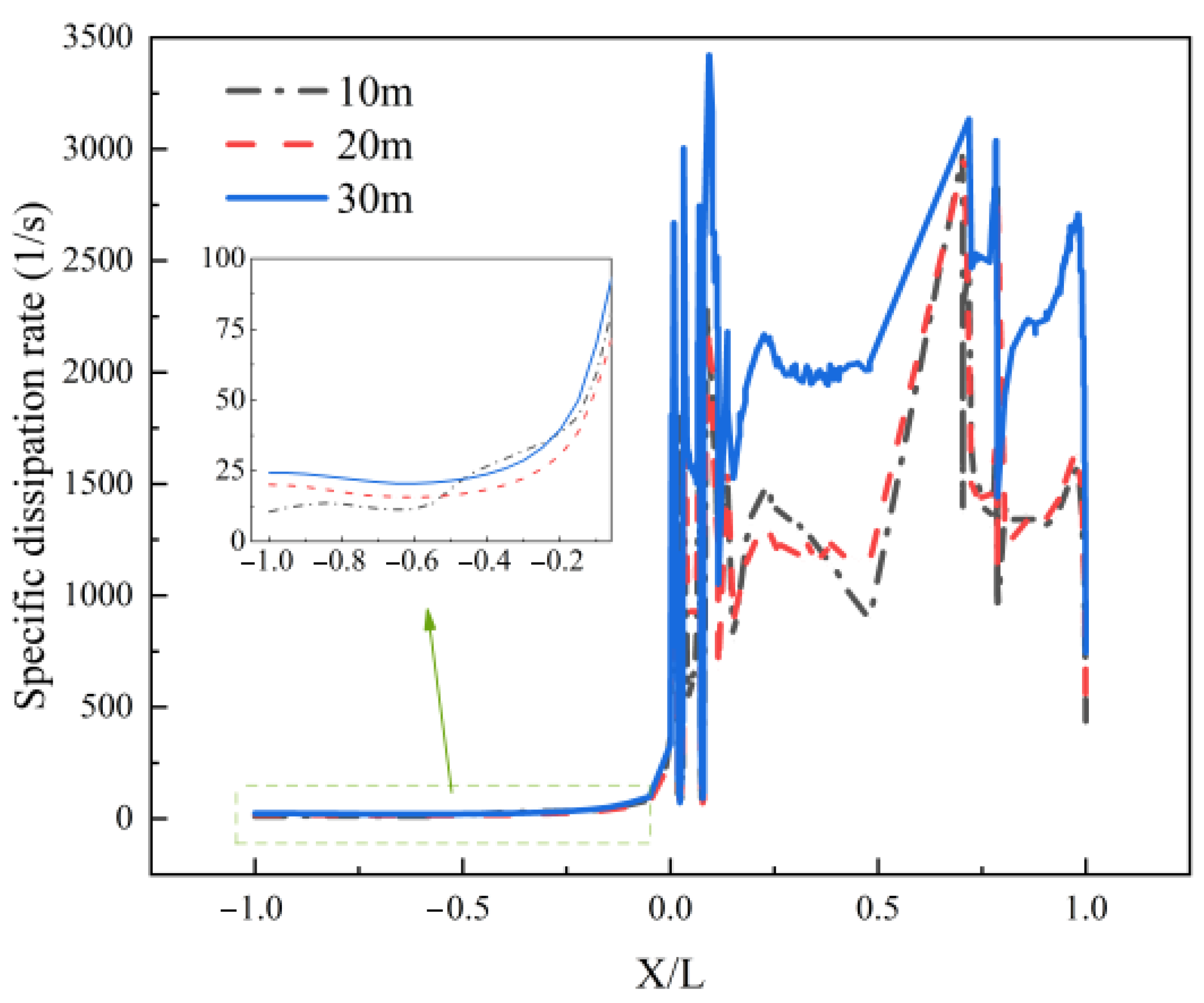
4.3.1. Influence of Speed on Hydrodynamic Wake Characteristics
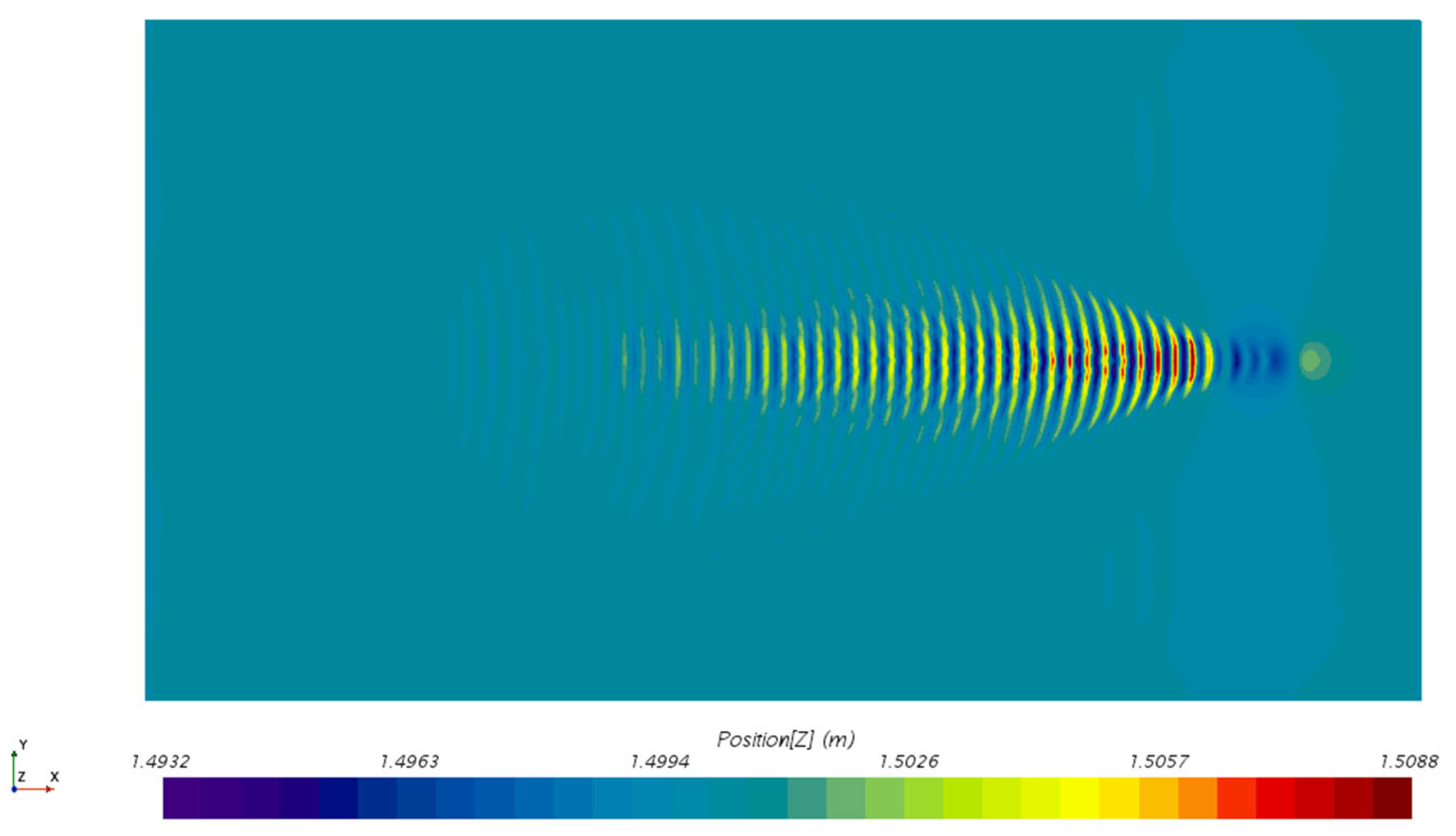
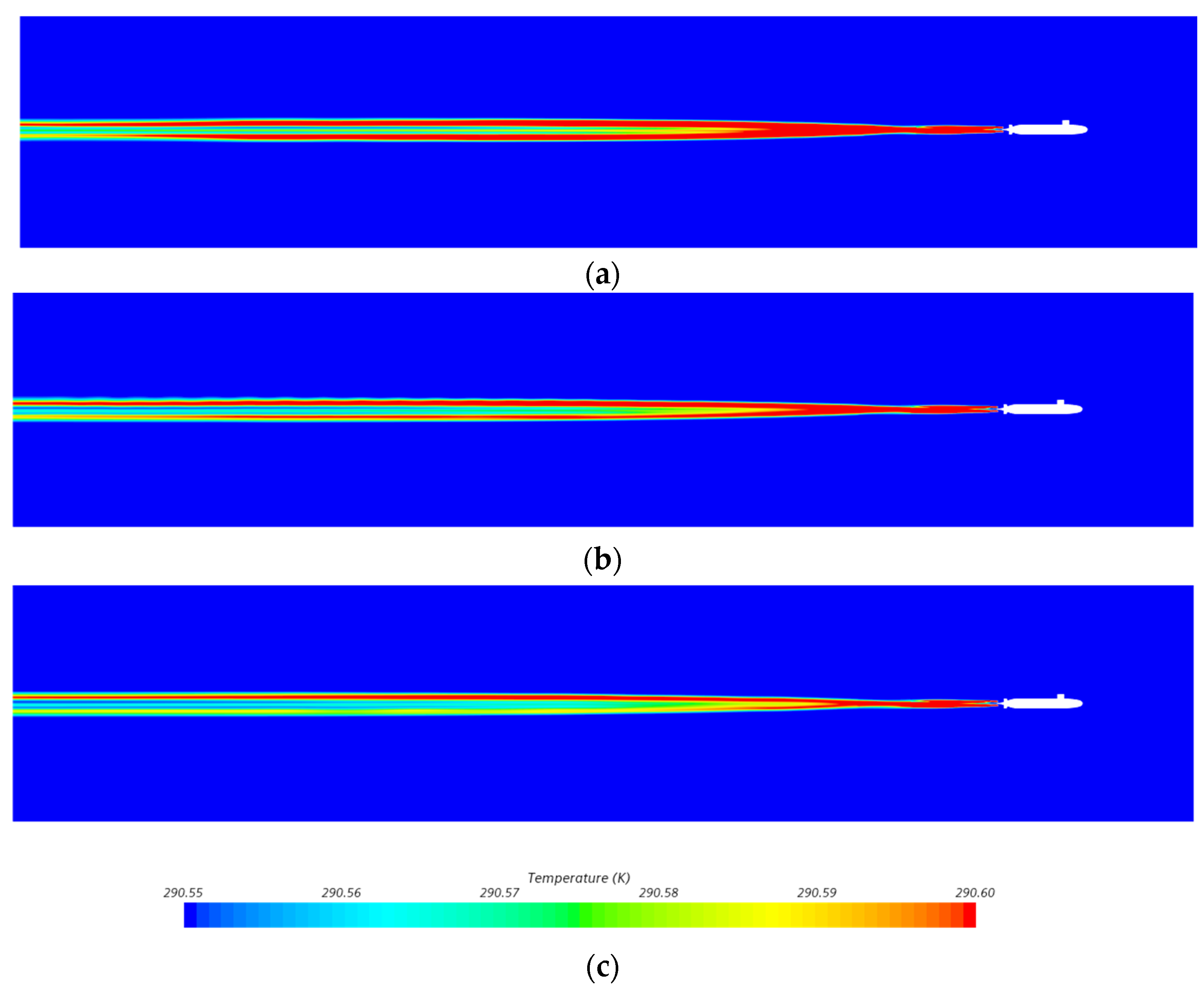
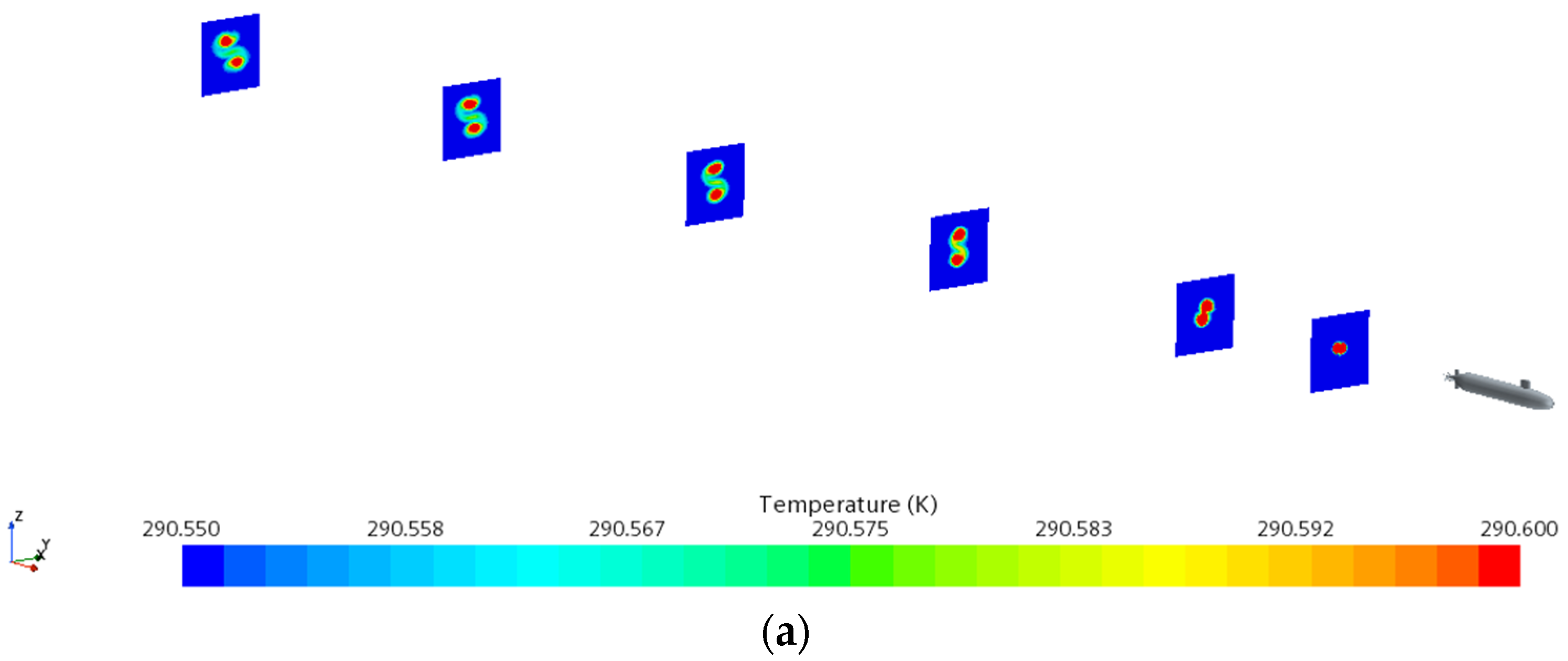
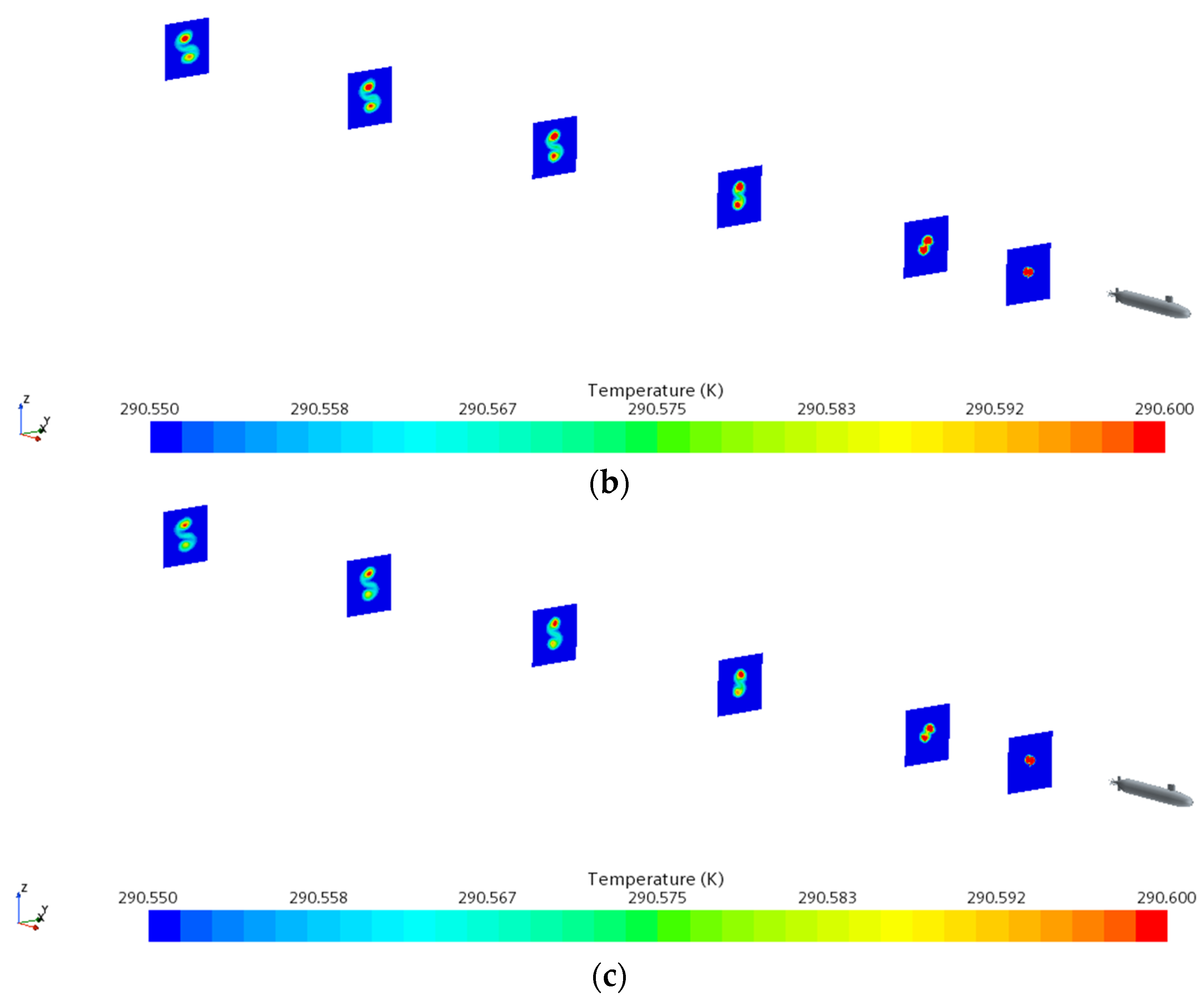
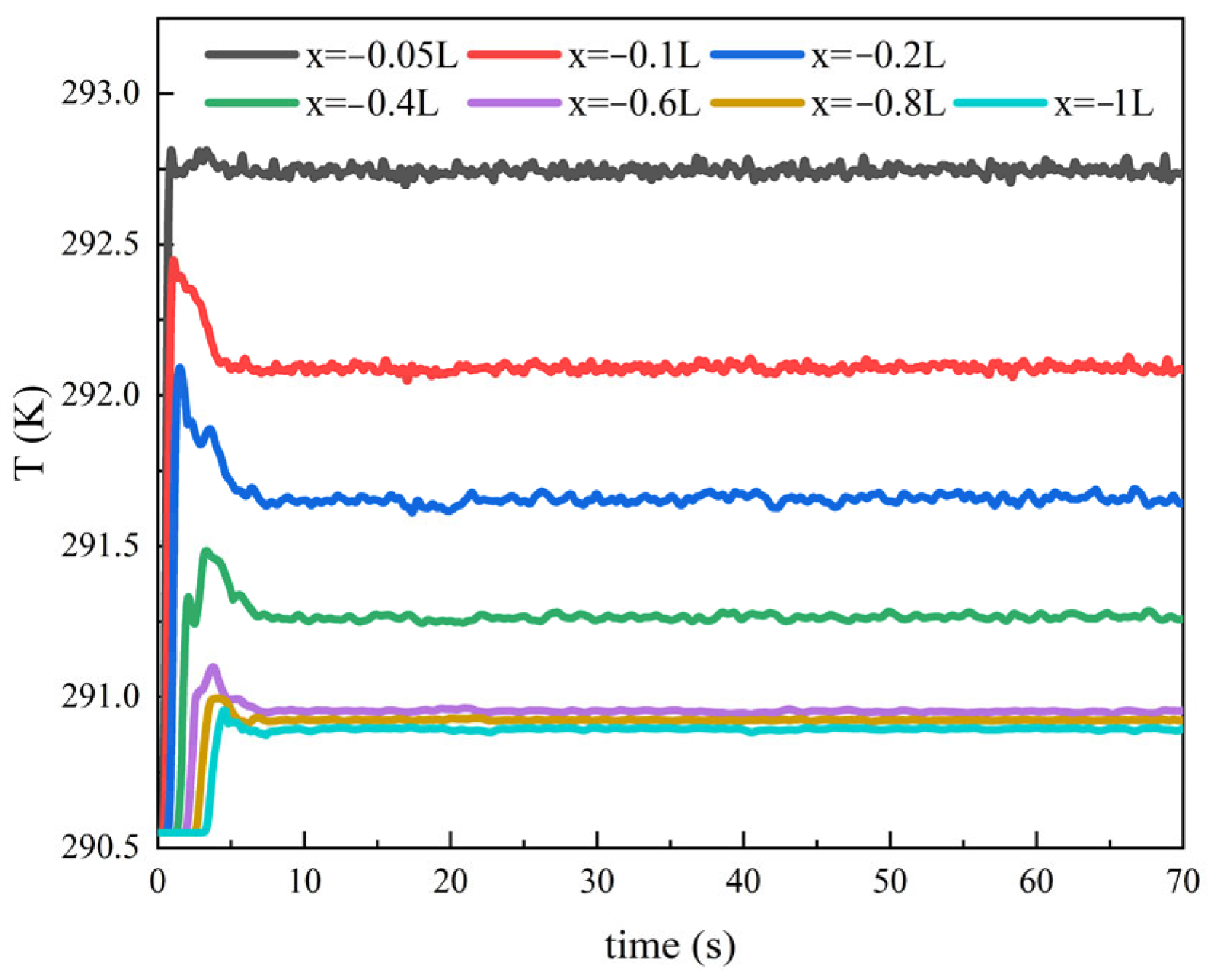
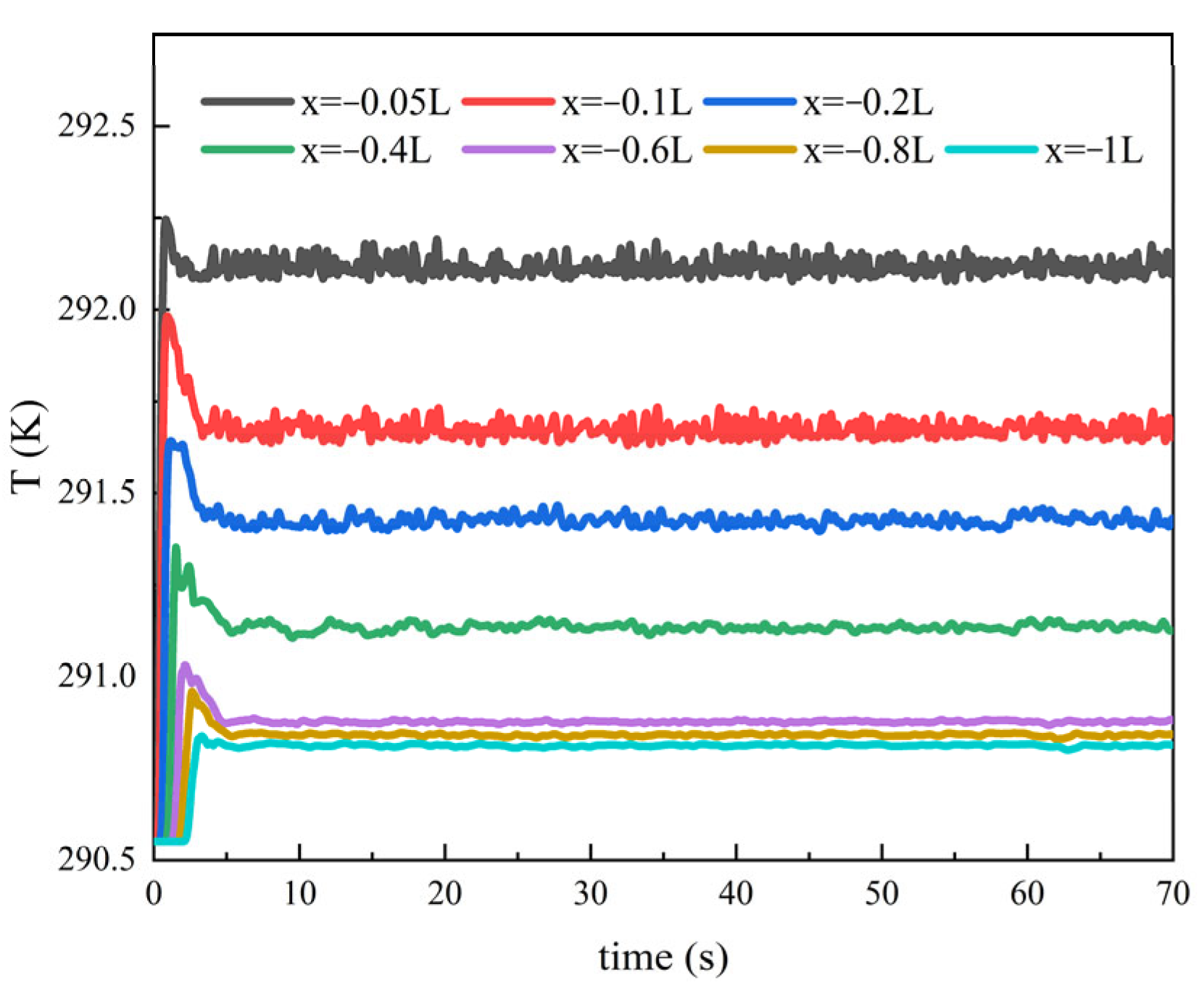
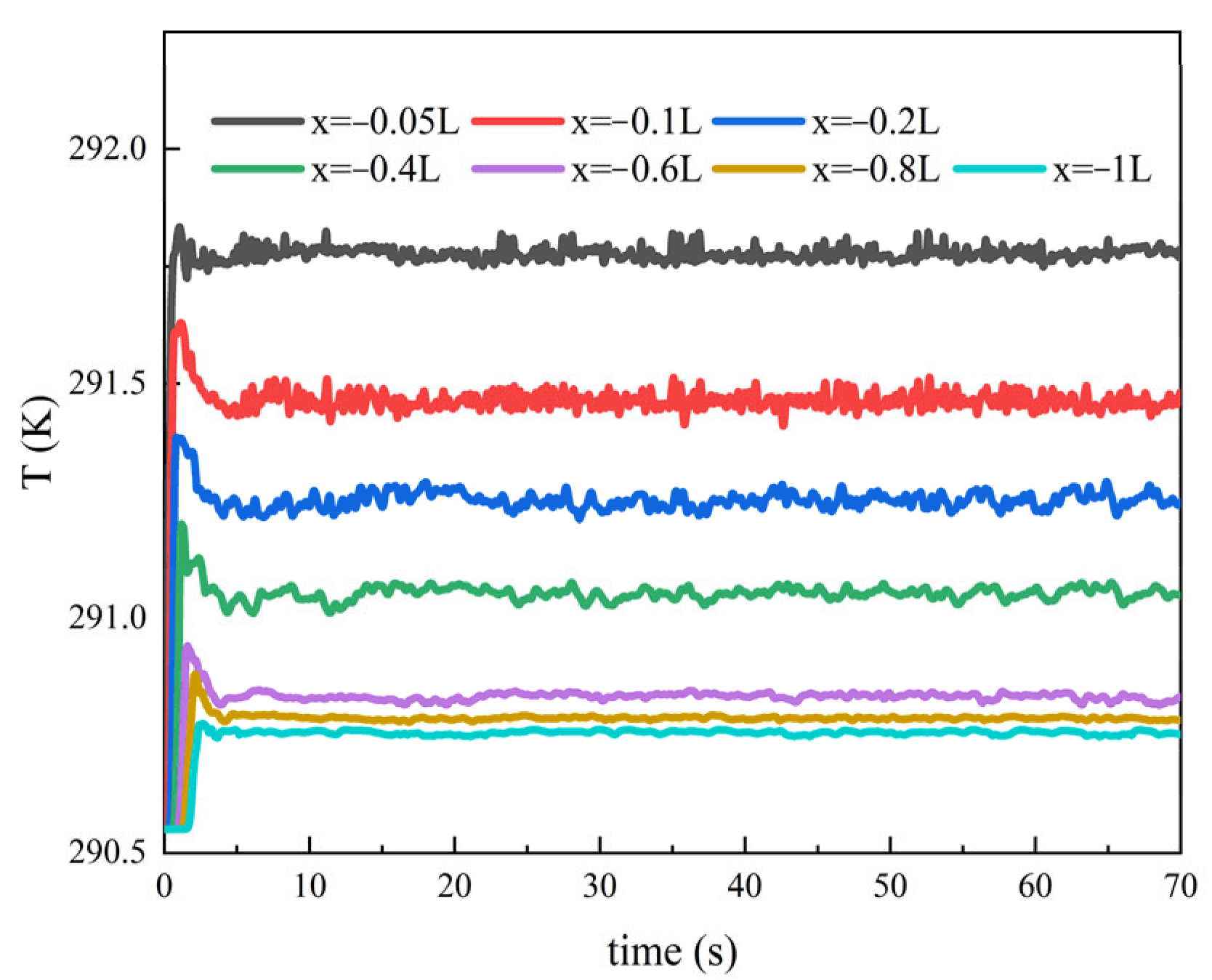
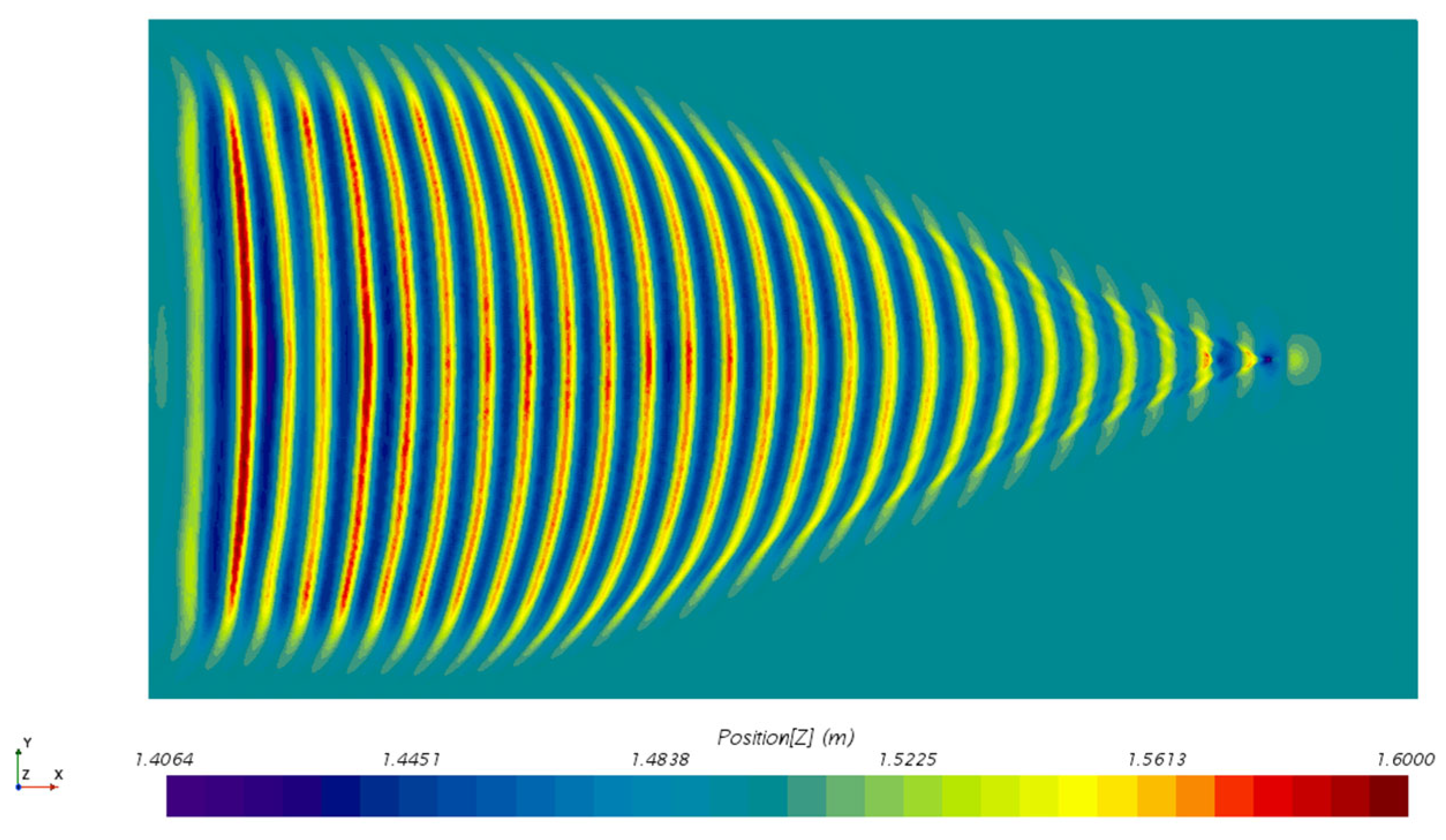
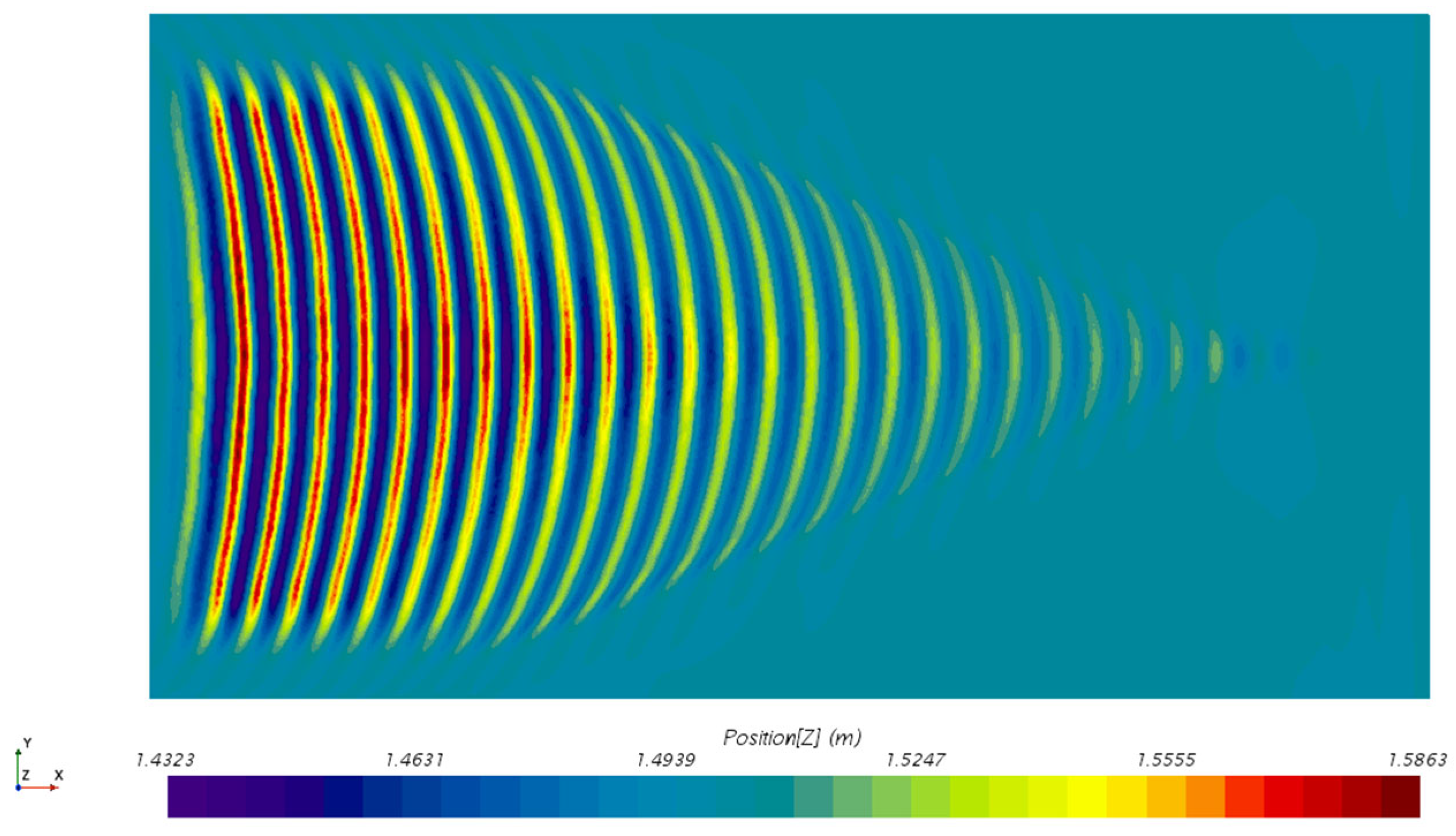
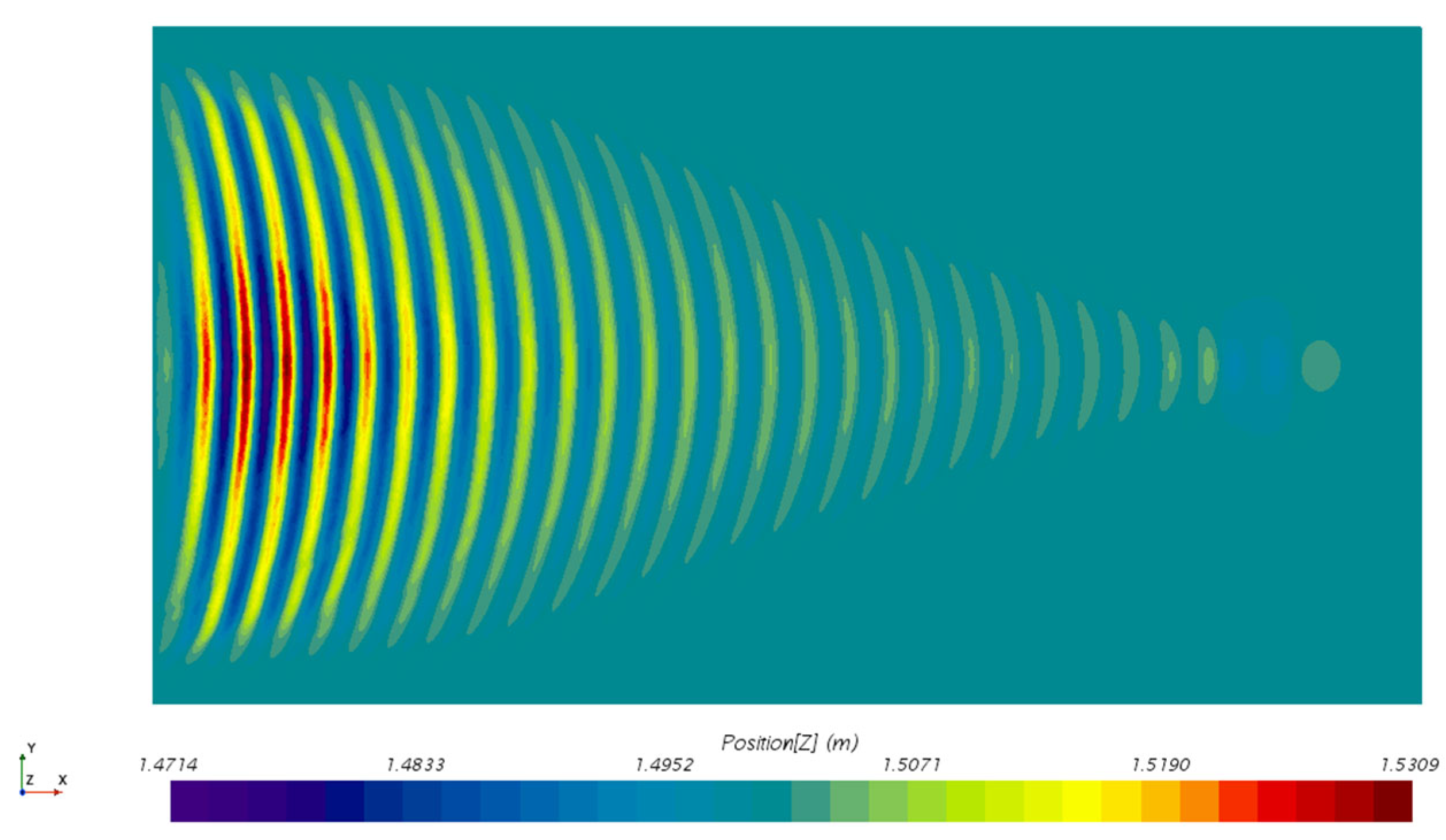
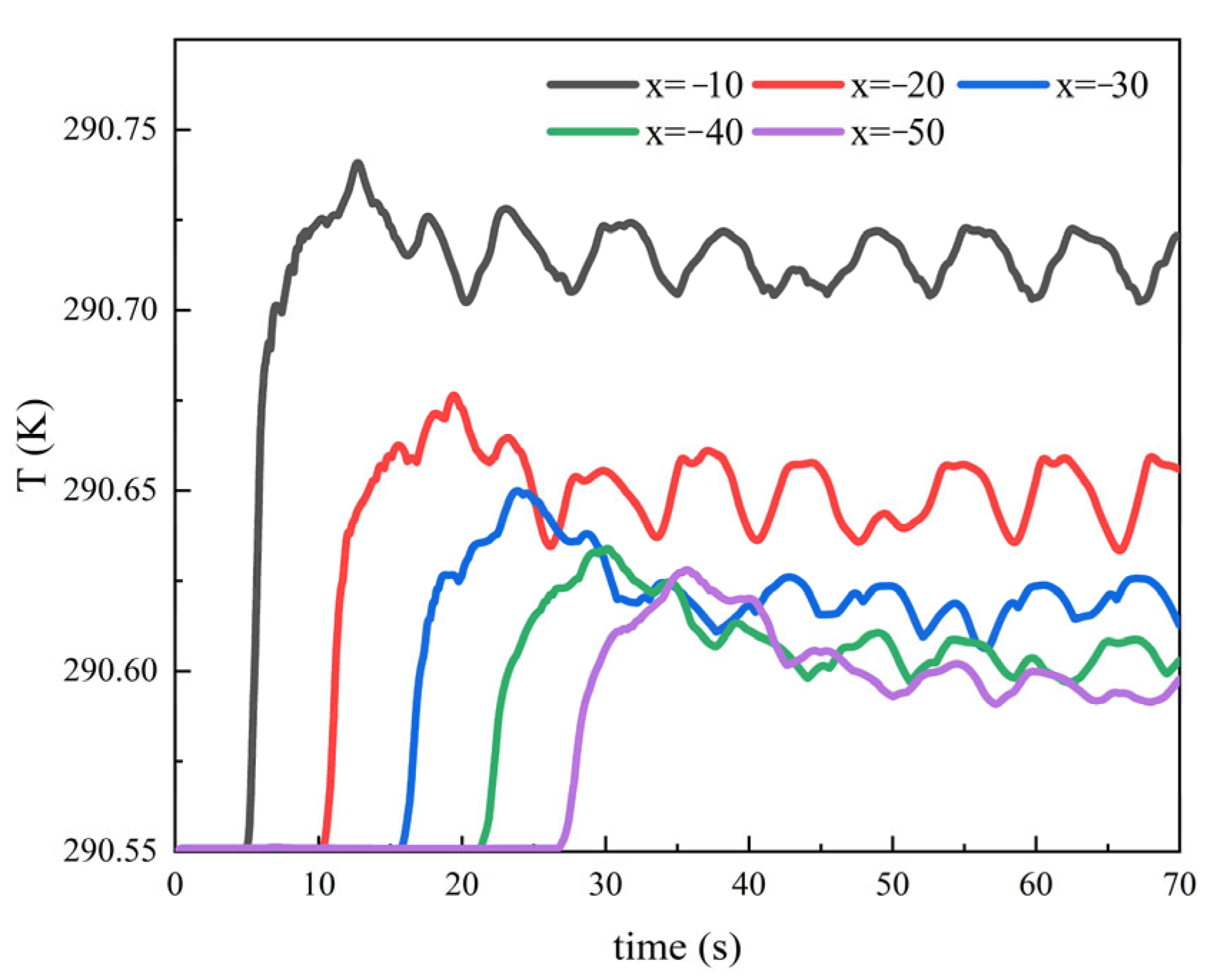
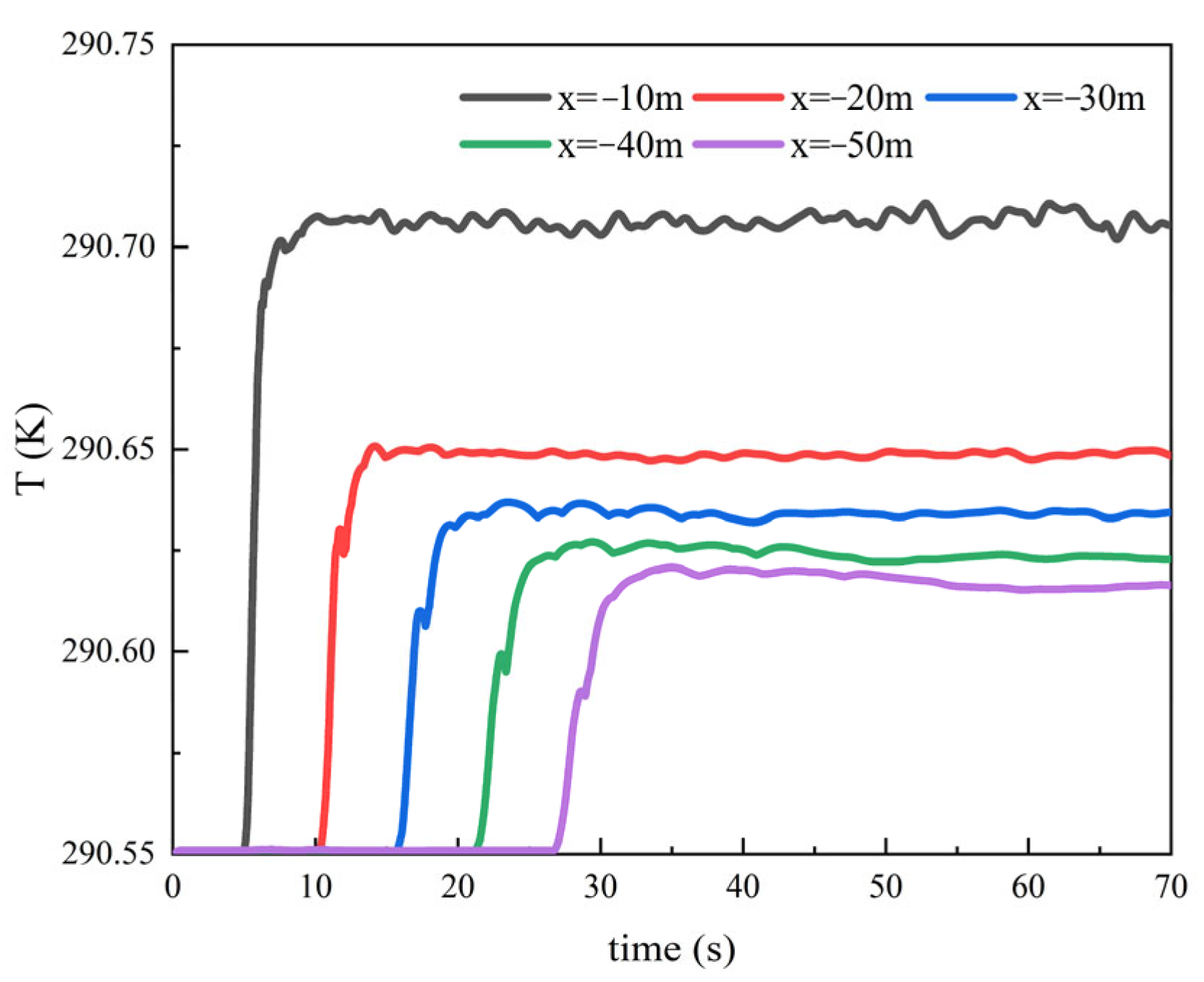
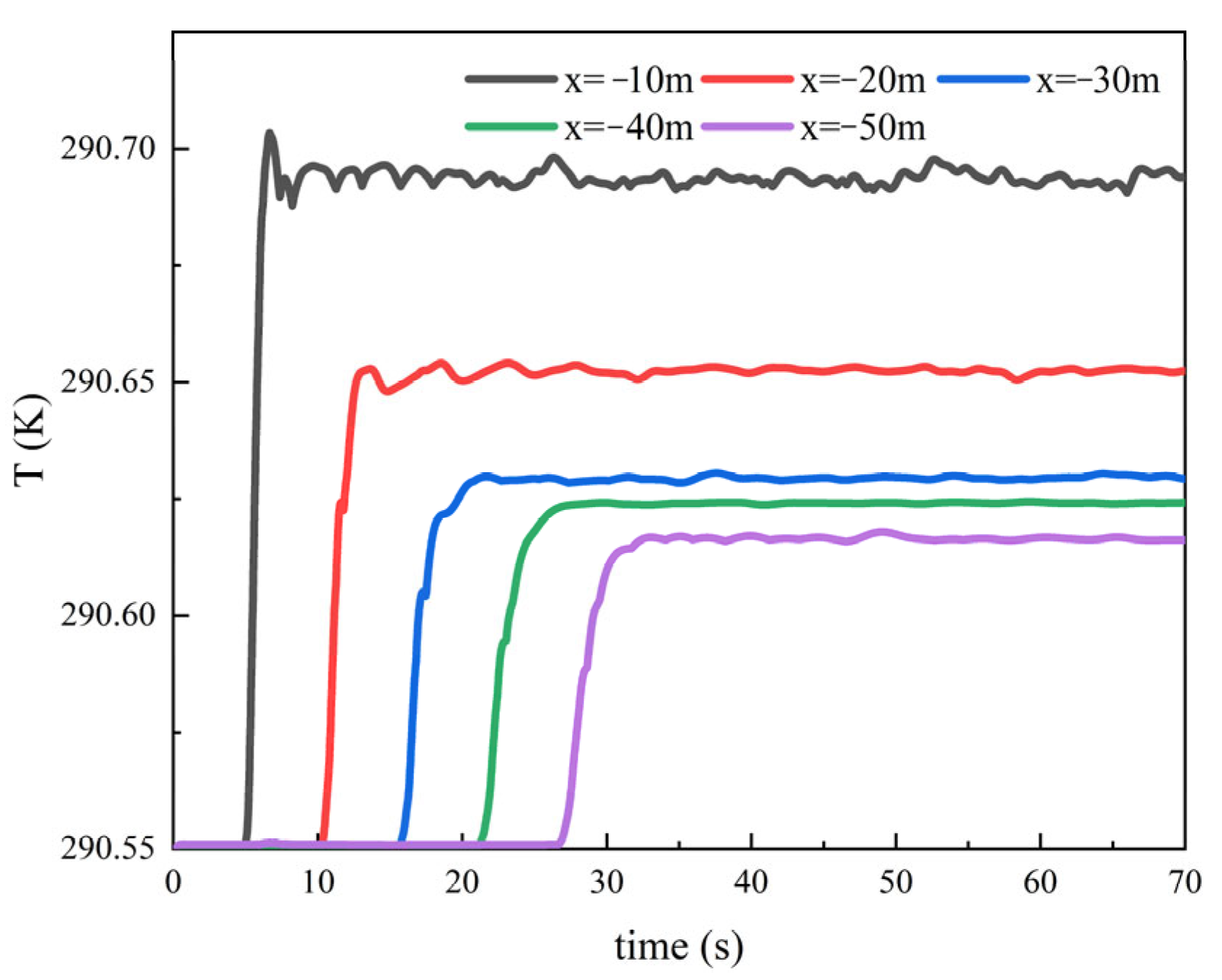
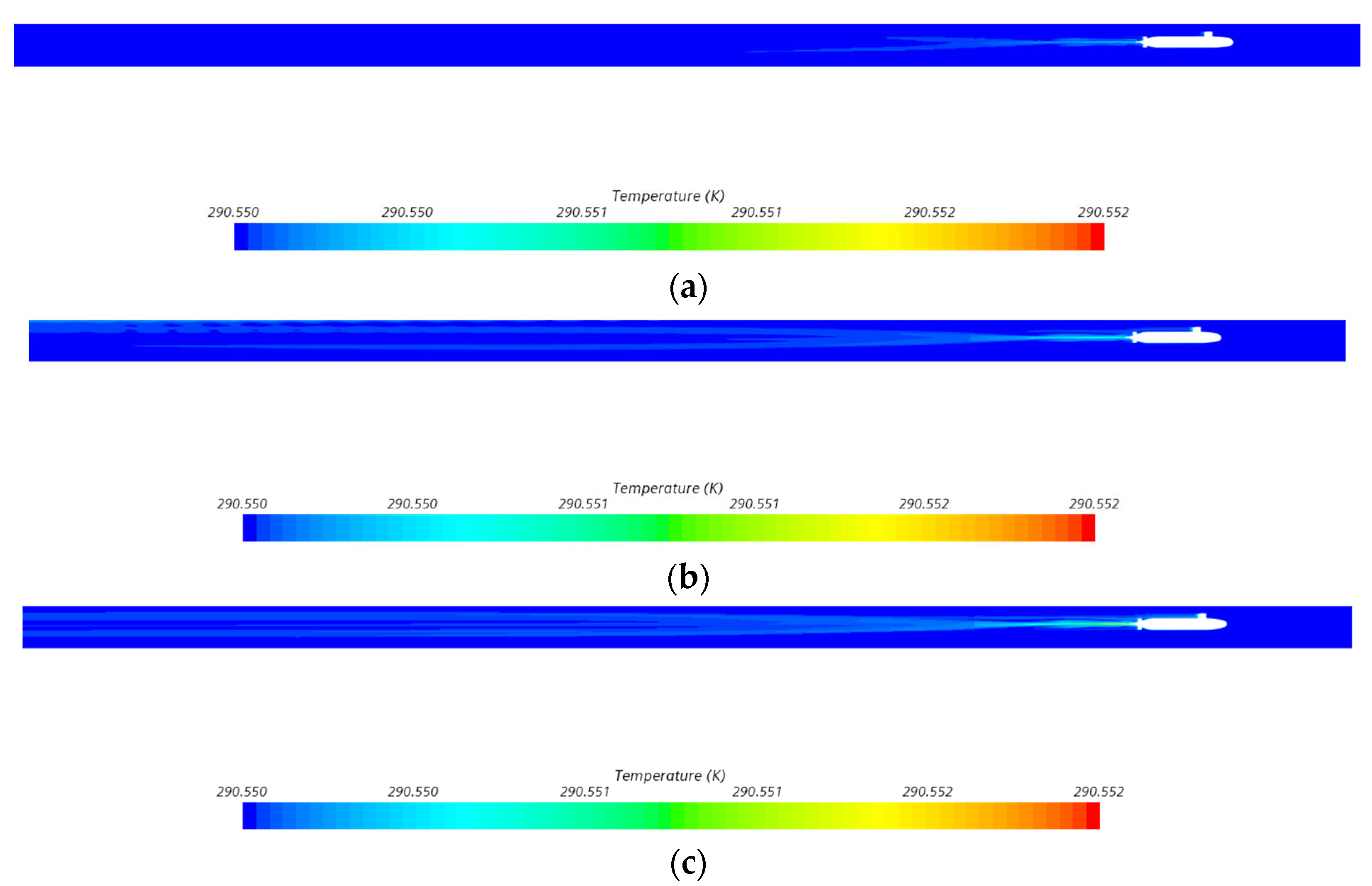
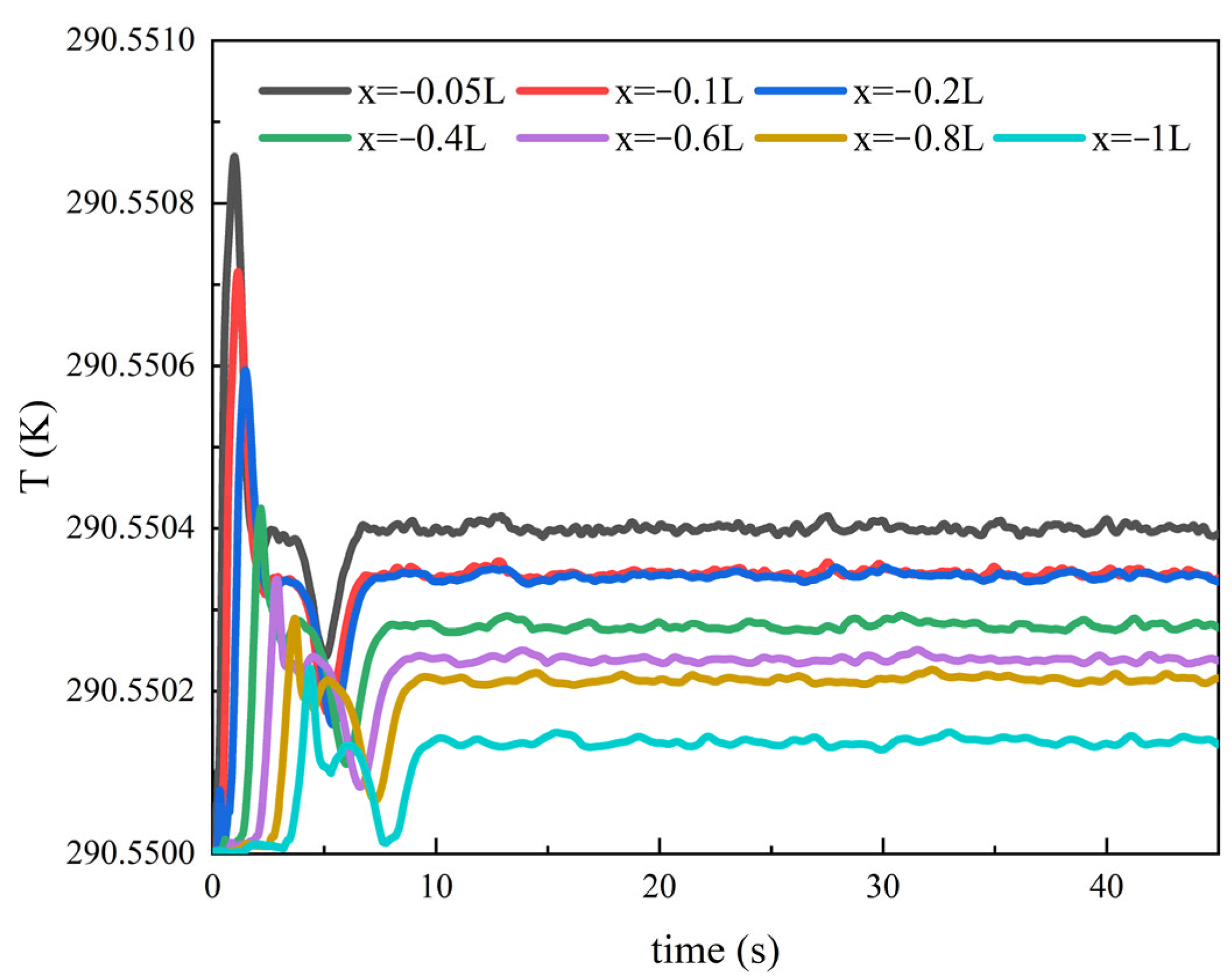
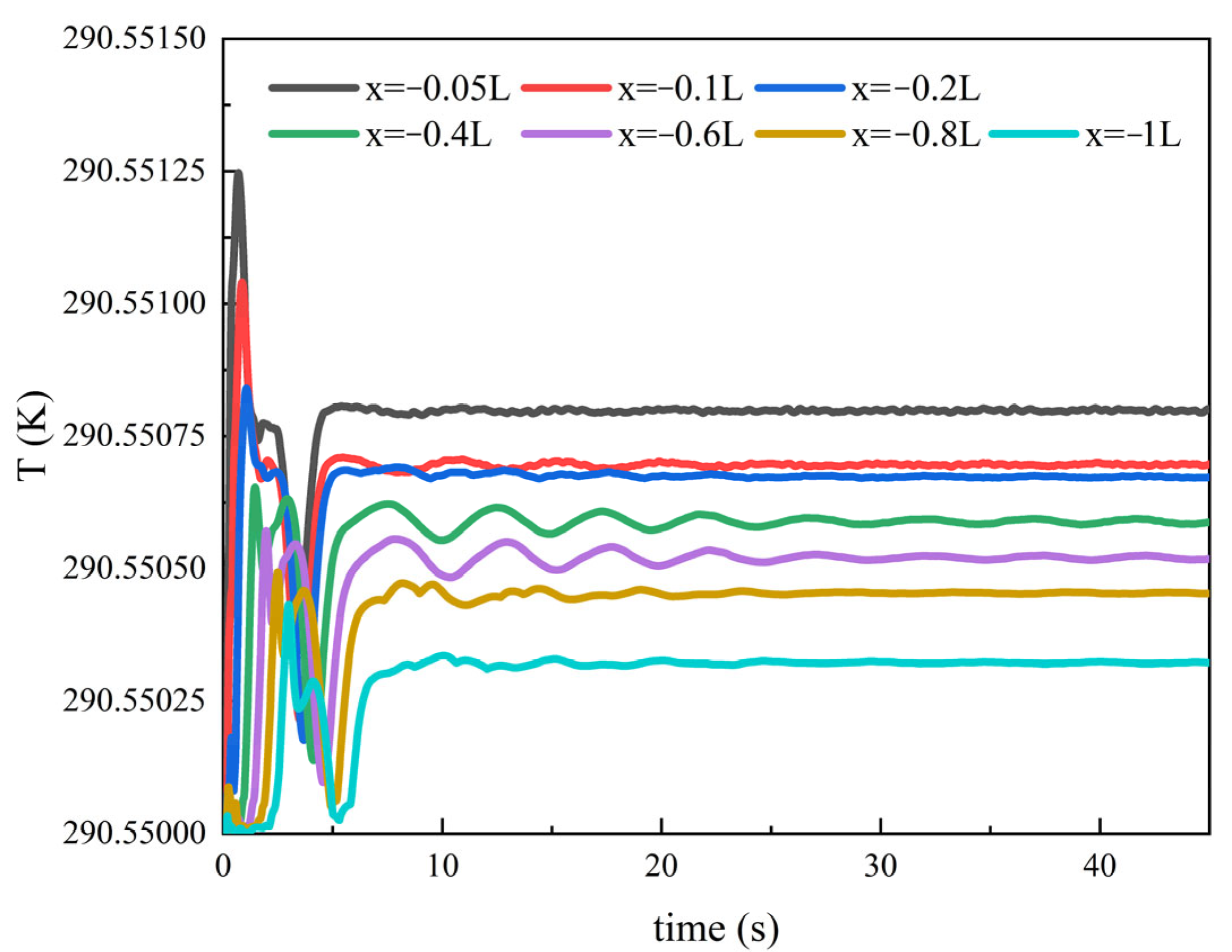
4.3.2. Influence of Speed on Thermal Wake Diffusion Characteristics
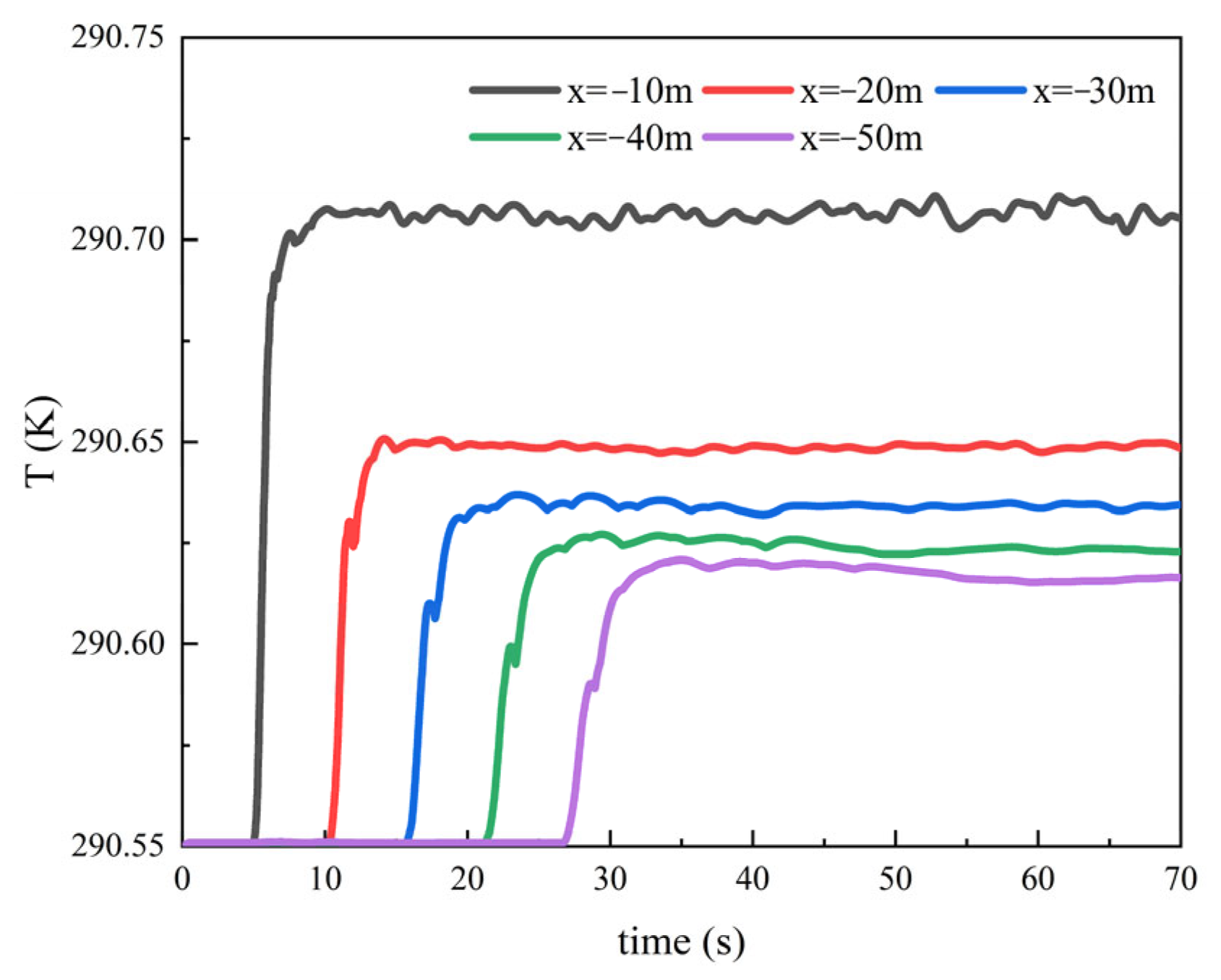
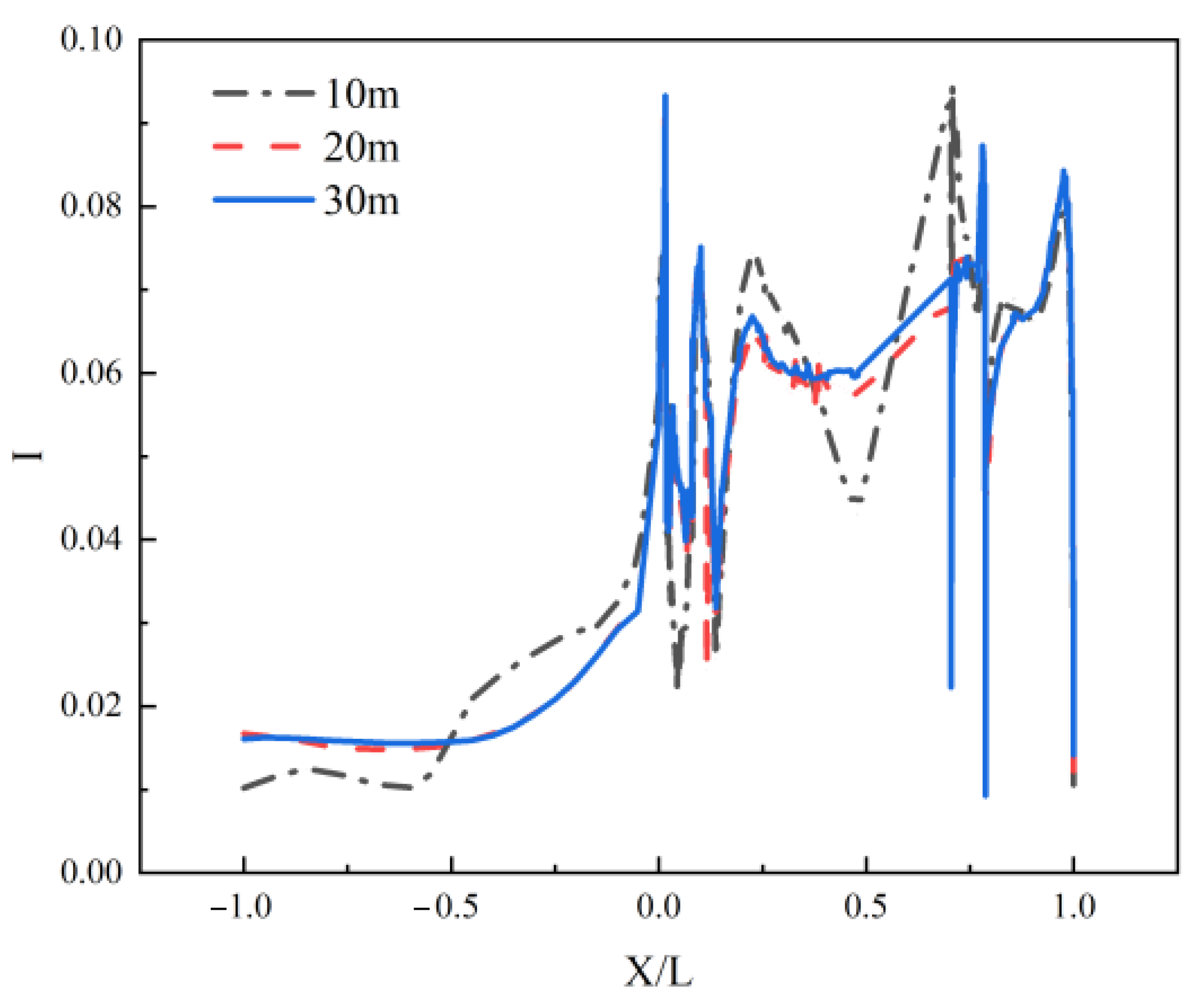
4.3.3. Influence of Submersible Depth on Hydrodynamic Wake Characteristics
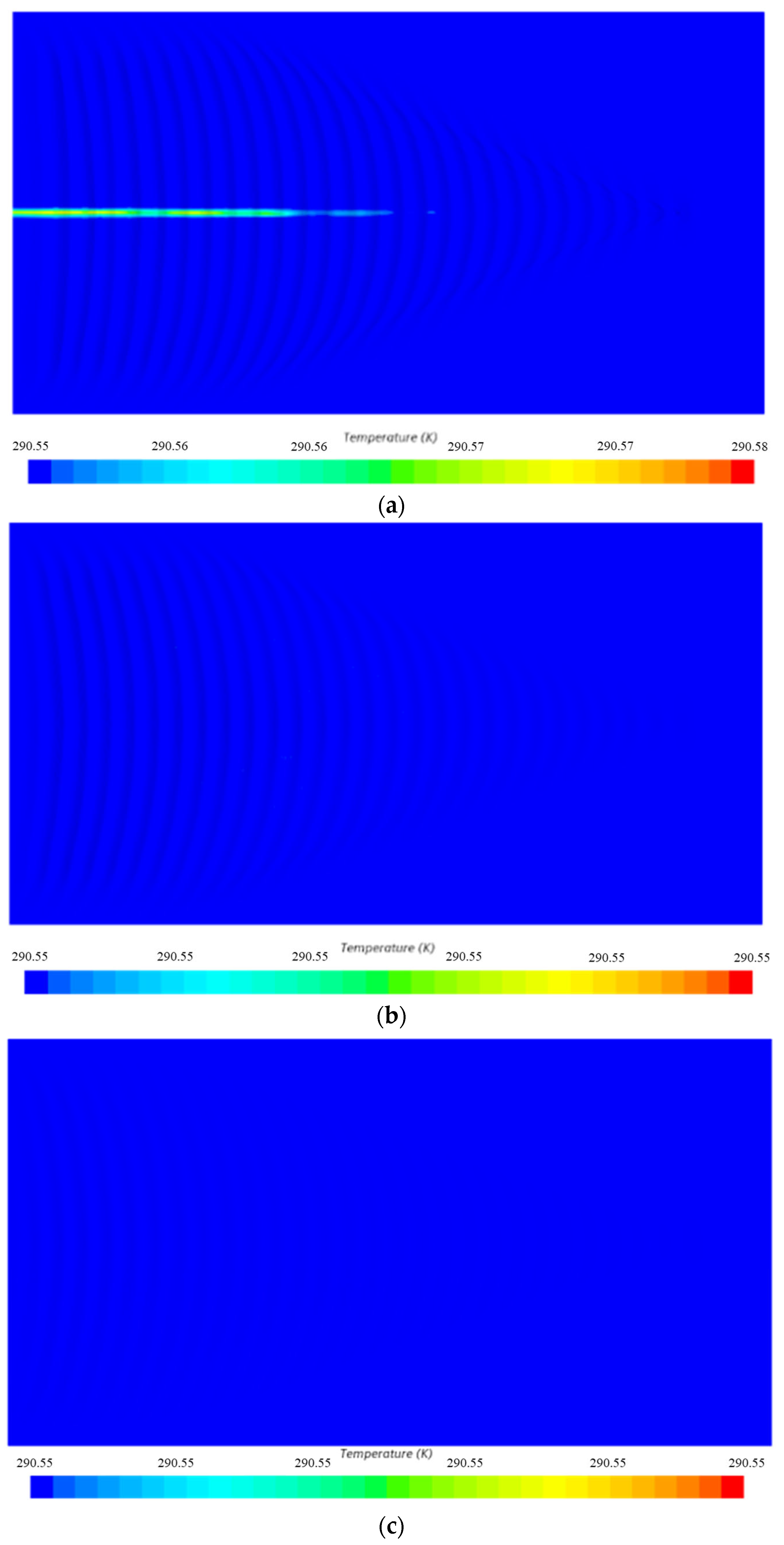
4.3.4. Influence of Depth on Thermal Wake Diffusion Characteristics
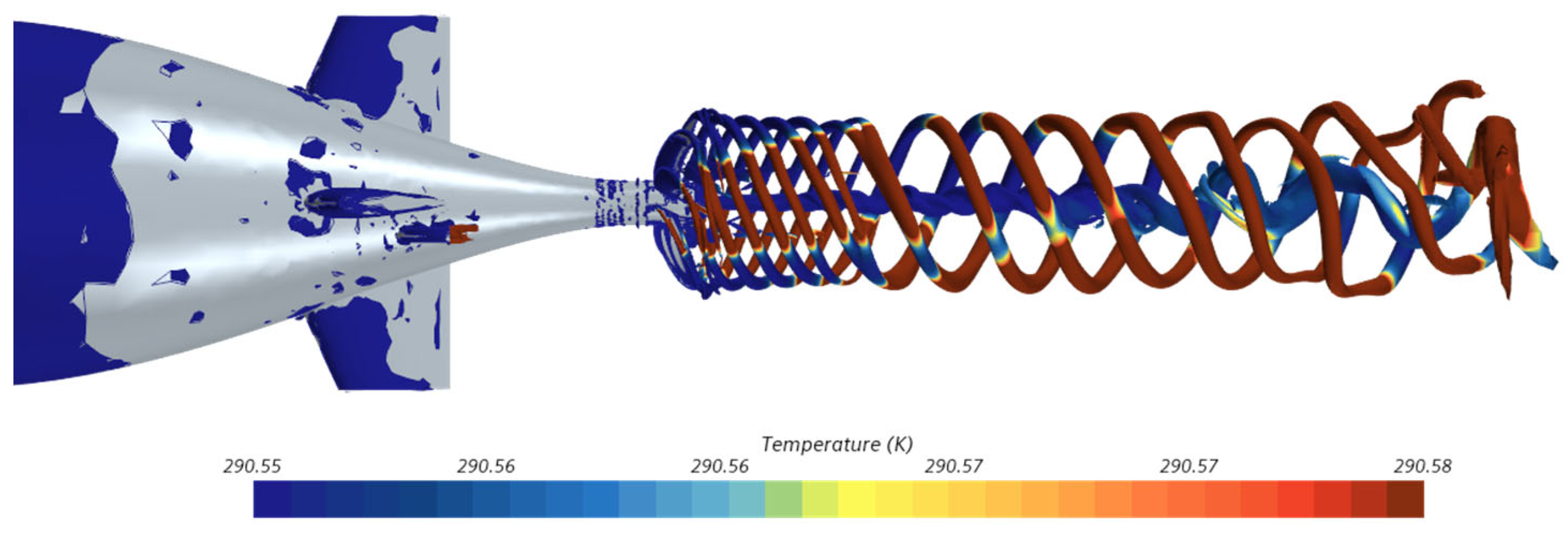
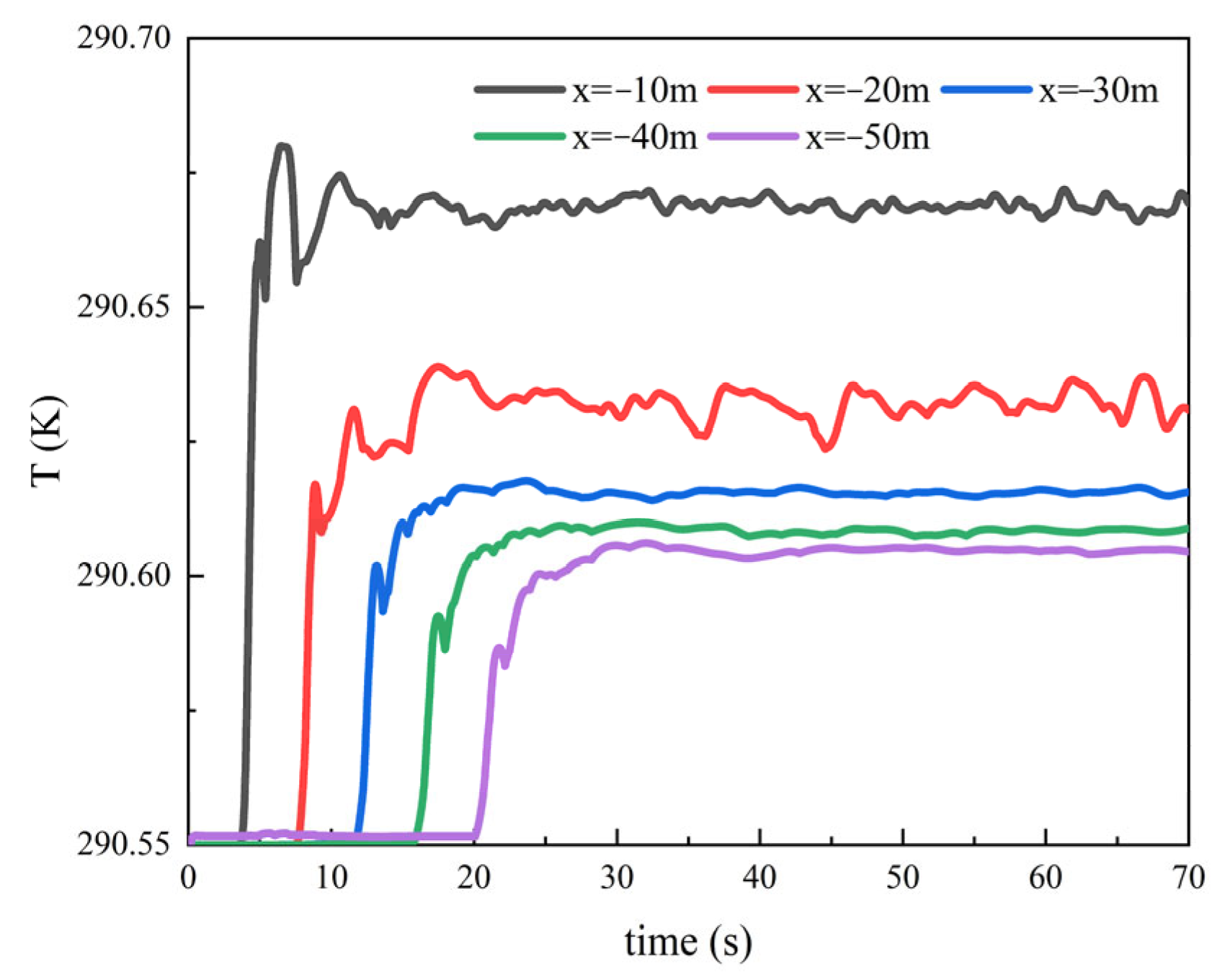
4.3.5. Underwater Vehicle Wake Thermal Characteristics Without Heat Emission
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Fluid density | |
| , , | The velocity components in the Cartesian coordinate system (in the x, y, and z directions) |
| Time | |
| , , | Spatial coordinates |
| Pressure | |
| Dynamic viscosity | |
| , , | Body force components |
| Temperature | |
| Specific heat capacity | |
| Turbulent kinetic energy | |
| Energy source term | |
| The effective diffusion rates of | |
| The effective diffusion rates of | |
| The turbulent kinetic energy that is generated by the average velocity gradient | |
| The generation of special turbulent kinetic energy dissipation | |
| Turbulence dissipation | |
| Turbulence dissipation | |
| Turbulent length scale in DDES |
References
- Xiao, Y.; Qiu, Z.; Shi, Z. On Current Research Status of UUV and Its Critical Technologies. Electron. Opt. Control 2014, 21, 46–49. [Google Scholar]
- Yan, Y. The overview study of non-acoustic detection technology base on UUV application in searching target underwater. Ship Sci. Technol. 2017, 39, 10–13. [Google Scholar]
- Wu, M.; Gong, W.; Yuan, B. Study of Surface Temperature Features of Thermal Wake Caused by Underwater Vehicle. Infrared Technol. 2011, 32, 29–34. [Google Scholar]
- Wu, M.; Chen, B.; Zhang, X. The Study on the Varied Laws of Surface Feature Parameters Caused by a Going Body Underwater in the Temperature Stratification Ocean. Infrared Technol. 2010, 32, 242–246. [Google Scholar]
- Gran, R. An Experiment on the Wake of a Slender Propeller-Driven Body; National Technical Information Service, U.S. Department of Commerce: Springfield, VA, USA, 1973. [Google Scholar]
- Schetz, J.A.; Jakubowski, A.K. Experimental Studies of the Turbulent Wake behind Self-Propelled Slender Bodies. AIAA J. 1975, 13, 1568–1575. [Google Scholar] [CrossRef]
- Schetz, J.A.; Daffan, E.B.; Jakubowski, A.K.; Cannon, S.; Cox, R.; Dubberley, D. Mean Flow and Turbulence Measurements in the Wake of Slender Propeller-Driven Bodies Including Effects of Pitch Angle; Virginia Polytechnic Institute and State University Blacksburg Department of Aerospace and Ocean Engineering: Blacksburg, VA, USA, 1976; Volume 77, p. 12337. [Google Scholar]
- Schetz, J.A.; Daffan, E.B.; Jakubowski, A.K. Turbulent Wake behind Slender Propeller-Driven Bodies at Angle of Attack. AIAA J. 1978, 16, 6–7. [Google Scholar] [CrossRef]
- Rudolf, A.; Walther, T. Laboratory Demonstration of a Brillouin Lidar to Remotely Measure Temperature Profiles of the Ocean. Opt. Eng. 2014, 53, 051407. [Google Scholar] [CrossRef]
- Hong, F. Numerical simulation of surface wake for submarine moving in homogeneous fluid. J. Ship Mech. 2005, 9, 9–17. [Google Scholar]
- Peng, J. Research on diffusion characteristics of submarine thermal wake based on multiphase flow. SHIP Sci. Technol. 2024, 46, 47–52. [Google Scholar]
- Chen, S.; Zhong, J.; Sun, P. Numerical Simulation and Experimental Study of the Submarine’s Cold Wake Temperature Character. J. Therm. Sci. 2014, 23, 253–258. [Google Scholar] [CrossRef]
- Hu, R. Experimental study on infrared signature of thermal wake of remote control submarine. SHIP Sci. Technol. 2017, 39, 53–56. [Google Scholar]
- Zhang, X. The Analysis and Carculation of Infrared Signature of Thermal Wake of Submarines. Laser Infrared 2007, 37, 1054–1057. [Google Scholar]
- Luo, H. The Numerical Simulation of Interaction between Free-Surface Wake Generated by a Moving Submerged Body and Stochastic Ocean Waves. J. Shanghaijiaotong Univ. 2007, 41, 1435–1440. [Google Scholar] [CrossRef]
- Wang, F. Computational Fluid Dynamics Analysis: Principles and Applications of CFD Software; Tsinghua University Press Co., Ltd.: Beijing, China, 2004. [Google Scholar]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Pan, Y. Analysis on Diffusion Characteristics of Submerged Body Thermal Wake in Ocean Stratified Flow. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.h.; Travin, A. A New Version of Detached-Eddy Simulation, Resistant to Ambiguous Grid Densities. Theoret. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Huang, T.; Liu, H.L. Measurements of Flows over an Axisymmetric Body with Various Appendages in a Wind Tunnel: The DARPA SUBOFF Experimental Program; British Maritime Technology: London, UK, 1994. [Google Scholar]








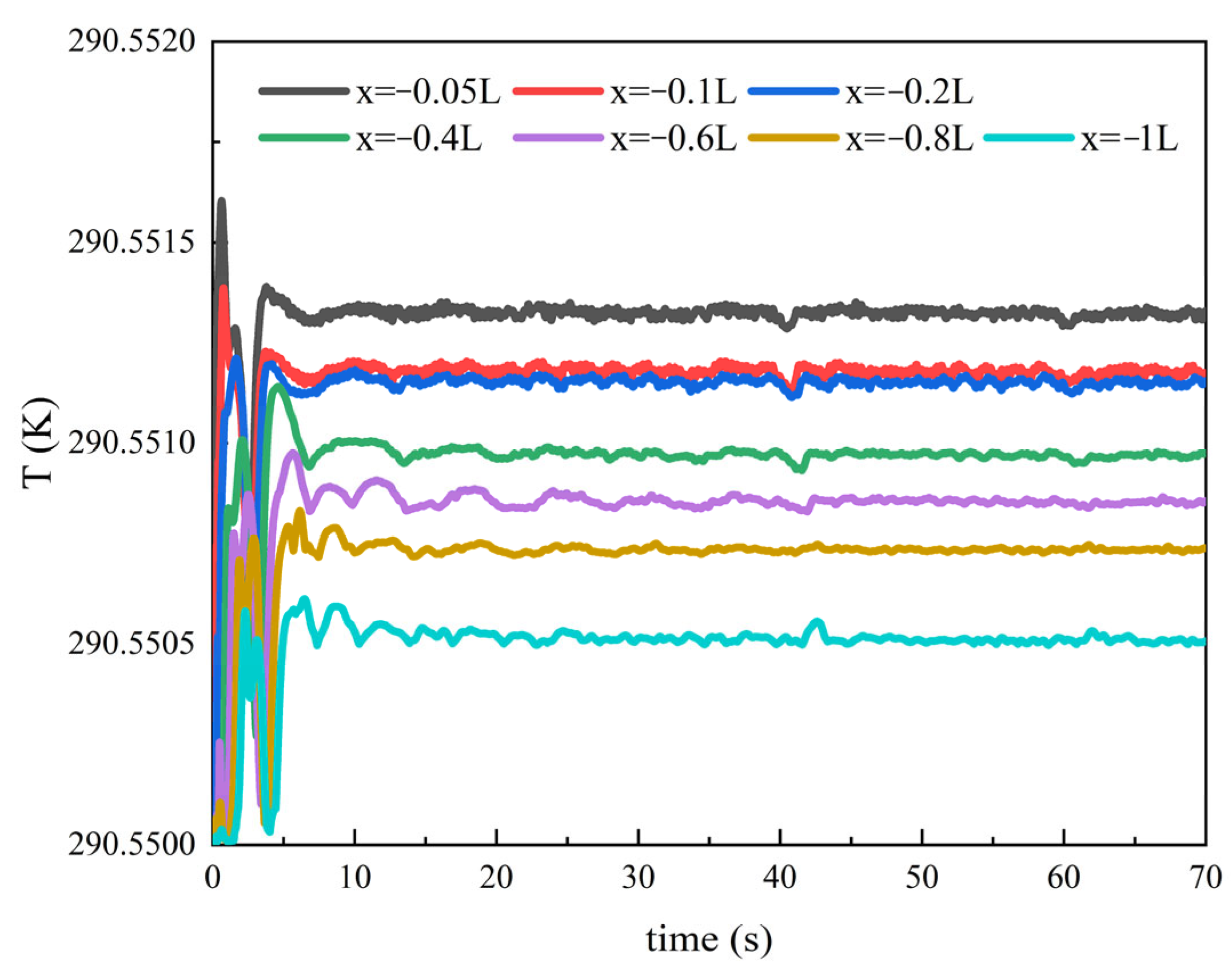
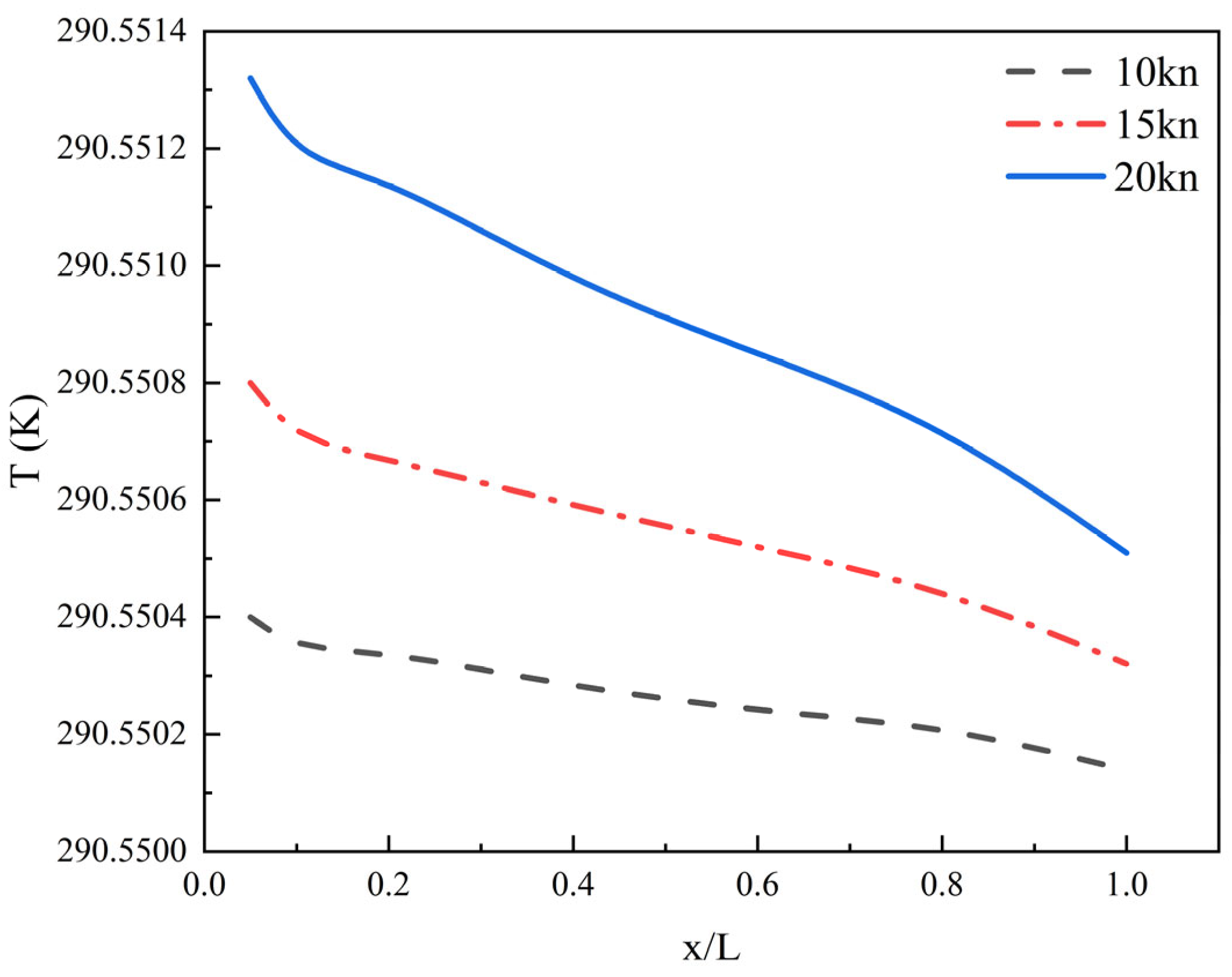
| Speed (m/s) | Resistance (N) | Error % | |
|---|---|---|---|
| Numerical Simulation | Basin Test | ||
| 3.045 | 101.0 | 102.2 | 1.2 |
| uniform flow field | operating condition | speed (kn) | depth (m) | thermal discharge |
| 1 | 10 | 20 | with | |
| 2 | without | |||
| 3 | 15 | 10 | with | |
| 4 | 20 | with | ||
| 5 | without | |||
| 6 | 30 | with | ||
| 7 | 20 | 20 | with | |
| 8 | without |
| Numerical Value | Theory | Error |
|---|---|---|
| 0.816 | 0.847 | −0.0370 |
| 1.920 | 1.916 | 0.0021 |
| 3.520 | 3.390 | 0.0383 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Cui, J.; Liu, B.; Shi, S.; Shao, W. Wake Characteristics and Thermal Properties of Underwater Vehicle Based on DDES Numerical Simulation. J. Mar. Sci. Eng. 2025, 13, 1371. https://doi.org/10.3390/jmse13071371
Lu Y, Cui J, Liu B, Shi S, Shao W. Wake Characteristics and Thermal Properties of Underwater Vehicle Based on DDES Numerical Simulation. Journal of Marine Science and Engineering. 2025; 13(7):1371. https://doi.org/10.3390/jmse13071371
Chicago/Turabian StyleLu, Yu, Jiacheng Cui, Bing Liu, Shuai Shi, and Wu Shao. 2025. "Wake Characteristics and Thermal Properties of Underwater Vehicle Based on DDES Numerical Simulation" Journal of Marine Science and Engineering 13, no. 7: 1371. https://doi.org/10.3390/jmse13071371
APA StyleLu, Y., Cui, J., Liu, B., Shi, S., & Shao, W. (2025). Wake Characteristics and Thermal Properties of Underwater Vehicle Based on DDES Numerical Simulation. Journal of Marine Science and Engineering, 13(7), 1371. https://doi.org/10.3390/jmse13071371






