Characterization of the Internal and External Flow Field of a Semi-Submersible Aquaculture Platform with Multiple Net Cage Configuration

Abstract

To achieve efficient and sustainable marine aquaculture, STAR-CCM+ was used to simulate the internal and external field characteristics of a semi-submersible aquaculture platform based on a porous media model, focusing on the influence of incoming flow velocity and net solidity ratio. The results indicate that the flow field distribution around the platform exhibits no significant regularity and that low-velocity vortex regions are primarily concentrated near the pillars and nets. After velocity attenuation, the velocity reduction coefficients at the centers of the three cages are 90.26%, 63.65%, and 52.56%, respectively. Furthermore, the velocity attenuation inside the cages is minimally influenced by incoming flow velocity, with a maximum difference of 3.10%. In contrast, differences in net solidity ratio significantly affect velocity attenuation, particularly in downstream regions. The velocity reduction coefficient in the third cage varies by up to 43.25% depending on the net solidity ratio. These findings provide practical insights for the engineering design and application of aquaculture platforms.

1. Introduction

Amid intensifying competition for global marine resources and the escalating deterioration of the offshore aquaculture environment [1,2], deep-sea aquaculture has emerged as a pivotal direction for the sustainable development of marine fisheries. A series of innovative aquaculture facilities have been developed in recent years, including the aquaculture workboat JOSTEIN ALBERT, the fully submersible net cage ‘Deep Blue 1’, and the semi-submersible aquaculture platforms ‘Ocean Farm 1’ and ‘Strait Farm 1’. Among these, a truss-type aquaculture platform characterized by its semi-submersible structural design and superior resistance to wind and waves has been deployed in Guangdong, China. However, aquaculture platforms in deep and remote sea areas are often subjected to extreme environmental loads such as intense wind, waves, and currents, which can adversely affect farmed fish. Consequently, the hydrodynamic problems of deep-sea aquaculture platforms have garnered significant attention from researchers [3].

The net is a critical factor influencing the flow field around aquaculture platforms; its flexible, small-scale structure results in an exceptionally complex flow field distribution. To study the hydrodynamic characteristics of the net, extensive research has been conducted using both experimental and numerical methods [4,5,6]. In response to the structural complexity of the net, researchers have proposed various simplified models, including the Morrison model [7,8,9] and the screen model [6,10,11]. Among these, the porous media model has been widely adopted in computational fluid dynamics (CFD) methods. Patursson et al. [12] pioneered the use of the porous media model to simulate the net, optimizing the process of determining the best-fitting porous media coefficients. Subsequently, Zhao et al. [13] simulated the flow field around the net and validated the accuracy of the numerical model through experimental studies. Bi et al. [14] employed the porous media model in conjunction with particle image velocimetry (PIV) and acoustic Doppler velocimetry (ADV) techniques to research the flow velocity attenuation downstream of the net. Furthermore, Chen et al. [15] integrated the porous media model with the concentrated mass method to analyze the fluid-structure interaction between water flow and the net.

Currently, aquaculture equipment is evolving from traditional net cages to advanced farming platforms that integrate flexible nets with rigid structural frameworks. The stability and safety of these aquaculture platforms in marine environments are fundamental prerequisites for ensuring the sustainable development of marine fisheries [16,17,18]. Moreover, the flow velocity within the net cages is a critical factor influencing the survival and growth of cultured fish [19]. Accurately predicting and analyzing the flow field characteristics inside aquaculture platforms can provide a vital theoretical foundation for optimizing the aquaculture environment and enhancing fish survival rates. Zhao et al. [20] and Liu et al. [21] introduced a novel approach combining the porous media model and rigid wall boundary conditions to analyze the flow field both inside and around semi-submersible aquaculture platforms. Their findings revealed that the presence of nets significantly expanded the low-velocity flow regions and increased the hydrodynamic load on the nets. Yang et al. [22] conducted a detailed investigation into the effects of flow velocity, angle of attack, and $S_n$ on the flow field around bottom-fixed aquaculture platforms (BFAF), providing valuable suggestions for optimizing platform layout. Furthermore, Ji et al. [23,24] explored the hydrodynamic mechanisms of double-layer nets on bottom-supported platforms. Their results demonstrated that platforms equipped with double-layer nets exhibit more pronounced flow velocity attenuation compared to those with single-layer nets. They also recommended selecting an appropriate $S_n$ and number of net layers to achieve efficient water exchange.

However, existing studies have primarily focused on prediction and analysis of the flow field distribution within individual net cages. In contrast, the flow field characteristics of a specific truss-type aquaculture platform representing a complex structural system comprising multiple net cages are influenced not only by the nets but also by the integrated interactions between multiple pillar structures and the nets. Currently, research on such aquaculture platforms remains limited, necessitating further exploration.

To address the aforementioned challenges, this study employs STAR-CCM+ (17.04.007) to discretize the governing equations using the finite volume method (FVM). The discretized equations are solved to obtain the velocity field and pressure field of the fluid. We incorporate a porous media model to simulate the net’s effect on the flow field, thereby conducting simulation analysis of the internal and external flow field characteristics of the semi-submersible aquaculture platform with multiple cage configuration. The rest of this paper is structured as follows: Section 2 provides a detailed introduction to the physical model, mathematical equations, boundary conditions, and mesh division; Section 3 conducts convergence analysis and rigorously validates results; Section 4 offers a detailed analysis of the flow field characteristics of semi-submersible aquaculture platforms with multiple net cage configurations as well as the influences of $u_0$ and $S_n$ on the platform’s flow field; finally, Section 5 summarizes the key findings and conclusions of the study.

2. Numerical Model

2.1. Physical Models

As shown in Figure 1, a truss-type aquaculture platform is a complex structural system mainly consisting of several components, including the truss, pillars, nets, and mooring system, with all cages employing a planar net configuration. Its main parameters are shown in Table 1. As illustrated in Figure 2, considering computational efficiency and engineering practicability, this study simplifies the three-dimensional model of the truss-type aquaculture platform such that only the underwater part of the pillar structure and the net system are retained, while the deformation of the net and pillar structure caused by the action of water currents is ignored.

Figure 1. Three-dimensional model of the truss-type aquaculture platform.

Table 1. Main parameters of the truss-type aquaculture platform.

Parameter	Symbol	Value
Length	L	86.00 m
Breadth	B	32.00 m
Operating draft	H	10.50 m
Aquaculture volume	-	36,000 m3

Figure 2. Simplified model of the truss-type aquaculture platform.

2.2. Mathematical Model

2.2.1. Control Equations

The objects of study in this research are all incompressible viscous fluids, for which the basic governing equations are the continuity equation, momentum conservation equation, and energy conservation equation. The continuity equation (mass conservation equation) and Navier–Stokes equation (momentum conservation equation) are expressed in Cartesian tensor notation as shown below.

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial p{\overline{u}}_i}{\partial x_i}}=0$$

(1)

$${\displaystyle \frac{\partial p{\overline{u}}_i}{\partial t}}+{\displaystyle \frac{\partial p{\overline{u}}_i{\overline{u}}_j}{\partial x_j}}=-{\displaystyle \frac{\partial {\overline{p}}_i}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\mu {\displaystyle \frac{\partial {\overline{u}}_i}{\partial x_j}}-\rho {\overline{u}}_i{\overline{u}}_j\right)+S_i$$

(2)

2.2.2. Turbulence Model

The realizable k-$\epsilon$ model is a turbulence model with wider applicability. Due to the flow resistance effect of the net, there is a large pressure gradient before and after the net cage, meaning that the water movement near the net cage is more intense. The realizable k-$\epsilon$ model has a good effect on the simulation of this problem [13]; thus, in this paper we choose this model for numerical simulation.

k-equation:

$${\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho k{u}_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{u_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+G_k-\rho \epsilon$$

(3)

$\epsilon$-equation:

$${\displaystyle \frac{\partial \left(\rho \epsilon \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \epsilon u_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{u_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+\rho C_{1}E\epsilon -\rho C_2{\displaystyle \frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}}$$

(4)

where k in the turbulence model represents the turbulent kinetic energy and $\epsilon$ is dissipation rate.

2.2.3. Porous Media Model

The porous media are modeled as a continuum containing a fluid and a fine solid structure. The pressure drop is approximated by introducing a source term into the momentum transfer equation, which is calculated from Forchheimer’s equation [25,26]:

$$-\nabla p=\mu v/k+\rho \left|v\right|v\tau /k$$

(5)

where k in the porous media model is the permeability tensor.

Laminar flows through porous media are characterized by peristaltic flow, where the pressure drop is usually proportional to the velocity. Thus, Equation (5) is reduced to Darcy’s law, as follows:

$$-\nabla p=\mu v/k.$$

(6)

The commercial CFD software STAR-CCM+ (17.04.007) introduces source terms $S_i$ into the momentum transport equations to approximate the pressure drop. The momentum equation incorporating $S_i$ is expressed as follows:

$$\partial \left(\rho v\right)/\partial t+\nabla \left(\rho vv\right)=-\nabla P+\nabla \left(T\right)+S_i.$$

(7)

In STAR-CCM+ (17.04.007), $S_i$ denotes the momentum sink of the porous media that generates the pressure drop, which is determined by the velocity and porous resistance tensor, as follows:

$$S_i=-P_{v}v-P_i\left|v\right|v.$$

(8)

Similarly, Zhao et al. [13] also used $S_i$ to denote the damping properties of the net, defined as follows:

$$S_i=-\mu Dv-\rho C\left|v\right|v/2.$$

(9)

The value of the porous media coefficient of the net is usually determined by parameters such as the size and solidity of the net, which can be obtained by fitting the drag results or using empirical equations. If D and C are known, $P_v$ and $P_i$ can be obtained by calculating Equations (10) and (11).

$$P_v=\mu D=\mu /k$$

(10)

$$P_i=\rho C/2=\rho \tau /k$$

(11)

2.3. Boundary Conditions and Meshing

As shown in Figure 3, a full-scale model is used in this study. Based on the Cartesian coordinate system, the coordinate origin is set at the center projection of the truss-type aquaculture platform on the water surface. The X-axis negative direction is defined as the current direction, the Y-axis is perpendicular to the current direction, and the Z-axis is vertically upward. The inlet, the lateral wall, and the top and bottom of the computational domain are provided as velocity inlet conditions [27], while the outlet is provided as a pressure outlet condition. The porous media model is used to simulate the net, with the pillar structure defined as a full-wall surface. For the net, the porous media is configured to produce the same flow resistance effect as the actual net by setting reasonable $P_v$, $P_i$, and $S_n$. In addition, the finite volume method is used in this study to discretize the governing equations in numerical calculations. The governing equations are solved using a pressure-based discrete solver, while the SIMPLE algorithm is chosen to achieve pressure–velocity coupling.

Figure 3. Boundary conditions and meshing.

To ensure better mesh quality, the mesh division of the computational domain is performed using the trimmed cell mesher. The surface of the pillar structure is used to capture the boundary layer flow through prismatic layers. The total thickness of the prismatic layer is 0.068 m, the number of prismatic layers is 7, and the stretching ratio is 1.2. For the flow field near the net cage, a two-layer mesh transition zone is set up to ensure the accuracy of the calculation. The dimensions of the computational domain and the specific grid refinement methods are provided in Table 2.

Table 2. Computational domain and grid refinement.

Encryption Zone	Dimensions	Grid Size
Domain	$2.7L\times 1.7L\times 4.8H$	1.28–2.56 m
Transition Zone 1	$2.0L\times 0.9L\times 1.9H$	0.64 m
Transition Zone 2	$1.4L\times 0.7L\times 1.6H$	0.32 m
Pillar	–	0.08 m
Net	–	0.05–0.20 m

3. Model Validation and Convergence Analysis

3.1. Model Validation

To verify the accuracy of the numerical method, this study simulates the working condition of a planar net perpendicular to the flow direction using the planar net model from Zhao et al. [13]. The numerical flume has a depth of 0.7 m and a width of 1.0 m. The planar net is simulated as a porous medium with a height of 0.4 m, a width of 1.0 m, and $\lambda =100\mathrm{mm}$. In addition, $P_{vn}=135.0661\mathrm{kg}·{\mathrm{m}}^{-3}·{\mathrm{s}}^{-1}$ and $P_{in}=8067.2758\mathrm{kg}·{\mathrm{m}}^{-4}$ can be derived from Equations (10) and (11) based on $D_n=75,990{\mathrm{m}}^{-2}$ and $C_n=8.087{\mathrm{m}}^{-1}$ respectively, as shown experimentally by Zhao et al. [13]. Notably, Liu et al. [27] demonstrated that the product of the coefficient and the thickness of a porous medium should be constant, i.e., the coefficient is inversely proportional to the thickness. Figure 4 shows the arrangement of the conditions and the velocity distribution under $u_0=0.5579\mathrm{m}/\mathrm{s}$. The location of the detection point and the physical modeling are consistent with Zhao et al. [13]. Figure 5 compares the simulation results of the flow velocity at the detection point with the experimental results from Zhao et al. [13]. The results indicate that the numerical method used in this study exhibits good agreement with the experimental data, verifying the reliability and accuracy of the numerical model in simulating problems related to porous media.

Figure 4. Layout of measuring points (a: horizontal view; b: vertical view) and velocity distribution at $u_0=0.5579$ m/s (c: horizontal view; d: vertical view).

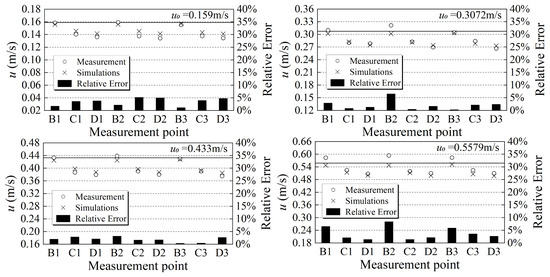
Figure 5. Flow velocity comparison.

3.2. Convergence Analysis

To ensure the stability of the simulation results, in this study we select the average value of $u/u_0$ at each point in the flow field as the basis for convergence judgment under the conditions of $u_0=1\mathrm{m}/\mathrm{s}$, $S_n$ = 0.2, and $\lambda =100\mathrm{mm}$; the arrangement of the monitoring points and monitoring planes is shown in Figure 6. Additionally, sensitivity analysis of porous media parameters by Patursson et al. [12] and others has demonstrated that the viscous term has a limited effect on the calculation error. Therefore, only the inertial resistance is considered in this study; based on the experiments of Patursson et al. [12], $P_{in}=1271.391\mathrm{kg}·{\mathrm{m}}^{-4}$ and $P_{it}=423.564\mathrm{kg}·{\mathrm{m}}^{-4}$ are obtained for the net, with $S_n=0.2$.

Figure 6. Arrangement of monitoring points and monitoring planes.

To ensure the accuracy of the numerical simulation, the residual values of the continuity equation, turbulent kinetic energy k, and specific dissipation rate $\epsilon$ are all set to 0.001. The computation time is set to 900 s, which allows the numerical simulation to achieve the predetermined accuracy. The temporal discretization utilizes a first-order implicit unsteady scheme, with the time step determined to ensure a convective Courant number of less than 1.

As shown in Table 3, our study first conducted a convergence analysis for different numbers of grids at the same time step, followed by a convergence analysis for the time step based on the optimal grid scheme. Figure 7 demonstrates the comparison of $u/u_0$ at each point under three sets of grids and three time steps. Considering computational accuracy and efficiency along with the need to prevent excessively coarse grids and avoid large time steps that fail to capture critical hydrodynamic phenomena, for this study we selected $N=9.70$ million and $\Delta t=0.20\mathrm{s}$ as the total number of grids and time steps, respectively.

Table 3. Case settings for different total meshes and time steps.

No.	Time Steps $\Delta \mathit{t}\mathbf{/}\mathbf{s}$	Total Grids N/Million	No.	Total Grids N/Million	Time Steps $\Delta \mathit{t}\mathbf{/}\mathbf{s}$
Mesh 1		4.50	TimeStep 1		0.50
Mesh 2	0.20	9.70	TimeStep 2	9.70	0.20
Mesh 3		22.50	TimeStep 3		0.10

Figure 7. Mesh convergence analysis and time step convergence analysis.

4. Results and Discussion

4.1. Characterization of the Flow Field in the Vicinity of the Aquaculture Platforms

A truss-type aquaculture platform is a system of multiple net cages consisting of pillars and nets, which together exhibit an extremely complex flow field structure due to intricate interactions. To study the characteristics of the flow field around the aquaculture platform, this study takes $u_0=1\mathrm{m}/\mathrm{s}$ and $S_n=0.2$ as an example. The computational conditions are consistent with those in Section 3.2, and both flow pattern analysis and flow velocity distribution analysis are conducted.

4.1.1. Analysis of Flow Patterns

Figure 8 illustrates the flow velocity contours inside and outside the aquaculture platform for different profiles. It can be observed that there are some common features among the different location profiles. The aquaculture platform has a significant resistance effect on the water flow, and $u/u_0$ generally exhibits a characteristic of decreasing first and then increasing. The water flow near the pillars is nearly stagnant, forming low-velocity vortex regions of varying sizes. This phenomenon is caused by the mutual conversion of kinetic energy and pressure energy when the viscous fluid passes through the impermeable wall. Additionally, the complex interactions between the pillars, net, and water flow result in a lack of fixed regularity in the flow field near the aquaculture platform.

Figure 8. Flow velocity contours inside and outside the aquaculture platform at different profiles.

Figure 8a shows the flow velocity contours of the XY profiles at $z=-1\mathrm{m}$, $-5\mathrm{m}$, and $-9\mathrm{m}$, illustrating the flow characteristics at different water depth locations. It is evident that the flow velocity attenuation and disturbance regions vary at different water depths. The lower layer exhibits a wider zone of low-velocity vortices compared to the upper layer. This phenomenon arises from the structural complexity of the aquaculture platform, leading to distinct spatial variations in the flow field distribution. These observations are consistent with the findings of Liu et al. [21], Yang et al. [22], and Ji et al. [24].

Figure 8b illustrates the flow velocity contours of the XZ profiles at $y=0$ m, 5 m, and 10 m, illustrating the flow characteristics near and away from the pillars. Due to the presence of the pillars, the flow velocity distribution from the inside to the outside is influenced by different vortices. Near the longitudinal profile within the aquaculture platform, i.e., away from the pillars, the vortex zone is smaller and the flow velocity distribution is relatively stable. On the other hand, at the edges of the platform, i.e., near the pillars, the vortex area is wider and the flow velocity distribution is more chaotic. It can be observed that the flow field within the aquaculture platform is uniformly distributed along the $u_0$ direction at locations away from the pillars, which is further discussed in the data analysis in Section 4.1.2.

Figure 8c shows the YZ profiles at $x=27.5\mathrm{m}$, $0\mathrm{m}$, and $-27.5\mathrm{m}$, representing the state of the internal and external flow fields in the three cages before and after. The results indicate that the flow velocity inside the cage is relatively stable, but decreases layer by layer due to the accumulation of the drag effect along the length scale. This is consistent with the observations in Figure 8a,b. It should be noted that along the $u_0$ direction, the vortex zone inside the first cage ($x=27.5\mathrm{m}$) has the lowest flow velocity, the vortex zone inside the third cage ($x=-27.5\mathrm{m}$) is the widest, and the situation in the middle cage ($x=0\mathrm{m}$) is relatively better. This suggests that the first cage provides good protection for the middle cage, while the vortex zone inside the third cage is relatively more disorganized due to the influence of the upstream vortex zone.

The flow field near the aquaculture platform is highly complex due to the presence of vortices. To observe the global flow field characteristics more intuitively, the Q-criterion isosurface ($Q=0.01{\mathrm{s}}^{-1}$) is used in this study to illustrate the three-dimensional vortex structure in the vicinity of the aquaculture platform, as shown in Figure 9. It can be observed that along the $u_0$ direction, the vortex region induced by the first pillar structure exhibits a broader lateral scale accompanied by significant energy dissipation of the flow. This phenomenon substantially reduces the downstream flow velocity, resulting in diminished velocity gradients around the second pillar structure. Consequently, this generates only localized vortex regions, while the combined influence of pressure near the third and fourth pillar structures and the flow resistance of the multi-layer net results in the vortex zone shrinking toward the inner part of the net cage. Under the combined effects of the residual vortex shedding from the pillar structures, the cumulative effect of multiple cages, and the drag effect of the net, the $u/u_0$ inside the first cage is highest near the center and lower at the edges. In contrast, the $u/u_0$ inside the third cage is lower and the flow field disturbance is the most complex. The middle cage, shielded by the front and rear nets, exhibits flow field conditions that are significantly more favorable for fish movement. These phenomena are also illustrated in Figure 8 and are further discussed in the data analysis in Section 4.1.2.

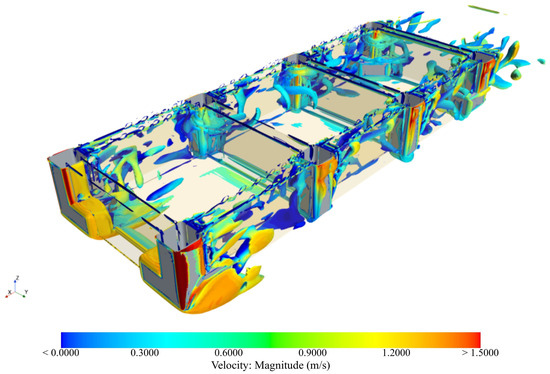
Figure 9. Three-dimensional vortex structure by Q-criterion isosurfaces.

4.1.2. Velocity Distribution Analysis

Figure 10 shows the $u/u_0$ for different profile lines, providing a data-driven basis for interpreting the flow pattern analysis in the previous section.

Figure 10. The $u/u_0$ for different profile lines.

Figure 10a demonstrates the variation of $u/u_0$ in the X-direction. Inside the aquaculture platform, the $u/u_0$ near the pillar side ($y=10\mathrm{m}$) decreases more significantly and fluctuates sharply, while the $u/u_0$ away from the pillar side ($y=0\mathrm{m},5\mathrm{m}$) shows a smooth decreasing trend. All $u/u_0$ values near the pillar side are lower than those away from the side, a phenomenon caused by the different distribution of vortices. Taking the profile lines $z=-5\mathrm{m}$, $y=0\mathrm{m},5\mathrm{m}$, and $10\mathrm{m}$, the $u/u_0$ from the entry to the exit of the aquaculture platform ($x=\pm 43\mathrm{m}$) is cumulatively attenuated by $41.59\%$, $49.66\%$, and $64.63\%$, respectively, demonstrating the significant effect of the pillar vortices on $u/u_0$. In contrast, the height factor has less impact on $u/u_0$, especially on the side away from the pillar, where the $u/u_0$ values for profile lines at different heights exhibit high consistency. Taking the profile lines $y=0\mathrm{m}$ with $z=-1\mathrm{m}$, $-5\mathrm{m}$, and $-9\mathrm{m}$, the $u/u_0$ is cumulatively attenuated by $42.88\%$, $41.59\%$, and $42.74\%$, respectively, showing very little difference. Near the pillar side, however, the curve fluctuations at different heights exhibit obvious differences, indicating that the vortices amplify the effect of the height factor on $u/u_0$. At the rear of the aquaculture platform, the $u/u_0$ recovers significantly after the water flow exits the platform, with faster recovery near the pillar side. Observing the profile lines $z=-5\mathrm{m}$ with $y=0\mathrm{m},5\mathrm{m}$, and $10\mathrm{m}$, it can be seen that the final $u/u_0$ values recover to $67.74\%$, $74.30\%$, and $85.44\%$, respectively. This is due to the conversion of pressure energy to kinetic energy outside the aquaculture platform and the greater pressure difference at locations with vortices. An interesting phenomenon is that the $u/u_0$ decreases and then increases in front of the first net layer of the aquaculture platform. The underlying principle involves mutual energy conversion: upstream of the net, $u/u_0$ decreases due to the obstruction effect of the net and the water surface slightly elevates. During this process, part of the kinetic energy converts to potential energy. Subsequently, as water flows from the elevated surface toward the net, potential energy converts back to kinetic energy, again causing an increase in $u/u_0$. This is consistent with part of the study by Yang et al. [22], who referred to this phenomenon as a “hydraulic jump”.

Figure 10b demonstrates the variation of $u/u_0$ in the Y-direction. It can be observed that the figure exhibits a clear symmetrical pattern in which $u/u_0$ gradually increases as it approaches the aquaculture platform, decreases sharply after passing through the net, and then gradually increases and stabilizes inside each cage. Similar to Figure 10a, it can also be noted that the curves of $u/u_0$ at different heights are nearly overlapping, indicating that the height factor has a negligible effect on $u/u_0$. Taking a fixed height $z=-5$ m at the center of the three cages ($x=27.5$ m, 0 m, and $-27.5$ m), the $u/u_0$ values are $90.26\%$, $63.65\%$, and $52.56\%$, respectively. This shows that $u/u_0$ is continuously attenuated under the influence of the multi-layer net, but that the attenuation effect gradually weakens due to the reduction in $u/u_0$. Additionally, due to the interaction of the double-layer nets, a sudden increase in $u/u_0$ occurs between the nets, similar to a squeezing effect. This is similar to the mechanism of the “hydraulic jump” phenomenon mentioned earlier. It should be noted that the flow field is not completely symmetric due to the presence of vortices and that the fluctuations in $u/u_0$ on both sides are not identical near the net and the pillar.

Figure 10c shows the variation of $u/u_0$ in the Z-direction. As can be seen from the figure, the bottom net divides the $u/u_0$ curves into two distinct forms inside and outside the net. Except for the positions near the pillars, which are still influenced by vortices, the $u/u_0$ inside the net is significantly more stable compared to that outside the net. This indicates that a certain low-velocity vortex region exists outside the net due to the effect of the bottom net, but that the vortices at the bottom do not significantly affect the interior of the net. Taking the central axis of the aquaculture platform ($y=0$ m) and the interior of the middle cage ($x=0$ m) as an example, the maximum and minimum values of $u/u_0$ with height are 63.84% and 63.41%, respectively, showing a very small difference. The situation inside the other cages is similar, reflecting the result that the flow field inside the aquaculture platform exhibits stable $u/u_0$ in the vertical direction at fixed locations and is uniformly distributed along $u_0$ direction. This is consistent with the discussion in Section 4.1.1.

From the perspective of aquaculture, this configuration of the aquaculture platform exhibits distinct flow velocity distribution characteristics: the first cage maintains a relatively higher $u/u_0$, the middle cage sustains moderate flow conditions, and the third cage experiences significantly slower $u/u_0$. Leveraging these characteristics, precision-classified aquaculture operations can be implemented based on species-specific optimal flow velocity requirements. For example, Salmo salar thrive in moderate flow velocity environments, which enhance their growth and physiological performance [28], whereas Micropterus salmoides demonstrate accelerated growth rates under high flow velocity conditions [29].

4.2. Effects of Different Incoming Flow Velocity

Appropriate flow velocity helps to promote the exchange of water inside and outside the net cage, thereby optimizing the survival environment of cultured fish. The calculation conditions in this section are consistent with those in Section 4.1, with the $u_0$ variable set to 0.5 m/s, 1.0 m/s, and 2.0 m/s, respectively.

Figure 11 illustrates the profile-specific flow velocity contours of the aquaculture platform for different $u_0$. As shown in Figure 11a, as $u_0$ decreases, the vortex zone near the first pillar expands, which provides a more significant shielding effect on the downstream cage, resulting in a relatively lower level of flow field chaos in the downstream cage. This is because fluid with high kinetic energy accelerates the vortex shedding frequency, leading to concentrated energy loss, while the pressure difference caused by $u_0$ variation also affects the extent of the low-velocity vortex region. As shown in Figure 11b,c, the influence of $u_0$ on the flow at the center of the aquaculture platform is minimal and can be neglected. The flow field still maintains the characteristics of a small vortex zone and a uniform stable flow velocity distribution. It can be observed that the vortex zone near the pillar is significantly affected by $u_0$, while this factor has less influence on flow velocity attenuation effect of the net. Therefore, if necessary, deflector plates can be installed behind the pillars or the pillar shape can be optimized to reduce flow velocity fluctuations and make the flow velocity distribution around the platform more stable.

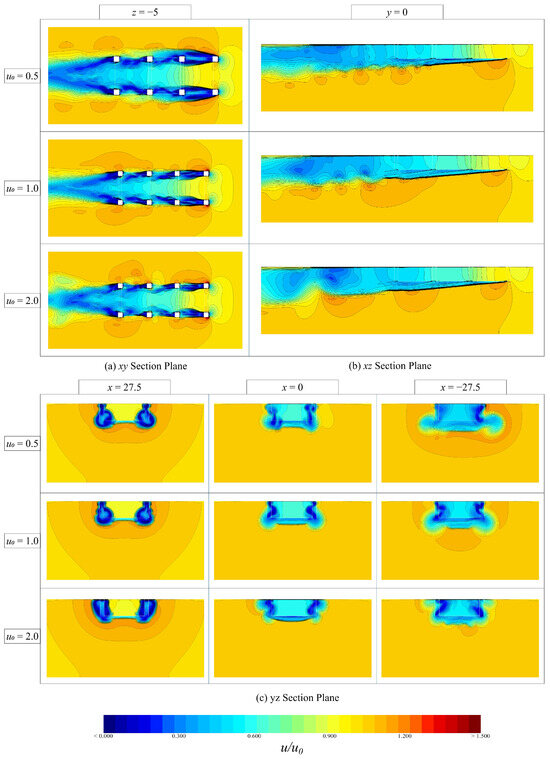
Figure 11. Contours of flow velocity in specific profiles of the aquaculture platform for different $u_0$.

Figure 12 demonstrates $u/u_0$ for specific profile lines under different $u_0$. As shown in Figure 12a, the locations near the pillar side ($x=10\mathrm{m}$) and inside the first cage ($x=14.55\mathrm{m}-39.45\mathrm{m}$) were selected. The $u/u_0$ values for $u_0=1.0\mathrm{m}/\mathrm{s}$ and $2.0\mathrm{m}/\mathrm{s}$ exhibit a decreasing trend followed by an increase, with attenuations of 48.36% and 29.95%, respectively. In contrast, $u/u_0$ for $u_0=0.5\mathrm{m}/\mathrm{s}$ displays a linear decreasing trend with an attenuation of 77.95%. As shown in Figure 12b, the $u/u_0$ curves are more stable within each cage and the range of the curve stabilization stage gradually decreases along $u_0$ direction. Taking $u_0=2.0\mathrm{m}/\mathrm{s}$ as an example, the $u/u_0$ values at the center profile lines of the three cages are 17.60 m, 16.00 m, and 7.68 m, respectively, along the $u_0$ direction. Figure 12c reveals that $u_0$ has minimal influence on the bottom net. Specifically, at the bottom net location of the first cage ($x=27.5$ m, $z=-10.5$ m), the $u/u_0$ values for $u_0=0.5$ m/s, $1.0$ m/s, and $2.0$ m/s are $34.73\%$, $32.60\%$, and $36.88\%$, respectively. Subsequently, $u/u_0$ shows an upward trend after moving away from the bottom grid. Figure 13 shows the $u/u_0$ at the centers of the cages under different $u_0$. Taking the center of the middle cage ($x=0$ m) as an example, the $u/u_0$ corresponding to $u_0=0.5\mathrm{m}/\mathrm{s}$, $1.0\mathrm{m}/\mathrm{s}$, and $2.0\mathrm{m}/\mathrm{s}$ are $60.55\%$, $63.65\%$, and $63.30\%$, respectively, with a maximum difference of $3.10\%$. Clearly, the above data reflect the phenomenon described in Section 4.1.1, further indicating that $u_0$ has a limited influence on the internal flow velocity of the aquaculture platform.

Figure 12. The $u/u_0$ for specific profile lines under different $u_0$.

Figure 13. The $u/u_0$ at the centers of the cages under $u_0$.

4.3. Effect of Different Net Solidity Ratios

In deep-sea aquaculture, the net belongs to a relatively rough porous medium; its structural robustness ensures that $S_n$ typically lies within the range of 0.1 to 0.4 [30]. Based on the phenomenon observed in the previous section, $u_0=1.0\mathrm{m}/\mathrm{s}$ is selected as the benchmark in this section. The computational conditions are consistent with Section 4.1, with $S_n$ of 0.111, 0.2, and 0.269, respectively. The corresponding parameters $P_{in}$ and $P_{it}$ are derived from Liu et al. [27], as shown in Table 4.

Table 4. The $S_n$ and corresponding $P_{in}$ and $P_{it}$ values.

${\mathit{S}}_{\mathit{n}}$	${\mathit{P}}_{\mathit{in}}$ (kg/$m^4$)	${\mathit{P}}_{\mathit{it}}$ (kg/$m^4$)
0.111	564.312	33.457
0.2	1271.391	423.564
0.269	2244.421	961.895

Figure 14 illustrates the profile-specific flow velocity contours of the aquaculture platform for different $S_n$. As shown in Figure 14a, the vortex zones of the flow field in the inner and downstream portions of the aquaculture platform become more concentrated, stable, and uniformly distributed with increasing $S_n$, while the attenuation effect of $u/u_0$ becomes more significant. This phenomenon can be explained by the fact that the denser structure of the high-solidity net increases the obstruction of the water flow, leading to greater deflection of the flow lines and forming a more concentrated and stable vortex structure. At the same time, this effect is combined with the cumulative impact of multiple cages, further exacerbating the energy loss of the water flow. As shown in Figure 14b,c, the $u/u_0$ decreases significantly near the water surface and the low-velocity zone is concentrated near the bottom net and pillar structure. As the $S_n$ increases, the low-velocity zone downstream becomes wider and the flow velocity attenuation becomes more pronounced. As the depth of the water increases, the disturbance effect of the low-solidity net diminishes compared to the high-solidity net. In the deeper region, there is no longer an obvious low-velocity zone, and the flow tends to approach a free-flowing state. It can be observed that the high-solidity net increases the energy loss inside the aquaculture platform, while the low-solidity net promotes the recovery of the deep flow velocity. By matching the appropriate $S_n$ and depth requirements, the flow field of the aquaculture platform can be optimized efficiently.

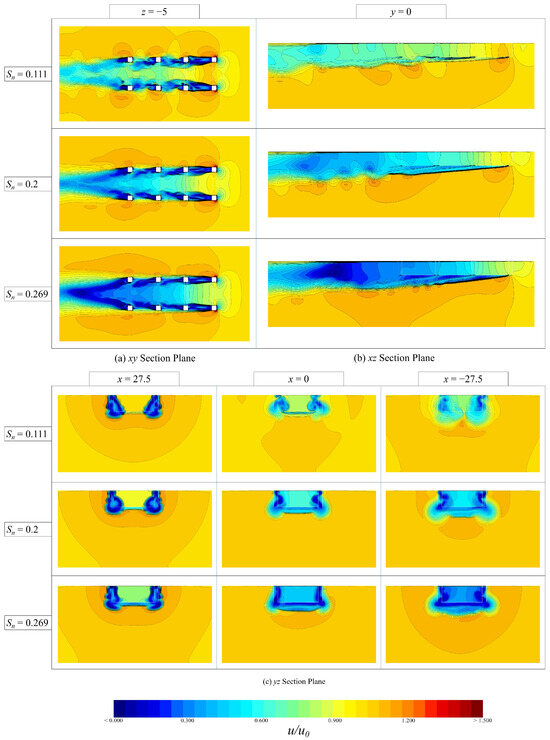
Figure 14. Contours of flow velocity in specific profiles of aquaculture platforms with different $S_n$.

Figure 15 demonstrates the $u/u_0$ for specific profile lines under different $S_n$. As shown in Figure 15a, the $u/u_0$ curves exhibit significant stratification according to the different attenuation effects of $S_n$, indicating that $S_n$ has a significant influence on flow velocity attenuation which can trigger a substantial degree of change. Taking the positions away from the side ($y=0\mathrm{m}, 5\mathrm{m}$) and inside the culture platform ($x=\pm 39.45\mathrm{m}$) as an example, the attenuation effect for $S_n=0.111$ is the weakest, with attenuation of $23.20\%$ and $37.89\%$, respectively. In contrast, the attenuation effect is the strongest for $S_n=0.269$, with attenuation of $61.95\%$ and $63.65\%$, respectively. As shown in Figure 15b and Figure 16, the $u/u_0$ at the center of the third cage ($x=-27.5\mathrm{m}$) is $76.83\%$, $52.56\%$, and $33.58\%$ for $S_n=0.111$, $0.2$, and $0.269$, respectively, with the maximum difference reaching 43.25%. As shown in Figure 15c, at the bottom net position ($z=-10.5\mathrm{m}$) of the first cage ($x=27.5\mathrm{m}$), the $u/u_0$ values corresponding to $S_n=0.111$, $0.2$, and $0.269$ are attenuated by $19.88\%$, $32.31\%$, and $49.72\%$, respectively. In summary, the $u/u_0$ reduction ratio of this aquaculture platform configuration is positively correlated with the $S_n$; the higher the $S_n$, the more significant the effect of the netting on flow obstruction. This phenomenon is consistent with the findings of Yao et al. [31] and Winthereig et al. [32].

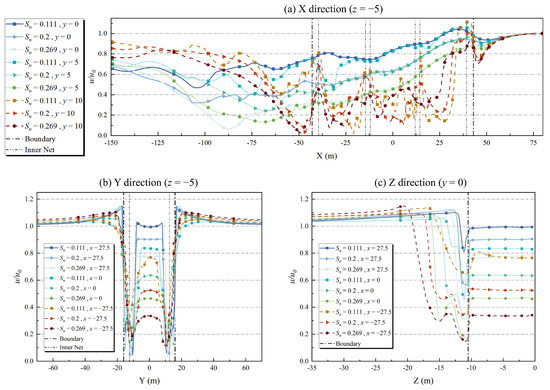
Figure 15. The $u/u_0$ for specific profile lines under different $S_n$.

Figure 16. The $u/u_0$ at the centers of the cages under different $S_n$.

5. Conclusions

Based on the porous media model, STAR-CCM+ (17.04.007) is used to conduct a comprehensive and systematic investigation into the flow field characteristics inside and outside a semi-submersible aquaculture platform with a multiple net cage configuration. First, the accuracy of the numerical method and stability of the numerical model are verified. Subsequently, the flow field characteristics of the aquaculture platform are analyzed and the effects of different $u_0$ and $S_n$ on the internal and external flow fields of the aquaculture platform are explored. The conclusions of this study are as follows:

(1)

Due to the combined effects of the pillar, net, and water flow, the flow field near the aquaculture platform is highly complex and lacks a fixed pattern. The low-velocity vortex region is concentrated near the pillar and net.

(2)

After velocity attenuation, the $u/u_0$ at the centers of the three cages is 90.26%, 63.65%, and 52.56%, respectively. By leveraging these characteristics, precision-classified aquaculture operations can be implemented based on species-specific optimal flow velocity requirements.

(3)

The $u_0$ has minimal effects on the flow velocity inside the cages, with a maximum difference of 3.10%.

(4)

Variations in the $S_n$ markedly impact velocity attenuation, particularly in downstream areas. The $u/u_0$ in the third cage varies by up to 43.25% due to differences in the $S_n$.

Investigating the internal and external flow field characteristics of aquaculture platforms holds significant importance for practical marine aquaculture engineering. Flow field analysis not only provides scientific foundations for rationally planning aquaculture density and feeding strategies that can ensure stable growth environments for fish but also offers theoretical support for net selection and platform layout design, effectively reducing trial-and-error costs in engineering. However, certain challenges remain in our current research. Cross-sectional analyses and probe lines struggle to deliver a reliable quantitative method for assessing the suitability of fish to specific flow conditions. In order to achieve precise evaluations, more appropriate metrics or statistical analysis methods should be adopted. Additionally, due to physiological differences among fish species, their optimal flow velocity ranges vary significantly, necessitating further studies on species-specific requirements. It should be noted that in practical engineering, semi-submersible aquaculture platforms typically apply pre-tension to nets in order to maintain the entire structure in a taut state with minimal deformation; hence, these are modeled as rigid structures. However, under wave–current coupling conditions or extreme environmental loads, the deformation of flexible nets, fluid–structure interactions, and corresponding flow field characteristics require further investigation. Furthermore, low-velocity vortex regions within aquaculture platforms may lead to sediment and fish waste accumulation, increasing the $S_n$ of the nets and compromising velocity attenuation effect. Despite these limitations, the methodologies and conclusions of this study can provide valuable references for practical engineering applications.