FTT: A Frequency-Aware Texture Matching Transformer for Digital Bathymetry Model Super-Resolution
Abstract
1. Introduction
- (1)
- Limited terrain feature-extraction capabilities: The local receptive field and translation invariance are powerful tools for CNNs to extract natural image features, but they may not be as effective for terrain features. A local receptive field has a limited capacity to capture large-scale topographic features [16,30], and translation invariance conflicts with the multi-scale spatial heterogeneity of terrain.
- (2)
- Loss of high-frequency priors: High-frequency priors refer to sharp changes in elevation, indicating steep terrain such as ridges or deep canyons. These topographic features are crucial for geological analysis and ocean resource management. However, convolutional operations and attention mechanisms may dampen high-frequency priors [31,32], which adversely affects the quality of DBM SR reconstruction.
- (3)
- Texture distortion and position shift: In our observations, increasing the depth of neural-network layers enhances the model’s ability to extract features but may lead to texture distortion and positional offsets. Although residual structures help to mitigate this phenomenon, further improving the fidelity of the generated HR DBM is a pressing problem given the high accuracy requirement of DBM.
- (1)
- We developed global terrain feature extraction (GTFE), which can effectively capture large-scale terrain features while maintaining sensitivity to spatial heterogeneity and spatial structure.
- (2)
- The high-frequency feature extraction (HFFE) is employed to alleviate the low-pass filtering characteristics of the swin transformer, thereby better preserving the high-frequency priors.
- (3)
- The terrain matching block (TMB) can integrate high-fidelity shallow features and deep features with rich semantics to improve fidelity.
2. Materials and Methods
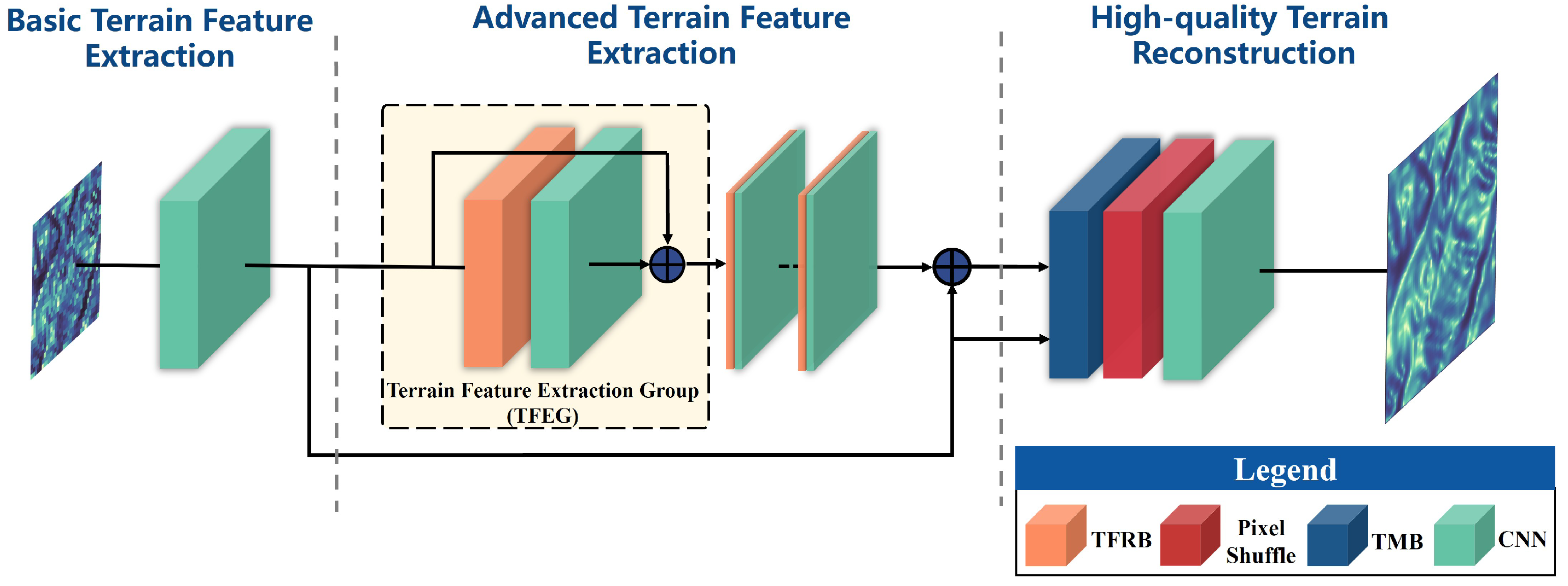
2.1. Model Overview
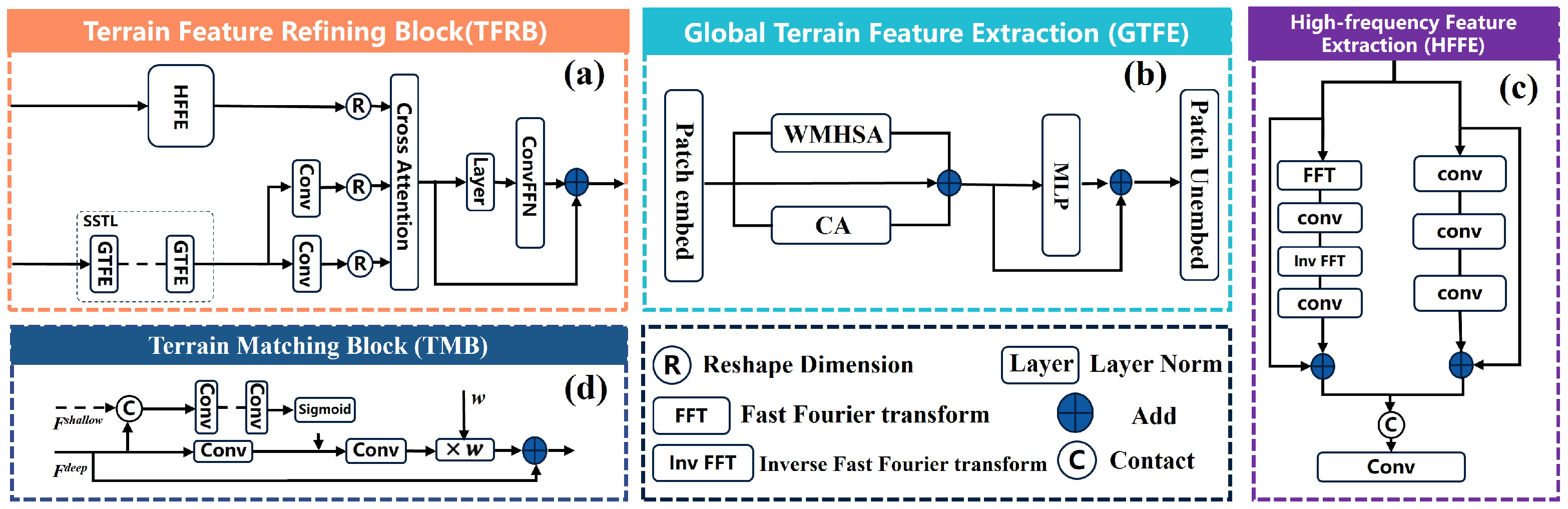
2.2. GTFE
- Impact of LN: The LN reduces the contrast between different terrain features. For instance, normalized peaks may appear flattened, making it difficult for the model to capture spatial heterogeneity and resulting in overly smooth outputs. Removing LN helps the model retain more terrain detail;
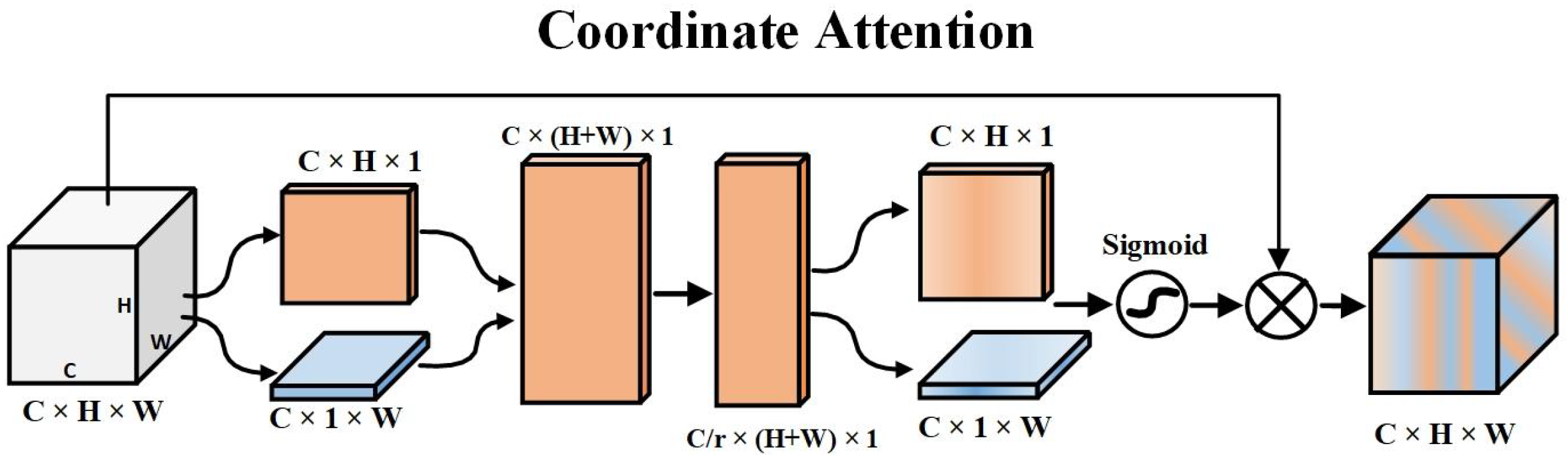
- Limitations of Patch Embedding: The patch embedding in STL limits the model’s ability to explicitly understand the 2D spatial structure of the DBM. To address this issue, we added the CA branch too. As shown in Figure 3, the CA branch generates attention maps in both vertical and horizontal directions, enhancing the model’s ability to perceive 2D coordinates and better handle terrain information.
2.3. HFFE
2.4. TMB
3. Experiments and Results
3.1. Datasets and Elevation Metrics
3.1.1. Study Area
3.1.2. Data Preprocessing
3.1.3. Elevation Metrics
3.2. Training Details
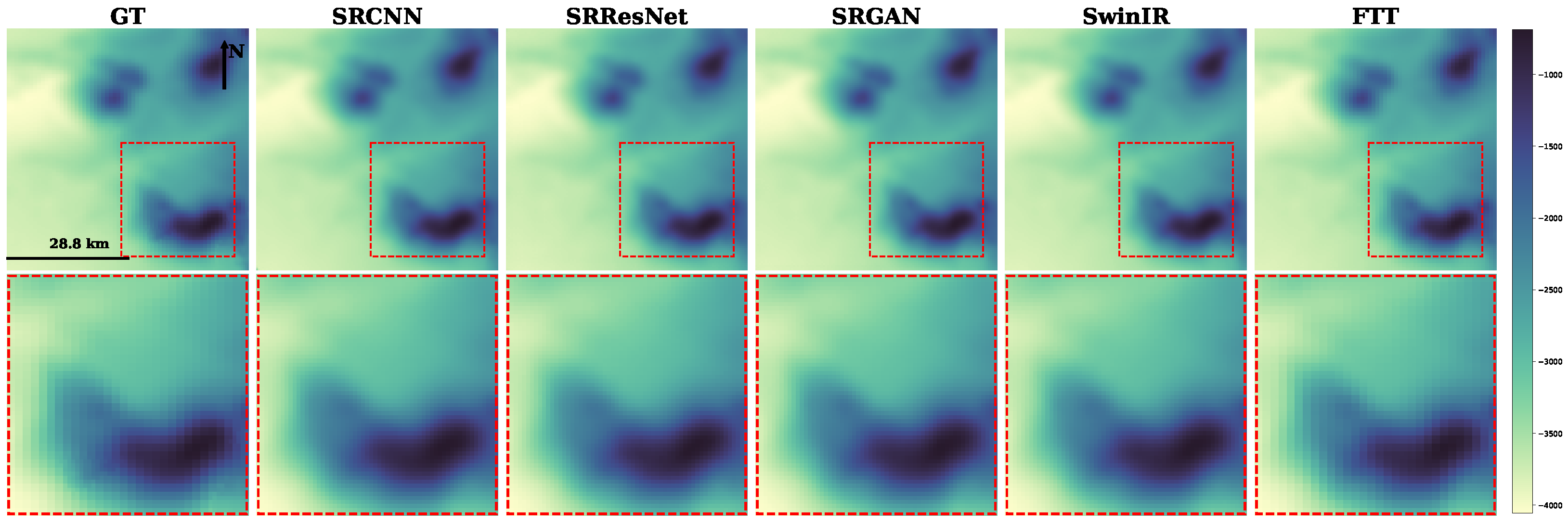
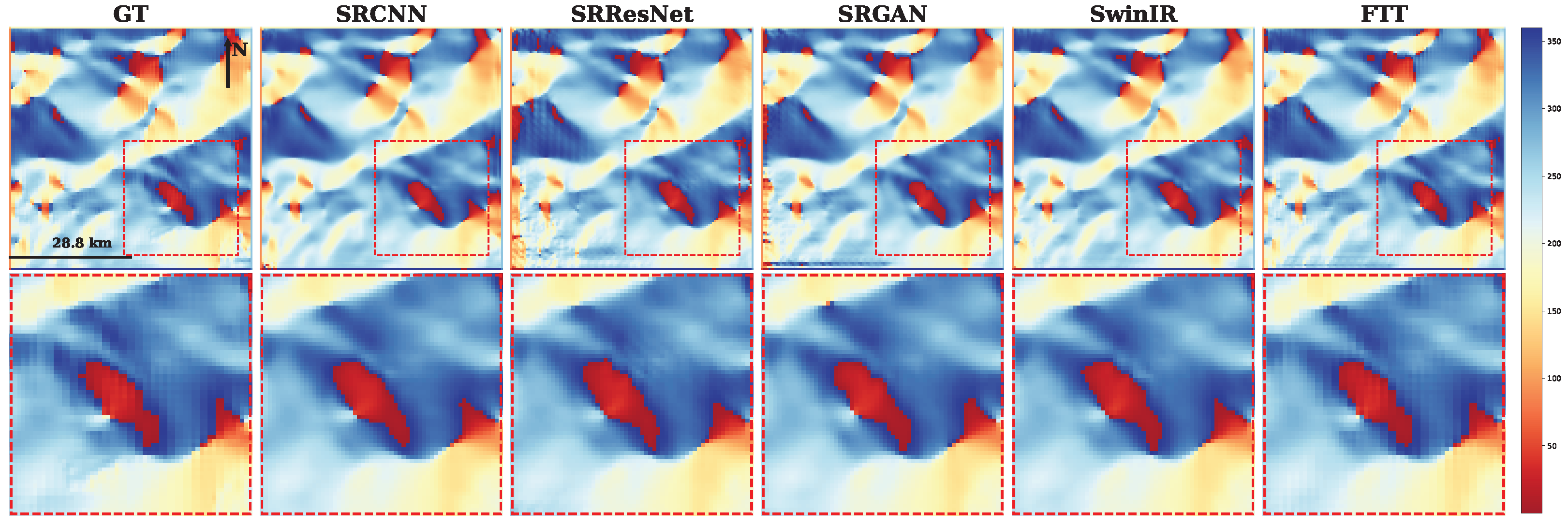
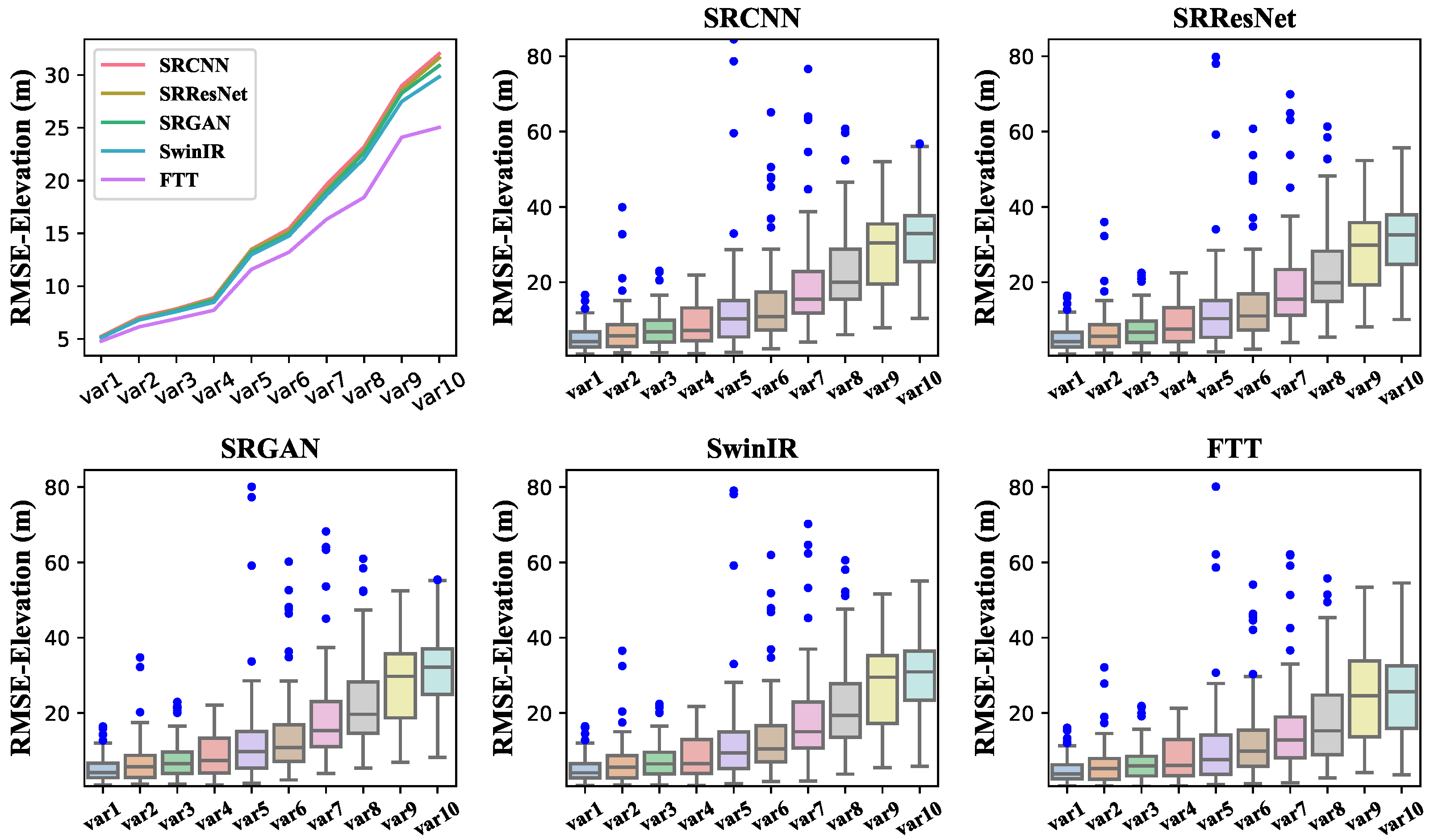
3.3. Results
4. Discussion
Ablation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SBES | Single-beam Echo Sounder |
| MBES | Multi-beam Echo Sounder |
| ALB | Airborne LiDAR Bathymetry |
| SAR | Synthetic Aperture Radar |
| SA | Satellite Altimeter |
| SDB | Satellite-Driven Bathymetry |
References
- Wölfl, A.C.; Snaith, H.; Amirebrahimi, S.; Devey, C.W.; Dorschel, B.; Ferrini, V.; Huvenne, V.A.I.; Jakobsson, M.; Jencks, J.; Johnston, G.; et al. Seafloor Mapping—The Challenge of a Truly Global Ocean Bathymetry. Front. Mar. Sci. 2019, 6, 283. [Google Scholar] [CrossRef]
- Lecours, V.; Dolan, M.F.J.; Micallef, A.; Lucieer, V.L. A review of marine geomorphometry, the quantitative study of the seafloor. Hydrol. Earth Syst. Sci. 2016, 20, 3207–3244. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, J.; Ruan, X.; Li, J.; Ye, L.; Chu, S.; Cheng, L.; Zhang, K. Satellite remote sensing and bathymetry co-driven deep neural network for coral reef shallow water benthic habitat classification. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104054. [Google Scholar] [CrossRef]
- Thompson, A.F.; Sallée, J.B. Jets and Topography: Jet Transitions and the Impact on Transport in the Antarctic Circumpolar Current. J. Phys. Oceanogr. 2012, 42, 956–972. [Google Scholar] [CrossRef]
- Ellis, J.; Clark, M.; Rouse, H.; Lamarche, G. Environmental management frameworks for offshore mining: The New Zealand approach. Mar. Policy 2017, 84, 178–192. [Google Scholar] [CrossRef][Green Version]
- He, J.; Zhang, S.; Feng, W.; Lin, J. Quantifying earthquake-induced bathymetric changes in a tufa lake using high-resolution remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103680. [Google Scholar] [CrossRef]
- Bandini, F.; Olesen, D.; Jakobsen, J.; Kittel, C.M.M.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Technical note: Bathymetry observations of inland water bodies using a tethered single-beam sonar controlled by an unmanned aerial vehicle. Hydrol. Earth Syst. Sci. 2018, 22, 4165–4181. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Y.; Le, Y.; Qian, Y.; Zhang, D.; Wang, L. A high-precision fusion bathymetry of multi-channel waveform curvature for bathymetric LiDAR systems. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103770. [Google Scholar] [CrossRef]
- Viaña-Borja, S.P.; Fernández-Mora, A.; Stumpf, R.P.; Navarro, G.; Caballero, I. Semi-automated bathymetry using Sentinel-2 for coastal monitoring in the Western Mediterranean. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103328. [Google Scholar] [CrossRef]
- Sharr, M.B.; Parrish, C.E.; Jung, J. Automated classification of valid and invalid satellite derived bathymetry with random forest. Int. J. Appl. Earth Obs. Geoinf. 2024, 129, 103796. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z.; Zhang, Z.; Chu, Y.; Xu, C.; Yao, S.; Zhu, X.; Yue, Y.; Levers, A.; Zhang, J.; et al. Exploring modern bathymetry: A comprehensive review of data acquisition devices, model accuracy, and interpolation techniques for enhanced underwater mapping. Front. Mar. Sci. 2023, 10, 1178845. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation—GEBCO Seabed 2030 Project: The Quest to See the World’s Oceans Completely Mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Farsiu, S.; Robinson, D.; Elad, M.; Milanfar, P. Advances and challenges in super-resolution. Int. J. Imaging Syst. Technol. 2004, 14, 47–57. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, W.; Guo, S.; Zhang, P.; Fang, H.; Mu, H.; Du, P. UnTDIP: Unsupervised neural network for DEM super-resolution integrating terrain knowledge and deep prior. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103430. [Google Scholar] [CrossRef]
- Zhou, A.; Chen, Y.; Wilson, J.P.; Chen, G.; Min, W.; Xu, R. A multi-terrain feature-based deep convolutional neural network for constructing super-resolution DEMs. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103338. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, S.; Yang, Z.; Guan, H.; Ren, Y.; Cheng, K.; Zhao, X.; Liu, X.; Chen, M.; Liu, Y.; et al. TTSR: A transformer-based topography neural network for digital elevation model super-resolution. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4403719. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. arXiv 2015, arXiv:1501.00092. [Google Scholar] [CrossRef]
- Jiao, J.; Tu, W.C.; He, S.; Lau, R.W.H. FormResNet: Formatted Residual Learning for Image Restoration. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1034–1042. [Google Scholar] [CrossRef]
- Fan, Y.; Shi, H.; Yu, J.; Liu, D.; Han, W.; Yu, H.; Wang, Z.; Wang, X.; Huang, T. Balanced Two-Stage Residual Networks for Image Super-Resolution. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition Workshops, CVPRW 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1157–1164. [Google Scholar] [CrossRef]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. arXiv 2017, arXiv:1708.02209. [Google Scholar] [CrossRef]
- Ren, H.; El-Khamy, M.; Lee, J. Image Super Resolution Based on Fusing Multiple Convolution Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017; pp. 1050–1057. [Google Scholar] [CrossRef]
- Li, W.; Tao, X.; Guo, T.; Qi, L.; Lu, J.; Jia, J. MuCAN: Multi-Correspondence Aggregation Network for Video Super-Resolution. arXiv 2020, arXiv:2007.11803. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image Super-Resolution Using Dense Skip Connections. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, J.; Wang, J.; Chen, Q.; Cao, J.; Deng, Z.; Xu, Y.; Tan, M. Closed-Loop Matters: Dual Regression Networks for Single Image Super-Resolution. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 5406–5415. [Google Scholar] [CrossRef]
- Shocher, A.; Cohen, N.; Irani, M. Zero-Shot Super-Resolution Using Deep Internal Learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3118–3126. [Google Scholar] [CrossRef]
- Xu, Y.S.; Tseng, S.Y.R.; Tseng, Y.; Kuo, H.K.; Tsai, Y.M. Unified Dynamic Convolutional Network for Super-Resolution with Variational Degradations. arXiv 2020, arXiv:2004.06965. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. arXiv 2017, arXiv:1609.04802. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Loy, C.C.; Qiao, Y.; Tang, X. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. arXiv 2018, arXiv:1809.00219. [Google Scholar] [CrossRef]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Real-ESRGAN: Training Real-World Blind Super-Resolution with Pure Synthetic Data. arXiv 2021, arXiv:2107.10833. [Google Scholar]
- Ma, X.; Li, H.; Chen, Z. Feature-Enhanced Deep Learning Network for Digital Elevation Model Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5670–5685. [Google Scholar] [CrossRef]
- Park, N.; Kim, S. How Do Vision Transformers Work? arXiv 2022, arXiv:2202.06709. [Google Scholar] [CrossRef]
- Li, A.; Zhang, L.; Liu, Y.; Zhu, C. Feature Modulation Transformer: Cross-Refinement of Global Representation via High-Frequency Prior for Image Super-Resolution. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 1–6 October 2023; pp. 12480–12490. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Guo, C.L.; Liu, L.; Cheng, M.M.; Hou, Q. SRFormerV2: Taking a Closer Look at Permuted Self-Attention for Image Super-Resolution. arXiv 2024, arXiv:2303.09735. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. arXiv 2016, arXiv:1609.05158. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar] [CrossRef]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13708–13717. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiong, L.; Huang, X.; Li, S.; Shen, W. Super-resolution for terrain modeling using deep learning in high mountain Asia. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103296. [Google Scholar] [CrossRef]
- Cai, W.; Liu, Y.; Chen, Y.; Dong, Z.; Yuan, H.; Li, N. A Seabed Terrain Feature Extraction Transformer for the Super-Resolution of the Digital Bathymetric Model. Remote Sens. 2023, 15, 4906. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, W.; Ma, M.; Wang, M.; Wang, D.; Huang, X.; Yu, L.; Zhang, Q.; Lu, H.; Hong, D.; et al. Super-resolution reconstruction of a 3 arc-second global DEM dataset. Sci. Bull. 2022, 67, 2526–2530. [Google Scholar] [CrossRef]





| Methods | Sensors | Strength | Limitations |
|---|---|---|---|
| Shipborne | SBES | Highly reliable | Limited range |
| MBES | High resolution | High operating costs | |
| Airborne | ALB | High accuracy | Limited water depth |
| SAR | Ignore clouds and fog | High uncertainty | |
| Spaceborne | SA | Wide range | Low accuracy |
| SDB | Wide range | Limited water depth |
| Model | RMSE of Elevation (m) ↓ | RMSE of Slope (°) ↓ | RMSE of Aspect (°) ↓ | SSIM ↑ |
|---|---|---|---|---|
| SRCNN | 16.30 | 5.29 | 68.29 | 0.968 |
| SRResNet | 16.07 | 5.39 | 71.06 | 0.968 |
| SRGAN | 16.23 | 5.19 | 68.10 | 0.968 |
| SwinIR | 15.43 | 5.12 | 67.43 | 0.969 |
| FTT (ours) | 13.48 | 4.81 | 65.25 | 0.973 |
| CA | HFFE | TMB | RMSE of Elevation (m) ↓ | RMSE of Slope (°) ↓ | RMSE of Aspect (°) ↓ | SSIM ↑ | |
|---|---|---|---|---|---|---|---|
| I | ✓ | 13.90 | 4.91 | 65.74 | 0.972 | ||
| II | ✓ | 13.79 | 4.88 | 65.53 | 0.973 | ||
| III | ✓ | 13.93 | 4.92 | 66.11 | 0.973 | ||
| IV | ✓ | ✓ | 13.76 | 4.87 | 65.65 | 0.973 | |
| V | ✓ | ✓ | 13.84 | 4.90 | 65.55 | 0.973 | |
| VI | ✓ | ✓ | 13.76 | 4.87 | 65.51 | 0.973 | |
| VII | ✓ | ✓ | ✓ | 13.48 | 4.81 | 64.97 | 0.973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Wu, J.; Wang, Y. FTT: A Frequency-Aware Texture Matching Transformer for Digital Bathymetry Model Super-Resolution. J. Mar. Sci. Eng. 2025, 13, 1365. https://doi.org/10.3390/jmse13071365
Xiao P, Wu J, Wang Y. FTT: A Frequency-Aware Texture Matching Transformer for Digital Bathymetry Model Super-Resolution. Journal of Marine Science and Engineering. 2025; 13(7):1365. https://doi.org/10.3390/jmse13071365
Chicago/Turabian StyleXiao, Peikun, Jianping Wu, and Yingjie Wang. 2025. "FTT: A Frequency-Aware Texture Matching Transformer for Digital Bathymetry Model Super-Resolution" Journal of Marine Science and Engineering 13, no. 7: 1365. https://doi.org/10.3390/jmse13071365
APA StyleXiao, P., Wu, J., & Wang, Y. (2025). FTT: A Frequency-Aware Texture Matching Transformer for Digital Bathymetry Model Super-Resolution. Journal of Marine Science and Engineering, 13(7), 1365. https://doi.org/10.3390/jmse13071365






