Abstract
Underwater explosion ice-breaking technology is critical for Arctic development and ice disaster prevention due to its high efficiency, yet it faces challenges in understanding the coupled dynamics of shock waves, pulsating bubbles, and heterogeneous ice fracture. This review synthesizes theoretical models, experimental studies, and numerical simulations investigating damage mechanisms. Key findings establish that shock waves initiate brittle fracture via stress superposition while bubble pulsation drives crack propagation through pressure oscillation; optimal ice fragmentation depends critically on charge weight, standoff distance, and ice thickness. However, significant limitations persist in modeling sea ice heterogeneity, experimental replication of polar conditions, and computational efficiency. Future advancements require multiscale fluid–structure interaction models integrating brine migration effects, enhanced experimental diagnostics for transient processes, and optimized numerical algorithms to enable reliable predictions for engineering applications.
1. Introduction
The Arctic region harbors abundant resources of global strategic significance. Its hydrocarbon reserves constitute approximately 20% to 32% of the global marine gas hydrate resources [1], while its coal deposits exceed the world’s total proven reserves [2]. For decades, the immense mineral resource potential and development prospects of the Arctic have remained a central focus of global geopolitics and economics [3,4,5]. Accelerated melting of the Arctic ice cap, driven by global climate change, has expanded the region’s strategic significance beyond mere resource endowment to encompass geostrategic transit corridors. Currently, both the Northern Sea Route and the Northwest Passage are commercially navigable during summer months. Research and practical experience demonstrate that utilizing Arctic shipping routes can reduce voyage distances by up to 40% and significantly lower transportation costs by approximately 30% compared to traditional routes (e.g., the Suez Canal route) [6]. This unlocking of navigational potential positions Arctic routes as a critical variable in reshaping global trade patterns and geopolitical dynamics, with their strategic importance becoming increasingly pronounced [7]. Against this backdrop, competition among circumpolar states for strategic dominance has intensified. Consequently, highly efficient and reliable ice-breaking technology has become an indispensable core capability for securing critical shipping lanes, supporting sustainable polar resource development, and ensuring operational mobility. However, conventional ice-breaking techniques, such as icebreaker propulsion and mechanical ice-breaking, face limitations including slow response times and low energy efficiency. These shortcomings render them inadequate for meeting the demands of precise resource extraction in polar regions, efficient waterway maintenance, and the rapid deployment of infrastructure. In contrast, underwater explosion ice-breaking technology has become the research focus in the field of Polar Engineering and ice disaster prevention due to its high energy efficiency ratio and fast response characteristics [8,9].
In summary, given the Arctic’s escalating strategic value and its criticality across multiple dimensions—resources, shipping lanes, and security—in-depth research and the advancement of sophisticated underwater explosion ice-breaking technology hold substantial scientific and engineering significance. Moreover, they represent an urgent imperative directly relevant to national strategic interests and the evolving landscape of international competition.
The coupled effects of shock wave loading and bubble loading on the dynamic damage of ice layers constitute the core scientific problem in underwater explosion ice-breaking research [10,11,12]. As illustrated in Figure 1, the underwater explosion ice-breaking process can be divided into four distinct phases. During the initial explosion phase, the shock wave, acting as the dominant load, reaches the underside of the ice layer. Due to its extremely high peak pressure, the underwater explosion shock wave rapidly transforms into a compressive stress wave upon interacting with the ice–water interface. As the stress wave propagates through the ice layer, tensile stresses develop. When the tensile stress exceeds the tensile strength of the ice, radial and circumferential cracks initiate. Subsequent damage to the ice layer is primarily induced by bubble pulsation. The expansion of the bubble drives an upward surge of water, subjecting the ice layer to significant tensile stresses. This tensile loading causes pre-existing cracks to propagate further. As the bubble continues to expand, a prominent water jet forms, imposing continued tensile and shear stresses on the ice, leading to progressive damage. Upon sufficient degradation of the ice layer’s integrity, the water jet penetrates and erupts through the ice surface, resulting in the ice root breaking. Concurrently, the bubble begins to shrink, forming the bubble jet and moving towards the bottom of the water. Following bubble pulsation, the ultimate collapse of the bubble occurs. The collapse phase will absorb the ice layer moving downward, causing further damage to it. Moreover, it is noteworthy that localized disturbances induced by underwater explosions can excite hydroelastic surface waves that propagate radially from the blast zone, generating large-scale dynamic loading. Numerical simulations by Guyenne and Parau [13] demonstrate that localized pressure distributions acting on ice covers generate large-amplitude nonlinear hydroelastic solitary waves, which propagate stably while imposing cyclic stresses on the ice. Furthermore, Guyenne et al. [14] reveal that compressive stresses within ice sheets—compared to bending stresses—exhibit stronger wave-focusing effects, significantly amplifying hydroelastic wave amplitudes to levels capable of direct ice fracture. This persistent fatigue mechanism drives secondary fracturing beyond the initial blast region, thereby extending the overall ice-breaking range. Consequently, the propagation and evolution of hydroelastic waves represent a fifth phase in the underwater explosion ice-breaking process, whose role in exacerbating ice fatigue damage becomes particularly critical under diminishing Arctic ice stability due to climate change.
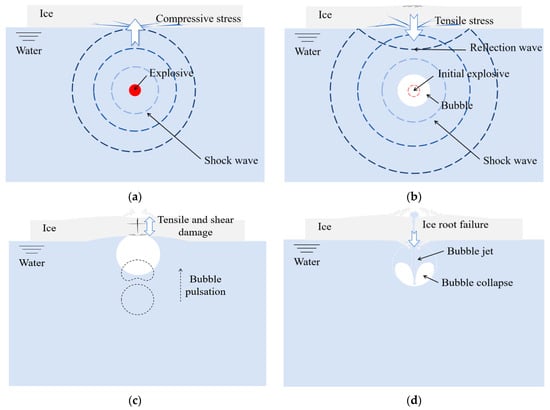
Figure 1.
Sketch of underwater explosion ice-breaking process: (a) shock wave compression loading and initial ice damage; (b) tensile stress and crack initiation induced by reflection waves; (c) crack propagation and water spike evolution driven by bubble pulsation; (d) jet impact and suction damage during bubble collapse.
Furthermore, the mechanical properties of sea ice exhibit marked temperature dependence [15,16,17]. As shown in Figure 2, temperature significantly influences the tensile strength and elastic modulus of sea ice. The elastic modulus data presented in Figure 2b were obtained from three-point bending tests conducted at strain rates ranging from approximately 0.03 to 1.65 MPa/s [16]. This corresponds to an estimated loading frequency range of 0.03–1.7 Hz, characteristic of quasi-static conditions. Recent work by Marchenko [18] demonstrates that the elastic modulus of sea ice exhibits significant frequency dependence, particularly within the 10–500 Hz range, where E may increase by up to 60% due to viscoelastic effects. This frequency sensitivity is intrinsically linked to strain-rate-dependent mechanical behavior. Consequently, the E relationship shown in Figure 2b reflects low-frequency measurements, and higher loading rates would yield substantially elevated modulus values. The observed scatter in data points and discrepancies among empirical E formulations may be partially attributed to variations in effective strain rates across different experimental methodologies, as systematically compared in Figure 18 of Marchenko [18]. As a non-homogeneous brittle material, the damage process in ice demonstrates pronounced anisotropy and strain rate sensitivity [19,20,21]. These characteristics further complicate the fluid–structure interaction (FSI) mechanism between the explosion loading and the ice response.
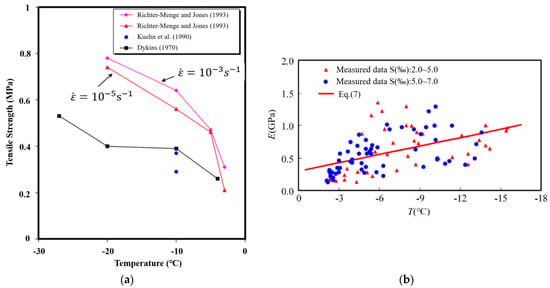
Figure 2.
Effect of temperature on partial mechanical properties of sea ice: (a) effect of temperature on tensile strength of sea ice [15] (Data sources: Richter-Menge and Jones 1993 [22], Kuehn et al., 1990 [23], Dykins 1967/1968 [24,25] via [15]; Figure labels Dykins (1970) as published in [15]); (b) effect of temperature on elastic modulus of sea ice [16]. Note: Ji et al. tested the strain rate range (0.03–1.65 MPa/s), where the elastic modulus has no strain rate dependence.
Underwater explosion ice-breaking, as an efficient method for ice fragmentation, relies heavily on the synergistic advancement of three primary research methodologies: theoretical analysis, experimental measurement, and numerical simulation. These approaches are interdependent and mutually validating, collectively forming a research framework for understanding the complex physical processes involved. However, each possesses inherent limitations.
Theoretical research focuses on elucidating fundamental physical mechanisms, aiming to establish quantitative relationships between critical parameters (e.g., charge weight, water depth, standoff distance, and ice thickness) and ice-breaking outcomes (e.g., damage extent and crater radius). Such theoretical frameworks heavily rely on experimental data for both hypothesis validation and model calibration. For instance, Barash [26] and Mellor [27] developed a predictive formula for ice damage extent based on systematic test data. Liu et al. [28] formulated a theoretical model for crater radius, demonstrating excellent agreement with measurements (mean relative error < 8.5%). These models provide essential foundations for explosion parameter design and safety zone demarcation. Theoretical complexity is significantly amplified by the unique properties of sea ice. The proportional distribution of ice with closed brine pockets (ICPs, which refer to brine pockets enclosed within the ice matrix) and liquid brine in permeable channels (BPCs, which constitute a connected pore network allowing brine flow under pressure gradients) varies with temperature, profoundly influencing the macroscopic mechanical properties of sea ice. Based on this, Marchenko and Lishman [29] established a thermoelastic model coupling phase transitions and brine migration mechanisms. This model systematically investigated the impact of brine phase distribution on thermal expansion and thermoelastic wave propagation, providing a key theoretical framework for understanding ice response under thermo-mechanical coupling loads.
Experimental measurement provides the most direct means for validating theoretical hypotheses and quantifying ice damage patterns and extent while serving as a primary source for computational model parameters. Orlova [30] demonstrated that under 4 kg emulsion explosive loading, a burial depth of 130 cm maximizes ice damage extent (41.7%) and ice channel diameter (156 cm), recommending mid-ice explosive placement for optimal fragmentation efficacy. Subsequent studies [31,32] determined that underwater explosion has higher ice-breaking efficiency than other explosive detonation locations. Therefore, underwater explosion ice-breaking has gradually become the mainstream research direction. Separately, Orlov [33] examined the effect of ice formation temperature on damage outcomes, revealing that lower temperatures enhance ice strength, thereby reducing the diameter of ice channels after explosions and altering debris size distributions. Through orthogonal experimental method and the gray system theory, Wang et al. [34] quantified key influencing factors in descending order of significance: standoff distance > charge weight > ice thickness. However, full-scale explosion ice-breaking experiments face inherent challenges such as high cost, poor repeatability, and high risk, which seriously restrict the systematic accumulation of data and mechanistic investigation. Cui et al. [35] first systematically studied the interaction between collapsing bubbles and ice layers. Subsequent research [36,37] delved into the interactions and ice-breaking effects of bubble pairs and multiple bubbles, particularly focusing on the shock wave-induced ice damage mechanism. These studies suggest that leveraging bubble collapse characteristics to design efficient, directional ice-breaking schemes holds promise as a revolutionary technological approach.
With the advent of efficient computational technologies, numerical methods have become increasingly adept at addressing a wide array of complex physical problems, multiphase coupling issues, and large-scale model calculations. In the specific domain of underwater explosion ice-breaking, numerical simulation plays a pivotal role in understanding and predicting the intricate interactions between shock waves, bubble pulsations, and the mechanical properties of ice. Mansur and Sereg [38], based on the principle of the finite element method (FEM), developed a computer simulation program to investigate ice-breaking by impulsive loading. Meng et al. [39] used LS-DYNA numerical simulation and shaped charge technology to research the 20 cm thick ice failure characteristics when under a certain amount of TNT underwater explosion, and finally determined the optimal explosion point. However, the FEM is difficult to use to accurately predict the location of cracks [40]. Orlov et al. [41] summarized the experimental and numerical research results of ice destruction under explosion loading and proposed a solid mechanics numerical model for studying modern multi-impact deformation events. This provides a new approach for extracting the crack surface of materials. Furthermore, meshfree particle methods provide an effective approach for addressing ice fragmentation and structural damage caused by explosion loading. Smooth particle hydrodynamics (SPH) has been widely applied in numerical simulation research of underwater explosions [42,43,44,45].
In summary, theoretical research, experimental techniques, and numerical simulation collectively advance underwater explosion ice-breaking technology. These approaches are complementary: theoretical models elucidate fundamental physics and guide engineering design; experiments provide validation benchmarks and critical empirical data; and numerical simulation enables the efficient replication of complex scenarios while overcoming experimental constraints. However, significant challenges remain in fulfilling these core functions. Theoretical models lack precision in characterizing complex multiphysics processes within sea ice. Experimental methods face challenges in recreating extreme environments, achieving high-precision dynamic parameter measurements, and controlling costs and safety risks. Numerical techniques require improvements in computational efficiency, multiphysics coupling model accuracy, and predictive capability for failure modes. Future research necessitates a tighter integration of these three methodologies, focusing on overcoming traditional experimental bottlenecks and enhancing the predictive accuracy of numerical models for complex ice damage and failure mechanisms. To address these imperatives, this paper reviews research advances in underwater explosion ice-breaking from theoretical, experimental, and numerical perspectives, providing theoretical and technical references for studying ice structure damage under explosion loading.
2. Theoretical Research
Ice-breaking by underwater explosion (UNDEX) is essentially the dynamic fracture behavior of the ice–water–air three-phase medium under transient multiphysics field coupling. Its theoretical framework covers microsecond-level high-strain-rate loads dominated by shock waves, millisecond-level low-frequency dynamic pressure fields induced by bubble pulsation, and sub-millisecond-level local secondary impacts caused by cavitation collapse. The above-mentioned multiphysics fields interact with the strain rate sensitive and anisotropic damage characteristics of the ice layer through a bidirectional FSI mechanism [46,47,48,49]. Therefore, the study of ice-breaking by underwater explosion requires the establishment of a theoretical framework that couples multiple physical fields to reveal the intrinsic relationship between explosion energy transfer, ice dynamic response, and damage threshold.
This section first starts with the spatiotemporal evolution law of UNDEX loading (Section 2.1), and then combines with the unique mechanical properties of ice to introduce the damage characteristics of ice layers under UNDEX loading (Section 2.2), forming a complete theoretical chain from load input to material failure.
2.1. Mathematical Models
Mathematical modeling is fundamental for quantifying the complex multiphysics processes in underwater explosion ice-breaking, including fluid–structure interaction (FSI), fracture of heterogeneous ice, and the propagation of secondary phenomena like hydroelastic waves. This section provides a categorized overview of key models used in this field, focusing on those describing ice damage, fracture mechanics, and wave–ice interaction.
Table 1 summarizes key mathematical models employed in underwater explosion ice-breaking research, with emphasis on ice fracture prediction and wave–ice interaction. The core formulations, specific applications within the context of ice-breaking, and inherent limitations of these selected models will be elaborated in the following subsections. While models describing shock wave propagation and bubble dynamics (e.g., Cole [50], Zamyshlyayev and Yakovlev [51], Rayleigh–Plesset equation [52,53], Keller–Miksis equation [54], Zhang et al. [55]) are critical for characterizing the initial UNDEX loading, their detailed formulations fall outside the immediate focus on ice response and fracture mechanisms covered here.

Table 1.
Key mathematical models for underwater explosion ice-breaking analysis.
2.2. UNDEX Loading
The theoretical research on UNDEX loading has long focused on the two core physical processes of shock waves and bubble pulsation. After decades of development, it has formed a complete system from empirical formulas to multifield coupling models.
The physics of underwater explosion shock waves governs ice-breaking efficiency through three interrelated physical processes. First, upon detonation, chemical energy conversion generates a high-pressure gas bubble that radially compresses the surrounding water, producing a shock wave characterized by exponential temporal decay with spatial attenuation governed by exponent n. Subsequently, when the shock wave impinges on the ice–water interface, the acoustic impedance mismatch between water and ice induces partial wave reflection. This converts compressive waves into tensile stress waves within the ice layer. Consequently, due to the significantly lower tensile strength of ice compared to compressive strength within the temperature range of −10 °C to −20 °C [59], the resulting tensile stress can cause brittle fracture, which is the main ice-breaking mechanism. These principles underpin classical empirical models and inform damage thresholds analyzed in Section 2.3.
Early research mainly focused on shock wave loads. Cole [46] established a shock wave overpressure index attenuation model and an empirical formula for the maximum radius of bubbles through systematic experiments. Their far-field prediction error was less than 5%, laying the foundation for engineering prediction. The book “Underwater Explosion” is still recognized as a classic, authoritative work today. Zamyshlyayev and Yakovlev [51] introduced a boundary reflection correction factor based on Cole’s research, further establishing an analytical formula for pressure waves in water containing bubble pulsation processes, and providing an empirical formula for near-field UNDEX loading. The book “Dynamic Load in Underwater Explosion” has become another authoritative work. The response problem of underwater explosion shock wave loads interacting with simple structures such as plates has also been extensively studied [60,61,62,63,64]. However, the propagation characteristics of near-field shock waves still lack a universal theoretical description due to their strong discontinuity and strong nonlinearity.
At the initial stage of an explosion, the shock wave pressure attenuation follows the empirical formula [50,51]:
For a TNT spherical charge, the empirical formula for the initial pressure peak of the shock wave is as follows:
In the above equation, is the pressure change in the underwater explosion shock wave with time; is the initial pressure peak of the shock wave; is the exponential time attenuation constant of the shock wave, that is, the time required for the shock wave pressure peak to decay to ; is the shock wave action time; is the shock wave barotropic time; is the charge amount; is the standoff distance; and is the spherical charge radius. The value of is used to define the near-field and far-field underwater explosion, where less than 12 is the near-field explosion, and more than or equal to 12 is the far-field explosion.
In the field of bubble dynamics research, Besant [65] first described the flow field characteristics during the spherical pulsation process of bubbles through sources and sinks. Rayleigh [52] and Plesset [53] established the Rayleigh–Plesset equation for spherical bubbles in incompressible fluid, laying the foundation for subsequent theoretical development. However, the model can not deal with complex coupling problems such as phase transition, migration, compressibility, boundary effect, and so on at the same time. Subsequently, scholars studied spherical bubbles in a compressible liquid, attempting to address the limitations of the Rayleigh–Plesset equation and considering the effects of surface tension and viscosity [66,67]. The Keller–Kolodner equation [68] solved the problem of traditional models being unable to predict damping oscillations, while the Keller–Miksis equation [54] constructed a more universal bubble dynamics model based on this, which can simultaneously describe the dynamic behavior of macroscopic explosion bubbles and microscopic cavitation bubbles. Prosperetti and Lezzi [69,70] proposed first-order and second-order theoretical models for bubble dynamics. Storey and Szeri [71] proposed a simplified model of a single bubble collapse, which considers phase change, mass diffusion, heat diffusion, and chemical reactions. Zhang et al. [72] established a new dynamic theory of oscillating bubbles, which achieved the unification of classical bubble theories such as the Rayleigh–Plesset equation, the Gilmore equation, and the Keller–Miksis equation. Presently, Equation (3) proposed by Zhang et al. [55] is the latest progress in bubble dynamics research. The formula significantly improves the prediction accuracy of bubble dynamics by unifying the multiphysical coupling effects (e.g., phase transition, migration, fluid compressibility, etc.) for the first time, reveals the nonlinear mechanism of the coordinated regulation of energy loss and pressure radiation by steam ratio and fluid compressibility, and provides a universal theoretical framework for engineering problems such as explosion and cavitation.
In the equation, is the sound speed, is the bubble radius, denotes the time derivative of , denotes the second derivative of , is the net evaporation rate of mass per unit area of the bubble surface, and is the liquid density; the normal velocity of fluids at the bubble surface is , the relative velocity vector v represents the velocity difference between the bubble migration velocity and the ambient flow velocity , is the enthalpy difference at the bubble surface, and its leading order term can be expressed as , where represents the ambient pressure at the bubble center, and denotes the liquid pressure at the bubble surface.
With the deepening of research, scholars have found that buoyancy has a significant effect on the large-scale bubbles generated by underwater explosions. Therefore, they have begun to consider the influence of buoyancy on bubbles. Wilkerson [73] proposed a boundary integral formulation for numerical calculation of bubbles’ expansion and collapse in underwater explosions. Klaseboer and Khoo [74] based on the Rayleigh–Plesset equation, an equivalent bubble radius and an equivalent bubble wall velocity were introduced, extending the analytical solution of the equation to the much more general (non-spherically symmetric) bubble configuration. Liu et al. [75] systematically investigated the pressure characteristics of non-spherical underwater explosion bubbles in a compressible fluid using an improved boundary element method (BEM) combined with an auxiliary function model. Their study revealed the significant influence of fluid compressibility on multiperiod pulsating pressures and jet impact dynamics, and identified a critical bubble–wall distance to avoid bubble splitting. Figure 3 visually demonstrates the marked differences in bubble pressure peaks and attenuation caused by compressibility, validating the necessity of accounting for compressibility in pressure calculations.
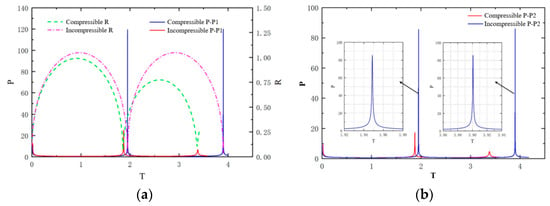
Figure 3.
Comparisons of bubble radius and pressures at the measurement points in compressible and incompressible flow fields for two bubble pulsation periods: (a) comparisons of bubble equivalent radii and pressures at P1 (2, 0) and (b) comparison of the pressures at P2 (2, 2) [75].
However, the current theoretical framework has significant bottlenecks in describing multiphase coupled dynamic processes. Firstly, there is a lack of accurate characterization of the dynamic mixing mechanism of water vapor and non-condensable gases inside bubbles, as well as the phase change mass transfer process. The existing models are difficult to use to quantify the nonlinear effects of gas vapor ratio changes on key parameters such as pulse frequency and energy dissipation rate. Especially under the boundary conditions of ice water gas three-phase coupling, overly simplified thermodynamic closure assumptions (such as isothermal and adiabatic conditions) further exacerbate prediction bias. Secondly, the theoretical system generally relies on the assumption of spherical bubbles, ignoring non-spherical distortions such as bubble jets and annular collapse caused by near-field fluid structure coupling and non-uniform constraints of ice layers in actual working conditions, resulting in the inability to analyze the spatiotemporal distribution characteristics of collapsed jet loads. Jet impact is precisely one of the dominant mechanical mechanisms of ice layer fracture. The above defects seriously restrict the applicability of theoretical models in predicting the ice-breaking efficiency of polar engineering. These limitations in modeling the loading dynamics directly impact the accuracy of predicting the resulting ice damage, which is examined next.
2.3. The Damage Characteristics of Ice Layers Under UNDEX Loading
At present, the research on the damage effects of underwater explosions on ice layers mainly considers the shock wave and bubble pulsation loads. Based on the latest progress in the mechanical properties of ice layers, this section preliminarily explores the ice-breaking mechanism of shock waves and bubble pulsation loads in order to provide some reference for the damage mechanism of ice layers under the action of multiple physical fields.
The core mechanism of ice-breaking by UNDEX technology is the time–space coupling effect of shock wave and bubble pulsation loads. The mechanical properties of ice, particularly its tensile strength being merely 1/5 to 1/10 of its compressive strength, fundamentally govern its susceptibility to shockwave-induced fracture [76]. Shockwaves generated by underwater explosions exhibit extreme characteristics, including GPa-level peak pressures and microsecond-scale transient action. Bubble pulsation generates low-frequency pressure oscillations with a second-level cycle, forming jets and secondary shock waves through periodic expansion and contraction, leading to fatigue damage to the ice layer.
To the best of the authors’ knowledge, there is a lack of theoretical research on UNDEX ice-breaking due to the strong nonlinear interactions. Vazic B et al. [77,78,79] used peridynamics, a non-local continuum mechanics formula, to analyze the failure of materials. They enabled cracks to occur naturally in the formula without imposing any external crack propagation laws. A theoretical method based on the elastic vibration theory was proposed to analyze the dynamic response of the icecap plate structure under the explosion loading [80]. And it was found that the bottleneck shape of the crater is identical to the blasting phenomenon of general brittle material. Due to the significantly lower tensile strength of ice compared to its compressive strength, this characteristic is consistent with typical brittle materials such as glass and ceramics. And under high-strain-rate loads such as explosion shock waves, the ice layer directly undergoes brittle fracture, and there is no obvious plastic deformation during the crack propagation process [15,81,82]. Therefore, the study of the damage characteristics of ice layers under explosion loading can refer to the damage characteristics of brittle materials under explosion loading. Wang et al. [56] used a regression method to establish Equation (4) representing the relationship between the radius of blasting craters and ice thickness, charge weight, and water depth below the ice layer. This equation is applicable to both natural rivers with a thin ice layer and shallow rivers with a thick ice layer, with an average relative error between the predicted and measured values was no more than 8.5%.
In this equation, is the scaled blasting crater radius; is the charge weight; is the ice thickness; and is the water depth.
Underwater explosion ice-breaking technology demonstrates practical utility in engineering applications. However, its theoretical underpinnings lag significantly behind operational requirements. This fundamental limitation stems from an incomplete understanding and oversimplified modeling of the complex underlying physics. Specifically, the current theoretical frameworks inadequately characterize key properties of sea ice. Prevalent models simplistically treat ice as a homogeneous elastic solid, disregarding the heterogeneous microstructure of polar sea ice constituted by ICPs and BPCs. These models fail to account for the dynamic evolution of permeability with brine volume fraction and lack consideration of interaction mechanisms between pore gases within the ice and the explosion-generated bubble. Furthermore, theoretical formulations excessively simplify dynamic processes, neglecting critical aspects such as the rheological behavior of ice at high strain rates and the influence of sea ice’s negative thermal expansion characteristics on thermally induced stresses. Consequently, refining the existing theoretical models is imperative to more accurately characterize the heterogeneity of sea ice and its dynamic response during explosive events. Simultaneously, physical models describing blast wave propagation, attenuation, and ice interaction must incorporate pre-existing defects inherent in natural ice—including gas pores, microcracks, and stratified layering—along with their evolution under shock loading. This integration is essential to elucidate the critical mechanisms through which these defects influence ice-breaking efficiency.
3. Experimental Research
Underwater explosion ice-breaking experiments provide critical validation data for investigating the dynamic fracture mechanisms of ice–water–air multiphase media under transient multiphysics strong coupling effects. To overcome the limitations of conventional single-paradigm experimental approaches, this section establishes a dual-track research framework integrating “engineering validation and mechanistic complementarity”. The experimental system was categorized into field explosion experiments (Section 3.1) and mechanistic model experiments (Section 3.2) for comprehensive analysis. Through the two-way verification of full-scale experiments and small-scale experiments, a comprehensive research chain covering explosion energy transfer, ice dynamic response, and failure threshold was constructed, aiming to serve the refined reconstruction of multi-scale theoretical models for underwater explosion ice-breaking and the optimized design of polar ice-breaking engineering technologies.
3.1. Full-Scale Explosion Experiments
Full-scale explosion experiments serve as the critical validation bridge connecting theoretical research with engineering applications in underwater explosion ice-breaking. The central scientific challenge lies in elucidating the dynamic coupling mechanisms between explosive multiphysics and strain-rate-sensitive damage evolution in ice media. This section reviews the underwater explosion ice-breaking experiment based on a progressive research framework of single-charge parameter study to multi-charge synergistic enhancement. The analysis reveals the regulatory effects of explosion parameters such as charge weight, standoff distance, detonation depth, and the superposition effect of energy field on ice damage patterns, aiming to provide reproducible and adjustable explosive parameter design criteria for polar ice-breaking operations and ice disaster prevention.
Systematic research on underwater explosion ice-breaking originated in the mid-20th century, primarily driven by polar development and military demands. Lyon [24] conducted the first systematic evaluation of ice-breaking efficiency in Arctic sea ice operations, comparing three detonation methods: surface-laid, tamped, and under-ice. Key findings demonstrated that tamped charges significantly outperformed surface detonations in ice-breaking efficiency, while under-ice explosions generated exponentially greater radial damage. Subsequently, underwater explosions gradually became the mainstream technology for explosion ice-breaking. Through integrated numerical simulation and field experiments, Liang et al. [83] and Xie et al. [84] quantitatively substantiated the energy transfer superiority of shockwave-bubble coupled loading mechanisms in water media, thereby consolidating the hydrodynamic foundations of modern underwater explosion ice-breaking technology.
Single-charge ice-breaking experiments primarily focus on analyzing the influence of explosion parameters and ice thickness on ice-breaking effectiveness. Barash [26] conducted extensive underwater explosion ice-breaking experiments to investigate the effects of charge weight, standoff distance, and ice thickness, revealing that both optimal standoff distance and ice-breaking radius increased linearly with the increase in charge weight. Mellor [27,85] systematically analyzed the relationships between ice-breaking radius and charge weight, standoff distance, and ice thickness through dimensionless analysis and regression modeling of historical experimental data, ultimately deriving empirical formulas for ice-breaking radius prediction. Wu et al. [86] measured the underwater shock wave pressure caused by a large equivalent underwater explosion through ice-breaking experiments and obtained the optimal combination design of charge weight and detonation depth. Zhang et al. [87] conducted a comprehensive experiment on explosion ice-breaking, demonstrating that the optimal standoff distance ranges between 0.3 and 0.45 times ice thickness based on quantitative correlations between the standoff distance and the breaking area of the ice surface. Zhang et al. [88] conducted underwater explosion ice-breaking experiments in the Dengkou section of the Yellow River and summarized the relationship between charge submersion depth, charge weight, and ice-breaking volume parameters. Wang et al. [34] implemented maritime explosion ice-breaking experiments, applying the gray system theory to calculate correlation coefficients between ice-breaking radius and three critical parameters (charge weight, standoff distance, and ice thickness), thereby proposing a novel optimization framework for underwater explosion ice-breaking parameters.
Multi-charge collaborative ice-breaking experiments have elucidated nonlinear mechanisms governing energy field superposition and crack network evolution through controlled variables including temporal sequencing, spatial distribution, and phase difference. Kurtz et al. [89] expanded the research of underwater explosion ice-breaking from the single-charge effect to the multi-charge synergy field, and revealed the stress wave superposition mechanism of multi-charge collaborative ice-breaking through three groups of comparative experiments of underwater explosion. Their research results show that when the distance between adjacent charges was less than or equal to twice the damage radius of a single charge, the superposition of explosive stress waves generated a continuous interconnected fracture zone, expanding the damage range by over 40% compared to single-charge detonation. Van der Kley [90] developed the stratified blasting method, while Nikolayev [91] proposed the direct blasting technique, both achieving directional energy focusing through the sequential detonation of differential-weight charges. Liang et al. [92] executed comprehensive ice-breaking trials beneath thick ice layers in the Yellow River basin, analyzing shock wave velocity, pressure characteristics, and fracture mechanisms to establish a multi-charge synergistic ice-breaking framework. Wang et al. [56] conducted multi-point explosion field experiments in the Heilongjiang River section and obtained several typical ice failure patterns as shown in Figure 4.

Figure 4.
Typical blasting crater types and post-blasting features: (a) mountain-shaped; (b) standard; (c) fully broken; (d) post-blasting ice cracks (width: 10 cm, depth: 35 cm). Note: The inclination toward the crack center may result from radial debris displacement or snow cover; no slope measurement was reported in the source study [56].
Despite over a century of development in underwater explosion ice-breaking [93], its research progress is still constrained by multiple factors. Firstly, there are significant technical bottlenecks in experimental observation and theoretical verification: limited by traditional measurement methods, it is difficult to accurately capture the propagation characteristics of stress waves and the details of ice layer crack propagation during the explosion process, resulting in an insufficient analysis of damage mechanisms. Meanwhile, the high cost and safety risks of large-yield explosive experiments further limit the depth and breadth of systematic research [94,95]. Secondly, the environmental universality of the existing research is insufficient: most conclusions are based on river ice layers (usually less than 1.5 m thick) and shallow water conditions, and the adaptability to polar thick ice (>3 m), high-salinity sea ice, and complex ice–water–air coupling boundaries has not been fully validated, making it difficult to support practical needs such as Arctic navigation development. Thirdly, there is an urgent need for breakthroughs in multi-charge collaborative ice-breaking technology: although experiments on multi-charge collaborative ice-breaking have revealed the superposition effect of energy fields, the existing technologies are difficult to use to achieve precise matching between microsecond-level temporal control and ice layer dynamic response, resulting in significant fluctuations in energy focusing efficiency. In addition, the influence of multi-charge spatial configurations (such as linear arrays and circular distributions) on the fractal characteristics of cracks lacks theoretical model support, and engineering practice still relies on empirical parameter adjustments. Finally, the ecological impact assessment system is weak: research on the damage mechanism of explosion shock waves to aquatic organisms mostly focuses on short-term effects [96], neglecting chronic damage to organs such as the liver and kidneys, as well as sensitivity differences among different species. Meanwhile, the lack of long-term ecological monitoring data and the unquantifiable cumulative toxic effects of explosive residues (such as TNT) on polar ecosystems have hindered the development of green ice-breaking technologies.
In response to the above issues, in the future, machine learning and adaptive control algorithms can be used to develop an adaptive matching model for charge weight–standoff distance–ice thickness, which can improve the adaptability to complex ice conditions. Focusing on green ice-breaking technology, exploring the synergistic application of low-weight charge and energy-focusing technology can help us reduce the impact of explosive residues on polar ecosystems. Establishing a biodiversity tracking database after an underwater explosion ice-breaking to quantify long-term ecological effects is also important. Through the collaborative innovation of theory, technology, and ecology, we aim to promote the next generation of precise, controllable, and environmentally friendly technologies for underwater explosion ice-breaking, providing reliable support for polar development and ice disaster prevention.
3.2. Small-Scale Mechanism Experiment
As a pivotal discipline in polar engineering and ice disaster prevention, the study of underwater explosion mechanisms fundamentally relies on the precise characterization of multiphysics coupling effects in explosion loading. While conventional full-scale field explosion ice-breaking experiments can replicate authentic operational scenarios, their high cost, safety risks, and difficulty in capturing dynamic parameters severely restrict systematic investigations into damage evolution mechanisms. Additional experimental uncertainties arise from water turbidity, ambient light interference, and ice layer heterogeneity. In recent years, the concept of using underwater high-pressure bubbles to break ice has also been proposed [97], and the scientific community has developed small-scale experimental techniques including electric-spark-generated bubble and high-pressure air-gun bubble ice-breaking simulations, enabling the high-resolution analysis of explosive energy transfer, bubble dynamics, and ice–water coupling interactions.
This technique employs high-voltage pulsed discharge to generate cavitation bubbles in water, utilizing shockwaves and jet energy from bubble pulsation and collapse to fracture ice layers. Compared to traditional explosive methods, it offers superior controllability, reduced environmental risks, and enhanced experimental repeatability, garnering significant attention in polar engineering and ice disaster prevention.
Cui et al. [35] conducted electric-spark-generated bubble ice-breaking experiments in glass water tanks, systematically revealing the dynamic interaction mechanisms between shockwaves and ice layers during bubble collapse. Figure 5 illustrates ice fracture patterns under large bubble–ice standoff distances, with visualization confirming shockwave reflection as the dominant fracture mechanism.

Figure 5.
High-speed image of a bubble collapse under a 20 mm-thick ice layer: (a) side view; (b) bottom view. Scale bars, 10 mm [35].
Yuan et al. [98] conducted electric-spark-generated bubble experiments in a water tank in a cold room, combined with high-speed cameras and new observation techniques, and revealed three typical patterns of ice damage caused by bubble collapse, as shown in Figure 6, including crevasse pattern, radial and circumferential cracks pattern, and radial cracks pattern. Figure 7 further presents the relationship between these three ice-breaking patterns and dimensionless parameters (bubble–ice standoff distance γ, hole radius λ, and ice thickness τ).
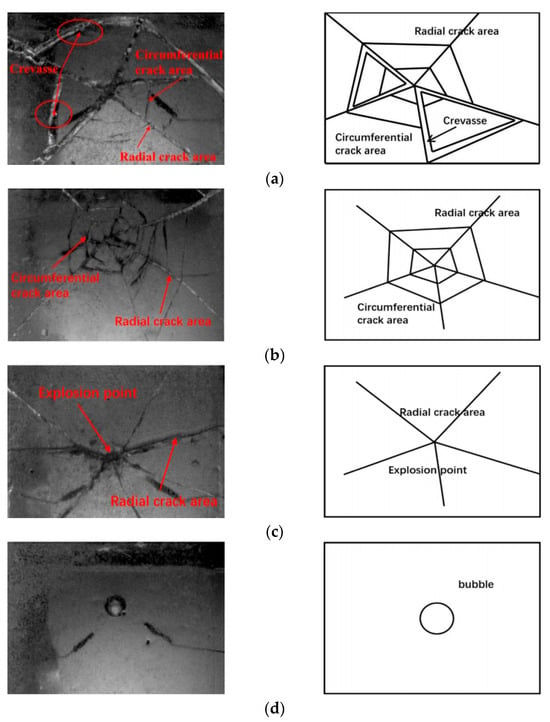
Figure 6.
Typical damage patterns of the ice under bubble loads with sketch maps: (a) crevasse pattern; (b) radial and circumferential cracks pattern; (c) radial cracks pattern; (d) no cracks [98]. Schematic representation (not to scale).
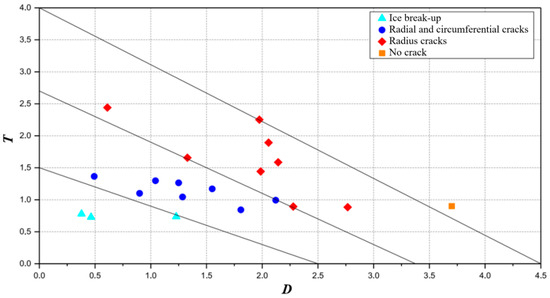
Figure 7.
Damage patterns of the ice depending on the distance parameter and thickness parameter [98].
Ni et al. [99] studied the interaction between electric-spark-generated bubbles and perforated ice layers through experiments. Research has found that compared to intact ice layers with the same parameters, ice layers with a hole were easier to be cracked by the initial shock wave with bubble generation. Figure 8 clearly illustrates three typical ice-breaking patterns, revealing the unique response mechanism of perforated ice layers under specific conditions by comparing the rupture patterns under different parameter combinations.

Figure 8.
Diagram of three typical crack patterns: (a) initial radial cracks and subsequent circumferential cracks/radial cracks; (b) no initial cracks and subsequent radial cracks; (c) initial radial cracks with no subsequent cracks, with side view in the right figure [99]. Schematic representation (not to scale).
Cui et al. [37] generated four in-phase pulsating bubbles through underwater electric discharge and employed high-speed photography combined with shadowgraph imaging to observe phenomena such as non-spherical collapse, splitting, and coalescence of multiple bubbles beneath an ice layer. The study systematically investigated the interaction of multiple bubbles and their damage effects on the ice layer. Figure 9 visually illustrates the fracture patterns and characteristics of the ice layer under different bubble configurations. The results demonstrate that vertically aligned bubbles concentrate shock waves at the ice layer’s center, generating radial cracks, whereas horizontally aligned bubbles induce dominant transverse fractures. This work highlights the critical role of bubble arrangement in ice-breaking efficiency and dynamic load distribution.
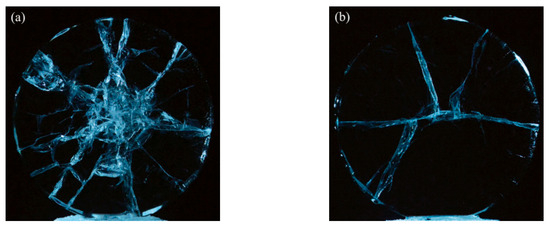
Figure 9.
Photographs of the ice layer fractured: (a) four vertically positioned bubbles; (b) four horizontally positioned bubbles under the ice layer. Frame width: 120 mm [37].
Yuan et al. [100] conducted experiments on high-speed water jet impact on ice layers using a self-developed water jet generator in a transparent water tank, revealing the effects of different parameters on ice fracture patterns. Figure 10 illustrates the damage evolution process of ice layers under high-speed water jet impact under typical experimental conditions, showcasing the sequential development of radial cracks, penetration, and circumferential cracking.

Figure 10.
Temporal evolution of ice layers damage under high-speed water jet impact: (a) t = 0 μs; (b) t = 50 μs; (c) t = 100 μs; (d) t = 1800 μs; (e) t = 6450 μs; (f) t = 6500 μs; (g) t = 7650 μs and (h) t = 40,000 μs. Ice thickness: 10 mm [100].
Small-scale mechanism experiments provide an effective solution to overcome the bottlenecks associated with conventional explosion ice-breaking experiments—namely, high costs, significant safety hazards, and challenges in acquiring dynamic parameters. This technique generates bubbles in water through electrical discharges or high-pressure air guns, harnessing energy from bubble pulsation, collapse-induced shock waves, and liquid jets to fracture ice. It offers the distinct advantages of high repeatability and low environmental risk. However, the existing experiments are exclusively conducted in transparent quiescent water tanks, failing to account for realistic polar environmental conditions such as turbulent flows, salinity gradients, thermal stratification, and inherent ice heterogeneity. Furthermore, these experiments utilize freshwater ice specimens, neglecting the critical influence of polar sea ice properties. Consequently, future small-scale ice-breaking experiments must incorporate considerations of environmental fidelity and ice complexity.
4. Numerical Simulation
While conventional theoretical models and experimental observations have established foundational frameworks for underwater explosion ice-breaking research, their practical implementation faces persistent challenges. On the one hand, theoretical models usually rely on idealized assumptions (such as infinite water domains and homogeneous ice layers), which makes it challenging to describe the dynamic coupling effect between explosion bubbles and ice–water boundary in practical engineering. On the other hand, the field experiments are limited by the high cost of extreme environments (such as polar cryogenic temperatures and deep-water hydrostatic pressure) and the spatiotemporal resolution constraints of measurement means.
In this context, advancements in computational mechanics and multiphysics coupling theories have elevated numerical simulation as a pivotal methodology for deciphering complex explosion loading–ice response interactions. At present, numerical simulation not only enables predictive optimization pre-experiment but also extends the mechanism research to non-idealized conditions through multi-phase coupling frameworks. In light of these considerations, this section will focus on the two dominant numerical simulation methods in this field: mesh-based nonlinear finite element method (FEM) (Section 4.1) and particle-based peridynamics (PD) (Section 4.2), analyze their theoretical framework, applicable scenarios and validation cases, and further explore how the coupling modeling strategy of multimethod collaboration (Section 4.3) can achieve high-precision capture of cross-scale failure process.
4.1. FEM
As a classical numerical method in the field of continuum mechanics, the core idea of FEM is based on the spatial discretization of continua and the numerical solution of weak-form governing equations. In this method, the solution domain is discretized into a finite number of elements, and the displacement interpolation function is constructed to approximate the real solution. Combined with the variational principle or the weighted residual method, the linear equations are established, so as to realize the quantitative analysis of the dynamic response of the ice layer, crack propagation, and other complex mechanical behaviors. In the field of underwater explosion ice-breaking, the technical advantages of the finite element method are mainly reflected in two aspects: first, its mature material constitutive model can accurately describe the nonlinear mechanical behavior of ice under explosion load; secondly, the flexible adaptive mesh generation ability can effectively capture the local stress concentration and crack propagation.
Mansour and Seireg [38] developed a finite element-based dynamic simulation code for shock wave-induced ice-breaking, which incorporated various fracture theories to facilitate the simulation of diverse ice types. However, as the conventional FEM is rooted in continuum mechanics theory, its governing equations inherently require the displacement field to remain continuously differentiable. When addressing displacement discontinuities caused by ice damage and fracture, the undefined spatial derivatives in such discontinuous regions result in numerical solution failures, thereby hindering accurate modeling of dynamic crack propagation processes. To address this issue, Belytschko and Black [101] proposed a minimal remeshing finite element method by introducing discontinuous enrichment functions to characterize the presence of cracks. This approach allows cracks to be arbitrarily aligned within the mesh, significantly reducing the frequent global remeshing required by conventional methods. The accuracy of this method was validated through extensive numerical experiments on two-dimensional crack problems.
Meng et al. [39,102] combined LS-DYNA numerical simulation with experimental validation to explore the dynamic response mechanism of shaped charge technology in underwater explosion ice-breaking. The study revealed correlations between underwater blast position, charge weight, ice layer failure radius, and stress distribution. It validated the effectiveness of optimizing explosion parameters to enhance ice-breaking efficiency, providing theoretical and technical support for engineering applications in ice disaster prevention. Wang et al. [9,12] employed the ALE method in the LS-DYNA software to investigate the damage characteristics and mechanisms of ice layers under underwater explosion loading, demonstrated the effects of shock waves and bubble dynamics on ice damage, confirmed the numerical simulation’s reliability through experimental comparison, and analyzed the impact of various factors on ice-breaking efficiency. Figure 11 directly compares the ice layer damage radius from numerical simulations and experimental measurements, showing that the computational error was only 5.15%, which validates the accuracy of the established ALE model and parameter settings.

Figure 11.
A comparison of the size of the ice layer damage between the numerical and experimental results: (a) the damage size of the ice layer by the numerical result; (b) the damage size of the ice layer by the experimental result [12].
Wang et al. [32] established a numerical model based on the ALE method to investigate the ice damage characteristics under underwater explosions and air-contact explosion loading. The study revealed the effects of explosive type, shape, and length-to-diameter ratio on ice damage. Figure 12 compares the damage ranges of six explosives under underwater explosions, clearly demonstrating that HMX and OCTOL exhibit the largest failure diameters, thereby validating the superiority of high-energy explosives.
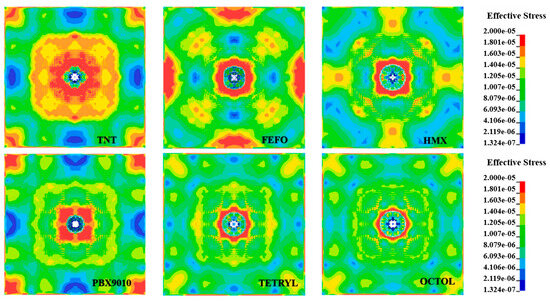
Figure 12.
The damage to the ice layer subjected to different explosive types for underwater explosions beneath the ice layer. Simulation scale: ice layer thickness 0.5 m [32].
Yu et al. [103] vestablished an ice–water–gas bidirectional coupling numerical model using the ALE method, compared the ice-breaking mechanisms of underwater explosion bubbles (UEXB) and compressed gas bubbles (CGB), and revealed the differences in their ice-breaking mechanisms and optimal standoff distances. Figure 13 shows the final damage pattern of the ice layer caused by UEXB and CGB, including the distribution of radial cracks (RC) and circumferential cracks (CC).
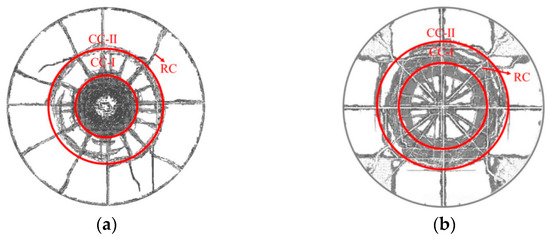
Figure 13.
Final damage pattern of ice layer: (a) UEXB; (b) CGB. Specimen thickness: 10 mm [103].
The core advantage of the finite element method lies in its flexible mesh generation strategy. This strategy enables the accurate capture of local deformation characteristics and stress concentration areas within the structure. Furthermore, the method’s calculation accuracy is reliably verified by experiments. However, in the large deformation scene, the mesh distortion problem needs to be improved by the adaptive mesh reconstruction technology. At the same time, the refined simulation of the propagation mechanism of secondary pressure wave and cavitation effect caused by the explosion bubble pulsation still depends on the innovation and breakthrough of the multifield coupling algorithm.
4.2. PD
PD is a computational non-local continuum mechanics method proposed by Silling [57]. PD overcomes the theoretical limitations of continuum mechanics in fracture problems by defining bond potential functions between material particles, where crack initiation and propagation are intrinsically represented through bond rupture processes. Currently, it has been widely used to predict the damage and fracture processes of brittle materials [104], composite laminated structures [105], and reinforced concrete materials [106]. Unlike traditional FEM constrained by local continuity assumptions, PD requires no a priori assumptions on crack nucleation sites or propagation paths, enabling the spontaneous capture of initial crack formation in ice under explosion loading. In addition, it can also capture the radial main crack, circumferential secondary cracks, and microcrack network of the ice layer under explosion load at the same time, avoiding the computational failure caused by mesh distortion in FEM.
Vazic et al. [77] demonstrated that peridynamics is an effective method for simulating crack propagation in ice-structure interactions. Wang et al. [107] applied and verified a bond-based peridynamic model, effectively simulating the ice layer fragmentation caused by underwater explosion loading, and analyzed the key factors affecting the ice layer breaking radius. Figure 14 visually shows the ice layer destruction process under underwater explosion shock waves, clearly revealing the central damaged area’s expansion over time and thus verifying the model’s ability to simulate ice layer damage.
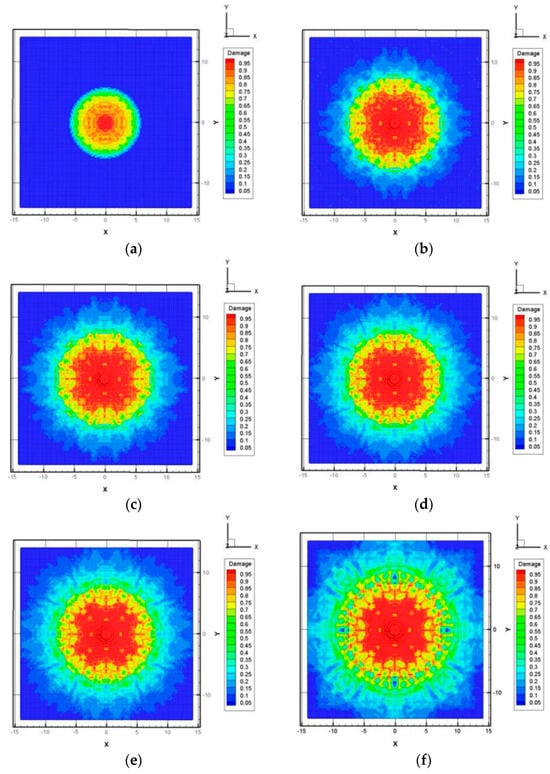
Figure 14.
Destruction process of ice layer for explosive 1.2 m under water: (a) t = 3.3706 ms; (b) t = 11.7971 ms; (c) t = 13.4842 ms; (d) t = 15.1677 ms; (e) t = 16.1789 ms; (f) t = 21.2348 ms [107].
Xu et al. [108] established a dynamic model of crack propagation around ice holes using the PD method, revealing the coupled interaction mechanisms of hydraulic pressure and fracture toughness on crack evolution. Figure 15 visually demonstrates the three-stage progression of cracks—from elastic deformation to stable penetration—validating the PD model’s capability to simulate complex crack propagation patterns in ice under hydraulic loading. This work highlights the critical role of pressure and material toughness in controlling fracture dynamics while experimentally verifying the accuracy of the PD approach for ice damage prediction.
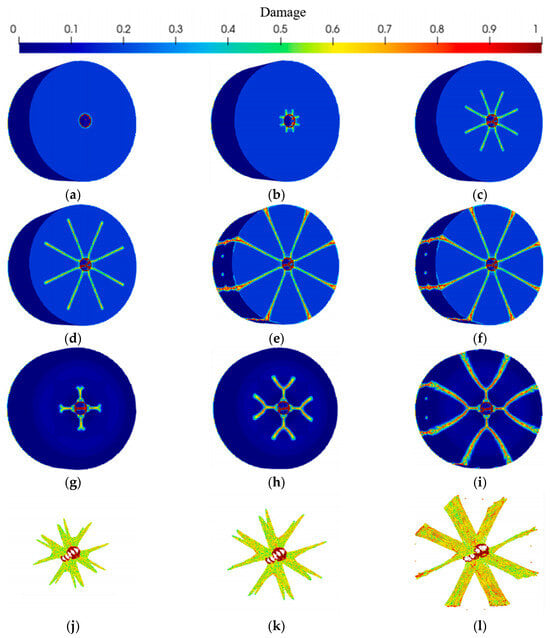
Figure 15.
Cracks initiation and propagation process of ice hole PD model: (a–f) surface cracks initiation and propagation process; (g–i) cracks shape of central cross-section; (j–l) three-dimensional cracks morphology [108].
Wang et al. [109] proposed a particle-paired algorithm and its optimized version, and achieved significant improvements in computational efficiency and memory usage through MPI parallelization. Figure 16 intuitively shows the memory footprint changes in different models as the number of particles increases, directly reflecting the advantage of the optimized particle-paired algorithm in memory usage.
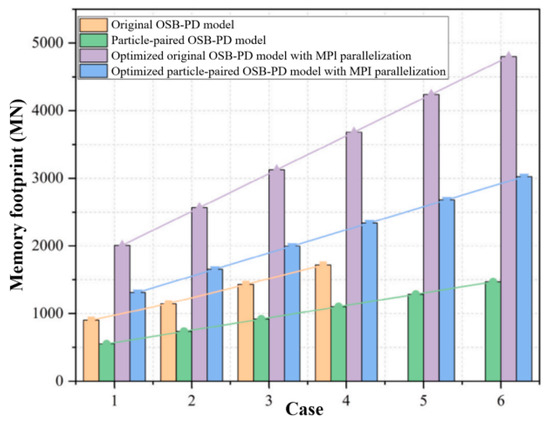
Figure 16.
Memory footprint of different models [109].
As an important branch of non-local continuum mechanics, PD has made significant progress in the field of underwater explosion ice-breaking in recent years. Its theoretical framework, based on bond potential functions between particles, breaks through the strict limitation of traditional continuum methods on the continuous differentiability of displacement fields, providing a new modeling perspective for discontinuous fracture behaviors of ice layers under explosion loading. However, the existing research still faces multiple challenges. First, most studies adopt bond-based elastic models to simulate ice layers, whose fixed Poisson’s ratio cannot reflect the true mechanical response of ice, leading to significant simulation errors under high-speed impact or low-temperature conditions [110,111]. Second, when the size and thickness of ice layers increase, the number of particles rises sharply, resulting in reduced computational efficiency and extremely high computational resource demands. Third, underwater explosions may induce local melting or phase-change damage in ice, but current models focus solely on mechanical responses and do not couple thermal conduction or phase-change effects.
To address these issues, future work could develop more efficient numerical algorithms and optimize programs to reduce computational time and resource consumption, enabling simulations of large-scale problems. Additionally, the constitutive models of ice should be further refined to improve the simulation accuracy of ice layer failure processes. Research on fluid–structure coupling problems should be strengthened to develop PD methods capable of accurately simulating fluid–structure interactions and multiphysics coupling. Exploring the integration of PD with other numerical methods, such as the finite element method and smoothed particle hydrodynamics, could leverage their respective advantages to solve complex problems.
4.3. Coupling Methods
In order to take into account the computational efficiency and physical accuracy, researchers have developed a variety of coupling methods, combining the advantages of different numerical techniques to overcome the limitations of a single method.
Kan et al. [112] revealed the dynamic mechanisms of crack initiation and propagation in the interaction between a high-pressure bubble and an ice layer using a coupled BEM and PD model, demonstrating the critical influence of bubble–ice distance, ice thickness, and bubble size on fracture patterns. Figure 17 clearly illustrates key phenomena such as jet impact and crack branching, validating the model’s capability to simulate complex fracture mechanisms.
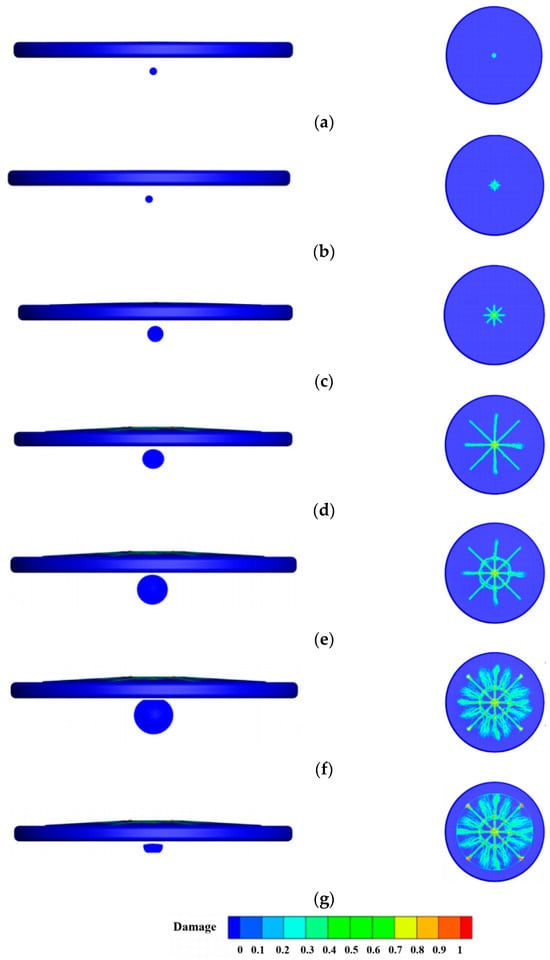
Figure 17.
Evolution of the bubble and ice layer; the left column represents the interaction of the bubble and ice, and the right column represents the damage of the ice layer: (a) t = 0.86 ms; (b) t = 1.24 ms; (c) t = 2.19 ms; (d) t = 7.64 ms; (e) t = 10.00 ms; (f) t = 14.56 ms; (g) t = 205.13 ms [112].
Kan et al. [113] investigated the dual-bubble ice-breaking effect using a coupled BEM and PD approach, revealing the critical influence of bubble spacing and bubble–ice distance on ice fracture patterns. Figure 18 demonstrates the reliability of the BEM-PD model through consistent crack propagation paths and bubble morphology between the experimental and numerical results.
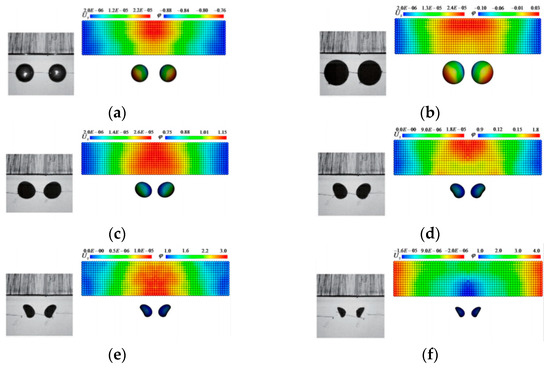
Figure 18.
Comparison of the interaction results between double bubbles and ice, the left is the experimental results of Cui et al. [29]; the right is the results of the coupled BEM-PD numerical simulations, where Uz (m) depicts the vertical displacement of the ice structure, and ϕ stands for the velocity potential of bubbles: (a) t = 0.36 ms; (b) t = 1.09 ms; (c) t = 1.93 ms; (d) t = 2.04 ms; (e) t = 2.12 ms; (f) t = 2.18 ms [113].
He [10] developed an EFEM-PD coupled numerical model to investigate the integral ice-breaking characteristics of underwater explosion bubbles. The model simulates the dynamic behavior of underwater explosion bubbles by the Eulerian finite element method (EFEM), and the peridynamics (PD) captures the discontinuous fracture process of the ice layer, which can accurately simulate the formation process of bifurcation ice cracks and capture the evolution laws of ice cracks and broken ice under various complex conditions.
Shi et al. [58] developed a novel PD-SPH coupling model and validated it through experiments. This model unveiled the ice-breaking mechanisms under high-velocity water jet impacts, particularly the formation and propagation of circumferential and radial cracks. Figure 19 visually presents the damage evolution during ice-breaking, showing the initiation and spread of these cracks.
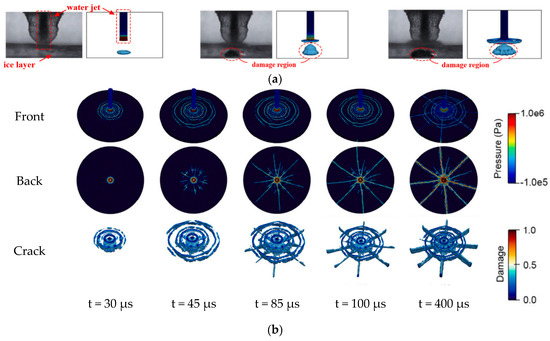
Figure 19.
PD-SPH simulation of ice-breaking by a high-speed water jet impact—a typical case with V = 62.52 m/s, T = 10 mm: (a) Experimental snapshots illustrate the initial impact of the water jet upon the ice layer [92]. The evolution of initial damage on the lower surface is in good agreement with the PD-SPH simulation. (b) Snapshots of damage evolution at five time points, front view (top), back view (middle), and crack topology (bottom). Ice layer thickness: 10 mm (as per experimental setup) [58].
Numerical simulation coupling methods demonstrate unique advantages in multiphysics collaborative modeling for underwater explosion ice-breaking, yet their practical applications still face significant challenges. First, data interaction between disparate algorithms and cross-scale matching substantially increases computational complexity. For instance, in PD-FEM coupling, the non-local particle interactions in PD rely on GPU parallel acceleration; even so, million-particle models still require days of computational time, failing to meet real-time simulation demands for engineering applications. Second, physical quantity transfer at fluid–structure coupling interfaces is prone to distortion due to mesh deformation or particle interpolation errors, resulting in significant errors in the simulation results. Third, the existing studies predominantly focus on mechanical responses while largely neglecting transient melting effects in ice layers caused by explosive high temperatures. Additionally, the dynamic environmental adaptability of numerical simulations is insufficient, and complex boundary conditions such as polar ice layers’ motion, heterogeneity of fractured ice layers, and energy absorption by muddy substrates remain oversimplified. Most current numerical models idealize scenarios as infinite water domains or rigid walls, ignoring critical real-world factors like sediment damping effects.
In the future, heterogeneous parallel algorithms based on GPU/TPU can be developed to optimize the computational efficiency of coupling models. By combining the deep learning inversion of ice constitutive parameters, reliance on experimental data from extreme environments can be reduced. Adaptive mesh and particle refinement techniques can be adopted to balance the resolution requirements of global accuracy and local details.
5. Summary and Prospects
Underwater explosion ice-breaking technology, with its high efficiency and controllability, holds significant promise for applications in polar waterway development and ice disaster prevention. However, the strongly coupled mechanical interactions among high-pressure shock waves, pulsating bubbles, and dynamic ice damage present formidable challenges. Despite advancements in theoretical, experimental, and numerical research, significant limitations persist across these domains.
Theoretical models inadequately address ice complexity, predominantly oversimplifying sea ice as a homogeneous elastic medium. This approach severely neglects its heterogeneous microstructure, dynamic permeability evolution under blast loading, strongly coupled thermo-mechanical-phase transition effects, and multiphase characteristics. Additional shortcomings include oversimplified dynamic process modeling, insufficient characterization of ice mechanical behavior under extreme conditions, and the absence of effective frameworks for key processes such as brine migration and phase transition kinetics.
Experimental research faces dual bottlenecks in observational accuracy and environmental applicability. Conventional techniques struggle to precisely capture critical transient phenomena—including microcrack initiation and dynamic shockwave pressure distribution—while bubble generation methods in small-scale ice-breaking experiments diverge substantially from actual explosive conditions. The existing findings predominantly derive from laboratory settings or specific thin-ice scenarios, lacking validation for polar thick ice, high-salinity sea ice, complex ice–water–air boundaries, and natural ice heterogeneity. Influences of water currents and thermal stratification remain unaddressed, with high costs and safety risks further constraining investigative depth.
Numerical simulations confront critical challenges in computational efficiency and physical model fidelity. Meshless methods incur prohibitive computational costs while adaptive mesh techniques remain underutilized. Constitutive models fail to adequately incorporate ice’s strain-rate dependence, anisotropy, and thermosalinity effects, employing oversimplified damage criteria. Multiphysics coupling remains incomplete, particularly regarding bidirectional strong coupling between bubble dynamics and ice fracture, as well as integrated modeling of brine migration and phase transitions. Engineering validation is deficient, with simulations typically addressing idealized ice conditions rather than comprehensively benchmarking against complex polar ice scenarios.
In conclusion, the integration of theoretical advancements, experimental validations, and numerical simulations will drive the development of more precise, controllable, and environmentally friendly underwater explosion ice-breaking technologies. These innovations will play a crucial role in supporting polar strategies and enhancing ice disaster prevention engineering.
6. Future Work
To address the limitations outlined above, future research should focus on the following key areas:
- At the theoretical level, efforts should prioritize advancing dynamic multiphysics coupling models for heterogeneous ice, with a key focus on developing quantitative characterizations of phase transition kinetics and brine migration mechanisms. This necessitates establishing strain-rate-sensitive constitutive equations and creating a defect-dominated predictive framework for shock wave propagation. In addition, further investigation into hydroelastic wave propagation induced by UNDEX is warranted, particularly regarding wave–ice crack interactions and long-range fatigue effects under realistic polar conditions.
- At the experimental level, research should prioritize developing novel sensors and imaging techniques tailored to extreme transient processes. Such technologies must enable the in situ, real-time, multiphysics synchronous capture of key phenomena, including stress wave propagation through ice, microcrack initiation and propagation, phase transition zones, and bubble–ice interfacial dynamics. Concurrently, simulation methods must be developed to replicate polar thick ice, heterogeneous saline ice containing bubbles/cracks, and complex boundary conditions at small-scale mechanism experiments.
- Numerical simulation research necessitates coordinated progress across key dimensions. First, the synergistic integration of diverse algorithms is essential to comprehensively investigate ice’s mechanical response under varying strain rates, temperatures, and salinity levels. Subsequently, constitutive models require refinement to accurately characterize ice anisotropy and capture microcrack propagation and coalescence during damage evolution. Second, substantial enhancements to explosion multiphysics models are imperative: simulations must achieve higher fidelity in representing underwater explosion bubble dynamics—including generation, expansion, contraction, and collapse—with rigorous consideration of intra-bubble gas compressibility, heat transfer, and mass diffusion. Concurrently, the precise characterization of explosive product dispersion, energy release mechanisms, and media interactions is crucial to significantly enhance blast loading prediction reliability.
- The refinement of ice dynamic fracture criteria. The existing ice dynamic fracture criteria need to be refined to better capture the complex damage mechanisms of ice under explosion loading. This includes considering the effects of temperature, salinity, and ice layer heterogeneity on fracture behavior.
- Ecological impact assessment. A comprehensive ecological impact assessment system should be established to evaluate the short-term and long-term effects of explosion shock waves on aquatic organisms and ecosystems. This includes monitoring the cumulative toxic effects of explosive residues on polar environments.
By addressing these critical areas, future research will contribute to the advancement of underwater explosion ice-breaking technology, providing reliable support for polar development and ice disaster prevention engineering.
Author Contributions
Conceptualization, Z.-X.Z. and Y.-D.W.; investigation, Z.-X.Z.; resources, X.H.; writing—original draft preparation, Z.-X.Z.; writing—review and editing, X.H.; visualization, Z.-X.Z.; supervision, X.H.; project administration, X.L.; funding acquisition, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 52471345), the Shenzhen Science and Technology Program (No. JCYJ20230807145621043), the Innovation Capability Support Program of Shaanxi (No. 2024RS-CXTD-15), and the Innovation Foundation for Doctoral Dissertation of Northwestern Polytechnical University (No. CX2025047).
Data Availability Statement
There are no publicly available data for this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BEM | Boundary element method |
| BPCs | Liquid brine in permeable channels |
| CC | Circumferential cracks |
| CGB | Compressed gas bubbles |
| EFEM | Eulerian Finite Element Method |
| FEM | Finite Element Method |
| FSI | Fluid–structure interaction |
| ICPs | Ice with closed brine pockets |
| PD | Peridynamics |
| RC | Radial cracks |
| SPH | Smooth particle hydrodynamics |
| UEXB | Underwater explosion bubbles |
| UNDEX | Ice-breaking by underwater explosion |
References
- Yoon, J.R.; Kim, Y.D. Reviews on natural resources in the Arctic: Petroleum, gas, gas hydrates and minerals. Ocean Polar Res. 2001, 23, 51–62. [Google Scholar]
- Orheim, A. Coal resources in Arctic areas outside USSR. Cold Reg. Sci. Technol. 1983, 7, 167–177. [Google Scholar] [CrossRef]
- Gautier, D.L.; Bird, K.J.; Charpentier, R.R.; Grantz, A.; Houseknecht, D.W.; Klett, T.R.; Moore, T.E.; Pitman, J.K.; Schenk, C.J.; Schuenemeyer, J.H.; et al. Assessment of undiscovered oil and gas in the Arctic. Science 2009, 324, 1175–1179. [Google Scholar] [CrossRef] [PubMed]
- Andreassen, N. Arctic energy development in Russia—How “sustainability” can fit? Energy Res. Soc. Sci. 2016, 16, 78–88. [Google Scholar] [CrossRef]
- Gulas, S.; Downton, M.; D’Souza, K.; Hayden, K.; Walker, T.R. Declining Arctic Ocean oil and gas developments: Opportunities to improve governance and environmental pollution control. Mar. Policy 2017, 75, 53–61. [Google Scholar] [CrossRef]
- Aksenov, Y.; Popova, E.E.; Yool, A.; Nurser, A.G.; Williams, T.D.; Bertino, L.; Bergh, J. On the future navigability of Arctic sea routes: High-resolution projections of the Arctic Ocean and sea ice. Mar. Policy 2017, 75, 300–317. [Google Scholar] [CrossRef]
- Verny, J.; Grigentin, C. Container shipping on the northern sea route. Int. J. Prod. Econ. 2009, 122, 107–117. [Google Scholar] [CrossRef]
- Xia, L.F. Research and practice of underwater ice jam breaking by manual-operated blasting. Blasting 2014, 31, 126–130. [Google Scholar]
- Wang, Y.; Qin, Y.; Yao, X.L. A combined experimental and numerical investigation on damage characteristics of ice sheet subjected to underwater explosion load. Appl. Ocean Res. 2020, 103, 102347. [Google Scholar] [CrossRef]
- He, M.; Yan, J.; Lv, P.; Duan, H.; Zhang, A.-M. Research on ice-breaking characteristics of underwater explosion bubbles based on an effective coupled model. Appl. Ocean Res. 2024, 153, 104259. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, D.; Feng, B.; Liu, T. Analysis of meso-mechanism of ice damage under two loads of underwater explosion. In Proceedings of the Second International Conference on Mechanical Design and Simulation (MDS 2022), Wuhan, China, 18–20 March 2022; Volume 12261, pp. 44–49. [Google Scholar]
- Wang, Y.; Qin, Y.; Wang, Z.; Yao, X. Numerical study on ice damage characteristics under single explosive and combination explosives. Ocean Eng. 2021, 223, 108688. [Google Scholar] [CrossRef]
- Guyenne, P.; Parau, E.I. Computations of fully nonlinear hydroelastic solitary waves on deep water. J. Fluid Mech. 2012, 713, 307–329. [Google Scholar] [CrossRef]
- Guyenne, P.; Kairzhan, A.; Sulem, C. A Hamiltonian Dysthe equation for hydroelastic waves in a compressed ice sheet. J. Fluid Mech. 2025, 1002, A24. [Google Scholar] [CrossRef]
- Timco, G.W.; Weeks, W.F. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Ji, S.; Wang, A.; Su, J.; Yue, Q.-J. Experimental studies on elastic modulus and flexural strength of sea ice in the Bohai Sea. J. Cold Reg. Eng. 2011, 25, 182–195. [Google Scholar] [CrossRef]
- Thomas, D.N. Sea Ice; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Marchenko, A. Elastic moduli of first-year sea ice calculated from tests with vibrating beams. Ocean Model. 2024, 189, 102365. [Google Scholar] [CrossRef]
- Bogorodsky, V.V.; Gavrilo, V.P. Ice: Physical Properties. In Modern Methods of Glaciology; Gidrometeoizdat: Saint Petersburg, Russia, 1980. [Google Scholar]
- Wu, S.; Shuzhi, L. The strain-rate sensitivity of strength of Bohai Sea one-year ice under uniaxial compression. J. Dalian Inst. Technol. 1984, 23, 45–49. [Google Scholar]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Menge, J.A.R.; Jones, K.F. The tensile strength of first-year sea ice. J. Glaciol. 1993, 39, 609–618. [Google Scholar] [CrossRef][Green Version]
- Kuehn, G.A.; Lee, R.W.; Nixon, W.A.; Schulson, E.M. The structure and tensile behavior of first-year sea ice and laboratory-grown saline ice. J. Offshore Mech. Arct. Eng. 1990, 112, 357–363. [Google Scholar] [CrossRef]
- Dykins, J.E. Tensile Properties of Sea Ice Grown in a Confined System; Physics of Snow and Ice; Bunyeido Printing Co.: Sapporo, Japan, 1967; Volume 1, pp. 523–537. [Google Scholar]
- Dykins, J.E. Tensile and Flexural Properties of Saline Ice; Physics of Ice; Plenum Press: New York, NY, USA, 1968; pp. 251–270. [Google Scholar]
- Barash, R.M. Underwater Explosion Beneath Ice; United States Naval Ordnance Laboratory Report; United States Naval Ordnance Laboratory: White Oak, MD, USA, 1962; pp. 62–96. [Google Scholar]
- Mellor, M. Breaking Ice with Explosive; U.S Army Cold Regions Research and Engineering Laboratory, Office of the Chief of Engineer: Hanover, NH, USA, 1983; pp. 1–57. [Google Scholar]
- Liu, Z.P.; Wang, T.; Guo, X.L.; Fu, H.; Yang, K.; Peng, X. Breaking ice with explosive in Heilongjiang River. J. Hydraul. Eng. 2017, 48, 253–260. [Google Scholar][Green Version]
- Marchenko, A.; Lishman, B. The influence of closed brine pockets and permeable brine channels on the thermo-elastic properties of saline ice. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2017, 375, 20150351. [Google Scholar] [CrossRef] [PubMed]
- Orlova, Y.N.; Orlov, M.Y. The study of the process of explosive loading of ice. Vestn. Tomsk. Gos. Univ. Mat. I Mekhanika 2015, 6, 81–89. [Google Scholar]
- Lyon, W.K. Experiments in the use of explosives in sea ice. Polar Rec. 1960, 10, 237–247. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.; Qin, Y. Investigation on influence factors about damage characteristics of ice sheet subjected to explosion loads: Underwater explosion and air contact explosion. Ocean Eng. 2022, 260, 111828. [Google Scholar] [CrossRef]
- Orlov, M.Y. Investigation of the process of explosive loading of freshwater ice. Therm. Sci. 2019, 23 (Suppl. 2), 561–567. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, W.; Yao, X.L.; Qin, Y.Z. Fragmentation of ice cover subjected to underwater explosion shock wave load and its influence factors. Explos. Shock Waves 2019, 39, 073103. [Google Scholar]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Khoo, B.C. Ice breaking by a collapsing bubble. J. Fluid Mech. 2018, 841, 287–309. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Liu, Y.-L. Experimental study on interaction, shock wave emission and ice breaking of two collapsing bubbles. J. Fluid Mech. 2020, 897, A25. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, A.M.; Wang, S.P. Shock wave emission and ice breaking effect of multiple interacting bubbles. Ocean Eng. 2021, 234, 109175. [Google Scholar] [CrossRef]
- Mansour, A.; Seireg, A. A computer-based simulation of ice-breaking by impact. J. Energy Resour. Technol. 1983, 105, 448–453. [Google Scholar] [CrossRef]
- Meng, W.Y.; Liu, X.; Hu, J.Q. Based on the technology of shaped charge numerical simulation and experiment research of ice blasting. Adv. Mater. Res. 2013, 753–755, 2704–2708. [Google Scholar] [CrossRef]
- Chen, Y.P.; Lee, J.D.; Eskandarian, A. Dynamic meshless method applied to nonlocal crack problems. Theor. Appl. Fract. Mech. 2002, 38, 293–300. [Google Scholar] [CrossRef]
- Orlov, M.Y.; Glazyrin, V.P.; Orlov, Y.N.; Orlova, Y.N. Research of ice behavoir under shock and explosive loads. Numerical simulation and experiment. J. Phys. Conf. Ser. 2019, 1214, 012001. [Google Scholar] [CrossRef]
- Ming, F.R.; Zhang, A.M.; Cao, X.Y. A robust shell element in meshfree SPH method. Acta Mech. Sin. 2013, 29, 241–255. [Google Scholar] [CrossRef]
- Zhang, A.; Ming, F.; Cao, X. Total Lagrangian particle method for the large-deformation analyses of solids and curved shells. Acta Mech. 2014, 225, 253–275. [Google Scholar] [CrossRef]
- Ming, F.R.; Zhang, A.M.; Wang, S.P. Smoothed particle hydrodynamics for the linear and nonlinear analyses of elastoplastic damage and fracture of shell. Int. J. Appl. Mech. 2015, 7, 1550032. [Google Scholar] [CrossRef]
- Ming, F.; Zhang, A.; Xue, Y.; Wang, S. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Myland, D.; Ehlers, S. Influence of bow design on ice breaking resistance. Ocean Eng. 2016, 119, 217–232. [Google Scholar] [CrossRef]
- Xue, Y.; Wang, X.; Yuan, G.; Ni, B.-Y.; Xu, X.; Song, J. Numerical simulation study on ice breaking by a submerged water jet. Phys. Fluids 2024, 36, 113302. [Google Scholar] [CrossRef]
- Luo, X.; Huang, X.; Zhong, Z.X.; Hu, H.-B.; Chen, X.-P. Research on the load characteristics of deep water explosions near curved boundaries. Phys. Fluids 2024, 36, 077165. [Google Scholar] [CrossRef]
- Huang, X.; Mao, J.W.; Li, Q.; Wang, Z.; Pan, G.; Hu, H.-B. On the interaction between the underwater explosion and the double-layer structure with an orifice on the outer plate. Ocean Eng. 2024, 306, 118050. [Google Scholar] [CrossRef]
- Cole, R.H. Underwater Explosion; Princeton University Press: Princeton, NJ, USA, 1948. [Google Scholar]
- Zamyshlyaev, B.V.; Yakovlev Yu, S. Dynamic Loads in Underwater Explosion: AD 757183; Naval Intelligence Support Center: Washington, DC, USA, 1973. [Google Scholar]
- Rayleigh, L. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. Ser. 1917, 6, 94–98. [Google Scholar] [CrossRef]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Zhang, A.M.; Li, S.M.; Xu, R.Z.; Pei, S.-C.; Li, S.; Liu, Y.-L. A theoretical model for compressible bubble dynamics considering phase transition and migration. J. Fluid Mech. 2024, 999, A58. [Google Scholar] [CrossRef]
- Wang, T.; Guo, X.L.; Fu, H.; Guo, Y.; Peng, X.; Wu, Y.; Li, J.; Xia, Y. Effects of water depth and ice thickness on ice cover blasting for ice jam flood prevention: A case study on the Heilong River, China. Water 2018, 10, 700. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Shi, H.T.; Yuan, G.Y.; Ni, B.Y.; Zhang, L.-W. Quasi-brittle ice breaking mechanisms by high-velocity water jet impacts: An investigation based on PD-SPH coupling model and experiments. J. Mech. Phys. Solids 2024, 191, 105783. [Google Scholar] [CrossRef]
- Petrovic, J.J. Review mechanical properties of ice and snow. J. Mater. Sci. 2003, 38, 1–6. [Google Scholar] [CrossRef]
- Taylor, G.I. The pressure and impulse of submarine explosion waves on plates. Underw. Explos. Res. 1950, 1, 1155–1173. [Google Scholar]
- Snay, H.G.; Christian, E.A. The Response of Air-Backed Plates to High-Amplitude Underwater Shockwaves; Technical Report No. 2462; Naval Ordnance Laboratory: White Oak, MD, USA, 1952. [Google Scholar]
- Huang, H. A Qualitative Appraisal of the Doubly Asymptotic Approximation for Transient Analysis of Submerged Structures Excited by Weak Shock Waves; Naval Research Lab: Washington, DC, USA, 1975. [Google Scholar]
- Schechter, R.S.; Bort, R.L. The Response of Two Fluid-Coupled Plates to an Incident Pressure Pulse; Memorandum Report; Naval Research Laboratory: Washington, DC, USA, 1981; No. 4647. [Google Scholar]
- Rajendran, R. Reloading effects on plane plates subjected to non-contact underwater explosion. J. Mater. Process. Technol. 2008, 206, 275–281. [Google Scholar] [CrossRef]
- Besant, W.H. A Treatise on Hydrostatics and Hydrodynamics; Deighton, Bell, & Company: Cambridge, UK, 1859. [Google Scholar]
- Herring, C. Theory of the Pulsations of the Gas Bubble Produced by an Underwater Explosion; Columbia University, Division of National Defense Research: New London, CT, USA, 1941. [Google Scholar]
- Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid; California Institute of Technology: Pasadena, CA, USA, 1952. [Google Scholar]
- Keller, J.B.; Kolodner, I.I. Damping of underwater explosion bubble oscillations. J. Appl. Phys. 1956, 27, 1152–1161. [Google Scholar] [CrossRef]
- Prosperetti, A.; Lezzi, A. Bubble dynamics in a compressible liquid. Part 1. First-order theory. J. Fluid Mech. 1986, 168, 457–478. [Google Scholar] [CrossRef]
- Lezzi, A.; Prosperetti, A. Bubble dynamics in a compressible liquid. Part 2. Second-order theory. J. Fluid Mech. 1987, 185, 289–321. [Google Scholar] [CrossRef]
- Storey, B.D.; Szeri, A.J. A reduced model of cavitation physics for use in sonochemistry. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 457, 1685–1700. [Google Scholar] [CrossRef]
- Zhang, A.; Li, S.M.; Cui, P.; Li, S.; Liu, Y.-L. A unified theory for bubble dynamics. Phys. Fluids 2023, 35, 033323. [Google Scholar] [CrossRef]
- Wilkerson, S.A. A Boundary Integral Approach to Three-Dimensional Underwater Explosion Bubble Dynamics; The Johns Hopkins University: Baltimore, MD, USA, 1990. [Google Scholar]
- Klaseboer, E.; Khoo, B.C. A modified Rayleigh–Plesset model for a non-spherically symmetric oscillating bubble with applications to boundary integral methods. Eng. Anal. Bound. Elem. 2006, 30, 59–71. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, W.; Yao, X. Pressure characteristics of a nonspherical underwater explosion bubble in a compressible fluid. Phys. Fluids 2024, 36, 057145. [Google Scholar] [CrossRef]
- Parameswaran, V.R.; Jones, S.J. Brittle fracture of ice at 77 K. J. Glaciol. 1975, 14, 305–315. [Google Scholar] [CrossRef][Green Version]
- Vazic, B.; Ji, X.; Oterkus, E.; Oterkus, S. Ice-structure interactions by using peridynamics. In Proceedings of the ASME 2017 International Mechanical Engineering Congress & Exposition, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Vazic, B. Multi-Scale Modelling of Ice-Structure Interactions. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2020. [Google Scholar]
- Vazic, B.; Oterkus, E.; Oterkus, S. In-plane and out-of plane failure of an ice sheet using peridynamics. J. Mech. 2020, 36, 265–271. [Google Scholar] [CrossRef]
- Ma, W.; Xie, W.; Liu, D.; Zhang, D. Analysis of the dynamic response of the icecap structure under the action of explosion wave. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 95–98. [Google Scholar]
- Dykins, J.E. Tensile Properties of Sea Ice Grown in a Confined System. Phys. Snow Ice Proc. 1967, 1, 523–537. [Google Scholar]
- Jones, S.J. High Strain-Rate Compression Tests on Ice. J. Phys. Chem. B 1997, 101, 6099–6101. [Google Scholar] [CrossRef]
- Liang, X.Q.; He, B.S.; Xie, W.H. Experimental Study on Blasting Effect upon Thick Ice of the Yellow River. Eng. Blasting 2012, 18, 83–85. [Google Scholar]
- Xie, W.H.; He, B.S.; Li, H.X. The effect of ice breaking by explosion for the yellow river ice flood prevention. Eng. Blasting 2014, 20, 29–31. [Google Scholar]
- Mellor, M. Derivation of guidelines for blasting floating ice. Cold Reg. Sci. Technol. 1987, 13, 193–206. [Google Scholar] [CrossRef]
- Wu, R.B.; Hao, M.S.; Wu, C.G.; Liang, X. The parameter optimization experiment of ice breaking by underwater blasting. Eng. Blasting 2014, 20, 25–28. [Google Scholar]
- Zhang, Z.H.; Liang, X.Q.; Wang, S.L. Numerical simulation of ice breaking mechanism of underwater blasting. Blasting 2015, 32, 150–155. [Google Scholar]
- Zhang, M.F.; Zhang, F.G.; Liang, X.Q.; Han, X.; Zhang, C. Ice-breaking experimental study on blasting with concentrated charge. Eng. Blasting 2015, 21, 43–46. [Google Scholar]
- Kurtz, M.K.; Benfer, R.H.; Chrktopher, W.G.; Frankenstein, G.E.; Van Wyhe, G.; Roguski, E.A. Consolidated Report, Operation Break-Up, FY 66. Ice Cratering Experiments, Blair Lake, Alaska; Nuclear Cratering Group, Lawrence Radiation Laboratory: Livermore, CA, USA, 1966; pp. 66–67. [Google Scholar]
- Van der Kley, J. The Use of Explosives for Clearing Ice; Rijkswaterstaat: Hague, The Netherlands, 1965. [Google Scholar]
- Nikolaev, S.E. Cutting Sea Ice by Directed Blasting; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1973. [Google Scholar]
- Liang, X.Q.; Xiong, F.; Lu, X.L. Experimental Research on Underwater Shock Wave Characteristic of Ice Blasting at Yellow River. Blasting 2014, 31, 1–4. [Google Scholar]
- Shen, H.T. Research on River Ice Processes: Progress and Missing Links. J. Cold Reg. Eng. 2003, 17, 135–142. [Google Scholar] [CrossRef]
- Shen, H.T. River ice transport theories: Past, present, and future. In Proceedings of the 15th IAHR International Symposium on Ice, Gdansk, Poland, 28 August–1 September 2000. [Google Scholar]
- Tao, W.; Kailin, Y.; Yongxin, G. Application of artificial neural networks to forecasting ice conditions of the Yellow River in the Inner Mongolia Reach. J. Hydrol. Eng. 2008, 13, 811–816. [Google Scholar] [CrossRef]
- Fan, Y.; Liao, H.; Yang, G.; Zhou, T.; Deng, K.; Tian, B. Dynamic behaviour of fish with swim bladders subjected to underwater explosions and methods for mitigating injuries. Biol. Conserv. 2024, 300, 110849. [Google Scholar] [CrossRef]
- Ni, B.Y.; Wang, Q.; Xue, Y.Z.; Wang, Y.; Wu, Q. Numerical Simulation on the Damage of Ice Floe by High-Pressure Bubble Jet Loads, 3rd ed.; Workshop and Symposium on Safety and Integrity Management of Operations in Harsh Environments: St. John’s, ON, Canada, 2017. [Google Scholar]
- Yuan, G.Y.; Ni, B.Y.; Wu, Q.G.; Xue, Y.-Z.; Zhang, A.-M. An experimental study on the dynamics and damage capabilities of a bubble collapsing in the neighborhood of a floating ice cake. J. Fluids Struct. 2020, 92, 102833. [Google Scholar] [CrossRef]
- Ni, B.Y.; Pan, Y.T.; Yuan, G.Y.; Xue, Y. An experimental study on the interaction between a bubble and an ice floe with a hole. Cold Reg. Sci. Technol. 2021, 187, 103281. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Ni, B.Y.; Wu, Q.G.; Xue, Y.-Z.; Han, D.-F. Ice breaking by a high-speed water jet impact. J. Fluid Mech. 2022, 934, A1. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Meng, W.Y.; Hu, J.Q.; Liu, X. Based on the Technology of Shaped Charge Numerical Simulation Research of the Ice Model’s Combination Blasting. Adv. Mater. Res. 2013, 753–755, 1002–1006. [Google Scholar] [CrossRef]
- Yu, Z.; Ni, B.Y.; Wu, Q.; Wang, Z.; Liu, P.; Xue, Y. Numerical Simulation of Icebreaking by Underwater-Explosion Bubbles and Compressed-Gas Bubbles Based on the ALE Method. J. Mar. Sci. Eng. 2023, 12, 58. [Google Scholar] [CrossRef]
- Ha, Y.D.; Bobaru, F. Dynamic brittle fracture captured with peridynamics. In Proceedings of the ASME 2011 International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011; pp. 437–442. [Google Scholar]
- Askari, E.; Xu, J.; Silling, S. Peridynamic analysis of damage and failure in composites. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Kilic, B.; Madenci, E. Structural stability and failure analysis using peridynamic theory. Int. J. Non-Linear Mech. 2009, 44, 845–854. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Zan, Y.; Lu, W.; Bai, X.; Guo, J. Peridynamics simulation of the fragmentation of ice cover by blast loads of an underwater explosion. J. Mar. Sci. Technol. 2018, 23, 52–66. [Google Scholar] [CrossRef]
- Xu, H.; Liu, Y.; Hou, Z.; Dou, Z.; Zhang, J.; Yang, G. Study on hydraulic cracking mechanism and propagation characteristics of ice hole based on Peridynamics. Appl. Ocean Res. 2023, 139, 103719. [Google Scholar] [CrossRef]
- Wang, C.; Cao, C.; Ye, L.; Wang, C.; Guo, C. An efficient peridynamic method and its MPI parallelization for simulating the continuous icebreaking process. Ocean Eng. 2023, 279, 114460. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Q.; Lu, W. Peridynamic simulation of brittle-ice crushed by a vertical structure. Int. J. Nav. Archit. Ocean. Eng. 2017, 9, 209–218. [Google Scholar] [CrossRef]
- Asgari, M.; Kouchakzadeh, M.A. An equivalent von Mises stress and corresponding equivalent plastic strain for elastic–plastic ordinary peridynamics. Meccanica 2019, 54, 1001–1014. [Google Scholar] [CrossRef]
- Kan, X.Y.; Zhang, A.M.; Yan, J.L.; Wu, W.-B.; Liu, Y.-L. Numerical investigation of ice breaking by a high-pressure bubble based on a coupled BEM-PD model. J. Fluids Struct. 2020, 96, 103016. [Google Scholar] [CrossRef]
- Kan, X.; Wang, J.; Yan, J.; Wang, C.; Wang, Y. Numerical analysis of ice-breaking effects induced by two interacting bubbles using the coupled boundary element method and peridynamics model. Phys. Fluids 2024, 36, 097110. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).