Optimization Design of Dynamic Cable Configuration Considering Thermo-Mechanical Coupling Effects

Abstract

During operation, dynamic cables endure coupled thermo-mechanical loads (mechanical: tension/bending; thermal: power transmission) that degrade stiffness, amplifying extreme responses and impairing configuration optimization. To address this, this study pioneers a multi-objective optimization framework integrating stiffness characteristics from mechanical/thermo-mechanical analyses, with objectives to minimize dynamic extreme tension and curvature under constraints of global configuration variables and safety thresholds. The framework employs a Radial Basis Function (RBF) surrogate model coupled with NSGA-II algorithm, yielding validated Pareto solutions (≤6.15% max error vs. simulations). Results demonstrate universal reduction in extreme responses across optimized configurations, with the thermo-mechanically optimized solution achieving 20.24% fatigue life enhancement. This work establishes the first methodology quantifying thermo-mechanical coupling effects on offshore cable safety and fatigue performance. This configuration design scheme exhibits better safety during actual service conditions.

1. Introduction

Dynamic cables are critical components in offshore wind systems, connecting floating platforms to seabed infrastructure. As illustrated in Figure 1, buoyancy modules enable wave-shaped configurations that accommodate platform motion while mitigating cable loads [1]. These cables endure complex multi-source loads: self-weight, hydrodynamic forces (waves/currents), buoyancy, and platform-induced motions [2]. In engineering design, sectional stiffness is integrated into global models for dynamic response analysis. Time-domain simulations under varying sea states extract extreme values to verify compliance with safety standards.

However, dynamic cables must also fulfill the function of power transmission. With the increasing scale of offshore wind turbines and the growing capacity of individual units, some dynamic cables are now required to meet 66 kV voltage levels, and in the future, high-voltage dynamic cables of 132 kV may emerge [3]. As a result, dynamic cables are required to carry high-voltage power, generating a significant amount of heat. This leads to elevated internal temperatures within the cable, causing thermal expansion of certain components and a reduction in material properties such as elastic modulus and yield strength, thereby altering the cable’s stiffness and mechanical characteristics. Li developed a 3D electro-thermal-mechanical multi-physics coupling model, focusing on the effect of conductor temperature on the bending behavior of cables. Their results showed that cable stiffness decreases to some extent as temperature rises [4]. Qiao investigated the effect of thermo-mechanical coupling on the stiffness of dynamic cables and revealed the mechanisms by which thermal loads induce expansion and softening, affecting stiffness variation [5]. Liu conducted pull-out tests on Galfan-coated cables under high-temperature conditions and observed a decline in cable stiffness with increasing temperature. They also proposed predictive formulas for tensile strength at different temperatures [6]. Yan performed a thermo-mechanical coupling analysis on the cross-section of dynamic cables used for floating wind turbines, finding that thermal loads significantly increased the peak stress responses of the cable, indicating that designs considering only mechanical loads may be unsafe [7]. While thermo-mechanical effects on cable components are established, no study integrates these into global configuration optimization—particularly for fatigue life enhancement under combined environmental extremes.

The global dynamic analysis of dynamic cables involves multiple operating conditions and a large number of interdependent design parameters, which can lead to low optimization efficiency. The cable’s response primarily depends on configuration design variables with varying sensitivities, and its hydrodynamic behavior is inherently nonlinear. Thus, surrogate models are required to link dynamic response to configuration parameters as the foundation for optimization design. Neural networks have become a popular choice for building such surrogates because they can learn complex variable-response relationships from training data and generalize to unseen scenarios. Guarize developed a hybrid artificial neural network-finite element procedure for predicting the dynamic response of subsea cable configurations, achieving a 20-fold efficiency gain over pure finite element methods [8]. Chen constructed a surrogate using a Radial Basis Function (RBF) network for the optimization of flexible riser configurations in shallow water, demonstrating that RBF models are simpler to build and more accurate than traditional Kriging [9]. Yang assessed the influence of both local cross-sectional and global configuration variables on cable design, comparing NSGA-II, AMGA, and NCGA for multi-objective optimization of bending curvature and effective tension [10]. Rentschler integrated MATLAB and OrcaFlex to perform the optimization design of lazy-wave dynamic cables within a depth range of 70–200 m, using a genetic algorithm and considering evaluation criteria such as fatigue life, extreme responses, and economic factors [11]. Schnepf pioneered gradient-based SLSQP optimization for tethered lazy-wave cable configurations, achieving reduced cable length while maintaining design compliance under extreme multidirectional loads [12]. Ahamd developed a buoy-suspended inter-array cable configuration for 5 MW FOWTs, validating feasibility through dynamic optimization while conducting safety margin trade-offs analysis between copper and aluminum conductors [13].

In summary, incorporating thermo-mechanical coupling effects into dynamic cable configuration optimization is essential for accurate stiffness input, enabling precise computation of dynamic responses and fatigue life. This approach critically enhances the safety and cost-effectiveness of cable designs. This study establishes a thermo-mechanical-coupled optimization framework for dynamic cable configurations, integrating temperature-dependent stiffness degradation to accurately capture mechanical responses. We develop an RBF-NSGA-II surrogate model minimizing effective tension and bending curvature under extreme constraints. The primary objectives are (1) quantifying thermal effects on global configuration safety, (2) deriving optimal parameters via multi-objective optimization, and (3) validating fatigue life enhancement in floating wind systems.

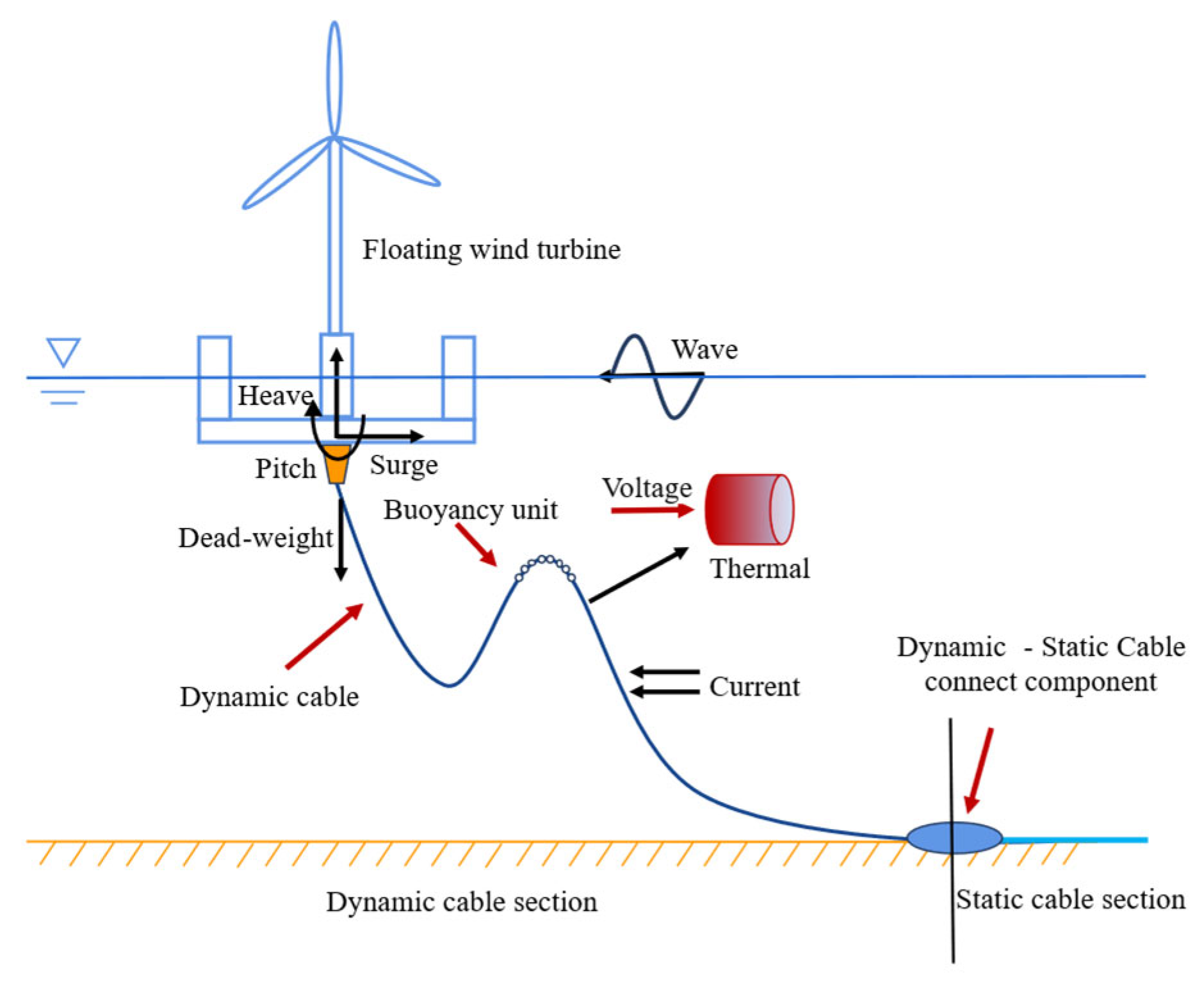
2. Coupling Analysis Model of Floating Wind Turbine

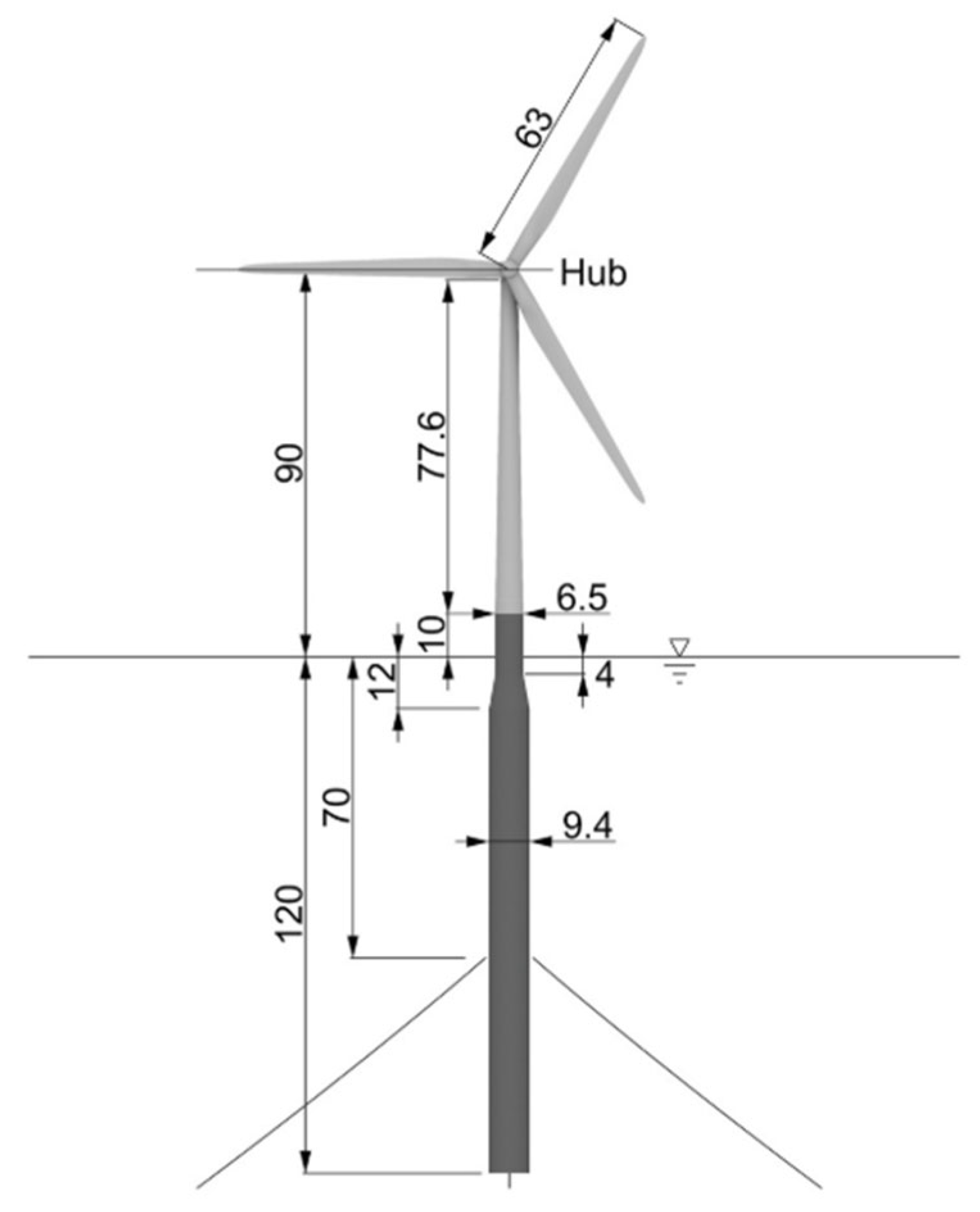
2.1. OC3-Hywind Floating Wind Turbine

The OC3-Hywind floating wind turbine is selected as the research model in this study. Developed by the National Renewable Energy Laboratory (NREL) in the United States, the OC3-Hywind model has been validated through numerical simulations and experimental studies by multiple research groups, demonstrating high reliability [13,14,15]. The model is primarily built using the OrcaFlex 11.3c numerical simulation software and coupling with a Python 3.8-based controller to adjust the blade pitch angle, enabling the realization of a wind-wave-current coupling model. Relevant resources are available on the official OrcaFlex website [16].

The OC3-Hywind platform adopts a spar-type structure and is moored using three catenary lines arranged symmetrically at 120° intervals around the platform center, as shown in Figure 2. The center of gravity of the floating platform and ballast tank is located 89.9 m below the still water level, while the platform extends 10 m above the water surface. The designed draft is 120 m, and the detailed geometry is illustrated in Figure 3. The OC3-Hywind wind turbine has a rated power of 5 MW, a rotor diameter of 126 m, and a hub height of 87.6 m. The key parameters are listed in

Table 1. OC3-Hywind floating wind turbine parameters.

Name	Parameters
Rated power	5 MW
Rotor orientation, configuration	Upwind, 3 blades
Rotor, hub diameter	126, 3 m
Hub height	90 m
Cut-in, rated, cut-out speed	3, 11.4, 25 m/s
Cut-in, rated rotor speed	6.9 rpm, 12.1 rpm
Rotor mass	110,000 kg
Nacelle mass	240,000 kg
Tower mass	347,460 kg

.

2.2. Marine Environmental Loading

In this study, the water depth is set to 320 m, with seabed stiffness specified as 100 N/m in both axial and tangential directions, and a friction coefficient of 0.5. According to standard recommendations, two loading conditions are considered: the first is the rated condition, during which the wind turbine is in operation; the second is the extreme condition, where the turbine is shut down and only freewheeling, as shown in

Table 2. Marine environmental parameters.

Name	Wind Speed [m/s]	Wave Height [m]	Period [s]	Current at Surface [m/s]	Turbine Status
Rated loads	11.4	6.0	10.0	0.486	Operating
Extreme loads	29.0	13.2	15.1	1.070	Shutdown

. The wave spectrum follows the JONSWAP model, and the rated loads of wave parameters are taken from the OC3 report by Jonkman and Musial [17]. The wave parameters for the extreme loads are taken from the Visund field based on the 2016 Tor storm from the report by Kvitrud and Løland [18]. The wind speed spectrum adopts the NPD (Norwegian Petroleum Directorate) model, and the current velocity is estimated using the power-law profile provided by DNV.

In general, extreme response analysis of dynamic cables involves hundreds of load cases; therefore, it is essential to extract representative scenarios to improve computational efficiency and analytical accuracy. Given that floating wind turbines are subjected to combined wind, wave, and current loads, the platform may drift from its initial position. Under relatively calm sea conditions, the floating wind turbine is maintained near its nominal position due to the constraint of the mooring system. However, in severe sea states, the platform may drift to any location within the circular area shown in Figure 4. In the design process, four typical extreme offset conditions are usually considered, namely the far, near, and two lateral positions. The far-offset condition refers to the case where wind, wave, and current loads act in the 180° direction, causing the top end of the dynamic cable to experience increasing horizontal drag forces and gradually drift outward, leading to the cable transitioning from its normal configuration toward a straightened shape. During this process, the bending curvature changes smoothly, while the tension continuously increases until it reaches the breaking limit, resulting in tensile failure. Conversely, the near-offset condition occurs when the environmental loads act in the 0° direction, pulling the dynamic cable inward. In this scenario, the maximum tension remains nearly constant, but the cable experiences compression, and the bending curvature gradually increases until it exceeds the allowable limit, resulting in bending failure. According to engineering experience, the near and far offset conditions typically represent the most critical scenarios for dynamic cables and are sufficient to encompass other offset cases.

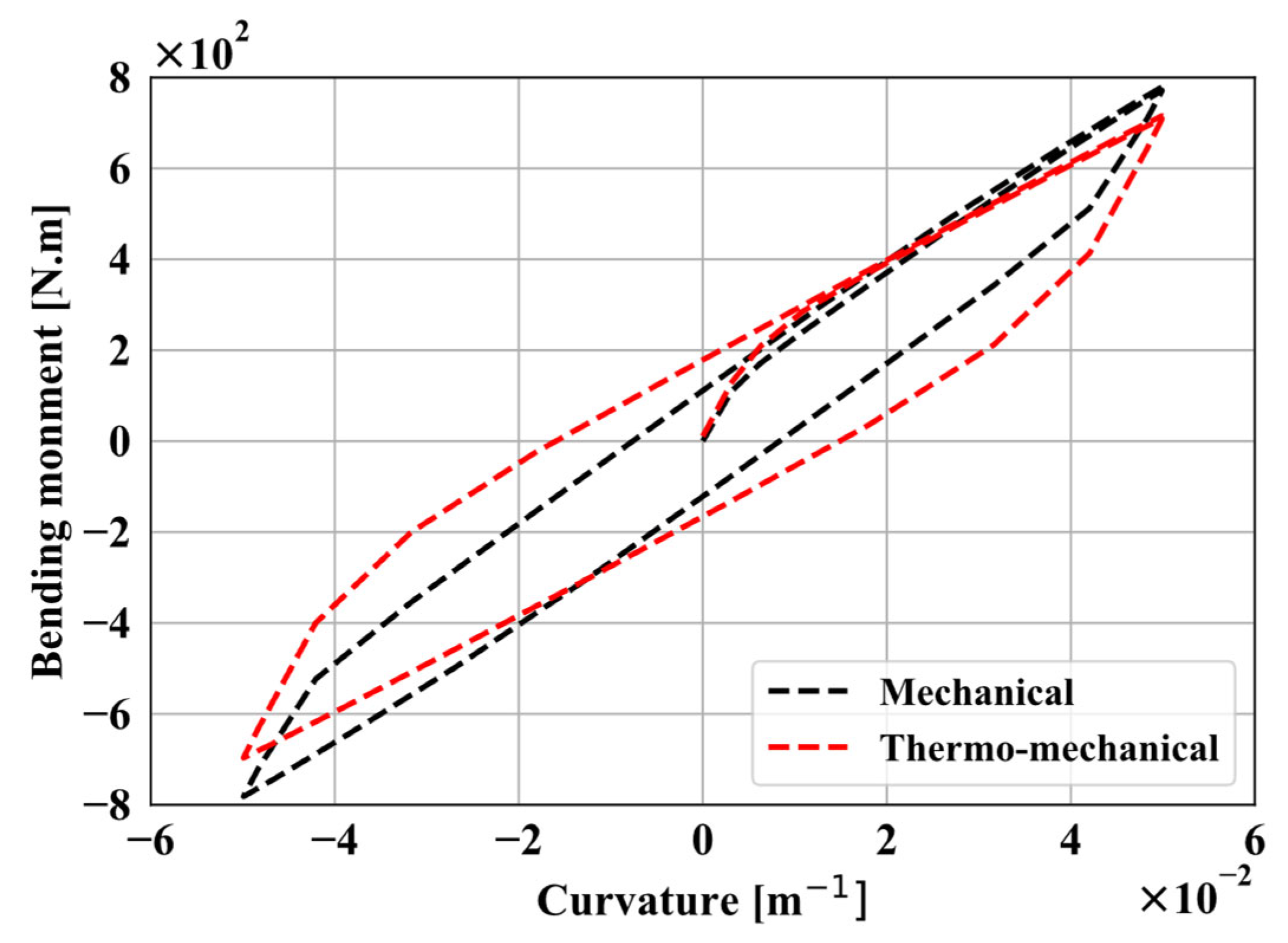
2.3. Dynamic Cable

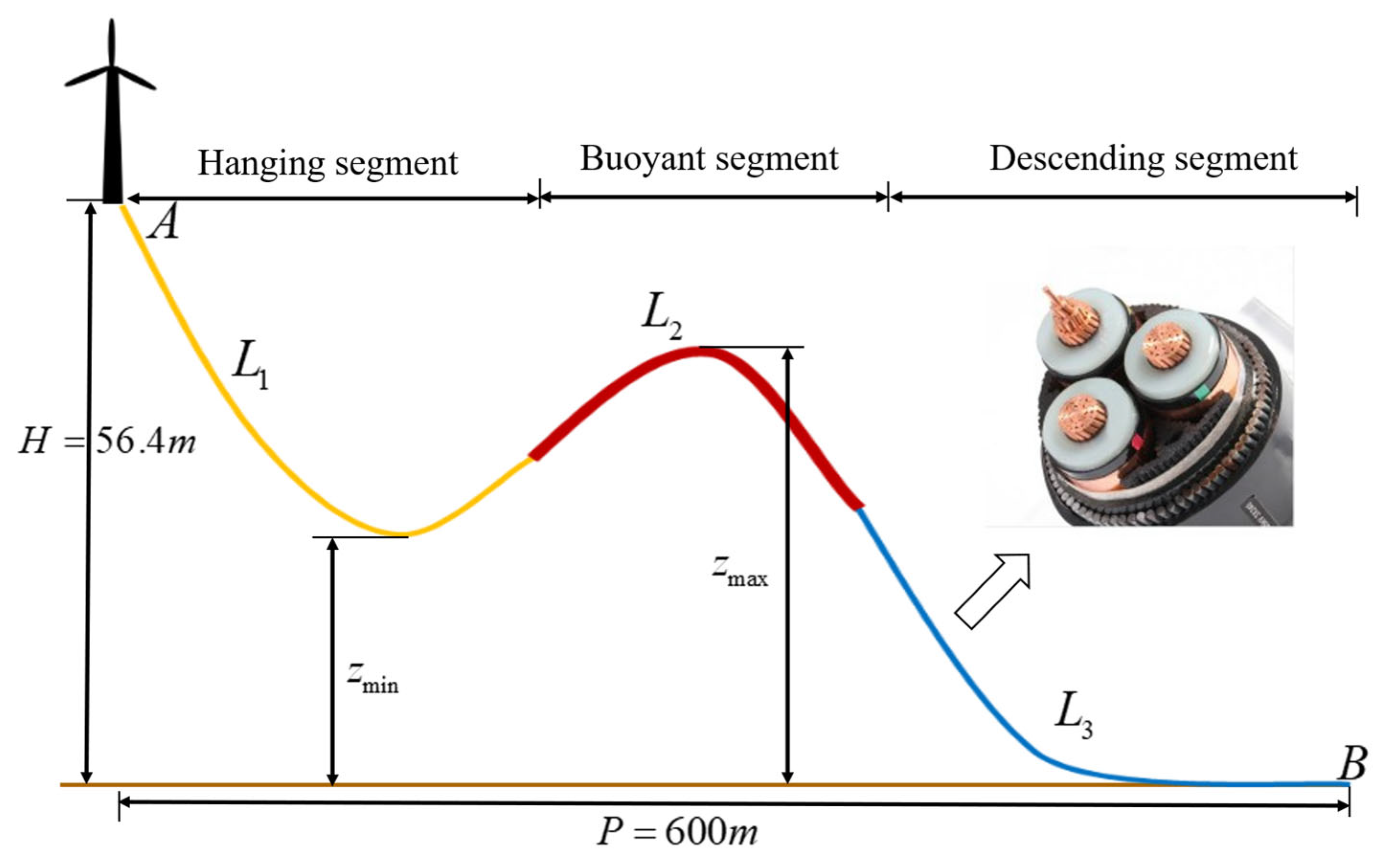
2.3.1. Global Configuration Design

For dynamic cables used in deep-sea wind power development, the lazy-wave configuration is commonly adopted to cope with harsh marine environments. The global configuration design of the dynamic cable is illustrated in Figure 5, where buoyancy modules are installed along the middle segment, making the net buoyancy greater than the weight and forming an inverted catenary shape. Typically, the lazy-wave configuration is decomposed into three connected catenary segments in sequence [10]: Hanging segment ($L_1$): the cable length between the top float connection point (Point A) and the beginning of the buoyant segment; Buoyant segment ($L_2$); Descending segment ($L_3$): the cable length between the end of the buoyant segment and the touchdown point on the seabed (Point B).

Based on the above-mentioned lazy-wave configuration, according to different engineering experiences [10,11,12], the preliminary layout of the dynamic cable is designed as follows: the hanging segment ($L_1$) is 400 m, the buoyant segment ($L_2$) is 80 m, and the descending segment ($L_3$) is 270 m, resulting in a total length of 750 m. The hang-off point A is located 4.95 m horizontally from the vertical centerline of the floating platform and 56.4 m above the bottom of the platform, aiming to reduce the impact of marine biofouling on the suspended segment of the dynamic cable. The touchdown point B is located on the seabed 600 m away from the platform’s vertical centerline and is arranged at an angle of 60° with respect to the adjacent mooring line.

2.3.2. Equivalent Stiffness Calculation

In general, for global dynamic analysis of dynamic cables, the cable is typically simplified as a single, uniform line. The structural stiffness characteristics (such as axial stiffness and bending stiffness) are assigned to this line model, where accurate stiffness input is essential for more precise load response and fatigue life predictions. Moreover, due to significant contact and friction interactions among the cable components, when the bending curvature exceeds a certain critical value, relative sliding occurs between components, leading to distinctly nonlinear bending stiffness behavior. Based on the equivalent stiffness analysis method proposed by Qiao [5], this study calculates the axial stiffness under both mechanical analysis and thermo-mechanical coupling analysis, as presented in

Table 3. Performance parameters of the dynamic cable.

Name	Parameter
	Mechanical Analysis	Thermo-Mechanical Coupling Analysis
Outer diameter	0.116 m
Weight in air	25.0 kg/m
Axial stiffness	345.0 MN	233.0 MN
Nonlinear bending stiffness	$E_{\mathrm{Mechanical}}^{F_1}$	$E_{\mathrm{Thermo}\text{-}\mathrm{mechanical}}^{F_1}$
Tension at conductor yield	885 kN
Maximum bending curvature	0.555 m−1
Drag coefficient (normal, axial)	1.2, 0.008
Added mass coefficient (normal, axial)	1.0, 0.0

. The nonlinear bending stiffness $E_{\mathrm{Mechanical}}^{F_1}$ and $E_{\mathrm{Thermo}\text{-}\mathrm{mechanical}}^{F_1}$ is illustrated in Figure 6. Other specific performance parameters of the dynamic cable are also listed in Table 3, and the buoyant segment parameters are shown in

Table 4. Performance parameters of buoyant segment.

Name	Parameter
	Mechanical Analysis	Thermo-Mechanical Coupling Analysis
Outer diameter	0.361 m
Weight in air	59.0 kg/m
Axial stiffness	345.0 MN	Axial stiffness
Nonlinear bending stiffness	$E_{\mathrm{Mechanical}}^{F_1}$	Nonlinear bending stiffness
Drag coefficient (normal, axial)	2.617, 0.345
Added mass coefficient (normal, axial)	1.0, 0.469

.

3. Dynamic Cable Configuration Optimization Model

3.1. Optimization Parameters and Objectives

As previously described, in the global configuration design of dynamic cables, geometric parameters such as the hanging segment, buoyant segment, and descending segment directly determine the total cable length and influence the cable’s dynamic responses, particularly the extreme effective tension and bending curvature. These design parameters effectively reflect the geometric shape of the cable configuration and enable calculation of its dynamic response. Therefore, $L_1$, $L_2$, and $L_3$ are selected as optimization parameters for the global configuration design. Sensitivity analysis is conducted on these parameters to identify their relative importance in the design process and to understand the variation patterns of the cable’s mechanical performance.

Under rated operating conditions, the influence of each configuration parameter on the extreme values of dynamic cable tension and bending curvature was analyzed using OrcaFlex. The results are shown in Figure 7. The effective tension decreases with the increase in the hanging segment length, mainly because the additional slack reduces the risk of excessive stretching. However, further increases in the hanging segment length lead to greater self-weight-induced tension at the top connection point. Additionally, increasing the hanging segment length intensifies the fluctuation amplitude of the cable configuration, resulting in higher curvature. Before the hanging segment length reaches 350 m, tension and curvature exhibit a competitive relationship. The influence of the buoyant segment on the hydrodynamic response of the dynamic cable follows a pattern similar to that of the hanging segment. However, when the length of the buoyant segment exceeds a certain threshold, the maximum curvature begins to decrease. This is because a longer buoyant segment provides a buffering effect on the global configuration. In contrast, the maximum tension and curvature in the descending segment show monotonic trends and consistently exhibit a competitive relationship. When the global dynamic tension response of the cable is small, the configuration tends to exhibit excessive curvature; conversely, configurations with small dynamic curvature response are often accompanied by large tension response. Optimizing one objective usually comes at the cost of sacrificing the performance of another, resulting in a set of trade-off solutions rather than a single optimal solution. This is known as the Pareto frontier. Therefore, the multi-objective optimization problem can be expressed as shown in Equation (1).

$$\begin{array}{l}\mathrm{Find} \mathrm{X}=(L_1,L_2,L_3)\\ \mathrm{Min} (T_{\max },{\kappa }_{\max })\\ s.t\left\{\begin{array}{l}{T}_{\max }\le MBL\\ {\kappa }_{\max }\le MAC\\ 300\le L_1\le 450\\ 50\le L_2\le 150\\ 250\le L_3\le 350\\ 700\le L_1+L_2+L_3\le 900\end{array}\right.\end{array}$$

(1)

where $T_{\max }$ and ${\kappa }_{\max }$ represent the maximum effective tension and the maximum bending curvature of the dynamic cable response, respectively, while MBL and MAC denote the maximum breaking tension and the maximum allowable curvature, respectively.

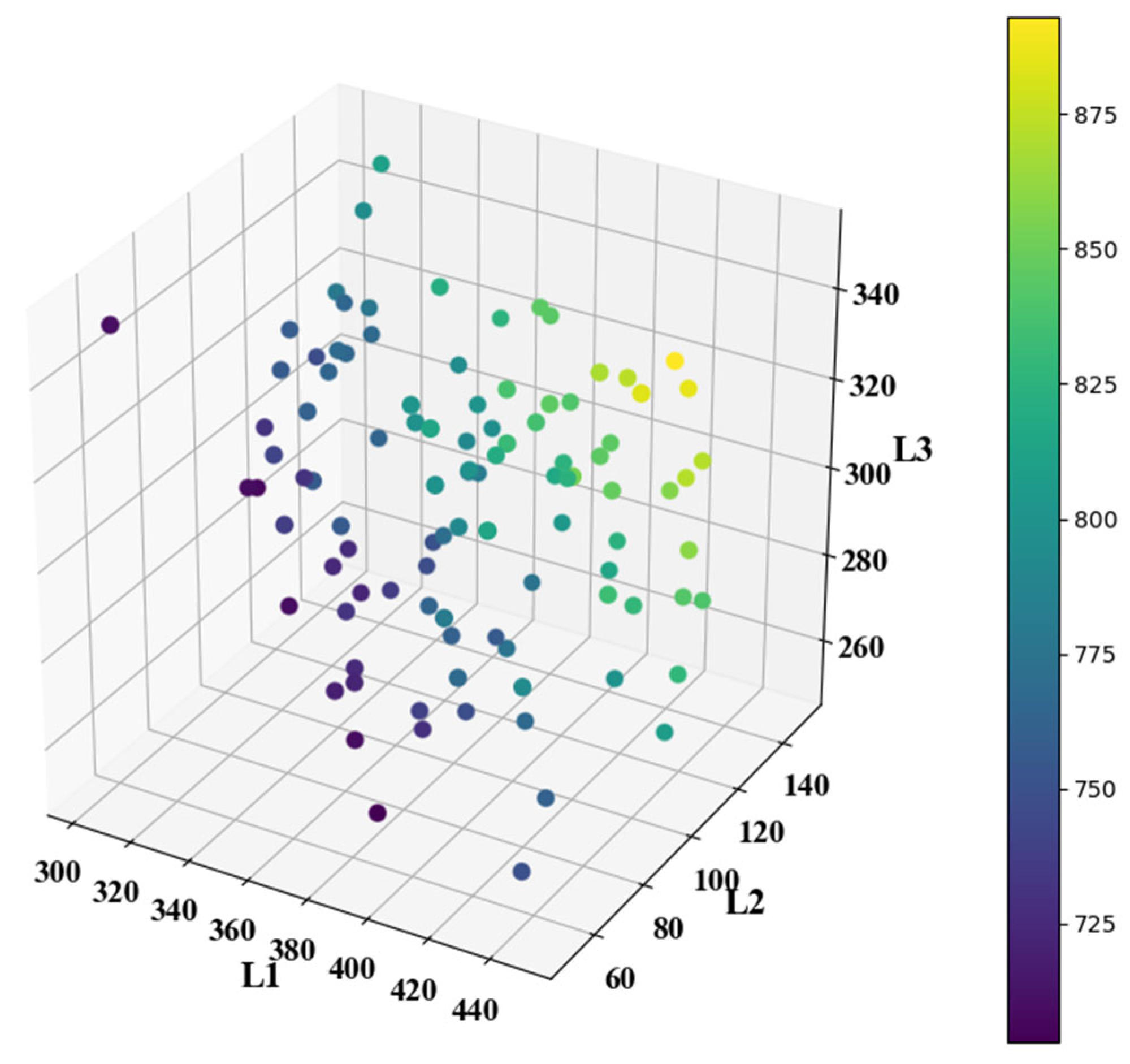
3.2. Optimal Latin Hypercube Sampling (OLHS)

The objective of experimental design for sampling is to select a relatively small number of sample points to maximize the acquisition of information about the relationship between design variables and performance parameters while minimizing experimental cost. This approach reduces unnecessary computational redundancy and improves the training efficiency of surrogate models. The Optimal Latin Hypercube Sampling (OLHS) method is adopted to ensure a uniform distribution of sample points within a high-dimensional design space, thereby enhancing computational efficiency and model accuracy. Based on this method, 100 sample points are generated within the defined ranges of $L_1$, $L_2$, and $L_3$ in Equation (1). The Optimal Latin Hypercube Sampling (OLHS) provides comprehensive coverage of the design space with non-repeating, uniformly random distributed points [19]. Their three-dimensional distribution is illustrated in Figure 8.

3.3. RBF Surrogate Model

The extreme response of dynamic cables is closely related to the parameters of the global line configuration, and its sensitivity varies with different design parameters. By appropriately adjusting these parameters to optimize the dynamic response, the dynamic cable’s ability to withstand environmental loads can be effectively improved. However, due to the complexity of marine loads and the dynamic responses of floating wind turbines, the global dynamic analysis of dynamic cables often exhibits strong nonlinear characteristics, making it difficult to derive explicit analytical expressions. Therefore, constructing a surrogate model based on pre-designed sample data becomes a necessary approach, laying the foundation for subsequent optimization design. Neural networks, known for their advantages in surrogate modeling, have been widely applied to solve complex engineering problems. Among them, the Radial Basis Function (RBF) network is an efficient multi-layer feedforward model that features a simple structure, easy implementation, and fast training convergence. Its fundamental idea is to establish a mapping relationship through the linear superposition of radial basis functions, enabling the construction of high-precision surrogate models from limited sample data [20]. It is typically expressed as follows:

$${\tilde{y}}_j(x)={\displaystyle {\sum }_{i=1}^N{w}_{ij}}\phi (‖x-x^i‖) (j=1,2\cdot \cdot \cdot p)$$

(2)

where $w_{ij}$ denotes the weight coefficients, $\phi$ represents the radial basis functions, typically Gaussian functions, N is the number of RBF neurons, and $p$ is the number of objective functions. The RBF neural network approximates input data by adjusting the weights between the input layer and the hidden layer, as well as the weights between the hidden layer and the output layer. During the training process, the network continuously optimizes these weights to effectively fit complex nonlinear relationships. As a result, a high-efficiency surrogate model is constructed, which can be applied in subsequent optimization design and prediction tasks.

To validate the effectiveness of the constructed surrogate model, the coefficient of determination is commonly used to evaluate the fitting accuracy. The coefficient of determination measures the strength of the linear relationship between the predicted and actual values, and is calculated as follows:

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n{(y_i-{\tilde{y}}_i)}^2}}{{\displaystyle {\sum }_{i=1}^n{(y_i-\overline{y})}^2}}}$$

(3)

where $y_i$ represents the actual value, ${\tilde{y}}_i$ is the value predicted by the surrogate model, $\overline{y}$ denotes the mean of all actual values, and n is the number of sample points used for testing. This coefficient reflects the goodness of fit of the model to the data. When the value of $R^2$ approaches 1, it indicates that the model’s predictions are very close to the actual results, demonstrating a good fitting performance. The error of the RBF surrogate model is shown in

Table 5. RBF surrogate model error.

Analysis Methods	Maximum Effective Tension	Maximum Bending Curvature	${\mathit{R}}^2$ > 0.95
	Error (${\mathit{R}}^2$)	Error (${\mathit{R}}^2$)
Mechanical Analysis	0.969	0.994	Yes
Thermo-Mechanical Coupling Analysis	0.968	0.995	Yes

. From the data in the table, it can be observed that the surrogate model meets the accuracy requirements for subsequent optimization computations.

3.4. NSGA-II Optimization Algorithm

In this study, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) is employed to perform optimization [21]. As an improved genetic algorithm, NSGA-II guides the search process using non-dominated sorting and crowding distance, while maintaining the diversity of the solution set through a penalty function mechanism. Compared to traditional genetic algorithms, NSGA-II can efficiently obtain high-quality Pareto-optimal solutions with lower computational cost, making it suitable for complex multi-objective optimization problems.

For the multi-objective optimization design of dynamic cables, the main steps using NSGA-II are as follows:

(1)

The Optimal Latin Hypercube Sampling (OLHS) method is used to generate a sufficient number of sample points that are uniformly distributed in the design space, ensuring comprehensive coverage of the key design variable ranges. To avoid issues such as touchdown of the hanging segment or excessive arching of the buoyant segment in the static configuration of the dynamic cable, initial screening is conducted to filter out inappropriate configurations, thereby improving computational efficiency. Based on the filtered samples, extreme responses under two working conditions—maximum effective tension and maximum bending curvature—are calculated using time-domain models of the dynamic cable under different stiffness conditions.

(2)

Based on the sampled data, a Radial Basis Function (RBF) neural network is used to construct a surrogate model that captures the nonlinear relationships between key design variables and response indicators. The prediction accuracy of the surrogate model is evaluated through error analysis, ensuring that the error between the model predictions and validation samples is minimized, thereby enhancing the model’s accuracy and reliability.

(3)

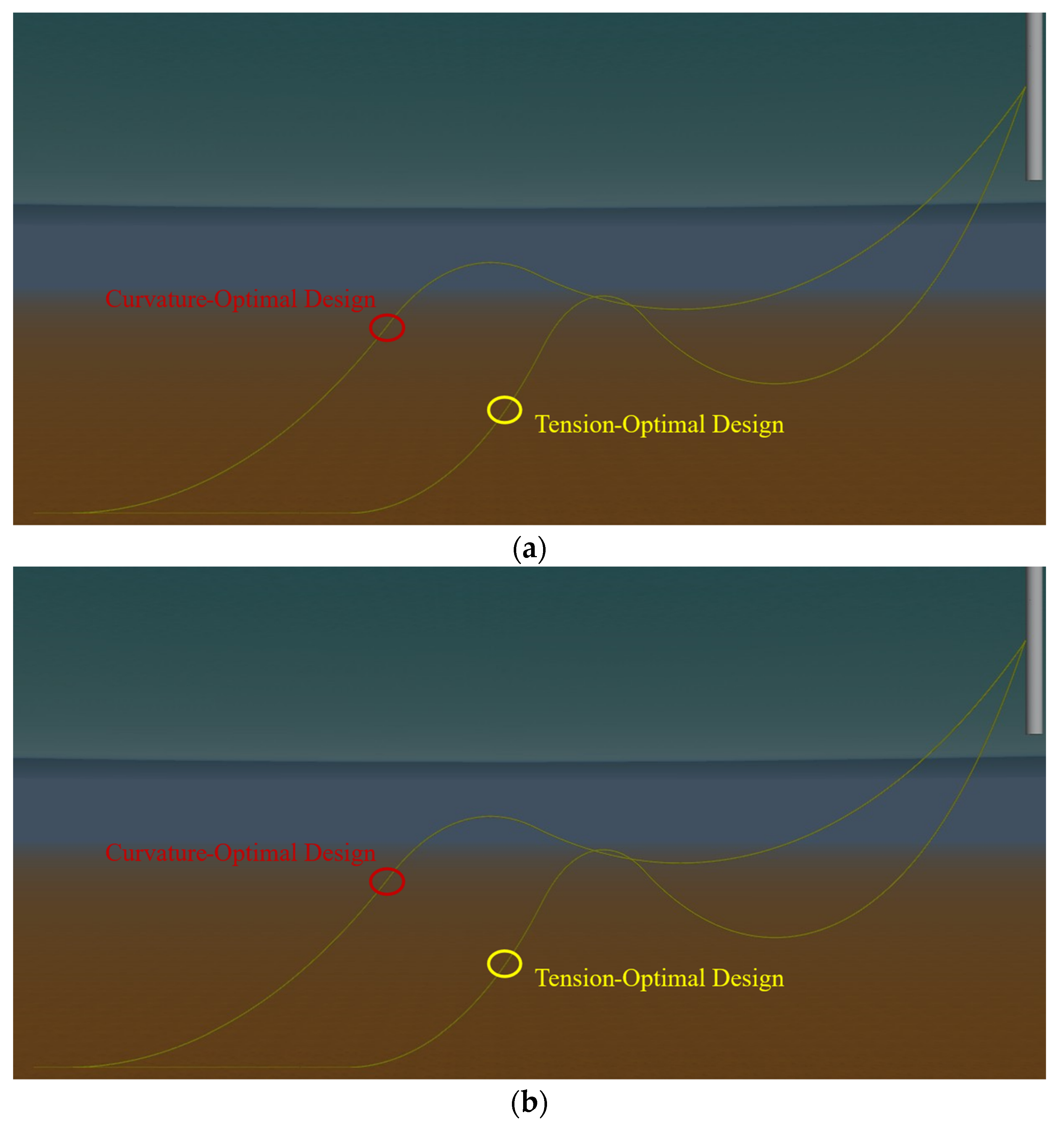
Using the nonlinear relationships established by the RBF surrogate model, the NSGA-II algorithm is applied to search for the Pareto-optimal front within the design variable space, achieving multi-objective optimization of cable tension and curvature. This ensures that multiple objectives are optimized simultaneously under different design variable combinations, providing a scientific basis for evaluating and selecting design solutions. The specific steps of the optimization process are illustrated in Figure 9.

4. Discussion of Optimization Results

From the sensitivity analysis of the optimization parameters above, it is evident that there is a competitive relationship between the effective tension and curvature performance of the dynamic cable. In the actual design of the dynamic cable shape, it is necessary to use multi-objective optimization to balance effective tension and bending curvature. Based on this, the NSGA-II optimization algorithm was employed to solve the optimization problem using the surrogate model constructed by the RBF neural network. The specific parameter settings for the optimization algorithm are shown in

Table 6. NSGA-II algorithm main parameters.

Parameter	Population Size	Number of Generations	Crossover Probability	Mutation Probability
Value	50	100	0.9	0.1

, which follows the recommendation from Refs. [8,11] to use initial conditions from pre-design. After 100 iterations, the Pareto front for the shape optimization design based on both static and thermo-mechanical coupling analyses was obtained, as shown in Figure 10. The optimization process, which is based on the dynamic cable stiffness characteristics calculated from both mechanical and thermo-mechanical coupling analyses, successfully balances effective tension and bending curvature in the multi-objective optimization process, providing a more reasonable optimization scheme for the dynamic cable shape design.

To verify the feasibility and accuracy of the proposed bi-objective optimization model, representative design parameters corresponding to single-objective optimization solutions were selected, specifically Pareto Front No. A and No. B in Figure 10a, and Pareto Front No. A’ and No. B’ in Figure 10b. The corresponding cable configurations are illustrated in Figure 11. A global dynamic analysis of the dynamic cable was conducted using the coupling floating wind turbine model introduced in Section 2. The optimization results were then compared with numerical simulation results, as summarized in

Table 7. Comparison of single-objective optimization results with numerical results (mechanical analysis).

Calculation Method	Tension Optimal Design		Curvature Optimal Design
	Maximum Effective Tension/[kN]	Maximum Bending Curvature/[m−1]	Maximum Effective Tension/[kN]	Maximum Bending Curvature/[m−1]
Surrogate model	35.68	0.05049	80.73	0.02596
Numerical simulation	38.02	0.05124	82.24	0.02729
Error/%	6.15%	0.29%	1.84%	4.87%

and

Table 8. Comparison of single-objective optimization results with numerical results (thermo-mechanical coupling analysis).

Calculation Method	Tension Optimal Design		Curvature Optimal Design
	Maximum Effective Tension/[kN]	Maximum Bending Curvature/[m−1]	Maximum Effective Tension/[kN]	Maximum Bending Curvature/[m−1]
Surrogate model	37.85	0.04939	80.98	0.02756
Numerical simulation	40.27	0.04976	82.71	0.02833
Error/%	6.01%	0.07%	2.09%	2.72%

. The comparison indicates that the maximum deviations in effective tension and bending curvature are both less than 6.15%. It is acceptable when considering the stochastic nature of the ocean environment [11].

In practical engineering applications, the two aforementioned single-objective optimal design schemes represent extreme cases and should be avoided. The curvature-optimal design typically results in a shorter cable configuration, which is prone to straightening under 180° directional loading. This phenomenon hinders the cable’s ability to accommodate the floating platform’s motions, thereby causing excessive tension and potential cable failure. Conversely, the tension-optimal design usually exhibits a significantly undulated shape, leading to a globally longer cable length. This may result in interference between the cable and either the seabed or sea surface, increasing the risk of mechanical damage.

Therefore, the optimal design should simultaneously consider both effective tension and bending curvature as optimization objectives, striking a balance between their relative importance. From the Pareto front, a specific solution can be selected based on practical performance requirements. In general, selecting a design from the central region of the Pareto front yields a balanced trade-off between the two objectives, ensuring that both tension and curvature remain within acceptable limits. Accordingly, the design parameters corresponding to Pareto Front No. C in Figure 10a and Pareto Front No. C’ in Figure 10b are selected as the optimal design solutions under mechanical and thermo-mechanical coupling analyses, respectively. These optimized configurations are compared with the initial design for further evaluation, as illustrated in Figure 12.

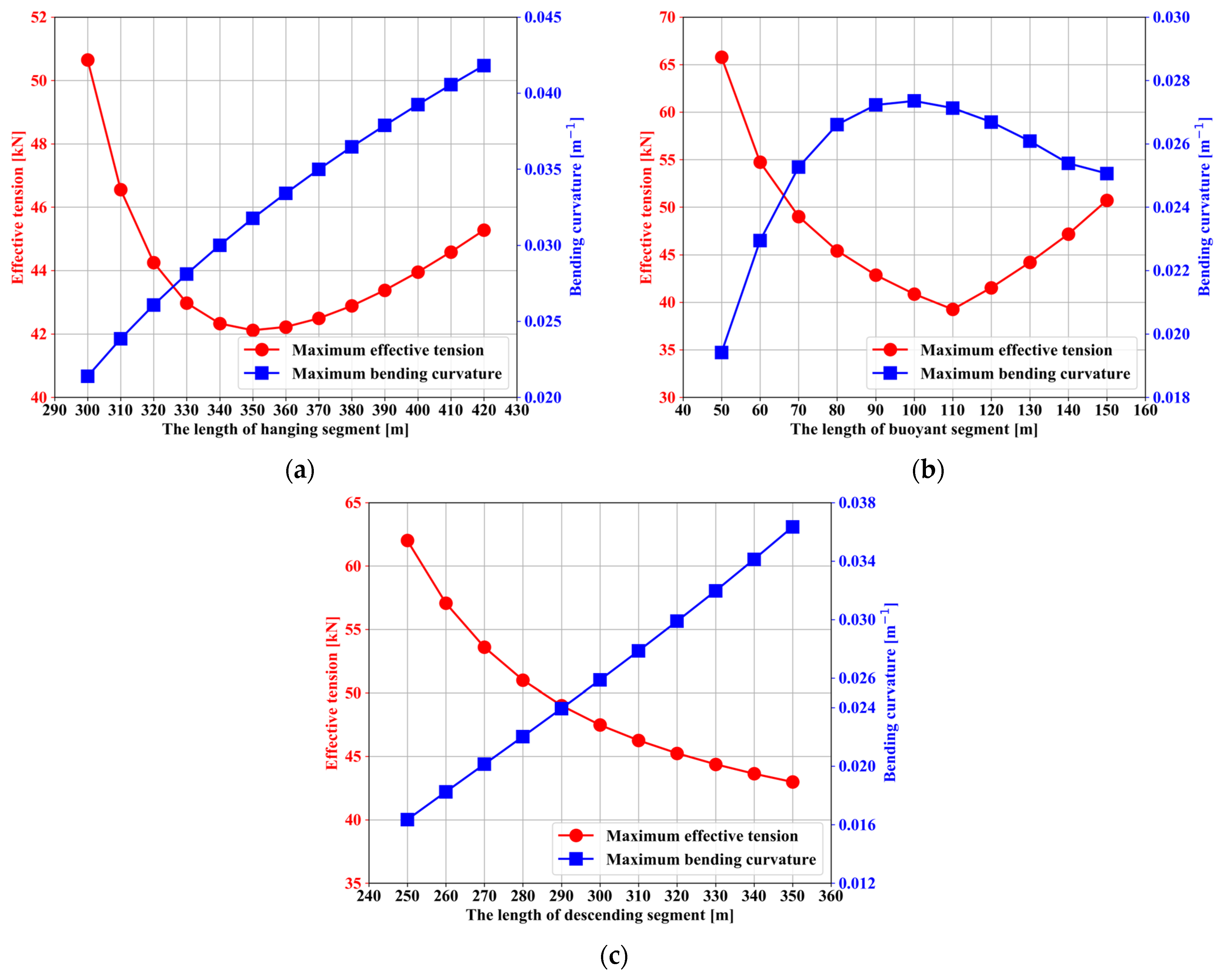
4.1. Effective Tension

The global dynamic analysis was conducted based on the design parameters corresponding to Pareto Front No. C and Pareto Front No. C’, with a comparison of the effective tension extracted from the initial design results, as shown in Figure 13. The numerical comparison of the maximum effective tension is presented in

Table 9. Comparison of effective tension between initial design and dual-objective optimization design.

Comparison of Design Schemes	Optimization Objective	Global Configuration Parameters
	Maximum Effective Tension/[kN]	Hanging Segment/[m]	Buoyant Segment/[m]	Descending Segment/[m]	Total Length/[m]
Initial design	54.44	400.0	80.0	270.0	750.0
Mechanical analysis	51.88	365.5	100.4	279.8	745.7
Change rate	−4.93%	-	-	-	−0.57%
Thermo-mechanical coupling analysis	53.03	369.4	99.8	273.5	742.7
Change rate	−2.59%	-	-	-	−0.97%

. The results indicate that, under both static and thermo-mechanical coupling analysis, the optimized cable configurations lead to a reduction in tension within the hanging segment compared to the initial design. Meanwhile, the length of the buoyant segment is increased, effectively alleviating the tension at the hang-off point. Specifically, the maximum effective tension is reduced by 4.93% under static analysis and by 2.59% under thermo-mechanical coupling analysis. In addition to the improvement in tensile performance, the global cable length is also reduced to some extent, potentially lowering material costs. Compared to the static case, the reduction in effective tension under thermo-mechanical coupling is slightly smaller. This is attributed to the fact that the coupling thermal-mechanical effect decreases the axial stiffness of the cable, making it more susceptible to deformation under dynamic loading, which in turn increases the effective tension at the hang-off point.

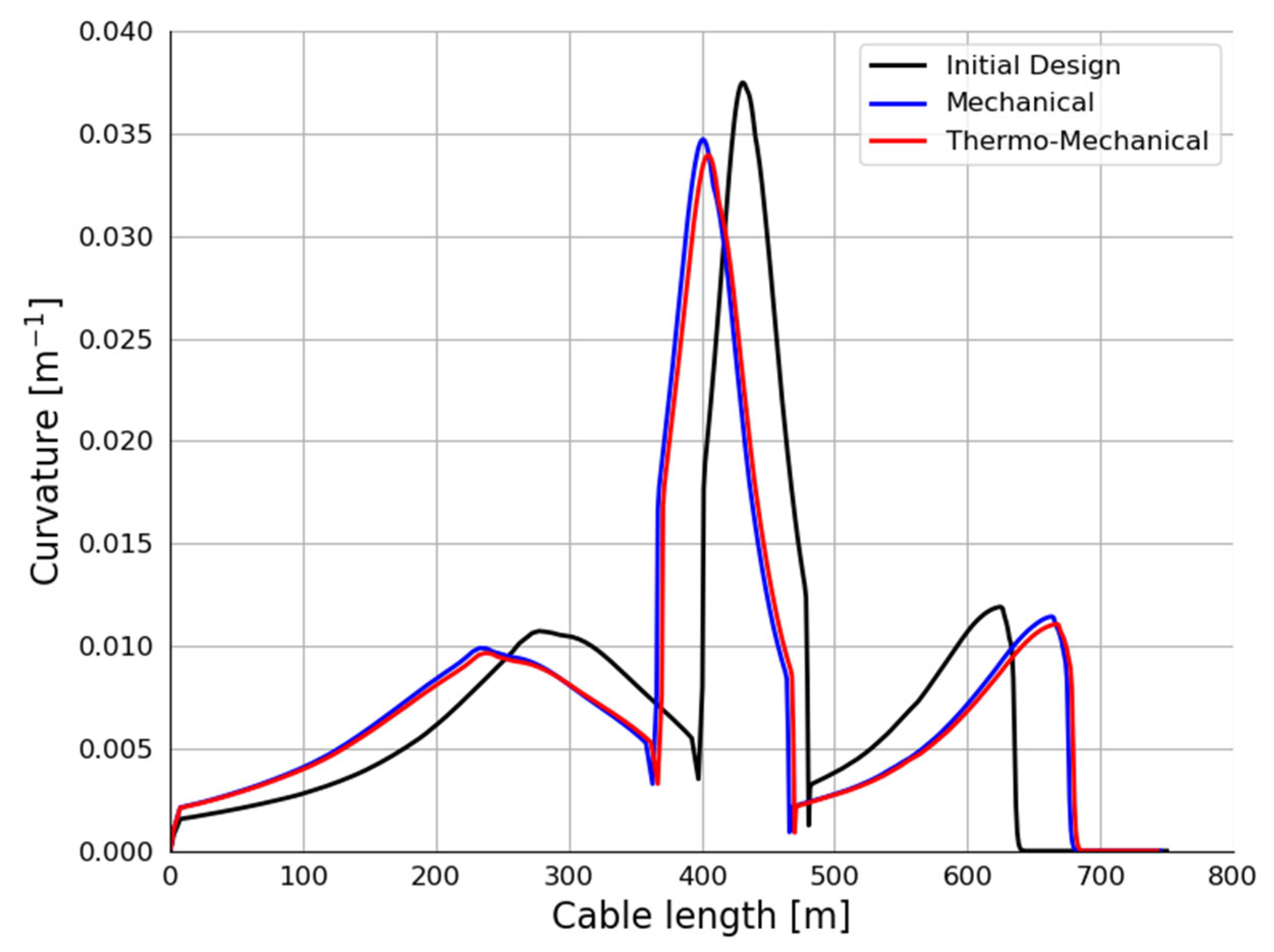
4.2. Bending Curvature

Based on the design parameters corresponding to Pareto Front No. C and Pareto Front No. C’, a global dynamic analysis was conducted, and the resulting bending curvature was compared with that of the initial design, as illustrated in Figure 14. The comparison of the maximum bending curvature values is presented in

Table 10. Comparison of bending curvature between initial design and dual-objective optimization design.

Comparison of Design Schemes	Optimization Objective	Global Configuration Parameters
	Maximum Bending Curvature/[m−1]	Hanging Segment/[m]	Buoyant Segment/[m]	Descending Segment/[m]	Total Length/[m]
Initial design	0.03747	400.0	80.0	270.0	750.0
Mechanical analysis	0.03470	365.5	100.4	279.8	745.7
Change rate	−7.39%	-	-	-	−0.57%
Thermo-mechanical coupling analysis	0.03394	369.4	99.8	273.5	742.7
Change rate	−9.42%	-	-	-	−0.97%

. The optimization results show that the maximum bending curvature decreased by 7.39% and 9.42%, respectively. Observing the changes in the cable configuration, the waveform of the buoyant segment becomes more gradual after optimization, resulting in a reduction in bending curvature. This effect is particularly evident under thermo-mechanical coupling analysis, where the curvature reduction is more pronounced. This can be attributed to the material softening caused by the thermo-mechanical coupling effect, which leads to a reduction in bending stiffness and consequently results in a more flexible global cable configuration. Such flexibility allows the dynamic cable to better accommodate the motions of the floating platform and mitigates curvature variations induced by external environmental loads.

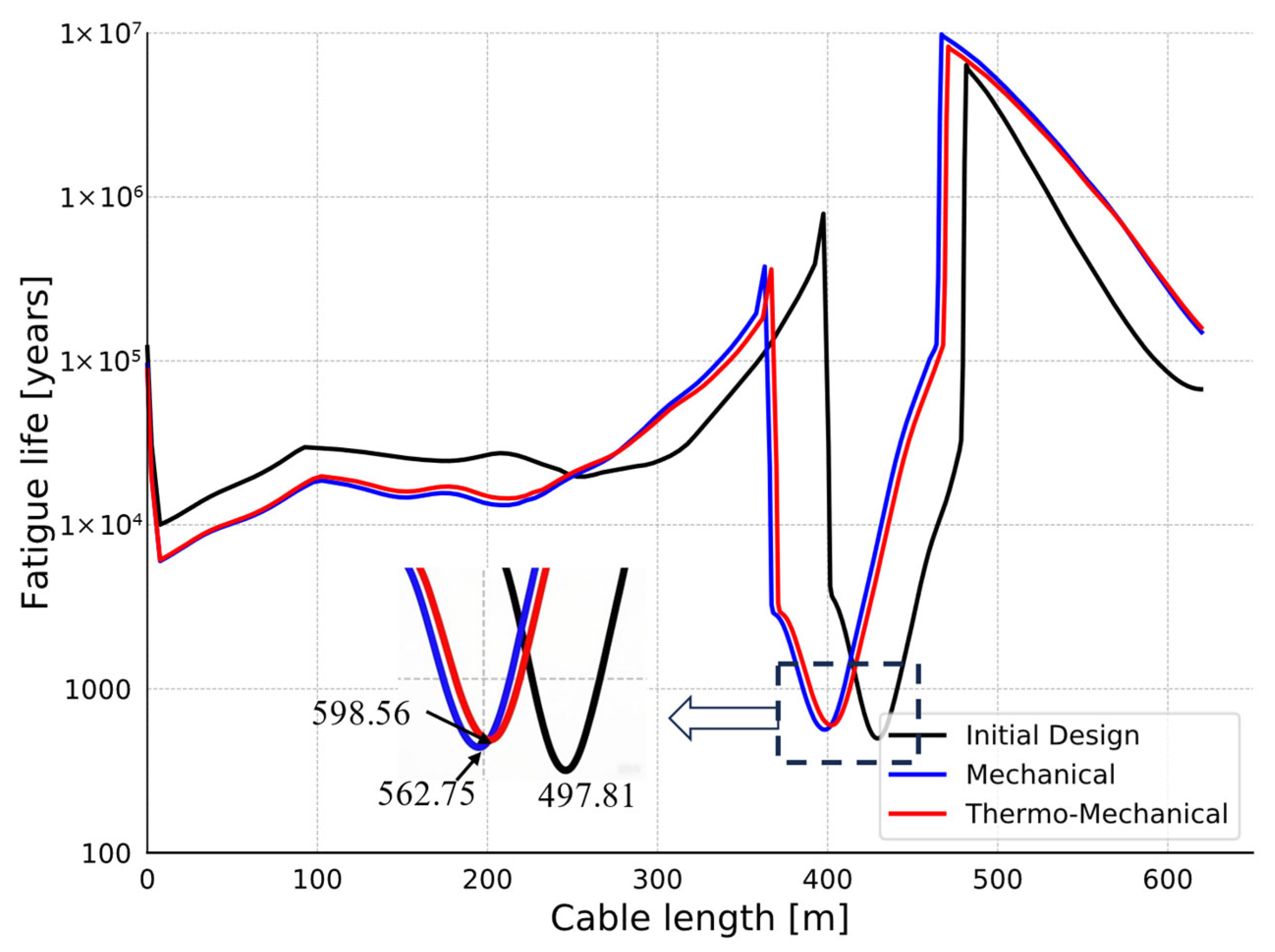
4.3. Fatigue Life

To further validate the reliability of the proposed multi-objective optimization strategy, the fatigue performance of three design schemes was evaluated based on statistical ocean environmental data from a specific sea area. Fatigue life prediction was adopted as an assessment metric before and after optimization. The fatigue life calculation for the dynamic cable involves the following steps: (1) collecting and processing environmental loading data (e.g., wave scatter diagrams); (2) conducting global time-domain dynamic analysis of the cable to obtain time histories of effective tension and curvature; (3) computing stress concentration factors using a local finite element model of the cable, namely, the effective tension-to-stress and curvature-to-stress coefficients; (4) calculating the fatigue life distribution along the cable length based on the S-N curve of the material, rain-flow counting method, and Miner’s linear damage accumulation rule. The results are shown in Figure 15, where the minimum fatigue life occurs in the central region of the buoyant segment—corresponding to the location of maximum curvature. This is primarily due to the fact that, although the effective tension is relatively low compared to catenary-type configurations, the buoyant segment is more susceptible to repeated bending induced by the platform’s heave and drift motions. During the stress distribution analysis, the curvature-to-stress coefficient was found to be significantly greater than the tension-to-stress coefficient, indicating that curvature-induced fatigue dominates the damage process, while the contribution of effective tension is comparatively minor. After optimization, the fatigue life of the dynamic cable improved by 13.04% and 20.24% under mechanical and thermo-mechanical coupling analyses, respectively, compared to the initial design. The optimization results under thermo-mechanical coupling show a more pronounced enhancement. These findings validate the accuracy of the proposed optimization model and underscore the importance of considering thermo-mechanical coupling effects in the optimization process. Incorporating these effects enables a more accurate reflection of the cable’s operational conditions, significantly enhancing its fatigue life, long-term stability, and operational safety.

5. Conclusions

Axial and bending stiffness are key parameters influencing the global dynamic response of dynamic cables, directly determining the extreme dynamic responses such as maximum effective tension and bending curvature. Thermo-mechanical coupling significantly affects the stiffness characteristics of the cable and should be thoroughly considered in the optimal configuration design of dynamic cables. In this study, a global dynamic analysis in the time domain was conducted for a dynamic cable used in the OC3-Hywind floating wind turbine system, taking into account the coupling interactions among the floating platform, mooring system, and the dynamic cable. During the optimization process, a surrogate model was constructed using the Radial Basis Function (RBF) neural network to relate design parameters to objective functions, and the NSGA-II algorithm was applied for tension-curvature multi-objective optimization, resulting in a set of Pareto Frontiers of optimal solution. The main conclusions are as follows:

(1)

The maximum deviation between the single-objective optimization results and numerical simulations is 6.15%, verifying the feasibility and accuracy of the proposed optimization model.

(2)

Compared to the initial design, the optimized configurations based on mechanical and thermo-mechanical coupling analyses achieved reductions in effective tension by 4.93% and 2.59%, respectively, and reductions in curvature by 7.39% and 9.42%, respectively.

(3)

While the total length of the dynamic cable was slightly reduced, its global dynamic response was significantly improved, and its fatigue life was markedly enhanced, with improvements of 13.04% and 20.24%, respectively, relative to the initial design. Notably, the optimization based on thermo-mechanical coupling demonstrated superior performance, offering a new perspective for dynamic cable configuration optimization.

However, it should be noted that these improvements come with a significant increase in buoyant section length, potentially raising manufacturing complexity and economic cost due to the need for additional buoyancy modules. We will include consideration of such factors in future optimization studies.