Influence of Geometric Effects on Dynamic Stall in Darrieus-Type Vertical-Axis Wind Turbines for Offshore Renewable Applications
Abstract
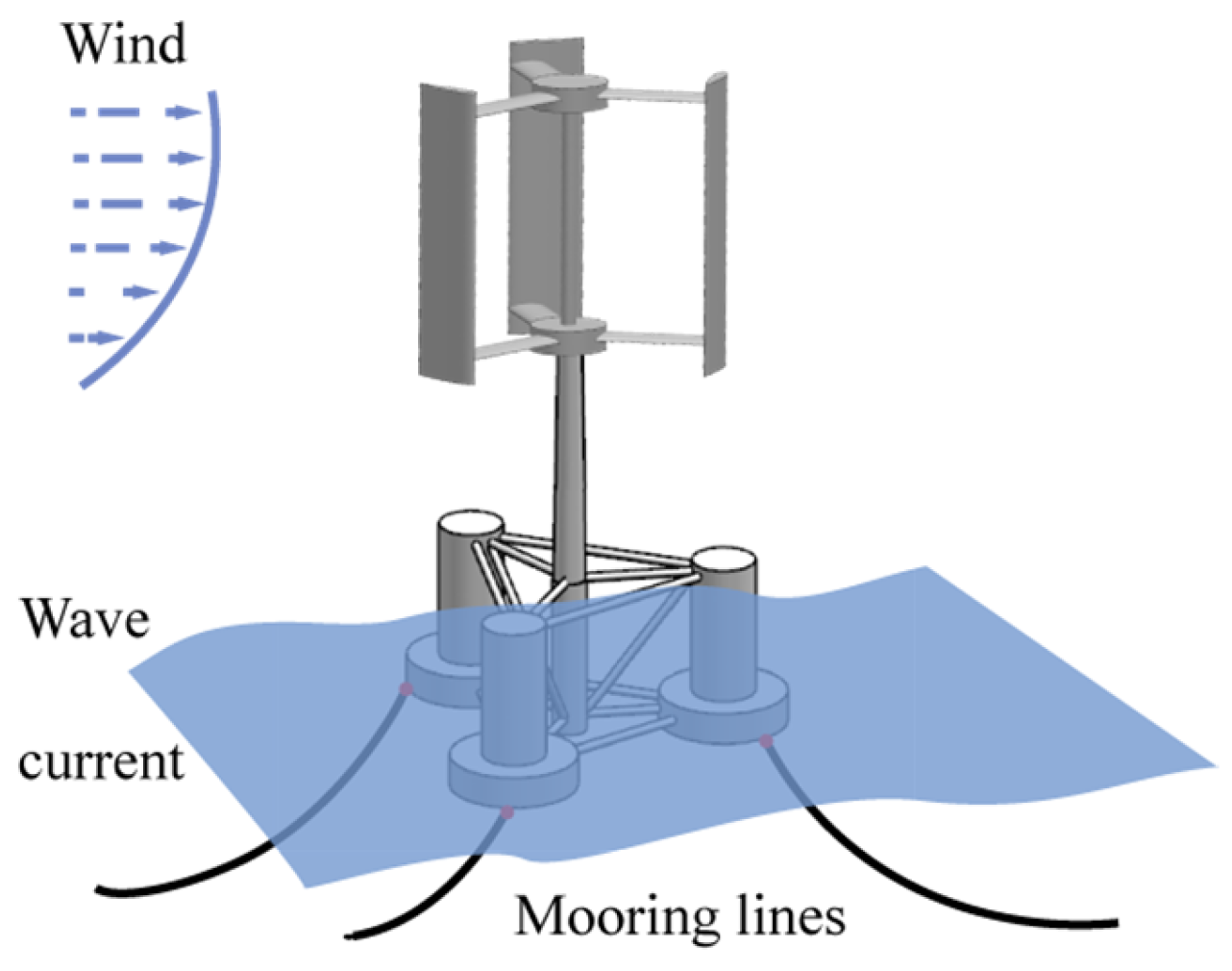
1. Introduction
- Detailed flow field analysis is conducted through high-fidelity CFD simulations to investigate the generation, development, and evolution of dynamic stall under DPM, providing a comprehensive understanding of the aerodynamic behavior of VAWT blades.
- A surrogate model based on a radial basis function neural network (RBFNN) is developed to efficiently predict aerodynamic responses from geometric parameters, thereby significantly reducing the computational cost of large-scale parametric analysis.
- A global sensitivity analysis framework based on Sobol′s indices is established to quantify the individual and interactive effects of airfoil geometric parameters on dynamic stall characteristics.
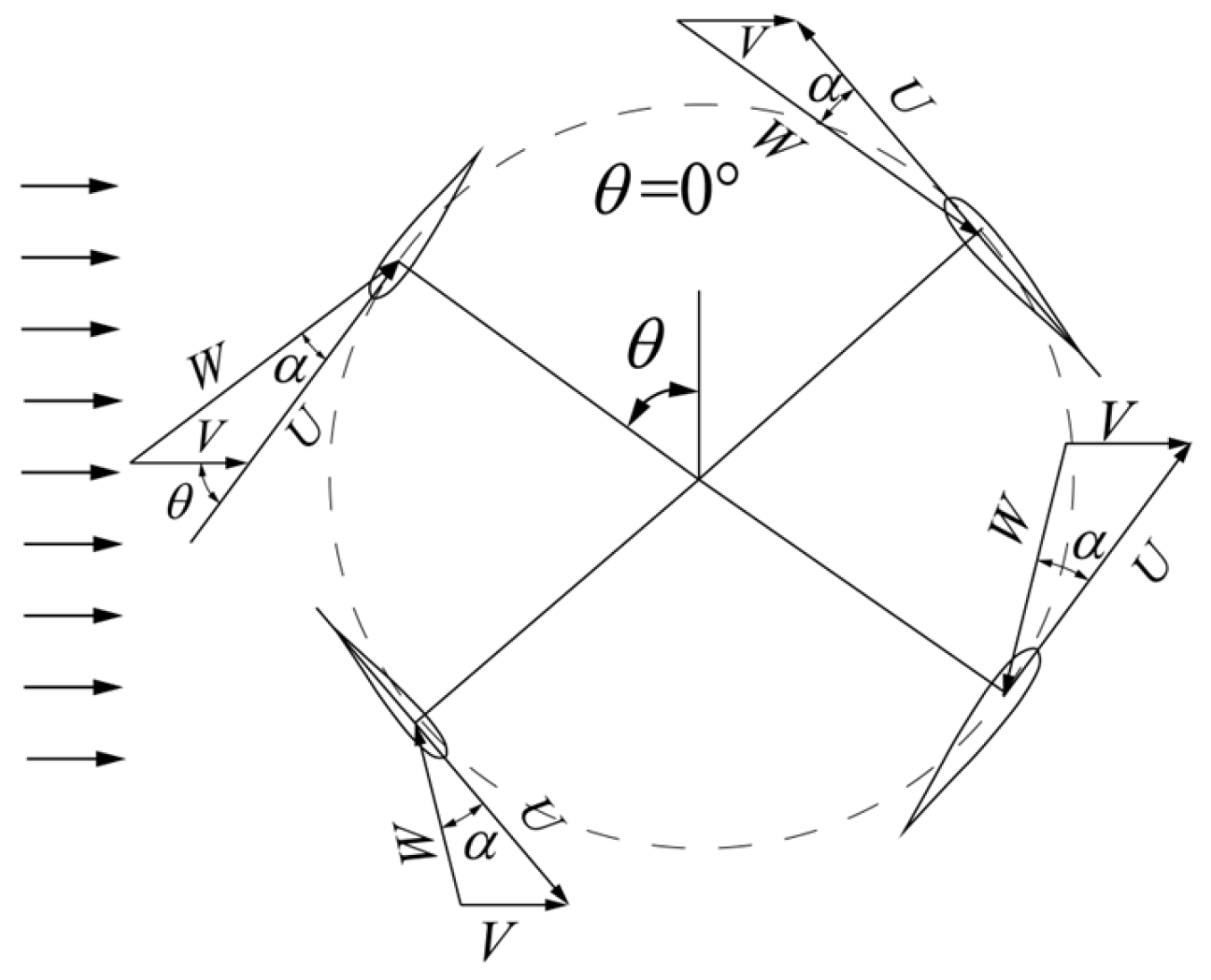
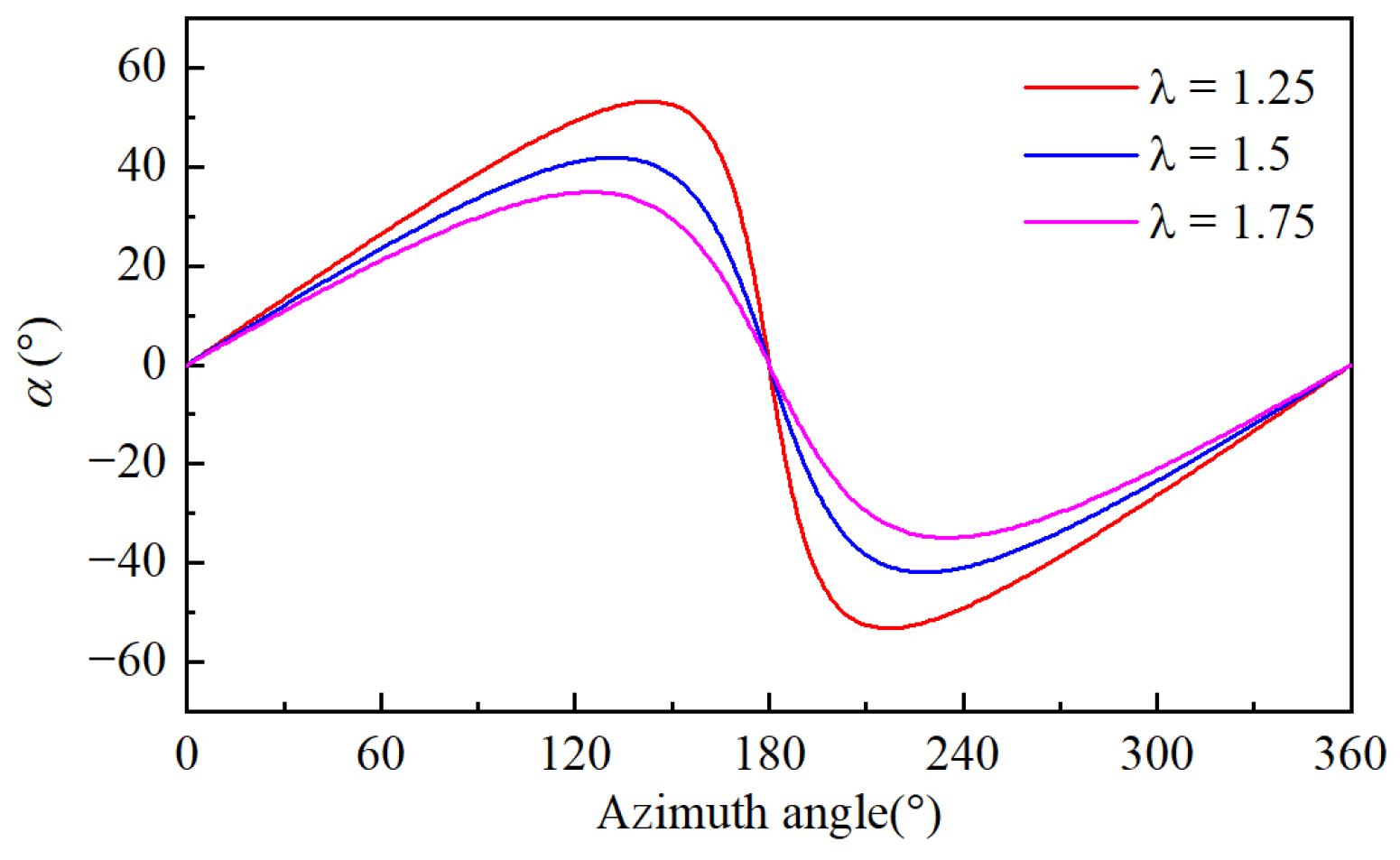
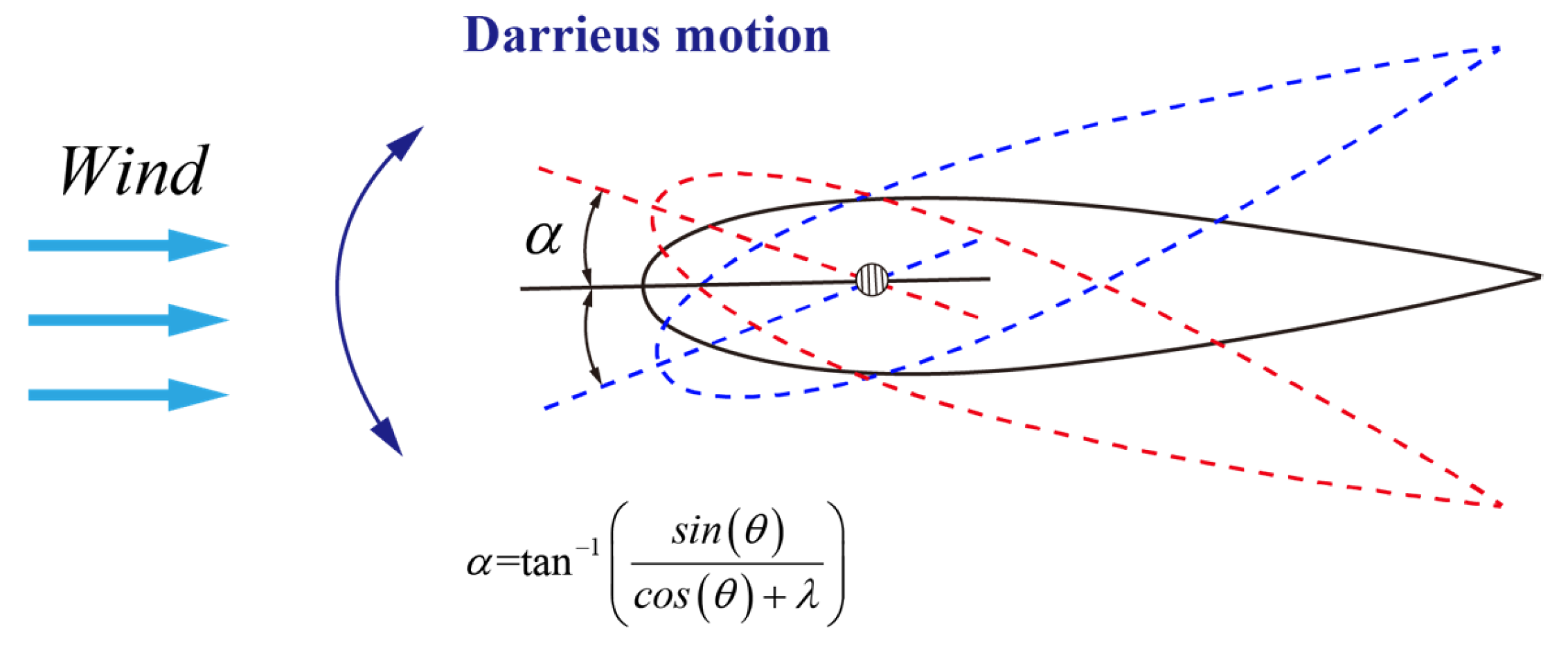
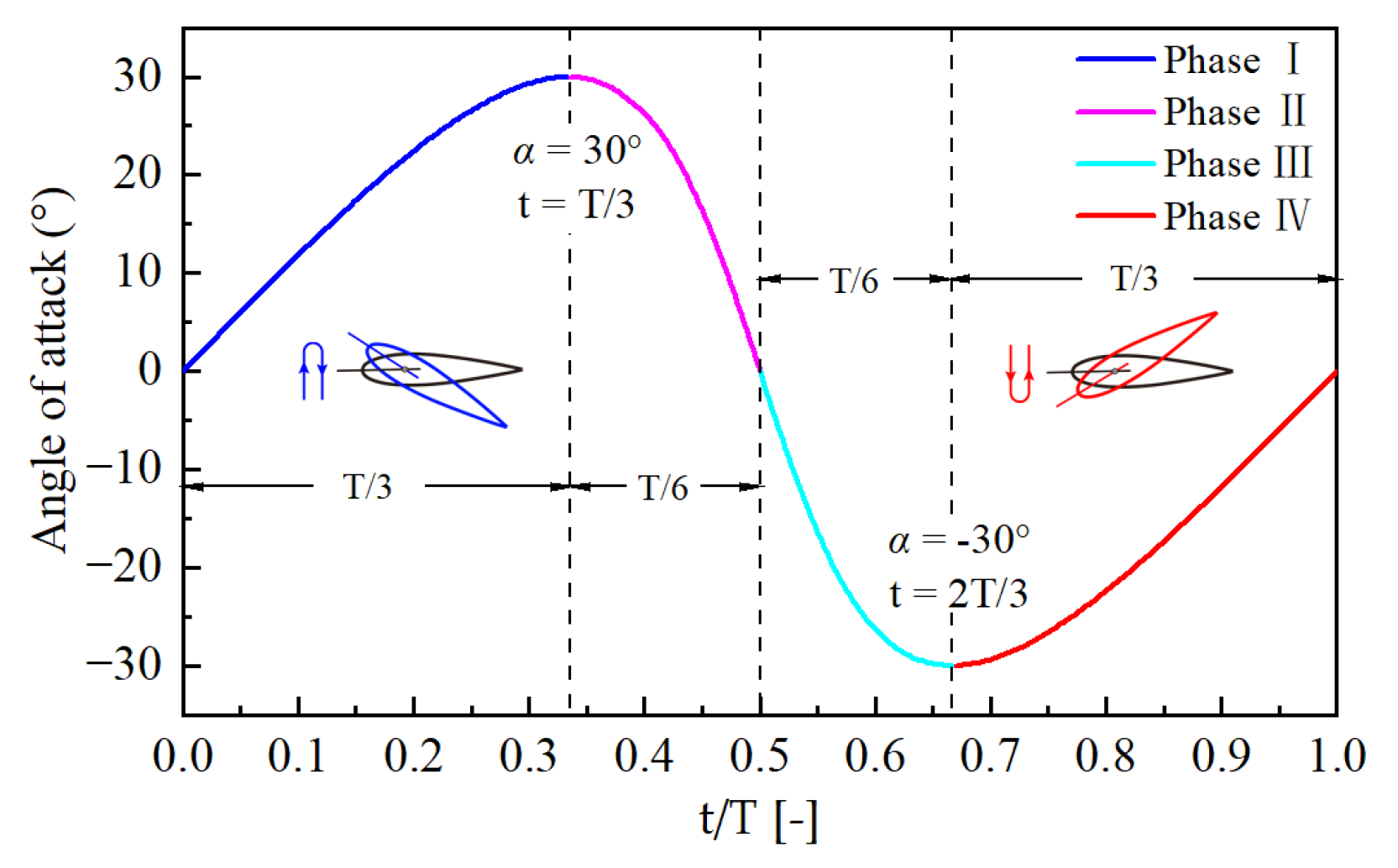
2. Darrieus-Type Pitching Motion (DPM)
3. Methodology for Sensitivity Analysis
3.1. Sobol Sensitivity Analysis Method
- (1)
- Generate Monte Carlo samples, which typically requires two sets of input matrices A and B of size (N, n), where n is the number of design variables, and N is the number of samples used for the sensitivity analysis.
- (2)
- Construct the mixed matrices A(i) and B(i). Replace the i-th column of matrix B with the i-th column of A and keep the rest of the columns to form A(i). Conversely, replace the i-th column of A with the i-th column of B to get B(i).
- (3)
- Obtain column vectors (YA, YB, , and ) of size (N, 1) by evaluating the model from A, B, A(i), and B(i), which defined as:
- (4)
- Calculate the first-order index and the total index for the i-th input variable using the following equations:
3.2. Surrogate Model Method
3.2.1. PARSEC Parameterization
3.2.2. Optimized Latin Hypercube Sampling (OLHS)
3.2.3. Radial Basis Function Neural Network (RBFNN)
3.2.4. Validation of Surrogate Model
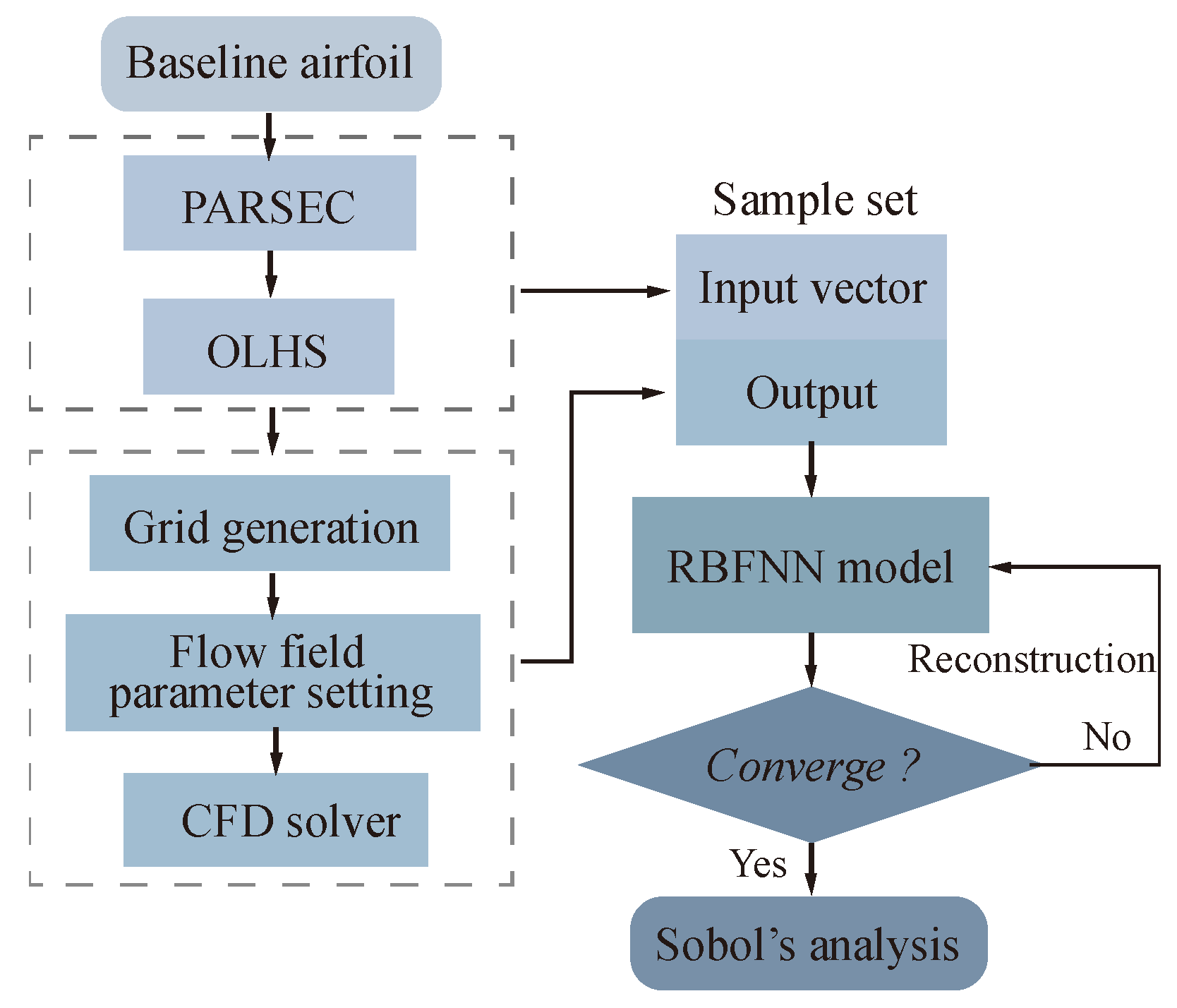
3.3. Sensitivity Analysis Process
- (1)
- Using the PARSEC parameterization method, we obtain the 12 geometric parameters for the upper and lower surfaces of the airfoil NACA0018.
- (2)
- The OLHS method is applied to obtain 200 initial samples in the design space as the input vector x. The aerodynamic coefficients are solved using the CFD method as the output response y.
- (3)
- The RBFNN model is constructed using the dataset (x, y). There are 180 samples in the training set and 20 in the test set. The accuracy of the model is verified by the MSE, RMSE, and R2. If the convergence error is not satisfied, we retrain the model by adjusting the neural network parameters.
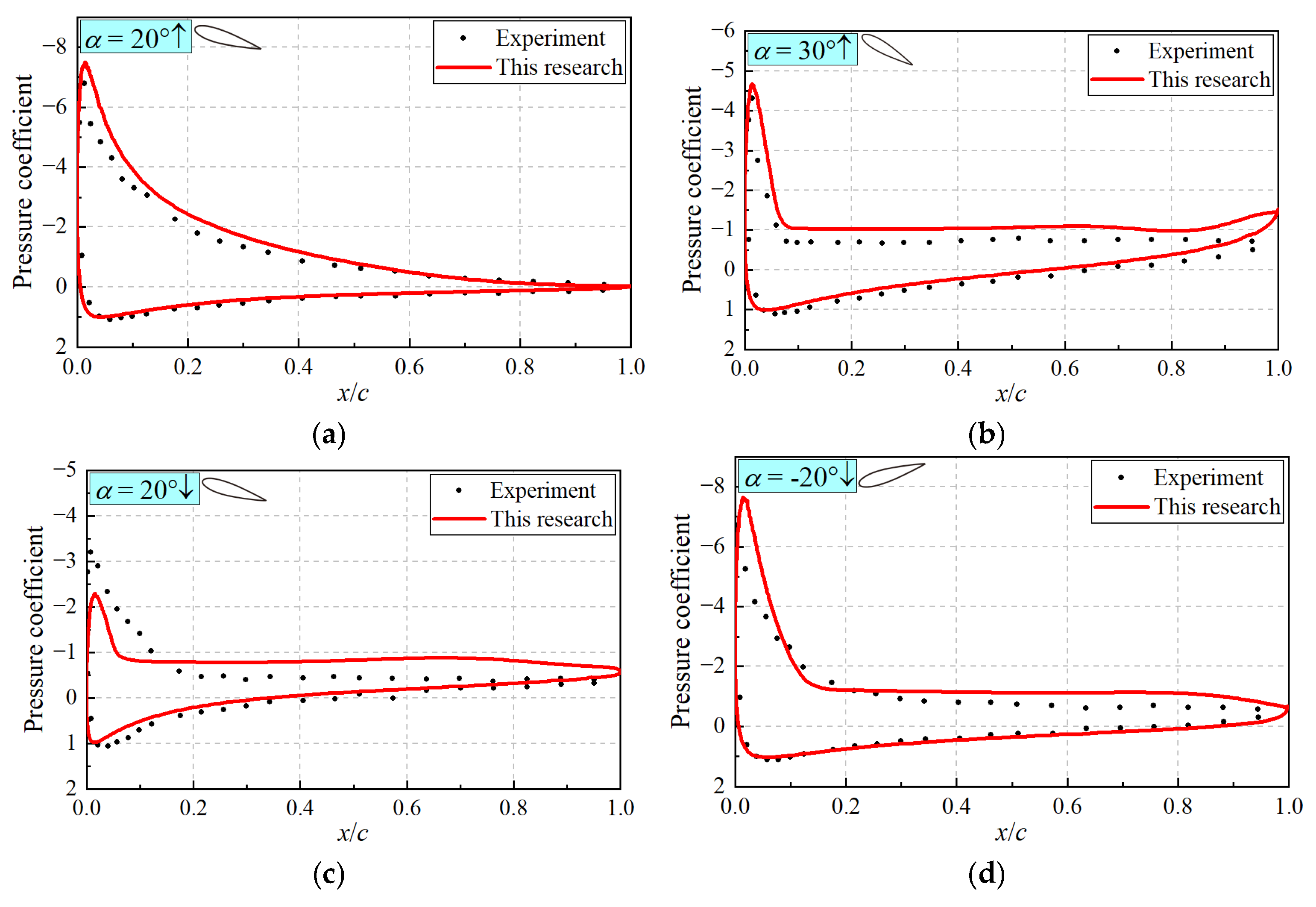
4. Numerical Modeling and Verification
4.1. Reference Case
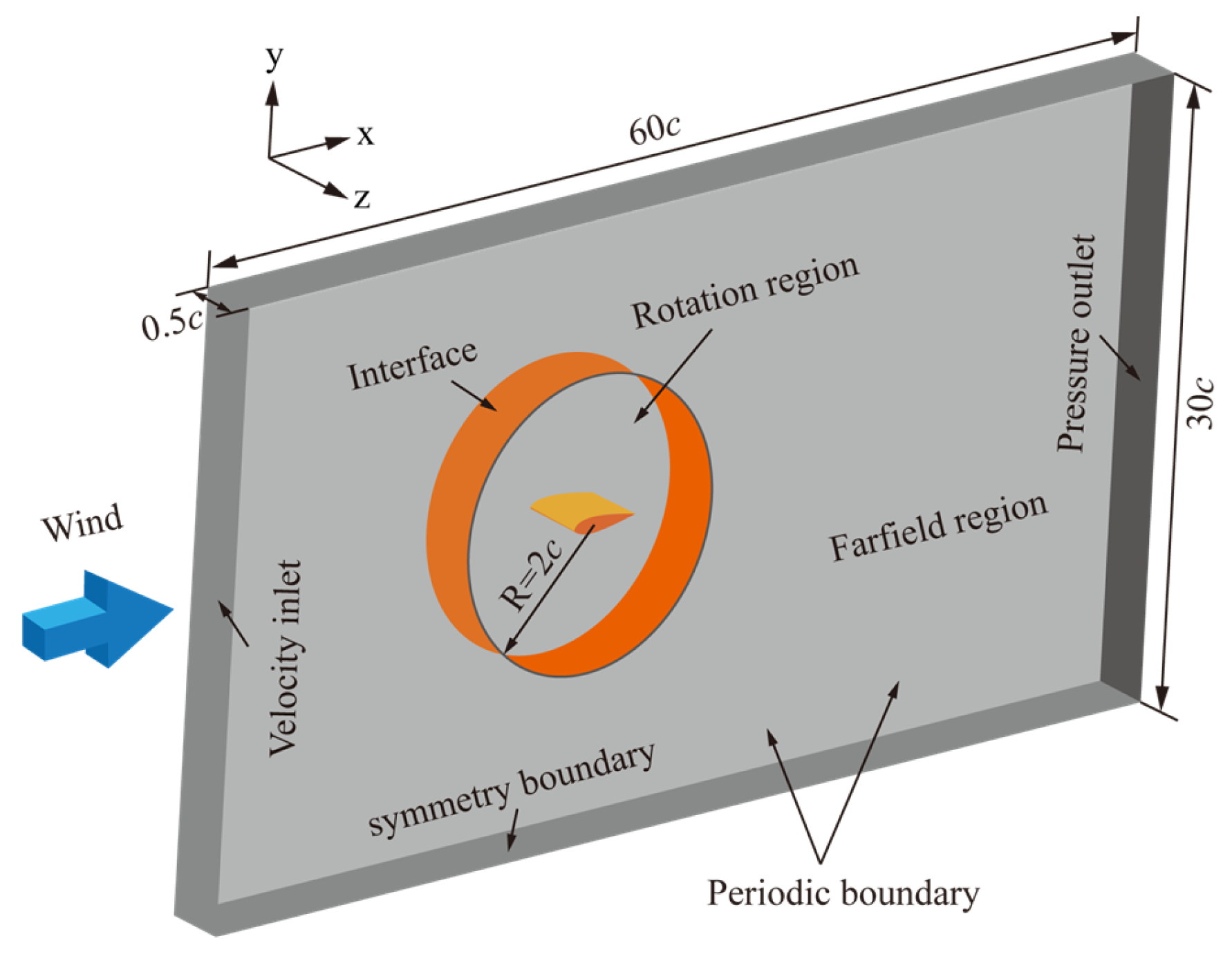
4.2. Computational Domain and Grid
4.3. Independence Verification
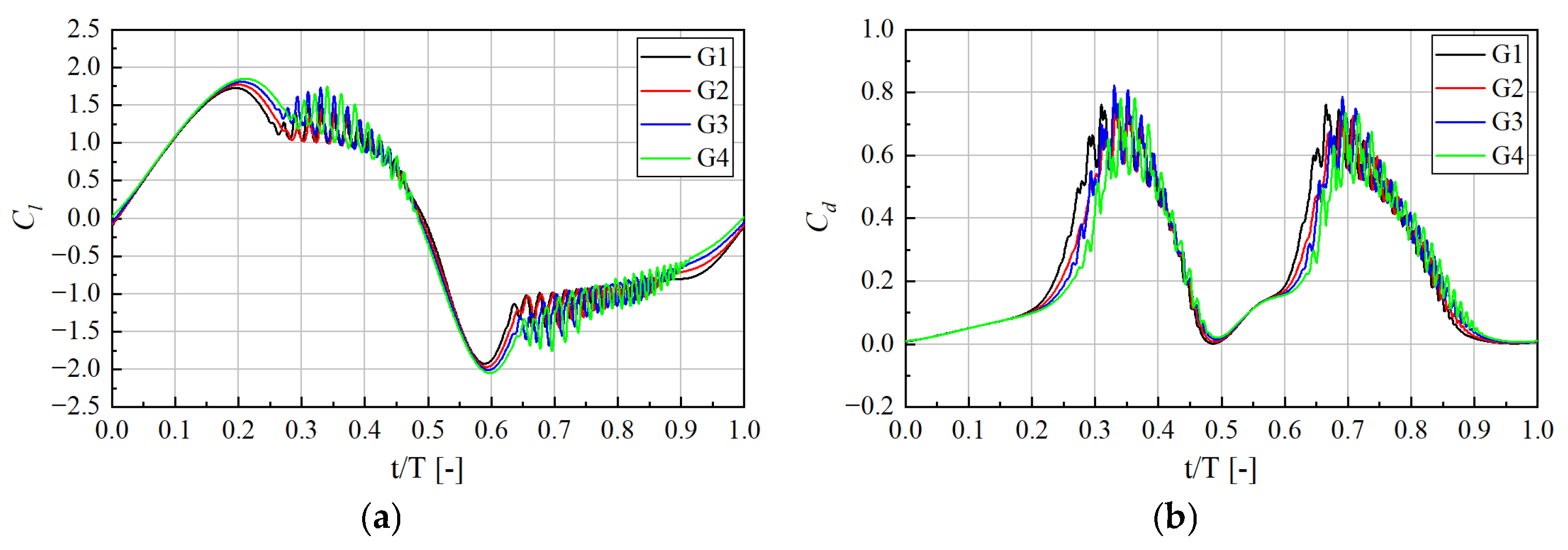
4.3.1. Grid Independence Verification
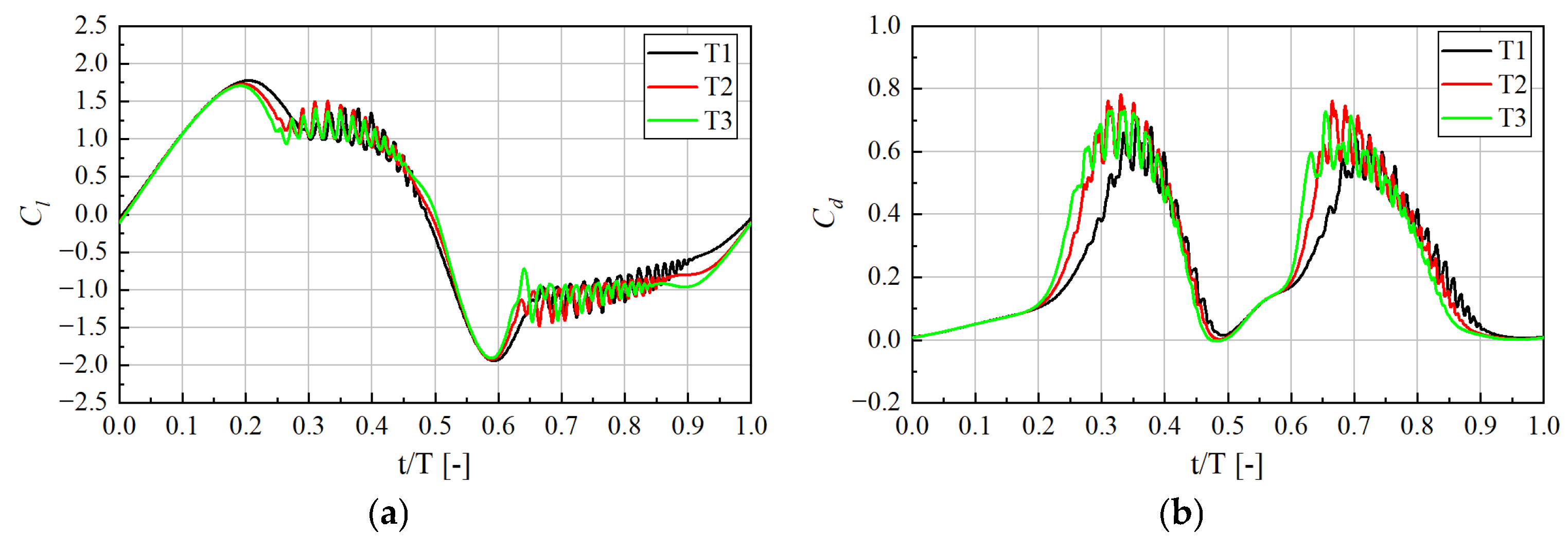
4.3.2. Time Independence Verification
5. Results and Discussion
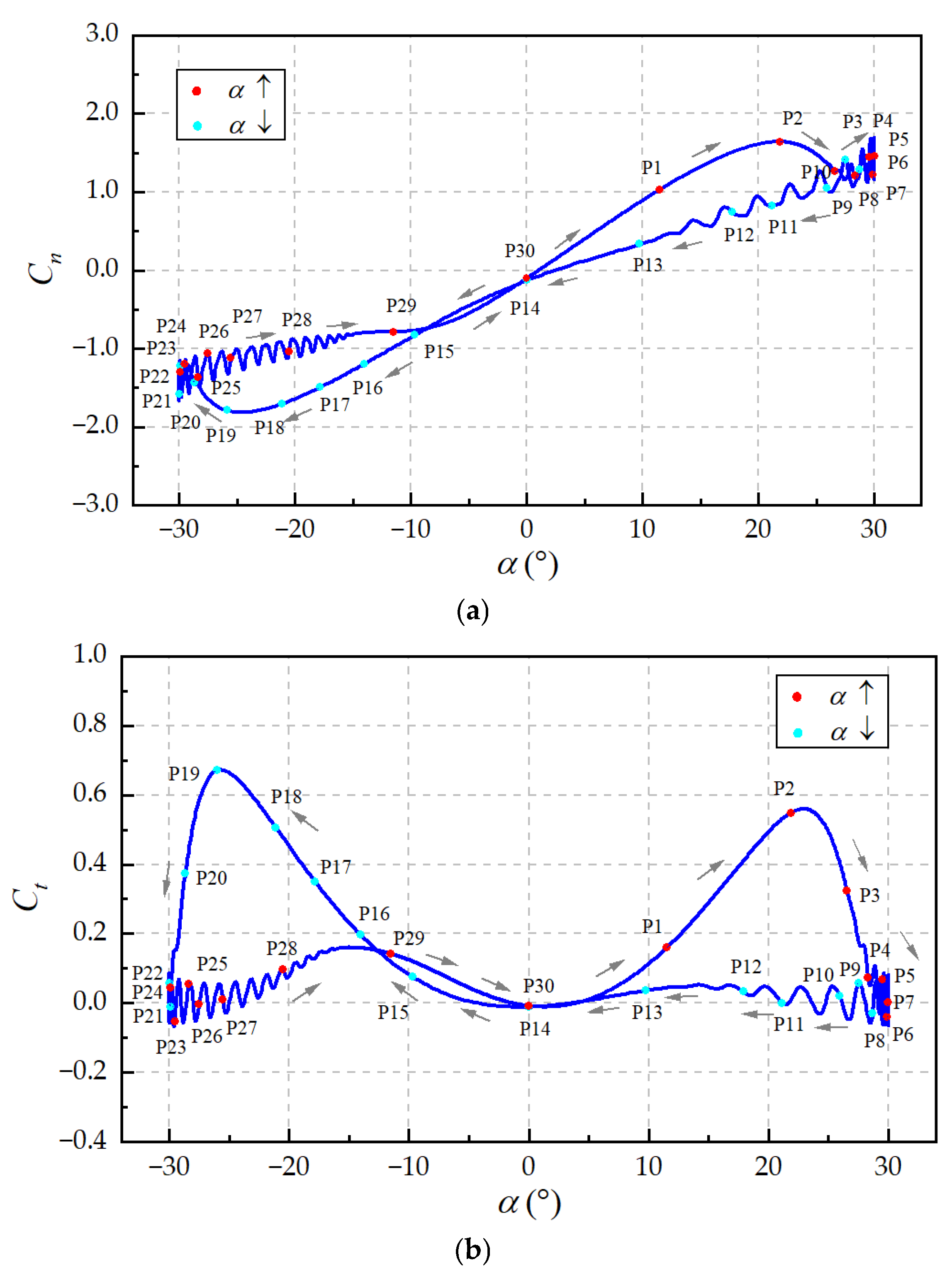
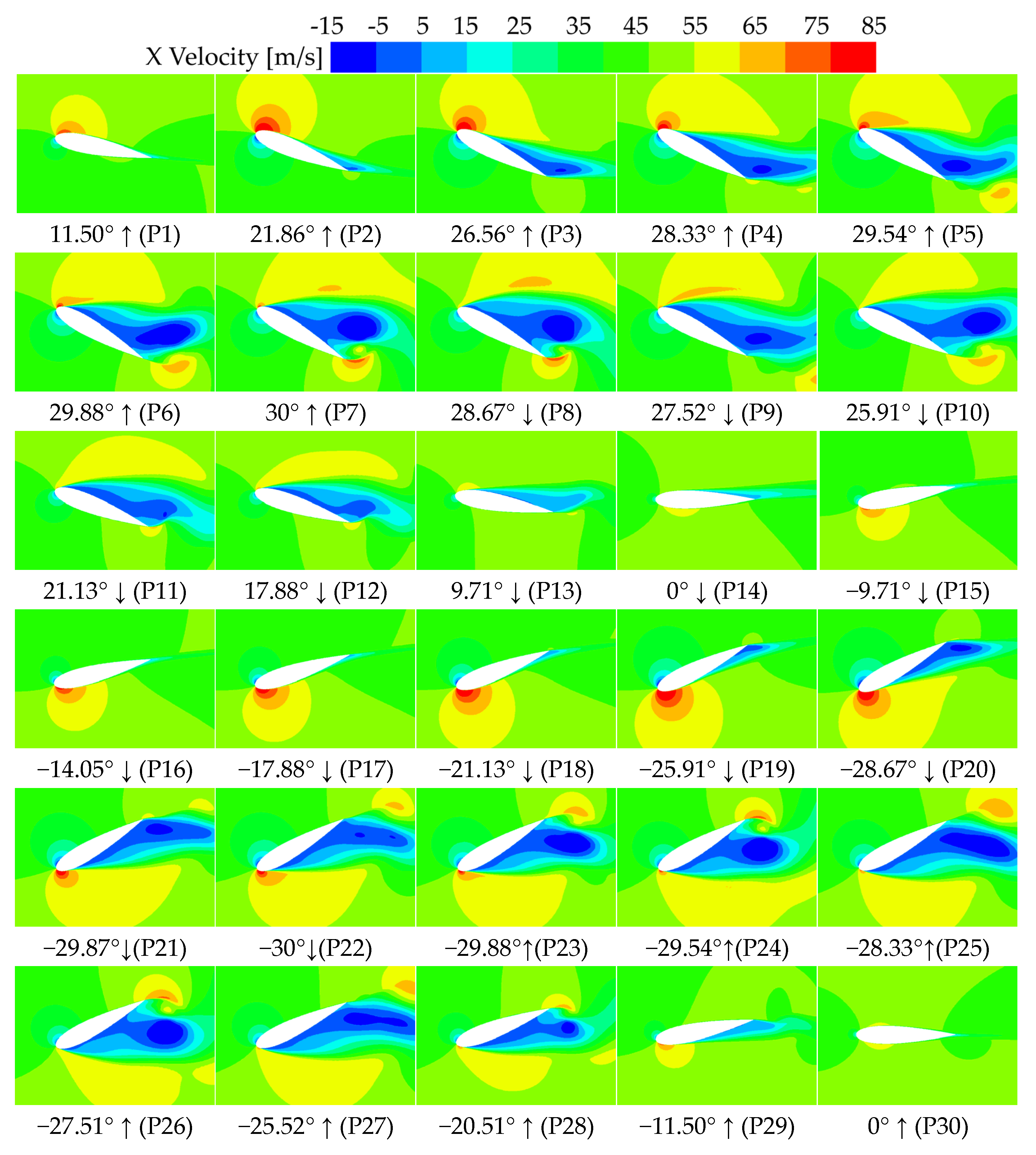
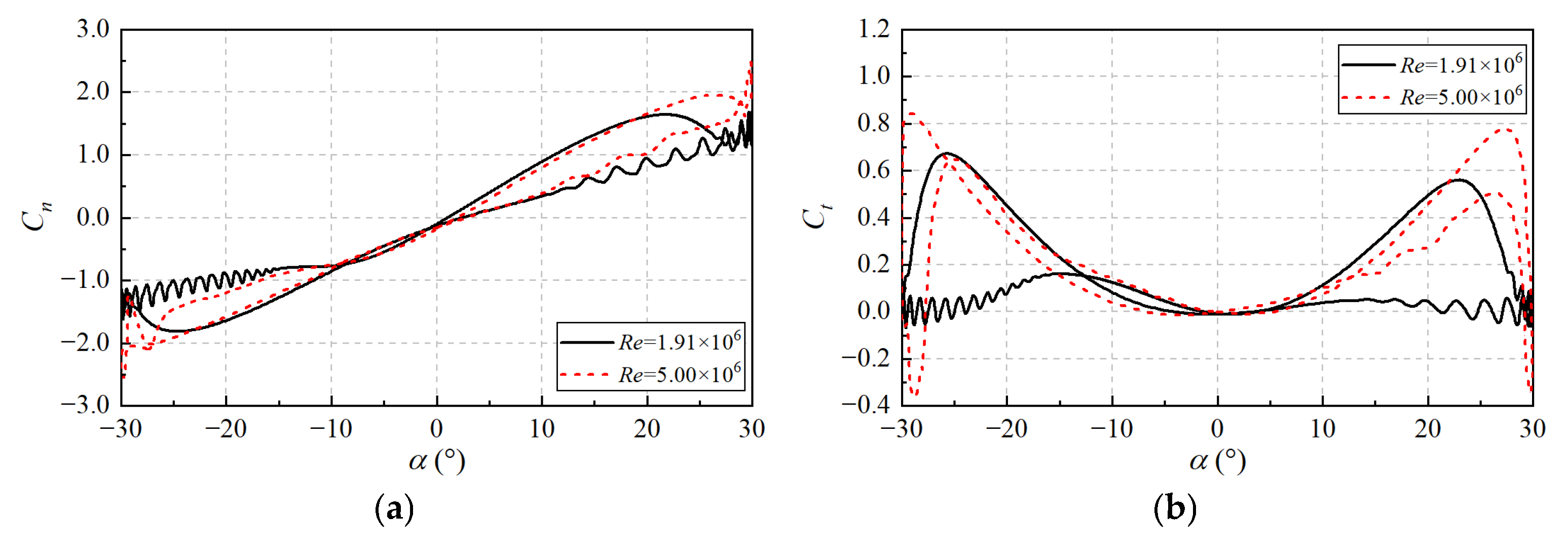
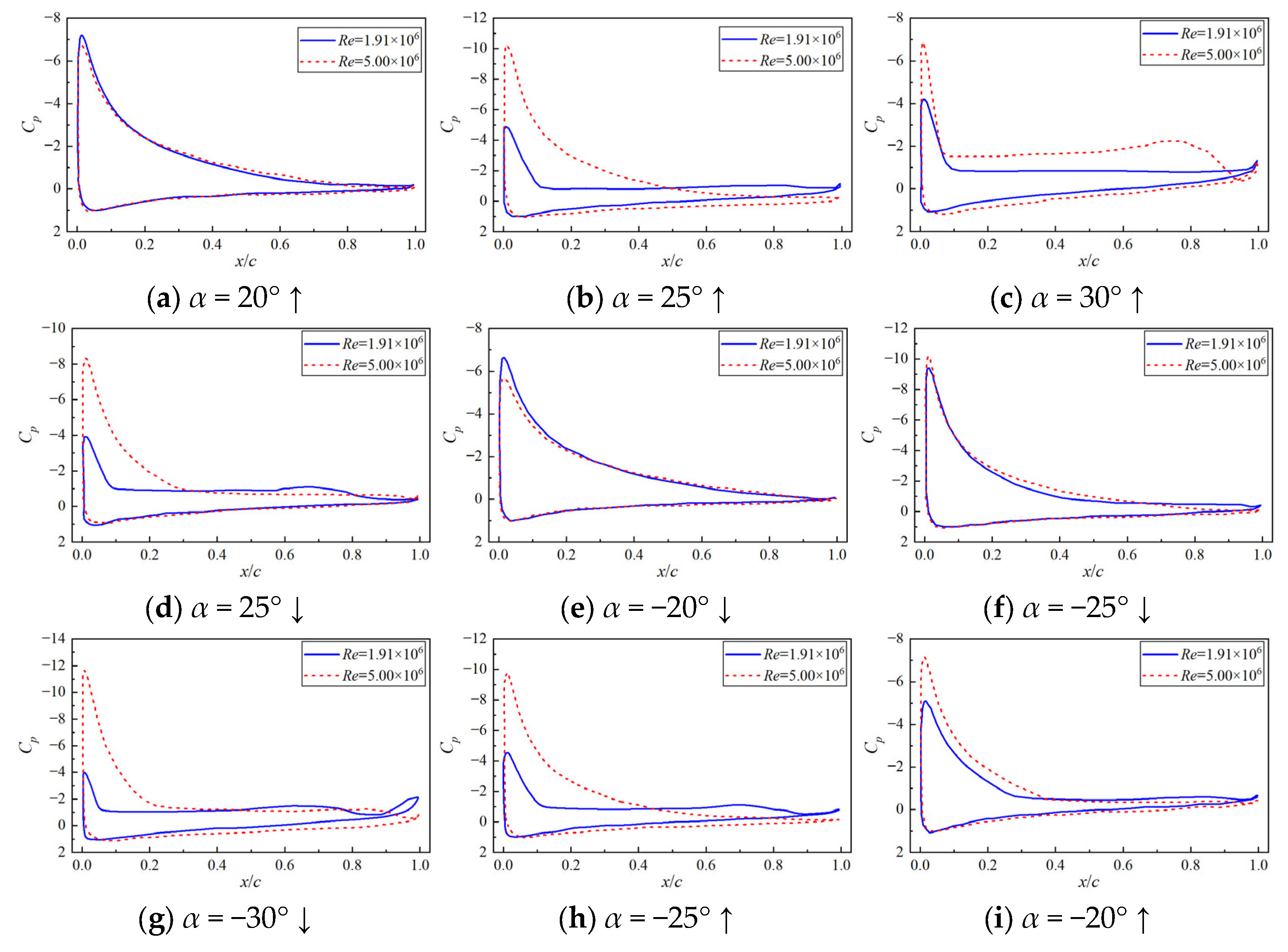
5.1. Flow Field Structure of DPM
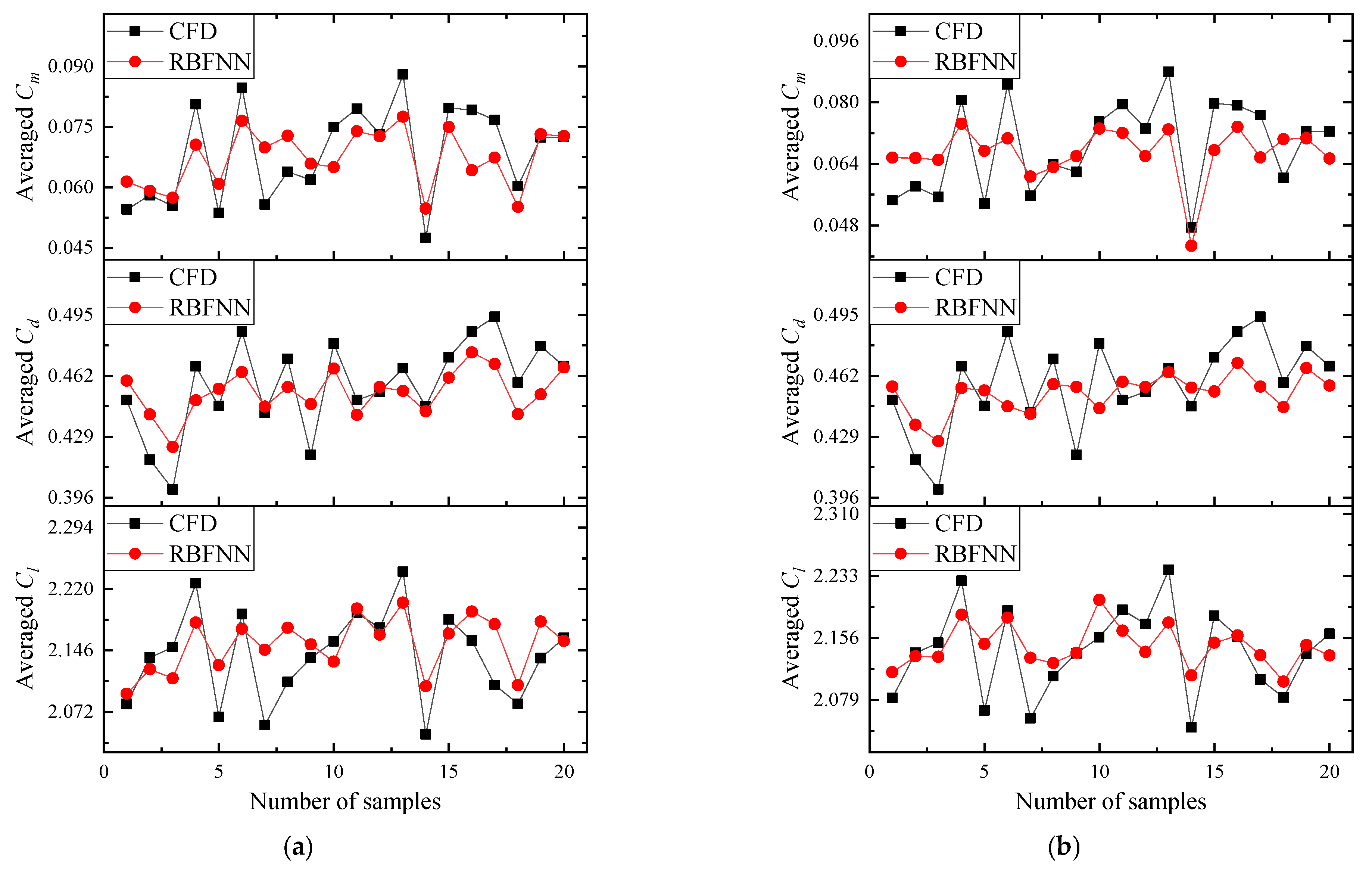
5.2. RBFNN Surrogate Model
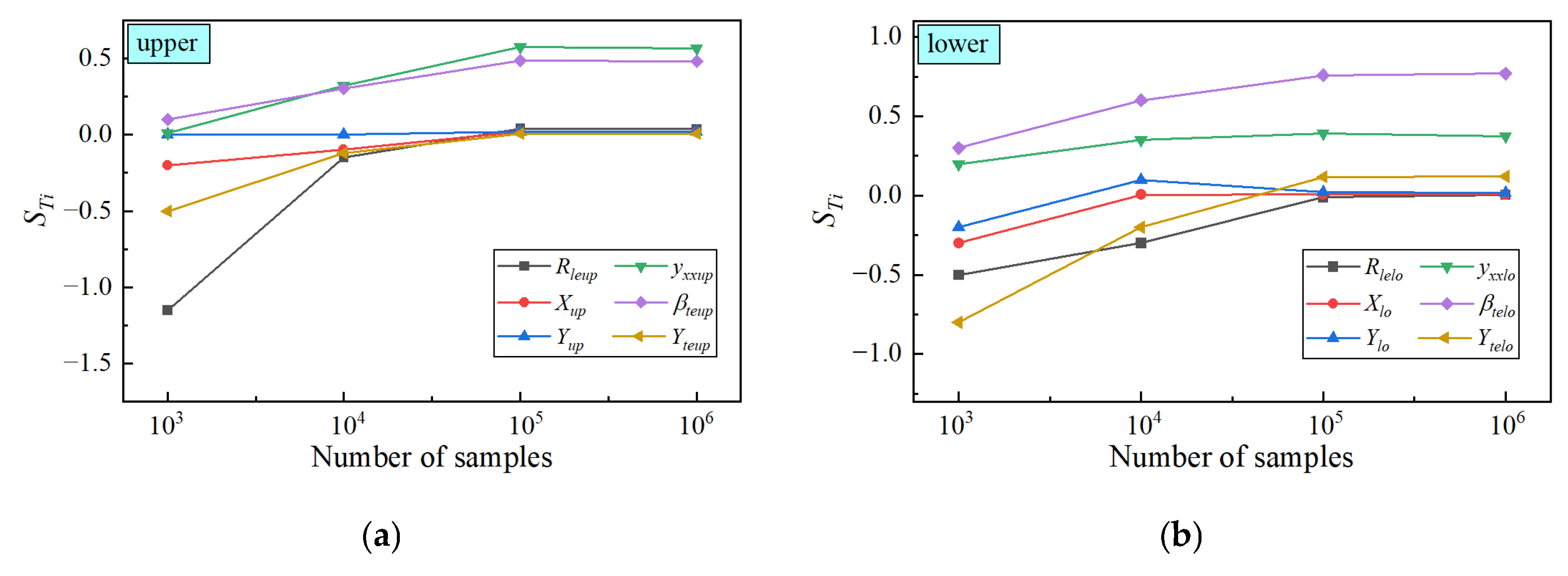
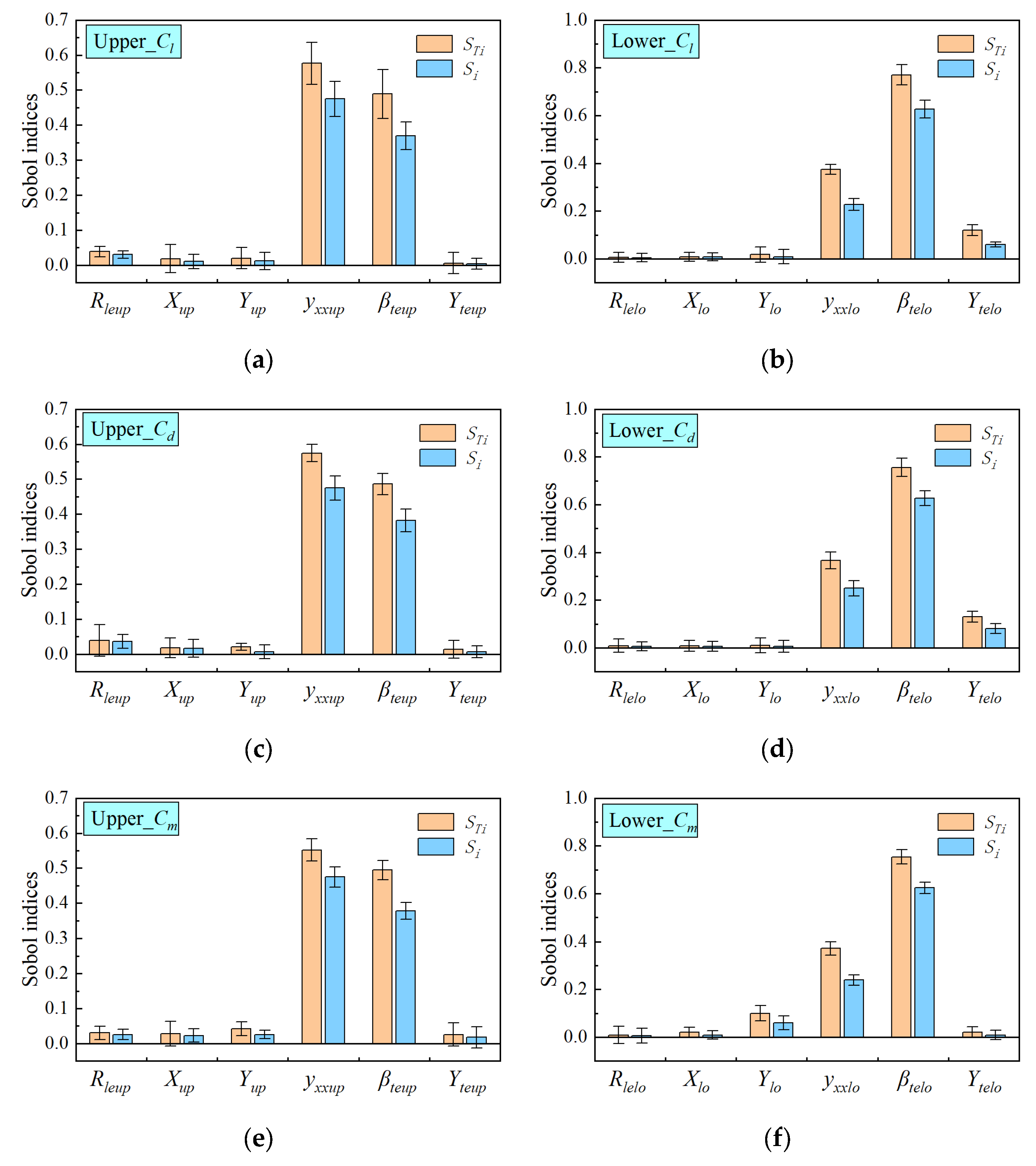
5.3. Sensitivity Analysis
6. Conclusions
- (i).
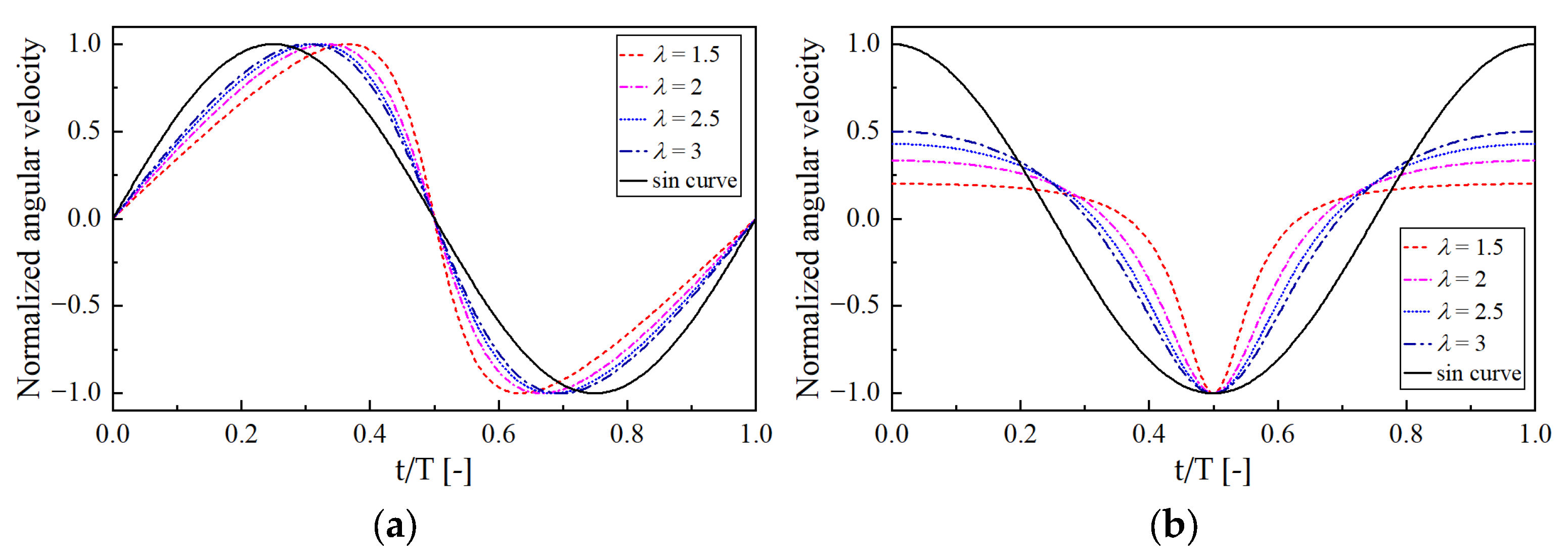
- Under DPM conditions, as the angle of attack (α) increases, reverse flow originating at the trailing edge extends toward the leading edge, causing diffusion of the high-velocity regions and ultimately triggering dynamic stall at the leading edge, with a decrease in aerodynamic forces. In Phases II and IV, the leading edge fails to accumulate high-velocity flow due to the adverse flow direction relative to the pitching motion, resulting in intense aerodynamic oscillations. In Phase III, the large pitch angular velocity delays leading-edge stall, with flow separation occurring only near the trailing edge. During the decrease of α, despite the relatively low pitch angular velocity in Phase IV, the leading-edge flow recovers more effectively compared to Phase II, indicating that slower pitching facilitates aerodynamic recovery.
- (ii).
- The RBFNN surrogate model, trained on 200 samples (including 20 test samples), achieves fitting accuracies of 0.982 and 0.975 (R2) for the upper and lower surfaces, respectively. This model enables the rapid prediction of aerodynamic forces based on blade geometry, making it feasible to generate a large of samples (exceeding 104) required for Sobol′s sensitivity analysis.
- (iii).
- Global sensitivity analysis reveals that the curvature at the maximum thickness and the trailing-edge deflection angle are the dominant geometric parameters influencing dynamic stall behavior under DPM. Their first-order effects on aerodynamic performance are significantly greater than their interaction effects. In contrast, the leading-edge radius and location of maximum thickness exhibit relatively minor influence and should be constrained in the VAWT blade optimization process. The maximum thickness is found to significantly affect the average moment coefficient. Overall, the geometric parameters that most strongly influence DPM behavior are those shaping the mid-to-aft region of the blade, which primarily governs the surrounding flow dynamics.
7. Future Work
- (i).
- In this work, we study the generation and evolution of the DPM at λ = 2, and the difference in the flow field structure for different λ will be analyzed in future work.
- (ii).
- A global sensitivity analysis of the blade geometry parameters on the aerodynamic characteristics is performed. In a follow-up study, a sensitivity analysis of the flow conditions, such as the variation of the incoming velocity and the Reynolds number, will be introduced. This can reveal how other parameters affect the dynamic stall characteristics to better contribute to the VAWT blade design.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VAWT | Vertical-axis wind turbine |
| HAWT | Horizontal-axis wind turbine |
| FOWT | Floating offshore wind turbine |
| DPM | Darrius-type pitching motion |
| CFD | Computational fluid dynamics |
| RBFNN | Radial basis function neural network |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| OLHS | Optimized Latin hypercube sampling |
| UDF | User-defined function |
References
- Leung, D.Y.C.; Yang, Y. Wind energy development and its environmental impact: A review. Renew. Sustain. Energy Rev. 2012, 16, 1031–1039. [Google Scholar] [CrossRef]
- Keivanpour, S.; Ramudhin, A.; Ait Kadi, D. The sustainable worldwide offshore wind energy potential: A systematic review. J. Renew. Sustain. Energy 2017, 9, 065902. [Google Scholar] [CrossRef]
- Global Wind Energy Council. Global Wind Report 2024; Global Wind Energy Council: Brussels, Belgium, 2024. [Google Scholar]
- Rehman, S.; Rafique, M.M.; Alam, M.M.; Alhems, L.M. Vertical axis wind turbine types, efficiencies, and structural stability—A Review. Wind Struct. 2019, 29, 15–32. [Google Scholar]
- Tjiu, W.; Marnoto, T.; Mat, S.; Ruslan, M.H.; Sopian, K. Darrieus vertical axis wind turbine for power generation I: Assessment of Darrieus VAWT configurations. Renew. Energy 2015, 75, 50–67. [Google Scholar] [CrossRef]
- Liu, J.; Lin, H.; Zhang, J. Review on the technical perspectives and commercial viability of vertical axis wind turbines. Ocean Eng. 2019, 182, 608–626. [Google Scholar] [CrossRef]
- Dabachi, M.A.; Rahmouni, A.; Bouksour, O. Design and aerodynamic performance of new floating H-darrieus vertical Axis wind turbines. Mater. Today Proc. 2020, 30, 899–904. [Google Scholar] [CrossRef]
- Dabachi, M.A.; Rahmouni, A.; Rusu, E.; Bouksour, O. Aerodynamic simulations for floating darrieus-type wind turbines with three-stage rotors. Inventions 2020, 5, 18. [Google Scholar] [CrossRef]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. Measurement of the flow field around straight-bladed vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2016, 151, 70–78. [Google Scholar] [CrossRef]
- Day, H.; Ingham, D.; Ma, L.; Pourkashanian, M. Adjoint based optimisation for efficient VAWT blade aerodynamics using CFD. J. Wind Eng. Ind. Aerodyn. 2020, 208, 104431. [Google Scholar] [CrossRef]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. The influence of flow field and aerodynamic forces on a straight-bladed vertical axis wind turbine. Energy 2016, 111, 260–271. [Google Scholar] [CrossRef]
- Allet, A.; Hallé, S.; Paraschivoiu, I. Numerical simulation of dynamic stall around an airfoil in Darrieus motion. J. Sol. Energy Eng. 1999, 121, 69–76. [Google Scholar] [CrossRef]
- Zouzou, B.; Dobrev, I.; Massouh, F.; Dizene, R. Experimental and numerical analysis of a novel Darrieus rotor with variable pitch mechanism at low TSR. Energy 2019, 186, 115832. [Google Scholar] [CrossRef]
- Zhou, L.; Shen, X.; Ma, L.; Chen, J.; Ouyang, H.; Du, Z. Unsteady aerodynamics of the floating offshore wind turbine due to the trailing vortex induction and airfoil dynamic stall. Energy 2024, 304, 131845. [Google Scholar] [CrossRef]
- Khalifa, N.M.; Rezaei, A.; Taha, H.E. On computational simulations of dynamic stall and its three-dimensional nature. Phys. Fluids 2023, 35, 105143. [Google Scholar] [CrossRef]
- Dyachuk, E.; Goude, A.; Bernhoff, H. Dynamic stall modeling for the conditions of vertical axis wind turbines. AIAA J. 2014, 52, 72–81. [Google Scholar] [CrossRef]
- Lam, H.F.; Peng, H.Y. Study of wake characteristics of a vertical axis wind turbine by two-and three-dimensional computational fluid dynamics simulations. Renew. Energy 2016, 90, 386–398. [Google Scholar] [CrossRef]
- Leishman, J.G. Dynamic stall experiments on the NACA 23012 aerofoil. Exp. Fluids 1990, 9, 49–58. [Google Scholar] [CrossRef]
- Tsai, H.C.; Colonius, T. Coriolis effect on dynamic stall in a vertical axis wind turbine. AIAA J. 2016, 54, 216–226. [Google Scholar] [CrossRef]
- Brunner, C.E.; Kiefer, J.; Hultmark, M. Comparison of dynamic stall on an airfoil undergoing sinusoidal and VAWT-shaped pitch motions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2265, p. 032006. [Google Scholar]
- Hand, B.; Kelly, G.; Cashman, A. Numerical simulation of a vertical axis wind turbine airfoil experiencing dynamic stall at high Reynolds numbers. Comput. Fluids 2017, 149, 12–30. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A review on global sensitivity analysis methods. Uncertainty management in simulation-optimization of complex systems: Algorithms and applications. In Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2015; pp. 101–122. [Google Scholar]
- Dela, A.; Shtylla, B.; de Pillis, L. Multi-method global sensitivity analysis of mathematical models. J. Theor. Biol. 2022, 546, 111159. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z.; Zhou, Y.; Shi, Y.; Wei, Y. Global sensitivity analysis using support vector regression. Appl. Math. Model. 2017, 49, 587–598. [Google Scholar] [CrossRef]
- Castillo, E.; Hadi, A.S.; Conejo, A.; Fernández-Canteli, A. A general method for local sensitivity analysis with application to regression models and other optimization problems. Technometrics 2004, 46, 430–444. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Echeverría, F.; Mallor, F.; San Miguel, U. Global sensitivity analysis of the blade geometry variables on the wind turbine performance. Wind Energy 2017, 20, 1601–1616. [Google Scholar] [CrossRef]
- Shum, J.G.; Lee, S. Computational Study of Airfoil Design Parameters and Sensitivity Analysis for Dynamic Stall. AIAA J. 2024, 62, 1611–1617. [Google Scholar] [CrossRef]
- Mohamed, A.S.; Raj, L.P. Sensitivity analysis of geometric parameters on the aerodynamic performance of a multi-element airfoil. Aerosp. Sci. Technol. 2023, 132, 108074. [Google Scholar]
- Wu, X.; Zhang, W.; Song, S. Uncertainty quantification and sensitivity analysis of transonic aerodynamics with geometric uncertainty. Int. J. Aerosp. Eng. 2017, 2017, 8107190. [Google Scholar] [CrossRef]
- Raul, V.; Leifsson, L. Surrogate-based aerodynamic shape optimization for delaying airfoil dynamic stall using Kriging regression and infill criteria. Aerosp. Sci. Technol. 2021, 111, 106555. [Google Scholar] [CrossRef]
- Raj, L.P.; Yee, K.; Myong, R.S. Sensitivity of ice accretion and aerodynamic performance degradation to critical physical and modeling parameters affecting airfoil icing. Aerosp. Sci. Technol. 2020, 98, 105659. [Google Scholar]
- Rahman, S. Global sensitivity analysis by polynomial dimensional decomposition. Reliab. Eng. Syst. Saf. 2011, 96, 825–837. [Google Scholar] [CrossRef]
- Feng, K.; Lu, Z.; Yang, C. Enhanced Morris method for global sensitivity analysis: Good proxy of Sobol’index. Struct. Multidiscip. Optim. 2019, 59, 373–387. [Google Scholar] [CrossRef]
- Rosolem, R.; Gupta, H.V.; Shuttleworth, W.J.; Zeng, X.; de Gonçalves, L.G.G. A fully multiple-criteria implementation of the Sobol′ method for parameter sensitivity analysis. J. Geophys. Res. Atmos. 2012, 117, D07103. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Li, C.; Mahadevan, S. An efficient modularized sample-based method to estimate the first-order Sobol׳ index. Reliab. Eng. Syst. Saf. 2016, 153, 110–121. [Google Scholar] [CrossRef]
- Wang, Y.X.; Zhang, L.L.; Liu, W.; Cheng, X.H.; Zhuang, Y.; Chronopoulos, A.T. Performance optimizations for scalable CFD applications on hybrid CPU+ MIC heterogeneous computing system with millions of cores. Comput. Fluids 2018, 173, 226–236. [Google Scholar] [CrossRef]
- Lange, C.; Barthelmäs, P.; Rosnitschek, T.; Tremmel, S.; Rieg, F. Impact of HPC and automated CFD Simulation processes on virtual product development—A case study. Appl. Sci. 2021, 11, 6552. [Google Scholar] [CrossRef]
- Sobieczky, H. Parametric airfoils and wings. In Recent Development of Aerodynamic Design Methodologies: Inverse Design and Optimization; Vieweg+ Teubner Verlag: Wiesbaden, Germany, 1999; pp. 71–87. [Google Scholar]
- Della Vecchia, P.; Daniele, E.; D’Amato, E. An airfoil shape optimization technique coupling PARSEC parameterization and evolutionary algorithm. Aerosp. Sci. Technol. 2014, 32, 103–110. [Google Scholar] [CrossRef]
- Sun, Y.B.; Meng, X.Y.; Long, T.; Wu, Y. A fast optimal Latin hypercube design method using an improved translational propagation algorithm. Eng. Optim. 2020, 52, 1244–1260. [Google Scholar] [CrossRef]
- Li, Y.; Li, N.; Gong, G.; Yan, J. A novel design of experiment algorithm using improved evolutionary multi-objective optimization strategy. Eng. Appl. Artif. Intell. 2021, 102, 104283. [Google Scholar] [CrossRef]
- Seshagiri, S.; Khalil, H.K. Output feedback control of nonlinear systems using RBF neural networks. IEEE Trans. Neural Netw. 2000, 11, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Peng, J.X.; Bai, E.W. Two-stage mixed discrete–continuous identification of radial basis function (RBF) neural models for nonlinear systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 56, 630–643. [Google Scholar]
- Montazer, G.A.; Giveki, D.; Karami, M.; Rastegar, H. Radial basis function neural networks: A review. Comput. Rev. J 2018, 1, 52–74. [Google Scholar]
- Chen, Z.; Huang, F.; Chen, W.; Zhang, J.; Sun, W.; Chen, J.; Gu, J.; Zhu, S. RBFNN-based adaptive sliding mode control design for delayed nonlinear multilateral telerobotic system with cooperative manipulation. IEEE Trans. Ind. Inform. 2019, 16, 1236–1247. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Wickens, R.H. Wind Tunnel Investigation of Dynamic Stall of a NACA 0018 Airfoil Oscillating in Pitch; Aeronautical Note NAE-AN-27, NRC no 24262; National Aeronautical Establishment: Bedford, UK, 1985.
- Balduzzi, F.; Bianchini, A.; Carnevale, E.A.; Ferrari, L.; Magnani, S. Feasibility analysis of a Darrieus vertical-axis wind turbine installation in the rooftop of a building. Appl. Energy 2012, 97, 921–929. [Google Scholar] [CrossRef]
- Imran, R.M.; Hussain, D.M.A.; Soltani, M. An experimental analysis of the effect of icing on Wind turbine rotor blades. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
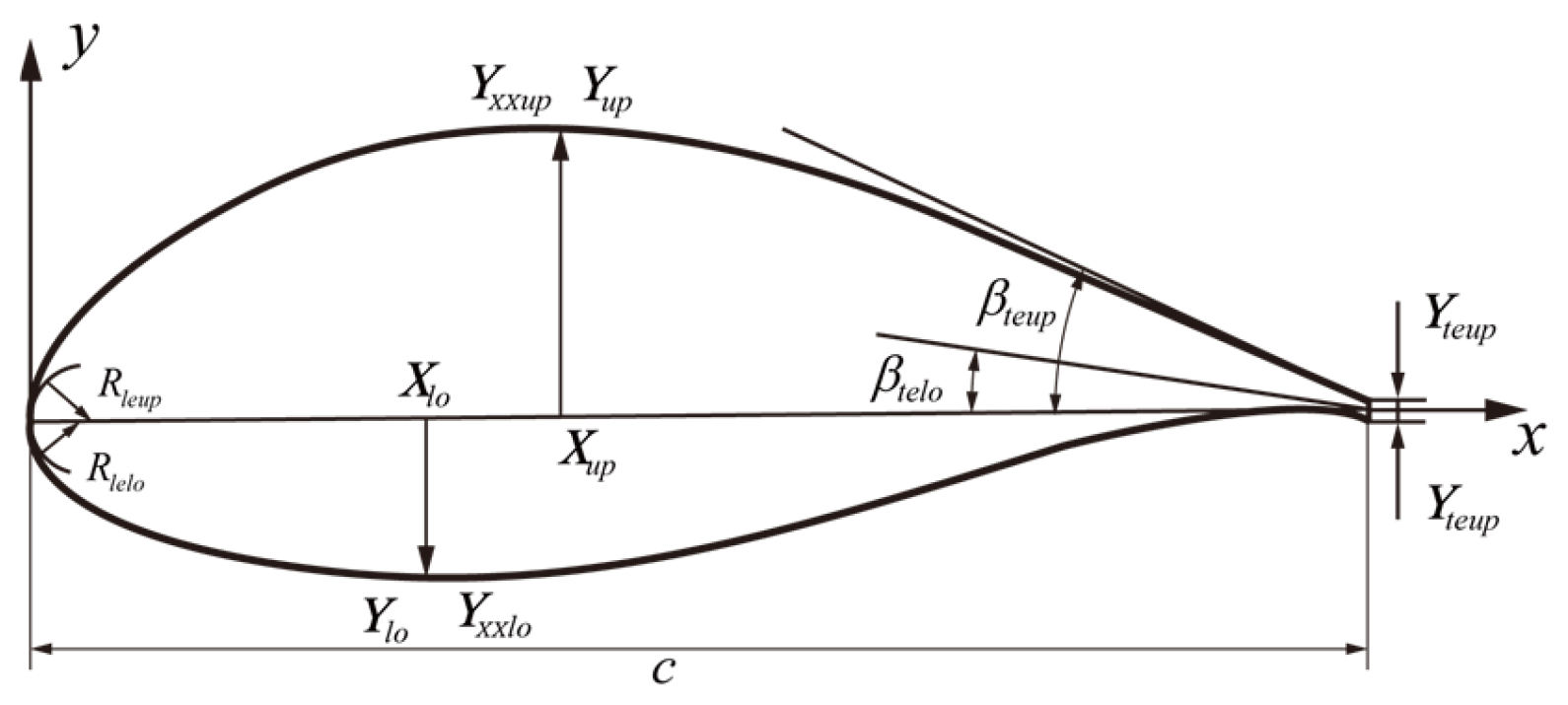
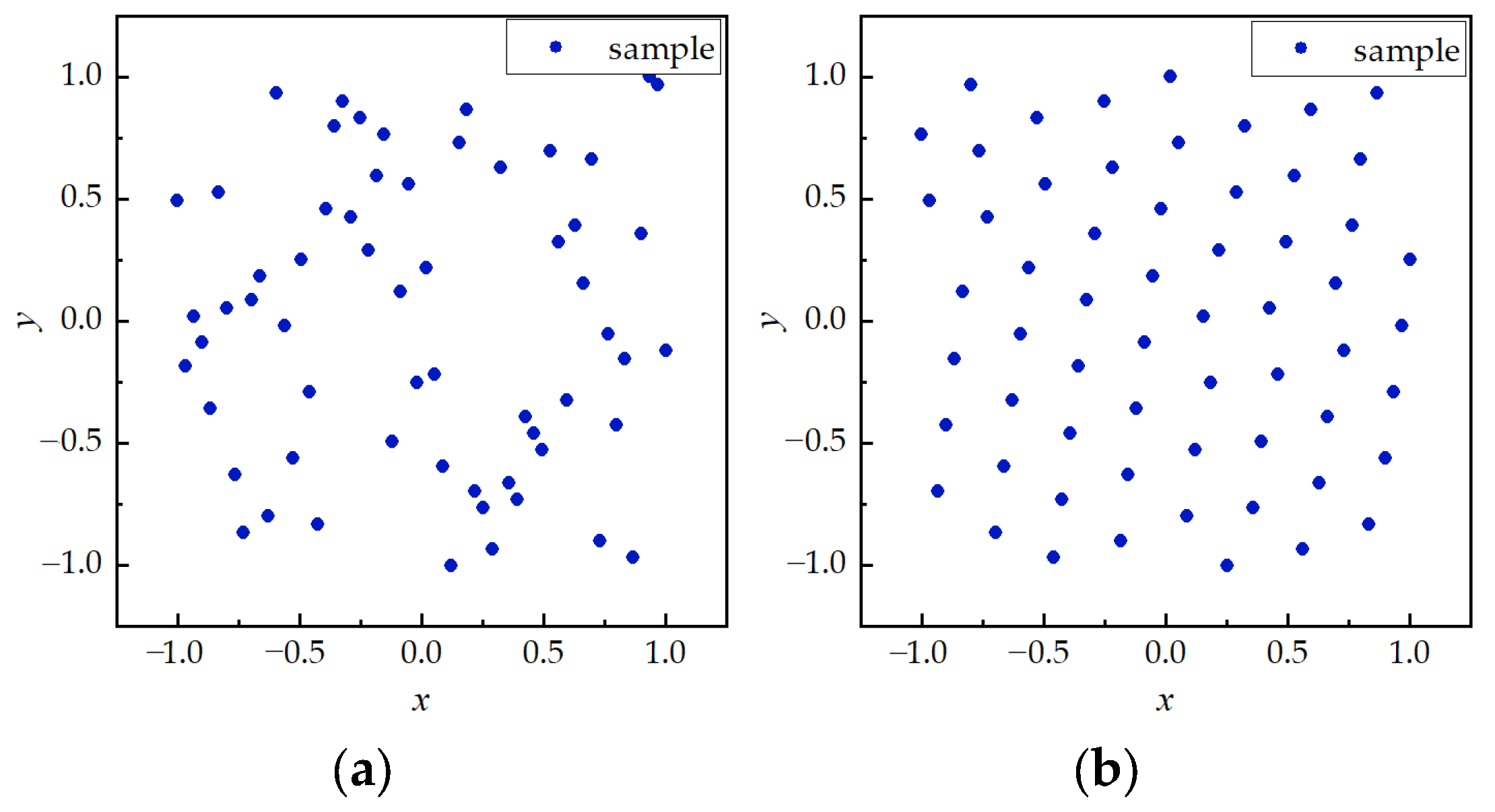
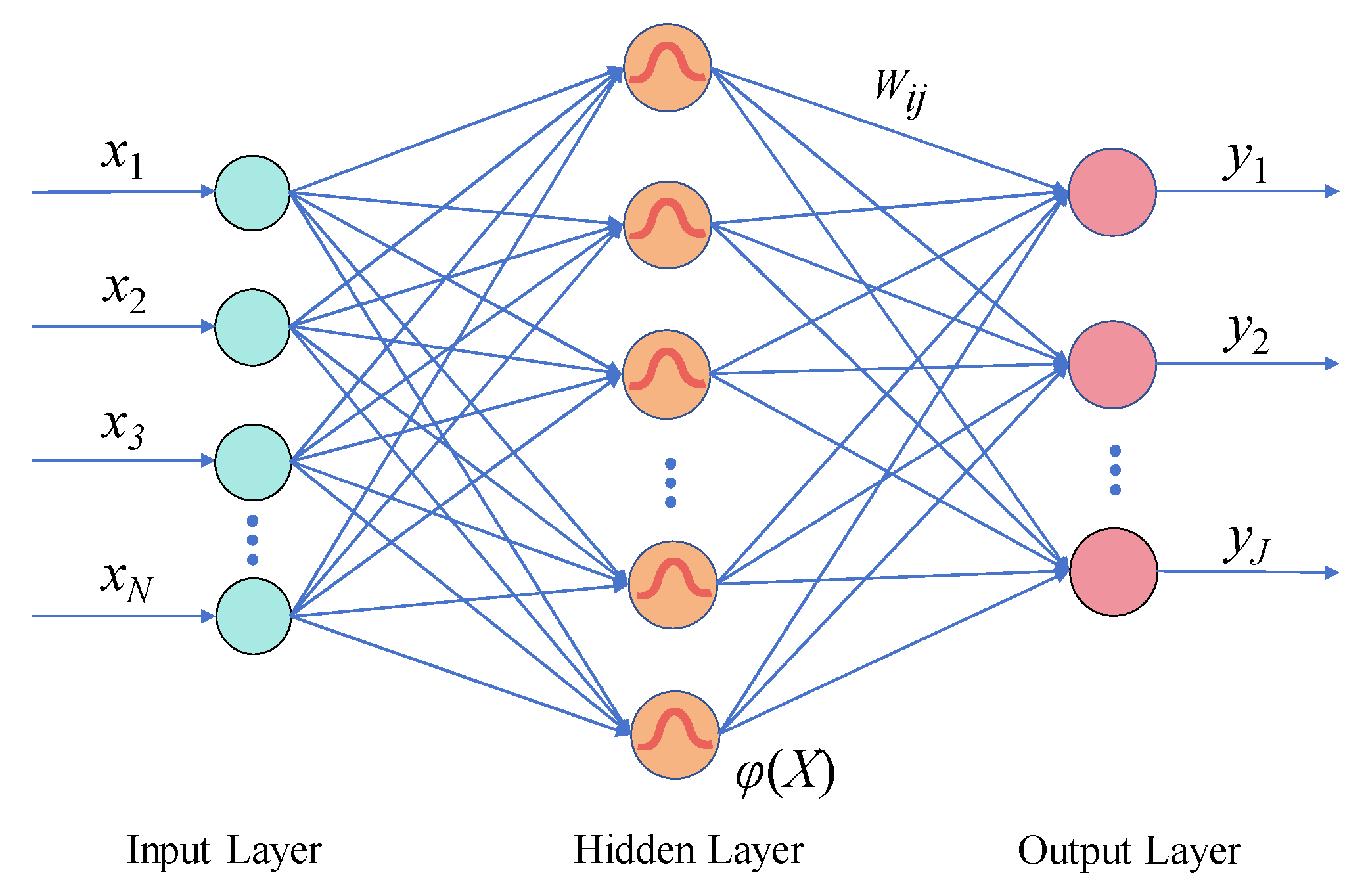

| PARSEC Parameters | Description |
|---|---|
| () | Upper (low) surface leading-edge radius |
| () | Upper (low) surface maximum thickness position |
| () | Upper (low) surface maximum thickness |
| () | Upper (low) surface curvature at the position of maximum thickness |
| () | Upper (low) surface trailing-edge thickness |
| () | Upper (low) surface deflection angle of the trailing edge |
| Upper | Value | Lower | Value |
|---|---|---|---|
| 0.1412 | 0.1412 | ||
| 0.2974 | 0.2974 | ||
| 0.0900 | 0.0900 | ||
| 0.6719 | −0.6719 | ||
| 0.0019 | −0.0019 | ||
| 11.7751 | −11.7751 |
| Parameters | Number of Grids | Height of First Layer/(mm) | Surface Grid Growth Rate | Volume Grid Growth Rate |
|---|---|---|---|---|
| G1 | 145 × 104 | 0.04 | 1.10 | 1.15 |
| G2 | 191 × 104 | 0.02 | 1.05 | 1.10 |
| G3 | 227 × 104 | 0.01 | 1.02 | 1.05 |
| G4 | 255 × 104 | 0.01 | 1.02 | 1.02 |
| Parameters | Time Steps/(10−4) | VAWT Rotation Angle at Each Time Step | Wall Clock/Hour |
|---|---|---|---|
| T1 | 25.25 | 0.5° | 5.51 |
| T2 | 12.62 | 0.25° | 11.25 |
| T3 | 6.31 | 0.125° | 22.05 |
| Evaluation Index | MSE | RMSE | R2 |
|---|---|---|---|
| Upper | 0.000875 | 0.0295 | 0.982 |
| Lower | 0.000953 | 0.0324 | 0.975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Miao, W.; Zhao, K.; Li, C.; Chang, L.; Yue, M.; Xu, Z. Influence of Geometric Effects on Dynamic Stall in Darrieus-Type Vertical-Axis Wind Turbines for Offshore Renewable Applications. J. Mar. Sci. Eng. 2025, 13, 1327. https://doi.org/10.3390/jmse13071327
Zhang Q, Miao W, Zhao K, Li C, Chang L, Yue M, Xu Z. Influence of Geometric Effects on Dynamic Stall in Darrieus-Type Vertical-Axis Wind Turbines for Offshore Renewable Applications. Journal of Marine Science and Engineering. 2025; 13(7):1327. https://doi.org/10.3390/jmse13071327
Chicago/Turabian StyleZhang, Qiang, Weipao Miao, Kaicheng Zhao, Chun Li, Linsen Chang, Minnan Yue, and Zifei Xu. 2025. "Influence of Geometric Effects on Dynamic Stall in Darrieus-Type Vertical-Axis Wind Turbines for Offshore Renewable Applications" Journal of Marine Science and Engineering 13, no. 7: 1327. https://doi.org/10.3390/jmse13071327
APA StyleZhang, Q., Miao, W., Zhao, K., Li, C., Chang, L., Yue, M., & Xu, Z. (2025). Influence of Geometric Effects on Dynamic Stall in Darrieus-Type Vertical-Axis Wind Turbines for Offshore Renewable Applications. Journal of Marine Science and Engineering, 13(7), 1327. https://doi.org/10.3390/jmse13071327







