A Review of Experimental and Numerical Research on the Slamming Problem of High-Performance Vessels
Abstract
1. Introduction
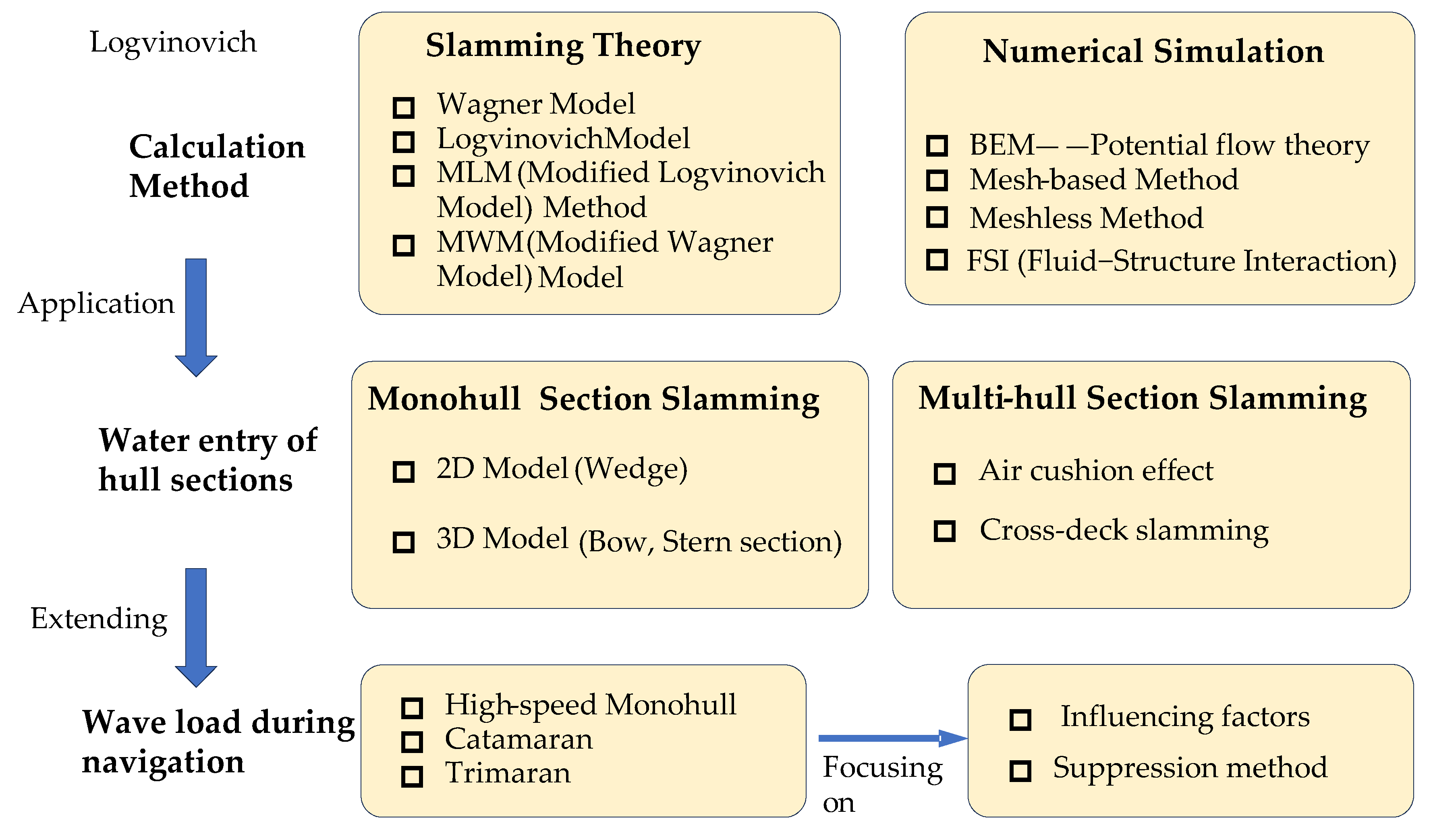
2. Calculation Methods
2.1. Slamming Theory
2.2. Numerical Calculation
2.2.1. Boundary Element Method
2.2.2. CFD Method
Mesh-Based Method
Meshless Method
3. Water Entry of Hull Section
3.1. Wedge Slamming
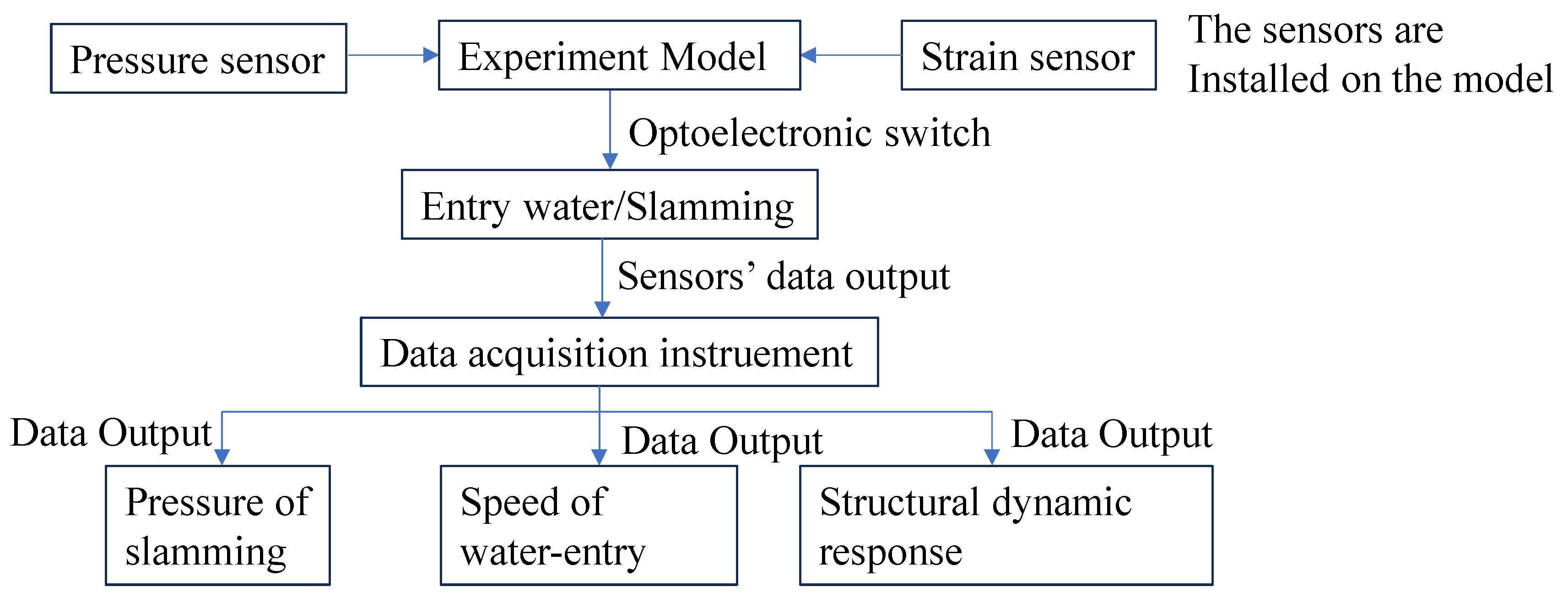
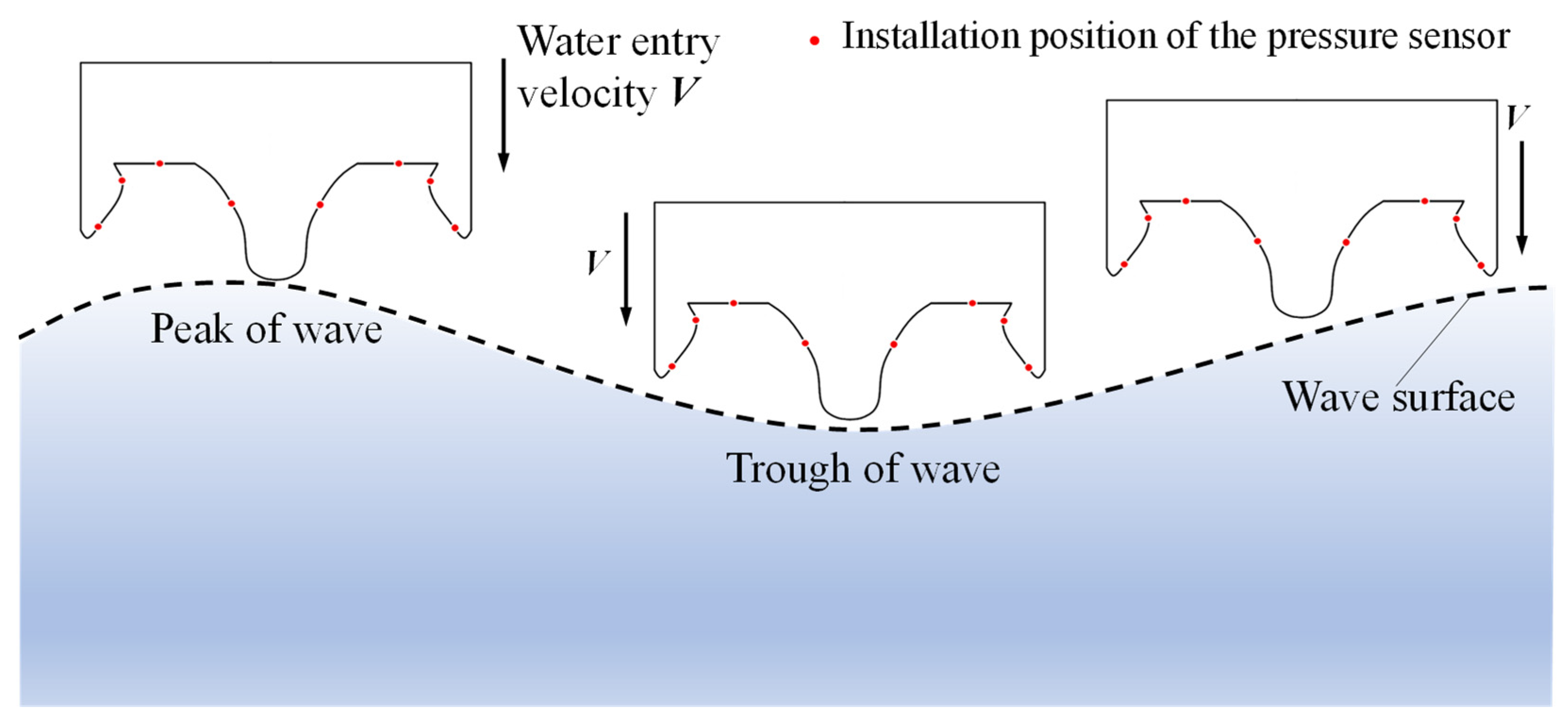
3.1.1. Experimental Study
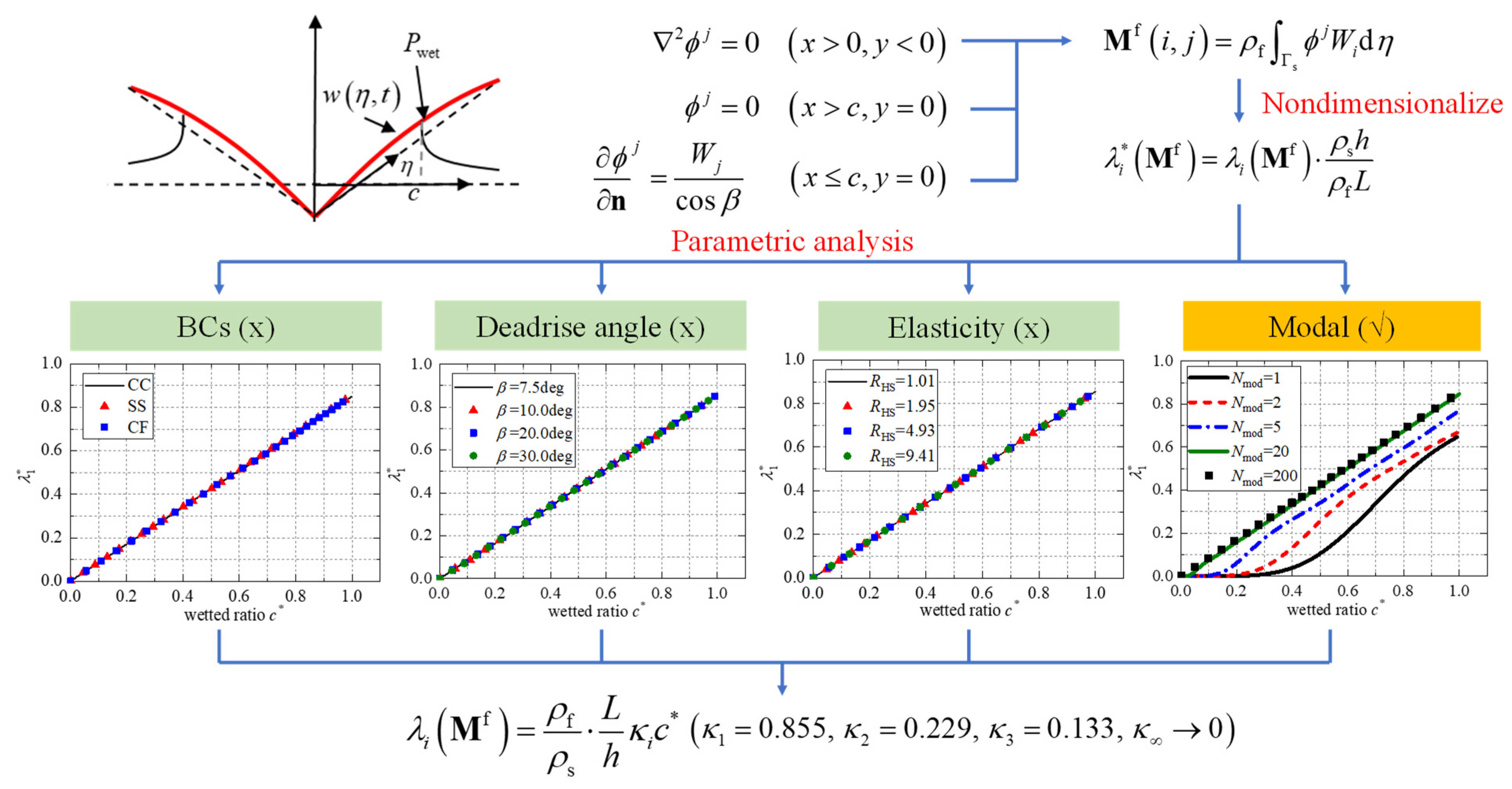
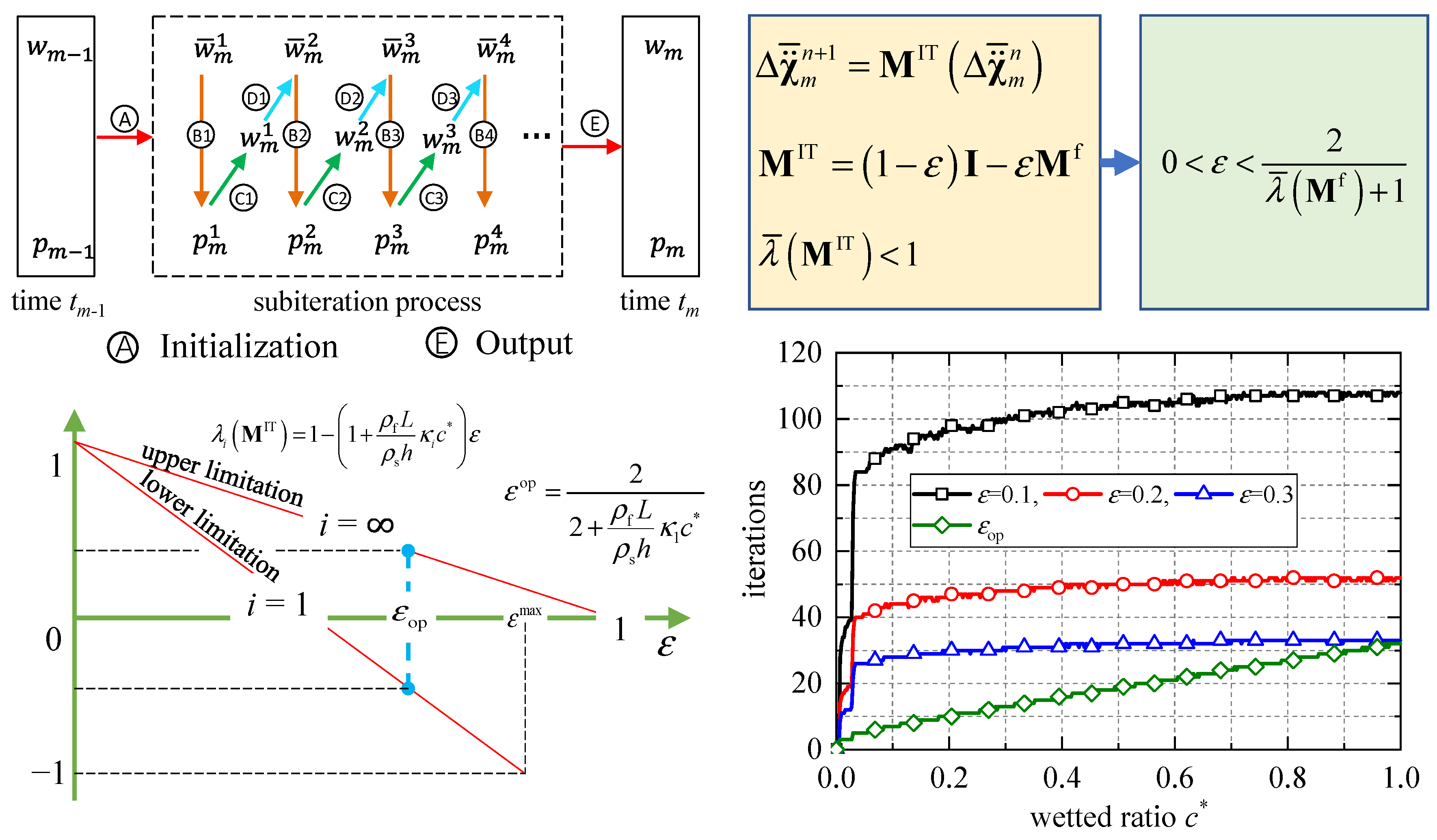
3.1.2. Calculation of Fluid–Structure Interaction for Wedge’s Slamming
3.2. Multi-Hull Section Slamming
3.2.1. Air Cushion Effect
3.2.2. Pressure of Wet-Deck Slamming
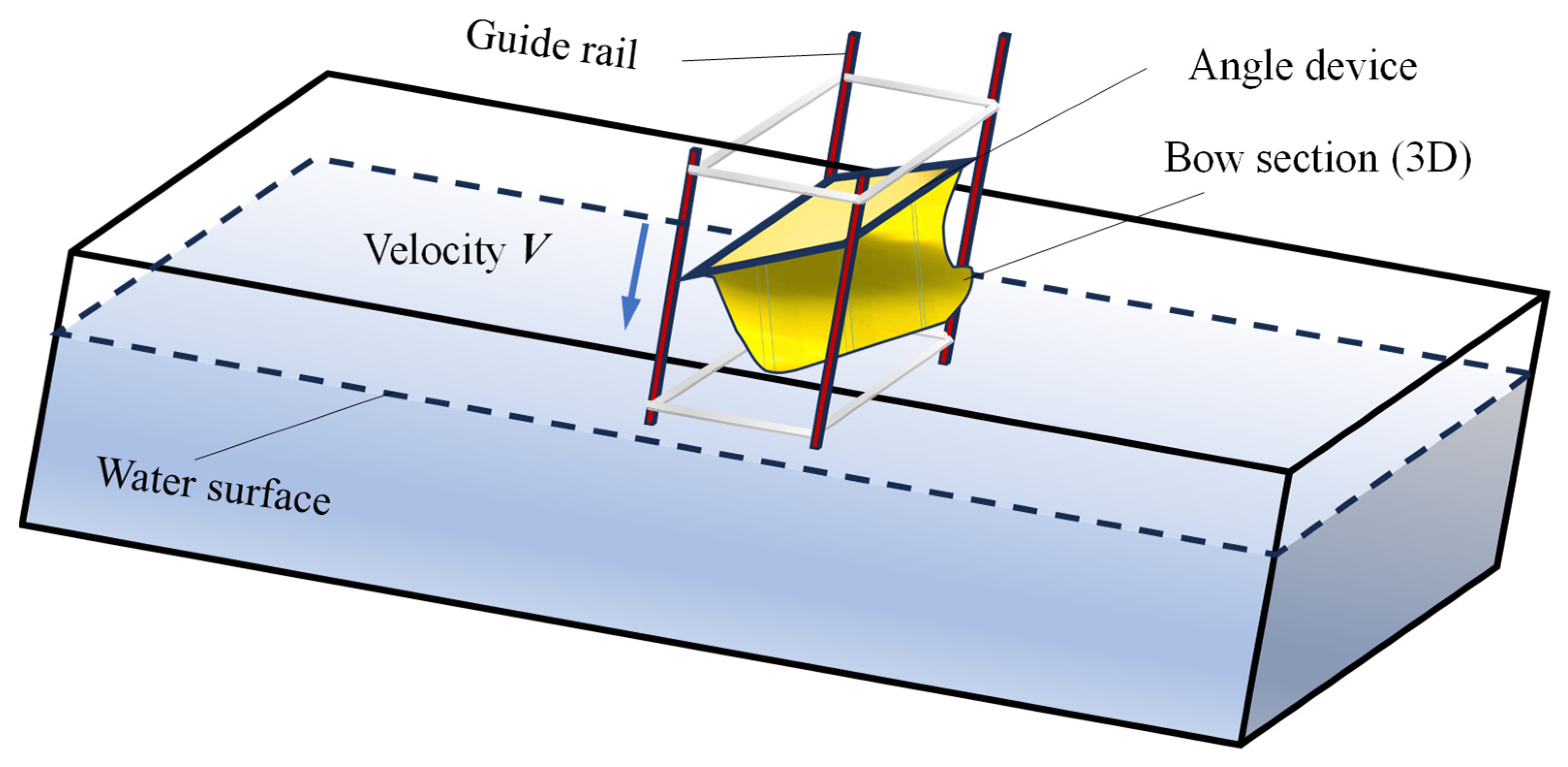
3.3. Water Entry of 3D Hull Model
4. Wave Load During Navigation
4.1. Slamming of High-Speed Monohull
4.1.1. Numerical Solution
4.1.2. Model Test
4.2. Slamming of Catamaran
4.2.1. Influencing Factors of Slamming Load
4.2.2. Suppression Method
4.3. Slamming of Trimaran
5. Conclusions
- (1)
- Coupling of Numerical Methods. By combining CFD (computational fluid dynamics) with the BEM (boundary element method), the far flow field is modeled using potential flow theory while the near field employs viscous models. This approach balances the high accuracy of CFD in handling nonlinear problems with the computational efficiency of the BEM, reducing dimensionality and more precisely capturing hydroelastic effects. Similarly, hybrid methods coupling particle-based techniques (e.g., SPH, MPS) with grid-based methods can be adopted, applying particle methods at slamming interfaces to accommodate large deformations while retaining grid methods elsewhere. For free-surface tracking, integrating level set with VOF (volume of fluid) enhances air–liquid interface resolution.
- (2)
- Application of Machine Learning. High-fidelity CFD simulations (e.g., DNS, LES) require an extremely fine mesh resolution and small time steps, making them impractical for rapid multi-condition evaluations in engineering applications. Neural networks can be employed to predict numerical solutions (e.g., pressure peaks, time-history curves) and replace traditional iterative processes, thereby improving computational efficiency for large-scale simulations. However, current slamming tests often rely on repeated experiments to mitigate data fluctuations, resulting in a scarcity of high-quality datasets. Additionally, biases inherent in numerical models may propagate into machine learning models, necessitating further calibration.
- (3)
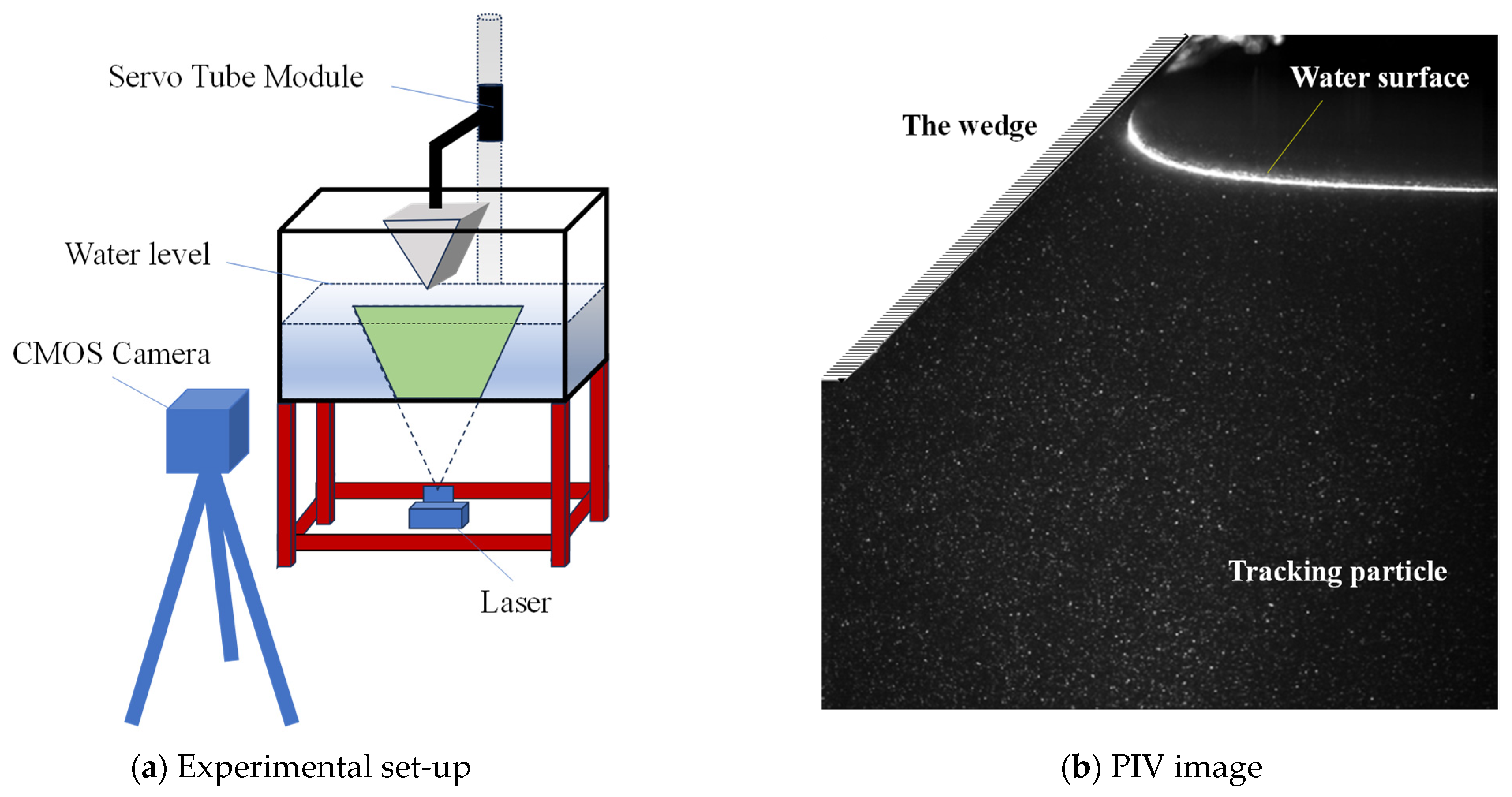
- Slamming Flow Field Measurement Techniques. The measurement of flow fields and pressure distribution on ship hull sections is often achieved using particle image velocimetry (PIV). This method enables the real-time measurement of fluid particle velocities and reconstructs the pressure field from the velocity field via pressure reconstruction techniques. It overcomes the limitations of traditional pressure sensors, which are prone to dynamic impact interference, particularly offering advantages in high-speed water-entry scenarios. However, existing pressure reconstruction methods (e.g., multi-path integration schemes) typically assume incompressible flow and neglect viscous effects. In reality, water-entry processes may involve complex phenomena such as cavitation and turbulence, leading to error accumulation. Additionally, PIV is predominantly applied to 2D models, making it challenging to fully capture the flow field characteristics in 3D scenarios (e.g., ship bow water entry).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sairam Prasad, B.; Ravi Kiran Sastry, G.; Das, H.N. A comprehensive review study on multiphase analysis of water entry bodies. Ocean Eng. 2024, 292, 116579. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Truelock, D.; Lavroff, J.; Pearson, D.; Czaban, Z.; Luo, H.B.; Wang, F.H.; Catipovic, I.; Begovic, E.; Takaoka, Y.; Loureiro, C.; et al. 5: Special Vessels. Soc. Nav. Archit. Mar. Eng. 2022, 2, 313–377. [Google Scholar]
- Aertssen, G. Laboring of ships in rough seas with special emphasis on the fast ships. In Proceedings of the SNAME Diamond Jubilee International Meeting, New York, NY, USA, 18–21 June 1968. [Google Scholar]
- Andrews, D.J.; Zhang, J.W. Trimaran Ships: The Configuration for the Frigate of the Future. Nav. Eng. J. 2010, 107, 77–94. [Google Scholar] [CrossRef]
- Yang, Q.; Jones, V.; McCue, L. Free-surface flow interactions with deformable structures using an SPH-FEM model. Ocean Eng. 2012, 55, 136–147. [Google Scholar] [CrossRef]
- Akbarzadeh, P.; Krieger, M.; Hofer, D.; Thumfart, M.; Gittler, P. Parallel water entry of hydrophobic-hydrophilic sphere pairings: Particle image velocimetry and High-Speed camera analysis. J. Fluids Struct. 2025, 133, 104272. [Google Scholar] [CrossRef]
- Von Karman, T. The Impact on Seaplane Floats During Landin; Techinical Note No. 321; National Advisory Committee for Aeronatics: Washington, DC, USA, 1932; pp. 309–313.
- Wagner, H. Uber stoss-und gleitvergange an der oberflache von flussigkeiten. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1932, 12, 193–235. [Google Scholar] [CrossRef]
- Dobrovol’Skaya, Z.N. On some problems of similarity flow of fluids with a free surface. J. Fluid Mech. 1969, 36, 805–829. [Google Scholar] [CrossRef]
- Hughes, O.F. Solution of wedge entry problem by numerical conformal mapping. J. Fluid Mech. 1972, 56, 173–192. [Google Scholar] [CrossRef]
- Logvinovich, G.V. Hydrodynamics Offlows with Free Boundaries; Naukova Dumka: Kiev, Ukraine, 1969. [Google Scholar]
- Korobkin, A.A. Analytical models of water impact. Eur. J. Appl. Math. 2004, 15, 821–838. [Google Scholar] [CrossRef]
- Duan, W.Y.; Xu, G.D.; Wu, G.X. Similarity solution of oblique impact of wedge-shaped water column on wedged coastalstructures. Coast. Eng. 2009, 56, 400–407. [Google Scholar] [CrossRef]
- Liu, L.; Zeng, K.; Ding, J.; Wang, Q.B.; Bu, S.X.; Cheng, C. A two-dimensional high-order explicit analytical solution model for symmetric wedges entering water. J. Ocean Eng. Sci. 2025, 10, 109–122. [Google Scholar] [CrossRef]
- Tassin, A.; Korobkin, A.A.; Cooker, M.J. On analytical models of vertical water entry of a symmetric body with separation and cavity initiation. Appl. Ocean Res. 2014, 48, 33–41. [Google Scholar] [CrossRef]
- Fairlie-Clarke, A.C.; Tveitnes, T. Momentum and gravity effects during the constant velocity water entry of wedge-shaped sections. Ocean Eng. 2008, 35, 706–716. [Google Scholar] [CrossRef]
- Wen, X.L.; Qu, Q.L.; Liu, P.Q.; Ding, S.L. Theoretical study on slamming and transition stages of normal impacts of symmetrical bodies on calm and wavy water surfaces. Appl. Ocean Res. 2022, 119, 102986. [Google Scholar] [CrossRef]
- Khabakhpasheva, T.I.; Korobkin, A.A.; Malenica, S. Water entry of an elastic conical shell. J. Fluid Mech. 2024, 980, A34. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, G.Y.; Jiang, S.Q.; Jiang, S.C.; el Moctar, O.; Ma, Y.X. Investigation of fluid added mass matrix during hydroelastic slamming of wedges. Phys. Fluids 2024, 36, 012133. [Google Scholar] [CrossRef]
- Liu, W.T.; Zhang, A.M.; Miao, X.H.; Ming, F.R.; Liu, Y.L. Investigation of hydrodynamics of water impact and tail slamming of high-speed water entry with a novel immersed boundary method. J. Fluid Mech. 2023, 958, A42. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.M.; Aarsnes, J. Water entry of arbitrary two-dimensional sections with and without separation. In Proceedings of the 21st Symposium on Naval Hydrodynamics 1996, Trondheim, Norway, 24–28 June 1996; pp. 118–133. [Google Scholar]
- Zhao, R.; Faltinsen, O.M. Water entry of two-dimensional bodies. J. Fluid Mech. 1993, 246, 593–612. [Google Scholar] [CrossRef]
- Battistin, D.; Iafrati, A. Hydrodynamic loads during water entry of two-dimensional and axisymmetric bodies. J. Fluids Struct. 2003, 17, 643–664. [Google Scholar] [CrossRef]
- Wu, G.X.; Sun, H.; He, Y.S. Numerical simulation and experimental study of water entry of a wedge in free fall motion. J. Fluids Struct. 2004, 19, 277–289. [Google Scholar] [CrossRef]
- Cheng, Y.; Yuan, D.C.; Ji, C.Y.; Li, G. Solitary wave slamming induced by an asymmetric wedge through three degrees of freedom free motions. Phys. Fluids 2019, 31, 097103. [Google Scholar] [CrossRef]
- Liu, B.W.; Sun, S.L.; Ren, H.L. Hydrodynamic performance of a cone falling into waves in 3DOFs free fall motion. Ocean Eng. 2021, 242, 110132. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, G.Y.; el Moctar, O.; Sun, Z.; Zhang, Z.F. A semi-analytical method to simulate hydroelastic slamming of 2D structural sections by coupling Wagner theory with the finite element method. Ocean Eng. 2021, 240, 109998. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, G.Y.; Wan, D.C.; Jiang, S.C.; Sun, Z.; Zong, Z. On the treatment of hydroelastic slamming by coupling boundary element method and modal superposition method. Appl. Ocean Res. 2021, 112, 102595. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, G.Y.; Ma, Y.X.; Sun, L.; Zhou, B. Study on the hydroelastic slamming of elastic wedges vertically entering shallow water. Ocean Eng. 2024, 311, 118848. [Google Scholar] [CrossRef]
- Wen, X.L.; Del Buono, A.; Liu, P.Q.; Qu, Q.L.; Iafrati, A. Acceleration effects in slamming and transition stages for the water entry of curved wedges with a varying speed. Appl. Ocean Res. 2022, 128, 103294. [Google Scholar] [CrossRef]
- Reddy, D.N.; Scanlon, T.J.; Kuo, C. Prediction of slam loads on a wedge section using computational fluid dynamics (CFD) techniques. In Proceedings of the Twenty-Fourth Symposium on Naval Hydrodynamics 2002, Fukuoka, Japan, 8–13 July 2002. [Google Scholar]
- Swidan, A.; Amin, W.; Ranmuthugala, D.; Thomas, G.; Penesis, I. Numerical Prediction of Symmetric Water Impact Loads on Wedge Shaped Hull Form Using CFD. World J. Mech. 2013, 3, 311–318. [Google Scholar] [CrossRef]
- Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Ma, S.; Shao, W.B.; Zhang, Y.X. Numerical investigation on the water entry of curved wedge-shaped sections into waves. Ocean Eng. 2023, 275, 114155. [Google Scholar] [CrossRef]
- Vepa, K.S.; Seetharamaiah, N. Performance study of different numerical methods for modeling the vertical water entry of a wedge. Int. J. Interact. Des. Manuf. 2024, 19, 2431–2447. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astrophys. J. 1977, 8, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, P.; Ming, F. An SPH modeling of bubble rising and coalescing in three dimensions. Comput. Methods Appl. Mech. Eng. 2015, 294, 189–209. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating free surface flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Ferrari, A. SPH simulation of free surface flow over a sharp-crested weir. Adv. Water Resour. 2010, 33, 270–276. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Cerqueiro, D.; Crespo, C.; Dalrymple, R.A. Green water overtopping analyzed with a SPH model. Ocean Eng. 2005, 32, 223–238. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M. Using a 3D SPH method for wave impact on a tall structure. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 630–669. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J.C. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48 (Suppl. 1), 6–27. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH without a tensile instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Rogers, B.D.; Dalrymple, R.A.; Stansby, P.K. SPH modeling of floating bodies in the surf zone. Coast. Eng. 2009, 5, 204–215. [Google Scholar]
- Cui, J.; Gu, C.J.; Chen, X.; Li, M.Y.; Masvaya, B. Numerical study of wedge entry in still water and waves using smoothed particle hydrodynamics methods. Ocean Eng. 2023, 280, 114776. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Shu, C.; Khalid, M.S.U.; Yuan, Z.Y.; Liu, W. Investigations on the hydroelastic slamming of deformable wedges by using the smoothed particle element method. J. Fluids Struct. 2022, 114, 103732. [Google Scholar] [CrossRef]
- Chen, D.; Huang, W.; Huang, D.; Liang, C. An adaptive multi-resolution SPH approach for three-dimensional free-surface flow with fluid impacting. Eng. Anal. Bound. Elem. 2023, 155, 642–651. [Google Scholar] [CrossRef]
- Rezavand, M.; Zhang, C.; Hu, X. A weakly compressible SPH method for violent multi-phase flows with high density ratio. J. Comput. Phys. 2020, 402, 109092. [Google Scholar] [CrossRef]
- Wang, P.P.; Zhang, A.M.; Meng, Z.F.; Ming, F.R.; Fang, X.L. A new type of WENO scheme in SPH for compressible flows with discontinuities. Comput. Methods Appl. Mech. Eng. 2021, 381, 113770. [Google Scholar] [CrossRef]
- Yang, Q.Z.; Xu, F.; Yang, Y.; Wang, J.Y. Two-phase SPH model based on an improved Riemann solver for water entry problems. Ocean Eng. 2020, 199, 107039. [Google Scholar] [CrossRef]
- Meng, Z.F.; Ming, F.R.; Wang, P.P.; Zhang, A.M. Numerical simulation of water entry problems considering air effect using a multiphase Riemann-SPH model. Adv. Aerodyn. 2021, 3, 244–259. [Google Scholar]
- Zhang, G.Y.; Yang, X.; Zhang, Z.F.; Hui, D.; Sun, Z.; Liang, G.Q.; Li, P. Numerical investigation of free surface flow impact using an accelerated three-dimensional smoothed particle hydrodynamics. Ocean Eng. 2024, 314 Pt 2, 119772. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 1996, 123, 421–433. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure. Coast. Eng. 2009, 56, 419–440. [Google Scholar] [CrossRef]
- Shibata, K.; Koshizuka, S.; Sakai, M.; Tanizawa, K. Lagrangian simulations of ship-wave interactions in rough seas. Ocean Eng. 2012, 42, 13–25. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Wan, D.C. MPS-FEM coupled method for sloshing flows in an elastic tank. Ocean Eng. 2018, 152, 416–427. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.Y.; Zong, Z.; Djidjeli, K.; Xing, J.T. Numerical analysis of violent hydroelastic problems based on a mixed MPS-mode superposition method. Ocean Eng. 2019, 179, 285–297. [Google Scholar] [CrossRef]
- Matsunaga, T.; Koshizuka, S. Improvement of the time marching method in a particle method. Trans. JSME 2021, 87, 20-00437. (In Japanese) [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 2011, 230, 3093–3118. [Google Scholar] [CrossRef]
- Iida, T.; Yokoyama, Y. Investigation of Numerical Conditions of Moving Particle Semi-implicit for Two-Dimensional Wedge Slamming. J. Mar. Sci. Appl. 2021, 20, 585–594. [Google Scholar] [CrossRef]
- Zha, R.S.; Peng, H.; Qiu, W. An improved higher-order moving particle semi-implicit method for simulations of two-dimensional of two-dimensional hydroelastic slamming. Phys. Fluids 2021, 33, 037104. [Google Scholar] [CrossRef]
- Zha, R.S.; Peng, H.; Qiu, W. Solving 2-D Slamming Problems by an Improved Higher-Order Moving Particle Semi-Implicit Method. J. Ship Res. 2021, 65, 194–222. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 2003, 30, 329–364. [Google Scholar] [CrossRef]
- De Rosis, A.; Falcucci, G.; Porfiri, M.; Ubertini, F.; Ubertini, S. Hydroelastic analysis of hull slamming coupling lattice Boltzmann and finite element methods. Comput. Struct. 2014, 138, 24–35. [Google Scholar] [CrossRef]
- Islam, A.; Taravella, B. A numerical investigation of cambered wedge impact using the Lattice Boltzmann method. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 258. [Google Scholar] [CrossRef]
- Zan, L.R.; Sun, H.B.; Zou, J.; Cang, J.Y.; Wan, L. The effect of flexible step on the resistance of planing boat and motion mitigation. Ocean Eng. 2024, 303, 117265. [Google Scholar] [CrossRef]
- Chuang, S.L. Experiments on slamming of wedge-shaped bodies. J. Ship Res. 1967, 11, 190–198. [Google Scholar] [CrossRef]
- Chuang, S.L. Theoretical Investigations on Slamming of Cone-shaped Bodies. J. Ship Res. 1969, 13, 276–283. [Google Scholar] [CrossRef]
- Chu, W.; Abramson, H.N. Hydrodynamic theories of ship slamming-review and extension. J. Ship Res. 1961, 5, 9–21. [Google Scholar] [CrossRef]
- Barjasteh, M.; Zeraatgar, H.; Javaherian, M.J. An experimental study on water entry of asymmetric wedges. Appl. Ocean Res. 2016, 58, 292–304. [Google Scholar] [CrossRef]
- Nikfarjam, M.; Yaakob, O.B.; Seif, M.S.; Koto, J. Investigation of Wedge Water-Entry Under Symmetric Impact Loads by Experimental Tests. Lat. Am. J. Solids Struct. 2017, 14, 861–873. [Google Scholar] [CrossRef]
- Seo, B.; Truong, D.D.; Cho, S.; Kim, D.; Park, S.; Shin, H. A study on accumulated damage of steel wedges with dead-rise 10° due to slamming loads. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 520–528. [Google Scholar] [CrossRef]
- Seo, B.; Shin, H. Experimental Study of Slamming Effects on Wedge and Cylindrical Surfaces. Appl. Sci. 2020, 10, 1503. [Google Scholar] [CrossRef]
- Korkmaz, F.C.; Güzel, B. Water entry of cylinders and spheres under hydrophobic effects; Case for advancing deadrise angles. Ocean Eng 2017, 129, 240–252. [Google Scholar] [CrossRef]
- Ren, Z.S.; Javaherian, M.J.; Gilbert, C.M. Kinematic and inertial hydroelastic effects caused by vertical slamming of a flexible V-shaped wedge. J. Fluids Struct. 2021, 103, 103257. [Google Scholar] [CrossRef]
- Ren, Z.S.; Javaherian, M.J.; Gilbert, C.M. Vertical Wedge Drop Experiments as a Model for Slamming. J. Ship Res. 2022, 66, 297–314. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Tabri, K.; Sahk, T.; Tear, R. Experimental dataset on aluminium wedge slamming: Measurements of acceleration, pressure, strain, and video data. Data Brief 2024, 56, 110818. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Tabri, K.; Topa, A.; Hirdaris, S. Slamming loads and responses on a non-prismatic stiffened aluminium wedge: Part II. Numerical simulations. Ocean Eng. 2023, 279, 114309. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Tabri, K.; Topa, A.; Hirdaris, S. Slamming loads and responses on a non-prismatic stiffened aluminium wedge: Part I. Experimental study. Ocean Eng. 2023, 279, 114510. [Google Scholar] [CrossRef]
- Han, B.B.; Li, H.; Zhang, B.Y.; Zou, J.; Zhao, W.Z. Experimental investigation of slamming characteristics of stiffened elastic wedges with different deadrise angles: Part I—Slamming pressure. Ocean Eng. 2024, 303, 117728. [Google Scholar] [CrossRef]
- Han, B.B.; Li, H.; Zhang, B.Y.; Zou, J.; Zhao, W.Z. Experimental investigation of slamming characteristics of stiffened elastic wedges with different deadrise angles: Part II—Structural response. Ocean Eng. 2024, 303, 118288. [Google Scholar] [CrossRef]
- Han, B.B.; Peng, Y.H.; Li, H.; Liu, S.N.; Sun, S.L.; Shan, Y.H.; Sun, Z.Y. Numerical investigations of a 2D bow wedge asymmetric free-falling into still water. Ocean Eng. 2022, 266 Pt 3, 112905. [Google Scholar] [CrossRef]
- Duan, L.L.; Zhu, L.; Chen, M.S.; Pedersen, P.T. Experimental study on the propagation characteristics of the slamming pressures. Ocean Eng. 2020, 217, 107868. [Google Scholar] [CrossRef]
- Güzel, B.; Korkmaz, F.C. Experimental investigation of water entry of bodies with constant deadrise angles under hydrophobic effects. Exp. Fluids 2021, 62, 107. [Google Scholar] [CrossRef]
- Zhang, J.; You, Y.; Yao, Z.; Huo, F.L. Sensitivity Analysis of the Effect of Speed and Inclination Angle on Water-Entry Slamming Pressure of the Bow. China Ocean Eng. 2020, 34, 432–440. [Google Scholar] [CrossRef]
- Meziane, B.; Alaoui, A.E.; Neme, A.; Leble, B.; Bellanger, D. Experimental investigation of the influence of the panel stiffness on the behaviour of a wedge under slamming. J. Fluids Struct. 2022, 114, 103702. [Google Scholar] [CrossRef]
- Meziane, B.; Alaoui, A.E.; Neme, A.; Leble, B.; Bellanger, D. Water impact of V-shaped wedge at constant velocity: Influence of deadrise angle and stiffness panels. Appl. Ocean Res. 2025, 158, 104494. [Google Scholar] [CrossRef]
- Jain, U.; Novakovic, V.; Bogaert, H.; van der Meer, D. On wedge-slamming pressures. J. Fluid Mech. 2022, 934, A27. [Google Scholar] [CrossRef]
- Korobkin, A.; Khabakhpasheva, T.; Malenica, S.; Kim, Y. A comparison study of water impact and water exit models. Int. J. Nav. Archit. Ocean Eng. 2014, 6, 1182–1196. [Google Scholar] [CrossRef]
- Nila, A.; Vanlanduit, S.; Vepa, S.; Van Paepegem, W. A PIV-based method for estimating slamming loads during water entry of rigid bodies. Meas. Sci. Technol. 2013, 24, 436–475. [Google Scholar] [CrossRef]
- Shams, A.; Jalalisendi, M.; Porfiri, M. Experiments on the water entry of asymmetric wedges using particle image velocimetry. Phys. Fluids 2015, 27, 027103. [Google Scholar] [CrossRef]
- Panciroli, R.; Porfiri, M. Evaluation of the pressure field on a rigid body entering a quiescent fluid through particle image velocimetry. Exp. Fluids 2013, 54, 1630. [Google Scholar] [CrossRef]
- Jalalisendi, M.; Shams, A.; Panciroli, R.; Porfiri, M. Experimental reconstruction of three-dimensional hydrodynamic loading in water entry problems through particle image velocimetry. Exp. Fluids 2015, 56, 41. [Google Scholar] [CrossRef]
- Panciroli, R.; Porfiri, M. Analysis of hydroelastic slamming through particle image velocimetry. J. Sound Vib. 2015, 347, 63–78. [Google Scholar] [CrossRef]
- Panciroli, R.; Porfiri, M. A Particle Image Velocimetry Study of Hydroelastic Slamming. Procedia Eng. 2014, 88, 180–185. [Google Scholar] [CrossRef]
- Zhang, P.; Porfiri, M. A combined digital image correlation/particle image velocimetry study of water-backed impact. Compos. Struct. 2019, 224, 111010. [Google Scholar] [CrossRef]
- Guo, C.Y.; Fan, Y.W.; Han, Y.; Xu, P.; Kuai, Y.F. Deep-learning-based liquid extraction algorithm for particle image velocimetry in two-phase flow experiments of an object entering water. Appl. Ocean Res. 2021, 108, 102526. [Google Scholar]
- Dessi, D.; Sanchez-Alayo, D.; Shabani, B.; Ali-Lavroff, J. Bow slamming detection and classification by Machine Learning approach. Ocean Eng. 2023, 287, 115646. [Google Scholar] [CrossRef]
- Izadi, M.; Ghadimi, P.; Fadavi, M.; Tavakoli, S. Hydroelastic analysis of water impact of flexible asymmetric wedge with an oblique speed. Meccanica 2018, 53, 2585–2617. [Google Scholar] [CrossRef]
- Jiao, J.L.; Chen, Z.W.; Xu, W.H.; Bu, S.X.; Zhang, P.J. Asymmetric water entry of a wedged grillage structure investigated by CFD-FEM co-simulation. Ocean Eng. 2024, 302, 117612. [Google Scholar] [CrossRef]
- Xiao, J.W.; Liu, C.; Han, B.B.; Wan, D.C.; Wang, J.H. A two-way coupled fluid-structure interaction method for predicting the slamming loads and structural responses on a stiffened wedge. Phys. Fluids 2015, 36, 077123. [Google Scholar] [CrossRef]
- Sun, S.L.; Sun, J.Y.; Wang, S.; Li, Y.H. Fluid–structure interaction analysis of curved wedges entering into water. Phys. Fluids 2024, 36, 102121. [Google Scholar] [CrossRef]
- Chen, Z.W.; Jiao, J.L.; Wang, S.; Soares, C.G. CFD-FEM simulation of water entry of a wedged grillage structure into Stokes waves. Ocean Eng. 2023, 275, 114159. [Google Scholar] [CrossRef]
- Sun, Z.; Sui, X.P.; Korobkin, A.; Zou, L.; Zong, Z. Slamming force decomposition with gravity effect. J. Fluids Struct. 2022, 114, 103694. [Google Scholar] [CrossRef]
- Wen, X.L.; Liu, P.D.; Del Buono, A.; Qu, Q.L.; Iafrati, A. Formulations of hydrodynamic force in the transition stage of the water entry of linear wedges with constant and varying speeds. J. Fluids Struct. 2022, 115, 103759. [Google Scholar] [CrossRef]
- Moore, M.R. Introducing pre-impact air-cushioning effects into the Wagner model of impact theory. J. Eng. Math. 2021, 129, 6. [Google Scholar] [CrossRef]
- Hasheminasab, H.; Zeraatgar, H.; Moradi, H.; Sakaki, A. Experimental study on water entry of twin wedge. Proc. Inst. Mech. Eng. Part M–J. Eng. Marit. Environ. 2020, 234, 388–398. [Google Scholar] [CrossRef]
- Tang, S.Q.; Zhang, Y.; Sun, S.L.; Ren, H.L.; Zhang, H.B.; He, J.H. Experimental investigation on the air-cushion effect during free fall of a trimaran section using an air escape control method. Ocean Eng. 2022, 254, 111417. [Google Scholar] [CrossRef]
- Ma, S.; Duan, W.Y.; Cao, Z.H.; Liu, J.Y.; Zhang, M.H.; Li, X.H.; Liu, D.D. Experimental study on the drop test on wet deck slamming for a SWATH segment model. Ocean Eng. 2022, 285 Pt 2, 115377. [Google Scholar] [CrossRef]
- Masoomi, M.; Rezanejad, K.; Mosavi, A.H. Numerical study of a novel ventilation system added to the structure of a catamaran for different slamming conditions using OpenFOAM. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100512. [Google Scholar] [CrossRef]
- Swidan, A.; Thomas, G.; Ranmuthugala, D.; Amin, W.; Penesis, I.; Allen, T.; Battley, M. Experimental drop test investigation into wetdeck slamming loads on a generic catamaran hullform. Ocean Eng. 2016, 117, 143–153. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Bai, J.Y.; Dong, Y.; Sun, T.Z.; Sun, Z.; Liu, S.J. Investigations of air cushion effect on the slamming load acting on trimaran cross deck during water entry. Ocean Eng. 2022, 251, 111161. [Google Scholar] [CrossRef]
- Yu, P.Y.; Qu, S.; Wang, Q.; Xie, H. Numerical investigation on the slamming loads of a truncated trimaran hull entering regular waves. Appl. Ocean Res. 2024, 153, 104253. [Google Scholar] [CrossRef]
- Wu, J.X.; Sun, Z.; Jiang, Y.C.; Zhang, G.Y.; Sun, T.Z. Experimental and numerical study of slamming problem for a trimaran hull. Ships Offshore Struct. 2021, 16, 46–53. [Google Scholar] [CrossRef]
- Liu, J.Y.; Duan, W.Y.; Liao, K.P.; Ma, S.; Shao, W.B.; Zhang, Y.F. Numerical analysis of wet-deck slamming characteristics for trimaran section with different main-hull profiles. Ocean Eng. 2024, 301, 117542. [Google Scholar] [CrossRef]
- Sun, Z.; Deng, Y.Z.; Zou, L.; Jiang, Y.C. Investigation of trimaran slamming under different conditions. Appl. Ocean Res. 2020, 104, 102316. [Google Scholar] [CrossRef]
- Sun, Z.; Sui, X.P.; Deng, Y.Z.; Zou, L.; Korobkin, A.; Xu, L.X.; Jiang, Y.C. Characteristics of Slamming Pressure and Force for Trimaran Hull. J. Mar. Sci. Eng. 2021, 9, 564. [Google Scholar] [CrossRef]
- Duan, W.Y.; Liu, J.Y.; Liao, K.P.; Ma, S. Experimental study of slamming pressure for a trimaran section with different drop heights and heel angles. Ocean Eng. 2022, 263, 112400. [Google Scholar] [CrossRef]
- Pan, J.; Zhang, W.Z.; Sun, Z.M.; Qu, X.; Xu, M.C. Experimental study on the dynamical response of elastic trimaran model under slamming load. J. Mar. Sci. Technol. 2024, 29, 20–35. [Google Scholar] [CrossRef]
- Li, J.Q.; Sun, S.L. Impact Force Mechanism of a Trimaran Model and Its Experimental Validation. Appl. Sci. 2023, 13, 10382. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, P.Y.; Fan, G.J.; Li, G.Z. Experimental drop test investigation into cross deck slamming loads on a trimaran. Ocean Eng. 2021, 240, 109999. [Google Scholar] [CrossRef]
- Li, H.; Deng, B.L.; Zou, J.; Dong, C.R.; Liu, C.L.; Liu, P.L. Experimental free-drop test investigation into wet-deck slamming loads on a generic trimaran section considering the influence of main hull profile. Ocean Eng. 2021, 242, 110114. [Google Scholar] [CrossRef]
- Dong, L.Y.; Wei, Z.Y.; Zhou, H.Y.; Yao, B.H.; Lian, L. Numerical Study on the Water Entry of a Freely Falling Unmanned Aerial-Underwater Vehicle. J. Mar. Sci. Eng. 2023, 11, 552. [Google Scholar] [CrossRef]
- Wang, Y.W.; Wang, M.Z.; Zheng, C.; Yang, L.; Zhang, H.T.; Li, Y.R.; Ruan, X.Y. Experimental investigation of slamming impact on fiber-reinforced composite sandwich bow structure. Ocean Eng. 2024, 319, 120162. [Google Scholar] [CrossRef]
- Shan, Y.H.; Li, H.; Han, B.B.; Sun, Z.Y.; Lu, L.; Liu, R.X.; Liu, Y.; Guo, H. E Experimental investigation of slamming pressure on 3D bow flare. Ocean Eng. 2024, 312 Pt 1, 118898. [Google Scholar] [CrossRef]
- Ping, Y.N.; Wang, J.Z.; Xie, H.; Liu, F.; Liu, X.Y. Experimental and CFD analysis: Effects of bottom appendages on the slamming characteristics of rigid hull structures during water entry. Ocean Eng. 2025, 319, 120195. [Google Scholar] [CrossRef]
- Xie, H.; Dai, X.L.; Liu, F.; Liu, X.Y. Experimental study on the slamming pressure distribution of a 3D stern model entering water with pitch angles. Ocean Eng. 2024, 291, 116404. [Google Scholar] [CrossRef]
- Xie, H.; Dai, X.L.; Ren, H.L.; Liu, F. Experimental characterization on slamming loads of a truncated ship bow under asymmetrical impact. Ocean Eng. 2023, 284, 115195. [Google Scholar] [CrossRef]
- Xie, H.; Liu, F.; Yu, P.Y.; Ren, H.L. Comparative study on fluid dynamic behavior and slamming loads of two bow-flare sections entering into water. Int. J. Mech. Sci. 2020, 166, 105177. [Google Scholar] [CrossRef]
- Liu, X.Y.; Liu, F.; Ren, H.L.; Chen, X.; Xie, H. Experimental investigation on the slamming loads of a truncated 3D stern model entering into water. Ocean Eng. 2022, 252, 110873. [Google Scholar] [CrossRef]
- Mutsuda, H.; Kanehira, T.; Kawawaki, K.; Doi, Y.; Yasukawa, H. Occurrence of stern slamming pressure and its characteristics in following irregular waves. Ocean Eng. 2018, 170, 222–236. [Google Scholar] [CrossRef]
- Ochi, M. Prediction of slamming characteristics and hull responses for ship design. Trans. SNAME 1973, 81, 144–177. [Google Scholar]
- Li, P.; Xie, H.; Liu, F.; Liu, X.Y.; Li, H. Experimental study on the water entry of a 3D bow-flared model with various inclination angles. Ocean Eng. 2022, 259, 111834. [Google Scholar] [CrossRef]
- Liu, B.; Wang, S.; Villavicencio, R.; Soares, C.G. Slamming load and hydroelastic structural response of bow flare areas of aluminium fast displacement crafts. Ocean Eng. 2020, 218, 108207. [Google Scholar] [CrossRef]
- Bao, C.M.; Sun, S.Y.; Xu, G.; Chen, L.F. Numerical prediction of slamming loads during water entry of a slender hull. Ocean Eng. 2020, 201, 107136. [Google Scholar] [CrossRef]
- Prini, F.; Benson, S.; Dow, R.S.; Phillips, H.J.; Sheppard, P.J.; Birmingham, R.W. Model scale prediction of seakeeping and global bending moment on a high speed craft. Eng. Struct. 2021, 231, 111738. [Google Scholar] [CrossRef]
- Parunov, J.; Badalotti, T.; Feng, Q.D.; Gu, X.C.; Iijima, K.; Ma, N.; Qiu, W.; Wang, S.; Wang, X.L.; Yang, P.; et al. Benchmark on the prediction of whipping response of a warship model in regular waves. Mar. Struct. 2024, 94, 103549. [Google Scholar] [CrossRef]
- Bilandi, R.N.; Mancini, S.; Vitiello, L.; Miranda, S.; De Carlini, M. A Validation of Symmetric 2D + T Model Based on Single-Stepped Planing Hull Towing Tank Tests. J. Mar. Sci. Eng. 2018, 6, 136. [Google Scholar] [CrossRef]
- Tavakoli, S.; Bilandi, R.N.; Mancini, S.; De Luca, F.; Dashtimanesh, A. Dynamic of a planing hull in regular waves: Comparison of experimental, numerical and mathematical methods. Ocean Eng. 2020, 217, 107959. [Google Scholar] [CrossRef]
- Shao, W.B.; Ma, S.; Duan, W.Y.; Liu, J.Y.; Zhang, Y.F. Vertical force prediction of planing craft in calm water based on varia-ble section slamming model. Ocean Eng. 2023, 287 Pt 1, 115693. [Google Scholar] [CrossRef]
- Mousaviraad, S.M.; Wang, Z.Y.; Stern, F. URANS studies of hydrodynamic performance and slamming loads on high-speed planing hulls in calm water and waves for deep and shallow conditions. Appl. Ocean Res. 2015, 51, 222–240. [Google Scholar] [CrossRef]
- Thodal, R.S. On Full Scale Slamming Testing of High-Speed Boats. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2016. [Google Scholar]
- Judge, C.; Mousaviraad, M.; Stern, F.; Lee, E.; Fullerton, A.; Geiser, J.; Schleicher, C.; Merrill, C.; Weil, C.; Morin, J.; et al. Experiments and CFD of a high-speed deep-V planing hull—Part II: Slamming in waves. Appl. Ocean Res. 2020, 97, 102059. [Google Scholar] [CrossRef]
- Judge, C.Q.; Ibrahim, A.M. Experimental investigation of motions and global hull girder bending moment of a semi-displacement vessel. Ocean Eng. 2025, 320, 120295. [Google Scholar] [CrossRef]
- Yousefnia, M.; Heirani, N.M.R. Global hydroelastic effects on hull girder deflection due to bow flare slamming. Mar. Syst. Ocean Technol. 2021, 16, 99–110. [Google Scholar] [CrossRef]
- Liu, W.Q.; Qin, Y.X.; Hu, Y.C.; Vladimir, N.; Xu, S.X.; Wu, Y.C. Numerical Research on Impacting Load and Structural Response for a Model Experiment of High-Speed Craft. J. Offshore Mech. Arct. Eng. 2025, 147, 011901. [Google Scholar] [CrossRef]
- Lee, E.J.; Die, M.; Harrison, E.L.; Jiang, M.J.; Snyder, L.A.; Powers, A.M.R.; Bay, R.J.; Serani, A.; Nadal, M.L.; Kubina, E.R.; et al. Experimental and computational fluid-structure interaction analysis and optimization of Deep-V planing-hull grillage panels subject to slamming loads—Part II: Irregular waves. Ocean Eng. 2024, 292, 116346. [Google Scholar] [CrossRef]
- Shan, L.; Xu, G.D. Numerical study of the green water on a wave-piercing tumblehome vessel and the hydrodynamic loads. Ocean Eng. 2024, 309 Pt 1, 118313. [Google Scholar] [CrossRef]
- Begovic, E.; Bertorello, C.; Bove, A.; Garme, K.; Lei, X.Y.; Persson, J.; Petrone, G.; Razola, M.; Rosén, A. Experimental modelling of local structure responses for high-speed planing craft in waves. Ocean Eng. 2020, 216, 107986. [Google Scholar] [CrossRef]
- Camilleri, J.; Taunton, D.J.; Temarel, P. Full-scale measurements of slamming loads and responses on high-speed planing craft in waves. J. Fluids Struct. 2018, 81, 201–229. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Judge, C.Q. Investigations of hull girder slamming factor for a semi-displacement vessel using model testing. Appl. Ocean Res. 2024, 150, 104084. [Google Scholar] [CrossRef]
- Zou, J.; Li, H.; Sun, Z.Y.; Han, B.B.; Wang, Z.Y. Experimental analysis of bow flare slamming and whipping responses in a ship at different sailing speeds. Ocean Eng. 2024, 305, 117896. [Google Scholar] [CrossRef]
- Magoga, T.; Aksus, S.; Cannon, S.; Ojeda, R.; Thomas, G. Identification of slam events experienced by a high-speed craft. Ocean Eng. 2017, 140, 309–321. [Google Scholar] [CrossRef]
- Davis, M.R.; Watson, N.L.; Holloway, D.S. Measurement of response amplitude operators for an 86 m high-speed catamaran. J. Ship Res. 2005, 49, 121–143. [Google Scholar] [CrossRef]
- Al-Furjan, M.S.H.; Kolahchi, R.; Shan, L.; Hajmohammad, M.H.; Farrokhian, A.; Shen, X. Slamming impact induced hydrodynamic response in wave-piercing catamaran beam elements with controller. Ocean Eng. 2022, 266 Pt 4, 112908. [Google Scholar] [CrossRef]
- Lavroff, J.; Davis, M.R.; Holloway, D.S.; Thomas, G. Wave slamming loads on wave-piercer catamarans operating at high-speed determined by hydro-elastic segmented model experiments. Mar. Struct. 2013, 33, 120–142. [Google Scholar] [CrossRef]
- Gebrezgabir, S.; Holloway, D.S.; Ali-Lavroff, J. Slam and wave load response reconstruction in high speed catamarans using transmissibility on full scale sea trials. Ocean Eng. 2023, 271, 113822. [Google Scholar] [CrossRef]
- French, B.J.; Thomas, G.A.; Davis, M.R. Slam occurrences and loads of a high-speed wave piercer catamaran in irregular seas. Proc. Inst. Mech. Eng. Part M–J. Eng. Marit. Environ. 2015, 229, 45–57. [Google Scholar] [CrossRef]
- Davis, M.R.; French, B.J.; Thomas, G.A. Wave slam on wave piercing catamarans in random head seas. Ocean Eng. 2017, 135, 84–97. [Google Scholar] [CrossRef]
- Shabani, B.; Lavroff, J.; Davis, M.R.; Holloway, D.S.; Thomas, G.A. Slam loads and pressures acting on high-speed wave-piercing catamarans in regular waves. Mar. Struct. 2019, 66, 136–153. [Google Scholar] [CrossRef]
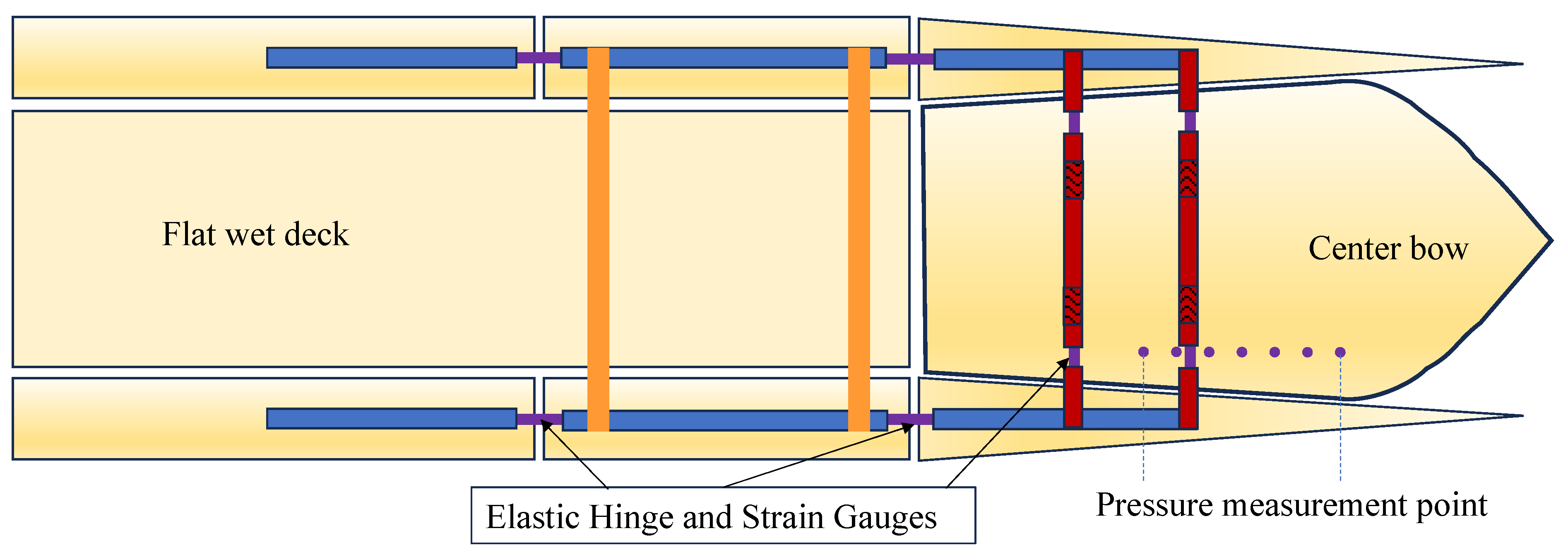
- Shabani, B.; Lavroff, J.; Davis, M.R.; Holloway, D.S.; Davis, M.R.; Thomas, G.A. The effect of centre bow and wet-deck geometry on wet-deck slamming loads and vertical bending moments of wave-piercing catamarans. Ocean Eng. 2018, 169, 401–417. [Google Scholar] [CrossRef]
- Shabani, B.; Lavroff, J.; Davis, M.R.; Holloway, D.S.; Davis, M.R.; Thomas, G.A. Centre bow and wet-deck design for motion and load reductions in wave piercing catamarans at medium speed. Ships Offshore Struct. 2021, 16, 83–99. [Google Scholar] [CrossRef]
- Liu, T.; Halse, K.H.; Leira, B.J.; Jiang, Z.Y.; Chai, W.; Brathaug, H.P.; Hildre, H.P. Dynamic response of a SWATH vessel for installing pre-assembled floating wind turbines. Mar. Struct. 2023, 88, 103341. [Google Scholar] [CrossRef]
- Ma, S.; Zhu, M.Y.; Liu, D.D.; Liu, J.C.; Wang, W. Experimental study of wet deck slamming for a SWATH in regular waves. Ocean Eng. 2023, 288 Pt 1, 115996. [Google Scholar] [CrossRef]
- McVicar, J.; Lavroff, J.; Davis, M.R.; Thomas, G. Fluid-structure interaction simulation of slam-induced bending in large high-speed wave-piercing catamarans. J. Fluids Struct. 2018, 82, 35–58. [Google Scholar] [CrossRef]
- Almallah, I.; Ali-Lavroff, J.; Holloway, D.S.; Davis, M.R. Slam load estimation for high-speed catamarans in irregular head seas by full-scale computational fluid dynamics. Ocean Eng. 2021, 234, 109160. [Google Scholar] [CrossRef]
- Almallah, I.; Ali-Lavroff, J.; Holloway, D.S.; Davis, M.R. Estimation of torsional and global loads for a wave-piercing high-speed catamaran at full-scale in irregular bow quartering seas using CFD simulation. Ocean Eng. 2022, 266, 113006. [Google Scholar] [CrossRef]
- Almallah, I.; Ali-Lavroff, J.; Holloway, D.S.; Davis, M.R. High-speed wave-piercing catamaran global loads determined by fea and sea trials. Int. J. Marit. Eng. 2021, 161, 139–153. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Farrokhian, A.; Kolahchi, R. Dynamic analysis in beam element of wave-piercing Catamarans undergoing slamming load based on mathematical modelling. Ocean Eng. 2021, 234, 106269. [Google Scholar] [CrossRef]
- Davis, M.R.; Watson, N.L.; Holloway, D.S. Measurement and prediction of wave loads on a high-speed catamaran fitted with active stern tabs. Mar. Struct. 2004, 17, 503–535. [Google Scholar] [CrossRef]
- Jacobi, G.; Thomas, G.; Davis, M.R.; Holloway, D.S.; Davidson, G.; Roberts, T. Full-scale motions of a large high-speed catamaran: The influence of wave environment, speed and ride control system. Int. J. Marit. Eng. 2012, 154, A143–A155. [Google Scholar] [CrossRef]
- Jacobi, G.; Thomas, G.; Davis, M.R.; Davidson, G. An insight into the slamming behaviour of large high-speed catamarans through full-scale measurements. J. Mar. Sci. Technol. 2014, 19, 15–32. [Google Scholar] [CrossRef]
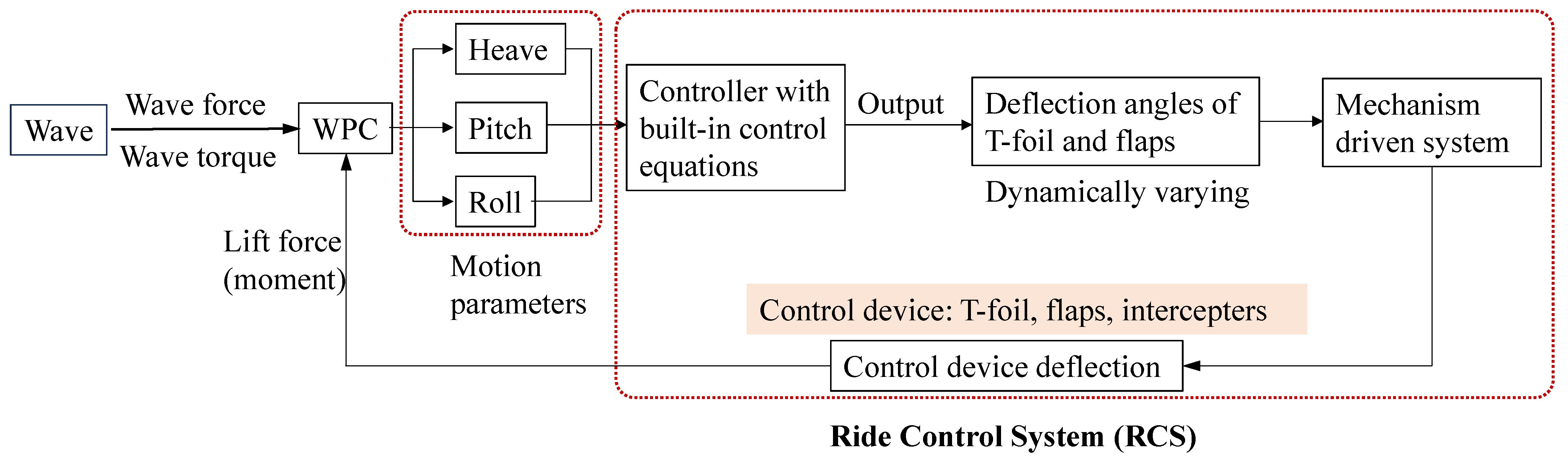
- AlaviMehr, J.; Lavroff, J.; Davis, M.R.; Holloway, D.S.; Thomas, G.A. An Experimental Investigation of Ride Control Algorithms for High-Speed Catamarans Part 2: Mitigation of Wave Impact Loads. J. Ship Res. 2017, 61, 51–63. [Google Scholar] [CrossRef]
- Hasheminasab, H.; Zeraatgar, H.; Malekmohammadi, J.; Azizi, A. Analysis of slamming loads on a catamaran section with a centre-bow appended by spray rail. Ships Offshore Struct. 2023, 18, 1025–1036. [Google Scholar] [CrossRef]
- Available online: https://www.hildstrom.com/publications/pub-StructuralTrialsOfTheRVTriton-Feb-10-2003-Final.pdf (accessed on 14 August 2003).
- Miao, S.H.; Price, W.G.; Temarel, P. The hydroelastic behavior of multi-hulls travelling in a seaway. In Proceedings of the 3rd International Conference Advances in Marine Structures 1997, Dunfermline, UK, 20–22 May 1997. [Google Scholar]
- Miao, S.H.; Temarel, P. Trimaran wave loading. In 2nd Report for DERA Contract SSDH100120; University of Southampton: Southampton, UK, 1998. [Google Scholar]
- Miao, S.H.; Temarel, P. Trimaran wave loading—Development of the software THAFTS. In Report for DERA Contract CU004-0000001635; University of Southampton: Southampton, UK, 2000. [Google Scholar]
- Tang, H.Y.; Ren, H.L.; Wan, Q. Investigation of Longitudinal Vibrations and Slamming of a Trimaran in Regular Waves. J. Ship Res. 2017, 61, 153–166. [Google Scholar] [CrossRef]
- Tang, H.Y.; Wan, Q.; Ren, H.L. Numerical study of trimaran wave load based on time-domain Rankine method. Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2023, 74, 107–129. [Google Scholar] [CrossRef]
- Tang, H.Y.; Zhang, X.K.; Ren, H.L.; Yu, P.Y. Numerical study of trimaran motion and wave load prediction based on time-domain Rankine-Green matching method. Ocean Eng. 2020, 214, 107605. [Google Scholar] [CrossRef]
- Askarian Khoob, A.; Ketabdari, M.J. Wave-induced loads on cross-deck of a wave-piercing trimaran with different hull forms of outriggers. Transport 2019, 34, 559–568. [Google Scholar] [CrossRef]
- Khoob, A.A.; Ketabdari, M.J. Short-term prediction and analysis of wave-induced motion and load responses of a wave-piercing trimaran. Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2020, 71, 123–142. [Google Scholar]
- Ghadimi, P.; Nazemian, A.; Sheikholeslami, M. Numerical simulation of the slamming phenomenon of a wave-piercing trimaran in the presence of irregular waves under various seagoing modes. Proc. Inst. Mech. Eng. 2019, 233, 1198–1211. [Google Scholar] [CrossRef]
- Xie, H.; Liu, F.; Liu, X.Y.; Tang, H.Y. Numerical prediction of asymmetrical ship slamming loads based on a hybrid two-step method. Ocean Eng. 2020, 208, 107331. [Google Scholar] [CrossRef]
- Liao, X.Y.; Chen, Z.Y.; Gui, H.B.; Du, M.C. CFD Prediction of Ship Seakeeping and Slamming Behaviors of a Trimaran in Oblique Regular Waves. J. Mar. Sci. Eng. 2021, 9, 1151. [Google Scholar] [CrossRef]
- Liao, X.Y.; Xia, J.S.; Chen, Z.Y.; Tang, Q.; Zhao, N.; Zhao, W.D.; Gui, H.B. Application of CFD and FEA Coupling to Predict Structural Dynamic Responses of A Trimaran in Uni- and Bi-Directional Waves. China Ocean Eng. 2024, 38, 81–92. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Gui, H.B.; Dong, P.S.; Yu, C.L. Numerical and experimental analysis of hydroelastic responses of a high-speed trimaran in oblique irregular waves. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 409–421. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Zhao, N.; Zhao, W.D.; Xia, J.S. Numerical prediction of seakeeping and slamming behaviors of a trimaran in short-crest cross waves compared with long-crest regular waves. Ocean Eng. 2023, 285, 115314. [Google Scholar] [CrossRef]
- Liu, J.Y.; Duan, W.Y.; Ma, S.; Liao, K.P.; Si, H.L. Experimental and numerical study of wet-deck slamming characteristic for a trimaran in regular head waves. Appl. Ocean Res. 2024, 150, 104136. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, D.; Wu, Z.; Yu, Y. A Review of Experimental and Numerical Research on the Slamming Problem of High-Performance Vessels. J. Mar. Sci. Eng. 2025, 13, 1310. https://doi.org/10.3390/jmse13071310
Sun Y, Zhang D, Wu Z, Yu Y. A Review of Experimental and Numerical Research on the Slamming Problem of High-Performance Vessels. Journal of Marine Science and Engineering. 2025; 13(7):1310. https://doi.org/10.3390/jmse13071310
Chicago/Turabian StyleSun, Yifang, Dapeng Zhang, Zongduo Wu, and Yiquan Yu. 2025. "A Review of Experimental and Numerical Research on the Slamming Problem of High-Performance Vessels" Journal of Marine Science and Engineering 13, no. 7: 1310. https://doi.org/10.3390/jmse13071310
APA StyleSun, Y., Zhang, D., Wu, Z., & Yu, Y. (2025). A Review of Experimental and Numerical Research on the Slamming Problem of High-Performance Vessels. Journal of Marine Science and Engineering, 13(7), 1310. https://doi.org/10.3390/jmse13071310





