Energetics of Eddy–Mean Flow Interaction in the Kuroshio Current Region
Abstract
1. Introduction
2. Diagnostic Framework and Model
2.1. Theoretical Framework
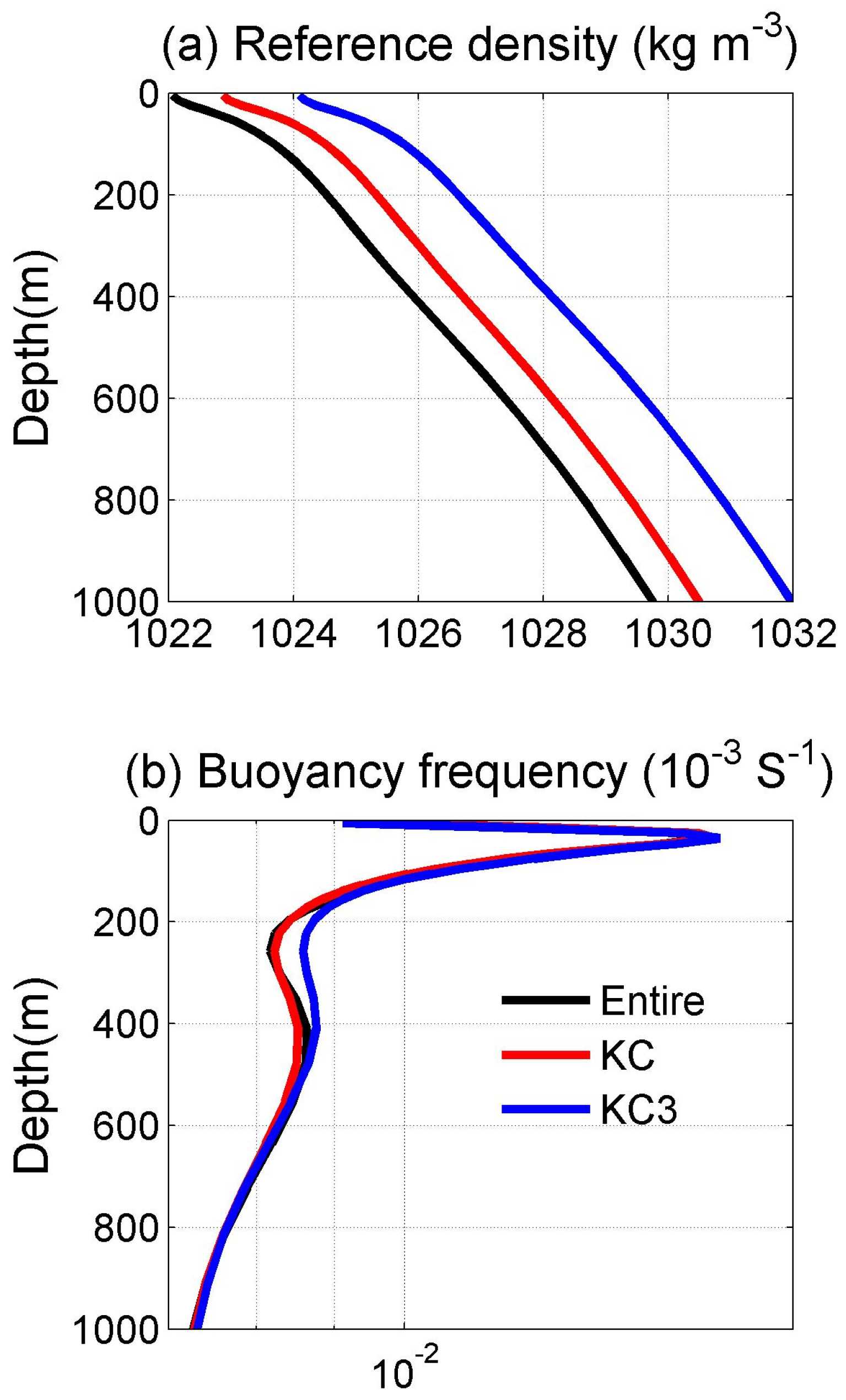
2.2. Numerical Simulation
3. Results
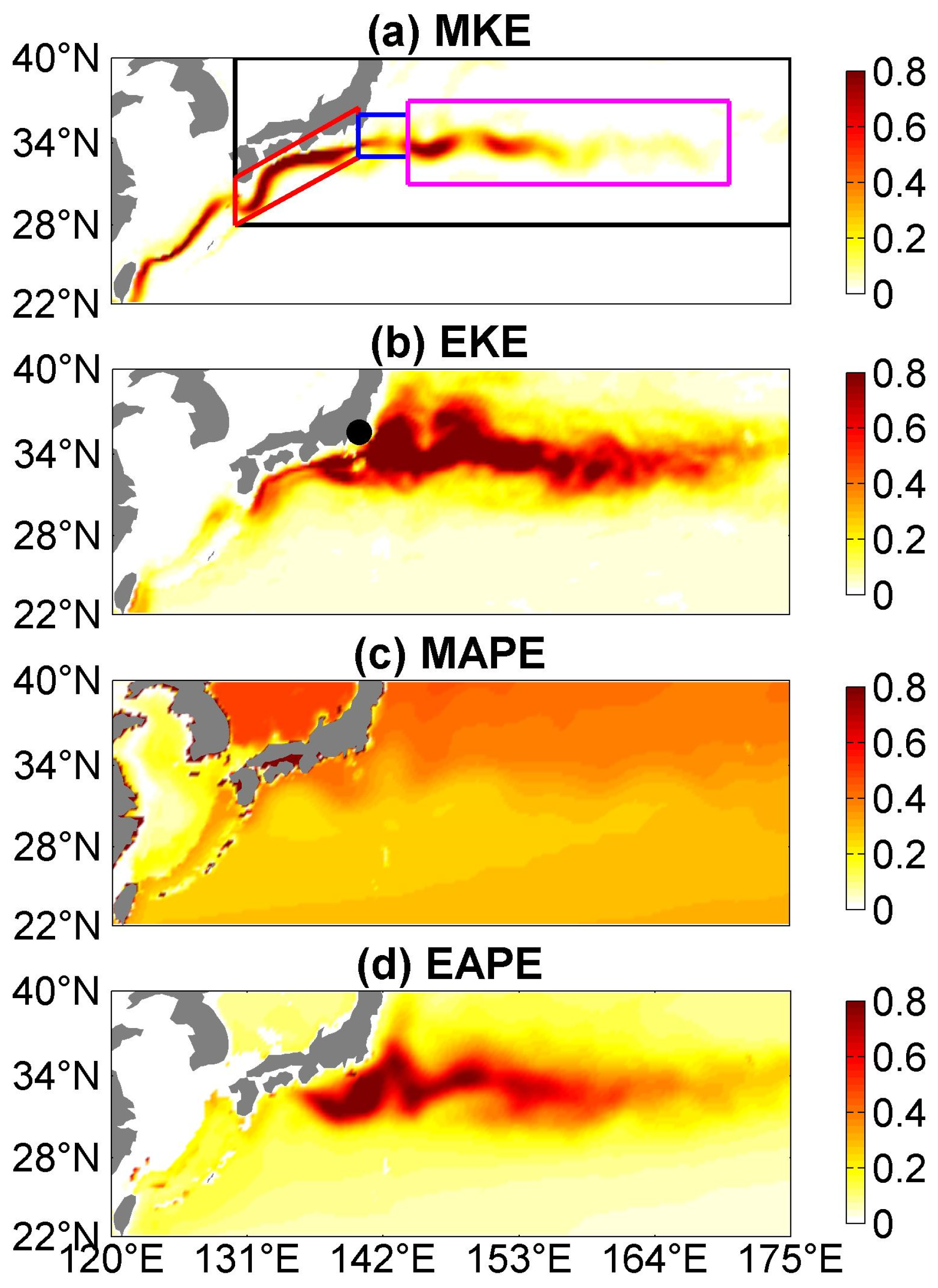
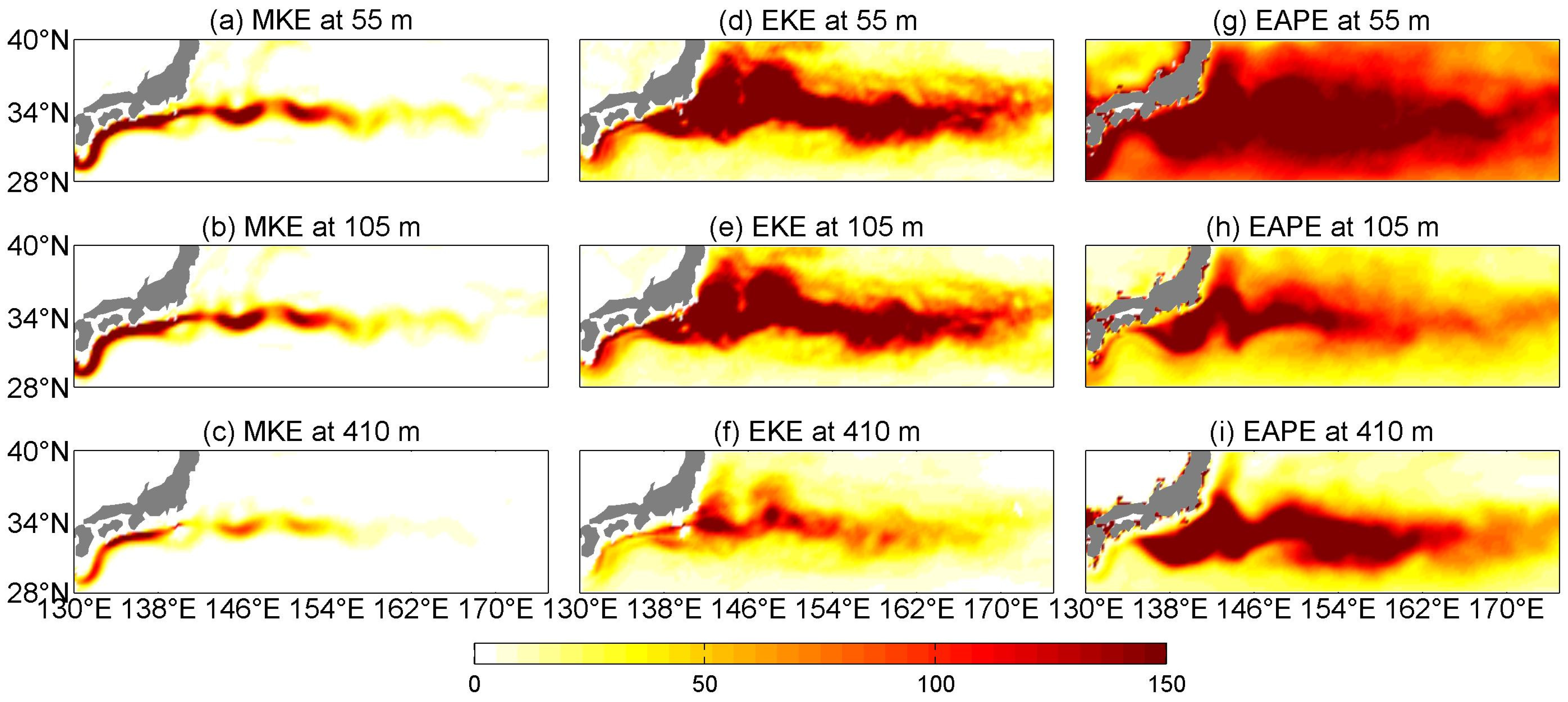
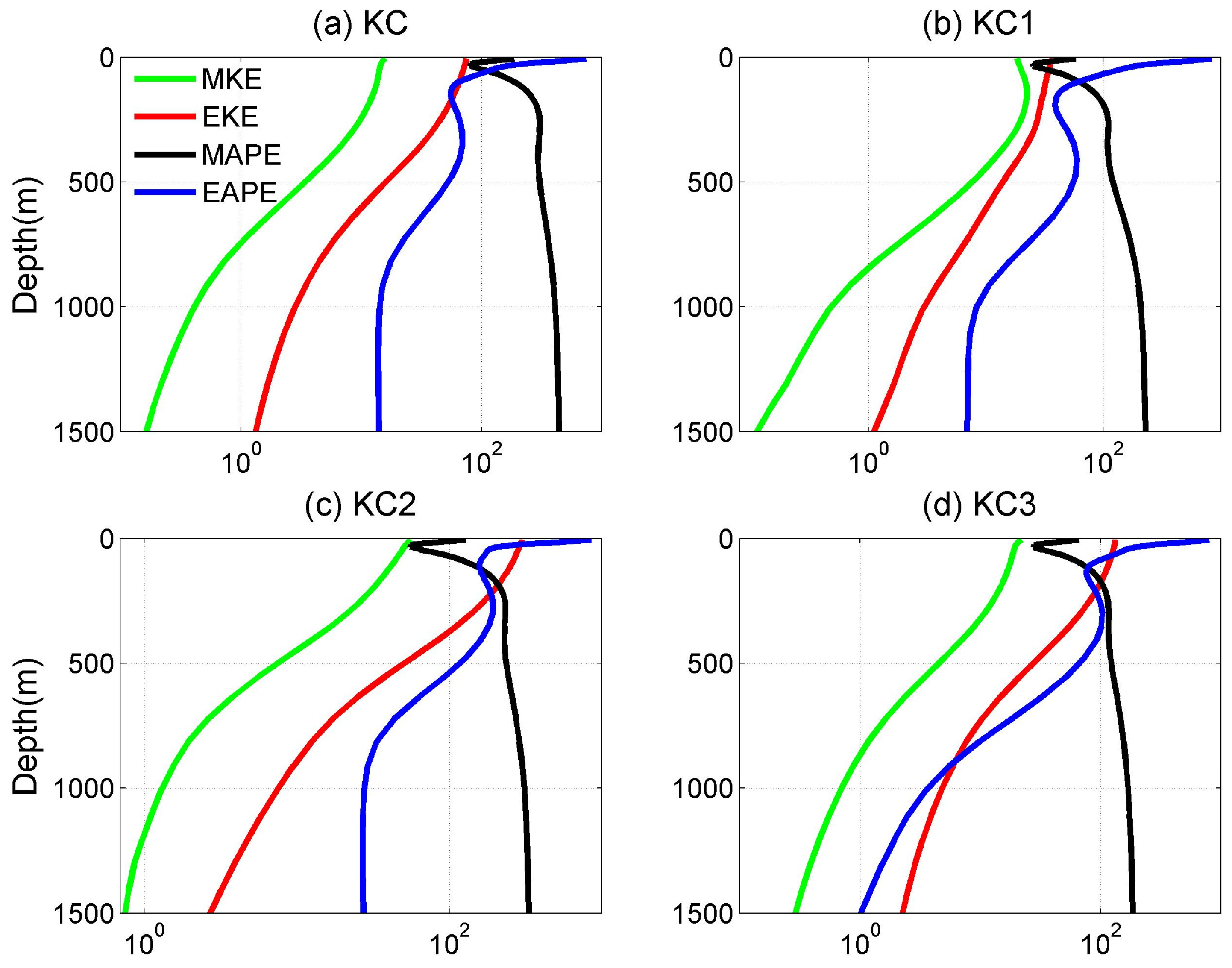
3.1. Energy Reservoirs
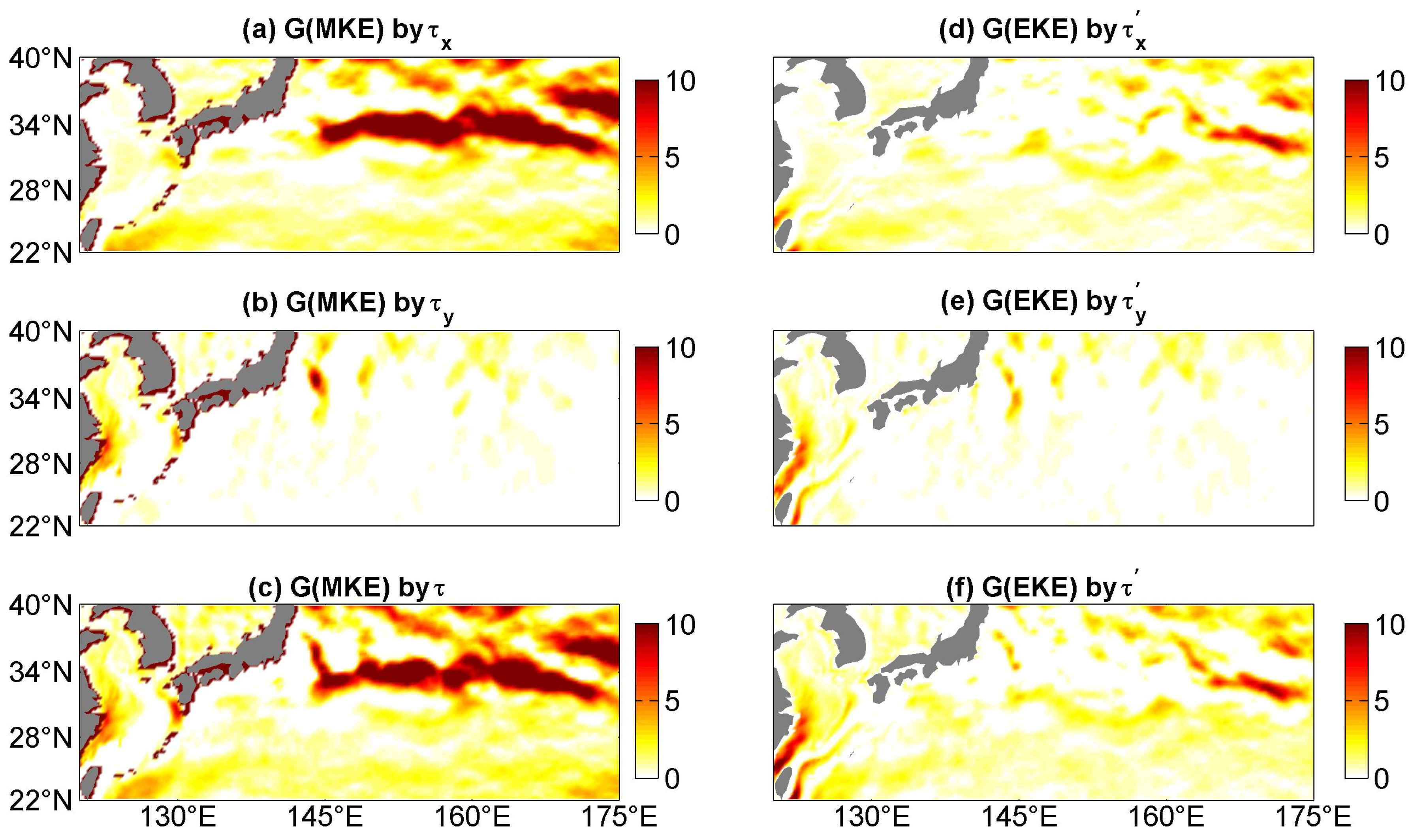
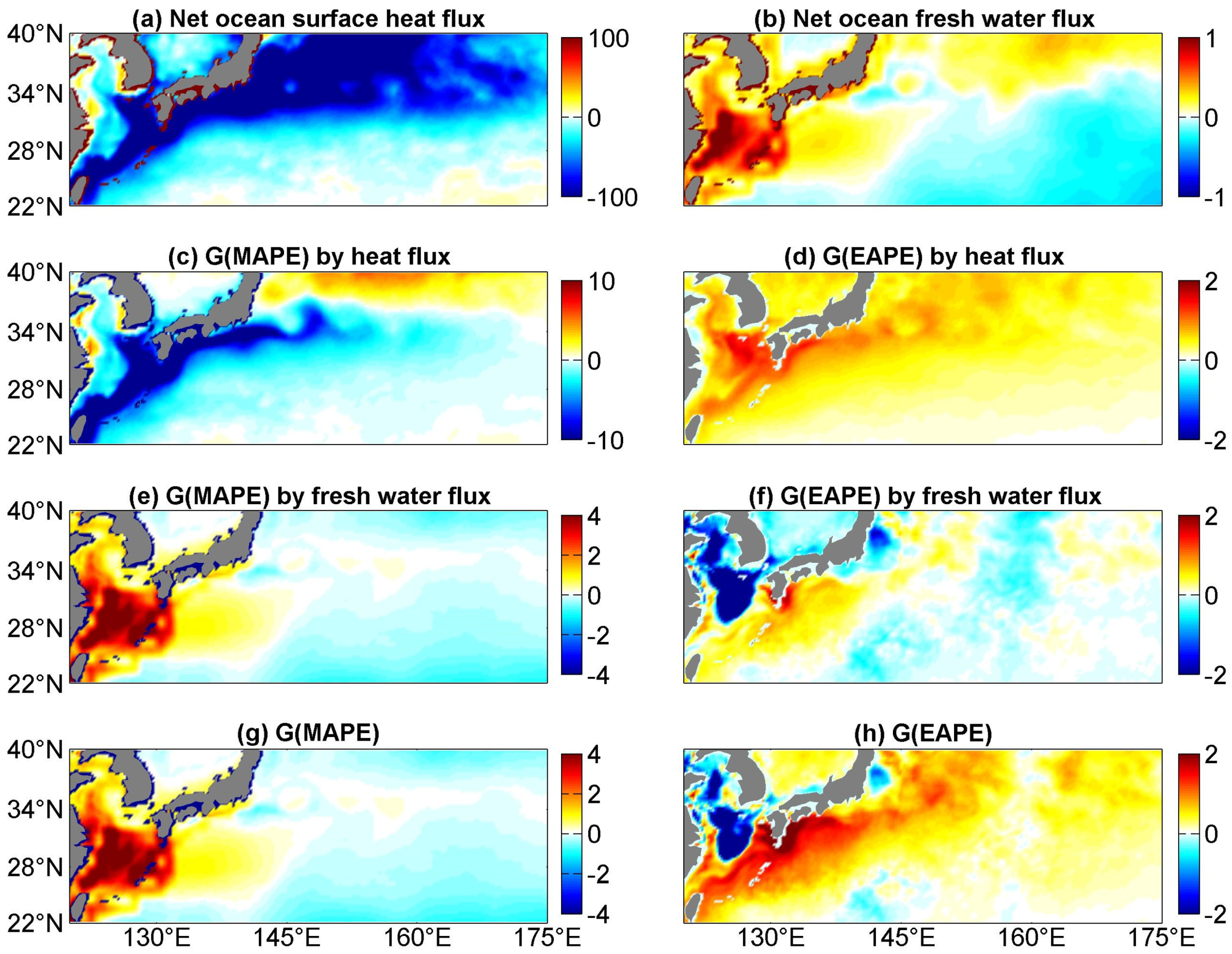
3.2. Energy Generations
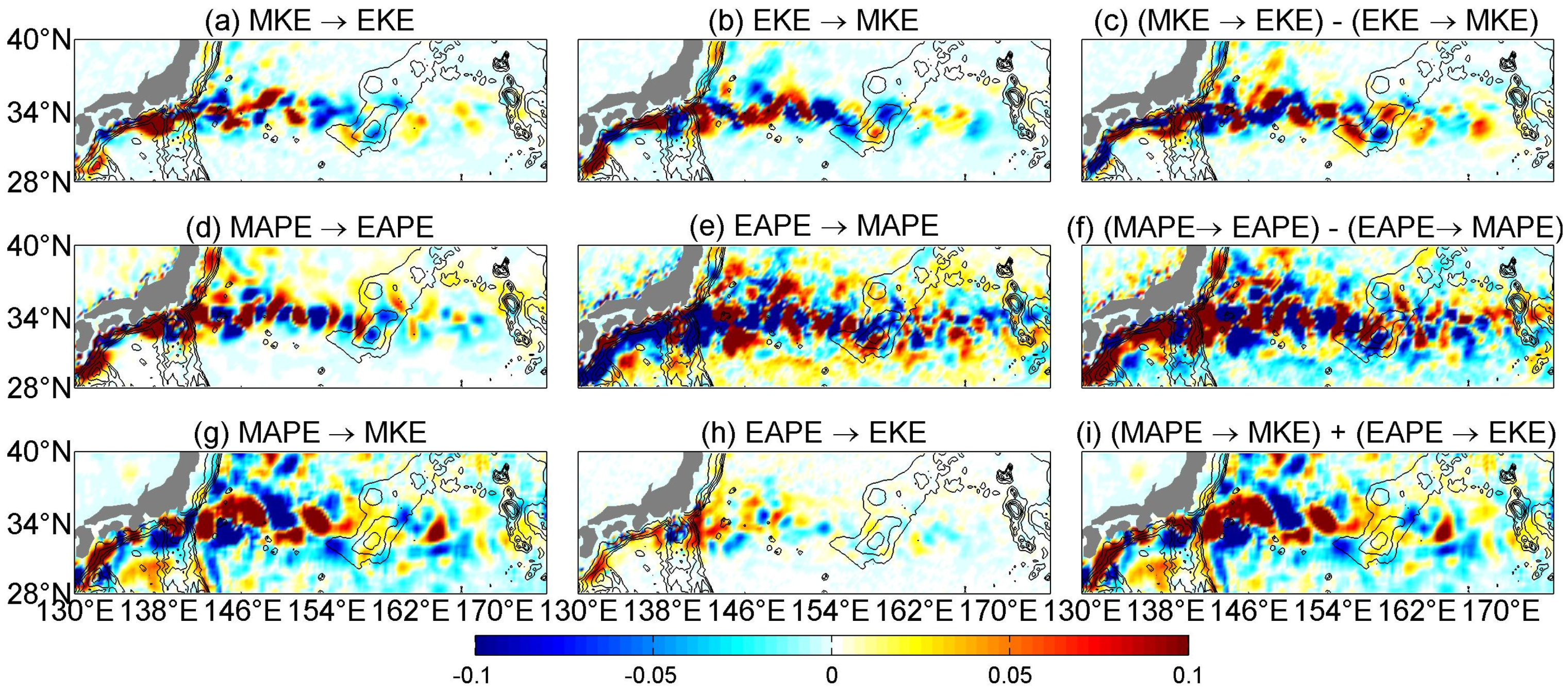
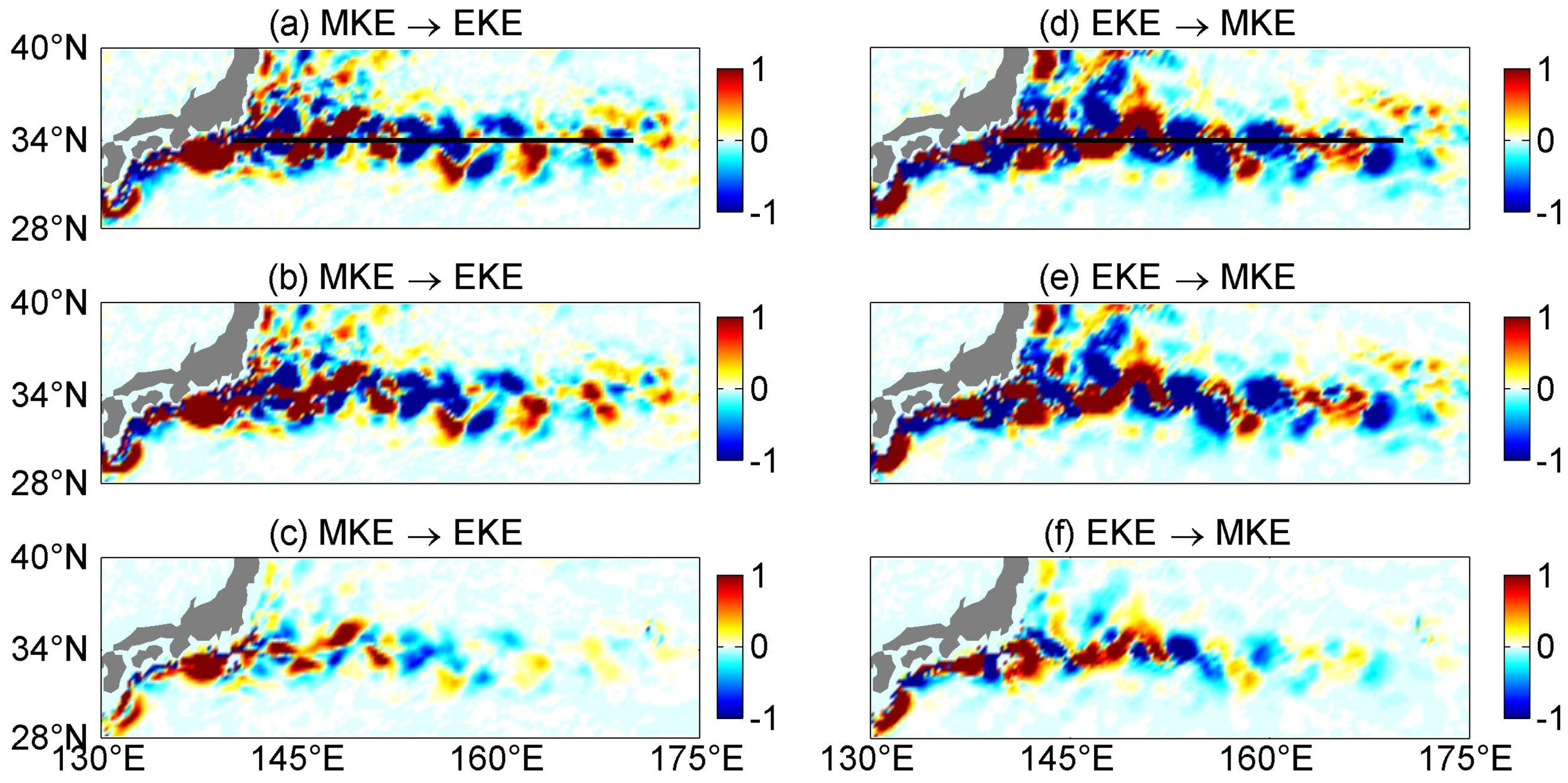
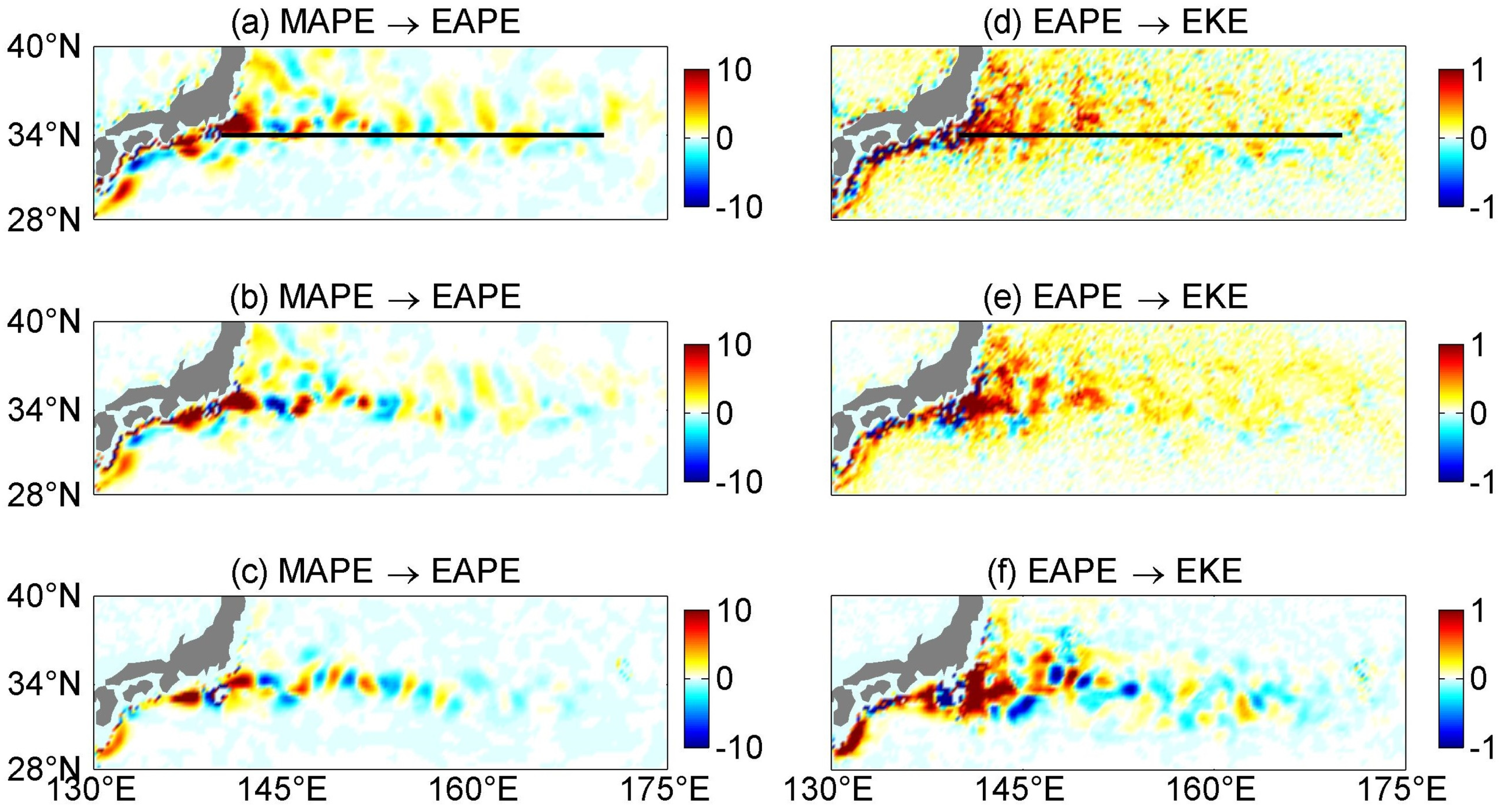
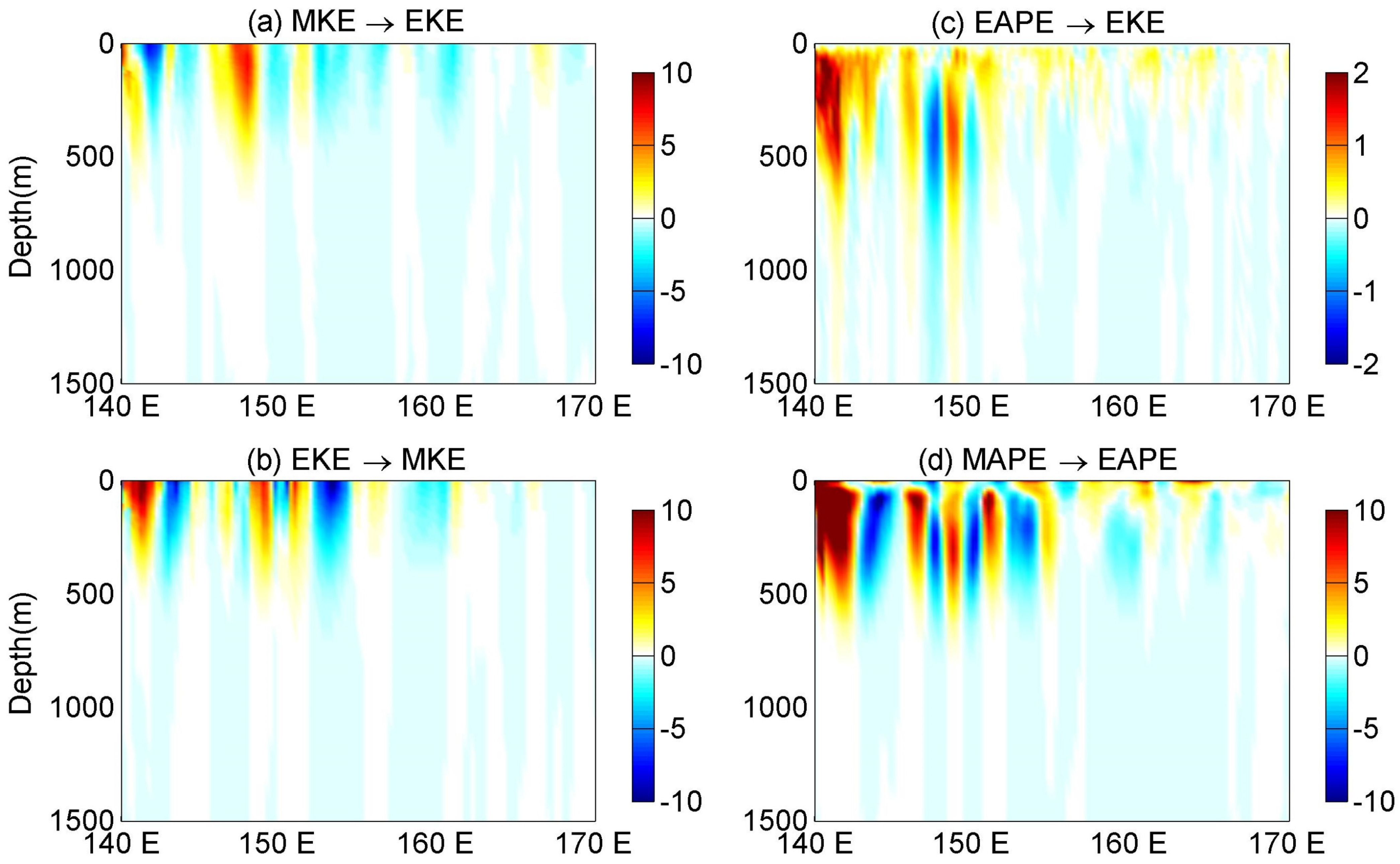
3.3. Energy Conversions
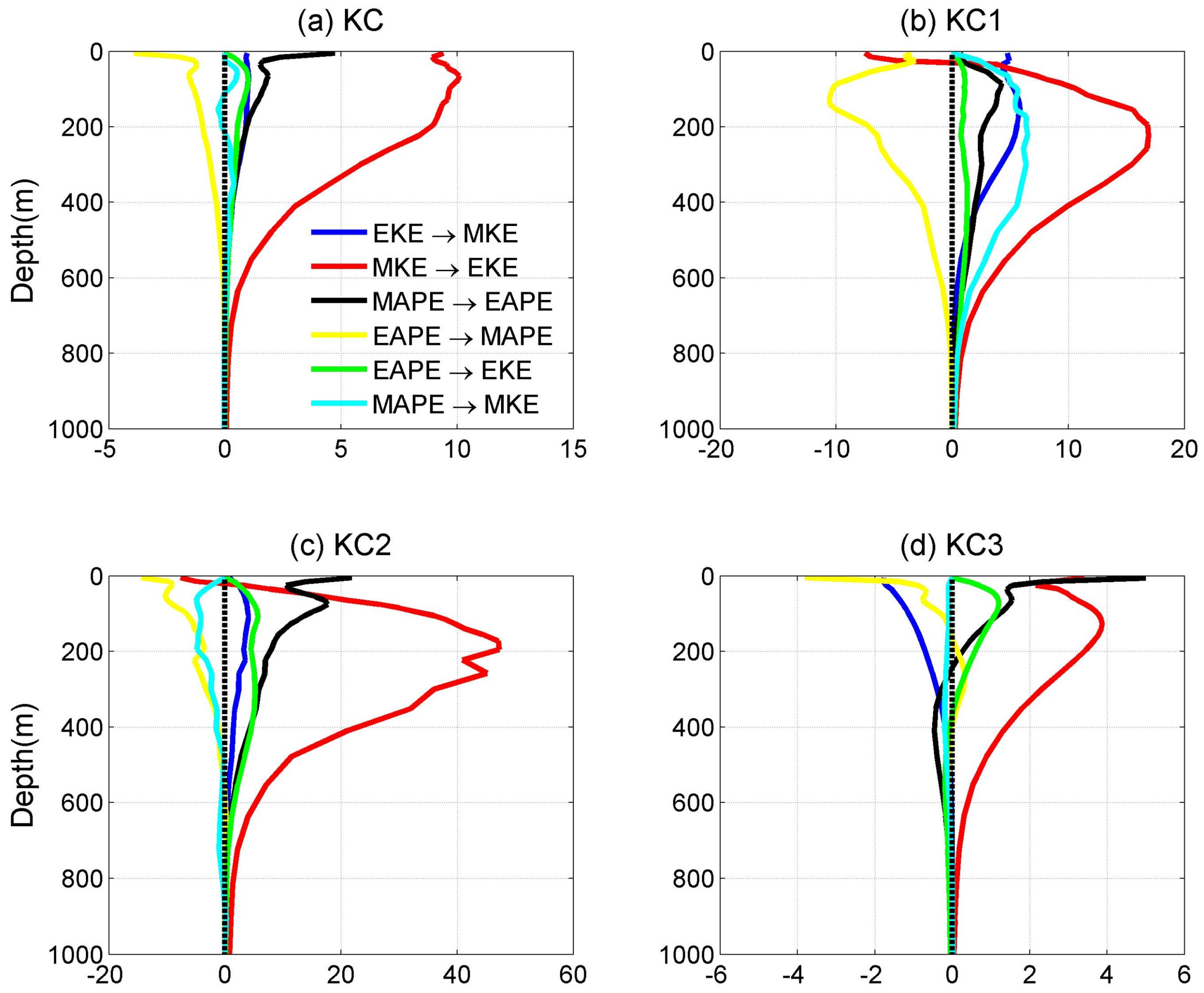
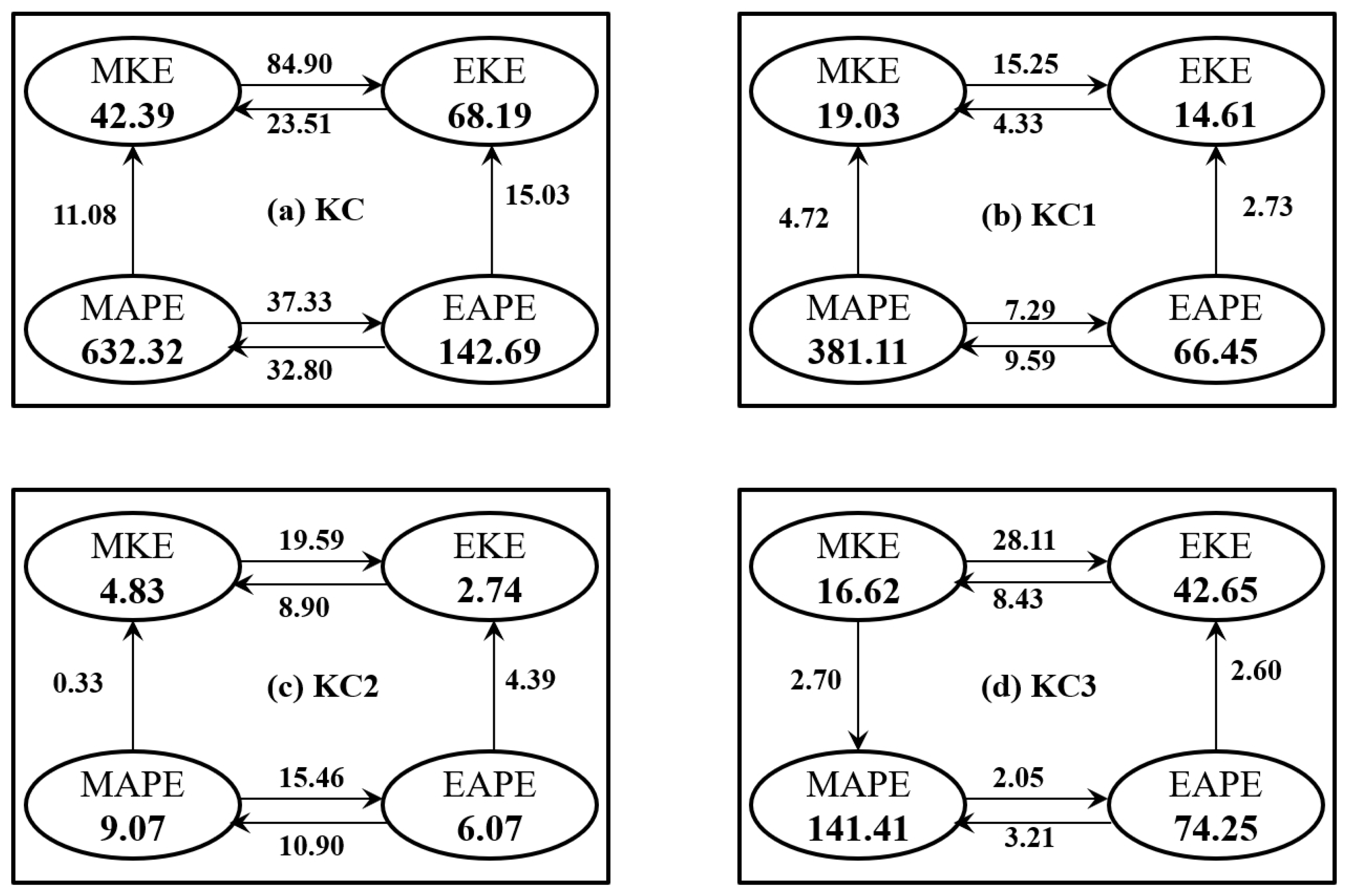
3.4. Energy Budget
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, B. Kuroshio Extension variability and forcing of the Pacific Decadal Oscillations: Responses and potential feedback. J. Phys. Oceanogr. 2003, 33, 2465–2482. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.M. Variability of the Kuroshio Extension jet, recirculation gyre and mesoscale eddies on decadal time scales. J. Phys. Oceanogr. 2005, 35, 2465–2482. [Google Scholar] [CrossRef]
- Greatbatch, R.J.; Zhai, X.; Kohlmann, J.D.; Czeschel, L. Ocean eddy momentum fluxes at the latitudes of the Gulf Stream and the Kuroshio extensions as revealed by satellite data. Ocean Dyn. 2010, 60, 617–628. [Google Scholar] [CrossRef]
- Scharffenberg, M.; Stammer, D. Seasonal variations of the large-scale geostrophic flow field and eddy kinetic energy inferred from the TOPEX/Poseidon and Jason-1 tandem mission data. J. Geophy. Res. 2010, 115, C02008. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S.; Qiu, B.; Chen, S. On the decadal variability of the eddy kinetic energy in the Kuroshio extension. J. Phys. Oceanogr. 2017, 47, 1169–1187. [Google Scholar] [CrossRef]
- Ferrari, R.; Wunsch, C. The distribution of eddy kinetic and potential energies in the global ocean. Tellus 2010, 62A, 92–108. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, B.; Chen, S.; Qi, Y.; Du, Y. Seasonal eddy kinetic energy modulations along the North Equatorial Countercurrent in the western Pacific. J. Geophys. Res. Oceans 2015, 120, 6351–6362. [Google Scholar] [CrossRef]
- Hui, Y.; Zhang, L.; Yan, X.; Li, M.; Wang, F.; Hu, D. Energetics of eddy-mean flow interactions in the western tropical Pacific Ocean. Deep Sea Res. 2024, 208, 12. [Google Scholar] [CrossRef]
- Waterman, S.; Jayne, S.R. Eddy-mean flow interaction in the along-stream development of a western boundary current jet: An idealized model study. J. Phys. Oceanogr. 2011, 41, 682–707. [Google Scholar] [CrossRef]
- Waterman, S.; Hogg, N.G.; Jayne, S.R. Eddy–Mean Flow Interaction in the Kuroshio Extension Region. J. Phys. Oceanogr. 2011, 41, 1182–1208. [Google Scholar] [CrossRef]
- von Storch, J.; Eden, C.; Fast, I.; Haak, H.; Hernndez-Deckers, D.; Maier-Reimer, E.; Marotzke, J.; Stammer, D. An estimate of Lorenz energy cycle for the world ocean based on the 1/10 STORM/NCEP simulation. J. Phys. Oceanogr. 2012, 42, 2185–2205. [Google Scholar] [CrossRef]
- Chen, R.; Flierl, G.R.; Wunsch, C. A Description of Local and Nonlocal Eddy–Mean Flow Interaction in a Global Eddy-Permitting State Estimate. J. Phys.Oceanogr. 2014, 44, 2336–2352. [Google Scholar] [CrossRef]
- Kang, D.J.; Curchitser, E.N. Energetics of Eddy-Mean Flow Interactions in the Gulf Stream Region. J. Phys. Oceanogr. 2015, 45, 1103–1120. [Google Scholar] [CrossRef]
- Lorenz, E.N. Available potential energy and the maintenance of the general circulation. Tellus 1955, 7, 157–167. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA, 1987; 710p. [Google Scholar]
- Li, L.; Ingersoll, A.P.; Jiang, X.; Feldman, D.; Yuk, L.Y. Lorenz energy cycle of the global atmosphere based on reanalysis datasets. Geophys. Res. Lett. 2007, 34, L16813. [Google Scholar] [CrossRef]
- Murakami, S. Atmospheric local energetics and energy interactions between mean and eddy fields. Part I: Theory. J. Atmos. Sci. 2011, 68, 760–768. [Google Scholar] [CrossRef]
- Murakami, S.; Ohgaito, R.; Abe-Ouchi, A. Atmospheric local energetics and energy interactions between mean and eddy fields. Part II: An example for the last glacial maximum climate. J. Atmos. Sci. 2011, 68, 533–552. [Google Scholar] [CrossRef]
- Jan, S.; Mensah, V.; Andres, M.; Chang, M.H.; Yang, Y.J. Eddy-Kuroshio interactions: Local and remote effects. J. Geophys. Res. Oceans 2017, 122, 9744–9764. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, S. Seasonal Variation of Submesoscale Ageostrophic Motion and Geostrophic Energy Cascade in the Kuroshio. J. Mar. Sci. Eng. 2024, 12, 1121. [Google Scholar] [CrossRef]
- Nakamura, H.; Nishina, A.; Ichikawa, H.; Nonaka, M.; Sasaki, H. Deep countercurrent beneath the Kuroshio in the Okinawa Trough. J. Geophys. Res. 2008, 113, C06030. [Google Scholar] [CrossRef]
- Lin, X.; Wu, D.; Li, Q.; Lan, J. An amplification mechanism of intraseasonal long rossby wave in subtropical ocean. J. Phys. Oceanogr. 2005, 61, 369–378. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Eddy-mean flow interaction in the decadally modulating Kuroshio Extension system. Deep Sea Res. 2010, 57, 1098–1110. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Wood, R.A. Unstable waves on oceanic fronts: Large amplitude behavior and mean flow generation. J. Phys. Oceanogr. 1988, 18, 775–787. [Google Scholar] [CrossRef]
- Tai, C.K.; White, W.B. Eddy variability in the Kuroshio Extension as revealed by GEOSAT altimetry: Energy propagation away from the jet, Reynolds stress, and seasonal cycle. J. Phys. Oceanogr. 1990, 20, 1761–1777. [Google Scholar] [CrossRef]
- Xu, C.; Shang, X.D.; Huang, R.X. Estimate of eddy energy generation/dissipation rate in the world ocean from altimetry data. Ocean Dyn. 2011, 61, 525–541. [Google Scholar] [CrossRef]
- Holland, W.R.; Lin, L.B. On the generation of mesoscale eddies and their contributionto the oceanic general circulation. I. A preliminary numerical experiment. J. Phys. Oceanogr. 1975, 5, 642–657. [Google Scholar] [CrossRef]
- Holland, W.R.; Lin, L.B. On the generation of mesoscale eddies and their contribution to the oceanic general circulation. II. A parameter study. J. Phys. Oceanogr. 1975, 5, 658–669. [Google Scholar] [CrossRef]
- Holland, W.R. The role of mesoscale eddies in the general circulation of the ocean-Numerical experiments using a wind-driven quasi-geostrophic model. J. Phys. Oceanogr. 1978, 8, 363–392. [Google Scholar] [CrossRef]
- Thompson, R.O.R.Y. Reynolds stress and deep countercurrents near the Gulf Stream. J. Mar.Res. 1978, 36, 611–615. [Google Scholar]
- Dewar, W.K.; Bane, J.M. Gulf Stream dynamics. Part II: Eddy energetics at 738W. J. Phys. Oceanogr. 1989, 19, 1574–1587. [Google Scholar] [CrossRef]
- Hogg, N.G. On the transport of the Gulf Stream between Cape Hatteras and the Grand Banks. J. Mar. Res. 1992, 50, 545–566. [Google Scholar] [CrossRef]
- Watts, D.R.; Tracey, K.L.; Bane, J.M.; Shay, T.J. Gulf Stream path and thermocline structure near 74 W and 68 W. J. Geophys. Res. 1995, 100, 18291–18312. [Google Scholar] [CrossRef]
- Hogg, N.G. A note on the deep circulation of the western North Atlantic: Its nature and causes. Deep-Sea Res. 1983, 30, 945–961. [Google Scholar] [CrossRef]
- Hogg, N.G. Evidence for baroclinic instability in the Gulf Stream recirculation. Prog. Oceanogr. 1985, 14, 209–229. [Google Scholar] [CrossRef]
- Hogg, N.G. Toward parameterization of the eddy field near the Gulf Stream. Deep-Sea Res. 1993, 40, 2359–2376. [Google Scholar] [CrossRef]
- Nishida, H.; White, W. Horizontal eddy fluxes of momentum and kinetic energy in the near-surface of the Kuroshio Extension. J. Phys. Oceanogr. 1982, 12, 160–170. [Google Scholar] [CrossRef]
- Hall, M.M. Energetics of the Kuroshio Extension at 35°N, 152°E. J. Phys. Oceanogr. 1991, 21, 958–975. [Google Scholar] [CrossRef]
- Eden, C.; Greatbatch, R.J.; Willebrand, J. A diagnosis of thickness fluxes in an eddy-resolving model. J. Phys. Oceanogr. 2007, 37, 727–742. [Google Scholar] [CrossRef]
- Nagai, T.; Hasegawa, D.; Tsutsumi, E.; Nakamura, H.; Nishina, A.; Senjyu, T.; Endoh, T.; Matsuno, T.; Inoue, R. The Kuroshio flowing over seamounts and associated submesoscale flows drive 100-km-wide 100–1000-fold enhancement of turbulence. Commun. Earth Environ. 2021, 2, 170. [Google Scholar] [CrossRef]
- Whalen, C.B.; Talley, L.D.; MacKinnon, J.A. Spatial and temporal variability of global ocean mixing inferred from Argo profiles. Geophys. Res. Lett. 2012, 39, L18612. [Google Scholar] [CrossRef]
- Kang, D.; Curchitser, E.N. On the evaluation of seasonal variability of the ocean kinetic energy. J. Phys. Oceanogr. 2017, 47, 1675–1683. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.; Liu, C. On the response of the Lorenz energy cycle for the Southern Ocean to intensified westerlies. J. Geophys. Res. Oceans 2017, 122, 2465–2493. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.M.; Liu, C.Y.; Lin, X. Impacts of high-frequency atmospheric forcing on Southern Ocean circulation and Antarctic sea ice. Adv. Atmos. Sci. 2020, 37, 515–531. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.M.; Liu, C.; Yan, L.J. Energetics of Eddy-Mean Flow Interactions in the Amery Ice Shelf Cavity. Front. Mar. Sci. 2021, 8, 638741. [Google Scholar] [CrossRef]
- Stewart, K.D.; Saenz, J.A.; Hogg, A.M.; Hughes, G.O.; Griffiths, R.W. Effect of topographic barriers on the rates of available potential energy conversion of the oceans. Ocean Model. 2014, 76, 31–42. [Google Scholar] [CrossRef]
- Zemskova, V.E.; White, B.L.; Scotti, A. Available potential energy and the general circulation: Partitioning wind, buoyancy forcing, and diapycnal mixing. J. Phys. Oceanogr. 2015, 45, 1510–1531. [Google Scholar] [CrossRef]
- Adcroft, A.; Campin, J.M.; Hill, C.; Marshall, J. Implementation of an atmosphere–ocean general circulation model on the expanded spherical cube. Mon. Wea. Rev. 2004, 132, 2845–2863. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. 1997, 102, 5753–5766. [Google Scholar] [CrossRef]
- Marshall, J.; Hill, C.; Perelman, L.; Adcroft, A. Hydrostatic, quasi-hydrostatic, and nonhydrostatic ocean modeling. J. Geophys. Res. 1997, 102, 5733–5752. [Google Scholar] [CrossRef]
- Losch, M.; Menemenlis, D.; Heimbach, P.; Campin, J.; Hill, C. On the formulation of sea-ice models. Part 1: Effects of different solver implementations and parameterizations. Ocean Model. 2010, 33, 129–144. [Google Scholar] [CrossRef]
- Large, W.; McWilliams, J.; Doney, S. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
- Menemenlis, D.; Hill, C.; Adcrocft, A.; Campin, J.-M.; Cheng, B.; Ciotti, B.; Fukumori, I.; Heimbach, P.; Henze, C.; Köhl, A.; et al. NASA supercomputer improves prospects for ocean climate research. EOS Trans. Amer. Geophys. Union 2005, 86, 89–96. [Google Scholar] [CrossRef]
- Menemenlis, D.; Fukumori, I.; Lee, T. Using Green’s functions to calibrate an ocean general circulation model. Mon. Wea. Rev. 2005, 133, 1224–1240. [Google Scholar] [CrossRef]
- Menemenlis, D.; Campin, J.; Heimbach, P.; Hill, C.; Lee, T.; Nguyen, A.; Schodlock, M.; Zhang, H. ECCO2: High Resolution Global Ocean and Sea Ice Data Synthesis; Mercator Ocean Quarterly News Letter, No. 31; Mercator Ocean: Ramonville Saint-Agne, France, 2008; pp. 13–21. [Google Scholar]
- Wunsch, C. The work done by the wind on the oceanic general circulation. J. Phys.Oceanogr. 1998, 28, 2332–2340. [Google Scholar] [CrossRef]
- Roquet, F.; Wunsch, C.; Madec, G. On the patterns of wind-power input to the ocean circulation. J. Phys.Oceanogr. 2011, 41, 2328–2342. [Google Scholar] [CrossRef]
- Qiu, B.; Kelly, K.A.; Joyce, T.M. Mean flow and variability in the Kuroshio extension from Geostat altimetry data. J. Phys. Oceanogr. 1991, 96, 18491–18507. [Google Scholar]
- Wunsch, C.; Ferrari, R. Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 2004, 36, 281–314. [Google Scholar] [CrossRef]
- Roullet, G.; Capet, X.; Maze, G. Global interior eddy available potential energy diagnosed from Argo floats. Geophys. Res. Lett. 2014, 41, 1651–1656. [Google Scholar] [CrossRef]
- Ji, J.; Dong, C.; Zhang, B.; Liu, Y.; Zou, B.; King, G.P.; Xu, G.; Chen, D. Oceanic eddy characteristics and generation mechanisms in the Kuroshio Extension region. J. Geophys. Res. Oceans 2018, 123, 8548–8567. [Google Scholar] [CrossRef]
- Kang, D.; Curchitser, E.N.; Rosati, A. Seasonal variability of the Gulf Stream kinetic energy. J. Phys. Oceanogr. 2016, 46, 1189–1207. [Google Scholar] [CrossRef]
- Yan, X.; Kang, D.; Curchitser, E.N.; Pang, C. Energetics of eddy-mean flow interactions along the western boundary currents in the North Pacific. J. Phys. Oceanogr. 2019, 49, 789–810. [Google Scholar] [CrossRef]
- Yan, X.; Kang, D.; Pang, C.; Zhang, L.; Liu, H. Energetics analysis of the eddy-Kuroshio interaction east of Taiwan. J. Phys. Oceanogr. 2022, 52, 647–664. [Google Scholar] [CrossRef]
- Rieck, J.K.; Boing, C.W.; Greatbatch, R.J.; Scheinert, M. Seasonal variability of eddy kinetic energy in a global high-resolution ocean model. Geophys. Res. Lett. 2015, 42, 9379–9386. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, X.S. On the seasonal eddy variability in the Kuroshio extension. J. Phys. Oceanogr. 2018, 48, 1675–1689. [Google Scholar] [CrossRef]
- Yan, X.; Kang, D.; Curchitser, E.N.; Liu, X.; Pang, C.; Zhang, L. Seasonal Variability of Eddy Kinetic Energy along the Kuroshio Current. J. Phys. Oceanogr. 2023, 53, 1731–1752. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Qiao, D.; Liu, C.; Yan, L.; Liu, K.; Qian, J.; Qin, Q.; Wei, J.; Chang, H.; Zhou, K.; et al. Energetics of Eddy–Mean Flow Interaction in the Kuroshio Current Region. J. Mar. Sci. Eng. 2025, 13, 1304. https://doi.org/10.3390/jmse13071304
Wu Y, Qiao D, Liu C, Yan L, Liu K, Qian J, Qin Q, Wei J, Chang H, Zhou K, et al. Energetics of Eddy–Mean Flow Interaction in the Kuroshio Current Region. Journal of Marine Science and Engineering. 2025; 13(7):1304. https://doi.org/10.3390/jmse13071304
Chicago/Turabian StyleWu, Yang, Dalei Qiao, Chengyan Liu, Liangjun Yan, Kechen Liu, Jiangchao Qian, Qing Qin, Jianfen Wei, Heyou Chang, Kai Zhou, and et al. 2025. "Energetics of Eddy–Mean Flow Interaction in the Kuroshio Current Region" Journal of Marine Science and Engineering 13, no. 7: 1304. https://doi.org/10.3390/jmse13071304
APA StyleWu, Y., Qiao, D., Liu, C., Yan, L., Liu, K., Qian, J., Qin, Q., Wei, J., Chang, H., Zhou, K., Qi, Z., Zhu, X., Li, J., Zhang, Y., & Guo, H. (2025). Energetics of Eddy–Mean Flow Interaction in the Kuroshio Current Region. Journal of Marine Science and Engineering, 13(7), 1304. https://doi.org/10.3390/jmse13071304






