Indirect Estimation of Seagrass Frontal Area for Coastal Protection: A Mask R-CNN and Dual-Reference Approach
Abstract
1. Introduction
2. Materials and Methods
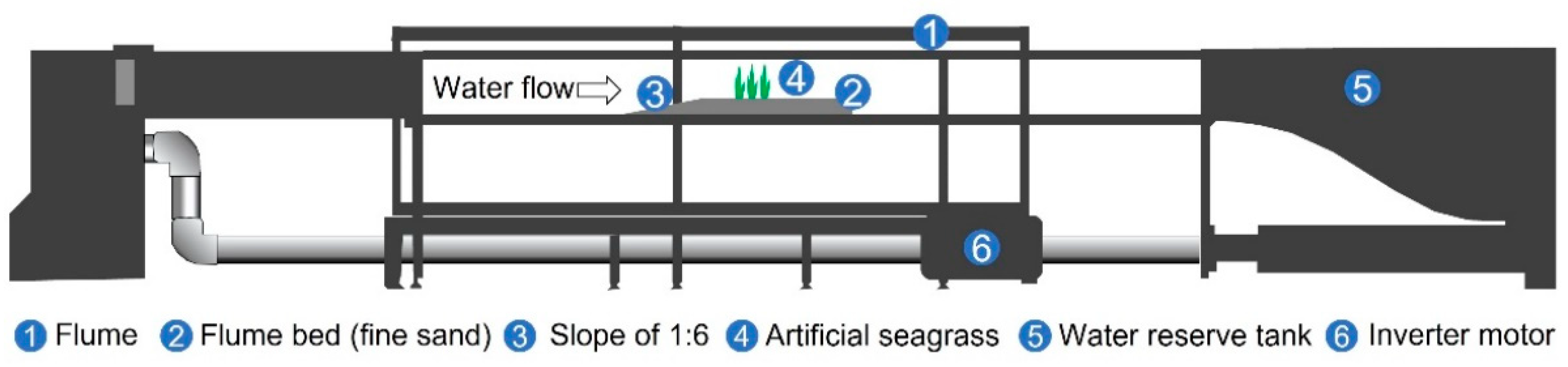
2.1. Experimental Setup
2.2. Image Augmentation of the Experimental Dataset
2.3. Real Seagrass Dataset
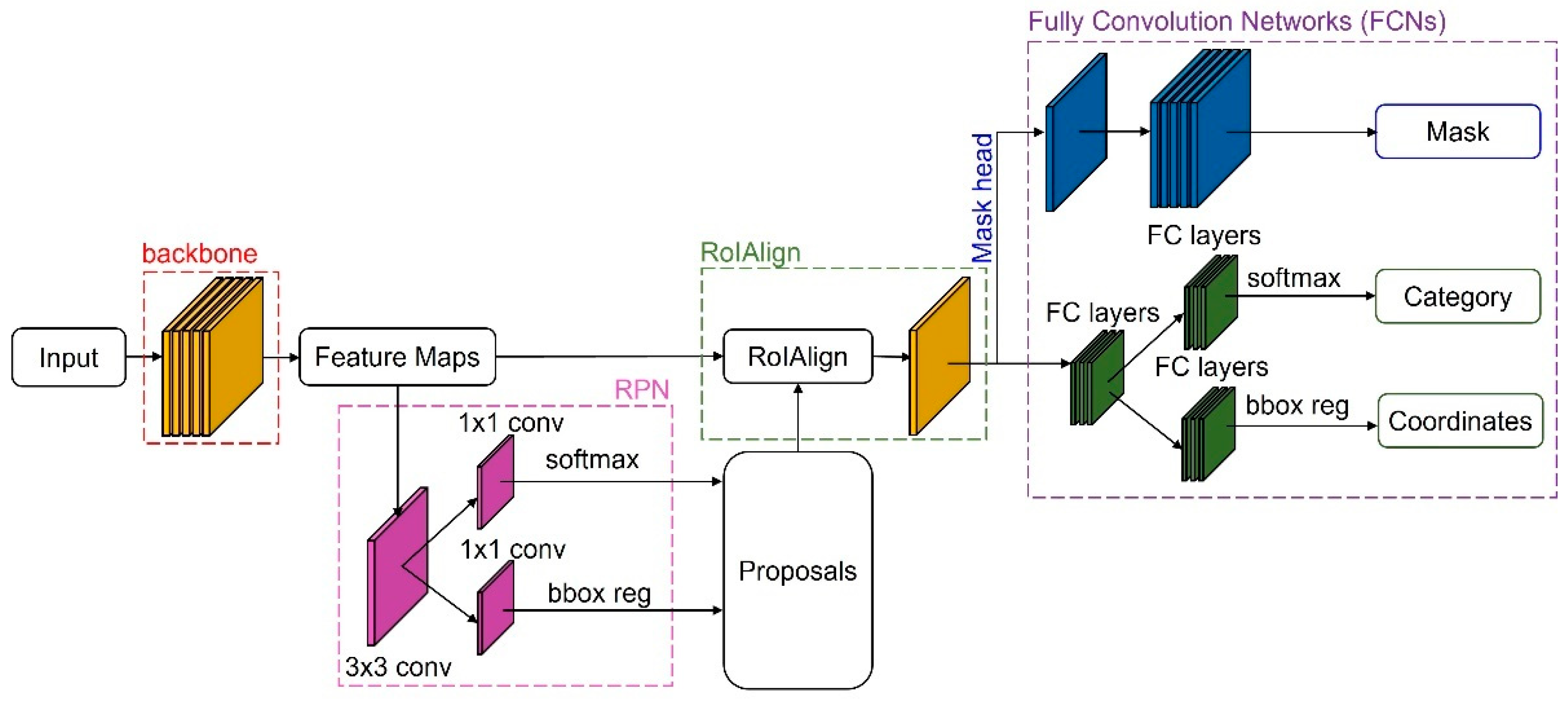
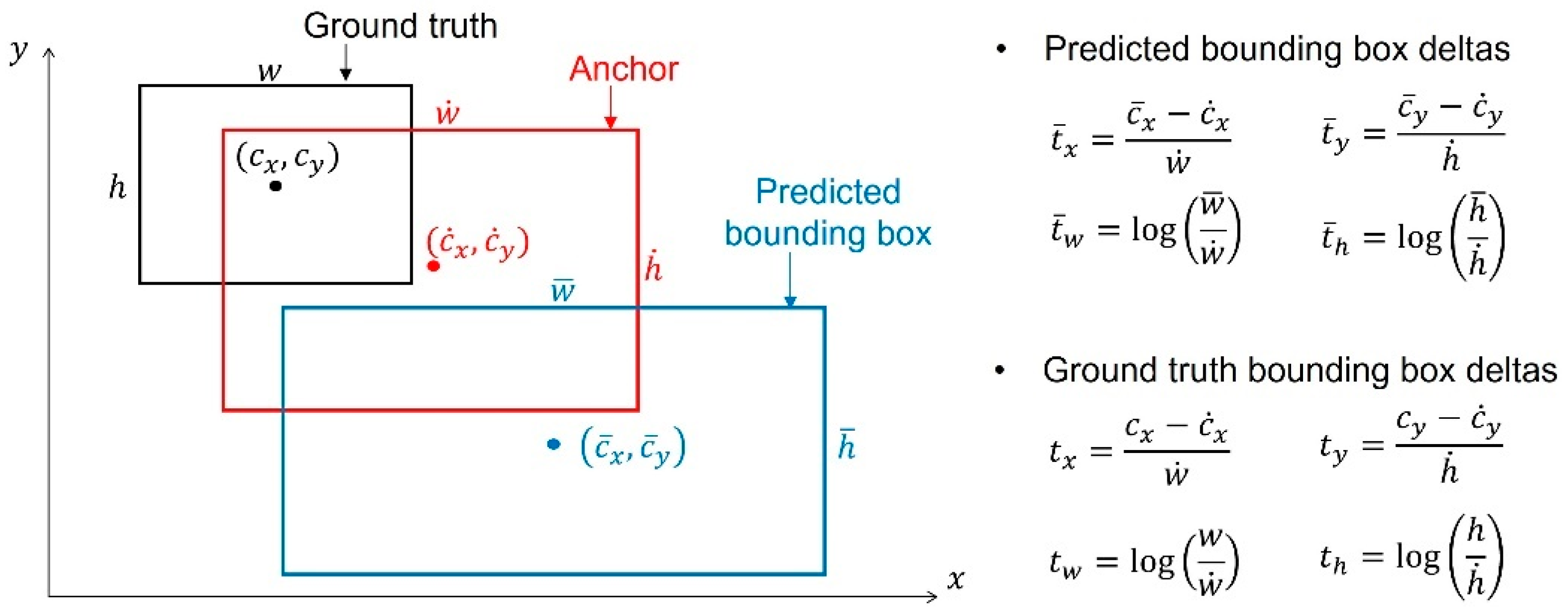
2.4. Mask R-CNN
2.5. Evaluation Metrics
2.5.1. Loss
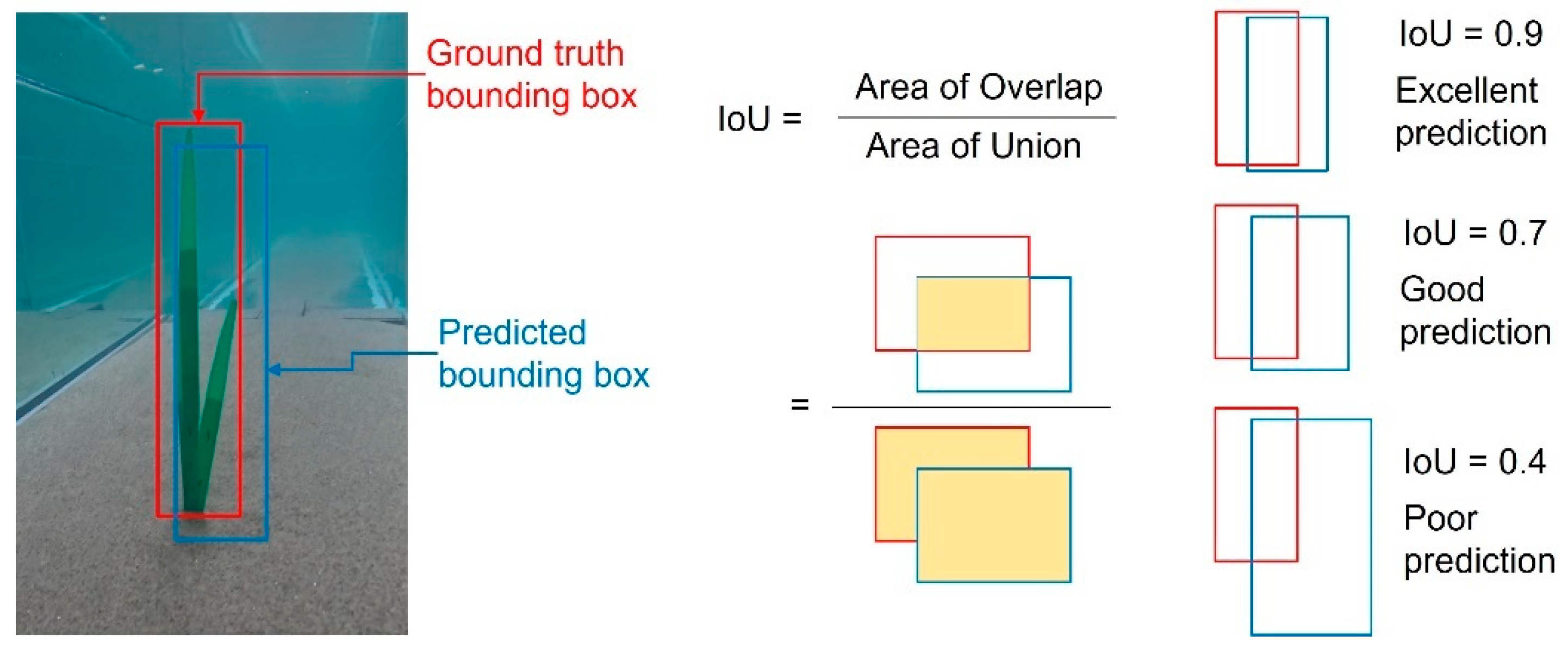
2.5.2. Intersection over Union
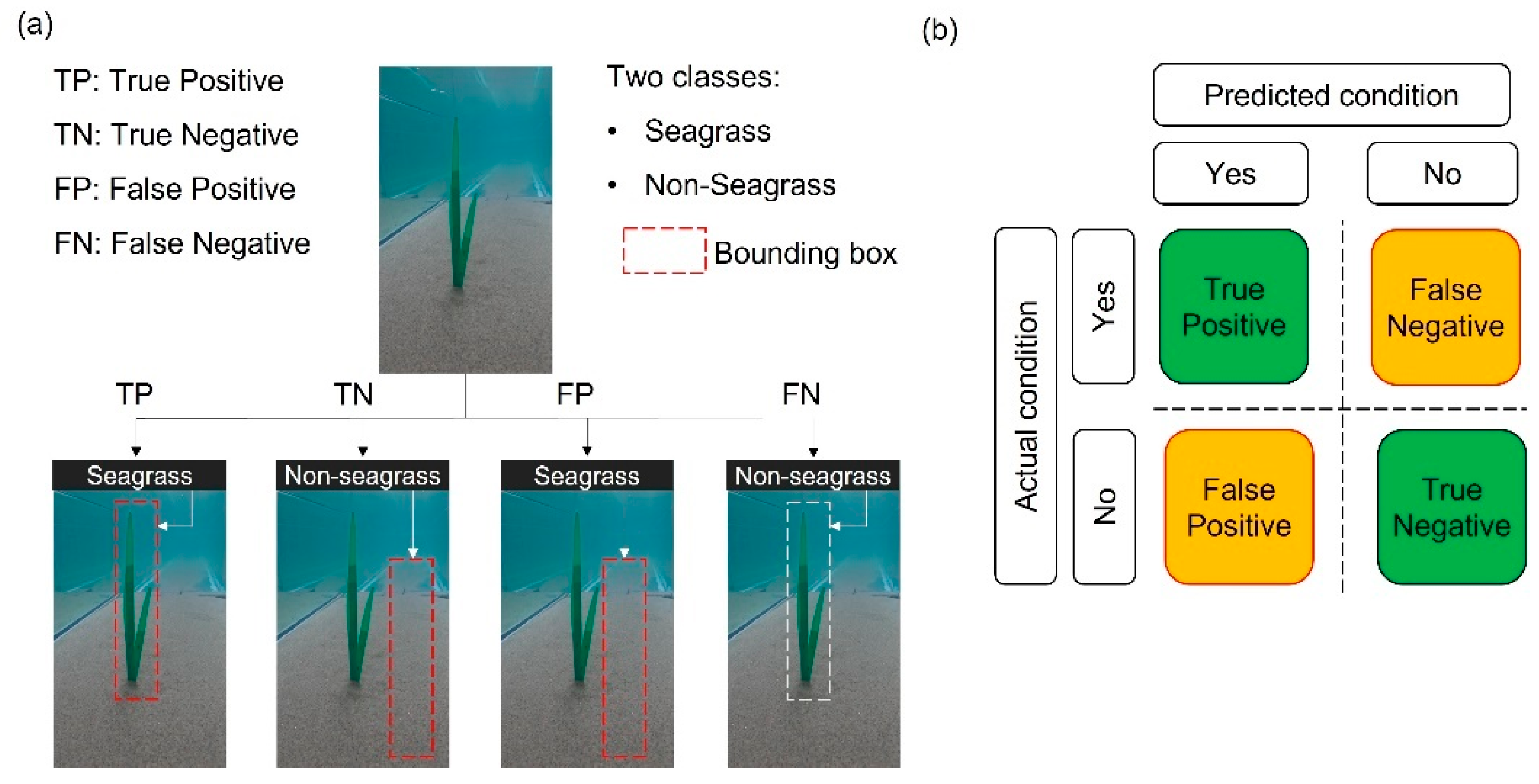
2.5.3. Confusion Matrix
2.5.4. Evaluation Thresholds
2.6. Frontal Area Estimation
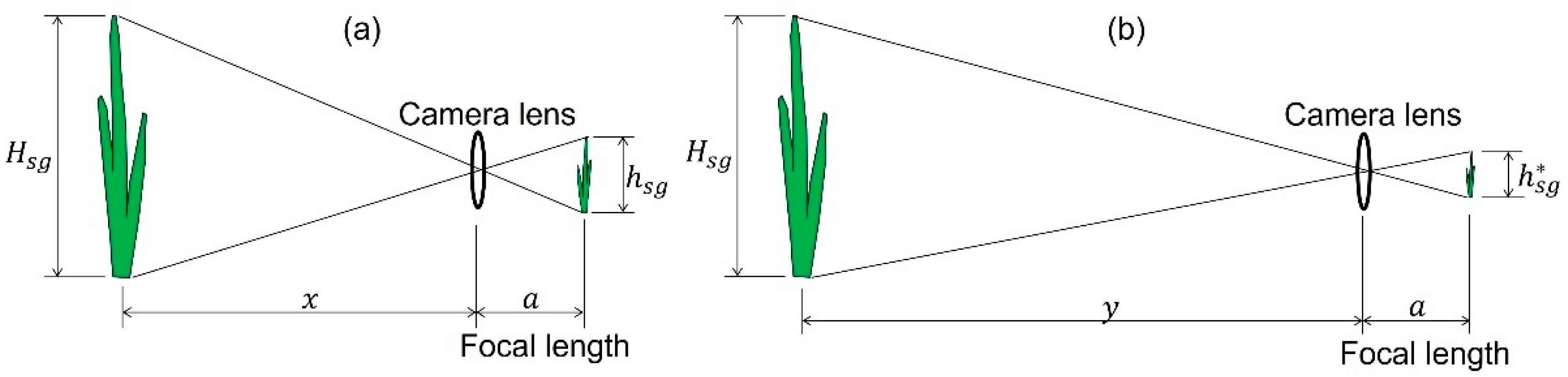
2.6.1. M1: Use of a Reference Object
2.6.2. M2: Use of the Distance Between the Camera and Seagrass
3. Results
3.1. Total Loss
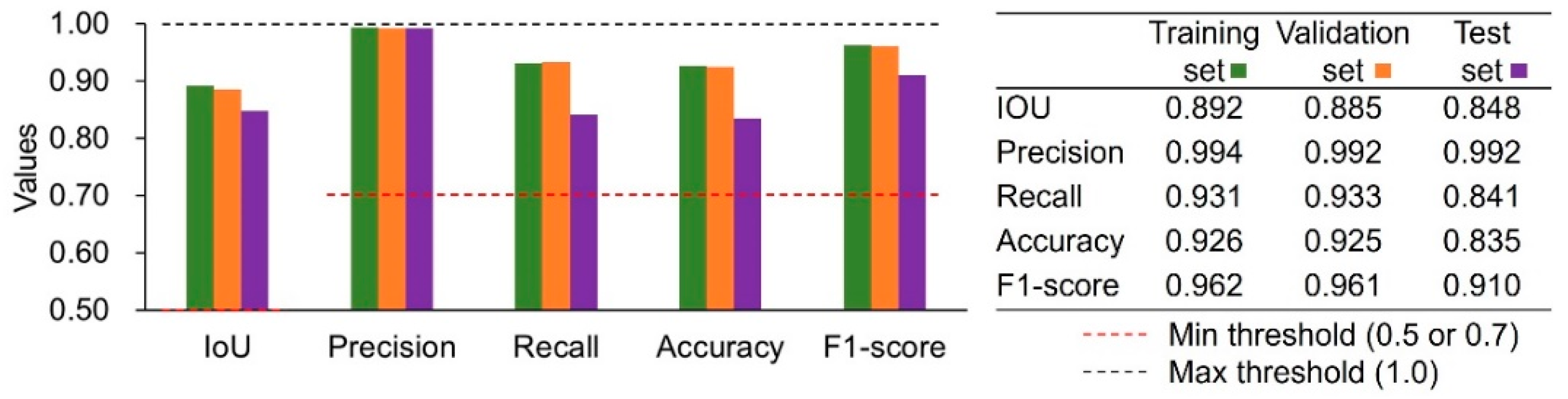
3.2. Model Metrics
3.3. Seagrass Detection
3.4. Estimation of Seagrass Frontal Area
3.4.1. Estimation Using a Reference Object (M1)
3.4.2. Estimation Using the Distance Between the Camera and Seagrasses (M2)
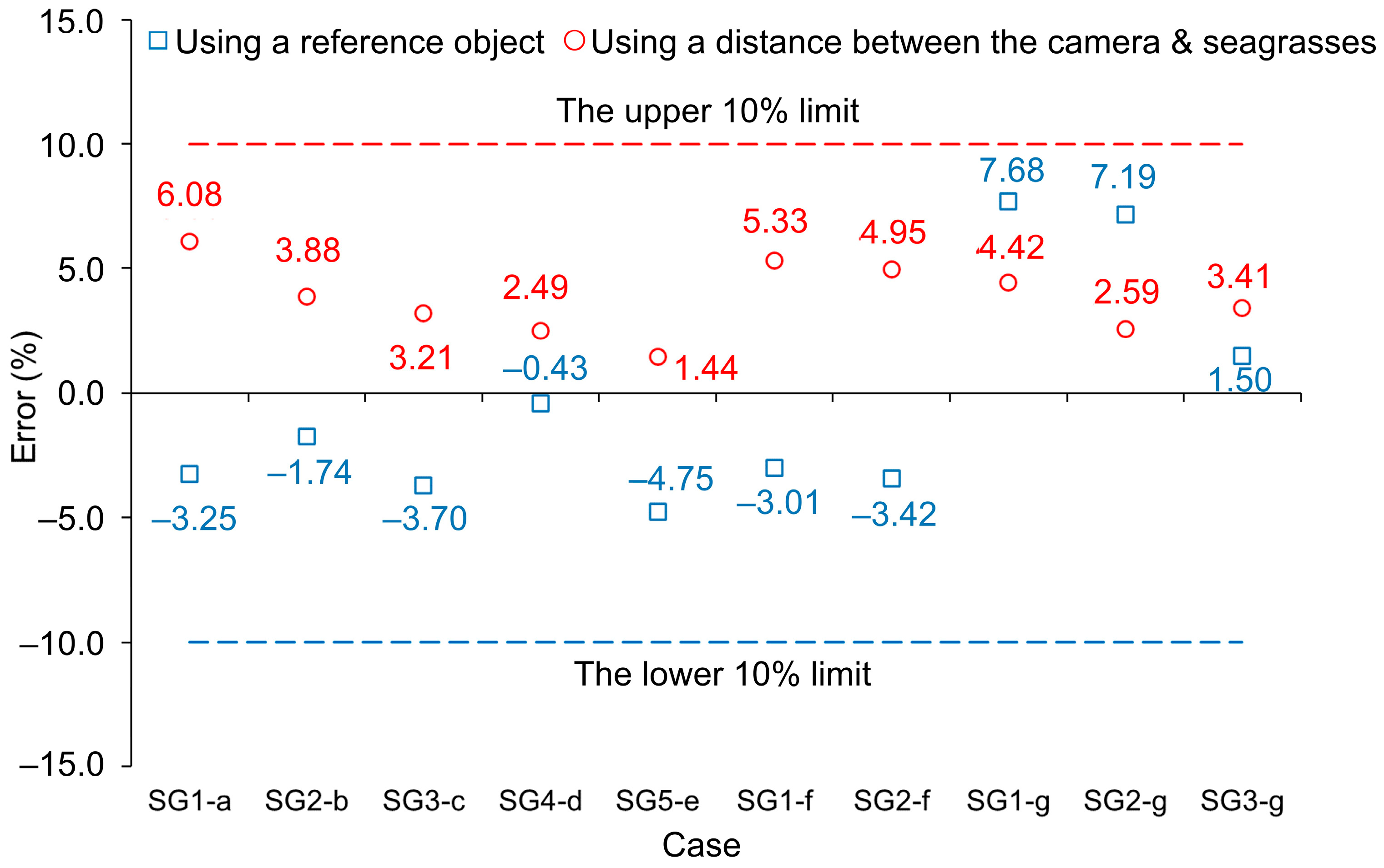
3.5. Comparison of the Two Frontal Area Estimation Methods
3.6. Results of the Real Seagrass Dataset
3.7. Applications of the Proposed Method
3.7.1. Estimation of Seagrass Bending Height
3.7.2. Estimation of Wave Height Reduction
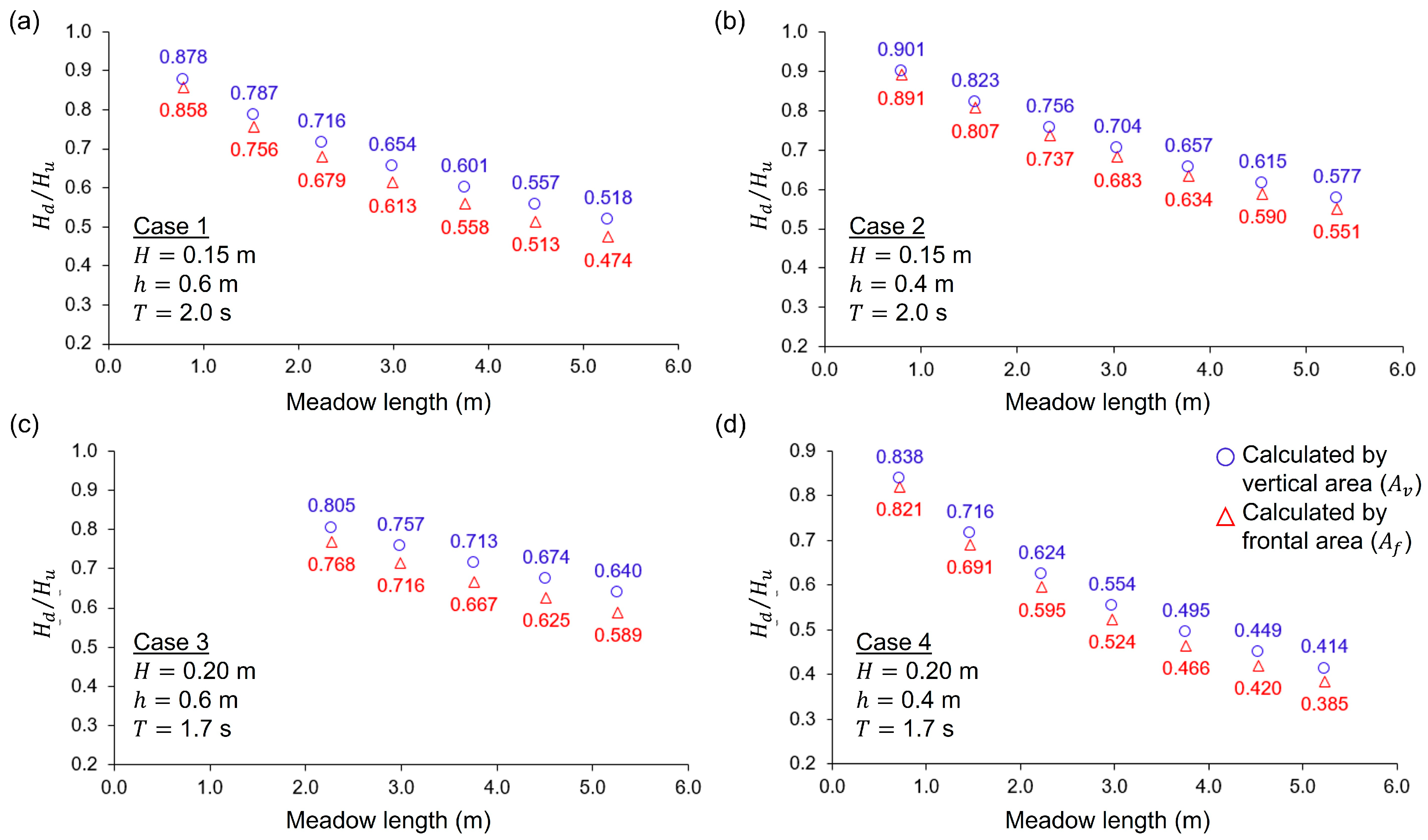
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duarte, C.M. The future of seagrass meadows. Environ. Conserv. 2002, 29, 192–206. [Google Scholar] [CrossRef]
- Orth, R.J.; Carruthers, T.J.B.; Dennison, W.C.; Duarte, C.M.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; Kendrick, G.A.; Kenworthy, W.J.; Olyarnik, S.; et al. A global crisis for seagrass ecosystems. Bioscience 2006, 56, 987–996. [Google Scholar] [CrossRef]
- Waycott, M.; Duarte, C.M.; Carruthers, T.J.B.; Orth, R.J.; Dennison, W.C.; Olyarnik, S.; Calladine, A.; Fourqurean, J.W.; Heck, K.L.; Hughes, A.R.; et al. Accelerating loss of seagrasses across the globe threatens coastal ecosystems. Proc. Natl. Acad. Sci. USA 2009, 106, 12377–12381. [Google Scholar] [CrossRef] [PubMed]
- Chau, V.T. Vision Image and Mask RCNN-Based Estimation of Frontal Area of Seagrass for Coastal Protection Function. Ph.D. Thesis, Pukyong National University, Busan, Republic of Korea, 2025; pp. 1–180. [Google Scholar]
- Kobayashi, N.; Raichle, A.; Asano, T. Wave attenuation by vegetation. J. Waterw. Port Coast. Ocean. Eng. 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Paul, M.; Bouma, T.J.; Amos, C.L. Wave attenuation by submerged vegetation: Combining the effect of organism traits and tidal current. Mar. Ecol. Prog. Ser. 2012, 444, 31–41. [Google Scholar] [CrossRef]
- Twomey, A.J.; O’Brien, K.R.; Callaghan, D.P.; Saunders, M.I. Synthesising wave attenuation for seagrass: Drag coefficient as a unifying indicator. Mar. Pollut. Bull. 2020, 160, 111661. [Google Scholar] [CrossRef]
- Phillips, R.C.; McRoy, C.P. Seagrass Research Methods; United Nations Educational, Scientific and Cultural Organization: Paris, France, 1990. [Google Scholar]
- Short, F.T.; Duarte, C.M. Methods for the measurement of seagrass growth and production. In Global Seagrass Research Methods; Elsevier Science: Amsterdam, The Netherlands, 2001; pp. 155–182. [Google Scholar] [CrossRef]
- Short, F.T.; Coles, R.G.; Short, C.A. SeagrassNet Manual for Scientific Monitoring of Seagrass Habitat; Worldwide edition; University of New Hampshire Publication: Durham, NH, USA, 2015. [Google Scholar]
- Riniatsih, I.; Ambariyanto, A.; Yudiati, E.; Redjeki, S.; Hartati, R. Monitoring the seagrass ecosystem using the unmanned aerial vehicle (UAV) in coastal water of Jepara. IOP Conf. Ser. Earth Environ. Sci. 2021, 674, 012075. [Google Scholar] [CrossRef]
- Paul, M.; Lefebvre, A.; Manca, E.; Amos, C.L. An acoustic method for the remote measurement of seagrass metrics. Estuar. Coast. Shelf Sci. 2011, 93, 68–79. [Google Scholar] [CrossRef]
- Morsy, S.; Suárez, A.B.Y.; Robert, K. 3D Mapping of Benthic Habitat Using XGBoost and Structure from Motion Photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 10, 1131–1136. [Google Scholar] [CrossRef]
- Komatsu, T.; Igararashi, C.; Tatsukawa, K.; Nakaoka, M.; Hiraishi, T.; Taira, A. Mapping of seagrass and seaweed beds using hydro-acoustic methods. Fish. Sci. 2002, 68, 580–583. [Google Scholar] [CrossRef][Green Version]
- Fonseca, M.S.; Koehl, M.A.R.; Kopp, B.S. Biomechanical factors contributing to self-organization in seagrass landscapes. J. Exp. Mar. Biol. Ecol. 2007, 340, 227–246. [Google Scholar] [CrossRef]
- Clarke, S.J. Vegetation growth in rivers: Influences upon sediment and nutrient dynamics. Prog. Phys. Geogr. 2002, 26, 159–172. [Google Scholar] [CrossRef]
- Rovira, A.; Alcaraz, C.; Trobajo, R. Effects of plant architecture and water velocity on sediment retention by submerged macrophytes. Freshw. Biol. 2016, 61, 758–768. [Google Scholar] [CrossRef]
- Chau, V.T.; Jung, S.; Kim, M.; Na, W.B. Analysis of the Bending Height of Flexible Marine Vegetation. J. Mar. Sci. Eng. 2024, 12, 1054. [Google Scholar] [CrossRef]
- Nanthini, K.; Sivabalaselvamani, D.; Chitra, K.; Gokul, P.; KavinKumar, S.; Kishore, S. A Survey on Data Augmentation Techniques. In Proceedings of the 2023 7th International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 23–25 February 2023; pp. 913–920. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Conrady, C.R.; Er, Ş.; Attwood, C.G.; Roberson, L.A.; de Vos, L. Automated detection and classification of southern African Roman seabream using mask R-CNN. Ecol. Inform. 2022, 69, 101593. [Google Scholar] [CrossRef]
- Song, Y.; Wu, Z.; Zhang, S.; Quan, W.; Shi, Y.; Xiong, X.; Li, P. Estimation of Artificial Reef Pose Based on Deep Learning. J. Mar. Sci. Eng. 2024, 12, 812. [Google Scholar] [CrossRef]
- Álvarez-Ellacuría, A.; Palmer, M.; Catalán, I.A.; Lisani, J.L. Image-based, unsupervised estimation of fish size from commercial landings using deep learning. ICES J. Mar. Sci. 2020, 77, 1330–1339. [Google Scholar] [CrossRef]
- Lestari, N.A.; Jaya, I.; Iqbal, M. Segmentation of seagrass (Enhalus acoroides) using deep learning mask R-CNN algorithm. IOP Conf. Ser. Earth Environ. Sci. 2021, 944, 012015. [Google Scholar] [CrossRef]
- Thammasanya, T.; Patiam, S.; Rodcharoen, E.; Chotikarn, P. A new approach to classifying polymer type of microplastics based on Faster-RCNN-FPN and spectroscopic imagery under ultraviolet light. Sci. Rep. 2024, 14, 3529. [Google Scholar] [CrossRef]
- Abdulrazzaq, M.M.; Yaseen, I.F.T.; Noah, S.A.; Fadhil, M.A. Multi-level of feature extraction and classification for X-ray medical image. Indones. J. Electr. Eng. Comput. Sci. 2018, 10, 154–167. [Google Scholar] [CrossRef]
- Joseph, V.R. Optimal ratio for data splitting. Stat. Anal. Data Min. 2022, 15, 531–538. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; pp. 1–675. ISBN 978-0387-31073-2. [Google Scholar]
- Thibaut, T.; Blanfuné, A.; Boudouresque, C.F.; Holon, F.; Agel, N. Distribution of the seagrass Halophila stipulacea: A big jump to the northwestern Mediterranean Sea. Aquat. Bot. 2022, 176, 103465. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Potrimba, P. What Is Mask R-CNN? The Ultimate Guide. Available online: https://blog.roboflow.com/mask-rcnn/ (accessed on 1 June 2024).
- Fang, S.; Zhang, B.; Hu, J. Improved Mask R-CNN Multi-Target Detection and Segmentation for Autonomous Driving in Complex Scenes. Sensors 2023, 23, 3853. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. arXiv 2015, arXiv:1506.01487. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous Structural Visual Inspection Using Region-Based Deep Learning for Detecting Multiple Damage Types. Comput. Civ. Infrastruct. Eng. 2017, 33, 731–747. [Google Scholar] [CrossRef]
- Rosebrock, A. Deep Learning for Computer Vision with Python; PyImageSearch: Philadelphia, PA, USA, 2017; pp. 29–140. [Google Scholar]
- Christen, R.; Hand, D.J.; Kirielle, N. A review of the F-measures: Its history, properties, criticism, and alternatives. ACM Comput. Surv. 2023, 56, 73. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The pascal visual object classes (VOC) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the Computer Vision—EECV 2014. EECV 2014. Lecture Notes in Computer Science, Zurich, Switzerland, 6–12 September 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar] [CrossRef]
- Boesch, G. What Is Intersection over Union (IoU)? Available online: https://viso.ai/computer-vision/intersection-over-union-iou/ (accessed on 5 July 2024).
- Cloudfactory, Confusion Matrix. Available online: https://wiki.cloudfactory.com/docs/mp-wiki/metrics/confusion-matrix (accessed on 1 December 2024).
- Barkved, K. How to Know If Your Machine Learning Model Has Good Performance. Available online: https://www.obviously.ai/post/machine-learning-model-performance (accessed on 15 January 2025).
- Logunova, I. A Guide to F1 Score. Available online: https://serokell.io/blog/a-guide-to-f1-score (accessed on 1 January 2025).
- Sergeev, A. Halophila Ovalis (R.Br.) Hook.f. Available online: https://www.floraofqatar.com/halophila_ovalis.htm (accessed on 1 June 2024).
- Mifsud, S. Halophila Stipulacea (Halophila Seagrass). Available online: https://www.maltawildplants.com/HYCH/Halophila_stipulacea.php (accessed on 1 June 2024).
- Okudan, E.Ş.; Dural, B.; Demir, V.; Erduğan, H.; Aysel, V. Biodiversity of marine benthic macroflora (seaweeds/macroalgae and seagrasses) of the Mediterranean Sea. In The Turkish Part of the Mediterranean Sea: Marine Biodiversity, Fisheries, Conservation and Governance; Publication No: 43; Turan, G., Salihoğlu, B., Özbek, E.Ö., Öztürk, B., Eds.; Turkish Marine Research Foundation (TUDAV): Istanbul, Turkey, 2016; pp. 107–135. ISBN 978-9-7588-2535-6. [Google Scholar]
- Algae Base, Zostera Stipulacea Forsskål 1775. Available online: https://www.algaebase.org/search/species/detail/?species_id=65451 (accessed on 1 June 2024).
- Sergeev, A. Algae Base, Seagrass (Halophila stipulacea) in Purple Island (Jazirat Bin Ghanim). Al Khor, Qatar, 9 October 2014. Available online: https://www.asergeev.com/pictures/archives/compress/2014/1488/13s.htm (accessed on 1 June 2024).
- Mittelmeer- und Alpenflora. Gattung: Halophila (Seagrass). Available online: https://www.mittelmeerflora.de/Einkeim/Hydocharitaceae/halophila.htm (accessed on 1 June 2024).
- Biologiamarina org. Halophila Stipulacea, Alofila. Available online: https://www.biologiamarina.org/halophila-stipulacea/ (accessed on 20 June 2025).
- iNaturalist. Halophila Stipulacea. Available online: https://inaturalist.ca/taxa/131137-Halophila-stipulacea/browse_photos (accessed on 20 June 2025).
- Fonseca, M.S.; Kenworthy, W.J. Effects of current on photosynthesis and distribution of seagrasses. Aquat. Bot. 1987, 27, 59–78. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef]
- Zeller, R.B.; Weitzman, J.S.; Abbett, M.E.; Zarama, F.J.; Fringer, O.B.; Koseff, J.R. Improved parameterization of seagrass blade dynamics and wave attenuation based on numerical and laboratory experiments. Limnol. Oceanogr. 2014, 59, 251–266. [Google Scholar] [CrossRef]
- Matweb. Material Property Data. Overview of Materials for Polypropylene, Molded. Available online: https://www.matweb.com/search/datasheet.aspx?MatGUID=08fb0f47ef7e454fbf7092517b2264b2&ckck=1 (accessed on 9 March 2025).
- Losada, I.J.; Maza, M.; Lara, J.L. A new formulation for vegetation-induced damping under combined waves and currents. Coast. Eng. 2016, 107, 1–13. [Google Scholar] [CrossRef]
- van Veelen, T.J.; Fairchild, T.P.; Reeve, D.E.; Karunarathna, H. Experimental study on vegetation flexibility as control parameter for wave damping and velocity structure. Coast. Eng. 2020, 157, 103648. [Google Scholar] [CrossRef]
- Liu, S.; Xu, S.; Yin, K. Optimization of the drag coefficient in wave attenuation by submerged rigid and flexible vegetation based on experimental and numerical studies. Ocean Eng. 2023, 285, 115382. [Google Scholar] [CrossRef]
- Mullarney, J.C.; Henderson, S.M. Wave-forced motion of submerged single-stem vegetation. J. Geophys. Res. Oceans 2010, 115, C12061. [Google Scholar] [CrossRef]






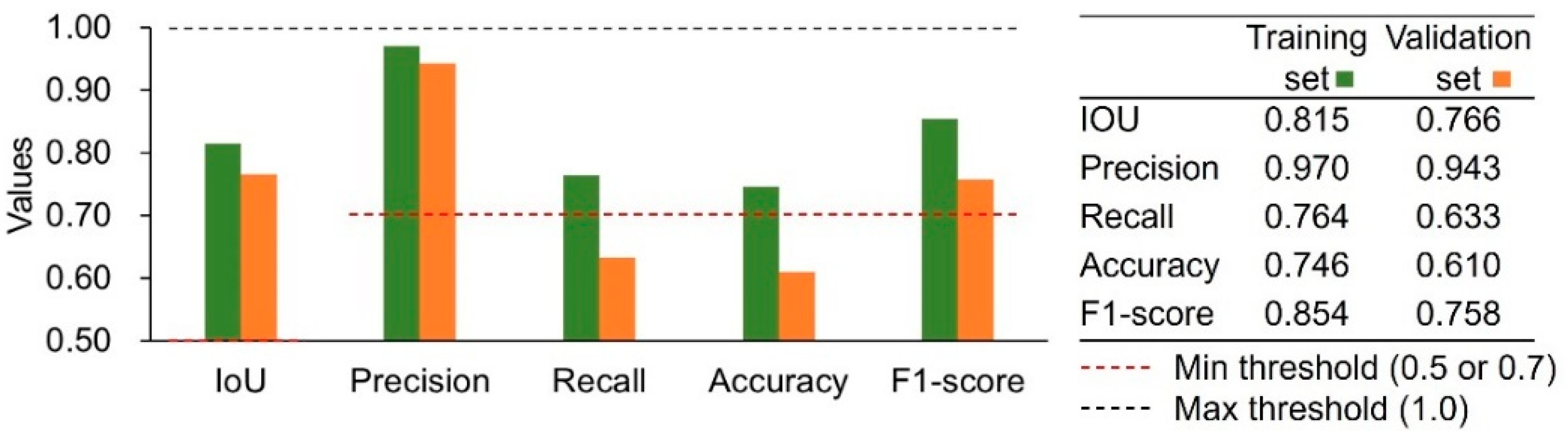



| Metric | Proposed Thresholds (References) |
|---|---|
| IOU | Required IoU at least 0.5 [21,30,36,38,39]; Acceptable IoU: >0.5; Good IoU: >0.7 [39]; Excellent IoU: >0.95; Good IoU: >0.7 [40] |
| Accuracy | Excellent score: >0.9; Good score: >0.7 [41]; Great model: >0.7 [42] |
| Precision | Excellent score: >0.85; Good score: >0.7 [41] |
| Recall | Excellent score: >0.85; Good score: >0.7 [41]; Good score: 0.70–0.75 [39] |
| F1-score | Excellent score: >0.85; Good score: >0.7 [41]; Good score: > 0.7 [43] |
| Image | Seagrass No. | (cm2) | (cm2) | Relative % Error |
|---|---|---|---|---|
| Figure 12a | SG1 | 53.87 | 55.62 | –3.25 |
| Figure 12b | SG2 | 59.34 | 60.37 | –1.74 |
| Figure 12c | SG3 | 55.74 | 57.80 | –3.70 |
| Figure 12d | SG4 | 53.65 | 53.88 | –0.43 |
| Figure 12e | SG5 | 60.33 | 63.20 | –4.75 |
| Figure 12f | SG1 | 47.67 | 49.10 | –3.01 |
| SG2 | 54.83 | 56.71 | –3.42 | |
| Figure 12g | SG1 | 51.75 | 47.77 | 7.68 |
| SG2 | 59.34 | 55.08 | 7.19 | |
| SG3 | 54.43 | 53.61 | 1.50 |
| Image | Seagrass No. | (cm2) | (cm2) | Relative % Error |
|---|---|---|---|---|
| Figure 13a | SG1 | 54.11 | 50.82 | 6.08 |
| Figure 13b | SG2 | 63.85 | 61.37 | 3.88 |
| Figure 13c | SG3 | 56.88 | 55.06 | 3.21 |
| Figure 13d | SG4 | 57.00 | 55.58 | 2.49 |
| Figure 13e | SG5 | 62.25 | 61.35 | 1.44 |
| Figure 13f | SG1 | 46.99 | 44.49 | 5.33 |
| SG2 | 60.20 | 57.22 | 4.95 | |
| Figure 13g | SG1 | 48.60 | 46.45 | 4.42 |
| SG2 | 59.95 | 58.40 | 2.59 | |
| SG3 | 52.47 | 50.68 | 3.41 |
| Seagrass | (m) | (m) | (m) | (kg m s–3) | (GPa) | (m s–1) | (m) | |
|---|---|---|---|---|---|---|---|---|
| SG1 | 0.030 | 0.210 | 0.001 | 931 | 1.69 | 0.123 | 0.191 | 0.912 |
| SG2 | 0.032 | 0.230 | 0.001 | 931 | 1.69 | 0.123 | 0.208 | 0.906 |
| SG3 | 0.031 | 0.217 | 0.001 | 931 | 1.69 | 0.123 | 0.197 | 0.910 |
| SG4 | 0.030 | 0.210 | 0.001 | 931 | 1.69 | 0.123 | 0.191 | 0.912 |
| SG5 | 0.030 | 0.237 | 0.001 | 931 | 1.69 | 0.123 | 0.214 | 0.903 |
| Std dev | 8.9 × 10–4 | 1.2 × 10–2 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 × 10–2 | 4.0 × 10–3 |
| Seagrass | Vertical Area (cm2) | Frontal Area (cm2) | |||||
|---|---|---|---|---|---|---|---|
| M1 | M2 | M1 | M2 | M1 | M2 | ||
| SG1 | 62.000 | 55.620 | 50.820 | 0.897 | 0.820 | –1.63 | –10.12 |
| SG2 | 74.172 | 60.370 | 61.370 | 0.814 | 0.827 | –10.16 | –8.67 |
| SG3 | 67.683 | 57.800 | 55.060 | 0.854 | 0.814 | –6.16 | –10.60 |
| SG4 | 62.006 | 53.880 | 55.580 | 0.869 | 0.896 | –4.72 | –1.72 |
| SG5 | 70.693 | 63.200 | 61.350 | 0.894 | 0.868 | –1.00 | –3.89 |
| Std dev | 5.4 | 3.7 | 4.5 | 3.4 × 10–2 | 3.5 × 10–2 | ||
| Case | Water Height (m) | Water Depth (m) | Wave Period (s) | Current Velocity (m s–1) |
|---|---|---|---|---|
| 1 | 0.15 | 0.60 | 2.0 | 0.3 |
| 2 | 0.15 | 0.40 | 2.0 | 0.3 |
| 3 | 0.20 | 0.60 | 1.7 | 0.3 |
| 4 | 0.20 | 0.40 | 1.7 | 0.3 |
| Young’s Modulus (MPa) | Stem Height (m) | Leaf Height (m) | Number of Leaves per Stem | Leaf Width (m) | Shoot Density (Shoots m−2) | |
|---|---|---|---|---|---|---|
| 13 | 7.8 | 0.473 | 0.230 | 5.5 | 0.003 | 2436 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chau, T.V.; Jung, S.; Kim, M.; Na, W.-B. Indirect Estimation of Seagrass Frontal Area for Coastal Protection: A Mask R-CNN and Dual-Reference Approach. J. Mar. Sci. Eng. 2025, 13, 1262. https://doi.org/10.3390/jmse13071262
Chau TV, Jung S, Kim M, Na W-B. Indirect Estimation of Seagrass Frontal Area for Coastal Protection: A Mask R-CNN and Dual-Reference Approach. Journal of Marine Science and Engineering. 2025; 13(7):1262. https://doi.org/10.3390/jmse13071262
Chicago/Turabian StyleChau, Than Van, Somi Jung, Minju Kim, and Won-Bae Na. 2025. "Indirect Estimation of Seagrass Frontal Area for Coastal Protection: A Mask R-CNN and Dual-Reference Approach" Journal of Marine Science and Engineering 13, no. 7: 1262. https://doi.org/10.3390/jmse13071262
APA StyleChau, T. V., Jung, S., Kim, M., & Na, W.-B. (2025). Indirect Estimation of Seagrass Frontal Area for Coastal Protection: A Mask R-CNN and Dual-Reference Approach. Journal of Marine Science and Engineering, 13(7), 1262. https://doi.org/10.3390/jmse13071262






