Influence of Principal Stress Orientation on Cyclic Degradation of Soft Clay Under Storm Wave Loading
Abstract
1. Introduction
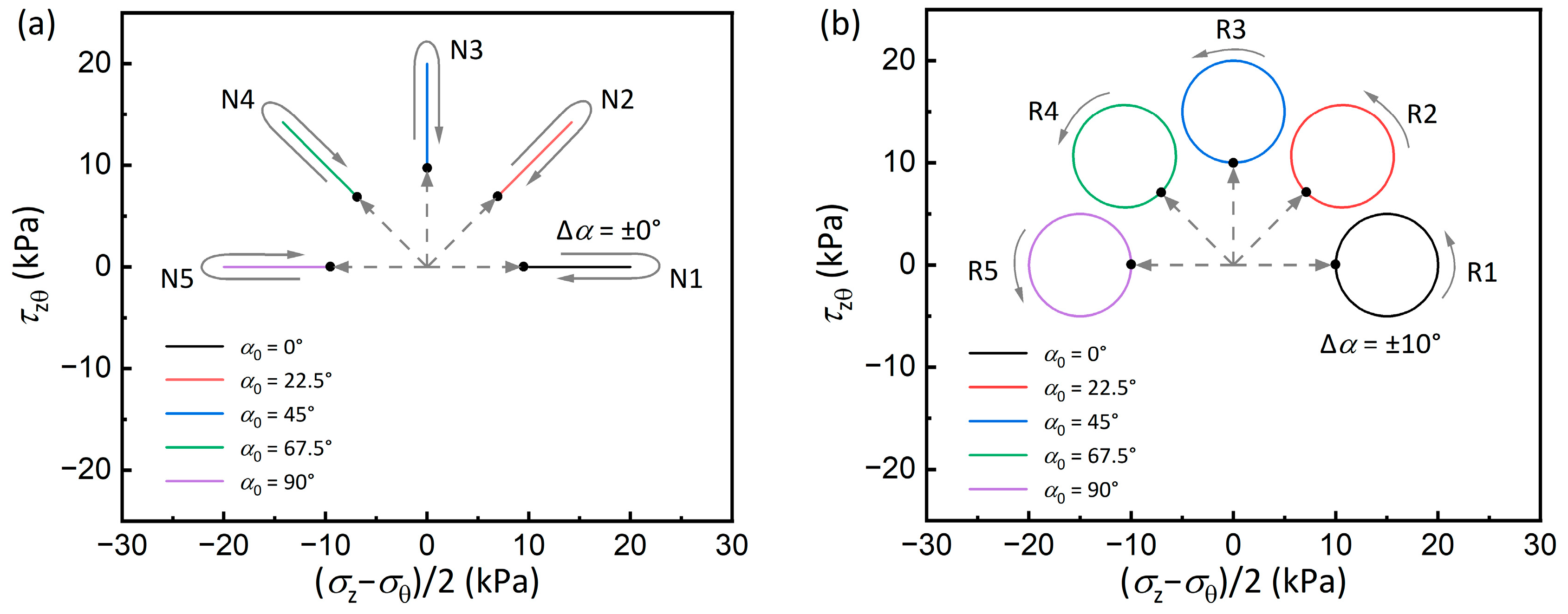
2. Sample Preparation and Test Procedures
3. Test Results and Discussion
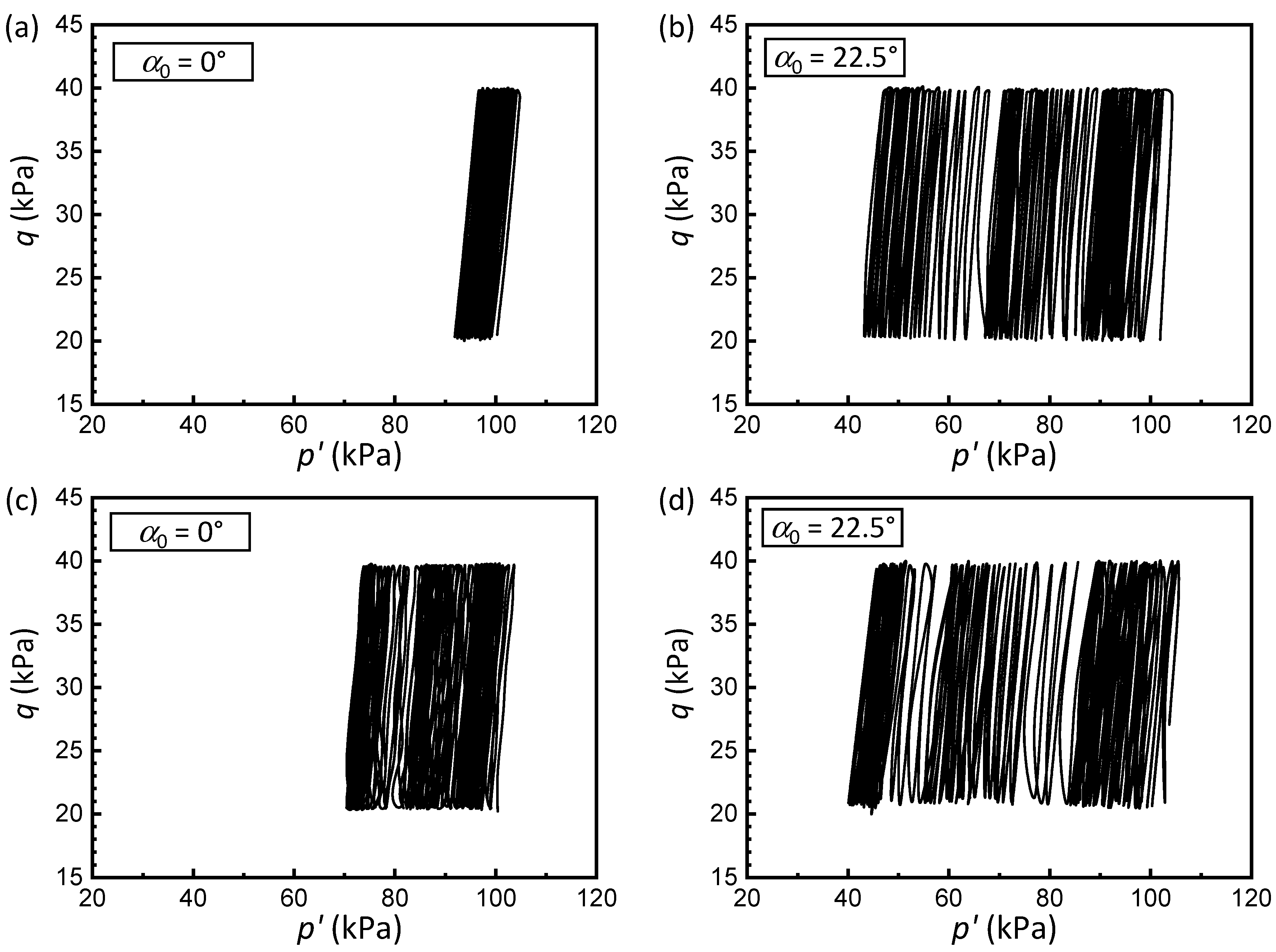
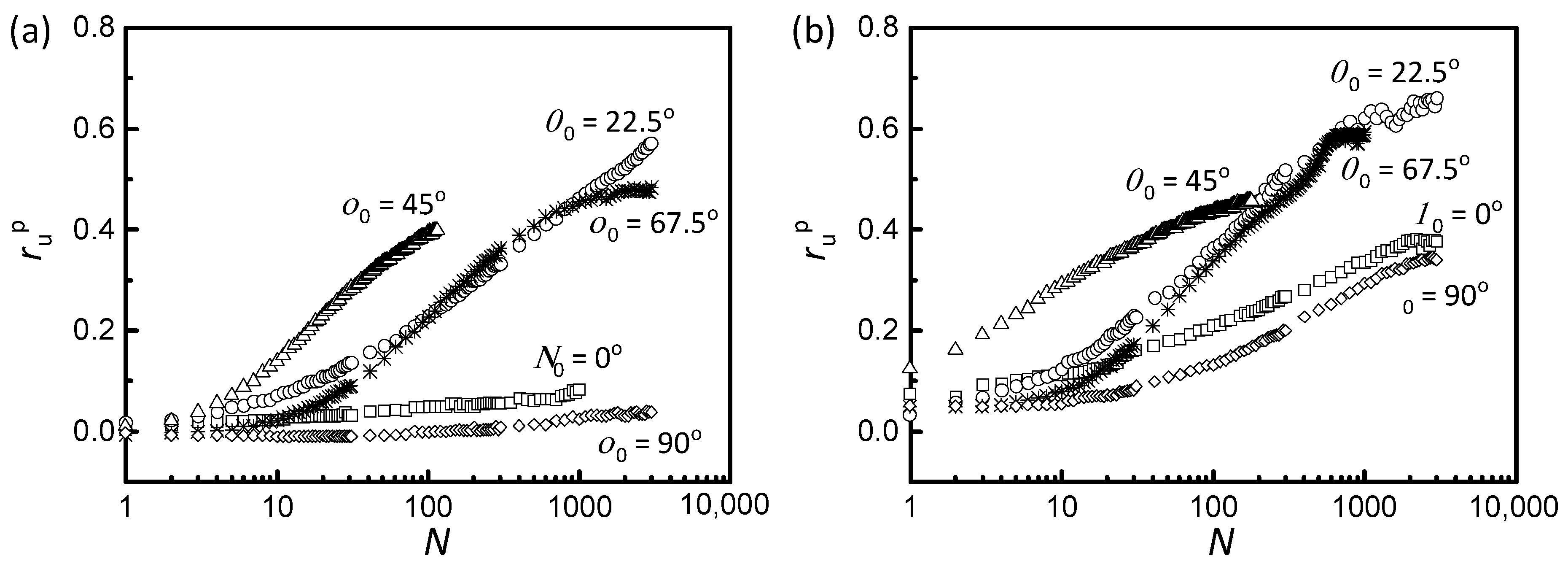
3.1. Pore Pressure Generation
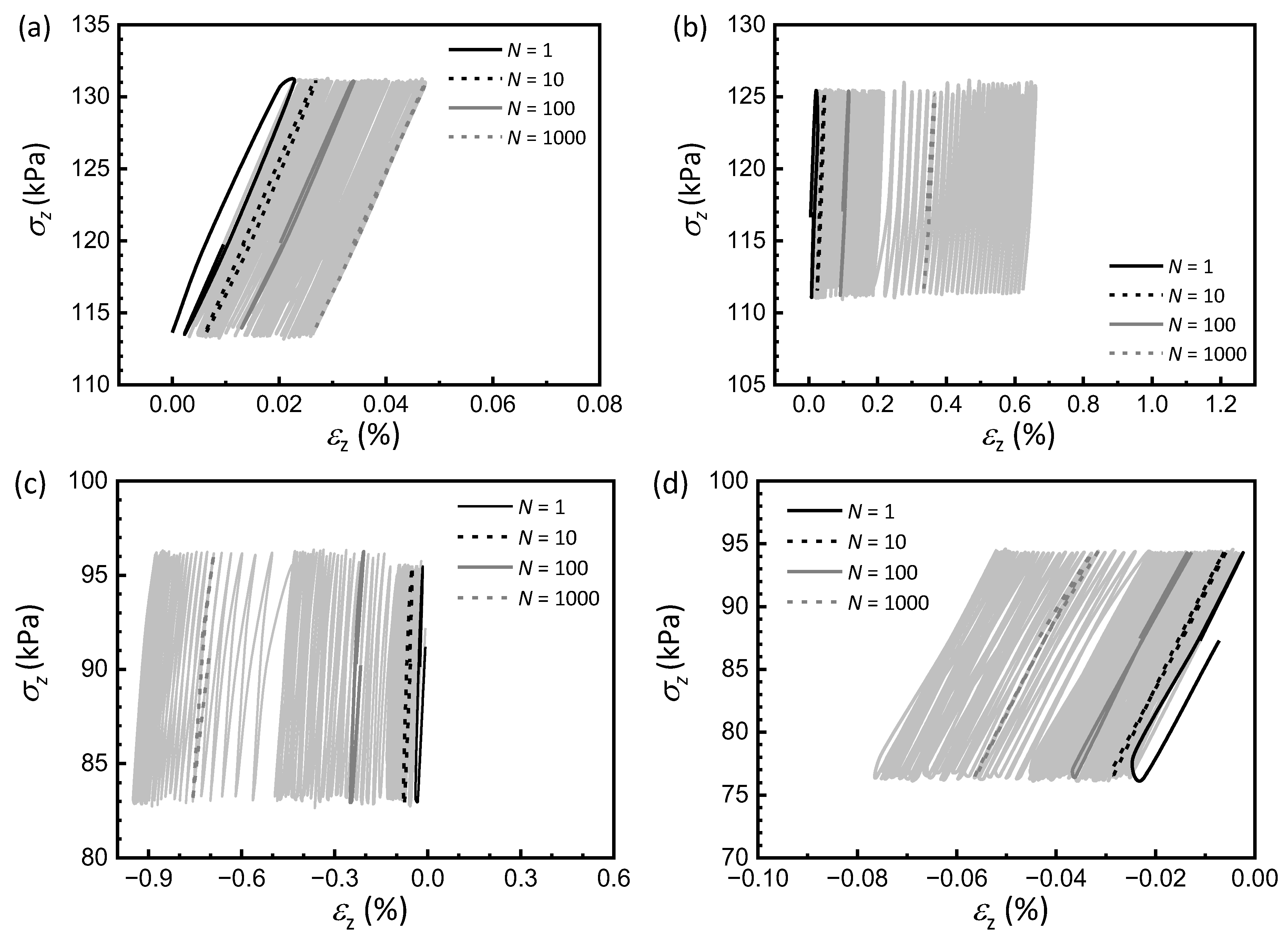
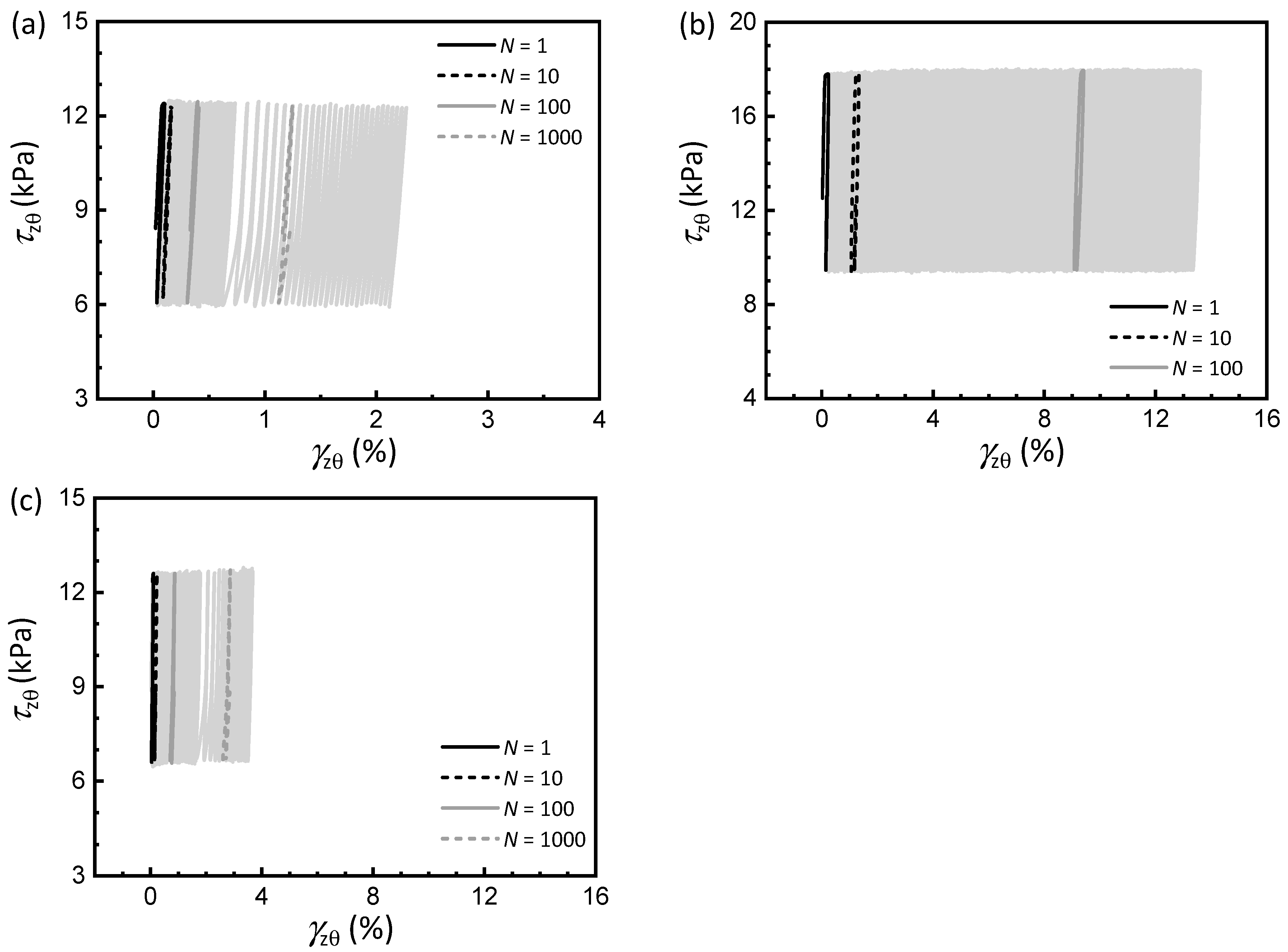
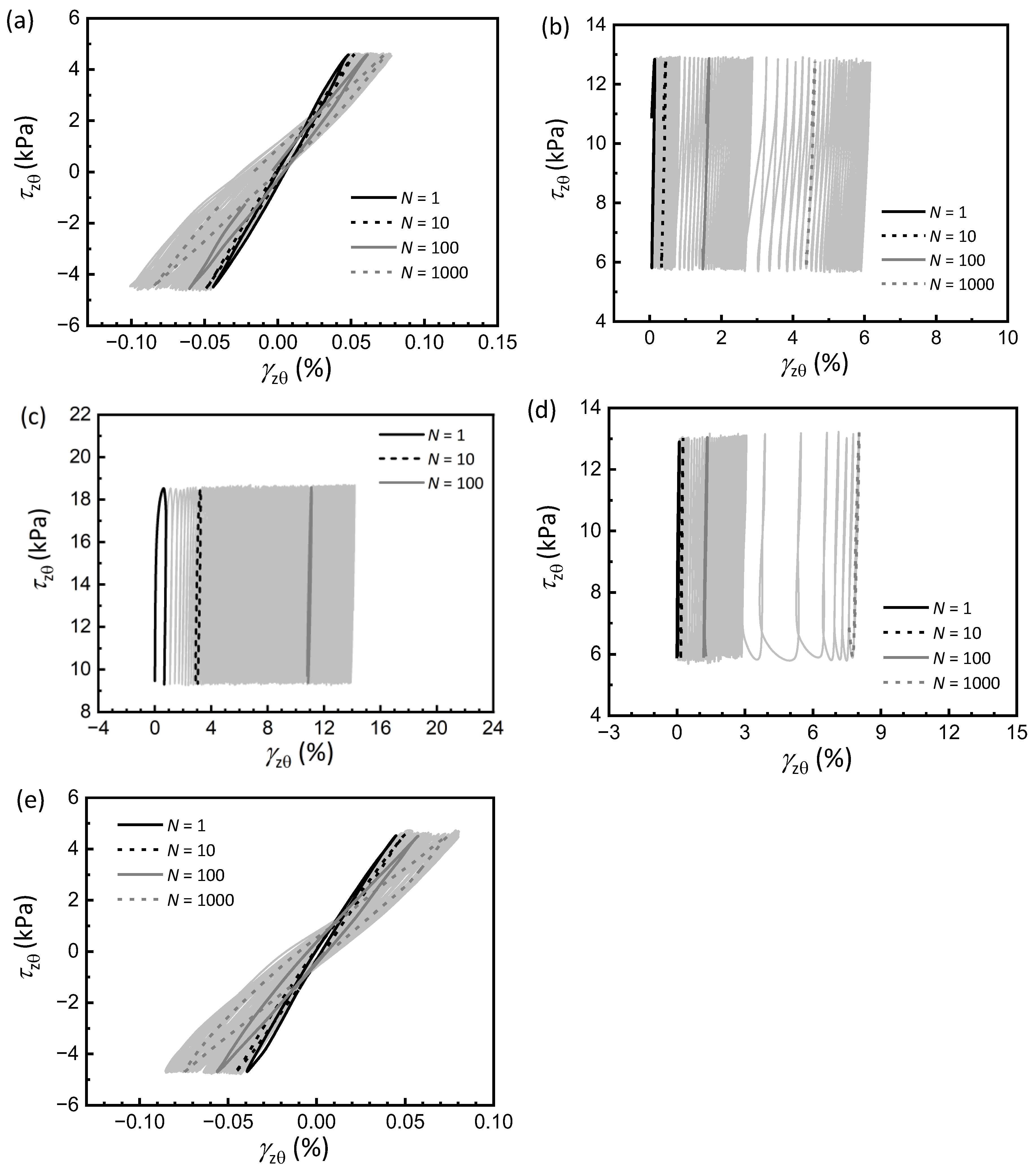
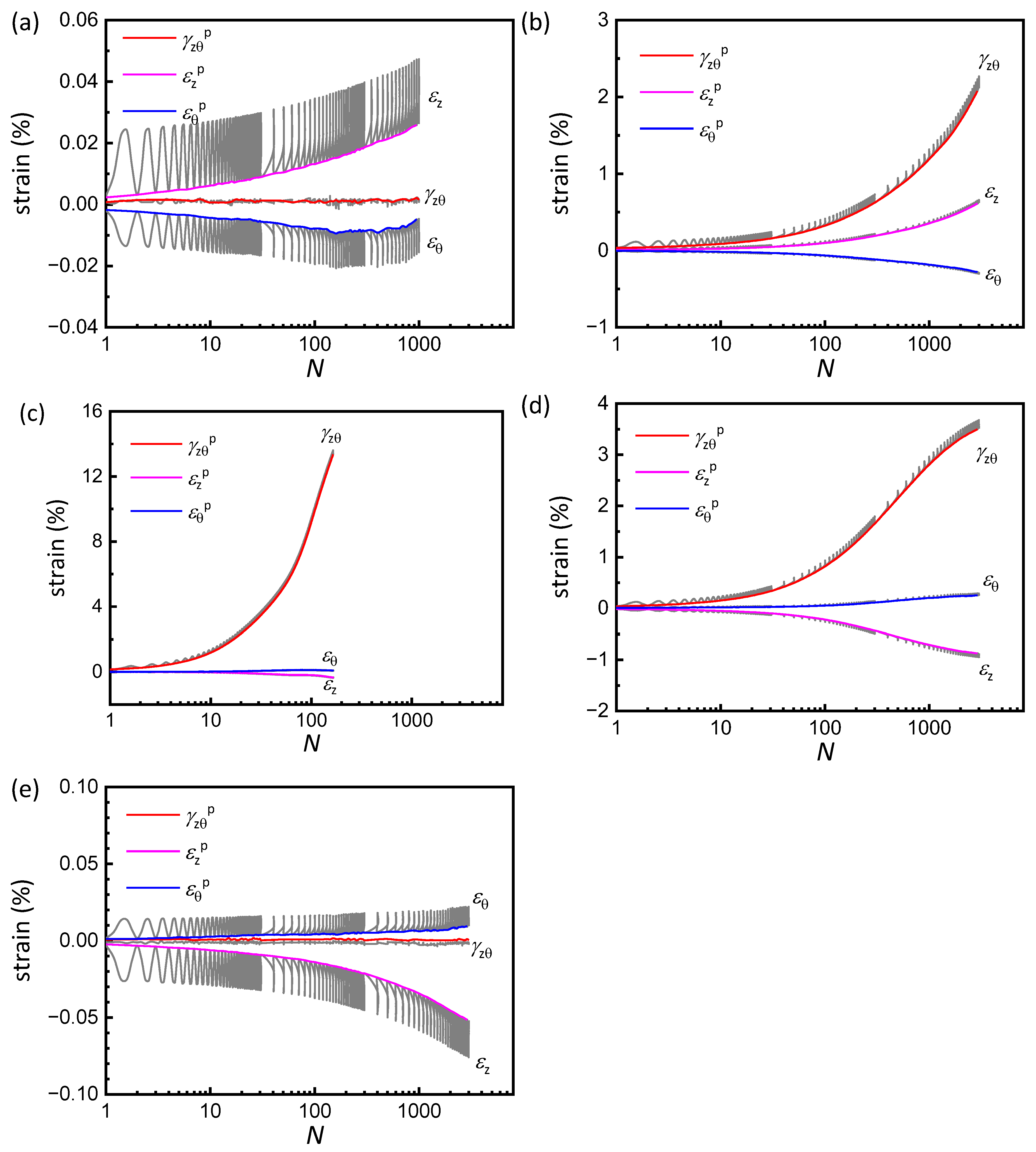
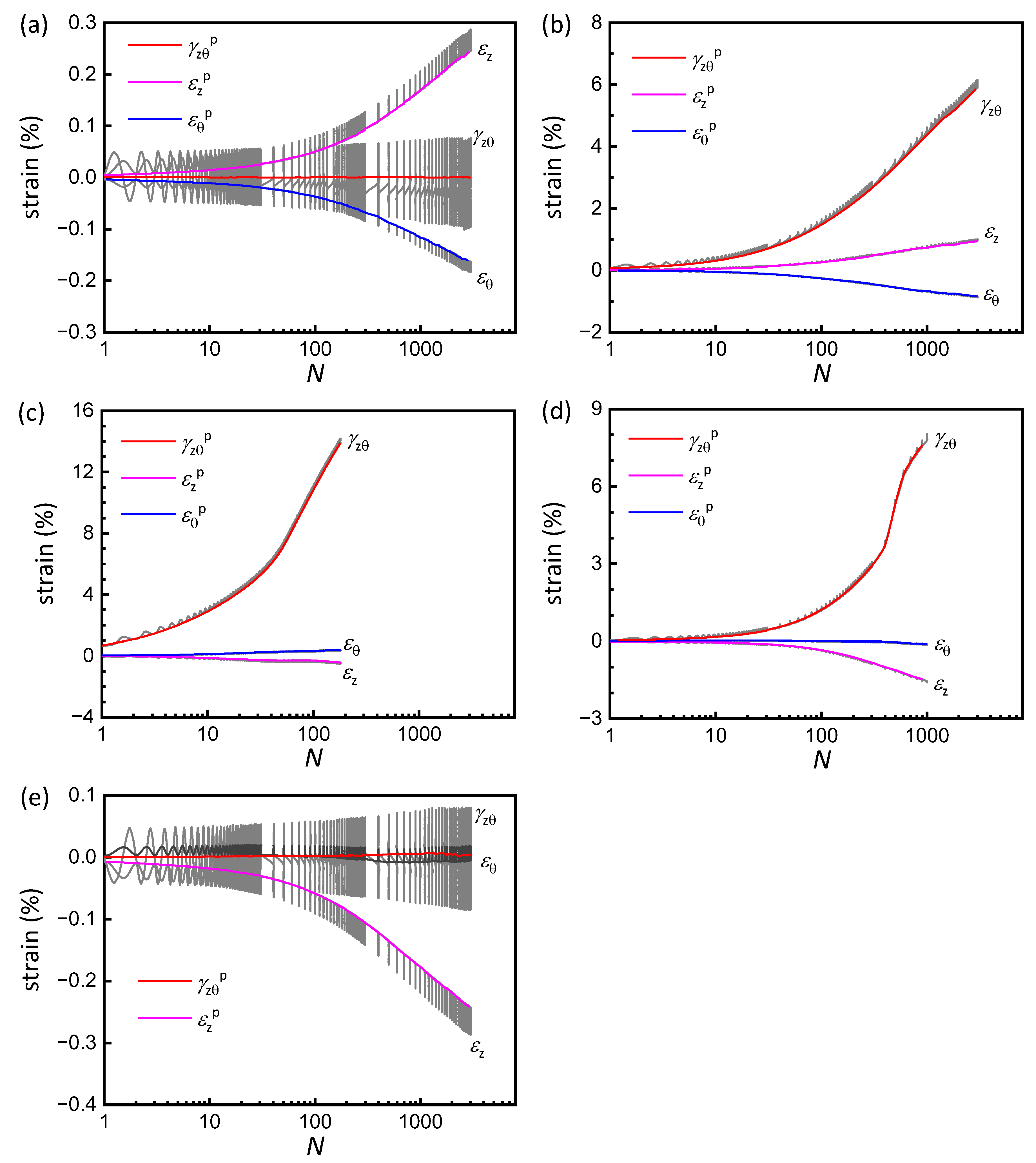
3.2. Cyclic and Permanent Strain Development
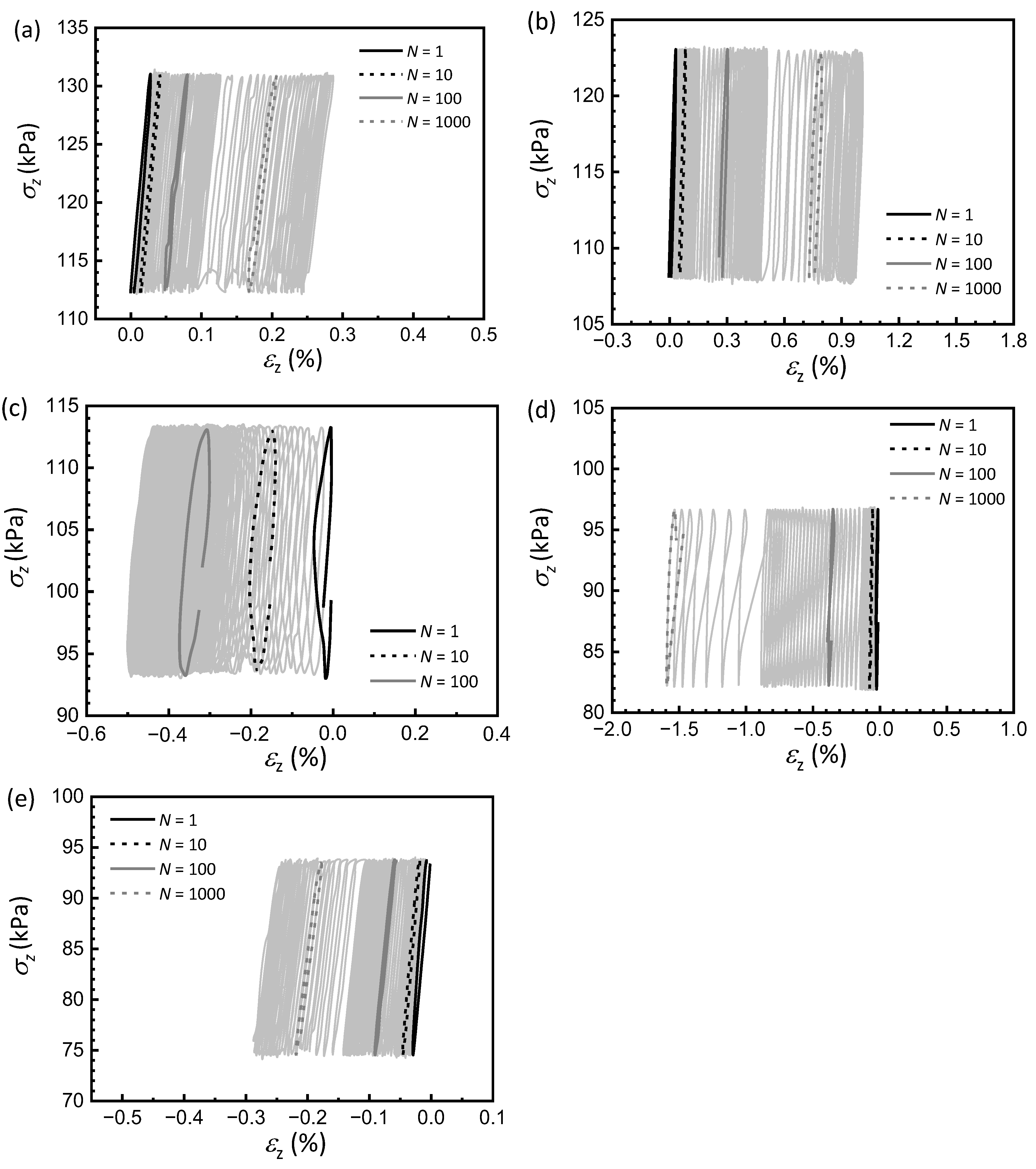
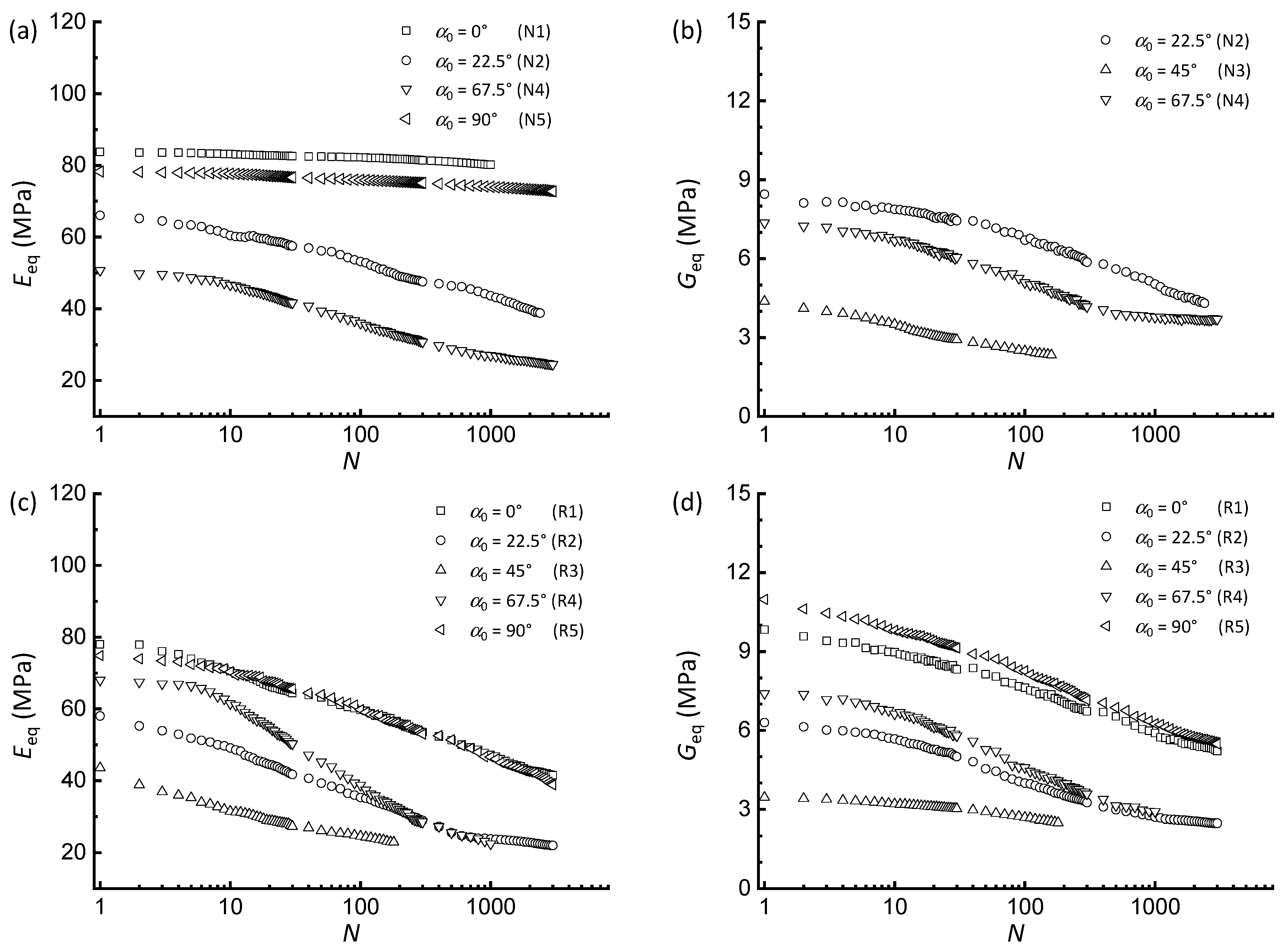
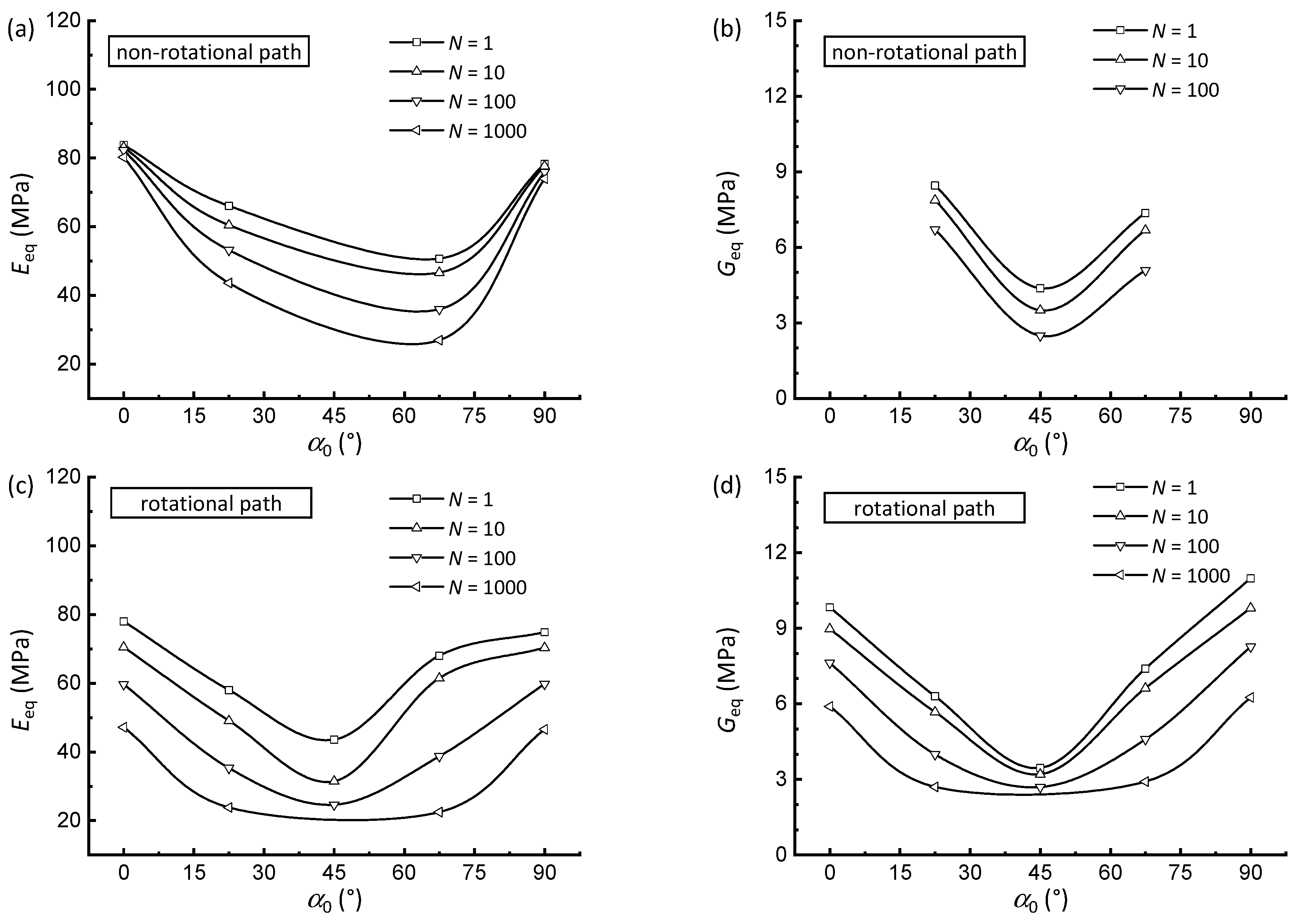
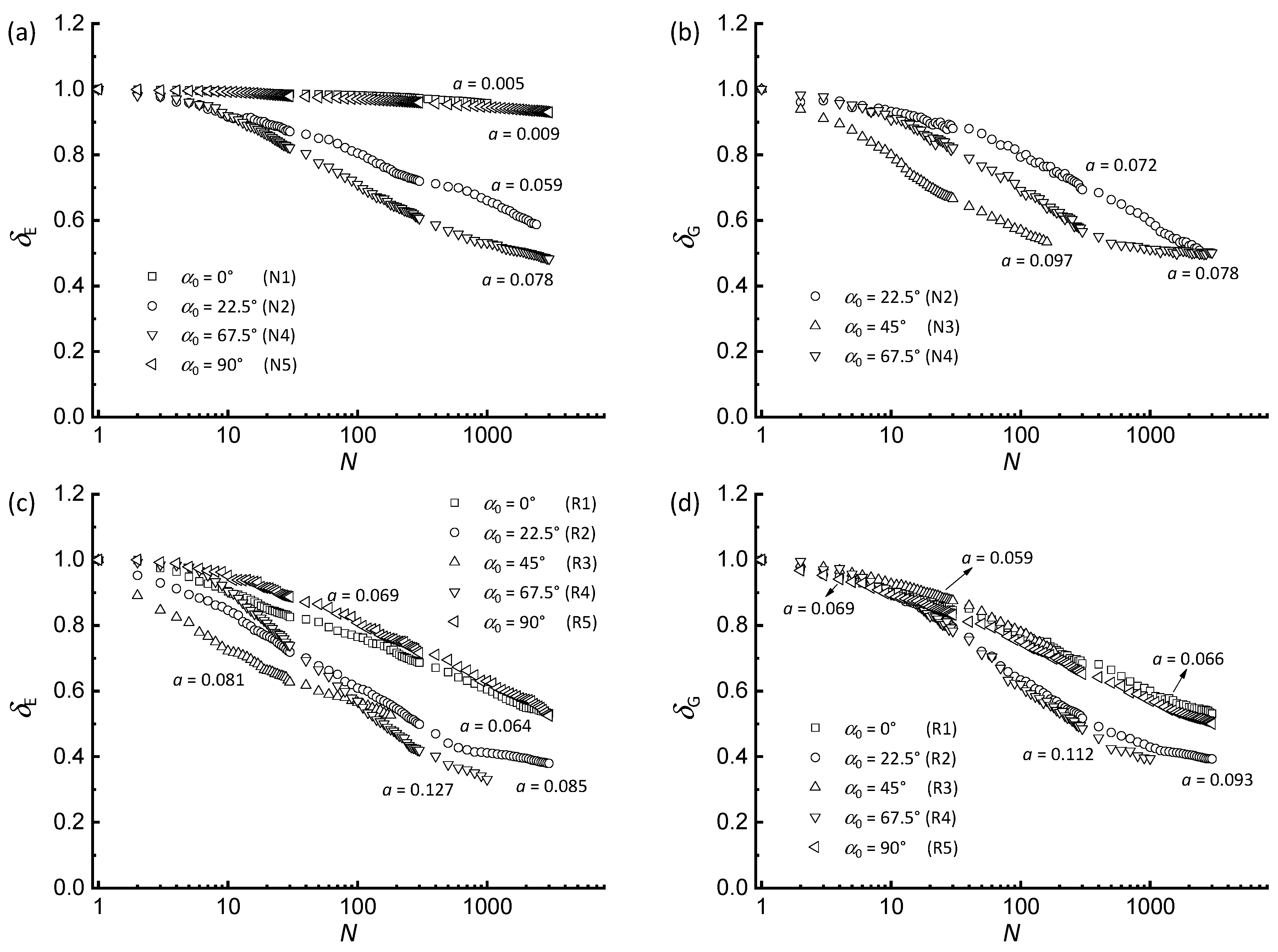
3.3. Stiffness Degradation Behavior
4. Conclusions
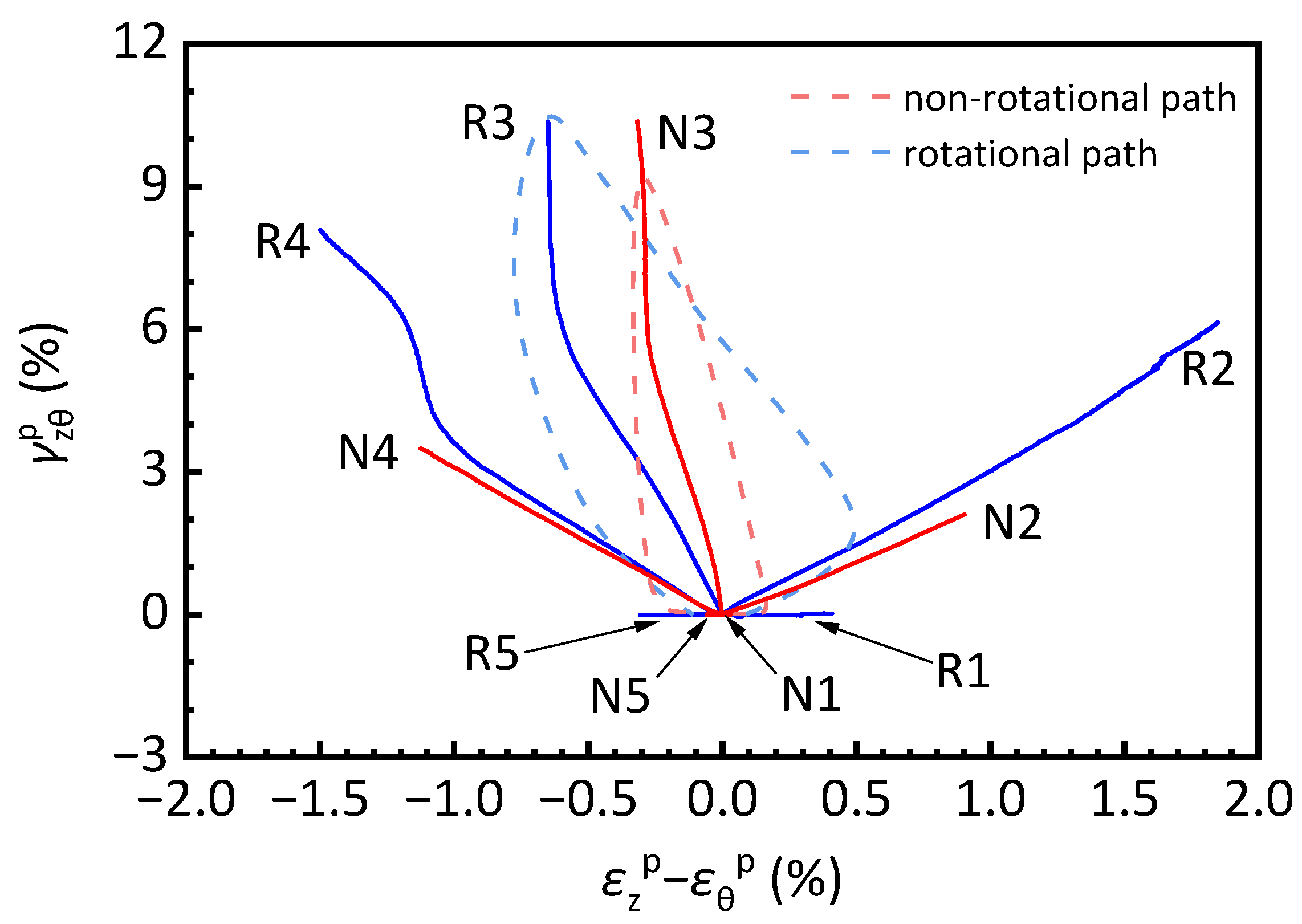
- Samples at α0 = 0° and 90° maintain stable pore pressure ratios with negligible permanent vertical, circumferential, and shear strain accumulation even at high cycle numbers. Conversely, orientations between 22.5 and 67.5° exhibit progressive degradation, with α0 = 45° triggering rapid shear strain development and earliest failure.
- The α0-dependent strain development demonstrates the significant anisotropy of the tested soft clay. Furthermore, compared with non-rotational cases, samples subjected to rotational loading exhibit higher generated pore pressure and more pronounced accumulation of permanent strain, underscoring that PSR significantly amplifies the anisotropic response of soft clay.
- Consistent with observations in permanent strains, PSR accelerates stiffness degradation, evidenced by more rapid declines in equivalent Young’s and shear moduli compared with non-rotational loading. Moreover, minimum stiffness values occur at α0 = 45°, where the degradation rate peaks due to non-coaxial shear disruption of anisotropic fabric. This peak response is systematically exacerbated by PSR across all orientations.
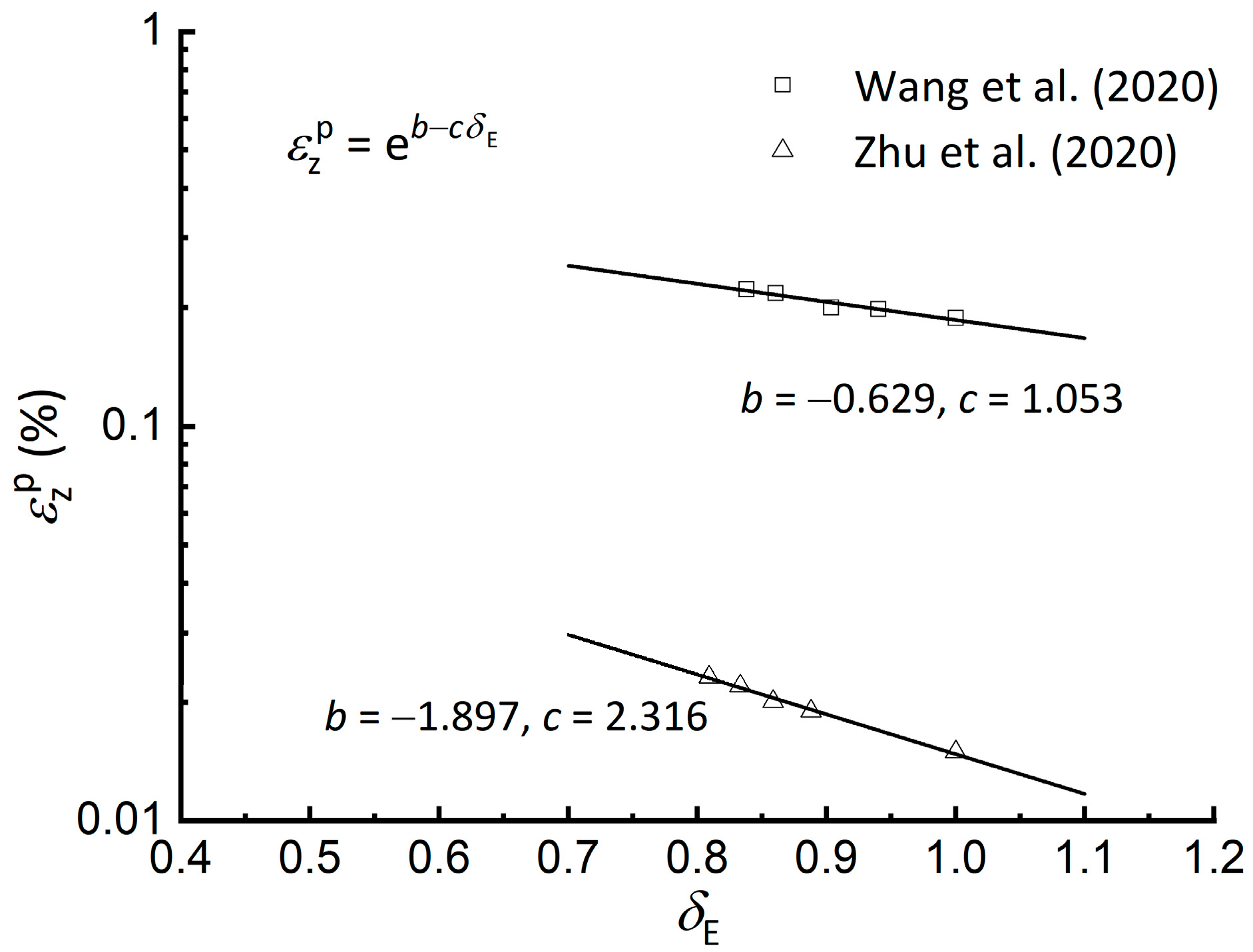
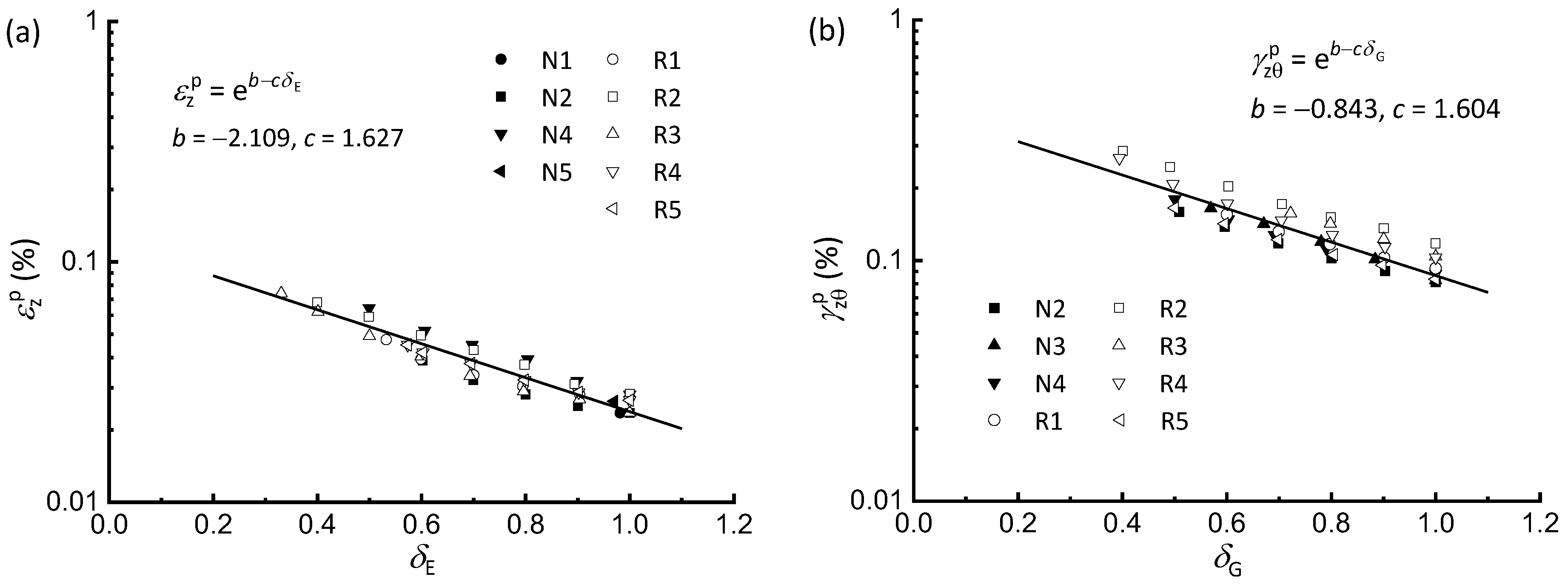
- The stiffness degradation index tends to uniquely correlate with the permanent axial or shear strain, which can be quantified by an exponential relationship that is independent of loading path. This correlation characterizes anisotropic effects from varying principal stress orientations by linking the cumulative damage on cyclic Young’s and shear moduli to permanent strain, providing a unified framework for long-term settlement prediction.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, L.; Wang, J.; Cai, Y.Q.; Liu, H.L.; Gao, Y.F.; Sun, H.L.; Mahfouz, A.H. Undrained deformation behavior of saturated soft clay under long-term cyclic loading. Soil Dyn. Earthq. Eng. 2013, 50, 28–37. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Wu, T.Y.; Guo, L.; Wang, J. Stiffness degradation and plastic strain accumulation of clay under cyclic load with principal stress rotation and deviatoric stress variation. J. Geotech. Geoenviron. Eng. 2018, 144, 04018021. [Google Scholar] [CrossRef]
- Li, Z.X.; Jeng, D.S.; Zhu, J.F.; Zhao, H.Y. Effects of principal stress rotation on the fluid-induced soil response in a porous seabed. J. Mar. Sci. Eng. 2019, 7, 123. [Google Scholar] [CrossRef]
- Zhu, J.F.; Zhao, H.Y.; Luo, Z.Y.; Liu, H.X. Investigation of the mechanical behavior of soft clay under combined shield construction and ocean waves. Ocean Eng. 2020, 206, 107250. [Google Scholar] [CrossRef]
- Vaid, Y.P.; Sivathayalan, S. Static and cyclic liquefaction potential of Fraser Delta sand in simple shear and triaxial tests. Can. Geotech. J. 1996, 33, 281–289. [Google Scholar] [CrossRef]
- Wu, Q.X.; Yang, Z.X. Novel undrained servomechanism in discrete-element modeling and its application in multidirectional cyclic shearing simulations. J. Eng. Mech. 2021, 147, 04020155. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, G.Y.; Wu, D.Z.; Li, Y.; Hu, J.T. Pre-and post-liquefaction behaviors of manufactured sand considering the particle shape and stress history effects. J. Mar. Sci. Eng. 2023, 11, 739. [Google Scholar] [CrossRef]
- Du, Z.B.; Qian, J.G.; Shi, Z.M.; Guo, Y.; Huang, M.S. Constitutive modeling for cyclic responses of saturated soft clay under principal stress rotation induced by wave loads. Ocean Eng. 2022, 252, 111243. [Google Scholar] [CrossRef]
- Wang, Y.K.; Guo, L.; Gao, Y.F.; Qiu, Y.; Hu, X.Q.; Zhang, Y. Anisotropic drained deformation behavior and shear strength of natural soft marine clay. Mar. Georesour. Geotechnol. 2016, 34, 191–202. [Google Scholar] [CrossRef]
- Finno, R.J.; Cho, W. Recent stress-history effects on compressible Chicago glacial clays. J. Geotech. Geoenviron. Eng. 2011, 137, 197–207. [Google Scholar] [CrossRef]
- Gu, C.; Wang, J.; Cai, Y.Q.; Liu, H.L.; Gao, Y.F. Undrained cyclic triaxial behavior of saturated clays under variable confining pressure. Soil Dyn. Earthq. Eng. 2012, 40, 118–128. [Google Scholar] [CrossRef]
- Yin, J.H.; Zhou, W.H.; Kumruzzaman, M.; Liu, J. A rigid-flexible boundary true triaxial apparatus for testing soils in a three-dimensional stress state. Geotech. Test. J. 2011, 34, 265–272. [Google Scholar] [CrossRef]
- Anantanasakul, P.; Yamamuro, J.A.; Lade, P.V. Three-dimensional drained behavior of normally consolidated anisotropic kaolin clay. Soils Found. 2012, 52, 146–159. [Google Scholar] [CrossRef]
- Yang, Z.X.; Li, X.S.; Yang, J. Undrained anisotropy and rotational shear in granular soil. Géotechnique 2007, 57, 371–384. [Google Scholar] [CrossRef]
- Wang, Y.; Wan, Y.; Liu, M.; Guo, C.; Zeng, C.; Wu, D. Undrained multi-dimensional deformation behavior and degradation of natural soft marine clay from HCA experiments. Soils Found. 2020, 60, 103–114. [Google Scholar] [CrossRef]
- Hight, D.W.; Gens, A.; Symes, M.J. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils. Géotechnique 1983, 33, 355–383. [Google Scholar] [CrossRef]
- Yoshimine, M.; Ishihara, K. Flow potential of sand during liquefaction. Soils Found. 1998, 38, 189–198. [Google Scholar] [CrossRef]
- Gasparre, A.; Nishimura, S.; Anh-Minh, N.; Coop, M.R.; Jardine, R.J. The stiffness of natural London Clay. Géotechnique 2007, 57, 33–47. [Google Scholar] [CrossRef]
- Brosse, A.M.; Jardine, R.J.; Nishimura, S. The undrained shear strength anisotropy of four Jurassic to Eocene stiff clays. Géotechnique 2017, 67, 653–671. [Google Scholar] [CrossRef]
- Wang, J.; Dai, M.; Cai, Y.Q.; Guo, L.; Du, Y.G.; Wang, C.L.; Li, M.F. Influences of initial static shear stress on the cyclic behaviour of over consolidated soft marine clay. Ocean Eng. 2021, 224, 108747. [Google Scholar] [CrossRef]
- Pan, K.; Liu, X.M.; Yang, Z.X.; Jardine, R.J.; Cai, Y.Q. Undrained cyclic response of K0-consolidated stiff cretaceous clay under wheel loading conditions. J. Geotech. Geoenviron. Eng. 2021, 147, 04021078. [Google Scholar] [CrossRef]
- Ishihara, K.; Towhata, I. Sand response to cyclic rotation of principal stress directions as induced by wave loads. Soils Found. 1983, 23, 11–26. [Google Scholar] [CrossRef]
- Sivathayalan, S.; Vaid, Y.P. Influence of generalized initial state and principal stress rotation on the undrained response of sands. Can. Geotech. J. 2002, 39, 63–76. [Google Scholar] [CrossRef]
- Lade, P.V.; Rodriguez, N.M.; Van Dyck, E.J. Effects of principal stress directions on 3D failure conditions in cross-anisotropic sand. J. Geotech. Geoenviron. Eng. 2014, 140, 04013001. [Google Scholar] [CrossRef]
- Jardine, R.J.; Potts, D.M.; Fourie, A.B.; Burland, J.B. Studies of the influence of non-linear stress-strain characteristics in soil-structure interaction. Géotechnique 1986, 36, 377–396. [Google Scholar] [CrossRef]
- Kokusho, T.; Yoshida, Y.; Esashi, Y. Dynamic properties of soft clay for wide strain range. Soils Found. 1982, 22, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, I.; Zhang, X. Unified dynamic shear moduli and damping ratios of sand and clay. Soils Found. 1993, 33, 182–191. [Google Scholar] [CrossRef]
- Idriss, I.M.; Dobry, R.; Singh, R.D. Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. Div. 1978, 104, 1427–1447. [Google Scholar] [CrossRef]
- Pan, K.; Zhou, G.Y.; Yang, Z.X.; Jardine, R.J. Undrained cyclic loading behavior of stiff Eocene-to-Jurassic plastic, high-OCR clays. Can. Geotech. J. 2024, 61, 717–731. [Google Scholar] [CrossRef]
- Gasparre, A.; Nishimura, S.; Coop, M.; Jardine, R.J.; Minh, N.A. The stiffness of natural London Clay. In Stiff Sedimentary Clays: Genesis and Engineering Behaviour; Thomas Telford Ltd.: London, UK, 2011; pp. 81–95. [Google Scholar] [CrossRef]
- Yang, Q.; Ren, Y.; Niu, J.; Cheng, K.; Hu, Y.; Wang, Y. Characteristics of soft marine clay under cyclic loading: A review. Bull. Eng. Geol. Environ. 2018, 77, 1027–1046. [Google Scholar] [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International West Conshohocken: Conshohocken, PA, USA, 2025. Available online: https://www.astm.org/ (accessed on 2 June 2025).
- Pillai, R.J.; Robinson, R.G.; Boominathan, A. Effect of microfabric on undrained static and cyclic behavior of kaolin clay. J. Geotech. Geoenviron. Eng. 2011, 137, 421–429. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Guo, L.; Fu, H.; Cai, Y.Q.; Wu, T.Y.; Shi, L. Anisotropic and noncoaxial behavior of K0-consolidated soft clays under stress paths with principal stress rotation. J. Geotech. Geoenviron. Eng. 2019, 145, 04019036. [Google Scholar] [CrossRef]
- Sivathayalan, S.; Logeswaran, P.; Manmatharajan, V. Cyclic resistance of a loose sand subjected to rotation of principal stresses. J. Geotech. Geoenviron. Eng. 2015, 141, 04014113. [Google Scholar] [CrossRef]
- Qian, J.G.; Du, Z.B.; Yin, Z.Y. Cyclic degradation and non-coaxiality of soft clay subjected to pure rotation of principal stress directions. Acta Geotech. 2018, 13, 943–959. [Google Scholar] [CrossRef]
- Cui, X.; Li, X.; Du, Y.; Bao, Z.; Zhang, X.; Hao, J.; Hu, Y. Macro-micro numerical analysis of granular materials considering principal stress rotation based on DEM simulation of dynamic hollow cylinder test. Constr. Build. Mater. 2024, 412, 134818. [Google Scholar] [CrossRef]
- Sharma, S.S.; Fahey, M. Degradation of stiffness of cemented calcareous soil in cyclic triaxial tests. J. Geotech. Geoenviron. Eng. 2003, 129, 619–629. [Google Scholar] [CrossRef]
- Clayton, C.R.I. Stiffness at small strain: Research and practice. Géotechnique 2011, 61, 5–37. [Google Scholar] [CrossRef]
- Liang, F.Y.; Zhang, Z.W.; Wang, C.; Gu, X.Q.; Lin, Y.F.; Yang, W. Experimental study on stiffness degradation and liquefaction characteristics of marine sand in the East Nan-Ao area in Guangdong Province, China. J. Mar. Sci. Eng. 2021, 9, 638. [Google Scholar] [CrossRef]
- Miura, K.; Miura, S.; Toki, S. Deformation behavior of anisotropic dense sand under principal stress axes rotation. Soils Found. 1986, 26, 36–52. [Google Scholar] [CrossRef]
- Gutierrez, M.; Ishihara, K. Non-coaxiality and energy dissipation in granular materials. Soils Found. 2000, 40, 49–59. [Google Scholar] [CrossRef]
- Qian, J.G.; Du, Z.B.; Lu, X.L.; Gu, X.Q.; Huang, M.S. Effects of principal stress rotation on stress–strain behaviors of saturated clay under traffic–load–induced stress path. Soils Found. 2019, 59, 41–55. [Google Scholar] [CrossRef]
- Zhuang, H.; Wang, J.; Gao, Z. Anisotropic and noncoaxial behavior of soft marine clay under stress path considering the variation of principal stress direction. Inter. J. Geomech. 2022, 22, 04022062. [Google Scholar] [CrossRef]
- AASHTO. Mechanistic-Empirical Pavement Design Guide; AASHTO: Washington, DC, USA, 2004. [Google Scholar]
- Muhanna, A.S.; Rahman, M.S.; Lambe, P.C. Model for resilient modulus and permanent strain of subgrade soils. Transp. Res. Rec. 1998, 1619, 85–93. [Google Scholar] [CrossRef]
- Niemunis, A.; Wichtmann, T.; Triantafyllidis, T. A high-cycle accumulation model for sand. Comput. Geotech. 2005, 32, 245–263. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Guo, L.; Cai, Y.; Li, B.; Qiu, Y.; Mahfouz, A.H. Cyclic response of natural soft marine clay under principal stress rotation as induced by wave loads. Ocean Eng. 2017, 129, 191–202. [Google Scholar] [CrossRef]
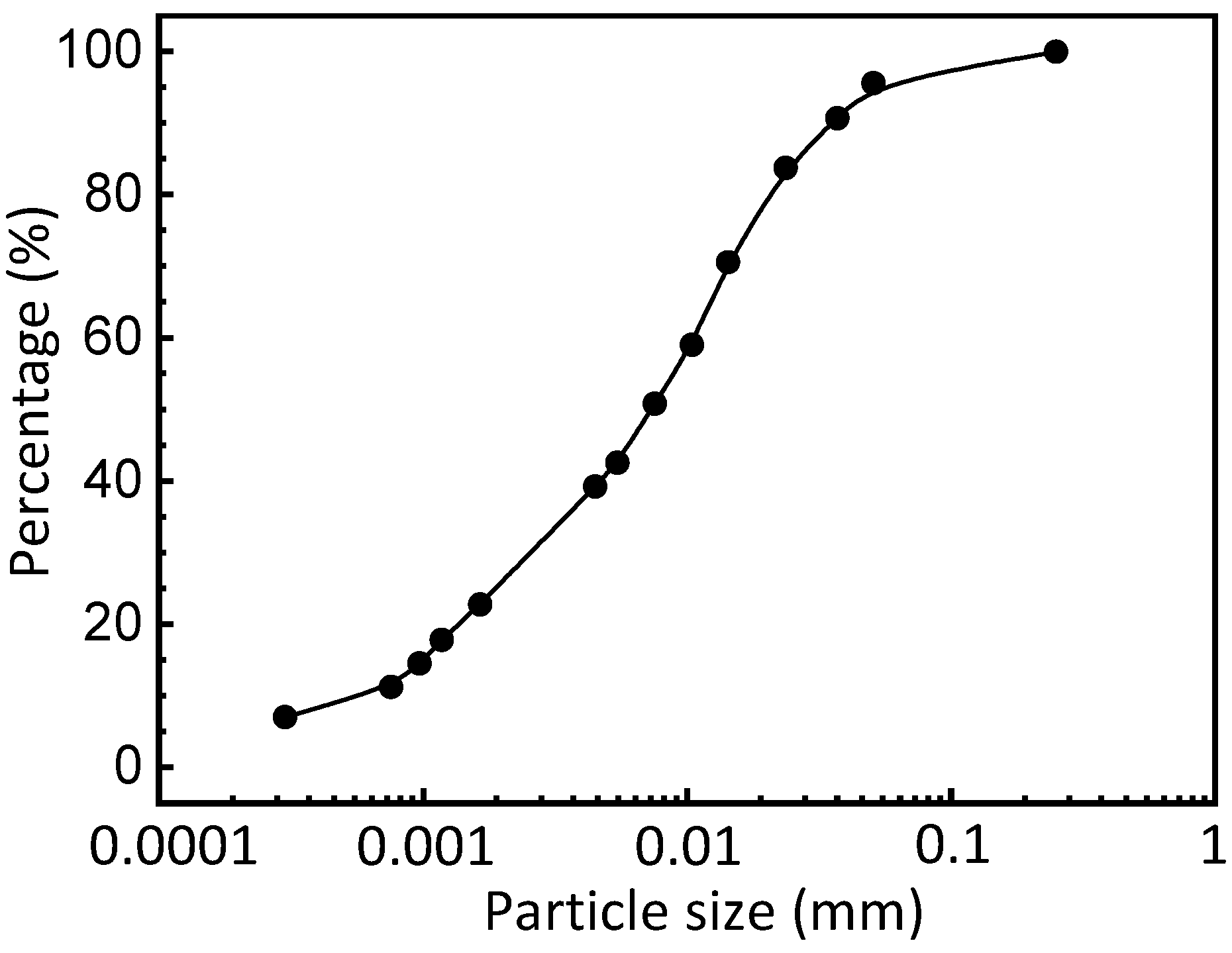
| Index Property | Value |
|---|---|
| Specific gravity, Gs | 2.68 |
| Initial density, ρ0 (g/cm3) | 1.78 |
| Water content, w (%) | 28.9 |
| Plastic limit, wP (%) | 23.7 |
| Liquid limit, wL (%) | 41.5 |
| Plastic index, IP | 17.8 |
| Unit weight of soil, γ (kN/m3) | 18.6 |
| Initial void ratio, e0 | 1.131–1.149 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Gao, F.; Huang, B.; Li, P.; Hu, Z.; Pan, K. Influence of Principal Stress Orientation on Cyclic Degradation of Soft Clay Under Storm Wave Loading. J. Mar. Sci. Eng. 2025, 13, 1227. https://doi.org/10.3390/jmse13071227
Hu C, Gao F, Huang B, Li P, Hu Z, Pan K. Influence of Principal Stress Orientation on Cyclic Degradation of Soft Clay Under Storm Wave Loading. Journal of Marine Science and Engineering. 2025; 13(7):1227. https://doi.org/10.3390/jmse13071227
Chicago/Turabian StyleHu, Chengcong, Feng Gao, Biao Huang, Peipei Li, Zheng Hu, and Kun Pan. 2025. "Influence of Principal Stress Orientation on Cyclic Degradation of Soft Clay Under Storm Wave Loading" Journal of Marine Science and Engineering 13, no. 7: 1227. https://doi.org/10.3390/jmse13071227
APA StyleHu, C., Gao, F., Huang, B., Li, P., Hu, Z., & Pan, K. (2025). Influence of Principal Stress Orientation on Cyclic Degradation of Soft Clay Under Storm Wave Loading. Journal of Marine Science and Engineering, 13(7), 1227. https://doi.org/10.3390/jmse13071227