Spatiotemporal Analysis of Sea-Surface pH in the Pacific Ocean Based on Interpretable Machine Learning
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area and Data
2.2. Calculation of the Seawater Carbonate System
2.3. Model and Methodology Description
2.4. An Interpretable Machine Learning Approach for Spatiotemporal Inversion of Sea Surface pH
- (1)
- Figure 2 illustrates the methodological framework of this study. The modeling of ocean carbonate system parameters was carried out through the following steps:
- (2)
- The preprocessing of the GLODAP and SOCAT datasets included standardization, spatial filtering, temperature–salinity screening, and outlier removal. In situ observations were integrated with satellite and reanalysis datasets to construct the TA inversion model. All remote sensing and reanalysis products were resampled to a uniform spatial resolution of 8 × 8 km using bilinear interpolation. For each in situ sampling location, the corresponding environmental variable values were extracted from the resampled datasets based on geographic coordinates and sampling date.
- (3)
- The construction of TA inversion models utilizing various machine learning methods based on two sets of input features: (SST, SSS) and (SST, SSS, Chl-a), with in situ TA measurements from GLODAP dataset.
- (4)
- The optimal TA inversion model is selected to expand the TA observational dataset by integrating it with the preprocessed SOCAT dataset. Surface pH values are then estimated using carbonate system calculations based on SOCAT fCO2 data and the optimal TA model.
- (5)
- The development of an expanded surface pH dataset for the Pacific Ocean. Using this dataset, an interpretable machine learning model was trained to produce pH inversion results, and SHAP analysis was applied to quantify and attribute the contributions of influencing factors to pH variability.

2.5. Model Evaluation Metrics and Model Configuration
3. Results
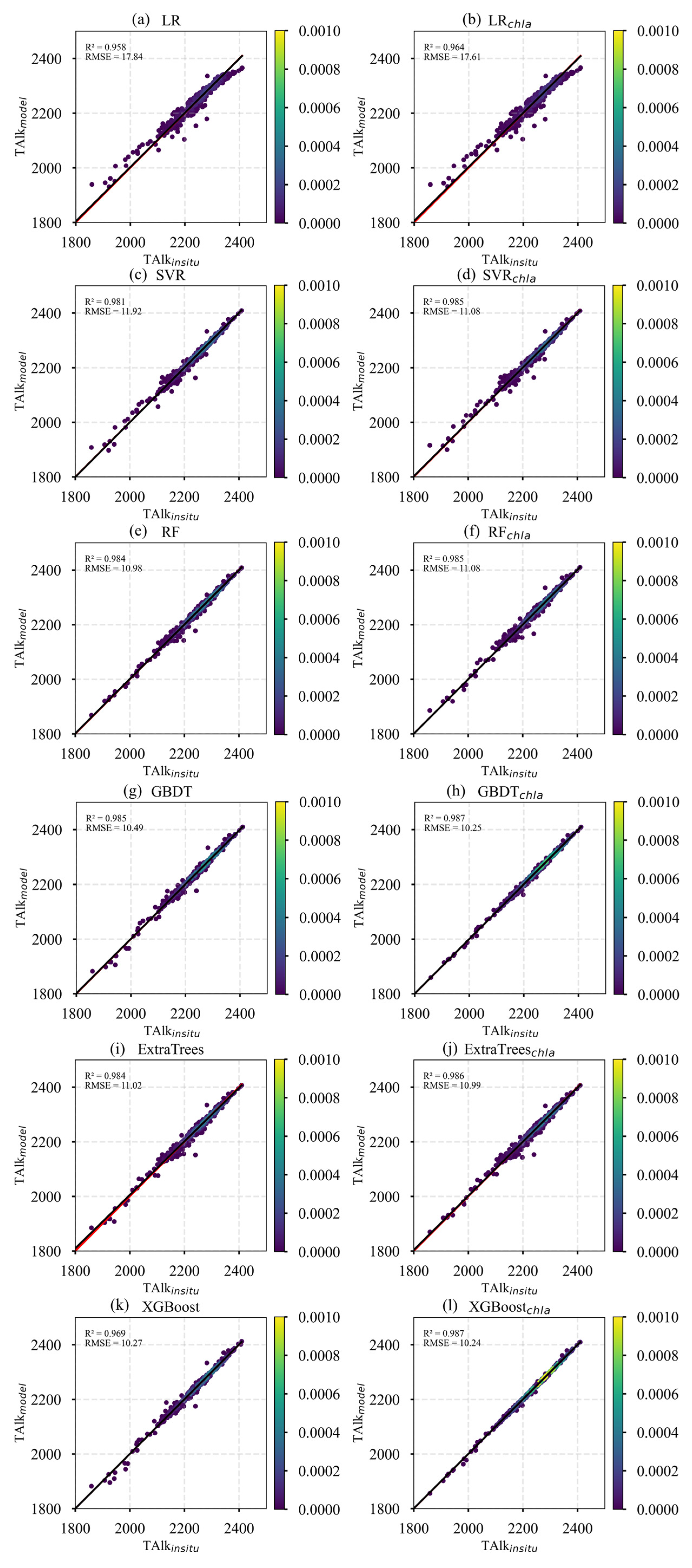
3.1. Reconstruction Results of Observed Total Alkalinity Data
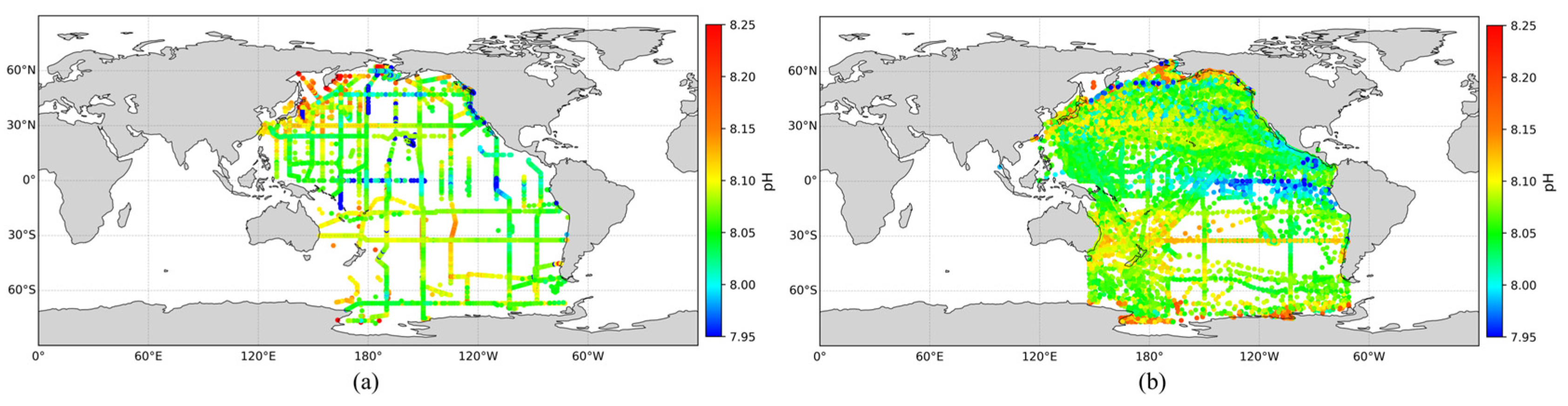
3.2. Reconstruction Results of Observed pH Data
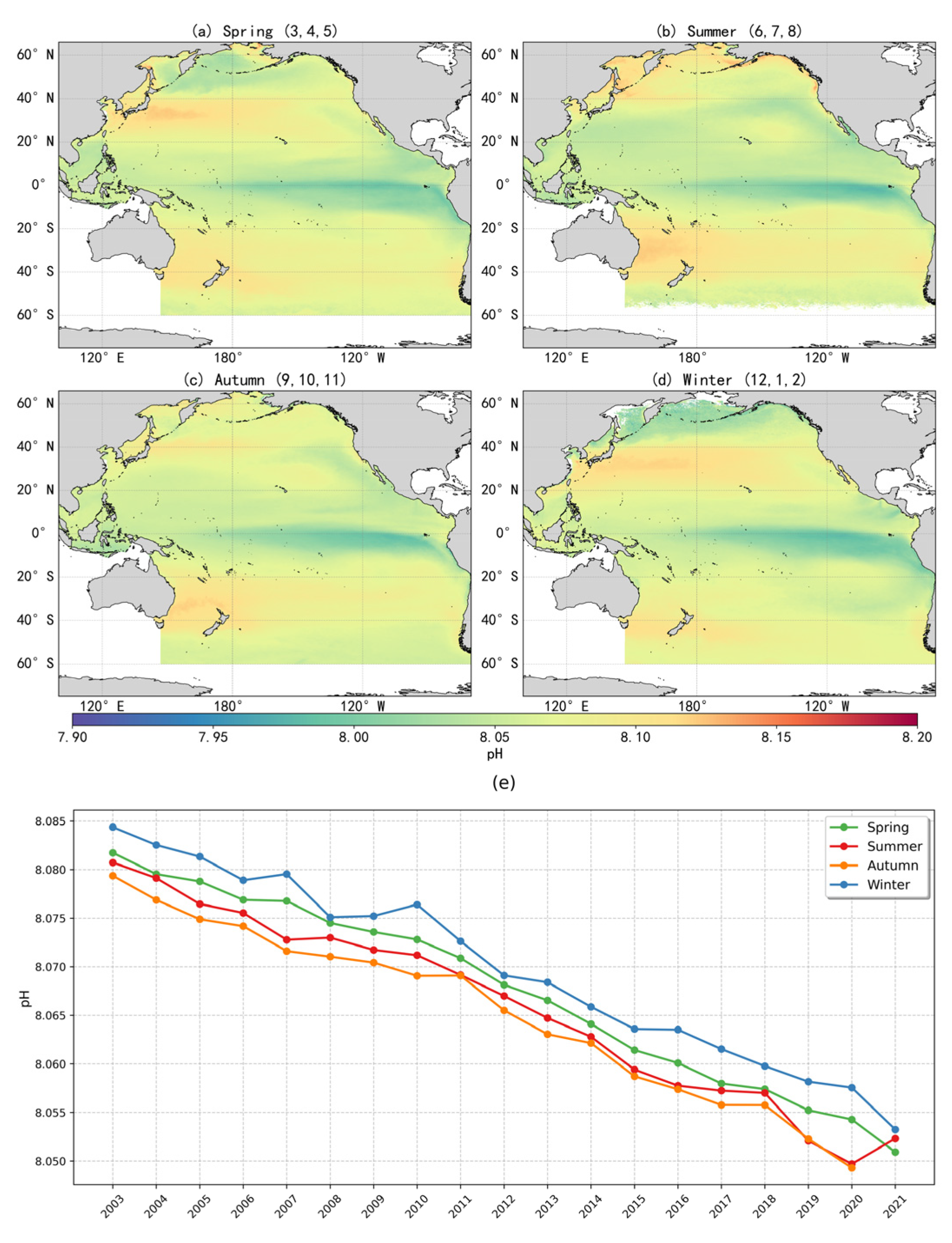
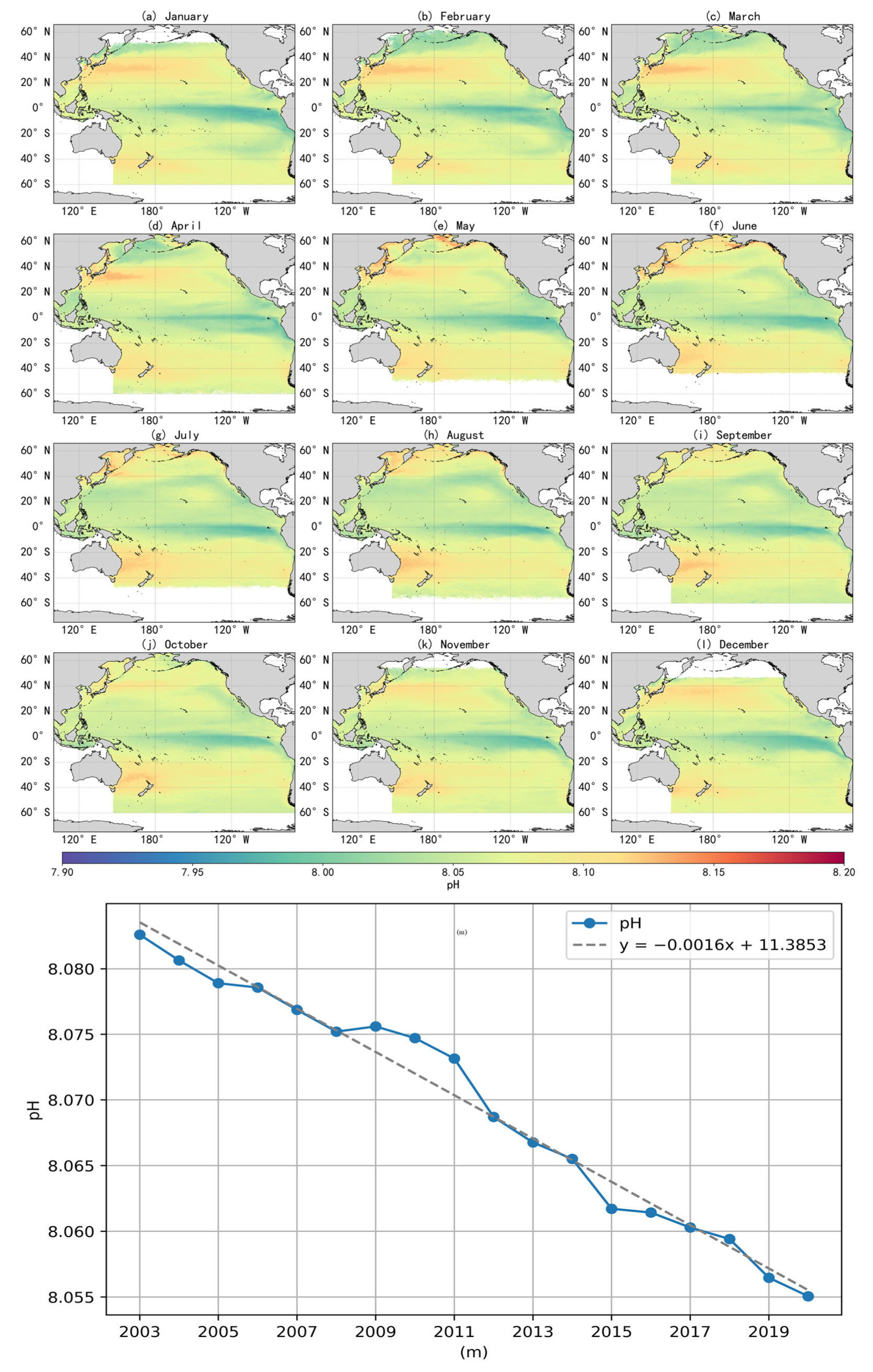
3.3. Spatiotemporal Inversion Results of Sea-Surface pH
4. Discussion
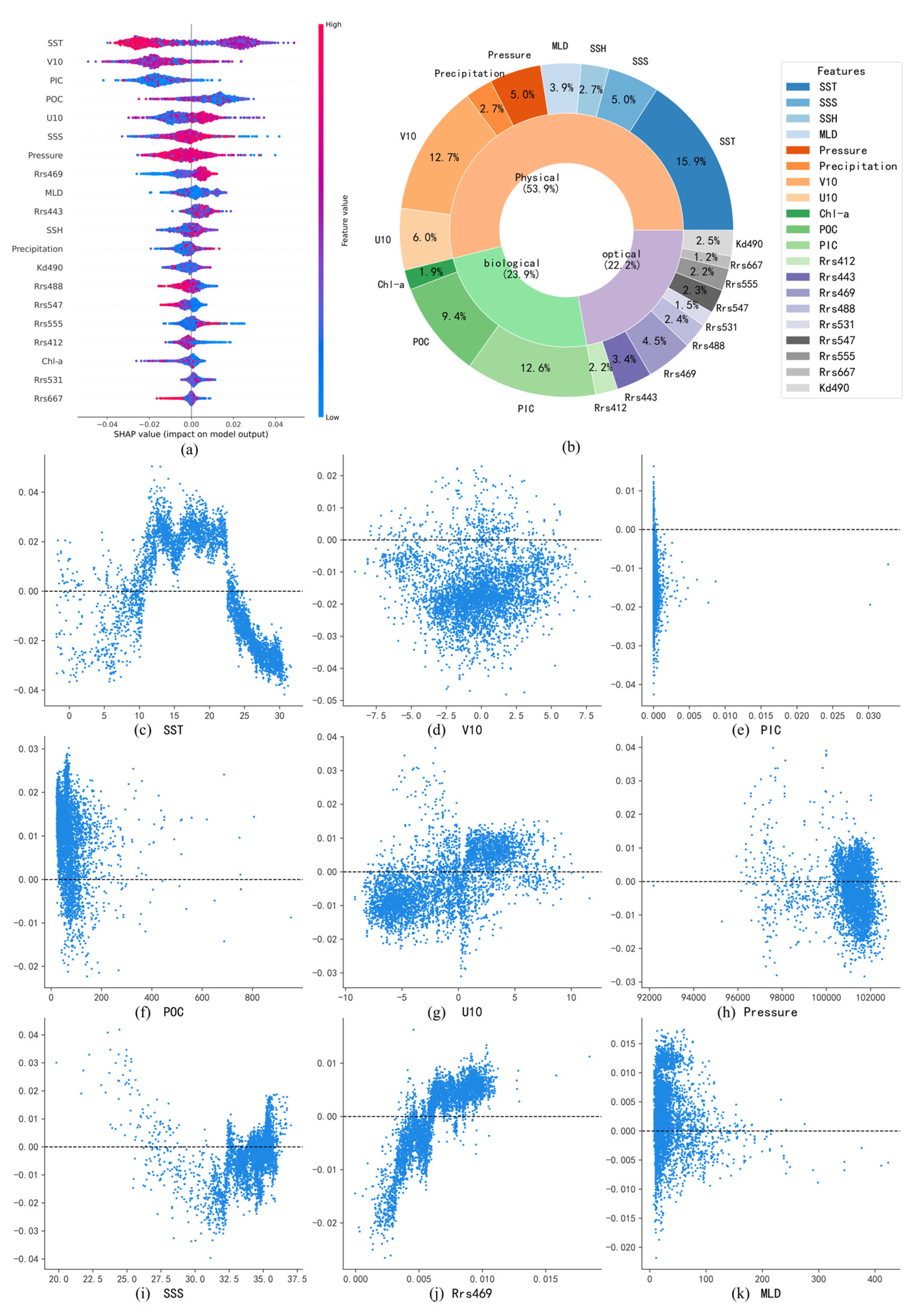
4.1. Analysis of Factors Influencing Surface pH in the Pacific Ocean
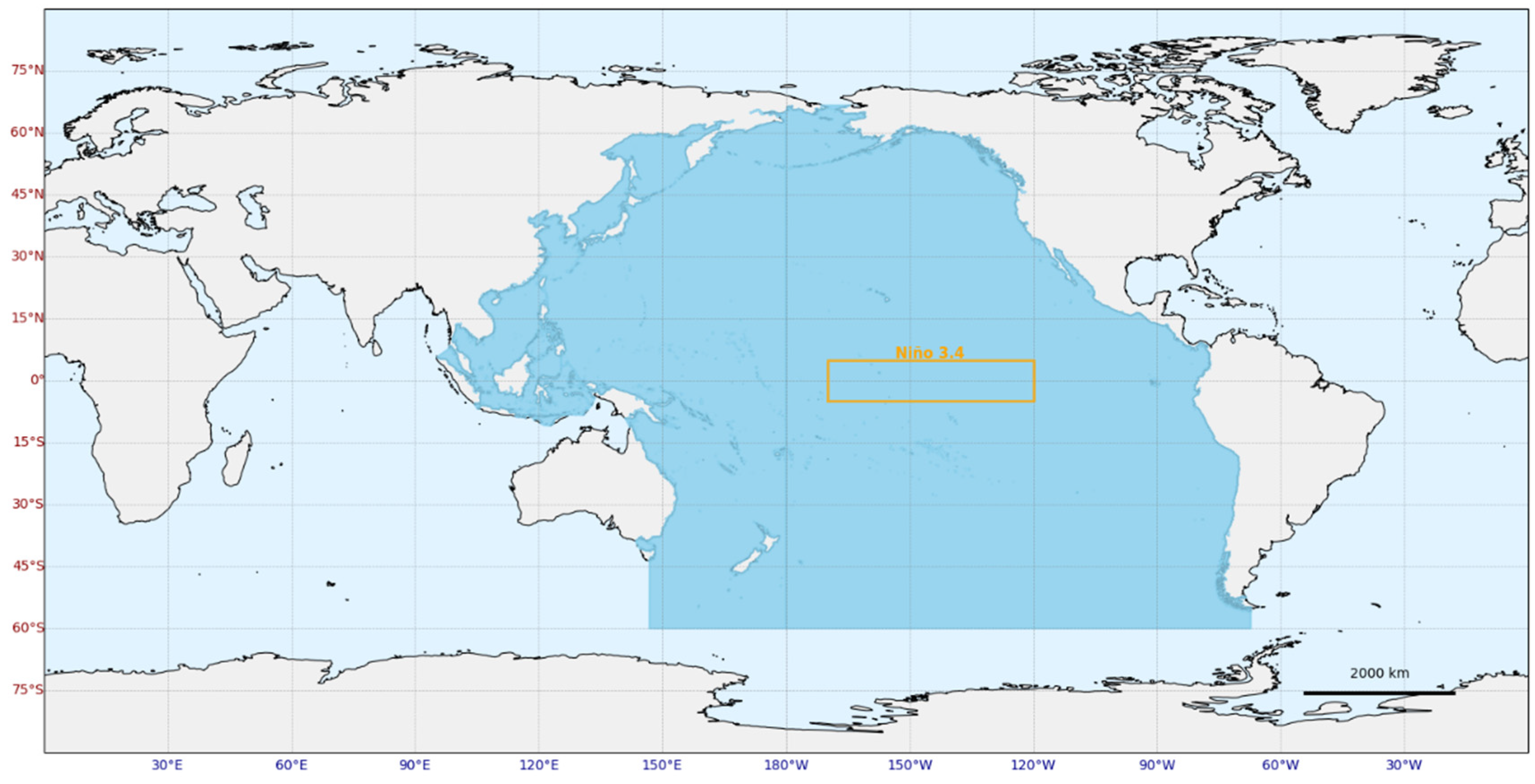
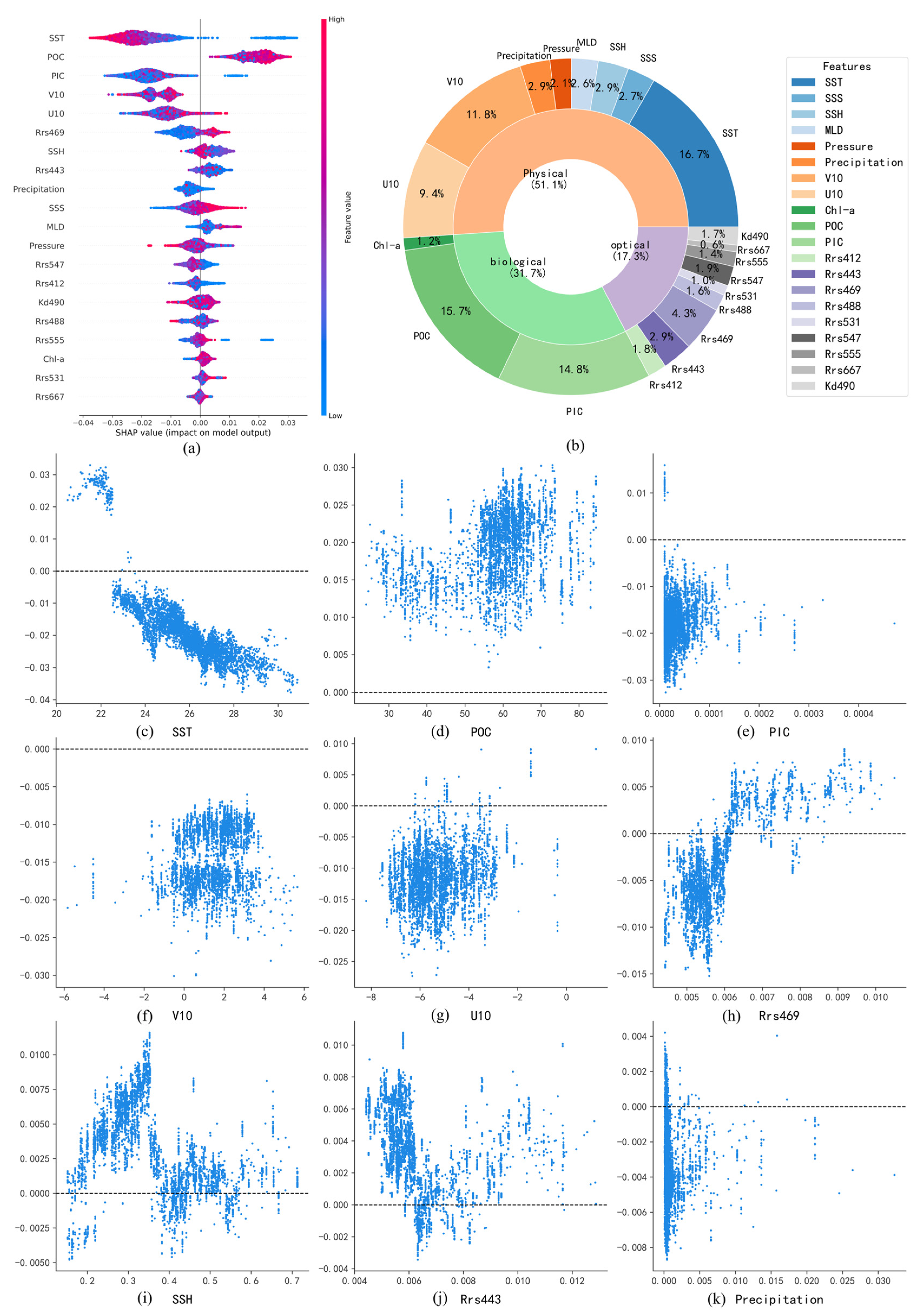
4.2. Analysis of pH Influencing Factors in the Niño 3.4 Region
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Chl-a | Chlorophyll a |
| CO2 | Carbon Dioxide |
| Carbon Dioxide Fugacity | |
| R2 | Coefficient of Determination |
| DIC | Dissolved inorganic carbon |
| DOC | Dissolved organic carbon |
| XGBoost | EXtreme Gradient Boosting |
| ExtraTrees | Extremely Randomized Trees |
| ENSO | El Niño—Southern Oscillation |
| FFNN | feedforward neural network |
| GBDT | Gradient Boosting Decision Tree |
| GODAP | Global Ocean Data Analysis Project |
| LR | Logistic Regression |
| MAE | Mean Absolute Error |
| MLD | Mixed-Layer Depth |
| OA | Ocean Acidification |
| POC | Particulate Organic Carbon |
| PIC | Particulate Inorganic Carbon |
| pCO2 | partial pressure of carbon dioxide |
| RF | Random Forest |
| SST | Sea-surface Temperature |
| SSS | Sea-surface Salinity |
| SVR | Support Vector Regression |
| SSH | Sea-surface Height |
| SHAP | SHapley Additive exPlanations |
| SOCAT | The Surface Ocean Co2 Atlas |
| TA | Total Alkalinity |
References
- Siegenthaler, U.; Sarmiento, J.L. Atmospheric carbon dioxide and the ocean. Nature 1993, 365, 119–125. [Google Scholar] [CrossRef]
- Orr, J.C.; Fabry, V.J.; Aumont, O.; Bopp, L.; Doney, S.C.; Feely, R.A.; Gnanadesikan, A.; Gruber, N.; Ishida, A.; Joos, F.; et al. Anthropogenic ocean acidification over the twenty-first century and its impact on calcifying organisms. Nature 2005, 437, 681–686. [Google Scholar] [CrossRef] [PubMed]
- Ayache, N.; Lundholm, N.; Gai, F.; Hervé, F.; Amzil, Z.; Caruana, A. Impacts of ocean acidification on growth and toxin content of the marine diatoms Pseudo-nitzschia australis and P. fraudulenta. Mar. Environ. Res. 2021, 169, 105380. [Google Scholar] [CrossRef] [PubMed]
- Sabine, C.L.; Feely, R.A.; Gruber, N.; Key, R.M.; Lee, K.; Bullister, J.L.; Wanninkhof, R.; Wong, C.S.; Wallace, D.W.R.; Tilbrook, B.; et al. The Oceanic Sink for Anthropogenic CO2. Science 2004, 305, 367–371. [Google Scholar] [CrossRef]
- Feely, R.A.; Fabry, V.J.; Guinotte, J.M. Ocean acidification of the North Pacific Ocean. PICES Press 2008, 16, 22–26. [Google Scholar]
- Takahashi, T.; Sutherland, S.C.; Chipman, D.W.; Goddard, J.G.; Ho, C.; Newberger, T.; Sweeney, C.; Munro, D.R. Climatological distributions of pH, pCO2, total CO2, alkalinity, and CaCO3 saturation in the global surface ocean, and temporal changes at selected locations. Mar. Chem. 2014, 164, 95–125. [Google Scholar] [CrossRef]
- Landschützer, P.; Gruber, N.; Haumann, F.A.; Rödenbeck, C.; Bakker, D.C.E.; Van Heuven, S.; Hoppema, M.; Metzl, N.; Sweeney, C.; Takahashi, T.; et al. The reinvigoration of the Southern Ocean carbon sink. Science 2015, 349, 1221–1224. [Google Scholar] [CrossRef]
- Wu, H.C.; Dissard, D.; Douville, E.; Blamart, D.; Bordier, L.; Tribollet, A.; Le Cornec, F.; Pons-Branchu, E.; Dapoigny, A.; Lazareth, C.E. Surface ocean pH variations since 1689 CE and recent ocean acidification in the tropical South Pacific. Nat. Commun. 2018, 9, 2543. [Google Scholar] [CrossRef]
- Caldeira, K.; Wickett, M.E. Anthropogenic carbon and ocean pH. Nature 2003, 425, 365. [Google Scholar] [CrossRef]
- Gruber, N.; Hauri, C.; Lachkar, Z.; Loher, D.; Froelicher, T.L.; Plattner, G.-K. Rapid Progression of Ocean Acidification in the California Current System. Science 2012, 337, 220–223. [Google Scholar] [CrossRef]
- Feely, R.A.; Doney, S.C.; Cooley, S.R. Ocean acidification: Present conditions and future changes in a high-CO2 world. Oceanography 2009, 22, 36–47. [Google Scholar] [CrossRef]
- Wootton, J.T.; Pfister, C.A.; Forester, J.D. Dynamic patterns and ecological impacts of declining ocean pH in a high-resolution multi-year dataset. Proc. Natl. Acad. Sci. USA 2008, 105, 18848–18853. [Google Scholar] [CrossRef]
- Li, B.; Watanabe, Y.W.; Yamaguchi, A. Spatiotemporal distribution of seawater pH in the North Pacific subpolar region by using the parameterization technique. J. Geophys. Res.-Ocean. 2016, 121, 3435–3449. [Google Scholar] [CrossRef]
- Krishna, K.V.; Shanmugam, P.; Nagamani, P.V. A multiparametric nonlinear regression approach for the estimation of global surface ocean pCO2 using satellite oceanographic data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6220–6235. [Google Scholar] [CrossRef]
- Iida, Y.; Takatani, Y.; Kojima, A.; Ishii, M. Global trends of ocean CO2 sink and ocean acidification: An observation-based reconstruction of surface ocean inorganic carbon variables. J. Oceanogr. 2021, 77, 323–358. [Google Scholar] [CrossRef]
- Jiang, Z.; Song, Z.; Bai, Y.; He, X.; Yu, S.; Zhang, S.; Gong, F. Remote Sensing of Global Sea Surface pH Based on Massive Underway Data and Machine Learning. Remote Sens. 2022, 14, 2366. [Google Scholar] [CrossRef]
- Zhong, G.; Li, X.; Song, J.; Qu, B.; Wang, F.; Wang, Y.; Zhang, B.; Cheng, L.; Ma, J.; Yuan, H.; et al. A global monthly 3D field of seawater pH over 3 decades: A machine learning approach. Earth Syst. Sci. Data 2025, 17, 719–740. [Google Scholar] [CrossRef]
- Nakano, Y.; Watanabe, Y.W. Reconstruction of pH in the Surface Seawater over the North Pacific Basin for All Seasons Using Temperature and Chlorophyll-a. J. Oceanogr. 2005, 61, 673–680. [Google Scholar] [CrossRef]
- Zeebe, R.E. History of Seawater Carbonate Chemistry, Atmospheric CO2, and Ocean Acidification. Annu. Rev. Earth Planet. Sci. 2012, 40, 141–165. [Google Scholar] [CrossRef]
- Lueker, T.J.; Dickson, A.G.; Keeling, C.D. Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: Validation based on laboratory measurements of CO2 in gas and seawater at equilibrium. Mar. Chem. 2000, 70, 105–119. [Google Scholar] [CrossRef]
- Wallace, R.B.; Baumann, H.; Grear, J.S.; Aller, R.C.; Gobler, C.J. Coastal ocean acidification: The other eutrophication problem. Estuar. Coast. Shelf Sci. 2014, 148, 1–13. [Google Scholar] [CrossRef]
- Mattsdotter Björk, M.; Fransson, A.; Torstensson, A.; Chierici, M. Ocean acidification state in western Antarctic surface waters: Controls and interannual variability. Biogeosciences 2014, 11, 57–73. [Google Scholar] [CrossRef]
- Hauri, C.; Gruber, N.; Vogt, M.; Doney, S.C.; Feely, R.A.; Lachkar, Z.; Leinweber, A.; McDonnell, A.M.P.; Munnich, M.; Plattner, G.-K. Spatiotemporal variability and long-term trends of ocean acidification in the California Current System. Biogeosciences 2013, 10, 193–216. [Google Scholar] [CrossRef]
- Lauvset, S.K.; Lange, N.; Tanhua, T.; Bittig, H.C.; Olsen, A.; Kozyr, A.; Álvarez, M.; Azetsu-Scott, K.; Brown, P.J.; Carter, B.R.; et al. The annual update GLODAPv2.2023: The global interior ocean biogeochemical data product. Earth Syst. Sci. Data 2024, 16, 2047–2072. [Google Scholar] [CrossRef]
- Lauvset, S.K.; Lange, N.; Tanhua, T.; Bittig, H.C.; Olsen, A.; Kozyr, A.; Álvarez, M.; Becker, S.; Brown, P.J.; Carter, B.R.; et al. An updated version of the global interior ocean biogeochemical data product, GLODAPv2.2021. Earth Syst. Sci. Data 2021, 13, 5565–5589. [Google Scholar] [CrossRef]
- Lewis, E.; Wallace, D. Program Developed for CO2 System Calculations; Environmental System Science Data Infrastructure for a Virtual Ecosystem 1998; Oak Ridge National Lab., Carbon Dioxide Information Analysis Center: Oak Ridge, TN, USA.
- Li, X.; Gan, B.; Zhang, Z.; Cao, Z.; Qiu, B.; Chen, Z.; Wu, L. Oceanic uptake of CO2 enhanced by mesoscale eddies. Sci. Adv. 2025, 11, eadt4195. [Google Scholar] [CrossRef]
- Bates, N.; Astor, Y.; Church, M.; Currie, K.; Dore, J.; Gonaález-Dávila, M.; Lorenzoni, L.; Muller-Karger, F.; Olafsson, J.; Santa-Casiano, M. A Time-Series View of Changing Ocean Chemistry Due to Ocean Uptake of Anthropogenic CO2 and Ocean Acidification. Oceanography 2014, 27, 126–141. [Google Scholar] [CrossRef]
- Carter, B.R.; Feely, R.A.; Williams, N.L.; Dickson, A.G.; Fong, M.B.; Takeshita, Y. Updated methods for global locally interpolated estimation of alkalinity, pH, and nitrate. Limnol. Oceanogr. Methods 2018, 16, 119–131. [Google Scholar] [CrossRef]
- Jiang, L.-Q.; Carter, B.R.; Feely, R.A.; Lauvset, S.K.; Olsen, A. Surface ocean pH and buffer capacity: Past, present and future. Sci. Rep. 2019, 9, 18624. [Google Scholar] [CrossRef]
- Chan, F.; Barth, J.A.; Blanchette, C.A.; Byrne, R.H.; Chavez, F.; Cheriton, O.; Feely, R.A.; Friederich, G.; Gaylord, B.; Gouhier, T.; et al. Persistent spatial structuring of coastal ocean acidification in the california current system. Sci. Rep. 2017, 7, 2526. [Google Scholar] [CrossRef]
- Yu, J.; Wang, X.; Murtugudde, R.; Tian, F.; Zhang, R.-H. Interannual-to-decadal variations of particulate organic carbon and the contribution of phytoplankton in the tropical pacific during 1981-2016: A model study. J. Geophys. Res. Oceans. 2021, 126, e2020JC016515. [Google Scholar] [CrossRef]
- Chakraborty, K.; Joshi, A.P.; Ghoshal, P.K.; Baduru, B.; Valsala, V.; Sarma, V.V.S.S.; Metzl, N.; Gehlen, M.; Chevallier, F.; Lo Monaco, C. Indian ocean acidification and its driving mechanisms over the last four decades (1980–2019). Glob. Biogeochem. Cycles 2024, 38, e2024GB008139. [Google Scholar] [CrossRef]



| Parameters | Data | Data Types | Time | Spatial Resolution |
|---|---|---|---|---|
| TA, pH, SSS, SST | GLODAP | In situ Data | 2003–2021 | Ship-Based Data |
| fCO2, SSS, SST | SOCAT | In situ Data | 2003–2021 | Ship-Based Data |
| Chl-a, KD, POC, PIC, Rrs | MODIS-Aqua | Satellite Data | 2003–2021 | 4 km × 4 km |
| Pressure, Precipitation, SST, u10, v10 | ERA | Reanalysis Data | 2003–2021 | 0.25°× 0.25° |
| SSS, SSH, MLD | CMEMS | Reanalysis Data | 2003–2021 | 0.83°× 0.83° |
| Model | Parameter | Tested Values |
|---|---|---|
| SVR | kernel | ‘rbf’ |
| Regularization Parameter | 0.001, 1, 1000 | |
| Kernel Coefficient | 0.001, 1, 1000 | |
| RF | n_estimators | 1000, 2000, 3000, 4000, 5000 |
| max_depth | 10, 20, 30, 40, 50, None | |
| GBDT | n_estimators | 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000 |
| max_depth | 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, None | |
| ExtraTrees | n_estimators | 1000, 2000, 3000, 4000, 5000 |
| max_depth | 10, 20, 30, 40, 50, None | |
| XGBoost | n_estimators | 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000 |
| max_depth | 5, 10, 15, 20, 25, 30, 35, 40, None |
| Model | Feature Selection | R2 | RMSE | MAE |
|---|---|---|---|---|
| LR | SST, SSS | 0.958 | 17.84 | 11.72 |
| SST, SSS, Chl-a | 0.964 | 17.61 | 11.26 | |
| SVR | SST, SSS | 0.981 | 11.92 | 5.54 |
| SST, SSS, Chl-a | 0.985 | 11.08 | 5.25 | |
| RF | SST, SSS | 0.984 | 10.98 | 5.80 |
| SST, SSS, Chl-a | 0.985 | 11.08 | 5.42 | |
| GBDT | SST, SSS | 0.985 | 10.49 | 4.92 |
| SST, SSS, Chl-a | 0.987 | 10.25 | 4.73 | |
| ExtraTrees | SST, SSS | 0.986 | 10.99 | 6.45 |
| SST, SSS, Chl-a | 0.984 | 11.02 | 6.01 | |
| XGBoost | SST, SSS | 0.986 | 10.27 | 5.36 |
| SST, SSS, Chl-a | 0.987 | 10.24 | 4.47 |
| Model | R2 | RMSE (×10−3) | MAE (×10−4) |
|---|---|---|---|
| LR | 0.289 | 4.69 | 33.22 |
| SVR | 0.231 | 4.87 | 35.22 |
| RF | 0.779 | 2.61 | 16.13 |
| GBDT | 0.830 | 2.29 | 14.34 |
| ExtraTrees | 0.711 | 2.98 | 18.79 |
| XGBoost | 0.887 | 1.86 | 10.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Qi, J.; Zhang, C.; Wang, Y.; Chen, Y.; Shao, J.; Wu, S. Spatiotemporal Analysis of Sea-Surface pH in the Pacific Ocean Based on Interpretable Machine Learning. J. Mar. Sci. Eng. 2025, 13, 1220. https://doi.org/10.3390/jmse13071220
Huang M, Qi J, Zhang C, Wang Y, Chen Y, Shao J, Wu S. Spatiotemporal Analysis of Sea-Surface pH in the Pacific Ocean Based on Interpretable Machine Learning. Journal of Marine Science and Engineering. 2025; 13(7):1220. https://doi.org/10.3390/jmse13071220
Chicago/Turabian StyleHuang, Minlong, Jin Qi, Can Zhang, Yuanyuan Wang, Yijun Chen, Jian Shao, and Sensen Wu. 2025. "Spatiotemporal Analysis of Sea-Surface pH in the Pacific Ocean Based on Interpretable Machine Learning" Journal of Marine Science and Engineering 13, no. 7: 1220. https://doi.org/10.3390/jmse13071220
APA StyleHuang, M., Qi, J., Zhang, C., Wang, Y., Chen, Y., Shao, J., & Wu, S. (2025). Spatiotemporal Analysis of Sea-Surface pH in the Pacific Ocean Based on Interpretable Machine Learning. Journal of Marine Science and Engineering, 13(7), 1220. https://doi.org/10.3390/jmse13071220





