A Novel Trajectory Repairing Model Based on the Artificial Potential Field-Enhanced A* Algorithm for Small Coastal Vessels
Abstract
1. Introduction
- Introduction of the A* algorithm for path planning, overcoming the impact of prolonged AIS data loss.
- Proposal of an improved A* algorithm integrated with an artificial potential field (APF-A*) model. Historical distribution characteristics of small coastal vessel trajectories are utilized to ensure the repaired paths align with actual navigation behavior.
- Development of a trajectory reconstruction method that considers vessel speed characteristics. Missing timestamps, planned route length, and speed ratios are incorporated to reconstruct temporal information in AIS records.
2. Literature Review
2.1. Classical Trajectory Repairing Methods
2.2. Artificial Intelligent Trajectory Repairing Methods
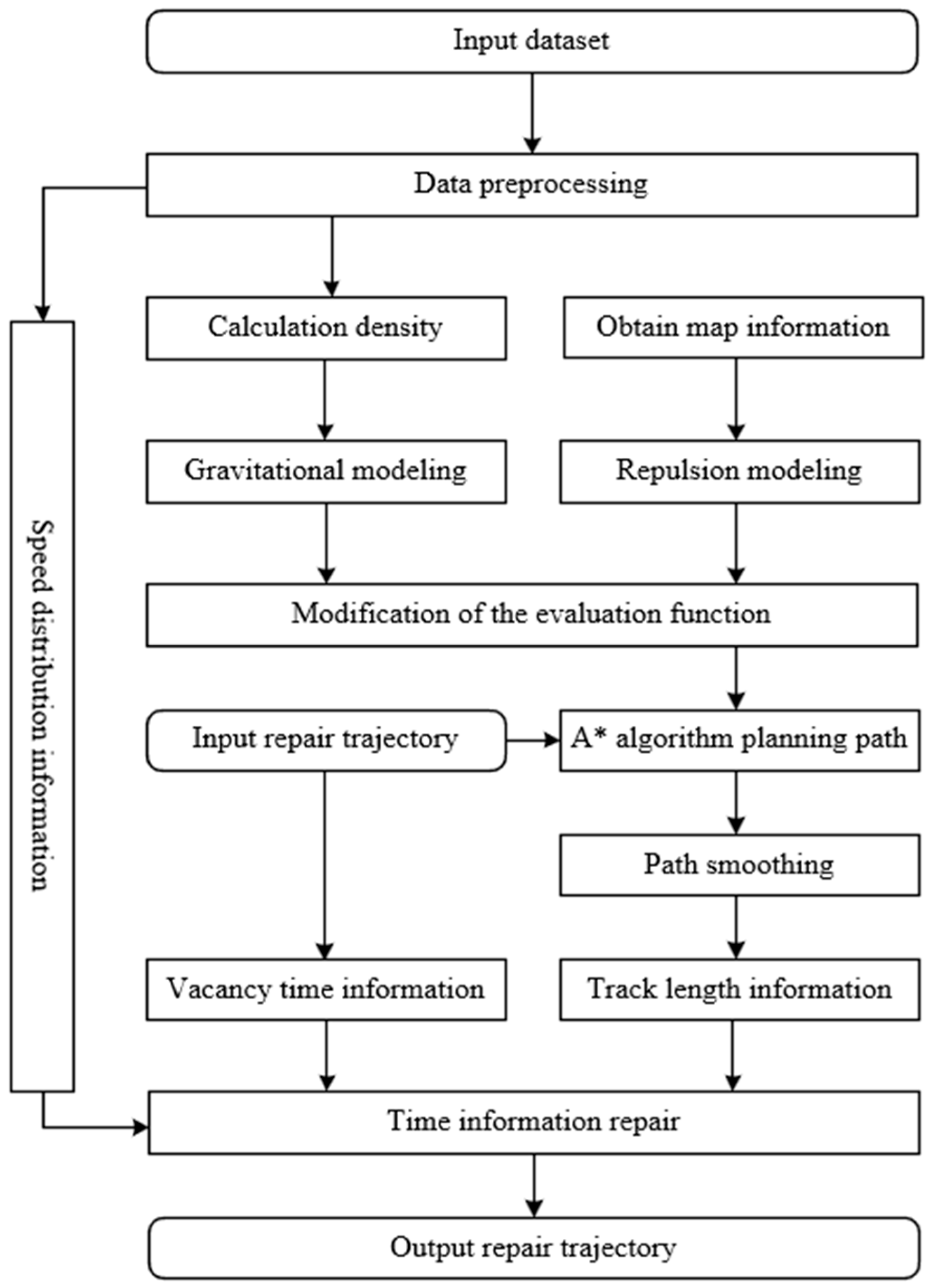
3. Methodology
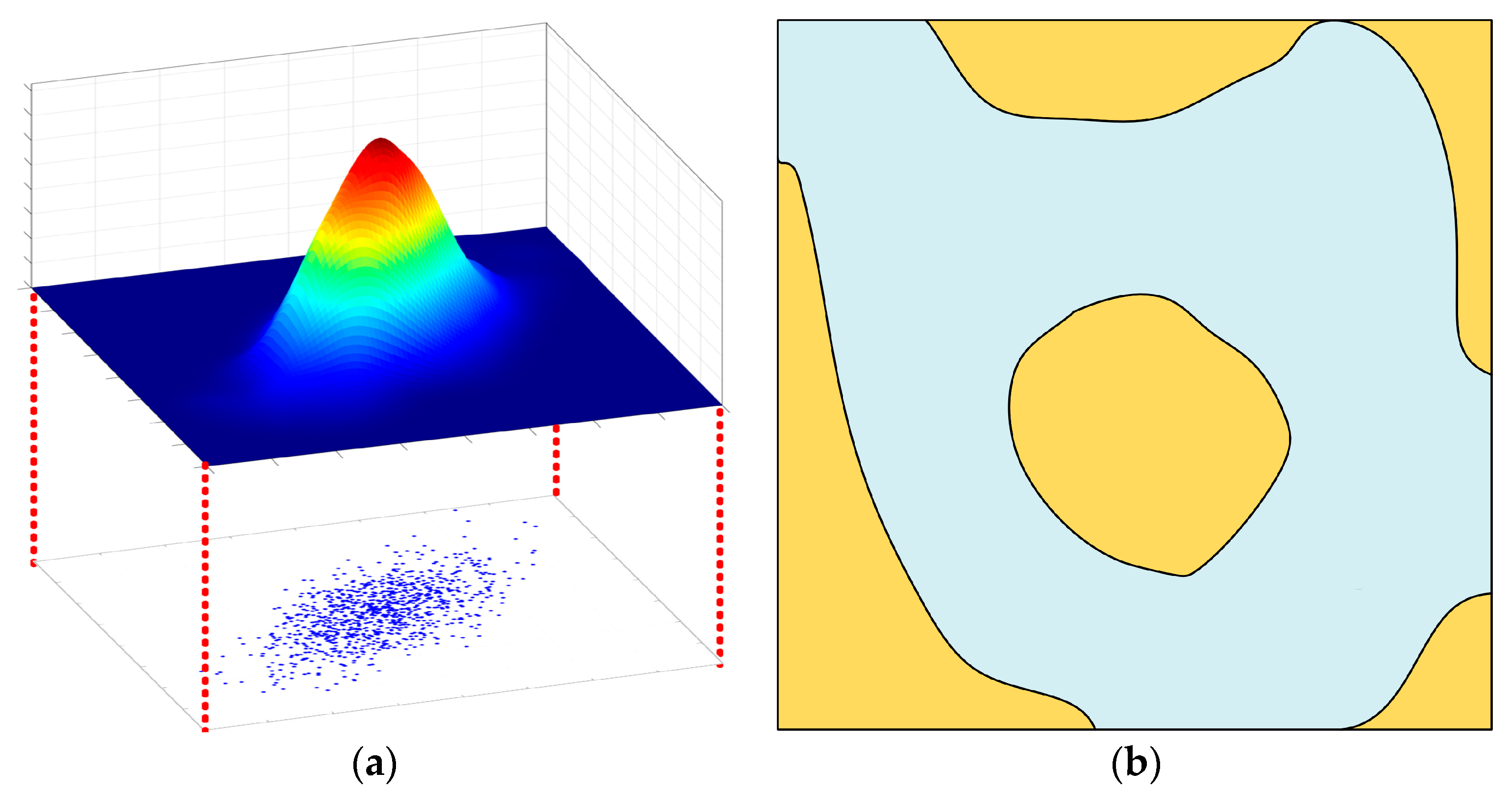
3.1. Artificial Potential Field Model
3.1.1. Gravitational Potential Field
3.1.2. Repulsive Potential Field
3.1.3. Resultant Potential Field
3.2. Introduction of A* Algorithm
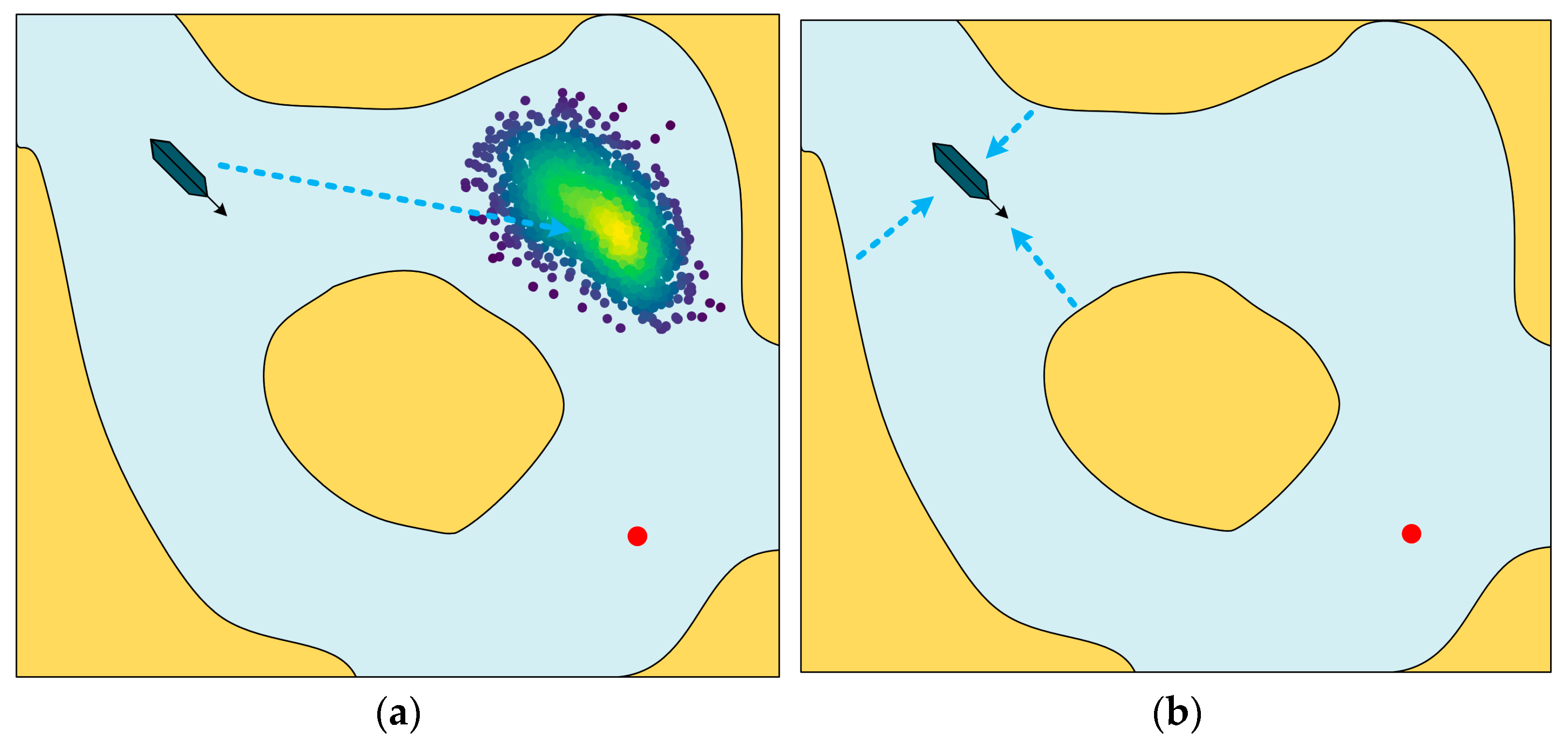
3.3. A* Algorithm Integrated with Artificial Potential Field Model (APF-A*)
3.3.1. Data Preprocessing and Potential Field Construction
3.3.2. Potential Field Function Reconstruction
3.3.3. Reconstruction of A* Algorithmic Evaluation Function
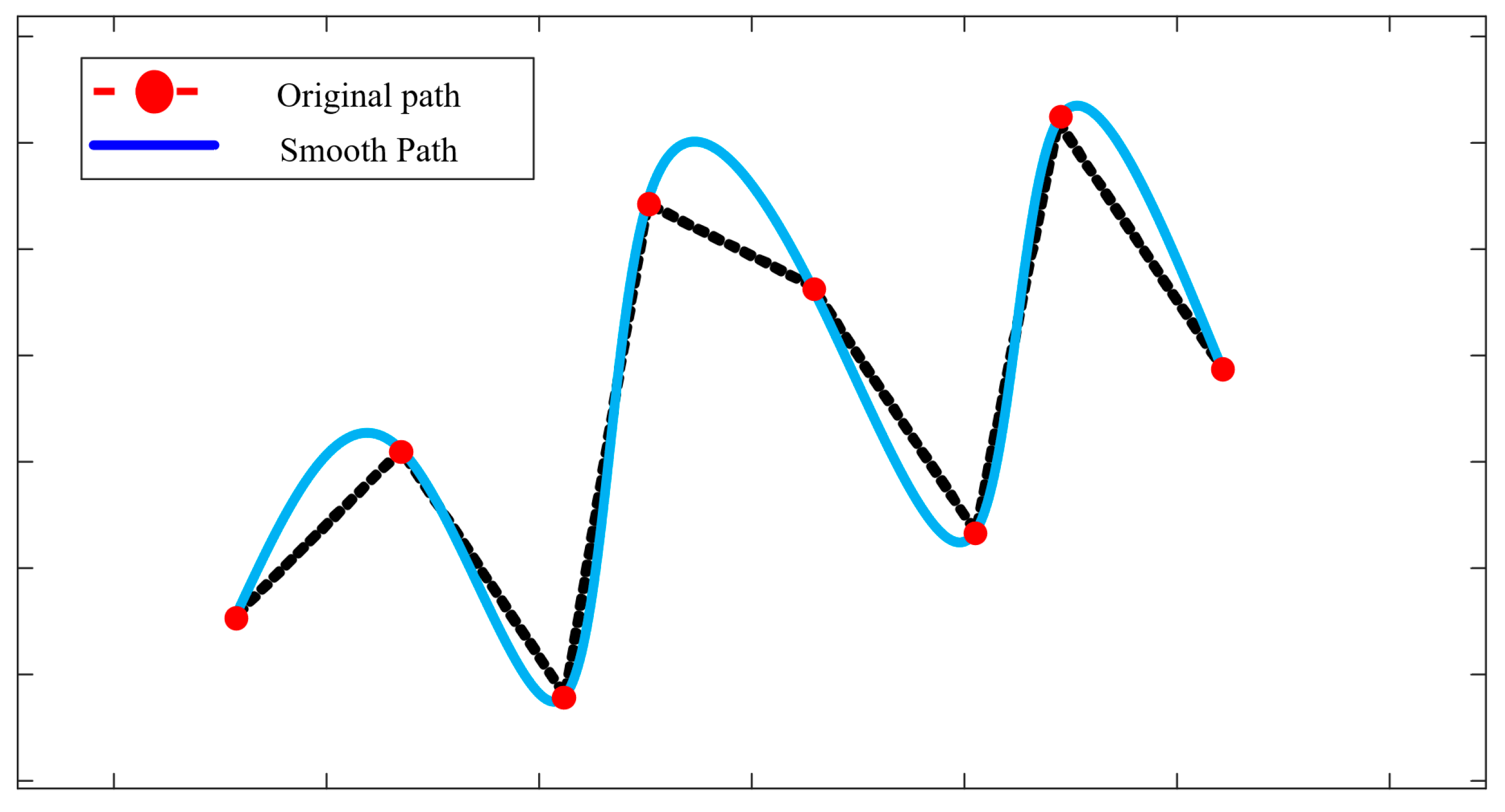
3.3.4. Path Smoothing
3.3.5. Temporal Information Repairing
4. Experimental Results
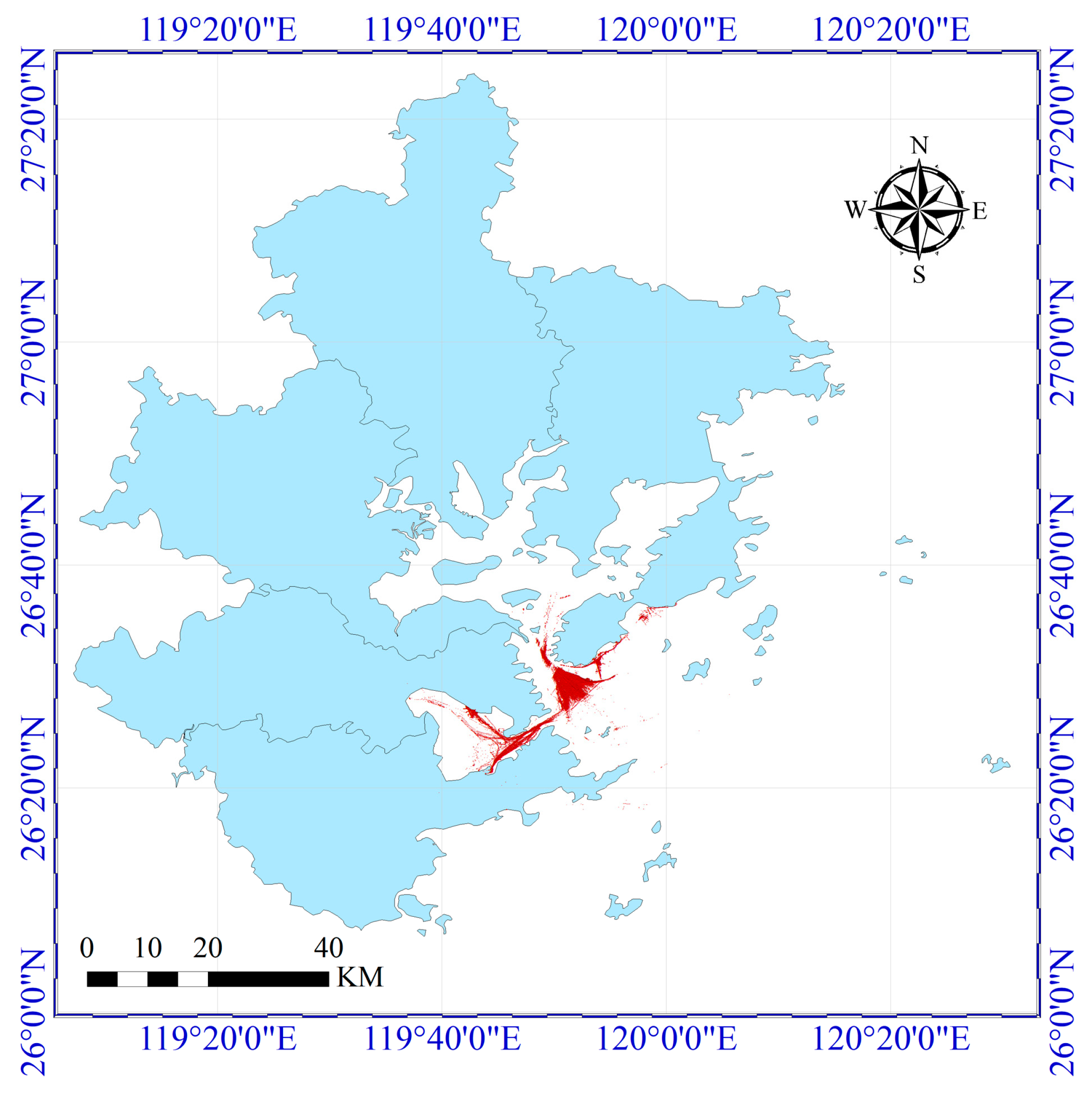
4.1. Description of the Study Area
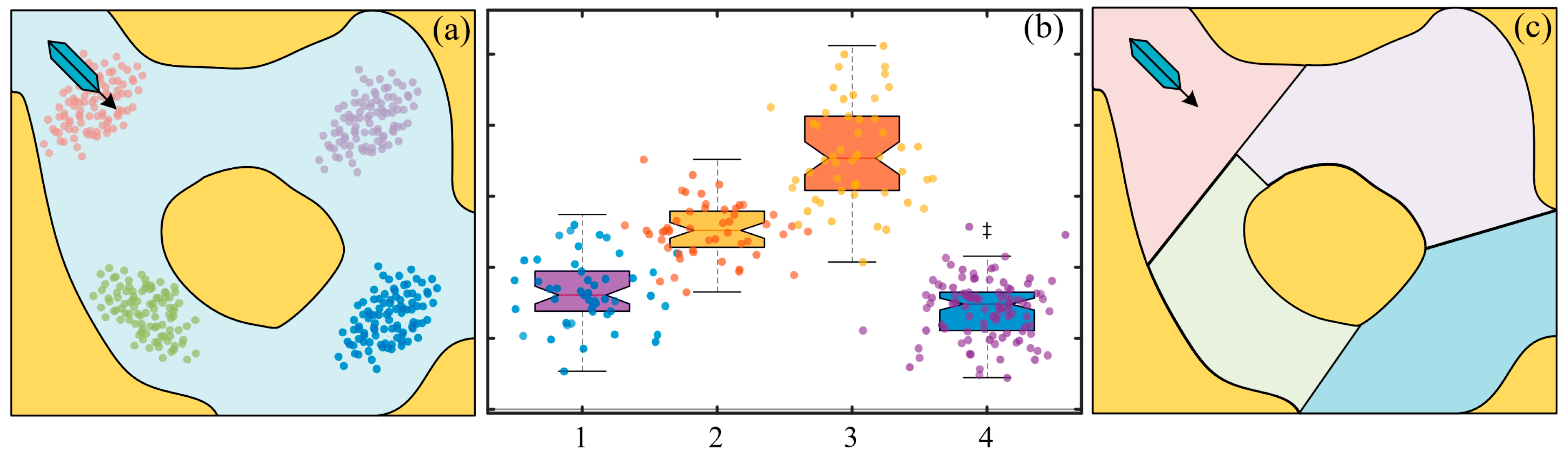
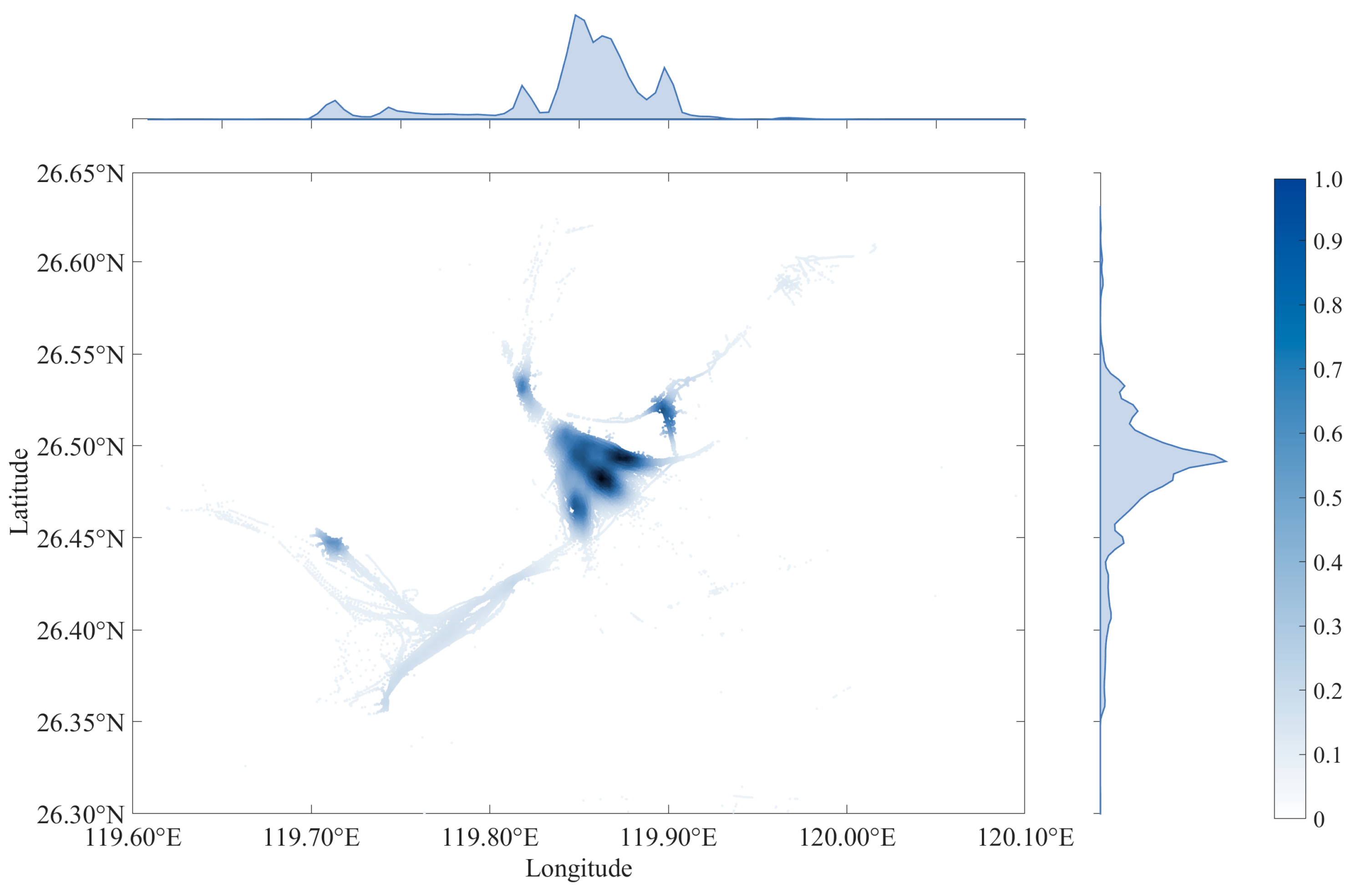
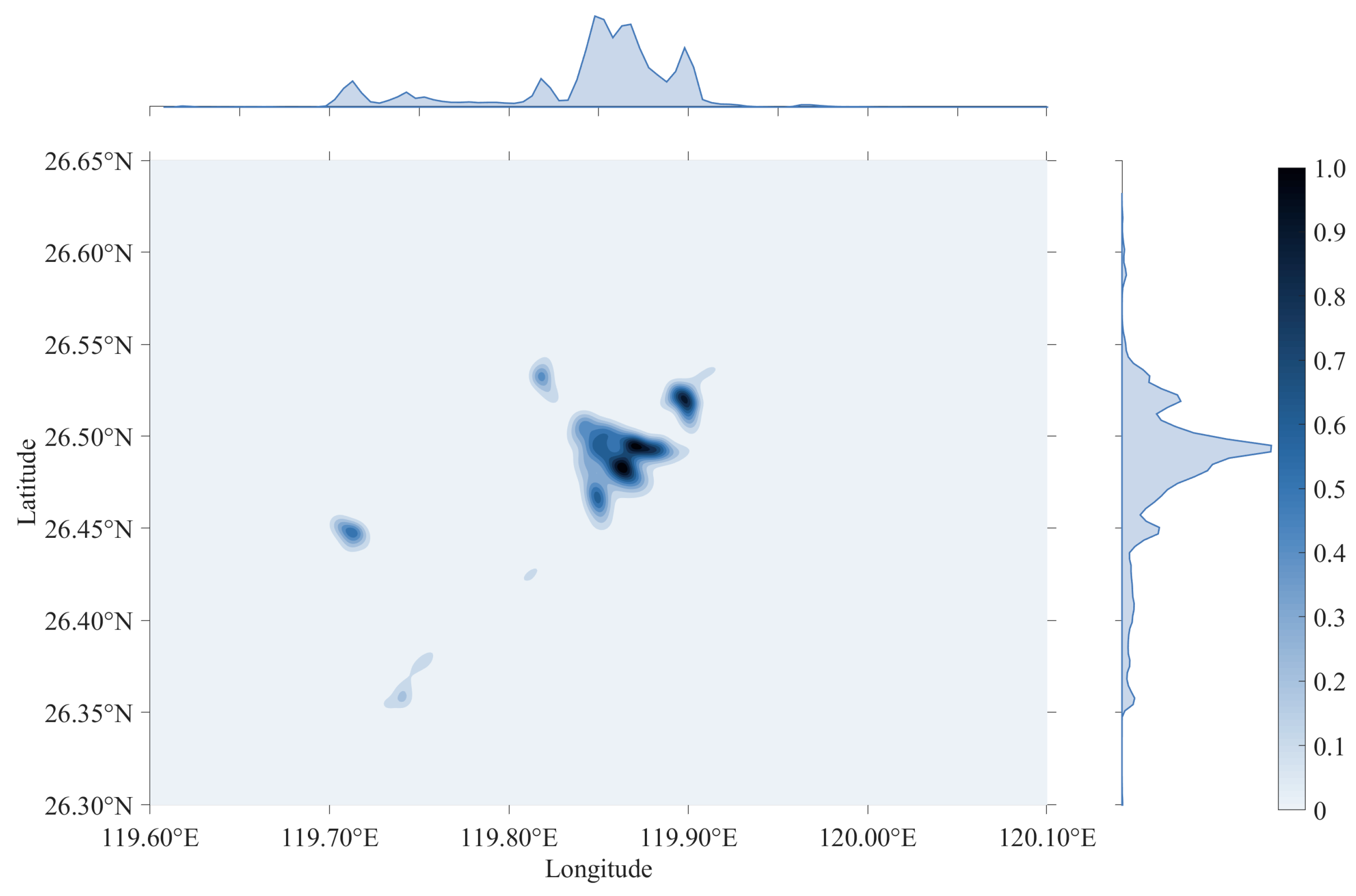
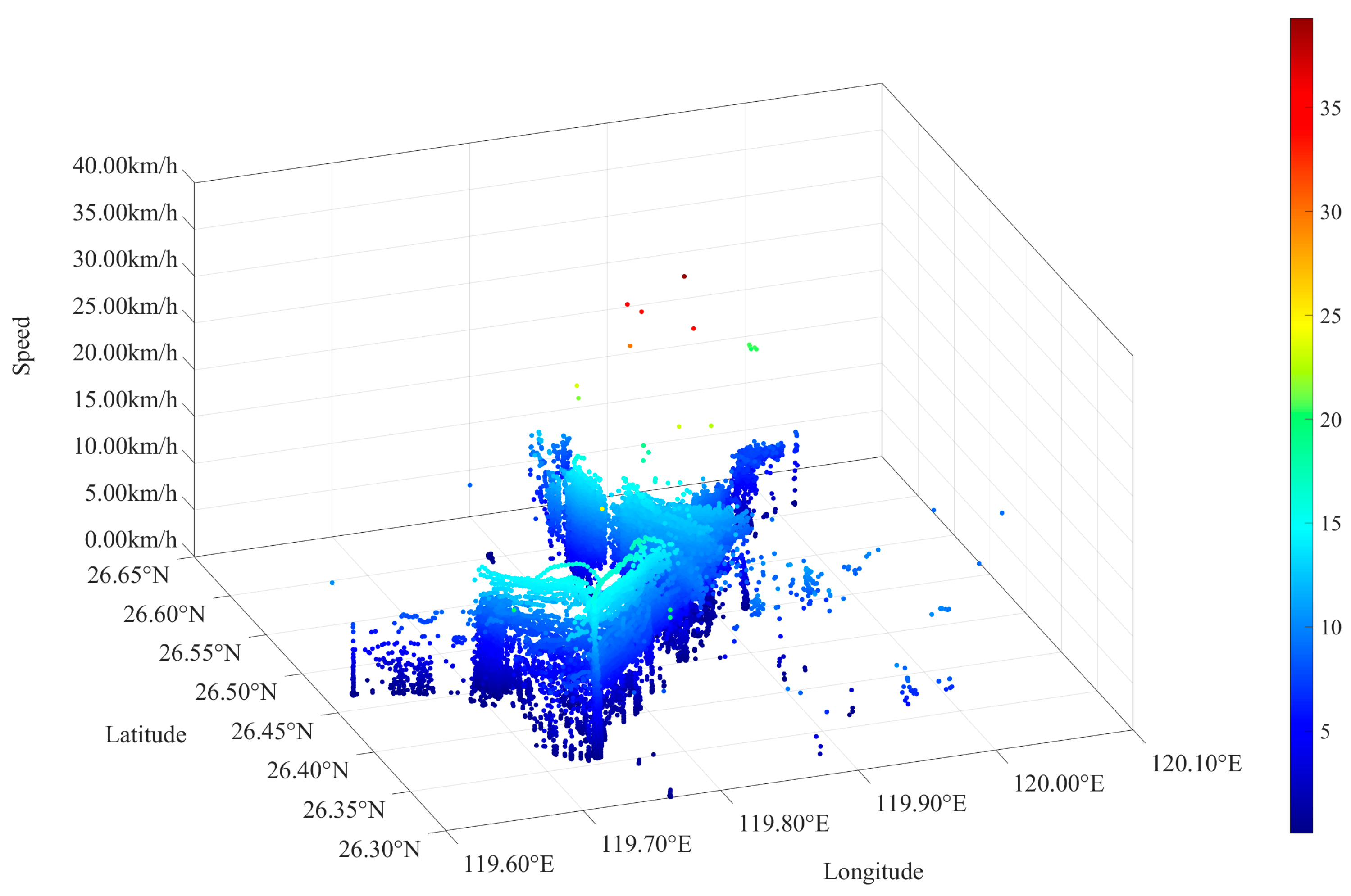
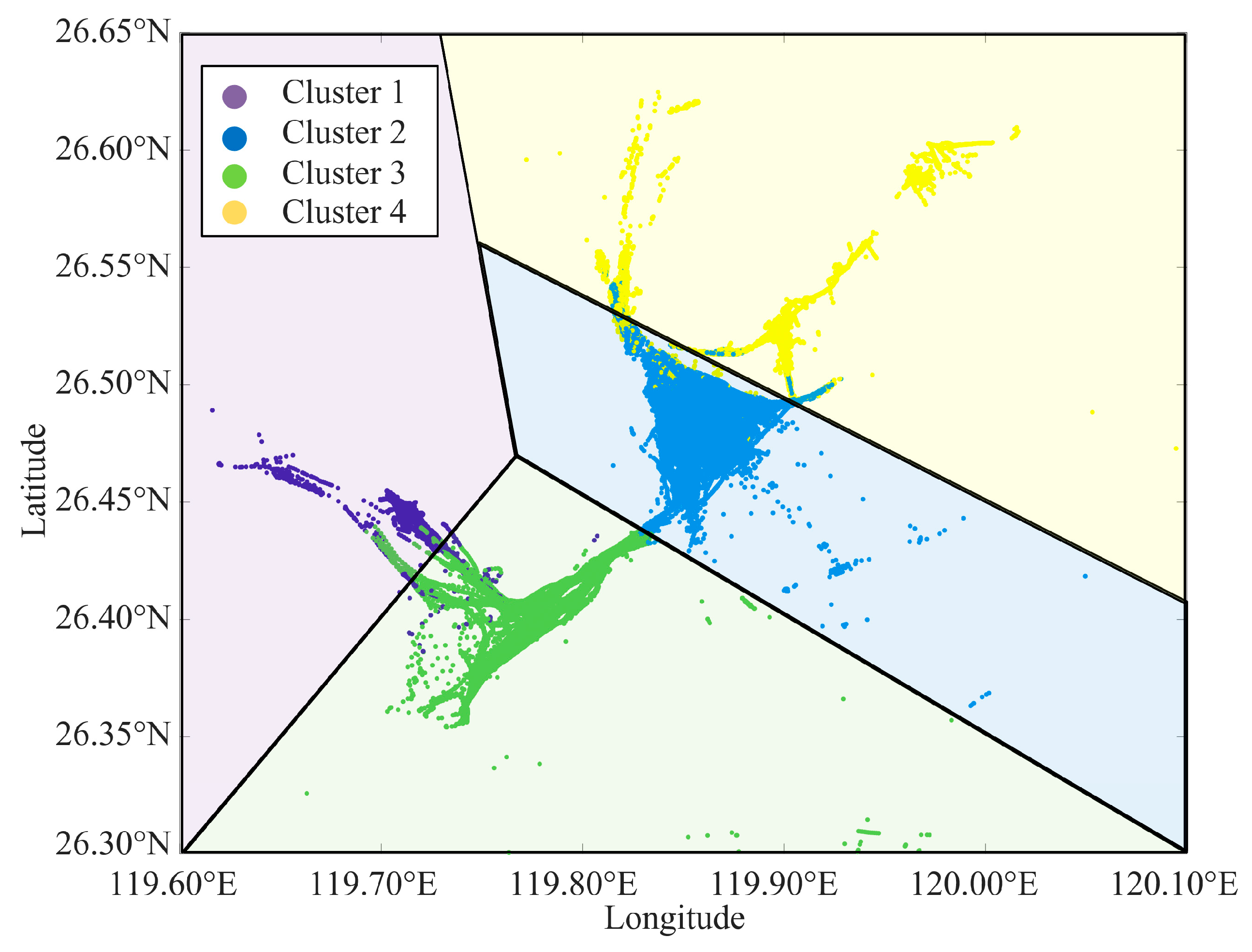
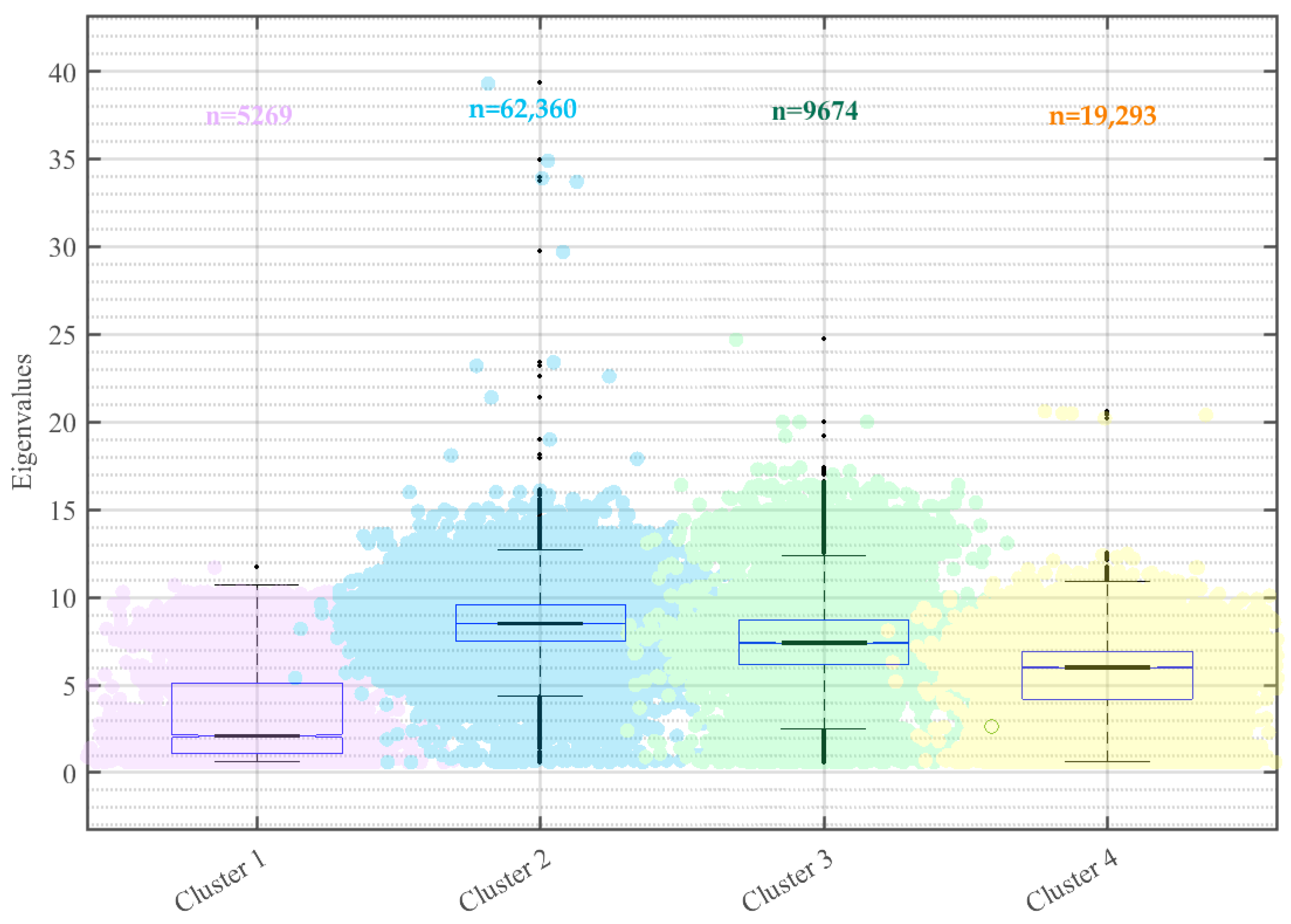
4.2. Density Calculation for Small Coastal Vessels
4.3. Feature Extraction of Vessel Speed
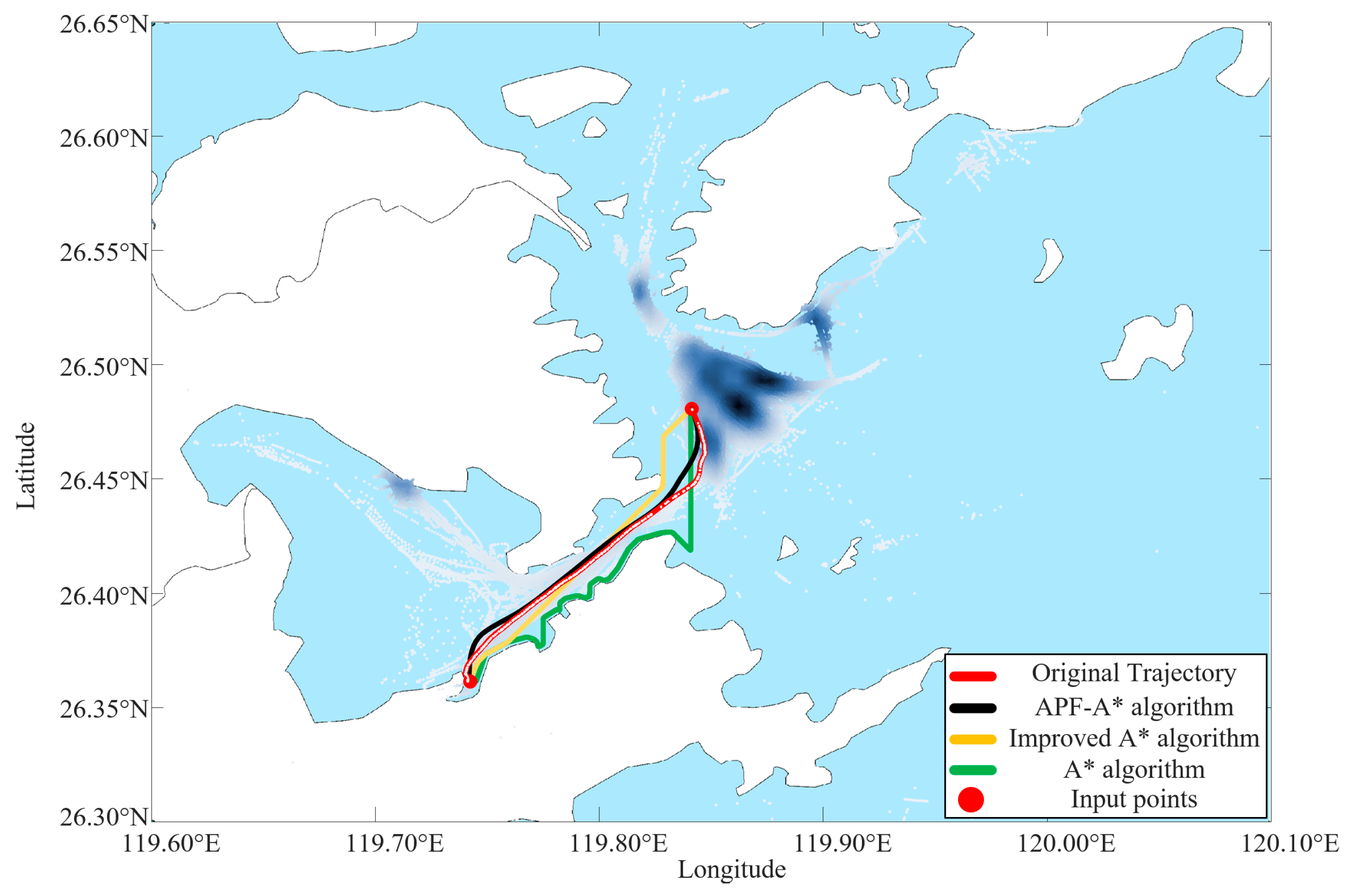
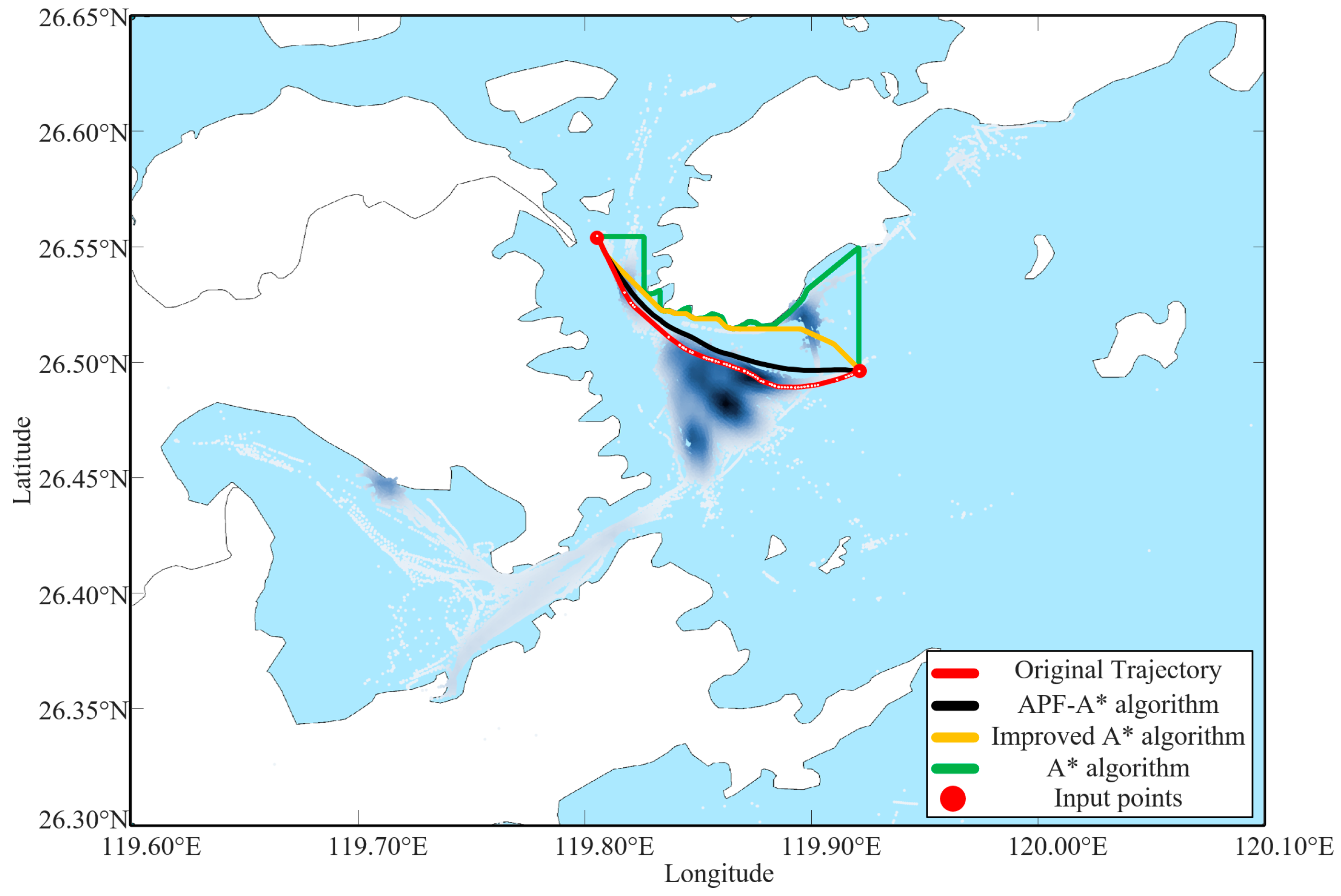
4.4. Comparative Study of Trajectory Repairing
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shipton, M.; Obradović, J.; Mišković, N.; Diamant, R. Underwater Radiated Noise Characteristics of Small Vessels—An Analysis of the HearMyShip Database. Mar. Pollut. Bull. 2025, 216, 117903. [Google Scholar] [CrossRef] [PubMed]
- Smith, T.A.; Grech La Rosa, A.; Wood, B. Underwater Radiated Noise from Small Craft in Shallow Water: Effects of Speed and Running Attitude. Ocean Eng. 2024, 306, 118040. [Google Scholar] [CrossRef]
- Alves, C.L.; Garcia, O.D.; Kramer, R.A. Fisher Perceptions of Belize’s Managed Access Program Reveal Overall Support but Need for Improved Enforcement. Mar. Policy 2022, 143, 105192. [Google Scholar] [CrossRef]
- Zhang, H.; Li, K. Assessment of Fishing Vessel Vulnerability to Pure Loss of Stability Using a Self-Developed Program. J. Mar. Sci. Eng. 2024, 12, 527. [Google Scholar] [CrossRef]
- Xiao, G.; Yang, D.; Xu, L.; Li, J.; Jiang, Z. The Application of Artificial Intelligence Technology in Shipping: A Bibliometric Review. J. Mar. Sci. Eng. 2024, 12, 624. [Google Scholar] [CrossRef]
- Ahn, S.; Pomeroy, R. Evaluating the Economic Impact of Distant Water Fleet Activities on Small-Scale Fishers in the South China Sea. Mar. Policy 2024, 168, 106324. [Google Scholar] [CrossRef]
- Zhang, L.; Zhu, Y.; Valdez Banda, O.A.; Du, L.; Gan, L.; Li, X. Navigational Risk Assessment of Inland Waters Based on Bi-Directional PSO-LSTM Algorithm and Ship Maneuvering Characteristics. Ocean Eng. 2024, 310, 118628. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, X.; Liu, S.; Zheng, Z.; Zhang, T.; Liao, Z.; Xia, X.; Li, Y. Multi-Level Localization Trajectory Alignment and Repairing in Complex Environment. Int. J. Appl. Earth Obs. Geoinf. 2024, 131, 103945. [Google Scholar] [CrossRef]
- Zaman, B.; Marijan, D.; Kholodna, T. Interpolation-Based Inference of Vessel Trajectory Waypoints from Sparse AIS Data in Maritime. J. Mar. Sci. Eng. 2023, 11, 615. [Google Scholar] [CrossRef]
- Du, H.; Xiao, Y.; Duan, L.; Gao, S. An Algorithm for Vessel’s Missing Trajectory Restoration Based on Polynomial Interpolation. In Proceedings of the 2017 4th International Conference on Transportation Information and Safety (ICTIS), Banff, AB, Canada, 8–10 August 2017; IEEE: New York, NY, USA, 2017; pp. 825–830. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, S.; Guo, M.; Liu, Y. A Novel Ship Trajectory Clustering Analysis and Anomaly Detection Method Based on AIS Data. Ocean Eng. 2023, 288, 116082. [Google Scholar] [CrossRef]
- Guo, S.; Mou, J.; Chen, L.; Chen, P. Improved Kinematic Interpolation for AIS Trajectory Reconstruction. Ocean Eng. 2021, 234, 109256. [Google Scholar] [CrossRef]
- Ye, L.; Chen, X.; Liu, H.; Zhang, R.; Li, J.; Lu, C.; Zhao, Y. A Study of Multi-Step Sparse Vessel Trajectory Restoration Based on Feature Correlation. Appl. Sci. 2024, 14, 4057. [Google Scholar] [CrossRef]
- Kim, T.; Park, T.-H. Extended Kalman Filter (EKF) Design for Vehicle Position Tracking Using Reliability Function of Radar and Lidar. Sensors 2020, 20, 4126. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Zhang, A.; Zhang, C.; Li, J.; Zhao, Q.; Rao, W. ATR: Automatic Trajectory Repairing With Movement Tendencies. IEEE Access 2020, 8, 4122–4132. [Google Scholar] [CrossRef]
- Luo, Q.; Xu, Z.; Zhang, Y.; Igene, M.; Bataineh, T.; Soltanirad, M.; Jimee, K.; Liu, H. Vehicle Trajectory Repair Under Full Occlusion and Limited Datapoints with Roadside LiDAR. Sensors 2025, 25, 1114. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Zhang, J.; He, Y.; Yan, K.; Yan, B. A Novel MP-LSTM Method for Ship Trajectory Prediction Based on AIS Data. Ocean Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Xue, H. Fractional-Order Gradient Descent with Momentum for RBF Neural Network-Based AIS Trajectory Restoration. Soft Comput. 2021, 25, 869–882. [Google Scholar] [CrossRef]
- Zhang, W.; Jiang, W.; Liu, Q.; Wang, W. AIS Data Repair Model Based on Generative Adversarial Network. Reliab. Eng. Syst. Saf. 2023, 240, 109572. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, D.; Tan, Y.; Duan, M.; Luo, L.; Wang, W.; Chen, X. LFPR: A Lazy Fast Predictive Repair Strategy for Mobile Distributed Erasure Coded Cluster. IEEE Internet Things J. 2023, 10, 704–719. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, W.; Guo, Z.; Peng, Y.; Tian, Q.; Xu, X. Navigation Mode Extraction and Trajectory Repair of Complex Waters in Multi-Harbor Port: An Optimal Semi-Supervised Clustering Method. Ocean Eng. 2024, 313, 119439. [Google Scholar] [CrossRef]
- Liang, M.; Su, J.; Liu, R.W.; Lam, J.S.L. AISClean: AIS Data-Driven Vessel Trajectory Reconstruction under Uncertain Conditions. Ocean Eng. 2024, 306, 117987. [Google Scholar] [CrossRef]
- Suo, Y.; Chen, X.; Yue, J.; Yang, S.; Claramunt, C. An Improved Artificial Potential Field Method for Ship Path Planning Based on Artificial Potential Field—Mined Customary Navigation Routes. J. Mar. Sci. Eng. 2024, 12, 731. [Google Scholar] [CrossRef]
- He, Z.; Liu, C.; Chu, X.; Negenborn, R.R.; Wu, Q. Dynamic Anti-Collision A-Star Algorithm for Multi-Ship Encounter Situations. Appl. Ocean Res. 2022, 118, 102995. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, S.; Zhao, S. Ship Trajectory Planning and Optimization via Ensemble Hybrid A* and Multi-Target Point Artificial Potential Field Model. J. Mar. Sci. Eng. 2024, 12, 1372. [Google Scholar] [CrossRef]
- Ni, Q.; Xie, C. Stretch-Energy-Minimizing B-Spline Interpolation Curves and Their Applications. Mathematics 2023, 11, 4534. [Google Scholar] [CrossRef]
- Ran, X.; Suyaroj, N.; Tepsan, W.; Ma, J.; Zhou, X.; Deng, W. A Hybrid Genetic-Fuzzy Ant Colony Optimization Algorithm for Automatic K-Means Clustering in Urban Global Positioning System. Eng. Appl. Artif. Intell. 2024, 137, 109237. [Google Scholar] [CrossRef]
- Chatzisavvas, A.; Dossis, M.; Dasygenis, M. Optimizing Mobile Robot Navigation Based on A-Star Algorithm for Obstacle Avoidance in Smart Agriculture. Electronics 2024, 13, 2057. [Google Scholar] [CrossRef]
- Kaklis, D.; Kontopoulos, I.; Varlamis, I.; Emiris, I.Z.; Varelas, T. Trajectory Mining and Routing: A Cross-Sectoral Approach. J. Mar. Sci. Eng. 2024, 12, 157. [Google Scholar] [CrossRef]
- Chang, S.-C.; Jeng, J.-T. Interval Generalized Improved Fuzzy Partitions Fuzzy C-Means Under Hausdorff Distance Clustering Algorithm. Int. J. Fuzzy Syst. 2025, 27, 834–852. [Google Scholar] [CrossRef]
- Herrmann, M.; Webb, G.I. Amercing: An Intuitive and Effective Constraint for Dynamic Time Warping. Pattern Recognit. 2023, 137, 109333. [Google Scholar] [CrossRef]
| Vessel Type | AIS Digital Coding |
|---|---|
| Fishing Boat | 3 |
| Self-use vessels | 0, 1 |
| Ferry | 2 |
| Agricultural transport ships | 1, 19 |
| Tourist sightseeing boats | 7, 14 |
| Law enforcement vessel | 10 |
| Engineering vessels | 17, 20 |
| Experiments | Algorithms | HD | DTW | DL |
|---|---|---|---|---|
| Case 1 | APF-A* | 0.0033 | 2.5468 | 0.1035 |
| Improve A* | 0.0180 | 12.3136 | 0.1192 | |
| A* | 0.0229 | 35.7881 | 0.2230 | |
| Case 2 | APF-A* | 0.0352 | 10.9357 | 0.1154 |
| Improve A* | 0.0947 | 129.5199 | 0.1098 | |
| A* | 0.1873 | 320.3494 | 0.1930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, C.; Jiang, Z.; Zhang, X.; He, W.; Zhong, C. A Novel Trajectory Repairing Model Based on the Artificial Potential Field-Enhanced A* Algorithm for Small Coastal Vessels. J. Mar. Sci. Eng. 2025, 13, 1200. https://doi.org/10.3390/jmse13071200
Yu C, Jiang Z, Zhang X, He W, Zhong C. A Novel Trajectory Repairing Model Based on the Artificial Potential Field-Enhanced A* Algorithm for Small Coastal Vessels. Journal of Marine Science and Engineering. 2025; 13(7):1200. https://doi.org/10.3390/jmse13071200
Chicago/Turabian StyleYu, Chengqiang, Zhonglian Jiang, Xinliang Zhang, Wei He, and Cheng Zhong. 2025. "A Novel Trajectory Repairing Model Based on the Artificial Potential Field-Enhanced A* Algorithm for Small Coastal Vessels" Journal of Marine Science and Engineering 13, no. 7: 1200. https://doi.org/10.3390/jmse13071200
APA StyleYu, C., Jiang, Z., Zhang, X., He, W., & Zhong, C. (2025). A Novel Trajectory Repairing Model Based on the Artificial Potential Field-Enhanced A* Algorithm for Small Coastal Vessels. Journal of Marine Science and Engineering, 13(7), 1200. https://doi.org/10.3390/jmse13071200







