The Novel Gravity-Matching Algorithm Based on Modified Adaptive Transformed Cubature Quaternion Estimation for Underwater Navigation
Abstract
1. Introduction
2. Problem Statement of Gravity-Matching Navigation System
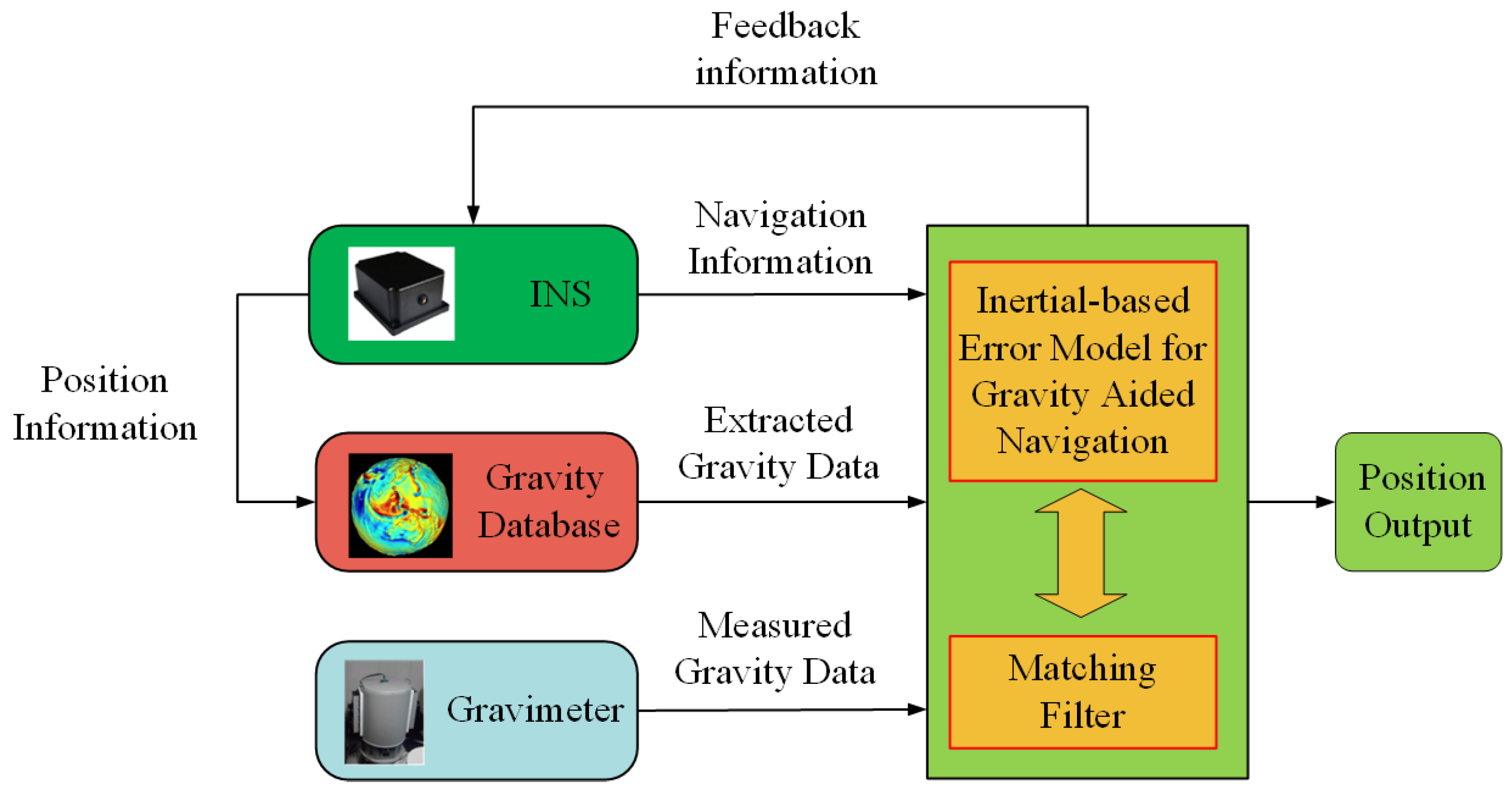
2.1. Gravity-Aided Navigation System
2.2. System Model for Gravity Aided Navigation System
3. Modified Adaptive Gravity-Matching Algorithms for Underwater Navigation
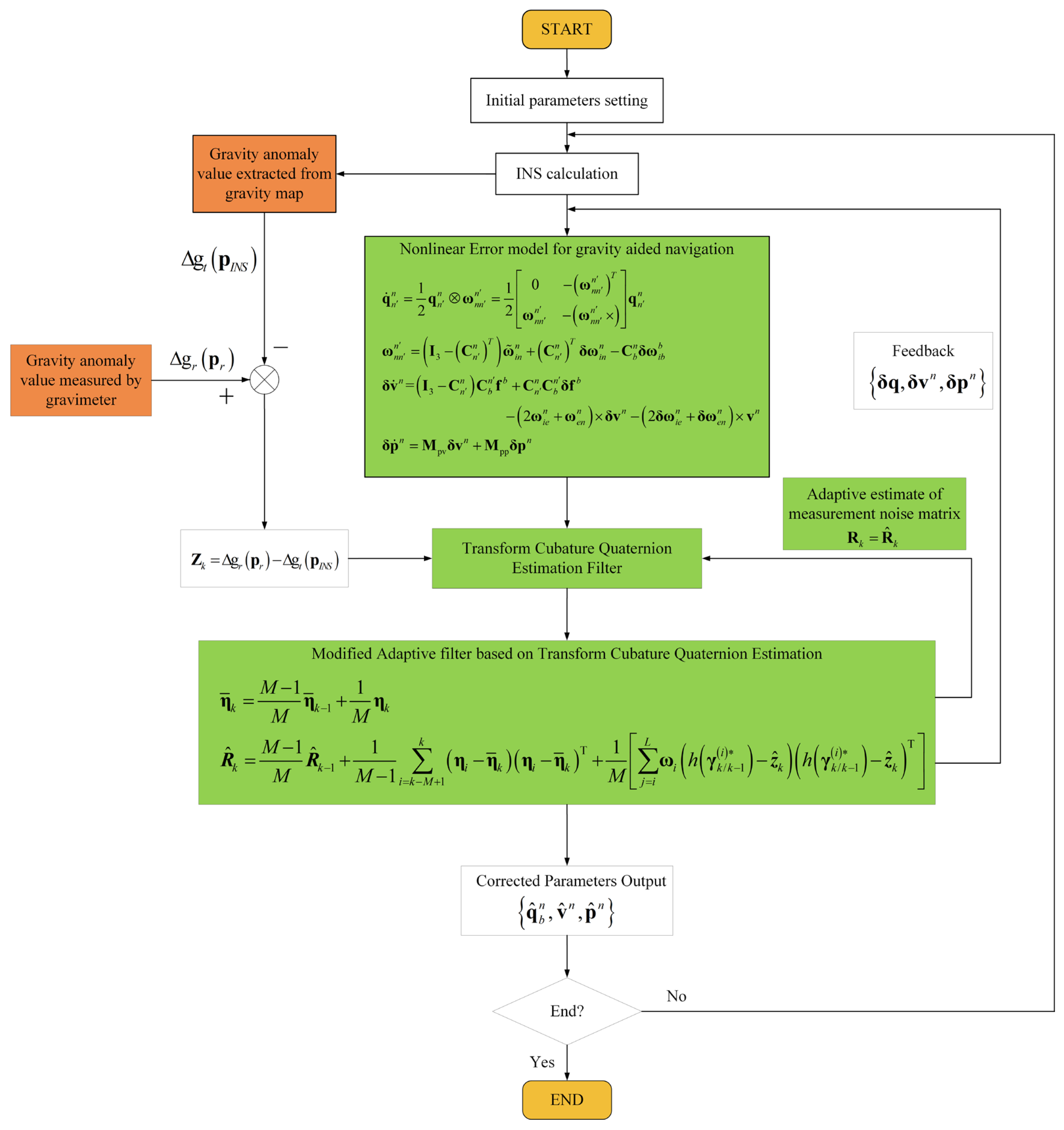
3.1. The Quaternion Based Error Model for Gravity-Aided Navigation
- Initialization:
- Time Propagation:
- Measurement Update:
3.2. The Modified Adaptive Transform Cubature Quaternion Estimation for Gravity-Aided Navigation
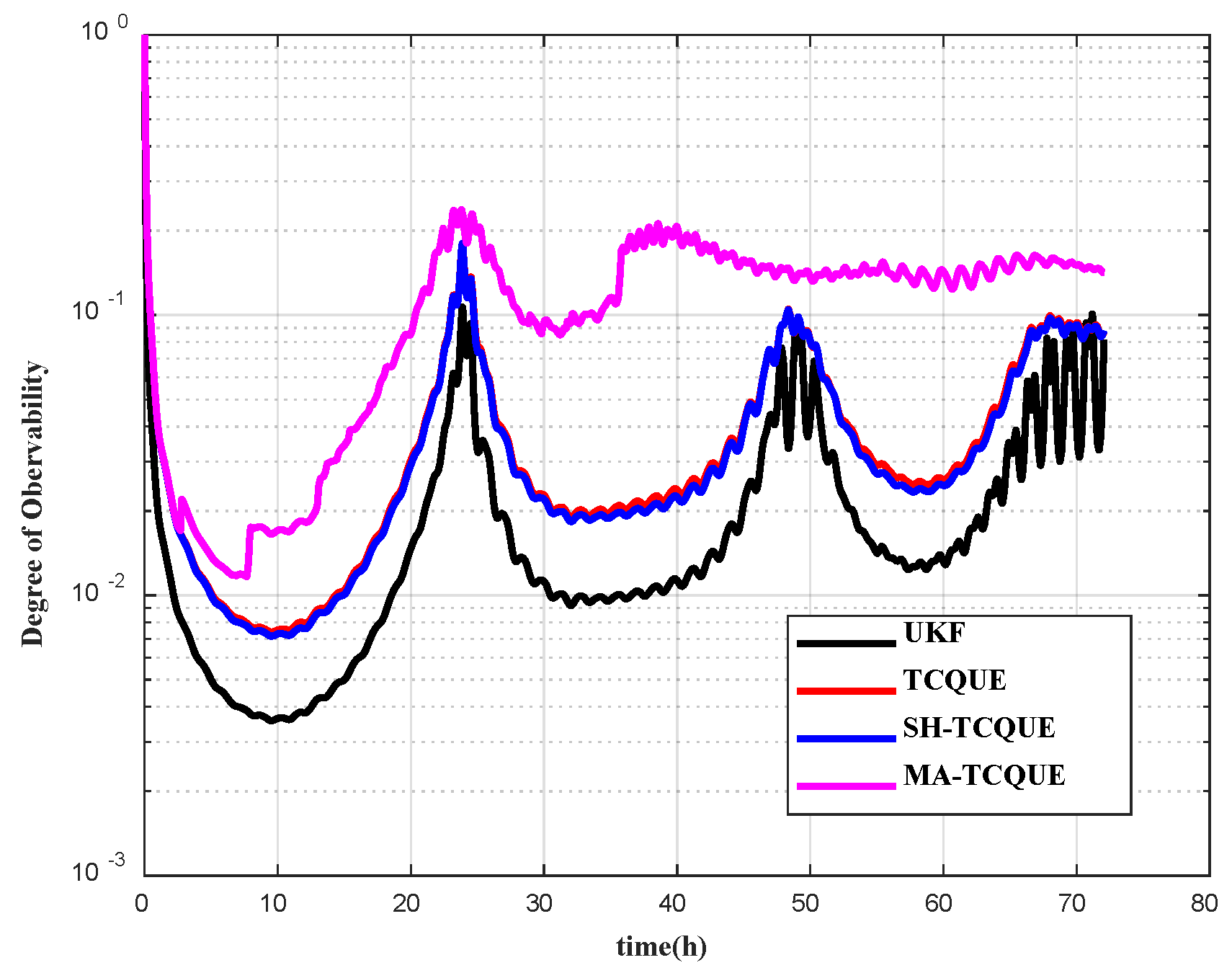
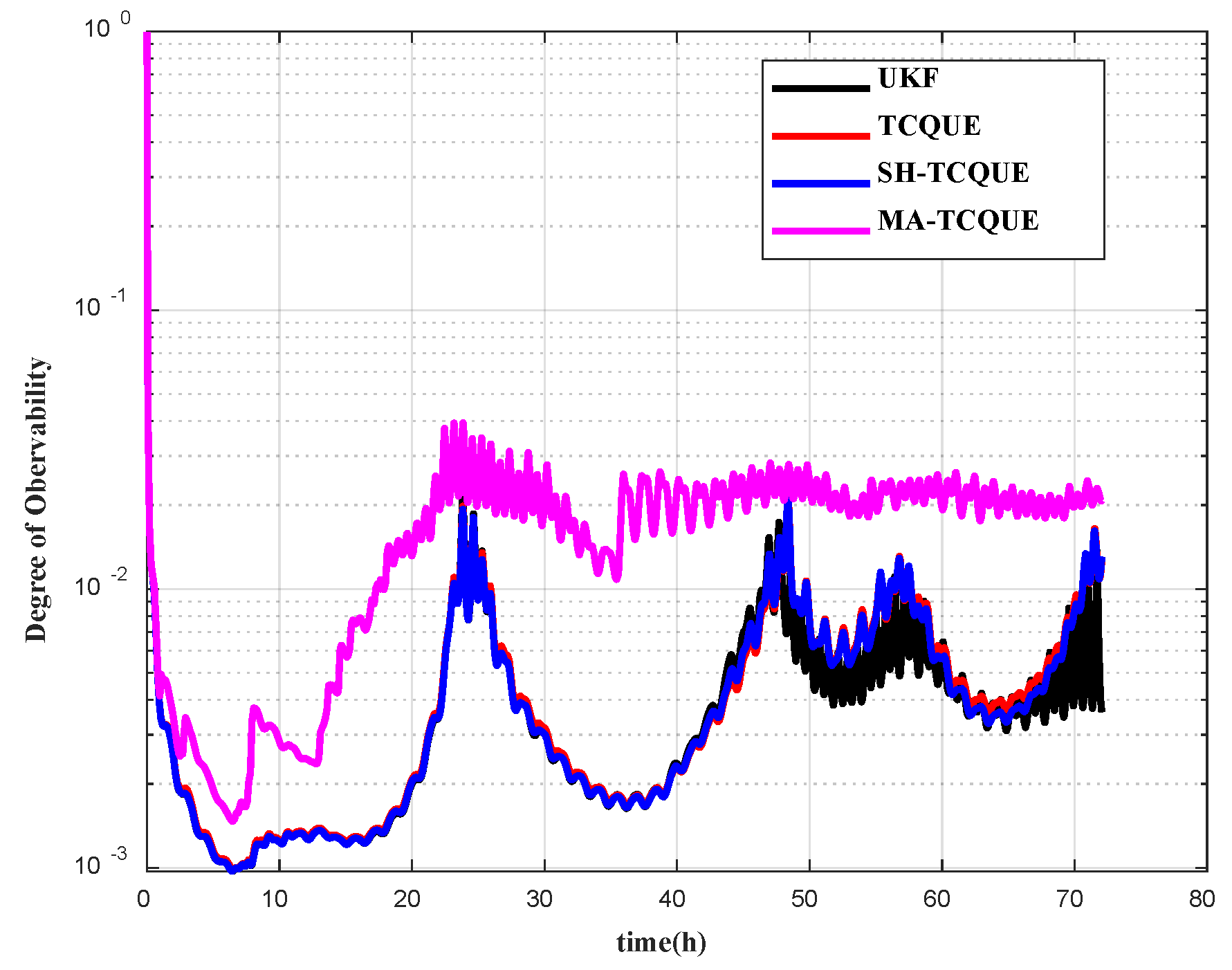
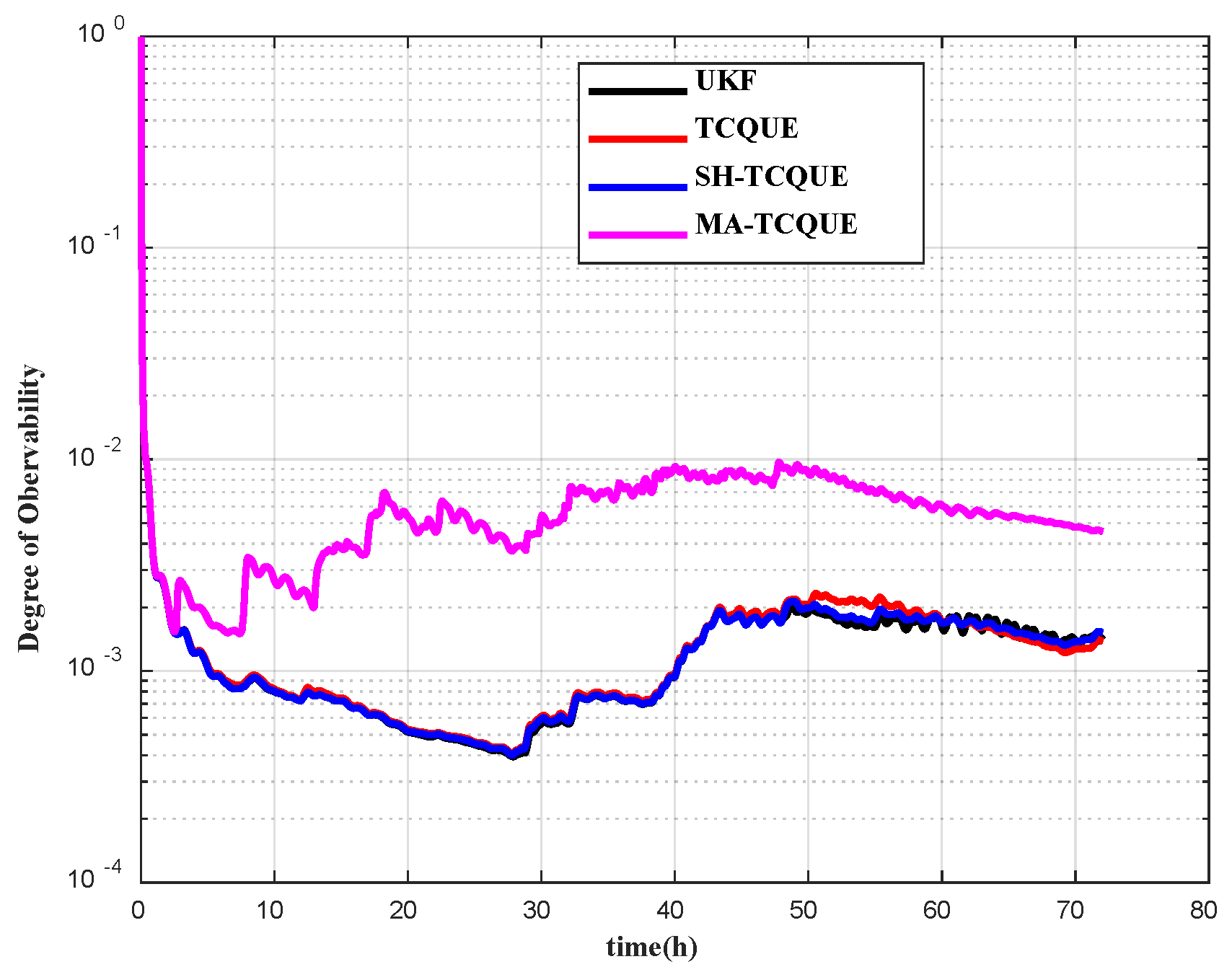
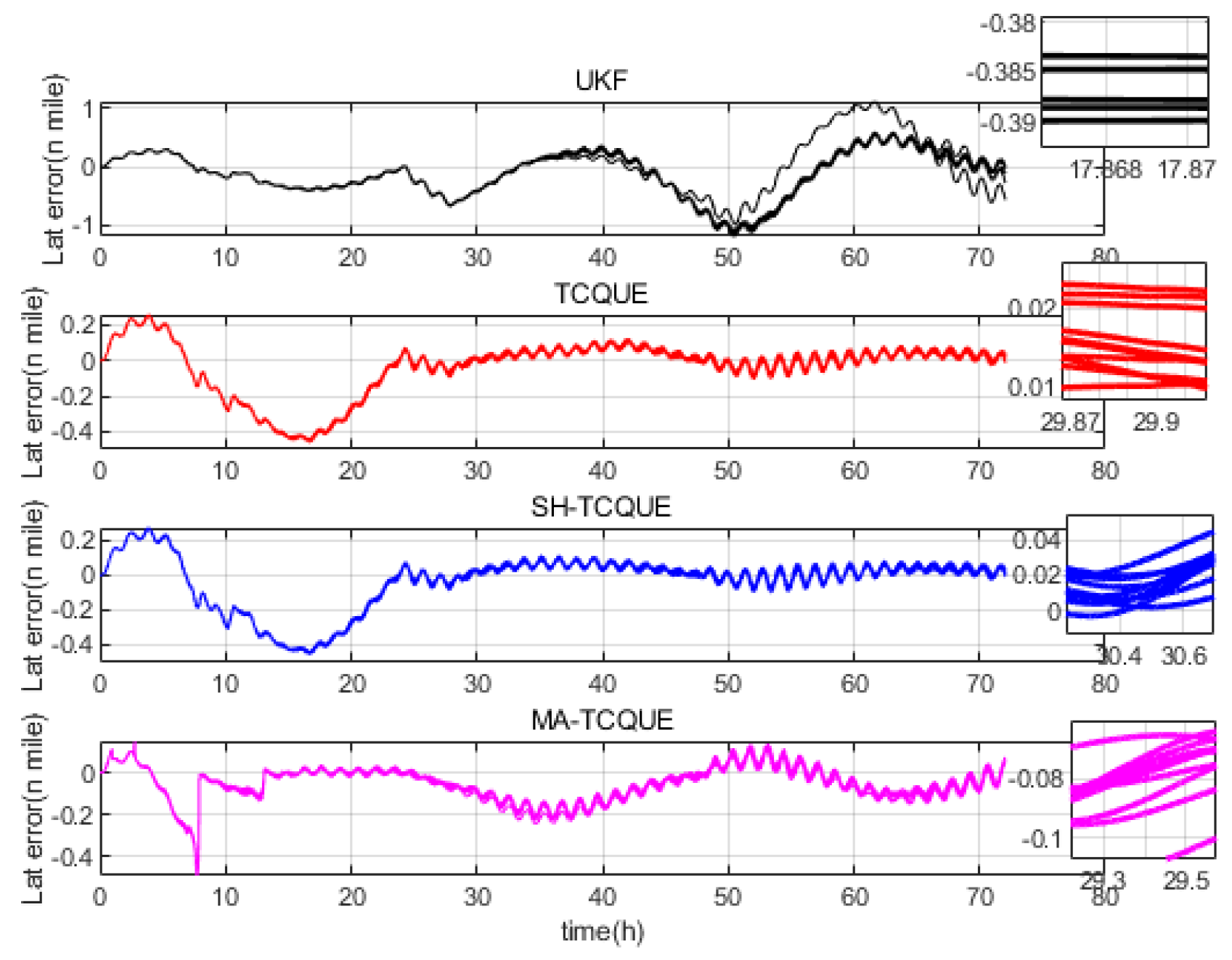
4. Experimental Study
4.1. Simulation Study
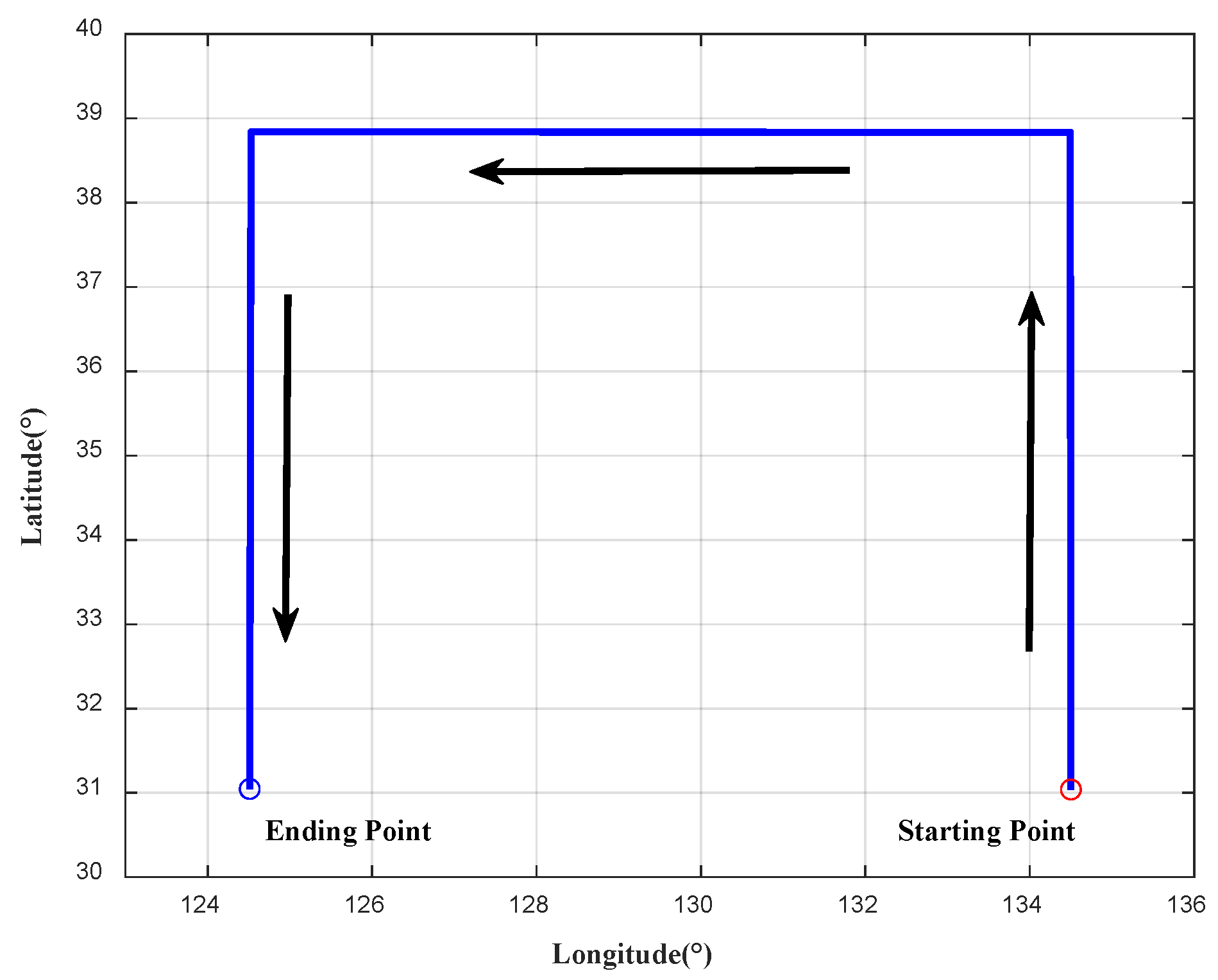
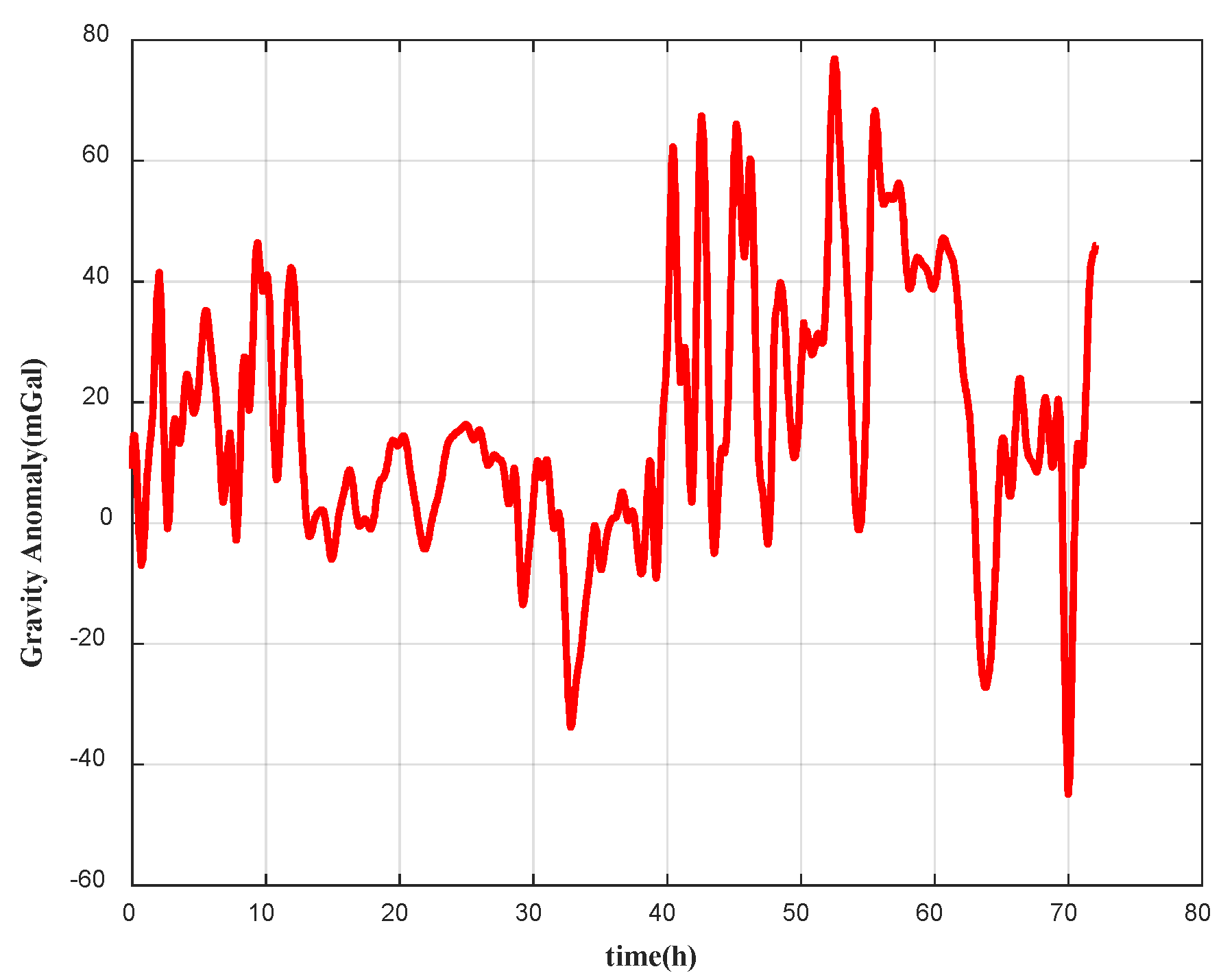
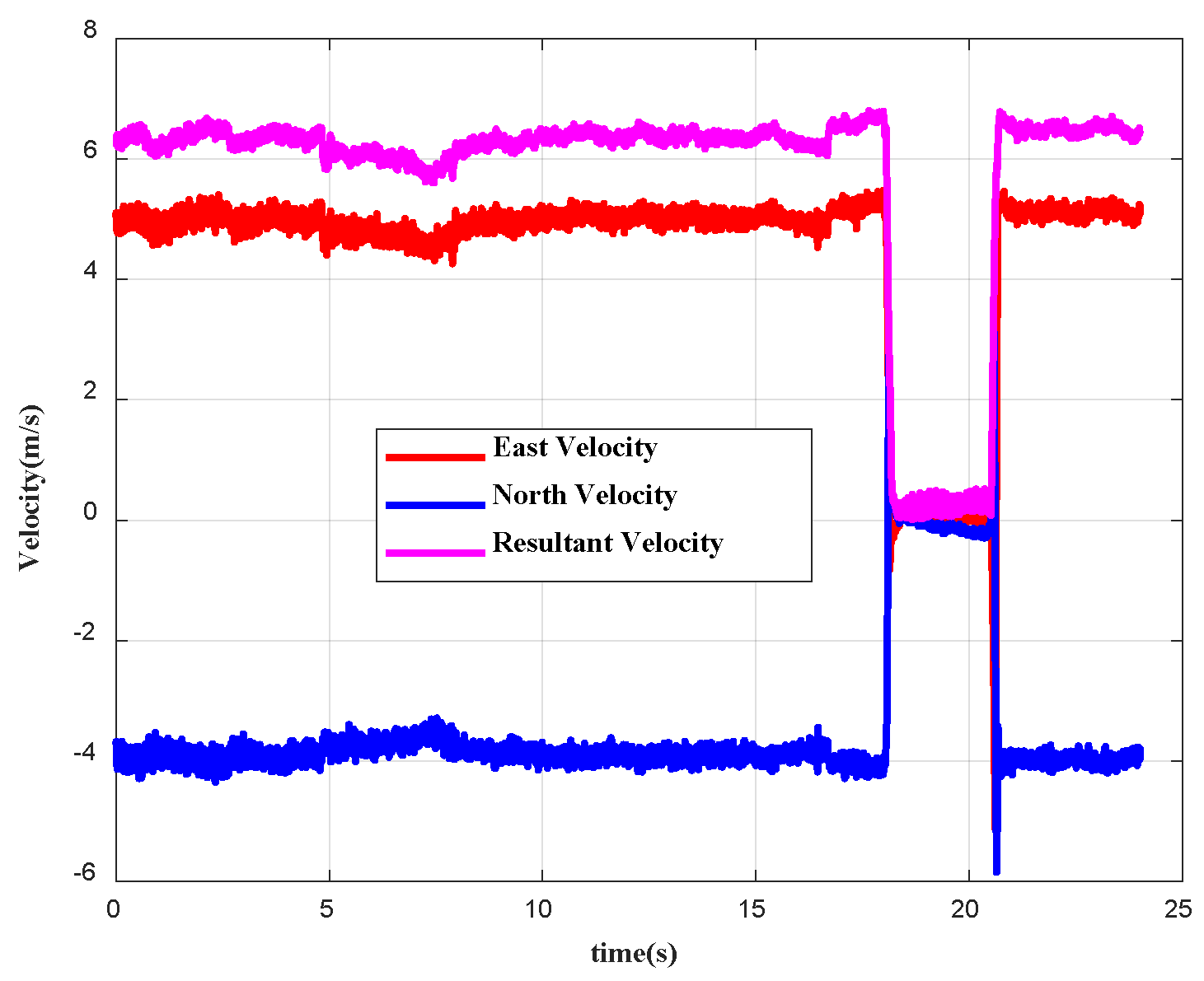
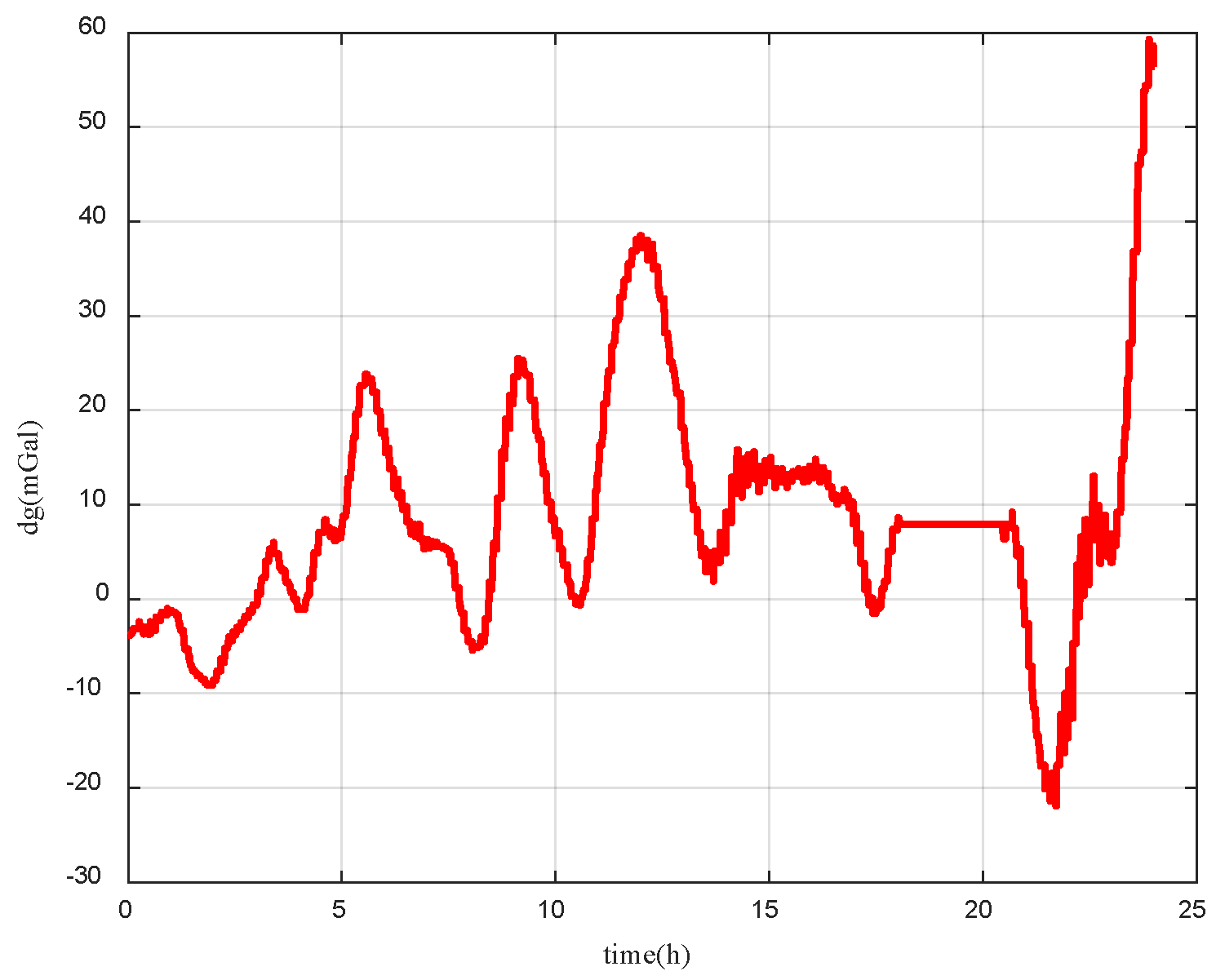
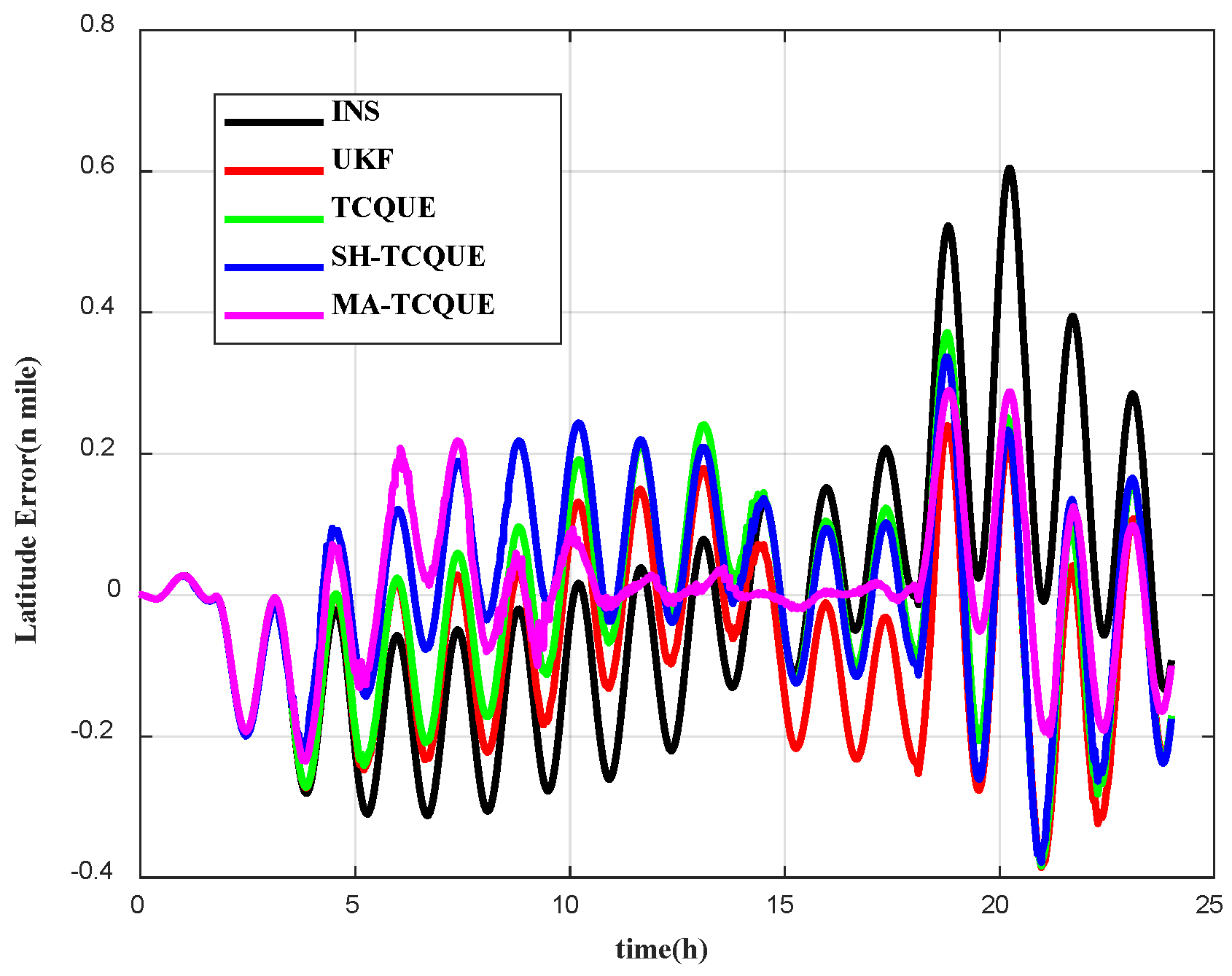
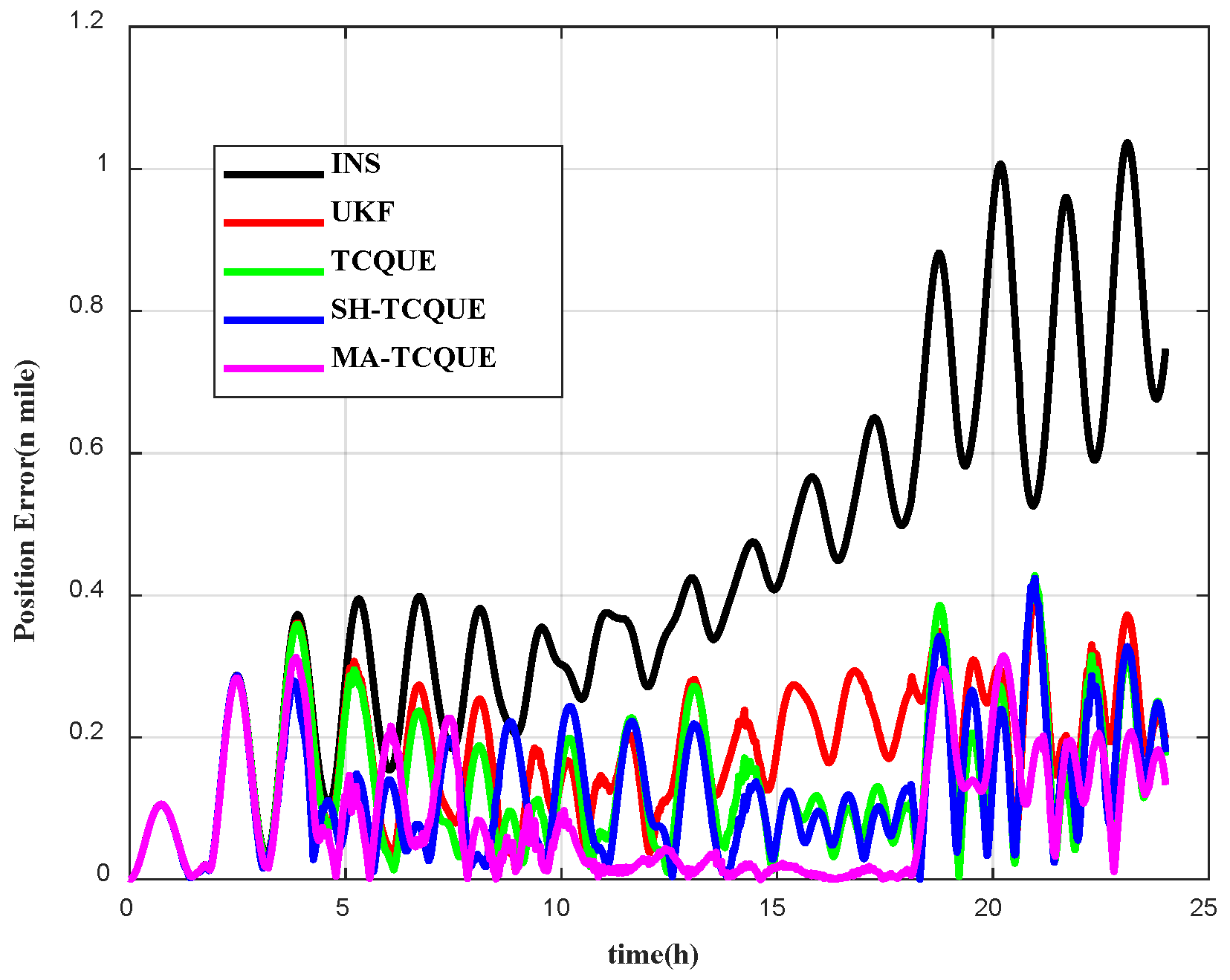
4.2. Field Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kayacan, E.; Zhao, Y.; Yao, W.; Chen, Y.; Li, S.; He, Y. Seamless INS/DVL Integrated Navigation System via Online Transfer Gaussian Process Regression. IEEE Trans. Instrum. Meas. 2024, 73, 2531013. [Google Scholar]
- Li, X.; Cai, Z.; Yu, X.; Huang, Y.; Lyu, X.; Meng, Z.; Li, C. A dual adaptive unscented Kalman filter algorithm for SINS-based integrated navigation system. J. Syst. Eng. Electron. 2024, 35, 732–740. [Google Scholar]
- Qin, F.; Li, A.; Zhu, J.; Qian, L.; Li, K. An INS/DVL integrated navigation filtering method against complex underwater environment. Ocean. Eng. 2023, 278, 114398. [Google Scholar] [CrossRef]
- Li, A.; Li, K.; Qin, F.; Zhu, T. The quaternion based error model based on se (3) of the ins. IEEE Sens. J. 2022, 22, 13067–13077. [Google Scholar]
- Di, J.; Chang, L.; Qin, F. Inertial-based integration with transformed INS mechanization in Earth frame. IEEE/ASME Trans. Mechatron. 2021, 27, 1738–1749. [Google Scholar]
- Hu, B.; Chang, L.; Li, K. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar]
- Chang, L.; Tang, H.; Hu, G.; Xu, J. SINS/DVL Linear Initial Alignment based on Lie Group SE3 (3). IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7203–7217. [Google Scholar] [CrossRef]
- Liu, Y.; Li, K.; Zhu, T.; Li, W. The quaternion-based attitude error for the nonlinear error model of the INS. IEEE Sens. J. 2021, 21, 25782–25795. [Google Scholar]
- Wang, Q.; Liu, K.; Cao, Z. System noise variance matrix adaptive Kalman filter method for AUV INS/DVL navigation system. Ocean. Eng. 2023, 267, 113269. [Google Scholar] [CrossRef]
- Pebody, M.; Allotta, B.; Topini, A.; Topini, E.; Phillips, A.B.; Ridolfi, A.; Fanelli, F. An experimental comparison of Deep Learning strategies for AUV navigation in DVL-denied environments. Ocean. Eng. 2023, 274, 114034. [Google Scholar]
- Golden, J.P. Terrain contour matching (TERCOM): A cruise missile guidance aid. In Proceedings of the 24th Annual Technical Symposium, San Diego, CA, USA, 23 December 1980; Volume 238, pp. 10–18. [Google Scholar]
- Yilmaz, G.; Eroglu, O. A terrain referenced UAV localization algorithm using binary search method. J. Intell. Robot. Syst. 2019, 73, 309–323. [Google Scholar]
- Xu, X.; Zhang, T.; Wang, H. Multipath parallel ICCP underwater terrain matching algorithm based on multibeam bathmetric data. IEEE Access 2018, 6, 48708–48715. [Google Scholar]
- Fu, M.; Deng, Z.; Han, Y.; Wang, B. A combined matching algorithm for underwater gravity-aided navigation. IEEE/ASME Trans. Mechatron. 2018, 23, 646–654. [Google Scholar]
- Fu, M.; Deng, Z.; Liu, M.; Wang, B. Improved ICCP algorithm and its application in gravity matching aided inertial navigation system. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 562–567. [Google Scholar]
- Lin, N.; Jing, X.; Li, F.; Liu, F. Gravity aided positioning based on real-time ICCP with optimized matching sequence length. IEEE Access 2018, 7, 97440–97456. [Google Scholar]
- Gao, N.; Wang, Q.; Huang, B.; Zhou, J.; Zhao, L. A novel terrain aided navigation algorithm combined with the TERCOM algorithm and particle filter. IEEE Sens. J. 2015, 15, 1124–1131. [Google Scholar]
- Fu, M.; Deng, Z.; Han, Y.; Wang, B. An improved TERCOM-based algorithm for gravity-aided navigation. IEEE Sens. J. 2016, 16, 2537–2544. [Google Scholar]
- Kang, C.; Dai, Z. Geomagnetic field aided inertial navigation using the SITAN algorithm. In Proceedings of the 2014 2nd International Conference on Systems and Informatics (ICSAI), Shanghai, China, 15–17 November 2014; pp. 79–83. [Google Scholar]
- Wang, W.; Li, S.S.; Xing, Z. The UKF matching algorithm using gravity anomaly based on correlative probability density add-weight. J. Geomat. Sci. Technol. 2015, 32, 349–352. [Google Scholar]
- Deng, Z.; Li, C.; Yin, L.; Wang, B.; Xiao, X. An adaptive robust unscented Kalman filter-based matching algorithm for underwater gravity aided navigation. IEEE/ASME Trans. Mechatron. 2023, 28, 2471–2482. [Google Scholar]
- Cai, S.; Guo, Y.; Cao, J.; Luo, K.; Yu, R. Robust two-stage filtering for INS/Gravity matching passive integrated navigation systems. IEEE Sens. J. 2020, 22, 3370–3381. [Google Scholar]
- Li, J.; Wu, M.; Mao, N.; He, H.; Xu, J.; Qin, F.; Li, A. Marine gravity anomaly from satellite altimetry: Interpolation and matching navigation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5918919. [Google Scholar]
- Zhu, B.; Li, J.; Mao, N.; He, H.; Xu, J.; Li, F.; Qin, F.; Li, A. Adaptive gravity-aided inertial navigation based on characteristic analysis of marine gravity anomaly from satellite altimetry. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5920813. [Google Scholar]
- Wang, Z.; Huang, Y.; Wang, M.; Wu, J.; Zhang, Y. A computationally efficient outlier-robust cubature kalman filter for underwater gravity matching navigation. IEEE Trans. Instrum. Meas. 2022, 71, 8500418. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Zhang, L.; Xia, M.; Pan, S. A Novel DVL Aided Inertial Navigation Strategy for Long-Endurance Robust Positioning of AUVs. IEEE Trans. Intell. Veh. 2021, 14, 1–14. [Google Scholar]
- Dong, X.; Hu, G.; Gao, B.; Zhong, Y.; Ruan, W. Windowing-based Factor Graph Optimization with Anomaly Detection using Mahalanobis Distance for Underwater INS/DVL/USBL Integration. IEEE Trans. Instrum. Meas. 2024, 73, 8501213. [Google Scholar] [CrossRef]
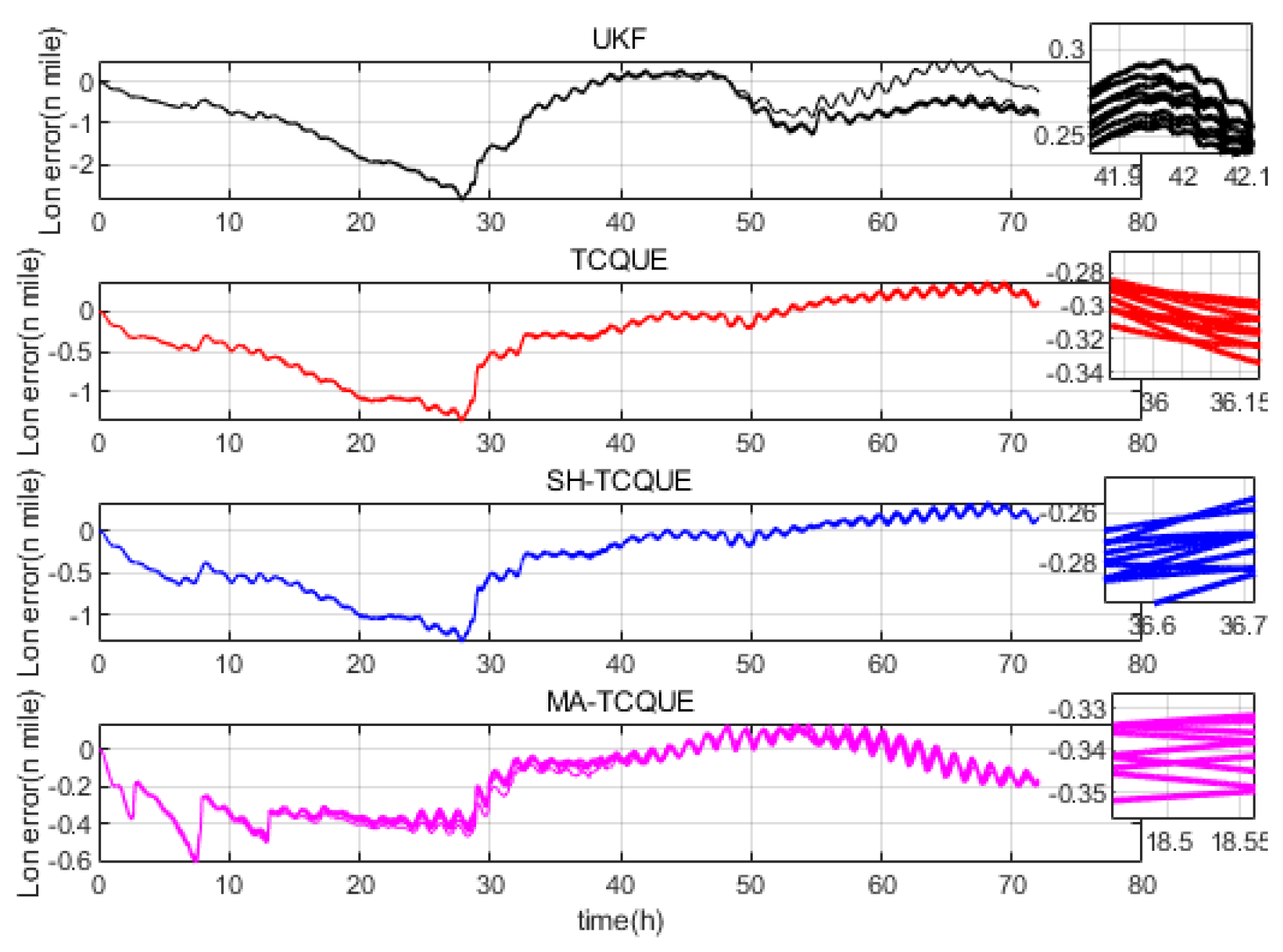
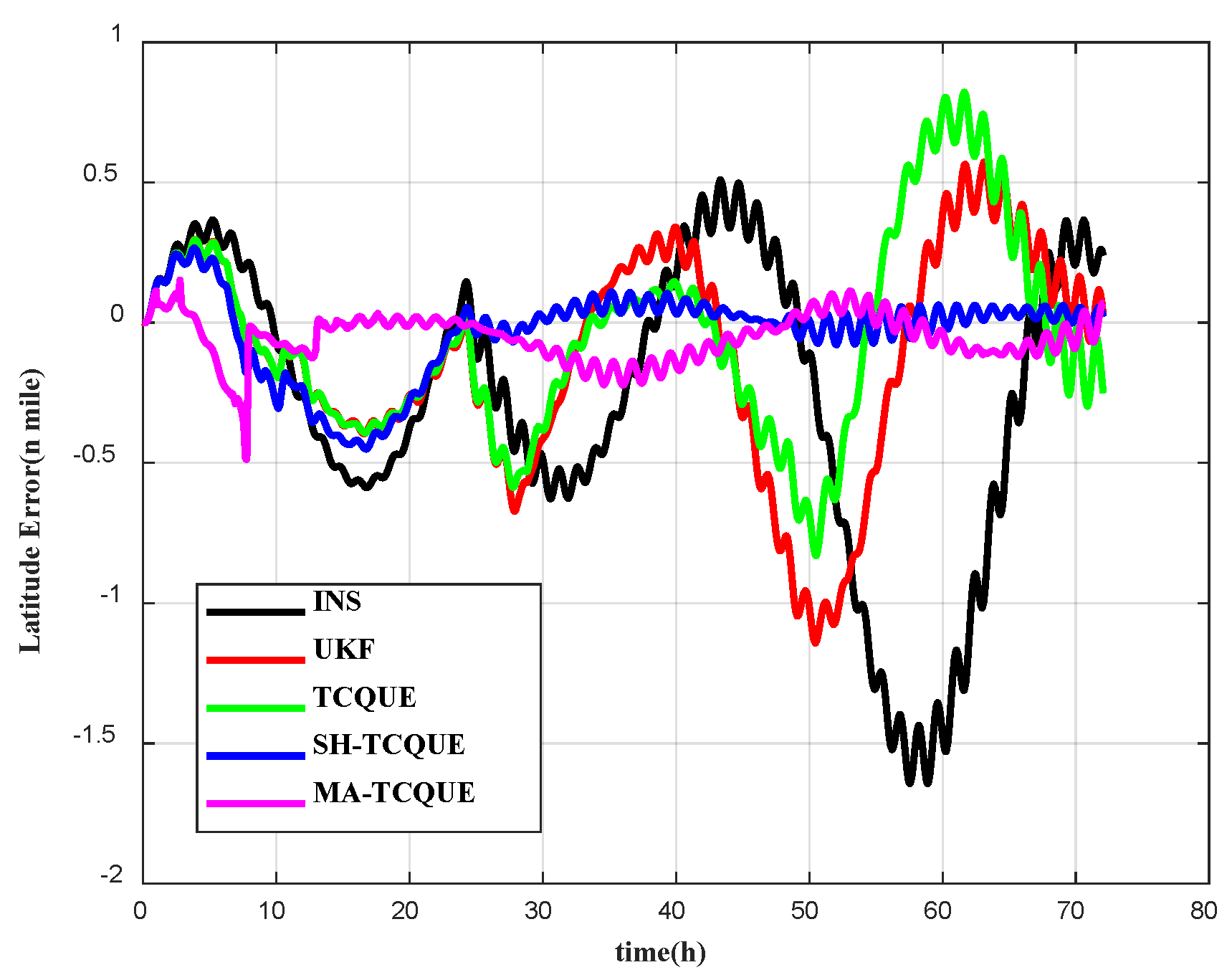

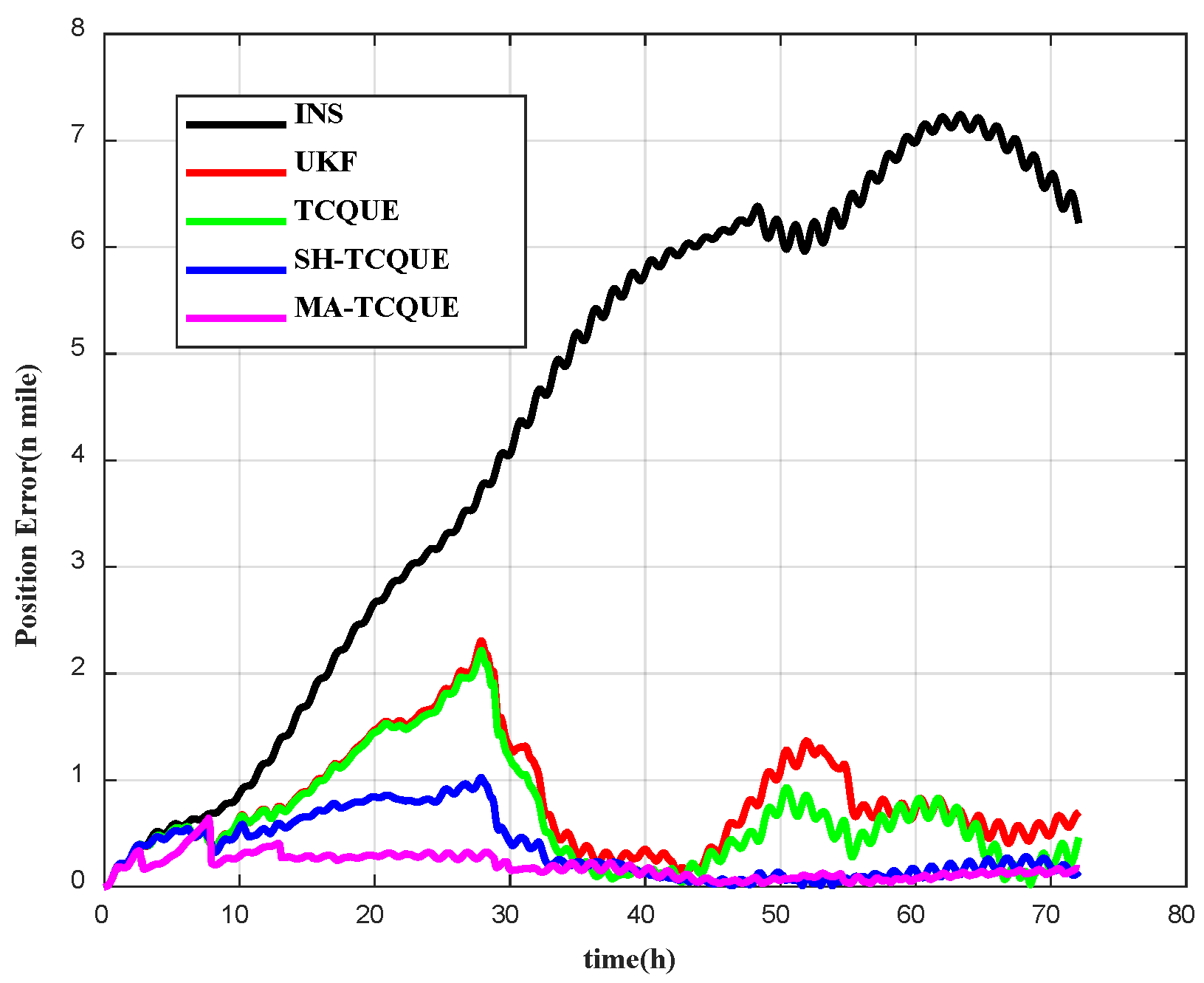

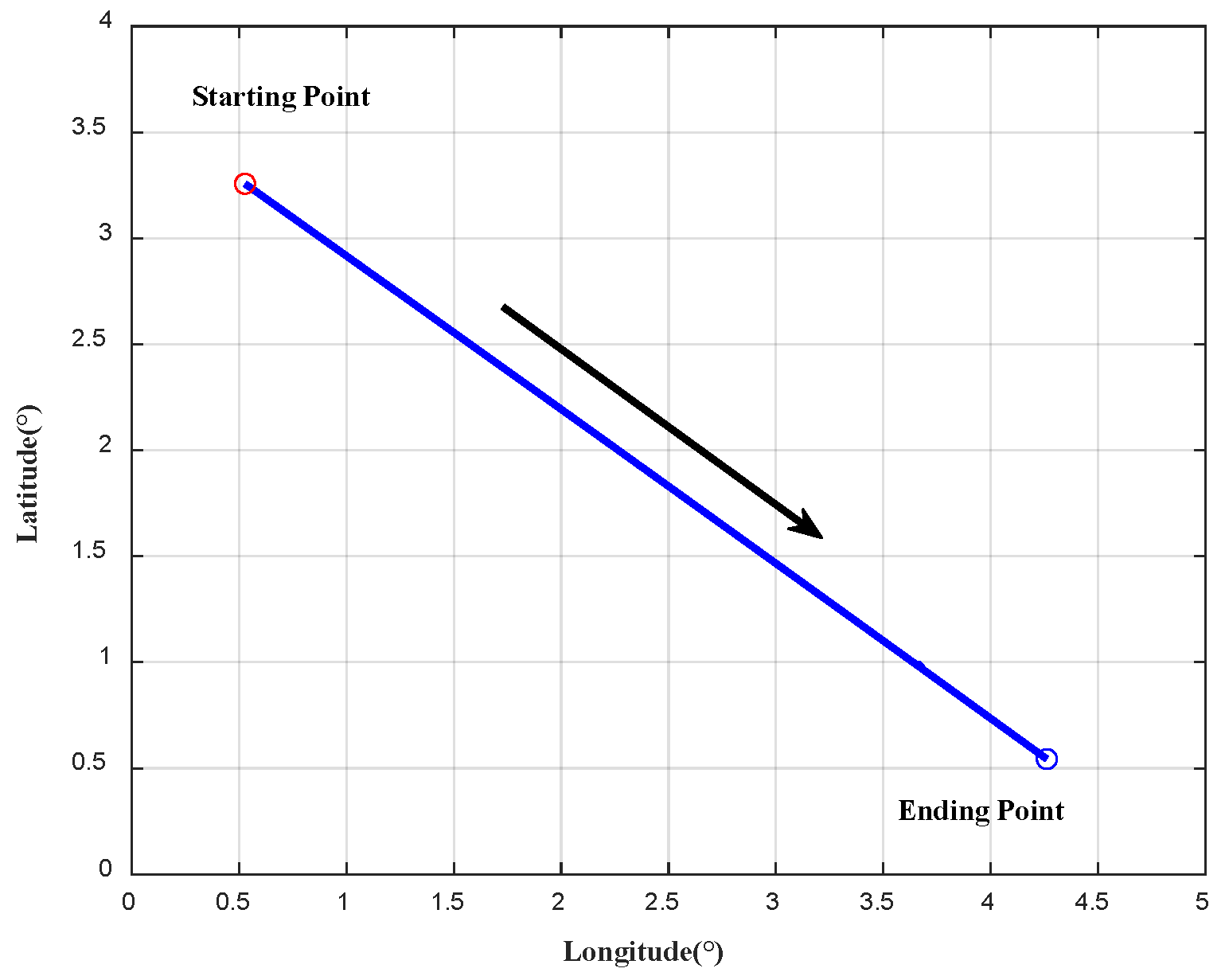

| Symbol | Characteristic |
|---|---|
| Initial position error | |
| Initial velocity error | |
| Gyroscope drift bias | |
| Gyroscope random walk | |
| Gyroscope update rate | |
| Accelerometer drift bias | |
| Accelerometer random walk | |
| Accelerometer update rate |
| Algorithm | UKF | TCQUE | SH-TCQUE | MA-TCQUE |
|---|---|---|---|---|
| Pitch | 0.320 | 0.076 | 0.075 | 0.126 |
| Roll | 0.024 | 0.040 | 0.039 | 0.059 |
| Yaw | 0.022 | 0.040 | 0.039 | 0.116 |
| East velocity | 1.013 | 1.449 | 1.436 | 2.679 |
| North velocity | 1.104 | 1.153 | 1.438 | 2.658 |
| Latitude | 0.004 | 0.005 | 0.005 | 0.017 |
| Longitude | 0.001 | 0.002 | 0.002 | 0.006 |
| x-axis gyroscope | 3.087 | 3.137 | 2.957 | 25.340 |
| y-axis gyroscope | 4.644 | 4.325 | 4.439 | 27.894 |
| z-axis gyroscope | 4.564 | 4.142 | 4.226 | 27.728 |
| x-axis accelerometer | 1.029 | 1.071 | 1.016 | 1.180 |
| y-axis accelerometer | 1.036 | 1.067 | 1.023 | 1.215 |
| z-axis accelerometer | 1.092 | 1.053 | 1.045 | 1.503 |
| Algorithm | Max | Mean | STD | RMS |
|---|---|---|---|---|
| INS | 7.24 | 4.36 | 2.34 | 4.96 |
| UKF | 2.26 | 0.81 | 0.49 | 0.95 |
| TCQUE | 2.21 | 0.67 | 0.51 | 0.84 |
| SH-TCQUE | 1.02 | 0.34 | 0.28 | 0.45 |
| MA-TCQUE | 0.64 | 0.18 | 0.11 | 0.21 |
| Algorithm Sensor | Max Characteristic | Value |
|---|---|---|
| Accelerometer | Bias | |
| Random walk | ||
| Update rate | ||
| SH-TCQUE | Bias | |
| Random walk | ||
| Update rate |
| Algorithm | Max | Mean | STD | RMS |
|---|---|---|---|---|
| INS | 1.03 | 0.42 | 0.25 | 0.49 |
| UKF | 0.37 | 0.18 | 0.09 | 0.20 |
| TCQUE | 0.31 | 0.14 | 0.08 | 0.17 |
| SH-TCQUE | 0.41 | 0.13 | 0.07 | 0.15 |
| MA-TCQUE | 0.31 | 0.08 | 0.06 | 0.12 |
| Algorithm | Theoretical FLOPs | Computational Time (s) |
|---|---|---|
| UKF | O(2n3) | 3144 |
| TCQUE | O(4n3) | 4429.3 |
| SH-TCQUE | O(4n3 + mn2) | 4584.1 |
| MA-TCQUE | O(4n3 + kmn2) | 4518.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Qin, F.; Li, A.; Li, K.; Yan, J.; Qian, L. The Novel Gravity-Matching Algorithm Based on Modified Adaptive Transformed Cubature Quaternion Estimation for Underwater Navigation. J. Mar. Sci. Eng. 2025, 13, 1150. https://doi.org/10.3390/jmse13061150
Zhu T, Qin F, Li A, Li K, Yan J, Qian L. The Novel Gravity-Matching Algorithm Based on Modified Adaptive Transformed Cubature Quaternion Estimation for Underwater Navigation. Journal of Marine Science and Engineering. 2025; 13(6):1150. https://doi.org/10.3390/jmse13061150
Chicago/Turabian StyleZhu, Tiangao, Fangjun Qin, An Li, Kailong Li, Jiujiang Yan, and Leiyuan Qian. 2025. "The Novel Gravity-Matching Algorithm Based on Modified Adaptive Transformed Cubature Quaternion Estimation for Underwater Navigation" Journal of Marine Science and Engineering 13, no. 6: 1150. https://doi.org/10.3390/jmse13061150
APA StyleZhu, T., Qin, F., Li, A., Li, K., Yan, J., & Qian, L. (2025). The Novel Gravity-Matching Algorithm Based on Modified Adaptive Transformed Cubature Quaternion Estimation for Underwater Navigation. Journal of Marine Science and Engineering, 13(6), 1150. https://doi.org/10.3390/jmse13061150






