1. Introduction
In underwater passive detection, the bearing time record (BTR), which is a visual tool for tracking the trajectory of underwater targets, plays a crucial role. BTRs are created by plotting the power of beamforming signals using beamforming algorithms like Conventional Beamforming (CBF) or Minimum Variance Distortionless Response (MVDR) over a two-dimensional (2D) plane of time and bearing angle [
1,
2]. In a BTR, the horizontal axis represents the bearing angle, while the vertical axis represents time. High-intensity regions correspond to strong signal returns from specific directions at particular times, indicating the presence and movement of targets, which can complete the task of target detection and tracking. The primary goal of underwater passive detection is to enhance the capability of detecting weak targets, with the expansion of the detection range being a key pursuit. Long-range detection performance is typically reflected in the identification of low-intensity signals in the BTR. An effective strategy for optimizing the design of acoustic arrays is to increase the number of array elements
N while maintaining a constant array aperture
, thereby improving resolution and array gain. According to the classical array gain formula, the theoretical gain is given by
[
3]. However, indiscriminately increasing the number of elements can result in an excessively long array, raising system design and deployment costs. Additionally, if the element spacing
d becomes too small, the assumption of noise orthogonality,
, may no longer hold, which would degrade the actual array gain and compromise detection performance [
4]. Ref. [
5] emphasized that effective separation of signal and noise spaces is essential for achieving optimal array gain. Therefore, array design must strike a balance between gain improvement, cost efficiency, and practical deployment to ensure overall system performance.
To reduce noise on the BTR, enhance the visibility of weak targets, and improve feature detectability, image processing techniques have been widely used in passive sonar post-processing for many years. Currently, popular image-denoising methods can be roughly classified into two categories: smoothing filter-based methods and block-based methods. In image processing, convolution operations are commonly employed for image filtering. By convolving an image with a kernel (or filter), the pixel values of the image are adjusted according to the weights of its neighboring pixels, resulting in noise reduction, edge detection, and feature enhancement. Commonly used image kernels include Gaussian filters, mean filters, and median filters [
6]. Li et al. [
7] proposed a method for processing non-uniform, non-stationary BTR images with noisy backgrounds by combining the median filter and sorted truncated mean for background balancing. However, all of these balancing methods are based on smoothing operations around the image areas, which will cause blurry details and information loss, especially in complex images containing more details. However, these methods are based on the smoothing operation applied to the peripheral areas of the image, which can lead to blurred details and loss of information, especially in complex images containing more detailed features.
The second method is a block-based approach, where the image is divided into blocks according to preset standards. Blocks with smoother textures are selected for matching. Ref. [
8] introduced the K-SVD algorithm, which uses an overcomplete dictionary to achieve sparse representation for signal and image compression and denoising. Ref. [
9] proposed the NLM (Non-Local Means) algorithm, which leverages non-local information within images to improve denoising while preserving details and texture information. Refs. [
10,
11] introduced a 3D block matching method (BM3D) that separates noise and signal in higher dimensions, achieving significant feature enhancement. However, all these algorithms require prior estimation of the noise level in the image and are overly dependent on poorly definable preset standards. Ref. [
12] proposed a new algorithm framework called Block Matching-Subband Extrema Energy Detection (BM-SEED) for denoising and enhancing the weak targets of BTRs. However, these algorithms require prior estimation of the image noise levels and are heavily reliant on preset standards that are difficult to determine. Ref. [
13] proposed a BTR image-denoising method based on principal component analysis (PCA) dimensionality reduction, but this method is unable to effectively enhance weak targets. Referencing [
14,
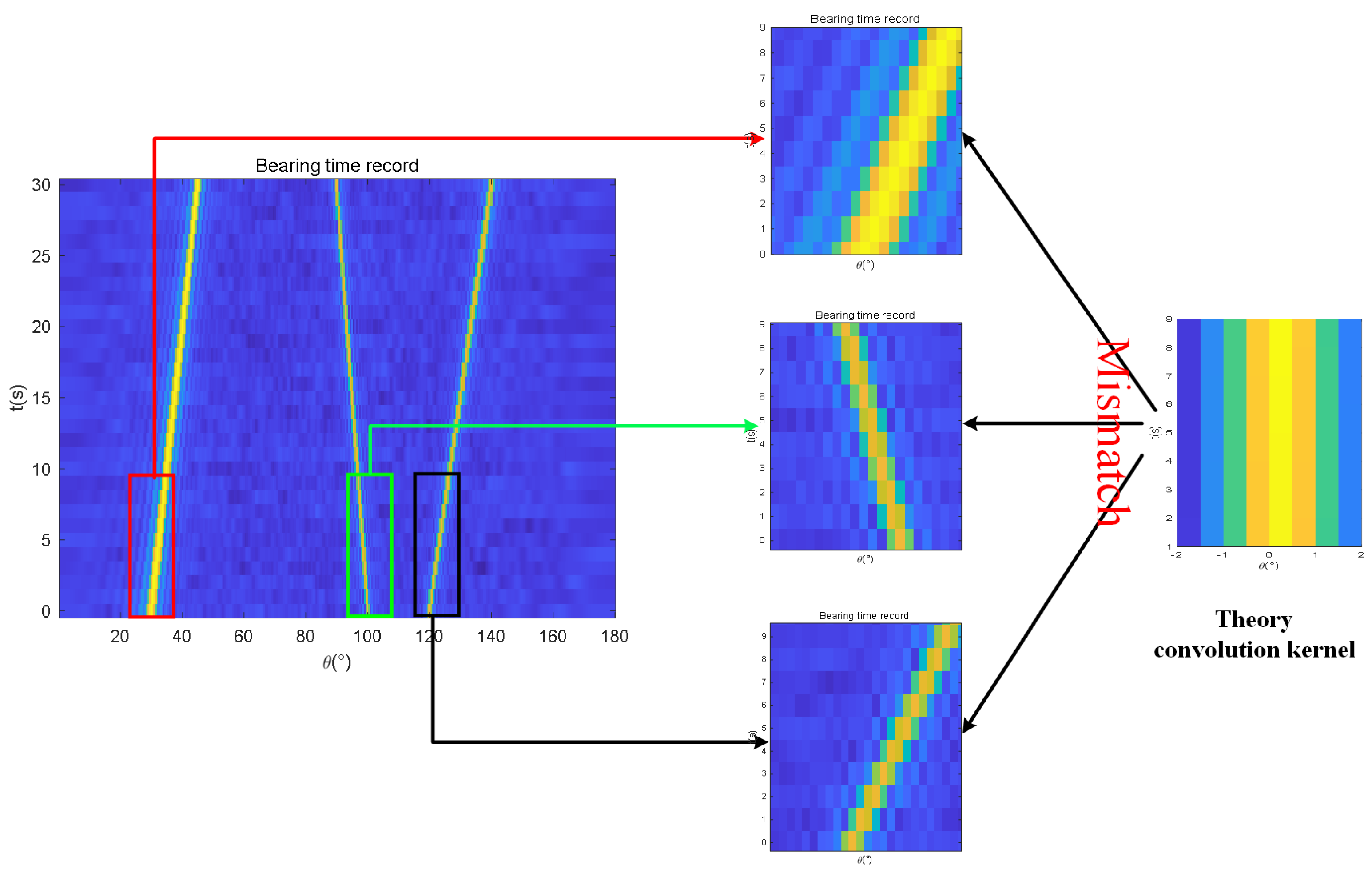
15], a deblurring algorithm is applied to an image via convolution to a uniform linear array (ULA). Deconvolution convention beamforming, which serves as an improved high-resolution algorithm for traditional beamforming, can significantly narrow the main lobe width and reduce the level of side lobes and has been widely used. However, under low signal-to-noise ratio (SNR) conditions, the point spread function (PSF) derived from array information is an idealized, theoretical representation, which may not accurately correspond to the actual noisy beam response. As a result, deconvolution may amplify noise in the original signal due to this mismatch. The BTR is a two-dimensional image, with the horizontal axis representing angles and the vertical axis representing time. Consequently, Ref. [
16] proposed extending the one-dimensional PSF into the temporal dimension to develop a 2D PSF with the horizontal axis denoting angles and the vertical axis representing time. This enables 2D deconvolution beamforming to acquire greater temporal gains. However, this approach has disadvantages: when targets undergo high-speed evasive maneuvers, their trajectories may shift in angle. The theoretical 2D PSF, lacking an inherent angular deviation, may not perform adequately if the time window
T is insufficient, failing to yield sufficient temporal gain. As a result, its performance may fall short of expectations for ideal temporal gains under rapid maneuvers and could even underperform compared with the CBF algorithm’s beam response.
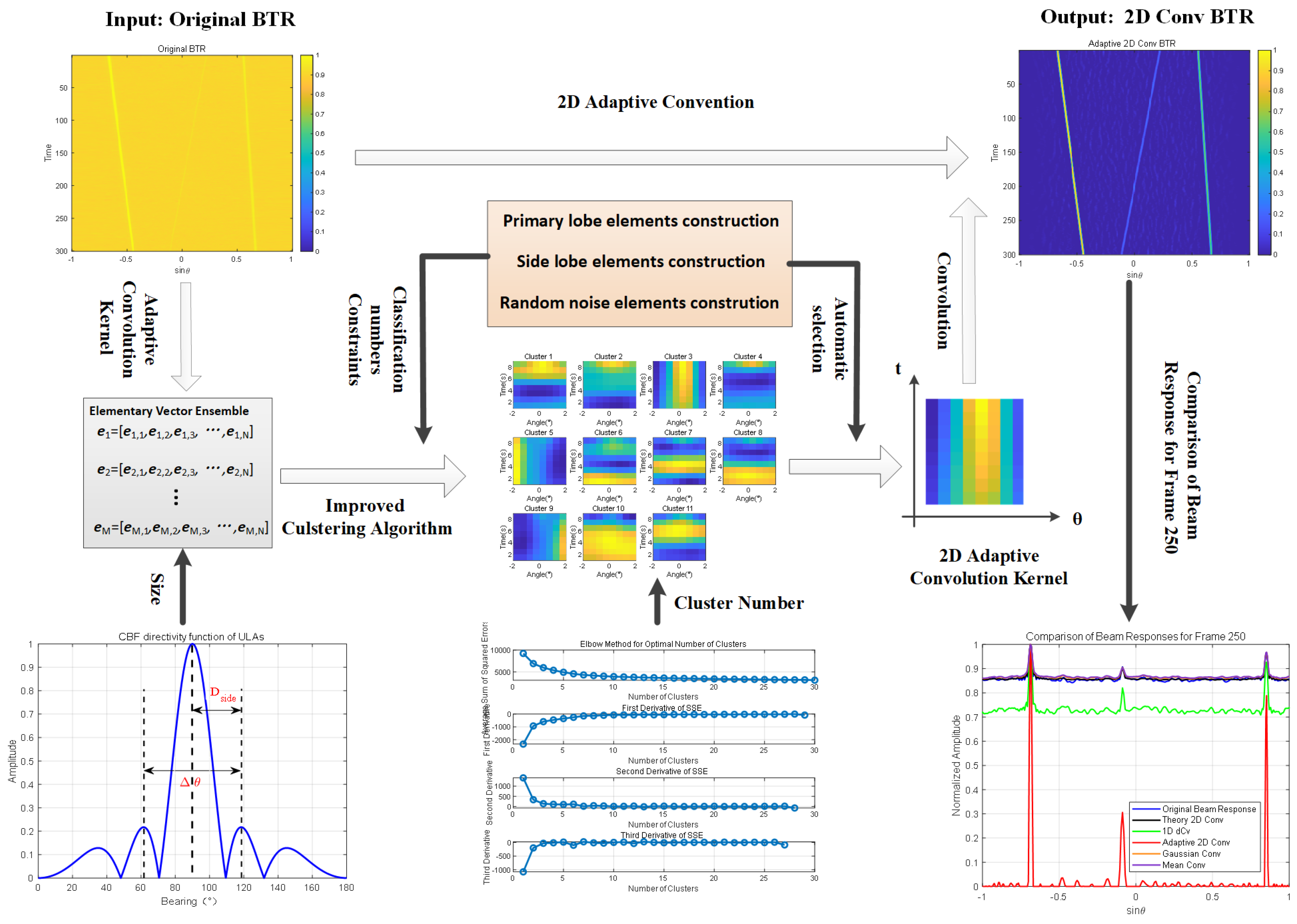
In passive detection, the parameters of the surrounding environment are unknown. To acquire these real-time parameters, we employ an adaptive method to extract the real-time parameters from the BTR. By adopting this approach, we can achieve feature enhancement. The core idea behind this method is to utilize a self-adaptive convolution kernel that matches the stripe pattern present in the current BTR for image processing. In image processing, convolution involves applying a small kernel over local areas of an image to extract features, reduce noise, or achieve other visual effects. The fundamental concept is to replace each pixel in the image with a weighted average value. By selecting appropriate kernel functions, various image processing tasks can be accomplished. Therefore, we construct a visual template representing the main lobe using the K-means algorithm, which serves as our self-adaptive convolution kernel. This approach offers two significant advantages: first, it is an artificial intelligence-based method that maximizes the extraction of real-time parameters from the stripe information on the BTR, avoiding the blind box process; second, it yields a self-adaptive convolution kernel that matches the actual probability statistical characteristics. Experimental results have shown that when compared with convolutional beamforming (CBF), Theory 2D convolution (Theory 2D Conv), 1D deconvolution beamforming (1D dCv), Gaussian convolution (Gaussian Conv), mean convolution (Mean Conv), and median convolution (Median Conv), our proposed Adaptive 2D convolution (adaptive 2D Conv) effectively suppresses background noise and side lobe levels while enhancing weak targets under low SNR conditions and reduces the main lobe width to improve resolution. The remainder of this paper is organized as follows:
Section 2 provides a comprehensive review of related work;
Section 3 presents the proposed Adaptive 2D Conv in detail;
Section 4 and
Section 5 analyze the simulation and experiment results, respectively; finally,
Section 6 gives the final conclusion of this work.
4. Simulations
In order to validate the algorithm’s performance, we subsequently conducted validation using both simulation data and real sea trial data. In the simulations, we conducted multiple targets under different low SNRs (from 0 dB to −20 dB); the results show that the proposed method performs well in both scenarios. The parameter for one-dimensional for deconvolution RL is 10 iterations.
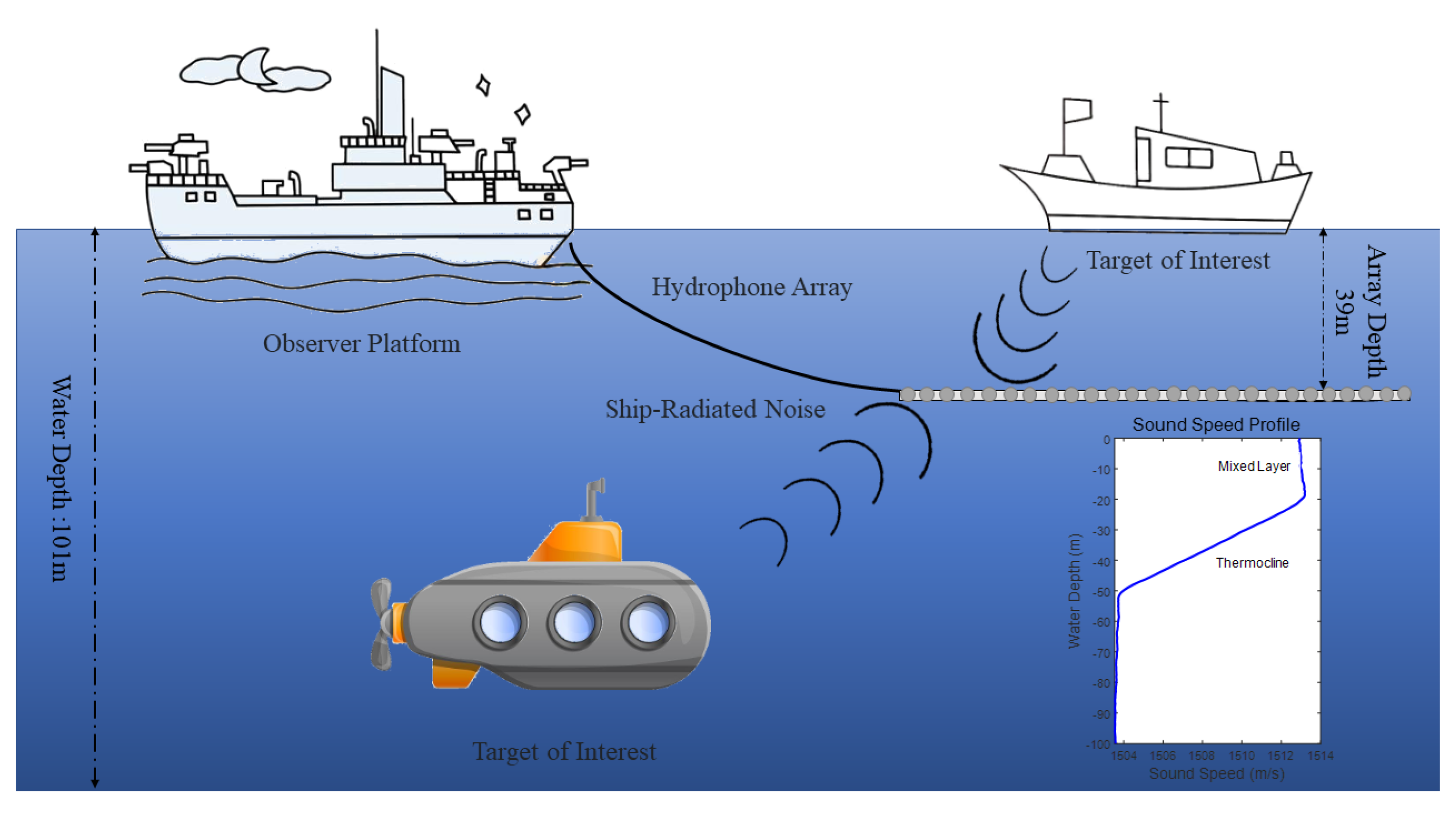
In multiple-target simulation, three targets initiated movement from , , and , moving to , , and , respectively, over a duration of 300 s with a time resolution of 1 s. Additionally, the amplitude ratios among these three targets were set at 1:0.33:0.5 over a duration of 300 s with a time resolution of 1 s per. The speed of sound of 1440 m/s is assumed, as well as a 256-unit uniform linear array spaced at d = 1.5 m. The frequency of the signal is 200 Hz, and the sampling frequency is 2000 Hz. The measuring signal angle ranges from 0 to , with a precision of . We employed CBF to process the received signals. Due to the translation invariance of the CBF directional function and considering the one-to-one mapping characteristics of the sine function, we observed that converting the original 0 to angular range using the sine transform could result in multiple x-values corresponding to the same y-value. To ensure the uniqueness of angle conversion, we adjusted the angular range from −90 to . This adjustment ensured the injectivity of the angular mapping, thus benefiting the accuracy and efficiency of subsequent data processing.
According to the steps in
Section 3, we first perform open peak extraction on the single-frequency signals, selecting 200 Hz as the representative frequency for calculation for the CBF method. When
f = 200 Hz,
d = 1.5 m, and
N = 256, the angle resolution of BTR is
. The main-to-sidelobe distance
is defined as the position of the maximum value of the first sidelobe. Since there is no analytical solution to Formula (
6), through numerical simulation, we can obtain the main-to-sidelobe distance
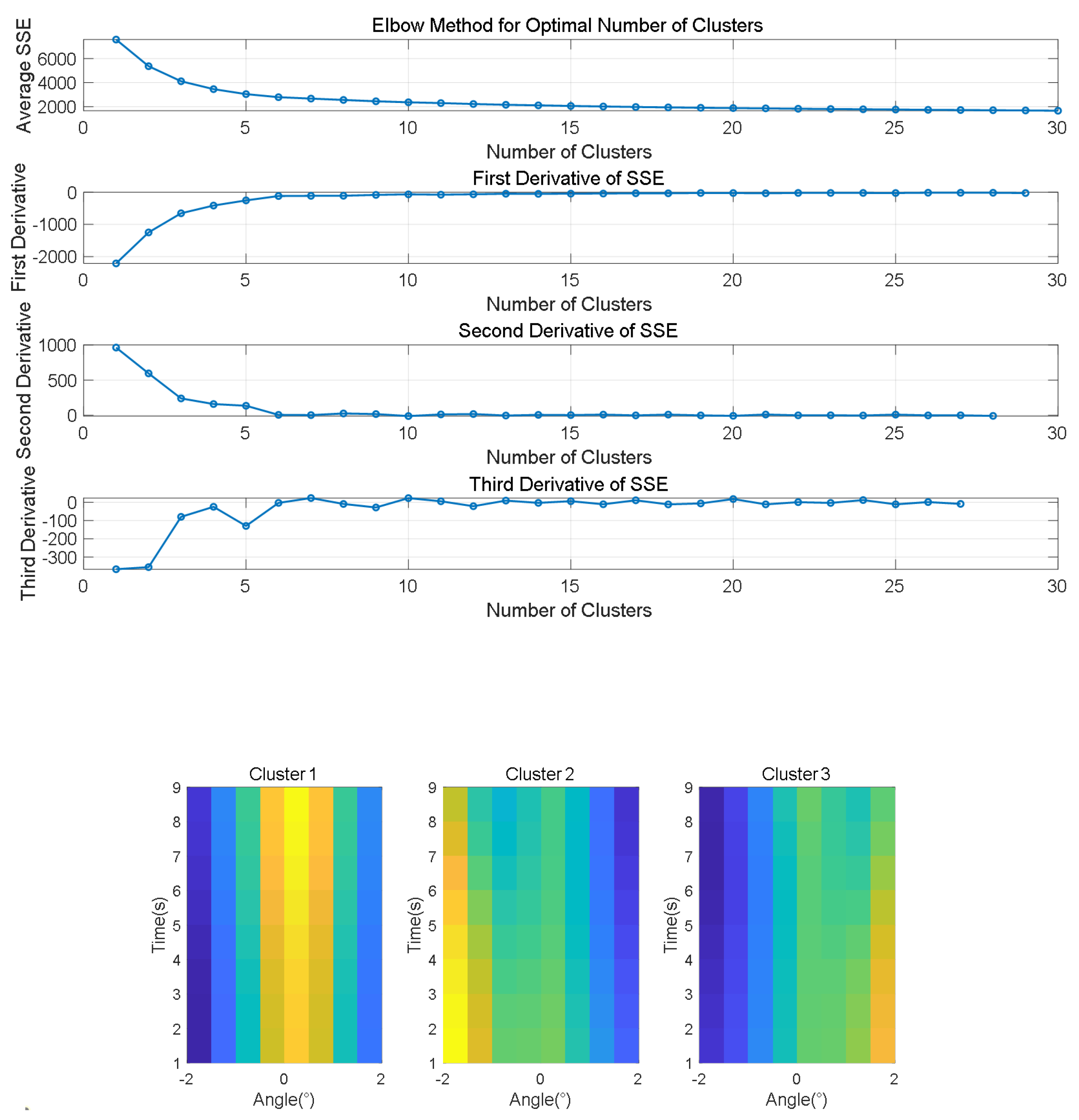
, so the width of the element should be nine pixels. We employed the improved k-means clustering algorithm on BTR for the first 300 frames. As shown in
Figure 4, it automatically determined the optimal number of clusters to be 6, 11, 11, and 7 at SNR of 0 dB, −10 dB, −15 dB, and −20 dB; subsequently, we extracted the main lobe visual pattern, with size of
, which corresponds to the
. We used the 1D dCv method, the Theory 2D Conv method, the Gaussian Conv method, the Mean Conv method, and the Median Conv method for baselines and compared them with our proposed adaptive 2D method. We calculated a one-dimensional conventional kernel based on the corresponding array information, then obtained the
by accumulating
along the time dimension and expanding it to two dimensions. To match the
, whose size is
, the sizes of
,
,
, and
are also
. Then, we performed the convolution algorithm with the six conventional kernels and deconvolution beamforming in the last 100 frames of BTR.
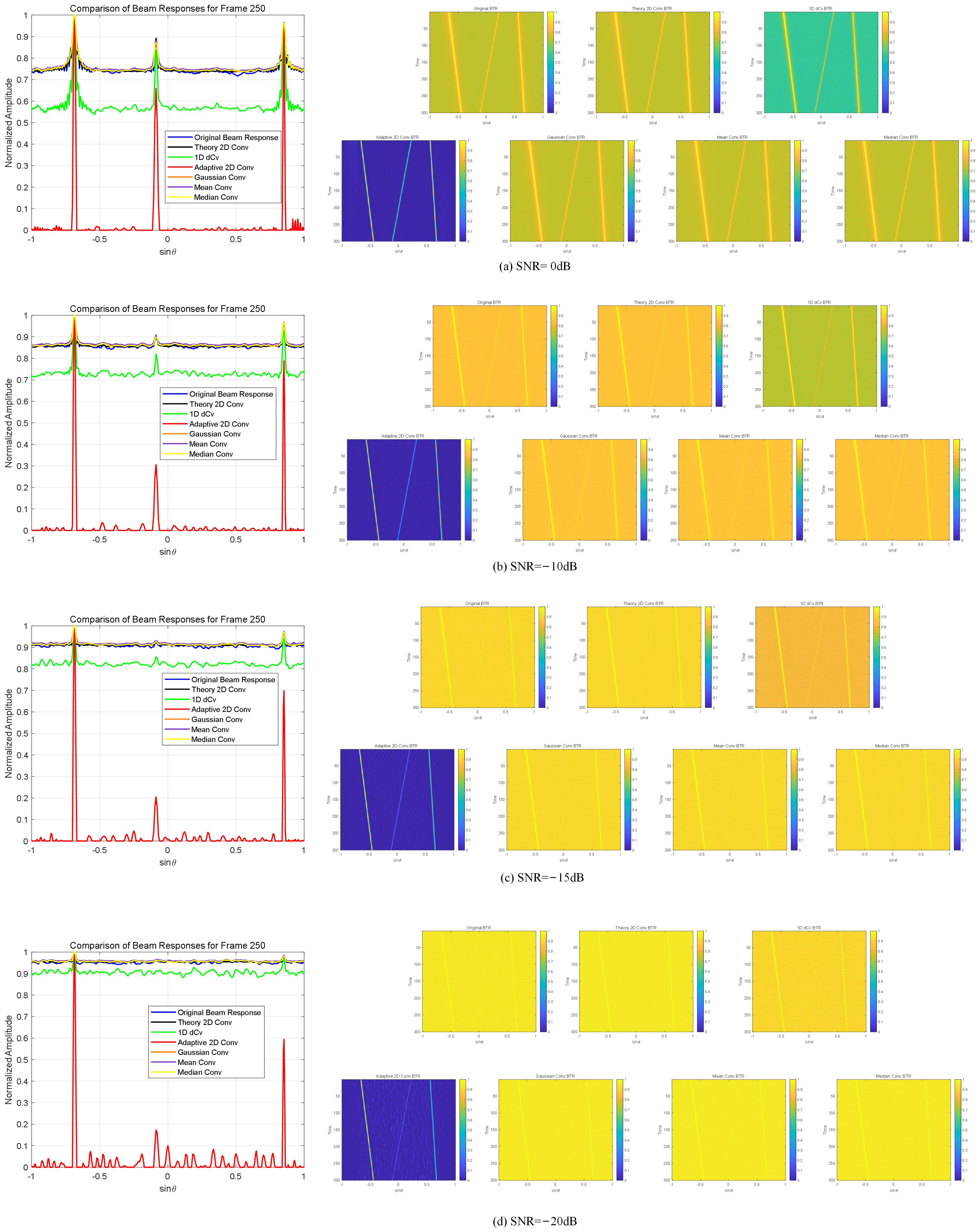
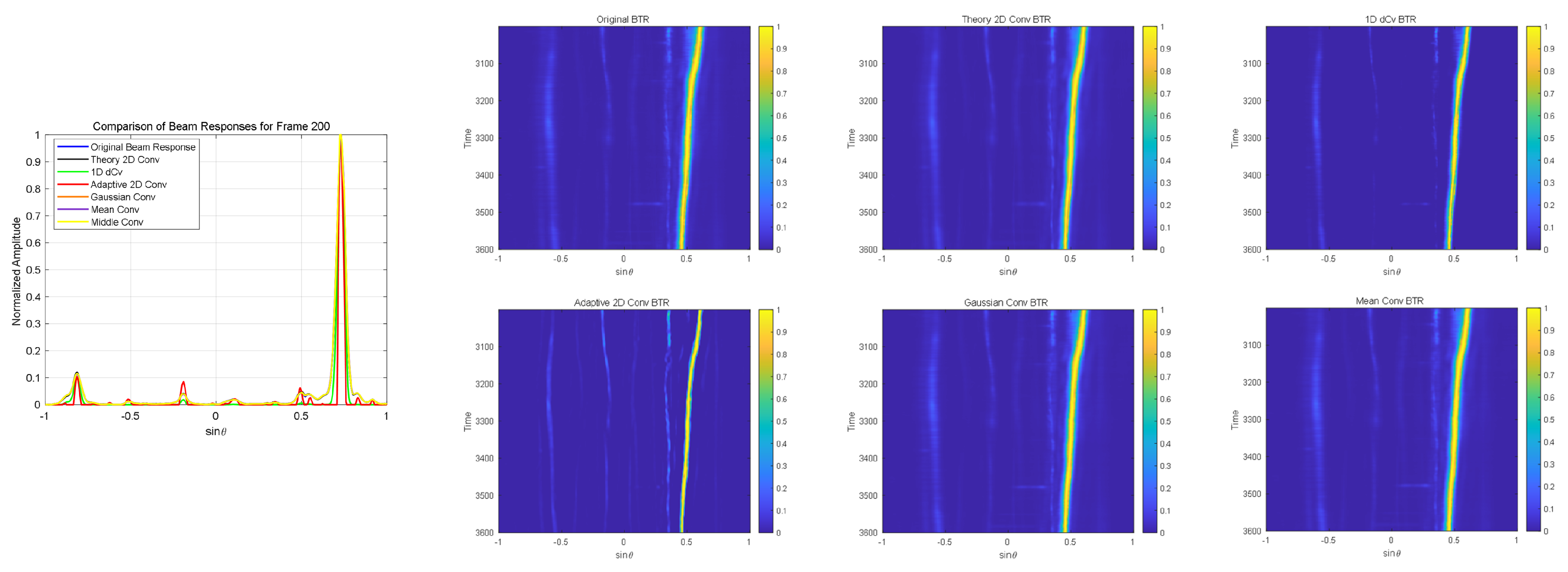
As shown in
Table 1, by comparing the SNRs of the three targets for each method, the performance of the targets under different SNR conditions can be clearly observed. When SNR = 0 dB, the SNRs for Target 1, Target 2, and Target 3 using the CBF method are 2.5 dB, 1.73 dB, and 2.17 dB, respectively. The Theory 2D Conv method shows even lower SNRs, with values of 2.5 dB, 1.63 dB, and 2.16 dB, performing worse than the CBF method. The 1D dCv method shows a slight improvement, with SNRs of 4.75 dB, 3.93 dB, and 4.32 dB for the three targets. However, the Adaptive 2D Conv method provides a significant enhancement, yielding SNRs of 26 dB, 22.5 dB, and 25.4 dB, outperforming all other methods. The results for the Gaussian Conv, Mean Conv, and Median Conv methods are relatively similar. The Gaussian Conv method yields SNRs of 2.5 dB, 1.6 dB, and 2.17 dB, while the Mean Conv method produces SNRs of 1.41 dB, 1.58 dB, and 2.19 dB. The Median Conv method shows SNRs of 2.5 dB, 1.54 dB, and 2.16 dB, which are comparable to those of the Gaussian and Mean Conv methods.
When SNR = −10 dB, the CBF method shows a decrease in SNR, with values of 1.41 dB, 0.45 dB, and 1.1 dB for Target 1, Target 2, and Target 3, respectively. The Theory 2D Conv method performs similarly, with SNRs of 1.41 dB, 0.55 dB, and 1.1 dB. The 1D dCv method provides a slight improvement, yielding SNRs of 2.71 dB, 1.18 dB, and 2.16 dB. However, the Adaptive 2D Conv method shows a significant enhancement, maintaining high SNRs of 18.85 dB, 24.07 dB, and 20 dB, outperforming all other methods. In comparison, the Gaussian Conv and Mean Conv methods show similar performance, with SNRs of 1.41 dB, 0.5 dB, and 1.1 dB for Gaussian Conv and 1.41 dB, 0.52 dB, and 1.11 dB for Mean Conv. The Median Conv method produces SNRs of 1.41 dB, 0.45 dB, and 1.11 dB, which are comparable to the Gaussian and Mean Conv methods.
When SNR = −15 dB, the SNRs for all methods further decrease. The CBF method shows relatively low SNRs, with values of 0.63 dB, 0.12 dB, and 0.37 dB for the three targets, while the 1D dCv method provides a slight improvement, with SNRs of 0.92 dB, 0.17 dB, and 0.56 dB. The Theory 2D Conv method performs the worst, yielding even lower SNRs of 0.63 dB, 0.11 dB, and 0.37 dB, which are worse than both the CBF and 1D dCv methods. In contrast, the Adaptive 2D Conv method demonstrates strong performance, maintaining higher SNRs of 8.94 dB, 17.27 dB, and 7.27 dB, significantly outperforming all other methods. The results for the Gaussian Conv and Mean Conv methods are similar, with SNRs of 0.63 dB, 0.12 dB, and 0.38 dB for Gaussian Conv and 0.63 dB, 0.05 dB, and 0.37 dB for Mean Conv. The Median Conv method shows SNRs of 0.63 dB, 0.09 dB, and 0.35 dB, which are comparable to those of the Gaussian and Mean Conv methods.
As shown in the last line of subfigures of
Figure 5, when SNR = −20 dB, due to the extremely low SNR, the weak energy targets are submerged by background noise, making it impossible to distinguish them in the original BTR obtained by CBF, as well as in the results obtained using other conventional or deconvolution algorithms. In contrast, our proposed Adaptive 2D Conv method is able to enhance the weak energy targets, allowing them to be differentiated from random noise. Notably, the Adaptive 2D Conv results show a more significant enhancement of the weak energy targets. Compared with the other methods, the Adaptive 2D Conv method has the narrowest main lobe width and nearly complete suppression of background noise. These results indicate that the Adaptive 2D Conv method significantly improves the target signal’s SNR under various conditions, especially in low SNR scenarios. This advantage makes the Adaptive 2D Conv method highly promising for practical applications, particularly for detecting weak targets by effectively suppressing background noise and maintaining high target distinguishability.