Abstract
The inherent randomness and intermittency of offshore renewable energy sources, such as wind and solar power, pose significant challenges to the stable and secure operation of the power grid. These fluctuations directly affect the performance of grid-connected systems, particularly in terms of harmonic distortion and load response. This paper addresses these challenges by proposing a novel harmonic control strategy and load response optimization approach. An integrated three-winding transformer filter is designed to mitigate high-frequency harmonics, and a control strategy based on converter-side current feedback is implemented to enhance system stability. Furthermore, a hybrid PI-VPI control scheme, combined with feedback filtering, is employed to improve the system’s transient recovery capability under fluctuating load and generation conditions. Experimental results demonstrate that the proposed control algorithm, based on a transformer-oriented model, effectively suppresses low-order harmonic currents. In addition, the system exhibits strong anti-interference performance during sudden voltage and power variations, providing a reliable foundation for the modulation and optimization of offshore wind–solar coupled hydrogen production power supply systems.
1. Introduction
Offshore wind and photovoltaic (PV) power generation have increasingly emerged as pivotal methods in the global transition to renewable energy and the pursuit of global carbon neutrality goals. As the global energy landscape shifts towards sustainability, these renewable sources play a critical role in reducing dependency on fossil fuels and mitigating environmental impacts. The wind–solar-electrolysis integrated hydrogen production system has attracted significant attention for its dual advantages in maximizing energy utilization efficiency and stabilizing power supply. This hybrid system not only facilitates flexible grid regulation but also enables the long-term storage of renewable energy through hydrogen, addressing the challenges of energy variability and enhancing grid resilience [1,2,3]. PV systems typically interface with the power grid through converters, which generate high-frequency harmonic components through their switching operations. These harmonics degrade power quality, significantly challenging the stability of the transmission network. Furthermore, offshore wind and solar installations are typically located in remote marine regions far from consumption centers, thereby requiring long-distance power transmission lines. This geographic configuration exacerbates harmonic distortion and compromises the disturbance immunity of the system. Additionally, the inherent intermittency and variability of wind and solar energy place stringent dynamic performance demands on the transmission network, increasing its susceptibility to power fluctuations and stability challenges [4,5,6].
In recent years, harmonic suppression and disturbance rejection have become key issues in the field of grid-connected power electronics, especially under renewable energy scenarios. Traditional approaches based on LCL/LLCL filters combined with PI controllers [7] are widely used for their simplicity and ease of implementation, yet they suffer from limited dynamic response and parameter sensitivity under grid fluctuations. Active damping techniques, such as capacitor current feedback or virtual impedance methods [8], improve stability but often increase control complexity or noise sensitivity.
Advanced control strategies, such as repetitive control [9], model predictive control (MPC), and resonance suppression using notch filters [10], can achieve better harmonic attenuation, but their implementation relies on accurate system modeling and high computational resources. In the field of disturbance rejection, disturbance observer-based control (DOBC) and sliding mode control (SMC) [11] are robust against parameter variations but may induce chattering or require complex tuning. Power electronic transformers (PETs) with multi-port configurations [12] offer enhanced flexibility for AC/DC hybrid interfaces. Fault-tolerant control strategies, such as the subspace current residual-based approach for DTP-PMSM [13], ensure system reliability under fault conditions. Accurate short-term forecasting of PV output using meteorological reconstruction and spatiotemporal features [14] helps balance supply and demand more effectively. Meanwhile, advanced pitch control methods [15] enhance wind energy capture while reducing structural loads. The application of these methods can improve the efficiency, reliability and prediction accuracy of renewable energy systems, which provide a valuable basis for the optimal design and control strategy of hybrid power systems.
Furthermore, machine learning and artificial intelligence have shown great potential in time-series modeling and prediction, offering new opportunities for harmonic forecasting and control optimization in power systems. For example, LSTM networks have demonstrated strong capabilities in capturing spatiotemporal data patterns [16], while reinforcement learning has been effectively applied to control design in complex dynamic systems [17]. In addition, feature-driven learning models have achieved notable success in analyzing high-dimensional data across diverse fields, such as genomics and network topology exploration [18,19]. Inspired by these advances, this study proposes to explore the integration of LSTM and reinforcement learning techniques into the harmonic prediction and control framework for offshore wind–solar coupled hydrogen production systems. This direction holds great promise for enhancing the intelligence and adaptability of such systems in future research.
This study focuses on optimizing harmonic control and disturbance rejection in the transmission system to address the aforementioned challenges. The proposed solution integrates innovative control strategies with harmonic suppression techniques to enhance system stability and significantly improve power quality. By combining advanced harmonic filtering devices with optimized disturbance rejection algorithms, the transmission system’s power quality is effectively enhanced. Moreover, this approach increases the system’s adaptability to fluctuations in wind and solar power output, thereby ensuring the long-term stability of offshore hydrogen production systems. Overall, the proposed methodologies offer a comprehensive and practical framework for improving grid resilience, supporting the reliable integration of renewable energy into hydrogen-based energy systems, and advancing the development of intelligent, adaptive power transmission infrastructures for future energy networks.
2. Design Method for Integrated Filtering of Transformers
2.1. Transformer Filtering Characteristics
Figure 1 illustrates a typical offshore wind–PV coupled hydrogen production system. In this configuration, wind and PV power serve as the primary energy for electrolysis, with the generated electrical energy converted into direct current (DC) by a power conversion system to supply the electrolytic cells. These cells then electrolyze seawater to produce hydrogen gas. This study focuses on the power conversion and transmission section of the wind–PV coupled hydrogen production system, specifically addressing the challenges of efficient energy conversion, harmonic suppression, and system stability.
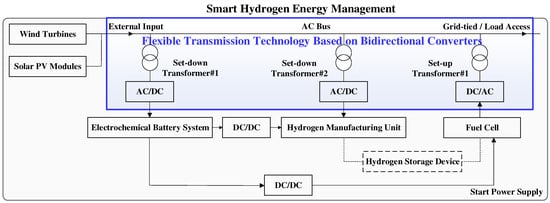
Figure 1.
Offshore wind–photovoltaic power coupled hydrogen production.
In high-power converters, reactive power compensation, harmonic suppression, and other methods typically require the installation of independent filters on the grid side. The advantage of this approach lies in its ability to mitigate the flow of harmonic currents into the grid, thereby enhancing overall power quality. However, the design and integration of these filtering branches are often intricate, and their interaction with the transformer can lead to undesirable consequences such as increased losses, larger physical dimensions, and complex coupling [20,21]. Moreover, the performance and capacity of the filters frequently fail to meet the desired outcomes. Previous studies have demonstrated that the secondary leakage inductance and the AC inductance of the transformer exhibit a series–parallel relationship, indicating that the secondary leakage inductance can theoretically replace part or all of the AC inductance [22]. In this context, leveraging the equivalent impedance of the transformer to directly configure the filter emerges as a highly effective solution to both economic and harmonic challenges. This approach not only minimizes harmonic interference, thus ensuring the stable operation of the power grid, but also satisfies the rapid response requirements for dynamic voltage control in four-quadrant converters. Furthermore, it optimizes the cost of converters, operational losses, and current harmonic distortion, which makes it an efficient and economically viable strategy. Figure 2 illustrates the main structure of a flexible transmission system.
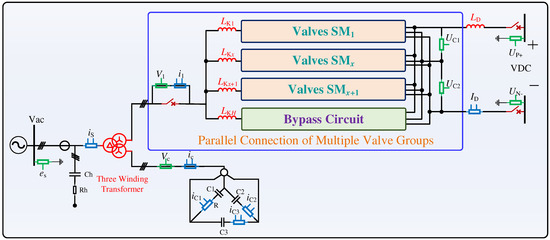
Figure 2.
Electrical main circuit of offshore wind power coupled hydrogen production system.
As shown in Figure 3. Through the equivalent relationship between mutual and self-impedances, each winding of the three-winding transformer can be equivalently represented by an inductance model scaled to the same voltage level. By connecting a capacitor in series with the third winding, the integrated transformer structure becomes equivalent to an LLCL circuit model. When a three-level converter is used in transmission systems, the basic filtering principle is that the branch of the third winding provides a low-impedance path to shunt high-frequency harmonics. This structure causes almost no attenuation of low-frequency signals (such as DC or fundamental current), but exhibits significant attenuation in the high-frequency harmonic band, effectively suppressing high-frequency noise generated by the converter or power system. It has a strong attenuation effect at specific frequencies, particularly harmonic frequencies. Compared with traditional L-type or LC-type filters, the LLCL structure offers superior performance in high-frequency harmonic suppression.
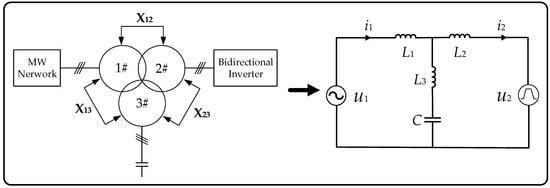
Figure 3.
Integrated design of transformers and equivalent filtering circuit.
X12, X13, and X23 represent the equivalent inter-winding short-circuit impedances of the transformer, referred to a common voltage level. Under the assumption that only mutual winding impedances are considered, the corresponding equivalent inductances L1, L2, and L3 can be calculated using the transformer’s self and mutual impedance relationships.
where Un is the rated voltage at the transformer’s voltage level, fn is the fundamental frequency, k is the turns ratio between the high-voltage and low-voltage windings, and S is the rated apparent power at that voltage level.
From the equivalent filter circuit, the relevant transfer functions are derived and employed as the plant model to facilitate systematic controller design.
The filtering characteristics can be analyzed based on these derived transfer functions.
The ripple current peak of the converter should be minimized to ensure stable operation and reduce system losses. Excessive ripple current increases system control complexity and shortens the lifespan of switching devices. The equivalent inductance on the converter side primarily affects the converter’s ripple current by limiting the current rate of change through the filter and acting as an isolation element to prevent high-frequency currents from directly flowing into the grid. The grid-side inductance mainly serves to further attenuate high-frequency noise and interference passing through the filter, particularly filtering harmonic frequencies originating from the grid. Together with the third winding inductance, the capacitor forms a resonant circuit that functions as a notch filter, diverting high-frequency noise to ground [23,24].
2.2. Parameter Design Rules
The evaluation of a three-winding transformer filter design involves two key aspects: First, the filter must effectively attenuate harmonic clusters generated by the converter, achieving high filtering efficiency. The grid-side current harmonic distortion rate, denoted as σ, is used to quantify the attenuation performance. A lower σ indicates reduced harmonic content in the grid-side current and improved harmonic suppression effectiveness. Second, while satisfying system design requirements, efforts should aim to minimize equivalent inductance and appropriately configure capacitance values. This not only reduces costs, but also enhances the system’s dynamic performance.
During the design process, the inductance value on the converter-side is typically determined first. The inductance values of the grid-side and filtering branch are chosen based on the actual transformer impedance. It is crucial to ensure that the resonance frequency meets design specifications while keeping the capacitor capacity within acceptable limits [25,26]. Meanwhile, filter parameters must satisfy further constraints. For example, the total inductance should not be excessively large to maintain the four-quadrant operational boundary of the bidirectional converter. Additionally, transformers must satisfy manufacturing requirements for short-circuit impedance while minimizing core and winding losses. Furthermore, the application scenario necessitates that the filtering device remains as compact as possible. Therefore, parameter design must comprehensively balance these constraints to achieve an optimal solution.
2.3. Parameter Design Constraints
A larger inductor on the converter side can effectively attenuate peak ripple current, thereby mitigating switching losses and enhancing system stability and reliability. However, increased inductance typically necessitates a larger magnetic core, potentially leading to larger transformer size and higher cost. Additionally, a higher inductance results in a larger time constant, thereby reducing the response speed of the system to load variations. Conversely, employing a smaller inductor on the converter side contributes to a more compact system design and enables a faster response to load fluctuations. Nevertheless, a reduction in inductance increases the ripple current, exacerbating switching device losses and potentially shortening their operational lifespan, so the inductance value on the converter side must be carefully considered:
where Im is the peak value of the rated phase current, fsw is the switching frequency, and Udc is the DC voltage.
The converter needs to operate stably in both positive and negative voltage and current directions in the four-quadrant operation mode. Therefore, it is required that the peak output voltage of the converter be high enough to cover the entire voltage vector range. In order to make the voltage vector endpoint run at any point on the unit circle, the total inductance range should be constrained:
where E is the fundamental wave vector of the grid phase voltage, and ω is the fundamental frequency.
The equivalent inductance range of the third winding is determined after establishing the inductance values for the converter side and the grid side. A capacitor with excessive capacitance absorbs excessive reactive power, causing the system voltage to rise, which may result in overvoltage or damage to electrical equipment; when the system is disturbed, changes in the reactive power output of capacitors may exacerbate the response fluctuations of the system and reduce its stability. To avoid the above problems, it is usually limited so that the reactive power absorption of capacitors does not exceed a certain proportion λ of the rated capacity, and the reactive power absorption of capacitors is controlled within a safe range to ensure the stability and reliability of the system:
where PN is the rated power and fn is the fundamental frequency.
The output voltage harmonics of a three-phase three-level PWM converter are mainly concentrated in the sideband harmonic clusters near the switching frequency and harmonics. The selection of inductance and capacitance values should ensure the maximum attenuation effect on the main secondary current harmonics, so that the filtered output current harmonics meet the grid connection standards. A multi-objective optimization model of LLCL filter parameters based on NSGA-II is established to minimize the total harmonic distortion (THD) of output current and maximize the system stability margin, and jointly optimize the parameters of the LLCL filter. Firstly, we set the maximum values of L1, L2, L3, and C as L1max, L2max, L3max, and Cmax, and the minimum step sizes as L1step, L2step, L3step, and Cstep according to the transformer design requirements, four quadrant operation constraints, ripple current constraints, etc. Secondly, based on the PWM of the inverter, we calculate the amplitudes of all characteristic subharmonic voltages (Vn,..., Vn+k, Vm,..., Vm+l).
The input of the application is the PWM calculation of the characteristic subharmonic voltage of the inverter, and the output is the transfer function GVI1 (s) of the inductance L1 corresponding to each harmonic current. The amplitude sum of each harmonic current can be obtained.
The total sum of the amplitudes of each harmonic current can be obtained.
The pseudocode of Algorithm 1 is as follows:
| Algorithm 1. Multi-objective optimization algorithm of LLCL filter parameters based on NSGA-II |
| Input: L1∈ [L1min, L1max], step: L1step L2 ∈ [L2min, L2max], step: L2step L3 ∈ [L3min, L3max], step: L2step N: population size M: maximum number of generations Output: Pareto-optimal set of filter parameters {L1, L2, L3, C} 1: Initialize population P(0) with N individuals, each with parameters {L1, L2, L3, C} within defined bounds 2: Evaluate each individual in P(0) using the following two objectives: (a) f1: Minimize THD of output current (b) f2: Maximize system stability margin 3: t ← 0 4: while t < M do 5: Perform non-dominated sorting on P(t) to form ranked fronts F1, F2, ... 6: Compute crowding distance for individuals in each front 7: Apply binary tournament selection based on rank and crowding distance 8: Generate offspring Q(t) using simulated binary crossover and polynomial mutation 9: Evaluate f₁ and f₂ for all individuals in Q(t) as in Step 2 10: R(t) ← P(t) ∪ Q(t) 11: Perform non-dominated sorting on R(t), and select the best N individuals to form P(t+1) 12: t ← t + 1 13: end while 14: Return Pareto-optimal set obtained from final generation P(M) |
In summary, the three-winding transformer filter demonstrates a high attenuation capability for specific harmonic components. By appropriately configuring transformer parameters and selecting capacitance values to adjust the resonant frequency, the filter effectively suppresses harmonics within clustered harmonic groups and leverages high-frequency attenuation to mitigate higher-order harmonics. The implementation of a three-winding transformer equivalent structure for harmonic filtering not only eliminates harmonics introduced by PWM modulation but also provides electrical solation between the grid and the power source. Additionally, this approach reduces both the cost and energy losses of the converter system, highlighting its significant practical value in enhancing system performance and reliability. The amplitude frequency characteristics are shown in Figure 4.

Figure 4.
Amplitude frequency characteristics of LLCL.
3. Closed Loop Control Strategy and Parameter Tuning Method
3.1. Comparison of Current Feedback Control Strategies
There are two primary current feedback methods for current control: one utilizes feedback from the grid-side current, while the other employs feedback from the converter-side current. Grid-side current feedback directly reflects variations in the grid current, enabling a more immediate response to grid fluctuations and disturbances. This allows the converter to adjust its output current in real time, thereby ensuring stable power transmission. However, due to the inherent delay introduced by the transformer when transmitting the grid-side current feedback signal, the system response is relatively slow. As shown in Figure 5a (x—pole, o—zero), regardless of how the system’s zero and pole points are configured, they cannot both enter the stability region, leading to poor stability and necessitating the incorporation of damping measures.
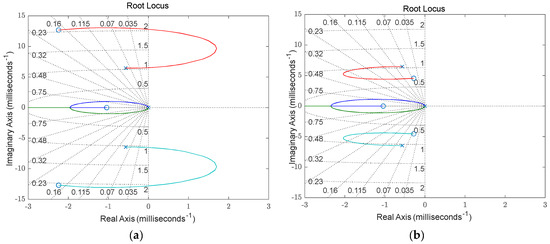
Figure 5.
Root locus diagrams of systems under different control strategies. (a) Root locus of the system during grid side current feedback. (b) Root locus of the system during current feedback on the converter side.
In contrast, converter-side current feedback enables precise control of the output current, effectively mitigating issues such as overload and overcurrent, while enhancing the overall performance and efficiency of the converter. This approach reduces the impact of grid disturbances on the control system, lessens the need for extensive grid current monitoring and processing, and achieves a faster dynamic response. As shown in Figure 5b (x—pole, o—zero), while converter-side current feedback eliminates the necessity for damping algorithms, their implementation may still improve the system’s stability margin. Considering these advantages, this study adopts a control strategy based on converter-side current feedback to optimize system stability and dynamic performance.
3.2. Controller Parameter Tuning Method Based on Fast Response
3.2.1. Double Closed-Loop Control Structure
The purpose of controlling a three-phase PWM converter is to maintain a constant current and voltage of the hydrogen manufacturing unit, ensuring stable operation under various working conditions; we control the current waveform on the AC side to approach a sine wave, track the voltage phase, and achieve high power factor operation. According to the control purpose, a dual closed-loop control structure is usually designed. As is shown in Figure 6, which includes a current inner loop and a voltage outer loop [25,26,27,28].
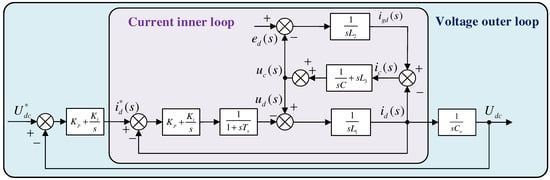
Figure 6.
Block diagram of current inner loop structure based on converter side current feedback.
3.2.2. Control Parameter Tuning Rules
The parameter tuning method of dual closed-loop control is commonly applied in engineering, a tuning approach based on bandwidth and stability margins which provides a foundation for achieving desirable dynamic characteristics. Due to the relatively small equivalent inductance value of L3, it is temporarily neglected when analyzing the dynamic response of the controlled system model. To prevent resonance frequency from adversely affecting system stability, the bandwidth (ωBW) of the current inner loop control system should be much smaller than the resonance frequency (ωres). Based on design experience, ωBW is generally taken as ≤(0.1~0.3) ωres. In response to the energy management requirements of higher-level intelligent collaborative control, the wind–solar coupling hydrogen production system requires a voltage response time in milliseconds. Consequently, the bandwidth of the inner loop should be 5–10 times greater than that of the outer voltage loop. Therefore, the upper limit of the current loop bandwidth is ωres, while the lower limit is 5 to 10 times the voltage loop bandwidth. Control parameters should be flexibly selected within this range to ensure optimal system stability.
This study investigates the impact of ωBW variation on the system’s step response while maintaining a fixed phase margin of φ = 80°. As shown in Figure 7a, selecting a small bandwidth results in a prolonged response time, characterized by increased rise time and settling time. Although this configuration offers relatively stable dynamic performance, it is better suited for applications where stability is prioritized over rapid response. With a medium bandwidth, the rise time and settling time are both reduced, achieving a balanced trade-off between dynamic performance and system stability. This configuration exhibits strong practical applicability for engineering scenarios that require both reasonable response speed and robustness. As the bandwidth further increases, the rise and settling times become significantly shorter, enhancing reference tracking performance. However, this improvement comes at the expense of reduced phase margins, increased oscillations, and amplified high-frequency noise, potentially causing system instability. Thus, such a configuration is more appropriate for applications demanding high dynamic response speeds but with less stringent stability requirements. In summary, bandwidth selection must strike a balance between response speed and stability. For traction power supply systems, a medium bandwidth presents a reasonable compromise, offering both a fast dynamic response and high stability.
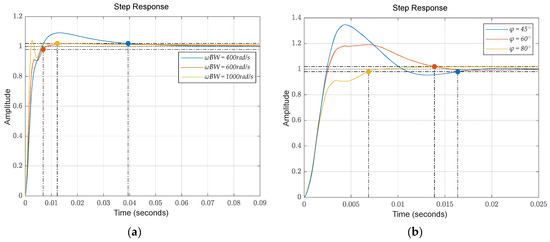
Figure 7.
The influence of control parameters on voltage response. (a) The influence of different bandwidths on voltage step. (b) The influence of different phase margins on voltage step.
Another study investigates the effect of phase margin variation on the step response of system with a fixed ωBW of 600 rad/s. As shown in Figure 7b, when a low stability margin is chosen, significant overshoot occurs, causing the voltage to exceed the power device’s threshold. Additionally, the time constant is prolonged, leading to poor dynamic performance. As the stability margin increases, the system’s damping ratio improves, resulting in a decrease in both overshoot and oscillation frequency, which leads to a smoother response curve. In complex traction power supply systems, increasing the phase margin enhances voltage stability and strengthens the system’s resilience to load disturbances, thereby reducing the risk of oscillations and instability under perturbations.
The current inner loop’s ωBW, constrained by the resonance frequency and the outer loop’s response speed limit, provides crucial guidance for PI controller parameter tuning. This ensures rapid tracking of the reference current while limiting overshoot, simultaneously addressing disturbance rejection and maintaining sufficient phase margin. When tuning the voltage outer loop parameters, the DC capacitor value in the bidirectional converter topology must be considered, as it increases the current bandwidth to compensate for the hysteresis effect caused by large capacitors. Maintaining a high stability margin allows the traction power supply system to operate safely within the specified voltage range under flexible and variable working conditions. Furthermore, it enables wide-range DC voltage adjustment, thereby optimizing power supply quality [29,30].
4. Non-Static Error Current Tracking and Transient Process Optimization
4.1. PI-VPI Low-Order Harmonic Suppression Control Algorithm
Considering the impact of dead time, the error voltage on the AC side contains odd harmonic components, including the 3rd, 5th, and 7th harmonics. However, due to the three-phase star-symmetrical structure of the bidirectional converter, harmonic components that are multiples of 3 in the grid-side current are effectively suppressed by the combined influence of the grid voltage and error voltage. Consequently, the AC side current harmonics primarily appear as 6k ± 1 (k = 1, 2, ...) harmonics, such as 5th, 7th, 11th, and 13th harmonics.
The 5th negative-sequence and 7th positive-sequence harmonics, when transformed into the d-q coordinate system, correspond to angular frequencies of −6ωg and 6ωg, respectively. Since cos(−6ωgt) = cos(6ωgt), the 5th and 7th harmonics combine to form a harmonic component at 6 times the fundamental angular frequency. Thus, by implementing tracking regulation and zero static error control of the 6k (k = 1, 2, ...) harmonic currents in the d-q coordinate system, effective suppression of low-order harmonics can be achieved. Figure 8 shows the PI-VPI control structure diagram.
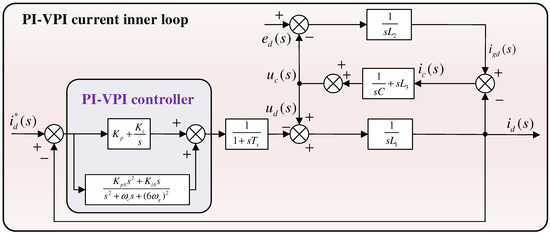
Figure 8.
PI-VPI control structure diagram.
The VPI controller expression in the s domain is defined as [31,32]
where Kph is the proportionality coefficient, Kih is the integration coefficient, ωc is the cutoff frequency, ωg is the fundamental frequency, and h is the number of resonances.
As is shown in Figure 9. The PI-VPI controller exhibits significant gain at the designated resonance frequencies, enabling it to track specified harmonic currents with zero steady-state error. For the 5th and 7th harmonics, the resonance frequency is set at six times the fundamental frequency, while for the 11th and 13th harmonics, it is set at twelve times the fundamental frequency. Analysis of the phase-frequency response shows that the controller’s phase shift is approximately 90° at 300 Hz and 600 Hz. Considering the phase delay introduced by digital control and the filter structure, the phase lead provided by the VPI effectively compensates for these delays, thereby facilitating precise control of the harmonic currents.
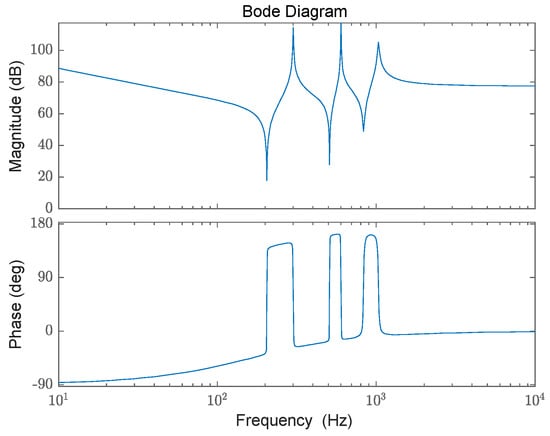
Figure 9.
PI-VPI amplitude frequency characteristics.
4.2. Band-Stop Filter Suppresses DC Pulsation
4.2.1. Improvement of Band-Stop Filter
The 6th harmonic ripple in the DC voltage is introduced into the voltage outer loop controller. Since the PI controller is a linear element, it cannot effectively suppress this pulsation component. Therefore, the same 6th harmonic component is superimposed onto the amplitude of the current reference output by the voltage outer loop. At this time, the current tracking command on the converter side fluctuates, and after inverse Park transformation in the d-q coordinate system, it manifests as 5th and 7th harmonics in the α-β coordinate system. Because the inverse Clarke transformation is a linear amplitude-preserving operation, the three-phase current in the a-b-c coordinate system also contains low-order harmonics at 5 to 7 times the fundamental frequency.
Previous research on suppressing the second harmonic component of the DC-side voltage in single-phase PWM rectifiers has shown that a point impedance filter with a notch frequency of 100 Hz can effectively filter the DC voltage sampling signal and suppress iterative current harmonics. The improved band-stop filter presented in this study exhibits superior filtering performance at specific notch frequencies, is designed with relative independence, and is well-suited for practical engineering applications [33,34]. The mathematical model of the second-order band-stop filter is as follows:
where K is the gain, ξ is the damping ratio, and ωn is the notch frequency.
The frequency response characteristics of BSF under different damping ratios are shown in Figure 10. The notch filter attenuates significantly in the amplitude of ωn and has little effect on other frequencies. As the value of ξ increases, the amplitude attenuation at ωn intensifies, providing better filtering performance. The wider the bandwidth, the more robust the parameter tolerance (such as frequency deviation). However, a large value of ξ may cause phase changes in a wide frequency range near the frequency ωn, resulting in a significant loss of stability margin in the voltage loop. When the value of ξ is large, the impact of the filter on the phase frequency characteristics of the voltage loop will be more pronounced. Therefore, when selecting the parameters of the filter, it is necessary to comprehensively consider the voltage loop-controlled object and controller parameters. Appropriately reducing the value of ξ can reduce the impact of the filter on the amplitude and phase frequency characteristics of the frequency range near ωn. Therefore, this article selects a moderate ξ = 0.5.
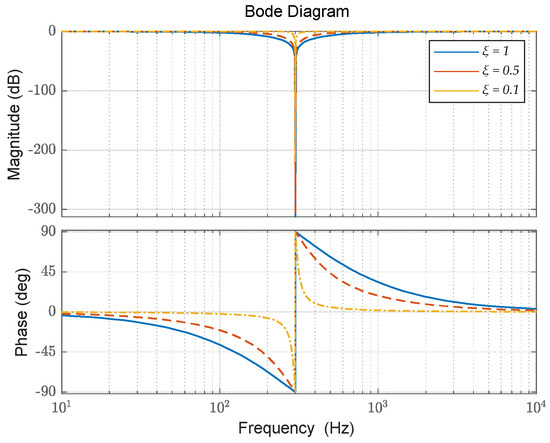
Figure 10.
Bode plots of notch filters with different quality factors.
4.2.2. Selection of Feedback Location
There are two options for introducing the digital filter in Figure 11: one method is to insert it into the DC voltage feedback path at position, filtering out the transmission of DC side voltage pulses to the control loop; another method is to insert it in front of the outer loop controller at position 2, filtering out harmonic components on the given current value, which is mathematically equivalent.
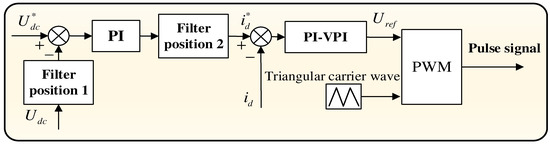
Figure 11.
Schematic diagram of filter position selection.
As shown in Figure 12, when introducing a band stop filter into the DC voltage feedback path, the amplitude–frequency characteristics remain nearly unchanged compared to when no filter is added. When introduced before the outer loop controller, the notch resonance peak is significantly increased, resulting in a decrease in the phase margin of the system and exacerbating the overshoot of the system. From the root locus (x—pole, o—zero), the stable open-loop gain is greater when there is no filtering and when filtering position 1 is introduced, while the gain is smaller and the steady-state error is larger when filtering position 2 is introduced, resulting in a slower response to input signal changes.

Figure 12.
Dynamic stability analysis of different filter introduction positions. (a) Bode plot at different filtering positions. (b) Root plot at different filtering positions.
We analyze the impact of filters on dynamic response according to Figure 13. BSF increases the overshoot of the system by changing the damping ratio and introducing unnecessary frequency components, resulting in typical second-order system oscillation characteristics. Differently, the introduction of position 1 in the filter is a negative feedback path, which directly affects the speed of DC voltage transmission. Subtracting the reference voltage value increases the error magnitude, leading to an increase in the response of the outer loop controller to the error and indirectly improving the response speed; the cutoff frequency at position 2 introduced by the filter is close to the excitation signal frequency, causing phase delay and resulting in a lagged frequency response that slows the system’s response speed. In summary, selecting the filter at position 1 represents a balanced choice that optimizes both system stability and dynamic response capability.
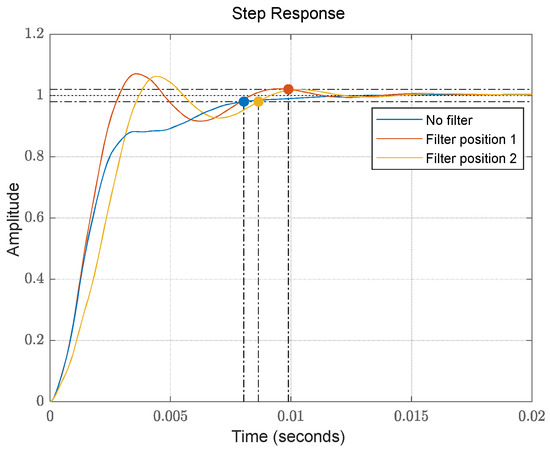
Figure 13.
Comparison of dynamic response performance at different filtering positions.
5. Simulation and Experimental Verification
5.1. Harmonic Suppression Experiment
The relevant experiments were conducted on the main circuit of a wind–solar coupled hydrogen production system to further validate the effectiveness of different low-order harmonic suppression algorithms. Relevant main parameters are shown in Table 1.

Table 1.
Main parameters related to hardware in the loop experiment.
There are twelve valve groups in the inverter, which adopt the carrier synchronous modulation scheme between them. The control signal transmission rate is the same (the current sharing effect between each valve group is consistent, without zero sequence current), and a midpoint voltage balance strategy and current sharing algorithm are added. The simulation step size is 2 μs, and the oscilloscope step size is 10 μs. Before starting the electrolytic cell, the DC side capacitor is charged through a charging resistor. When the PV power is greater than the DC load, power is supplied to the hydrogen production unit; when the PV power is less than the DC load, the energy of the hydrogen production device is fed back to the grid.
When the PV power is fully transmitted to the DC load, the experimental results are shown in Figure 14. The voltage of the high-voltage power line is 10.5 kV, the amplitude of the phase voltage is about 7.42 kV, and the amplitude of the current is about 77 A. The voltage and current phase characteristics are consistent. The total current amplitude on the converter side is about 1.9 kA. Due to the ∆-Y type of transformer, the converter-side current leads the grid-side voltage and current by 30 degrees. High-frequency currents on the converter side are extracted through the third-winding filtering branch, leaving only low-order amplified harmonics in the grid-side current. When no harmonic suppression strategy is adopted, the low-order harmonic current content is relatively high, and the current waveform’s sinusoidal quality is poor. After the original 6k ± 1st harmonic frequency shift, the DC voltage mainly shows 6th harmonic pulsation, and the high-frequency harmonic components are obvious, with the highest ripple peak reaching around 20 V. Algorithm 2 uses a PI-VPI controller, which suppresses voltage ripple on the DC side to around 7 V. The converter-side current shows high-frequency harmonic components with good sinusoidal waveform quality, and no significant distortion is observed in the grid-side voltage.
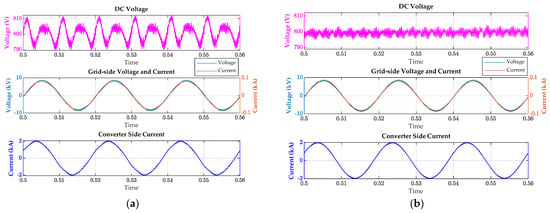
Figure 14.
Experimental waveform of undistorted current. (a) Algorithm 1: Pure PI. (b) Algorithm 2: PI-VPI combined with BSF.
To enable a more intuitive and quantitative comparison of the harmonic suppression capabilities of different algorithms, a frequency spectrum analysis was performed on the converter-side current, as summarized in Table 2. To verify the configuration effect of the three winding transformer filter, a cutoff frequency of 255 fundamental waves was set for THD statistics. When using Algorithm 1, the 5th harmonic content in converter-side current is 0.4%, and the 7th harmonic content is 0.25%, resulting in a THD255 of 2.11%. After equivalent filtering by the three-winding transformer, the 5th and 7th harmonics on the high-voltage grid side increase to 0.48% and 0.35%, respectively, while THD255 is reduced to 1.65%. When using Algorithm 2, the 5th and 7th harmonics of the low-voltage side current are significantly suppressed to 0.076% and 0.1%, respectively, while THD255 was 2.01%. Additionally, the 5th and 7th harmonics of the grid side were 0.077% and 0.14%, respectively, while THD255 is reduced to 1.27%, demonstrating Algorithm 2’s superior suppression of low-order harmonics. Algorithm 3 reduces the THD of the converter-side and grid-side currents by 5.6% and 69%, respectively. This indicates that the 5th and 7th harmonic currents of the converter are affected by DC voltage fluctuations, and therefore BSF can play a major inhibitory role. The experimental results demonstrate that Algorithm 2 has a better low-order harmonic suppression effect.

Table 2.
Current spectrum analysis.
As illustrated in the frequency domain spectrum, the fundamental component of the converter-side current is 1.897 kA, with the dominant harmonic components concentrated around the switching frequency and its second harmonic. The PWM strategy employed in this study is the SPWM with third-harmonic injection, which is functionally equivalent to the space vector PWM (SVPWM) method. This modulation introduces a characteristic six-segment timing pattern during vector synthesis, which is reflected as 6k (k = 1, 2, …) ripple components in the DC-side voltage. The converter-side current, tracking the reference signal, exhibits 6k ± 1 (k = 1, 2, …) residual harmonics in the three-phase stationary coordinate system after inverse Park transformation (Figure 15).
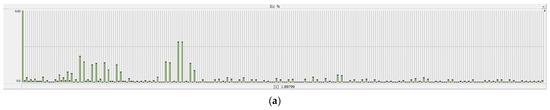
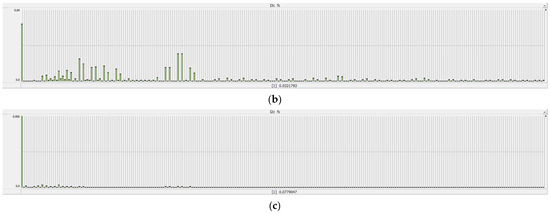
Figure 15.
Spectrum distribution. (a) FFT spectrum of single-phase current at the side of bidirectional converter. (b) FFT spectrum of single-phase current in filter branch of transformer. (c) FFT spectrum of single-phase current at grid-side.
The third winding of the transformer is configured as a filtering branch, designed to divert high-frequency components based on its cut-off frequency. Together with the optimized selection of the transformer’s equivalent parameters, this configuration ensures that only minimal low-order residual harmonics remain in the grid-side current. Specifically, the 5th and 7th harmonic currents are effectively suppressed by the VPI + BSF controller, with amplitudes of only 2.57 A and 4.59 A, well within the grid interconnection standard limits defined by IEEE 1547 (THD ≤ 5%) [35]. These results validate the rationality and engineering applicability of the integrated three-winding transformer design and the proposed PI–VPI + BSF control strategy.
5.2. Immunity Recovery Experiment
5.2.1. Power Mutation
Due to the fluctuation and intermittency of new energy generation, the system is often subject to power or load interference in the offshore wind–solar coupling hydrogen production system. This study tests the stability of the power supply system under sudden power changes caused by fluctuations in energy storage in the power grid through power anti-interference experiments.
Figure 16 shows the voltage and current waveforms of the grid side and the AC/DC side of the converter during a sudden change in hydrogen production state load. As shown in Figure 16a, when the system power suddenly increases at 0.7 s, the system cannot provide sufficient energy instantly, and the DC voltage shows a significant short-term drop at the moment of power sudden change. Then, it is quickly adjusted to the given value of 900 V after 5 ms and gradually stabilizes after 15 ms. The grid side and converter side provide more current to meet the load demand, so the current amplitude increases instantly and enters a stable state after a 5 ms fluctuation. As shown in Figure 16b, when the system power suddenly decreases at 0.7 s, due to the decrease in load, the excess energy on the DC side leads to a sharp rise in voltage, which then falls back to a stable value. The current demand provided by the grid side and converter side decreases, resulting in a decrease in current amplitude, which remains stable after a 5 ms fluctuation. The oscillation indicates that the system has undergone a transitional process during the transient period, and the rapid decay of oscillation demonstrates the effectiveness and high-bandwidth response capability of the current inner loop controller. Overall, the voltage on the high-voltage grid side is basically stable, reflecting the strong power supply capacity of the power grid; and the voltage fluctuation on the low-voltage side is relatively small, indicating that the system control effect is good. The damping ratio calculated from Figure 16a (ζ = 0.344) meets the recommended threshold (≥0.3) according to the IEEE 1547 grid-connection standard, and the settling time of 15 ms is well below the IEEE 1547 requirement of ≤30 ms. In Figure 16b, the calculated damping ratio is ζ = 0.267 based on the corrected peak value. Although slightly below the recommended value of 0.3, the system still complies with IEEE 1547 through an overshoot of 15% and a settling time of 13 ms. The current total harmonic distortion also meets the IEEE 1547 grid-connection requirement of ≤5%.
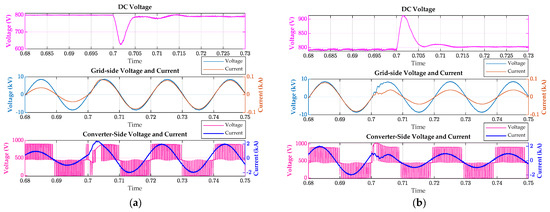
Figure 16.
Sudden load changes in rectification state, voltage, and current waveforms on the converter side, grid side, and DC side. (a) Sudden increase in load. (b) Sudden reduction in load.
Figure 17 shows the voltage and current waveforms of the grid side and the AC/DC side of the converter under sudden load changes in electric energy feedback (inverter) mode. As shown in Figure 17a, when the system power suddenly increases at 0.7 s, the efficiency of the dynamic response of the DC voltage becomes worse than that during traction, and the system cannot provide sufficient energy instantly. The DC voltage first shows a significant decrease, and then rises to 90% of the given value at 15 ms. With the adjustment of the controller, the voltage gradually increases and eventually returns to stability. The phase of the current on the AC side is opposite to that of the voltage. When the power decreases, the demand for current on the grid side and converter side decreases, resulting in a decrease in current amplitude. The transient process shows a basic stability after 10 ms. The step response exhibits a 7.41% overshoot, a settling time of 25 ms, and only a single mild oscillation. The damping ratio (ζ = 0.78) indicates an overdamped system, and together with a low Integral of Absolute Error (IAE = 0.75), it confirms the robustness of the controller. Overall, the performance complies with the IEEE 1547 grid-connection standard. Figure 17b shows the situation where the power of the system suddenly decreases at 0.7 s. At this time, the system gradually stabilizes after the DC voltage rises due to energy release, the load power decreases, and the current demand decreases, gradually decreasing to a stable value. The step response shows an overshoot of only 4.75% and a settling time of 30 ms. The damping ratio ζ = 0.91 further confirms an overdamped system. Compared to the rectifier mode, the proposed design demonstrates significant improvements in both stability and accuracy. From the perspective of the DC voltage recovery process, there is a certain adjustment delay in the system during sudden load changes, and DC-side energy storage devices can be added to ensure a stable DC voltage. Overall performance is stable.

Figure 17.
Sudden load changes in inversion state, voltage and current waveforms on the converter side, grid side, and DC side. (a) Sudden increase in load. (b) Sudden reduction in load.
5.2.2. Voltage Transients
The DC voltage mutation experiment was conducted in this study to simulate the rapid power fluctuations caused by complex weather conditions, such as sudden changes in offshore wind speed or sharp drops in solar irradiance. In wind–solar hydrogen production systems, where electrolyzers are directly powered by renewable sources, abrupt variations in generation can lead to significant transients in the DC bus voltage. Specifically, a sudden increase in wind speed may cause voltage overshoot, while cloud shading can lead to a sharp voltage drop. These mutations have a pronounced impact on the performance of the electrolytic hydrogen production system. On the one hand, voltage overshoot may result in overloading of the electrolyzer, accelerating degradation of the electrode materials or even causing permanent damage. On the other hand, voltage sags can interrupt hydrogen production, reducing energy conversion efficiency and compromising the stable operation of the entire system.
Figure 18 presents the voltage and current waveforms at the grid side, as well as the AC and DC sides of the converter, during rectification mode, when the grid delivers power and the DC voltage undergoes a sudden change. As shown in Figure 18a, when the DC voltage increases from the lower limit of four-quadrant operation to 800 V, the voltage rises rapidly. Due to the lag in the system’s dynamic response, this may cause transient small-scale oscillations, which subside and stabilize within approximately 12 ms. The voltage on the high-voltage grid side remains nearly unchanged, while the converter draws more current from the grid to maintain power balance. Consequently, the current increases instantaneously, and the fluctuation is a transient phenomenon during the adjustment process. Figure 18b shows that when the DC voltage drops from the setpoint of 800 V to the lower limit, it decreases rapidly with minor oscillations and stabilizes within 10 ms. The current drawn by the converter from the high-voltage grid decreases, resulting in a lower current amplitude. The grid voltage remains essentially unaffected due to the strong grid capacity. The converter-side current decreases significantly with slight fluctuation, gradually stabilizing after approximately 8 ms. The current rises sharply when the voltage increases and falls quickly when the voltage decreases, demonstrating the controller’s fast dynamic response to DC voltage variations. This meets the dynamic and transient performance requirements of the bidirectional converter system under load voltage changes. The stability of the grid voltage indicates strong grid robustness in handling load power fluctuations.
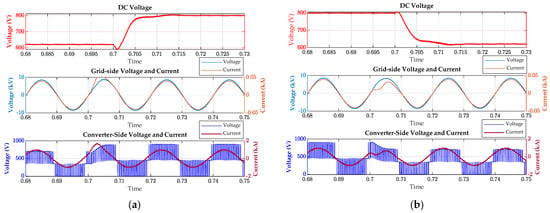
Figure 18.
Sudden voltage changes in rectification state, voltage and current waveforms on the converter side, grid side, and DC side. (a) Sudden increase in voltage. (b) Sudden reduction in voltage.
Figure 19 shows the voltage and current waveforms at the AC and DC sides of the grid side and converter under the energy feedback mode. It can be seen from Figure 19a that in order to prevent the system from generating voltage overshoot due to too-fast energy feedback, it is usually necessary to limit the feedback current or increase the delay of voltage control to reduce the dynamic response speed. The DC voltage gradually increased to 800 V, and then remained stable. At this time, the DC voltage rise time is about 8 ms, and it is adjusted to a stable state in 14 ms. When the DC voltage rises, the system needs to absorb more current from the high-voltage network side to meet the power balance requirements. The load power demand at the low-voltage side increases, resulting in a significant rise in the current, and the transient process lasts about 10 ms. It can be seen from Figure 19b that when the step-down operation is performed, the voltage gradually drops down and reaches a stable state after 10 ms. From the perspective of fluctuation degree, the controller can complete voltage regulation in a short time and tend to be stable, with strong dynamic performance. The stability time and overshoot all meet IEEE 1547 standards.
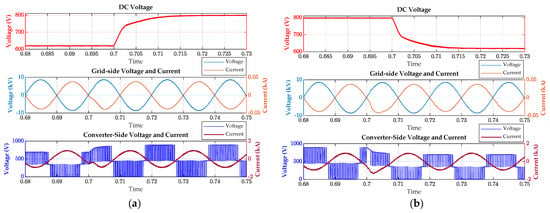
Figure 19.
Sudden voltage changes in inversion state, voltage and current waveforms on the converter side, grid side, and DC side. (a) Sudden increase in voltage. (b) Sudden reduction in voltage.
The above experimental results indicate that the PI–VPI + BSF control strategy proposed in this paper has good control stability and dynamic adjustment ability. The rapid recovery of voltage fluctuations indicates that the controller parameter tuning is reasonable, and the AC voltage changes show good adaptability to load transients. The rapid decay of current oscillations proves that the system has high dynamic performance and control accuracy. If further optimization is needed, the anti-interference ability of the voltage outer loop PI controller can be improved to reduce the amplitude of voltage overshoot or enhance reactive power compensation capability to reduce the impact of reactive power fluctuations on the system.
5.2.3. Fault Protection
To enhance system reliability and ensure operational robustness under fault conditions, the proposed system design follows the N-1 reliability criterion commonly adopted in power systems. Specifically, the converter is composed of twelve T-type three-level power modules, with each module functioning as an independent valve group. In accordance with the N-1 principle, the system’s performance is evaluated under the failure of any single valve group, representing the loss of one out of twelve key modules. The remaining valve groups will be evenly distributed again, while the total valve group current remains unchanged. The system maintains stable operation.
The bypass circuit, introduced earlier as part of the system architecture, serves as a key protection component in the event of DC-side short-circuit faults. Its primary function is to enable the rapid transfer and diversion of fault current during a bipolar short-circuit fault at the DC terminal. Under normal operating conditions, the bidirectional converter functions as intended, and the bypass thyristor remains in the off state due to the absence of a trigger signal. However, when the system encounters abnormal conditions such as inverter overload, internal faults, or short circuits on the AC side of the grid, the DC-side capacitors rapidly discharge toward the fault point. This results in a sharp voltage drop across the capacitors and a substantial increase in the voltage differential between the AC and DC sides. Consequently, a current surge occurs on the AC side of the inverter, potentially exceeding the overcurrent tolerance of power switching devices and risking damage to circuit components. We have designed an experiment to verify the short-circuit current shunt protection effect of the bypass circuit. The protective action is to lock all IGBT pulses and trigger the start of the bypass thyristor.
As shown in Figure 20a, the first subplot illustrates Udc and output power throughout the test period. Initially, Udc rises steadily as the DC-side capacitor charges, marking the transition to normal operation. At t = 0.6 s, a power command is issued, resulting in a noticeable increase in Idc. A grid fault is introduced at t = 1.0 s, causing a sharp voltage oscillation and transient disturbance in the output power. Following the activation of fault isolation and the bypass circuit, the system begins to recover, and the DC bus voltage gradually re-stabilizes at t = 1.2 s, indicating a total recovery time of around 200 ms. The second subplot presents Idc and its predefined protection threshold (Iset = 2.5 kA). As the load demand increases, Idc rises and eventually approaches Iset. When the fault-induced disturbance causes Idc to exceed the threshold, the protection logic is triggered at t ≈ 1.013 s, and the bypass thyristor is activated to divert the fault current away from the main converter path. The third subplot displays the voltage and current waveforms of the faulty valve group. During normal operation, the current remains stable. However, when the grid fault occurs, the current exhibits strong oscillations. Upon activation of the bypass path, the current through the valve group rapidly attenuates, and the voltage across it drops to approximately 280 V. This transition occurs within approximately 50 ms, indicating a fast fault-clearing and valve protection response. The fourth subplot shows the current flowing through the bypass thyristor. Once the fault is detected and protection is triggered, the thyristor conducts and redirects the high fault current away from the valve group. The bypass current stabilizes within 50 ms, reflecting effective fault current management and fast recovery capability. As shown in Figure 20b, under the energy feedback mode, the voltage stabilization time is approximately 10 ms longer than that in rectification mode. The Idc rises finally to 6.16 kA, which is 1.46 times higher than the predefined protection threshold. The valve group voltage drops to 280 V, and the total peak current reaches 0.7 kA. The bypass thyristor successfully commutates and shunts the fault current, carrying a peak current of 28.97 kA.

Figure 20.
Current distribution of bypass circuit fault protection. (a) Rectification state power grid fault. (b) Inversion state power grid fault.
These results confirm that the proposed system architecture is capable of withstanding typical grid-side faults and converter-level failures. The incorporation of bypass thyristors for fault current commutation significantly enhances the system’s fault ride-through capability, and protects IGBT components from operating at a rated current. This approach lays a solid foundation for improving the reliability and resilience of modular high-voltage DC transmission systems, particularly in complex and dynamic application scenarios.
6. Conclusions
This article aims to solve the problems of harmonic control and power disturbance recovery arising from fluctuations in wind and solar resources within offshore wind–solar integrated hydrogen production and transmission systems. The step-up transformer and high-power bidirectional converter are the research objects, and the filter design and converter control are studied. This article proposes harmonic suppression control and control strategy-related algorithms based on the harmonic characteristics of three-level topology, and verifies the theoretical research through simulation and experimental methods. Firstly, an integrated three-winding filter is designed to mitigate high-order harmonics generated by the bidirectional inverter. The parameter design method and optimization algorithm for the transformer are summarized, which can suppress harmonics, reduce converter losses and costs, and achieve improved dynamic performance and modulation efficiency. Secondly, a converter-side current feedback control strategy is proposed. A controller parameter tuning method with dual closed-loop bandwidth and stability margin is proposed based on dynamic and stability indicators. Finally, the suppression of low-order harmonic currents should be approached from a control perspective. In this paper, a PI-VPI controller is designed to effectively regulate the content of low-order harmonics. The introduction of a filtering element in the voltage outer loop can optimize response speed and suppress the transmission of sixth harmonic in the control loop of DC voltage. Simulation and experimental results confirm that the proposed PI–VPI + BSF control algorithm, based on converter-side current feedback, offers superior suppression of low-order harmonics. Under conditions of sudden voltage and power fluctuations, the control strategy exhibits strong anti-disturbance capability, making it a viable solution to enhance the stability of high-power offshore wind–solar coupled hydrogen production transmission systems.
Future work will focus on developing a unified mathematical framework that integrates the three-winding LLCL filter, converter dynamics, and control strategy to enable frequency-domain performance prediction. Nonlinear control approaches such as Lyapunov-based or sliding mode control will be explored to enhance system robustness under extreme conditions. The model will be extended to account for variable grid impedance caused by long offshore transmission lines, using small-signal and impedance-based stability analysis. Additionally, machine learning methods such as LSTM will be investigated for harmonic prediction based on fluctuating wind/solar inputs. Statistical metrics (e.g., mean THD, voltage ripple variance) will be incorporated to validate control robustness, and system efficiency under varying conditions will be evaluated and compared with conventional LCL filters to highlight practical and economic advantages.
Author Contributions
Conceptualization and funding acquisition, L.M.; writing—original draft, R.D. and Q.F.; writing—review and editing, C.W. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (grant number 2023YFB4005105).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nasser, M.; Megahed, T.F.; Ookawara, S.; Hassan, H. A Review of Water Electrolysis–Based Systems for Hydrogen Production Using Hybrid/Solar/Wind Energy Systems. Env. Sci. Pollut. Res. 2022, 29, 86994–87018. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, H.; Zhang, L.; Du, L.; Wang, Q.; Zhou, D. Optimization of a Wind-PV-Hydrogen Production Coupling System Considering Economy, Environment, and Reliability. Int. J. Hydrogen Energy 2025, 105, 441–457. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Rezazadeh, A. Hydrogen Fuel and Electricity Generation from a New Hybrid Energy System Based on Wind and Solar Energies and Alkaline Fuel Cell. Energy Rep. 2021, 7, 2594–2604. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Evaluation of Offshore Wind Energy Zones within Marine Spatial Planning: A Case Study in the Spanish Mediterranean Sea. Energy Rep. 2024, 11, 3461–3473. [Google Scholar] [CrossRef]
- Sun, Y.; Ai, H.; Li, Y.; Wang, R.; Ma, R. Data-Driven Large-Scale Spatial Planning Framework for Determining Size and Location of Offshore Wind Energy Development: A Case Study of China. Appl. Energy 2024, 367, 123388. [Google Scholar] [CrossRef]
- Su, X.; Wang, X.; Xu, W.; Yuan, L.; Xiong, C.; Chen, J. Offshore Wind Power: Progress of the Edge Tool, Which Can Promote Sustainable Energy Development. Sustainability 2024, 16, 7810. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Applicat. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Dannehl, J.; Fuchs, F.W.; Hansen, S.; Thøgersen, P.B. Investigation of Active Damping Approaches for PI-Based Current Control of Grid-Connected Pulse Width Modulation Converters with LCL Filters. IEEE Trans. Ind. Applicat. 2010, 46, 1509–1517. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. A Method for Synchronization of Power Electronic Converters in Polluted and Variable-Frequency Environments. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar] [CrossRef]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized Design of High Performance Shunt Active Power Filter With Output LCL Filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, X.; Zhang, H.; Yang, F.; Wu, Z.-G. A Novel Sliding Mode Estimation for Microgrid Control with Communication Time Delays. IEEE Trans. Smart Grid 2019, 10, 1509–1520. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Kong, X.; Zhou, J.; Shi, G.; Zang, J.; Wang, J. A Novel Multiple-Medium-AC-Port Power Electronic Transformer. IEEE Trans. Ind. Electron. 2024, 71, 6568–6578. [Google Scholar] [CrossRef]
- Hang, J.; Wang, X.; Li, W.; Ding, S. Interturn Short-Circuit Fault Diagnosis and Fault-Tolerant Control of DTP-PMSM Based on Subspace Current Residuals. IEEE Trans. Power Electron. 2025, 40, 3395–3404. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Zhang, W.; Li, Y.; Su, X. Short-Term Interval Prediction Strategy of Photovoltaic Power Based on Meteorological Reconstruction with Spatiotemporal Correlation and Multi-Factor Interval Constraints. Renew. Energy 2024, 237, 121834. [Google Scholar] [CrossRef]
- Wan, A.; Gong, W.; Iqbal, A.; AL-Bukhaiti, K.; Ji, Y.; Duer, S.; Ma, S.; Yao, F. Robust Loop Shaping Design Pitch Control of Wind Turbine for Maximal Power Output and Reduced Loading. Energy 2025, 319, 135136. [Google Scholar] [CrossRef]
- Wood, D.A. Spatio-Temporal Attributes of Varicella-Zoster Case Number Trends Assist with Optimizing Machine Learning Predictions. Mar. Environ. Data Inf. Netw. 2023, 1, 43–53. [Google Scholar] [CrossRef]
- Valadbeigi, A.P.; Sedigh, A.K.; Lewis, F.L. H∞ Static Output-Feedback Control Design for Discrete-Time Systems Using Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 396–406. [Google Scholar] [CrossRef]
- Charles, S.; Natarajan, J. Identification of Key Gene Modules and Novel Transcription Factors in Tetralogy of Fallot Using Machine Learning and Network Topological Features. Mar. Environ. Data Inf. Netw. 2023, 1, 27–34. [Google Scholar] [CrossRef]
- Adeyanju, S.A.; Ogunjobi, T.T. Machine Learning in Genomics: Applications in Whole Genome Sequencing, Whole Exome Sequencing, Single-Cell Genomics, and Spatial Transcriptomics. Mar. Environ. Data Inf. Netw. 2024. [Google Scholar] [CrossRef]
- Adamas-Pérez, H.; Ponce-Silva, M.; Mina-Antonio, J.D.; Claudio-Sánchez, A.; Rodríguez-Benítez, O.; Rodríguez-Benítez, O.M. A New LCL Filter Design Method for Single-Phase Photovoltaic Systems Connected to the Grid via Micro-Inverters. Technologies 2024, 12, 89. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Wang, T.; Wang, K. Optimization of Passive Damping for LCL-Filtered AC Grid-Connected PV-Storage Integrated Systems. Electronics 2025, 14, 801. [Google Scholar] [CrossRef]
- Jena, K.; Kesh, R.; Kumar, D.; Padhy, A.P.; Ahmed, M.I.; Panigrahi, C.K. Transformer-Less Multilevel Inverter (TMLI) with Reduced Device Count and Voltage Stress. e-Prime-Adv. Electr. Eng. Electron. Energy 2024, 7, 100417. [Google Scholar] [CrossRef]
- Wang, X.; Zhuang, R.; Cai, J. Theoretical Analysis of a Fractional-Order LLCL Filter for Grid-Tied Inverters. Fractal Fract. 2023, 7, 135. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Q.; Zhang, G.; Zhang, H.; Liu, K.; Yue, X. Novel Active Damping Design Based on a Biquad Filter for an LLCL Grid-Tied Inverter. Energies 2023, 16, 1093. [Google Scholar] [CrossRef]
- Bolsi, P.C.; Prado, E.O.; Sartori, H.C.; Lenz, J.M.; Pinheiro, J.R. LCL Filter Parameter and Hardware Design Methodology for Minimum Volume Considering Capacitor Lifetimes. Energies 2022, 15, 4420. [Google Scholar] [CrossRef]
- Abbas, H.H.; Shafiee, Q.; Bevrani, H. Optimal Passive LCL Filter Design for Grid-Connected Converters in Weak Grids. Electr. Power Syst. Res. 2024, 235, 110896. [Google Scholar] [CrossRef]
- Blachuta, M.; Bieda, R.; Grygiel, R. High Performance Single and Double Loop Digital and Hybrid PID-Type Control for DC/AC Voltage Source Inverters. Energies 2022, 15, 785. [Google Scholar] [CrossRef]
- Zhou, Z.; Song, J.; Yu, Y.; Xu, Q.; Zhou, X. Research on High-Quality Control Technology for Three-Phase PWM Rectifier. Electronics 2023, 12, 2417. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Hussain, S.M.S.; Ustun, T.S. Optimal PI Controller Based PSO Optimization for PV Inverter Using SPWM Techniques. Energy Rep. 2022, 8, 1003–1011. [Google Scholar] [CrossRef]
- Suid, M.H.; Ahmad, M.A. Optimal Tuning of Sigmoid PID Controller Using Nonlinear Sine Cosine Algorithm for the Automatic Voltage Regulator System. ISA Trans. 2022, 128, 265–286. [Google Scholar] [CrossRef]
- Marzo, I.; Muguruza, I.; Sanchez-Ruiz, A.; Abad, G.; Fernandez-Rebolleda, H.; Costa-Iriarte, J.J.; Barrena, J.A. Zero-Sequence Controller Requirements and Comparison for a Delta-CHB STATCOM under Unbalanced Operation. Int. J. Electr. Power Energy Syst. 2024, 156, 109785. [Google Scholar] [CrossRef]
- Zhou, L.; Han, W.; Qi, J.; Zhou, Z. Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions. Appl. Sci. 2023, 13, 5983. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, Y.; Ma, Y.; Yang, L.; Yang, X.; Zhang, B. DC Bus Voltage Control of Grid-Side Converter in Permanent Magnet Synchronous Generator Based on Improved Second-Order Linear Active Disturbance Rejection Control. Energies 2020, 13, 4592. [Google Scholar] [CrossRef]
- Kwon, J.-H.; Zhou, G.; Kim, C.-S.; Park, S.-J.; Wang, Y. A Second Harmonic Current Suppression Strategy Based on a Digital Band-Stop Filter with Center Frequency Tracking Grid Frequency. IEEE Access 2025, 13, 13250–13263. [Google Scholar] [CrossRef]
- IEEE 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: New York, NY, USA, 2018. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).