Experimental Study on Dynamic Responses of Floating Offshore Wind Turbines and Its Validation Against the Vector-Form Intrinsic Finite Element Method

Abstract

In this study, a novel rigid–flexible coupled computational model for floating offshore wind turbines (FOWTs) is developed using the vector-form intrinsic finite element (VFIFE) method, named VFIFE-FOWT. This framework integrates multi-body dynamics and the VFIFE method to establish a comprehensive dynamic model for FOWTs, enabling high-fidelity simulations of FOWT systems. Validation of the VFIFE-FOWT model is conducted through comparisons with results from the industry-standard software OpenFAST, together with experimental data from a 1:80 scale model test of a shallow-draft stepped Spar platform equipped with a NREL 5MW wind turbine. The results demonstrate good agreement, verifying the accuracy and reliability of the proposed VFIFE-FOWT framework for predicting the dynamic behavior of FOWTs.

1. Introduction

As the global transition toward renewable energy accelerates, floating offshore wind turbines (FOWTs) have emerged as a cornerstone technology for unlocking deepwater wind resources, offering scalability and adaptability to harsh offshore environments. The 2024 report by the Global Wind Energy Council (GWEC) underscores the critical role of floating wind turbines in achieving net-zero goals, projecting a tenfold increase in installed capacity by 2035 [1,2,3]. However, their dynamic behavior under combined wind, wave, and current loads introduces complex challenges, including nonlinear fluid–structure interactions (FSI) and multi-body couplings that demand advanced modeling frameworks for reliable design optimization [4,5].

Conventional finite element methods (FEMs) are widely used in offshore engineering. A nonlinear finite element (FEM) of a spar-type FOWT is established to investigate the collision motion caused by a ship [6]. Gu and Chen developed a dynamic calculation program for mooring lines using the FEM method. They then integrated this program with a platform hydrodynamic analysis program based on the computational fluid dynamic (CFD) method to analyze the motion response of a semi-submersible floating wind turbine [7]. Song et al. proposes a coupled CFD and finite element analysis (FEA) approach to numerically simulate the motion and deformation responses of an NREL 5 MW FOWT with a catenary mooring system [8].

While the FEM method faces limitations in accurately resolving large-amplitude motions and flexible component deformations in FOWTs, studies such as Liu et al. [9] have shown that Lagrangian-based FEMs experience up to 20% errors in mooring line tension predictions during extreme wave conditions due to mesh distortion. Therefore, many scholars adopted multi-body dynamics (MBD) methods to establish a motion analysis framework for FOWTs, within which FEMs are integrated to locally analyze structural deformations, aerodynamic forces, and hydrodynamic forces. Al-Solihat and Nahon [10] developed a nonlinear flexible multi-body dynamic model for a spar-type FOWT using Lagrange’s equations, considering the coupled rigid body motions of the platform and elastic deformations of the tower. Using Kane’s approach, Liu et al. [11] establish an 8-DOF multi-rigid-body (MRB) module with quasi-coordinate Lagrange’s equation considering a flexible tower module. Luo et al. [12] develop a 14-DOF semi-submersible FOWT using the Lagrange energy method to derive governing equations by integrating kinetic/potential energies and external wind–wave loads in a global coordinate system. Barooni et al. [13] present an open-source comprehensive numerical model that integrates wind inflow, rotor aerodynamics, structural dynamics, wave hydrodynamics, and mooring-line dynamics using methods like blade element momentum theory and Morison’s equation. Guo et al. [14] published an open-source multi-body modeling framework for FOWT (TorqTwin), which uses Kane’s method and the SymPy (1.14.0) library to handle rigid and flexible bodies. Beginners researching the modeling of floating wind turbines should give more attention to these open-source programs and are advised to develop their own analysis programs based on them.

This study adopts a numerical modeling method different from all of the research approaches described above. Here, a motion analysis model is developed for floating wind turbines, which is the vector-form intrinsic finite element (VFIFE) method [15,16]. The VFIFE method is a numerical analysis approach based on vector mechanics theory, avoids global stiffness matrix assembly, and efficiently handles complex mechanical behaviors. It contrasts in basic theory with traditional finite element methods, and has shown progress in various applications [17]. In recent years, the VFIFE method has been widely applied to the analysis of offshore engineering structures, especially in the complex motion analysis of marine risers. Li et al. [18,19], respectively, apply the VFIFE method to conduct nonlinear analysis of three-dimensional marine risers and introduce a novel integrated model with a wake oscillator for vortex-induced vibration (VIV) prediction in top-tensioned risers. Yu et al. [20] propose a modified lateral riser–seabed interaction model integrated with the VFIFE method to simulate three-dimensional trench formation induced by cyclic out-of-plane motions of steel catenary risers (SCRs). Xu et al. [21,22] present refined VFIFE models integrated with an equivalent beam particle technique to investigate the dynamic behaviors of deepwater S-lay pipelines in the overbend section and J-laying pipelines in the touchdown zone (TDZ), enabling precise simulations of complex pipeline dynamics under different laying configurations. Wu et al. [23] employ the VFIFE method to develop a three-dimensional dynamic model for deep-sea flexible pipes, enabling efficient analysis of static and dynamic behaviors under large displacements and small strains, and validate its reliability through comparisons with commercial software, demonstrating its applicability to complex marine engineering problems like flexible mining pipes. Additionally, the VFIFE method has been used in the motion analysis of FOWTs [24,25], integral vertical transport system of deep-sea mining [26], the stress analysis of offshore substation structures [27], and the motion analysis of offshore mooring systems [28].

The Hywind Spar concept was one of the first applied in practical engineering and remains one of the most mature technologies to date. However, due to the greater water depth in European seas compared to the South China Sea, where the water depth is only around 100 m even 20 km offshore, the Hywind Spar concept is unsuitable for Chinese waters. Thus, Jiang et al. [29] developed a shallow draft stepped Spar platform suitable for 100 m water depth based on the Hywind Spar concept. This paper describes the numerical modeling and model test research on the shallow draft stepped Spar platform using the VFIFE method. The purpose of the current study is to establish the FOWT coupled model based on the VFIFE method (VFIFE-FOWT), and the scaled FOWT model test is conducted to verify the accuracy of the coupled VFIFE-FOWT model. Considering Froude number and elasticity similarity, the similarity theory for the FOWT is investigated in Section 2; Section 3 describes the experimental model design, including the hub, nacelle and tower models, FOWT supporting structure model, and mooring anchor chain models. The numerical simulation study of the FOWT coupled model under typical wave loads on the basis of the VFIFE method is reported in Section 4. Furthermore, the model tests of the FOWT under regular wave conditions were performed; the test results are compared with the numerical simulation by taking the shallow draft stepped Spar platform as the research object, and the correctness of the time-domain coupled motion analysis model of the VFIFE-FOWT is verified. Finally, Section 6 summarizes the conclusions drawn from the study.

2. Similarity Theory

For the model test results to realistically reflect the forces and movements of the prototype structure, there are some similar criteria that need to be met when performing the FOWT dynamic model test, which are the basis for scaling the prototype wind turbine and returning the test results to the prototype scale. In this experiment, only wave load tests were conducted, and wind loads were not considered. Therefore, geometric similarity and the Froude similarity law were adopted for the design of the scaled model, and the similarity in thrust was not simulated in the experiment. Therefore, the relevant similarity theories for wind load scaling are not introduced in this section. The correctness of the scaled model of the NREL 5MW wind turbine and tower has been verified in Reference [30]. In this study, the geometric scale ratio is represented by $\lambda$, the prototype size is represented by the subscript s, and the model size is represented by the subscript m.

2.1. Geometric Similarity

The linear dimensions between the prototype and the model need to meet the geometric similarity relationship, including length, thickness, wave height, wavelength, draft, etc., and the geometric similarity can be expressed as [31]:

$${\displaystyle \frac{L_s}{L_m}}=\lambda$$

(1)

2.2. Froude Similarity

Gravity and inertia forces also need to be satisfied between the model and prototype wind turbine; therefore, the Froude number is introduced in this FOWT dynamic model test, which can be described as [32]:

$$Fr={\displaystyle \frac{U_m}{\sqrt{g{L}_m}}}={\displaystyle \frac{U_s}{\sqrt{g{L}_s}}}$$

(2)

where $U$ is the wave velocity; g is the gravity acceleration; L is the geometric length.

Waves based on laboratory wave-making machine simulations should be like the Strouhal number, which is expressed as [32]:

$$St={\displaystyle \frac{U_m{T}_m}{L_m}}={\displaystyle \frac{U_s{T}_s}{L_s}}$$

(3)

where T is the wave period.

The similarity of the viscous forces between the model and the prototype can be expressed by the Reynolds number, as shown in Equation (5) [32].

$$\mathit{Re}={\displaystyle \frac{L_m{V}_m}{\nu }}={\displaystyle \frac{L_s{V}_s}{\nu }}$$

(4)

where $\nu$ is the kinematic viscosity of the fluid.

2.3. Structural Stiffness Similarity

The flexibility of the wind turbine tower has a significant impact on the motion of the FOWT system, especially the pitch motion response of the structure, so the wind turbine model and the prototype tower need to meet the similar requirements of structural stiffness, namely [32]:

$${\displaystyle \frac{E_s{I}_s}{{\left(EI\right)}_m}}={\lambda }^5$$

(5)

where E is the elasticity modulus of the tower material; I is the cross-section moment of inertia of the tower. The similar stiffness of the towers ensures that the natural frequencies and deformations in the model and prototype are consistent.

Without considering Reynolds number similarity, the scaling relationships between the physical quantities in the model test and those in the prototype wind turbine can be derived based on geometric similarity, Froude number similarity, Strouhal number similarity, and structural stiffness similarity; the results as listed in

Table 1. Scaling factors between the experimental model and prototype of FOWT.

Project	Symbol	Scale	Project	Symbol	Scale
Length	[L]	$\lambda$	Mass	[M]	${\lambda }^3$
Area	[L2]	${\lambda }^2$	Time	[T]	$\sqrt{\lambda }$
Volume	[L3]	${\lambda }^3$	Frequency	[T−1]	$1/\sqrt{\lambda }$
Water density	[ML−3]	$\lambda \rho =1$	Force	[MLT−2]	${\lambda }^3$

. The derivation process can be found in Reference [32].

3. Experimental Model Design

3.1. Wind Turbine Blade Model

The blade model employed in this test is derived from the NREL 5 MW wind turbine. Subsequently, scaling is performed based on geometric similarity and Froude number similarity. The same blade scaling method as that described in Reference [33] is adopted. The blade model is made into a hollow structure wrapped by two layers of carbon fiber composite materials, and a lightweight aluminum alloy base that can be manually adjusted for pitch angle is installed at the root of the blade, which is shown in Figure 1. The total weight of a single blade, including the metal base, is 97.53 g, which is a large difference from the expected 34.5 g. When scaled according to geometric similarity and Froude number similarity, the final blade model should have a length of 0.769 m and a mass of 34.5 g, respectively. It should be owing to the mass of the aluminum base and the larger scale ratio of the model test, which magnifies the error. Therefore, if a smaller scaling ratio is chosen in the experiment, the experimental model will be more accurate.

3.2. Hub, Nacelle and Tower Models

The test model of the hub and nacelle is shown in Figure 2a,b, which is made of lightweight, high-strength aluminum alloy material. To facilitate the control of the quality of the nacelle, a hollow design is adopted for this study, and a servo motor is installed at the nacelle tail to drive the rotating blades, as shown in Figure 2b.

The mass of the land-based tower for the NREL 5 MW is 347,460 kg, and the mass of the scaled tower is 0.514 kg [34]. To meet the requirements of the scaled mass, the tower is made of lightweight 6061 aluminum, and the tower model is designed as an internal hollow structure with an external equal cross-section, as shown in Figure 3. A six-component force sensor is installed at the top of the tower, which is located at the lower end of the nacelle. Including the six-component force sensor, the mass of the scaled tower model is 0.514 kg. Considering the mass of the scaled model’s tower, six-component force sensor, and flange at both tower ends, the overall center of mass position is obtained through the center of mass calculation formula. Additionally, the first-order mode of the scaled tower is consistent with the value reported in the NREL 5 MW documentation.

The mass values of the prototype and scaled model of the blade, hub, nacelle, and tower are summarized in

Table 2. Parameters of the prototype and scaled model of the NREL 5MW wind turbine.

Project	Prototype/kg	Scaled Model/g
Blade (three)	53,220.00	292.60
Hub	56,780.00	89.00
Nacelle	240,000.00	523.10
Tower	291,995.77	514.50

.

3.3. Floating Foundation Model

In this study, the shallow draft stepped Spar platform designed by Tian et al. [29] is adopted to support the NREL 5 MW wind turbine. The design of the stepped Spar platform is inspired by the OC3 Hywind Spar, based on which the draft of the platform is greatly reduced through the stepped design, and the stepped changing cross-section can act as a heave plate to reduce the heave of the platform. The platform is scaled using geometric similarity and Froude number similarity to ensure that geometric dimensions, mass distribution, and moment of inertia meet the similarity theory. The installed water depth of the platform is 80 m, the drainage is 17,938 m³, the buoyancy position is −31.286 m, and the center of gravity position is −34.925 m. The still water surface is used as the reference plane, and vertical upward is designed as positive. The catenary mooring system is used for positioning, and the fairlead hole is located 6 m below the still water surface. The prototype geometry of the platform is shown in Figure 4. The scale ratio is 80, and the parameters for the prototype and scaled model are listed in

Table 3. Parameters of the prototype and scaled model of the shallow draft stepped Spar platform.

Parameter	Unit	Prototype	Scaled Model
Draft	m	50	0.625
Total mass	kg	18,324,466.890	32.790
Center of mass below SWL	m	−34.755	−0.434
Center of buoyancy below SWL	m	−31.286	−0.391
Drainage	m3	17,938.035	0.035
Longitudinal radius of inertia	m	49.750	0.622

.

The scaled model of the platform in SolidWorks 2020 is shown in Figure 5a, in which considering that the diameter of the lowest cylinder of the platform is larger, the cabin design is made in the interior by means of partition. The whole cylinder is divided into four cabins, and each cabin adopts a certain height of aluminum ingot ballast. The geometry of the ingot used for ballast is shown in Figure 5b, and the height of the ingot is 55 mm.

3.4. Mooring Line Model

The scaled mooring line model used in the experiment is shown in Figure 6. Due to the insufficient width of the test tank (the wide of tank is 4 m), the three mooring lines of the catenary-type floating wind turbine cannot be arranged at 120-degree intervals as in a traditional mooring system. Instead, in the process of this test, the arrangement of the three mooring anchor chains of the FOWT in the water tank is designed in the form shown in Figure 7, in which the direction of the No. 1 mooring from the fairlead hole to the anchor point is the wave propagation direction, and the distance between the anchor points of the No. 2 and No. 3 moorings is 4 m wide in the test tank. During the scaling of the mooring lines, we focused on ensuring the similarity in length, mass, and stiffness between the prototype and the scaled model. What needs illustration is that the objective of this experiment was not to match the real model, but to validate the calculation accuracy of the VFIFE-FOWT model. Therefore, the delta connection was excluded in the experimental setup, and the additional yaw stiffness introduced by the delta connection was also not considered in the numerical model.

According to the scheme of Figure 7, if the No. 1 mooring and the No. 2 and No. 3 moorings are the same, then due to the asymmetry of moorings, the mooring force in the horizontal direction is no longer balanced; hence, the static balance position of the platform will deviate to the left from the preset position. To make the static equilibrium position of the platform as close as possible to the predetermined equilibrium position, the length of the prototype mooring anchor chain No. 1 is selected as 520 m, and the length of the No. 2 and 3 moorings is 528 m. Parameters of the mooring lines are shown in

Table 4. Prototype and scaled model parameters of the mooring lines.

Parameter	Unit	Prototype	Scaled Model
Radius	m	500	6.250
Length	m	#1: 520	#1: 6.50
		#2: 528	#2: 6.60
Distance between the fairlead and the still water surface	m	6	0.075
Depth of the anchor points from the still water surface	m	80	1.00
Axial stiffness	N	2.3597 × 109	4608.789
Breaking force	N	2.580 × 107	49.16
Mass	kg/m	656.775	0.103
Wet weight	kg/m	571	0.089
Pre-tension	N	#1: 1.5 × 106	#1: 2.93, 2.84
		#2: 9.8 × 105	#2: 1.91, 1.68

.

3.5. Load Cases

The wave-making equipment uses a servo motor to drive the push plate. According to the characteristics of the wave-making equipment, the Siemens servo control system is selected in this model test, and the host computer directs the controller in real time through the network. The wave-making period range of the tank is 0.5–5.0 s, the maximum effective wave height of the irregular wave is 0.35 m, and the maximum wave-making depth is 1.8 m, which can fully meet all the wave conditions for this test. In addition, the wave height and wave period errors are less than 5%, which ensures the accuracy of the test.

The main purpose of this study is to carry out the coupled model test of an FOWT under only wave loads, and the correctness and accuracy of the time-domain coupled numerical model of the FOWT are verified through the test results. The dynamic response of the FOWT was limited to wave-only scenarios and the wind conditions were not tested in this experiment. Then, the six degrees of freedom motion of the floating platform and the mooring tension data of the three anchor chains are measured, and finally the test results are compared with the numerical calculation results.

The parameter settings for the test conditions are shown in

Table 5. Parameters defined for the regular wave conditions.

Regular Wave Load Case	Wave Period T (s)	Wave Height H (m)
Re 1	8.0	3.5
Re 2	10.0	5.0
Re 3	12.0	5.5
Re 4	13.0	6.0
Re 5	15.0	6.0

, including five regular wave conditions with different wave heights and periods and the hydrostatic load case.

4. Numerical Simulation

4.1. FOWT Calculation Model

Based on the combination of the 3D dynamic mooring model and the rigid body dynamics model of the VFIFE-FOWT, the time-domain coupling analysis model of the floating wind turbine is established in this section. In [35], the study highlights the necessity of direct time-domain methods to accurately capture coupled dynamics and wave-structure interactions. The developed framework of the model calculation program is shown in Figure 8. The coupling model program of the floating wind turbine mainly includes the wave generation module, the mooring hydrodynamic calculation module, the mooring internal force calculation module, the aerodynamic load calculation module, the platform hydrodynamic calculation module, and the core solver central difference module, based on MATLAB 2022a. The calculation of turbulent wind conditions requires preprocessing with the TurbSim_v2.00 and OpenFASTv4.0.4 software, generating a wind speed information file that can be read by the BEM program, and then the aerodynamic load calculation is carried out by the aerodynamic module. Furthermore, in order to calculate the hydrodynamic loads, it is first necessary to input the wave parameters in the wave generation module, which can generate a regular wave or a random wave. The input parameters of the regular wave involve the wave period and wave height, and the random wave input parameters are the peak period, the significant wave height, and the peak factor. The generated wave is in the global coordinate system ${\mathit{e}}^{\left(g\right)}$, and after the data are transferred to the hydrodynamic module, the hydrodynamic load of the element is calculated in the body coordinate system ${\mathit{e}}^{\left(b\right)}$.

The VFIFE-FOWT model in MATLAB is illustrated in Figure 9. To calculate the hydrodynamic loads acting on the platform and mooring system, both components are discretized into numerous elements. The hydrodynamic forces are computed using Morison’s equation [36]:

$$F_h={\displaystyle \frac{1}{2}}{C}_D{\rho }_{w}D\left(u_x-\dot{x}\right)\left|u_x-\dot{x}\right|+{\rho }_w{\displaystyle \frac{\pi D^2}{4}}{\displaystyle \frac{\partial u_x}{\partial t}}+C_m{\rho }_w{\displaystyle \frac{\pi D^2}{4}}\left({\displaystyle \frac{\partial u_x}{\partial t}}-\ddot{x}\right)$$

(6)

where ${\rho }_w$ is the density of water, $C_D$ is the drag coefficient perpendicular to the axis of the cylinder, D is the diameter of the cylinder, $C_m$ is the added mass coefficient, $u_x$ and ${\displaystyle \frac{\partial u_x}{\partial t}}$ are the velocity and acceleration of water particles, respectively, while $\dot{x}$ and $\ddot{x}$ are the velocity and acceleration of structural element nodes.

It should be noted that the position information of the tower, nacelle, and rotor can be calculated based on the relative motion between the rigid bodies, so there is no division of elements in MATLAB. Since the calculation of the wind load does not involve air elasticity, and the blade element momentum (BEM) program in this paper only needs the relevant information of the rotor plane to calculate the aerodynamic thrust; the blade is not divided into elements in the modeling, as shown in Figure 9.

The aerodynamic forces acting on the rotor are determined by the geometric components of the sectional lift (L) and drag forces (D). These forces are highly reliant on the airfoil’s aerodynamic properties [37]:

$$\left(L,D\right)=1/2{\rho }_{air}{V}_{rel}^{2}cB\left(C_L{e}_L,C_D{e}_D\right)$$

(7)

where ${\rho }_{air}$ is the density of air, V_rel is the relative velocity between wind and blade element, c is the chord length of the airfoil, B is the number of blades of the turbine, $C_L$ and $C_D$ are the lift and drag coefficients, respectively, and $e_L$ and $e_D$ are the unit vectors. When estimating V_rel, the rotational effects are factored in. The formula of the V_rel is

$$V_{rel}^2={\left(U_{\infty }-W_z\right)}^2+{\left(\mathsf{\Omega }{r}_l+W_{\theta }\right)}^2$$

(8)

where $W_z$ is the induced velocity, $r_l$ is the local radius of the considered annular section, and $W_{\theta }$ is the induced angular velocity.

The axial and tangential forces are calculated based on the low angle; for ${\varphi }_l$, which is defined as the angle formed between the direction of V_rel and the rotor plane:

$${\varphi }_l={tan}^{-1}\left({\displaystyle \frac{U_{\infty }-W_z}{\mathsf{\Omega }{r}_l+W_{\theta }}}\right)$$

(9)

and the sectional forces become

$$F_{air}^a=L\cos {\varphi }_l+D\sin {\varphi }_l,F_{air}^t=L\sin {\varphi }_l-D\cos {\varphi }_l$$

(10)

The governing equations of motion for the FOWT can be written in the following form:

$${\mathit{M}}^g\ddot{\mathit{X}}+{\mathit{C}}^g\dot{\mathit{X}}+{\mathit{K}}^g\mathit{X}={\mathit{F}}_h+{\mathit{F}}_{air}$$

(11)

where M, C, and K represent the mass matrix, damping matrix, and stiffness matrix of the FOWT system, respectively. ${}_{}{}^g\mathit{X}$ is the position vector in the global coordinate system, and ${}_{}{}^g\dot{\mathit{X}}$ and ${}_{}{}^g\ddot{\mathit{X}}$ are the velocity and acceleration, respectively. Their expressions can be found in References [24,28].

In the VFIFE method, the central difference scheme is employed to solve the governing equations of motion. The core idea is to approximate velocity and acceleration through position information at different time steps, and then solve for the motion response via an iterative approach:

$${}_{}{}^g\ddot{\mathit{X}}={\displaystyle \frac{1}{h^2}}\left({}_{}{}^g{\mathit{X}}^{n+1}-2{}_{}{}^g{\mathit{X}}^n+{}_{}{}^g{\mathit{X}}^{n-1}\right)$$

(12)

$${}_{}{}^g\dot{\mathit{X}}={\displaystyle \frac{1}{2h}}\left({}_{}{}^g{\mathit{X}}^{n+1}-{}_{}{}^g{\mathit{X}}^{n-1}\right)$$

(13)

where h is the time increment.

Substituting Equations (12) and (13) into Equation (11) and defining three coefficients $P_1,P_2,P_3$, then the final iteration format represented by the central difference scheme can be obtained:

$${}_{}{}^g{\mathit{X}}^{n+1}=P_1{h}^2\left({\mathit{F}}_h+{\mathit{F}}_{air}\right)-P_2{}_{}{}^g{\mathit{X}}^{n-1}-P_3{}_{}{}^g{\mathit{X}}^n$$

(14)

The expressions of three coefficients are

$$\left\{\begin{array}{c}{P}_1=1/\left(\mathit{M}+{\displaystyle \frac{h\mathit{C}}{2}}\right)\\ P_2=P_1\left(\mathbf{M}-{\displaystyle \frac{h\mathit{C}}{2}}\right)\\ P_3=P_1\left(h^2\mathit{K}-2\mathit{M}\right)\end{array}\right.$$

(15)

Additionally, the output content of the program mainly includes the six degrees-of-freedom motion response of the platform, the mooring motion, the time-domain results of the mooring tension, and the variation in hydrodynamic and aerodynamic loads under the time domain.

4.2. FOWT Motion Response Analysis

The MoorDyn module in OpenFAST v3.3.0 is selected to establish the moorings to validate the VFIFE-FOWT coupled model. In addition, the MAP++1.15 model in OpenFAST v3.3.0 is used in this section to compare the calculation differences between the dynamic model and the quasi-static model.

The steady-state wind–regular wave load cases are used to verify the proposed FOWT model, and the detailed parameters are wave height 6 m, wave period 10 s, wind and speed 10 m/s.

Under the combined steady-state wind and regular waves, the time histories and statistical results of the surge and pitch motion of the platform are shown in Figure 10 and Figure 11, and the statistical results of the mooring tension are indicated in Figure 12. As shown in the figures, the time history curves of platform motion responses and mooring tensions computed by the VFIFE-FOWT coupled model demonstrate strong agreement with the results from OpenFAST (MoorDyn), with highly consistent maximum/minimum values and waveform characteristics. Statistical analysis indicates that the relative errors for platform surge and pitch are 1.36% and 1.01%, respectively, while those for the mooring tensions of anchor lines #1 and #2 are 0.23% and 0.28%, respectively. Additionally, it can be observed that all relative errors fall within a small range, demonstrating the accuracy and reliability of the VFIFE model in simulating the dynamic behavior of the FOWT system. Consequently, the VFIFE-FOWT coupled model shows good agreement with the OpenFAST calculation results under the combined steady-state wind and regular wave analysis. From the comparison of the calculation results between the dynamic and quasi-static models, it can be seen that the mooring tension results from OpenFAST (MSQS) significantly differ from those of OpenFAST (MoorDyn) and VFIFE. It is evident that the dynamic effect of the mooring has minimal influence on the motion of the calculation platform but exerts a notable impact on the mooring tensions.

The numerical calculation results clearly demonstrate that the calculation accuracy of the VFIFE-FOWT model is basically consistent with that of OpenFAST. Next, the accuracy of the VFIFE-FOWT model is verified by means of experimental results.

5. Comparison Analysis of Dynamic Response Test Results

5.1. Hydrostatic Free Decay Test

A free decay test was performed under still water in the presented study. The free attenuation characteristics of the floating foundation model are obtained by applying the initial linear displacement in the surge and heave motion directions, and the initial angular displacement in the pitch direction. Figure 13, Figure 14 and Figure 15 show the comparisons of the test measured and numerical values of the time history curves and frequency spectrum based on the free attenuation of the surge, heave, and pitch motions, respectively.

As indicated in the figures, the test and numerical results of the hydrostatic free attenuation motion histories of the floating wind turbine and the natural period of the rigid body motion are in good agreement, and the natural period of the rigid body motion has a small natural frequency, which reasonably avoids the frequency range of wave energy concentration [38].

Table 6. Free decay period of the floating offshore wind turbine.

Motions	Natural Period (s)		Error (%)
	Test Results	Numerical Results
Surge	111.36	103.10	−7.42
Heave	29.27	30.03	2.60
Pitch	42.01	42.89	2.09

shows the model test results and numerical calculation values for the natural period of the FOWT rigid body motions calculated by Fourier transform. The relative error for surge motions between the calculated numerical results and the test results is −7.42%, and the relative errors of the natural period of the heave and pitch motions are 2.60% and 2.09%, respectively. The platform surge period error is negative and the heave and pitch error is positive, as can be distinctly observed; such phenomenon is attributed to the platform surge motion period, which is mainly controlled by the moorings, and the heave and pitch periods are mainly determined by the static resilience matrix of the platform.

5.2. Model Test Results Under Regular Wave Loads

Comparison of the motion response calculated by the VFIFE time-domain coupled numerical model and the test data under regular wave loads are developed in this section, and the established test FOWT model is shown in Figure 16.

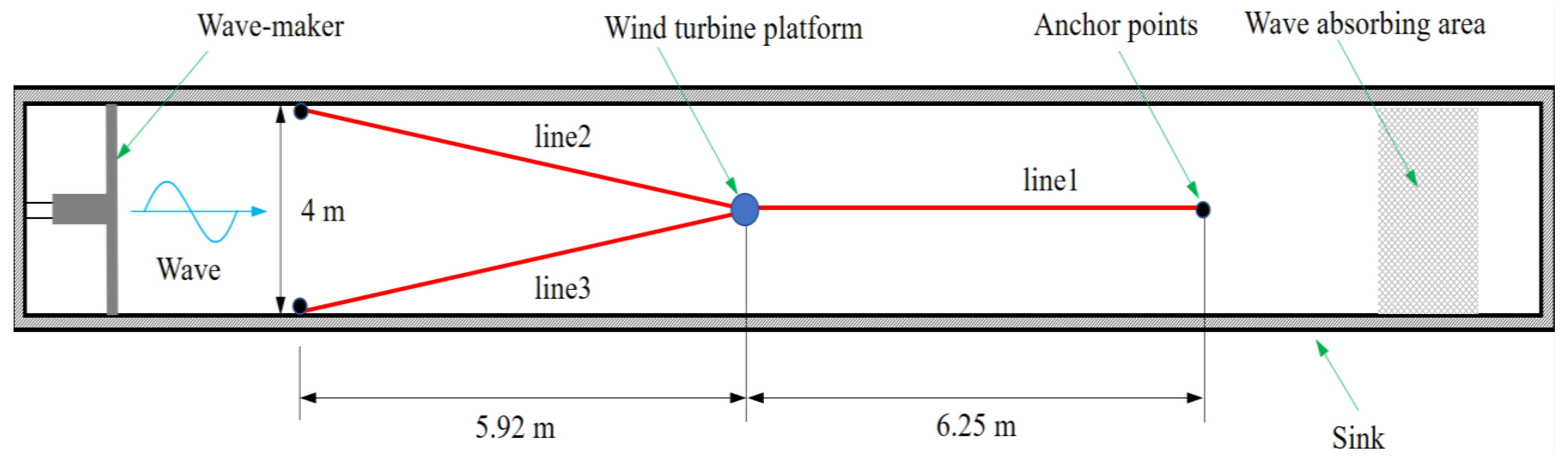
The selected comparison objects are the surge and pitch of the floating wind turbine platform and the mooring tension of anchor chains 1 and 2 (anchor chains 2 and 3 are symmetrically distributed, and the tension variation is consistent, so only anchor chain 2 is analyzed). Figure 17 shows the comparisons of the motion response calculated by the coupled time-domain numerical model of the VFIFE-FOWT and the experimental results under the regular wave condition Re 1. As shown in the figure, although the dynamic response of the FOWT model is measured under the action of regular waves, the experimental motion response curve is not an ideal regular wave shape, and the amplitude of motion responses shows small periodic fluctuations in the time domain; while, the steady-state response of the numerical simulation results is in the shape of a sine wave. The main reason for this phenomenon is the wave reflection effect in the test tank, and the platform movement also produces radiation waves, which are superimposed with the incident waves to form a new wave field. However, the numerical results are in good agreement with the trend in the time histories for the experiment, as can be directly observed in Figure 17.

The statistical analysis and comparison of the motion response between and test and numerical results of the FOWT under regular wave conditions Re 1–5 are summarized in

Table 7. Statistical results for regular wave load case 1.

	Surge (m)		Pitch (deg)		Mooring Line-1 Tension (106 N)		Mooring Line-2 Tension (106 N)
	Test	Numerical	Test	Numerical	Test	Numerical	Test	Numerical
Maximum	1.46	1.39	0.81	0.74	1.41	1.41	0.85	0.85
Minimum	−0.66	−0.50	−0.50	−0.43	1.25	1.26	0.78	0.78
Mean	0.40	0.44	0.15	0.15	1.33	1.33	0.81	0.82
STD	0.69	0.67	0.44	0.41	0.04	0.05	0.02	0.02

,

Table 8. Statistical results for regular wave load case 2.

	Surge (m)		Pitch (deg)		Mooring Line-1 Tension (106 N)		Mooring Line-2 Tension (106 N)
	Test	Numerical	Test	Numerical	Test	Numerical	Test	Numerical
Maximum	1.85	1.75	0.94	0.91	1.57	1.57	0.90	0.90
Minimum	−1.27	−1.15	−0.67	−0.70	1.27	1.28	0.81	0.81
Mean	0.28	0.28	0.11	0.10	1.41	1.41	0.85	0.85
STD	1.08	1.02	0.54	0.57	0.08	0.09	0.02	0.03

,

Table 9. Statistical results for regular wave load case 3.

	Surge (m)		Pitch (deg)		Mooring Line-1 Tension (106 N)		Mooring Line-2 Tension (106 N)
	Test	Numerical	Test	Numerical	Test	Numerical	Test	Numerical
Maximum	2.41	2.29	1.23	1.20	1.68	1.65	0.90	0.91
Minimum	−1.87	−1.73	−1.02	−0.99	1.18	1.17	0.80	0.80
Mean	0.27	0.26	0.09	0.10	1.41	1.38	0.85	0.85
STD	1.48	1.41	0.62	0.77	0.14	0.14	0.02	0.03

,

Table 10. Statistical results for regular wave load case 4.

	Surge (m)		Pitch (deg)		Mooring Line-1 Tension (106 N)		Mooring Line-2 Tension (106 N)
	Test	Numerical	Test	Numerical	Test	Numerical	Test	Numerical
Maximum	2.92	3.09	1.27	1.16	1.73	1.754	0.933	0.938
Minimum	−2.24	−2.28	−1.01	−0.86	1.08	1.064	0.788	0.784
Mean	0.34	0.39	0.07	0.14	1.39	1.364	0.849	0.861
STD	1.72	1.80	0.65	0.70	0.19	0.190	0.037	0.042

and

Table 11. Statistical results for regular wave load case 5.

	Surge (m)		Pitch (deg)		Mooring Line-1 Tension (106 N)		Mooring Line-2 Tension (106 N)
	Test	Numerical	Test	Numerical	Test	Numerical	Test	Numerical
Maximum	3.10	2.89	1.23	1.18	1.84	1.81	1.12	1.13
Minimum	−2.95	−2.84	−1.05	−1.08	1.12	1.11	0.97	0.96
Mean	0.04	−0.04	0.09	0.00	1.45	1.43	1.04	1.04
STD	2.08	1.98	0.65	0.76	0.24	0.24	0.04	0.05

, and the statistical analysis mainly includes the maximum value (Max), the minimum value (Min), the mean value (Mean), and the standard deviation (STD). The maximum surge displacement response occurs in case 2, which can attain 3.102 m; while, compared with surge motions, mean responses of the FOWT under pitch motions are slightly affected by the wave period and wave height. Furthermore, for mooring tension, with the increase in the wave period, the mooring tension increases significantly; for example, the difference of maximum tension is 0.192 MN for line-2.

To more clearly illustrate the difference between the statistical analysis of the numerical simulation results and experimental data, Figure 18 gives the absolute difference between the numerical simulation and the experiment. Among which the thicker the height of the colored squares in the figure, the greater the difference between the values and the statistic values. As can be seen from the figures, the largest platform surge and pitch error between the numerical simulation and the test attain the maximum value in the statistical results of regular wave Re 5, and the calculated relative errors are 6.78% and 11.2%, respectively. In addition, the mooring tension error of mooring line-1 between the numerical simulation and the test is the largest under Re 3, and its relative error is 2.2%; while, such error of the mooring line-2 is the smallest value in the statistical results of regular wave Re 5, which is 1.1%. Further comparison shows that the relative error of the platform motion response is larger than that of the mooring tension. This is because using Morison’s equation to calculate the hydrodynamic loads of the platform will lead to significant errors due to the large diameter of the platform. Under regular wave conditions, the relative error becomes more pronounced in load cases with smaller wave heights and periods. This is because smaller wave heights and periods result in smaller response amplitudes in the experiment, making the data acquisition more susceptible to signal interference. Consequently, this leads to significant discrepancies between the experimental data and numerical simulations. Since the comparison of standard deviations does not directly reflect the difference between numerical and experimental results, standard deviations are not analyzed in this present study.

Although the mooring system in this model test is not deployed according to the normal interval of 120°, the maximum mooring response of the platform is 6.22 m, the maximum amplitude of pitch inclination is 2.56°, the maximum mooring tension of the mooring line-1 is 1.85 × 10⁶ N, and the maximum mooring tension of the mooring line-2 attains 1.13 × 10⁶ N. All test results show that the pitch amplitude of the platform does not exceed 1/10 (8 m) of the water depth, the pitch angle does not exceed 10°, and the maximum mooring tension is much less than the rated breaking force of 2.58 × 10⁷ N. These results show that the shallow draft stepped Spar platform has better motion performance under the condition of the single wave, and the resonance frequency can basically avoid the frequency range in wave energy concentration.

5.3. Discussion

The experiment conducted in this study has validated the correctness of the VFIFE-FOWT model, but there are still some discrepancies in the consistency of the results. The causes of these discrepancies include, firstly, the scale effects, and secondly, the insufficient calculation accuracy of the numerical model. This is because Morison’s equation was used to calculate the hydrodynamic loads of the platform in the model, but the large diameter of the platform introduces noticeable inaccuracies in the calculations. Since the purpose of this experiment was to validate the VFIFE-FOWT model using experimental data, and the width of the wave tank was limited, causing that the mooring system could not be fully deployed at 120-degree intervals. Therefore, the experimental model setup differs significantly from practical applications, yielding limited guiding significance for real-world engineering. To explore the performance of this shallow draft stepped Spar platform, more comprehensive tank model tests should be conducted, such as investigating the platform’s motion performance under extreme operating conditions.

Furthermore, as the water depth in this experiment was 1 m and the wave tank bottom was relatively flat, the influence of the tank bottom on waves was relatively minor in the experiment.

6. Conclusions

In this study, a 1:80 model text of a shallow draft stepped Spar platform was carried out to validate the correctness of a proposed numerical model for the FOWT based on the VFIFE method. The paper introduces the modeling approach of the VFIFE-FOWT model and its validation through comparison with calculation results from OpenFAST. It then describes the experimental setups of this test, and finally compares the calculation results of the VFIFE-FOWT model with the experimental data, leading to the following conclusions:

• The VFIFE method exhibits high accuracy in calculating the rigid–flexible coupling dynamics of FOWTs. Comparative analysis between OpenFAST and the VFIFE method confirms the reliability of the proposed model under typical regular wave conditions.
• A regular wave test of the FOWT was conducted in a wave tank, and the relative errors between numerical simulation results and experimental data were compared. It was found that the relative errors in platform motion responses were larger than those of mooring tensions. This is because the large diameter of the platform leads to significant inaccuracies when using Morison’s equation to calculate platform hydrodynamic loads, while the smaller diameter of the mooring lines allows for more accurate hydrodynamic calculations using Morison’s equation.
• In general, under regular wave load case conditions, the results calculated by the VFIFE-FOWT model are in good agreement with the experimental results (with a maximum relative error of 11.2%), thus verifying the correctness of the VFIFE-FOWT model. However, its calculation accuracy still needs to be improved.

The VFIFE-FOWT model presented in this paper also has certain limitations. The explicit central difference method adopted in the program to solve the motion control equations leads to slightly lower computational efficiency, resulting in higher requirements for computer performance. Additionally, using Morison’s equation to calculate the platform’s hydrodynamic loads is inappropriate. Therefore, it is necessary to develop a calculation module for platform hydrodynamic loads based on potential flow theory.