Abstract
Autonomous ship berthing requires advanced path planning to balance multiple objectives, such as minimizing berthing time, reducing energy consumption, and ensuring safety under dynamic environmental constraints. However, traditional planning and learning methods often suffer from inefficient search or sparse rewards in such constrained and high-dimensional settings. This study introduces a double deep Q-network (DDQN)-guided dual-population constrained multi-objective evolutionary algorithm (CMOEA) framework for autonomous ship berthing. By integrating deep reinforcement learning (DRL) with CMOEA, the framework employs DDQN to dynamically guide operator selection, enhancing search efficiency and solution diversity. The designed reward function optimizes thrust, time, and heading accuracy while accounting for vessel kinematics, water currents, and obstacles. Simulations on the CSAD vessel model demonstrate that this framework outperforms baseline algorithms such as evolutionary multitasking constrained multi-objective optimization (EMCMO), DQN, Q-learning, and non-dominated sorting genetic algorithm II (NSGA-II), achieving superior efficiency and stability while maintaining the required berthing angle. The framework also exhibits strong adaptability across varying environmental conditions, making it a promising solution for autonomous ship berthing in port environments.
1. Introduction
Autonomous ship berthing is a critical task in intelligent maritime transportation, aiming to achieve high-precision, low-energy, and low-risk docking operations with minimal human intervention, thereby improving the overall efficiency and safety of berthing procedures [1,2,3]. With the continuous growth of global port traffic, autonomous berthing systems must generate globally feasible, smooth, and collision-free trajectory sequences that satisfy multiple constraints, including minimized berthing time, reduced energy consumption, collision avoidance, and precise pose alignment with the geometric structure of the berth [4,5]. Unlike navigation in open waters, berthing typically takes place in spatially constrained and structurally complex port environments, such as quays, berths, and narrow channels. Although these environments appear relatively stable on a macro scale, the presence of fixed infrastructure, moored vessels, shallow-water effects, and disturbances from wind and currents pose significant challenges to path planning [4]. Studies have shown that a majority of berthing accidents are attributed to human operational errors; thus, reducing manual intervention during the final docking phase can enhance control precision and system reliability in port scenarios [6,7]. To this end, autonomous surface vessels must be equipped with guidance modules capable of integrating environmental perception, obstacle distribution, and the geometric profile of the berthing target. Such integration is essential for generating smooth, safe, and collision-free trajectories, thereby enabling efficient and fully autonomous berthing [8,9].
Autonomous berthing, conceptualized as a motion planning task, necessitates meticulous consideration of vessel dynamics, kinematics, and dimensional constraints, rendering path validation both complex and computationally intensive [10,11]. Concurrently, the task demands a delicate balance in multi-objective optimization, striving for minimized berthing time, reduced energy expenditure, assured collision-free navigation, and precise final pose attainment relative to the berth. The development of robust path planning algorithms to address these requirements encounters several intrinsic challenges. Firstly, the high-dimensional continuous state space inherent to ship systems, compounded by the dynamic uncertainties of the port environment, significantly impairs the efficiency of conventional search algorithms. Secondly, sparse reward signals, particularly under fault conditions or adverse environments, lead to limited successful experiences, causing agents to converge to suboptimal strategies [12]. Furthermore, stringent posture control requirements result in a predominance of failure experiences, increasing the risk of suboptimal convergence. A core challenge in algorithm design is enhancing exploration capabilities to ensure solution diversity. Thus, developing advanced motion planning algorithms that manage multi-objective trade-offs, maintain search efficiency, and preserve solution diversity in challenging berthing environments remains a critical research direction.
To address the aforementioned challenges, researchers have proposed a series of methodologies. For instance, Song et al. [13] introduced a practical path planning framework predicated on a smoothed A* algorithm, validating its efficacy across different berthing phases through high-fidelity simulations and real-ship trials. Han et al. [14] presented a non-uniform Theta* algorithm for global planning, demonstrating its efficiency on grid maps, although this method primarily covers the route planning aspect. Considering safety zones and kinematic constraints, Zhang et al. [15] developed the KS-RRT* algorithm, which, by applying a prioritized multi-objective strategy in diverse berthing environments, achieves superior planning time compared to traditional RRT*. However, within the specific context of berthing operations, such approaches can be constrained by low initial search efficiency or insufficient solution diversity.
In recent years, with the advancement of computational intelligence, bio-inspired optimization algorithms have garnered significant attention in the path planning of unmanned surface vehicles (USVs) and similar autonomous systems. Among these, Genetic Algorithms (GAs) [16,17,18], Particle Swarm Optimization (PSO) [19,20], and Differential Evolution (DE) [21] have been widely adopted. To address the multi-objective nature of USV path planning, which parallels ship berthing tasks, researchers have introduced optimization frameworks incorporating Pareto dominance [22]. However, these conventional bio-inspired algorithms face several bottlenecks when applied to berthing problems: low efficiency in the initial search phase, resulting in slow convergence; susceptibility to local optima and a lack of global robustness; and limited adaptability in dynamic, multi-constrained environments. To mitigate these issues, several studies have proposed structural improvements. For instance, Peng et al. [23] developed a decomposition-based multi-objective evolutionary algorithm (MOEA) for unmanned aerial vehicle path planning, incorporating a local infeasibility mechanism to enhance the reliability and stability of feasible solutions. Similarly, Liu et al. [21] introduced the MOEA/D-DE-C-ACO algorithm for multiple autonomous underwater vehicles path planning in complex underwater environments, aiming to maintain population diversity and achieve high-quality solutions. Despite these advancements, traditional bio-inspired algorithms struggle to balance exploration breadth, convergence speed, and solution quality in the highly constrained, dynamic, and multi-objective context of ship berthing motion planning.
To further enhance the performance of global path planning for ship berthing, employing CMOEAs with dual-population strategies presents a promising approach to improve global search capability and maintain solution diversity. Existing multi-objective optimization algorithms often struggle to balance exploration breadth and solution diversity when addressing the competing multi-dimensional objectives. Recent studies have demonstrated that dual-population frameworks can significantly expand the search space through collaborative mechanisms. For example, a coevolutionary constrained multiobjective optimization algorithm enhanced global coverage by leveraging weak coupling between subpopulations [24]; a push and pull search strategy maintained a balance between exploration and exploitation, although it may suffer from reduced diversity in later stages [25]; and a two-archive evolutionary algorithm promoted solution diversity via a dual-archive structure, despite the potential limitations imposed by strong inter-population interactions [26]. In complex scenarios such as maritime scheduling, dual-population strategies have shown potential in broadening the solution space [27]. Building upon these insights, this study adopts a dual-population CMOEA framework tailored to the kinematic characteristics of berthing path planning. Through coordinated population evolution and structured information exchange, the proposed method aims to improve global optimization performance and generate high-quality berthing trajectories.
According to the “No Free Lunch” theorem [28], no universal optimal operator exists for all optimization problems, underscoring the importance of selecting appropriate operators in multi-objective optimization problems (MOPs), particularly for complex tasks such as ship berthing path planning. In recent years, deep reinforcement learning (DRL) has garnered significant attention for its potential in multi-objective optimization, primarily due to its ability to leverage neural networks (NNs) to approximate action–value functions, thereby effectively handling high-dimensional continuous state spaces [29,30,31,32,33]. Notably, integrating NNs within reinforcement learning frameworks can mitigate the curse of dimensionality, enhancing decision-making capabilities in complex systems [34]. In contrast, evolutionary algorithms (EAs) exhibit strong adaptability in solving high-dimensional constrained multi-objective optimization problems (CMOPs) through global search and population-based collaboration mechanisms. Incorporating DRL into EA frameworks enables dynamic operator selection, thereby effectively adapting to the complex scenarios with diverse optimization requirements [35]. Concurrently, dual-population CMOEAs enhance global search capabilities through population collaboration, demonstrating advantages in solution set diversity for scenarios like ship scheduling [27]. However, existing methods still face challenges in coordinating evolutionary processes and improving search efficiency for constrained problems. To address this, this study proposes integrating DRL with EAs—combined with a dual-population coordinated evolutionary strategy that accounts for constraints—to optimize operator selection and population collaboration mechanisms, thereby enhancing the global performance of ship berthing path planning. Specifically, DRL will be employed to dynamically adjust operators, while coordinated evolution between dual populations balances search breadth and constraint satisfaction, aiming to achieve efficient and diverse berthing path solutions.
The specific contributions of this study are as follows:
(1) The adoption of multiple crossover operators, including crossover from genetic algorithms and mutation from differential evolution, enriches the operator selection space. A dual-population algorithm is employed to better adapt to the demands of complex path planning.
(2) An improved DRL approach addresses existing shortcomings by utilizing DDQN to dynamically evaluate operator performance, mitigating the exploration–exploitation dilemma and enhancing global search capabilities.
(3) The integration of DRL and EA is applied to ship berthing path planning, optimizing multiple objectives, including berthing time, energy consumption, and safety. Experimental results demonstrate that the proposed method outperforms traditional single- and dual-population approaches in terms of diversity and convergence, highlighting its applicability in port environments.
The remainder of this paper is organized as follows: Section 2 presents the ship berthing control system and reviews related work on path planning and optimization algorithms. Section 3 details the DDQN-guided evolutionary multitasking framework, including path encoding, reward function design, and the DDQN-EMCMO algorithm for autonomous berthing. Section 4 describes the experimental setup and presents a comprehensive analysis of the simulation results on the ship berthing problem. Section 5 concludes the paper.
2. Theory
2.1. Navigation and Control of Maritime Vessels
Ludvigsen et al. [9] introduced the concept of autonomy levels, which refers to a vessel’s ability to autonomously perceive, model, make decisions, and control in complex tasks and environments, enabling berthing, collision avoidance, and re-planning after fault detection. A vessel’s berthing control system primarily includes a guidance system, control system, and navigation system. The guidance system interacts with the autonomous system to execute path planning, path generation, and re-planning in complex scenarios. To evaluate the path-planning capabilities of the intelligent system, this study’s intelligent algorithm interacts with the guidance system to generate berthing trajectories, after which the control system issues commands to the propellers to drive the vessel. The vessel’s state is then fed back through a passive observer to the guidance and control systems for further adjustments, as shown in Figure 1 [36].
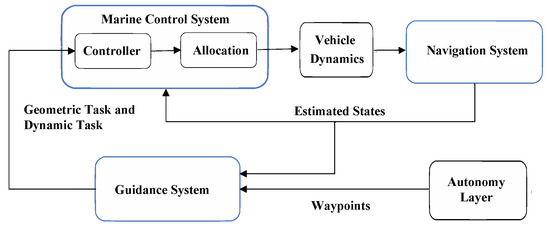
Figure 1.
Block diagram of ship berthing control system.
During the berthing process, the dock environment can be assumed to be calm and at low speed. Under these conditions, the berthing process for an intelligent vessel can be simplified to a three-degree-of-freedom (3-DOF) model, allowing the omission of roll, pitch, and heave motions. This study adopts Fossen’s ship model, incorporating a thrust allocation module [37]. The vessel’s 3-DOF state space model is represented by three generalized coordinates , , and , along with body frame velocities , , and , as well as the ship’s rigid-body and added mass terms.
where represents the vessel’s position state, denotes the velocity state, and indicates the control forces. Here, M is the inertia matrix, D is the damping matrix, and is the transformation matrix, used to convert between the NED and body reference frames. Additionally, represents the environmental disturbance forces, specifically modeled as water currents in this study.
To better represent the relationship between the guidance layer and thrust in the ship’s control system, allowing the vessel to follow a given berthing path, path-tracking control is addressed as a maneuvering problem [38], where position tracking and heading control tasks are separated, permitting path parameters to rely solely on position feedback. The desired path is continuous, and the control objective satisfies both geometric and dynamic requirements. Assuming a constant desired speed along the path tangent, the thrust equation can be derived using the backstepping maneuvering control design presented in [11]:
where , , and represents the virtual control rate with its derivative . Here, s is the path parameter vector, denotes the speed distribution , is the thrust configuration matrix containing the angles of the thrusters, and is the magnitude of the thrust force.
2.2. Related Work on DRL and MOEA Algorithm
A central challenge in the design of algorithms for CMOPs lies in effectively managing the interplay between feasible and infeasible solutions within the objective space. Current research often focuses on the relationship between the unconstrained Pareto front (UPF) and the constrained Pareto front (CPF) as a means to improve search efficiency and enhance both the convergence and diversity of the algorithm. A critical feature of CMOPs is the topological relationship between the UPF and the CPF, which can be categorized into four distinct types (Type-I through Type-IV) [39], as depicted in Figure 2. The specific nature of the UPF-CPF relationship directly impacts the choice of optimization strategy. For instance, in Type-I and Type-II scenarios, characterized by substantial or partial overlap between the UPF and CPF, information derived from the UPF can effectively guide the search process and help prevent convergence to local optima. Consequently, researchers have proposed methods that leverage UPF information to enhance CMOP performance. One such approach involves dual-population co-evolutionary algorithms, which employ coordinated evolution to explore the UPF and CPF spaces somewhat independently. This strategy aims to effectively balance broad exploration with constraint satisfaction, ultimately improving solution set diversity and global convergence.
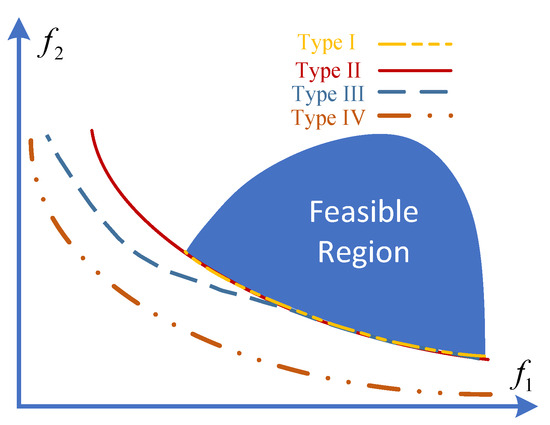
Figure 2.
Four categories of CMOP.
RL, a key area within machine learning, offers significant potential for addressing complex optimization problems. In applications such as automated ship berthing path planning, DQN, a prominent RL algorithm, guide decision-making by optimizing the Q-value function [40]. This function, approximated using deep neural networks based on the Bellman equation, estimates the expected cumulative reward for state-action pairs. To enhance stability and adaptability, particularly in dynamic environments characteristic of ship berthing, DQN incorporates an experience replay mechanism. This technique mitigates issues arising from sample correlation and non-stationary data distributions, thereby stabilizing the learning process. Despite its strengths, applying DQN directly to ship berthing encounters significant challenges. The inherent complexity of the task, involving numerous state variables (e.g., position, velocity) and control inputs (e.g., thrust), results in a high-dimensional action space, leading to the well-known “curse of dimensionality”. Furthermore, the initial scarcity of successful trajectories during exploration phases can severely impede learning progress and hinder convergence towards effective policies. Consequently, hybrid approaches that integrate optimization algorithms, notably EAs, with RL have emerged as a promising direction to improve both the efficiency and success rate of automated berthing systems.
Within these frameworks, EAs can effectively explore the solution space and accelerate the generation of diverse and relevant experience data. Concurrently, RL can leverage these data to learn sophisticated control policies, thereby guiding the evolutionary search towards high-quality solutions more rapidly. This synergistic interaction is particularly advantageous when addressing CMOPs. In such problems, the presence of constraints often makes the identification of feasible solutions challenging; RL’s capacity for adaptive learning through continuous interaction allows it to effectively refine search strategies for navigating these complex, constrained landscapes. In related developments, research has explored the integration of evolutionary multitasking (EMT) with RL. By facilitating knowledge transfer from auxiliary or related tasks, EMT can guide the training of the RL policy network more effectively. This aims to enhance the adaptability and generalization capabilities of the resulting optimization method, making it more robust across varying conditions. For instance, combining EAs and RL has demonstrated success in accelerating experience accumulation and optimizing search trajectories for improved efficiency [31]. Moreover, the fusion of RL and EMT, particularly through auxiliary task-guided policy learning, has been shown to enhance the robustness required for effectively solving CMOPs [41].
3. Path Planning Algorithm
The autonomous berthing scheme proposed in this study is not merely based on simple kinematic planning using electronic nautical charts, but it comprehensively considers the actual movement scenarios, including the kinematic constraints of the ship itself and detailed dynamical physical constraints. The path points proposed in this paper are first encoded into the population of the optimization algorithm for comparison with traditional path planning algorithms. We have adopted the same action space used in reinforcement learning-generated automatic berthing path planning as the decision variables for heuristic learning algorithms in order to facilitate a more effective comparison and application.
3.1. Path Coding
To guide the ship in successfully completing the automatic berthing task, we systematically encoded the ship’s operations, enabling the crossover and mutation processes in the proposed algorithm to more effectively optimize the ship’s operational path. We adopted a method that combines reinforcement learning’s action space with heuristic algorithm encoding strategies, which not only enhances the algorithm’s global search capability but also simplifies the decision-making process through encoding, providing smarter decision support and navigation for the ship.
To ensure smooth navigation during berthing and to complete the necessary left and right turns, we designed a specialized stable trajectory encoding method for ship berthing. The action space expression proposed in this paper uses the variable to adjust the tangent angle of the berthing path, , with the adjustment based on the starting point . By extending the length of the path segment , new directions suitable for different actions are generated, further enriching the options within the action space. Therefore, the action space consists of carefully designed actions, where action aims to maintain the ship’s heading by holding the current , while other actions adjust the heading precisely through variations in .
As shown in Equation (2), action does not change the tangent angle of the ship, with and the path length remaining constant. Other actions adjust the heading by altering either positively or negatively. Each action corresponds to a different angle variation and path length, providing flexible heading adjustments for the ship, thereby improving the flexibility and accuracy of path planning during the berthing process.
As shown in Equation (3), the first step is to calculate the tangent angle from the current position to the target position . Based on the selected action , and by considering the current heading information, the tangent angle is dynamically adjusted by applying the corresponding angle variation . With the new tangent angle and the specified path length, the new route point is generated by extending from the current position . This process calculates the new waypoint . This method not only improves the flexibility and accuracy of path planning but also enhances adaptability to complex navigation environments, ensuring the safety and efficiency of the automatic berthing process.
3.2. Design of Path Reward Function
To achieve the desired objective of automatic berthing path planning, it is essential to design appropriate reward components. Since this objective requires generating a berthing path that considers both external environmental factors and the vessel’s own dynamics, the final design of the reward function will be more complex. The angle is defined as the tangent to the path, and the action space formula provides limited turning possibilities, resulting in a strong interdependence between the selected actions and the future actions. Therefore, early mistakes in action selection can have irreversible effects on the generated berthing trajectory. Thus, from the beginning of the berthing process to the final docking stage, the reward function plays a critical role in influencing the vessel’s actions.
One of the key functions of the agent is to guide the vessel in the direction of movement. This is likely the most crucial part of the reward, with the primary objective of ensuring the vessel reaches the dock. The simplest way to achieve this is to provide the agent with feedback on whether its chosen actions bring it closer to the target. In this paper, this feedback is provided by using the Euclidean distance d between the current position p and the waypoint as a measure. Based on this, the reward function is defined as follows:
The reward is designed based on the deviation angle from the desired heading when reaching the dock. Since a deviation angle of 90° poses the greatest risk during berthing, the reward function is developed accordingly. For , the reward is defined to increase linearly from the minimum at to the maximum at .
where is a tuning constant in the reward function, used to adjust the magnitude of the reward based on the deviation angle .
In addition to reaching the dock with the correct heading, this paper introduces the sub-objective of reducing thrust. To balance these two factors, a terminal reward is proposed, triggered when the vessel enters the target berthing area. The reward for total thrust is expressed as a function of the entry heading reward, resulting in a comprehensive terminal reward upon achieving the berthing state.
Additionally, an immediate thrust reward is introduced to enhance the agent’s focus on reducing thrust throughout the entire process.
To minimize the time the vessel takes to move along the path, a terminal time reward and an immediate time reward are designed.
where and represent the time the vessel spends at waypoints and , respectively. and are tuning constants that encourage the agent to take actions aimed at minimizing time.
So far, the reward function has been able to guide the vessel to the dock at the optimal angle while minimizing thrust and time throughout the process. To prevent the agent from becoming confused about whether to prioritize reducing distance or minimizing , this paper adopts a distance-dependent reward. By utilizing potential field characteristics, it continuously provides the desired heading indication throughout the process.
The reward indicates that the offset angle is not critical when the vessel is far from the dock, but it increases exponentially as the distance decreases. As a result, the agent can prioritize reducing distance in the early stages of berthing and focus more on the heading as it approaches the berth. This prioritization is further adjusted by the reward priority tuning constants and . Finally, since the objective of this paper is to develop a sufficiently safe path, a negative reward is defined in the event of a collision, where is a tuning constant. Thus, the complete reward function becomes the following:
In traditional reinforcement learning reward function design, rewards are typically maximized to satisfy path planning objectives, such as minimizing path length, time, and energy consumption. By inverting the sign of the relevant constant, a maximization problem can be reformulated as a minimization problem, enabling seamless integration with the proposed approach. Additionally, this study adopts a multi-objective framework, treating thrust and time as independent objective functions to achieve balanced optimization.
3.3. Generation of Reference Trajectory
To generate a feasible trajectory for the vessel to follow, this paper introduces several improvements to the path generation method based on [37]. Reinforcement learning is employed to expand the path, allowing the agent to continuously select and evaluate actions under different states. In this context, only the characteristics of the upcoming segment of the path can be determined in advance, meaning only the next waypoint can be predicted. In this paper, represents the previously visited starting waypoint, while denotes the current target waypoint.
The generation of the trajectory begins with the geometric task of knowing only the previous waypoint and the current destination waypoint . To ensure the continuity at the connection points, the rule is applied, and the tangential vectors of adjacent trajectory segments are aligned.
where represents the first derivative of the current path segment, and represents the first derivative of the upcoming path segment. is a tuning constant. The parameterized trajectory segment is presented by the following equation, where :
To satisfy the connection criteria between trajectory segments as shown in Equation (13), the following formula is used in this paper to generate the coefficients of the trajectory segments by continuously evaluating the coefficient vector of a k-th order polynomial, :
These are solved according to the aforementioned parametric continuity criteria, as follows: continuity, which ensures connection with the next trajectory segment by maintaining continuity between them.
According to Equation (13), continuity is achieved by ensuring that the slopes at the connection points are equal.
continuity is achieved by further setting the following path derivatives to zero at the connection points. Specifically, when , and . Under the assumption that the relative velocity is maximized along the tangent direction of the vessel’s velocity, this generates the trajectory tangent representing the path as follows:
As the foundation of the vessel agent’s learning process, it is necessary to define specific objectives to be achieved and the termination conditions. The termination conditions for the automatic berthing path planning in this paper include reaching a waypoint or failure to track the waypoint. The learning process terminates when either condition is met. While the desired heading angle can be used to generate the berthing path, there are challenges, as the probability of the vessel accurately reaching this state is low. To increase the likelihood of reaching the target, the target area is expanded to a larger region , which encompasses the selected docking position with a radius around .
where is defined as the terminal state of a training episode. Instead of using as a termination condition, the desired state is achieved through rewards. Since the goal is to allow the vessel to freely navigate under the assumption of feasible path tracking, there is a possibility that the vessel will continuously explore during navigation. To prevent this and limit computational complexity, constraints are imposed on the state space. If the vessel’s state exceeds this defined space, the episode is terminated.
3.4. Algorithm Design
This section presents the design of the DDQN-EMCMO algorithm, a CMOEA that leverages DRL with a DDQN for adaptive operator selection, enhancing the optimization of CMOPs through the co-evolution of two populations and . Building upon the EMCMO framework proposed by Qiao et al. [42], DDQN-EMCMO introduces a DDQN-based operator selection strategy to improve search efficiency and convergence stability.
3.5. EMCMO Framework Overview
The EMCMO framework employs a dual-phase evolutionary process with inter-task knowledge transfer to address CMOPs efficiently. It co-evolves two populations: optimizes the CMOP task considering both objectives and constraints, while tackles an auxiliary MOP task focusing on objectives only. The process is divided into two phases:
Early-Phase Diversity and Knowledge Sharing: When the number of function evaluations satisfies , where is a phase transition parameter and is the maximum allowed evaluations, EMCMO prioritizes population diversity and cross-task knowledge sharing. For each task (), a subset of individuals is randomly selected from as mating parents to generate offspring . A temporary population is constructed as , where denotes offspring from the auxiliary task. Environmental selection retains the top individuals to update , reusing constraint violation information from for to reduce computational overhead. This phase ensures broad exploration and accumulates transferable knowledge.
Later-Phase Solution Refinement and Knowledge Transfer: When , the focus shifts to solution refinement and adaptive knowledge transfer. Mating parents are selected based on fitness, generating offspring . A temporary population is evaluated, and the top individuals are selected using environmental selection from the auxiliary task . Transfer success rates are computed as and , where and are the counts of parent and offspring individuals among the selected solutions, respectively. If , offspring are chosen as the transfer population ; otherwise, individuals are randomly selected from . The updated population is , followed by environmental selection to update , enhancing convergence toward the Pareto-optimal front.
Despite its strengths, EMCMO relies on static operator selection, which may lead to suboptimal performance in dynamic or highly constrained scenarios due to the lack of adaptability in operator choice.
3.5.1. DDQN-Enhanced Operator Selection
To address the limitations of static operator selection in EMCMO, DDQN-EMCMO integrates a DDQN-based strategy to dynamically select operators, improving both stability and efficiency in solving CMOPs. The operator set is defined as , where corresponds to genetic algorithm operator, and to differential evolution operator. The DDQN enhancement consists of the following components:
Population State Representation: The population state is characterized by three metrics: convergence , feasibility f, and diversity d, computed as
where is the k-th objective value, is the constraint violation, and are the maximum and minimum values of objective k. The state vector is thus .
Reward Mechanism: The reward measures the operator’s effectiveness in improving the population state
where are the next-generation state values. Each transition is stored in an experience replay buffer .
DDQN Learning and Decision-Making: DDQN employs a primary Q-network and a target Q-network to mitigate Q-value overestimation. Q-values are updated as
where is the discount factor. The operator is selected as , ensuring stable and precise decisions compared to traditional DQL.
3.5.2. The Integrated DDQN-EMCMO Algorithm
The DDQN-EMCMO algorithm integrates adaptive operator selection into the two-phase EMCMO structure, as shown in Figure 3. The process is outlined as follows:
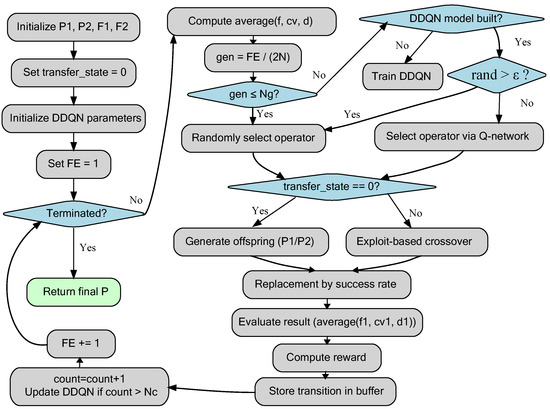
Figure 3.
Flowchart illustrating the proposed DDQN-EMCMO algorithm.
- 1.
- Initialize and , compute their fitness values, and set up DRL parameters, including networks, buffer , exploration parameters, update counter count, and initial exploration phase length . Set transfer_state = 0.
- 2.
- Enter the main loop (while NotTerminated):
- 3.
- Compute the state for the relevant population.
- 4.
- Select operator : If gen ≤ , select randomly. Otherwise, if gen > , proceed as follows: if the DDQN model is not yet built, construct it using data from and select randomly for this generation; if the model is built, apply an epsilon-greedy approach, selecting randomly with probability 1-greedy, or set otherwise.
- 5.
- Check whether updates transfer_state from 0 to 1. Early stages share across tasks, and later stages adaptively migrate based on success rate to update and .
- 6.
- Compute the new state of the updated population.
- 7.
- Calculate the reward based on and , store the transition in the buffer , and trim if it exceeds its maximum size.
- 8.
- Update DDQN model: If the model is built and the update counter count exceeds the update frequency , use batches sampled from to train the main network, update the target network regularly, and increase count.
- 9.
- Terminate the loop when the termination criterion is met, returning the final optimized population .
This integrated approach leverages the structural benefits of EMCMO’s phased evolution and knowledge transfer while using DDQN to make intelligent, adaptive decisions about which evolutionary operator to employ at each step, leading to a potentially more robust and efficient optimization process.
4. Results
To validate the effectiveness and superiority of the proposed autonomous berthing path planning scheme, comprehensive simulation experiments were conducted on the well-known C/S Inocean Cat I Arctic Drillship(CSAD) [43]. The key simulation parameters are summarized in Table 1. All computational experiments were carried out on a workstation equipped with a 16-core Intel Core i7-13700K processor (3.40 GHz) and 32 GB of RAM. The optimization algorithm was specifically tailored and tested in accordance with the dynamic and kinematic characteristics of the vessel model. By explicitly incorporating both physical dynamics and maneuverability constraints, the proposed method ensures high fidelity to realistic berthing conditions, thereby enhancing the practical relevance and applicability of the research findings.

Table 1.
Key Parameters of the CSAD Vessel Model.
To evaluate the effectiveness of the proposed DDQN-guided dual-population evolutionary multitasking framework for autonomous ship berthing, a simulation environment was established using the CSAD vessel model. The target berthing zone is defined as a circular region centered at with a radius of . The training state space is constrained as follows: , with a constant reference speed of . Initial conditions include a starting position , an initial target waypoint , an initial pose , and an initial velocity . To address the high-dimensional complexity of berthing trajectory planning, 3000 training episodes were implemented to optimize exploration and convergence efficiency. To balance computational efficiency with search performance, the DDQN-guided framework employs a population size of 15, while comparative optimization algorithms use a population size of 200. The deep reinforcement learning component is implemented using a backpropagation neural network configured with two hidden layers (each with 40 neurons), four input nodes, one output node, a batch size of 200, a learning rate of , and ReLU activation functions. The hyperparameters for the EMCMO component are adapted from [42] to ensure algorithmic robustness. The reward function parameters were carefully calibrated through iterative experiments, with the following values: distance reward weight , heading deviation weight , instantaneous thrust weight , terminal thrust reward , instantaneous time weight , terminal time reward , collision penalty , distance priority , and heading priority . These parameters enable the reward function to effectively guide the vessel toward efficient and safe berthing while addressing multi-objective optimization requirements.
4.1. Performance Comparison of Berthing Algorithms
To achieve the objective of parallel berthing, this study mandates that the vessel reaches the berth at a precise angle of 90 degrees, with a relaxed positional constraint allowing the final position to be within 0.4 m of the quay wall. Under the same current speed and direction, six algorithms were compared: DDQN-EMCMO, DQN-EMCMO, EMCMO, DQN, Q-learning, and NSGAII. The performance metrics, including required thrust, berthing time, and total reward, were analyzed, with results summarized in Table 2. The autonomous berthing trajectories for each algorithm are illustrated in Figure 4, while Figure 5 provides a detailed comparison of the total thrust and time relationship across these algorithms.

Table 2.
Comparison of thrust, time, and average reward for different algorithms.
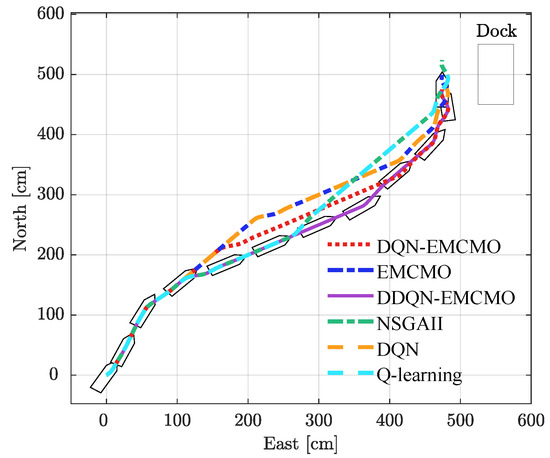
Figure 4.
Autonomous berthing trajectories under different algorithms.
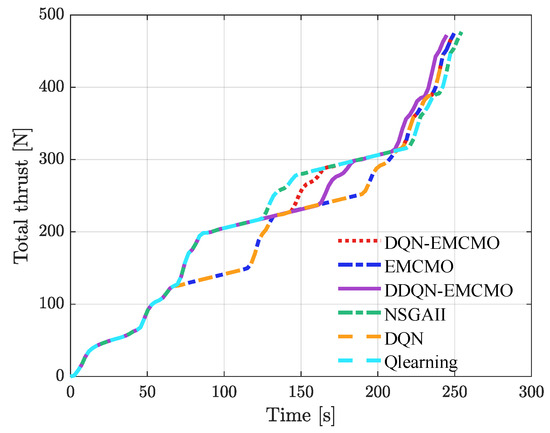
Figure 5.
Total thrust and time relationship for different berthing algorithms.
Table 2 presents the optimal thrust, berthing time, and total reward, along with their standard deviations, to provide a robust statistical representation of each algorithm’s performance. The total reward reflects the cumulative performance of the algorithm, integrating factors such as positional accuracy, angle precision, and efficiency in thrust and time, with higher values indicating better overall berthing performance. These statistical measures highlight the consistency and stability of the results. DDQN-EMCMO outperforms all other algorithms, achieving the lowest mean thrust of , the shortest mean berthing time of , and the highest mean total reward of 15,440.37 ± 9.67. The tight standard deviations across all metrics reflect high reliability and minimal variability. DQN-EMCMO matches DDQN-EMCMO in thrust () but requires a longer mean time () and yields a lower total reward (15,318.77 ± 17.69), with slightly higher variability. Other algorithms, such as DQN (, , ) and Q-learning (, , 14,640.15 ± 20.15), exhibit higher thrust, longer times, and lower total rewards, with greater variability, indicating less stable performance. NSGAII (, , ) performs marginally better than Q-learning but remains less efficient than the evolutionary multitasking-based approaches. The consistently low standard deviations of DDQN-EMCMO, especially in total reward, underscore its superior balance of efficiency and precision.
Figure 4 visually illustrates the berthing trajectories generated by each algorithm, demonstrating that DDQN-EMCMO produces smooth, efficient, and safe paths to the target berth. Figure 5 depicts the relationship between total thrust and berthing time for the six algorithms under consideration. This figure distinctly positions DDQN-EMCMO at the Pareto-optimal frontier, achieving the most efficient combination of minimal thrust and time, closely followed by DQN-EMCMO. In contrast, other algorithms, particularly Q-learning and NSGAII, are positioned farther from the optimal region, reflecting their higher resource demands and extended berthing durations. When combined with the statistical data presented in Table 2, DDQN-EMCMO exhibits superior performance in thrust efficiency, time minimization, and total reward, with the latter encapsulating overall berthing effectiveness through positional accuracy, angle precision, and resource optimization. The low standard deviations across these metrics further underscore its robust stability and adaptability. This reliability significantly enhances the algorithm’s applicability in real-world port scenarios, where consistent and high-reward performance is of paramount importance.
4.2. Comparison Results in Different Environments
This study investigates the vessel’s berthing process using the DDQN-EMCMO algorithm under varying current speeds and directions. The experimental setup included five distinct current conditions: [0 cm/s, 0°], [2.24 cm/s, 30°], [2.24 cm/s, 60°], [2.24 cm/s, 45°], and [3.36 cm/s, 45°]. Following smoothing of the collected data, curves illustrating the convergence trend of total thrust and berthing time over 3000 training episodes were plotted, as shown in Figure 6. The corresponding berthing trajectory diagrams for different current conditions are presented in Figure 7. Concurrently, the average thrust and average time required for successful berthing were recorded, as detailed in Table 2.
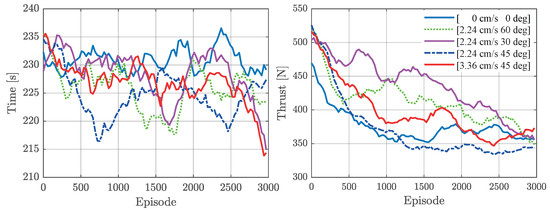
Figure 6.
Convergence trend of total thrust and berthing time with respect to training episodes for the DDQN-EMCMO algorithm under different environmental conditions.
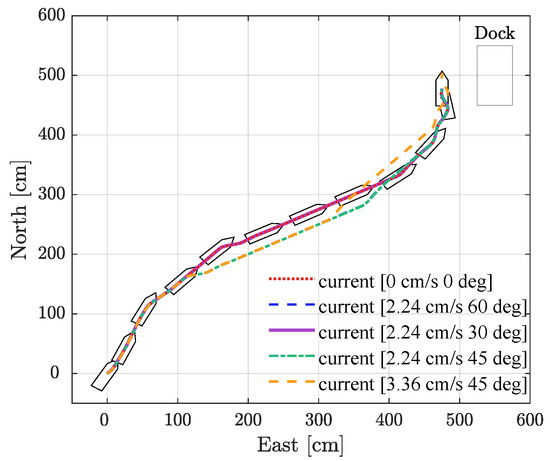
Figure 7.
Berthing trajectories and training performance under different current conditions.
Figure 6 displays the convergence characteristics of the DDQN-EMCMO algorithm’s total thrust and berthing time across 3000 optimization iterations under the different current conditions. The figure demonstrates a favorable convergence in both key performance indicators as training progresses. The curves for total thrust and time stabilize across various current environments, indicating the algorithm’s capacity to learn effective berthing strategies. Particularly under more challenging current conditions, such as [2.24 cm/s, 45°] and [3.36 cm/s, 45°], although the algorithm might exhibit some fluctuation during the early training phases, it consistently converges to lower thrust consumption and shorter berthing times. This highlights its robust learning ability and adaptability to environmental disturbances. As depicted in Figure 7, the DDQN-EMCMO algorithm consistently achieves stable and safe berthing under diverse water flow conditions. The vessel’s heading is maintained at approximately 90 degrees throughout the berthing process, fulfilling the predefined requirements. The trajectory plots clearly illustrate the vessel’s path from the initial position to the final berth. Even when subjected to water flow interference of varying directions and intensities, the algorithm successfully plans smooth and efficient trajectories, guiding the vessel to its precise docking location. This further substantiates the algorithm’s robustness in complex environments.
As listed in Table 3, under still water conditions ([0 cm/s, 0°]), the average total thrust is , and the required berthing time is . When the current speed increases to 2.24 cm/s with directions of 30°, 60°, and 45°, the required total thrust fluctuates between and , with corresponding times ranging from to . Specifically, under the [2.24 cm/s, 45°] condition, the berthing task is most challenging, necessitating a thrust of and for completion. Even in stronger currents, such as [3.36 cm/s, 45°], the algorithm maintains commendable control performance, completing the berthing with a thrust of in . The berthing angle consistently remained at approximately 90 degrees across all tested environments, satisfying the berthing requirements. In conclusion, the DDQN-EMCMO algorithm demonstrates significant adaptability and robustness when subjected to various complex current disturbances. It effectively accomplishes parallel berthing tasks with minimal performance degradation, validating its potential for practical applications.

Table 3.
Optimal thrust–time combination under different current conditions.
4.3. Berthing Path Planning Under Obstacle Constraints
To evaluate the robustness and path planning capability of the proposed DDQN-EMCMO algorithm in port environments, we designed a berthing scenario with an embedded obstacle. The experimental results are illustrated in Figure 8, which depicts the berthing trajectory and dynamic response in the presence of an obstacle. The obstacle is modeled as a square with a side length of 50 cm, located in the cm region of the NED coordinate frame. It is strategically placed between the vessel’s initial position and the target berthing area to simulate typical port obstacles such as moored ships or dock structures. The obstacle’s size and position effectively block a direct path to the berth, thus testing the algorithm’s ability to generate a collision-free trajectory while maintaining a 90-degree berthing orientation.
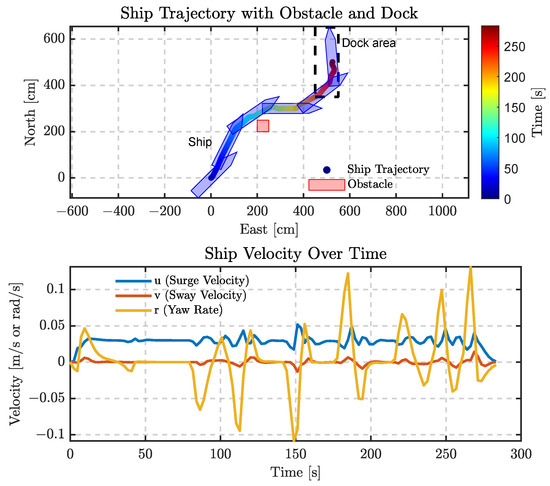
Figure 8.
Berthing trajectory and dynamic response of the ship under obstacle constraints.
Collision detection is performed by ensuring that the vessel’s geometry does not intersect the obstacle region. According to Table 1, the CSAD vessel is 257.8 cm in length and 44.0 cm in width, with a triangular bow approximated by five key vertices: stern-left, stern-right, bow-tip, bow-right, and bow-left. These vertices are transformed from the vessel’s body-fixed coordinate system to the NED frame based on the vessel’s current position and heading. A collision is detected if any of these vertices fall within the obstacle’s bounding box. Upon detection, a collision penalty is triggered, as detailed in Section 3.2. This mechanism ensures reliable identification of intersections between the vessel and the obstacle, facilitating safe path generation.
As shown in the upper part of Figure 8, the vessel successfully avoids the defined obstacle (marked with a red rectangle) while maintaining a reasonable safety margin, effectively reducing collision risk. The trajectory is color-coded to represent time progression, demonstrating continuous heading adjustments as the vessel approaches the berth, eventually completing the berthing maneuver with a pose perpendicular to the quay. The trajectory remains smooth and continuous throughout, indicating that the algorithm achieves well-balanced coordination between obstacle avoidance and berthing control.
The lower part of Figure 8 presents the dynamic responses, including surge, sway, and yaw rates. While minor fluctuations occur during the obstacle avoidance phase, the responses stabilize rapidly during final docking. The simplicity and realistic dimensions of the rectangular obstacle test the adaptability of the algorithm. Its positioning necessitates an optimized trade-off between safety and efficiency. Iterative testing and optimization of the collision detection mechanism contributed to the stable trajectory observed in Figure 8, further validating the algorithm’s performance in simulated port scenarios. It is worth noting that the current berthing strategy assumes a fully observable and deterministic environment. However, real-world uncertainties such as surrounding traffic dynamics, variable currents, and limited observability can significantly affect berthing safety. To enhance robustness in such scenarios, short-term traffic and trajectory prediction techniques may be incorporated into the planning module [44,45,46].
5. Conclusions
This study proposed a DDQN-guided dual-population evolutionary multitasking framework to address the constrained multi-objective optimization challenges of autonomous ship berthing. By leveraging a DDQN to guide operator selection within a dual-population evolutionary structure, the framework effectively balances competing objectives, including berthing time, energy consumption, and safety. The integrated reward function ensures efficient path planning by optimizing thrust, time, and heading accuracy while adapting to environmental dynamics such as water currents and obstacles.
Simulations on the CSAD vessel model confirm that this framework surpasses baseline algorithms, including DQN-EMCMO, EMCMO, DQN, Q-learning, and NSGAII, demonstrating enhanced efficiency and stability while consistently achieving the required berthing angle. The framework’s adaptability is evident in its robust performance across diverse environmental conditions, generating safe and smooth trajectories through dynamic adjustments of vessel kinematics. These results highlight the framework’s potential as a reliable solution for autonomous ship berthing in challenging port environments. Future work could focus on real-world validation, incorporating additional environmental factors such as wind disturbances, shallow water effects, and wave-induced motions, and extending the framework to multi-vessel coordination scenarios. Additionally, underactuated ships and thruster failure scenarios will be considered to further validate the framework’s robustness and applicability.
Author Contributions
Conceptualization, J.M. and Q.Z.; methodology, J.M.; software, J.M.; validation, J.M. and Q.Z.; formal analysis, J.M.; investigation, Q.Z.; resources, Q.Z.; data curation, Q.Z.; writing—original draft preparation, J.M.; writing—review and editing, J.M.; visualization, J.M.; supervision, Q.Z.; project administration, Q.Z.; funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China grant number 52171299.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cai, J.; Chen, G.; Yin, J.; Ding, C.; Suo, Y.; Chen, J. A review of autonomous berthing technology for ships. J. Mar. Sci. Eng. 2024, 12, 1137. [Google Scholar] [CrossRef]
- Lexau, S.J.; Breivik, M.; Lekkas, A.M. Automated docking for marine surface vessels—A survey. IEEE Access 2023, 11, 132324–132367. [Google Scholar] [CrossRef]
- Wang, K.; Guo, X.; Zhao, J.; Ma, R.; Huang, L.; Tian, F.; Dong, S.; Zhang, P.; Liu, C.; Wang, Z. An integrated collaborative decision-making method for optimizing energy consumption of sail-assisted ships towards low-carbon shipping. Ocean Eng. 2022, 266, 112810. [Google Scholar] [CrossRef]
- Öztürk, Ü.; Akdağ, M.; Ayabakan, T. A review of path planning algorithms in maritime autonomous surface ships: Navigation safety perspective. Ocean Eng. 2022, 251, 111010. [Google Scholar] [CrossRef]
- Wu, G.; Li, D.; Ding, H.; Shi, D.; Han, B. An overview of developments and challenges for unmanned surface vehicle autonomous berthing. Complex Intell. Syst. 2024, 10, 981–1003. [Google Scholar] [CrossRef]
- Mou, J.; Zhu, Q.; Liu, Y.; Bai, Y. Multi-objective optimal thrust allocation strategy for automatic berthing of surface ships using adaptive non-dominated sorting genetic algorithm III. Ocean Eng. 2024, 299, 117288. [Google Scholar] [CrossRef]
- Murdoch, E.; Dand, I.W.; Clarke, C. A Master’s Guide to Berthing; Witherby Seamanship International Ltd.: Edinburgh, UK, 2012. [Google Scholar]
- Utne, I.B.; Rokseth, B.; Sørensen, A.J.; Vinnem, J.E. Towards supervisory risk control of autonomous ships. Reliab. Eng. Syst. Saf. 2020, 196, 106757. [Google Scholar] [CrossRef]
- Ludvigsen, M.; Sørensen, A.J. Towards integrated autonomous underwater operations for ocean mapping and monitoring. Annu. Rev. Control 2016, 42, 145–157. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, S.; Wen, Y.; Du, Z.; Xiao, C.; Huang, L.; Zhu, M. The review unmanned surface vehicle path planning: Based on multi-modality constraint. Ocean Eng. 2020, 200, 107043. [Google Scholar] [CrossRef]
- Zhou, H.; Ren, Z.; Marley, M.; Skjetne, R. A guidance and maneuvering control system design with anti-collision using stream functions with vortex flows for autonomous marine vessels. IEEE Trans. Control Syst. Technol. 2022, 30, 2630–2645. [Google Scholar] [CrossRef]
- Andrew, B.; Richard S, S. Reinforcement Learning: An introduction; Bradford Books: Bradford, UK, 2018. [Google Scholar]
- Song, R.; Liu, Y.; Bucknall, R. Smoothed A* algorithm for practical unmanned surface vehicle path planning. Appl. Ocean Res. 2019, 83, 9–20. [Google Scholar] [CrossRef]
- Han, S.; Wang, L.; Wang, Y.; He, H. A dynamically hybrid path planning for unmanned surface vehicles based on non-uniform Theta* and improved dynamic windows approach. Ocean Eng. 2022, 257, 111655. [Google Scholar] [CrossRef]
- Zhang, X.; Xia, S.; Li, X.; Zhang, T. Multi-objective particle swarm optimization with multi-mode collaboration based on reinforcement learning for path planning of unmanned air vehicles. Knowl.-Based Syst. 2022, 250, 109075. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, J.; Wu, D.; Tian, W. A novel path planning algorithm for ships in dynamic current environments. Ocean Eng. 2023, 288, 116091. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, J. A ship performance and genetic algorithm-based decision support system for vessel speed optimisation of ocean route. Int. J. Shipp. Transp. Logist. 2023, 17, 107–145. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Xia, Y.; Chai, S. Solving multiobjective constrained trajectory optimization problem by an extended evolutionary algorithm. IEEE Trans. Cybern. 2018, 50, 1630–1643. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, W. An efficient UAV localization technique based on particle swarm optimization. IEEE Trans. Veh. Technol. 2022, 71, 9544–9557. [Google Scholar] [CrossRef]
- Guo, X.; Ji, M.; Zhao, Z.; Wen, D.; Zhang, W. Global path planning and multi-objective path control for unmanned surface vehicle based on modified particle swarm optimization (PSO) algorithm. Ocean Eng. 2020, 216, 107693. [Google Scholar] [CrossRef]
- Liu, X.F.; Fang, Y.; Zhan, Z.H.; Jiang, Y.L.; Zhang, J. A cooperative evolutionary computation algorithm for dynamic multiobjective multi-AUV path planning. IEEE Trans. Ind. Inform. 2023, 20, 669–680. [Google Scholar] [CrossRef]
- Ouelmokhtar, H.; Benmoussa, Y.; Benazzouz, D.; Ait-Chikh, M.A.; Lemarchand, L. Energy-based USV maritime monitoring using multi-objective evolutionary algorithms. Ocean Eng. 2022, 253, 111182. [Google Scholar] [CrossRef]
- Peng, C.; Qiu, S. A decomposition-based constrained multi-objective evolutionary algorithm with a local infeasibility utilization mechanism for UAV path planning. Appl. Soft Comput. 2022, 118, 108495. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X. Push and Pull Search: Balancing Exploration and Exploitation in Multi-objective Optimization. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Deb, K. CTAEA: A Two-Archive Evolutionary Algorithm for Promoting Diversity in Optimization. IEEE Trans. Evol. Comput. 2019, 23, 109–123. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Zhang, Q. Dual-Population Strategies for Global Optimization in Maritime Scheduling. Transp. Res. Part C Emerg. Technol. 2021, 129, 103–117. [Google Scholar]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Schneider, S.; Khalili, R.; Manzoor, A.; Qarawlus, H.; Schellenberg, R.; Karl, H.; Hecker, A. Self-learning multi-objective service coordination using deep reinforcement learning. IEEE Trans. Netw. Serv. Manag. 2021, 18, 3829–3842. [Google Scholar] [CrossRef]
- Caviglione, L.; Gaggero, M.; Paolucci, M.; Ronco, R. Deep reinforcement learning for multi-objective placement of virtual machines in cloud datacenters. Soft Comput. 2021, 25, 12569–12588. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.; Zhang, T.; Li, K.; Li, W.; Ishibuchi, H.; Liao, X. Hybridization of evolutionary algorithm and deep reinforcement learning for multiobjective orienteering optimization. IEEE Trans. Evol. Comput. 2022, 27, 1260–1274. [Google Scholar] [CrossRef]
- Jo, S.; Oh, J.Y.; Yoon, Y.T.; Jin, Y.G. Self-healing radial distribution network reconfiguration based on deep reinforcement learning. Results Eng. 2024, 22, 102026. [Google Scholar] [CrossRef]
- Zhao, F.; Di, S.; Wang, L. A hyperheuristic with Q-learning for the multiobjective energy-efficient distributed blocking flow shop scheduling problem. IEEE Trans. Cybern. 2022, 53, 3337–3350. [Google Scholar] [CrossRef]
- Liu, X.; Qiu, L.; Fang, Y.; Wang, K.; Li, Y.; Rodríguez, J. Event-Driven Based Reinforcement Learning Predictive Controller Design for Three-Phase NPC Converters Using Online Approximators. IEEE Trans. Power Electron. 2024, 40, 4914–4926. [Google Scholar] [CrossRef]
- Tian, Y.; Li, X.; Ma, H.; Zhang, X.; Tan, K.C.; Jin, Y. Deep reinforcement learning based adaptive operator selection for evolutionary multi-objective optimization. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 7, 1051–1064. [Google Scholar] [CrossRef]
- Hinostroza, M.A.; Lekkas, A. Temporal mission planning for autonomous ships: Design and integration with guidance, navigation and control. Ocean Eng. 2024, 297, 117104. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Skjetne, R. The Maneuvering Problem. Ph.D. Thesis, NTNU, Trondheim, Norway, 2005. Volume 1. pp. 95–98. [Google Scholar]
- Ma, Z.; Wang, Y. Evolutionary constrained multiobjective optimization: Test suite construction and performance comparisons. IEEE Trans. Evol. Comput. 2019, 23, 972–986. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D. Human-level Control Through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Zhang, H.; Wang, J. Meta-learning-Based Deep Reinforcement Learning for Multiobjective Optimization Problems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7978–7991. [Google Scholar] [CrossRef]
- Qiao, K.; Yu, K.; Qu, B.; Liang, J.; Song, H.; Yue, C. An evolutionary multitasking optimization framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2022, 26, 263–277. [Google Scholar] [CrossRef]
- Bjørnø, J.; Heyn, H.M.; Skjetne, R.; Dahl, A.R.; Frederich, P. Modeling, parameter identification and thruster-assisted position mooring of c/s inocean cat i drillship. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Trondheim, Norway, 25–30 June 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 57748, p. V07BT06A019. [Google Scholar]
- Chen, X.; Wei, C.; Zhou, G.; Wu, H.; Wang, Z.; Biancardo, S.A. Automatic identification system (AIS) data supported ship trajectory prediction and analysis via a deep learning model. J. Mar. Sci. Eng. 2022, 10, 1314. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Li, Y.; Yu, Q.; Yang, Z. Vessel Trajectory Prediction for Enhanced Maritime Navigation Safety: A Novel Hybrid Methodology. J. Mar. Sci. Eng. 2024, 12, 1351. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).