Seismic Prediction of Shallow Unconsolidated Sand in Deepwater Areas
Abstract
1. Introduction
2. Materials and Methods
2.1. Geological Settings
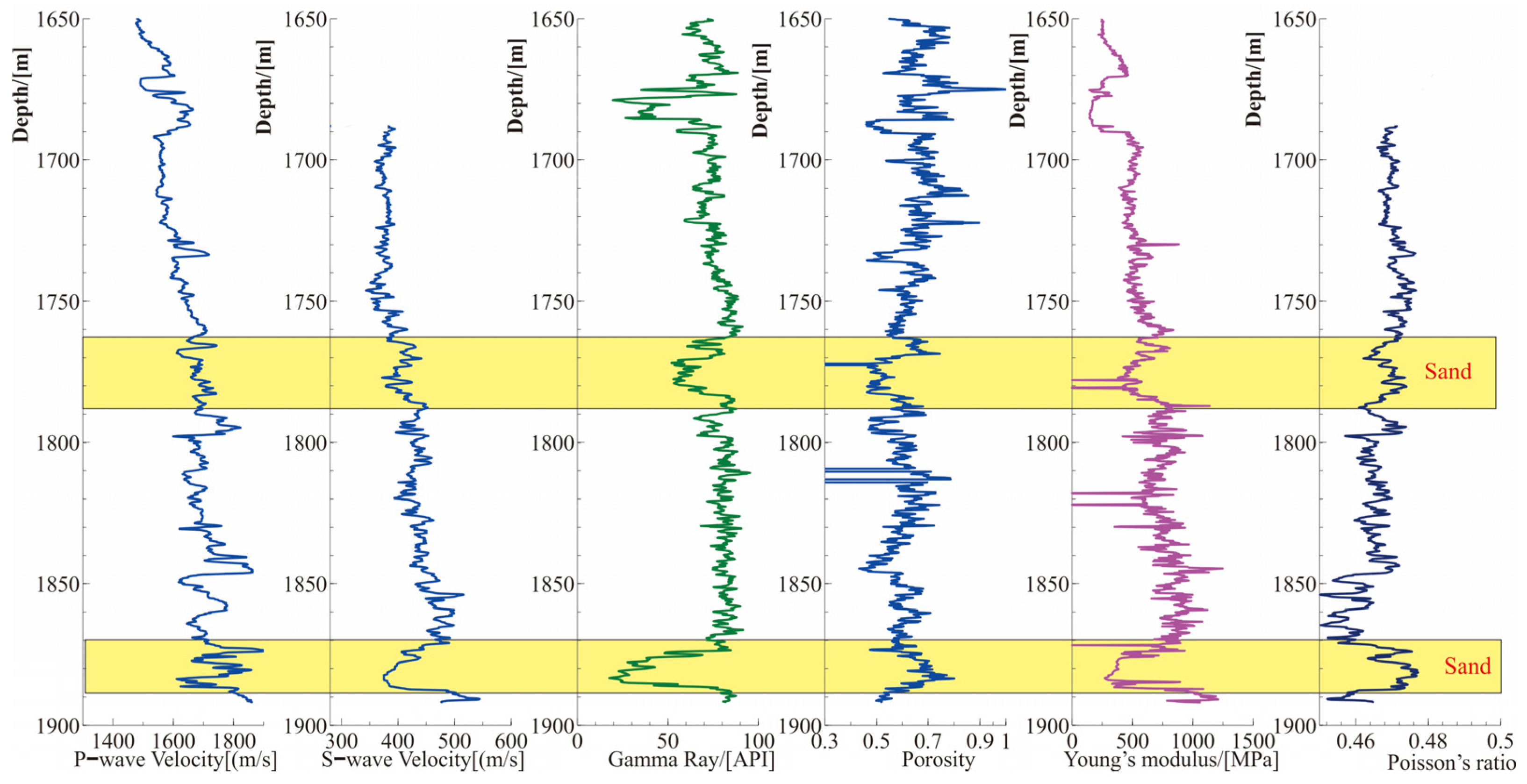
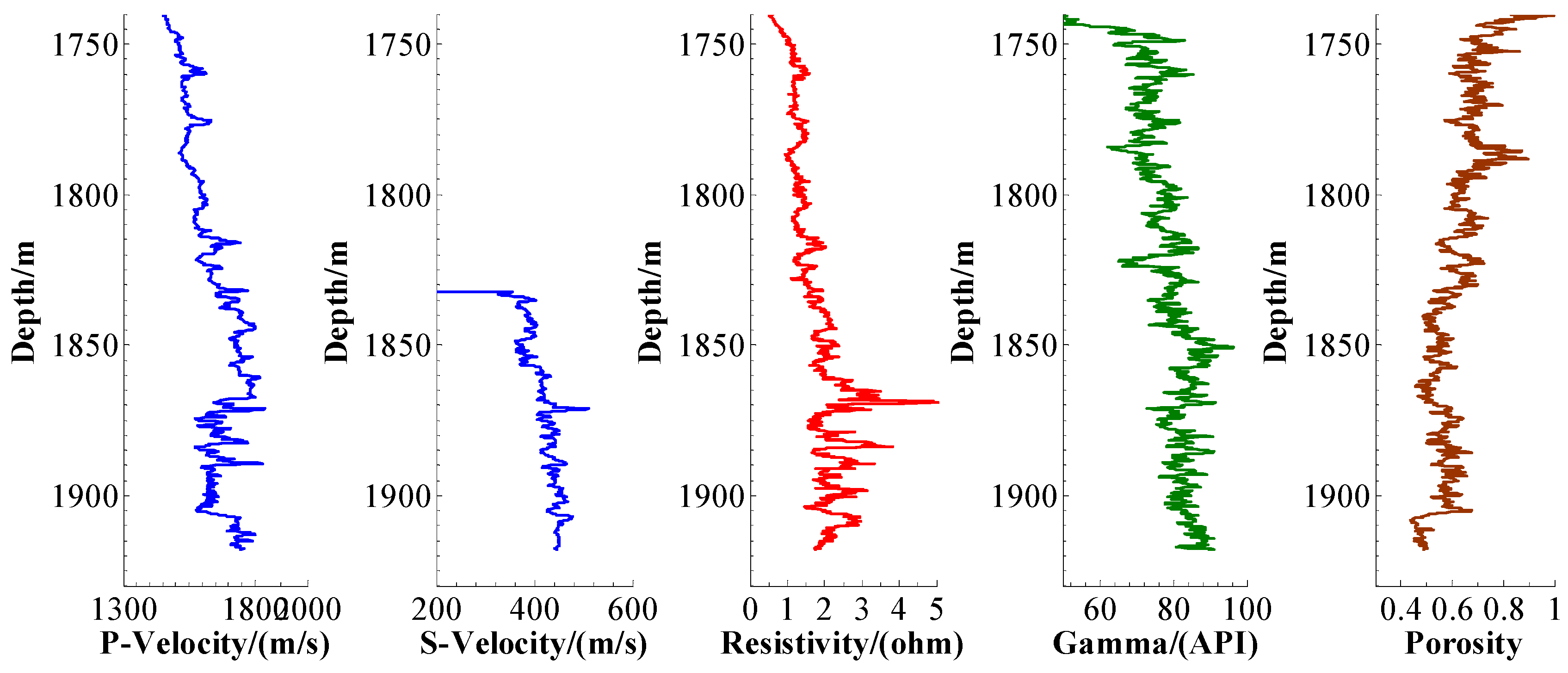
2.2. Well Logs and Seismic Data
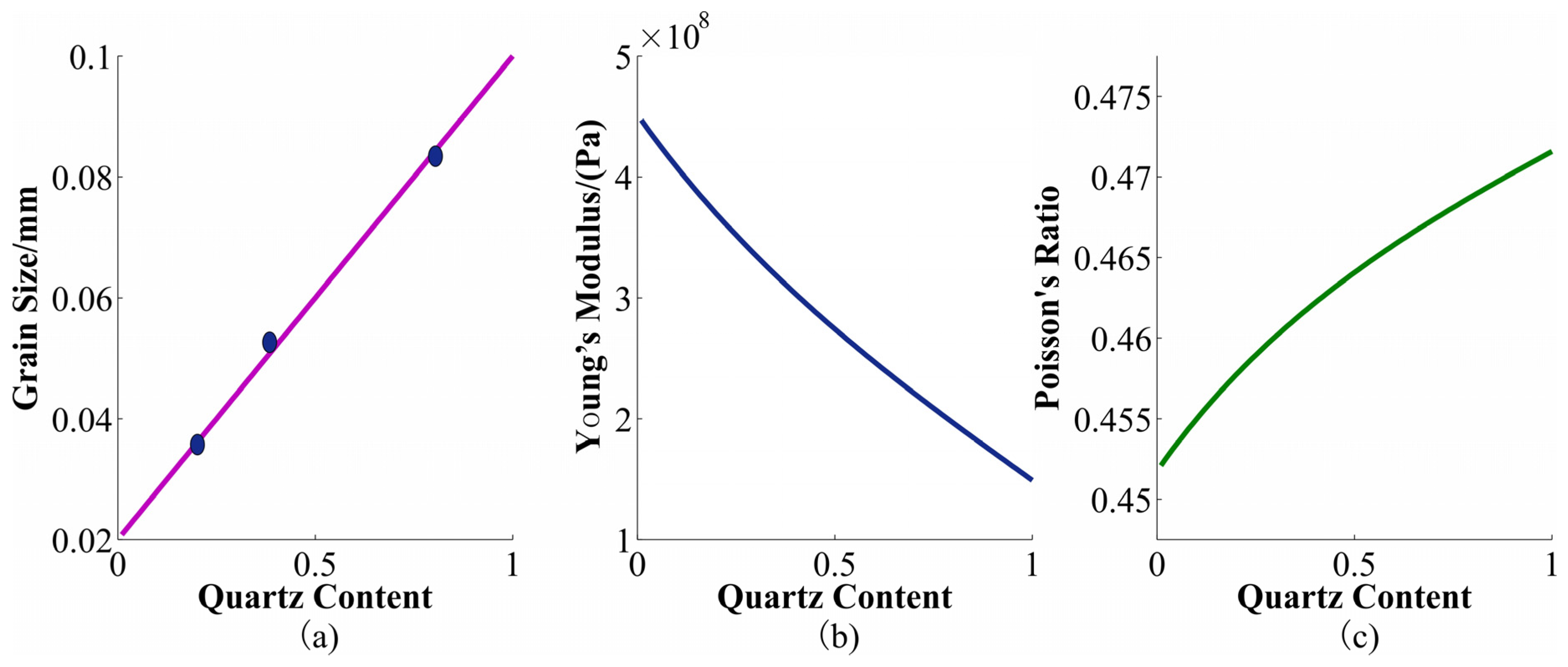
2.3. Rock Physics Modeling
2.4. Seismic Inversion
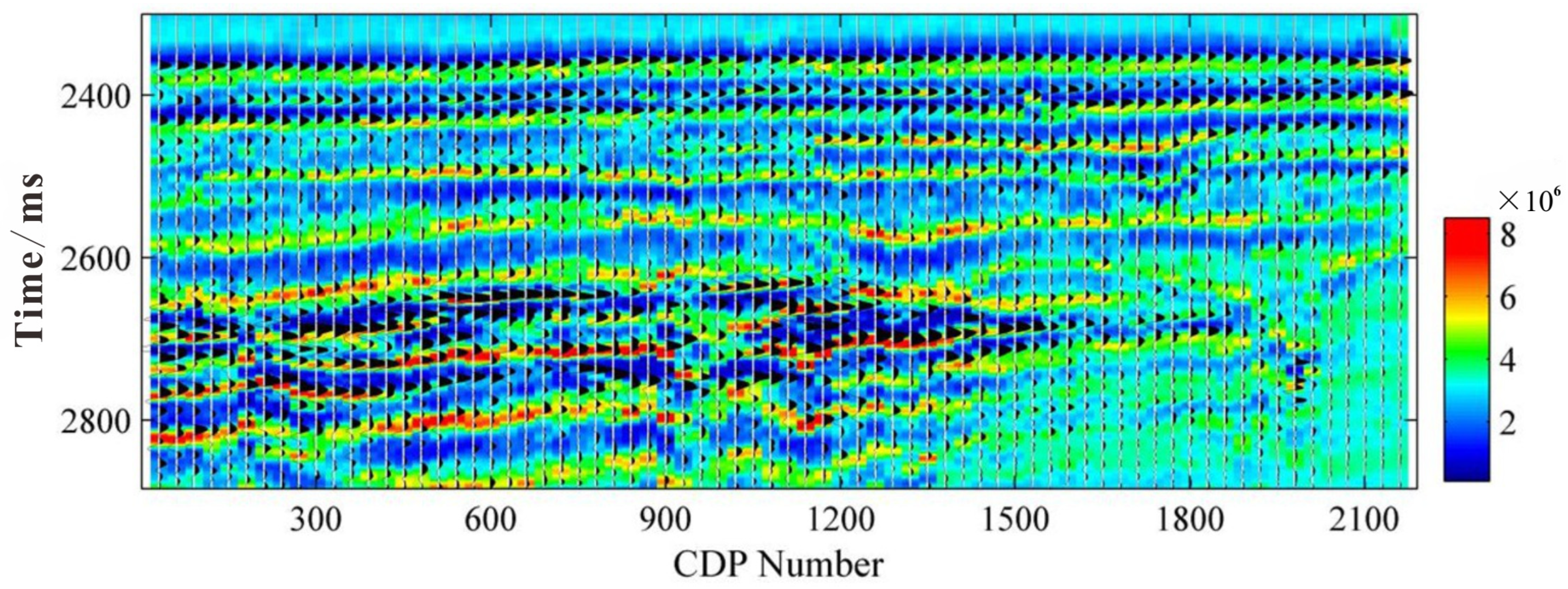
3. Results
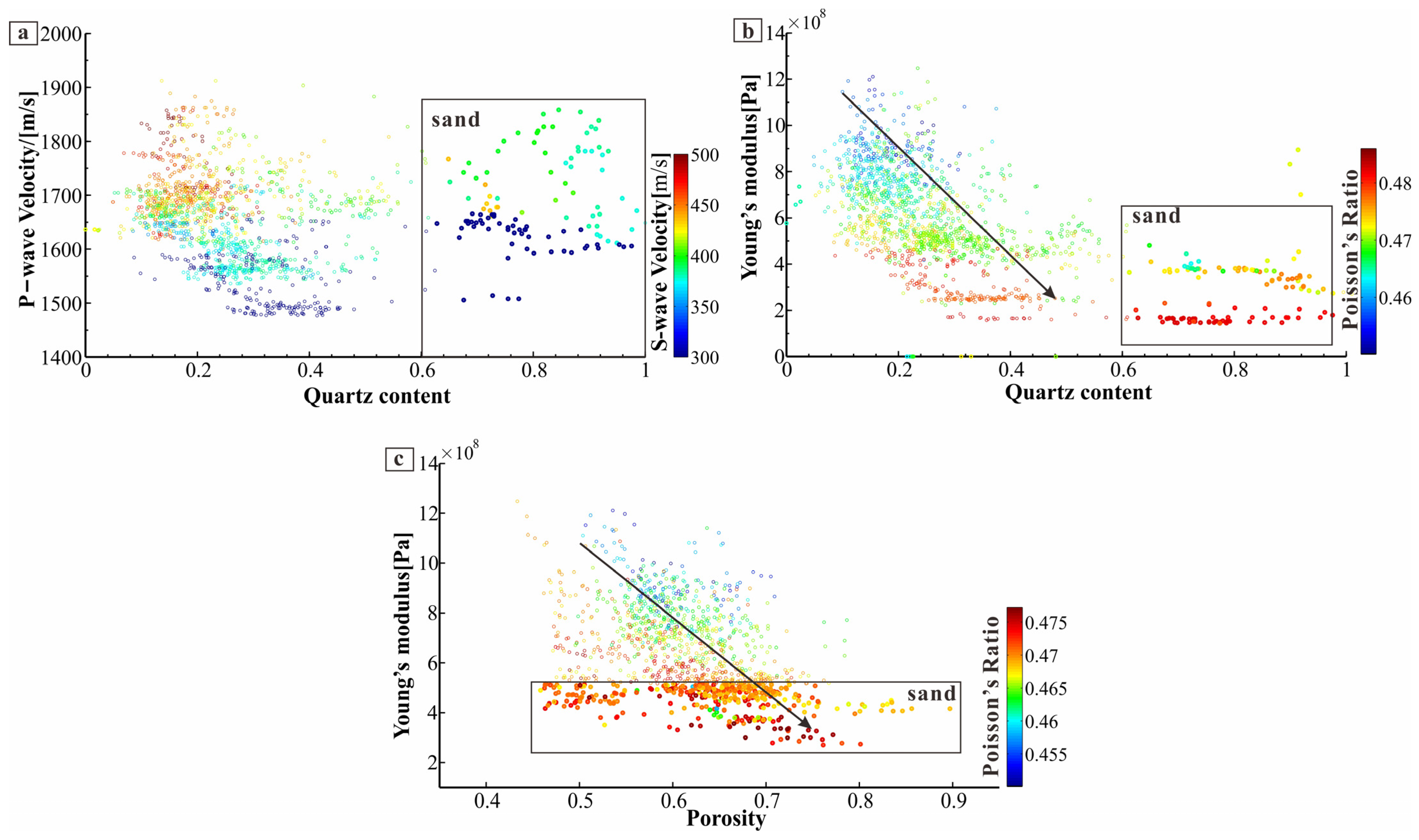
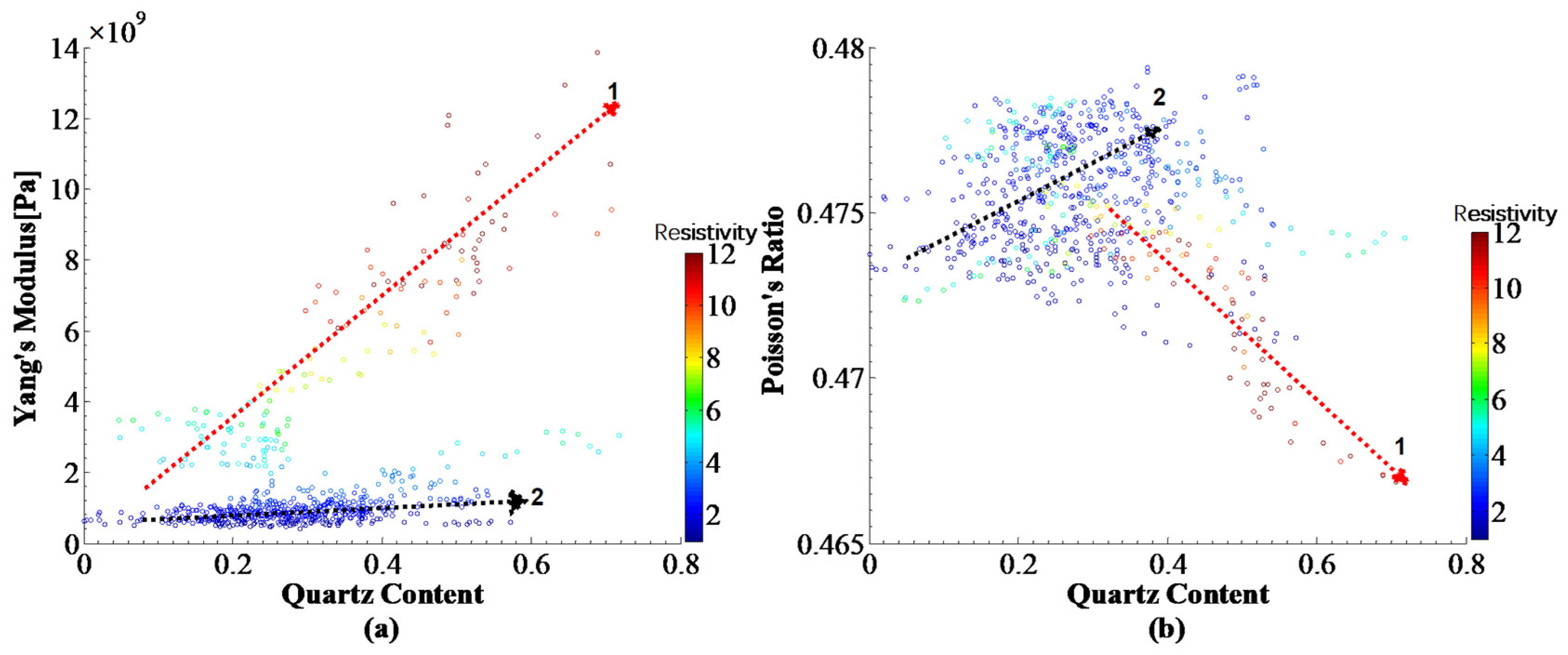
3.1. The Elastic Characteristic of Sandy Sediments
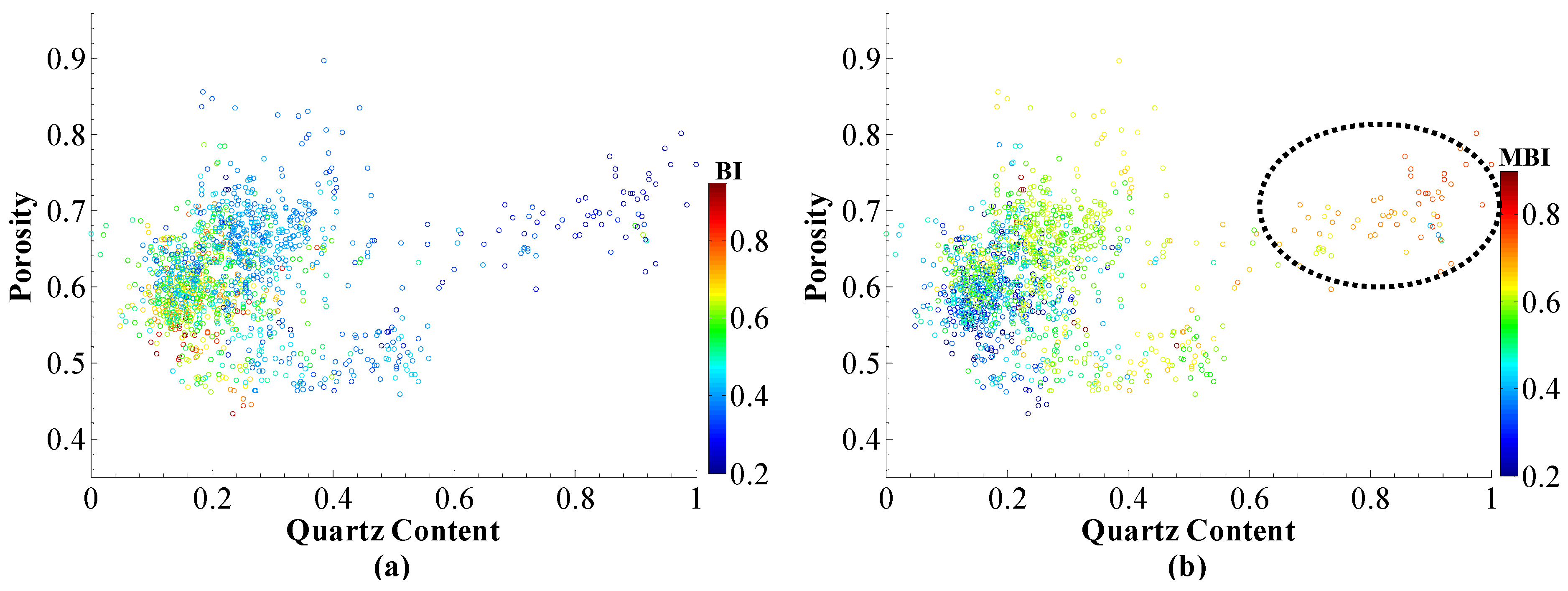
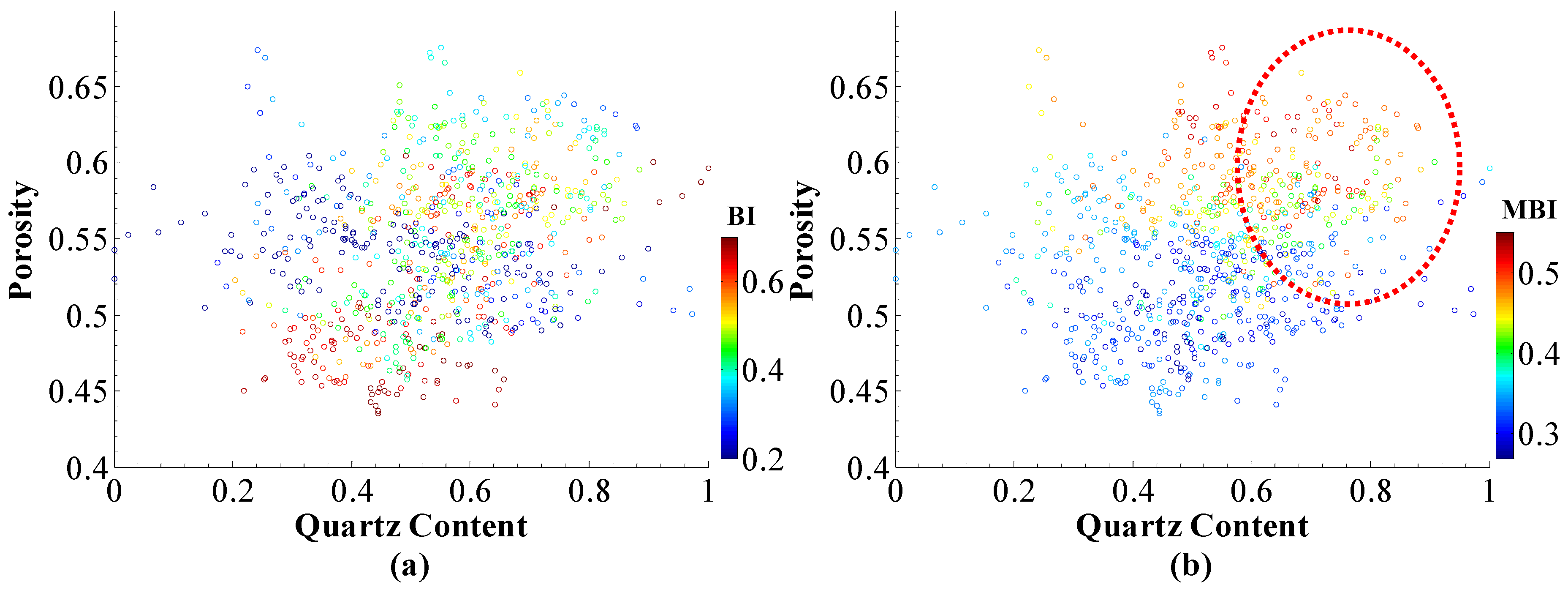
3.2. Elastic Indicator of Sand Content
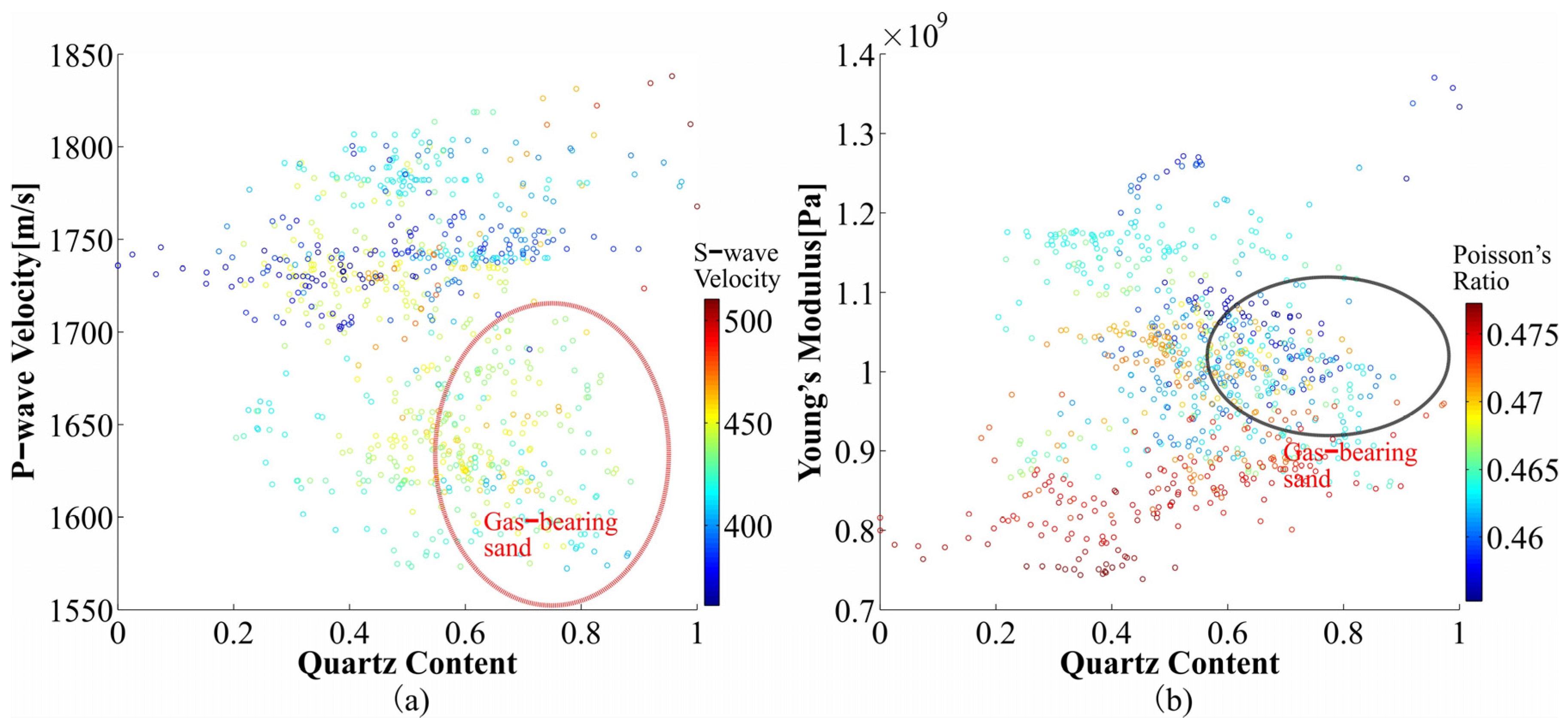
3.2.1. Water Saturated Sandy Sediments
3.2.2. Gas-Bearing Sediments
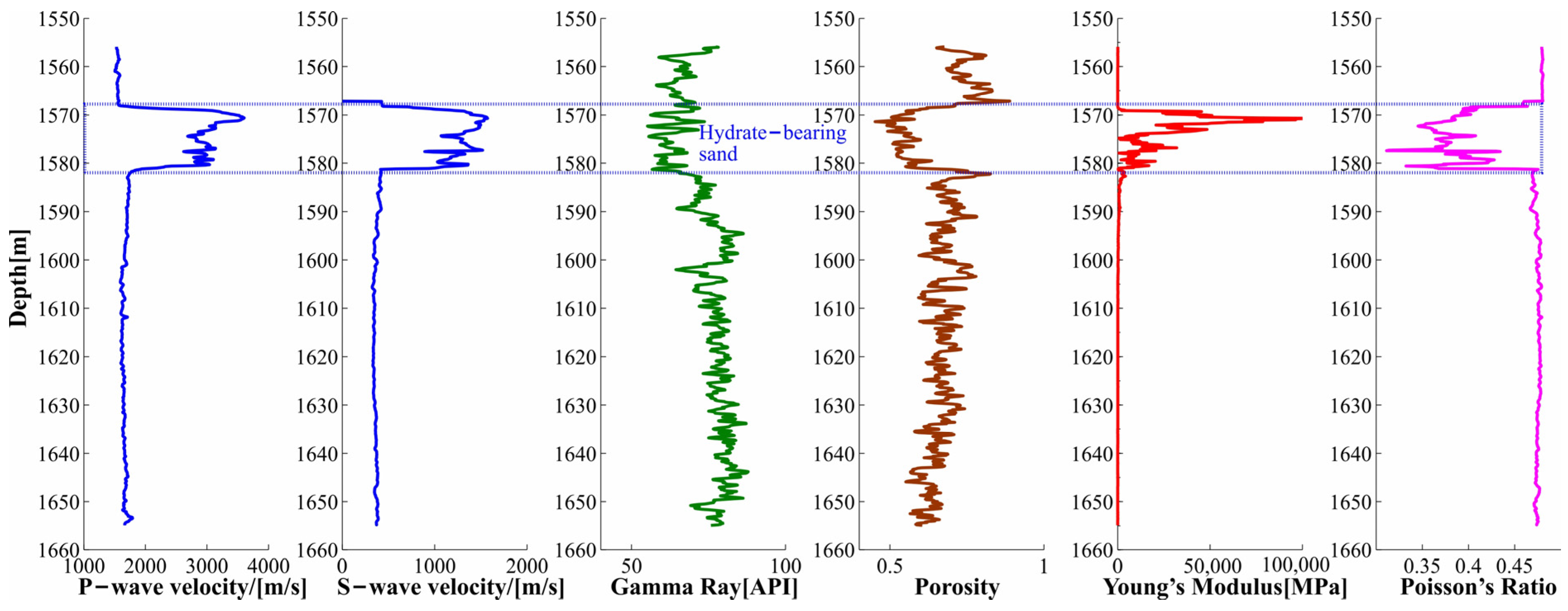
3.2.3. Hydrate-Bearing Sand
3.3. Seismic Inversion Results
4. Discussion
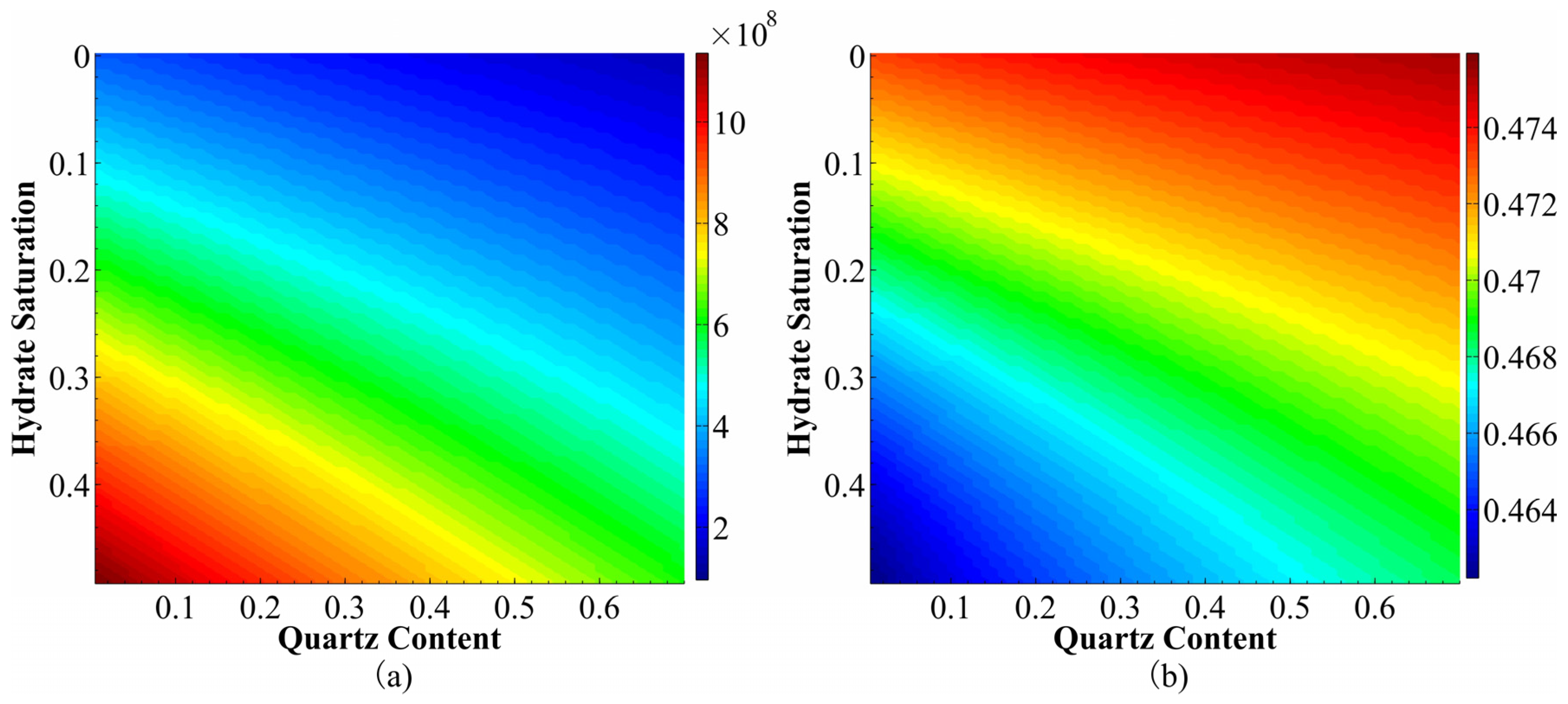
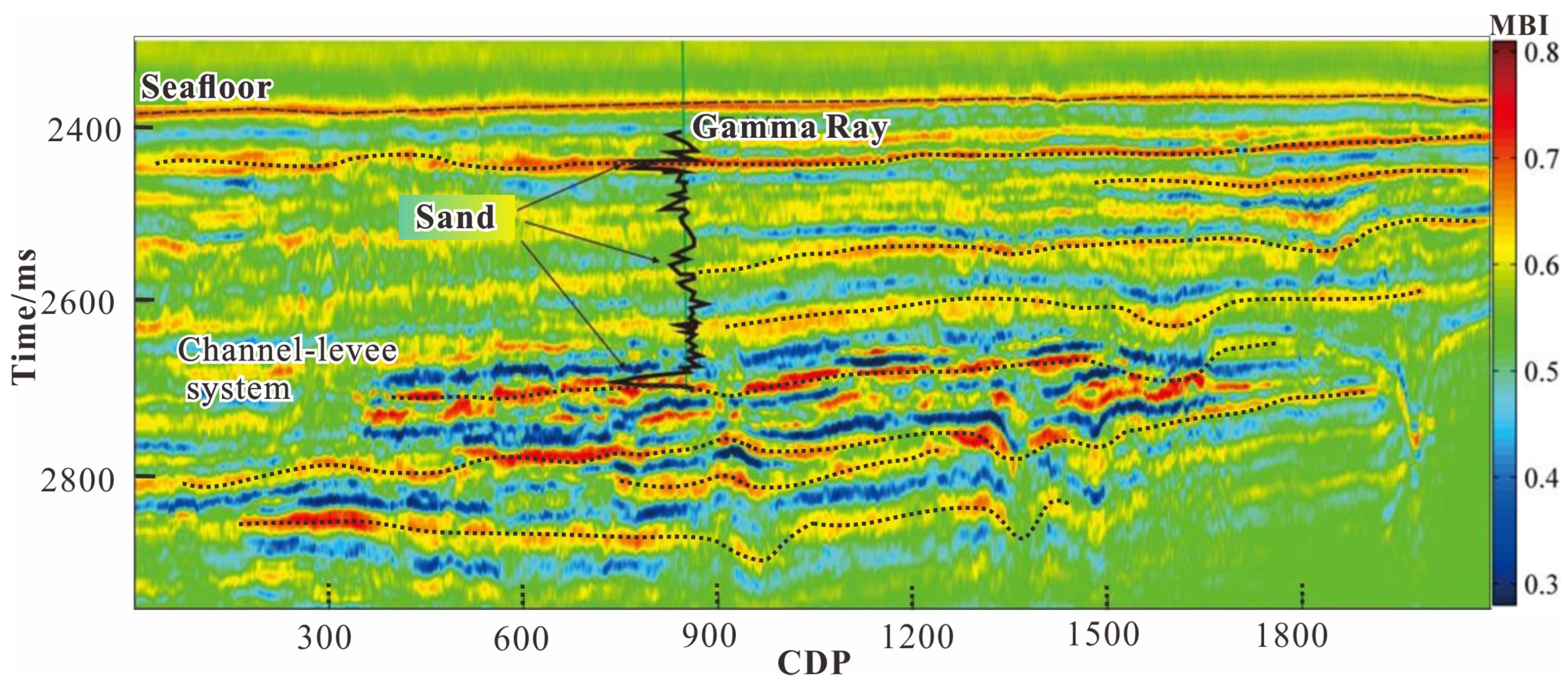
4.1. Effectiveness of MBI
4.2. Geological Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dickens, G.R.; Quinby, H.M.S. Methane hydrate stability in seawater. Geophys. Res. Lett. 1994, 21, 2115–2118. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Methane hydrate a major reservoir of carbon in the shallow geosphere? Chem. Geol. 1988, 71, 41–51. [Google Scholar] [CrossRef]
- Kvenvolden, K.A. Gas hydrates: Geological perspective and global change. Rev. Geophys. 1993, 31, 173–187. [Google Scholar] [CrossRef]
- Collett, T.S.; Lee, M.W.; Zyrianova, M.V.; Mrozewski, S.A.; Guerin, G.; Cook, A.E.; Goldberg, D.S. Gulf of Mexico gas hydrate Joint industry Project leg II logging-while-drilling data acquisition and analysis. Mar. Petrol. Geol. 2012, 34, 41–61. [Google Scholar] [CrossRef]
- Fang, Y.; Flemings, P.B.; Daigle, H.; Phillips, S.; Meazell, K.; You, K. Petrophysical properties of the Green Canyon Block 955 hydrate reservoir inferred from reconstituted sediments: Implications for hydrate formation and production. AAPG Bull. 2020, 104, 1997–2028. [Google Scholar] [CrossRef]
- Colwell, F.; Matsumoto, R.; Reed, D. A review of the gas hydrates, geology, and biology of the Nankai Trough. Chem. Geol. 2004, 250, 391–404. [Google Scholar] [CrossRef]
- Kuang, Z.; Cook, A.; Ren, J.; Deng, W.; Cao, Y.; Cai, H. A flat-lying transitional free gas to gas hydrate system in a sand layer in the Qiongdongnan Basin of the South China Sea. Geophys. Res. Lett. 2023, 50, e2023GL105744. [Google Scholar] [CrossRef]
- Xu, C.; Wu, K.; Pei, J.; Hu, L. Enrichment mechanisms and accumulation model of ultra-deep water and ultra-shallow gas: A case study of Lingshui 36-1 gas field in Qiongdongnan Basin, South China Sea. Pet. Explor. Dev. 2025, 51, 50–63. [Google Scholar] [CrossRef]
- Ruppel, C. Permafrost-associated gas hydrate: Is it really approximately 1% of the global system? J. Chem. Eng. Data 2015, 60, 429–436. [Google Scholar] [CrossRef]
- Kessler, J.D.; Ruppel, C.D. Characterizing Ocean Acidification and Atmospheric Emission caused by Methane Released from Gas Hydrate Systems along the US Atlantic Margin (No. DOE-ROCHESTER-0028980); Univeristy of Rochester, Ed.; National Energy Technology Laboratory (NETL): Pittsburgh, PA, USA; Morgantown, WV, USA; Albany, OR, USA, 2020.
- Farahani, M.V.; Guo, X.; Zhang, L.; Yang, M.; Hassanpouryouzband, A.; Zhao, J.; Yang, J.; Song, Y.; Tohidi, B. Effect of thermal formation/dissociation cycles on the kinetics of formation and pore-scale distribution of methane hydrates in porous media: A magnetic resonance imaging study. Sustain. Energy Fuels 2021, 5, 1567–1583. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the climate-driven evolution of gas hydrate-bearing permafrost sediments: Implications for prediction of environmental impacts and security of energy in cold regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Maslin, M.; Owen, M.; Day, S.; Long, D. Linking continental-slope failures and climate change: Testing the clathrate gun hypothesis. Geology 2004, 32, 53–56. [Google Scholar] [CrossRef]
- Meng, M.; Li, L.; Liang, J.; Xu, J.; Feng, J.; Kuang, Z.; Zhang, W.; Huang, W.; Ren, J.; Deng, W.; et al. Quantifying the relative provenance contributions to submarine channel systems in the Qiongdongnan Basin since the Miocene: Implications for tectonic responses and channel migration. Basin Res. 2024, 36, 1365–2117. [Google Scholar]
- Meng, M.; Liang, J.; Lu, J.A.; Zhang, W.; Kuang, Z.; Fang, Y.; He, Y.; Deng, W.; Huang, W. Quaternary Deep-Water Sedimentary Characteristics and Their Relationship with the Gas Hydrate Accumulations in the Qiongdongnan Basin, Northwest South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2021, 177, 103628. [Google Scholar] [CrossRef]
- Yang, Y.; Aplin, A.C. Influence of lithology and compaction on the pore size distribution and modelled permeability of some mudrocks from the Norwegian margin. Mar. Petrol. Geol. 1998, 15, 163–175. [Google Scholar] [CrossRef]
- Yang, Y.; Aplin, A.C. Definition and practical application of mudstone porosity-effective stress relationships. Petrol. Geosci. 2004, 10, 153–162. [Google Scholar] [CrossRef]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47, RG4003. [Google Scholar] [CrossRef]
- Harris, N.B.; Miskimins, J.L.; Mnich, C.A. Mechanical anisotropy in the Woodford Shale, Permian Basin: Origin, magnitude, and scale. Lead. Edge 2011, 30, 284–291. [Google Scholar] [CrossRef]
- Sena, A.; Castillo, G.; Chesser, K.; Voisey, S.; Estrada, J.; Carcuz, J.; Carmona, E.; Schneider, R.V. Seismic reservoir characterization in resource shale plays: “Sweet spot” discrimination and optimization of horizontal well placement. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2011; p. 4424. [Google Scholar]
- Mehrabi, A.; Bagheri, M.; Bidhendi, M.N.; Delijani, E.B.; Behnoud, M. Improved porosity estimation in complex carbonate reservoirs using hybrid CRNN deep learning model. Earth Sci. Inf. 2024, 17, 4773–4790. [Google Scholar] [CrossRef]
- Riahi, Z.T.; Sarkarinejad, K.; Faghih, A.; Soleimany, B.; Payrovian, G.R. Frature detection using multi seismic attributes ant-tracking in the Rag-e-Sefid oilfield, SW Iran. EGU 2024, 21, 12039. [Google Scholar]
- Rickman, R.; Mullen, M.; Petre, E.; Grieser, B.; Kundert, D. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 21–24 September 2008; p. 115258. [Google Scholar]
- Sondergeld, C.H.; Newsham, K.E.; Comisky, J.T.; Rice, M.C.; Rai, C.S. Petrophysical consideration in evaluation and producing shale gas resources. In Proceedings of the SPE Unconventional Gas Conference, Calgary, AB, Canada, 19–21 October 2010. [Google Scholar]
- Shelander, D.; Dai, J.; Bunge, G. Predicting saturation of gas hydrates using pre-stack seismic data, Gulf of Mexico. Mar Geophys. Res. 2010, 31, 39–57. [Google Scholar] [CrossRef]
- Lee, M.W.; Hutchinson, D.R.; Collett, T.S.; Dillon, W.P. Seismic velocities for hydrate-bearing sediments using weighted equation. J. Geophys. Res.-Solid Earth 1996, 101, 20347–20358. [Google Scholar] [CrossRef]
- Lee, M.W.; Collett, T.S.; Inks, T.L. Seismic-attribute analysis for gas-hydrate and free-gas prospects on the North Slope of Alaska. In Natural Gas Hydrates-Energy Resource Potential and Associated Geologic Hazards; Collett, T., Johnson, A., Knapp, C., Boswell, R., Eds.; AAPG Memoir: Tulsa, OK, USA, 2009; Volume 89, pp. 541–554. [Google Scholar]
- Waite, W.F.; Helgerud, M.B.; Nur, A.; Pinkston, J.C.; Stern, L.A.; Kirby, S.H.; Durham, W.B. Laboratory measurements of compressional and shear wave speeds through methane hydrate. Ann. N. Y. Acad. Sci. 2000, 912, 1003–1010. [Google Scholar] [CrossRef]
- Yun, T.S.; Francisca, F.M.; Santamarina, J.C.; Rupple, C. Compressional and shear wave velocities in uncemented sediment containing gas hydrate. Geophys. Res. Lett. 2005, 32, L10669. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Elasticity of high-porosity sandstones: Theory for two North Sea data sets. Geophysics 1996, 61, 1363–1370. [Google Scholar] [CrossRef]
- Helgerud, M.B.; Dvorkin, J.; Nur, A.; Sakai, A.; Collett, T. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling. Geophys. Res. Lett. 1999, 26, 2021–2024. [Google Scholar] [CrossRef]
- Lee, M.W. Modifed Biot-Gassmann theory for calculating elastic velocities for unconsolidated and consolidated sediments. Mar. Geophys. Res. 2002, 23, 403–412. [Google Scholar] [CrossRef]
- Duffaut, K.; Landrø, M.; Sollie, R. Using Mindlin theory to model friction-dependent shear modulus in granular media. Geophysics 2010, 75, E143–E152. [Google Scholar] [CrossRef]
- Fujii, T.; Saeki, T.; Kobayashi, T.; Inamori, T.; Hayashi, M.; Takano, O.; Takayama, T.; Kawasaki, T.; Nagakubo, S.; Nakamizu, M.; et al. Resource assessment of methane hydrate in the eastern Nankai Trough, Japan. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008; OnePetro: Richardson, TX, USA, 2008. [Google Scholar]
- Pan, H.; Li, H.; Chen, J.; Zhang, Y.; Cai, S.; Huang, Y.; Zheng, Y.; Zhao, Y.; Deng, J. A unified contact cementation theory for gas hydrate morphology detection and saturation estimation from elastic-wave velocities. Mar. Petrol. Geol. 2020, 113, 104146. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Zhu, W.; Huang, B.; Mi, L.; Wilkins, R.W.; Fu, N.; Xiao, X. Geochemistry, origin, and deep-water exploration potential of natural gases in the Pearl River Mouth and Qiongdongnan basin, South China Sea. AAPG Bull. 2009, 93, 741–761. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, W.; Lu, J.A.; Wei, J.; Kuang, Z.; He, Y. Geological occurrence and accumulation mechanism of natural gas hydrates in the eastern Qiongdongnan Basin of the South China Sea: Insights from site GMGS5-W9-2018. Mar. Geol. 2019, 418, 106042. [Google Scholar] [CrossRef]
- Deng, W.; Kuang, Z.; Liang, J.; Yan, P.; Lu, J.; Meng, M. The seismic and rock-physics evidences of the different migration efficiency between different types of gas chimneys. Deep Sea Res. Part I: Oceanogr. Res. Pap. 2023, 191, 103942. [Google Scholar] [CrossRef]
- Deng, W.; Liang, J.; Zhang, W.; Kuang, Z.; Zhong, T.; He, Y. Typical characteristics of fracture-filling hydrate-charged reservoirs caused by heterogeneous fluid flow in the Qiongdongnan Basin, northern South China Sea. Mar. Pet. Geol. 2021, 124, 104810. [Google Scholar]
- Wei, J.; Liang, J.; Lu, J.; Zhang, W.; He, Y. Characteristics and dynamics of gas hydrate systems in the northwestern South China Sea-results of the fifth gas hydrate drilling expedition. Mar. Pet. Geol. 2019, 110, 287–298. [Google Scholar] [CrossRef]
- Xie, X.; Müller, R.D.; Ren, J.; Jiang, T.; Zhang, C. Stratigraphic architecture and evolution of the continental slope system in offshore Hainan, northern South China Sea. Mar. Geol. 2008, 247, 129–144. [Google Scholar] [CrossRef]
- Meng, M.; Liang, J.; Kuang, Z.; Ren, J.; He, Y.; Deng, W.; Gong, Y. Distribution characteristics of Quaternary channel systems and their controlling factors in the Qiongdongnan basin, South China Sea. Front. Earth Sci. 2022, 10, 902517. [Google Scholar] [CrossRef]
- Winkler, K.W. Contact stiffness in granular and porous meterials: Comparison between theory and experiment. Geophys. Res. Lett. 1983, 10, 1073–1076. [Google Scholar] [CrossRef]
- Walton, K. The effective elastic moduli of a random packing of spheres. J. Mech. Phys. Solids. 1987, 35, 213–226. [Google Scholar] [CrossRef]
- Dai, S.; Santamarina, J.C.; Waite, W.F.; Kneafsey, T.J. Hydrate morphology: Physical properties of sands with patchy hydrate saturation. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- White, J.E.; Martineau-Nicholetis, L.; Monash, C. Measured anisotropy in Pierre shale. Geophys. Prospect. 1983, 31, 709–729. [Google Scholar] [CrossRef]
- Backus, G.E. Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res. 1962, 67, 4427–4440. [Google Scholar] [CrossRef]
- Brown, R.; Korringa, J. On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid. Geophysics 1975, 40, 608–616. [Google Scholar] [CrossRef]
- Lu, S.; McMechan, G.A. Elastic impedance inversion of multichannel seismic data from unconsolidated sediments containing gas hydrate and free gas. Geophysics 2004, 69, 164–179. [Google Scholar] [CrossRef]
- Lu, S.; McMechan, G.A.; Liaw, A. Identification of shallow-water-flow sands by Vp/Vs inversion of conventional 3D seismic data. Geophysics 2005, 70, O29–O37. [Google Scholar] [CrossRef]
- Downton, J.E. Seismic Parameter Estimation from AVO Inversion. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Russell, B.H.; Hedlin, K.; Hilterman, F.J.; Lines, L.R. Fluid-property discrimination with AVO: A Biot-Gassmann perspective. Geophysics 2003, 68, 29–39. [Google Scholar] [CrossRef]
- Russell, B.H.; Gray, D.; Hampson, D.P. Linearized AVO inversion and poroelasticity. Geophysics 2011, 76, C19–C29. [Google Scholar] [CrossRef]
- Wang, B.; Yin, X.; Zhang, F. Lamé parameters inversion based on elastic impedance and its application. Appl. Geophys. 2006, 3, 120–123. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, S. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation. Geophysics 2014, 79, R221–R232. [Google Scholar] [CrossRef]
- Zong, Z.; Yin, X.; Wu, G. Elastic impedance parameterization and inversion with Young’s modulus and Poisson’s ratio. Geophysics 2012, 77, N17–N24. [Google Scholar] [CrossRef]
- Zong, Z.; Yin, X.; Wu, G. Geofluid discrimination incorporating poroelasticity and seismic reflection inversion. Surv. Geophys. 2015, 36, 659–681. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology: Theory and Methods; University Science Books: Herndon, VA, USA, 2002. [Google Scholar]
- Connolly, P. Elastic impedance. Lead. Edge 1999, 18, 438–452. [Google Scholar] [CrossRef]
- Shelander, D.; Dai, J.; Bunge, G.; Singh, S.; Eissa, M.; Fisher, K. Estimating saturation of gas hydrates using conventional 3D seismic data, Gulf of Mexico Joint Industry Project Leg II. Mar. Pet. Geol. 2012, 34, 96–110. [Google Scholar] [CrossRef]

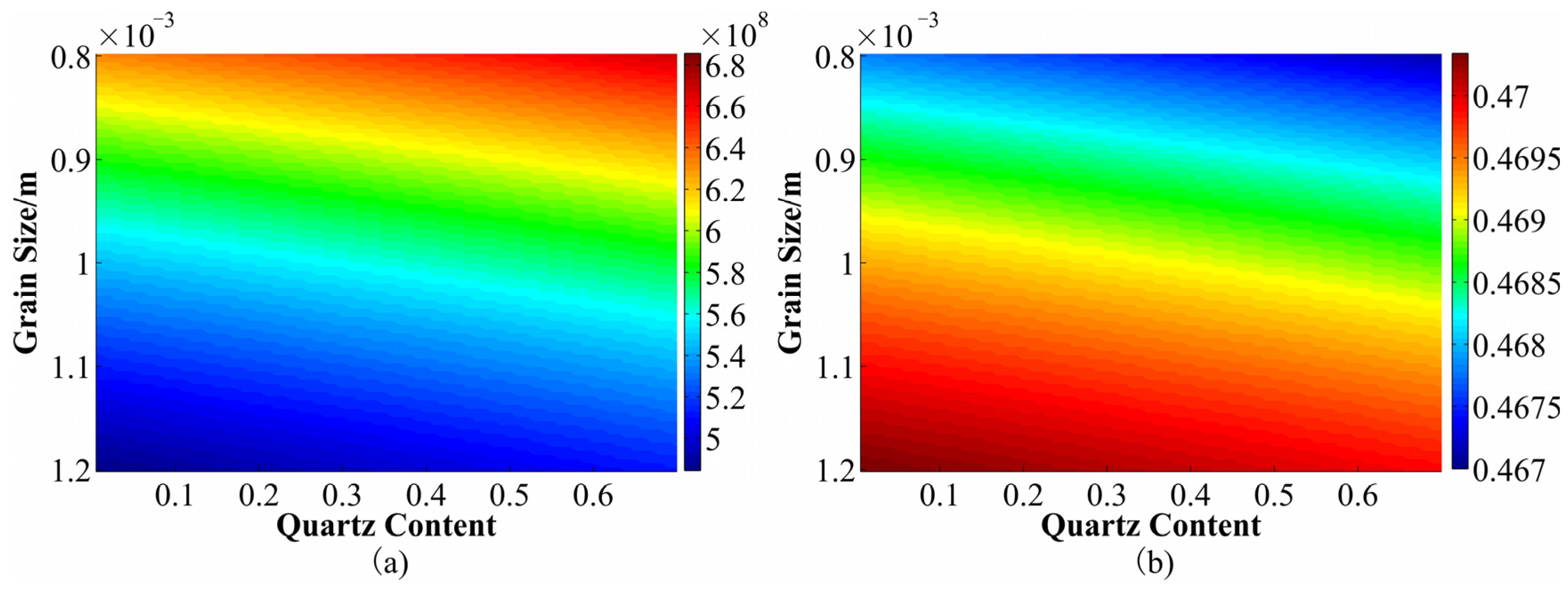
| Mineral Components | Bulk Modulus (Gpa) | Shear Modulus (Gpa) | Density (g/cm3) | |
|---|---|---|---|---|
| matrix | quartz | 36.6 | 45 | 2.65 |
| shale | 20.9 | 6.85 | 2.58 | |
| dolomite | 61.5 | 41.1 | 2.79 | |
| calcite | 76.8 | 32 | 2.71 | |
| fluid | water | 2.55 | - | 1.05 |
| gas | 0.01 | - | 0.1 | |
| hydrate | - | 7.7 | 3.2 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xie, Y.; Wang, T.; Zhou, H.; Zhang, Z.; Li, Y.; Zhang, S.; Deng, W. Seismic Prediction of Shallow Unconsolidated Sand in Deepwater Areas. J. Mar. Sci. Eng. 2025, 13, 1044. https://doi.org/10.3390/jmse13061044
Chen J, Xie Y, Wang T, Zhou H, Zhang Z, Li Y, Zhang S, Deng W. Seismic Prediction of Shallow Unconsolidated Sand in Deepwater Areas. Journal of Marine Science and Engineering. 2025; 13(6):1044. https://doi.org/10.3390/jmse13061044
Chicago/Turabian StyleChen, Jiale, Yingfeng Xie, Tong Wang, Haoyi Zhou, Zhen Zhang, Yonghang Li, Shi Zhang, and Wei Deng. 2025. "Seismic Prediction of Shallow Unconsolidated Sand in Deepwater Areas" Journal of Marine Science and Engineering 13, no. 6: 1044. https://doi.org/10.3390/jmse13061044
APA StyleChen, J., Xie, Y., Wang, T., Zhou, H., Zhang, Z., Li, Y., Zhang, S., & Deng, W. (2025). Seismic Prediction of Shallow Unconsolidated Sand in Deepwater Areas. Journal of Marine Science and Engineering, 13(6), 1044. https://doi.org/10.3390/jmse13061044






