An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels
Abstract
1. Introduction
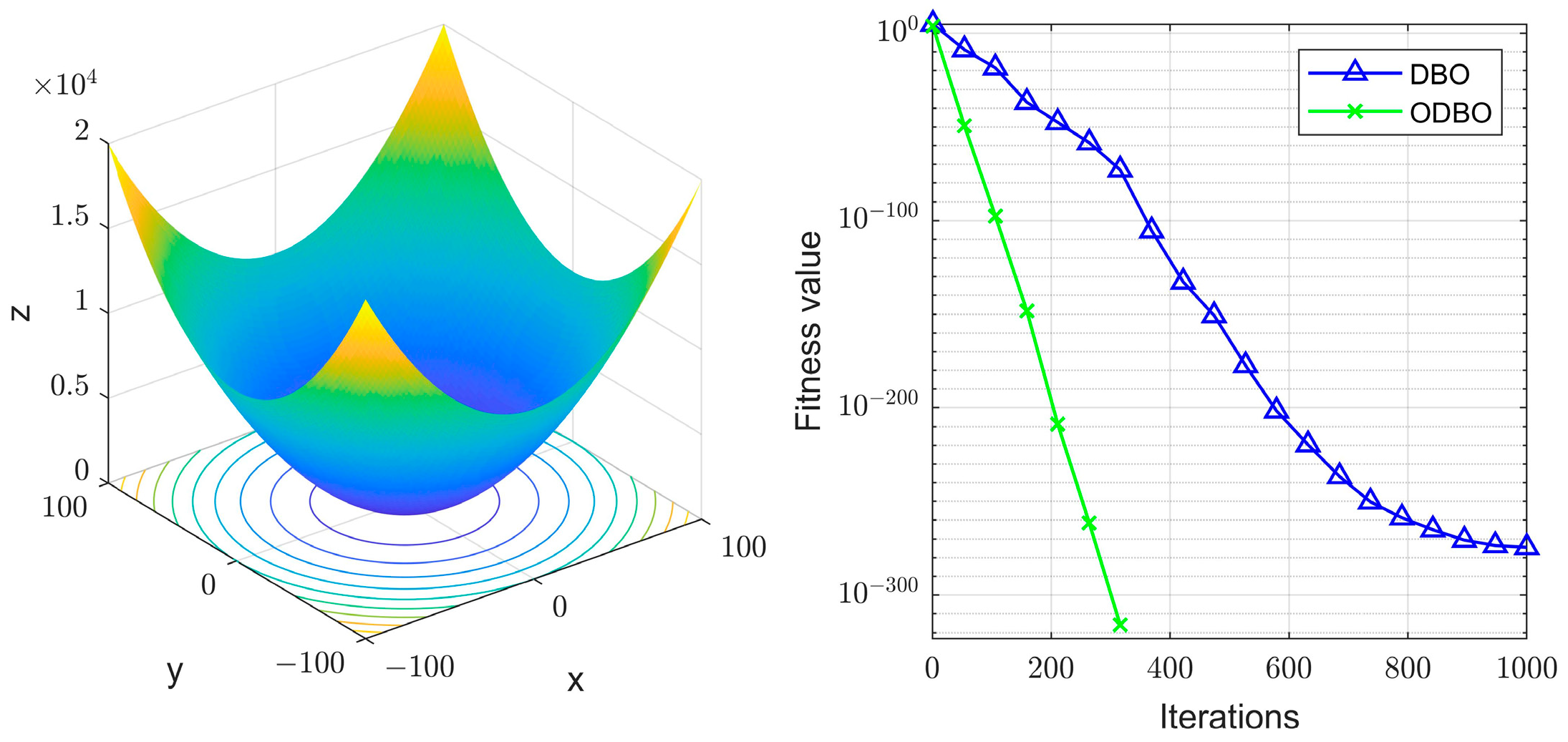
- In the DBO algorithms [34,35,36,37], the rolling behavior relies only on the worst solution, lacks communication with other beetles, and requires more parameters. Luckily, in our proposed HOATDBO algorithm, a global exploration strategy inspired by the OOA is proposed to overcome the aforementioned drawbacks of rolling behavior. Moreover, HOATDBO incorporates adaptive t-distribution perturbations to perturb the foraging behavior of the small dung beetle, thus expanding the selection of the population, enhancing the diversity of the population, and increasing the ability to escape from local optimal solutions. Based on the improvement strategies presented above, our HOATDBO algorithm can enhance global and local exploration capabilities, improve convergence speed, and reduce computational complexity.
- To the best of my knowledge, this is the first time that the DBO algorithm has been applied in the TA of DPS. In contrast to other intelligent algorithms applied to the TA of DPS [38], our proposed HOATDBO algorithm can reduce the error between the commanded and achieved generalized control forces, improve the positioning accuracy, and reduce the energy consumption of DPS, which has great prospects in solving the TA optimization problem of DPS.
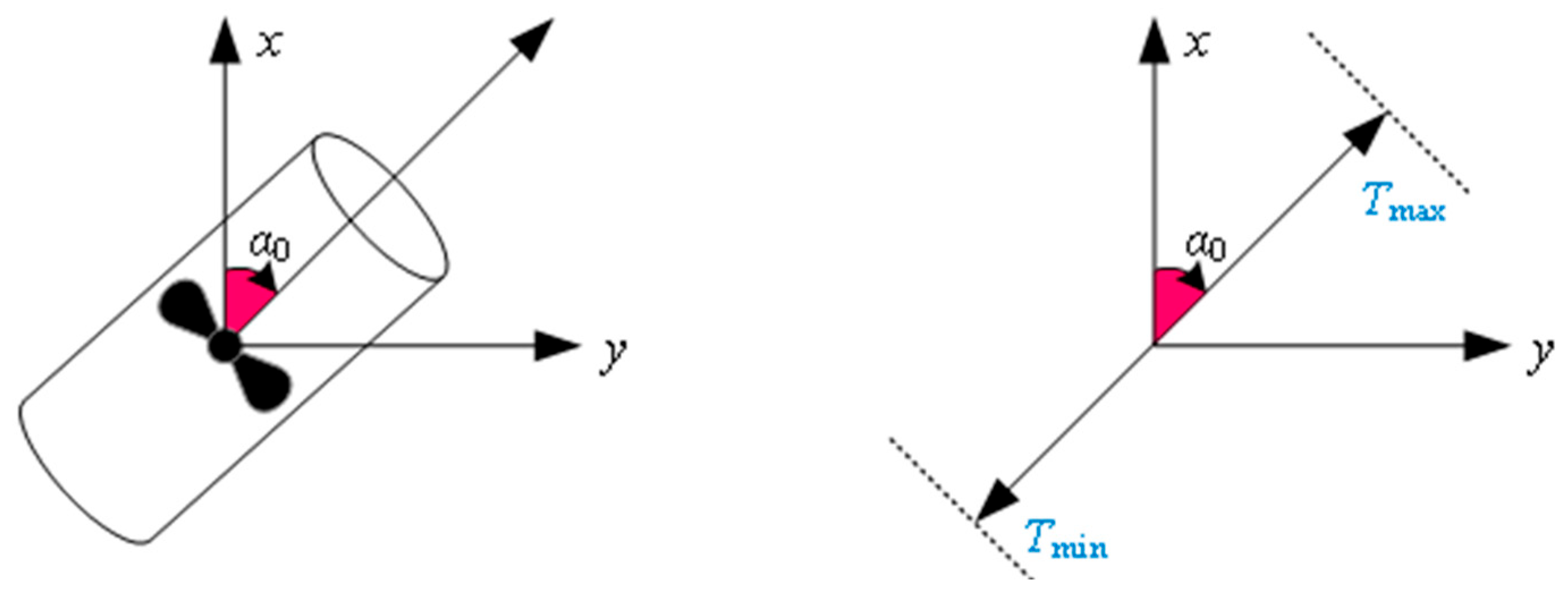
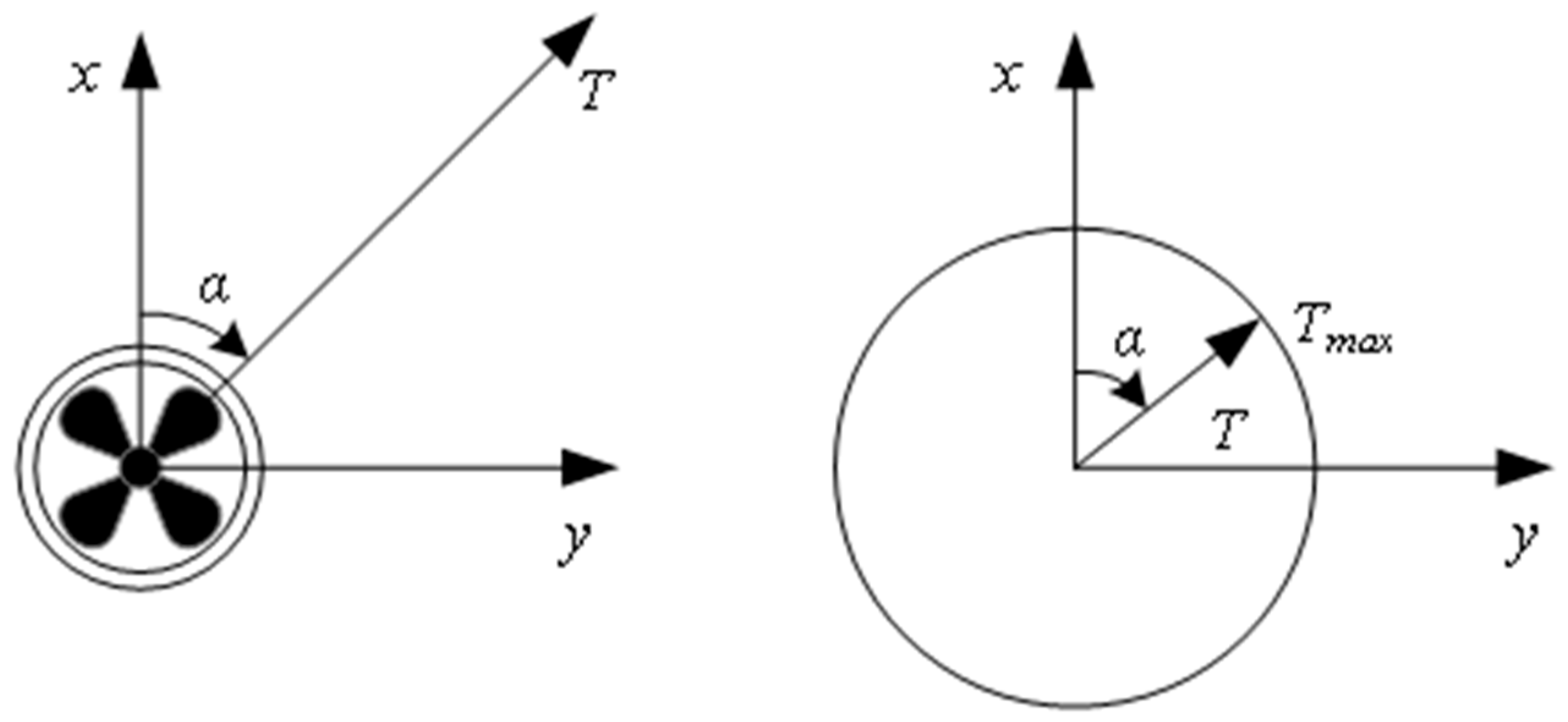
2. Thrust Allocation Model for the DPS of Vessels
2.1. Objective Function of Thrust Allocation Model
2.2. Constraints of Thrust Allocation Model
3. Thrust Allocation Based on the HOATDBO Algorithm
3.1. Proposed HOATDBO
- (1)
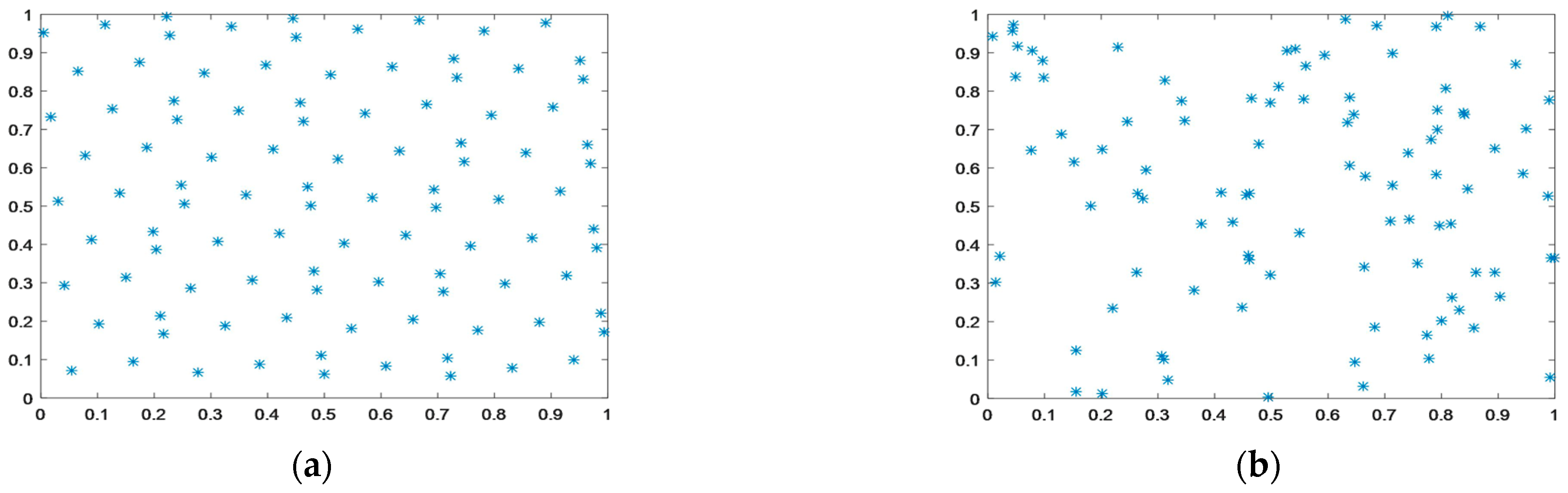
- In the original DBO algorithm, random population initialization is used to initialize the population, which inevitably brings uncertainty. Therefore, the GPSPI is introduced to eliminate the uncertainty caused by random population initialization. The GPSPI method is a uniformly distributed and effective technique for selecting points. By utilizing the uniformity of the GPSPI, the population diversity can be improved. At present, the GPSPI has been applied to many intelligent algorithms. The results of two population initialization methods are given as follows:
- (2)
- According to Ref. [32], dung beetles only depend on the worst position on a global scale and cannot interact with others in DBO. Therefore, this paper uses the global exploration strategy in the OOA to replace the strategy on position updates for rolling dung beetles. The global exploration strategy imitates the behavior of Osprey, which randomly searches for the position of a fish and attacks it. By simulating the motion of Osprey towards the fish, the formula for updating the position of Osprey can be derived as follows:
- (3)
- The t-distribution variation perturbation is employed to disrupt the foraging behavior of the small dung beetle. The method of position update is designed as follows:
| Algorithm 1: The pseudocode of the HOATDBO algorithm |
| Input and . 1 Initializing the Population with the GP-S . 2 while do 3 for do 4 if then 5 6 if then 7 Select and update the position of the global dung beetle 8 else 9 Update the position of global dung beetle 10 end if 11 end if 12 if then 13 Update the position of the brood ball 14 end if 15 if then 16 Update the position of the small dung beetle 17 end if 18 if then 19 Update the position of the thief 20 end if 21 Disturb the position of the thief 22 if the new position of the thief is superior to the previous one then 23 Update it; 24 end if 25 end for 26 if the new position is superior to the previous one then 27 Update it; 28 end if 29 ; 30 end while 31 return and the fitness value |
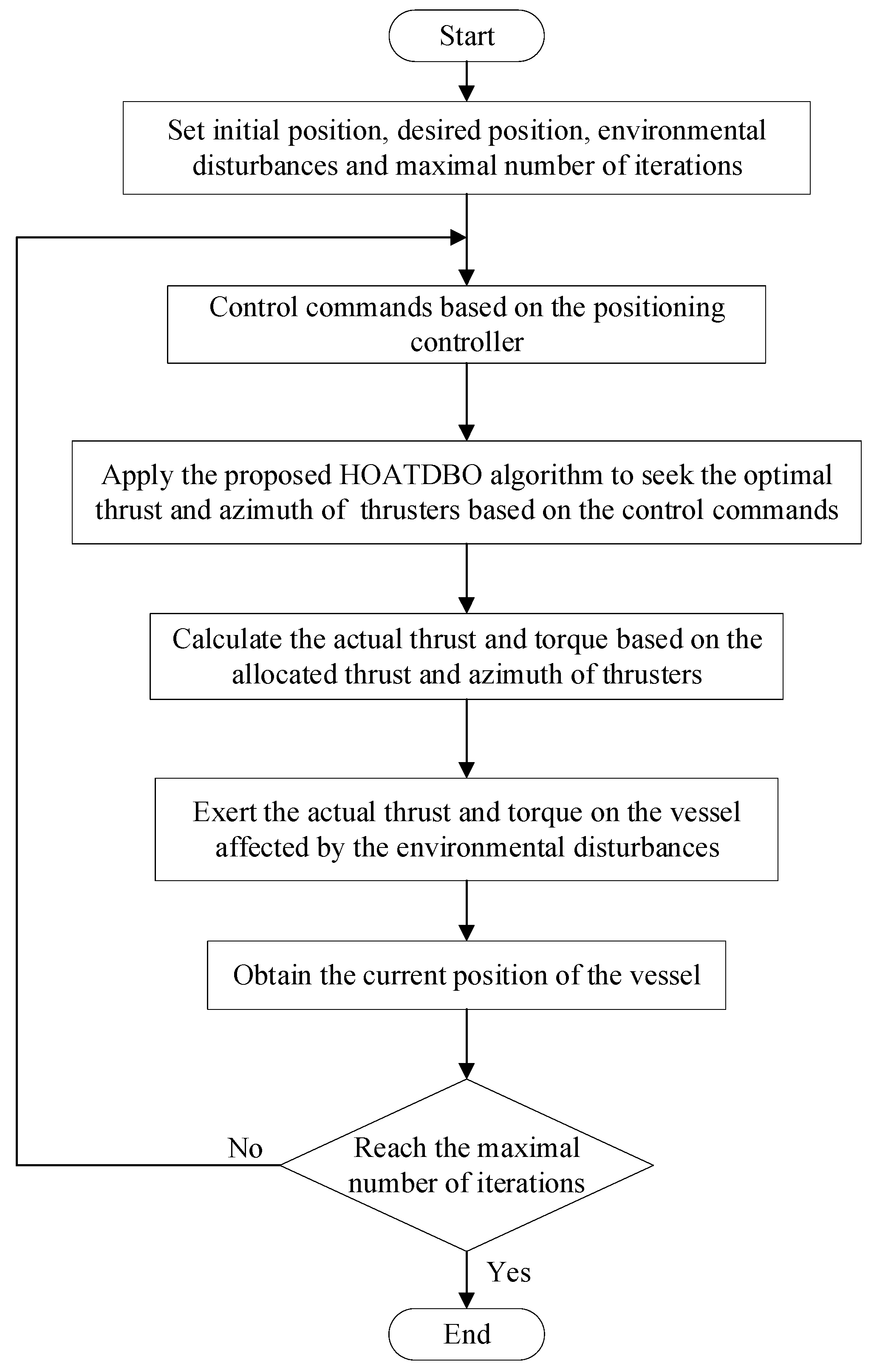
3.2. HOATDBO-Based Thrust Allocation
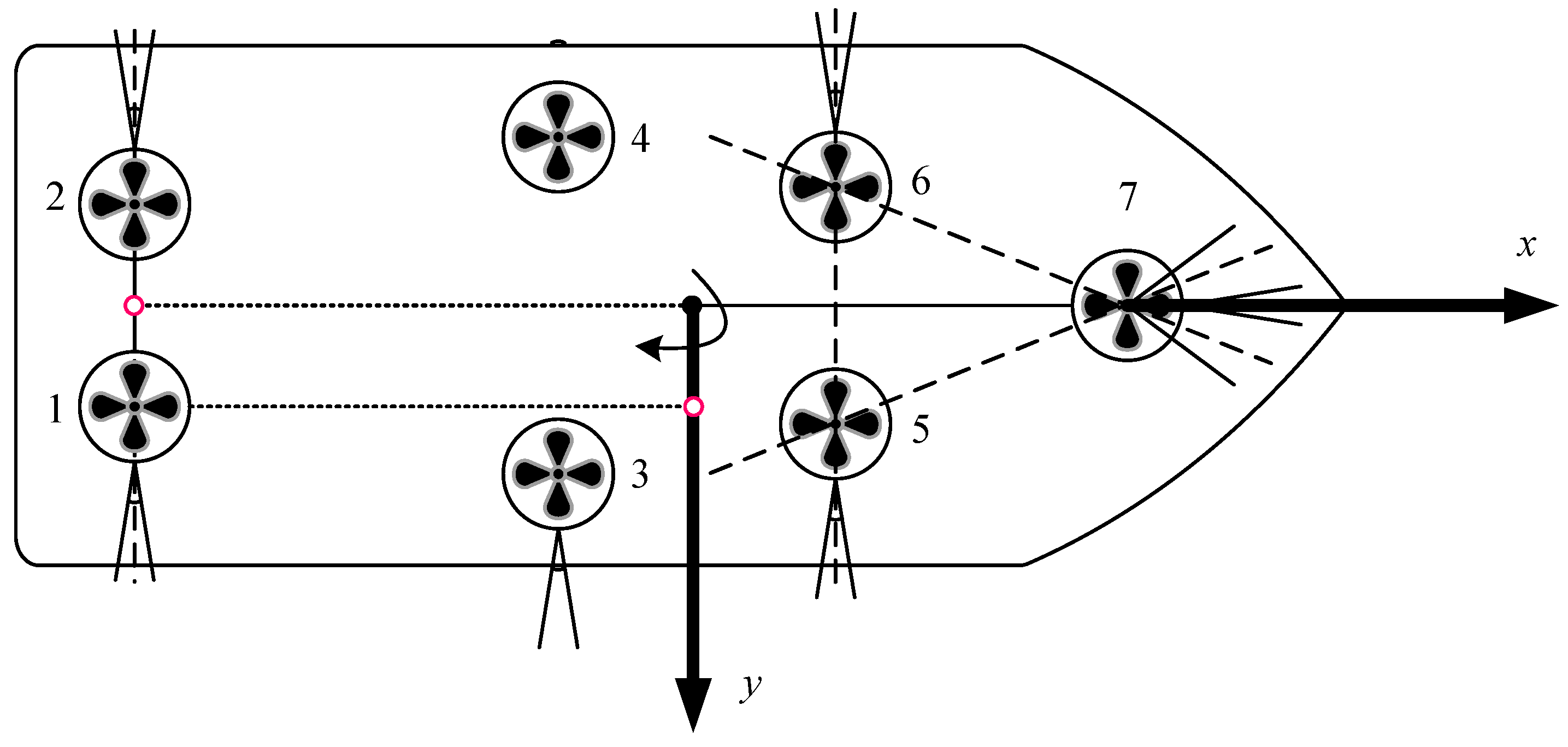
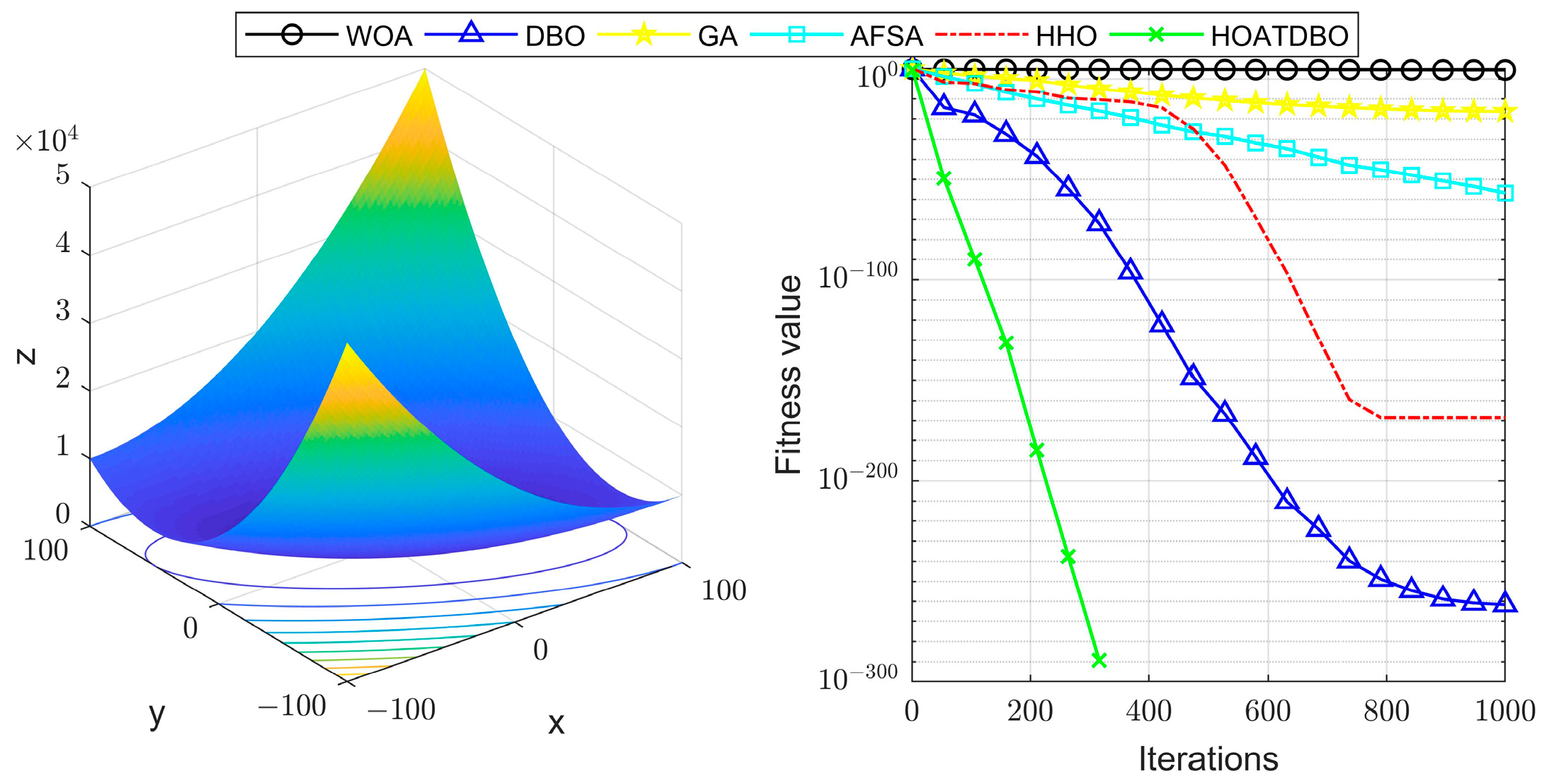
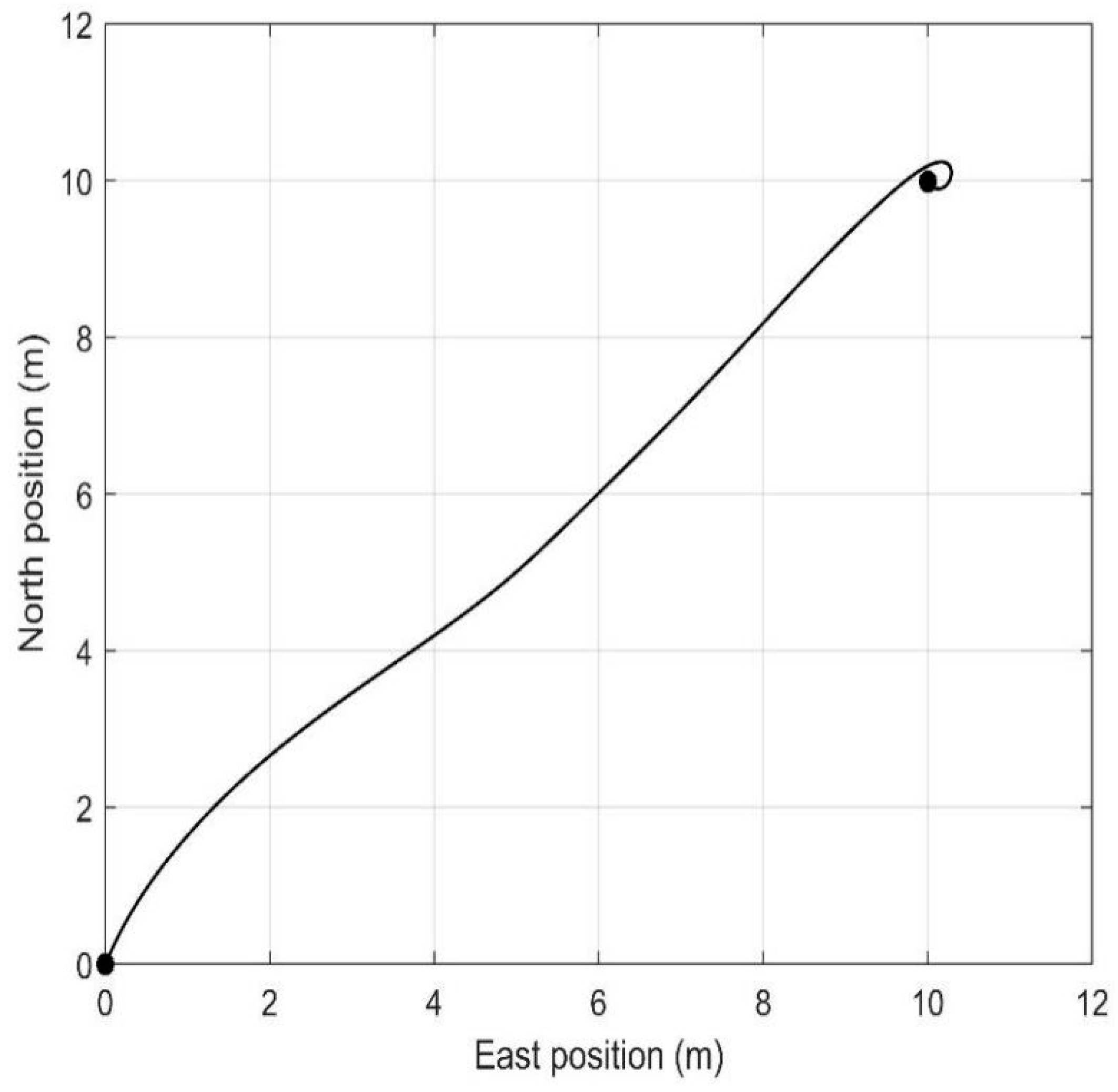
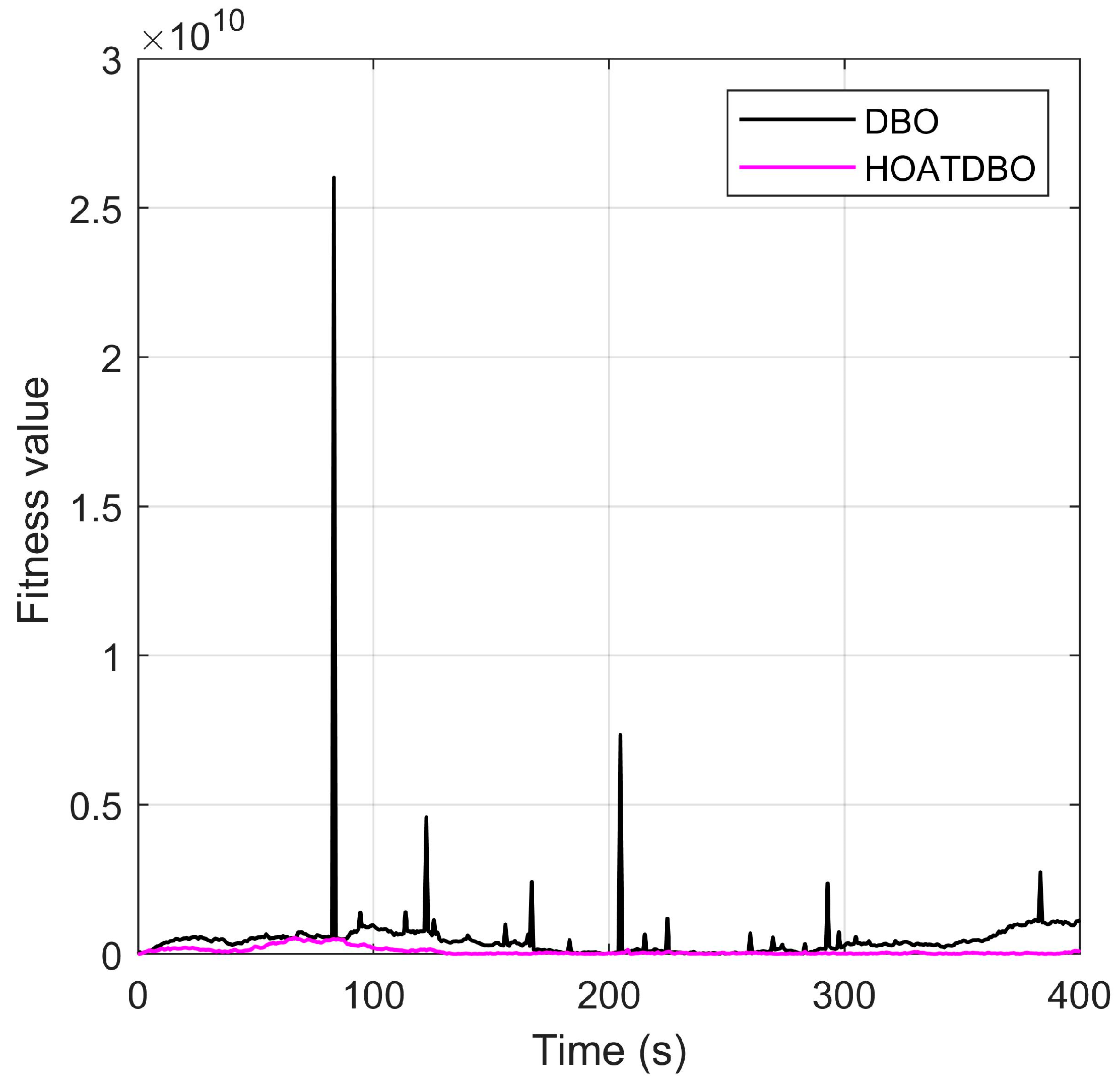
4. Simulation Results and Comparative Analysis
5. Conclusions
6. Limitations and Future Work
- (1)
- The thrust allocation model established in this paper takes into account the impact of power changes on vessel dynamic positioning but does not consider solutions for different loads and circuit breaker on–off situations, which also affects the accuracy and stability of dynamic positioning. Therefore, further research in this area should be conducted.
- (2)
- The effectiveness of our proposed HOATDBO-based thrust allocation method was validated through simulations. Nevertheless, this paper does not consider the influence of sensor noise and actuator faults, which are unavoidable in the practical dynamic positioning system of vessels. Therefore, future research should also focus on the field of nonlinear filtering and fault-tolerant control.
- (3)
- For further implementation in real dynamic positioning systems, real-time performance should also be given special attention. Hence, we will explore swarm intelligence optimization algorithms with lower computational complexity to meet the real-time requirement of the dynamic positioning system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johansen, T.A.; Bø, T.I.; Mathiesen, E.; Veksler, A.; Sørensen, A.J. Dynamic positioning system as dynamic energy storage on diesel-electric ships. IEEE Trans. Power Syst. 2014, 29, 3086–3091. [Google Scholar] [CrossRef]
- Torben, T.R.; Teel, A.R.; Kjerstad, I.K.; Wittemann, E.H.T.; Skjetne, R. A resetting observer for linear time-varying systems with application to dynamic positioning of marine surface vessels. IEEE Trans. Control Syst. Technol. 2024, 32, 1048–1056. [Google Scholar] [CrossRef]
- Du, J.; Hu, X.; Liu, H.; Chen, C.L.P. Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2775–2786. [Google Scholar] [CrossRef] [PubMed]
- Veksler, A.; Johansen, T.A.; Skjetne, R.; Mathiesen, E. Thrust allocation with dynamic power consumption modulation for diesel-electric ships. IEEE Trans. Control Syst. Technol. 2016, 24, 578–593. [Google Scholar] [CrossRef]
- Skjong, S.; Pedersen, E. Nonangular MPC-based thrust allocation algorithm for marine vessels study of optimal thruster commands. IEEE Trans. Transp. Electrif. 2017, 3, 792–807. [Google Scholar] [CrossRef]
- Ye, B.; Xiong, J.; Wang, Q.; Luo, Y. Design and implementation of pseudo-inverse thrust allocation algorithm for ship dynamic positioning. IEEE Access 2020, 8, 16830–16837. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Coraddu, A.; Oneto, L.; Anguita, D. Optimizing fuel consumption in thrust allocation for marine dynamic positioning systems. IEEE Trans. Autom. Sci. Eng. 2022, 19, 122–142. [Google Scholar] [CrossRef]
- Taborda, P.; Matias, H.; Silvestre, D.; Loureno, P. Convex MPC and thrust allocation with deadband for spacecraft rendezvous. IEEE Control Syst. Lett. 2024, 8, 1132–1137. [Google Scholar] [CrossRef]
- Willis, J.B.; Beard, R.W. Pitch and thrust allocation for full-flight-regime control of winged eVTOL UAVs. IEEE Control Syst. Lett. 2022, 6, 1058–1063. [Google Scholar] [CrossRef]
- Ruth, E.; Smogeli, Y.N.; Perez, T.; Sorensen, A.J. Antispin thrust allocation for marine vessels. IEEE Trans. Control Syst. Technol. 2009, 17, 1257–1269. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, X.; Wei, N.; Liu, Z.; Liu, C.; Wang, F. A thrust allocation method for DP vessels equipped with rudders. Ocean Eng. 2023, 285, 115342. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2022, 79, 7305–7336. [Google Scholar] [CrossRef]
- Lang, X.; Ruiter, A. Distributed optimal control allocation for 6-dof spacecraft with redundant thrusters. Aerosp. Sci. Technol. 2021, 118, 106971. [Google Scholar] [CrossRef]
- Arditti, F.; Souza, F.L.; Martins, T.C.G.; Tannuri, E.A. Thrust allocation algorithm with efficiency function dependent on the azimuth angle of the actuators. Ocean Eng. 2015, 105, 206–216. [Google Scholar] [CrossRef]
- Li, X. Dynamic multiobjective optimization for thrust allocation in ship application. Ocean Eng. 2020, 218, 108187. [Google Scholar]
- Chieu, N.H.; Jeyakumar, V.; Li, G. Convexifiability of continuous and discrete nonnegative quadratic programs for gap-free duality. Eur. J. Oper. Res. 2017, 280, 441–452. [Google Scholar] [CrossRef]
- Shi, D.; Yin, J.; Bai, C. An effective global optimization algorithm for quadratic programs with quadratic constraints. Symmetry 2019, 11, 424. [Google Scholar] [CrossRef]
- Anitescu, M. A superlinearly convergent sequential quadratically constrained quadratic programming algorithm for degenerate nonlinear programming. SIAM J. Control Optim. 2002, 12, 949–978. [Google Scholar] [CrossRef]
- Ammar, E. On fuzzy random multiobjective quadratic programming. Eur. J. Oper. Res. 2009, 193, 329–341. [Google Scholar] [CrossRef]
- Li, H.; Zhang, K. A decomposition algorithm for solving large-scale quadratic programming problems. Appl. Math. Comput. 2006, 173, 394–403. [Google Scholar] [CrossRef]
- PiekAo, A.; Witkowska, A.; Zubowicz, T. Dynamic positioning capability assessment based on optimal thrust allocation. Pol. Marit. Res. 2023, 30, 28–38. [Google Scholar] [CrossRef]
- Sun, G.; Xie, J.; Qu, J. Multistep thrust allocation method based on priority idea for remotely operated underwater vehicle with horizontal thrusters configured as X shape. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221090077. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, J.M.H.; Choi, J.W.; You, Y.J. Fuel optimized thrust allocation algorithm development using penalty-method for the dynamic positioning FPSO. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Republic of Korea, 19–24 June 2016; pp. 1–6. [Google Scholar]
- Peng, Z.; Liu, E.; Pan, C. Model-based deep reinforcement learning for data-driven motion control of an under-actuated unmanned surface vehicle: Path following and trajectory tracking. J. Frankl. Inst. 2023, 360, 4399–4426. [Google Scholar] [CrossRef]
- Ji, X.; Sun, G.; Er, J. Adaptive correction of landmark for visual homing in mobile vehicles. IEEE Trans. Intell. Veh. 2022, 8, 3418–3430. [Google Scholar] [CrossRef]
- Ji, X.; Tang, L.; Lu, T. Dbenet: Dual-branch ensemble network for sea–land segmentation of remote-sensing images. IEEE Trans. Instrum. Meas. 2023, 72, 5503611. [Google Scholar] [CrossRef]
- Zhao, D.; Ding, F.; Feng, T.; Liu, Y.; Bian, X. Optimal thrust allocation based GA for dynamic positioning ship. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 1254–1258. [Google Scholar]
- Ji, M.; Yi, B. The optimal thrust allocation based on QPSO algorithm for dynamic positioning vessels. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1365–1370. [Google Scholar]
- Guang, C.; Da, W.; Kai, W.; Jing, H. Multi-agent chaos particle swarm optimization algorithm of thrust allocation for dynamic positioning vessels. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 2389–2396. [Google Scholar]
- Leng, P.; Xiang, L.; Lin, Y.; Xiao, W.; Yang, Z.; Li, D.; Nai, W. Logistic regression based on artificial fish swarm algorithm with t-distribution parameters. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 11–13 December 2020; Volume 9, pp. 1912–1915. [Google Scholar]
- Yuan, M.; Kan, X.; Chi, C. An adaptive simulated annealing and artificial fish swarm algorithm for the optimization of multi-depot express delivery vehicle routing. Intell. Data Anal. 2022, 26, 239–256. [Google Scholar] [CrossRef]
- Xue, B.; Lu, C. Nonlinear fault-accommodation thrust allocation for overactivated vessels using artificial neural network and multivariate analysis. Ocean Eng. 2022, 266, 112936. [Google Scholar]
- Zhang, Y.; Liu, P. Research on reactive power optimization based on hybrid osprey optimization algorithm. Energies 2023, 16, 7101. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2023, 236, 121219. [Google Scholar] [CrossRef]
- Wang, X.; Wei, Y.; Guo, Z.; Wang, J.; Yu, H.; Hu, B. A sinh-cosh-enhanced DBO algorithm applied to global optimization problems. Biomimetics 2024, 9, 271. [Google Scholar] [CrossRef]
- Jin, H.; Ji, H.; Yan, F. An effective obstacle avoidance and motion planning design for underwater telescopic arm robots based on a tent chaotic dung beetle algorithm. Electronics 2023, 12, 4128. [Google Scholar] [CrossRef]
- Lyu, L.; Jiang, H.; Yang, F. Improved dung beetle optimizer algorithm with multi-strategy for global optimization and UAV 3D path planning. IEEE Access 2024, 12, 69240–69257. [Google Scholar] [CrossRef]
- Deng, F.; Zhang, H.; Ding, Q.; Zhang, S.; Du, Z.; Yang, H. PSO and NNPC-base integrative control allocation for dynamic positioning ships with thruster constraints. Ocean Eng. 2024, 292, 116553. [Google Scholar] [CrossRef]
- Ou, Y.; Yin, P.; Mo, L. An improved grey wolf optimizer and its application in robot path planning. Biomimetics 2023, 8, 84. [Google Scholar] [CrossRef]
- Qu, C.; He, W.; Peng, X. Harris hawks optimization with information exchange. Appl. Math. Model. 2020, 84, 52–75. [Google Scholar] [CrossRef]





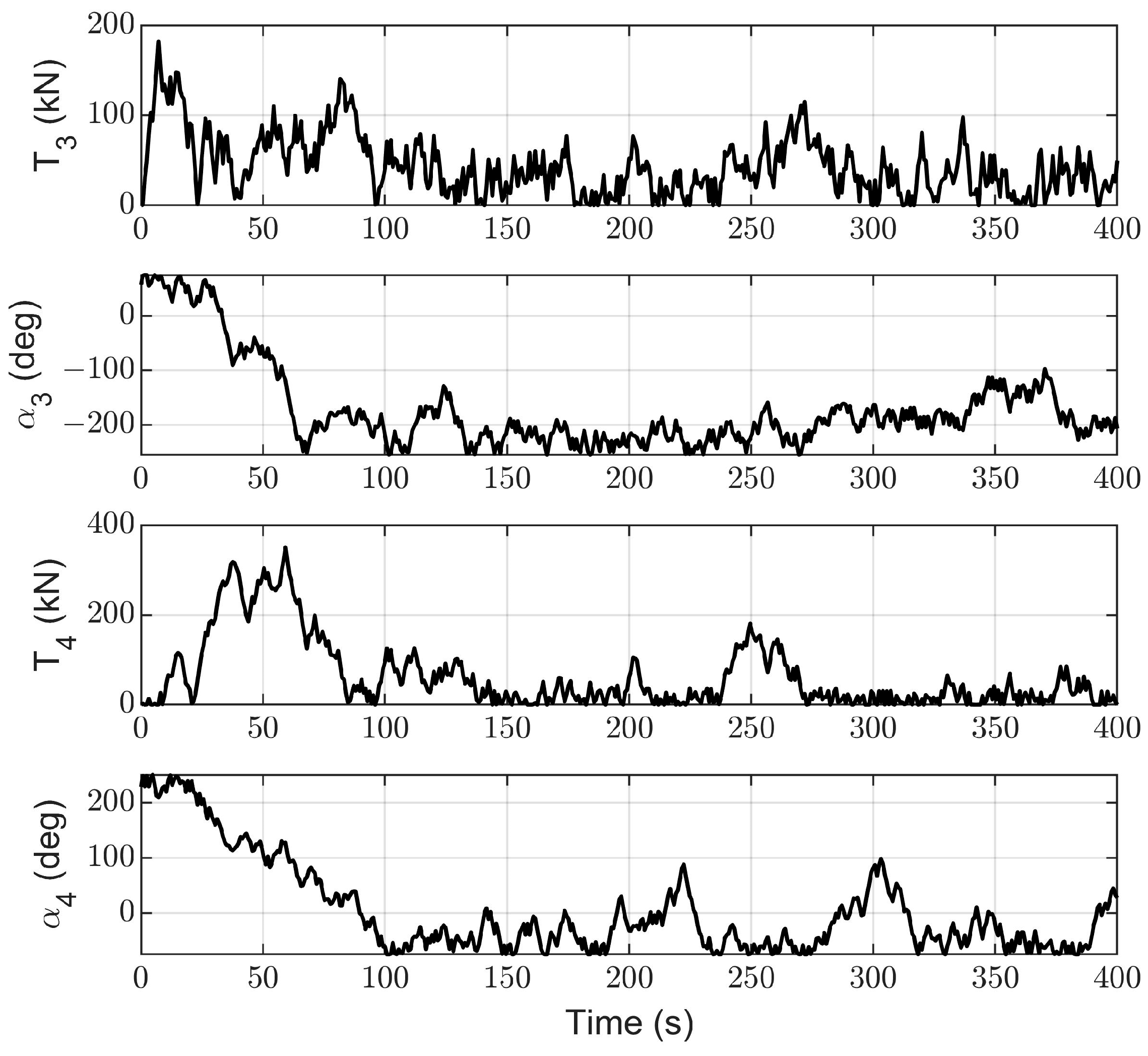
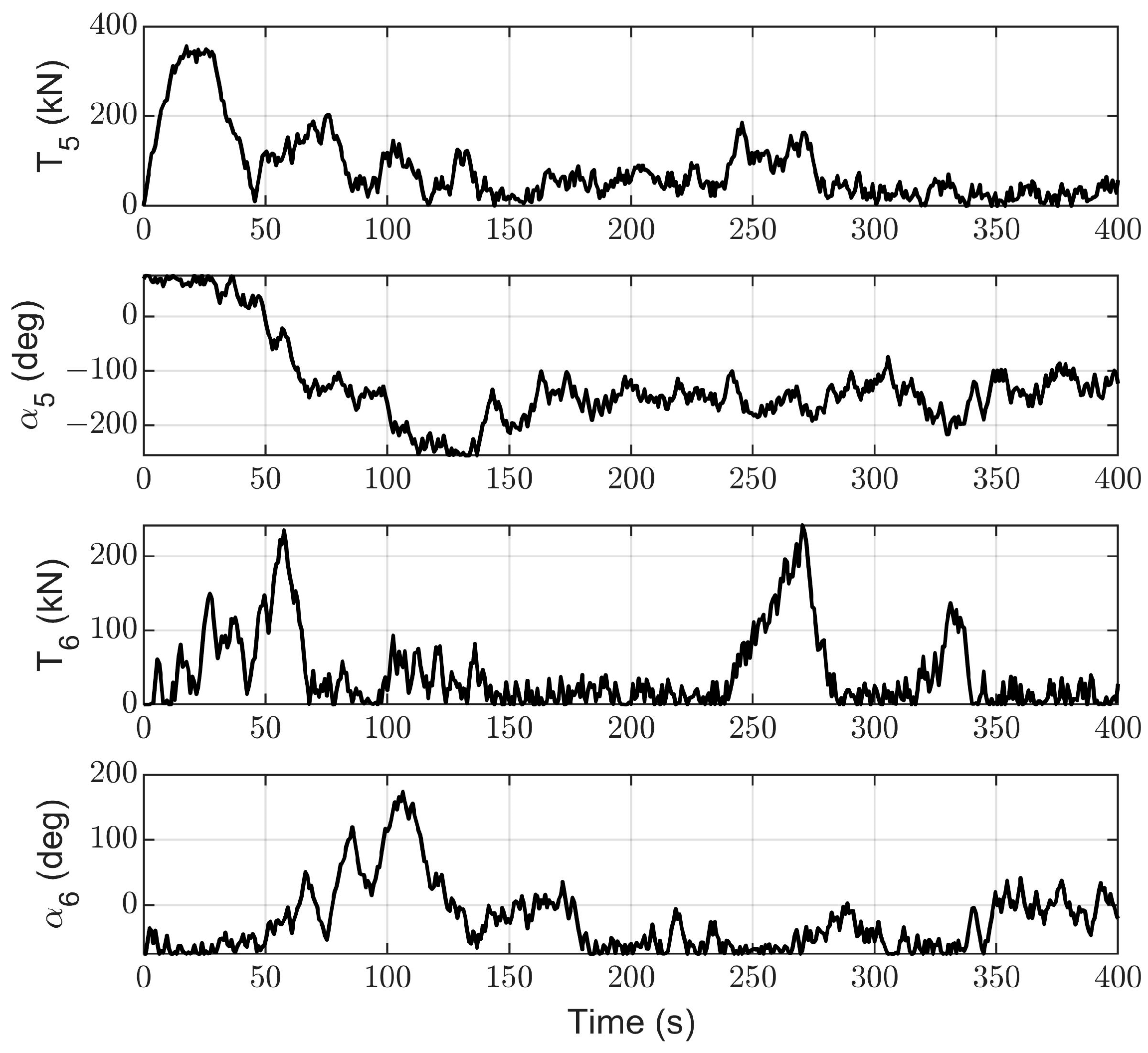
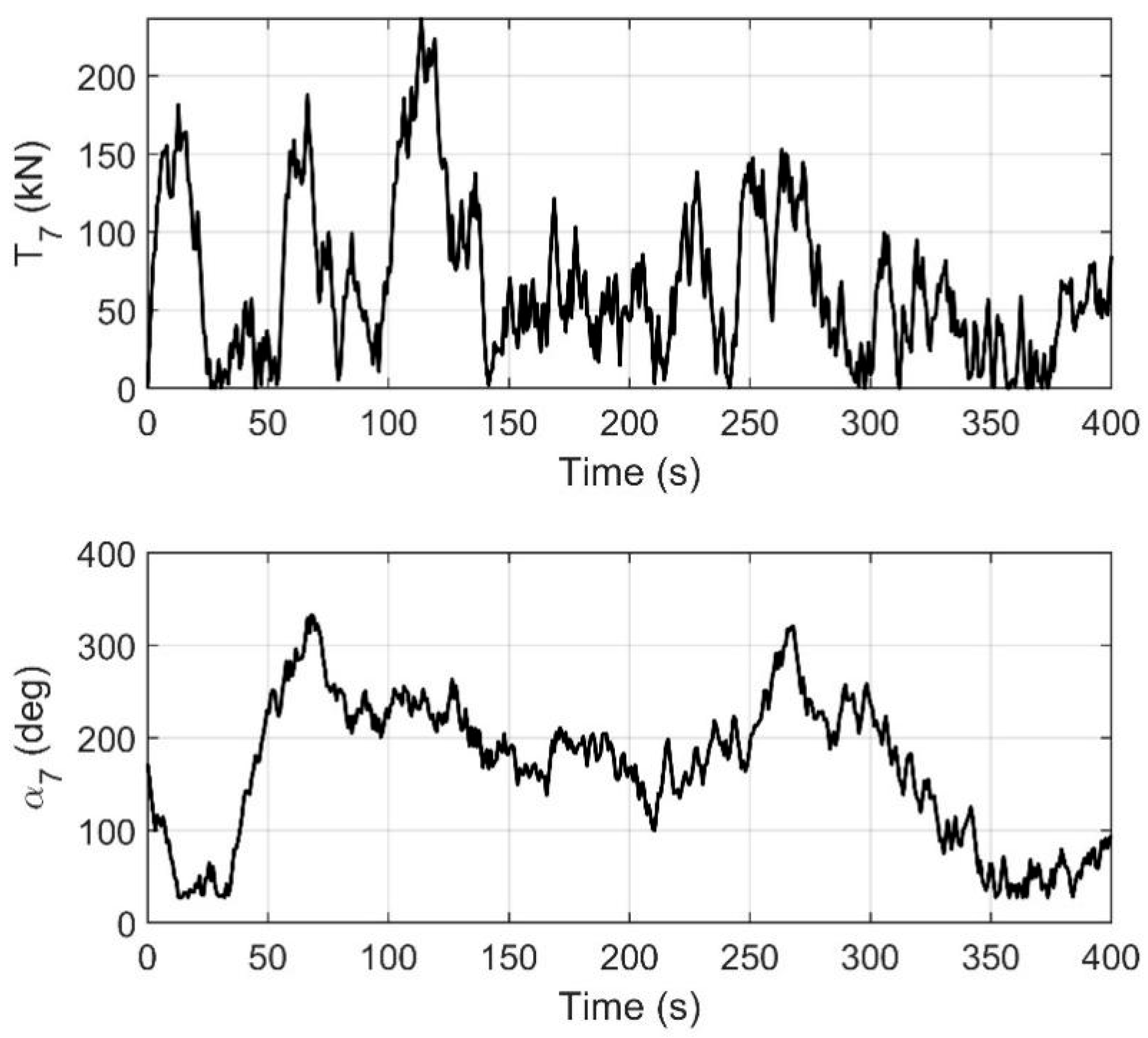
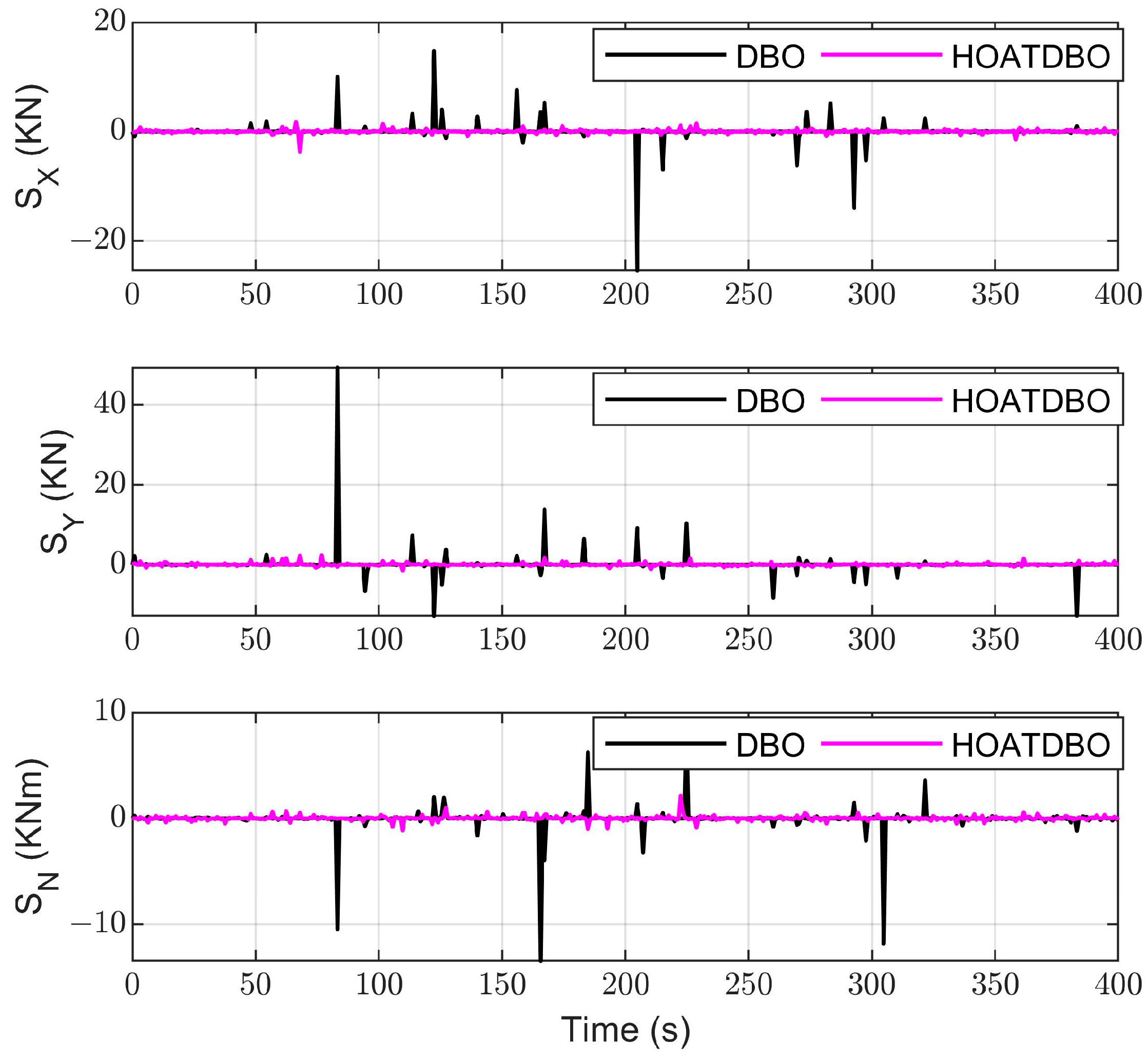

| Sea Condition | Value |
|---|---|
| Wind velocity | |
| Wind direction | |
| Current direction | |
| Wave direction | |
| Current velocity |
| Algorithm | ||||
|---|---|---|---|---|
| DBO | ||||
| HOATDBO | ||||
| Algorithm | Energy Consumption (kW) |
|---|---|
| GA | |
| AFSA | |
| DBO | |
| HOATDBO |
| Algorithm | Average Time of 30 Simulations (s) |
|---|---|
| DBO | |
| HOATDBO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuo, Y.; Lin, J.; Peng, Z.; Wang, Y.; Wang, S. An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels. J. Mar. Sci. Eng. 2025, 13, 1041. https://doi.org/10.3390/jmse13061041
Tuo Y, Lin J, Peng Z, Wang Y, Wang S. An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels. Journal of Marine Science and Engineering. 2025; 13(6):1041. https://doi.org/10.3390/jmse13061041
Chicago/Turabian StyleTuo, Yulong, Jianlong Lin, Zhouhua Peng, Yuanhui Wang, and Shasha Wang. 2025. "An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels" Journal of Marine Science and Engineering 13, no. 6: 1041. https://doi.org/10.3390/jmse13061041
APA StyleTuo, Y., Lin, J., Peng, Z., Wang, Y., & Wang, S. (2025). An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels. Journal of Marine Science and Engineering, 13(6), 1041. https://doi.org/10.3390/jmse13061041







