An Energy-Efficient Thrust Allocation Based on the Improved Dung Beetle Optimizer for the Dynamic Positioning System of Vessels

Abstract

This paper investigates the constrained nonlinear thrust allocation problem for the dynamic positioning system of vessels. Considering the wear, energy consumption, and allocation error of thrusters, a constrained nonlinear mathematical optimization model of thrust allocation is established based on the “Hai Yang Shi You 201”. Based on the dung beetle optimizer (DBO) algorithm, a hybrid Osprey adaptive t-distribution DBO (HOATDBO) algorithm is presented to achieve the thrust allocation. The HOATDBO algorithm introduces the global exploration strategy of the Osprey algorithm, with the addition of the initialization of the good point set and adaptive t-distribution perturbations. The proposed HOATDBO algorithm has perfect global and local optimization capabilities, which can quickly and reliably obtain the optimal thrust solution, improve the thrust allocation accuracy of vessels, and reduce energy consumption. Finally, the simulation and comparison results are presented to verify the superiority of the proposed HOATDBO algorithm.

1. Introduction

With the development of ocean engineering, the positioning system has become a key support system for the offshore operation of vessels. Due to the increasing depth of water in the operation environment, the mooring positioning system finds it hard to meet the positioning requirement. Compared with the mooring positioning system, the dynamic positioning system (DPS) can achieve high-precision positioning in different water depths, thus becoming a hot research topic [1,2,3]. The DPS consists of a thrust allocation (TA) system, a control system, a position measurement system, and a propulsion system. TA is a bridge connecting the control system and propulsion system in DPS, which allocates the angle and force commands to the thrusters to achieve the desired moment and forces from the control system [4,5,6,7,8]. Since the TA affects the accuracy of the DPS and energy consumption of thrusters, it is significant to conduct relevant research on improving the performance of TA [9,10].

Nowadays, numerous methods have been put forward to handle the TA optimization problems [11,12,13,14,15]. In general, the aforementioned optimization algorithms can be categorized as quadratic programming (QP) methods and swarm intelligent optimization algorithms. The QP algorithm is a special type of nonlinear programming method, which is good at solving investment portfolio problems and constrained least squares problems [16,17,18,19,20]. In recent years, the QP algorithm has been widely utilized for solving TA problems owing to the advantages of its instant application and optimization capability [21,22,23]. Nevertheless, the global optimization capability of QP is relatively weak. With the development of computer technology, machine learning algorithms have been applied in various fields [24,25,26] due to their good global optimization capability. The machine learning algorithm can handle a large amount of experimental data, but it requires powerful computing equipment with sufficient computing time. On the contrary, the swarm intelligent optimization algorithms use multiple individuals to search for the solution space in parallel, which is equivalent to comprehensively searching the solution space from multiple starting points at the same time, greatly increasing the scope and efficiency of the search. Compared to the aforementioned algorithms [16,17,18,19,20,21,22,23,24,25,26], swarm intelligent optimization algorithms have faster computing speed and better global optimization capabilities. Thus, many swarm intelligent optimization algorithms have been presented to compensate for the aforesaid deficiency [27,28,29,30,31]. Ref. [27] presents a TA solution, which is inspired by the genetic algorithm (GA). Refs. [28,29] solved the TA problem by proposing a particle swarm optimization (PSO) with simple parameters. But the PSO may fall into the local optimal solution and have poor local search ability. Luckily, the artificial fish swarm algorithm (AFSA) [30,31] can solve the issues above to a certain extent. However, the AFSA still has a deficiency in global searching ability. In addition, these swarm intelligent optimization algorithms still have room for improvement in terms of computational complexity and randomness, which restricts their application in the TA of dynamic positioning vessels.

To overcome these limitations in existing optimization algorithms [27,28,29,30,31], an advanced population-based dung beetle optimizer (DBO) algorithm has been presented by [32], which draws its design principles from the behaviors of the dung beetle in stealing, reproduction, dancing, foraging, and ball-rolling. The proposed DBO has the characteristics of satisfactory solution accuracy and fast convergence speed. Nevertheless, there also exists an imbalance between local and global exploitation capabilities, which may easily lead to local optimal solutions and a weak global exploration ability. Inspired by the Osprey Optimization Algorithm (OOA) [33], this study designed a hybrid Osprey adaptive t-distribution dung beetle optimizer algorithm (HOATDBO). The HOATDBO is described as follows: (1) the rolling ball behavior of the original DBO is replaced by the global exploration strategy of the OOA; (2) the random population initialization is replaced by the good point set population initialization (GPSPI); and (3) the t-distribution perturbation is introduced to solve the local optimal solutions. Based on the improvements above, the HOATDBO is presented to enhance the performance of TA in DP vessels. The main contributions are characterized below:

• Compared with the random population initialization methods [30,31], the proposed GPSPI can avoid the uncertain and uneven population spatial distribution caused by random initialization, thus improving the solution quality of our proposed HOATDBO algorithm.
• In the DBO algorithms [34,35,36,37], the rolling behavior relies only on the worst solution, lacks communication with other beetles, and requires more parameters. Luckily, in our proposed HOATDBO algorithm, a global exploration strategy inspired by the OOA is proposed to overcome the aforementioned drawbacks of rolling behavior. Moreover, HOATDBO incorporates adaptive t-distribution perturbations to perturb the foraging behavior of the small dung beetle, thus expanding the selection of the population, enhancing the diversity of the population, and increasing the ability to escape from local optimal solutions. Based on the improvement strategies presented above, our HOATDBO algorithm can enhance global and local exploration capabilities, improve convergence speed, and reduce computational complexity.
• To the best of my knowledge, this is the first time that the DBO algorithm has been applied in the TA of DPS. In contrast to other intelligent algorithms applied to the TA of DPS [38], our proposed HOATDBO algorithm can reduce the error between the commanded and achieved generalized control forces, improve the positioning accuracy, and reduce the energy consumption of DPS, which has great prospects in solving the TA optimization problem of DPS.

The other parts of this paper consist of the following sections. Section 2 presents the mathematical model of TA. The research on the HOATDBO algorithm is shown in Section 3. The performance of the HOATDBO algorithm is verified by simulations and comparisons in Section 4. Finally, the conclusions are shown in Section 5.

2. Thrust Allocation Model for the DPS of Vessels

First, we established the objective function of the TA model by considering the energy consumption, allocation error, thruster azimuth changes amplitude, and energy variation constraint in Section 2.1. Then, we gave the constraints of the TA model based on physical constraints and the forbidden area of thrusters in Section 2.2.

2.1. Objective Function of Thrust Allocation Model

The commanded control force $\tau$ was computed by the dynamic positioning controller using the error between the desired and current positions of the vessels. Then, $\tau$ needed to be allocated as the thrust and azimuth of thrusters before being sent to the propulsion system. The expression for this is shown below:

$$\tau =B(\alpha )T$$

(1)

where $T={\left[T_1{T}_2\dots T_n\right]}^T\in {ℝ}^n$ and $\alpha ={\left[{\alpha }_1{\alpha }_2\dots {\alpha }_n\right]}^T\in {ℝ}^n$ are the force and azimuth of thrusters, and $B(\alpha )\in {ℝ}^{3\times n}$ is the matrix of thruster configuration. The expression of $B(\alpha )\in {ℝ}^{3\times n}$ is shown below:

$$B(\alpha )=\left[b_1{b}_2\dots b_n\right]$$

(2)

Each thruster corresponds to a column vector of $B(\alpha )$ with the following form:

$$b_i=\left[\begin{array}{c}\cos ({\alpha }_i)\\ \sin ({\alpha }_i)\\ l_{xi}\sin ({\alpha }_i)-l_{yi}\cos ({\alpha }_i)\end{array}\right]$$

(3)

where $\left(l_{xi},l_{yi}\right)$ is the installation position of the $i$-th thruster.

The aim of solving the TA problem is to reduce energy consumption. Our proposed TA objective function includes four parts, as shown below:

$$MINJ(\alpha ,T)=W{P}_{total}+s^{T}Qs+{(\alpha -{\alpha }_0)}^T\mathsf{\Omega }(\alpha -{\alpha }_0)+{({\dot{P}}_m-{\dot{P}}_f)}^{T}K({\dot{P}}_m-{\dot{P}}_f)$$

(4)

where $W$ is a weight parameter reflecting the proportion of $W{P}_{total}$ in the objective function. In the actual optimization process, the proportion of energy consumption in the entire optimization objective can be adjusted by changing the weight matrix. The weight matrix $Q$ decides the proportion of $s^{T}Qs$ in the objective function and should be set as large as possible to ensure $s\approx 0$. $\mathsf{\Omega }$ is a weight coefficient matrix, determining the proportion of ${(\alpha -{\alpha }_0)}^T\mathsf{\Omega }(\alpha -{\alpha }_0)$. The weight matrix $K$ determines the proportion of ${({\dot{P}}_m-{\dot{P}}_f)}^{T}K({\dot{P}}_m-{\dot{P}}_f)$ in the entire objective function. A larger $K$ value represents smoother power change, and the selection of $K$ should be based on the actual needs. The specific explanation of the remaining parts is as follows:

The mathematical expression of the total energy consumption $P_{total}$ is as follows:

$$P_{total}={\displaystyle \sum _{i=1}^n{P}_i}$$

(5)

where $P_i$ represents the energy consumption of each thruster.

The second term is the penalty item for the allocation error. The purpose is to impose a penalty for the discrepancy between the achieved and the commanded generalized control forces. The error is represented by the relaxation variable $s$ and defined as follows:

$$s=\tau -B_1(\alpha )T_1$$

(6)

The third item is the penalty term for the amplitude of change in the thruster azimuth angle. $\alpha$ and ${\alpha }_0$ represent the azimuth of thrusters at the current and previous moment.

The fourth item is the energy variation constraint term. ${\dot{P}}_m$ is the current energy change rate of the thrusters and ${\dot{P}}_f$ is the desired energy change rate of the thrusters.

2.2. Constraints of Thrust Allocation Model

Besides the fitness function, the TA model also includes some constraints. As for fixed azimuth thrusters, thrust is confined to the linear region due to the static characteristics of the thrusters. The thrust constraint is presented in Figure 1.

$$\left\{\begin{array}{l}{T}_{\min }\le T\le T_{\max }\\ \alpha ={\alpha }_0\end{array}\right.$$

(7)

where $T_{\min }$ and $T_{\max }$ signify the highest and lowest thrust levels and ${\alpha }_0$ indicates the fixed azimuth of the thrusters. For the azimuth thrusters, the azimuth angle can be adjusted within the specified range as needed without other constraints. It demonstrates significant agility and versatility. The structure is shown in Figure 2.

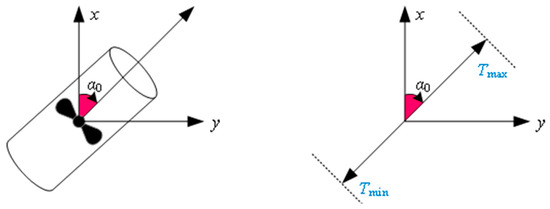
Figure 1. The thrust constraint of thrusters with a fixed azimuth.

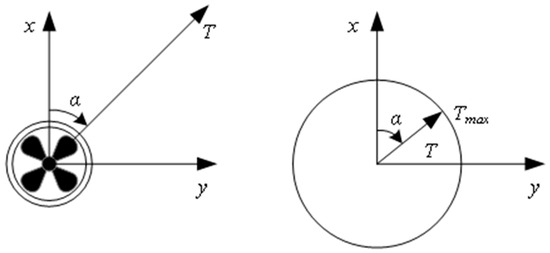
Figure 2. Thrust variation range of azimuth thrusters.

The thrust variation range can be mathematically expressed as follows:

$$\left\{\begin{array}{c}{T}_{\min }\le T\le T_{\max }\\ {\alpha }_{\min }\le \alpha \le {\alpha }_{\max }\\ \Delta T_{\min }\le T-T_0\le \Delta T_{\max }\\ \Delta {\alpha }_{\min }\le \alpha -{\alpha }_0\le \Delta {\alpha }_{\max }\end{array}\right.$$

(8)

This paper conducts research based on “Hai Yang Shi You 201”. Seven rotary thrusters were installed on the vessel, as shown in Figure 3.

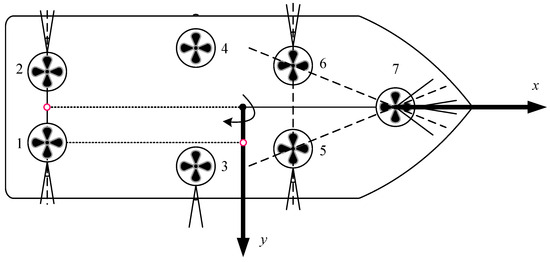
Figure 3. The thruster installation layout diagram of “Hai Yang Shi You 201”.

According to the given mathematical functions and constraint conditions and combining this with the material model of “Hai Yang Shi You 201”, the final TA mathematical model is obtained as follows:

$$MINJ(\alpha ,T)=W{\displaystyle \sum _{i=1}^7{C}_i{T}_i^{3/2}}+s^{T}Qs+{(\alpha -{\alpha }_0)}^T\mathsf{\Omega }(\alpha -{\alpha }_0)+K{\left({\displaystyle \sum _{i=1}^7{C}_i{T}_i^{3/2}-C_i{T}_{0i}^{3/2}}\right)}^2$$

(9)

$$\left\{\begin{array}{ll}s=\tau -B_1(\alpha )T_1& \\ 0\le T_i\le 680& i=1,2\\ 0\le T_i\le 540& i=3,4,\cdots ,7\\ -255\le {\alpha }_i\le 75& i=1,3,5\\ -75\le {\alpha }_i\le 255& i=2,4,6\\ 27.6\le {\alpha }_7\le 332.4& \\ \left|T_i-T_{0i}\right|\le 35& i=1,2\\ \left|T_i-T_{0i}\right|\le 30& i=3,4,\cdots ,7\\ \left|{\alpha }_i-{\alpha }_{0i}\right|\le 20& i=1,2,\cdots ,7\end{array}\right.$$

(10)

3. Thrust Allocation Based on the HOATDBO Algorithm

The specific behaviors of the improved HOATDBO algorithm and its application in the field of TA are discussed in this section, respectively.

3.1. Proposed HOATDBO

It is well known that the dung beetle feeds on the dung of animals. As an integral decomposer, the dung beetle plays an essential role in the ecological environment. This research has provided evidence that dung beetles have the behaviors of stealing, foraging, dancing, ball-rolling, and reproduction. And the details of these behaviors can be seen in [32]. In this part, some improvement strategies have been made to improve the DBO algorithm [32].

The specific improvements are shown below:

(1)

In the original DBO algorithm, random population initialization is used to initialize the population, which inevitably brings uncertainty. Therefore, the GPSPI is introduced to eliminate the uncertainty caused by random population initialization. The GPSPI method is a uniformly distributed and effective technique for selecting points. By utilizing the uniformity of the GPSPI, the population diversity can be improved. At present, the GPSPI has been applied to many intelligent algorithms. The results of two population initialization methods are given as follows:

Figure 4 shows the results of the GPSPI and the random population initialization. By comparison, it can be seen that the distribution result of the GPSPI is more homogeneous than the random population initialization.

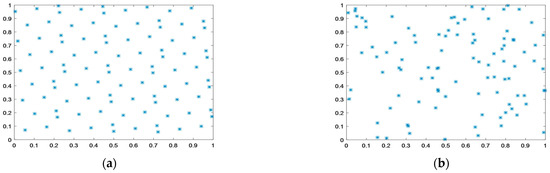
Figure 4. Initialize population comparison: (a) GPSPI; (b) random population initialization.

(2)

According to Ref. [32], dung beetles only depend on the worst position on a global scale and cannot interact with others in DBO. Therefore, this paper uses the global exploration strategy in the OOA to replace the strategy on position updates for rolling dung beetles. The global exploration strategy imitates the behavior of Osprey, which randomly searches for the position of a fish and attacks it. By simulating the motion of Osprey towards the fish, the formula for updating the position of Osprey can be derived as follows:

$$x_i(t+1)=x_i(t)+r_i\times \left(x_{i,rand}-I_i\times x_i(t)\right)$$

(11)

where $x_{i,rand}$ is the fecal ball randomly detected by the beetle and $r_i\in [0,1]$ and $I_i\in [1,2]$ are random numbers. Equation (11) solves the problem of the DBO’s rolling behavior relying only on the worst position and enhances the DBO’s exploration ability to escape from local optimal solutions.

To verify the superiority of our proposed improvement strategy, we compared the improved algorithm (ODBO) based on Equation (11) with the original algorithm (DBO) by using the classical test functions [32]. According to Ref. [32], the parameters are set as $K=0.1$, $b=0.3$, $S=0.5$, $N=30$, $t=1000$. The comparison result is shown below:

From Figure 5, we can see that the ODBO algorithm can reach the optimal solution faster than DBO, and the obtained optimal solution of ODBO is more accurate than DBO, which demonstrates the superiority of our proposed strategy based on Equation (11).

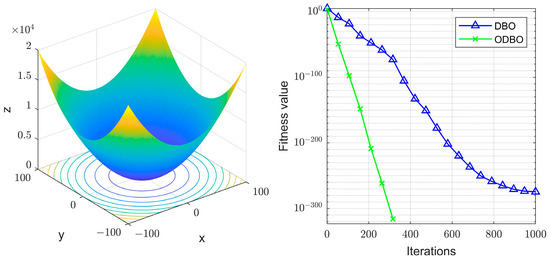
Figure 5. Convergence curves of ODBO and DBO in the test functions.

(3)

The t-distribution variation perturbation is employed to disrupt the foraging behavior of the small dung beetle. The method of position update is designed as follows:

$$x_i(t+1)=x_i(t)+\mathrm{trnd}\left(C\_iter\right)\times x_i(t)$$

(12)

where $x_i(t)$ is the $i$-th small dung beetle’s position information at the $t$-th iteration before the mutation disturbance, $\mathrm{trnd}\left(C\_iter\right)$ represents the generated t-distribution random number and $C\_iter$ is the number of iterations. Equation (12) endows the HOATDBO algorithm with excellent global exploitation capabilities during the initial iteration phase and effective local exploration skills in the subsequent iteration phase, thereby improving the convergence rate of the HOATDBO algorithm.

The pseudocode of the HOATDBO is shown as follows in Algorithm 1:

Algorithm 1: The pseudocode of the HOATDBO algorithm

Input $T_{\max }$ and $N$. 1 Initializing the Population with the GP-S $i\leftarrow 1,2,\dots ,N$. 2 while $(t\le T_{\max })$ do 3 for $i\leftarrow 1$$toN$ do 4  if $i==\mathrm{the}\mathrm{global}\mathrm{dung}\mathrm{beetle}$ then 5   $\delta =\mathrm{rand}\left(1\right)$ 6   if $\delta <0.9$ then 7    Select $\alpha$ and update the position of the global dung beetle 8   else 9    Update the position of global dung beetle 10  end if 11 end if 12 if $i==\mathrm{brood}\mathrm{ball}$ then 13  Update the position of the brood ball 14 end if 15 if $i==\mathrm{small}\mathrm{dung}\mathrm{beetle}$ then 16  Update the position of the small dung beetle 17 end if 18 if $i==\mathrm{thief}$ then 19  Update the position of the thief 20 end if 21 Disturb the position of the thief 22 if the new position of the thief is superior to the previous one then 23  Update it; 24 end if 25 end for 26 if the new position is superior to the previous one then 27  Update it; 28 end if 29 $t=t+1$; 30 end while 31 return $X^b$ and the fitness value

3.2. HOATDBO-Based Thrust Allocation

At present, some swarm intelligence optimization algorithms have been applied to the fields of TA, such as GA, AFSA, and so on. These optimization algorithms have the disadvantages of complex calculations, slow convergence, unsatisfactory solution accuracy, and local optimal solutions. The HOATDBO algorithm can effectively solve these problems. But it has not yet been applied to the field of TA. Therefore, we applied the HOATDBO to the field of TA in this paper; the basic steps are shown in Figure 6.

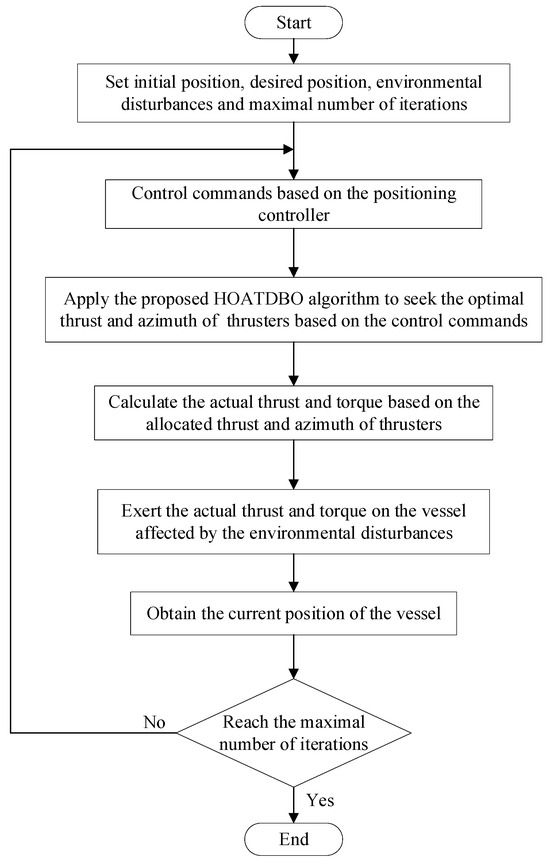
Figure 6. Flow chart of HOATDBO-based TA.

To verify the effectiveness of our proposed three improvement strategies, we compare the HOATDBO algorithm with several popular swarm intelligent optimization algorithms. The parameters of HOATDBO are set as $K=0.1$, $b=0.3$, $S=0.5$, $\delta =1$, $\mu =X_{best}$, $N=30$, and $t=1000$. The parameters of GA [27], AFSA [30], DBO [32], the Whale Optimization Algorithm (WOA) [39], and Harris Hawks Optimization (HHO) [40] can be seen in the corresponding references. The simulation result is as follows:

Figure 7 shows the convergence performance of our proposed HOATDBO algorithm with GA, AFSA, DBO, WOA and HHO on the classical test functions. We can see from the figure that our proposed HOATDBO algorithm has the best convergence speed and accuracy, which proves its superiority.

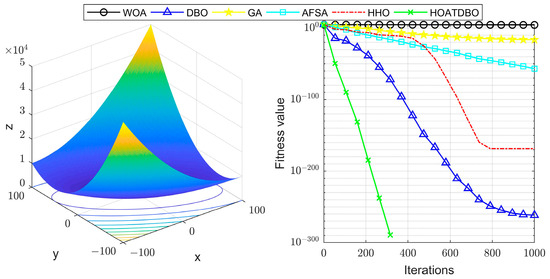
Figure 7. Convergence curves of different algorithms in the test functions.

4. Simulation Results and Comparative Analysis

The “Hai Yang Shi You 201” DP vessel was employed to validate the effectiveness of our proposed HOATDBO algorithm in this section. Inspired by typical values in references [32,37], the parameters of these improvement strategies had minor adjustments made to them based on the thrust allocation characteristics. After trial and error, the parameters of HOATDBO were set as $K=0.15$, $b=0.3$, $S=0.5$, $\delta =1$, $\mu =X_{best}$, $N=30$, $t=500$. The other details of the HOATDBO algorithm can be seen in Ref [32]. The details of “Hai Yang Shi You 201” refer to Ref. [31].

In the simulation, the initial and desired vectors for the positions and headings are set as $\left[0m,0m,0°\right]$ and $\left[10m,10m,10°\right]$, respectively. The details of the sea conditions are shown in Table 1:

Table 1. Sea conditions of simulations.

Sea Condition	Value
Wind velocity	$10\mathrm{m}/\mathrm{s}$
Wind direction	${225}^{°}$
Current direction	${10}^{°}$
Wave direction	${15}^{°}$
Current velocity	$0.8\mathrm{m}/\mathrm{s}$

The results from the simulation are given as follows:

Figure 8 describes the change curve of the environmental disturbance forces and moment exerted on the vessel. From Figure 8, we can see that environmental disturbance slowly varies over time, which is consistent with the marine environments in the real world. Figure 9 describes that the vessel can move from the initial position to the desired position and ultimately stabilize there. Figure 10 shows the response curves for positions and headings. It is evident from Figure 10 that the vessel can stabilize at around 100 s. Figure 11 shows the velocities and yaw rate of the vessel. Figure 8, Figure 9, Figure 10 and Figure 11 demonstrate that the HOATDBO-based TA can achieve dynamic positioning with high precision under dynamic environmental disturbance. Figure 12 shows the comparison between the output commands of the controller and thrusters. We can conclude from Figure 12 that the composite output command of the thrusters can track the controller command well, validating the effectiveness of our proposed HOATDBO-based TA algorithm.

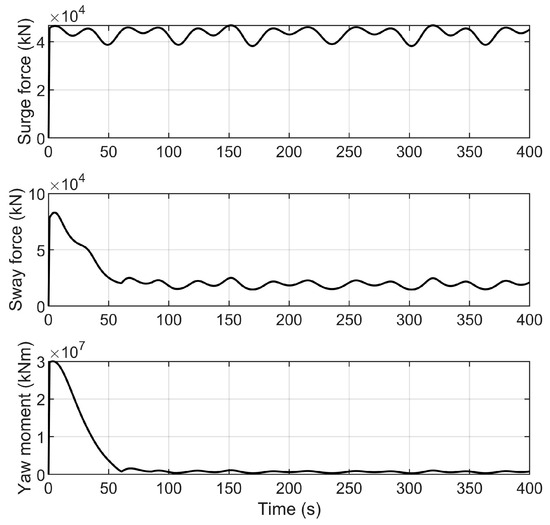
Figure 8. The environmental disturbance forces and moment exerted on the vessel.

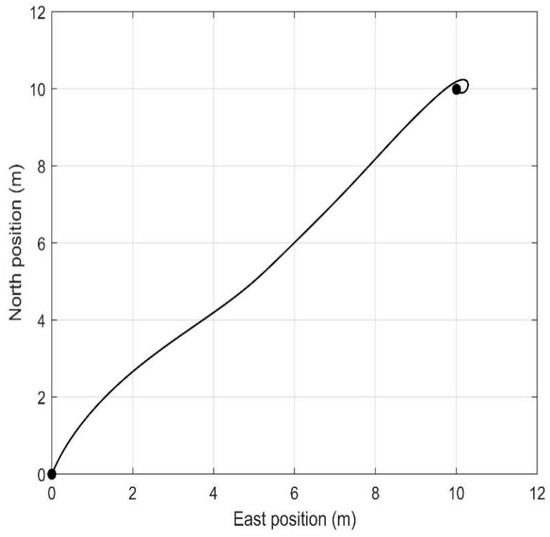
Figure 9. The motion trajectory of the vessel.

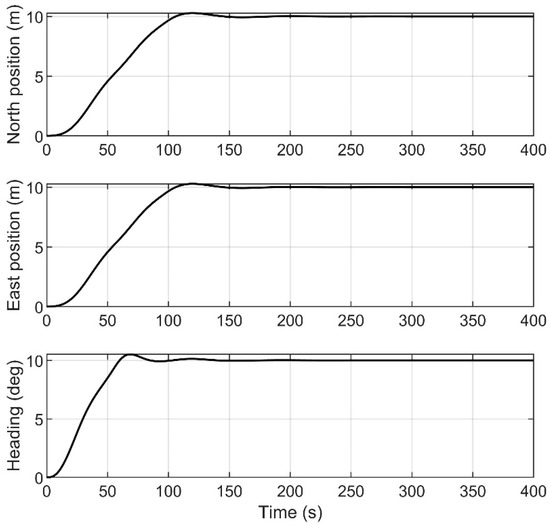
Figure 10. Response curves for positions and heading.

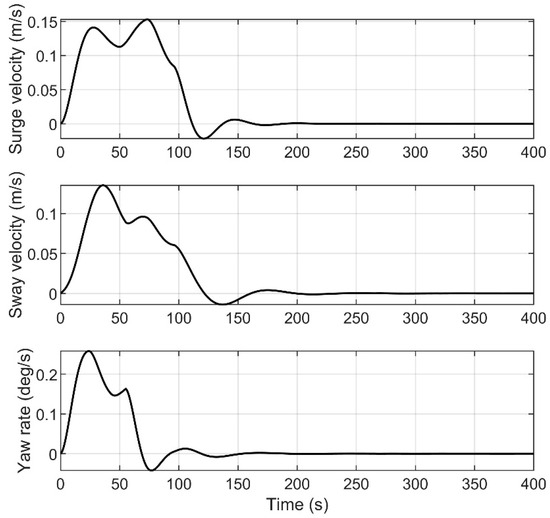
Figure 11. Velocities and yaw rate of vessels.

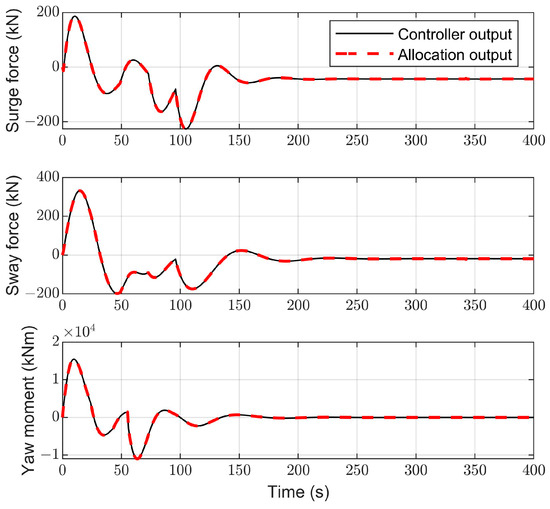
Figure 12. Output commands of controller and thrusters.

Figure 13, Figure 14, Figure 15 and Figure 16 represent the changes in the thrusts and azimuths of the seven thrusters. Figure 13, Figure 14, Figure 15 and Figure 16 demonstrate that the thrusts and azimuths of the thrusters, which are all within the allowable range. This is in line with the practical application requirements of thrusters.

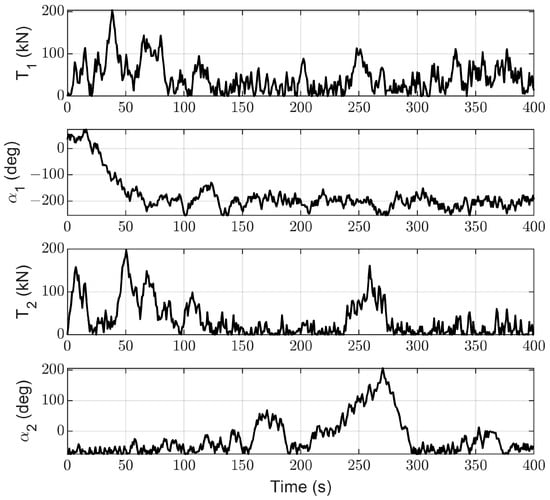
Figure 13. The thrusts and azimuths of thrusters 1# and 2#.

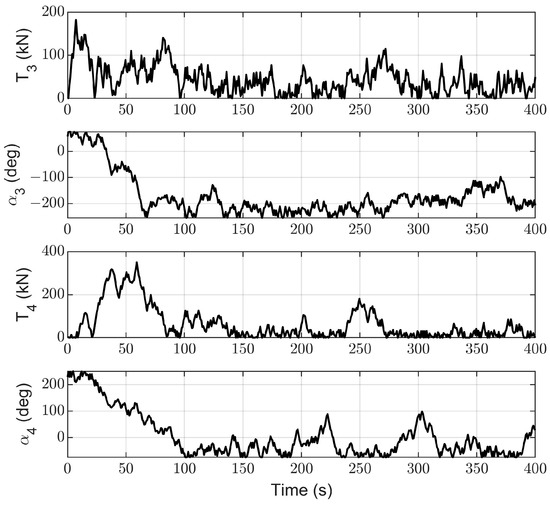
Figure 14. The thrusts and azimuths of thrusters 3# and 4#.

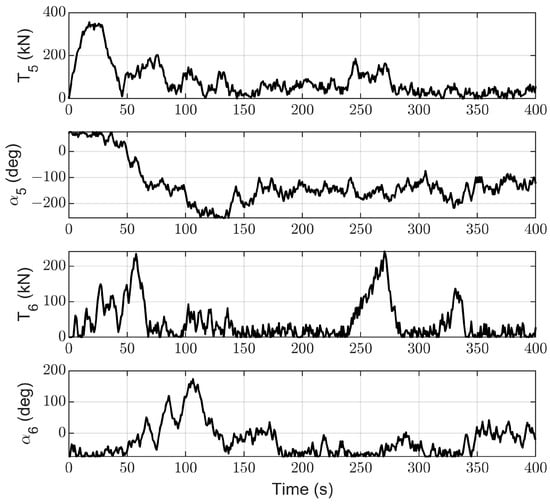
Figure 15. The thrusts and azimuths of thrusters 5# and 6#.

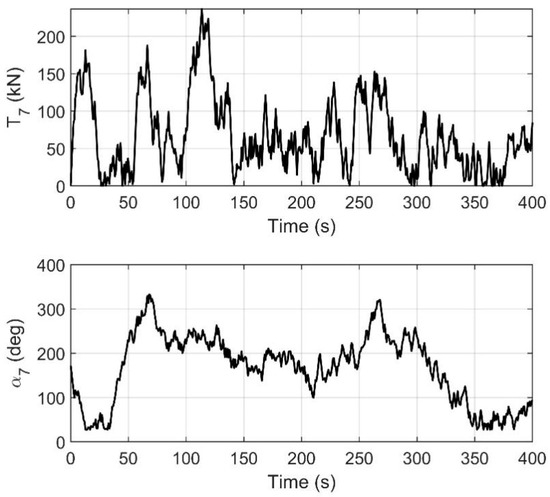
Figure 16. The thrust and azimuth of thruster 7#.

To further validate the superiority of the HOATDBO algorithm, we compared our proposed HOATDBO-based TA algorithm with the algorithms based on DBO, AFSA, and GA. Since the superiority of DBO over GA and AFSA has been demonstrated in [32], this section only provides the simulation results between HOATDBO and DBO. The comparison results are given in Figure 17, Figure 18 and Figure 19 and Table 2, Table 3 and Table 4.

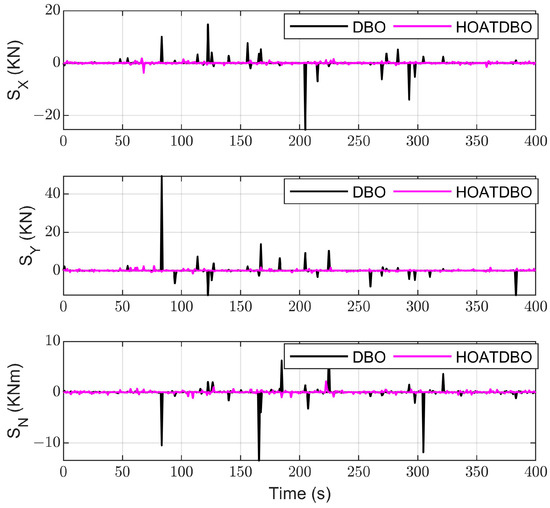
Figure 17. Allocation errors under DBO and HOATDBO methods.

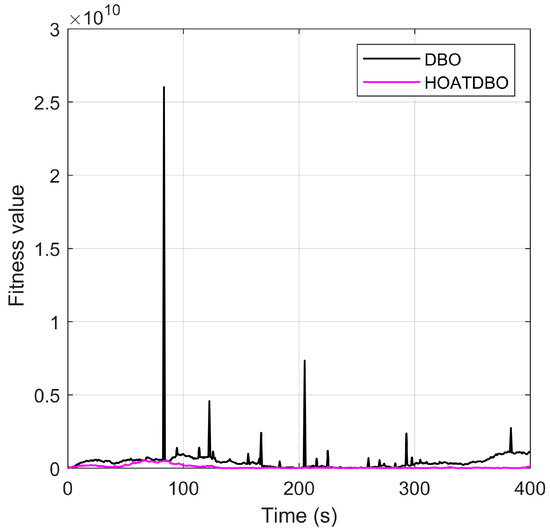
Figure 18. Fitness values of DBO and HOATDBO methods.

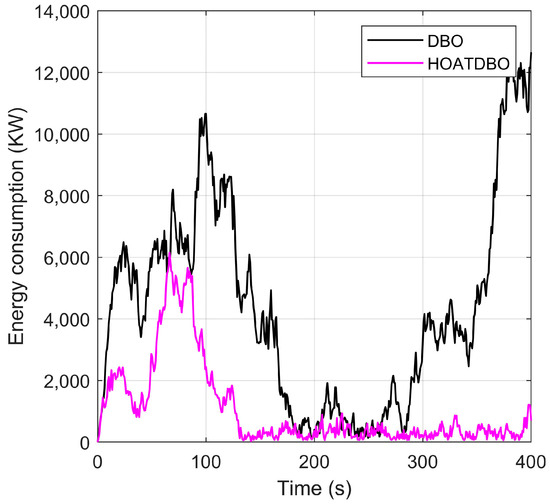
Figure 19. Energy consumption under DBO and HOATDBO methods.

Table 2. A comparison of the optimal value, average value, and variance under HOATDBO-based and DBO-based TA methods.

Algorithm	${\mathit{X}}_{\mathit{a}}(\mathit{m}/\mathit{m}/\mathit{r}\mathit{a}\mathit{d})$	${\mathit{X}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t}}(\mathit{m}/\mathit{m}/\mathit{r}\mathit{a}\mathit{d})$	$\overline{\mathit{X}}(\mathit{m}/\mathit{m}/\mathit{r}\mathit{a}\mathit{d})$	$\mathit{S}$
DBO	$10$	$9.866398$	$9.844831$	$3.29\times {10}^{-6}$
	$10$	$10.213566$	$10.255012$	$9.52\times {10}^{-6}$
	$0.174532$	$0.173921$	$0.173659$	$6.34\times {10}^{-10}$
HOATDBO	$10$	$9.993238$	$9.986887$	$5.41\times {10}^{-8}$
	$10$	$10.002272$	$10.003915$	$6.55\times {10}^{-8}$
	$0.174532$	$0.174532$	$0.174553$	$3.45\times {10}^{-12}$

Table 3. Energy comparison of algorithms.

Algorithm	Energy Consumption (kW)
GA	$5.0449\times {10}^9$
AFSA	$2.6871\times {10}^9$
DBO	$2.1325\times {10}^9$
HOATDBO	$6.0192\times {10}^8$

Table 4. Average time of algorithms.

Algorithm	Average Time of 30 Simulations (s)
DBO	$68.78$
HOATDBO	$65.42$

Figure 17 illustrates the force and moment allocation errors under the DBO and HOATDBO methods. It can be seen that the allocation errors under HOATDBO are much smaller than those under DBO. The allocation errors under HOATDBO have fewer mutation points and smaller overshoots than those under DBO. Figure 18 shows the fitness values of the DBO and HOATDBO methods. From Figure 18, we can see that the fitness value of HOATDBO tends towards stability earlier than that of DBO. It is demonstrated that HOATDBO has significantly faster convergence compared to DBO. Further, it implies that the HOATDBO method increases the probability of avoiding local optimums and obtaining optimal results.

Based on 30 simulations, Table 2 records the optimal value $X_{\mathrm{best}}$, average value $\overline{X}$, and variance $S$ of the final position for the vessel when solving the TA problem based on HOATDBO and DBO. From Table 2, we can see that the optimal and average values of HOATDBO are closer to the target value $X_a$ than those of DBO, and the variances of the HOATDBO method are smaller than those of DBO. This means that HOATDBO can enhance the accuracy and stability of the solution. In addition, it also reflects the fact that HOATDBO can enhance global and local exploration capabilities.

Figure 19 shows the total energy consumption under the DBO and HOATDBO methods from 0 s to 400 s. It is evident that the energy consumption under HOATDBO is lower than that under DBO. When the vessel arrives at the desired position, the energy consumption under HOATDBO tends to be stable. Nevertheless, the energy consumption under DBO is still oscillating. It illustrates that HOATDBO-based TA can reduce energy consumption. To further demonstrate the superiority of the HOATDBO algorithm in energy consumption, the total energy consumption of seven thrusters is listed in Table 3 based on the GA, AFSA, DBO, and HOATDBO algorithms. It is evident from Table 3 that the HOATDBO-based TA method has the lowest energy consumption during the process of vessel movement. Table 4 shows the average time taken for 30 simulations of HOATDBO and DBO based on TA. From the table, we can see that the computation time of HOATDBO is less than DBO, which demonstrates that our proposed HOATDBO algorithm can effectively reduce computational complexity.

In summary, we can conclude from the results and analysis that the proposed HOATDBO method can achieve satisfactory thrust allocation with high allocation accuracy and low energy consumption while reducing computational complexity.

5. Conclusions

This paper presents an energy-efficient TA method based on the proposed HOATDBO algorithm. First of all, to avoid the uncertain and uneven population spatial distribution caused by random initialization in DBO, the random population initialization is replaced by the GP-S population initialization in our HOATDBO algorithm. Subsequently, inspired by the OOA, a global exploration strategy is proposed in our HOATDBO method to enhance global exploration capability. Finally, we introduce the t-distribution perturbation to escape from the local optimal solutions that occurred in DBO. Based on the comparison analysis, we can conclude that our HOATDBO method can achieve satisfactory thrust allocation with high allocation accuracy and low energy consumption while reducing computational complexity.

6. Limitations and Future Work

(1)

The thrust allocation model established in this paper takes into account the impact of power changes on vessel dynamic positioning but does not consider solutions for different loads and circuit breaker on–off situations, which also affects the accuracy and stability of dynamic positioning. Therefore, further research in this area should be conducted.

(2)

The effectiveness of our proposed HOATDBO-based thrust allocation method was validated through simulations. Nevertheless, this paper does not consider the influence of sensor noise and actuator faults, which are unavoidable in the practical dynamic positioning system of vessels. Therefore, future research should also focus on the field of nonlinear filtering and fault-tolerant control.

(3)

For further implementation in real dynamic positioning systems, real-time performance should also be given special attention. Hence, we will explore swarm intelligence optimization algorithms with lower computational complexity to meet the real-time requirement of the dynamic positioning system.