The Numerical Analysis of Hydrodynamic Response and Structural Stability of an Eccentric Conical Floating Structure
Abstract
:1. Introduction
2. Theory
2.1. Theoretical Background
2.1.1. Control Theory
2.1.2. Wave Theory
3. Numerical Model Development and Validation
3.1. Environmental Conditions
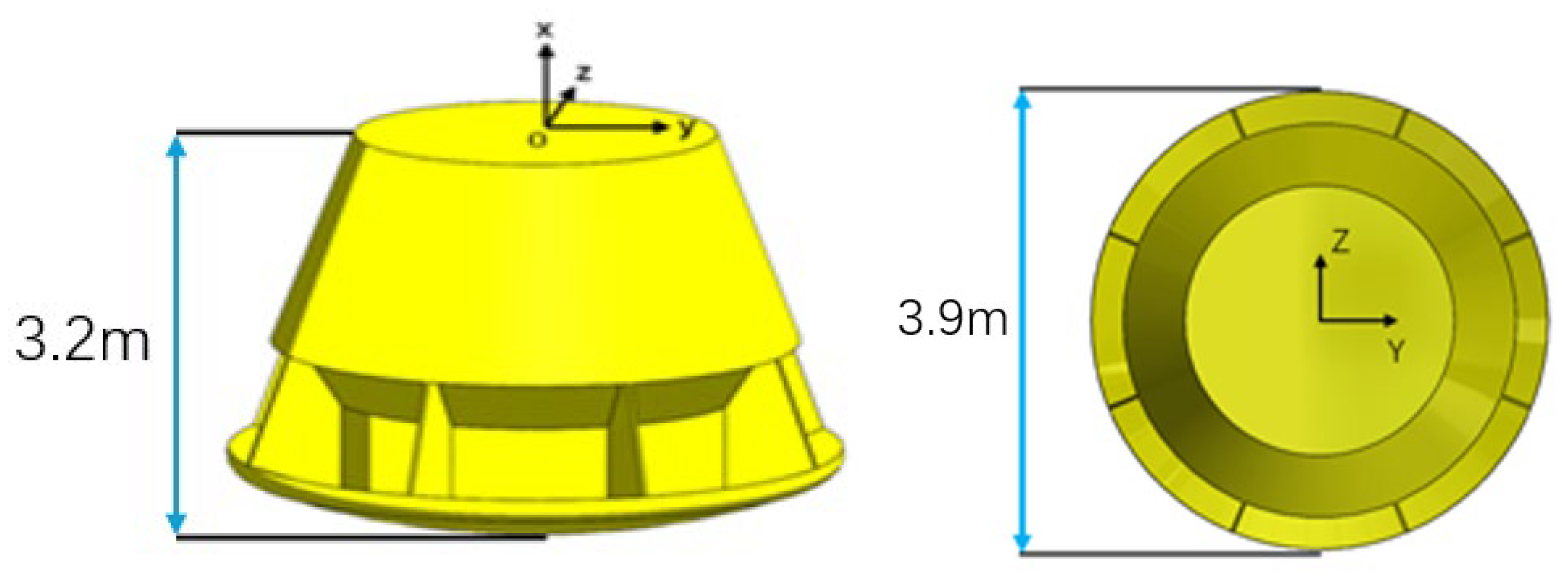
3.2. Eccentric Conical Structure Model
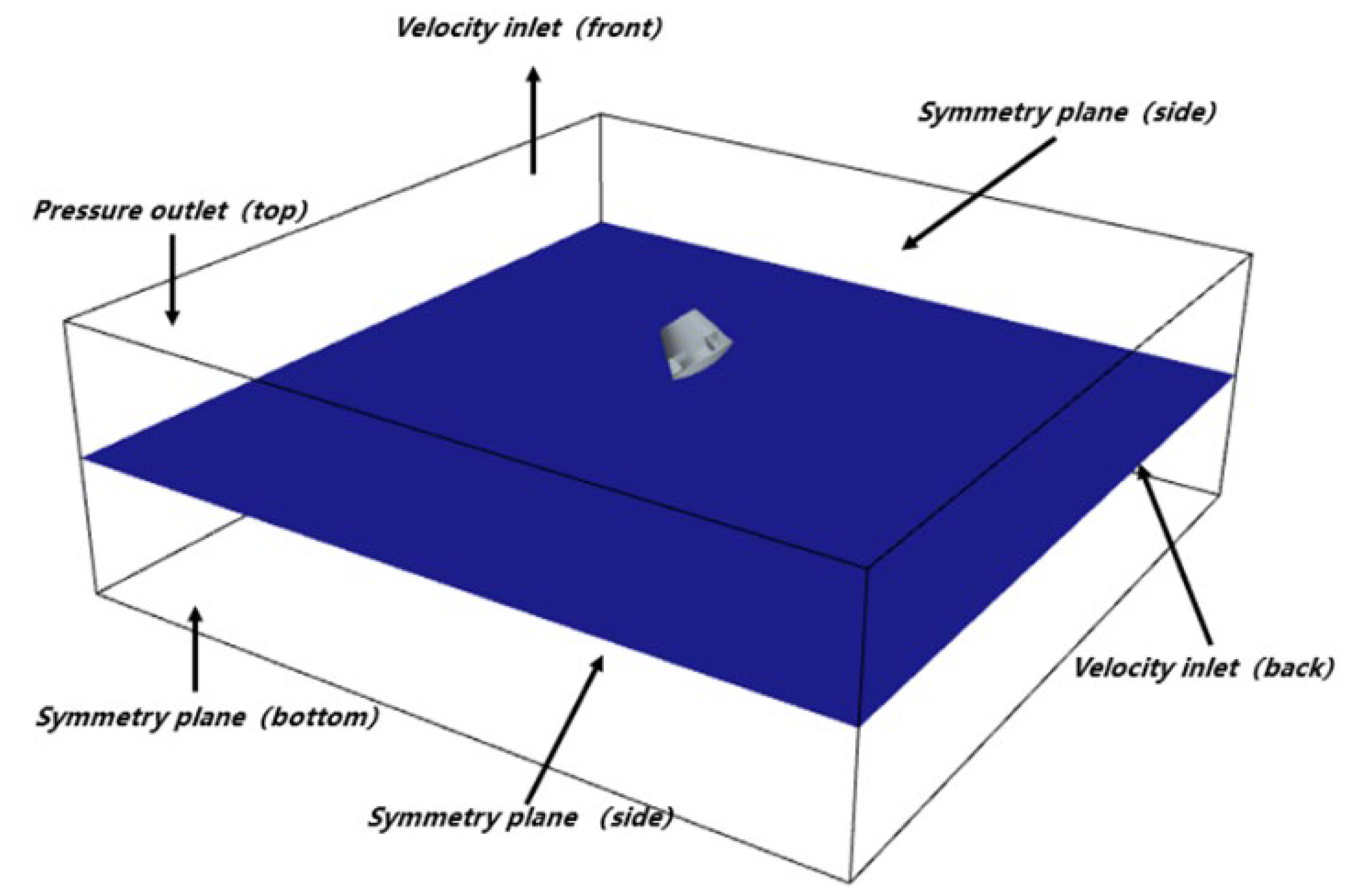
3.3. Simulation Setup
3.4. Experimental Pool Testing and Validation
3.4.1. Subsubsection Experimental Design
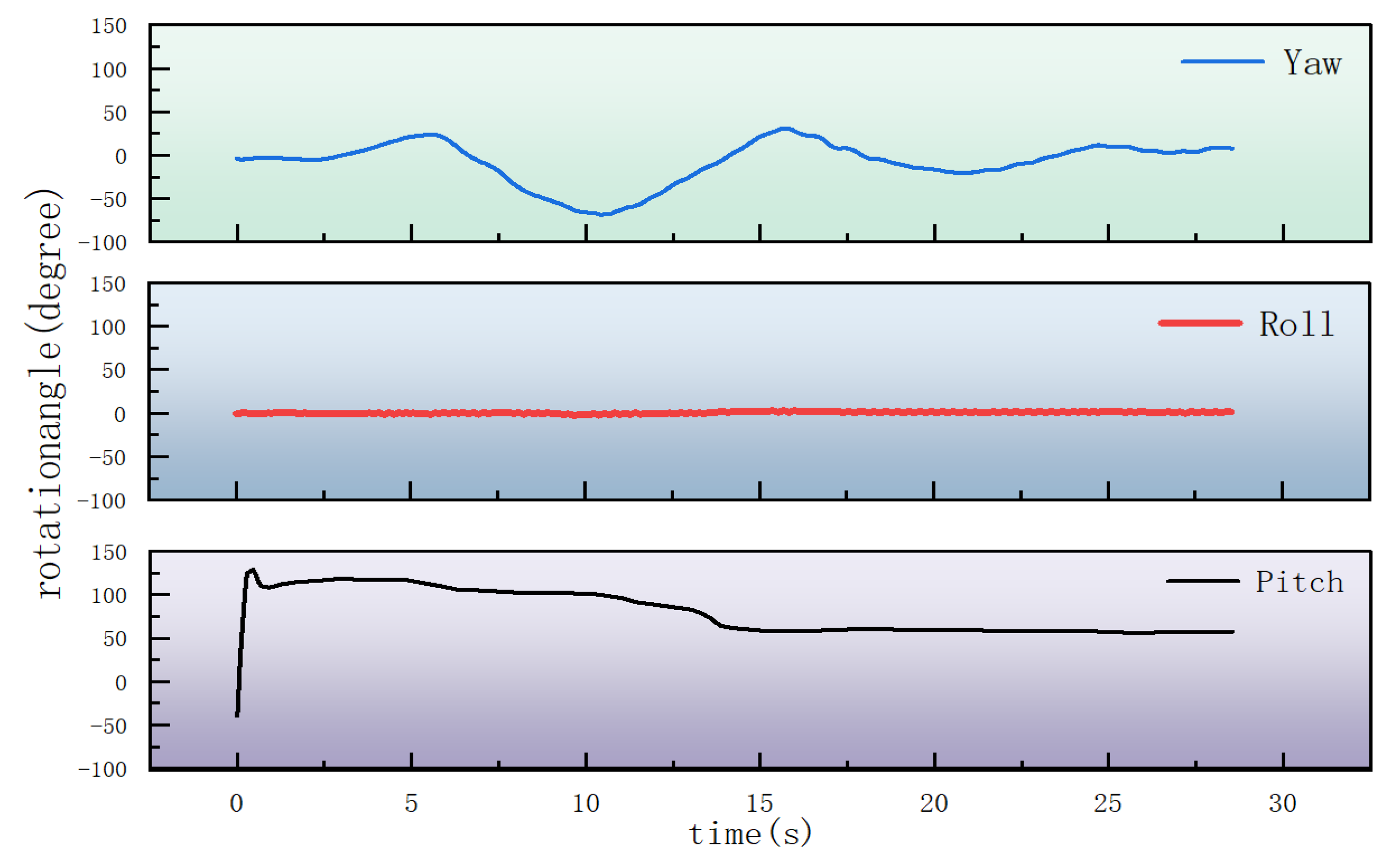
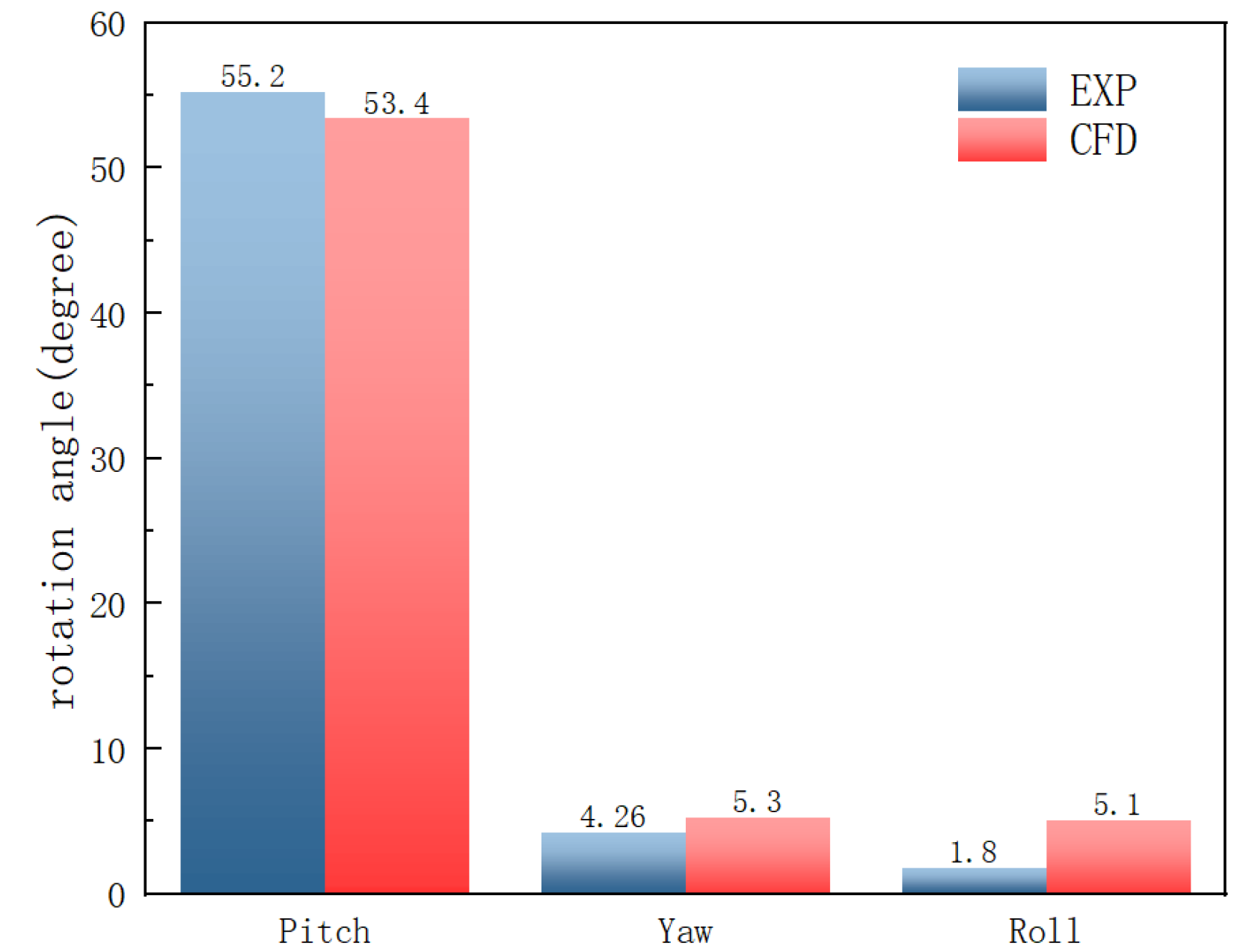
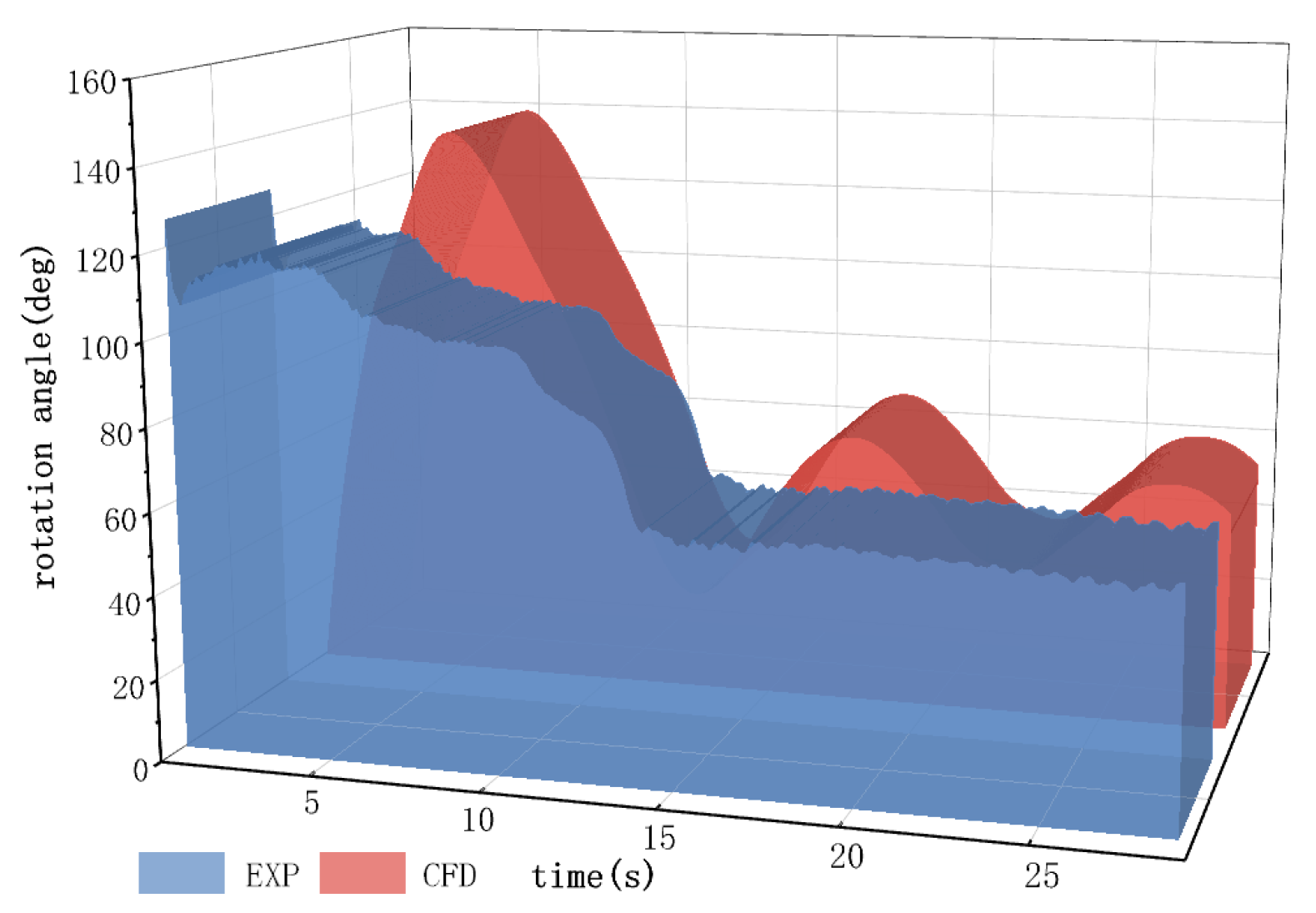
3.4.2. Results and Analysis
4. Steady-State Analysis
4.1. Impact of Mass Characteristics on Platform Floating Stability
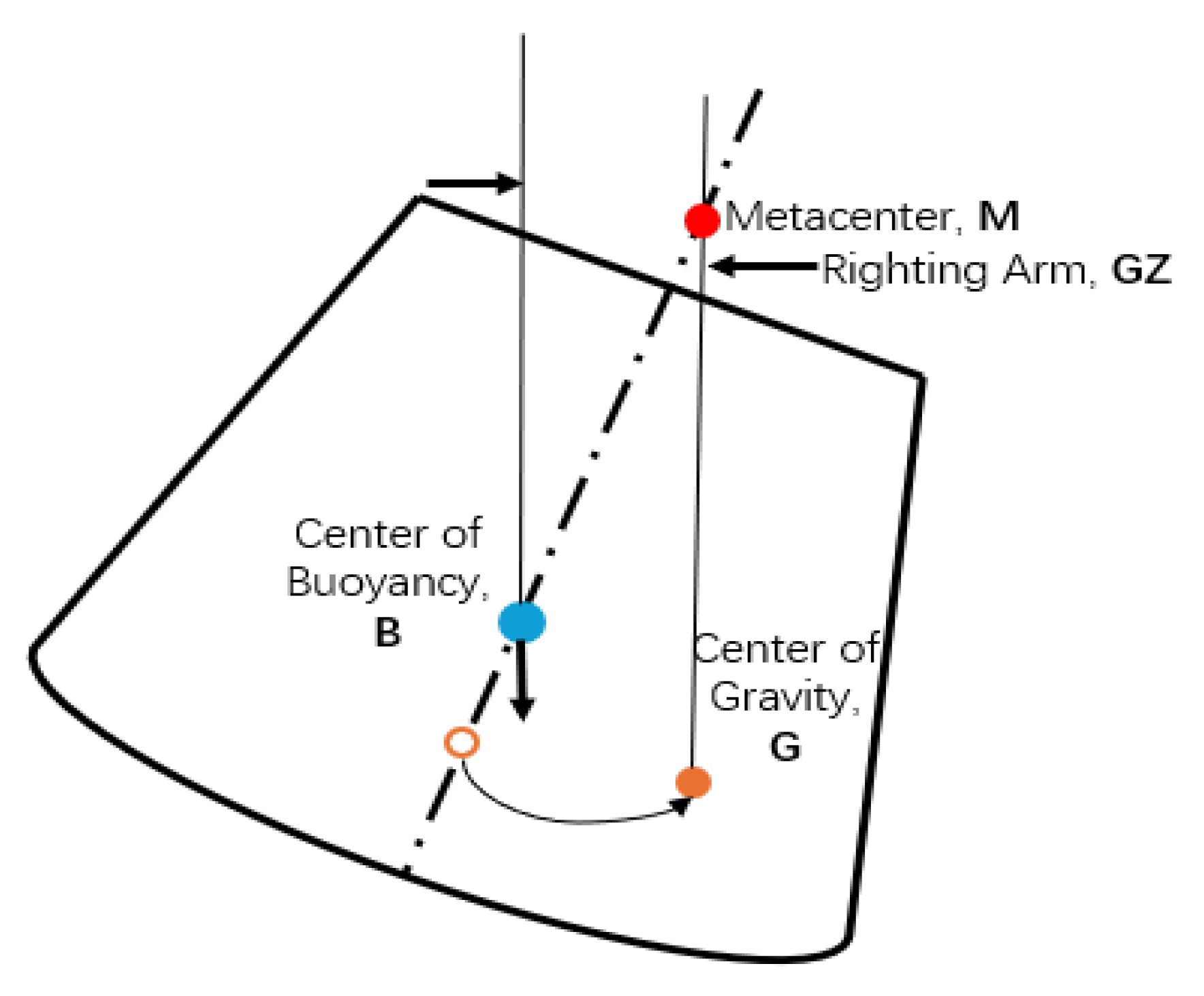
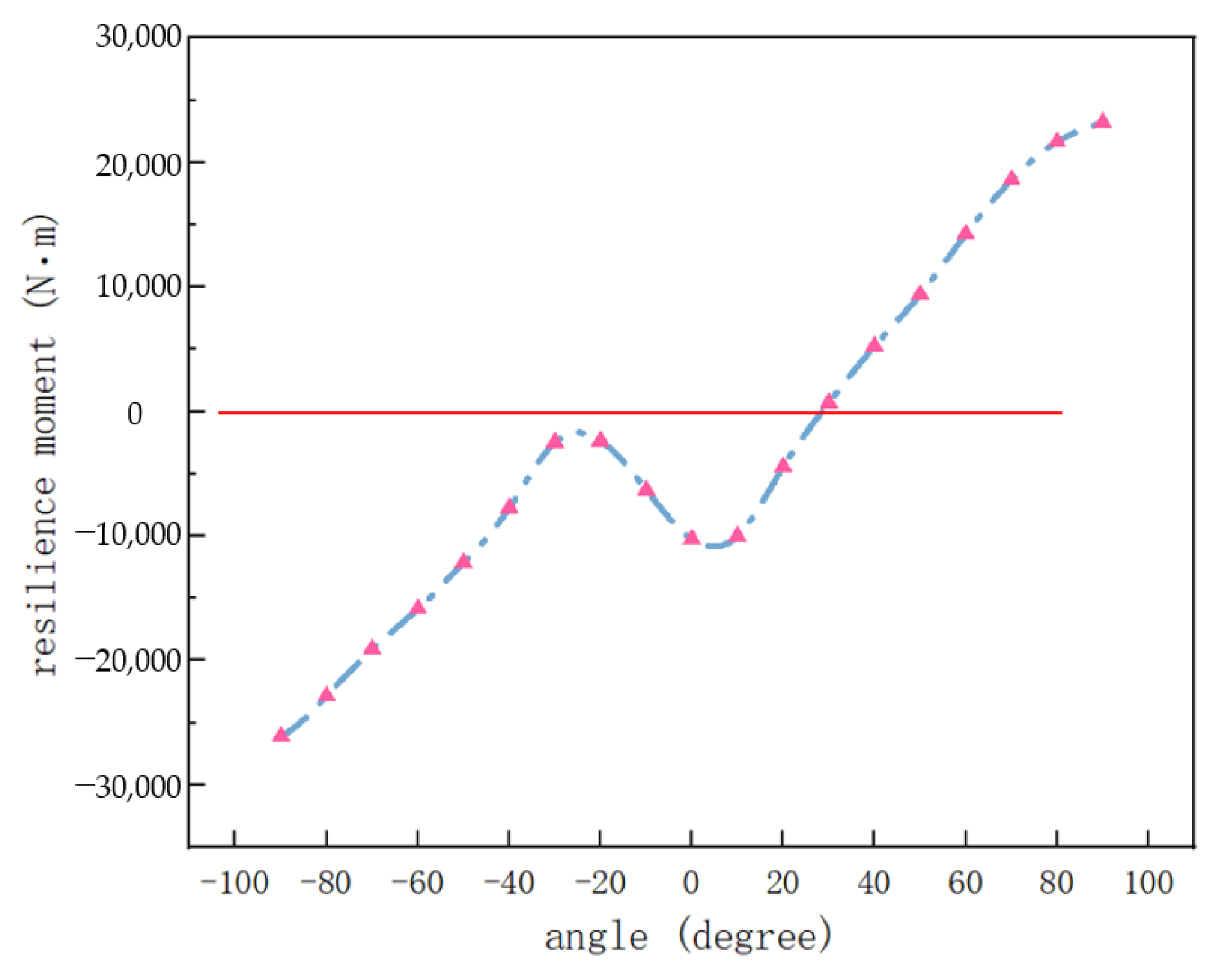
4.2. Restoring Moment Analysis of the Eccentric Conical Structure
4.3. Impact of Displacement Volume on Platform Floating Stability
5. Multi-Physics Coupling Analysis
6. Wave Parameter Effects
6.1. Wavelength Effects
6.2. Wave Height Effects
7. Conclusions and Discussion
- (1)
- In still water, the lateral (y-axis) center-of-mass offset sustains a single stable equilibrium via a nonlinear restoring moment driven by geometric asymmetry. Its stability sensitivity exceeds that of the longitudinal (x-axis) offset. The x-axis offset increases pitch response amplitude but does not exceed the instability threshold. Biaxial center-of-mass disturbances do not cause capsizing in still water, but wave excitation in real sea conditions may induce multi-stable equilibria.
- (2)
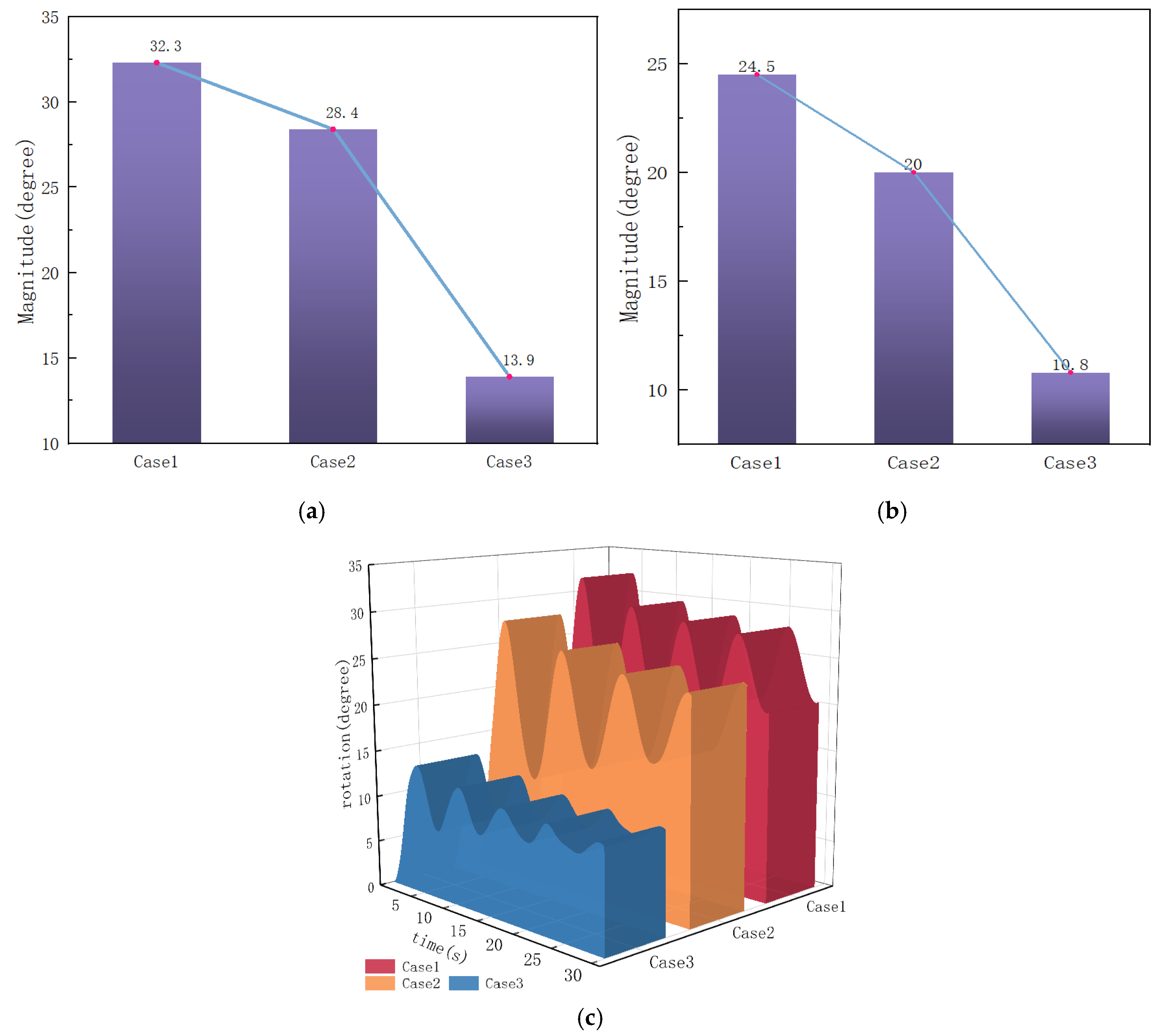
- For displacement volume control, uniform foam filling across all compartments reduces motion amplitude and steady-state tilt angle compared to the no-foam baseline. Directional filling in the +y-axis compartment provides superior stability correction, reducing the maximum tilt angle more effectively than uniform filling. In engineering applications, post-parachute +y-axis ballast control can rapidly right the capsule by adjusting the center of buoyancy and center of mass.
- (3)
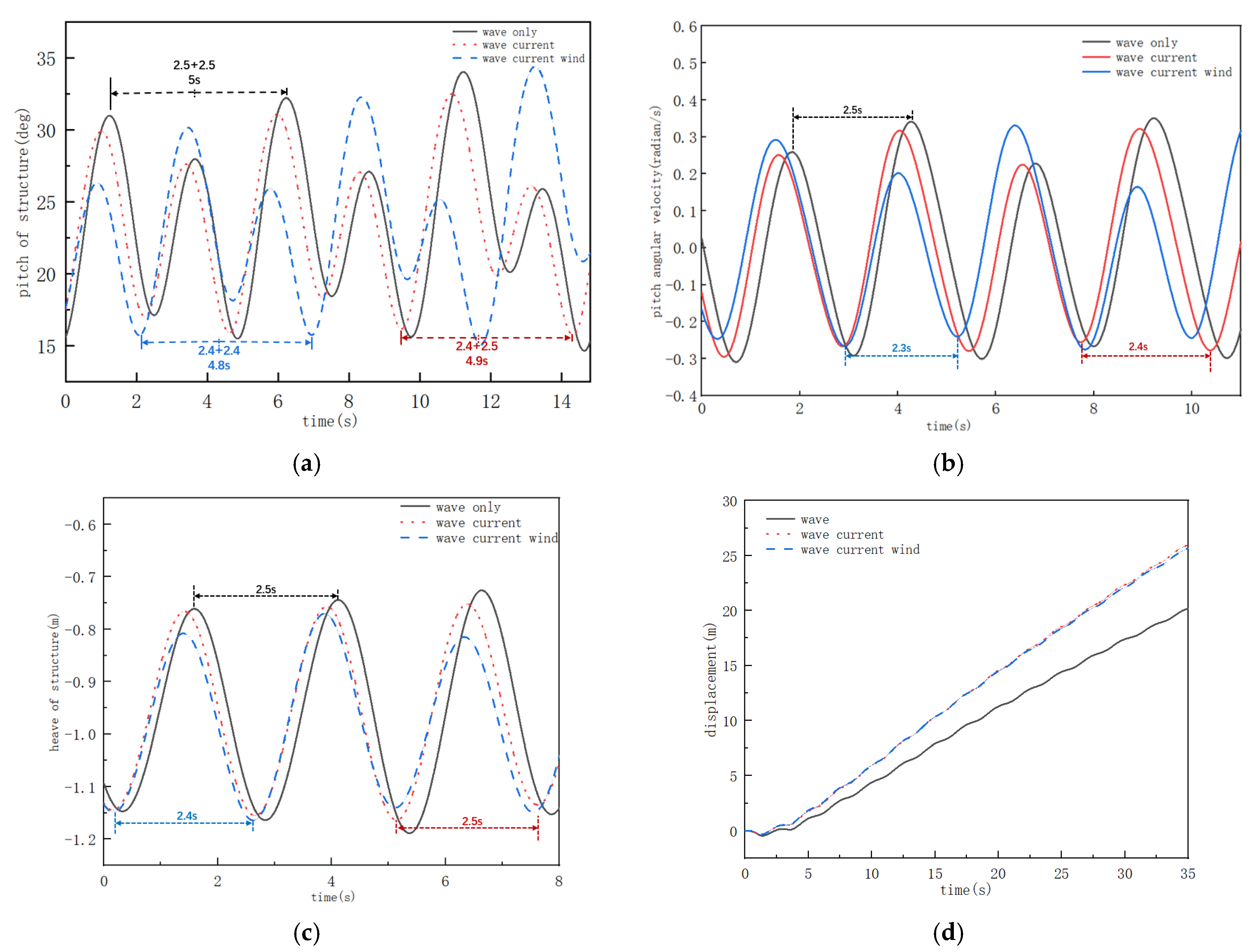
- Waves induce significant surge, heave, and pitch coupling in the platform, with response periods strictly synchronized with the wave period. Ocean currents and wind loads slightly alter motion amplitude and phase, but their effects are less significant than wave periodicity. Wave parameters are the primary determinants of the platform’s dynamic stability, while current and wind disturbances have limited effects on local motion modes.
- (4)
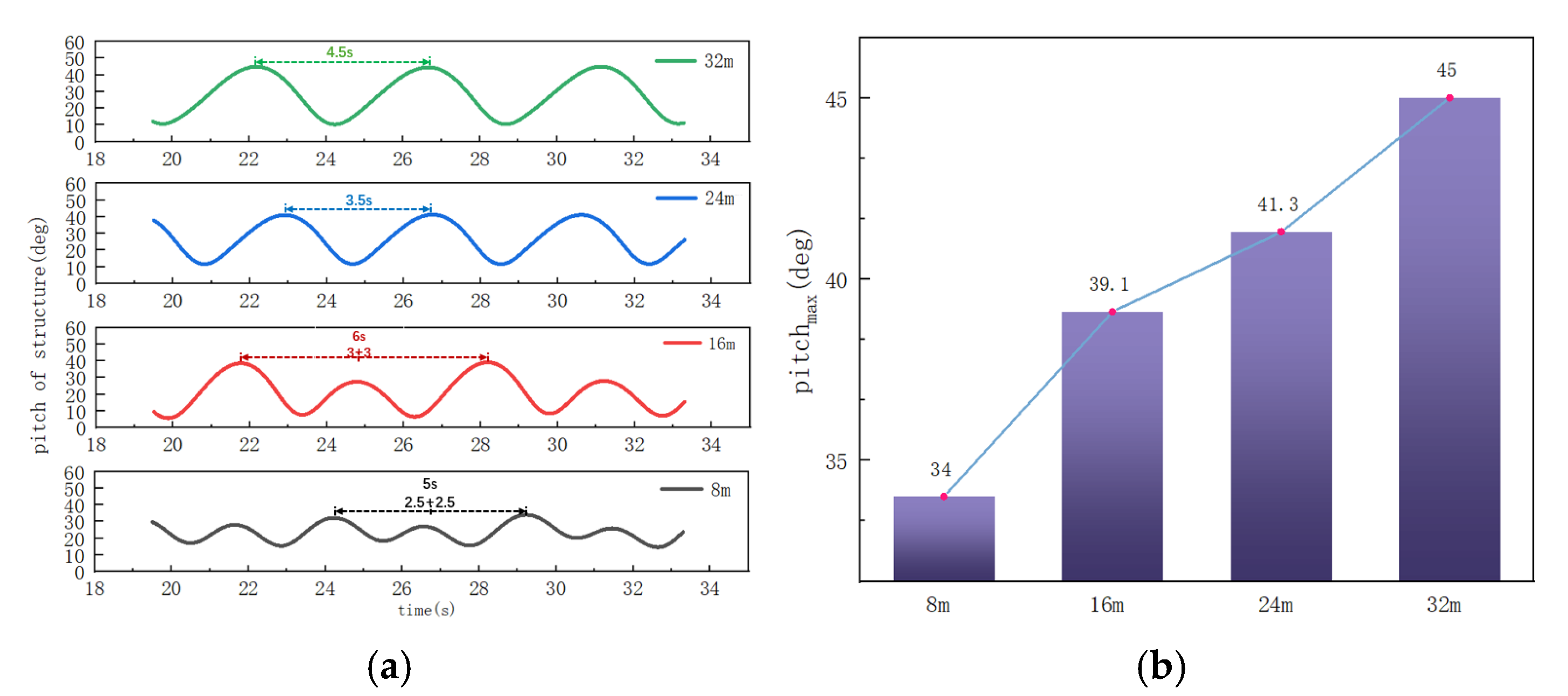
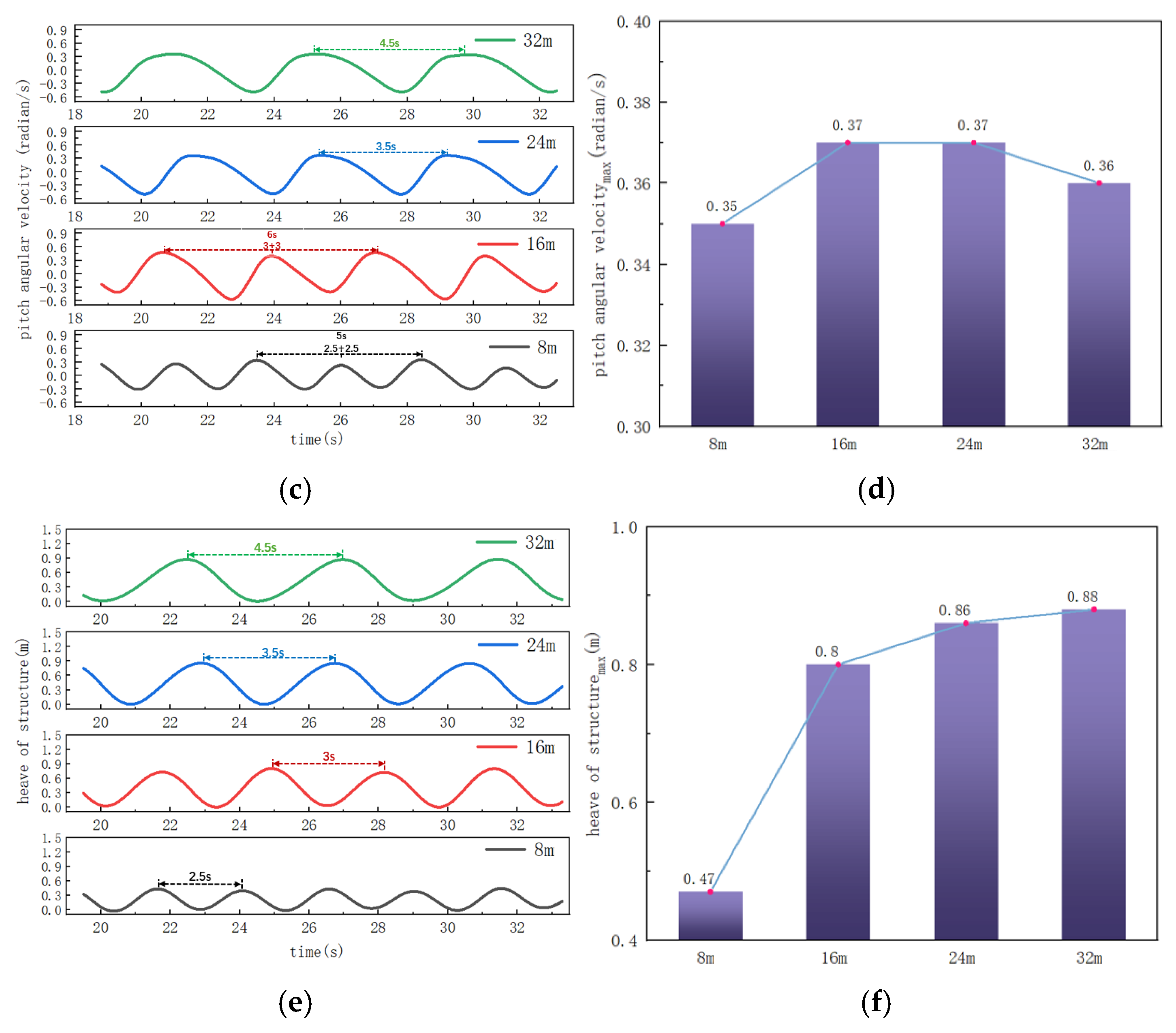
- As wavelength increases, the platform’s restoring moment and wave action moment balance more rapidly, reducing the motion period from twice the wave period to wave period synchronization. Surge displacement amplitude exhibits nonlinear growth, rising sharply up to a wavelength threshold, then leveling off. Pitch angle amplitude increases linearly with wavelength, while angular velocity remains stable, suggesting that wavelength primarily affects displacement response potential energy, not inertial forces.
- (5)
- In moderate sea conditions (Sea States 3–5), the platform’s motion frequency aligns with the wave fundamental frequency, maintaining stable pitch angle amplitudes. At a wave height of 5 m (Sea State 6), the system enters a strongly nonlinear regime, with subharmonic resonance and broadband vibrations causing a sharp increase in pitch angle extrema and a reduced safety margin. Notably, increasing wave steepness reduces energy input efficiency, attenuating heave displacement responses at extreme wave heights.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Shi, X. Current status and progress of research on water impact problems. Explos. Shock Waves 2008, 28, 276–282. [Google Scholar]
- Xuan, J.; Miao, Y.; Cheng, J. Experimental study and theoretical calculation of water impact characteristics of return capsules. Hydrodyn. Res. Prog. (Ser. A) 2000, 3, 276–286. [Google Scholar]
- Mei, C.; Zhang, J.; Pan, G. Multi-objective optimization design of airbag cushioning for manned spacecraft return capsules. Manned Spacefl. 2015, 21, 444–449. [Google Scholar]
- Takasawa, H.; Fujii, T.; Takahashi, Y.; Moriyoshi, T.; Takayanagi, H.; Nagata, Y.; Yamada, K. Static attitude stability of deep space sample return capsule with thin aeroshell. CEAS Space J. 2025, 17, 55–69. [Google Scholar] [CrossRef]
- Lin, W.; Wang, N.; Gao, Z. Optimization of joint search and rescue by rescue ships and helicopters in remote sea areas. J. Transp. Eng. 2021, 21, 187–199. [Google Scholar]
- Peng, Z.; Yang, H.; Wei, J. Current status and prospects of China’s maritime search and rescue equipment development. World Shipp. 2023, 46, 26–29. [Google Scholar]
- Vaughan, V.L. Landing Characteristics and Flotation Properties of a Reentry Capsule. Unpublished report, 1961. Vaughan, V. L. Landing Characteristics and Flotation Properties of a Reentry Capsule; NASA Langley Research Center: Hampton, VA, USA, 1961. [Google Scholar]
- Herting, D.; Pohlen, J.; Pollock, R. Analysis and design of the Apollo landing impact system. In Proceedings of the AIAA 3rd Manned Space Flight Meeting, Houston, TX, USA, 4–6 November 1964. [Google Scholar] [CrossRef]
- Stubbs, S.M. Landing Characteristics of the Apollo Spacecraft with Deployed-Heat-Shield Impact Attenuation Systems; NASA Langley Research Center: Hampton, VA, USA, 1966. [Google Scholar]
- Benson, H.E. Water impact of the Apollo spacecraft. J. Spacecr. 1966, 3, 1282–1284. [Google Scholar] [CrossRef]
- Baker, W.E.; Westine, P.S. Model tests for determination of the structural response of the Apollo command module to water impact. Arch. Int. Pharmacodyn. Ther. 2013, 23, 165–174. [Google Scholar] [CrossRef]
- Thompson, W.C. Dynamic Model Investigation of the Rough-Water Landing Characteristics of a Spacecraft; NASA Langley Research Center: Hampton, VA, USA, 1967. [Google Scholar]
- Wang, J.T.; Lyle, K.H. Simulating Space Capsule Water Landing with Explicit Finite Element Method. In Proceedings of the AIAA Conference, San Antonio, TX, USA, 7–10 January 2007. [Google Scholar] [CrossRef]
- Anghileri, M.; Spizzica, A. Experimental validation of finite element models for water impacts. J. Spacecraft Rockets 1995, 32, 621–628. [Google Scholar]
- Song, S.; Demirel, Y.K.; Atlar, M. An investigation into the effect of biofouling on the ship hydrodynamic characteristics using CFD. Ocean Eng. 2019, 175, 122–137. [Google Scholar] [CrossRef]
- Jasak, H.; Vukevi, V.; Gatin, I.; Lalović, I. CFD validation and grid sensitivity studies of full scale ship self propulsion. Int. J. Nav. Archit. Ocean Eng. 2019, 1, 45–58. [Google Scholar] [CrossRef]
- Wang, J.; Wan, D. CFD study of ship stopping maneuver by overset grid technique. Ocean Eng. 2020, 197, 106895. [Google Scholar] [CrossRef]
- Jiao, J.; Huang, S.; Soares, C.G. Numerical investigation of ship motions in cross waves using CFD. Ocean Eng. 2021, 223, 108711. [Google Scholar] [CrossRef]
- Islam, H.; Ventura, M.; Guedes Soares, C.; Tadros, M.; Abdelwahab, H.S. Comparison between Empirical and CFD Based Methods for Ship Resistance and Power Prediction. J. Mar. Sci. Eng. 2022, 10, 258. [Google Scholar] [CrossRef]
- Kim, D.; Tezdogan, T. CFD-based hydrodynamic analyses of ship course keeping control and turning performance in irregular waves. Ocean Eng. 2022, 248, 110808. [Google Scholar] [CrossRef]
- Andersson, J.; Shiri, A.A.; Bensow, R.E.; Jin, Y.; Wu, C.; Qiu, G.; Deng, G.; Queutey, P.; Yan, X.-K.; Horn, P.; et al. Ship-scale CFD benchmark study of a pre-swirl duct on KVLCC2. Appl. Ocean Res. 2022, 123, 103134. [Google Scholar] [CrossRef]
- Huang, S.; Jiao, J.; Soares, C.G. Uncertainty analyses on the CFD–FEA co-simulations of ship wave loads and whipping responses. Mar. Struct. 2022, 82, 103129. [Google Scholar] [CrossRef]
- Mi, C.; Gao, J.; Song, Z.; Liu, Y. Hydrodynamic Wave Forces on Two Side-by-Side Barges Subjected to Nonlinear Focused Wave Groups. Ocean Eng. 2025, 317, 120056. [Google Scholar] [CrossRef]
- Gong, S.; Gao, J.; Yan, M.; Song, Z.; Shi, H. Effects of Floater Motion on Wave Loads during Steady-State Gap Resonance Occurring between Two Non-Identical Boxes. Ocean Eng. 2025, 323, 120649. [Google Scholar] [CrossRef]
- Song, Z.; Jiao, Z.; Gao, J.; Mi, C.; Liu, Y. Numerical Investigation on the Hydrodynamic Wave Forces on the Three Barges in Proximity. Ocean Eng. 2025, 316, 119941. [Google Scholar] [CrossRef]
- Lari, K.S. Comparison and verification of turbulence Reynolds-averaged Navier–irregular waves closures to model spatially varied flows. Sci. Rep. 2020, 10, 76128. [Google Scholar] [CrossRef]
- Zhan, J.; Li, Y. A hybrid turbulence model for wave breaking simulation. Chin. J. Theor. Appl. Mech. 2019, 51, 1712–1719. [Google Scholar] [CrossRef]
- Babaji, B. Computational Aerodynamic Analysis of Flow Around Apollo Reentry Capsule with Anisotropic Mesh Adaptation. Ph.D. Thesis, Cranfield University, Bedford, UK, 2021. [Google Scholar]
- Wheeler, M.P.; Matveev, K.I.; Xing, T. Numerical study of hydrodynamics of heavily loaded hard-chine hulls in calm water. J. Mar. Sci. Eng. 2021, 9, 184. [Google Scholar] [CrossRef]
- Yuan, R.; Guo, B.; Liu, M.Q. Flexible sliced Latin hypercube designs with slices of different sizes. Stat. Pap. 2021, 62, 137–157. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, C.; Fan, T.; Lu, H. Research on the Dynamic Behaviors of a Spar Floating Offshore Wind Turbine with an Innovative Type of Mooring System. Front. Energy Res. 2022, 10, 853448. [Google Scholar] [CrossRef]
- Arredondo-Galeana, A.; Brennan, F. Floating Offshore Vertical Axis Wind Turbines: Opportunities, Challenges and Way Forward. Energies 2021, 14, 8000. [Google Scholar] [CrossRef]
- Fang, H.; Liu, L.F.; Tang, L.; Lin, P. The theory of fifth-order Stokes waves in a linear shear current. Proc. R. Soc. A 2023, 479, 19. [Google Scholar] [CrossRef]
- Ahn, H.; Shin, H. Experimental and numerical analysis of a 10 MW floating offshore wind turbine in regular waves. Energies 2020, 13, 2608. [Google Scholar] [CrossRef]
- Jana, O.; Taylor, P.H.; Wolgamot, H.A.; Madsen, F.J.; Pegalajar-Jurado, A.M.; Bredmose, H. Wave- and drag-driven subharmonic responses of a floating wind turbine. J. Fluid Mech. 2021, 929, A50. [Google Scholar]








| Sea Condition Levels | Level 3 | Level 4 | Level 5 |
|---|---|---|---|
| Wave Height (m) | 1 | 2 | 3 |
| Wavelength (m) | 8 | 16 | 24 |
| Wave Period (s) | 2.5 | 3.6 | 4.7 |
| Wind Speed (m/s) | 4 | 8 | 11 |
| Parameter Name | Parameter Value |
|---|---|
| Total Mass (kg) | 7800 |
| Center of Mass (mm) | −1750 |
| Center of Mass (mm) | 30 |
| Center of Mass (mm) | 0 |
| Inertia Tensor (kg ·m2) | 9675.11 |
| Inertia Tensor (kg·m2) | 11,805.97 |
| Inertia Tensor (kg·m2) | 11,266.03 |
| Group | Cells (Millions) | ||||||
|---|---|---|---|---|---|---|---|
| Coarse | 1.5 | 4.70 | 5.86% | 1.31 | 4.8% | 28.13 | 1.7% |
| Medium | 2.6 | 4.50 | 1.35% | 1.27 | 1.6% | 27.72 | 0.22% |
| Fine | 3.3 | 4.44 | 0% | 1.25 | 0% | 27.66 | 0% |
| Condition | Initial Pitch Angle (°) | Oscillation (J) | Energy Dissipation Rate (J/s) |
|---|---|---|---|
| Baseline | 24.5 | 1030.3 | 41.2 |
| Uniform Filling | 20.0 | 686.7 | 31.6 |
| Directional Filling | 10.8 | 200.2 | 10.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, F.; Chen, S.; Zhang, K. The Numerical Analysis of Hydrodynamic Response and Structural Stability of an Eccentric Conical Floating Structure. J. Mar. Sci. Eng. 2025, 13, 1032. https://doi.org/10.3390/jmse13061032
Qu F, Chen S, Zhang K. The Numerical Analysis of Hydrodynamic Response and Structural Stability of an Eccentric Conical Floating Structure. Journal of Marine Science and Engineering. 2025; 13(6):1032. https://doi.org/10.3390/jmse13061032
Chicago/Turabian StyleQu, Fei, Shengtao Chen, and Kang Zhang. 2025. "The Numerical Analysis of Hydrodynamic Response and Structural Stability of an Eccentric Conical Floating Structure" Journal of Marine Science and Engineering 13, no. 6: 1032. https://doi.org/10.3390/jmse13061032
APA StyleQu, F., Chen, S., & Zhang, K. (2025). The Numerical Analysis of Hydrodynamic Response and Structural Stability of an Eccentric Conical Floating Structure. Journal of Marine Science and Engineering, 13(6), 1032. https://doi.org/10.3390/jmse13061032







