Abstract
Offshore wind power is one of the primary forms of utilizing marine green energy in China. Currently, near-shore wind power predominantly employs monopile foundations, with designs typically being overly conservative, resulting in high construction costs. Precise characterization of the interaction mechanisms between marine piles and surrounding soils is crucial for foundation design optimization. Traditional p-y curve methods, with simplified fitting functions, inadequately capture the complex pile–soil behaviors, limiting predictive accuracy and model uncertainty quantification. To address these challenges, this research collected 1852 empirical datasets of offshore wind monopile foundation pile–soil interactions, developing p-y curve and horizontal displacement prediction models using artificial neural network (ANN) expressions and comprehensive uncertainty statistical analysis. The constructed ANN model demonstrates a simple structure with satisfactory predictive performance, achieving average error margins below 6% and low to moderate prediction accuracy dispersion (26%~45%). In contrast, traditional p-y curve models show 30%~50% average biases with substantial accuracy dispersion near 80%, while conventional finite element methods exhibit approximately 40% error and dispersion. By strictly characterizing the probability cumulative function of the neural network model factors, a foundation is provided for reliability-based design. Through comprehensive case verification, it is demonstrated that the ANN-based model has significant advantages in terms of computational accuracy and efficiency in the design of offshore wind power foundations.
1. Introduction
Although fossil fuels such as coal and oil remain the backbone of the global energy mix, offshore wind power—a renewable and low-carbon energy source—has emerged as a critical component of international efforts to achieve carbon neutrality and energy transition []. Rapid advancements in technology, coupled with cross-border policy coordination and collaboration (e.g., in the North Sea [,], Baltic Sea [], and the Guangdong-Hong Kong-Macao Greater Bay Area [] as a regional exemplar), have propelled offshore wind into a vital supplement to the world energy supply. In near-shore shallow water areas, offshore wind turbine foundations primarily utilize large-diameter steel pipe piles. Statistics indicate that approximately 75% of marine engineering structures currently employ large-diameter monopile foundations [,].
The ideal objective in pile foundation design is to balance safety with economic efficiency. However, due to the potential catastrophic risks associated with complex wind, wave, and current loads in marine environments [], coupled with nonlinear pile–soil interactions and the significant uncertainty in existing pile design methodologies [,], designers are compelled to adopt conservative approaches to ensure the stability and service life of offshore platform structures while hedging against the exorbitant repair costs of pile failure []. The direct consequence of overly conservative design is elevated construction costs. Accurately quantifying pile–soil interaction is the key to designing marine pile foundations that balance safety with economic considerations.
Currently, common methods for analyzing pile–soil interaction primarily include theoretical approaches [,], empirical methods [,], and numerical techniques [,,]. Theoretical methods typically simplify piles as idealized models such as cantilever beams [,,]; however, due to excessive simplification, these approaches fail to adequately account for complex factors in pile–soil interaction, including soil nonlinear mechanical properties and variations in pile–soil interface friction []. Empirical methods are analytical approaches developed from extensive engineering practice or experimental data, with the p-y curve method being a typical representative model. Due to its simple expression and convenient application, this method has been widely adopted in various international specifications [,,]. The method constructs empirical expressions between pile displacement and soil reaction force by fitting experimental data [,].
The accuracy of the p-y curve method depends on the quantity of fitted data and the functional expressions employed. Additionally, the p-y curve method exhibits significant regional characteristics and typically cannot be directly applied to different regions [,]. Given the extreme complexity of marine environments, pile–soil interactions exhibit significant variability and uncertainty [,], imposing substantial limitations on applying the p-y curve method. Empirical investigations have demonstrated that the p-y curve method exhibits significantly compromised predictive accuracy when applied to large-diameter pile foundations and under specialized geotechnical conditions [,,,].
The finite element method (FEM) is a widely utilized numerical technique capable of accurately characterizing the boundary and initial conditions of pile–soil interaction systems []. However, the highly nonlinear mechanical properties inherent in marine soils present significant challenges to predictive modeling. Although FEM simulations are generally unbiased on average, they exhibit moderate variability in predictive accuracy due to these nonlinearities [,]. When confronted with complex environmental loads and unique geological formations, the FEM not only struggles to maintain precision but also encounters substantial hurdles, including significantly increased computational costs and prolonged processing times [,]. These limitations pose serious obstacles in practical engineering applications that demand high computational efficiency and rapid iterative analyses.
In recent years, machine learning methods have been widely applied to complex geotechnical engineering problem analysis due to their powerful nonlinear representation capabilities [,,,]. For example, support vector machines (SVMs) demonstrate high accuracy in landslide susceptibility analysis and rock deformation prediction [,], while artificial neural networks (ANNs) excel in soil classification [] and in predicting earth dam settlement and foundation settlement []. Machine learning methods effectively compensate for the deficiencies of traditional techniques in handling highly nonlinear problems, overcoming the oversimplification of theoretical approaches, the applicability limitations of empirical methods, and the accuracy and computational cost issues of numerical methods, making them highly suitable for analyzing pile–soil interactions in specialized marine geotechnical environments.
This study compiles a comprehensive dataset encompassing multi-dimensional parameters of marine large-diameter monopile foundations, including marine geological conditions, pile design specifications, horizontal displacement profiles, and soil pressure distribution characteristics. Leveraging this dataset, we develop a neural network model specifically tailored for analyzing pile–soil interactions in marine environments. The proposed framework achieves enhanced predictive accuracy for pile–soil interaction behaviors through systematic model training and rigorous application while significantly improving computational efficiency. This methodology substantially mitigates design risks associated with marine large-diameter pile foundations and provides a robust technical framework for cost-effective engineering solutions in offshore pile construction.
The subsequent section describes the database development process and its contents, while Section 3 details the construction of the neural network model, including fundamental concepts, development procedures, and the selection of key parameters. Section 4 and Section 5 analyze the prediction results of the neural network model, discuss its performance and influencing factors, and validate the model’s reliability using a real-world case study. Finally, the paper concludes with a summary of the research content and findings.
2. Database
This study collected 1852 datasets comprising field measurements and model test data from 29 monopile foundations across 24 offshore wind projects worldwide. Leveraging the compiled datasets, we established a marine geotechnical database to systematically investigate and predict pile–soil interactions of monopile foundations under complex loading and geological environments.
The database systematically documents three critical components for each monopile (Table 1): (i) soil parameters encompassing stratigraphic classification and strength characteristics (φ: internal friction angle; c: cohesion; E: elastic modulus; γ: soil’s unit weight, et al.); (ii) geometric design specifications of steel tubular piles (L: pile length; D: outer diameter; t: wall thickness, et al.); and (iii) operational loading regimes with horizontal force (F) applied at the pile head. Depth-dependent soil–structure interaction data are parametrized by l (depth from pile head), with pile geometric configuration schematically detailed in Figure 1.

Table 1.
Soil information and pile design parameters of the pile foundation in the database.
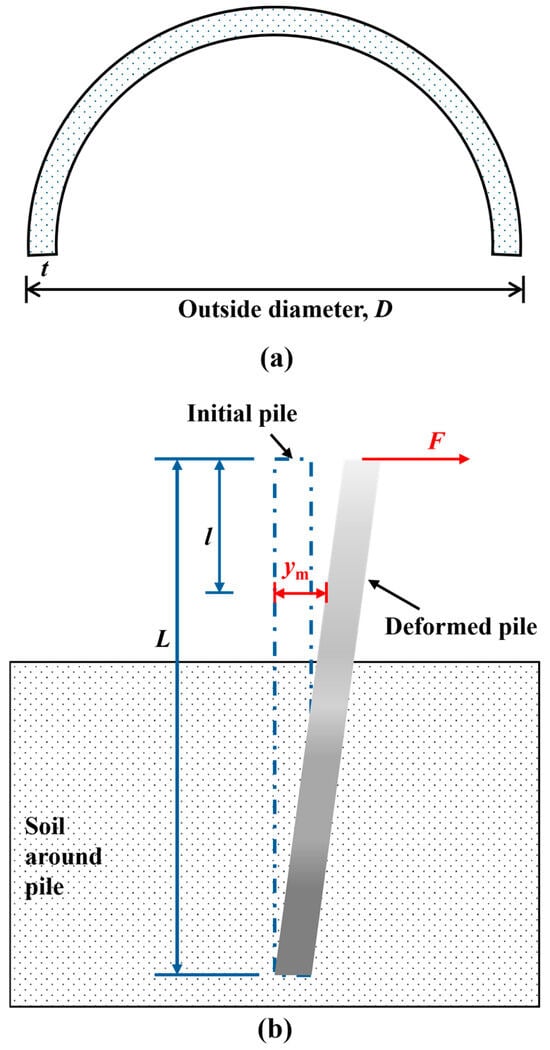
Figure 1.
Pile foundation design parameters. (a) Cross-section view, (b) side-elevation view.
Field-monitored monopiles were predominantly embedded in clay and sand strata, with three cases (P3, P4, and P19) terminating in weathered rock formations. Laboratory tests employed reconstituted sand-silt mixtures. The soil unit weight (γ) exhibited limited variation, predominantly between 18.8 and 19.5 kN/m3. While strength parameters demonstrated significant heterogeneity across the dataset. As illustrated in Figure 2, internal friction angle (φ) varied considerably from 5° to 42°; cohesion (c) predominantly clustered within 11–22 kPa, with only approximately 5% of specimens exceeding 50 kPa; the distribution of shear strength (cu) exhibited considerable variability, ranging from 10 kPa to 80 kPa, with values predominantly concentrated within the 35–42 kPa interval; and soil elastic modulus (E) exhibited a wide distribution from 6 to 180 MPa, with half below 30 MPa and 80% below 69 MPa.
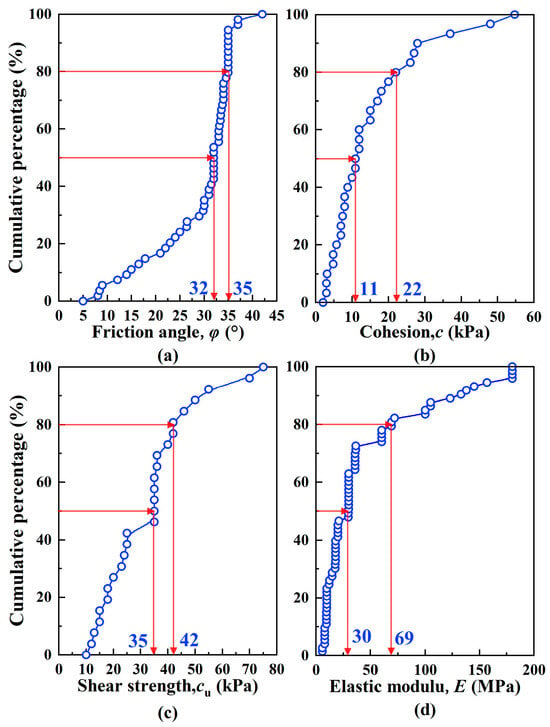
Figure 2.
Cumulative percentage of soil strength parameters from field tests in the database (a). Friction angle, φ (°), (b) cohesion, c (kPa), (c) shear strength, cu (kPa), (d) elastic modulus, E (MPa).
Figure 3 delineates the nonlinear correlation between lateral soil displacement (y) and mobilized soil resistance (p). Soil pressure on piles in clay typically ranged from 55 to 120 kN/m, whereas sand deposits demonstrated enhanced lateral resistance (215–412 kN/m) attributable to particulate interlocking and dilatant behavior.
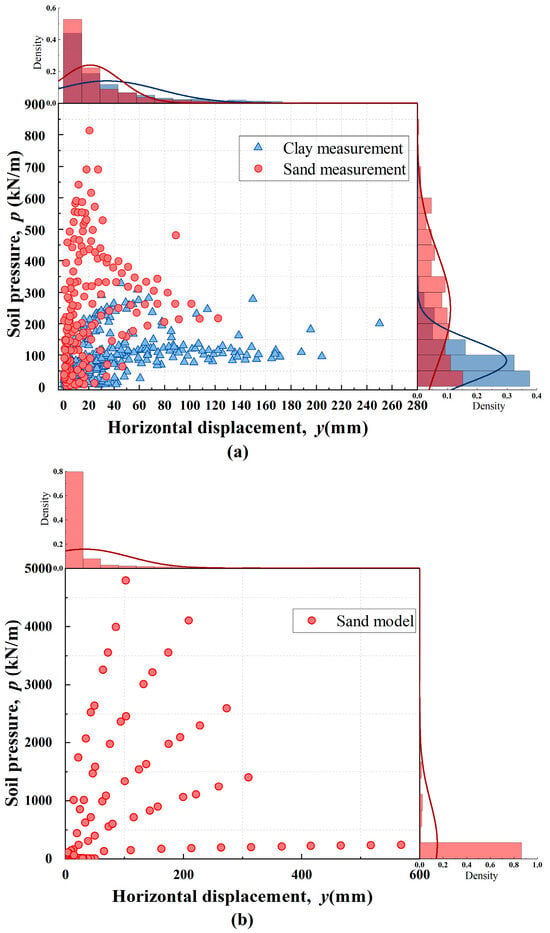
Figure 3.
Nonlinear correlation between horizontal displacement and soil pressure. (a) Field measurement results for clay and sand, (b) model test results for sand.
Field tests revealed significant discrepancies in horizontal displacement magnitudes between clay- and sand-embedded piles. The clay-pile systems exhibited maximum displacements up to 255 mm, contrasting sharply with the sand systems’ 122 mm maximum. The model test exhibited considerable scatter, with maximum displacements reaching 500 mm; however, 80% of the values were below 35 mm. This divergence underscores limitations in model testing: while capturing general load-displacement trends, scaled tests inadequately replicate in situ stress redistribution processes and strain localization patterns, particularly under large deformation regimes.
The database reveals geometric scaling characteristics between prototype and model piles. Prototype monopile lengths (L) generally exceeded 50 m, with maximum values reaching 105.4 m, whereas model piles exhibited significantly shorter dimensions ranging from 0.41 to 12.0 m. Diameter (D) distributions show marked divergence: prototype piles cluster in the 1.0–2.4 m range (80% within 1.8–2 m), while model diameters span three orders of magnitude (D: 0.032–2 m). Slenderness ratios (L/D) predominantly occupy 20–50 across both groups, satisfying prototype and model piles geometric proportional control criteria [].
As illustrated in Figure 4a, normalized horizontal displacement (y/L) exhibits inverse proportionality to relative depth (l/L) in both clay and sand. Thickness (t) of field-measured piles ranged from 16 to 30 mm, with a predominance of 30 mm, while model piles featured substantially thinner walls of only 1.2–7 mm. Notably, geometric parameter covariation emerges: increasing L correlates with proportional D and t enhancements, reflecting design optimization for structural stability and bearing capacity across varying embedment depths.
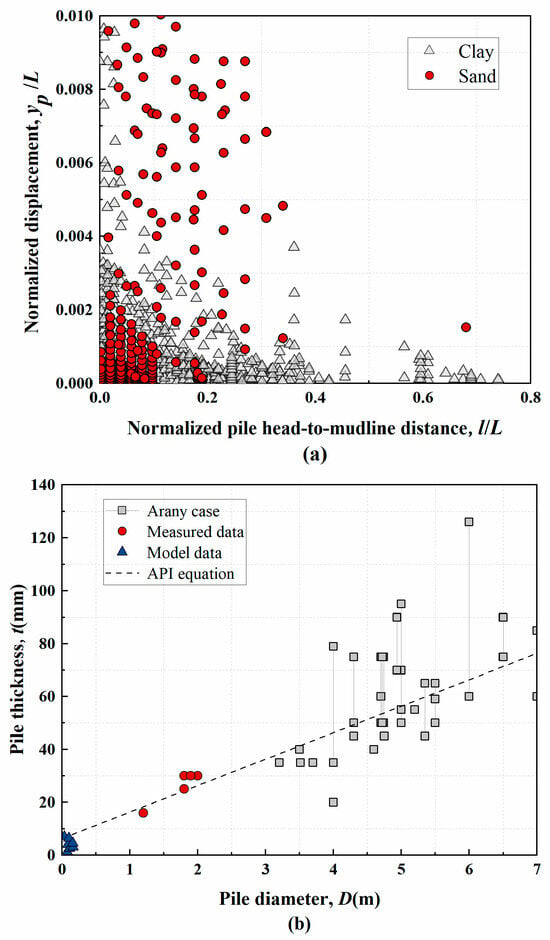
Figure 4.
The design parameters of the piles in the database. (a) Normalized displacement versus normalized pile head-to-mudline distance for clay and sand, (b) pile thickness versus pile diameter.
To satisfy the installation requirements of steel pipe piles and prevent local buckling when the pile reaches its yield strength, the thickness needs to comply with the following criterion []:
Figure 4b illustrates the relationship between thickness and diameter for piles in the database, compared with data from other case studies []. The straight line in the figure represents the minimum thickness value recommended by the API specification. A comparative analysis reveals that most field-tested piles in the database adhered to this standard, whereas the model test piles exhibited only basic compliance.
3. Neural Network Modeling of Pile–Soil Interaction
3.1. Artificial Neural Networks
Artificial neural networks (ANNs) are biologically inspired computational frameworks designed to emulate the information processing mechanisms of biological neural systems. As depicted in Figure 5, a standard ANN architecture consists of three hierarchical layers:
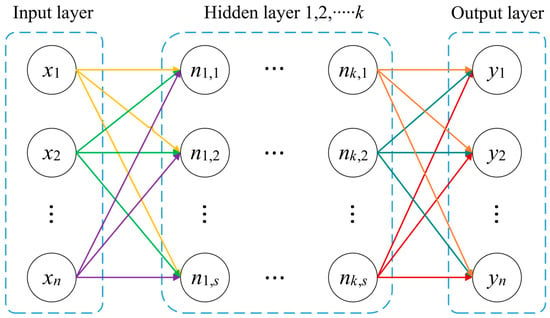
Figure 5.
Neural network architecture.
(i). Input Layer: Receives normalized geotechnical parameters (e.g., pile diameter D, soil elastic modulus E).
(ii). Hidden Layer: Extracts nonlinear relationships through weighted transformations and activation functions.
(iii). Predicts target variables (e.g., pile head displacement, soil reaction forces).
The performance of the ANN depends on the number of layers and neurons. Increasing neurons or adjusting weights reduces the mean squared error (MSE).
3.2. Architecture Design & Workflow
3.2.1. Data Preprocessing
Input–output parameters are normalized to the interval [0, 1] to mitigate numerical instability caused by disparate units (e.g., MPa vs. mm):
where is the normalized value; x is the raw data, and or denote the maximum or minimum values in the dataset.
3.2.2. Topology Structure
The hidden layer dimensionality is determined via Kolmogorov’s superposition theorem [], which prescribes a theoretical upper bound for the number of hidden nodes (m) as:
where n corresponds to the input dimension. This configuration balances model complexity and generalization capacity.
Equation (3) establishes the theoretical upper bound for nodes in the hidden layer. To systematically evaluate optimal network architecture, we conducted a parametric study by training networks with incrementally increasing hidden layer complexity (3, 5, 7, 9, 11, and 13 nodes) and assessed their performance against established metrics. Figure 6 plots the coefficient of determination (R2) across training, validation, and test datasets. Increasing node count initially enhances model performance, as evidenced by rising R2 values. However, beyond 5 nodes, R2 exhibits pronounced fluctuations across all datasets. Networks with more than 9 nodes show a declining R2 trend in training and test datasets, indicative of overfitting. This suggests that in geotechnical modeling, a moderate number of nodes (5–7 nodes) optimizes generalization capability, while excessive complexity degrades validation/test accuracy.
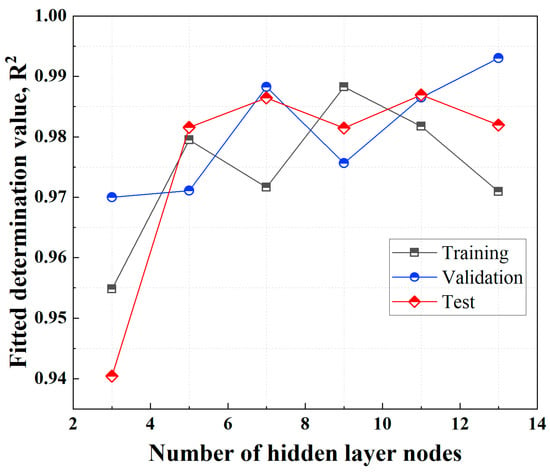
Figure 6.
Effect of hidden layer node number on model performance (R2) for training, validation and test datasets.
3.2.3. Propagation Mechanism & Training Algorithm
For an input vector x = [x1, x2,…, xn]T, the pre-activation (zk) and activation (ak) of the k-th hidden neuron are computed as:
where wk,p,t and bk,t denote the weight matrix and bias vector of the layer, respectively. f(x) represents activation functions (logistic) used to convey interlayer information.
The Levenberg–Marquardt (LM) optimization algorithm is employed for network training due to its hybrid mechanism that synergistically integrates the robustness of gradient descent in shallow regions of the error surface with the quadratic convergence properties of the Gauss–Newton method near minima. The weight update rule is formulated as:
where is the Jacobian matrix of partial derivatives, μ is a damping factor, and e is the residual vector.
3.2.4. Learning Rate & Iterations
The learning rate (η) regulates the step magnitude in gradient-based optimization, critically balancing convergence stability and rate. Elevated η values (e.g., η > 0.1) accelerate convergence yet risk overshooting minima or inducing oscillatory behavior, whereas diminished values (η < 0.001) prioritize stability at the cost of computational inefficiency. This study adopts η = 0.01, a heuristically calibrated value within the empirically effective range η ∈ [0.001, 0.1] for geotechnical systems [,,].
Concurrently, the maximum iteration threshold (Nmax = 1000) safeguards against overfitting by constraining parametric updates, with training termination triggered upon either reaching Nmax or validation loss plateau ( < 10−5 sustained over 50 epochs).
3.2.5. Validation and Regularization
To prevent overfitting, a 70-15-15 data partitioning (training-validation-testing) is implemented, coupled with Bayesian regularization to penalize excessive weight magnitudes:
where α and β are hyperparameters optimized via cross-validation.
4. Results
4.1. Predictions of p-y Curves
A critical consideration lies in the selection of input parameters for the neural network model. While using all parameters from the database as inputs may theoretically maximize data utilization, it introduces computational complexity and risks overfitting due to redundant or low-sensitivity variables. Thus, the selection of which influencing factors to incorporate as input parameters is a task that requires careful engineering judgment. Fortunately, based on the physico-mechanical properties of clay and sand foundations and in conjunction with prior research [,,], the primary influencing factors to be used as input parameters can be identified.
For the clay model, the selected inputs were pile diameter (D), length (L), depth (d), ultimate resistance (pu), undrained shear strength (cu), and lateral displacement (y). Similarly, the sand model incorporates D, L, d, internal friction angle (φ), soil unit weight (γ), and y as inputs, with soil pressure (p) as the output. The architecture of the clay p-y curve neural network is illustrated in Figure 7, while detailed structural hyperparameters for both models are tabulated in Table 2.
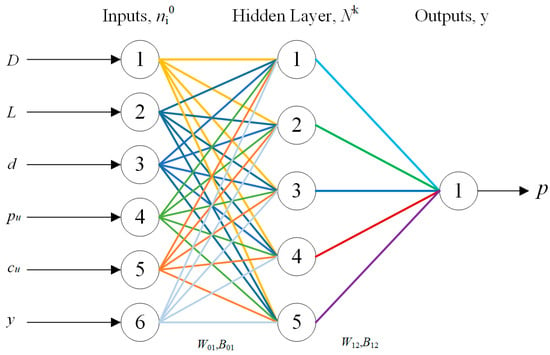
Figure 7.
The ANN model for the p-y curve of clay.

Table 2.
Neural network model structure parameters and predictive regression values.
It is also crucial to highlight another issue: the potential existence of size effects means that the results of model tests cannot fully replace those of field tests. Therefore, the data from model tests and field tests need to be separately employed to establish predictive models (primarily focused on sand). For ease of description in subsequent discussions, the predictive results from model tests and field tests are combined, and the use of ratios can effectively characterize these predictive outcomes. This will be elaborated in later sections.
The hidden layer neuron outputs are computed via the activation function as:
where W01 (5 × 6 weight matrix) and B01 (5 × 1 bias vector) govern the input-to-hidden layer transformations.
The output layer is expressed as:
where and denote the normalized bounds of measured input parameters (e.g., D, L, d, pu, cu, φ, γ, y) with subscript m indicating experimental measurements. W12 and B12 represent the hidden-to-output layer weight matrix and bias vector, respectively.
The squared error () is calculated by comparing the observed values with their corresponding predicted values generated by the model.
By iterating over all samples in the dataset and aggregating these squared differences, the mean squared error (MSE) is obtained as a quantitative measure of the model’s performance.
The MSE serves as the objective function in the training of the artificial neural network. Minimizing the MSE through appropriate optimization algorithms allows for the determination of the optimal weights and biases (W01, W12, B01, B12).
The optimized parameters of the neural network for clay p-y curves are mathematically expressed as follows:
Taking this model as an example, the simplified expression is as follows:
where subscript p denotes predicted values from the neural network, contrasting with subscript m for measured data. f(x) represents the activation function.
For sand soils, the optimal weights and biases are derived as:
As illustrated in Figure 8, the neural network demonstrates outstanding predictive performance. For the clay p-y curve model, both the training and testing phases exhibited strong convergence (R2 ≥ 0.95). The neural network model for sand p-y curves demonstrated robust correlation with experimental data, achieving a test set R2 = 0.96. This statistical validated confirms the model’s high predictive accuracy and reliability for both sandy soils and clayey soils.
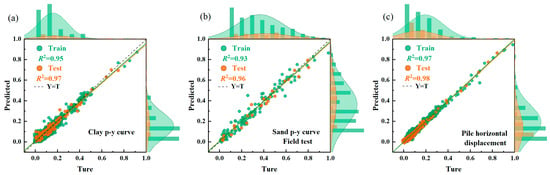
Figure 8.
(a) Regression performance for Clay p-y curve prediction, (b) Regression performance for Sand p-y curve prediction, (c) Regression performance for Pile horizontal displacement prediction.
4.2. Pile Horizontal Displacement Prediction
The data were randomly extracted from the pile horizontal displacement database to construct an ANN-based model for predicting pile horizontal displacement. The structural parameters of the model are presented in Table 2. The input parameters include pile horizontal load (F), pile length (L), pile diameter (D), penetration depth (d), distance from the test point to the pile top (l), soil elastic modulus (E), internal friction angle (φ), and cohesion (c), with the pile horizontal displacement serving as the output parameter. Given the strong correlation between t and D as well as L, and considering that the research focus lies on the global horizontal displacement of the pile rather than its internal deformation characteristics, the input parameters of the model excluded the pile t.
For the constructed ANN model of pile horizontal displacement, the optimal values of parameters W01, W12, and B01, B12 are determined.
The training and testing performance metrics of the model are systematically presented in Table 2 and Figure 8. The ANN framework demonstrated robust convergence characteristics, achieving exceptional agreement between predicted and observed displacements in the training dataset (R2 =0.97). During validation and testing phases, the model maintained superior predictive capability with R2 > 0.96 for both phases, confirming its reliability in horizontal displacement prediction across diverse geotechnical scenarios.
5. Discussion
5.1. Model Performance
To rigorously evaluate the performance of the neural network model, the model factor (λ) is used to evaluate the accuracy of the model:
where Pm and ym denote measured soil resistance and displacement, respectively, while Pp and yp represent predicted soil resistance and displacement, respectively.
Figure 9 presents the predicted p-y curves obtained from the neural network model and the API specification. It can be observed that the predictions from the neural network model closely align with the measured values along the 1:1 diagonal line, demonstrating a high degree of consistency. Only when the soil resistance is relatively low (less than 50 kN/m) do the data points exhibit some dispersion. In contrast, the values calculated using the API specification show significant deviations from the actual measurements, underestimating clay resistance by approximately 50% and overestimating sand resistance by about 30%, with a greater degree of data scatter.
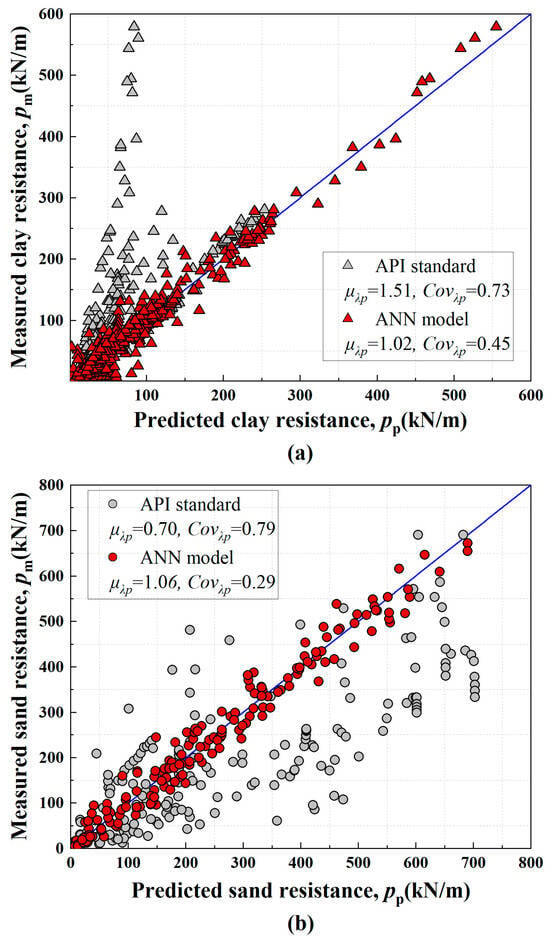
Figure 9.
Comparison of predicted and measured soil resistance for clay and sand using the ANN model and API standard. (a) Clay resistance, (b) sand resistance.
For the clay p-y curves, the model factor λ of the neural network model has a mean value = 1.02 and a coefficient of variation COVλ = 0.45. Compared to the clay p-y curves predicted by the API specification (μλ = 1.51, COVλ = 0.73), the mean model factor of the neural network model is closer to 1. Similarly, for the sand p-y curves, the neural network model yields a mean model factor μλ = 1.06 with a coefficient of variation COVλ = 0.29. In comparison, the API specification predicts a mean model factor of μλ =0.70 and COVλ =0.79 for sand p-y curves.
These results demonstrate that the neural network model provides more accurate predictions, with average errors ranging from only 2% to 6%. According to the model accuracy classification [], the variability in the prediction accuracy of the neural network model is classified as moderate to low. Overall, the soil resistance values computed by the neural network model, utilizing the selected input parameters and hidden nodes, effectively reflect the actual soil resistance behavior.
The measured data from field tests on the horizontal bearing capacity of offshore wind turbine pile foundations were input into the trained neural network model to obtain predicted values of horizontal displacement. These predicted values were then compared with the actual measured horizontal displacements, as illustrated in Figure 10. Observing the distribution of the data points, it is evident that the predictions from the neural network model are predominantly concentrated near the line along the 1:1 reference line, indicating low data dispersion. Specifically, the mean value of the model factor is μλ = 0.9, with a coefficient of variation COVλ = 0.26.
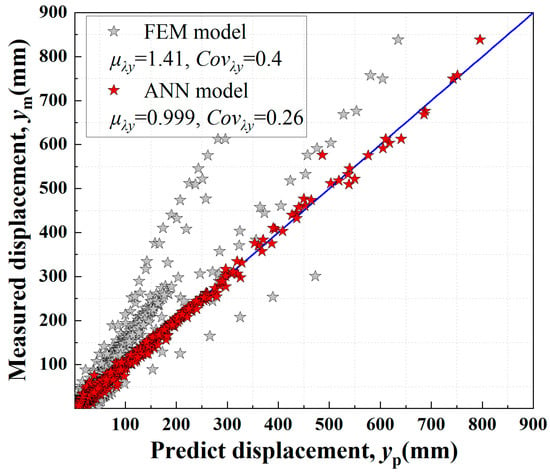
Figure 10.
Comparison of horizontal displacement predictions from ANN model and FEM model with measured data.
To achieve a more rigorous comparative analysis, a finite element model (FEM) was utilized to predict the horizontal displacement of offshore wind turbine monopile foundations. For conciseness, the detailed description of the FEM is omitted here; the specific methodologies and parameters can be found in the work of []. The FEM results exhibited considerable dispersion and lower predictive accuracy, significantly underestimating the horizontal displacement around the pile. Specifically, the average value of the μλ was 1.41 with COVλ = 0.4. The deviation of this result is closely related to the establishment of the model and the selection of data, and it may be attributed to issues such as the mixed use of model data and on-site measured data. This clearly demonstrates that the neural network model offers significant advantages and higher accuracy in predicting the horizontal displacement of offshore monopile foundations.
5.2. Parameter Sensitivity
Table 3 presents the Spearman rank correlation coefficients between the model factor λ and each input parameter at a significance level of 0.05. For the clay p-y curve model, λ exhibited positive correlations with Pu, d/L, y/D, and D/L; however, these correlations were relatively modest, with coefficients (ρ) not exceeding 0.20. Conversely, λ demonstrated slight negative correlations with D and L.

Table 3.
Spearman’s rank correlation test results.
For the sand p-y curve model, λ displayed more pronounced positive correlations with y/D and D/L, with ρ values of 0.191 and 0.201, respectively. Negative correlations were observed with φ, d/L, y/L, D, and L. Notably, the correlation coefficients for D and L fell below −0.2, indicating that pile diameter and pile length significantly influence the sand p-y curve behavior. From an engineering standpoint, the strong negative correlation with pile diameter (D) implies that the accuracy of the sand p-y curve model is particularly sensitive to this parameter. This underscores the importance of precise pile diameter specification and manufacturing control in design and construction, as variations can lead to considerable deviations in the predicted soil–pile interaction. Similarly, the significant influence of pile length (L) highlights its critical role in the overall response, demanding careful optimization during the design process.
In the pile horizontal displacement model, F, l/L, and D exhibited positive correlations with λ. Negative correlations were identified with φ, E, t/D, D/L, and L. Particularly, parameters E and L had ρ values less than −0.2, suggesting that both the design parameters of the pile and the stiffness of the soil are significant factors affecting its horizontal displacement. The engineering significance of the strong negative correlation with soil modulus (E) is substantial; it emphasizes that accurate determination of soil stiffness through thorough geotechnical investigation is paramount for reliable predictions of horizontal pile displacement. Even minor uncertainties or variations in E can disproportionately affect the model’s output, potentially impacting the safety and serviceability of the pile foundation. Likewise, the pile length (L), a fundamental design choice, also demonstrates a strong influence, reinforcing the need for its careful selection based on site conditions and load demands.
5.3. Probability Distribution
In reliability-based geotechnical design, the probability distribution of the λ, in addition to its μλ and COVλ, constitutes a critical consideration. Kolmogorov–Smirnov (K–S) normality tests were performed on both the λ and its natural logarithm ln(λ), revealing that the model factors generated by the neural network deviated significantly from normal or log-normal distributions. Further goodness-of-fit tests, including the corrected K-S test and Anderson–Darling (A-D) test, demonstrated that the model factor also failed to conform to Weibull, exponential, or gamma distributions.
To characterize the distribution pattern of the λ, a second-order Gaussian function was employed; this approach proves particularly effective in capturing the highly nonlinear distribution characteristics of model factors []. Figure 11 illustrates the fitting results, while Table 4 details the mathematical expression of the second-order Gaussian function and its optimized parameters. The coefficient of determination values approaching unity across all three investigated scenarios confirm the rationality and efficacy of utilizing Gaussian functions to model the distribution trends of the model factor λ.
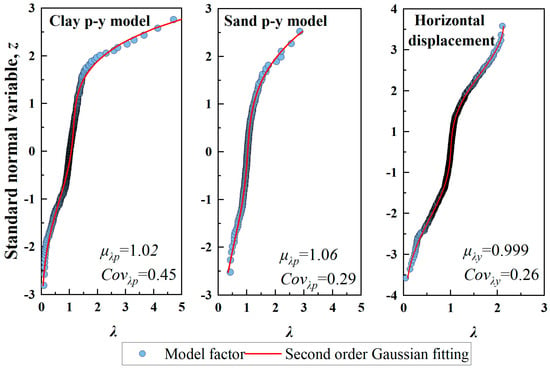
Figure 11.
Probability distribution of ANN model factors.

Table 4.
Gaussian fitting expression and parameters.
To provide a more intuitive comparison of the accuracy among different predictive models, the μλ and the COVλ for each model are summarized in Table 5. A comparative analysis reveals that the artificial neural network (ANN) model exhibits significant advantages in predictive accuracy over the API specification and the finite element model. Specifically, the average model factor of the ANN model is significantly closer to 1, and the relatively low coefficient of variation further validates the remarkable stability and reliability of the ANN model during the prediction process. In stark contrast, the FEM and the API approach, in practical applications, highly rely on precise parameter settings and simplified assumptions. When faced with complex and variable actual working conditions, it is difficult to comprehensively capture the subtle differences in the real environment, resulting in a significant reduction in the stability and reliability of their prediction results.

Table 5.
The degree of dispersion and accuracy of the prediction methods of API, ANN, and FEM.
5.4. Case Application
To further investigate the neural network model’s performance, a case study was conducted using a monopile foundation from [] work. It is critical to emphasize that the monopile analyzed here was excluded from the dataset used for prior model development and validation. The steel pipe pile has a length of 71.5 m, diameter of 2.0 m, and wall thickness of 30 mm. The surrounding soil strata consist of fine sand, silty sand, and clayey silt, with geotechnical properties detailed in Table 6.

Table 6.
Design parameters for the example monopile.
Lateral displacement predictions along the pile depth were generated using both FEM and ANN models. As demonstrated in Figure 12, under five distinct loading scenarios, the FEM model consistently underestimated displacements, particularly in the supralittoral zone (above the mudline). This systematic bias correlates with the model accuracy evaluation outcomes, where the μλ > 1 (refer to Figure 10). Such underestimation could lead to non-conservative design outcomes in engineering practice, potentially increasing operational risks for monopile foundations. Conversely, the ANN model predictions exhibit significantly better alignment with field monitoring data.
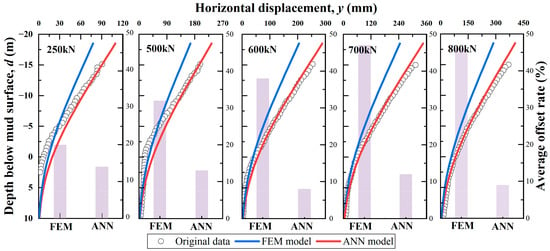
Figure 12.
Predicted vs. measured horizontal displacement (ANN and FEM).
Progressive refinement of the ANN model is achievable through continuous accumulation of field measurements, involving both architectural optimization (e.g., hidden layer configuration) and parameter calibration (e.g., activation function tuning). This iterative process enhances predictive capability while reducing output variance, thereby enabling more robust soil–pile interaction analysis for offshore foundation design. The ANN’s superior predictive accuracy compared to conventional FEM methodologies underscores this study’s contribution to advancing precision in geotechnical predictive modeling.
6. Conclusions
This study focuses on offshore wind turbine monopile foundations. By collecting data from literature sources, we established a marine pile–soil interaction database comprising 1852 datasets. Based on this database, predictive neural network models were developed for pile displacement and soil resistance around the pile, using pile design parameters, displacements, and soil strength parameters as input variables. The accuracy of these models was quantitatively evaluated, and their validity was verified. The main conclusions of this study are as follows:
(i) Artificial neural networks are established as p-y curve models for marine pile foundations in both clay and sand, as well as a predictive model for pile horizontal displacement. The developed pile–soil interaction ANN models exhibit nearly unbiased average accuracy, with an average error of less than 6%.
(ii) The cumulative distribution function of the model factor in the established neural network models can be approximated using a second-order Gaussian function. This simple expression can be directly applied to the reliability-based design of marine pile foundations.
(iii) Through analysis of practical cases and by comparing the finite element method with the neural network models developed in this study for predicting pile horizontal displacement, the superiority of the proposed ANN models in terms of computational accuracy and efficiency is highlighted.
Building upon the established model, subsequent research should prioritize the development of real-time data assimilation mechanisms for digital twin systems to achieve synchronized integration of monitoring data and numerical simulations, coupled with systematic expansion of engineering databases encompassing diverse marine geological conditions. The implementation of hybrid modeling frameworks that synergize 3D convolutional neural networks with physical principles is expected to significantly enhance predictive capabilities in pile–soil interaction analysis.
Author Contributions
Conceptualization, P.L.; methodology, P.L.; validation, K.L., X.Y. (Xiangwei Yu), T.L. and X.Y. (Xun Yuan); formal analysis, K.L. and X.Y. (Xiangwei Yu); data curation, H.L.; writing—original draft preparation, P.L. and K.L.; writing—review and editing, P.L.; supervision, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 52008408) and Natural Science Foundation of Guangdong Province (Grant Nos. 2021A1515012088). This financial support is gratefully acknowledged.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Abbreviations
The following abbreviations are used in this manuscript:
| ak | Activation of the k-th hidden neuron |
| A-D | Anderson–Darling |
| ANN | Artificial neural network |
| API | American Petroleum Institute |
| B01 | 5 × 1 bias vector |
| B12 | Hidden-to-output layer bias vector |
| bk,t | Bias vector of the layer |
| c | Cohesion |
| cu | Shear strength |
| COVλ | Coefficient of variation |
| d | Depth |
| D | Outer diameter |
| e | Residual vector |
| E | Elastic modulus |
| f(x) | Activation functions (logistic) |
| FEM | Finite element method |
| F | Horizontal force applied at the pile head |
| i | Total number of samples |
| Identity matrix | |
| Jacobian matrix of partial derivatives | |
| The transpose of the Jacobian matrix | |
| K-S | Kolmogorov–Smirnov |
| l | Distance from the test point to the pile top |
| L | Pile length |
| Regularized loss function | |
| LM | Levenberg–Marquardt |
| m | Number of hidden nodes |
| MSE | Mean squared error |
| n | Input dimension |
| The p-th input to the k-th neuron | |
| pu | Ultimate resistance |
| Pm | Measured soil resistance |
| Pp | Predicted soil resistance |
| Nmax | Maximum iteration threshold |
| Input vector | |
| Output vector of the first hidden layer | |
| p | Mobilized soil resistance |
| R2 | Coefficient of determination |
| SVM | Support vector machines |
| t | Wall thickness |
| wk,p,t | Weight matrix of the layer |
| W01 | 5 × 6 weight matrix |
| W12 | Hidden-to-output layer weight matrix |
| x | Raw data |
| Normalized value | |
| Maximum value | |
| Minimum value | |
| y | Lateral soil displacement |
| ym | Measured displacement |
| yp | Predicted displacement |
| Normalized bound of measured input parameters | |
| Normalized bound of measured input parameters | |
| Predicted value | |
| Actual value | |
| zk | Pre-activation of the k-th hidden neuron |
| Change in validation loss | |
| Weight update vector | |
| α | Hyperparameter optimized via cross-validation. |
| β | Hyperparameter optimized via cross-validation |
| φ | Internal friction angle |
| μ | Damping factor |
| η | Learning rate |
| γ | Soil’s unit weight |
| λ | Model factorMean value |
| μλ | |
| Squared error | |
| Mean squared error | |
| Regularization penalty term |
References
- IEA. Offshore Wind Outlook 2019; IEA: Paris, France, 2019. [Google Scholar]
- Hjelmeland, M.; Nøland, J.K. Correlation Challenges for North Sea Offshore Wind Power: A Norwegian Case Study. Sci. Rep. 2023, 13, 18670. [Google Scholar] [CrossRef] [PubMed]
- Santhakumar, S.; Meerman, H.; Faaij, A.; Martinez Gordon, R.; Florentina Gusatu, L. The Future Role of Offshore Renewable Energy Technologies in the North Sea Energy System. Energy Convers. Manag. 2024, 315, 118775. [Google Scholar] [CrossRef]
- Ponder, A.N.; Avdic, D.B. Offshore Wind and Power-to-Hydrogen in the Baltic Sea Region; BOWE2H Strategic Roadmap; IKEM: Berlin, Germany, 2024. [Google Scholar]
- Ren, L.; Wang, Y.; Zhang, W.; Yang, H.; Wang, H.; Wei, J.; Mateos, L.M.F. Characterizing Wind Fields at Multiple Temporal Scales: A Case Study of the Adjacent Sea Area of Guangdong–Hong Kong–Macao Greater Bay Area. Energy Rep. 2022, 8, 212–223. [Google Scholar] [CrossRef]
- Sun, Y. Experimental and Numerical Studies on a Laterally Loaded Monopile Foundation of Offshore Wind Turbine. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2016. [Google Scholar]
- Zhang, J.; Wang, H. Development of Offshore Wind Power and Foundation Technology for Offshore Wind Turbines in China. Ocean Eng. 2022, 266, 113256. [Google Scholar] [CrossRef]
- Buljac, A.; Kozmar, H.; Yang, W.; Kareem, A. Concurrent Wind, Wave and Current Loads on a Monopile-Supported Offshore Wind Turbine. Eng. Struct. 2022, 255, 113950. [Google Scholar] [CrossRef]
- Yang, Y.F.; Zheng, Y.Q.; Ge, H.; Wang, C.Z. Nonlinear Interactions between Solitary Waves and Structures in a Steady Current. Ocean Eng. 2023, 274, 113920. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Guo, Z.; Zhang, J.; Lü, Q. Robust Design of Monopiles for Offshore Wind Turbines Considering Uncertainties in Dynamic Loads and Soil Parameters. Ocean Eng. 2022, 266, 112822. [Google Scholar] [CrossRef]
- Qi, W.; Gao, F. Equilibrium Scour Depth at Offshore Monopile Foundation in Combined Waves and Current. Sci. China Technol. Sci. 2014, 57, 1030–1039. [Google Scholar] [CrossRef]
- Gupta, B.K. Soil-Structure Interaction Analysis of Monopile Foundations Supporting Offshore Wind Turbines. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2018. [Google Scholar]
- Poulos, H.G. Pile Behaviour—Theory and Application. Géotechnique 1989, 39, 365–415. [Google Scholar] [CrossRef]
- Hansen, N.M. Interaction Between Seabed Soil and Offshore Wind Turbine Foundations; DCAMM Special Report; DTU Mechanical Engineering: Lyngby, Denmark, 2012; ISBN 9788790416805. [Google Scholar]
- Zhu, B.; Wen, K.; Li, T.; Wang, L.; Kong, D. Experimental Study on Lateral Pile–Soil Interaction of Offshore Tetrapod Piled Jacket Foundations in Sand. Can. Geotech. J. 2019, 56, 1680–1689. [Google Scholar] [CrossRef]
- Sheil, B.B.; McCabe, B.A. An Analytical Approach for the Prediction of Single Pile and Pile Group Behaviour in Clay. Comput. Geotech. 2016, 75, 145–158. [Google Scholar] [CrossRef]
- Shi, S.; Zhai, E.; Xu, C.; Iqbal, K.; Sun, Y.; Wang, S. Influence of Pile-Soil Interaction on Dynamic Properties and Response of Offshore Wind Turbine with Monopile Foundation in Sand Site. Appl. Ocean Res. 2022, 126, 103279. [Google Scholar] [CrossRef]
- Tang, H.; Yue, M.; Yan, Y.; Li, Z.; Li, C.; Niu, K. Influence of Soil–Structure Interaction Models on the Dynamic Responses of An Offshore Wind Turbine Under Environmental Loads. China Ocean Eng. 2023, 37, 218–231. [Google Scholar] [CrossRef]
- Chow, Y.K.; Kencana, E.Y.; Leung, C.F.; Purwana, O.A. Spudcan-Pile Interaction in Thick Soft Clay and Soft Clay Overlying Sand: A Simplified Numerical Solution. Appl. Ocean Res. 2021, 112, 102684. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, Y.; Xiong, Y.; Xu, C.; Guo, Y.; Wang, C.; Fang, T. Analytical Solution for Displacement-Dependent Active Earth Pressure Considering the Stiffness of Cantilever Retaining Structure in Cohesionless Soil. Comput. Geotech. 2024, 170, 106258. [Google Scholar] [CrossRef]
- Randolph, M.F. The Response of Flexible Piles to Lateral Loading. Géotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Heidari, M.; Hesham El Naggar, M. Analytical Approach for Seismic Performance of Extended Pile-Shafts. J. Bridge Eng. 2018, 23, 04018069. [Google Scholar] [CrossRef]
- American Petroleum Institute. Planning, Designing, and Constructing Fixed Offshore Platforms: Working Stress Design; API: Washington, DC, USA, 2020. [Google Scholar]
- DET NORSKE VERITAS DNVGL-ST-N001; Marine Operations and Marine Warranty; DNV GL: Oslo, Norway, 2016.
- MOT China Communications Press. JTS 167-2018: Code for Design of Pile Foundations in Port and Waterway Engineering; China Communications Press: Beijing, China, 2022. [Google Scholar]
- Liu, P.; Jiang, C. A Modified P-y Curve Model for Offshore Piles near Sandy Slopes Considering the Soil-Pile-Slope Deformation Mechanism. Mar. Struct. 2024, 98, 103675. [Google Scholar] [CrossRef]
- Stevens, J.B.; Audibert, J.M.E. Re-Examination Of P-Y Curve Formulations. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 1979. [Google Scholar]
- Wang, H.; Wang, L.Z.; Hong, Y.; He, B.; Zhu, R.H. Quantifying the Influence of Pile Diameter on the Load Transfer Curves of Laterally Loaded Monopile in Sand. Appl. Ocean Res. 2020, 101, 102196. [Google Scholar] [CrossRef]
- White, D.J.; Doherty, J.P.; Guevara, M.; Watson, P.G. A Cyclic P-y Model for the Whole-Life Response of Piles in Soft Clay. Comput. Geotech. 2022, 141, 104519. [Google Scholar] [CrossRef]
- Lin, P.; Zhong, X.; Guo, C.; Yang, F.; Wang, F. Statistical Evaluation of Jacking-Installation Resistance Models for Suction Foundation of Offshore Wind Turbines in Sands. Ocean Eng. 2023, 279, 114605. [Google Scholar] [CrossRef]
- Yeter, B.; Garbatov, Y.; Guedes Soares, C. Uncertainty Analysis of Soil-Pile Interactions of Monopile Offshore Wind Turbine Support Structures. Appl. Ocean Res. 2019, 82, 74–88. [Google Scholar] [CrossRef]
- Byrne, B.W.; Houlsby, G.T.; Burd, H.J.; Gavin, K.G.; Igoe, D.J.P.; Jardine, R.J.; Martin, C.M.; McAdam, R.A.; Potts, D.M.; Taborda, D.M.G.; et al. PISA Design Model for Monopiles for Offshore Wind Turbines: Application to a Stiff Glacial Clay Till. Géotechnique 2020, 70, 1030–1047. [Google Scholar] [CrossRef]
- Haiderali, A.; Madabhushi, G. Three-Dimensional Finite Element Modelling of Monopiles for Offshore Wind Turbines. In Proceedings of the Advances in Civil, Environmental, and Materials Research, Seoul, Republic of Korea, 26–29 August 2012. [Google Scholar]
- McAdam, R.A.; Byrne, B.W.; Houlsby, G.T.; Beuckelaers, W.J.A.P.; Burd, H.J.; Gavin, K.G.; Igoe, D.J.P.; Jardine, R.J.; Martin, C.M.; Muir Wood, A.; et al. Monotonic Laterally Loaded Pile Testing in a Dense Marine Sand at Dunkirk. Géotechnique 2020, 70, 986–998. [Google Scholar] [CrossRef]
- Xiao-ling, Z.; Rui, Z.; Yan, H. Study on P-y Curve of Large Diameter Pile under Long-Term Cyclic Loading. Appl. Ocean Res. 2023, 140, 103736. [Google Scholar] [CrossRef]
- Sheil, B.; Finnegan, W. Numerical Simulations of Wave–Structure–Soil Interaction of Offshore Monopiles. Int. J. Geomech. 2017, 17, 04016024. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.; Bürg, M.; Andreykiv, A.; Lim, L. Beyond the Finite Element Method in Geotechnical Analysis; Bundesanstalt für Wasserbau: Karlsruhe, Germany, 2015; Volume 98, pp. 91–102. [Google Scholar]
- Lin, P.; Ding, M.; Liu, H.; Liu, Y.; Wang, K. Statistical Accuracy of Finite Element Method in Predicting Horizontal Displacement of Monopiles for Offshore Wind Turbines. Mar. Struct. 2024, 97, 103641. [Google Scholar] [CrossRef]
- Murphy, G.; Igoe, D.; Doherty, P.; Gavin, K. 3D FEM Approach for Laterally Loaded Monopile Design. Comput. Geotech. 2018, 100, 76–83. [Google Scholar] [CrossRef]
- Wang, S.; Han, B.; Jiang, J.; Telyatnikova, N. Machine Learning and FEM-Driven Analysis and Optimization of Deep Foundation Pits in Coastal Area: A Case Study in Fuzhou Soft Ground. Undergr. Space 2025, 22, 55–76. [Google Scholar] [CrossRef]
- Baghbani, A.; Choudhury, T.; Costa, S.; Reiner, J. Application of Artificial Intelligence in Geotechnical Engineering: A State-of-the-Art Review. Earth-Sci. Rev. 2022, 228, 103991. [Google Scholar] [CrossRef]
- Lin, P.; Zhao, C.; Zhang, W.; Xue, Y. Machine Learning Methods and Applications in Geotechnical Engineering; China Architecture & Building Press: Beijing, China, 2023. [Google Scholar]
- Vahab, M.; Shahbodagh, B.; Haghighat, E.; Khalili, N. Application of Physics-Informed Neural Networks for Forward and Inverse Analysis of Pile–Soil Interaction. Int. J. Solids Struct. 2023, 277–278, 112319. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of Deep Learning Algorithms in Geotechnical Engineering: A Short Critical Review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, S.; Chapman, D.; Meng, K. Dynamic Impedance of a Floating Pile Embedded in Poro-Visco-Elastic Soils Subjected to Vertical Harmonic Loads. Geomech. Eng. 2018, 15, 793–803. [Google Scholar] [CrossRef]
- Dong, Y.; Cui, L.; Zhang, X. Multiple-GPU Parallelization of Three-dimensional Material Point Method Based on Single-root Complex. Int. J. Numer. Methods Eng. 2022, 123, 1481–1504. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, S.; Yang, G.; Li, X. Vertical Vibration of a Floating Pile in a Saturated Viscoelastic Soil Layer Overlaying Bedrock. J. Cent. South Univ. 2016, 23, 220–232. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, W.; Li, Y.; Wen, L.; Sun, X. ResGRU: A Deep Learning Approach for Settlement Prediction in CFRD Based on the Spatiotemporal Feature Fusion Method. Comput. Geotech. 2024, 173, 106518. [Google Scholar] [CrossRef]
- Wang, W.; Yan, J.; Liu, J.P. Study on p-y Models for Large-Diameter Pile Foundation Based on In-Situ Tests of Offshore Wind Power. Chin. J. Geotech. Eng. 2021, 43, 1131–1138. [Google Scholar] [CrossRef]
- Hu, Z.; Zhai, E.; Luo, L.; Yang, X. Study of P-y Curves of Large-Monopiles for Offshore Wind Power in Sand. Acta Energiae Solaris Sin. 2019, 40, 3571–3577. [Google Scholar]
- Wu, R.; Ye, J.; Luo, G.; Shen, X.; Zhang, Q. Experimental Study on the Bearing Characteristics of Steel Pipe Pile in Radial Sandbar of Jiangsu Province. Ocean Eng. 2021, 39, 121–132. [Google Scholar] [CrossRef]
- Luo, L.; Wang, Y.; Zhai, E.; Hu, Z.; Yang, X.; Li, Q. Study on P-y Curves of Monopile in Layered Soil Based on Field Test. Acta Energiae Solaris Sin. 2019, 40, 3258–3264. [Google Scholar]
- Kim, Y.; Jeong, S.; Won, J. Effect of Lateral Rigidity of Offshore Piles Using Proposed P-y Curves in Marine Clay. Mar. Georesources Geotechnol. 2009, 27, 53–77. [Google Scholar] [CrossRef]
- Zhang, Y. Study on Horizontal Load Test of Large-Diameter Steel Pipe Piles for Offshore Wind Power. Energy Environ. 2022, 175, 18–20. [Google Scholar] [CrossRef]
- Gong, W.; Huo, S.; Yang, C.; Huang, X.; Guo, C. Experimental Study on Horizontal Bearing Capacity of Large Diameter Steel Pipe Pile for Offshore Wind Farm. J. Hydraul. Eng. 2015, 46, 34–39. [Google Scholar] [CrossRef]
- Bao, J.; Su, J.; Wu, F. Field Horizontal Loading Test and P-y Curve Applicability of Large-Diameter Single Pile Foundation in Deep Soft Clay Groundsill. J. Hohai Univ. (Nat. Sci.) 2023, 51, 127–134. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, F.; Dai, G. Research on P-y Curve of Pile Foundation in Clay Based on Cpt Data. Acta Energiae Solaris Sin. 2023, 44, 172–180. [Google Scholar] [CrossRef]
- Zhu, B.; Zhu, Z.; Li, T.; Liu, J.; Liu, Y. Field Tests of Offshore Driven Piles Subjected to Lateral Monotonic and Cyclic Loads in Soft Clay. J. Waterw. Port. Coast. Ocean Eng. 2017, 143, 05017003. [Google Scholar] [CrossRef]
- Cai, W.; Ye, J. Experimental Investigation of Large Diameter Pipe Piles Under Vertical and Lateral Load in Ocean Engineering. Shanghai Land Resour. 2011, 32, 81–86. [Google Scholar] [CrossRef]
- Zhu, Z.; Gong, W.; DAI, G. Field Test Research of Horizontal Bearing Capacity of Large Diameter Steel Pipe Pile. Build. Sci. 2010, 26, 32–36. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Wu, F. Research on Horizontal Load Testing of Large-Diameter Steel Pipe Piles. Ocean Dev. Manag. 2018, 35, 9–13. [Google Scholar] [CrossRef]
- Bi, M.; Liu, D.; Wang, H. Calculation Method Study for the Horizontal Bearing Capacity of Offshore Wind Turbine Steel-Pile. South. Energy Constr. 2018, 5, 77–82. [Google Scholar] [CrossRef]
- Lao, W.; Zhou, L.; Wang, Z. Field Test and Theoretical Analysis on Flexible Large-Diameter Rock-Socketed Steel Pipe Piles Under Lateral Load. Chin. J. Rock. Mech. Eng. 2004, 23, 1770–1777. [Google Scholar] [CrossRef]
- Choo, Y.W.; Kim, D. Experimental Development of the P-y Relationship for Large-Diameter Offshore Monopiles in Sands: Centrifuge Tests. J. Geotech. Geoenviron. Eng. 2016, 142, 04015058. [Google Scholar] [CrossRef]
- Wang, T.; Wang, T. Experimental Research on Silt P-Y Curves. Rock. Soil. Mech. 2009, 30, 1343–1346. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Lv, X. Model Tests on Lateral Bearing Capacity of Single Piles Under Cyclic Load Saturated Silt. Period. Ocean Univ. China 2015, 45, 76–82. [Google Scholar] [CrossRef]
- Lin, H.; Ni, L.; Suleiman, M.T.; Raich, A. Interaction between Laterally Loaded Pile and Surrounding Soil. J. Geotech. Geoenviron. Eng. 2015, 141, 04014119. [Google Scholar] [CrossRef]
- Zhu, B.; Zhu, R.; Chen, R.; Kong, L.; Luo, J. Model Tests on Characteristics of Ocean and Offshore Elevated Piles with Large Lateral Deflection. Chin. J. Geotech. Eng. 2010, 32, 521–530. [Google Scholar]
- Wu, T.; Lu, Z.; Dou, D.; Wu, Q. Model Tests and Finite Element Analysis of Behaviors of Ocean and Offshore Elevated Piles under Lateral Load. Sci. Technol. Eng. 2013, 13, 7697–7702. [Google Scholar]
- Zhu, B.; Chen, R.-P.; Guo, J.; Kong, L.; Chen, Y. Large-Scale Modeling and Theoretical Investigation of Lateral Collisions on Elevated Piles. J. Geotech. Geoenviron. Eng. 2012, 138, 461–471. [Google Scholar] [CrossRef]
- Li, W.; Zhu, B.; Yang, M. Static Response of Monopile to Lateral Load in Overconsolidated Dense Sand. J. Geotech. Geoenviron. Eng. 2017, 143, 04017026. [Google Scholar] [CrossRef]
- Yu, J.; Zhu, J.; Kanmin, S.; Huang, M.; Leung, C.; Tan, Q. Bounding-Surface-Based p-y Model for Laterally Loaded Piles in Undrained Clay. Ocean Eng. 2020, 216, 107997. [Google Scholar] [CrossRef]
- Wood, D.M. Geotechnical Modelling; CRC Press: London, UK, 2017; ISBN 9781315273556. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Macdonald, J.; Hogan, S.J. Design of Monopiles for Offshore Wind Turbines in 10 Steps. Soil Dyn. Earthq. Eng. 2017, 92, 126–152. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the Representation of Continuous Functions of Many Variables by Superposition of Continuous Functions of One Variable and Addition. Russ. Acad. Sci. 1957, 114, 953–956. [Google Scholar]
- Hsein Juang, C.; Lu, P.C.; Chen, C.J. Predicting Geotechnical Parameters of Sands from CPT Measurements Using Neural Networks. Comput.-Aided Civ. Infrastruct. Eng. 2002, 17, 31–42. [Google Scholar] [CrossRef]
- Liu, C.; Macedo, J.; Rodríguez, A. Leveraging Physics-Informed Neural Networks in Geotechnical Earthquake Engineering: An Assessment on Seismic Site Response Analyses. Comput. Geotech. 2025, 182, 107137. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Hong, L.; Han, L.; Wang, L. Comprehensive Review of Machine Learning in Geotechnical Reliability Analysis: Algorithms, Applications and Further Challenges. Appl. Soft Comput. 2023, 136, 110066. [Google Scholar] [CrossRef]
- Anglade, E.; Aubert, J.-E.; Sellier, A.; Papon, A. Physical and Mechanical Properties of Clay–Sand Mixes to Assess the Performance of Earth Construction Materials. J. Build. Eng. 2022, 51, 104229. [Google Scholar] [CrossRef]
- Ouendi, F.; Zentar, R. Investigating the Influence of Particle Size Ranges on the Physical, Mineralogical, and Environmental Properties of Raw Marine Sediment. Constr. Build. Mater. 2023, 409, 133987. [Google Scholar] [CrossRef]
- Wan, J.-H.; Zaoui, A. Mechanical Resistance behind Fiber-Reinforced Polymer Pile: Role of Clay Minerals. Comput. Geotech. 2024, 168, 106158. [Google Scholar] [CrossRef]
- Phoon, K.-K.; Tang, C. Characterisation of Geotechnical Model Uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 101–130. [Google Scholar] [CrossRef]
- Yuan, J.; Lin, P. Reliability Analysis of Soil Nail Internal Limit States Using Default FHWA Load and Resistance Models. Mar. Georesour. Geotechnol. 2019, 37, 783–800. [Google Scholar] [CrossRef]
- Xu, D.; Xu, X.; Li, W.; Fatahi, B. Field Experiments on Laterally Loaded Piles for an Offshore Wind Farm. Mar. Struct. 2020, 69, 102684. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).