Joint Allocation of Shared Yard Space and Internal Trucks in Sea–Rail Intermodal Container Terminals
Abstract
1. Introduction
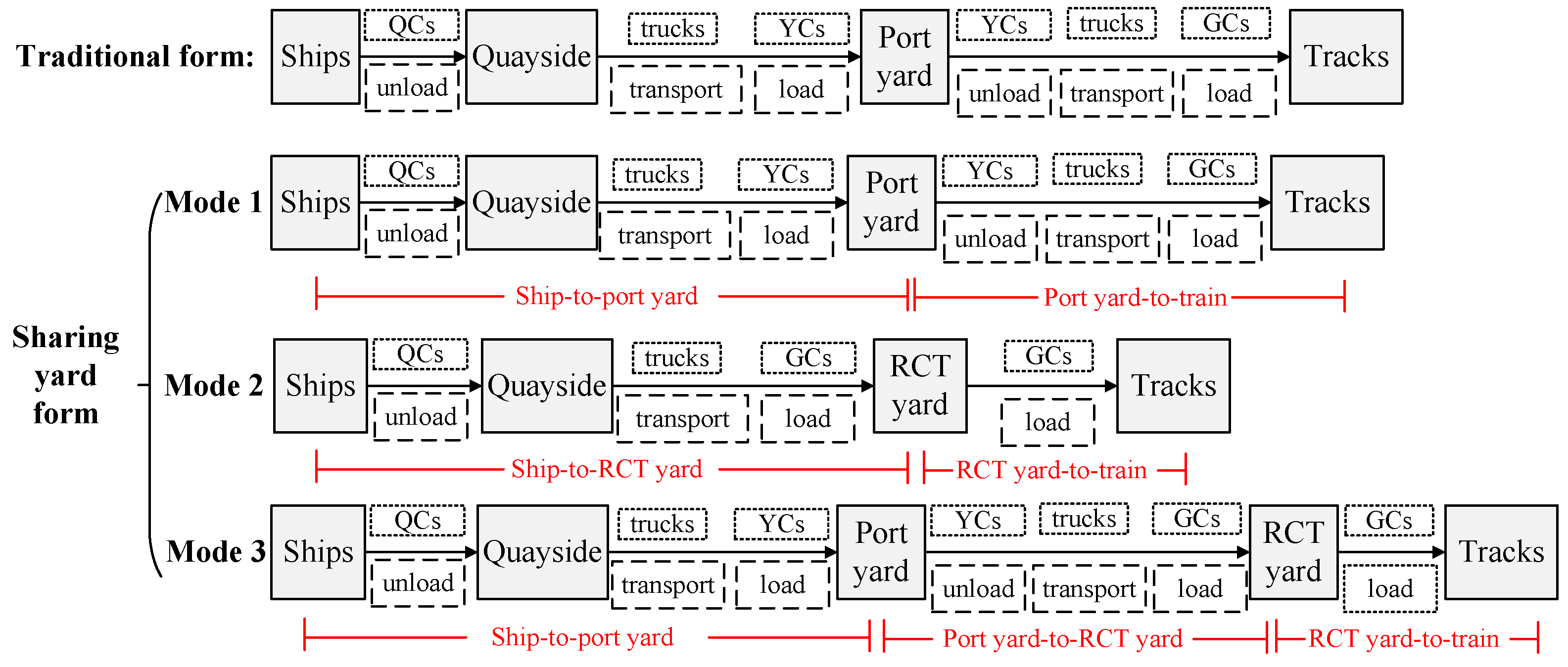
- Focusing on the seaport–RCT separation layout commonly used in practice, we introduce an innovative resource-sharing mechanism between two independent entities, namely the seaport and the RCT. A novel framework for joint allocation of shared yard space and trucks is investigated. This collaborative approach overcomes inefficiencies in ship and train turnaround operations.
- Considering practical constraints including yard capacities and equipment limitations, along with operational disparities between the port and the RCT, we develop a mixed-integer programming (i.e., MIP) model that integrates yard allocation, container transfers, and truck allocation to balance trans-shipment costs and handling efficiency. A two-layer hybrid heuristic algorithm incorporating Adaptive Particle Swarm Optimization and Greedy Rules (i.e., APSO-GR) is designed to obtain globally optimal solutions.
- The handling time continuity of vehicles (ships and trains are hereafter collectively termed “vehicles”) and all possible states of trans-shipment containers are presented. The optimization objectives are designed to align with the long-term strategic goals. Therefore, although this study primarily addresses a single-period resource coordination problem, the proposed framework can be extended to complex multi-period scenarios through decomposition into sequential independent single-period decisions, maintaining its practical applicability for strategic planning purposes.
2. Literature Review
2.1. Storage Space Allocation Problem
2.2. Truck Allocation Problem
2.3. Container Transshipment Operation
2.4. Research Motivation
3. Methodology
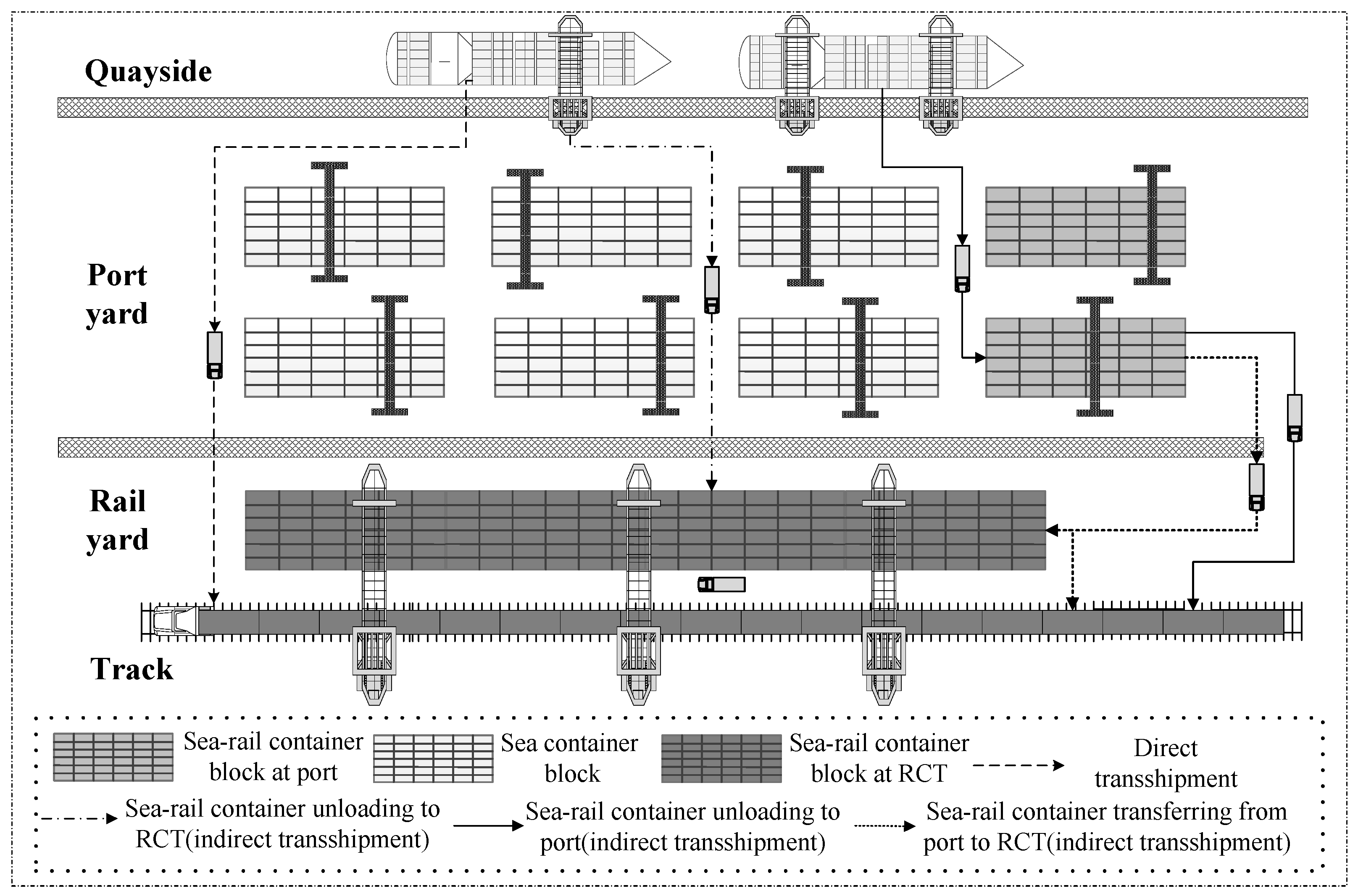
3.1. Problem Description
- Yard allocation: For arriving trans-shipment batches during the planning horizon, decide which yard containers are stored, RCT yard or port yard.
- Container transfer: Due to limited storage capacity and the turnaround efficiency of vehicles, containers may transfer from the port yard to the RCT yard. We conduct the quantity and time of container transfer. This sub-problem is intended for the import trans-shipment batches arriving and stored in the port during the planning horizon and pre-existing batches stored in the port before the planning horizon.
- Truck allocation: Allocate trucks for ships, trains, and container transfer within specified fleet constraints.
3.2. Model Formulation
3.2.1. Model Assumptions
3.2.2. Notations
3.2.3. Formulation
3.2.4. Model Validation
4. Solution Algorithm
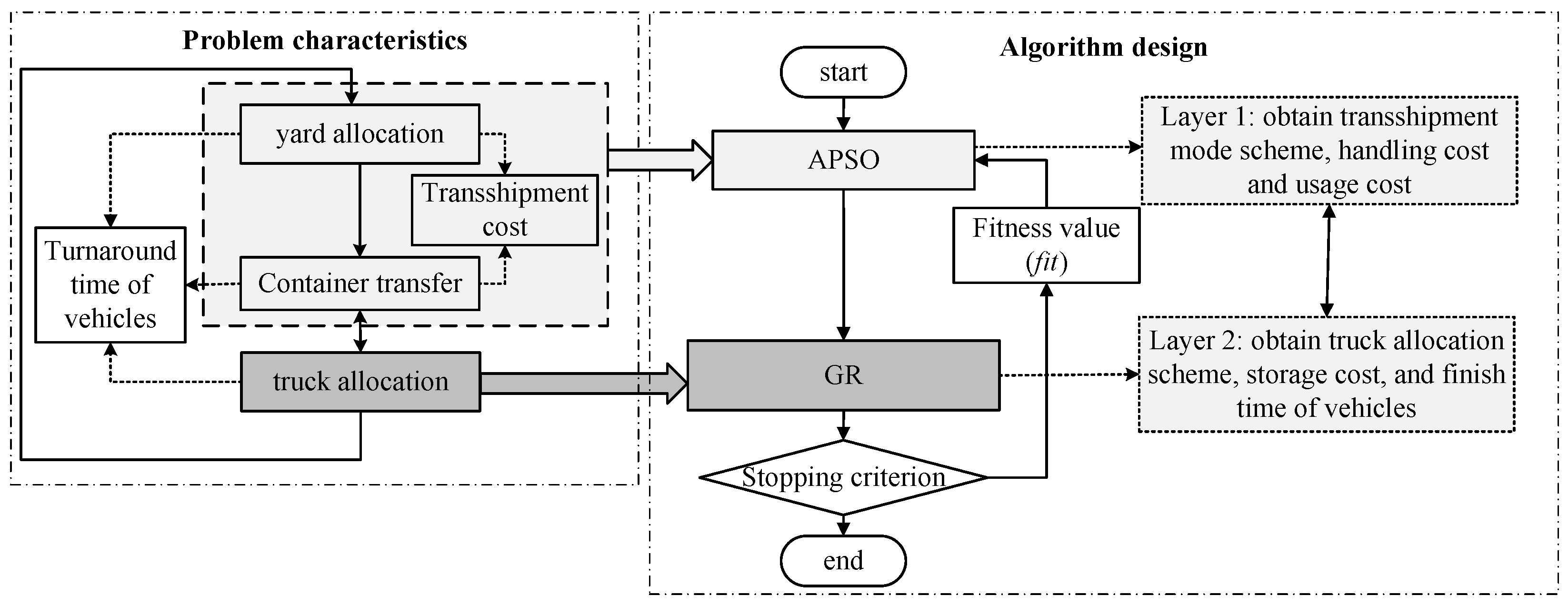
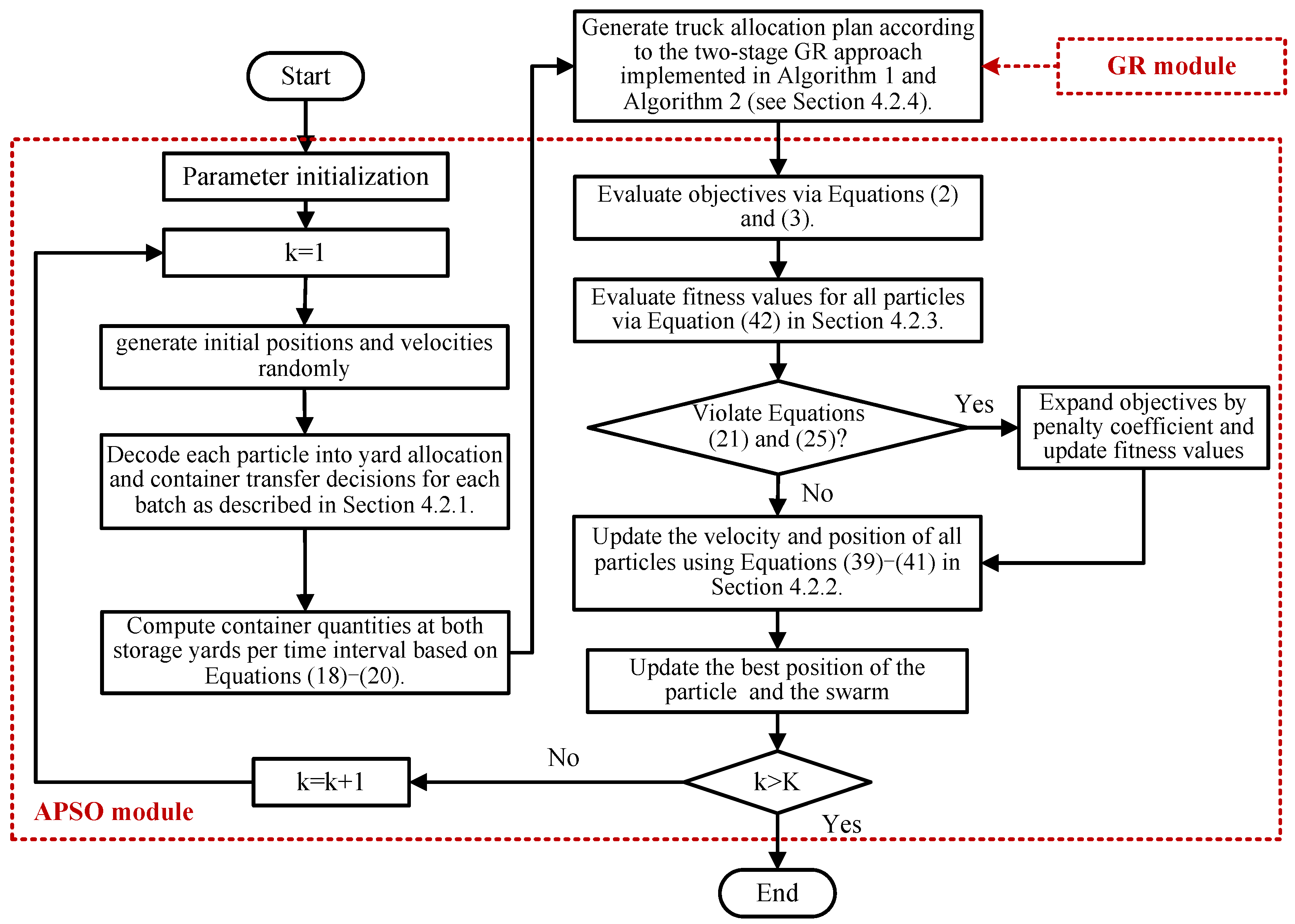
4.1. Algorithm Framework
4.2. Algorithm Tactics
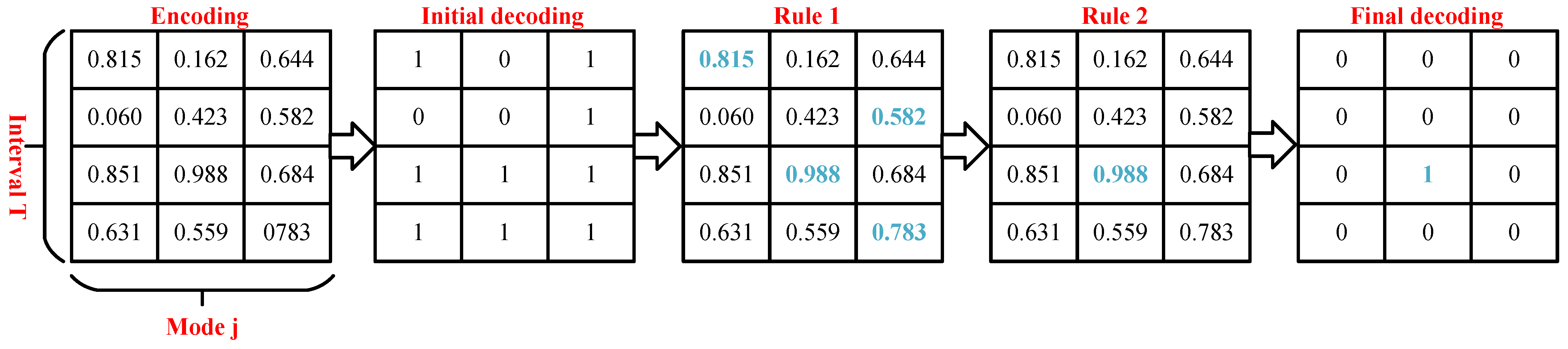
4.2.1. Encoding and Decoding Strategy
4.2.2. Adaptively Updating of Velocity and Position
4.2.3. Fitness Function
4.2.4. GR for Truck Allocation
| Algorithm 1 The first stage pseudocode: allocate trucks for vehicles |
|
| Algorithm 2 The second stage pseudocode: allocate trucks to container transfer |
|
5. Numerical Experiments
5.1. Text Instances
5.2. Experimental Results
5.3. Performance Analysis of the Model and Algorithm
5.3.1. Performance Analysis with Different Solving Methods
5.3.2. Performance Analysis for Truck Allocation Strategies
5.4. Comparative Experiment of Shared Yard Form and Traditional Storage Form
5.5. Sensitively Analysis
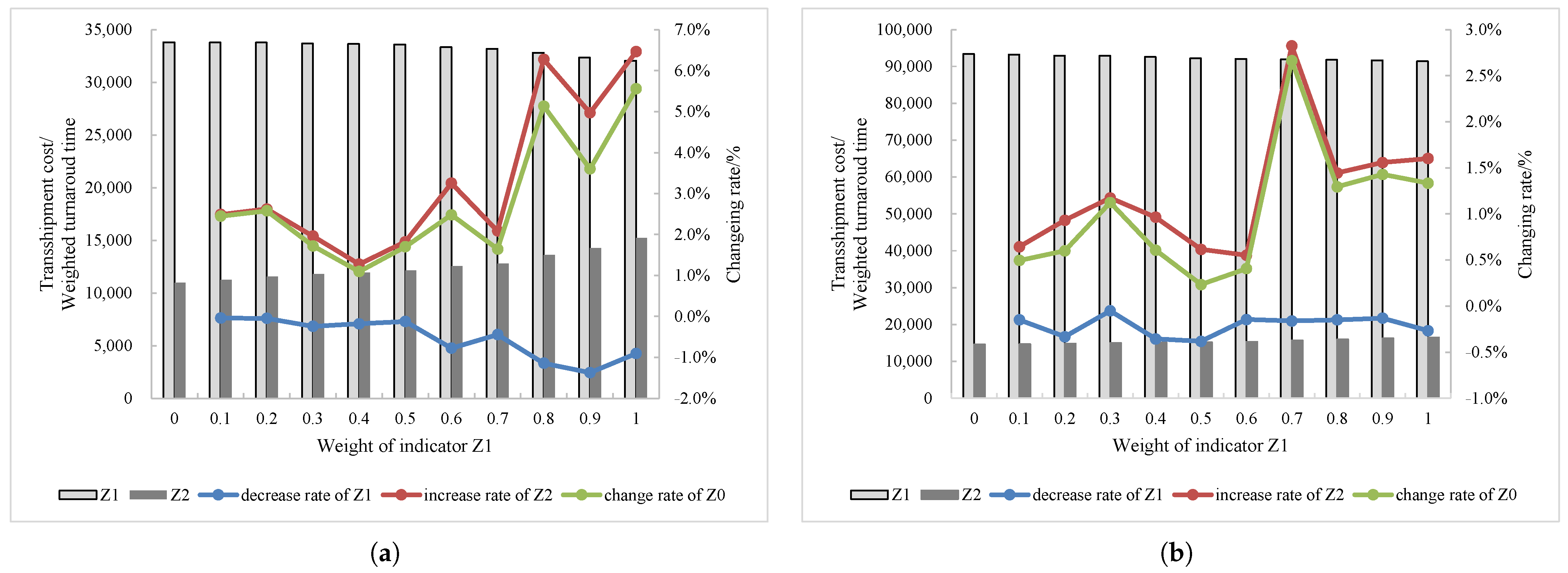
5.5.1. Sensitively Analysis for Objective Weights
5.5.2. Sensitively Analysis for Truck Configuration
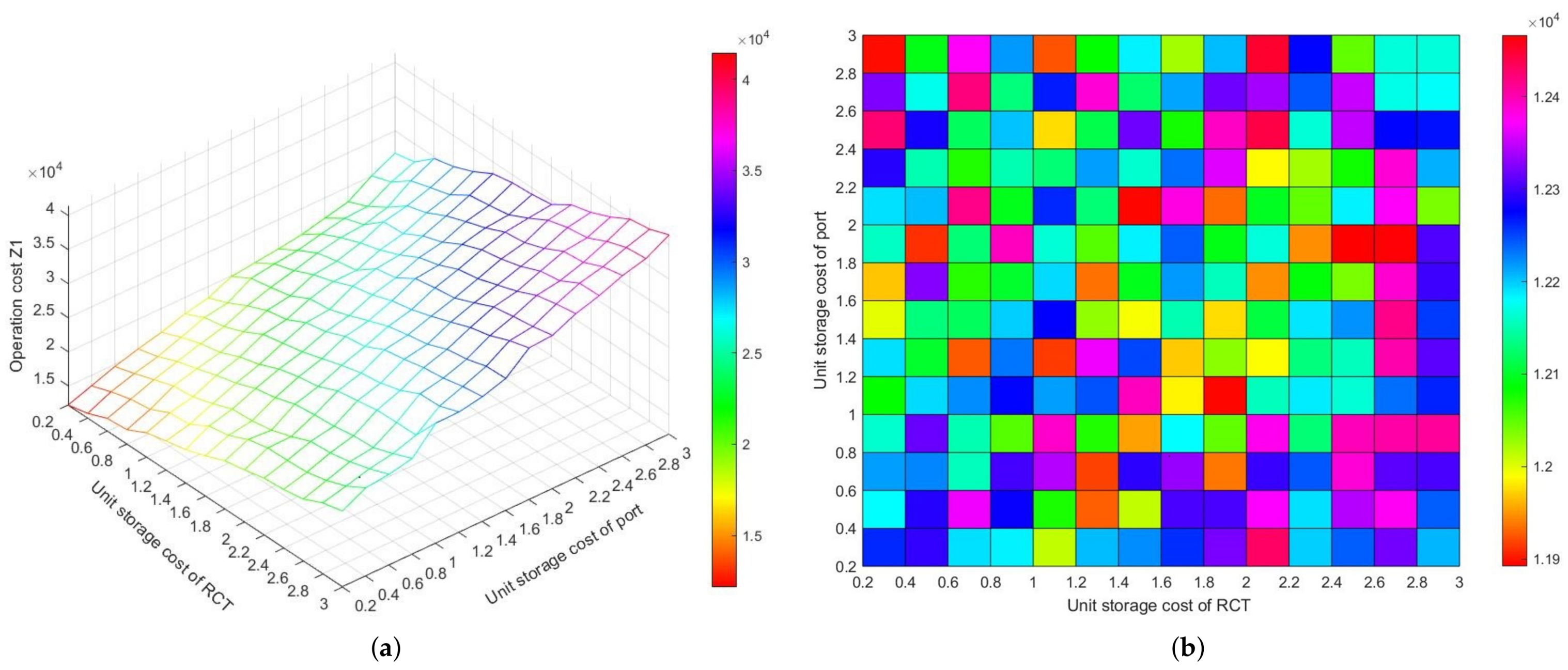
5.5.3. Sensitivity Analysis for Unit Storage Costs
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Operational Cost Breakdown
| Container State (S1/S2/S3/S4) | Equipment Deployment Frequency (QC/YC/GC/Truck) | Stacking Time in Port Yard | Stacking Time in RCT Yard |
|---|---|---|---|
| 1/1/1/1 | 0/1/2/1 | ||
| 1/1/1/2 | 0/1/1/1 | 0 | |
| 1/1/2/2 | 0/0/1/0 | 0 | |
| 1/2/1/1 | 0/1/1/1 | ||
| 1/2/1/2 | 0/0/0/0 | 0 | |
| 1/2/2/2 | 0/0/0/0 | 0 | |
| 2/1/1/1 | 1/2/2/2 | ||
| 2/1/1/2 | 1/2/1/2 | 0 | |
| 2/1/2/2 | 1/0/2/1 | 0 | |
| 2/2/1/1 | 1/2/1/2 | ||
| 2/2/1/2 | 1/1/0/1 | 0 | |
| 2/2/2/2 | 1/0/1/1 | 0 |
Appendix B. Model Linearization
References
- Liu, W.Q.; Zhu, X.N.; Wang, L.; Li, S.Y. Flexible yard crane scheduling for mixed railway and road container operations in sea-rail intermodal ports with the sharing storage yard. Trans. Res. Part E-Logist. Transp. Rev. 2024, 190, 103714. [Google Scholar] [CrossRef]
- Yan, B.C.; Jin, J.G.; Zhu, X.N.; Lee, D.H.; Wang, L.; Wang, H. Integrated planning of train schedule template and container transshipment operation in seaport railway terminals. Trans. Res. Part E-Logist. Transp. Rev. 2020, 142, 102061. [Google Scholar] [CrossRef]
- Hu, Q.; Corman, F.; Wiegmans, B.; Lodewijks, G. A tabu search algorithm to solve the integrated planning of container on an inter-terminal network connected with a hinterland rail network. Trans. Res. Part C-Emerg. Technol. 2018, 91, 15–36. [Google Scholar] [CrossRef]
- Guo, W.J.; Atasoy, B.; Beelaerts, W.; Negenborn, R.R. A dynamic shipment matching problem in hinterland synchromodal transportation. Decis. Support. Syst. 2020, 134, 113289. [Google Scholar] [CrossRef]
- Feng, Y.J.; Song, D.P.; Li, D. Smart stacking for import containers using customer information at automated container terminals. Eur. J. Oper. Res. 2022, 301, 502–522. [Google Scholar] [CrossRef]
- Lee, D.H.; Jin, J.G.; Chen, J.H. Terminal and yard allocation problem for a container transshipment hub with multiple terminals. Trans. Res. Part E-Logist. Transp. Rev. 2012, 48, 516–528. [Google Scholar] [CrossRef]
- Zhen, L.; Wang, S.A.; Wang, K. Terminal allocation problem in a transshipment hub considering bunker consumption. Nav. Res. Logist. 2016, 63, 529–548. [Google Scholar] [CrossRef]
- Hu, X.Y.; Liang, C.J.; Chang, D.F.; Zhang, Y. Container storage space assignment problem in two terminals with the consideration of yard sharing. Adv. Eng. Inform. 2021, 47, 101224. [Google Scholar] [CrossRef]
- Xie, Y.; Song, D.P. Optimal planning for container prestaging, discharging, and loading processes at seaport rail terminals with uncertainty. Trans. Res. Part E-Logist. Transp. Rev. 2018, 119, 88–109. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Storage yard operations in container terminals: Literature overview, trends, and research directions. Eur. J. Oper. Res. 2014, 235, 412–430. [Google Scholar] [CrossRef]
- Abouelrous, A.; Dekker, R.; Bliek, L.; Zhang, Y.Q. Real-time policy for yard allocation of transshipment containers in a terminals. Transp. Res. Part B-Methodol. 2025, 192, 103138. [Google Scholar] [CrossRef]
- Hu, H.T.; Mo, J.; Zhen, L. Integrated optimization of container allocation and yard cranes dispatched under delayed transshipment. Transp. Res. Part C-Emerg. Technol. 2024, 158, 104429. [Google Scholar] [CrossRef]
- Wang, T.T.; Ma, H.; Xu, Z.; Xia, J. A new dynamic shape adjustment and placement algorithm for 3D yard allocation problem with time dimension. Comput. Oper. Res. 2022, 138, 105585. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Gaudioso, M.; Laporte, G.; Moccia, L. The service allocation problem at the Giola Tauro Maritime Terminal. Eur. J. Oper. Res. 2007, 176, 1167–1184. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G.; Moccia, L.; Sorrentino, G. Optimizing yard assignment in an automotive transshipment terminal. Eur. J. Oper. Res. 2011, 215, 149–160. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Legato, P.; Mazza, R.M.; Trunfio, R. Simulation-based optimization for housekeeping in a container transshipment terminal. Comput. Oper. Res. 2015, 53, 81–95. [Google Scholar] [CrossRef]
- Kim, K.; Jin, X.; Woo, C. A survey on sharing economy and logistics resources sharing. J. Supply Chain Manag. 2017, 17, 89–115. [Google Scholar] [CrossRef]
- He, J.L.; Liu, Y.L.; Tan, C.M. A novel method for yard space allocation for the port with atypical container collection cycles. Adv. Eng. Inform. 2025, 64, 103040. [Google Scholar] [CrossRef]
- Tan, C.M.; Liu, Y.L.; He, J.L.; Wang, Y.; Yu, H. Yard space allocation for container transshipment ports with mother and feeder vessels. Ocean Coast. Manag. 2024, 25, 107048. [Google Scholar] [CrossRef]
- Jin, X.F.; Park, K.T.; Kim, K.H. Storage space sharing among container handling companies. Trans. Res. Part E-Logist. Transp. Rev. 2019, 127, 111–131. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.; Harraz, N.A. Simultaneous assignment of quay cranes and internal trucks in container terminals. Int. J. Ind. Syst. Eng. 2016, 24, 107–125. [Google Scholar] [CrossRef]
- Li, M.W.; Xu, R.Z.; Yang, Z.Y.; Hong, W.C.; An, X.G.; Yeh, Y.H. Optimization approach of berth-quay crane-truck allocation by the tide, environment and uncertainty factors based on chaos quantum adaptive seagull optimization algorithm. Appl. Soft Comput. 2024, 152, 111197. [Google Scholar] [CrossRef]
- Zhang, X.J.; Li, H.J.; Sheu, J.B. Integrated scheduling optimization of AGV and double yard cranes in automated container terminals. Transp. Res. Part B-Methodol. 2024, 179, 102871. [Google Scholar] [CrossRef]
- Wang, Z.X.; Chan, F.T.S.; Chung, S.H.; Niu, B. A decision support method for internal truck employment. Ind. Manag. Data Syst. 2014, 114, 1378–1395. [Google Scholar] [CrossRef]
- Karam, A.; Eltawil, A.B. Functional integration approach for the berth allocation, and specific quay crane assignment problems. Comput. Ind. Eng. 2016, 102, 458–466. [Google Scholar] [CrossRef]
- Chargui, K.; Zouadi, T.; EI Fallahi, A.; Reghioui, M.; Aouam, T. Berth and quay crane allocation and scheduling with worker performance variability and yard truck deployment in container terminals. Trans. Res. Part E-Logist. Transp. Rev. 2021, 154, 102449. [Google Scholar] [CrossRef]
- Vahdani, B.; Mansour, F.; Soltani, M.; Veysmoradi, D. Bi-objective optimization for integrating quay crane and internal truck assignment with challenges of trucks sharing. Knowl. Based. Syst. 2019, 163, 675–692. [Google Scholar] [CrossRef]
- He, J.; Zhang, W.; Huang, Y.; Yan, W. A simulation optimization method for internal trucks sharing assignment among multiple container terminals. Adv. Eng. Inform. 2013, 27, 598–614. [Google Scholar] [CrossRef]
- Schepler, X.; Stefan, B.; Michel, S.; Sanlaville, E. Global planning in a multi-terminal and multi-modal maritime container port. Trans. Res. Part E-Logist. Transp. Rev. 2017, 100, 38–62. [Google Scholar] [CrossRef]
- Yan, B.C.; Zhu, X.N.; Lee, D.H.; Jin, J.G.; Wang, L. Transshipment operations optimization of sea-rail intermodal container in seaport rail terminals. Comput. Ind. Eng. 2020, 141, 106296. [Google Scholar] [CrossRef]
- Heilig, L.; Voß, S. Inter-terminal transportation: An annotated bibliography and research agenda. Flex. Serv. Manuf. J. 2016, 29, 35–63. [Google Scholar] [CrossRef]
- Hu, Q.; Wiegmans, B.; Corman, F.; Lodewijks, G. Critical literature review into planning of inter-terminal transport: In port areas and the hinterland. J. Adv. Transp. 2019, 2019, 9893615. [Google Scholar] [CrossRef]
- Tierney, K.; Voß, S.; Stahlbock, R. A mathematical model of inter-terminal transportation. Eur. J. Oper. Res. 2014, 235, 448–460. [Google Scholar] [CrossRef]
- Hu, Q.; Wiegmans, B.; Corman, F.; Lodewijks, G. Integration of inter-terminal transport and hinterland rail transport. Flex. Serv. Manuf. J. 2019, 31, 807–831. [Google Scholar] [CrossRef]
- Ramadhan, M.H.; Kamal, I.M.; Kim, D.; Bae, H. Solving the inter-terminal truck routing problem for delay minimization using simulated annealing with normalized exploration rate. J. Mar. Sci. Eng. 2023, 11, 2103. [Google Scholar] [CrossRef]
- Fowler, R.J.; Paterson, M.S.; Tatimoto, S.L. Optimal packing and covering in the plane are NP-complete. Inf. Process. Lett. 1981, 12, 133–137. [Google Scholar] [CrossRef]
- Tole, K.; Moqa, R.; Zheng, J.Z.; He, K. A simulated annealing approach for the circle bin packing problem with rectangular items. Comput. Ind. Eng. 2023, 176, 109004. [Google Scholar] [CrossRef]
- Wang, X.H.; Jin, Z.H. Collaborative optimization of multi-equipment scheduling and intersection point allocation for U-shaped automated sea-rail intermodal container terminals. IEEE Trans. Autom. Sci. Eng. 2025, 22, 7373–7393. [Google Scholar] [CrossRef]
- Xu, B.W.; Jie, D.P.; Li, J.J.; Yang, Y.S.; Wen, F.R.; Song, H.T. Integrated scheduling optimization of U-shaped automated container terminal under loading and unloading mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Tengecha, N.A.; Zhang, X.Y. An efficient algorithm for the berth and quay crane assignments considering operator performance in container terminal using particle swarm model. J. Mar. Sci. Eng. 2022, 10, 1232. [Google Scholar] [CrossRef]
- Luo, Q.; Rao, Y.Q.; Peng, D. GA and GWO algorithm for the special bin packing problem encountered in field of aircraft arrangement. Appl. Soft Comput. 2022, 14, 108060. [Google Scholar] [CrossRef]
- Vecek, N.; Crepinsek, M.; Mernik, M. On the influence of the number of algorithms, problems, and independent runs in the comparison of evolutionary algorithms. Appl. Soft Comput. 2017, 54, 23–45. [Google Scholar] [CrossRef]
- Wieckowski, J.; Salabun, W. Sensitivity analysis approaches in multi-criteria decision analysis: A systematic review. Appl. Soft Comput. 2023, 148, 110915. [Google Scholar] [CrossRef]






| Literature | Research Area | Resource Allocation | Container Flow | Container Transfer | Objective | Solution Algorithm |
|---|---|---|---|---|---|---|
| Lee et al. (2012) [6] | Multiple sea terminals | Yard and block allocation | Sea containers | Yes | Cost | Two-stage algorithm |
| Zhen et al. (2016) [7] | Multiple sea terminals | Yard allocation | Sea containers | Yes | Cost | Local branching and PSO * |
| He et al. (2025) [18] | Seaport yard | Sub-block allocation | Sea containers | No | Yard utilization | PSO |
| Tan et al. (2024) [19] | Seaport yard | Sub-block allocation | Sea containers | No | Transportation distance and yard utilization | Upper-bound model |
| Hu et al. (2021) [8] | A seaport yard and a dry port yard | Yard allocation | Sea containers | No | Transportation distance and yard utilization | NSGA-II |
| Jin et al. (2019) [20] | Multi-terminals | Yard and cost allocation | Storage orders | No | Cost | Game theory |
| Xie and Song (2018) [9] | SRICT | Yard allocation | Sea–rail containers | Yes | Cost | Optimal strategy |
| This paper | SRICT | Yard and truck allocation | Sea–rail containers | Yes | Cost and turnaround efficiency | APSO-GR |
| Instance | /s | CPU/s | ||
|---|---|---|---|---|
| I1 | 5209.7 | 9288.6 | 4879.7 | 236 |
| I2 | 5906.7 | 7248.5 | 4854.9 | 577 |
| I3 | 7011.4 | 10,232.0 | 5773.7 | 1328 |
| I4 | 26,067.4 * | 10,392.7 * | 25,111.9 * | 7200 |
| I5 | — | — | — | 7200 |
| Instance | Intervals | Ships | Trains | Batches* | Container Number/FEU |
|---|---|---|---|---|---|
| I1 | 4 + 4 | 3 | 4 | 46/18/11/17 | 590 |
| I2 | 4 + 4 | 4 | 5 | 52/23/16/13 | 693 |
| I3 | 4 + 4 | 4 | 6 | 55/25/14/16 | 775 |
| I4 | 12 + 4 | 12 | 16 | 75/52/11/14 | 1338 |
| I5 | 12 + 4 | 12 | 20 | 90/60/16/14 | 1666 |
| I6 | 12 + 4 | 12 | 20 | 101/68/16/17 | 1763 |
| I7 | 20 + 4 | 16 | 27 | 140/100/21/19 | 2059 |
| I8 | 20 + 4 | 19 | 30 | 169/121/23/25 | 2537 |
| I9 | 20 + 4 | 19 | 33 | 181/134/22/25 | 2675 |
| I10 | 28 + 4 | 23 | 46 | 215/145/30/40 | 3212 |
| I11 | 28 + 4 | 26 | 46 | 235/164/33/38 | 3557 |
| I12 | 28 + 4 | 26 | 49 | 249/183/32/34 | 3492 |
| Parameter ℓ | Convergence Situation of I6 | Convergence Situation of I12 | ||
|---|---|---|---|---|
| Iterations | Objective | Iterations | Objective | |
| 10 | 364 | 29,111.78 | 369 | 93,573.7 |
| 100 | 228 | 28,571.3 | 195 | 90,214.2 |
| 500 | 185 | 28,738.47 | 226 | 91,874.4 |
| 1000 | 103 | 30,330.46 | 89 | 94,233.46 |
| Instance | Objective | Transshipment Cost | Turnaround Time | CPU/s | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average | Best | FR/% | Average/s | Best/s | FR/% | Average | Best | FR/% | Average | |
| I1 | 4931.0 | 4917.4 | 0.28 | 5312.4 | 5258.3 | 1.02 | 9287.6 | 9287.6 | 0.00 | 31 |
| I2 | 4978.3 | 4934.0 | 0.89 | 6081.7 | 6028.5 | 0.87 | 7385.6 | 7362.5 | 0.31 | 46 |
| I3 | 5905.4 | 5840.1 | 0.39 | 7177.1 | 7127.5 | 0.68 | 10,452.8 | 10,282.0 | 1.63 | 48 |
| I4 | 23,026.4 | 22,783.1 | 0.53 | 24,751.5 | 24,683.6 | 0.27 | 9164.3 | 9020.8 | 1.21 | 168 |
| I5 | 25,678.6 | 25,278.8 | 1.56 | 30,259.1 | 29,902.7 | 1.18 | 12,351.1 | 12,098.5 | 2.05 | 212 |
| I6 | 28,899.8 | 28,571.3 | 1.15 | 33,780.3 | 33,599.4 | 0.54 | 12,307.3 | 12,148.1 | 1.30 | 232 |
| I7 | 43,072.5 | 42,693.8 | 0.88 | 44,438.7 | 44,421.1 | 0.04 | 11,491.7 | 11,307.3 | 1.60 | 511 |
| I8 | 53,185.6 | 52,887.1 | 1.15 | 54,890.1 | 54,098.0 | 1.44 | 12,520.5 | 12,446.5 | 0.59 | 585 |
| I9 | 56,280.1 | 55,990.2 | 0.52 | 58,031.8 | 57,612.7 | 0.72 | 13,647.5 | 13,606.6 | 0.30 | 622.0 |
| I10 | 94,487.4 | 93,648.5 | 0.89 | 92,628.6 | 92,317.3 | 0.34 | 13,745.0 | 13,526.2 | 1.59 | 1006 |
| I11 | 98,188.1 | 96,901.6 | 1.34 | 98,112.5 | 97,288.7 | 0.84 | 13,874.0 | 13,614.7 | 1.87 | 1175 |
| I12 | 91,050.9 | 90,214.2 | 0.92 | 92,628.1 | 92,213.6 | 0.48 | 15,452.1 | 15,225.7 | 1.47 | 1397 |
| Instance | WPA-GR | SPAO-GR | Gap Value/% | ||||
|---|---|---|---|---|---|---|---|
| CPU/s | CPU/s | Gap*(1) | Gap*(2) | Gap*(3) | |||
| I1 | 5070.0 | 33 | 4944.1 | 30 | 2.82 | 0.27 | −1.25 |
| I2 | 5261.9 | 49 | 5066.4 | 50 | 5.70 | 1.77 | −2.50 |
| I3 | 6492.4 | 48 | 6007.9 | 53 | 9.94 | 1.74 | −1.73 |
| I4 | 24,710.8 | 174 | 23,722.4 | 163 | 7.32 | 3.02 | 9.08 |
| I5 | 27,483.0 | 221 | 26,408.1 | 198 | 7.03 | 2.84 | — |
| I6 | 31,327.8 | 250 | 29,803.2 | 244 | 8.40 | 3.13 | — |
| I7 | 45,905.5 | 536 | 44,613.1 | 587 | 6.58 | 3.58 | — |
| I8 | 57,096.2 | 636 | 55,490.8 | 581 | 7.35 | 4.33 | — |
| I9 | 61,037.2 | 648 | 59,022.5 | 693 | 8.45 | 4.87 | — |
| I10 | 100,754.7 | 1109 | 99,535.7 | 979 | 6.63 | 5.34 | — |
| I11 | 107,289.4 | 1289 | 104,528.5 | 1276 | 9.27 | 6.46 | — |
| I12 | 98,551.5 | 1467 | 96,602.9 | 1209 | 8.24 | 6.10 | — |
| APSO-GR | WPA-GR | SPSO-GR | |
|---|---|---|---|
| APSO-GR | 0/1 | 2/0.000003 | 1/0.038 |
| WPA-GR | 2/0.000003 | 0/1 | 1/0.038 |
| SPSO-GR | 1/0.038 | 1/0.038 | 0/1 |
| Instance | TA2 Strategy | TA3 Strategy | ||||||
|---|---|---|---|---|---|---|---|---|
| /s | Gap(2,1)/% | Gap(2,2)/% | /s | Gap(3,1)/% | Gap(3,2)/% | |||
| I1 | 5386 | 9989 | 1.37 | 7.03 | 5375 | 9288 | 1.16 | 0.00 |
| I2 | 6294 | 9573 | 3.37 | 22.85 | 6225 | 7689 | 2.31 | 3.95 |
| I3 | 7311 | 13,381 | 1.83 | 21.88 | 7188 | 11,463 | 0.15 | 8.81 |
| I4 | 25,535 | 11,794 | 3.07 | 22.30 | 24,972 | 9717 | 0.88 | 5.68 |
| I5 | 31,439 | 18,063 | 3.75 | 31.62 | 30,844 | 13,418 | 1.89 | 7.95 |
| I6 | 34,576 | 18,590 | 2.30 | 33.80 | 34,133 | 13,568 | 1.03 | 9.29 |
| I7 | 45,339 | 14,294 | 1.99 | 19.61 | 44,518 | 11,893 | 0.18 | 3.38 |
| I8 | 57,190 | 16,071 | 4.02 | 22.09 | 55,098 | 13,187 | 0.38 | 5.05 |
| I9 | 59,477 | 19,136 | 2.43 | 28.68 | 58,649 | 14,587 | 1.05 | 6.44 |
| I10 | 95,240 | 17,147 | 2.74 | 19.84 | 93,323 | 14,471 | 0.74 | 5.02 |
| I11 | 101,761 | 18,035 | 3.59 | 23.07 | 98,352 | 14,954 | 0.24 | 7.22 |
| I12 | 95,879 | 20,451 | 3.41 | 24.44 | 94,026 | 16,775 | 1.49 | 7.89 |
| CT | M1 | M2 | M3 | SP/(FEU·h) | SR/(FEU·h) | WTT-S/s | WTT-T/s | |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 16 | 48 | 10 | 10 | 7177.9 | 3171.3 | 4930.6 | 7179.4 |
| 0.4 | 22 | 40 | 12 | 16 | 6927.8 | 3459.8 | 5102.3 | 7137.8 |
| 0.6 | 17 | 45 | 12 | 11 | 6743.9 | 3664.3 | 5394.3 | 6993.3 |
| 0.8 | 17 | 40 | 16 | 12 | 6405.6 | 3948.8 | 5527.5 | 6537.4 |
| 1 | 22 | 33 | 18 | 17 | 6245.1 | 4120.1 | 5692.6 | 12,421.8 |
| 1.2 | 24 | 35 | 17 | 16 | 5968.6 | 4409.2 | 5344.2 | 6939.8 |
| 1.4 | 19 | 34 | 22 | 12 | 5836.8 | 4516.5 | 5456.2 | 6863.7 |
| 1.6 | 22 | 35 | 20 | 13 | 5521.9 | 4829.4 | 5852.7 | 6434.7 |
| 1.8 | 24 | 29 | 23 | 16 | 5312.1 | 4993.3 | 6104.9 | 5906.7 |
| 2.0 | 24 | 26 | 26 | 16 | 5106.9 | 5125.5 | 6554.3 | 5438.4 |
| 2.2 | 23 | 29 | 24 | 15 | 5092.5 | 5178.3 | 6408.3 | 5756.8 |
| 2.4 | 23 | 26 | 27 | 15 | 4846.0 | 5557.0 | 6529.6 | 5728.1 |
| 2.6 | 24 | 24 | 27 | 17 | 4785.1 | 5474.9 | 6285.6 | 5722.7 |
| 2.8 | 23 | 25 | 30 | 13 | 4591.5 | 5645.1 | 6340.2 | 5796.9 |
| 3 | 27 | 24 | 27 | 17 | 4212.6 | 6065.8 | 6503.1 | 5622.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jin, Z.; Luo, J. Joint Allocation of Shared Yard Space and Internal Trucks in Sea–Rail Intermodal Container Terminals. J. Mar. Sci. Eng. 2025, 13, 983. https://doi.org/10.3390/jmse13050983
Wang X, Jin Z, Luo J. Joint Allocation of Shared Yard Space and Internal Trucks in Sea–Rail Intermodal Container Terminals. Journal of Marine Science and Engineering. 2025; 13(5):983. https://doi.org/10.3390/jmse13050983
Chicago/Turabian StyleWang, Xiaohan, Zhihong Jin, and Jia Luo. 2025. "Joint Allocation of Shared Yard Space and Internal Trucks in Sea–Rail Intermodal Container Terminals" Journal of Marine Science and Engineering 13, no. 5: 983. https://doi.org/10.3390/jmse13050983
APA StyleWang, X., Jin, Z., & Luo, J. (2025). Joint Allocation of Shared Yard Space and Internal Trucks in Sea–Rail Intermodal Container Terminals. Journal of Marine Science and Engineering, 13(5), 983. https://doi.org/10.3390/jmse13050983






