DC-WUnet: An Underwater Ranging Signal Enhancement Network Optimized with Depthwise Separable Convolution and Conformer
Abstract
1. Introduction
- (1)
- A DC-WUnet network model is proposed, which employs an encoder-decoder structure to separate clean signals from ship noise and multipath Doppler effect interference, thereby enhancing the target signal.
- (2)
- In the encoder, the Conformer module and skip connections enhance the network’s ability to capture signal features. Multi-scale features are extracted through feature transfer facilitated by skip connections and convolutional kernels of varying sizes in each encoding layer. Additionally, depthwise separable convolutions are introduced to address the feature loss associated with traditional downsampling methods while reducing network parameters and improving computational efficiency. In the decoder, a slope-based linear upsampling method delivers superior reconstruction performance, particularly in regions of the signal with rapid variations.
- (3)
- In the network loss function, frequency-domain processing is introduced, and by performing joint computation in the time–frequency domain, the problem of information compression and loss caused by the inability to extract clean signals in the time domain is addressed.
2. Related Work
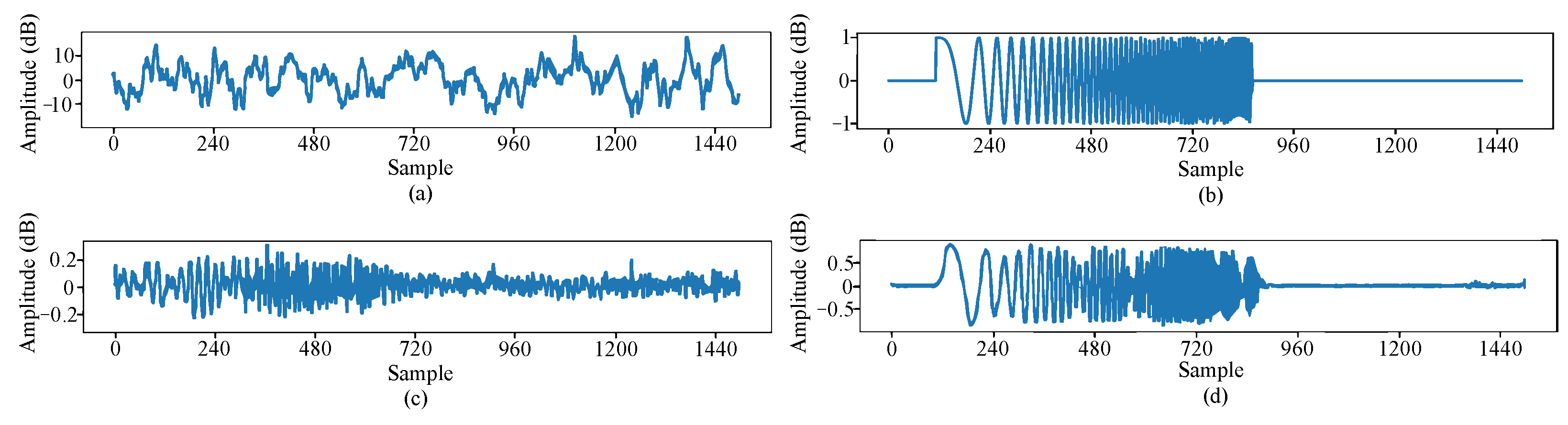
3. Ranging Signal Simulation Model
3.1. Ship-Radiated Noise Modeling
3.2. Interference Signal Model
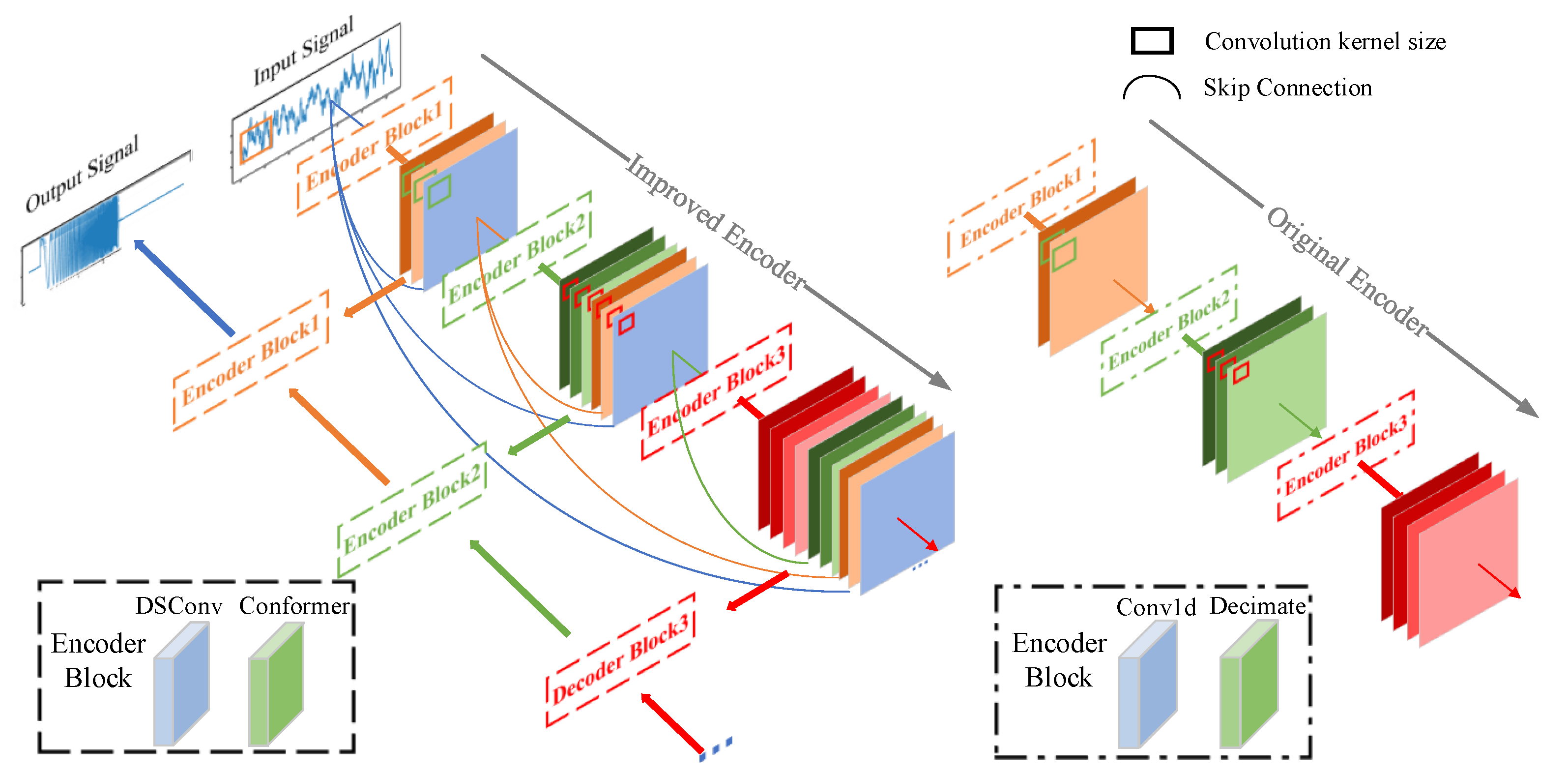
4. DC-WUnet Network
4.1. Loss Function
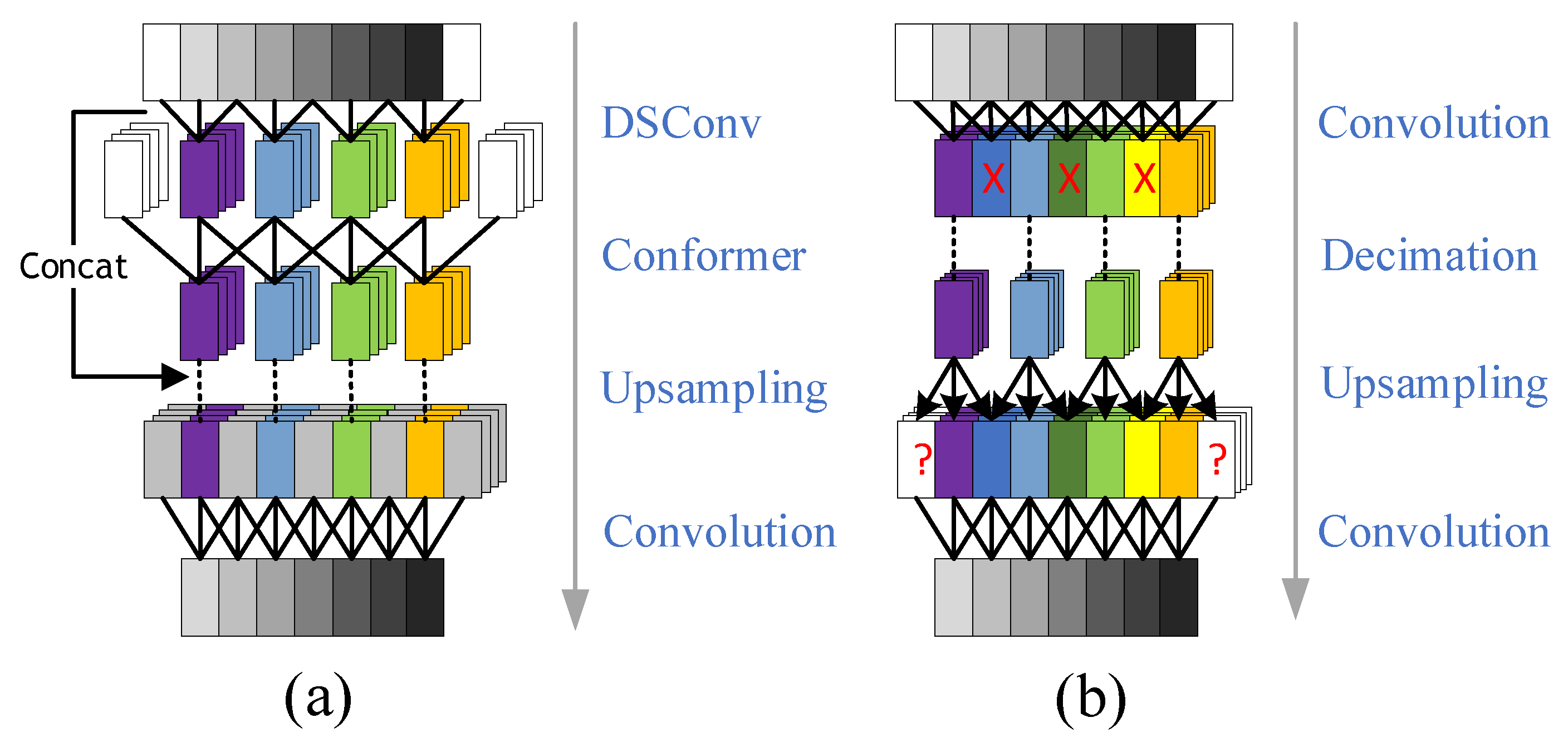
4.2. Upsampling and Downsampling
4.3. Skip Connections and Conformer Model
4.3.1. Feed Forward Module
4.3.2. Multi-Head Self-Attention Module
4.3.3. Convolution Module
5. Experiment Setup
5.1. Dataset
5.2. Experimental Configuration and Training Goal
| Algorithm 1: Network Training Algorithm |
 |
5.3. Evaluation Metrics
5.4. Comparison Algorithms
6. Experiments and Results
6.1. Training Results
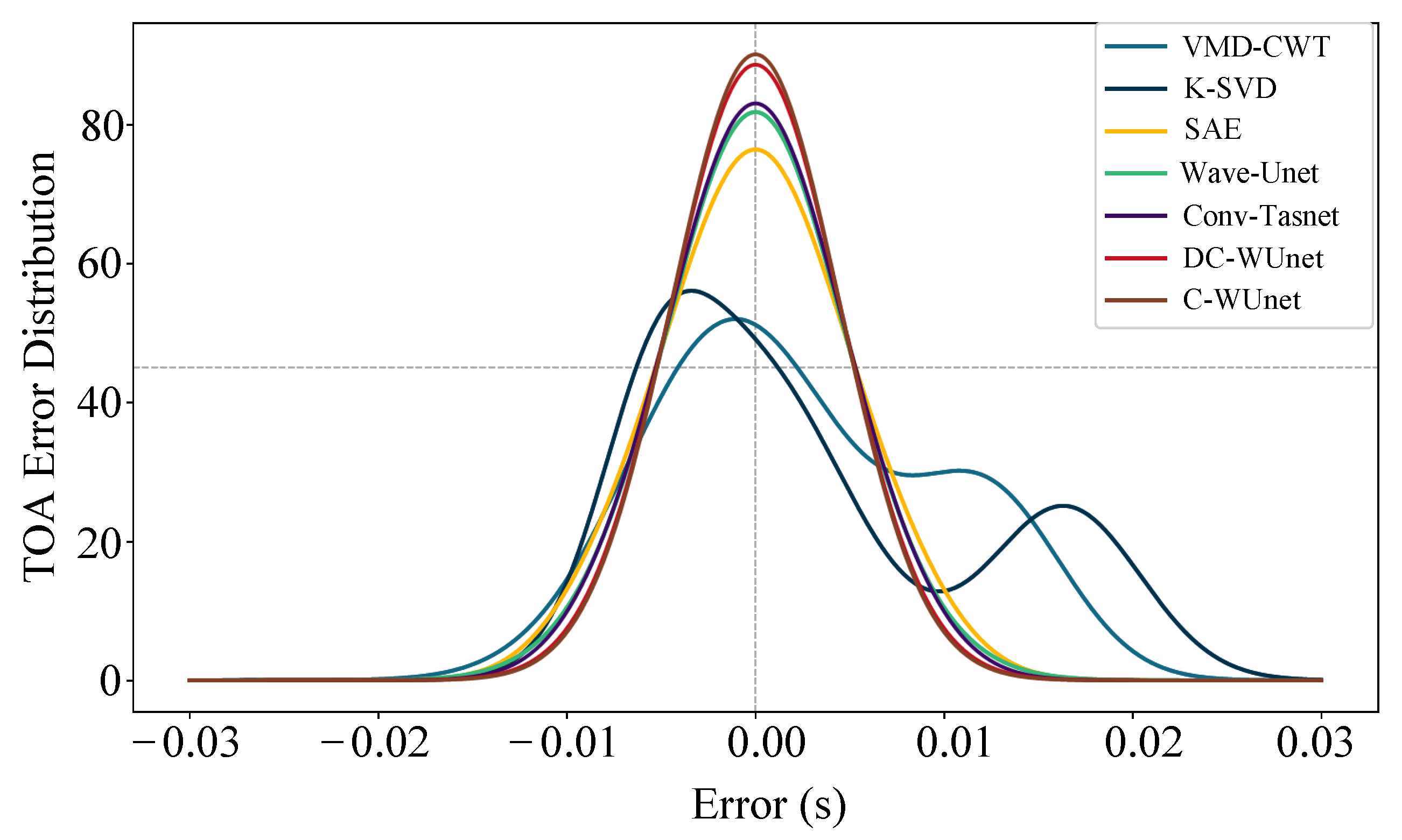
6.2. Comparison of TOA Accuracy and SNR Improvement
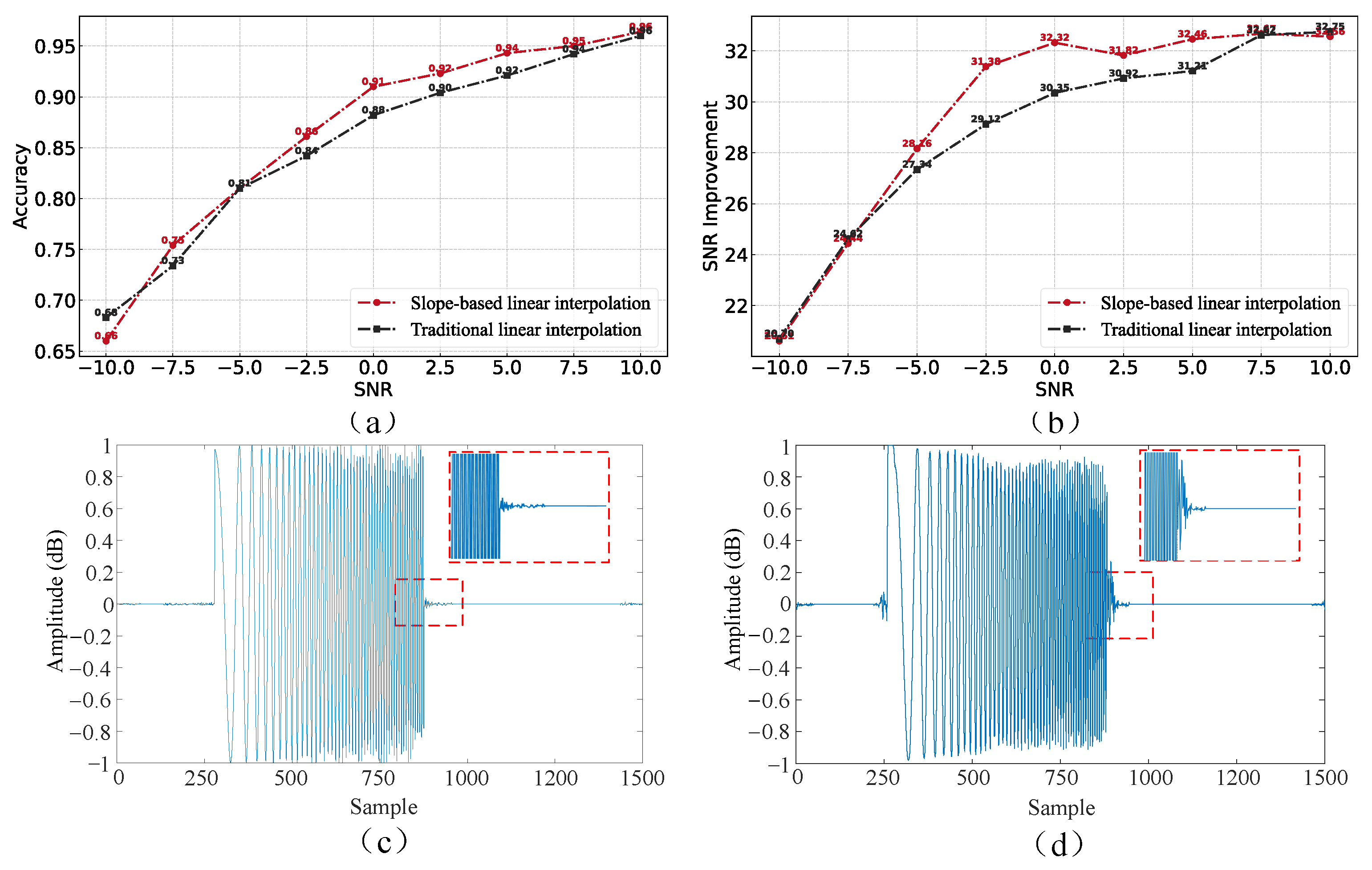
6.3. Different Interpolation Methods Performance
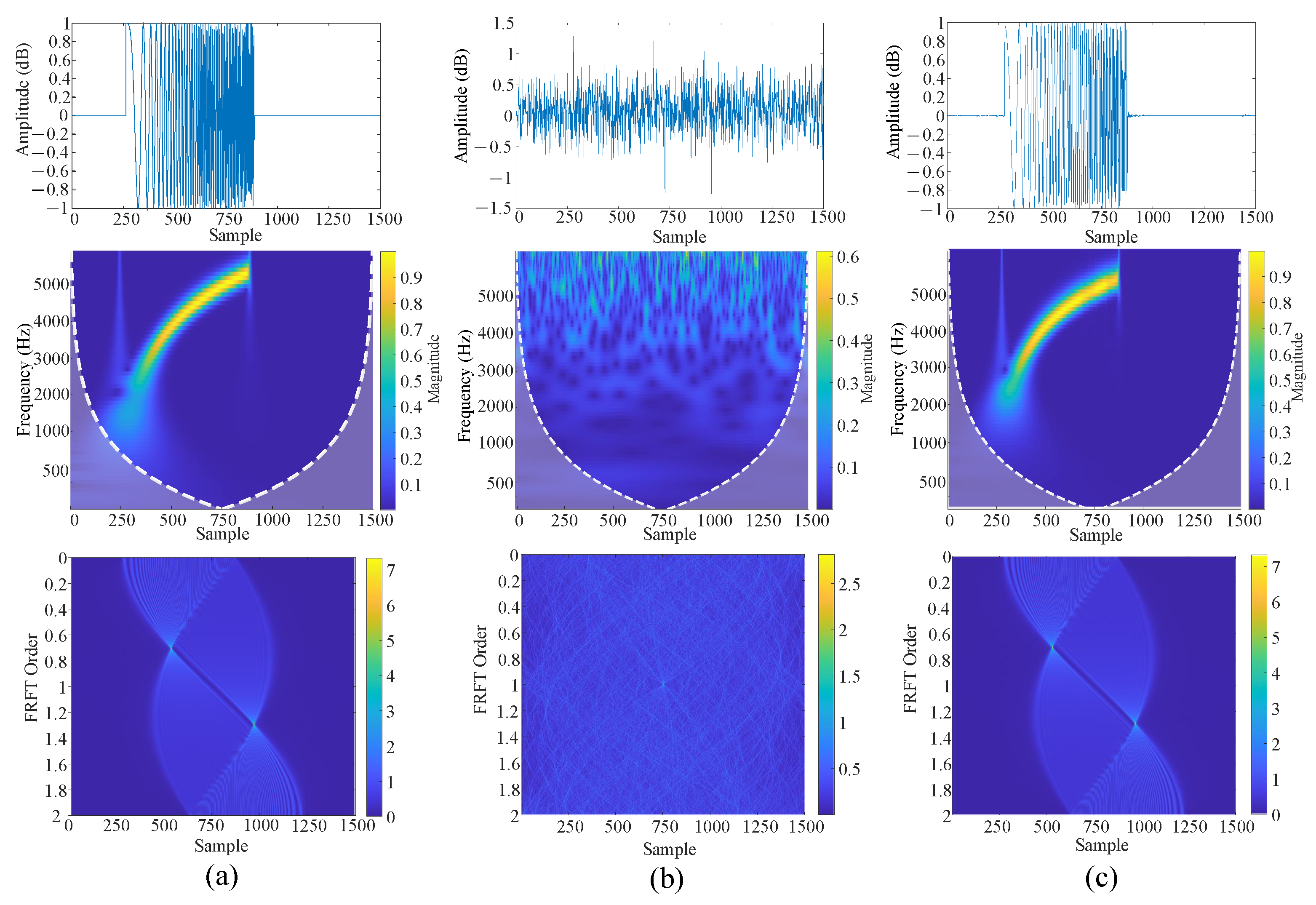
6.4. DC-WUnet Performance
6.5. Network Parameter and Execution Time Comparison
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reis, J.; Morgado, M.; Batista, P.; Oliveira, P.; Silvestre, C. Design and experimental validation of a usbl underwater acoustic positioning system. Sensors 2016, 16, 1491. [Google Scholar] [CrossRef] [PubMed]
- Kim, J. Hybrid toa–doa techniques for maneuvering underwater target tracking using the sensor nodes on the sea surface. Ocean Eng. 2021, 42, 110110. [Google Scholar] [CrossRef]
- Zhang, B.; Xiang, Y.; He, P.; Zhang, G.-j. Study on prediction methods and characteristics of ship underwater radiated noise within full frequency. Ocean Eng. 2019, 174, 61–70. [Google Scholar] [CrossRef]
- Smith, T.A.; Rigby, J. Underwater radiated noise from marine vessels: A review of noise reduction methods and technology. Ocean Eng. 2022, 266, 112863. [Google Scholar] [CrossRef]
- Tan, H.-P.; Diamant, R.; Seah, W.K.; Waldmeyer, M. A survey of techniques and challenges in underwater localization. Ocean Eng. 2011, 38, 1663–1676. [Google Scholar] [CrossRef]
- Rioul, O.; Duhamel, P. Fast algorithms for discrete and continuous wavelet transforms. IEEE Trans. Inf. Theory 1992, 38, 569–586. [Google Scholar] [CrossRef]
- Hariharan, S.M.; Kamal, S.; Pillai, S. Reduction of self-noise effects in onboard acoustic receivers of vessels using spectral subtraction. In Proceedings of the Acoustics 2012 Nantes Conference, Nantes, France, 23–27 April 2012. [Google Scholar]
- Czapiewska, A.; Luksza, A.; Studanski, R.; Zak, A. Reduction of the multipath propagation effect in a hydroacoustic channel using filtration in cepstrum. Sensors 2020, 20, 751. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, W.; Li, P.; Yang, S.; Tian, Y. An ultrahigh frequency partial discharge signal de-noising method based on a generalized s-transform and module time-frequency matrix. Sensors 2016, 16, 941. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-svd: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Yang, W.; Peng, Z.; Wei, K.; Shi, P.; Tian, W. Superiorities of variational mode decomposition over empirical mode decomposition particularly in time–frequency feature extraction and wind turbine condition monitoring. IET Renew. Power Gener. 2017, 11, 443–452. [Google Scholar] [CrossRef]
- Fu, S.-W.; Tsao, Y.; Lu, X.; Kawai, H. Raw waveform-based speech enhancement by fully convolutional networks. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 6–12. [Google Scholar] [CrossRef]
- Wang, H.; Wu, X.; Huang, Z.; Xing, E.P. High-frequency component helps explain the generalization of convolutional neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8684–8694. [Google Scholar]
- Yang, S.; Xue, L.; Hong, X.; Zeng, X. A lightweight network model based on an attention mechanism for ship-radiated noise classification. J. Mar. Sci. Eng. 2023, 11, 432. [Google Scholar] [CrossRef]
- Kumar Pc, K.; Palani, S.; Selvaraj, J.; Rajendran, V. De-noising algorithm for snr improvement of underwater acoustic signals using cwt based on fourier transform. Underw. Technol. 2018, 35, 23–30. [Google Scholar] [CrossRef]
- Barbarossa, S. Analysis of multicomponent lfm signals by a combined wigner-hough transform. IEEE Trans. Signal Process. 1995, 43, 1511–1515. [Google Scholar] [CrossRef]
- Dai, Y.; Xue, Y.; Zhang, J. A continuous wavelet transform approach for harmonic parameters estimation in the presence of impulsive noise. J. Sound Vib. 2016, 360, 300–314. [Google Scholar] [CrossRef]
- Li, S.; Zhao, J.; Wu, Y.; Bian, S.; Zhai, G. Prior frequency information assisted vmd method for sbp sonar data noise removal. IEEE Geosci. Remote Sens. Lett. 2023, 20, 7503905. [Google Scholar] [CrossRef]
- Xiao, F.; Yang, D.; Guo, X.; Wang, Y. Vmd-based denoising methods for surface electromyography signals. J. Neural Eng. 2019, 16, 056017. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Yang, H.; Li, L.; Li, G. A new denoising method for underwater acoustic signal. IEEE Access 2020, 8, 201874–201888. [Google Scholar] [CrossRef]
- Wu, Y.; Xing, C.; Zhang, D.; Xie, L. Low-frequency underwater acoustic signal denoising method in the shallow sea with a low signal-to-noise ratio. In Proceedings of the 2021 OES China Ocean Acoustics (COA), Harbin, China, 14–17 July 2021; pp. 731–735. [Google Scholar] [CrossRef]
- Ahmed, N.; Natarajan, T.; Rao, K.R. Discrete cosine transform. IEEE Trans. Comput. 1974, 100, 90–93. [Google Scholar] [CrossRef]
- Rubinstein, R.; Zibulevsky, M.; Elad, M. Efficient Implementation of the k-Svd Algorithm Using Batch Orthogonal Matching Pursuit. CS Technion Technical Report. 2008. Available online: https://www.researchgate.net/publication/251229200_Efficient_Implementation_of_the_K-SVD_Algorithm_Using_Batch_Orthogonal_Matching_Pursuit (accessed on 22 March 2025).
- Gogna, A.; Majumdar, A.; Ward, R. Semi-supervised stacked label consistent autoencoder for reconstruction and analysis of biomedical signals. IEEE Trans. Biomed. Eng. 2016, 64, 2196–2205. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhao, Y.; Teng, X.; Sun, W. A stacked convolutional sparse denoising autoencoder model for underwater heterogeneous information data. Appl. Acoust. 2020, 167, 107391. [Google Scholar] [CrossRef]
- Russo, P.; Ciaccio, F.D.; Troisi, S. Danae++: A smart approach for denoising underwater attitude estimation. Sensors 2021, 21, 1526. [Google Scholar] [CrossRef]
- Guimarães, H.R.; Nagano, H.; Silva, D.W. Monaural speech enhancement through deep wave-u-net. Expert Syst. Appl. 2020, 158, 113582. [Google Scholar] [CrossRef]
- Macartney, C.; Weyde, T. Improved speech enhancement with the wave-u-net. arXiv 2018, arXiv:1811.11307. [Google Scholar]
- Chu, H.; Li, C.; Wang, H.; Wang, J.; Tai, Y.; Zhang, Y.; Yang, F.; Benezeth, Y. A deep-learning based high-gain method for underwater acoustic signal detection in intensity fluctuation environments. Appl. Acoust. 2023, 211, 109513. [Google Scholar] [CrossRef]
- Luo, Y.; Mesgarani, N. Conv-tasnet: Surpassing ideal time–frequency magnitude masking for speech separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2019, 27, 1256–1266. [Google Scholar] [CrossRef]
- Irfan, M.; Jiangbin, Z.; Ali, S.; Iqbal, M.; Masood, Z.; Hamid, U. Deepship: An underwater acoustic benchmark dataset and a separable convolution based autoencoder for classification. Expert Syst. Appl. 2021, 183, 115270. [Google Scholar] [CrossRef]
- Gul, S.; Zaidi, S.S.H.; Khan, R.; Wala, A.B. Underwater acoustic channel modeling using bellhop ray tracing method. In Proceedings of the 2017 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 10–14 January 2017; pp. 665–670. [Google Scholar] [CrossRef]
- Kuniyoshi, S.; Oshiro, S.; Saotome, R.; Wada, T. An iterative orthogonal frequency division multiplexing receiver with sequential inter-carrier interference canceling modified delay and doppler profiler for an underwater multipath channel. J. Mar. Sci. Eng. 2024, 12, 1712. [Google Scholar] [CrossRef]
- Neipp, C.; Hernández, A.; Rodes, J.; Márquez, A.; Beléndez, T.; Beléndez, A. An analysis of the classical doppler effect. Eur. J. Phys. 2003, 24, 497. [Google Scholar] [CrossRef]
- Li, B.; Zhou, S.; Stojanovic, M.; Freitag, L.; Willett, P. Multicarrier communication over underwater acoustic channels with nonuniform doppler shifts. IEEE J. Ocean Eng. 2008, 33, 198–209. [Google Scholar] [CrossRef]
- Qu, F.; Wang, Z.; Yang, L.; Wu, Z. A journey toward modeling and resolving doppler in underwater acoustic communications. IEEE Commun. Mag. 2016, 54, 49–55. [Google Scholar] [CrossRef]
- Abdelkareem, A.E.; Sharif, B.S.; Tsimenidis, C.C. Adaptive time varying doppler shift compensation algorithm for ofdm-based underwater acoustic communication systems. Ad Hoc Netw. 2016, 45, 104–119. [Google Scholar] [CrossRef]
- Tanaka, S.; Nomura, H.; Kamakura, T. Doppler shift equation and measurement errors affected by spatial variation of the speed of sound in sea water. Ultrasonics 2019, 94, 65–73. [Google Scholar] [CrossRef]
- Porter, M.B. The Bellhop Manual and User’s Guide: Preliminary Draft; Heat, Light, and Sound Research, Inc.: La Jolla, CA, USA, 2011; Volume 260. [Google Scholar]
- Gulati, A.; Qin, J.; Chiu, C.-C.; Parmar, N.; Zhang, Y.; Yu, J.; Han, W.; Wang, S.; Zhang, Z.; Wu, Y.; et al. Conformer: Convolution-augmented transformer for speech recognition. arXiv 2020, arXiv:2005.08100. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A self-gated activation function. arXiv 2017, arXiv:1710.05941; Volume 7, p. 5. [Google Scholar]
- Bridle, J. Training Stochastic Model Recognition Algorithms as Networks Can Lead to Maximum Mutual Information Estimation of Parameters. Available online: https://proceedings.neurips.cc/paper_files/paper/1989/file/0336dcbab05b9d5ad24f4333c7658a0e-Paper.pdf (accessed on 22 March 2025).
- Dauphin, Y.N.; Fan, A.; Auli, M.; Grangier, D. Language modeling with gated convolutional networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, NSW, Australia, 6–11 August 2017; pp. 933–941. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
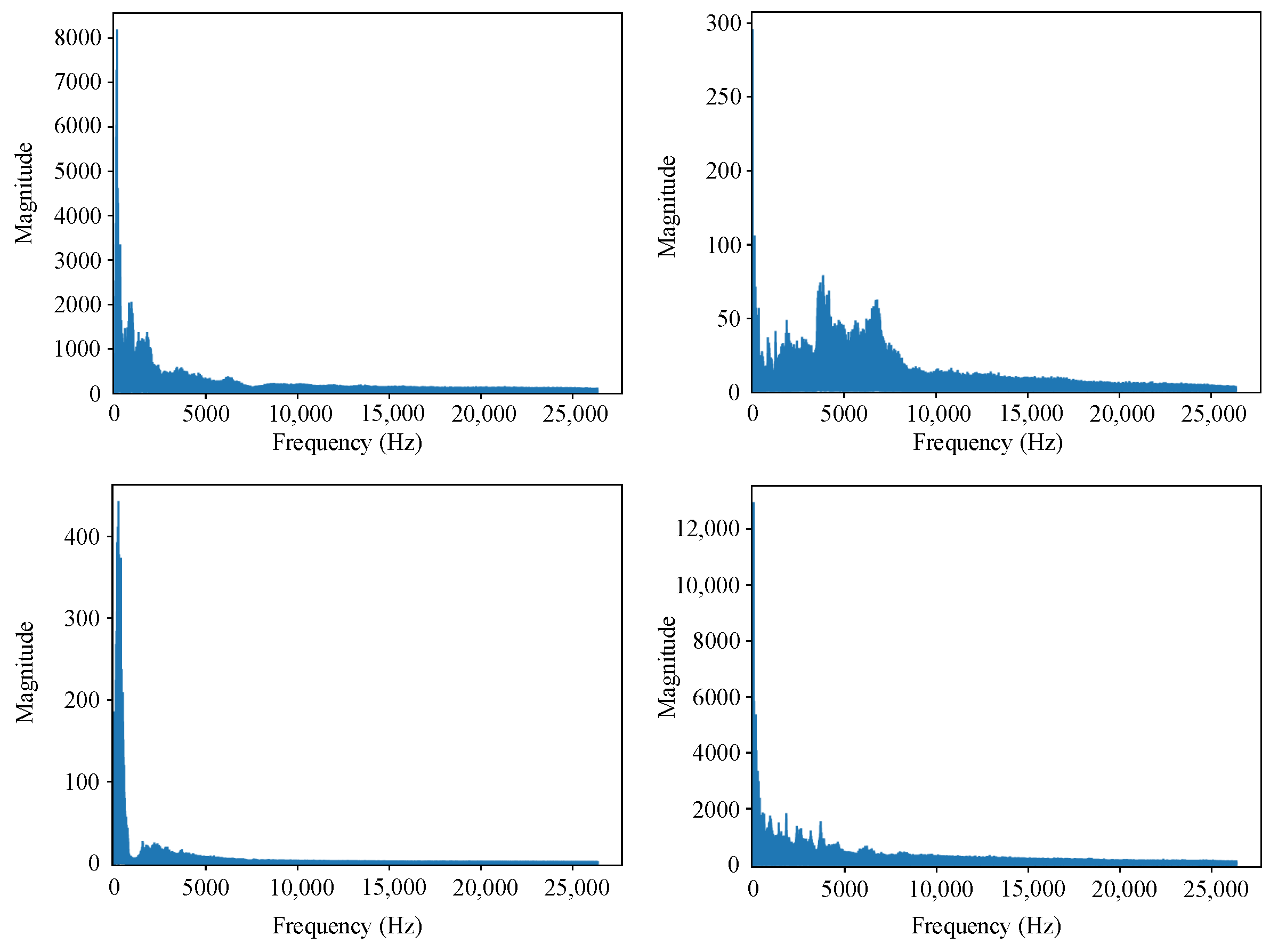







| Block | Operation | Shape (C,T) | |
|---|---|---|---|
| Input | (1, 1000) | ||
| Encoder () | DSConv | DWConv PWConv | (56, 4) |
| Conformer Add | |||
| Middle | DSConv | (64, 2) | |
| Decoder | Upsample Concat Conv | (8, 1000) | |
| Conv | (1, 1000) | ||
| Module | Parameter | Value |
|---|---|---|
| LFM | Amplitude A | 1 |
| Length T | 500 samples | |
| Initial phase | 0° | |
| FM slope | 600 kHz/s | |
| Starting frequency | 1 kHz | |
| Multipath Doppler | Channel environment | SWellEx96.env |
| Detection distance | 50∼200 m | |
| Launch angle | −10∼10° | |
| Relative vessel speed | 0.926∼9.260 km/h | |
| Relative ocean current speed | 9.260∼16.668 km/h |
| SNR | —10 | —7.5 | —5 | —2.5 | 0 | 2.5 | 5 | 7.5 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| Noisy | 0.281 | 0.317 | 0.343 | 0.408 | 0.436 | 0.481 | 0.479 | 0.489 | 0.500 |
| VMD-CWT [20] | 0.251 | 0.330 | 0.420 | 0.481 | 0.500 | 0.544 | 0.561 | 0.540 | 0.548 |
| K-SVD [23] | 0.315 | 0.343 | 0.373 | 0.421 | 0.450 | 0.485 | 0.497 | 0.490 | 0.511 |
| SAE [26] | 0.500 | 0.580 | 0.700 | 0.768 | 0.827 | 0.876 | 0.903 | 0.925 | 0.934 |
| Wave-Unet [29] | 0.540 | 0.671 | 0.721 | 0.819 | 0.870 | 0.902 | 0.929 | 0.948 | 0.958 |
| Conv-Tasnet [31] | 0.590 | 0.700 | 0.760 | 0.823 | 0.830 | 0.895 | 0.945 | 0.932 | 0.947 |
| DC-WUnet | 0.660 | 0.754 | 0.810 | 0.861 | 0.910 | 0.923 | 0.943 | 0.950 | 0.960 |
| C-WUnet | 0.700 | 0.776 | 0.795 | 0.889 | 0.917 | 0.941 | 0.955 | 0.986 | 0.971 |
| SNR | —10 | —7.5 | —5 | —2.5 | 0 | 2.5 | 5 | 7.5 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| VMD-CWT [20] | —4.54 | —2.92 | —1.21 | 1.45 | 6.38 | 8.26 | 11.40 | 14.53 | 17.57 |
| K-SVD [23] | —3.37 | —1.12 | —0.11 | 3.86 | 8.18 | 9.80 | 14.53 | 16.24 | 18.21 |
| SAE [26] | 16.42 | 20.27 | 23.77 | 25.54 | 26.85 | 27.22 | 28.91 | 29.42 | 30.12 |
| Wave-Unet [29] | 17.20 | 20.96 | 23.92 | 27.23 | 29.37 | 30.64 | 30.92 | 31.55 | 31.71 |
| Conv-Tasnet [31] | 18.38 | 21.70 | 25.94 | 28.11 | 29.85 | 30.12 | 31.50 | 31.24 | 30.94 |
| DC-WUnet | 20.61 | 24.44 | 28.16 | 31.38 | 32.32 | 31.82 | 32.46 | 32.67 | 32.56 |
| C-WUnet | 21.88 | 25.52 | 28.36 | 31.91 | 32.23 | 32.56 | 32.75 | 32.61 | 32.72 |
| Network | Number of Parameters | Speed (s) | FLOPs |
|---|---|---|---|
| SAE [26] | 1.404 M | 2.53 | 0.62 G |
| Conv-Tasnet [31] | 2.686 M | 5.72 | 1.27 G |
| Wave-Unet [29] | 1.505 M | 4.57 | 0.66 G |
| C-WUnet | 1.616 M | 4.53 | 0.72 G |
| DC-WUnet | 1.481 M | 2.15 | 0.56 G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, J.; Zhang, J.; Bai, Y.; Cui, Z. DC-WUnet: An Underwater Ranging Signal Enhancement Network Optimized with Depthwise Separable Convolution and Conformer. J. Mar. Sci. Eng. 2025, 13, 956. https://doi.org/10.3390/jmse13050956
Liu X, Li J, Zhang J, Bai Y, Cui Z. DC-WUnet: An Underwater Ranging Signal Enhancement Network Optimized with Depthwise Separable Convolution and Conformer. Journal of Marine Science and Engineering. 2025; 13(5):956. https://doi.org/10.3390/jmse13050956
Chicago/Turabian StyleLiu, Xiaosen, Juan Li, Jingyao Zhang, Yajie Bai, and Zhaowei Cui. 2025. "DC-WUnet: An Underwater Ranging Signal Enhancement Network Optimized with Depthwise Separable Convolution and Conformer" Journal of Marine Science and Engineering 13, no. 5: 956. https://doi.org/10.3390/jmse13050956
APA StyleLiu, X., Li, J., Zhang, J., Bai, Y., & Cui, Z. (2025). DC-WUnet: An Underwater Ranging Signal Enhancement Network Optimized with Depthwise Separable Convolution and Conformer. Journal of Marine Science and Engineering, 13(5), 956. https://doi.org/10.3390/jmse13050956





