YOLO-LPSS: A Lightweight and Precise Detection Model for Small Sea Ships
Abstract
1. Introduction
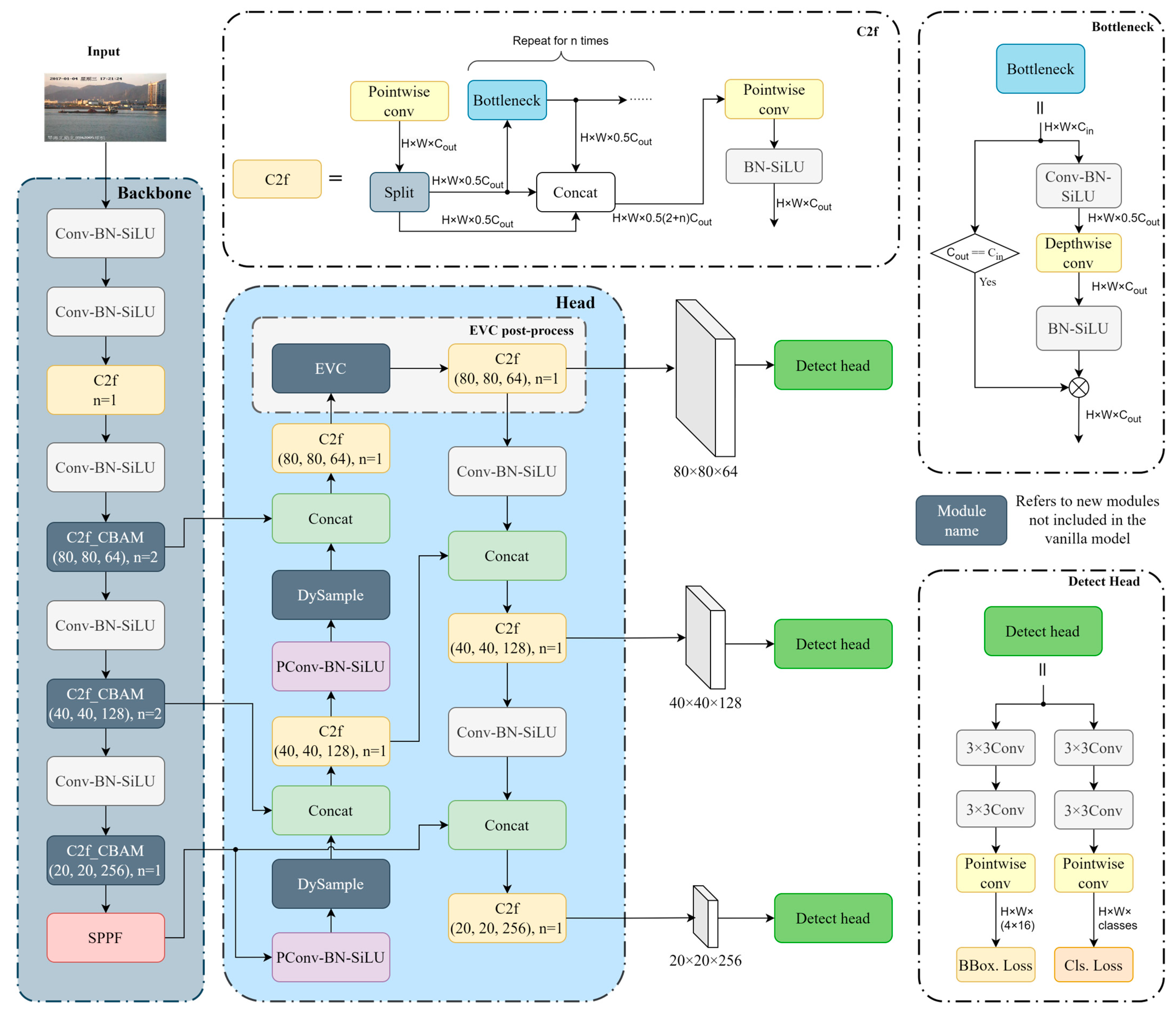
2. Proposed Model
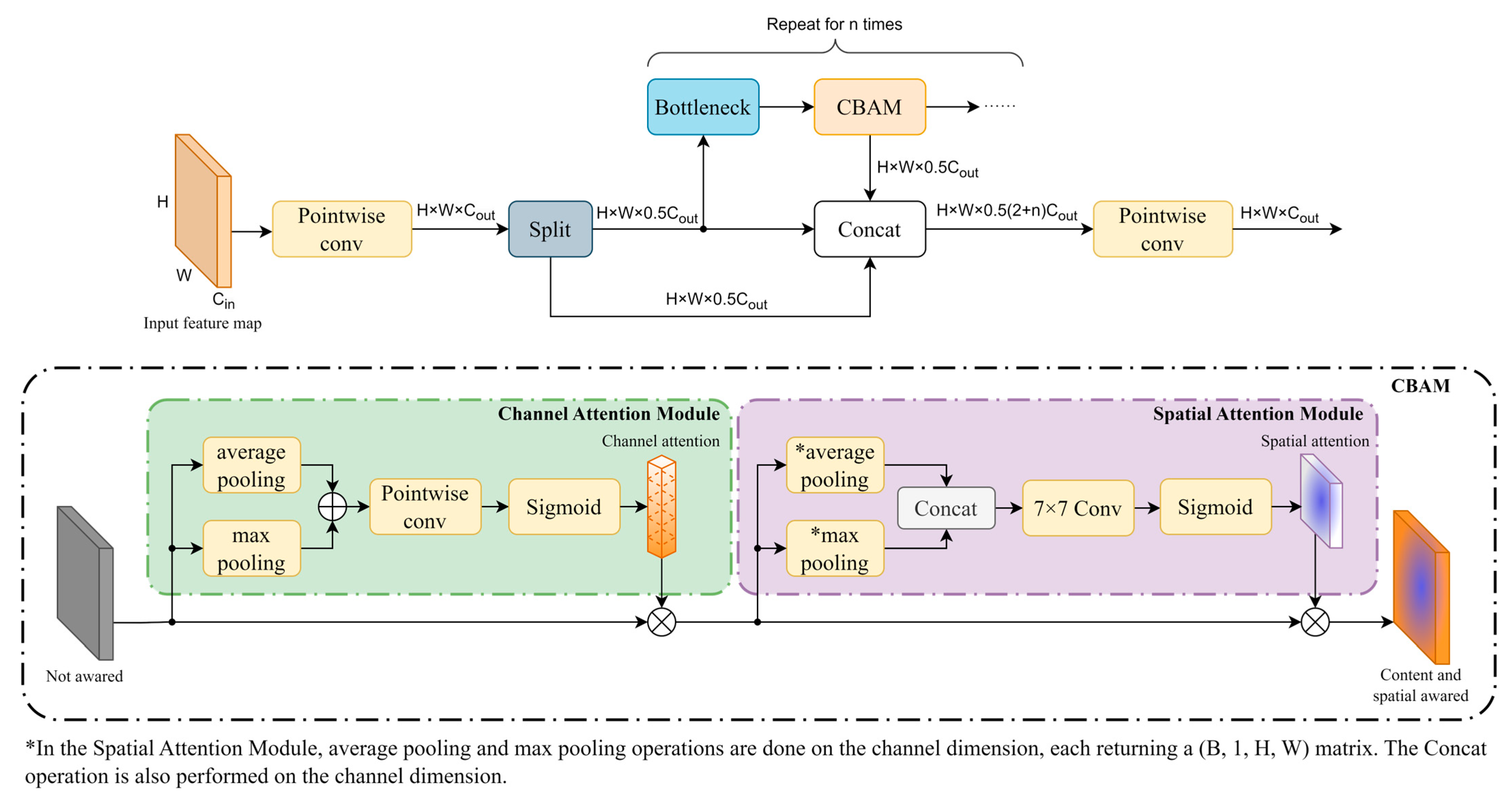
2.1. Attention Mechanism
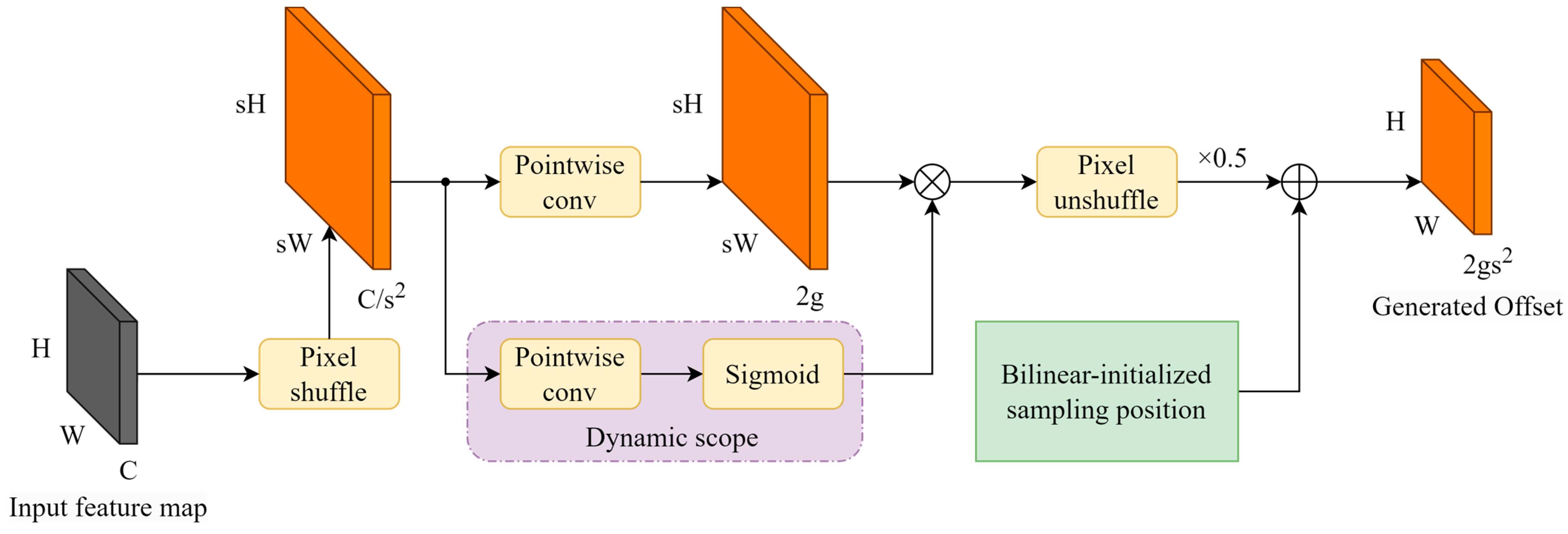
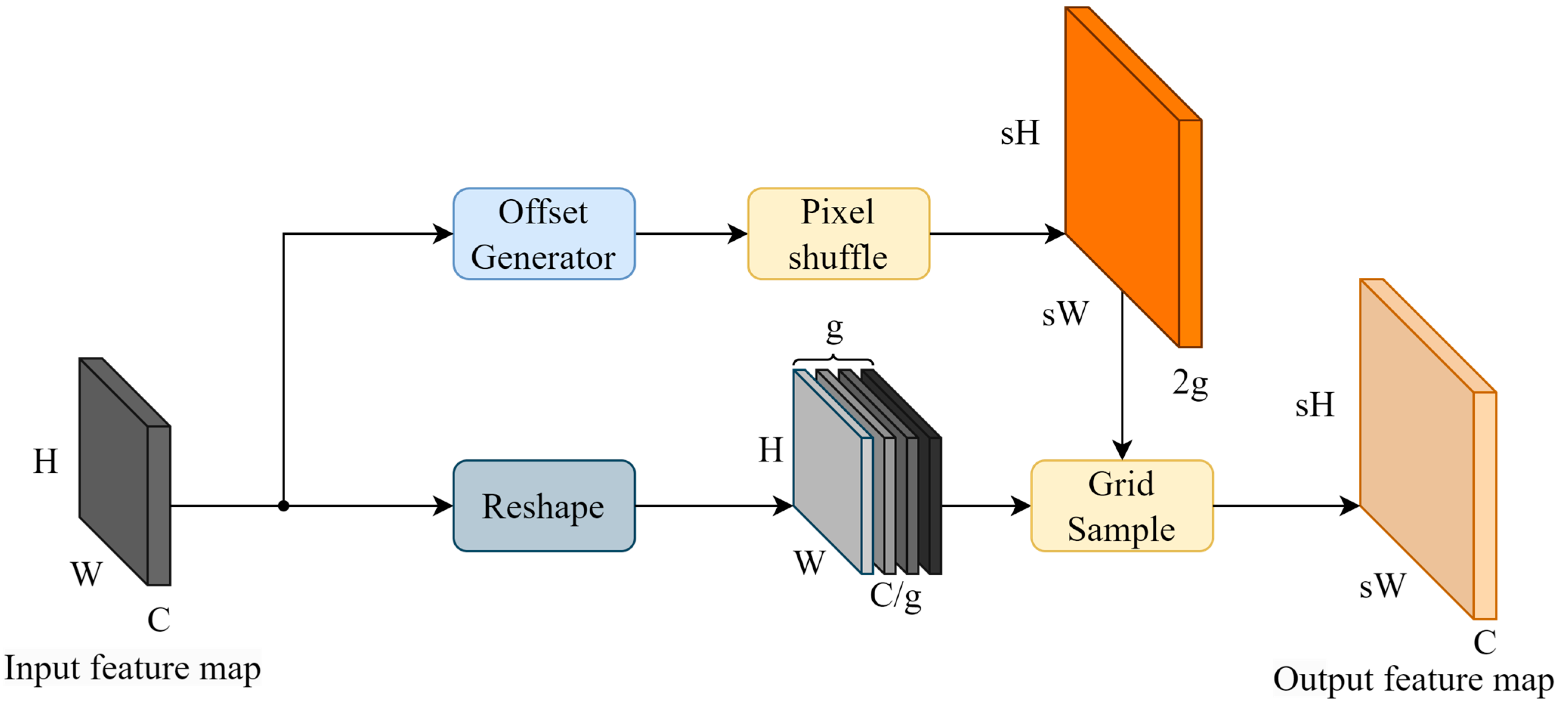
2.2. Learnable Up-Sample
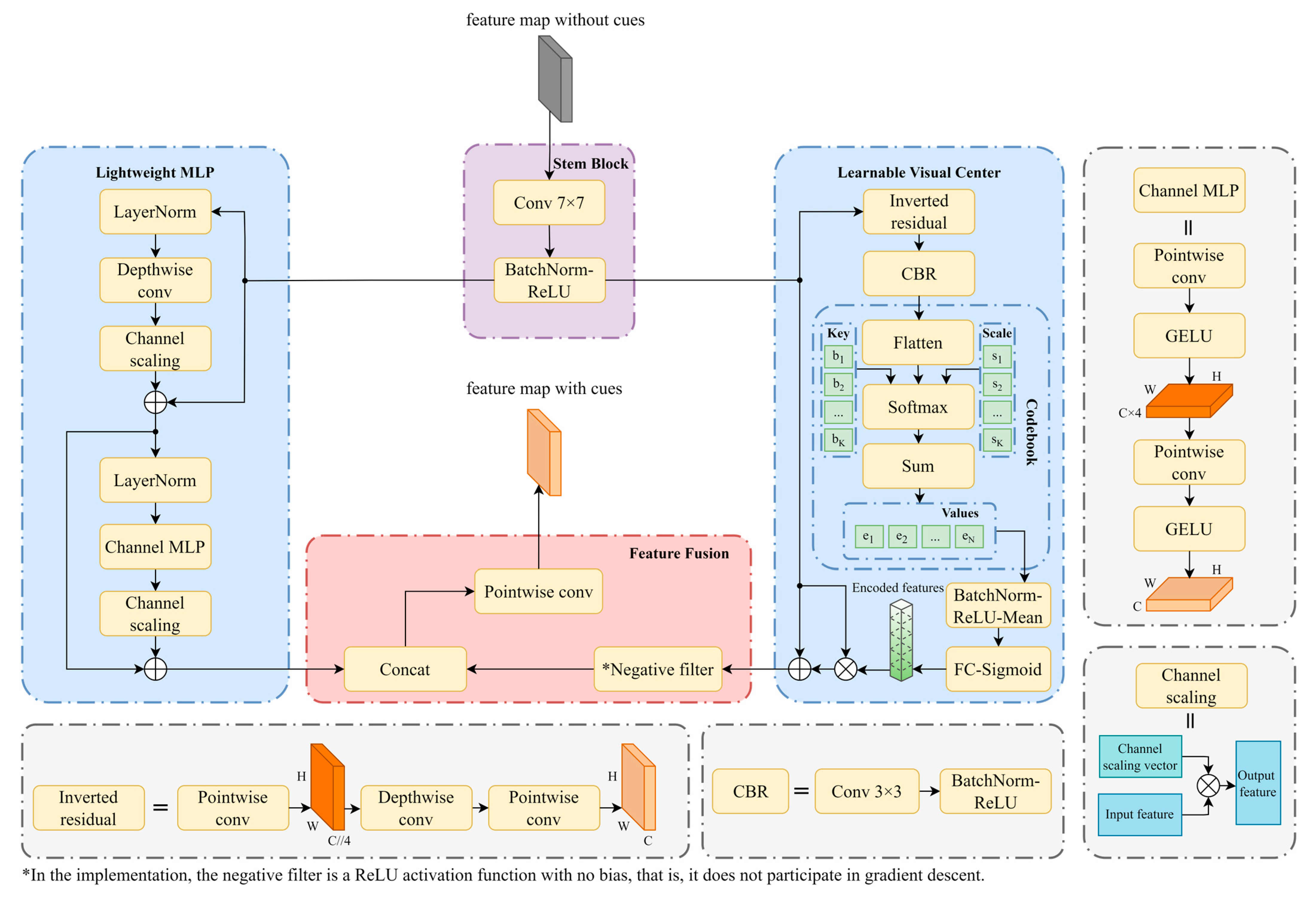
2.3. EVC Post-Process
2.3.1. LMLP Mechanism
2.3.2. LVC Mechanism
3. Experimental Results and Analysis
3.1. Subsection
3.2. Model Evaluation Metrics
3.3. Experimental Results of YOLO-LPSS
3.3.1. Ablation Experiments
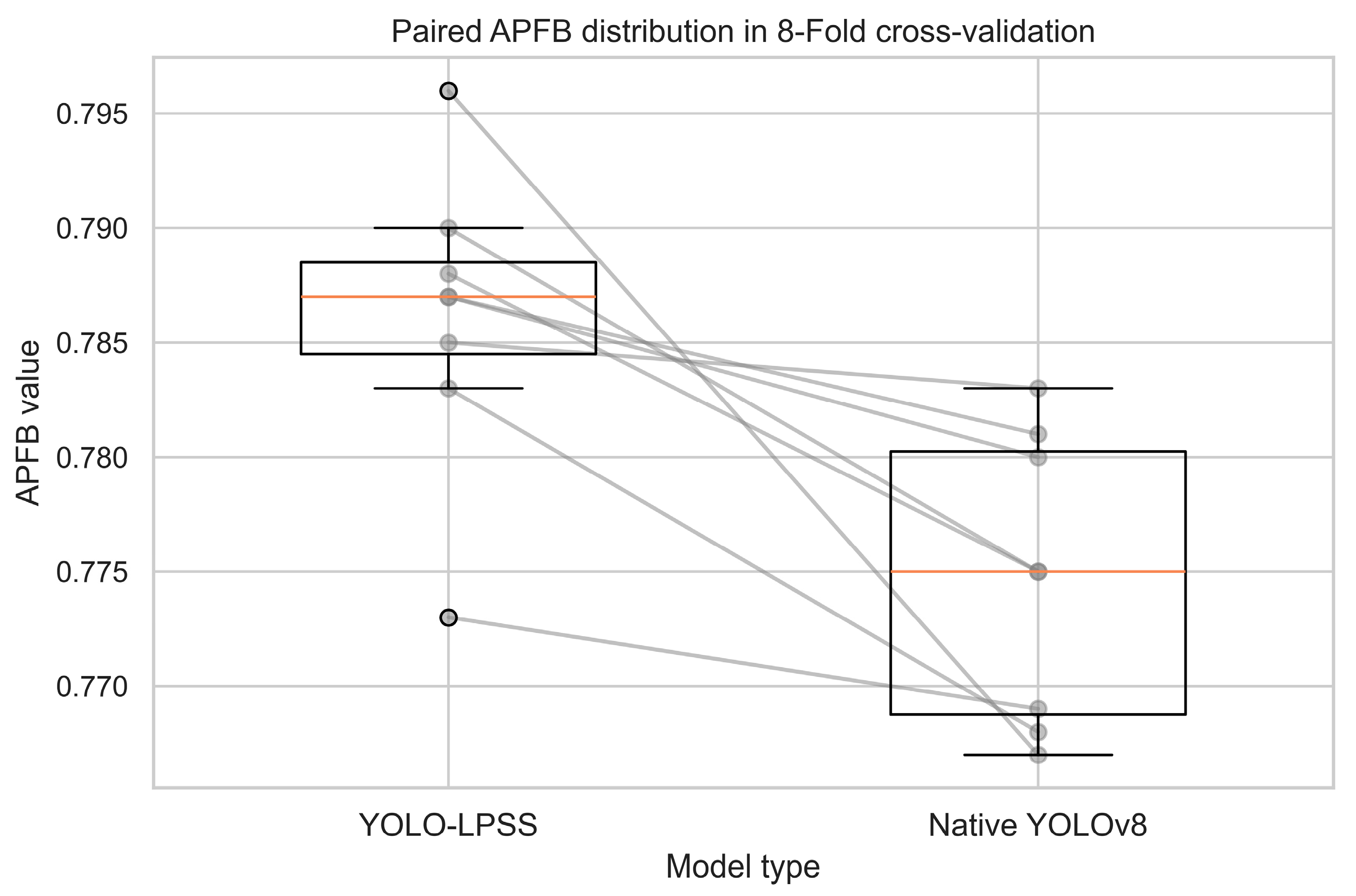
3.3.2. Paired Sample t-Test
3.3.3. Deep Look at the EVC
3.3.4. Comparisons with Different Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, X.; Cai, J.; Wang, B.A. Yoloseaship: A lightweight model for real-time ship detection. Eur. J. Remote Sens. 2024, 57, 2307613. [Google Scholar] [CrossRef]
- Cheng, B.; Xu, X.; Zeng, Y.; Ren, J.; Jung, S. Pedestrian trajectory prediction via the Social-Grid LSTM model. J. Eng. 2018, 2018, 1468–1474. [Google Scholar] [CrossRef]
- Corbane, C.; Najman, L.; Pecoul, E.; Demagistri, L.; Petit, M. A complete processing chain for ship detection using optical satellite imagery. Int. J. Remote Sens. 2010, 31, 5837–5854. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.; Zang, F. Ship detection for visual maritime surveillance from non-stationary platforms. Ocean Eng. 2017, 141, 53–63. [Google Scholar] [CrossRef]
- Chen, X.; Hu, R.; Luo, K.; Wu, H.; Biancardo, S.A.; Zheng, Y.; Xian, J. Intelligent ship route planning via an A∗ search model enhanced double-deep Q-network. Ocean Eng. 2025, 327, 120956. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chang, Y.; Anagaw, A.; Chang, L.; Wang, Y.C.; Hsiao, C.; Lee, W. Ship detection based on yolov2 for sar imagery. Remote Sens. 2019, 11, 786. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, J.; Weng, L.; Yang, Y. Rotated region based cnn for ship detection. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 900–904. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Uijlings, J.R.R.; van de Sande, K.E.A.; Gevers, T.; Smeulders, A.W.M. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1703–6870. [Google Scholar] [CrossRef]
- Li, Y.; Xie, S.; Chen, X.; Dollar, P.; He, K.; Girshick, R. Benchmarking detection transfer learning with vision transformers. arXiv 2021, arXiv:2111.11429. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Wang, C.; Bochkovskiy, A.; Liao, H.M. Yolov7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2022; pp. 2207–2696. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Lin, T.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2016; pp. 1612–3144. [Google Scholar] [CrossRef]
- Fu, K.; Li, Y.; Sun, H.; Yang, X.; Xu, G.; Li, Y.; Sun, X. A ship rotation detection model in remote sensing images based on feature fusion pyramid network and deep reinforcement learning. Remote Sens. 2018, 10, 1922. [Google Scholar] [CrossRef]
- Ziyu, W.; Tom, S.; Matteo, H.; Hado, H.; Marc, L.; Nando, F. Dueling network architectures for deep reinforcement learning. In Proceedings of the Machine Learning Research, New York, NY, USA, 19–24 June 2016; Maria, F.B., Kilian, Q.W., Eds.; JMLR. 2016; pp. 1995–2003. [Google Scholar]
- Wen, G.; Cao, P.; Wang, H.; Chen, H.; Liu, X.; Xu, J.; Zaiane, O. Ms-ssd: Multi-scale single shot detector for ship detection in remote sensing images. Appl. Intell. 2023, 53, 1586–1604. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, Y. Ship detection based on multi-scale weighted fusion. Displays 2023, 78, 102448. [Google Scholar] [CrossRef]
- Sun, Z.; Dai, M.; Leng, X.; Lei, Y.; Xiong, B.; Ji, K.; Kuang, G. An anchor-free detection method for ship targets in high-resolution sar images. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 7799–7816. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, C.; Fu, Q. Ofcos: An oriented anchor-free detector for ship detection in remote sensing images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6004005. [Google Scholar] [CrossRef]
- Feng, C.; Zhong, Y.; Gao, Y.; Scott, M.R.; Huang, W. Tood: Task-aligned one-stage object detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 3490–3499. [Google Scholar]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. arXiv 2020, arXiv:2006.04388. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.; Kweon, I.S. Cbam: Convolutional block attention module. arXiv 2018, arXiv:1807.06521. [Google Scholar] [CrossRef]
- Liu, W.; Lu, H.; Fu, H.; Cao, Z. Learning to upsample by learning to sample. arXiv 2023, arXiv:2308.15085. [Google Scholar] [CrossRef]
- Quan, Y.; Zhang, D.; Zhang, L.; Tang, J. Centralized feature pyramid for object detection. IEEE Trans. Image Process. 2023, 32, 4341–4354. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. arXiv 2016, arXiv:1610.02357. [Google Scholar] [CrossRef]
- Sergey, I.; Christian, S. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the Machine Learning Research, Lille, France, 6–11 July 2015; Francis, B., David, B., Eds.; JMLR. 2015; pp. 448–456. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar] [CrossRef]
- Kopf, J.; Cohen, M.F.; Lischinski, D.; Uyttendaele, M. Joint bilateral upsampling. ACM Trans. Graph. (ToG) 2007, 26, 96. [Google Scholar] [CrossRef]
- Wang, J.; Chen, K.; Xu, R.; Liu, Z.; Loy, C.C.; Lin, D. Carafe: Content-aware reassembly of features. arXiv 2019, arXiv:1905.02188. [Google Scholar] [CrossRef]
- Lu, H.; Liu, W.; Fu, H.; Cao, Z. Fade: Fusing the assets of decoder and encoder for task-agnostic upsampling. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2022; pp. 231–247. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. arXiv 2016, arXiv:1609.05158. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. arXiv 2015, arXiv:1506.02025. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Yu, W.; Luo, M.; Zhou, P.; Si, C.; Zhou, Y.; Wang, X.; Feng, J.; Yan, S. Metaformer is actually what you need for vision. arXiv 2021, arXiv:2111.11418. [Google Scholar] [CrossRef]
- Tolstikhin, I.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; et al. Mlp-mixer: An all-mlp architecture for vision. arXiv 2021, arXiv:2105.01601. [Google Scholar] [CrossRef]
- Larsson, G.; Maire, M.; Shakhnarovich, G. Fractalnet: Ultra-deep neural networks without residuals. arXiv 2016, arXiv:1605.07648. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. Mobilenetv2: Inverted residuals and linear bottlenecks. arXiv 2018, arXiv:1801.04381. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, W.; Wang, Z.; Du, W.; Li, C. Seaships: A large-scale precisely annotated dataset for ship detection. IEEE Trans. Multimed. 2018, 20, 2593–2604. [Google Scholar] [CrossRef]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the 19th International Conference on Computational Statistics, Paris, France, 22–27 August 2010; pp. 177–186. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. arXiv 2016, arXiv:1610.02391. [Google Scholar] [CrossRef]
- Jocher, G.; Chaurasia, A.; Stoken, A.; Borovec, J.; Kwon, Y.; Michael, K.; Fang, J.; Wong, C.; Yifu, Z.; Montes, D. Ultralytics/yolov5: v6.0—YOLOv5n ‘Nano’ Models, Roboflow Integration, TensorFlow Export, OpenCV DNN Support. Zenodo. 2021. Available online: https://zenodo.org/records/5563715 (accessed on 4 May 2025).
- Zhao, Y.; Lv, W.; Xu, S.; Wei, J.; Wang, G.; Dang, Q.; Liu, Y.; Chen, J. Detrs beat yolos on real-time object detection. arXiv 2023, arXiv:2304.08069. [Google Scholar] [CrossRef]
- Khalili, B.; Smyth, A.W. SOD-YOLOv8—Enhancing YOLOv8 for Small Object Detection in Aerial Imagery and Traffic Scenes. Sensors 2024, 24, 6209. [Google Scholar] [CrossRef]




| Bulk Cargo Carrier | Container Ship | Fishing Boat | General Cargo Ship | Ore Carrier | Passenger Ship | |
|---|---|---|---|---|---|---|
| Total instances | 1952 | 901 | 2190 | 1505 | 2199 | 474 |
| Small instances | 935 | 509 | 1927 | 542 | 1197 | 333 |
| Percentage | 47.90% | 56.49% | 87.99% | 36.01% | 54.43% | 70.25% |
| Categories | Bulk Cargo Carrier | Container Ship | Fishing Boat | General Cargo Ship | Ore Carrier | Passenger Ship | |
|---|---|---|---|---|---|---|---|
| Metrics | |||||||
| Precision | 0.965 | 0.999 | 0.957 | 0.993 | 0.976 | 0.965 | |
| Recall | 0.98 | 0.998 | 0.929 | 0.99 | 0.988 | 0.976 | |
| AP50 | 0.985 | 0.995 | 0.976 | 0.995 | 0.984 | 0.986 | |
| AP50:95 | 0.847 | 0.872 | 0.767 | 0.842 | 0.813 | 0.795 | |
| mAP50 | 0.987 | ||||||
| mAP50:95 | 0.823 | ||||||
| Metrics | Precision | Recall | mAP50 | mAP50:95 | APFB | APPS | GFLOPs | Parameters (M) | Inference Time (ms) | CPU FP32 Inference Time (ms) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | |||||||||||
| YOLOv8 nano (Baseline) | 0.974 | 0.977 | 0.987 | 0.823 | 0.767 | 0.795 | 8.1 | 3.01 | 2.9 | 11.4 | |
| YOLOv8-CBAM | 0.975 | 0.974 | 0.990 | 0.841 (+1.8%) | 0.781 (+1.4%) | 0.814 (+1.9%) | 8.1 | 3.03 | 3.0 | 13.1 | |
| YOLOv8-DySample | 0.974 | 0.976 | 0.986 | 0.828 (+0.5%) | 0.776 (+0.9%) | 0.808 (+1.3%) | 8.2 | 3.02 | 2.3 | 14.2 | |
| YOLOv8-EVC | 0.969 | 0.978 | 0.984 | 0.817 (−0.6%) | 0.777 (+1.0%) | 0.811 (+1.6%) | 11.8 | 3.31 | 3.2 | 16.3 | |
| YOLOv8-CBAM + EVC | 0.969 | 0.974 | 0.985 | 0.824 (−1.7%) | 0.790 (+0.9%) | 0.827 (+1.3%) | 11.8 | 3.34 | 3.3 | 20.6 | |
| YOLOv8-CBAM+ EVC + DySample(Ours) | 0.973 | 0.980 | 0.987 | 0.831 (+0.7%) | 0.796
(+0.6%) | 0.831
(+0.4%) | 11.8 | 3.34 | 2.4 | 23.9 | |
| t-Test Result | p-Value | T-Statistic | |
|---|---|---|---|
| Metrics | |||
| APFB | 0.008 | 3.698 | |
| APPS | 0.038 | 2.553 | |
| Metrics | Precision | Recall | mAP50 | mAP50:95 | APFB | APPS | GFLOPs | Parameters (M) | Inference Time (ms) | CPU FP32 Inference Time (ms) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | |||||||||||
| YOLO-LPSS (64 channels) | 0.973 | 0.980 | 0.987 | 0.838 | 0.796 | 0.831 | 11.8 | 3.34 | 2.4 | 23.9 | |
| YOLO-LPSS (128 channels) | 0.969 | 0.974 | 0.985 | 0.834 | 0.797 | 0.834 | 21.3 | 4.10 | 4.7 | 78.4 | |
| Metrics | Total CUDA Time (64 Channels) (ms) | Top 10 Time-Consuming CUDA Operator Calls (64 Channels) | Total CUDA Time (128 Channels) (ms) | Top 10 Time-Consuming CUDA Operator Calls (128 Channels) | |
|---|---|---|---|---|---|
| Precision | |||||
| Full precision (FP32) | 21.271 | 16 | 39.534 | 22 | |
| Half precision (FP16) | 15.509 | 16 | 27.446 | 16 | |
| Metrics | Precision | Recall | mAP50 | mAP50:95 | APFB | APPS | GFLOPs | Parameters (M) | Inference Time (ms) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Models | ||||||||||
| Faster R-CNN (ResNet-50-FPN) | 0.872 | 0.915 | 0.924 | 0.788 | 0.653 | 0.719 | 431.1 | 41.32 | 46.6 | |
| YOLOv3 | 0.958 | 0.969 | 0.983 | 0.809 | 0.740 | 0.792 | 19.0 | 12.13 | 2.3 | |
| YOLOv5 | 0.973 | 0.976 | 0.989 | 0.835 | 0.779 | 0.808 | 24.1 | 9.12 | 3.2 | |
| RT-DETR | 0.979 | 0.985 | 0.988 | 0.831 | 0.780 | 0.796 | 103.5 | 32.00 | 12.9 | |
| W. Zhou et al. | 0.958 | 0.978 | 0.989 | 0.812 | 0.764 | 0.813 | 27.7 | 12.40 | 3.5 | |
| YOLOSeaship | 0.953 | 0.944 | 0.977 | 0.751 | 0.702 | 0.732 | 24.7 | 6.48 | 2.5 | |
| SOD-YOLOv8 | 0.965 | 0.972 | 0.984 | 0.824 | 0.792 | 0.803 | 38.2 | 11.93 | 5.0 | |
| YOLO-LPSS | 0.973 | 0.980 | 0.987 | 0.831 | 0.796 | 0.831 | 11.8 | 3.34 | 2.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, L.; Gao, T.; Yin, Q. YOLO-LPSS: A Lightweight and Precise Detection Model for Small Sea Ships. J. Mar. Sci. Eng. 2025, 13, 925. https://doi.org/10.3390/jmse13050925
Shen L, Gao T, Yin Q. YOLO-LPSS: A Lightweight and Precise Detection Model for Small Sea Ships. Journal of Marine Science and Engineering. 2025; 13(5):925. https://doi.org/10.3390/jmse13050925
Chicago/Turabian StyleShen, Liran, Tianchun Gao, and Qingbo Yin. 2025. "YOLO-LPSS: A Lightweight and Precise Detection Model for Small Sea Ships" Journal of Marine Science and Engineering 13, no. 5: 925. https://doi.org/10.3390/jmse13050925
APA StyleShen, L., Gao, T., & Yin, Q. (2025). YOLO-LPSS: A Lightweight and Precise Detection Model for Small Sea Ships. Journal of Marine Science and Engineering, 13(5), 925. https://doi.org/10.3390/jmse13050925





