Hydrodynamic Analysis of Combined Offshore Wind Turbine and Net Cage Under Finite-Depth Waves
Abstract
1. Introduction
2. Methods
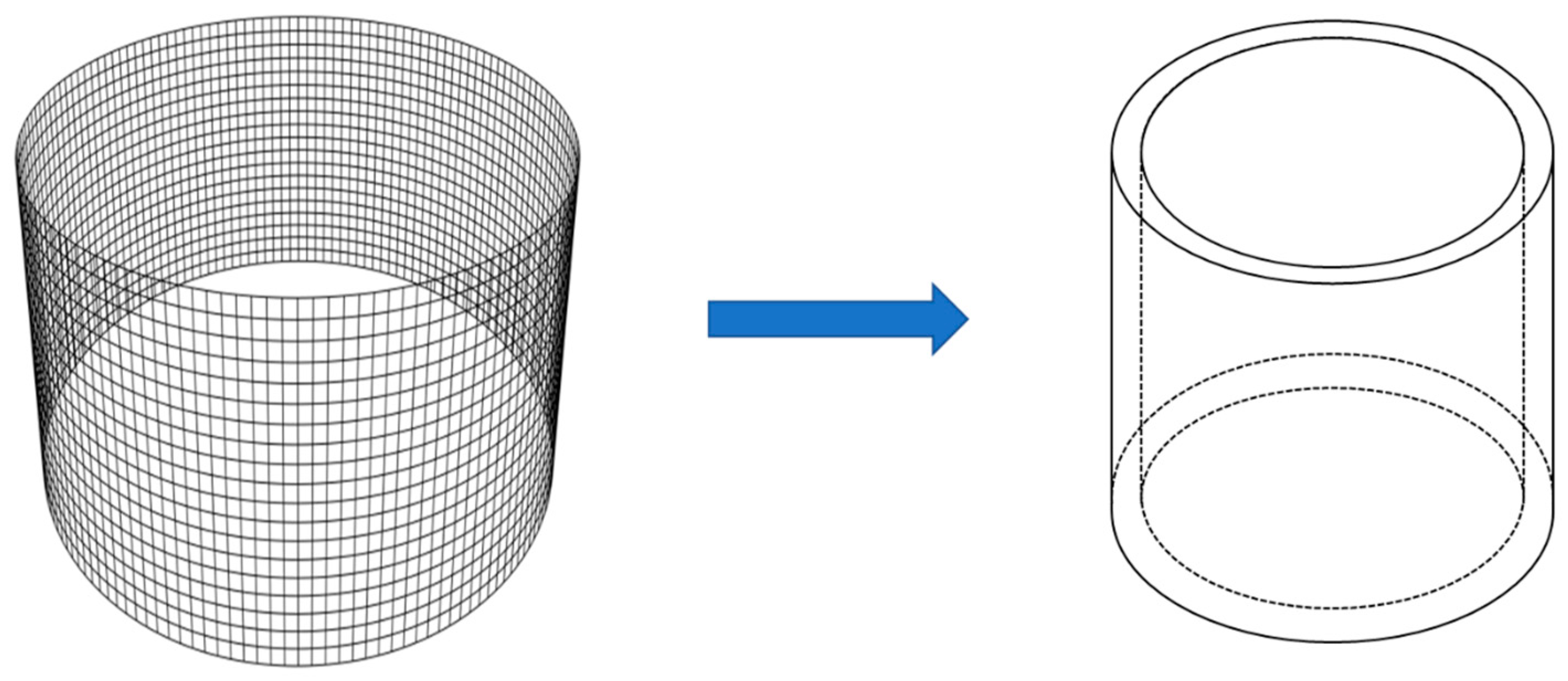
2.1. Porous Medium Model
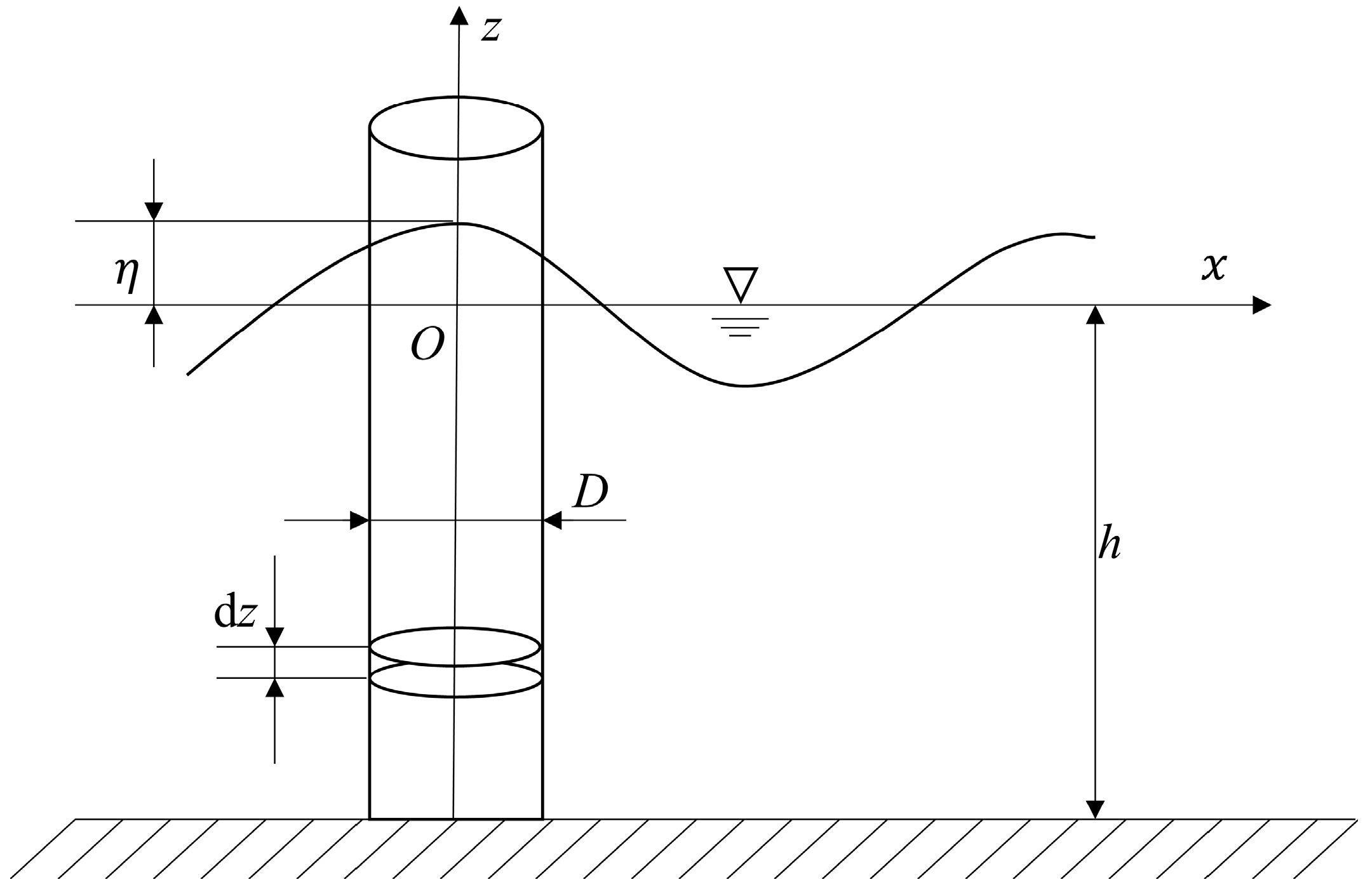
2.2. Morison’s Equation
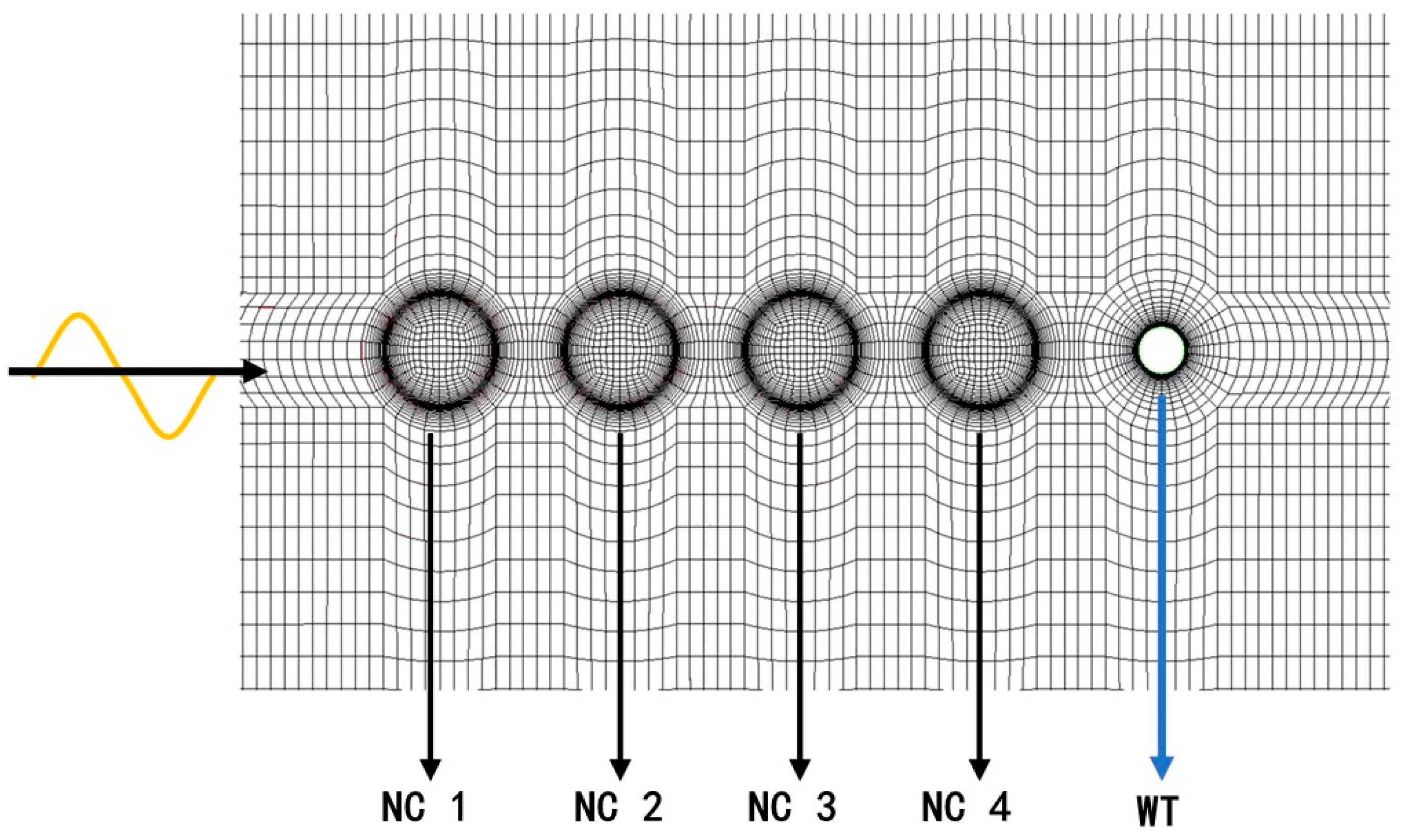
2.3. Flow Field Calculation Model
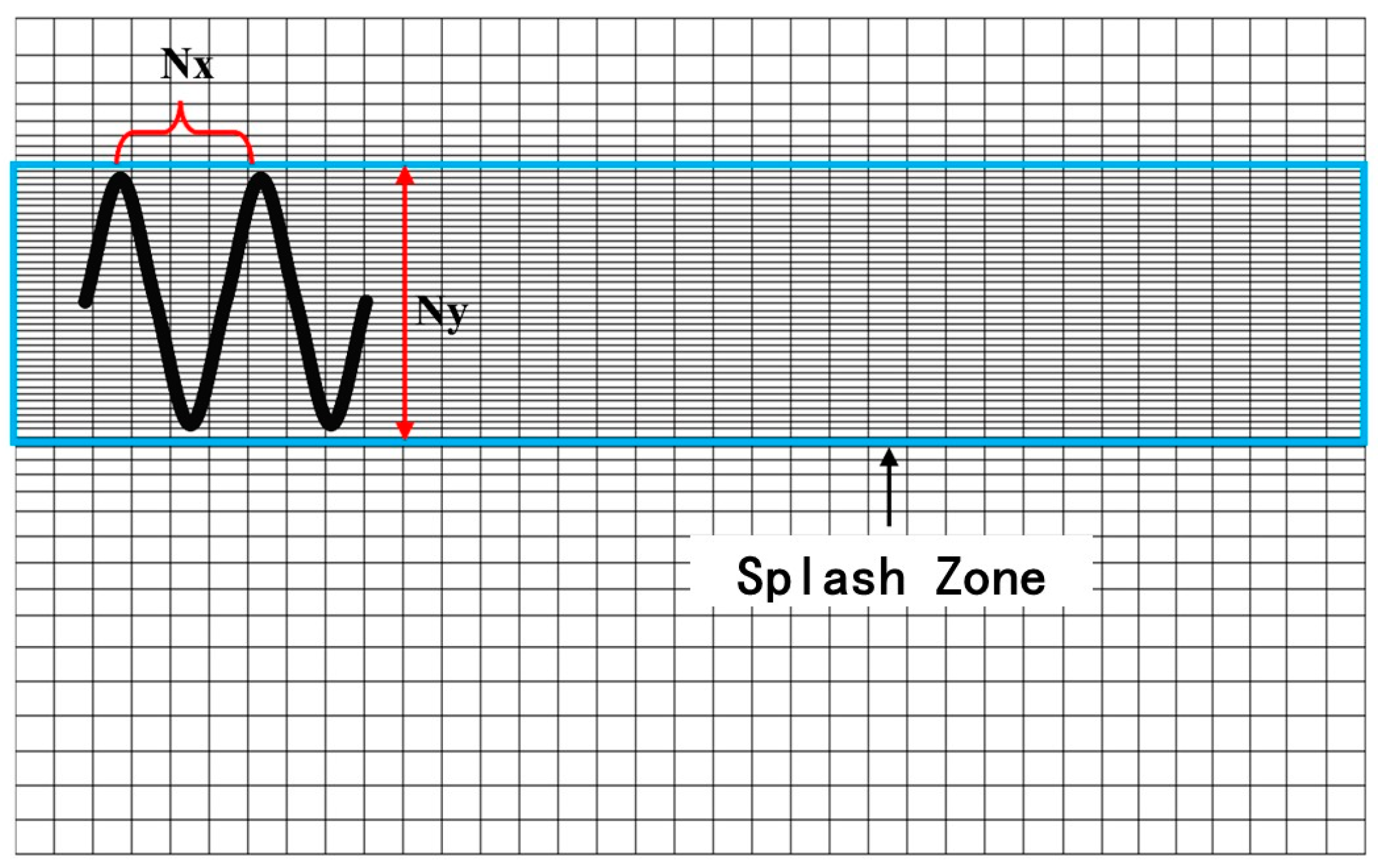
- Nx: Number of grids per wavelength in the wave propagation direction (along the wavelength);
- Ny: Number of grids per wave height in the y-direction (wave height direction) within the splash zone.
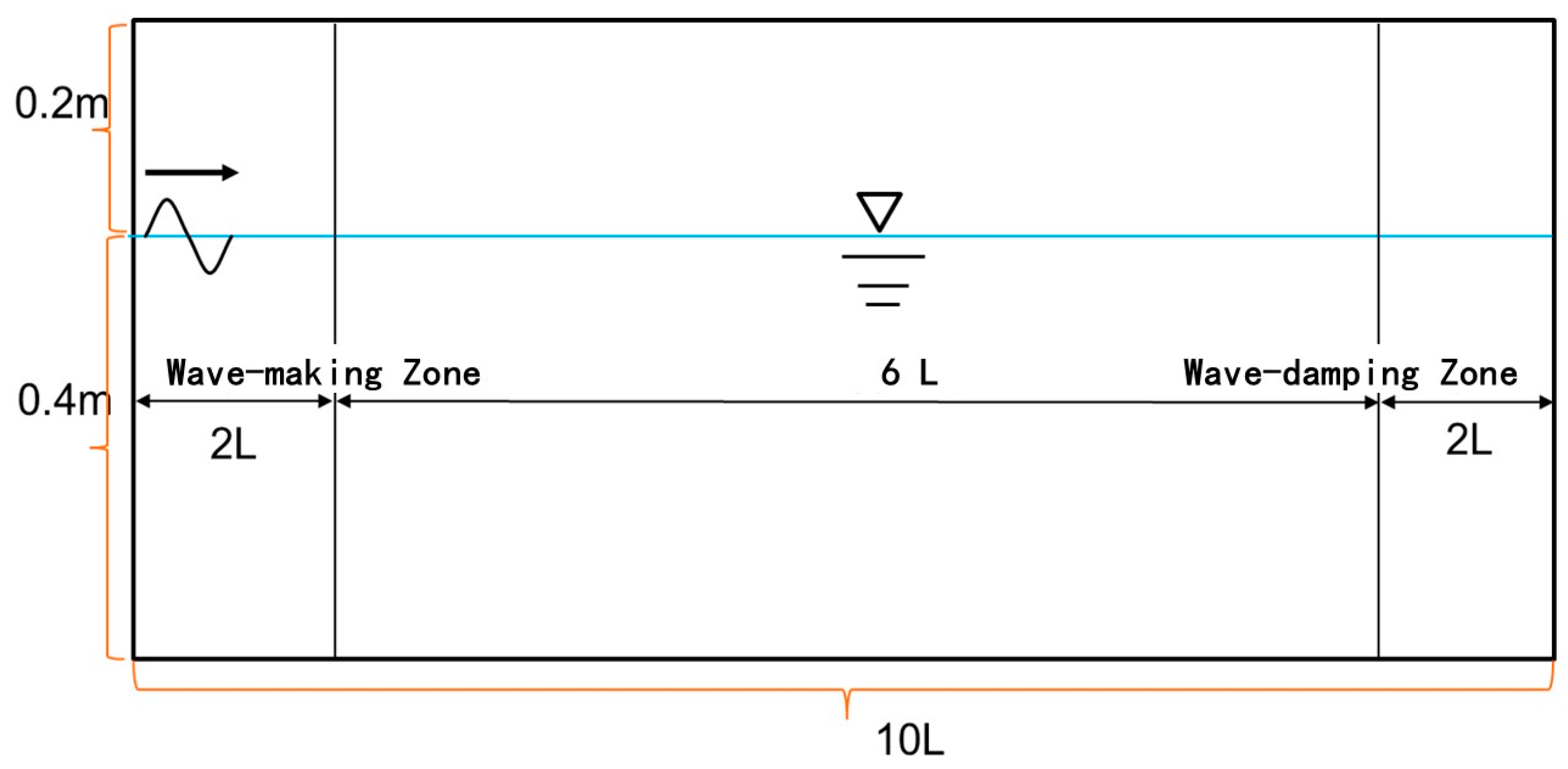
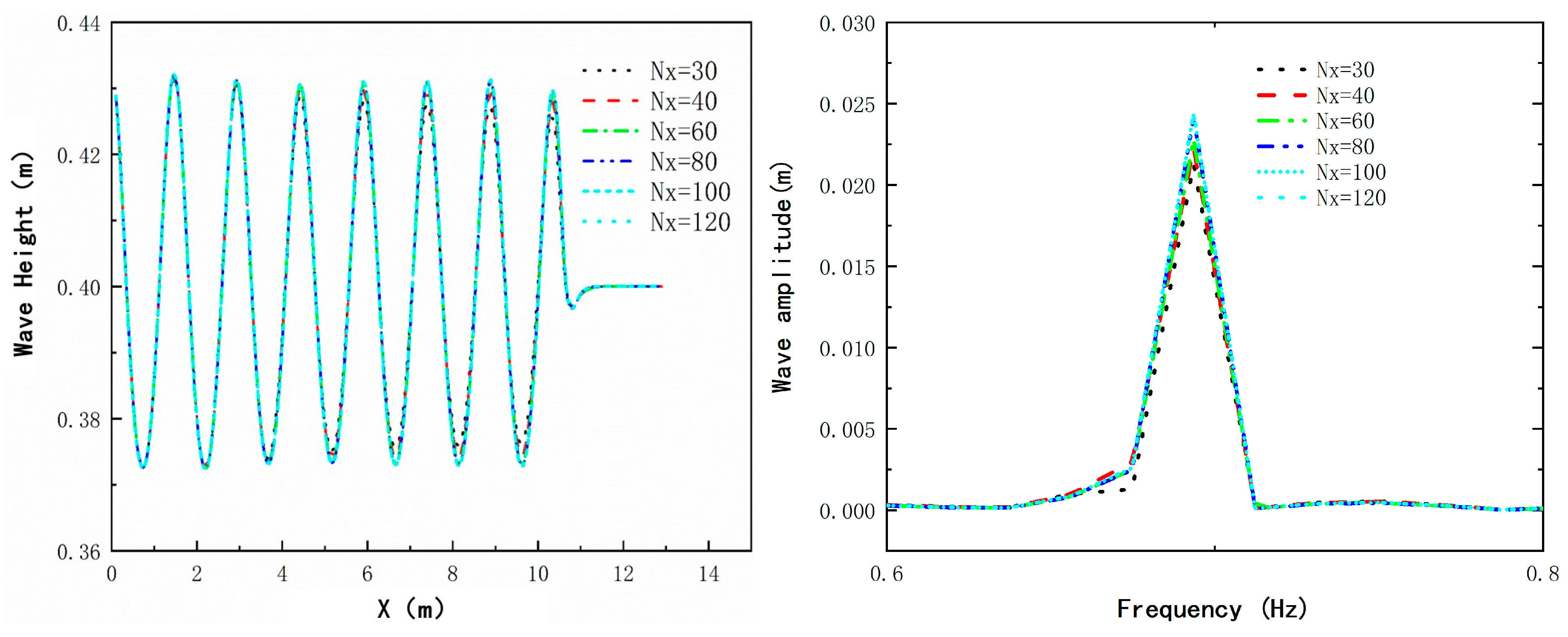
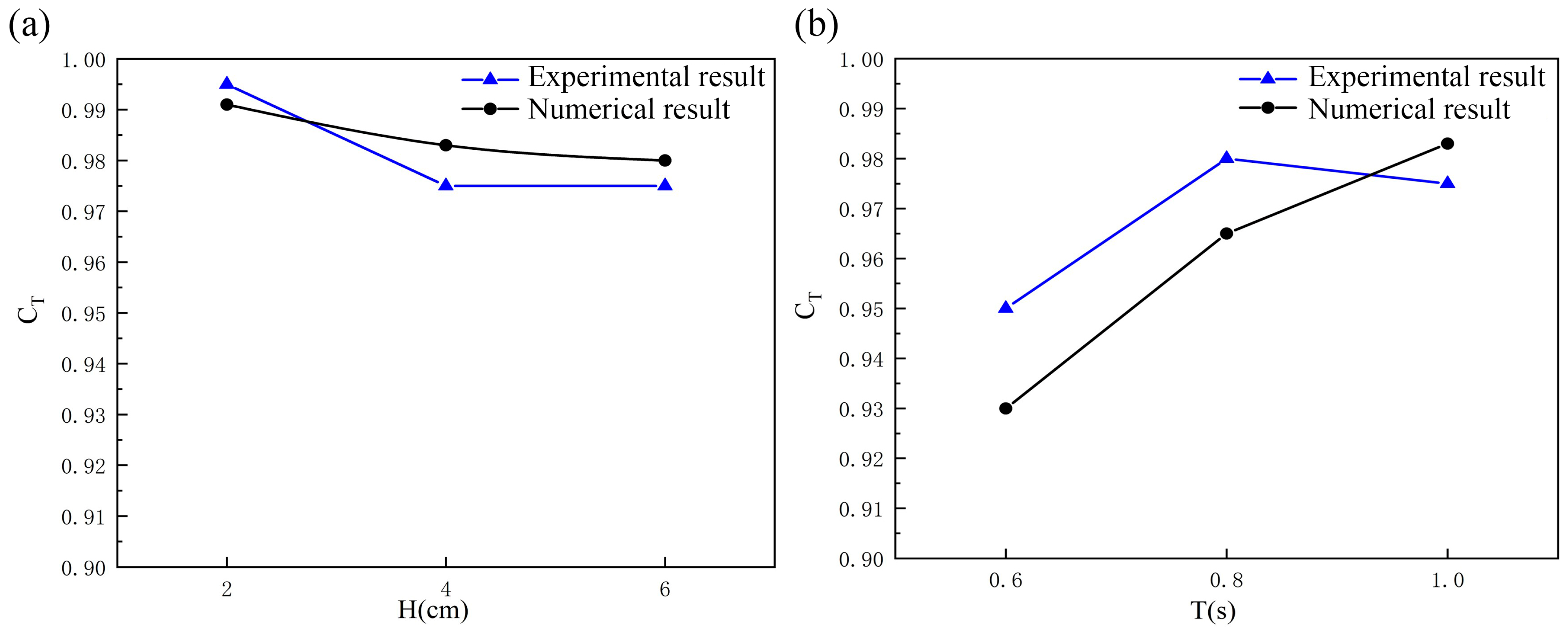
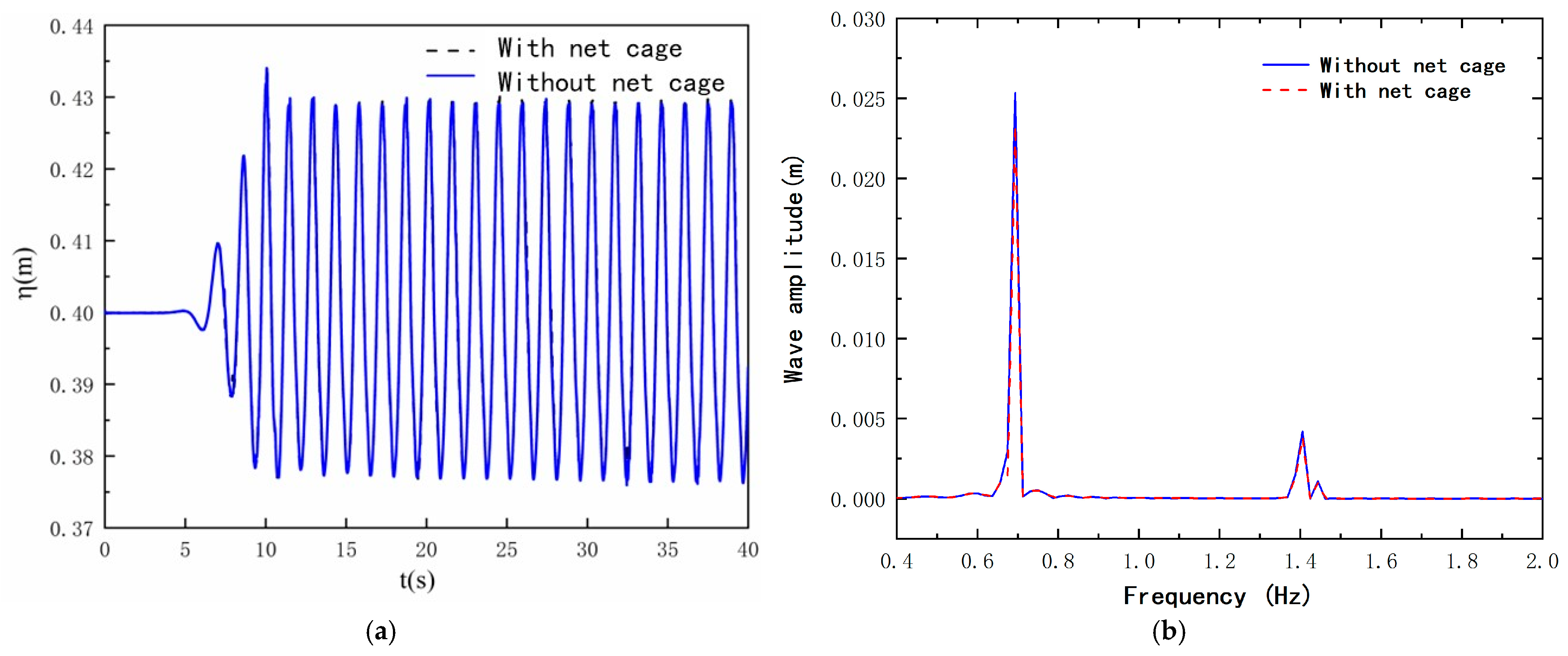
2.4. Numerical Model Validation
3. Results and Discussion
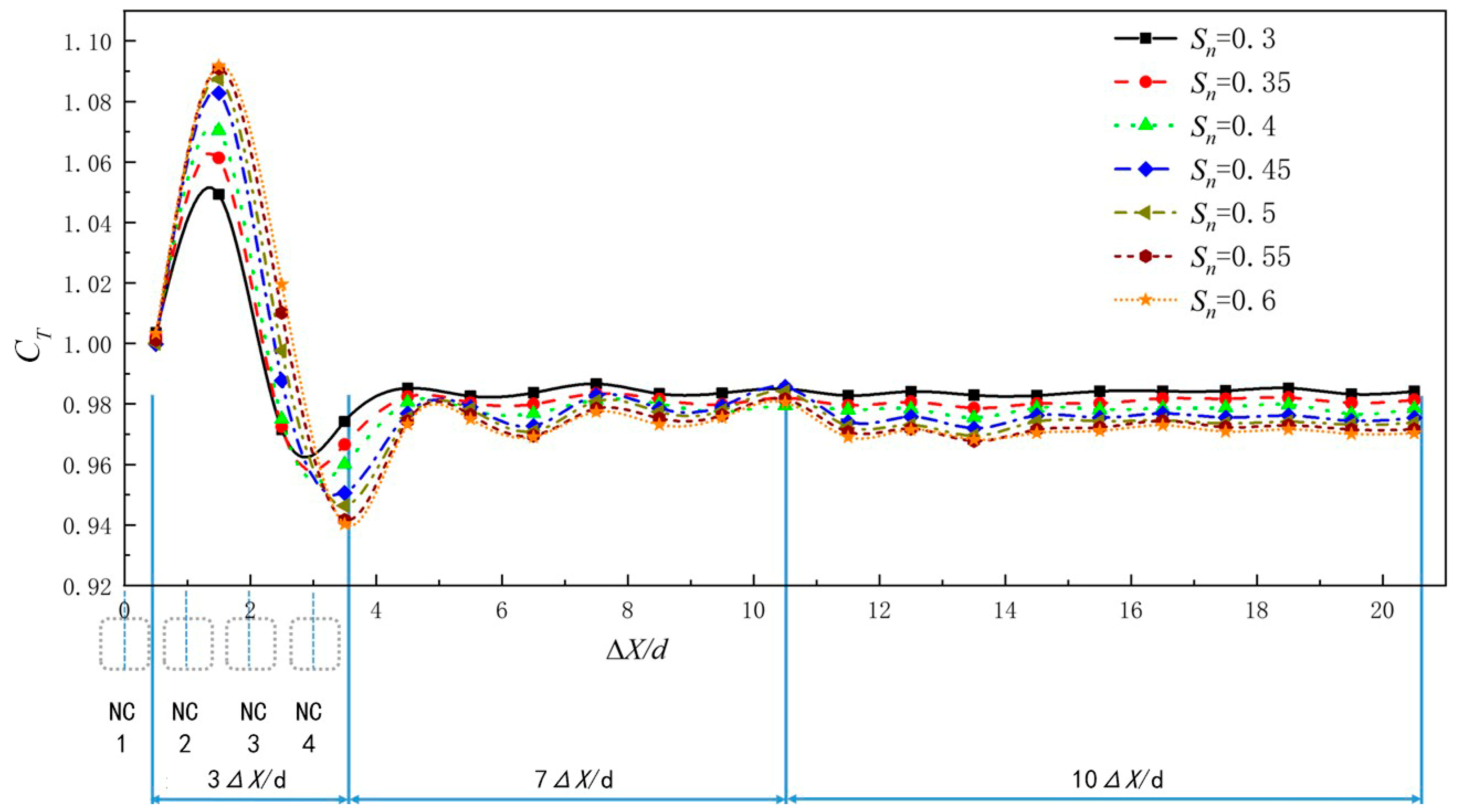
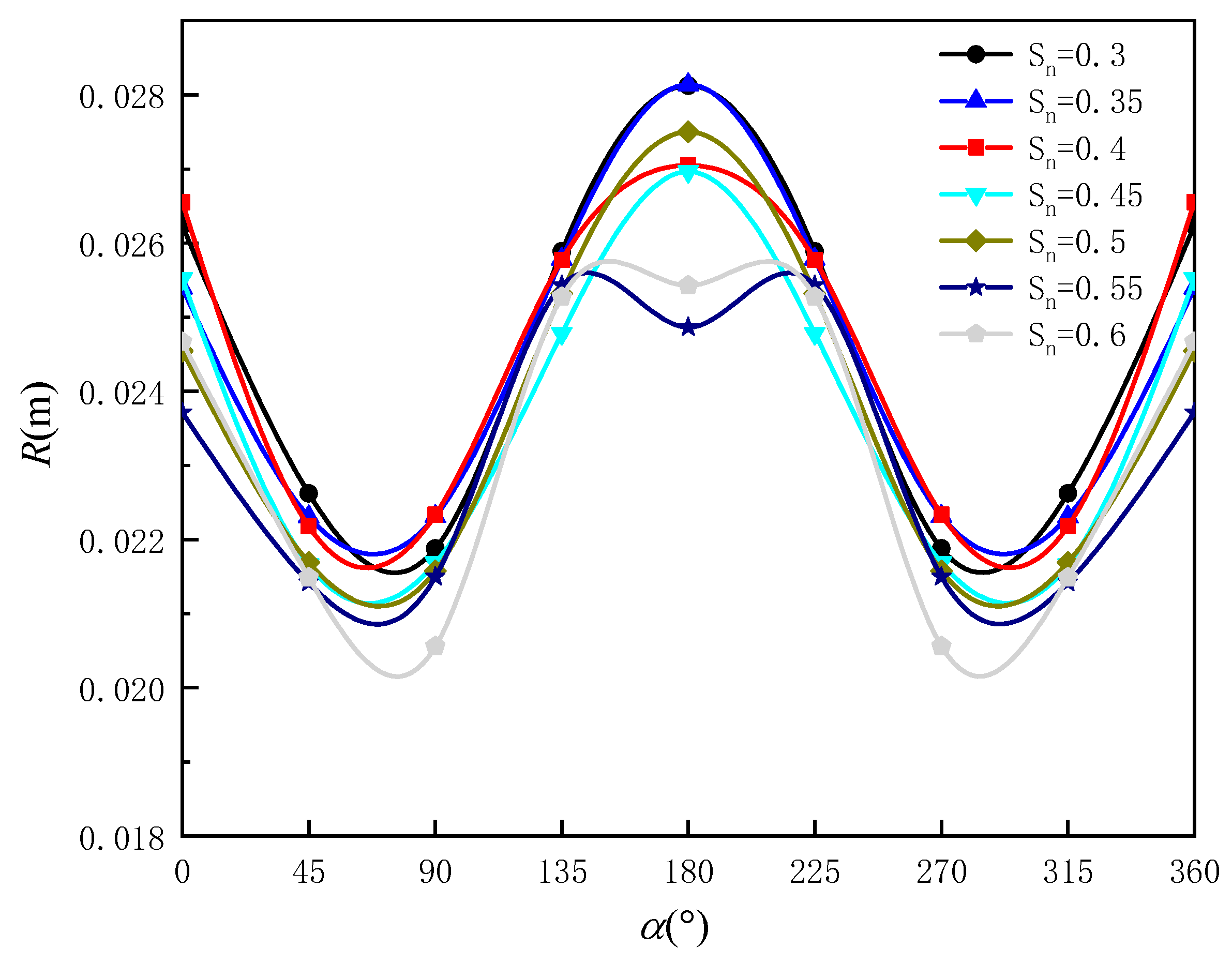
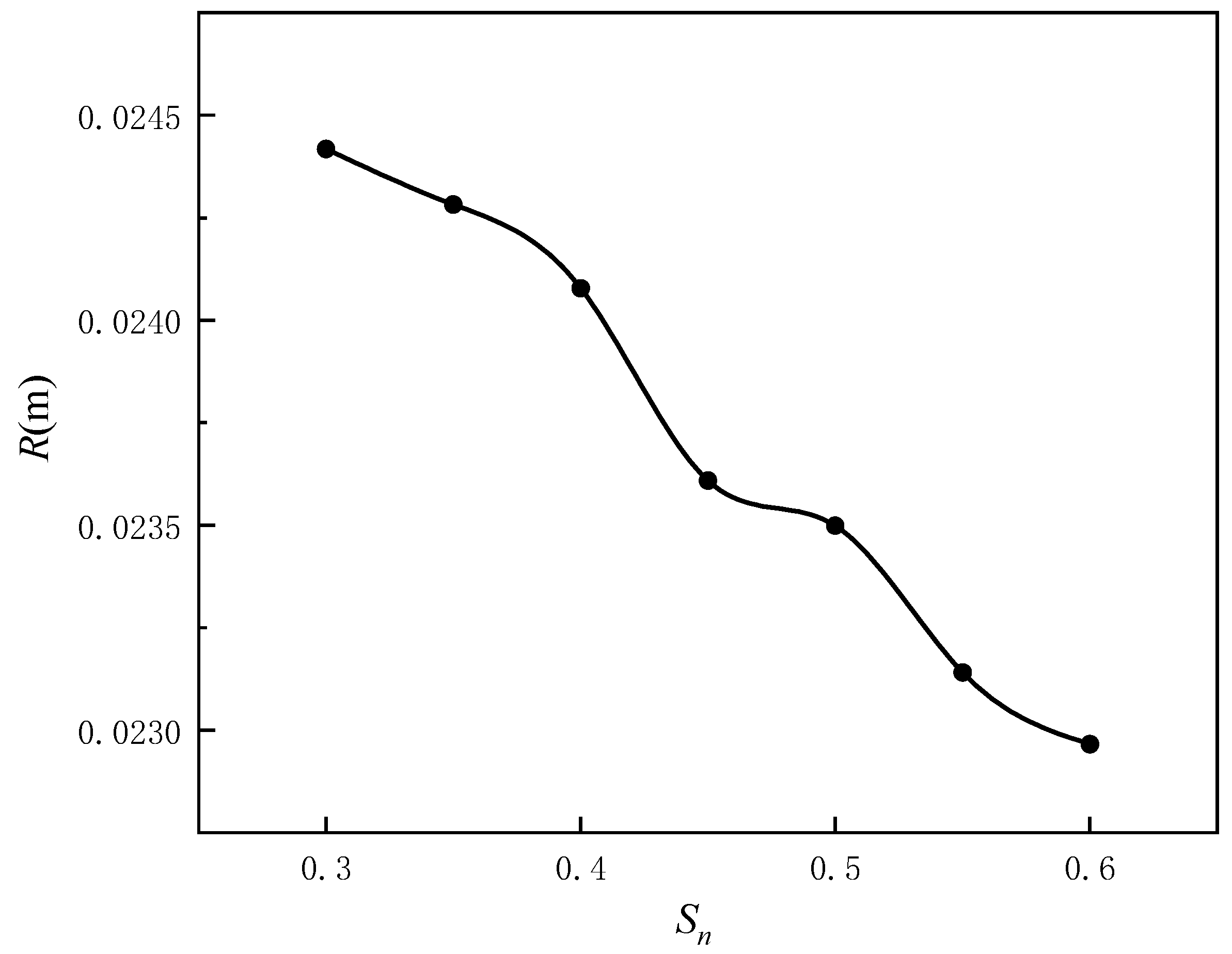
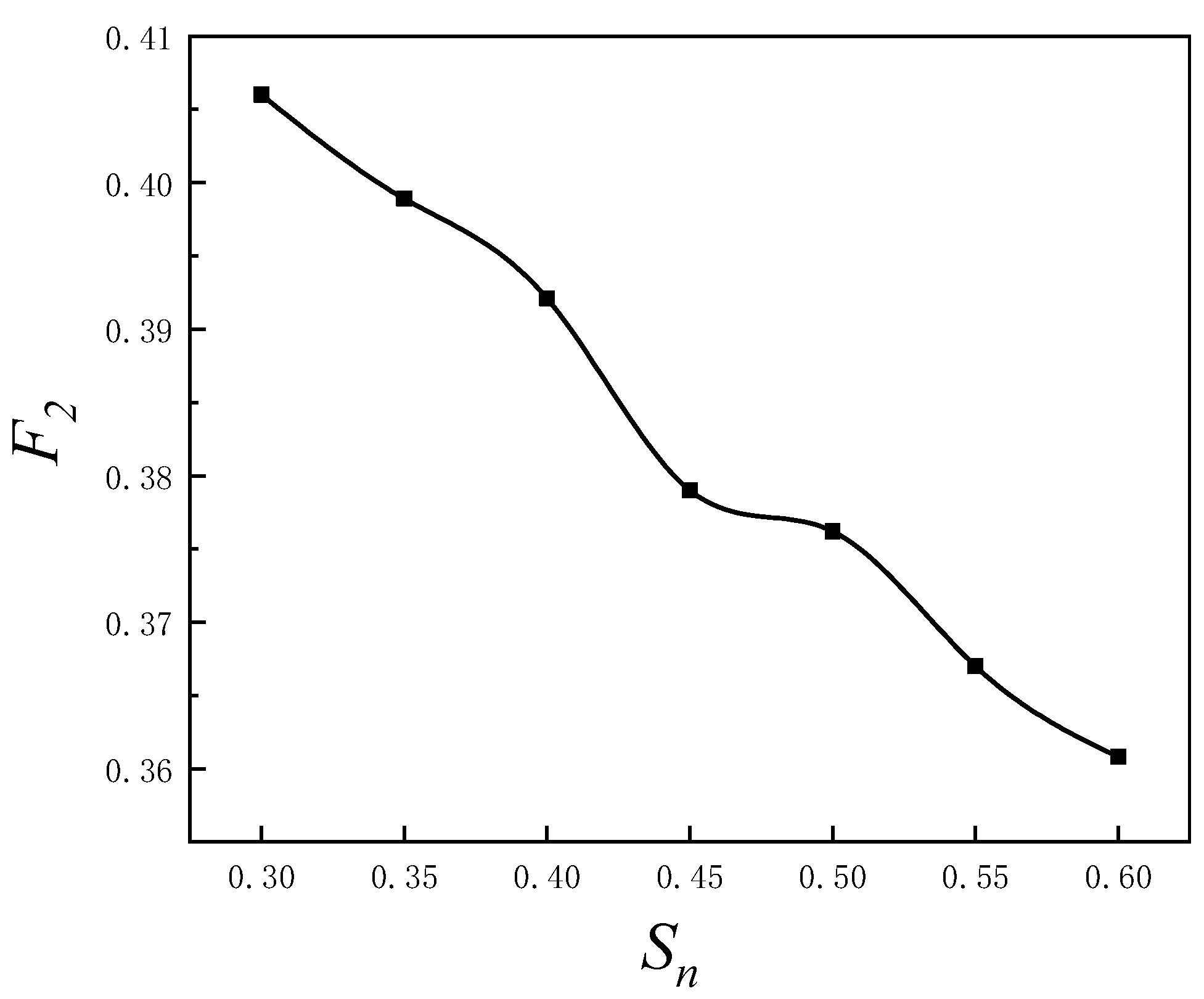
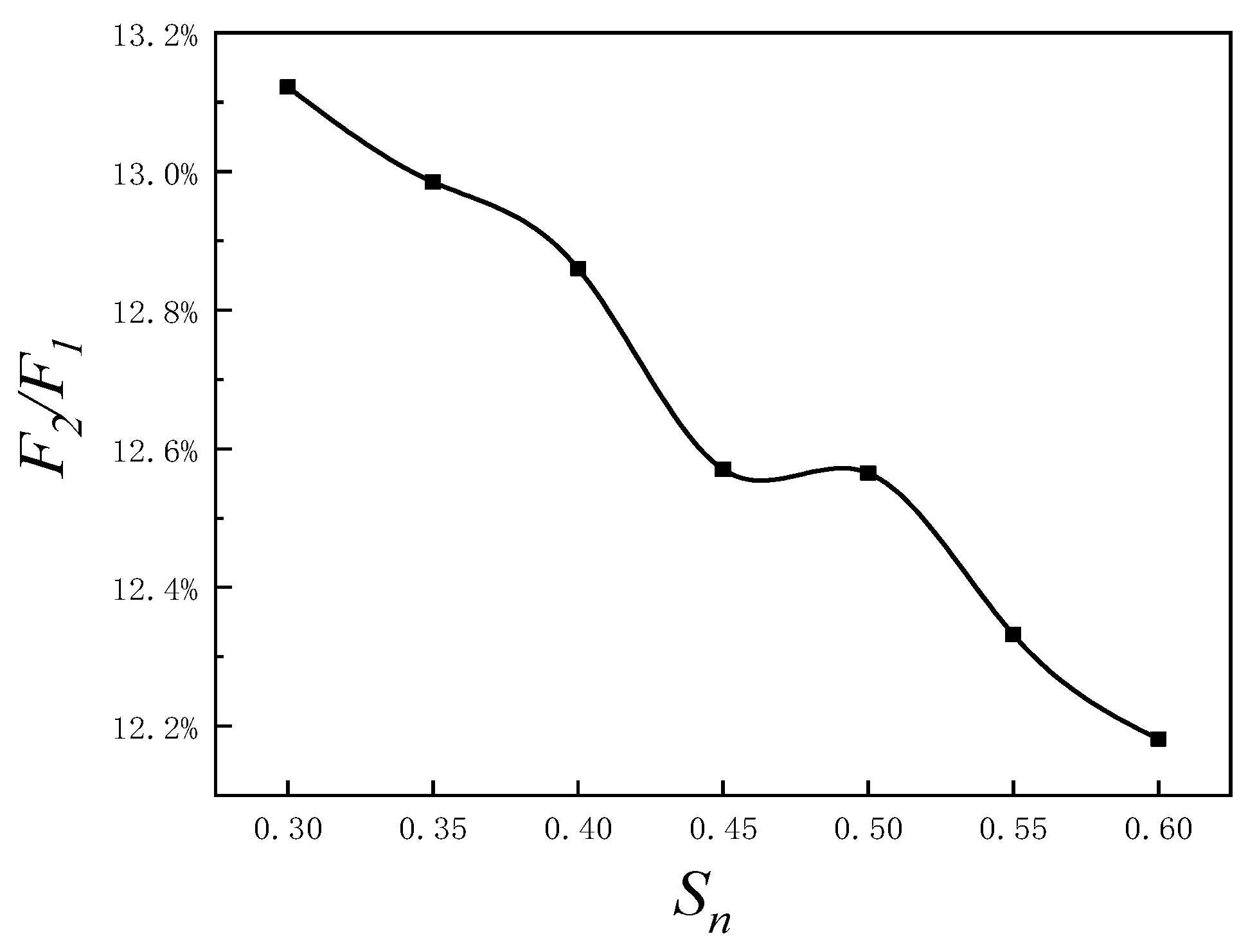
3.1. Influence of Net Solidity on Waves
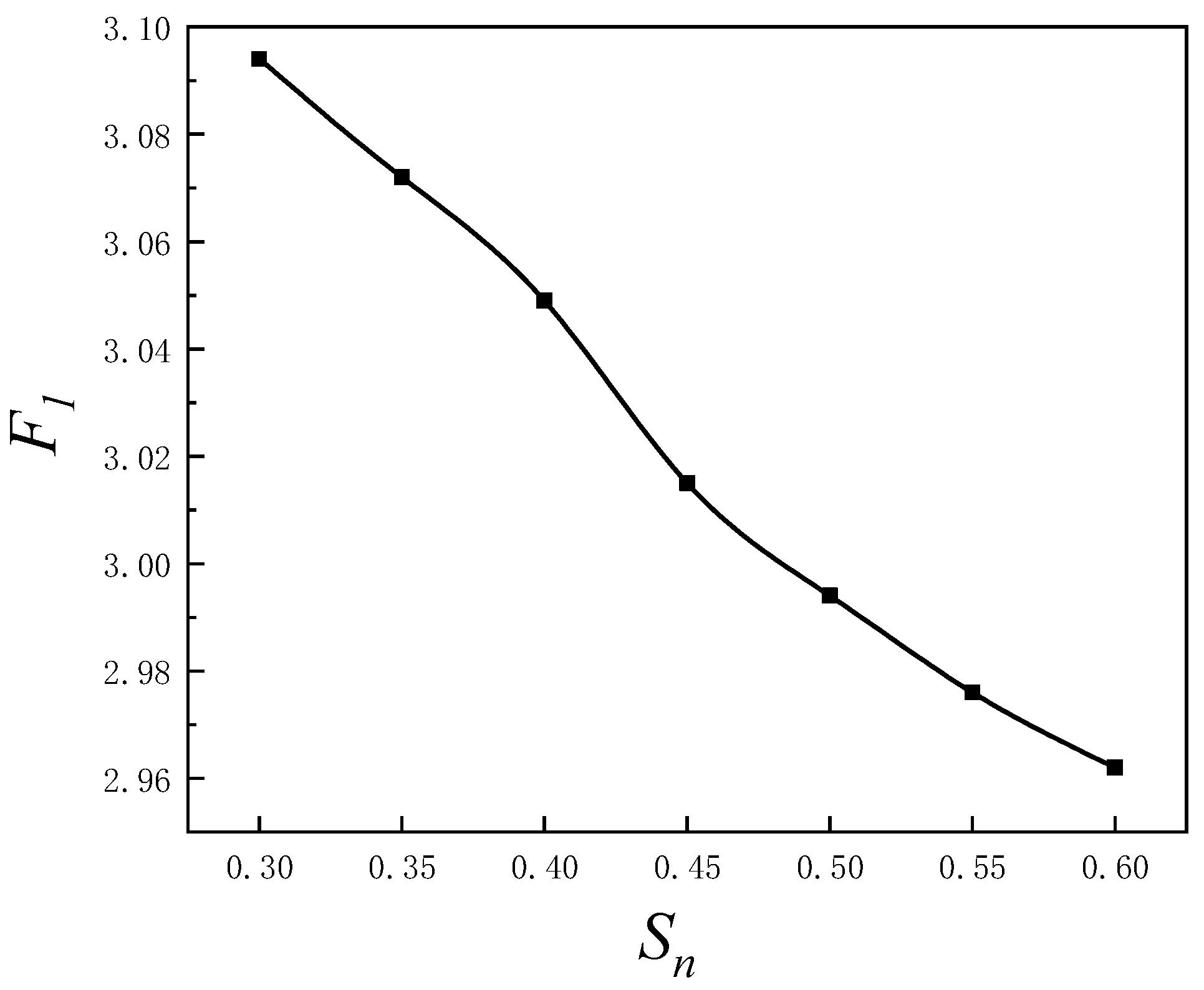
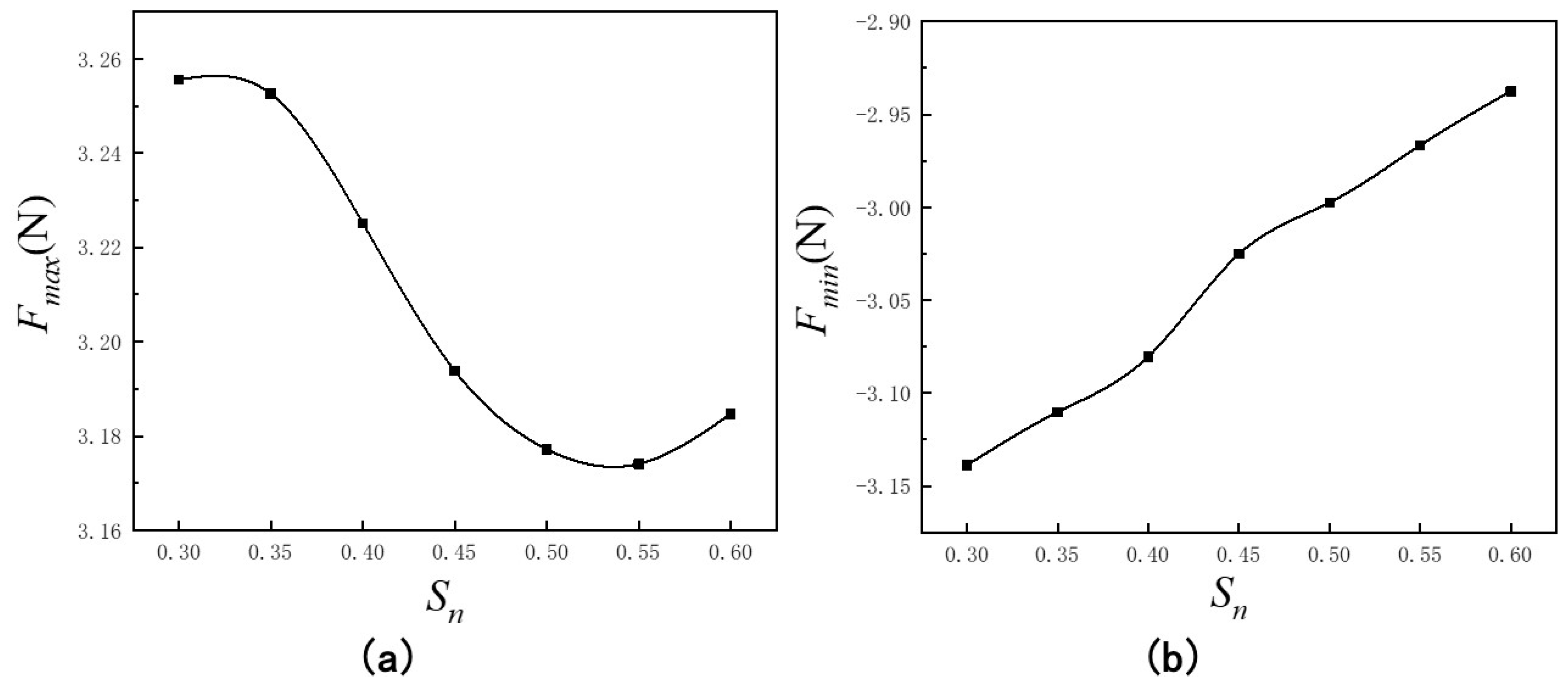
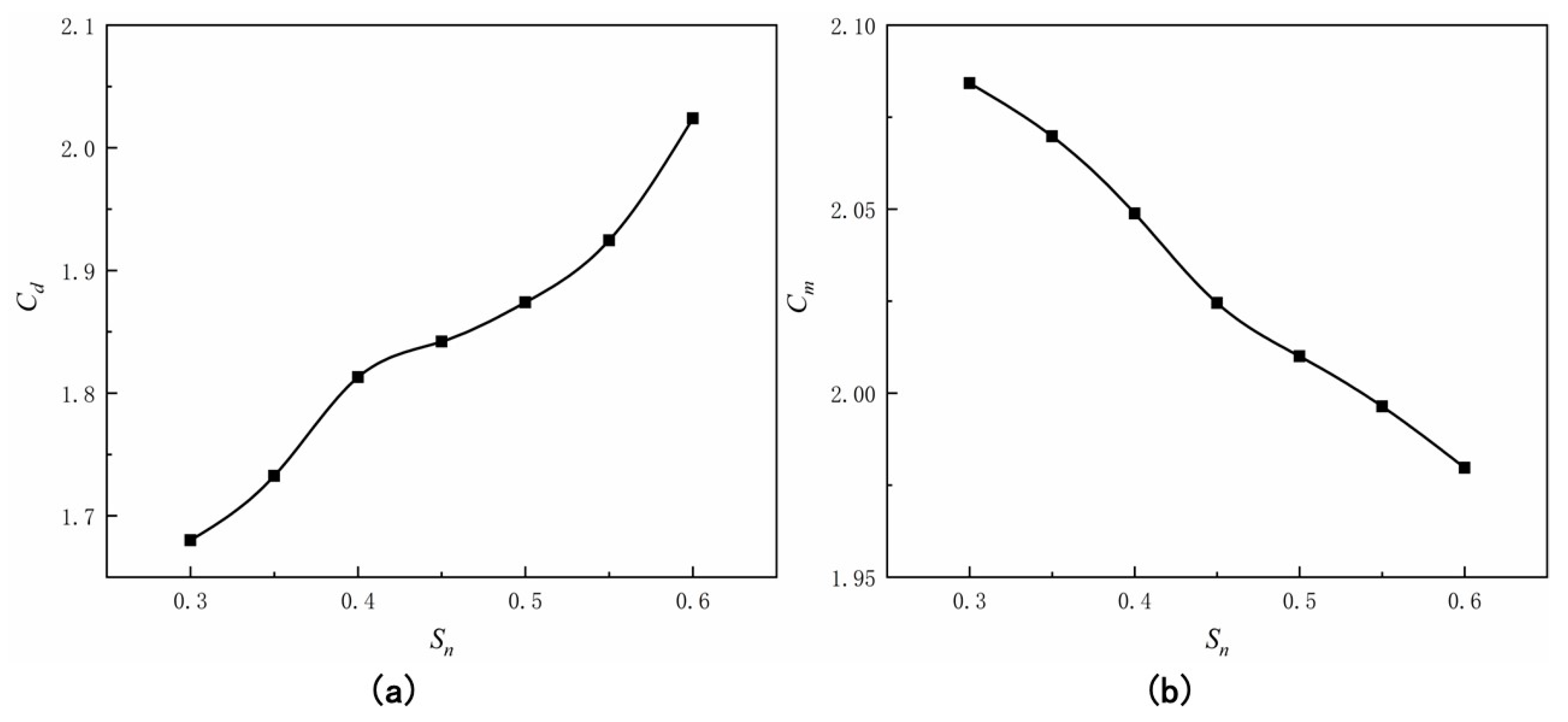
3.2. Influence of Net Solidity on Hydrodynamic Forces of the Turbine Foundation
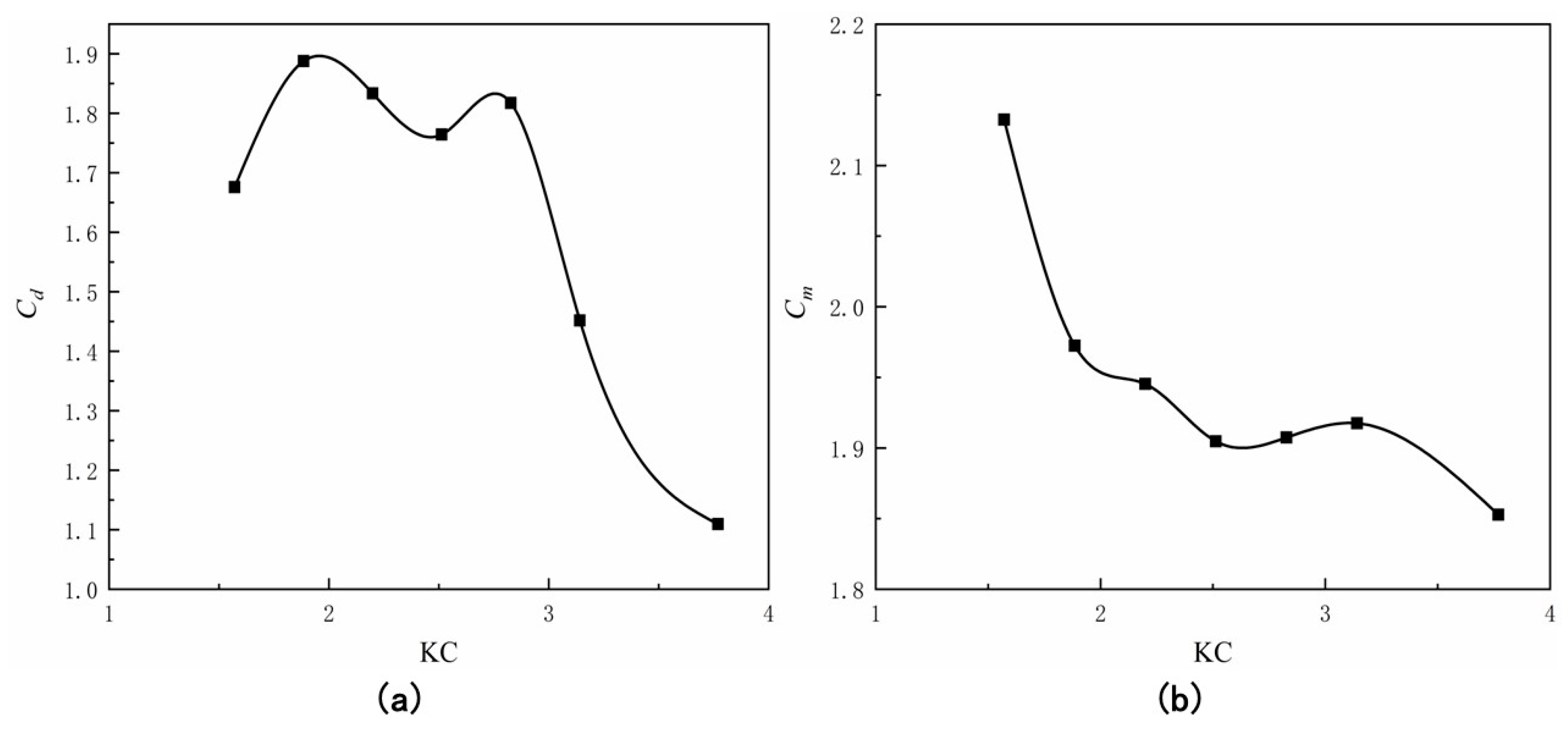
3.3. Influence of KC on Hydrodynamic Forces of the Turbine Foundation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, X.; Lei, Y. Stochastic Response Analysis for a Floating Offshore Wind Turbine Integrated with a Steel Fish Farming Cage. Appl. Sci. 2018, 8, 1229. [Google Scholar] [CrossRef]
- Guo, Z.C.; Dong, G.H.; Zheng, Z.J. Numerical study of flow regimes and force characteristics for cruciform cylinder in oscillatory flow. Ocean. Eng. 2023, 290, 116223. [Google Scholar] [CrossRef]
- Balash, C.; Colbourne, B.; Bose, N.; Raman-Nair, W. Aquaculture Net Drag Force and Added Mass. Aquac. Eng. 2009, 41, 14–21. [Google Scholar] [CrossRef]
- Wang, T.Y.; Xu, T.J.; Wang, S.; Dong, G.H.; Yan, L.H. Hydrodynamic analysis of the combined structure of offshore monopile wind turbine foundation and aquaculture cage. Ocean. Eng. 2023, 287 Pt 1, 115796. [Google Scholar] [CrossRef]
- Liu, Z.; Soares, C.G. Numerical study of rope materials of the mooring system for gravity cages. Ocean. Eng. 2024, 298, 9. [Google Scholar] [CrossRef]
- Gansel, L.C.; Plew, D.R.; Endresen, P.C.; Olsen, A.I.; Misimi, E.; Guenther, J.; Jensen, Ø. Drag of Clean and Fouled Net Panels—Measurements and Parameterization of Fouling. PLoS ONE 2015, 10, e0131051. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Ji, H.; Liu, J.; Huang, C.; Huang, Z.; Zhang, Y.; Lei, J.; Chen, W.; Dong, Q.; Chen, C. Comparative analysis of dynamic and structural responses of three floating offshore wind turbine foundations. Ocean. Eng. 2025, 320, 120252. [Google Scholar] [CrossRef]
- Cheng, H.; Li, L.; Ong, M.C. Comparative study of five commonly used gravity type fish cages under pure current conditions. Ocean. Eng. 2022, 250, 110977. [Google Scholar] [CrossRef]
- Martin, A.B.H. A Lagrangian approach for the coupled simulation of fixed net structures in a Eulerian fluid model. J. Fluids Struct. 2020, 94, 102962. [Google Scholar] [CrossRef]
- Dong, G.H.; Tang, M.F.; Xu, T.J.; Bi, C.W.; Guo, W.J. Experimental analysis of the hydrodynamic force on the net panel in wave. Appl. Ocean. Res. 2019, 87, 233–246. [Google Scholar] [CrossRef]
- Bi, C.W.; Chen, Q.P.; Zhao, Y.P.; Su, H.; Wang, X.Y. Experimental investigation on the hydrodynamic performance of plane nets fouled by hydroids in waves. Ocean. Eng. 2020, 213, 107839. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, H.; Soares, C.G. Experimental study on the mooring forces and motions of a fish cage under regular waves. Ocean. Eng. 2023, 280, 11. [Google Scholar] [CrossRef]
- Chen, Q.P.; Ma, C.; Zhao, Y.P.; Bi, C.W.; Liu, H.F. Hydrodynamics of focused waves acting on netting that extends above the mean sea level. Ocean. Eng. 2024, 309 Pt 1, 8. [Google Scholar] [CrossRef]
- Cheng, H.; Ong, M.C.; Li, L.; Chen, H. Development of a coupling algorithm for fluid-structure interaction analysis of submerged aquaculture nets. Ocean. Eng. 2022, 243, 110208. [Google Scholar] [CrossRef]
- Liu, H.F.; Zhao, T.H.; Liu, Y. Investigation on dynamic performance of semi-submersible aquaculture platform in two mooring forms. Ocean. Eng. 2024, 297, 14. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Dong, G.H.; Wu, Z.M.; Zhang, Y.; Xu, T.J. Drag on and flow through the hydroid-fouled nets in currents. Ocean. Eng. 2022, 161, 195–204. [Google Scholar] [CrossRef]
- Xie, M.; Li, S.; Mu, Y.; Wei, Y.; Xu, T.; Sun, Z.; Yuan, C. Experimental investigation on the mooring dynamics of the flexible trash intercept net under wave-current combined actions. Ocean. Eng. 2023, 268, 113544. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, J.; Baniotopoulos, C.; Wang, X.; Deng, X. Dynamic analysis of offshore steel wind turbine towers subjected to wind, wave and current loading during construction. Ocean. Eng. 2020, 216, 108084. [Google Scholar] [CrossRef]
- Ma, C.; Bi, C.W.; Xu, Z.; Zhao, Y.P. Dynamic behaviors of a hinged multi-body floating aquaculture platform under regular waves. Ocean. Eng. 2022, 243, 110278. [Google Scholar] [CrossRef]
- Liu, Z.; Soares, C.G. Sensitivity analysis of the cage volume and mooring forces for a gravity cage subjected to current and waves. Ocean. Eng. 2023, 287 Pt 1, 115715. [Google Scholar] [CrossRef]
- Bannister, J.; Sievers, M.; Bush, F.; Bloecher, N. Biofouling in marine aquaculture: A review of recent research and developments. Biofouling 2019, 35, 631–648. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Bi, C.W.; Sun, X.X.; Dong, G.H. A Prediction on Structural Stress and Deformation of Fish Cage in Waves Using Machine-Learning Method. Aquac. Eng. 2019, 85, 15–21. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Sun, X.X.; Zhang, Y.; Guo, Z.X.; Wang, B.; Dong, G.H. An efficient artificial neural network model to predict the structural failure of high-density polyethylene offshore net cages in typhoon waves. Ocean. Eng. 2020, 196, 106793. [Google Scholar] [CrossRef]
- Shi, W.; Zeng, X.; Feng, X.; Shao, Y.; Li, X. Numerical study of higher-harmonic wave loads and runup on monopiles with and without ice-breaking cones based on a phase-inversion method. Ocean. Eng. 2023, 267, 113221. [Google Scholar] [CrossRef]
- Tang, H.J.; Yeh, P.H.; Huang, C.C.; Yang, R.Y. Numerical study of the mooring system failure of aquaculture net cages under irregular waves and current. Ocean. Eng. 2020, 216, 108110. [Google Scholar] [CrossRef]
- Bi, C.W.; Ma, C.; Zhao, Y.P.; Xin, L.X. Physical model experimental study on the motion responses of a multi-module aquaculture platform. Ocean. Eng. 2021, 239, 109862. [Google Scholar] [CrossRef]
- Fan, Z.; Liang, Y.H.; Yun-Peng, Z. Review of the research on the hydrodynamics of fishing cage nets. Ocean. Eng. 2023, 276, 114192. [Google Scholar] [CrossRef]
- Klebert, P.; Su, B. Turbulence and flow field alterations inside a fish sea cage and its wake. Appl. Ocean. Res. 2020, 98, 102113. [Google Scholar] [CrossRef]
- Gharechae, A.; Ketabdari, M.J. Semi-analytical study of wave interaction with a submerged permeable sphere applied on a spherical aquaculture cage. Ocean. Eng. 2023, 272, 113839. [Google Scholar] [CrossRef]
- Patursson, Ø.; Swift, M.R.; Tsukrov, I.; Simonsen, K.; Baldwin, K.; Fredriksson, D.W.; Celikkol, B. Development of a porous media model with application to flow through and around a net panel. Ocean. Eng. 2010, 37, 314–324. [Google Scholar] [CrossRef]
- Bi, C.W.; Zhao, Y.P.; Dong, G.H.; Cui, Y.; Gui, F.K. Experimental and numerical investigation on the damping effect of net cages in waves. J. Fluids Struct. 2015, 55, 122–138. [Google Scholar] [CrossRef]

| Sn | Wave Height (m) | Wave Length (m) | Wave Steepness (H/L) | Period (s) | h/L |
|---|---|---|---|---|---|
| 0.30 | 0.05 | 2.5 | 0.02 | 1.4479 | 0.16 |
| 0.35 | |||||
| 0.40 | |||||
| 0.45 | |||||
| 0.50 | |||||
| 0.55 | |||||
| 0.60 |
| Sn | Wave Height (m) | Wave Length (m) | Wave Steepness (H/L) | Period (s) | h/L |
|---|---|---|---|---|---|
| 0.3 | 0.05 | 0.25 | 0.020 | 1.4479 | 0.16 |
| 0.06 | 0.024 | ||||
| 0.07 | 0.028 | ||||
| 0.08 | 0.032 | ||||
| 0.09 | 0.036 | ||||
| 0.10 | 0.040 | ||||
| 0.12 | 0.048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tang, M.; Jiang, Z.; Dong, G. Hydrodynamic Analysis of Combined Offshore Wind Turbine and Net Cage Under Finite-Depth Waves. J. Mar. Sci. Eng. 2025, 13, 924. https://doi.org/10.3390/jmse13050924
Wang B, Tang M, Jiang Z, Dong G. Hydrodynamic Analysis of Combined Offshore Wind Turbine and Net Cage Under Finite-Depth Waves. Journal of Marine Science and Engineering. 2025; 13(5):924. https://doi.org/10.3390/jmse13050924
Chicago/Turabian StyleWang, Bin, Mingfu Tang, Zhenqiang Jiang, and Guohai Dong. 2025. "Hydrodynamic Analysis of Combined Offshore Wind Turbine and Net Cage Under Finite-Depth Waves" Journal of Marine Science and Engineering 13, no. 5: 924. https://doi.org/10.3390/jmse13050924
APA StyleWang, B., Tang, M., Jiang, Z., & Dong, G. (2025). Hydrodynamic Analysis of Combined Offshore Wind Turbine and Net Cage Under Finite-Depth Waves. Journal of Marine Science and Engineering, 13(5), 924. https://doi.org/10.3390/jmse13050924





