Abstract
Accurate forecasting of offshore wind speed is crucial for the efficient operation and planning of wind energy systems. However, the inherently non-stationary and highly volatile nature of wind speed, coupled with the sensitivity of neural network-based models to parameter settings, poses significant challenges. To address these issues, this paper proposes an Adaptive Neuro-Fuzzy Inference System (ANFIS) optimized by CRGWAA. The proposed CRGWAA integrates Chebyshev mapping initialization, an elite-guided reflection refinement operator, and a generalized quadratic interpolation strategy to enhance population diversity, adaptive exploration, and local exploitation capabilities. The performance of CRGWAA is comprehensively evaluated on the CEC2022 benchmark function suite, where it demonstrates superior optimization accuracy, convergence speed, and robustness compared to six state-of-the-art algorithms. Furthermore, the ANFIS-CRGWAA model is applied to short-term offshore wind speed forecasting using real-world data from the offshore region of Fujian, China, at 10 m and 100 m above sea level. Experimental results show that the proposed model consistently outperforms conventional and hybrid baselines, achieving lower MAE, RMSE, and MAPE, as well as higher R2, across both altitudes. Specifically, compared to the original ANFIS-WAA model, the RMSE is reduced by approximately 45% at 10 m and 24% at 100 m. These findings confirm the effectiveness, stability, and generalization ability of the ANFIS-CRGWAA model for complex, non-stationary offshore wind speed prediction tasks.
1. Introduction
Offshore wind energy has emerged as a key component of the global transition towards sustainable power generation [1]. Compared to onshore wind farms, offshore wind resources offer higher and more stable wind speeds, making them an attractive option for large-scale renewable energy production. However, the stochastic nature of wind variations, influenced by atmospheric dynamics, ocean–atmosphere interactions, and mesoscale meteorological phenomena, poses a significant challenge for accurate wind speed prediction. Reliable forecasting is crucial for optimizing wind farm operations, improving grid integration, and mitigating the economic and technical risks associated with wind energy variability [2].
As a prominent form of renewable energy, wind energy has garnered increasing global attention due to its remarkable environmental and economic benefits [3,4]. As an inherently clean and sustainable source, wind power generation produces no greenhouse gas emissions or air pollutants during operation, thereby making a substantial contribution to carbon neutrality and climate change mitigation efforts. According to the Global Wind Energy Council’s (GWEC) 2024 report on offshore wind energy [5], the global offshore wind power installed capacity increased by 108 GW in 2023, representing a year-on-year growth of 24%. Notably, China led the global offshore wind market for the sixth consecutive year, with an additional installed capacity of 6.3 GW. This underscores the importance of offshore wind speed forecasting.
However, offshore wind speed forecasting faces numerous challenges, which significantly impact both prediction accuracy and model stability. One such challenge is the complexity of air–sea interactions [6], which exacerbates forecasting difficulties. The characteristics of the offshore atmospheric boundary layer differ markedly from those on land, with its stability influenced by multiple factors such as sea surface temperature, ocean currents, and humidity. These factors are not only highly variable but also subject to rapid changes, making them difficult to model effectively. Additionally, the spatiotemporal variability of wind speed is inherently complex [7]. Offshore wind speed exhibits pronounced diurnal fluctuations, seasonal variations, and sudden bursts, often accompanied by extreme events such as typhoons and storm surges. This strong non-stationarity presents a significant challenge to traditional forecasting methods.
To address these challenges, numerous researchers have explored various approaches to enhance wind speed forecasting accuracy. In recent years, wind speed prediction models can generally be categorized into three main types: physical models, statistical models, and artificial intelligence (AI)-based models. Physical models, exemplified by numerical weather prediction (NWP) methods [8], utilize atmospheric physical equations to simulate wind speed variations. For instance, Tuy et al. [9] employed the Weather Research and Forecasting (WRF) model to comprehensively assess offshore wind energy potential within Cambodia’s Exclusive Economic Zone (EEZ). While such models perform well in large-scale forecasting, their accuracy at local scales is often limited by physical parameterization schemes and resolution constraints. Particularly in coastal regions with complex microtopography, these models often struggle to deliver satisfactory forecasting precision and are associated with high computational costs.
Compared to physical models, statistical approaches rely on historical wind speed data. For example, Torres et al. [10] applied ARMA and persistence models for hourly average wind speed forecasting. Statistical methods, often based on time series analysis, are well suited for short-term forecasting but exhibit limited capability in handling nonlinearity and non-stationarity in wind speed data. To overcome these limitations, hybrid statistical models have been proposed. Zhang et al. [11], for instance, developed a VMD-PRBF-ARMA-E-based approach that effectively integrates the nonlinear, linear, and stochastic characteristics of wind speed data.
In recent years, the advancement of machine learning and deep learning techniques has made AI-based wind speed forecasting methods a major focus of research. Lin et al. [12] proposed a wind speed prediction framework for offshore wind farms that combines a Graph Attention Network (GAT) with a learnable graph matrix to adaptively fuse spatiotemporal features using a Transformer architecture. This model demonstrated excellent performance in capturing complex spatiotemporal dependencies. Similarly, Zhang et al. [13] introduced an improved pure two-dimensional convolutional neural network (CNN)-based model for spatiotemporal wind speed forecasting. These AI-driven methods can effectively extract latent patterns from historical meteorological data, enabling more accurate and robust wind speed predictions.
Although existing models based on physical principles, statistical methods, and AI techniques have demonstrated potential in wind speed forecasting, they still face notable limitations. These include inadequate generalization capabilities, limited interpretability, and significant challenges in accurately modeling the nonlinear and non-stationary characteristics of offshore wind dynamics. Moreover, conventional ANFIS models typically depend on manual parameter tuning, which constrains their performance and hinders adaptability across varying scenarios.
To address these challenges, this study proposes a novel wind speed forecasting framework that integrates ANFIS with CRGWAA. Swarm Intelligence Optimization Algorithms (SIOAs) [14,15,16] are a class of intelligent optimization techniques inspired by the collective behaviors observed in nature. By simulating the information exchange and cooperative interactions among individuals within biological populations, these algorithms are capable of efficiently approximating global optima in complex search spaces. Due to their strong global optimization capability, high robustness, and independence from gradient information, SIOAs have been widely applied across various domains, including communication networks [17,18], path planning [19,20], and medical information processing [21,22]. The ANFIS model combines the adaptive learning capability of neural networks with the transparent reasoning mechanism of fuzzy logic, offering superior interpretability and the ability to effectively capture the complex nonlinear dynamics inherent in wind speed sequences. Meanwhile, the integration of an intelligent optimization algorithm [23] mitigates the limitations of traditional ANFIS models, which typically rely on manually tuned parameters. By leveraging the global search ability and adaptive optimization features of CRGWAA, the proposed framework enables efficient and automatic tuning of model parameters, thereby significantly enhancing forecasting accuracy and model robustness. Finally, extensive experiments conducted on multiple offshore wind speed datasets demonstrate that the proposed model consistently outperforms baseline approaches across various scenarios, exhibiting superior predictive performance and strong generalization ability.
In comparison to advanced deep learning architectures such as the GAT-Transformer and CNN-based spatiotemporal models, the proposed ANFIS-CRGWAA framework demonstrates superior interpretability and adaptability. These advantages are especially evident in scenarios involving noisy, irregular, and non-stationary offshore wind data, where black-box models often struggle to maintain robustness and transparency. The hybrid structure of ANFIS-CRGWAA not only captures complex nonlinear patterns but also facilitates better insight into the decision-making process, which is critical for operational reliability in renewable energy forecasting.
The primary contributions of the present work are summarized below:
- CRGWAA integrates Chebyshev initialization, an elite-guided reflection refinement operator, and quadratic interpolation to enhance convergence, diversity, and local exploitation in ANFIS.
- CRGWAA achieves superior accuracy, convergence speed, and robustness on the CEC2022 benchmark suite.
- ANFIS-CRGWAA outperforms conventional and hybrid models in real-world offshore wind speed forecasting, demonstrating strong generalization.
2. Methodology
2.1. ANFIS
The Adaptive Neuro-Fuzzy Inference System (ANFIS), first introduced by Jang in 1993 [24], is a hybrid artificial intelligence framework that integrates the learning capabilities of neural networks with the reasoning mechanisms of fuzzy logic. By employing a set of fuzzy if–then rules to model the relationship between inputs and outputs, ANFIS effectively handles uncertainty and nonlinearity, offering a level of interpretability that closely mimics human decision-making processes. Given the inherently non-stationary and stochastic nature of offshore wind speed, ANFIS presents a particularly suitable modeling framework. Its ability to adaptively learn from data while incorporating linguistic knowledge allows it to effectively capture the temporal fluctuations and abrupt transitions commonly observed in offshore environments. Moreover, the modular structure of ANFIS enables efficient integration of external features such as meteorological inputs, spatial dependencies, and historical trends, thereby enhancing its predictive robustness. These characteristics have led to its widespread application in various domains such as medical diagnosis [25], industrial process control [26], and short-term load forecasting [27], among others. Despite its interpretability advantages, ANFIS suffers from certain limitations, particularly in terms of generalization ability and sensitivity to parameter selection.
To address these limitations, recent studies have focused on enhancing the ANFIS framework through hybridization with optimization algorithms and data preprocessing techniques. For instance, Feng et al. employed a complex-coded Artificial Hummingbird Algorithm (CAHA) to optimize the parameters of ANFIS [28], achieving notable improvements in short-term wind speed forecasting accuracy. Similarly, Rashed applied a Genetic Algorithm (GA) to optimize both the antecedent and consequent parameters of the ANFIS model [29], thereby enhancing the diagnostic accuracy of disease classification in medical imaging.
The core architecture of ANFIS is typically composed of a five-layer feedforward network, as is shown in Figure 1, where each layer performs a specific function in the fuzzy inference process. These layers correspond to the components of a Sugeno-type fuzzy inference system, allowing for the seamless integration of linguistic reasoning and numerical learning. The structure includes the following:
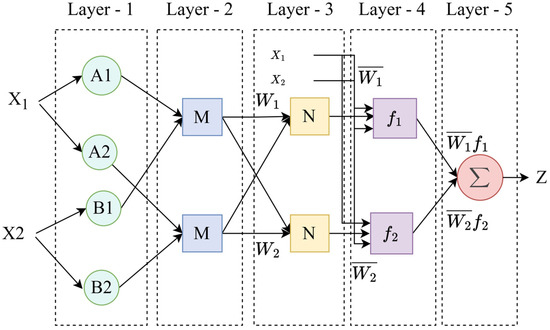
Figure 1.
The Architecture of ANFIS.
Layer 1 is the Fuzzification Layer. This layer is responsible for mapping crisp input values to fuzzy sets using predefined membership functions, such as Gaussian, triangular, or bell-shaped functions. As indicated in Equation (1), each node in this layer represents a linguistic label associated with one input variable, and the output of each node is the degree of membership of the input to that label, where and are variable parameters.
Layer 2 is the Rule Layer. In this layer, fuzzy rules are formulated by combining the membership values from Layer 1. Each node in Layer 2 corresponds to a fuzzy if–then rule, as presented in Equation (2), and the node output represents the firing strength of the rule, typically computed as the product (or another t-norm operator) of incoming membership values.
Then, the firing strengths obtained in the previous layer are normalized in the Normalization Layer. Each node calculates the ratio between a rule’s firing strength and the sum of all rules’ firing strengths, thereby ensuring that the contributions of all rules are weighted proportionally, as demonstrated in Equation (3).
Layer 4 is the Defuzzification Layer. In this layer, the normalized firing strengths are multiplied by linear functions of the input variables to compute the rule outputs, as can be seen in Equation (4). These linear functions represent the consequent parts of the fuzzy rules in a first-order Sugeno model. The parameters in this layer are adaptive and subject to optimization during training.
Finally, Layer 5 aggregates the outputs of all fuzzy rules by summing them to produce the final crisp output of the system. This output represents the system’s prediction or classification result:
Through this layered architecture, ANFIS effectively integrates the qualitative knowledge embedded in fuzzy rules with the quantitative learning capabilities of neural networks. During the training phase, a hybrid learning algorithm—typically combining least squares estimation and backpropagation—is employed to adjust both the antecedent and consequent parameters, enabling the system to learn efficiently from nonlinear data.
2.2. Weighted Averaging Algorithm
The Weighted Average Algorithm [30] (WAA), proposed in 2024, is a novel intelligent optimization algorithm centered around the idea of guiding the search process through the computation of weighted averages of candidate solutions. By updating each solution’s position based on a weighted combination of global and local information, WAA effectively balances exploration and exploitation, enabling it to escape local optima while accelerating convergence to the global optimum. Extensive experimental studies have demonstrated WAA’s superior performance and rapid convergence across various optimization tasks. In particular, its application in optimizing the surface waviness of WAAM components highlights its effectiveness in real-world engineering problems. Owing to these advantages, WAA has gained popularity in solving complex optimization problems. For instance, Wu et al. [31] proposed a PCA-VMD-WAA-TFT model for forecasting live hog futures prices, in which the WAA algorithm was employed to optimize the parameters of the Temporal Fusion Transformers (TFT), resulting in significantly improved predictive accuracy.
WAA incorporates a dynamic weighted average position and integrates information from each individual’s personal best, the global best solution, and the Lévy flight mechanism to achieve a dynamic balance between global exploration and local exploitation. Its exploration and exploitation balance, adaptive step-size adjustment, and weighted average position mechanisms enable WAA to efficiently escape local optima and navigate complex, high-dimensional search spaces. When applied to the parameter optimization of ANFIS, WAA enhances the model’s capacity to identify optimal membership function parameters and rule structures, which are critical for accurately capturing nonlinear and non-stationary wind dynamics. In the context of offshore wind speed forecasting, where the data are often noisy, volatile, and influenced by multifactorial environmental conditions, WAA’s global search ability helps accelerate the training process of ANFIS and improves predictive accuracy and generalization ability.
The algorithm consists of two main phases. The first phase, Exploration, leverages Lévy flight and randomized initialization strategies to escape local optima. These two strategies are governed by Equations (6) and (7), and are probabilistically selected using random numbers. In this context, represents the step length of the Lévy flight, denotes the -th dimension of the -th solution at iteration , and corresponds to the global best position found so far.
The parameter serves as a judging criterion to dynamically balance the exploration and exploitation phases during the optimization process. As shown in Equation (8), is a function of the current iteration number, is the maximum number of iterations, and is a predefined control parameter typically set to 10. This exponential decay function allows the algorithm to emphasize global exploration in the early stages, while gradually shifting towards local exploitation as the iterations proceed.
During the exploitation phase, three distinct update strategies are employed, with one randomly selected at each iteration to enhance local search dynamics. Strategy 1 integrates the weighted average position , the global best position , and the personal best position of the current solution for position updating, as defined in Equation (9), thereby balancing global guidance and individual experience. Strategy 2 combines with to emphasize individual-level refinement, shown in Equation (10), while Strategy 3 utilizes and to guide the search toward promising regions in the global space, as is illustrated in Equation (11). Here, denotes the dynamically updated weighted mean position of the population, which serves as a flexible anchor for enhancing convergence while preserving population diversity.
2.3. Improved CRGWAA for Optimization
WAA is a recently proposed lightweight population-based optimization method characterized by a simple computational process, low parameter dependency, and fast convergence speed. It has demonstrated satisfactory performance in various small- and medium-scale optimization problems. However, its performance remains limited when tackling high-dimensional and complex tasks, primarily due to three factors: (1) the lack of a well-established theoretical convergence framework, resulting in limited mathematical guarantees; (2) a unidirectional search strategy that may cause premature convergence by trapping the algorithm in local optima during early iterations; and (3) insufficient fine-grained exploitation in later stages, leading to slow improvements in solution accuracy.
To address these limitations and enhance WAA’s optimization capability, we proposed an improved CRGWAA, for which three improvements are proposed in this study. First, Chebyshev mapping is employed for population initialization, leveraging its strong chaotic properties to generate a uniformly distributed and well-covered set of initial solutions. This enhances population diversity and global exploration at the early stage. Second, an elite-based reflection refinement operator is designed to guide the search direction using the best individuals. By incorporating a reflection mechanism, local search intensification is achieved, thereby improving the algorithm’s ability to escape local optima. Finally, to boost solution precision in the later stages, a generalized quadratic interpolation strategy is introduced. This technique fits the objective function landscape within a local region to accurately estimate the optimal position, thus improving the stability and accuracy of the final solution.
2.3.1. Chebyshev Mapping Initialization
In the WAA, the initial population is generated through random initialization, which may result in an uneven population distribution, thereby affecting the global search capability. To address this issue, the Chebyshev map is introduced to provide a more uniform and diverse set of initial solutions, enhancing the algorithm’s exploration ability and helping to avoid premature convergence to local optima.
The expression of the a-order Chebyshev chaotic map is given in Equation (12), where a is typically set to 4. The state values of the resulting chaotic trajectory lie within the range [−1, 1]. Its visualization is illustrated in Figure 2, where Figure 2a presents a scatter plot of 1000 samples generated using the Chebyshev chaotic map, and Figure 2b shows the corresponding histogram distribution. Through an appropriate linear transformation, the Chebyshev map can be utilized to initialize the population of the optimization algorithm, thereby improving its diversity.
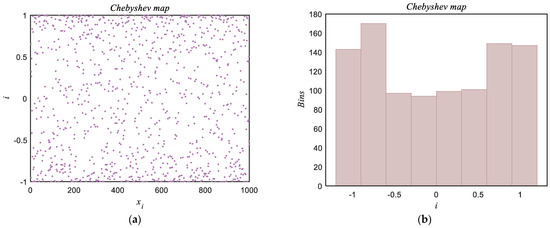
Figure 2.
Chaotic Sequence and its Statistical Characteristics. (a) Chebyshev Map Scatter Plot; (b) Chebyshev Map Frequency Histogram.
2.3.2. Elite-Guided Reflection Refinement Operator
The Reflection Refinement Operator is a strategy adopted in the Quadruple Parameter Adaptation Growth Optimizer [32] (QAGO) to address the issue of premature convergence, as formulated in Equation (13), where denotes the -th dimension of the elite solution , and represents the -th dimension of a randomly selected individual. By incorporating the random individual , this operator effectively enhances population diversity, enabling the search to transcend the current optimal region and thoroughly explore the entire solution space, thereby reducing the risk of premature convergence. However, directly applying this mechanism to the WAA fails to fully exploit the weighted mean position and elite information. To address this limitation, this study proposes the Elite-guided Reflection Refinement Operator, which leverages both the global elite and the weighted average to guide a more adaptive and targeted refinement process.
The improved Reflection Refinement Operator is defined in Equation (16). Compared to the original reflection operator, the GAGO reflection operator offers several advantages in optimization performance. It adopts a weighted average position, , to enhance search stability and integrates the individual best and the global best , thereby improving convergence efficiency. Additionally, it exhibits more stable convergence characteristics, stronger local search capabilities, and superior global exploration abilities, significantly enhancing the optimization performance of the WAA algorithm.
2.3.3. Generalized Quadratic Interpolation
The original WAA employs a weighted average strategy, where the search direction update depends on the population structure but lacks precise estimation capabilities. Generalized Quadratic Interpolation (GQI), through its interpolation method, provides a more accurate estimation of the region where the optimal solution resides, thus improving search precision and avoiding blind searches. The GQI is an enhanced version of quadratic interpolation, based on a three-point interpolation technique. It utilizes three distinct individuals and their corresponding fitness values to construct a quadratic interpolation function, which is then used to predict new solutions, thereby improving the search accuracy. The traditional Quadratic Interpolation (QI) method requires the three points to follow a specific order and depends on the direction of the interpolation polynomial, which limits its applicability. In contrast, GQI improves the construction of the interpolation function, allowing it to handle any combination of three points, regardless of their order or the shape of the quadratic function. This enhancement significantly increases the algorithm’s adaptability and robustness.
Furthermore, the GQI interpolation method adjusts the search intensity at different stages, aiding the population in moving towards better regions in the early stages and refining the search accuracy in the later stages. This results in a more balanced global and local search process. The GQI is formulated as shown in Equation (17), where , , represent three distinct sampling points, and , , denote the objective function values at these corresponding points.
2.4. Proposed ANFIS-CRGWAA for Offshore Wind Speed Prediction
The methodology of the proposed ANFIS-CRGWAA model for offshore wind speed prediction is illustrated in Figure 3 and consists of three major stages. Step 1, Data Preprocessing. Offshore wind speed data collected from the coastal region of Fujian Province, China, at heights of 10 m and 100 m above sea level are selected as the predictive targets. The raw time series data are divided into training and testing sets, with 70% used for training and 30% for testing. To construct the predictive samples, a sliding window approach is employed, whereby wind speed values from the previous three time steps are used as input features to predict the value at the subsequent time step. Step 2, Proposed ANFIS-CRGWAA prediction modal. An enhanced CRGWAA is introduced to optimize the parameters of the ANFIS. In this optimization framework, the RMSE is utilized as the fitness function to guide the global search process. The use of Chebyshev chaotic mapping for population initialization ensures diversity, while elite-guided reflection refinement and adaptive parameter adjustment enable effective exploration and exploitation of the solution space. The CRGWAA enhances the convergence speed and avoids local optima, thereby improving the prediction accuracy and generalization capability of the ANFIS model. The resulting optimized ANFIS parameters, including the best membership functions, are employed to construct the final prediction model. Step 3, Forecasting Result. The forecasting performance is rigorously evaluated using five statistical indicators: RMSE, MAE, MBE, MAPE, and R2. These evaluation metrics provide a comprehensive and quantitative assessment of the model’s accuracy, bias, and stability in offshore wind speed forecasting applications.
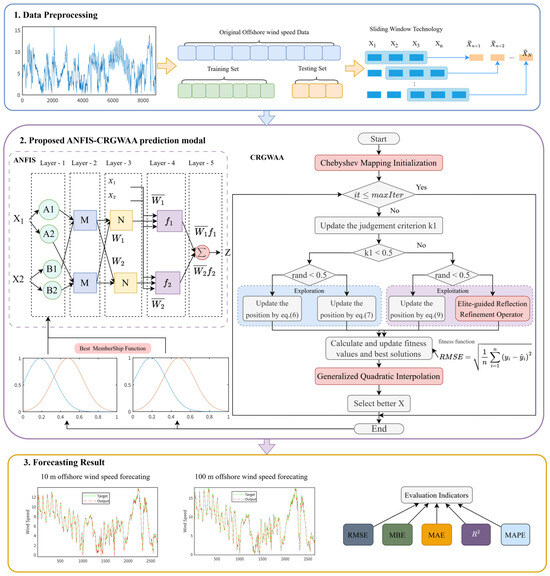
Figure 3.
Flowchart of the ANFIS-CRGWAA Model.
3. Experiment Results
The experimental evaluations were carried out on a 64-bit Windows 11 platform equipped with a 13th Generation Intel® Core™ i9-13980HX processor (base frequency: 2.20 GHz, turbo up to 2.30 GHz) and 16 GB of RAM. All implementations and simulations were conducted using MATLAB R2023b.
3.1. Benchmark Function Test for CRGWAA
3.1.1. Experimental Settings
To rigorously validate the optimization performance of the proposed CRGWAA, the CEC2022 benchmark function [33] suite is adopted as the evaluation platform, as is shown in Table 1. This benchmark set comprises a diverse collection of representative objective functions, encompassing key characteristics such as multimodality, high-dimensional nonlinearity, multiple local optima, and complex inter-variable coupling. The available dimensions are 2, 10, and 20. These features enable a comprehensive assessment of the algorithm’s generalization capability and robustness across varying degrees of problem complexity.

Table 1.
CEC2022 Benchmark Function.
For a fair and objective comparison, six well-established and emerging metaheuristic algorithms are selected as baselines: Genetic Algorithm [34] (GA), Whale Optimization Algorithm [35] (WOA), Sand Cat swarm optimization [36] (SCSO), Goose Optimization Algorithm [37] (GOOSE), Rat Swarm Optimizer [38] (RSO), and the original Weighted Aggregation Algorithm [30] (WAA). All algorithms are configured with a population size of 50, a maximum of 1000 iterations, and a problem dimensionality of 10. Each benchmark function is independently tested 10 times to account for stochastic variability, and the results are recorded for subsequent statistical analysis. The comparative study focuses on evaluating search accuracy, convergence speed, and global exploration capability, thereby demonstrating the overall superiority of CRGWAA in terms of optimization efficiency and solution quality.
3.1.2. Test Results of CEC2022
Table 2 presents the Mean and Standard Deviation values obtained by each of the seven comparative algorithms on the benchmark functions, serving as indicators of average optimization performance and stability. As shown in the table, CRGWAA demonstrates superior mean performance on the majority of the test functions (F1 to F12). Specifically, CRGWAA achieves the best results on 9 out of the 12 functions. For F1 and F9, although GOOSE and RSO obtain marginally better results, CRGWAA still exhibits highly competitive performance, highlighting its robustness.

Table 2.
Experimental Results of Seven Algorithms on the CEC2022 Benchmark Functions. (Bold font indicates the best performance in the comparison algorithms).
In addition to achieving the best average values, CRGWAA also delivers lower or comparable standard deviations on most functions, suggesting that the algorithm maintains strong stability and consistency across multiple independent runs. Notably, on functions F3 and F7, CRGWAA attains both the lowest mean and the smallest standard deviation, underscoring its reproducibility and reliability in diverse optimization environments.
The complex hybrid and composition functions (e.g., F5–F12) are characterized by numerous local optima and nonlinear interactions, posing significant challenges for global optimization. CRGWAA’s enhanced performance on these functions highlights the advantages of integrating the generalized quadratic interpolation (GQI) strategy and the elite-based reflection refinement operator. These enhancements significantly strengthen the algorithm’s diversity preservation and adaptive search capabilities, enabling it to more effectively escape local optima and refine solutions with higher precision.
Table 3 presents the results of the Rank Sum Test, which is used to statistically analyze the superiority of the CRGWAA algorithm compared to the other algorithms. The Rank Sum Test is a non-parametric method commonly employed to compare whether the ranks of two datasets are identical. This test helps determine whether the performance differences between different algorithms across multiple benchmark functions are statistically significant. From the table, it is evident that CRGWAA outperforms other algorithms on several benchmark functions (p-values less than 0.05), particularly on functions F1 to F8. However, for function F10, the p-value for GA and RSO is 0.4727, indicating that these algorithms do not show a significant difference in performance when compared to CRGWAA on F10.

Table 3.
Wilcoxon Rank Sum Test Results for Algorithm Evaluation.
3.1.3. Stability and Convergence Speed
The convergence curves and box plots presented in Figure 4 and Figure 5 compare the performance of the proposed CRGWAA with GA, WOA, RSO, WAA, SCSO, and GOOSE on the CEC2022 benchmark test functions, with a focus on convergence speed, global search capability, and result stability. Overall, CRGWAA demonstrates significant optimization superiority across most test functions. For instance, in the unimodal function F1, CRGWAA rapidly reduces the objective function value at the early stage and converges within fewer iterations.
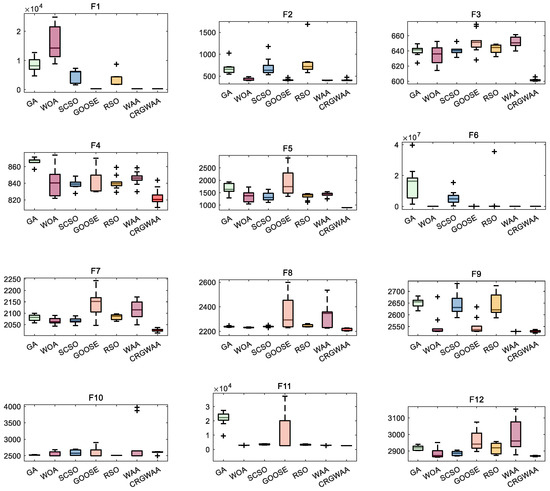
Figure 4.
Box Plot of Competitor Algorithms on CEC2022 Function.
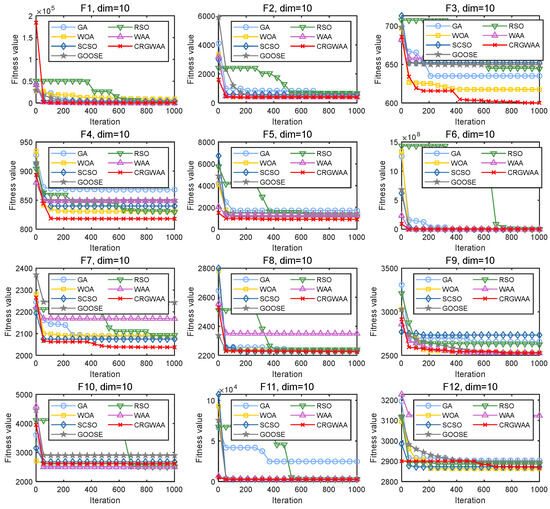
Figure 5.
Convergence of Competitor Algorithms on CEC2022 Function.
From Figure 5, it can be observed that CRGWAA demonstrates significantly improved convergence speed and stability compared to other six algorithms, as indicated by its smoother and faster descent in fitness values. In multimodal functions (F2, F3), the algorithm effectively avoids local optima, outperforming WOA and SCSO. It also maintains superior performance on complex coupled functions (F4, F5), achieving lower fitness values with fewer fluctuations. However, performance drops on F10 and F12 suggest limitations in handling functions with high-frequency disturbances.
In high-dimensional problems such as F6 and F11, CRGWAA achieves rapid and precise convergence, with less sensitivity to parameter tuning. Consistent trends across F7–F12 further highlight its robustness and adaptability. Box plot analysis supports these observations: CRGWAA produces compact distributions and lower medians, indicating high reliability across repeated runs, whereas GA and WOA show wider spreads and multiple outliers. Overall, CRGWAA demonstrates strong global search capabilities, convergence stability, and robustness, making it well-suited for a broad range of optimization tasks.
3.1.4. Search History Trajectory
Figure 6 illustrates the search history of WAA and CRGWAA across different test functions. The green points represent the path of WAA, while the pink points represent the path of CRGWAA. The black and red pentagrams indicate the best solutions for WAA and CRGWAA, respectively.
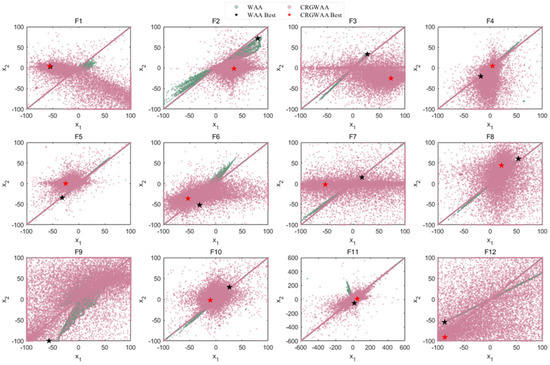
Figure 6.
Comparative Search History Trajectory of WAA and CRGWAA.
From the figure, it is evident that CRGWAA outperforms WAA in both global search and local optimization. For unimodal and multimodal functions (F1 to F4), the search path of CRGWAA is more focused and closer to the optimal solution, whereas the search path of WAA is more dispersed and prone to local optima. In more complex functions (F5 to F8), CRGWAA demonstrates stronger global search capabilities, with its best position being closer to the global optimum. For high-dimensional complex functions (F9 to F12), the search path of CRGWAA is more extensive and concentrated in the optimal region, significantly outperforming WAA. Overall, CRGWAA exhibits superior global search and local optimization capabilities compared to WAA.
3.2. Offshore Wind Speed Prediction Performance
3.2.1. Dataset Introduction
The dataset used in this study is derived from the Fujian offshore wind power forecasting dataset, publicly available on the Heywhale community platform (Heywhale.com), an open-source hub focused on data science and artificial intelligence applications. The dataset covers meteorological observations from January 2022 to January 2024, with a sampling frequency of every 15 min. It includes multiple meteorological variables such as wind speed, wind direction, and temperature, collected from five different meteorological stations. For the experiments, data from station f1 were selected, specifically the wind speed measurements at 10 m and 100 m above sea level during the period from May to July 2023. The corresponding wind speed rose diagrams are shown in Figure 7, where Figure 7a illustrates the 10 m wind speed and Figure 7b presents the 100 m wind speed distribution. It can be seen that the wind direction distributions at 10 m and 100 m above sea level exhibit a broadly similar pattern, indicating a relatively stable directional consistency across vertical layers. Notably, dominant wind occurrences are concentrated in the south–southwest and northeast sectors, reflecting persistent directional preferences in the local wind regime. However, despite this directional consistency, the wind speed distribution reveals significant non-stationarity across both spatial and directional dimensions.
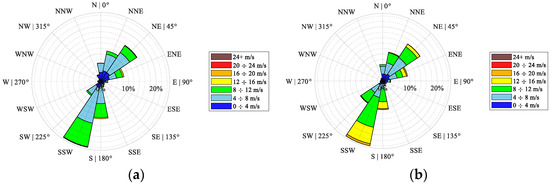
Figure 7.
Wind Rose Diagrams of Offshore Wind Speeds in Fujian Coastal Waters. (a) Ten Meters Offshore Wind Speed; (b) One Hundred Meters Offshore Wind Speed.
3.2.2. Data Preprocessing
The input dataset consists of historical offshore wind speed time series collected at two different heights: 10 m and 100 m above sea level. To improve the stability and accuracy of data-driven learning and modeling procedures, all input features are normalized to the range of [0, 1] using min–max scaling, as is described in Equation (18). This standardization ensures uniform feature contribution during training and avoids dominance of variables with larger magnitudes. A sliding window approach is applied to convert the time series into supervised learning samples. Specifically, a three-step prediction strategy is adopted, whereby the wind speeds from the previous three time steps are used as input features to forecast the wind speed at the next time step.
In the proposed ANFIS-CRGWAA model, these constructed input vectors serve as antecedents in the fuzzy inference framework. Each input is first mapped to corresponding fuzzy membership values using Gaussian membership functions. These fuzzy inputs are then processed through the inference mechanism of ANFIS, ultimately yielding the predicted wind speed. This structure allows the model to effectively capture both the nonlinear relationships and inherent uncertainties in offshore wind dynamics.
3.2.3. Performance Metrics
To comprehensively evaluate the performance of the proposed offshore wind speed forecasting model, five widely used statistical metrics are employed: RMSE, which quantifies the average magnitude of the prediction error; MBE, which indicates the directional tendency of the forecasted values relative to the observations; R2, which measures how well the predicted outcomes capture the variance of the observed data; MAPE, which expresses the error in relative terms; and the MAE, reflecting the average of the absolute deviations. The use of the Accuracy metric enables a more intuitive assessment of the model’s forecasting performance and the range is defined as the difference between the maximum and minimum values within the dataset. These metrics assess the model’s prediction accuracy and stability from different perspectives, including overall error magnitude, directional bias, goodness-of-fit, and relative error. The specific mathematical formulations of these performance indicators are summarized in Table 4, where denotes the total number of samples, represents the observed wind speed values, and indicates the predicted values generated by the model. By leveraging these evaluation criteria, the model’s adaptability and forecasting accuracy under various conditions can be systematically analyzed.

Table 4.
Performance Metrics.
3.2.4. Experimental Results
To evaluate the forecasting performance of various models for offshore wind speed at 10 m and 100 m heights, several statistical metrics including MAE, MBE, RMSE, MAPE, and R2 were computed across 10 time runs. Table 5 and Table 6 present the mean and standard deviation of each metric for all competing models, and its visualization result is shown in Figure 8. At the 10 m level, the ANFIS-CRGWAA model demonstrated outstanding performance, achieving the lowest MAE (0.065), RMSE (0.107), and MAPE (1.83%), as well as the highest R2 (0.999), outperforming all baseline and hybrid models. These results validate the efficacy of integrating ANFIS with the CRGWAA optimizer in accurately and consistently capturing wind speed dynamics. The low standard deviations associated with these metrics further confirm the robustness and reliability of the proposed model. At the 100 m height, a similar pattern emerged. ANFIS-CRGWAA again led in all key metrics, confirming its adaptability across different altitudes. Compared to the original ANFIS-WAA model, the proposed ANFIS-CRGWAA model achieves a substantial reduction in RMSE, by 45.2% at 10 m and 24.6% at 100 m. To further assess the predictive performance of the proposed ANFIS-CRGWAA model, the accuracy ratio was calculated. The model achieved an accuracy ratio of 99.32% at 10 m and 99.28% at 100 m, demonstrating its strong generalization ability and robustness in modeling the complex dynamics of offshore wind fields.

Table 5.
The Offshore Wind Speed Forecast Indicators of 10 m. (Bold font indicates the best performance in the comparison algorithms).

Table 6.
The Offshore Wind Speed Forecast Indicators of 100m. (Bold font indicates the best performance in the comparison algorithms).
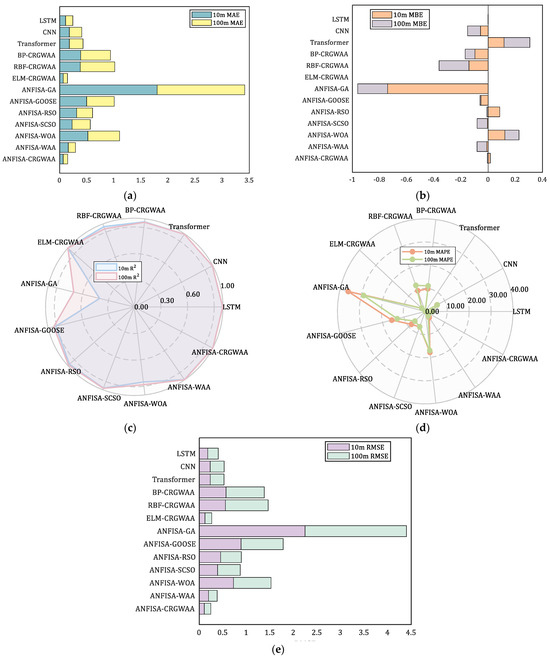
Figure 8.
Visualization Indicators Across Different Test Sets at 10 m and 100 m Heights. (a) Stacked Histogram of MAE for Each Model; (b) Stacked Histogram of MBE for Each Model; (c) Radar Chart of R2 for Each Model; (d) Radar Chart of MAPE (%) for Each Model; (e) Stacked Histogram of RMSE for Each Model.
Although the MBE of ANFIS-CRGWAA is slightly higher than that of the LSTM model, this can be attributed to the distinct focuses of RMSE and MBE. RMSE reflects the overall error magnitude and is particularly sensitive to large deviations, making it a more comprehensive indicator of predictive accuracy. In contrast, MBE captures systematic bias—whether the model tends to over- or under-predict. Therefore, the slightly elevated MBE does not undermine the superior overall performance of ANFIS-CRGWAA; rather, it highlights the model’s robustness and stability in mitigating extreme prediction errors.
Among conventional deep learning models, LSTM outperformed CNN and Transformer architectures, exhibiting lower error metrics and a higher R2 value (0.996). However, its performance still lagged slightly behind the best-performing ANFIS variant, particularly in terms of MAPE. A similar pattern was observed at the 100 m height, where ANFIS-CRGWAA again led across all key metrics, demonstrating its adaptability to different altitudinal conditions. The ELM-CRGWAA model also yielded excellent results, with a remarkably low MAE (0.0778) and a high R2 (0.999), underscoring the advantages of integrating CRGWAA with lightweight neural architectures such as ELM.
Figure 9 and Figure 10 illustrate the wind speed prediction results at 10 m and 100 m above sea level. In both figures, the black curves represent the actual observed data, while the red curves denote the predictions generated by the proposed ANFIS-CRGWAA model. As shown, the ANFIS-CRGWAA model exhibits strong fitting performance at both altitudes, with its predicted values closely following the overall trends of the observed wind speeds. Notably, in regions characterized by sharp wind speed fluctuations, the model demonstrates a remarkable ability to track the rapid changes, with the predicted curves aligning well with the true values. This highlights the model’s robustness and generalization capability under complex and highly dynamic wind conditions, affirming the superior performance of ANFIS-CRGWAA in modeling non-stationary and strongly volatile wind speed data.
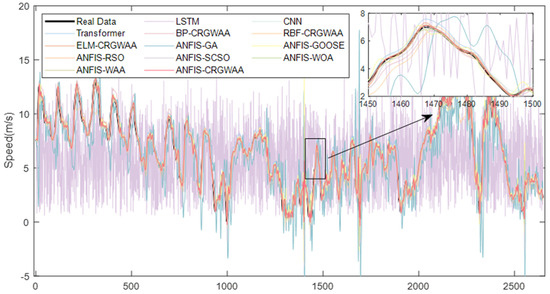
Figure 9.
Offshore Wind Speed Forecast Results in 10 m.
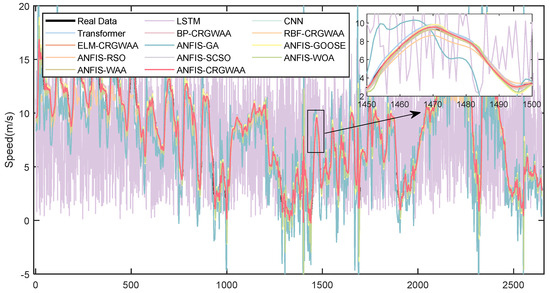
Figure 10.
Offshore Wind Speed Forecast Results in 100 m.
4. Discussion
The empirical results of offshore wind speed prediction using the proposed ANFIS-CRGWAA model demonstrate notable improvements in both predictive accuracy and robustness when compared to conventional models. These improvements are particularly evident in metrics such as RMSE, MAE, R2, MAPE, and MBE, where ANFIS-CRGWAA consistently achieves lower error values across multiple experimental runs. This suggests that the integration of the CRGWAA effectively enhances the parameter optimization process of the ANFIS model, allowing for better generalization on highly non-stationary offshore wind datasets.
To comprehensively validate the performance advantages of the proposed ANFIS-CRGWAA model, we evaluate its relative improvements compared to baseline models using four core performance indicators: , , , and , as specified in Equations (19)–(22). For each metric, the enhancement percentage is derived by subtracting the proposed model’s error from that of the corresponding baseline, thus quantifying the margin of improvement. This approach ensures a coherent and interpretable framework for assessing performance gains across diverse models and evaluation criteria.
Table 7 presents the percentage improvements in predictive performance when comparing the proposed ANFIS-CRGWAA model with three representative baselines: LSTM, ELM-CRGWAA, and ANFIS-WAA. In comparisons with the traditional deep learning architecture LSTM, the proposed hybrid model demonstrates consistently superior performance across all metrics. Specifically, for the offshore wind speed dataset at 10 m height, the ANFIS-CRGWAA achieves 40–45% improvements in MAE, RMSE, MAPE, and R2, while for the 100 m dataset, enhancements range from 37% to 43%, with noticeable gains in R2 as well. These findings highlight the superior generalization and prediction capabilities of the proposed model over standard deep neural networks under non-stationary offshore conditions. When compared to an already optimized neural model, ELM-CRGWAA, the ANFIS-CRGWAA still yields measurable benefits, with error reduction percentages ranging from 2.58% to 13.21% across the metrics. This further supports the hypothesis that ANFIS, especially when coupled with an effective optimization strategy, is better suited for capturing the complex dynamics inherent in offshore wind series. However, ELM-CRGWAA shows a negative MAE improvement (−7.52%) vs. ANFIS-CRGWAA, due to MAE’s weak sensitivity to extreme errors. RMSE, being more responsive to outliers, offers a clearer measure of robustness under large fluctuations. Furthermore, against the ANFIS model optimized by the original WAA algorithm, the proposed approach demonstrates the most significant gains, particularly at the 10-m height. Reductions in MAE, RMSE, and MAPE reach 59.05%, 45.71%, and 43.79%, respectively. Even at 100 m, RMSE decreases by 36.76% and R2 increases by 0.13%, illustrating that the enhanced CRGWAA algorithm facilitates more efficient convergence toward the global optimum in ANFIS parameter tuning.

Table 7.
The Percentage Changes in Forecasting Performance at 10 m and 100 m.
These findings support the initial hypothesis that a hybrid approach combining ANFIS with advanced metaheuristic optimization can better capture the nonlinear and dynamic nature of offshore wind speed patterns. Specifically, the random-guided mechanism in CRGWAA introduces controlled stochasticity that helps maintain population diversity, while the chaotic component enables efficient exploration of complex solution spaces. This synergy appears crucial in avoiding local optima and ensuring convergence towards global optimal solutions, thereby outperforming traditional deterministic or less adaptive methods.
In sum, the results not only validate the effectiveness of the proposed method but also highlight the importance of algorithmic innovation in advancing renewable energy forecasting. Future research may explore its adaptability to multivariate inputs, real-time data assimilation, or coupling with physical models for hybrid physics-informed learning frameworks.
5. Conclusions
This study proposes a novel hybrid forecasting model that integrates an Adaptive Neuro-Fuzzy Inference System (ANFIS) with the CRGWAA optimization algorithm to address the inherent non-stationarity and volatility of offshore wind speed. The CRGWAA algorithm incorporates Chebyshev mapping-based initialization, an elite-guided reflection refinement operator, and a generalized quadratic interpolation strategy, which together enhance population diversity, adaptive global exploration, and local exploitation capabilities. Extensive experiments conducted on the CEC2022 benchmark suite confirm that CRGWAA achieves superior optimization performance compared to several state-of-the-art algorithms. When applied to short-term offshore wind speed prediction in the Fujian region of China, the proposed ANFIS-CRGWAA model significantly outperforms both conventional and hybrid baseline models. Specifically, it achieves an up to 45% reduction in RMSE at 10 m and 24% at 100 m compared to the original WAA, indicating notable improvements in prediction accuracy and generalization performance. By improving the reliability of short-term wind forecasts, the model supports wind farm operators in reducing reserve margins, decreasing wind energy curtailment, and reducing marine disasters.
This study presents three key scientific contributions: (1) the development of a novel hybrid optimization strategy specifically designed to enhance ANFIS performance, (2) the empirical validation of the proposed model’s effectiveness in real-world offshore wind forecasting applications, and (3) the formulation of a generalizable modeling framework that can be adapted to a wide range of time series prediction problems within renewable energy systems.
Despite the significant improvements in predictive performance achieved by the proposed model, several limitations remain. First, offshore wind speed time series are inherently non-stationary and inevitably affected by noise, which can degrade the model’s predictability. Therefore, incorporating a denoising process during data preprocessing is essential. Techniques such as Variational Mode Decomposition (VMD) or wavelet decomposition can be employed to enhance data stability and improve the model’s generalization capability. Second, the ANFIS structure adopted in this study is relatively simple and may not fully capture deeper temporal dependencies. Future work could explore the integration of more sophisticated deep neural network architectures to further enhance prediction accuracy and better model complex dynamic behaviors.
Author Contributions
Conceptualization, Y.L. and F.M.; methodology, Y.L. and F.M.; software, Y.L.; validation, F.M.; formal analysis, Y.L.; investigation, F.M.; writing—original draft preparation, Y.L.; writing—review and editing, F.M.; visualization, Y.L.; supervision, F.M.; funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Engineering Research Center of Integration and Application of Digital Learning Technology, Ministry of Education (1411011), the National Natural Science Foundation of China (Grant No. 52201401), Shanghai Committee of Science and Technology (Grant No. 23010502000), and Chenguang Program of Shanghai Education Development Foundation and Shanghai Municipal Education Commission (Grant No. 24CGA52).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, C.; Mogollón, J.M.; Tukker, A.; Dong, J.; Von Terzi, D.; Zhang, C.; Steubing, B. Future Material Requirements for Global Sustainable Offshore Wind Energy Development. Renew. Sustain. Energy Rev. 2022, 164, 112603. [Google Scholar] [CrossRef]
- Gong, Z.; Wan, A.; Ji, Y.; AL-Bukhaiti, K.; Yao, Z. Improving Short-Term Offshore Wind Speed Forecast Accuracy Using a VMD-PE-FCGRU Hybrid Model. Energy 2024, 295, 131016. [Google Scholar] [CrossRef]
- Xu, X.; Hu, S.; Shi, P.; Shao, H.; Li, R.; Li, Z. Natural Phase Space Reconstruction-Based Broad Learning System for Short-Term Wind Speed Prediction: Case Studies of an Offshore Wind Farm. Energy 2023, 262, 125342. [Google Scholar] [CrossRef]
- Song, D.; Fan, T.; Li, Q.; Joo, Y.H. Advances in Offshore Wind. J. Mar. Sci. Eng. 2024, 12, 359. [Google Scholar] [CrossRef]
- Cem, E.; Cebi, S. Fuzzy Set-Based Approaches in Wind Energy Research: A Literature Review. In Intelligent and Fuzzy Systems; Kahraman, C., Cevik Onar, S., Cebi, S., Oztaysi, B., Tolga, A.C., Ucal Sari, I., Eds.; Lecture Notes in Networks and Systems; Springer Nature: Cham, Switzerland, 2024; Volume 1090, pp. 425–433. ISBN 978-3-031-67191-3. [Google Scholar]
- Das, P.; Mashiata, M.; Iglesias, G. Big Data Meets Big Wind: A Scientometric Review of Machine Learning Approaches in Offshore Wind Energy. Energy AI 2024, 18, 100418. [Google Scholar] [CrossRef]
- Dong, D.; Wang, S.; Guo, Q.; Ding, Y.; Li, X.; You, Z. Short-Term Marine Wind Speed Forecasting Based on Dynamic Graph Embedding and Spatiotemporal Information. J. Mar. Sci. Eng. 2024, 12, 502. [Google Scholar] [CrossRef]
- Dong, L.; Wang, L.; Khahro, S.F.; Gao, S.; Liao, X. Wind Power Day-Ahead Prediction with Cluster Analysis of NWP. Renew. Sustain. Energy Rev. 2016, 60, 1206–1212. [Google Scholar] [CrossRef]
- Tuy, S.; Lee, H.S.; Chreng, K. Integrated Assessment of Offshore Wind Power Potential Using Weather Research and Forecast (WRF) Downscaling with Sentinel-1 Satellite Imagery, Optimal Sites, Annual Energy Production and Equivalent CO2 Reduction. Renew. Sustain. Energy Rev. 2022, 163, 112501. [Google Scholar] [CrossRef]
- Torres, J.L.; García, A.; De Blas, M.; De Francisco, A. Forecast of Hourly Average Wind Speed with ARMA Models in Navarre (Spain). Sol. Energy 2005, 79, 65–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Kong, C.; Chen, B. A New Prediction Method Based on VMD-PRBF-ARMA-E Model Considering Wind Speed Characteristic. Energy Convers. Manag. 2020, 203, 112254. [Google Scholar] [CrossRef]
- Lin, S.; Wang, S.; Xu, X.; Li, R.; Shi, P. GAOformer: An Adaptive Spatiotemporal Feature Fusion Transformer Utilizing GAT and Optimizable Graph Matrixes for Offshore Wind Speed Prediction. Energy 2024, 292, 130404. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, J. Spatial-Temporal Offshore Wind Speed Characteristics Prediction Based on an Improved Purely 2D CNN Approach in a Large-Scale Perspective Using Reanalysis Dataset. Energy Convers. Manag. 2024, 299, 117880. [Google Scholar] [CrossRef]
- Hou, M.; Jin, S.; Cui, X.; Peng, C.; Zhao, K.; Song, L.; Zhang, G. Protein Multiple Conformation Prediction Using Multi-Objective Evolution Algorithm. Interdiscip. Sci. Comput. Life Sci. 2024, 16, 519–531. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhu, D.; Yang, C.; Zhou, C. H-ACO with Consecutive Bases Pairing Constraint for Designing DNA Sequences. Interdiscip. Sci. Comput. Life Sci. 2024, 16, 593–607. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Wang, S.; Zhu, D.; Hu, G.; Zhou, C. DNA Sequence Optimization Design of Arithmetic Optimization Algorithm Based on Billiard Hitting Strategy. Interdiscip. Sci. Comput. Life Sci. 2023, 15, 231–248. [Google Scholar] [CrossRef]
- Kooshari, A.; Fartash, M.; Mihannezhad, P.; Chahardoli, M.; AkbariTorkestani, J.; Nazari, S. An Optimization Method in Wireless Sensor Network Routing and IoT with Water Strider Algorithm and Ant Colony Optimization Algorithm. Evol. Intel. 2024, 17, 1527–1545. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Wang, D.; Xu, Y.; Hua, G. WOAD3QN-RP: An Intelligent Routing Protocol in Wireless Sensor Networks—A Swarm Intelligence and Deep Reinforcement Learning Based Approach. Expert Syst. Appl. 2024, 246, 123089. [Google Scholar] [CrossRef]
- Miao, F.; Li, H.; Yan, G.; Mei, X.; Wu, Z.; Zhao, W.; Liu, T.; Zhang, H. Optimizing UAV Path Planning in Maritime Emergency Transportation: A Novel Multi-Strategy White Shark Optimizer. J. Mar. Sci. Eng. 2024, 12, 1207. [Google Scholar] [CrossRef]
- Miao, F.; Li, H.; Mei, X. Three-Dimensional Path Planning of UAVs for Offshore Rescue Based on a Modified Coati Optimization Algorithm. J. Mar. Sci. Eng. 2024, 12, 1676. [Google Scholar] [CrossRef]
- Ling, L.; Huang, L.; Wang, J.; Zhang, L.; Wu, Y.; Jiang, Y.; Xia, K. An Improved Soft Subspace Clustering Algorithm Based on Particle Swarm Optimization for MR Image Segmentation. Interdiscip. Sci. Comput. Life Sci. 2023, 15, 560–577. [Google Scholar] [CrossRef]
- Tuo, S.; Jiang, J. A Novel Detection Method for High-Order SNP Epistatic Interactions Based on Explicit-Encoding-Based Multitasking Harmony Search. Interdiscip. Sci. Comput. Life Sci. 2024, 16, 688–711. [Google Scholar] [CrossRef]
- Zhu, A.; Zhao, Q.; Yang, T.; Zhou, L.; Zeng, B. Wind Speed Prediction and Reconstruction Based on Improved Grey Wolf Optimization Algorithm and Deep Learning Networks. Comput. Electr. Eng. 2024, 114, 109074. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Nguyen, T.-L.; Kavuri, S.; Park, S.-Y.; Lee, M. Attentive Hierarchical ANFIS with Interpretability for Cancer Diagnostic. Expert Syst. Appl. 2022, 201, 117099. [Google Scholar] [CrossRef]
- Saraswathi, K.; Vijayaraghavan, S. Design of TITO System Using ANFIS-PID Controller for Polymerization Industry. Meas. Sens. 2024, 31, 100996. [Google Scholar] [CrossRef]
- Urošević, V. Determining the Model for Short-Term Load Forecasting Using Fuzzy Logic and ANFIS. Soft Comput. 2024, 28, 11457–11470. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, Y.; Luo, Q.; Wei, Y. Complex-Valued Artificial Hummingbird Algorithm for Global Optimization and Short-Term Wind Speed Prediction. Expert Syst. Appl. 2024, 246, 123160. [Google Scholar] [CrossRef]
- Rashed, B.M.; Popescu, N. Medical Image-Based Diagnosis Using a Hybrid Adaptive Neuro-Fuzzy Inferences System (ANFIS) Optimized by GA with a Deep Network Model for Features Extraction. Mathematics 2024, 12, 633. [Google Scholar] [CrossRef]
- Cheng, J.; De Waele, W. Weighted Average Algorithm: A Novel Meta-Heuristic Optimization Algorithm Based on the Weighted Average Position Concept. Knowl.-Based Syst. 2024, 305, 112564. [Google Scholar] [CrossRef]
- Wu, B.; Zeng, H.; Hu, H.; Wang, L. A Novel Data-Driven Model for Explainable Hog Price Forecasting. Appl. Intell. 2025, 55, 444. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q.; Bu, X.; Zhang, H. Quadruple Parameter Adaptation Growth Optimizer with Integrated Distribution, Confrontation, and Balance Features for Optimization. Expert Syst. Appl. 2024, 235, 121218. [Google Scholar] [CrossRef]
- Kumar, A.; Price, K.V.; Mohamed, A.W.; Hadi, A.A. Problem Definitions and Evaluation Criteria for the CEC 2022 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2022. [Google Scholar]
- Montana, D.J.; Davis, L. Training Feedforward Neural Networks Using Genetic Algorithms. Int. Jt. Conf. Artif. Intell. 1989, 89, 762–767. [Google Scholar]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat Swarm Optimization: A Nature-Inspired Algorithm to Solve Global Optimization Problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Hamad, R.K.; Rashid, T.A. GOOSE Algorithm: A Powerful Optimization Tool for Real-World Engineering Challenges and Beyond. Evol. Syst. 2024, 15, 1249–1274. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A Novel Algorithm for Global Optimization: Rat Swarm Optimizer. J. Ambient. Intell. Hum. Comput. 2021, 12, 8457–8482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).