Abstract
Driven by the commercialization of intelligent ships, the increasingly complex mixed maritime traffic environment presents significant challenges for collision avoidance between multiple ships due to cognitive and behavioral differences between intelligent and traditional ships. Therefore, it is essential to develop a human-like collision avoidance strategy that incorporates traditional navigational experience and handling practices, enhancing explainability and autonomy. By addressing the actual decision-making needs for predicting other ships’ intentions and considering potential risk impacts, a hierarchical strategy is designed that first seeks course direction adjustment and then determines the magnitude of adjustment. A direction adjustment intention estimation model is proposed, accounting for risk membership and COLREGS, to predict other ships’ collision avoidance intentions. Additionally, an intention influence model and a state influence model are introduced to design decision-making objectives, forming an optimization function based on angle range and maneuvering time constraints to determine the appropriate adjustment magnitude. The results demonstrate the strategy’s effectiveness across various scenarios. Specifically, the distance between ships increased by nearly 25% during the process, significantly enhancing safety. It is worth mentioning that the model has the potential to enhance intelligent ships’ capabilities in complex situational handling and intention understanding.
1. Introduction
With the maturation of intelligent ship technology and the increasing commercial utilization, maritime transportation is facing a prolonged coexistence of intelligent and traditional ships [1]. This situation introduces unpredictability and risk to navigation safety, amplifying the complexity of inter-ship coordination and collision avoidance. Cognitive disparities and information asymmetry in collision avoidance rules and situational understanding between intelligent and traditional ships [2,3] can lead to intention misjudgment, misunderstandings, and operational conflicts, especially in densely trafficked waterways. Hence, there is a need to develop an intelligent ship collision avoidance strategy that mirrors human-like operational decision-making. This approach aims to align with traditional navigational decision-making experiences and practices, reducing operational discrepancies between ships and enhancing the explainability of intelligent ships. Such strategies offer practical insights for the scalable transition of maritime traffic towards intelligent ships while coexisting with traditional ships, thus holding significant promise for future applications.
Traditional ships typically select a primary threat and maneuver according to rules governing two-ship encounters while also considering the impact of surrounding ships and reacting promptly [4]. In contrast, intelligent ships can handle multiple threatening ships simultaneously, aiming for optimal strategic planning. Current literature focuses extensively on multi-ship collision avoidance decisions for intelligent ships, broadly categorized into centralized and distributed approaches [2,5].
Centralized multi-ship collision avoidance strategies typically involve a central controller or decision unit that collects information from all relevant ships and formulates unified collision avoidance plans based on a global perspective. These strategies are similar to single-ship collision avoidance methods and can generally be categorized into model-based analytical methods, optimization algorithms, vector or field theory models, artificial intelligence methods, and hybrid methods [6,7]. For example, Hu [8] used a collision risk index model to adjust the speeds and courses of multiple ships for collision avoidance; Li [9] proposed a rolling horizon optimization method that aims to minimize the time cost and course changes of avoidance maneuvers from a globally optimal perspective; Liu [10] constructed a multi-objective optimization problem by combining the quantifying degree of domain violation and the probability of domain violation to find the optimal collision avoidance path; Lee [11] used an artificial potential field and DCPA/TCPA evaluation models for course planning during multi-ship encounters. Some researches have quantified the International Regulations for Preventing Collisions at Sea (COLREGs). Wang [12] designed a collision avoidance plan based on multi-ship identification, adherence to and violations of international collision regulations, and corresponding adjustment procedures; Cho [13] developed a process framework starting from collision avoidance rules, including inter-ship encounter situation analysis, encounter type classification, and probabilistic velocity obstacle modeling to coordinate multi-ship collision avoidance; Wang [14] designed a centralized multi-ship collision avoidance system by observing the navigation states of other ships, estimating their situational intentions, predicting their actions, and determining collision avoidance decisions.
Centralized strategies involve a central controller that collects information from all ships to create optimized, global collision avoidance plans, thereby reducing conflicts and improving navigation efficiency. However, they rely on efficient data communication and high trust in the central node, and their effectiveness may be compromised in complex environments with limited information. So, distributed strategies treat each ship as an independent decision-maker, using local information and limited communication for coordination. They offer greater flexibility and robustness, reducing dependence on central control. While the methods are similar to centralized collision avoidance strategies, including optimization algorithms [15,16], vector or field theory models [17,18], deep learning [19,20,21], and others [22,23]. Both centralized and distributed strategies are primarily focused on intelligent ships, leveraging the advantages of algorithmic models to achieve precise collision avoidance.
However, in mixed-traffic environments, this undoubtedly increases the difficulty for traditional ships’ crews to comprehend these strategies, often leading to operational conflicts. In single-ship collision avoidance research, there is an increasing trend to incorporate crew experience and human-like maneuvering thinking [24,25]. Given the complexity and diversity of multi-ship adjustments, it is even more crucial to integrate traditional navigational practices. Huang [26] developed a collision avoidance system’s human-machine interface based on the generalized velocity obstacle algorithm, integrating traditional navigational experience to provide feasible collision avoidance solutions among multiple intelligent ships; Liu [3] analyzed multi-ship collision avoidance planning in mixed situations involving intelligent and traditional ships from the perspective of collision avoidance rule systems, taking into account the maneuvering habits of traditional ships. Therefore, this paper aims to consider the decision-making requirements of traditional navigation in multi-ship environments, integrating them into a multi-objective decision mode. This approach optimizes algorithm performance, enhances the explainability of decision intentions, and improves the generalizability of the algorithms, thereby demonstrating a human-like collision avoidance method. Such a method is designed to facilitate the coexistence of human and machine systems in modern maritime navigation.
This approach has the following advantages over the existing solutions: (1) Addressing the two critical factors of actual decision-making requirements and habits, including the intentions of other ships and potential risks, it constructs a hierarchical strategy that first seeks the course direction of adjustment and then determines the adjustment magnitude, which enhances the explainability of the strategy. (2) By incorporating COLREGs and a risk membership function based on the course danger sector, it designs a direction adjustment intention estimation model, which predicts the intentions of other ships even under limited information conditions. (3) Considering the current situation and potential risk impacts during the adjustment process, it uses a field model to quantify intention influences and combines with a state influence model to form a multi-objective planning function, thereby reducing operational conflicts and risk impacts for smooth collision avoidance. (4) Utilizing the geometric characteristics of turning maneuvers, it establishes target constraints to enhance the practical efficiency of the algorithm.
The rest of the paper is organized as follows. In Section 2, the preliminaries and overview are given. Section 3 describes models and methodologies. Ship collision avoidance strategies are presented in Section 4. Section 5 conducts case studies for different situations. Discussion is carried out in Section 6. Finally, we conclude this paper in Section 7.
2. Preliminaries and Overview
In actual multi-ship encounter scenarios, collision avoidance maneuvers often occur in high-density traffic environments with limited adjustment time. Ship operators face two primary challenges: estimating the intentions of other ships and managing potential risks. To address these challenges, operators must rely on rules or experience to determine the collision avoidance intentions of nearby threatening ships and then formulate their own avoidance strategies to prevent operational conflicts. Additionally, they must address both immediate risks arising from the current situation and those generated during the adjustment process while continuously refining their strategy to mitigate the impact of emerging risks.
Multi-ship simultaneous collision avoidance is one of the most complex scenarios in collision avoidance strategy planning due to the extensive data analysis required, which traditional ships often struggle to fully meet. In contrast, intelligent ships can leverage their advanced data analysis and computational capabilities to rapidly formulate optimal collision avoidance strategies. Based on this, this paper proposes an intelligent ship-distributed local collision avoidance architecture that aligns with real-world decision-making requirements and operational habits. The proposed approach includes the following key components:
(1) Direction intention estimation: Using the current navigation situation and COLREGS, the collision avoidance direction intentions of each threatening ship are estimated to predict their potential avoidance behaviors.
(2) Magnitude adjustment construction: A target function is constructed to determine the course magnitude of avoidance adjustment for each ship, ultimately forming a distributed multi-ship collision avoidance adjustment strategy. Here, and represents the sets of states and direction intentions of all involved ships, respectively. denotes the intention influence function, which assesses the impact of each ship’s direction adjustment intention on the overall collision avoidance strategy. represents the state influence function, reflecting the constraints imposed by the ships’ navigation states on the collision avoidance strategy. is the cost function for the ith ship, aiming to constrain the impact of adjustments on individual ships.
This approach employs a hierarchical design strategy that first identifies the adjustment direction and then solves for the adjustment magnitude when encountering risk, focusing solely on course adjustments. A structural illustration of this framework is provided in Figure 1. Here, it is assumed that each ship can receive the position, speed, and course information of the surrounding threatening ships, and each ship performs distributed collision avoidance according to the strategy designed in the paper.
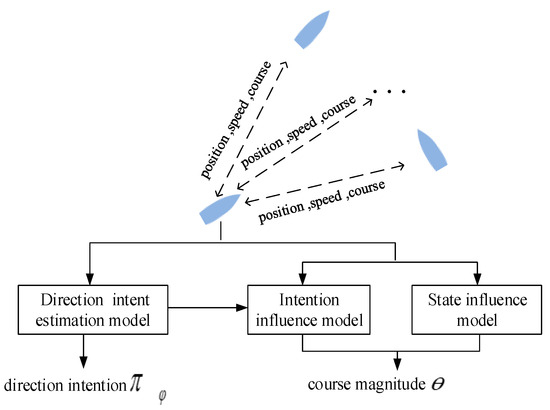
Figure 1.
Architecture of multi-ship distributed collision avoidance strategy.
3. Models and Methodologies
3.1. Collision Risk Model
When facing the complex environment of multi-ship collision avoidance, traditional maritime practices require assessing the risk between ships to initiate avoidance maneuvers. Therefore, it is essential to construct a collision risk model to evaluate these risks. Building upon the risk model proposed previously by the author [27], the model is expanded here to incorporate velocity factors, resulting in the collision risk index model of two ships as shown in Equation (1):
where
, U(D), and U(V) represent the membership functions for the nearest encounter situation, the distance between ships, and the speed, respectively. refer to the minimum distance and safest encounter distance between two ships, respectively; is the collision angle between two ships; this aforementioned parameter information can be found in reference [28]. represents the ratio of the target ship (TS) ‘s velocity to our own ship (OS) ‘s velocity ; denote the relative velocity and relative distance between them, with as the angle between them; DCPA and denote distance and time to the closest point of approach between OS and TS; , indicate the weighting parameters of three membership functions. When the CRI is larger, it indicates a higher collision risk, generally considered high when exceeding 0.6 [29]. Therefore, once the risk between ships exceeds the set threshold, collision avoidance planning actions are triggered.
3.2. Direction Adjustment Intent Estimation Model
Both the collision avoidance rules provided in COLREGS and daily decision-making and maneuvering habits emphasize guidance on adjusting course direction, while specific guidance on adjusting course magnitude is not explicitly provided [4,30]. Therefore, in the collision avoidance planning process, adjusting course direction is typically considered a prioritized factor. Despite this, most studies tend to integrate course direction and magnitude adjustment as a unified decision-making process [31,32], and a few have attempted to separate these factors for finer control of ship collision avoidance behaviors. For instance, Perera [33] proposed a fuzzy-logic-based parallel decision-making model for selecting course and speed adjustment directions; He [34] provided specific course turn strategies based on collision avoidance rules and seamanship practices and further designed action models based on the encounter situation discrimination model.
In addition, due to the difficulty in accurately predicting the intentions of other ships in a multi-ship environment, crews typically make initial predictions about the adjustment directions of other ships [4]. Moreover, to enhance the explainability and human-likeness of the strategies, the first step is to estimate the intentions of course adjustments for the involved ships. This helps in assisting the understanding of the general collision avoidance trends of other ships.
(1) Risk membership function based on course danger sector.
When making decisions, crews often assess whether to adjust course based on observing the minimum encounter distance with other ships. They rely on automatic radar plotting aids (ARPA) and guidance manuals to estimate specific course adjustments using geometric plotting methods for collision avoidance [30]. In the literature [35,36], the resultant range of course adjustments from this method is termed a “danger sector”, which comprises potentially risky courses. As illustrated in Figure 2, Dsda represents OS’s safe passing distance. When , OS makes course adjustments either left (TL) or right (TR) to achieve a safe passing distance. The range of course adjustments at this moment defines the course danger sector. Further details on the computation of TR and TL can be found in reference [35].
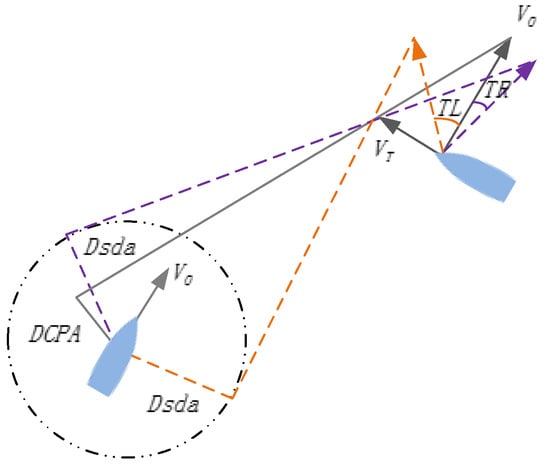
Figure 2.
Course danger sector illustration.
In actual collision avoidance scenarios, in addition to considering the danger sectors arising from relative positions and distances, the impact of the relative speeds of ships must also be taken into account. Research indicates that avoiding fast-moving ships is easier compared to slow-moving ones. Therefore, a risk membership function is formulated by integrating ship speed and course adjustments to assess the risk level when altering course to the left or right:
The risk membership functions for course adjustments to the right and left are denoted as respectively. represent the maximum extent of course adjustments to the right or left, which can be considered as 90°, while represent the minimum extent of course adjustments, which can be considered as 0°.
(2) Risk-based estimation of direction adjustment intention.
Practical directional adjustment choices are mainly influenced by two factors: collision avoidance rules and risk levels. Consequently, by integrating the collision avoidance direction guidance for different encounter situations with the risk membership functions based on the course danger sector, an intention estimation model for directional adjustments is designed. According to the classification of ship encounter situations and action interpretations from the author’s previous study [27] (as shown in Table 1), the preferences of collision avoidance rules are integrated into the estimation model. The model prioritizes selecting the adjustment direction with the lower risk as the intention.

Table 1.
The interpretation of ship encounter situation.
α, β denote the relative bearing angles. The collision avoidance rule preferences are only integrated into the estimation model for ship encounter scenarios where the CRI is greater than the threshold of 0.6. When the rule-guided preference is to turn right, the corresponding risk of adjusting to the right is weighted less, while the risk of adjusting to the left is weighted more. Conversely, when the rule-guided preference is to turn left, the opposite weighting applies. In other situations, the influence of weights is disregarded. The detailed estimation model is presented in Equations (7)–(9).
Therefore, by analyzing the total risk faced when a single ship chooses to adjust right or left in a multi-ship scenario, intention estimation is conducted to preliminarily determine each ship’s evasion tendency.
3.3. Intention Influence Model
After estimating the directional adjustments of the involved ships, their mutual influence is evaluated by analyzing pairwise interactions, categorized into receding or approaching trends. Receding trends show tendencies to repel or move apart, indicating no conflict in adjustment actions. Approaching trends show tendencies to attract or move closer, potentially leading to conflicts closely related to the adjustment magnitudes.
In receding trends, mutual influence between ships is not considered. In approaching trends, a theoretical field model assesses the influence of converging intentions, guiding course adjustments. Specifically, as shown in Figure 3, when the intentions and exhibit an approaching trend, a field model related to ship-to-ship distance is designed to describe the influence, where closer distances imply stronger effects. Conversely, when and exhibit a receding trend, no influence is assumed. This is formulated as described in Equation (10).
where represents the intention influence between two ships, ρ denotes the weighting parameter. The receding trend and approaching trend are jointly determined by the relative positions, relative courses, and directional intentions of the ships. During an approaching trend scenario, the influence of intentions is primarily constrained by the relative distance between ships. At greater distances, the influence is minimal, but it increases as the distance decreases. Within a range of less than 1 nautical mile, the quantified influence value exceeds 1, emphasizing the significant impact of close proximity.
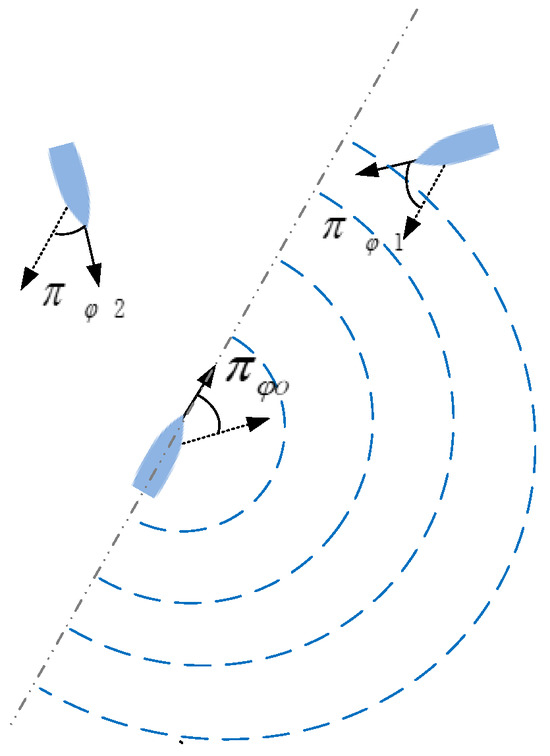
Figure 3.
Intention influence field illustration.
In summary, course intention not only influences direction adjustment but also plays a crucial role in magnitude adjustment. Ships can use the estimated intentions to analyze trends of approaching or receding and quantify the degree of influence on magnitude adjustment. The closer the ships are, the greater the impact becomes. By selecting an appropriate magnitude, the influence can be mitigated to maintain a suitable distance between ships, thereby enhancing safety.
3.4. State Influence Model
When multi-ships are simultaneously engaged in collision avoidance maneuvers, it is essential to consider potential risks beyond the estimated conflicts arising from intention adjustments. This includes the inherent risks associated with the navigation states of the ships themselves, specifically the risks posed to surrounding non-hazardous ships during avoidance maneuvers. Here, the complexity of the distance factor (DF) and the CRI are used to describe these risks.
In multi-ship environments, complex models are typically employed to represent the traffic flow conditions among encountering ships [37,38], including the degree of crowding and collision risk. Among these, the distance factor is the most significant traffic feature [39,40]. This study utilizes DCPA as the distance factor for construction.
are positive parameters. As the DCPA changes during the ship adjustment process, the complexity increases when DCPA is smaller than the safe passing distance Dsda, which, in turn, has a greater impact on the interaction between ships. The CRI is referenced according to Equation (1)’s description. These two indicators are used to assess the spatial distribution of ships, reflecting the degree of posture correlation during collision avoidance adjustments and revealing potential risk impacts.
4. Ship Collision Avoidance Strategies
Based on the collision avoidance framework outlined in Section 2, a multi-ship distributed collision avoidance strategy is structured. It adheres to the design principle of first determining the adjustment direction and then planning the adjustment magnitude. This approach allows each ship independently to adjust according to its own risk conditions, meeting practical requirements and operational conventions.
(1) Limiting the scope of handling.
Each time selecting the ith ship within the water area as OS (), the study focuses on TSs j () within a 5 nautical mile range. Using the risk model to assess the collision risk level; if the risk exceeds a preset threshold, OS initiates collision avoidance strategies.
(2) Adjustment of course direction.
Referring to Section 3.2, based on the relationship between the DCPA and Dsda, determine (The course magnitude adjustment to the right and left for ship i to safely pass ship j at Dsda), substitute them into Equations (5) and (6) to obtain the risk membership functions between two ships. Then, based on the anticipated encounter actions of ships, apply Equations (7)–(9) to calculate the total risk of adjusting to the right and to the left for OS. By comparing these, determine OS’s directional adjustment intention . Next, further estimate the directional adjustment intentions of surrounding TSs to guide subsequent course magnitude adjustments. Sequentially treat each surrounding TS j as OS, repeating steps (1) and (2). Ultimately, this process forms a set of directional intentions .
(3) Adjustment of course magnitude
Based on their respective adjustment risks, after estimating the course direction adjustment intentions of the involved ships and considering potential risk factors in practical decision-making needs, it designs an objective function for OS’s course magnitude adjustment. This objective function comprises intention influence functions, state influence functions, and course deviation cost functions:
where, represent the course magnitude after adjustment and the initial course magnitude of OS respectively, denotes a weighting parameter. The adjustment magnitude obtained when the objective function reaches its minimum value, corresponds to the desired course adjustment. ϑ is the range of magnitude adjustment.
The first constraint is the adjustment angle limit, determined by the maximum extent of the course danger sector, as specified in Equation (13):
The second constraint is the steering time constraint, which aims to consider the maneuvering characteristics when the course changes, ensuring that the maneuvering time does not exceed the time the ship invades the safe encounter distance. The maneuvering time [10,41] required to reach the specified course magnitude is , represents the reaction time before course adjustment, which is taken as 20 s [42], and is the simplified ship maneuvering radius, which is taken as 200 m. As shown in Figure 4, the time for segment OA is denoted as , and the time for segment OB is denoted as .
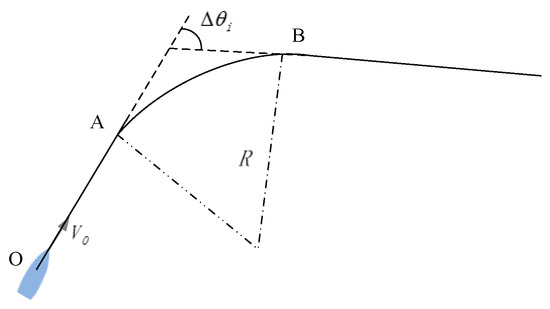
Figure 4.
Geometric illustration of collision avoidance steering path.
And T represents the range of the time constraint, which is estimated by the shortest time to reach DCPA or Dsda, satisfying the following Equation (14):
Furthermore, to reduce the operational complexity associated with frequent minor course adjustments, no course magnitude adjustment is executed during each adjustment process when the continuously estimated directional adjustment intentions of the own ship remain consistent, and the total risk change in the corresponding direction is below the set threshold. Ultimately, the initial course is gradually restored when all surrounding risks dissipate, or there are no ships within the influence distance.
The specific algorithm flow is shown in Algorithm 1.
| Algorithm 1: Algorithm flow. |
| Inputs: Ship parameters |
| Outputs: The new trajectory state of ships Procedure: Initiate collision avoidance if the risk threshold is exceeded for i = 1:N for j = 1:Mi if calculate by in (1)–(8) using direction adjustment intent estimation model end if end for gain end for summarize the collection of course directional intentions for i = 1:N for j = 1:Mi if design objective planning function according to Equations (10)–(14) using intention influence model and state influence model end if end for gain if restore the initial course of ship i end if end for obtain the new layout of ships At next time instant repeat procedure |
5. Case Study
The distributed collision avoidance adjustments for multi-ships are validated in various scenarios, focusing solely on the course adjustment strategy. The testing is performed on the MATLAB R2021 simulation platform. By setting up multiple-ship scenarios with different encounter situations, the trajectories, course changes, and trends in inter-ship distances during the collision avoidance process are analyzed to evaluate the collision avoidance effectiveness. The relevant model parameters are determined based on empirical data and algorithm tuning, with the values set as follows: . The initial parameters of the ships involved are shown in Table 2.

Table 2.
The initial parameters of the ships in simulated test scenarios.
(1) Scenario one.
Figure 5a–c respectively shows the trajectory changes, course adjustments, and the distances between ships. In Figure 5b, dashed lines are initial courses and circle-dashed lines are adjusted courses. Ships adjusted left and right by up to 90°, with minimum distances reaching 0.4 n miles. Adjustments were mainly within the first 4000 s. Ships then returned to initial courses if risk thresholds were not met or they moved beyond the influence distance, thus avoiding collisions. Each course adjustment considers the current scenario and risks during the process. New target ships may enter the influence distance during each assessment, requiring continuous adjustments until all ships were free from risk influence.
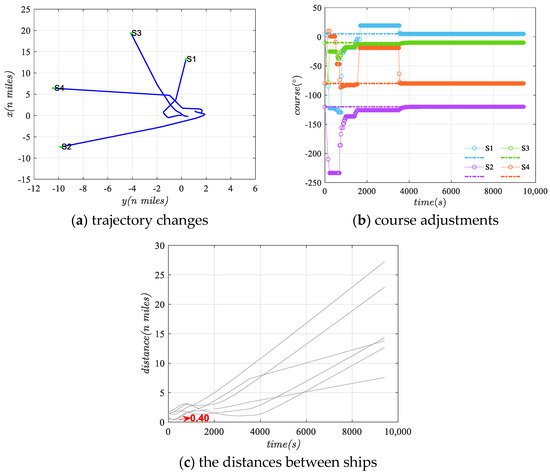
Figure 5.
Collision avoidance situation in scenario one.
S1 was continuously influenced by other ships, initially adjusting left, then right, and finally left again to return to its initial course, showing significant redundancy. Similarly, S2 to S4 undergo multiple adjustments to the right or the left. Among them, S3 exhibited the smallest adjustment magnitude, while S2 and S3 exited the risk influence earlier. The adjustment magnitude fluctuation frequency was relatively low throughout, maintaining a stable course until new risks prompted further adjustments.
The collision avoidance trajectories at different time instances are illustrated in Figure 6a–d. The specific time points are randomly selected based on the situation in Figure 5b. At t = 274 s, all ships were adjusting. At t = 1321 s, S2 and S3 had finished and were returning to their initial courses. At t = 2428 s, S1 and S4 were still adjusting. By t = 4428 s, all ships returned to initial courses with no new risks.
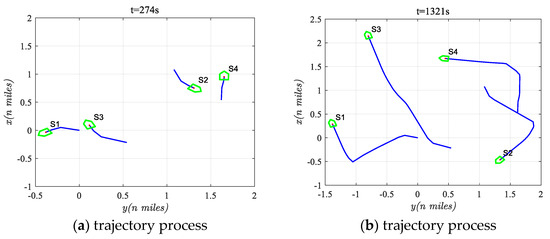
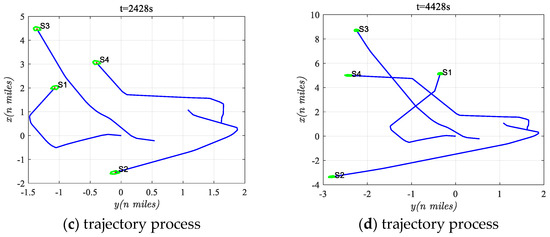
Figure 6.
Avoidance process at different time instances in scenario one.
(2) Scenario two.
Figure 7a–c respectively show the trajectory changes, course adjustments, and distances between ships. Ships adjusted left and right by up to 90°, with minimum distances reaching 0.41 n miles. Adjustments were mainly within the first 3500 s. In this scenario, the introduction of S5 affected the adjustment dynamics of S1 to S4 differently compared to Scenario 1. S1 was still significantly influenced by other ships, initially adjusted left twice, then right, and subsequently exited the risk zone. Later, influenced by S4 and S5, S1 adjusted left again, then right, until returning to its initial course. S5 exhibited the smallest adjustment magnitude, while S2 and S3 exited the risk zone earlier. Overall, the frequency of adjustment magnitude fluctuations is relatively low.
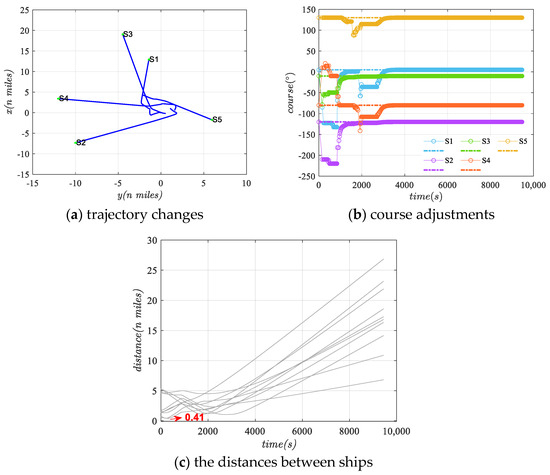
Figure 7.
Collision avoidance situation in scenario two.
Figure 8a–d provides an overview of the collision avoidance trajectories at various time instances. At t = 382 s, all ships except S5 were in collision avoidance mode. By t = 1076 s, S2 had completed its maneuvers and was returning to its original course, while S4 was also recovering but may face further adjustments later. At t = 2065 s, S1, S4, and S5 were still adjusting their courses, with S3 having completed its adjustments. Finally, at t = 3465 s, all ships had finished their collision avoidance maneuvers and were gradually returning to their initial courses.
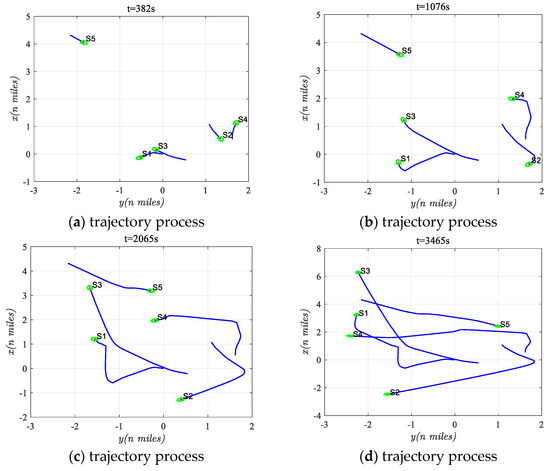
Figure 8.
Avoidance process at different time instances in scenario two.
(3) Scenario three.
Figure 9a–c respectively illustrate the trajectory changes, course adjustments, and distances between ships. Ships adjusted left and right by up to 90°, with minimum distances reaching 0.40 n miles. Adjustments were mainly within the first 4000 s. In this scenario, S6’s influence was introduced, impacting the adjustment dynamics of ships differently compared to previous scenarios. S1 and S5 experienced significant influence from other ships: S1 adjusted left twice, then continued right, followed by continuous left adjustments until returning to its initial course. Meanwhile, S5 initially adjusted right, then several left adjustments until returning right to its initial course. In contrast, S3 and S6 exhibited smaller adjustment magnitudes, with S3 exiting the risk zone earlier.
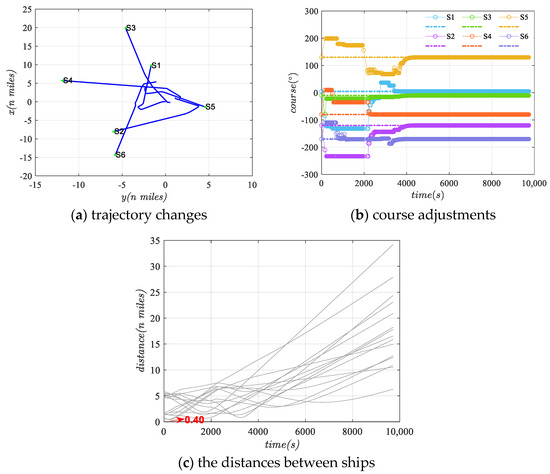
Figure 9.
Collision avoidance situation in scenario three.
Figure 10a–d provided an overview of the collision avoidance trajectories at various time instances. At t = 475 s, all ships were actively engaged in collision avoidance adjustments. By t = 1103 s, S3 had completed its maneuvers and returned to its initial course, while S6 was also recovering but faced further adjustments later. At t = 3088 s, S1, S2, and S5 were still adjusting their courses, with S4 having completed all adjustments. Finally, at t = 4736 s, all ships had finished their collision avoidance maneuvers and were gradually returning to their initial courses.
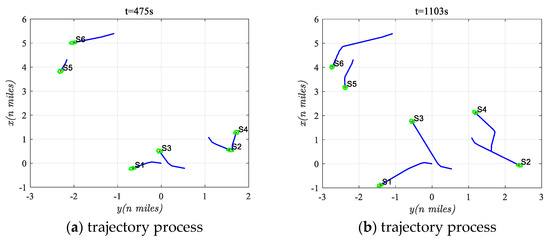
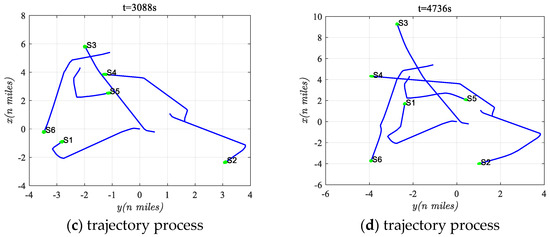
Figure 10.
Avoidance process at different time instances in scenario three.
(4) Scenario four.
Figure 11a–c, respectively, illustrates the trajectory changes, course adjustments, and distances between ships. Ships adjusted left and right by up to 105°, with minimum distances reaching 0.40 n miles. Adjustments were mainly within the first 4500 s. In this scenario, the introduction of S7 influenced the adjustment dynamics differently compared to previous scenarios. S5 and S1 experience significant influence from other ships: S5 adjusted right, then left, continued right, and then left again until returning to its initial course. Meanwhile, S1 initially adjusted left, then right, left again, and finally right to return to its initial course. In contrast, S3, S6, and S7 exhibited smaller adjustment magnitudes, with S3 exiting the risk zone earlier. Due to the complexity of ship dynamics in this scenario, the time taken for all ships to return to their initial courses is relatively delayed. The frequency of course adjustment fluctuations also increases for some ships.
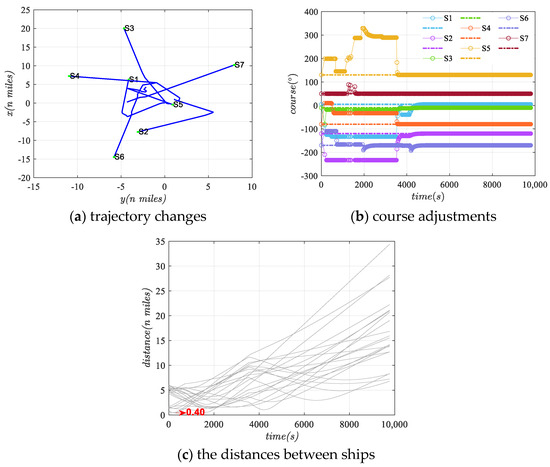
Figure 11.
Collision avoidance situation in scenario four.
Figure 12a–d depicts the collision avoidance trajectories at various time instances. At t = 487 s, all ships except S7 are actively engaged in collision avoidance adjustments. By t = 1588 s, S3 had completed all collision avoidance maneuvers and gradually returned to its initial course. S6 has also exited the risk zone and is in the process of returning to its original course, though it may encounter further risk influences later. At this time, S7 entered the collision avoidance phase. At t = 3795 s, S1, S2, S4, and S5 were still undergoing collision avoidance adjustments, while S7 had completed all collision avoidance maneuvers. Finally, at t = 5795 s, all ships had completed their collision avoidance maneuvers and were gradually returning to their initial courses.
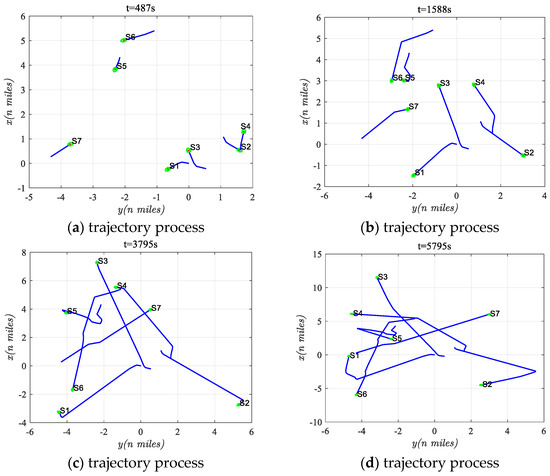
Figure 12.
Avoidance process at different time instances in scenario four.
In complex multi-ship interactions, ships use a collision avoidance strategy that first determines the adjustment direction, then the magnitude. This enables effective coordinated collision avoidance. During adjustments, ships follow a traditional decision-making model, independently controlling their maneuvers by considering other ships’ intentions and potential risks. The adjustment magnitudes are gradual with low fluctuation frequency, while directions are flexibly chosen based on real-time dynamics.
6. Discussion
In comparison with other common collision avoidance frameworks, the decision-making process typically considers both the direction and magnitude of course adjustments but often neglects the individual estimation of other ships’ course intentions. Here, a classic objective function-based collision avoidance method [43,44] is employed for comparative analysis. This compared algorithm disregards the constraints of angle and time of our algorithm as well as the intention influence function, focusing solely on the objective function composed of state influence functions and course deviation cost functions to select course adjustment strategies. The specific results are shown in Figure 13, based on the initial layout of Scenario Three, depicting trajectory changes (a) and inter-ship distances (b). From the trajectory trends, it can be observed that the trajectories exhibit greater abruptness in terms of smoothness, course fluctuation frequency, adjustment frequency, and amplitude compared to Figure 10a, and the minimum inter-ship distance drops to 0.28 n miles, which significantly increases the probability of ship collisions. Therefore, the early prediction of directional intentions can effectively improve the coordination and adjustment performance of multi-ship collision avoidance.
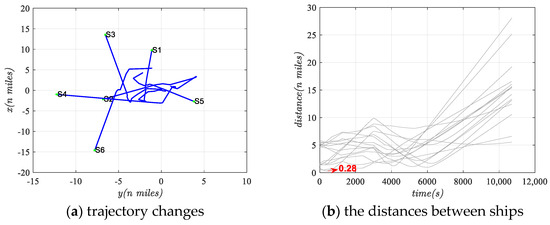
Figure 13.
The compared collision avoidance situation.
In the actual process of ship handling, owing to limitations in cognition and response, crews cannot fully consider the influence of all involved ships. However, intelligent ships can analyze potential risks from multiple ships simultaneously and generate more precise planning paths. Although this may lead to more frequent directional adjustments, it is a necessary adaptation to address unpredictable risks in complex situations. Despite efforts to minimize unnecessary adjustments, some redundancy is unavoidable to ensure safety. To reduce differences in cognitive understanding and ambiguities in actions compared to traditional ships, more in-depth research is needed in designing anthropomorphic strategies for intelligent ships. For example, empirical methods such as collecting and statistically analyzing the actual behavior or maneuvering trajectories of crews could be used to further narrow the gap between humans and machines. This approach not only enhances collision avoidance efficiency but also promotes synergistic navigation between intelligent and traditional ships.
In addition, the sensitivity analysis of the weighting parameters has not yet been addressed. To enhance the generalization ability of the model, further research should be conducted on methods such as online identification optimization and reinforcement learning. There is still significant potential for algorithm optimization in this area.
7. Conclusions
In response to the complex and dense multi-ship environments, this paper integrates actual decision-making habits and maritime experience to form an intelligent ship collision avoidance framework that first determines direction and then adjusts magnitude. This framework focuses on two key issues: assessing the intentions of other ships and evaluating potential risks. The proposed approach features a direction intention estimation model compliant with COLREGS and an objective planning function that combines intention influence and state influence models to optimize strategies. Combined with ship performance constraints, this framework enables efficient and smooth collision avoidance, aligning closely with practical needs and handling habits. By leveraging efficient, intelligent processing capabilities and integrating traditional ship handling experience, this strategy enhances the situational analysis and decision-making capabilities of intelligent ships in complex environments. The main innovations lie in: (1) considering practical decision-making needs to explore a hierarchical ship collision avoidance framework of “direction first, magnitude later”; (2) designing an objective planning function that integrates performance constraints with intention and state influence goals by incorporating potential risk impacts. This provides new perspectives and methods for the application and large-scale development of intelligent ships.
However, there are still some actual needs and scenarios that have not been considered and need further resolution. The current research does not adequately account for factors of special or restricted complex waters and external environmental disturbances, which may significantly impact the assessment of other ships’ intentions and risk analysis. For instance, Pan [45] proposed a ship domain model for scenarios where ship maneuverability is limited in busy waters, which can be used to develop customized collision avoidance strategies to meet various navigation requirements. Some constraints regarding navigational conditions can be considered to address the issue of restricted waters. To better reflect actual navigation scenarios, speed strategies need to be integrated to enhance collision avoidance performance. Quantitative empirical formulas [46] and geometric analytical models [47] can be employed to design speed strategies for more effective collision avoidance maneuvers. Moreover, this paper primarily focuses on planning strategies without addressing control strategies, neglecting related ship maneuvering dynamics and parameter constraints; future research endeavors will incorporate methods such as Model Predictive Control and adaptive control to enhance control performance, aligning it more closely with actual navigation and maneuvering requirements. In conclusion, there is still considerable development needed to achieve the general application of intelligent collision avoidance.
Author Contributions
Y.L.: conceptualization of this study, methodology, writing—original draft preparation. Y.P.: software. J.Z.: data curation, review. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52372416) and the Science and Technology Commission of Shanghai Municipality (20238003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ørnulf, J.R.; Lars, A.L.W.; Håvard, N. Improving safety of interactions between conventional and autonomous ships. Ocean Eng. 2023, 284, 115206. [Google Scholar]
- Akdağ, M.; Solnør, P.; Johansen, T.A. Collaborative collision avoidance for Maritime Autonomous Surface Ships: A review. Ocean Eng. 2022, 250, 110920. [Google Scholar] [CrossRef]
- Liu, J.J.; Zhang, J.F.; Yan, X.P.; Guedes, S. Multi-ship collision avoidance decision-making and coordination mechanism in Mixed Navigation Scenarios. Ocean Eng. 2022, 257, 111666. [Google Scholar] [CrossRef]
- Zhao, J.S.; Wang, F.C. The Principles of Collision Prevention at Sea; Dalian Maritime University Press: Dalian, China, 1999. [Google Scholar]
- Sharma, A.; Srinivasan, D.; Kumar, D.S. A comparative analysis of centralized and decentralized multi-agent architecture for service restoration. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 311–318. [Google Scholar]
- Zhang, X.Y.; Wang, C.B.; Jiang, L.L.; An, L.X.; Yang, R. Collision-avoidance navigation systems for Maritime Autonomous Surface Ships: A state of the art survey. Ocean Eng. 2021, 235, 109380. [Google Scholar] [CrossRef]
- Huang, Y.M.; Chen, L.Y.; Chen, P.F.; Rudy, R.N.; Gelder, P.H.A.J.M.V. Ship collision avoidance methods: State-of-the-art. Saf. Sci. 2020, 121, 451–473. [Google Scholar] [CrossRef]
- Hu, Y.J.; Zhang, A.M.; Tian, W.L.; Zhang, J.F.; Hou, Z.B. Multi-Ship collision avoidance decision-making based on collision risk index. J. Mar. Sci. Eng. 2020, 8, 640. [Google Scholar] [CrossRef]
- Li, S.J.; Liu, J.L.; Rudy, R.N.; Ma, F. Optimizing the joint collision avoidance operations of multiple ships from an overall perspective. Ocean Eng. 2019, 191, 106511. [Google Scholar] [CrossRef]
- Liu, K.Z.; Wu, X.L.; Zhou, Y.; Yuan, Z.T.; Xin, X.R.; Zhang, J.F. Coordinated multi-stage and multi-objective optimization approach for ship collision avoidance decision-making. Ocean Eng. 2023, 287, 115888. [Google Scholar] [CrossRef]
- Lee, M.C.; Nieh, C.Y.; Kuo, H.C.; Huang, J.C. A collision avoidance, method for multi ship encounter situations. J. Mar. Sci. Technol. 2020, 25, 925–942. [Google Scholar] [CrossRef]
- Wang, T.F.; Yan, X.P.; Wang, Y.; Wu, Q. Ship domain model for multi-ship collision avoidance decision-making with COLREGs based on artificial potential field. Int. J. Mar. Navig. Saf. Sea Transp. 2017, 11, 85–92. [Google Scholar] [CrossRef]
- Cho, Y.; Han, J.; Kim, J. Efficient COLREG-compliant collision avoidance in multi-ship encounter situations. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1899–1911. [Google Scholar] [CrossRef]
- Wang, T.F.; Wu, Q.; Zhang, J.F.; Wu, B.; Wang, Y. Autonomous decision-making scheme for multi-ship collision avoidance with iterative observation and inference. Ocean Eng. 2020, 197, 106837. [Google Scholar] [CrossRef]
- Li, J.X.; Wang, H.B.; Guan, Z.Y.; Pan, C. Distributed multi-objective algorithm for preventing multi-ship collisions at sea. J. Navig. 2020, 73, 971–990. [Google Scholar] [CrossRef]
- Kim, D. A study on intention exchange-based ship collision avoidance by changing the safety domain. J. Korean Soc. Mar. Environ. Saf. 2019, 25, 259–268. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, L.W.; He, Y.X.; Wang, B.; Chen, J.H.; Tian, Y.F.; Zhao, X.Y. A real-time multi-ship collision avoidance decision-making system for autonomous ships considering ship motion uncertainty. Ocean Eng. 2023, 278, 114205. [Google Scholar] [CrossRef]
- Yu, D.; Roh, M.-I. Method for anti-collision path planning using velocity obstacle and A* algorithms for maritime autonomous surface ship. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100586. [Google Scholar] [CrossRef]
- Xue, D.L.; Wu, D.F.; Andre, S.Y.; Li, Z.X. Proximal policy optimization with reciprocal velocity obstacle based collision avoidance path planning for multi-unmanned surface vehicles. Ocean Eng. 2023, 273, 114005. [Google Scholar] [CrossRef]
- Cui, Z.W.; Guan, W.; Zhang, X.K. Collision avoidance decision-making strategy for multiple USVs based on Deep Reinforcement Learning algorithm. Ocean Eng. 2024, 308, 118323. [Google Scholar] [CrossRef]
- Chun, D.-H.; Roh, M.-I.; Lee, H.-W.; Yu, D. Method for collision avoidance based on deep reinforcement learning with path-speed control for an autonomous ship. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100579. [Google Scholar] [CrossRef]
- Hornauer, S.; Hahn, A.; Blaich, M.; Reuter, J. Trajectory planning with negotiation for maritime collision avoidance. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2015, 9, 335–341. [Google Scholar] [CrossRef][Green Version]
- Zhao, L.; Roh, M. COLREGs-compliant multiship collision avoidance based on deep reinforcement learning. Ocean Eng. 2019, 191, 106436. [Google Scholar] [CrossRef]
- Ding, Z.G.; Zhang, X.Y.; Wang, C.B.; Li, Q.; An, L.X. Intelligent collision avoidance decision-making method for unmanned ships based on driving practice. Chin. J. Ship Res. 2021, 16, 96–104, 113. [Google Scholar]
- Jiang, L.L.; An, L.X.; Zhang, X.Y.; Wang, C.B.; Wang, X.J. A human-like collision avoidance method for autonomous ship with attention-based deep reinforcement learning. Ocean Eng. 2022, 264, 112378. [Google Scholar] [CrossRef]
- Huang, Y.M.; Chen, L.Y.; Negenborn, R.R.; Gelder, P.H.A.J.M.V. A ship collision avoidance system for human-machine cooperation during collision avoidance. Ocean Eng. 2020, 217, 107913. [Google Scholar] [CrossRef]
- Li, Y.; Peng, Y.; Zheng, J. Intelligent ship collision avoidance model integrating human thinking experience. Ocean Eng. 2023, 286, 115510. [Google Scholar] [CrossRef]
- Seo, C.; Nam, Y.; Misganaw, A.; Kim, Y.J.; Park, S.; Kim, C. Ship collision avoidance route planning using CRI-based A* algorithm. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100551. [Google Scholar] [CrossRef]
- Wang, S.B.; Zhang, Y.J.; Huo, R.; Mao, W.G. A real-time ship collision risk perception model derived from domain-based approach parameters. Ocean Eng. 2022, 265, 112554. [Google Scholar] [CrossRef]
- China navy hydrographic office. Ship Navigation Safety and Collision Prevention; Navigation Book Press: Tianjin, China, 2010. [Google Scholar]
- Song, L.; Sun, H.; Xu, K.; Huang, L.; Chen, H. Interference intention classification of moving obstacles used for USV collision avoidance. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100459. [Google Scholar] [CrossRef]
- Jadhav, A.K.; Pandi, A.R.; Somayajula, A. Collision avoidance for autonomous surface vessels using novel artificial potential fields. Ocean Eng. 2023, 288, 116011. [Google Scholar] [CrossRef]
- Perera, L.P.; Carvalho, J.; Guedes Soares, C. Intelligent Ocean Navigation and Fuzzy-Bayesian Decision/Action Formulation. IEEE J. Ocean. Eng. 2012, 37, 204–219. [Google Scholar] [CrossRef]
- He, Y.X.; Jin, Y.; Huang, L.W.; Xiong, Y.; Chen, P.F.; Mou, J.M. Quantitative analysis of COLREG rules and seamanship for autonomous collision avoidance at open sea. Ocean Eng. 2017, 140, 281–291. [Google Scholar] [CrossRef]
- Wang, W.Q.; Huang, L.W.; Liu, K.Z.; Zhou, Y.; Yuan, Z.T.; Xin, X.R.; Wu, X.L. 2024,Ship encounter scenario generation for collision avoidance algorithm testing based on AIS data. Ocean Eng. 2010, 291, 116436. [Google Scholar] [CrossRef]
- Liu, Z.H.; Wu, Z.L.; Zheng, Z.Y. A cooperative game approach for assessing the collision risk in multi-vessel encountering. Ocean Eng. 2019, 187, 106175. [Google Scholar] [CrossRef]
- Wen, Y.Q.; Huang, Y.M.; Zhou, C.H.; Yang, J.L.; Xiao, C.S.; Wu, X.C. Modelling of marine traffic flow complexity. Ocean Eng. 2015, 104, 500–510. [Google Scholar] [CrossRef]
- Sui, Z.Y.; Wen, Y.Q.; Huang, Y.M.; Zhou, C.H.; Xiao, C.S.; Chen, H.L. Empirical analysis of complex network for marine traffic situation. Ocean Eng. 2020, 214, 107848. [Google Scholar] [CrossRef]
- Geng, X.Q.; Huang, L.; Wen, Y.Q.; Zhou, C.H. Modelling of the Marine Traffic Situation Complexity. MATEC Web Conf. 2016, 68, 15002. [Google Scholar] [CrossRef]
- Li, Y.P.; Liu, Z.J.; Kai, J.S. Study on complexity model and clustering method of ship to shipencountering risk. J. Mar. Sci. Technol. 2019, 27, 153–160. [Google Scholar]
- Liu, K.Z.; Wu, X.L.; Zhou, Y.; Yuan, Z.T.; Yang, X.; Xin, X.R.; Zhuang, S.J. A conflict cluster-based method for collision avoidance decision-making in multi-ship encounter situations. Ocean Eng. 2023, 288, 116038. [Google Scholar] [CrossRef]
- T/CIN 017—2023; Group Standard: General Requirements for Perception Data of Ship Remote Control Driving. Chinese Institute of Navigation: Beijing, China, 2023.
- Liang, H.; Wasif, N.; Eshan, R.; Graham, W.; Terry, M.; Zakirul, B.; Ivor, S. COLREGs-Compliant Path Planning for Autonomous Surface Vehicles: A Multiobjective Optimization Approach. IFAC-PapersOnLine 2017, 50, 13662–13667. [Google Scholar]
- Yang, R.W.; Xu, J.S.; Wang, X.; Zhou, Q. Parallel trajectory planning for shipborne Autonomous collision avoidance system. Appl. Ocean. Res. 2019, 91, 101875. [Google Scholar] [CrossRef]
- Pan, W.; Xie, X.; Bao, T.; Li, M. Ship domain model for ships with restricted manoeuvrability in busy waters. J. Navig. 2021, 74, 673–697. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Li, W.; Shi, P. A real-time collision avoidance learning system for Unmanned Surface Vessels. Neurocomputing 2016, 182, 255–266. [Google Scholar] [CrossRef]
- Seo, J.; Kim, J.; Song, R.J. Modeling human’s collision avoidance direction in an encounter situation using an ensemble classifier. Ocean Eng. 2023, 271, 113738. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).