Transient Power Stabilization in Marine Microgrids: Improved Droop Control and Feedforward Strategies for Heterogeneous Gas Turbines with Hybrid Energy Storage
Abstract
1. Introduction
- To address the complex power allocation in heterogeneous single-shaft and split-shaft gas turbine generator parallel operation systems, an inter-unit power sharing strategy based on improved voltage droop control is proposed.
- A feedforward-integrated power sharing strategy is developed to resolve the significant power mismatch in two-unit parallel-operating systems with hybrid energy storage under Sudden load and rectangular-wave pulsed load changes.
- A comprehensive analysis is conducted on the synergistic complementarity and technical advantages among generators, power grids, loads, and energy storage devices in marine gas turbine power generation systems.
- Good power distribution between units and reasonable distribution of system power can be achieved. In steady-state conditions, and when the propulsion load increases or decreases, the power sharing deviation between units is less than 3.5%. During sudden load changes and when a pulsed load is connected, the power sharing deviation between units is less than 4%.
2. Model of the Power System with Two Gas Turbine Generator Sets Operating in Parallel
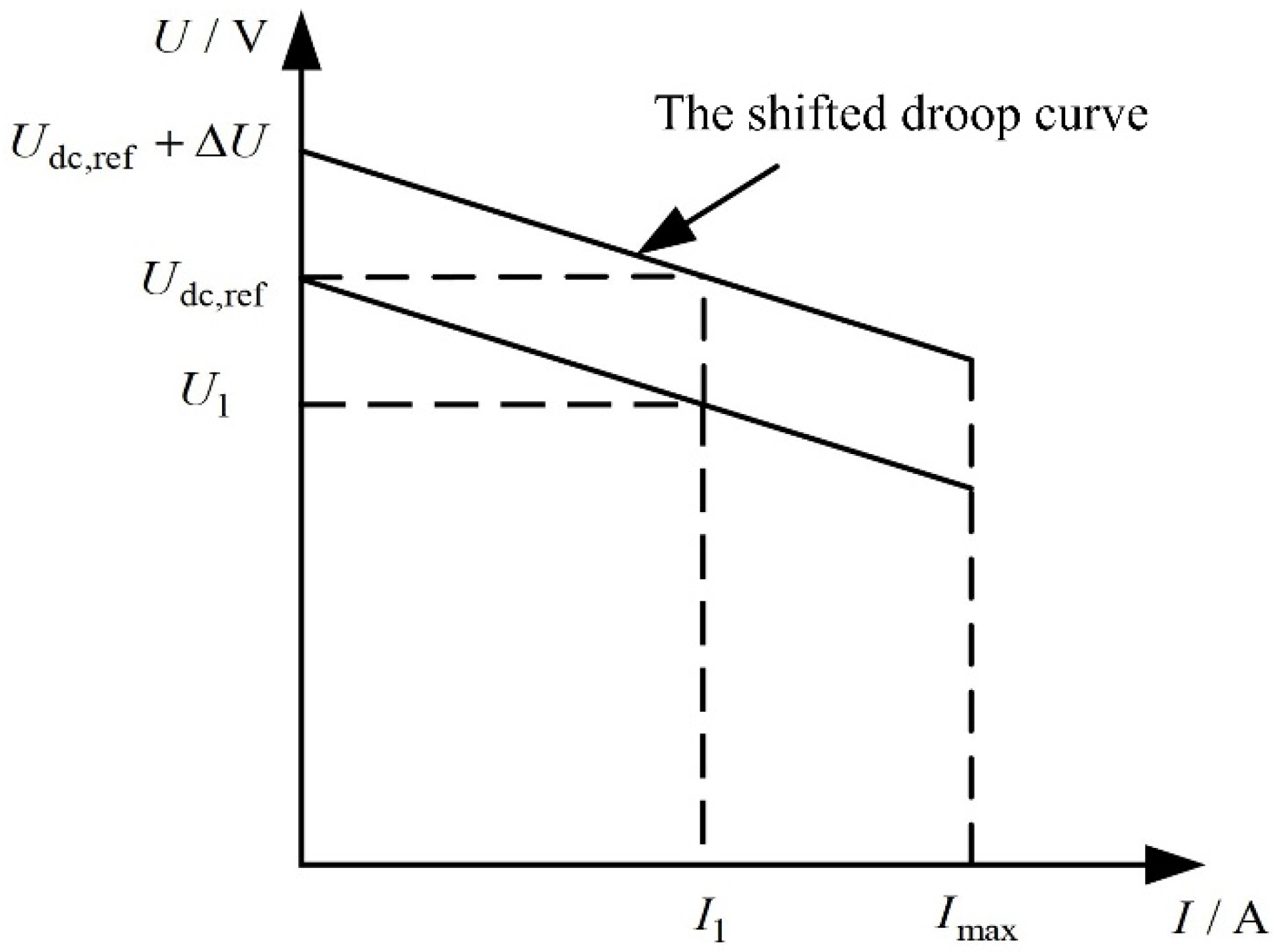
3. Research on Power Sharing Strategy for Parallel Generator Sets Based on Improved Voltage Droop Control
3.1. Power Sharing Strategy Between Parallel Gas Turbine Generator Sets
3.2. Simulation Verification Research on Power Sharing Strategy Among Parallel Gas Turbine Generator Sets
3.2.1. Simulation Verification for the Increase and Decrease in Propulsion Load
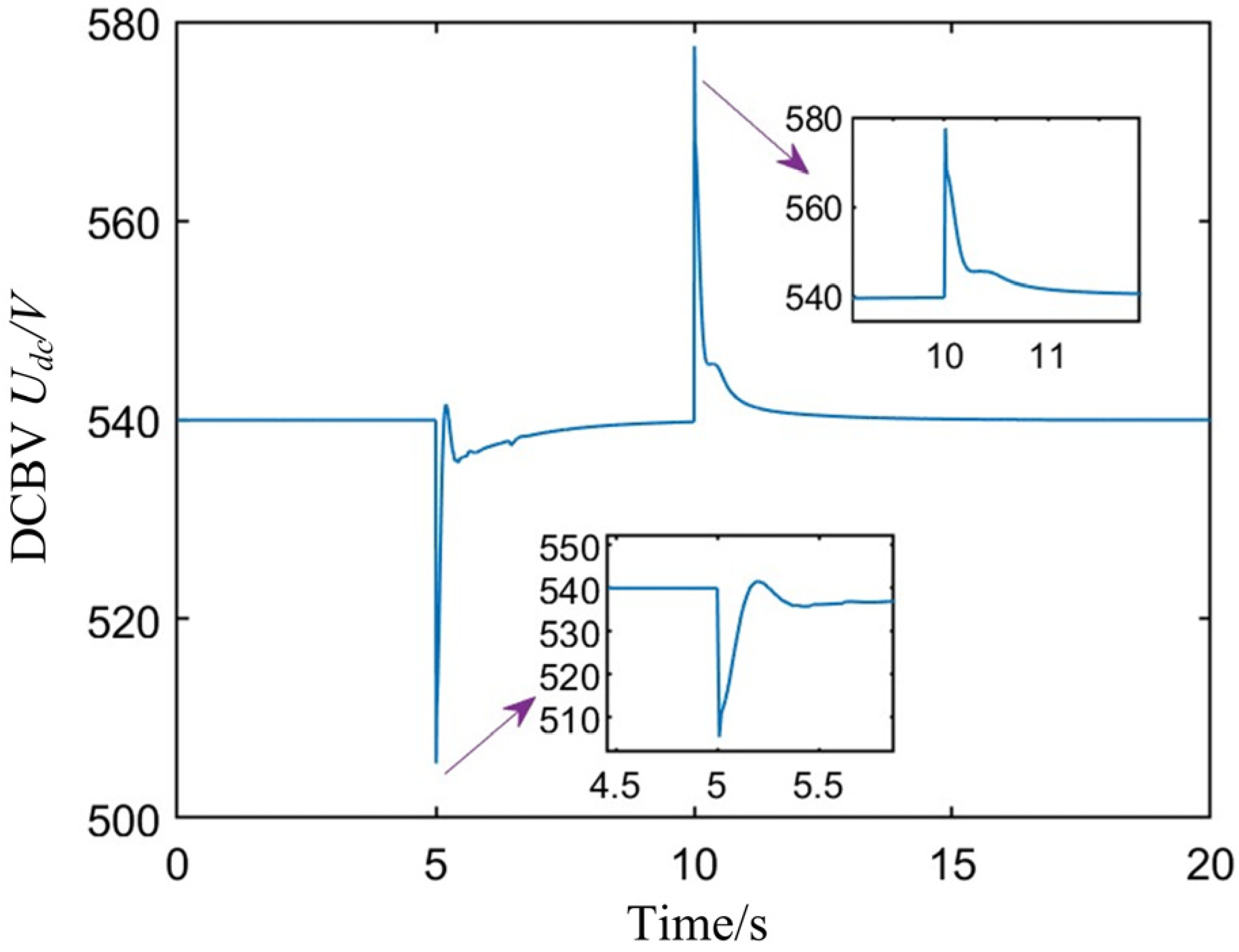
3.2.2. Simulation Verification of Sudden Load Changes
4. Research on Power Sharing Strategies for Parallel Generator Sets with Power Feedforward
4.1. Research on Power Sharing Strategy for a Two-Unit Parallel Operation System Under Sudden Load Changes
4.1.1. Power Sharing Strategy Under Sudden Load Changes
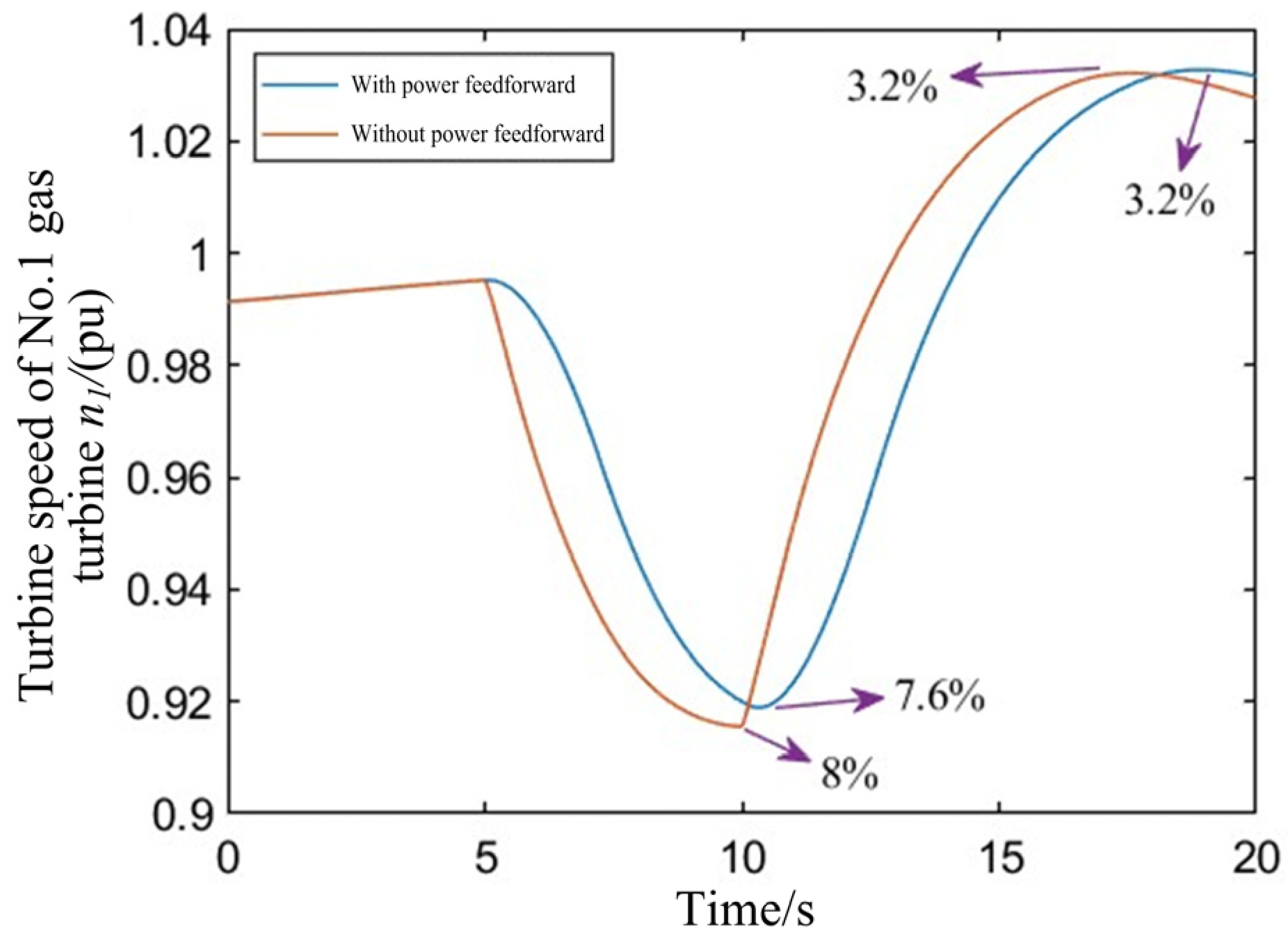
4.1.2. Simulation Verification of the Power Sharing Strategy of the System Under Sudden Load Changes
4.2. Research on a Power Sharing Strategy for a Two-Unit Parallel Operation System Under Rectangular-Wave Pulsed Load
4.2.1. Power Sharing Strategy of the System Under Rectangular-Wave Pulsed Load
4.2.2. Simulation Verification of the System Power Sharing Strategy Under Rectangular-Wave Pulsed Load
5. Experimental Verification
5.1. Experimental Objectives
5.2. Introduction to the Experimental Platform
5.3. Result Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Time intervals for power change | |
| Droop control coefficient | |
| Current | |
| voltage | |
| Power | |
| Self-defined stage for load increase and decrease | |
| Speed | |
| Time |
Abbreviations
| BESS | Battery energy storage system |
| DCBV | DC bus voltage |
| ESS | Energy storage system |
| FESS | Flywheel energy storage system |
| GTPGS | Gas turbine power generator set |
| HESS | Hybrid energy storage system |
| TSRR | Transient speed regulation rate |
References
- Xu, L.; Guerrero, J.M.; Lashab, A.; Wei, B.; Bazmohammadi, N.; Vasquez, J.; Abusorrah, A. A review of DC shipboard microgrids-Part I: Power architectures, energy storage, and power converters. IEEE Trans. Power Electron. 2021, 37, 5155–5172. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Shao, C.C.; Wang, G.Q.; Hou, Y.H. Resilience control of DC shipboard power systems. IEEE Trans. Power Syst. 2018, 33, 6675–6685. [Google Scholar] [CrossRef]
- Kim, S.; Kucka, J.; Ulissi, G.; Kim, S.-N.; Dujic, D. Solid-state technologies for flexible and efficient marine dc microgrids. IEEE Trans. Smart Grid 2021, 12, 2860–2868. [Google Scholar] [CrossRef]
- Li, Y.M.; Ding, Z.M.; Yu, Y.H.; Liu, Y.B. Mitigation effect of flywheel energy storage on the performance of marine gas turbine DC microgrid under high-power load mutation. Energy Rep. 2023, 9, 1380–1396. [Google Scholar] [CrossRef]
- Jia, K.Y.; Liu, C.; Li, S.H.; Jiang, D.X. Modeling and optimization of a hybrid renewable energy system integrated with gas turbine and energy storage. Energy Convers. Manag. 2023, 279, 116763. [Google Scholar] [CrossRef]
- Wu, S.; Li, T.; Chen, R.; Huang, S.; Xu, F.; Wang, B. Transient performance of gas-engine-based power system on ships: An overview of modeling, optimization, and applications. J. Mar. Sci. Eng. 2023, 11, 2321. [Google Scholar] [CrossRef]
- Yang, R.; Liu, Y.; He, X.; Liu, Z. An innovative online adaptive high-efficiency controller for micro gas turbine: Design and simulation validation. J. Mar. Sci. Eng. 2024, 12, 2150. [Google Scholar] [CrossRef]
- Ismail, M.S.; Moghavvemi, M.; Mahlia TM, I. Design of an optimized photovoltaic and microturbine hybrid power system for a remote small community: Case study of Palestine. Energy Convers. Manag. 2013, 75, 271–281. [Google Scholar] [CrossRef]
- Seljak, T.; Buffi, M.; Valera-Medina, A.; Chong, C.; Chiaramonti, D.; Katrašnik, T. Bioliquids and their use in power generation-A technology review. Renew. Sustain. Energy Rev. 2020, 129, 109930. [Google Scholar] [CrossRef]
- Escamilla, A.; Sánchez, D.; García-Rodríguez, L. Assessment of power-to-power renewable energy storage based on the smart integration of hydrogen and micro gas turbine technologies. Int. J. Hydrogen Energy 2022, 47, 17505–17525. [Google Scholar] [CrossRef]
- Javadi, M.A.; Khodabakhshi, S.; Ghasemiasl, R.; Jabery, R. Sensivity analysis of a multi-generation system based on a gas/hydrogen-fueled gas turbine for producing hydrogen, electricity and freshwater. Energy Convers. Manag. 2022, 252, 115085. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, L.; Xing, Y.; Guerrero, J.M. A distributed control strategy based on DC bus signaling for modular photovoltaic generation systems with battery energy storage. IEEE Trans. Power Electron. 2011, 26, 3032–3045. [Google Scholar] [CrossRef]
- Vu, T.V.; Gonsoulin, D.; Diaz, F.; Edrington, C.S.; El-Mezyani, T. Predictive control for energy management in ship power systems under high-power ramp rate loads. IEEE Trans. Energy Convers. 2017, 32, 788–797. [Google Scholar] [CrossRef]
- Duan, J.D.; Fan, S.G.; Wu, F.J.; Sun, L.; Wang, G.L. Power balance control of micro gas turbine generation system based on supercapacitor energy storage. Energy 2017, 119, 442–452. [Google Scholar] [CrossRef]
- Wang, S.; Duan, J.D.; Sun, L.; Fan, S.G. Power balance control based on super-capacitor energy storage for micro-turbine power generation system. Electr. Power Autom. Equip. 2017, 37, 126–133. [Google Scholar]
- Duan, J.D.; Liu, J.J.; Xiao, Q.; Fan, S.G.; Sun, L.; Wang, G.L. Cooperative controls of micro gas turbine and super capacitor hybrid power generation system for pulsed power load. Energy 2019, 169, 1242–1258. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.B.; Dakyo, B. Transient power control for diesel-generator assistance in electric boat applications using supercapacitors and batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 416–428. [Google Scholar] [CrossRef]
- Xiao, Z.X.; Li, H.M.; Fang, H.W.; Guan, Y.Z.; Guerrero, J.M. Operation control for improving energy efficiency of shipboard microgrid including bow thrusters and hybrid energy storages. IEEE Trans. Transp. Electrif. 2020, 6, 856–868. [Google Scholar] [CrossRef]
- Wang, X.B.; Huang, W.T.; Tai, N.L.; Wen, L.; Fan, F. A tie-line power smoothing strategy for microgrid with heat and power system using source-load-storage coordination control. Trans. China Electrotech. Soc. 2020, 35, 2817–2829. [Google Scholar]
- Li, Y.M.; Ding, Z.M.; Yu, Y.H.; Liu, Y.B. Hybrid energy storage power allocation strategy based on parameter-optimized VMD algorithm for marine micro gas turbine power system. J. Energy Storage 2023, 73, 109189. [Google Scholar] [CrossRef]
- Park, D.; Zadeh, M. Modeling and predictive control of shipboard hybrid DC power systems. IEEE Trans. Transp. Electrif. 2020, 7, 892–904. [Google Scholar] [CrossRef]
- Baek, G.H.; Choi, D.G.; Choi, I.G.; Kim, T.K. Research on optimal operation plan for parallel operation of marine diesel generator. J. Korea Ind. Inf. Syst. Res. 2023, 28, 11–19. [Google Scholar]
- Nyrkov, A.; Sokolov, S.; Zhilenkov, A.; Chernyi, S. Complex modeling of power fluctuations stabilization digital control system for parallel operation of gas-diesel generators. In Proceedings of the 2016 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRusNW), Petersburg, Russia, 2–3 February 2016; pp. 636–640. [Google Scholar]
- Zaccone, R.; Campora, U.; Martelli, M. Optimisation of a diesel-electric ship propulsion and power generation system using a genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 587. [Google Scholar] [CrossRef]
- Ji, F.; Fu, L.J.; Ye, Z.H.; Xiong, Y.X.; Ma, F. Experimental research of MVDC parallel operation generator sets for vessel integrated power system. J. Nav. Univ. Eng. 2017, 29, 11–16. [Google Scholar]
- Zhang, G.; Khan, I.A.; Daraz, A.; Basit, A.; Khan, M.I. Load frequency control of marine microgrid system integrated with renewable energy sources. J. Mar. Sci. Eng. 2023, 11, 844. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G.; Guerrero, J. Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage DC microgrids. IEEE Trans. Power Electron. 2012, 28, 1900–1913. [Google Scholar] [CrossRef]
- Wang, M.; Tang, F.; Chen, Q.Y.; Wu, X.Z.; Niu, J.K. Passivity-based control and large signal stability of DC-DC converter parallel system. Proc. CSEE 2022, 42, 6789–6803. [Google Scholar]
- Wang, P.B.; Lu, X.N.; Yang, X.; Wang, W.; Xu, D. An improved distributed secondary control method for DC microgrids with enhanced dynamic current sharing performance. IEEE Trans. Power Electron. 2016, 31, 6658–6673. [Google Scholar] [CrossRef]
- Muhammad, I.; Majid, M.G. Master-slave design for frequency regulation in hybrid power system under complex environment. IET Renew. Power Gener. 2022, 16, 3041–3057. [Google Scholar]
- Wang, G.; Song, Y.H.; Cao, S.X.; Duan, J. Novel adaptive power distribution master–slave control strategy for a biogas-solar-wind battery islanded microgrid based on a microturbine. Electr. Power Syst. Res. 2023, 224, 109743. [Google Scholar] [CrossRef]
- Zhang, B.; Gorbachev, S.; Dou, C.; Kuzin, V.; Park, J.H.; Zhang, Z.Q.; Yue, D. Source-storage-load coordinated master-slave control strategy for islanded microgrid considering load disturbance and communication interruption. IEEE Trans. Cybern. 2024, 54, 1768–1781. [Google Scholar] [CrossRef] [PubMed]
- Faddel, S.; Saad, A.A.; Youssef, T.; Mohammed, O. Decentralized control algorithm for the hybrid energy storage of shipboard power system. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 720–731. [Google Scholar] [CrossRef]
- Liu, Z.M.; Liu, Y.B.; Yu, Y.H.; Yang, R.; Chen, Y.Y. Improved design of transient power sharing strategy for AES multi-gensets in response to high power load mutation. Energy Rep. 2023, 9, 5323–5335. [Google Scholar] [CrossRef]
- Yang, C.; Gao, F.; Zhang, B. An improved nonlinear droop control strategy in DC microgrids. IEEE Trans. Power Electron. 2024, 39, 5058–5073. [Google Scholar] [CrossRef]
- Yehia, M.; Numair, M.; Mansour, D.A. Novel IoT-based droop control for battery SoC balancing among multiple microgrids. IEEE Trans. Smart Grid 2024, 15, 1304–1316. [Google Scholar] [CrossRef]
- Khersonsky, Y. New IEEE Power Electronics Standards for Ships. In Proceedings of the 2011 IEEE Electric Ship Technologies Symposium, Alexandria, VA, USA, 10–13 April 2011. [Google Scholar]
- Li, Y.M. Research on Control Strategies for Marine Micro Gas Turbine DC Power Generation Systems. Master’s Thesis, Wuhan Naval University of Engineering, Wuhan, China, 2024. [Google Scholar]
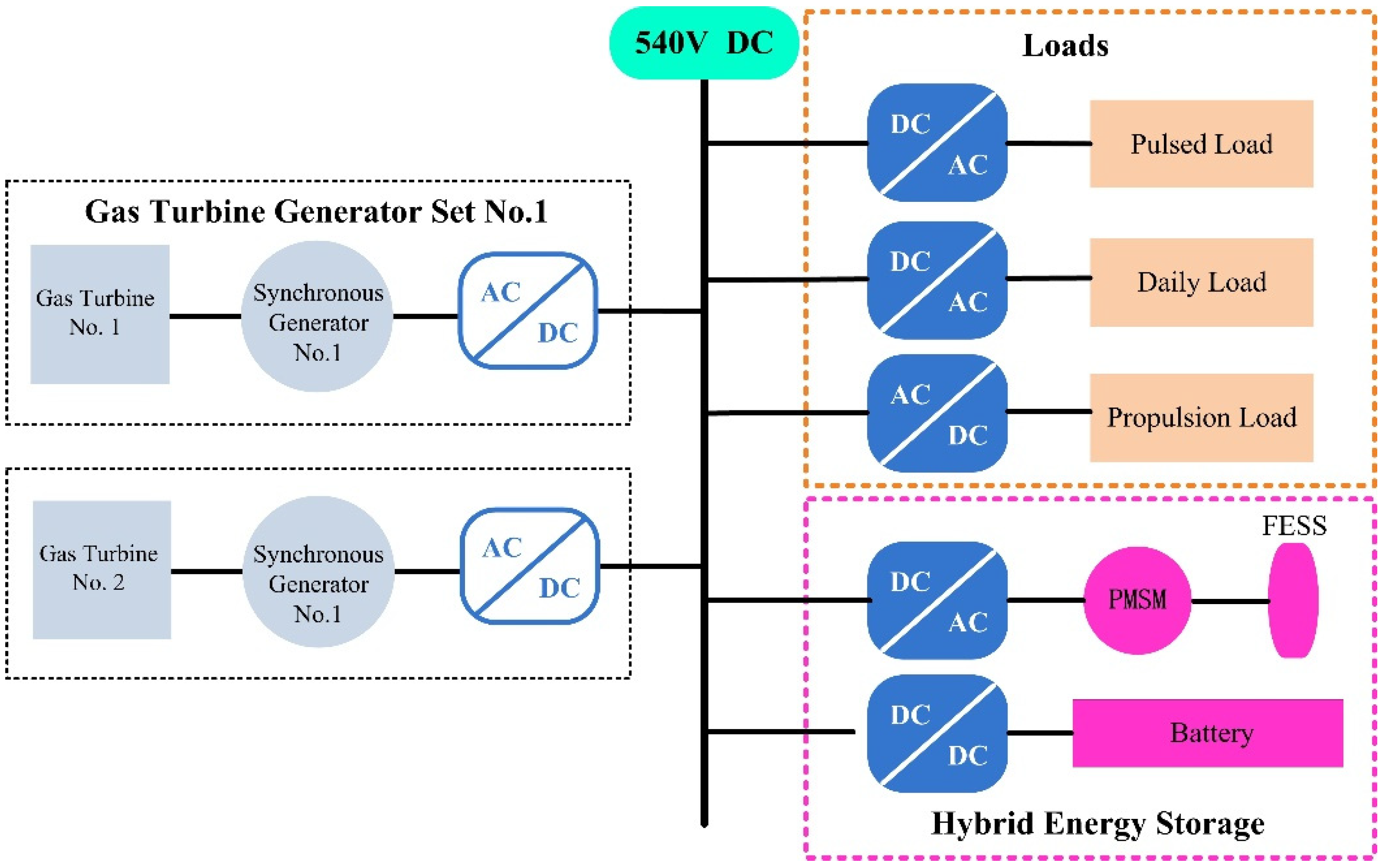

































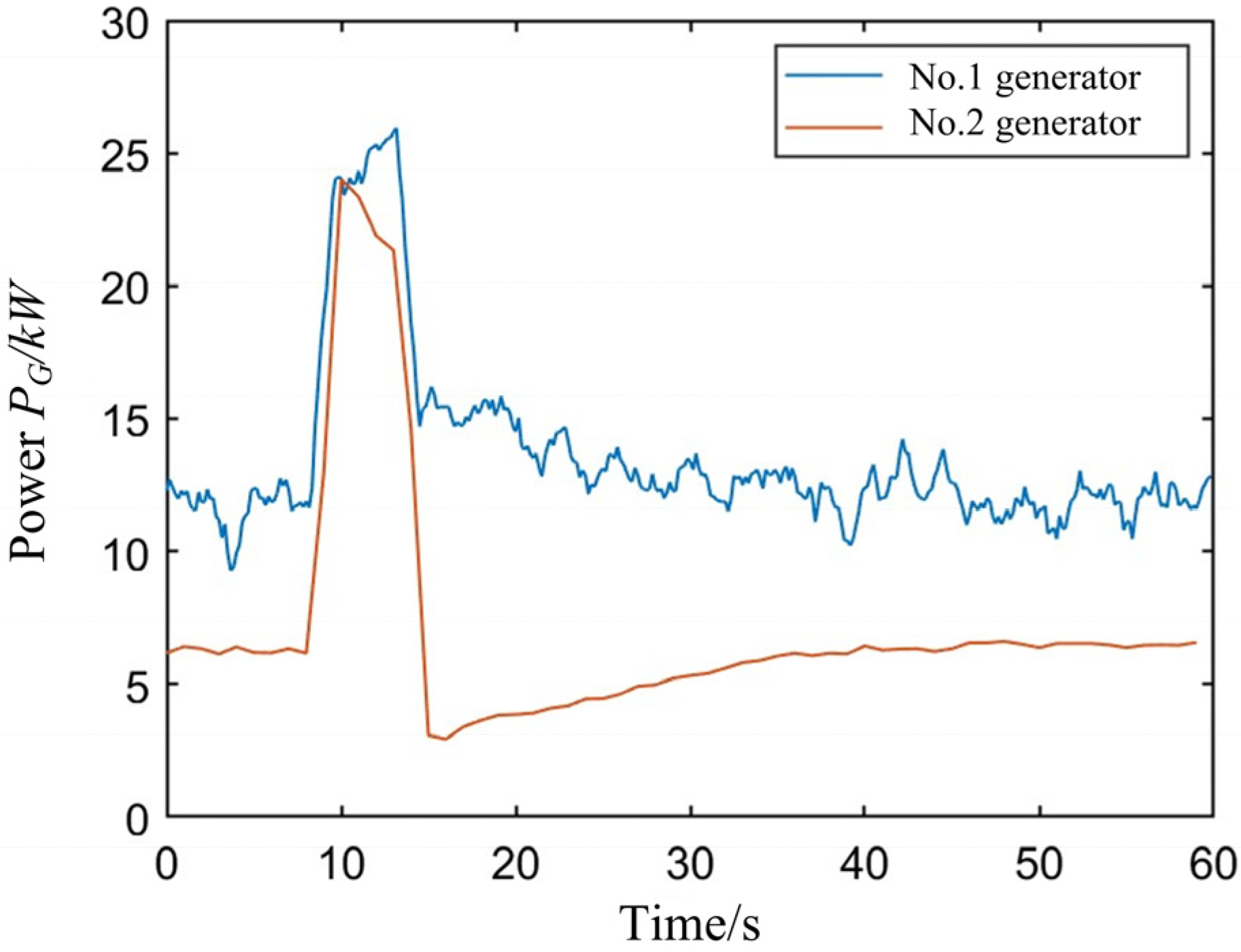


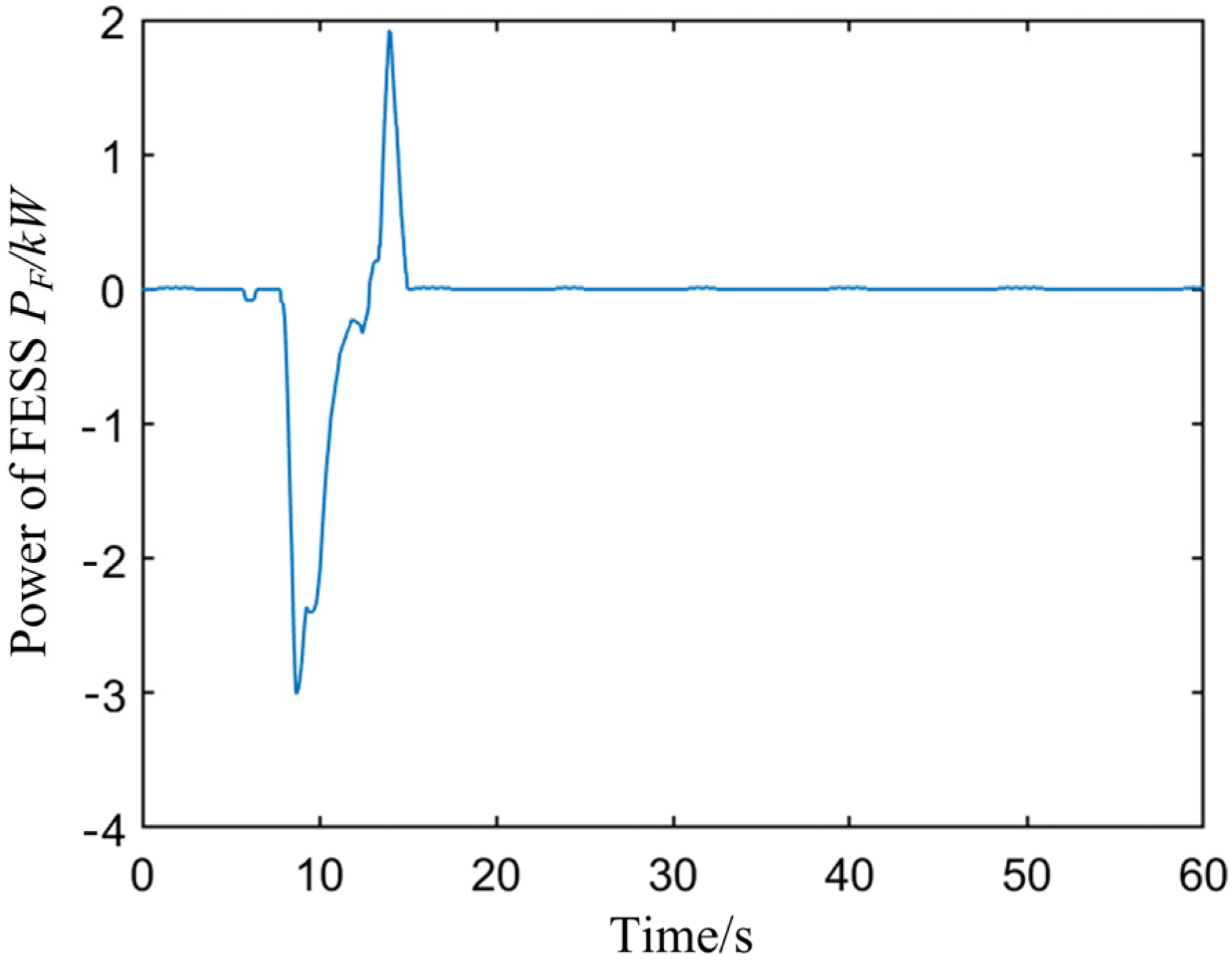



| Device | Design Parameters | ||||||
|---|---|---|---|---|---|---|---|
| No. 1 GTPGS | Rated power/kW | Rated speed of turbine/(r/min) | Maximum speed of turbine/(r/min) | Maximum acceleration of the rotor/(r/s) | Inertia constants/(s) | ||
| 200 | 39,000 | 44,000 | 500 | 5 | |||
| No. 2 GTPGS | Rated power/kW | Rated speed of turbine/(r/min) | Maximum speed of turbine/(r/min) | Maximum acceleration of the rotor/(r/s) | Inertia constants/(s) | ||
| 100 | 51,000 | 53,000 | 500 | 2 | |||
| FESS | Rated speed/(r/min) | Maximum speed /(r/min) | Maximum charge/discharge work/kW | Moment of inertia /(kg⋅m2) | |||
| 30,000 | 36,000 | 120 | 1.83 | ||||
| BESS | Rated voltage/V | Capacity/Ah | Initial SOC/% | Rated discharge current/A | |||
| 400 | 100 | 80 | 44 | ||||
| Case | Transient Fluctuations of Bus Voltage/V | Transient Fluctuation Rate of Bus Voltage | ||
|---|---|---|---|---|
| Without FESS | With FESS | Without FESS | With FESS | |
| Maximum transient drop | 9.3 | 7.5 | 1.72% | 1.39% |
| Maximum transient jump | 5.95 | 4.98 | 1.10% | 0.92% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Z.; Li, Y.; Liu, Y.; Yu, Y. Transient Power Stabilization in Marine Microgrids: Improved Droop Control and Feedforward Strategies for Heterogeneous Gas Turbines with Hybrid Energy Storage. J. Mar. Sci. Eng. 2025, 13, 771. https://doi.org/10.3390/jmse13040771
Ding Z, Li Y, Liu Y, Yu Y. Transient Power Stabilization in Marine Microgrids: Improved Droop Control and Feedforward Strategies for Heterogeneous Gas Turbines with Hybrid Energy Storage. Journal of Marine Science and Engineering. 2025; 13(4):771. https://doi.org/10.3390/jmse13040771
Chicago/Turabian StyleDing, Zemin, Yueming Li, Yongbao Liu, and Youhong Yu. 2025. "Transient Power Stabilization in Marine Microgrids: Improved Droop Control and Feedforward Strategies for Heterogeneous Gas Turbines with Hybrid Energy Storage" Journal of Marine Science and Engineering 13, no. 4: 771. https://doi.org/10.3390/jmse13040771
APA StyleDing, Z., Li, Y., Liu, Y., & Yu, Y. (2025). Transient Power Stabilization in Marine Microgrids: Improved Droop Control and Feedforward Strategies for Heterogeneous Gas Turbines with Hybrid Energy Storage. Journal of Marine Science and Engineering, 13(4), 771. https://doi.org/10.3390/jmse13040771






