Vortex-Induced Vibration Performance Prediction of Double-Deck Steel Truss Bridge Based on Improved Machine Learning Algorithm
Abstract
1. Introduction
2. Vertical Bending VIV Response Analysis Method for Large-Span Bridge
2.1. Scanlan Nonlinear VIV Model
2.2. Realization of Vertical Bending VIV Response Analysis Method for Large-Span Bridge
3. Prediction of Vertical Bending VIV Performance of Large-Span Bridge Based on Improved Machine Learning Algorithm
3.1. Determination of Input Parameters
3.2. Three Machine Learning Algorithms and the Optimization Algorithm
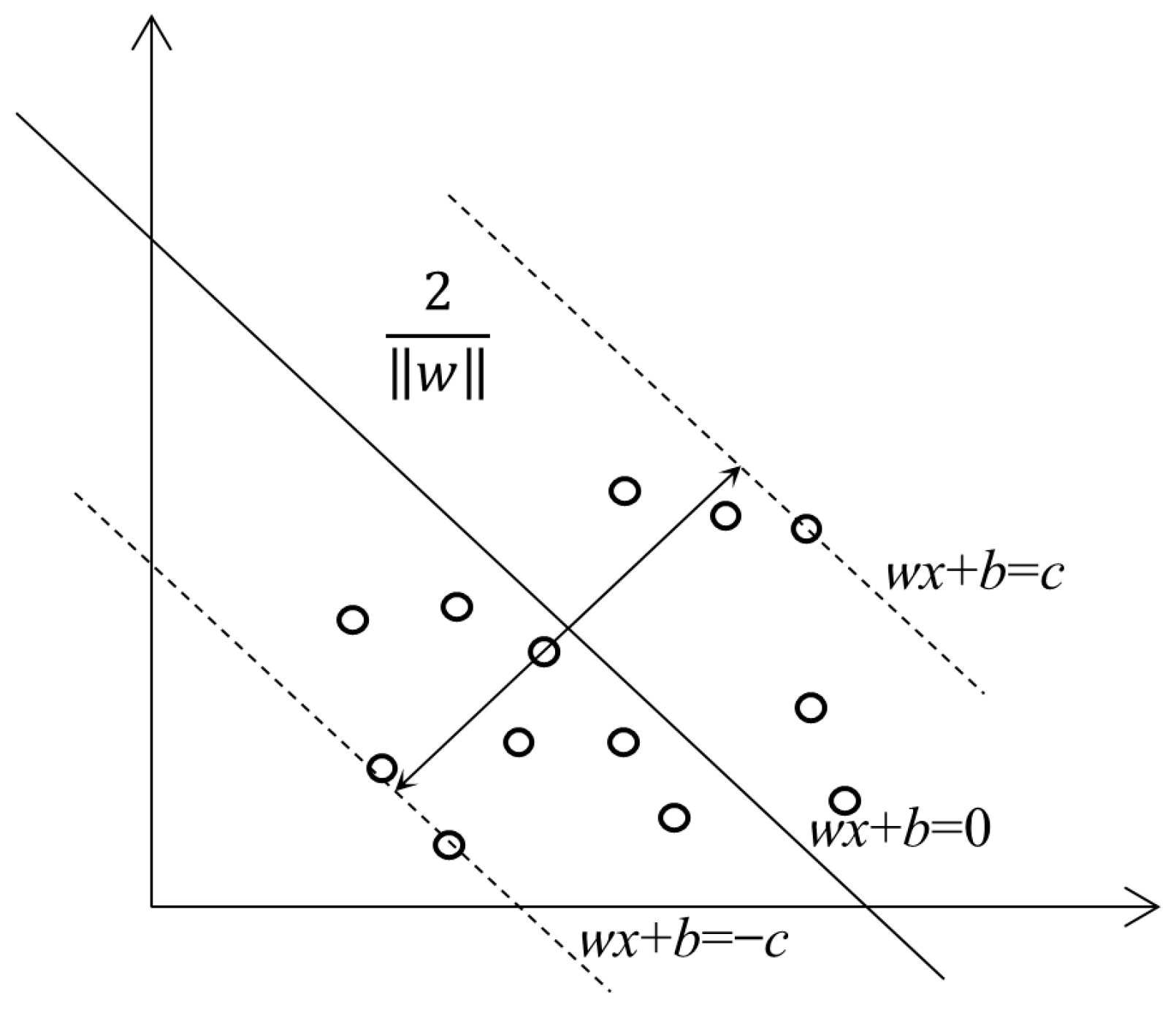
- Support Vector Regression Algorithm:
- 2.
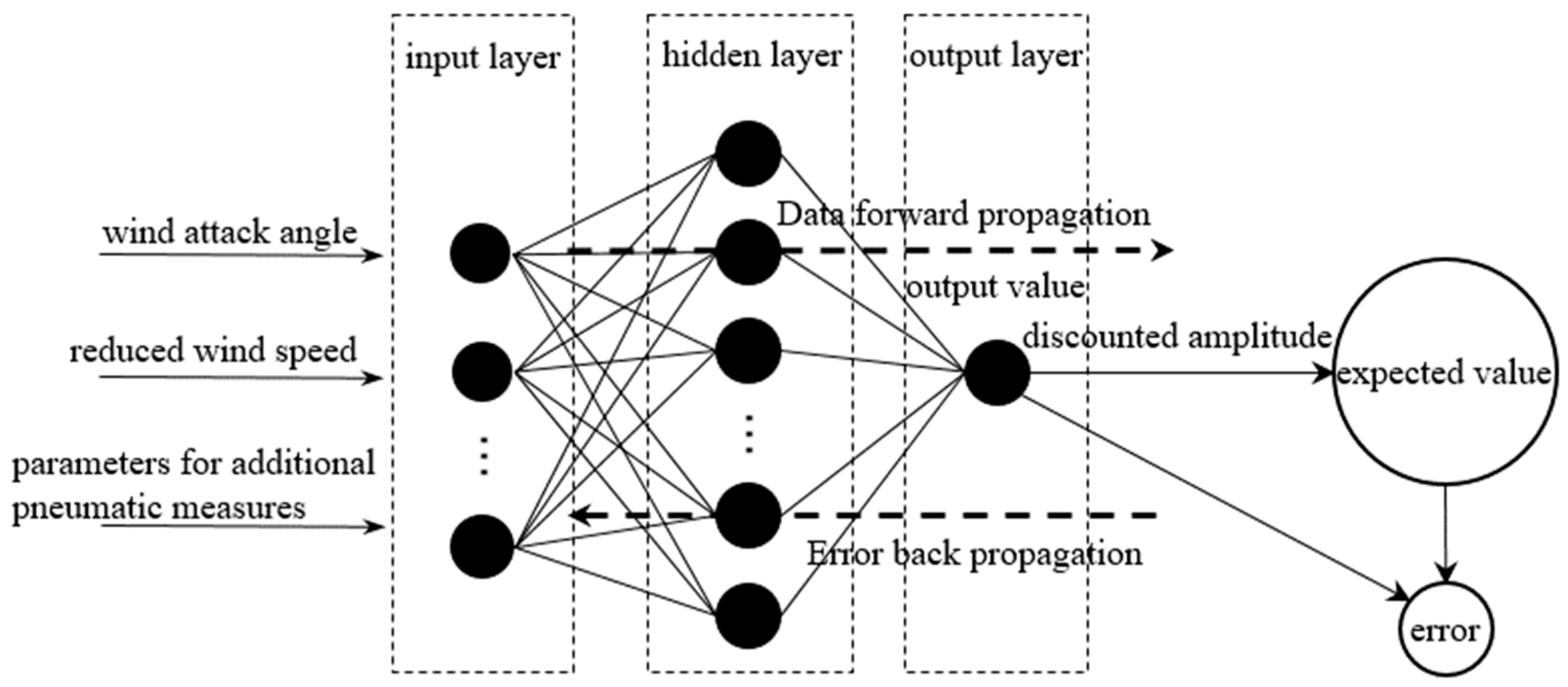
- Backpropagation Neural Network Algorithm:
- 3.
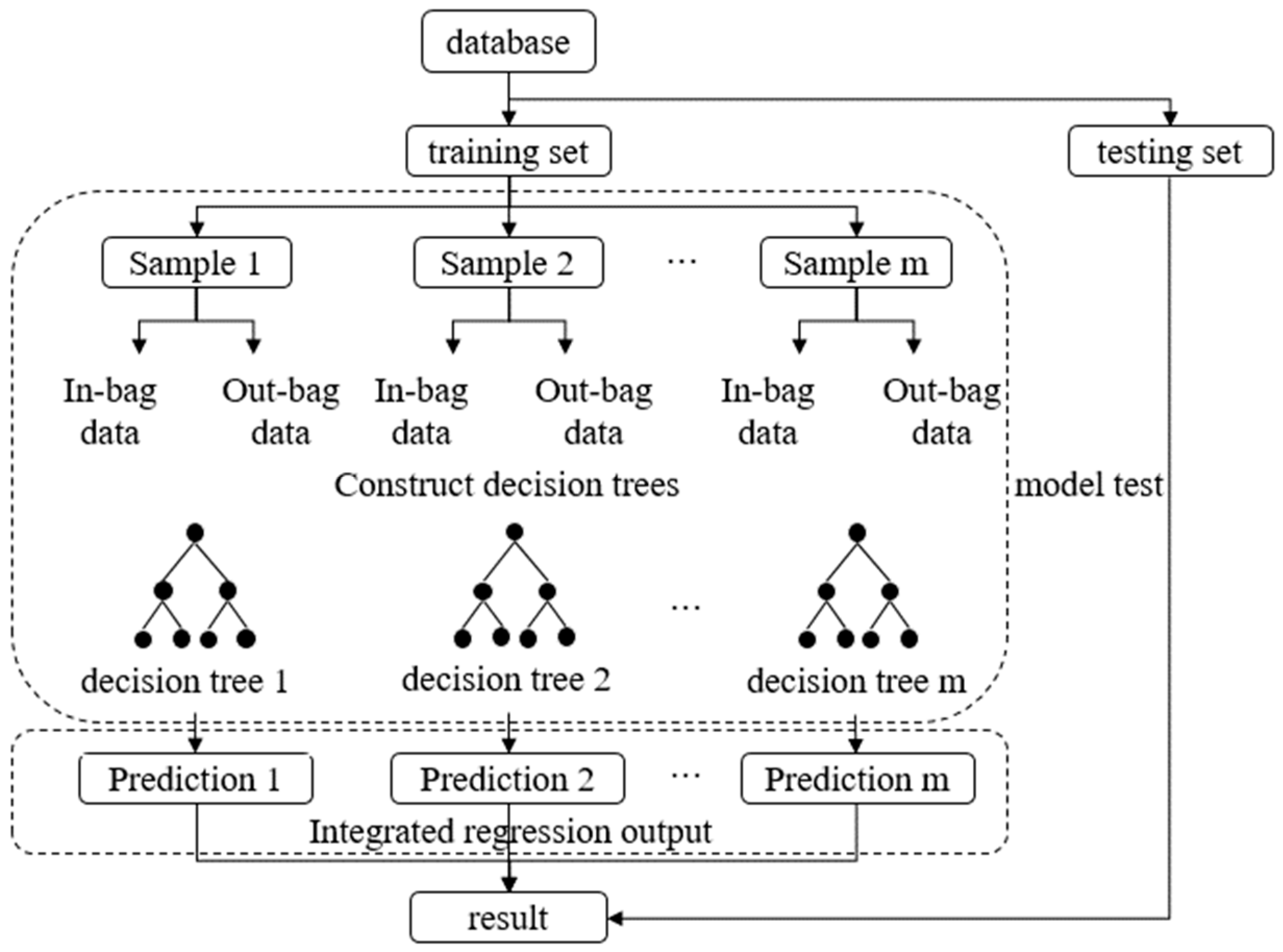
- Random Forest Algorithm:
- 4.
- Genetic Algorithm:
- 5.
- Particle Swarm Optimization:
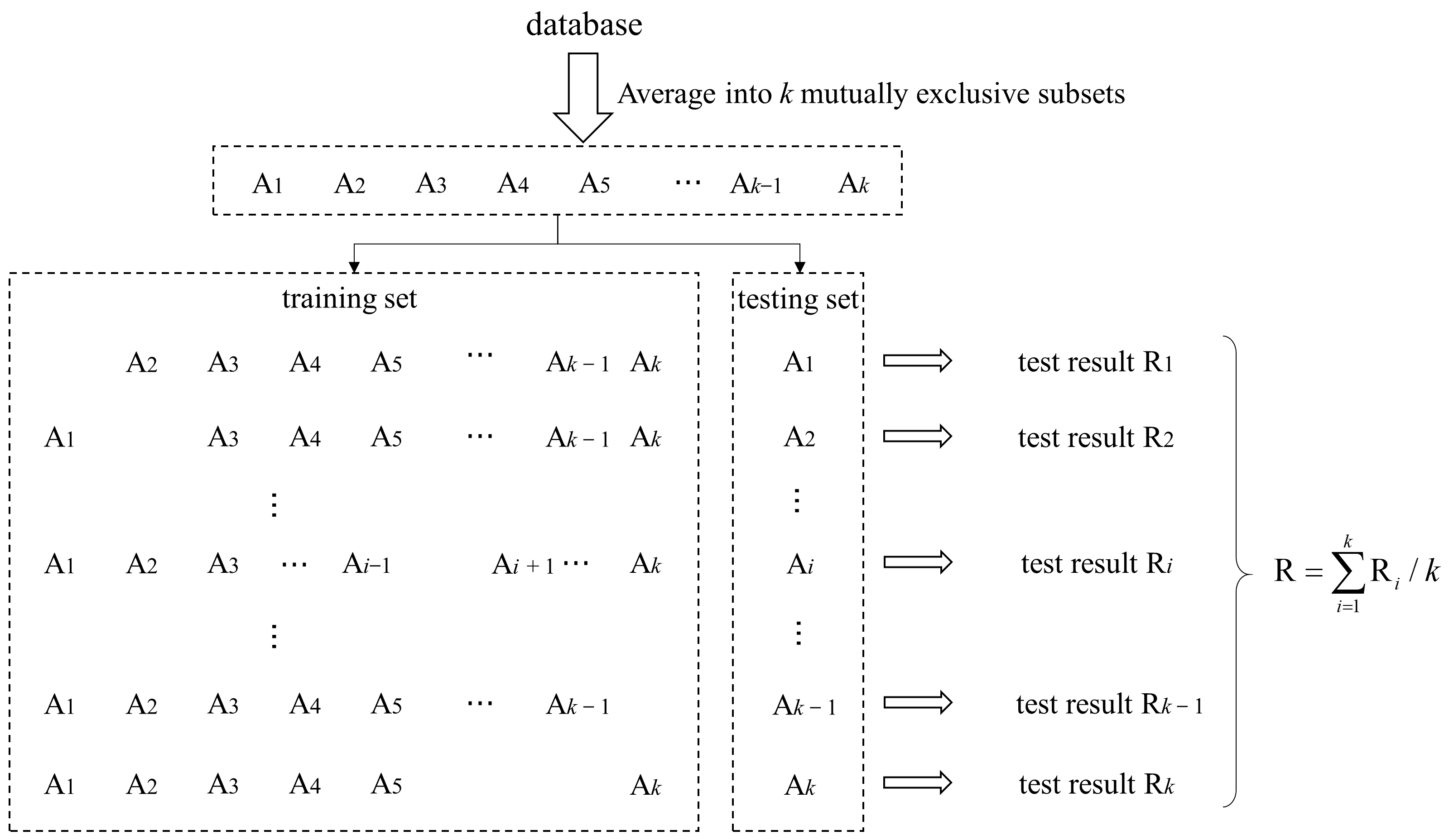
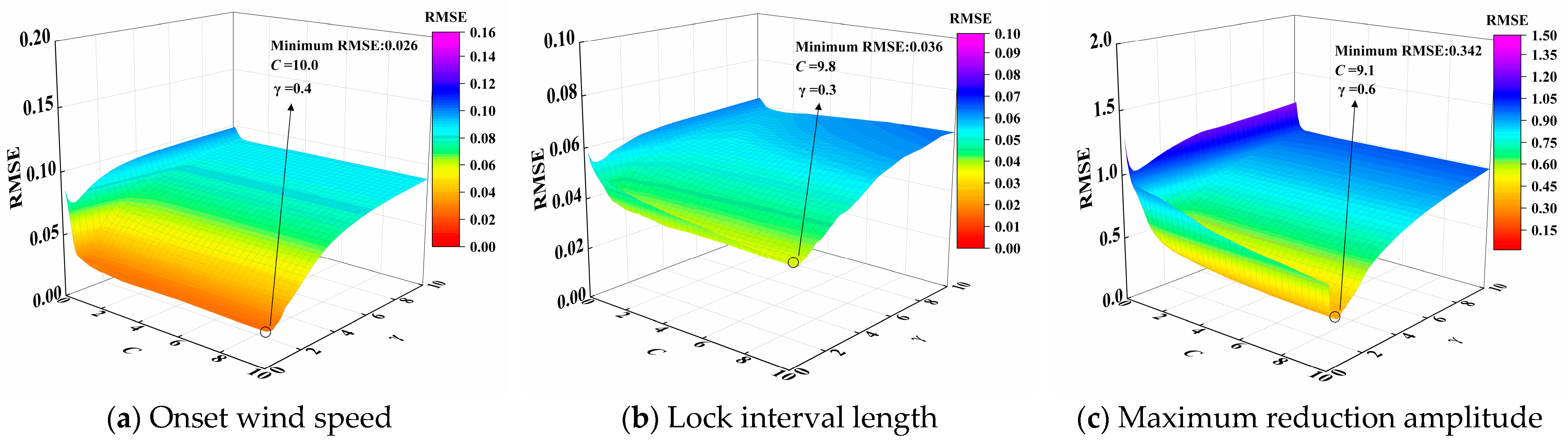
3.3. Performance Evaluation Methods and Parameter Optimization
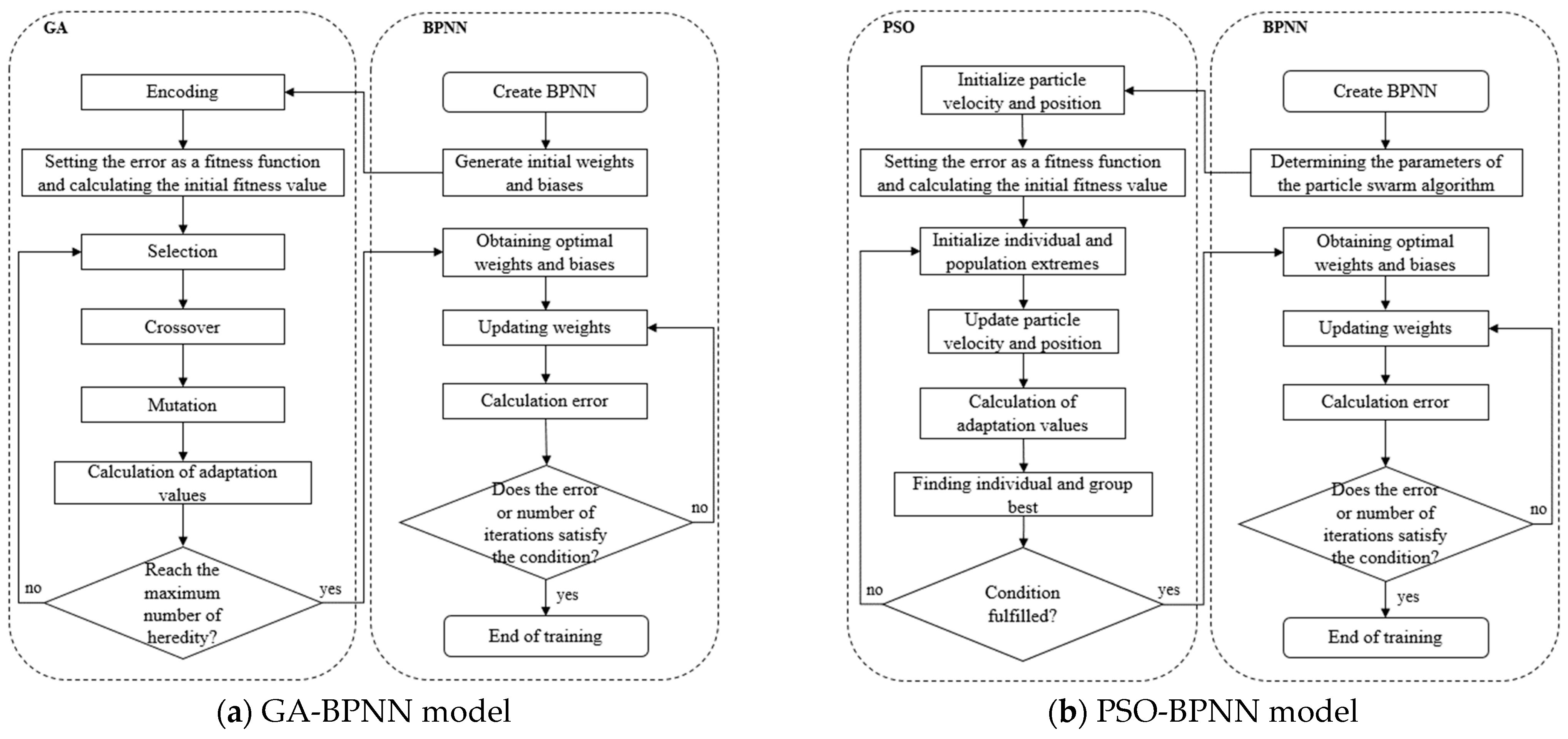
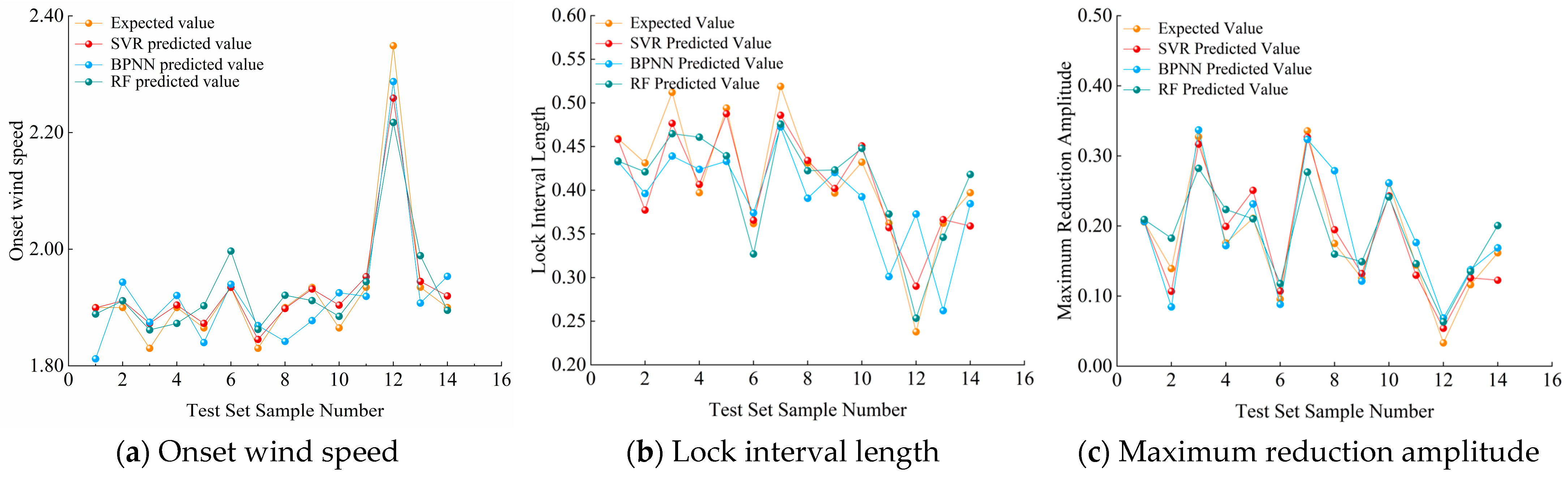
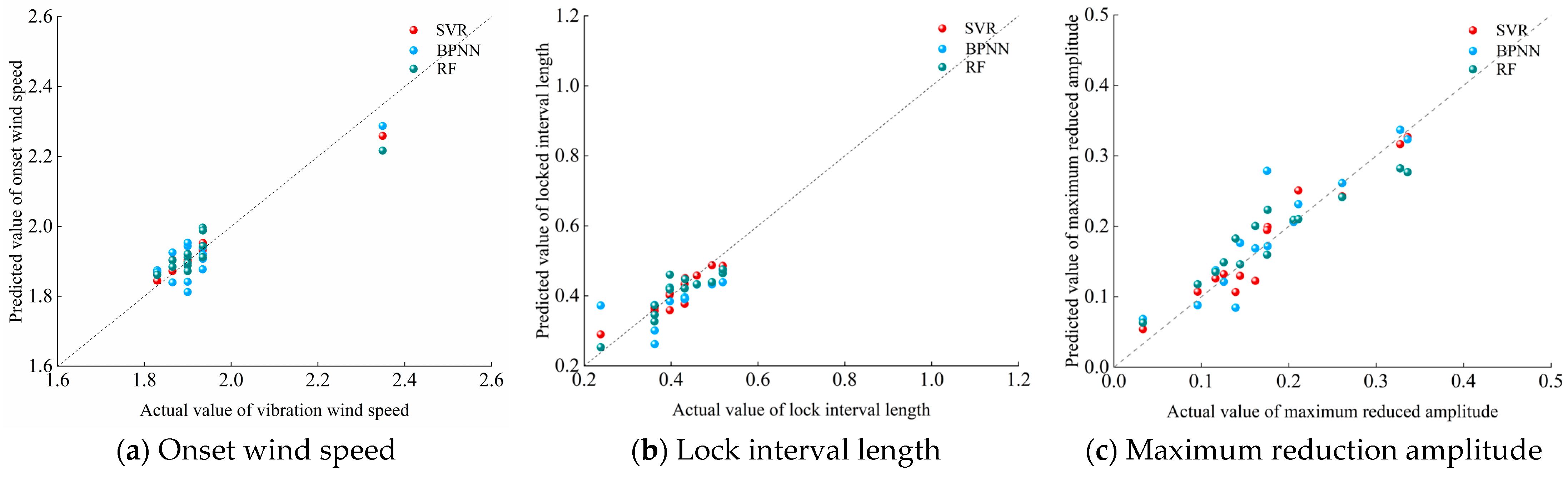
3.4. VIV Response Prediction Model Based on Improved Machine Learning Algorithm
4. Engineering Example Analysis
4.1. Engineering Background
4.2. Segment Model VIV Test
4.3. Numerical Simulation Results of Additional Aerodynamic Measures for Two Wind Attack Angles
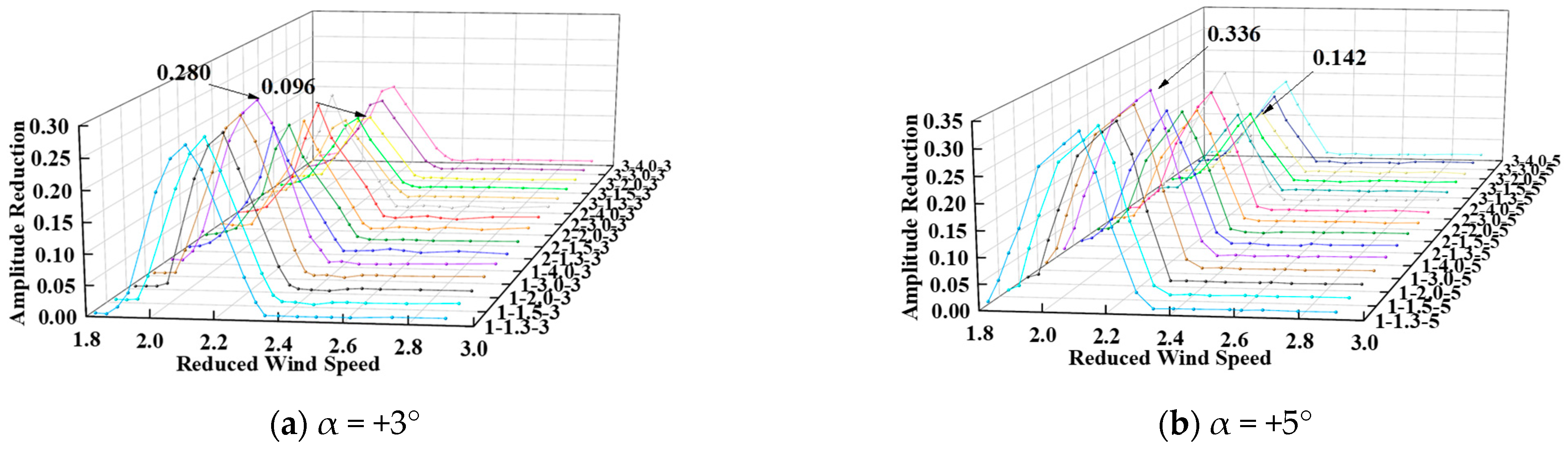
4.3.1. Vibration Suppression Rule for Wind Nozzle
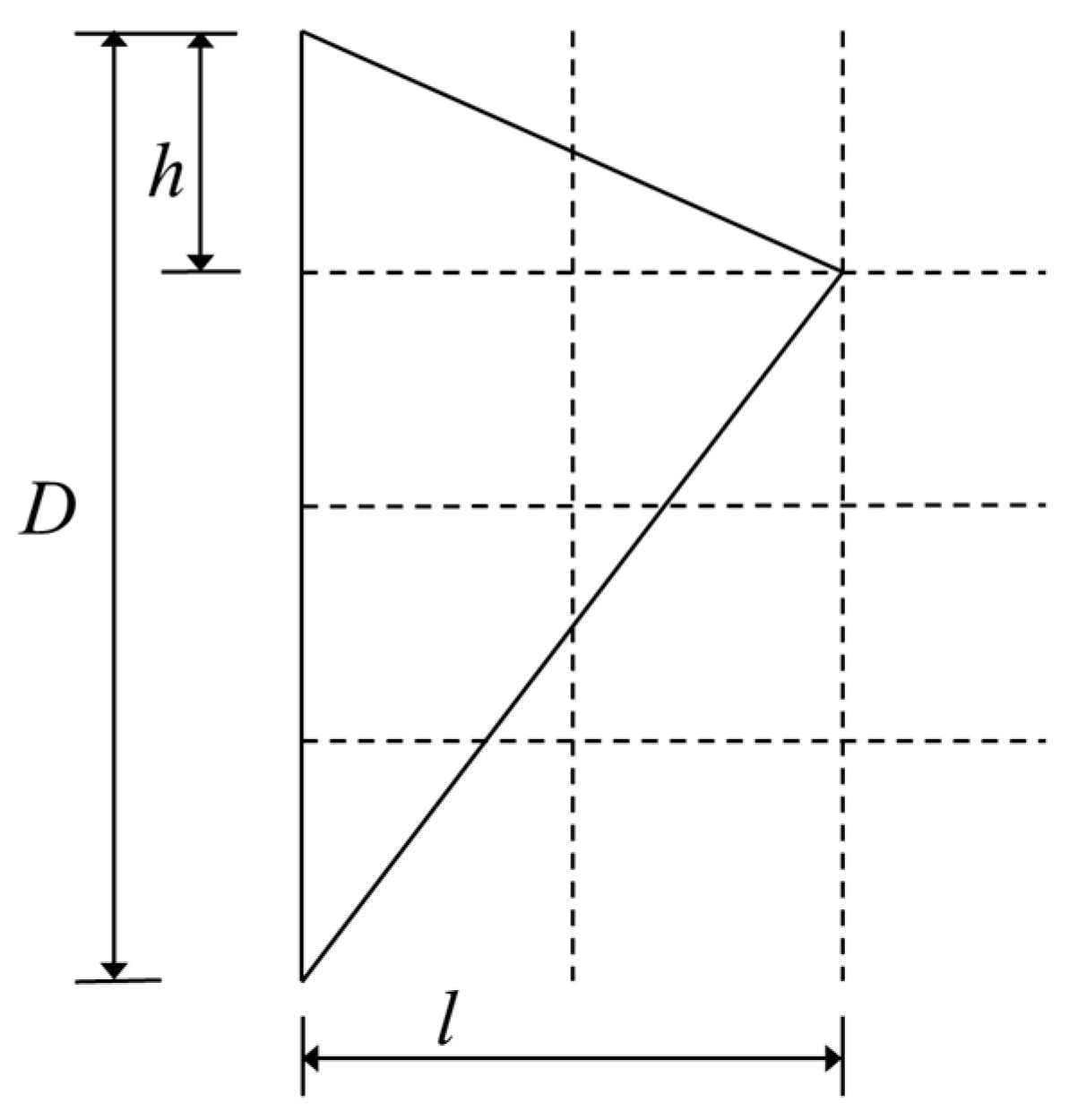
4.3.2. Vibration Suppression Rule for Deflector Plate
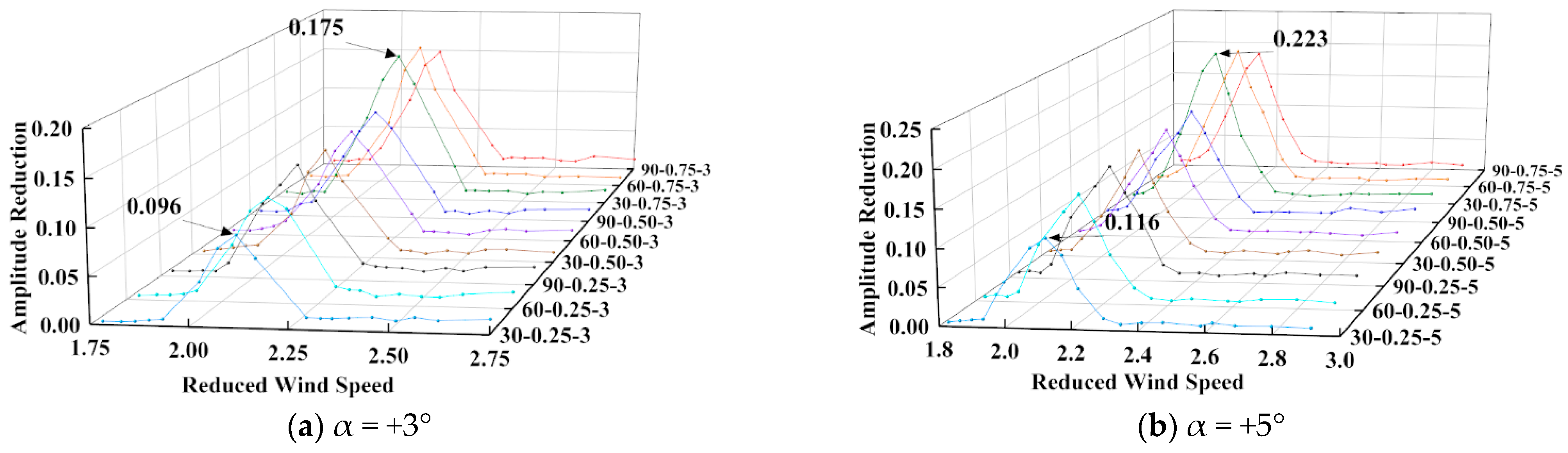
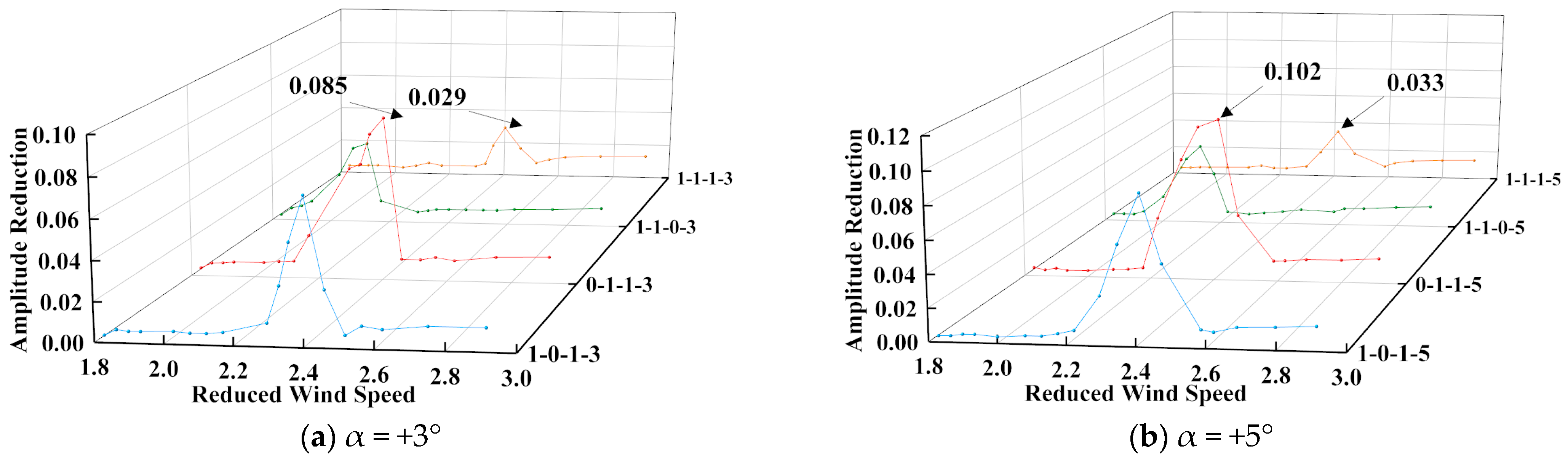
4.3.3. Vibration Suppression Rule for Combined Measures
- (1)
- After setting up the upper chord deflector plate, the separation point of the airflow at the front edge of the upper bridge deck was advanced, resulting in stronger vortex shedding. At the same time, the “unloading effect” of the leeward side guide plate weakens the energy of the vortex in the wake area of the upper bridge deck. Under the combined action of the two, the vertical bending VIV response of the DDST girder increases slightly.
- (2)
- After setting up the upper chord wind nozzle, the separated flow at the front edge of the upper bridge deck adheres to the surface of the wind nozzle. More airflow escapes from the gap of the railing, resulting in a significant reduction in the vortex intensity above the upper bridge deck and significant suppression of the vertical bending VIV of the DDST girder.
- (3)
- The “unloading effect” of the lower chord deflector plate significantly weakens the vortex strength in the wake area of the lower bridge deck, resulting in significant suppression of the torsional vortex response of the DDST girder, especially under high wind speeds.
- (4)
- After setting up the central stabilizer plate, a larger flow field appeared in front of it, further consuming the energy of the airflow and causing a slight reduction in the vertical bending VIV response. In addition, the central stabilizer plate effectively reduces the frequency of vortex shedding, resulting in the vertical bending VIV locking interval length towards higher wind speeds.
5. Prediction of VIV Response of the DDST Girder Section
5.1. Amplitude Prediction of DDST Girder Section
5.2. Characteristic Parameter Prediction of VIV of DDST Girder Section
6. Conclusions
- (1)
- In the VIV test, the segmental model will have vertical bending VIV at +3° and +5° wind angles of attack. The increase in the wind angle of attack leads to an increase in the locking interval length and maximum reduction amplitude, and the reduction wind speed of vibration onset is advanced.
- (2)
- Numerical simulation of the DDST girder was carried out to investigate the vertical bending VIV response of the section after changing the parameters of different additional aerodynamic measures and to summarize the effects of these variables on the VIV performance, which can provide reliable samples for the machine algorithm model.
- (3)
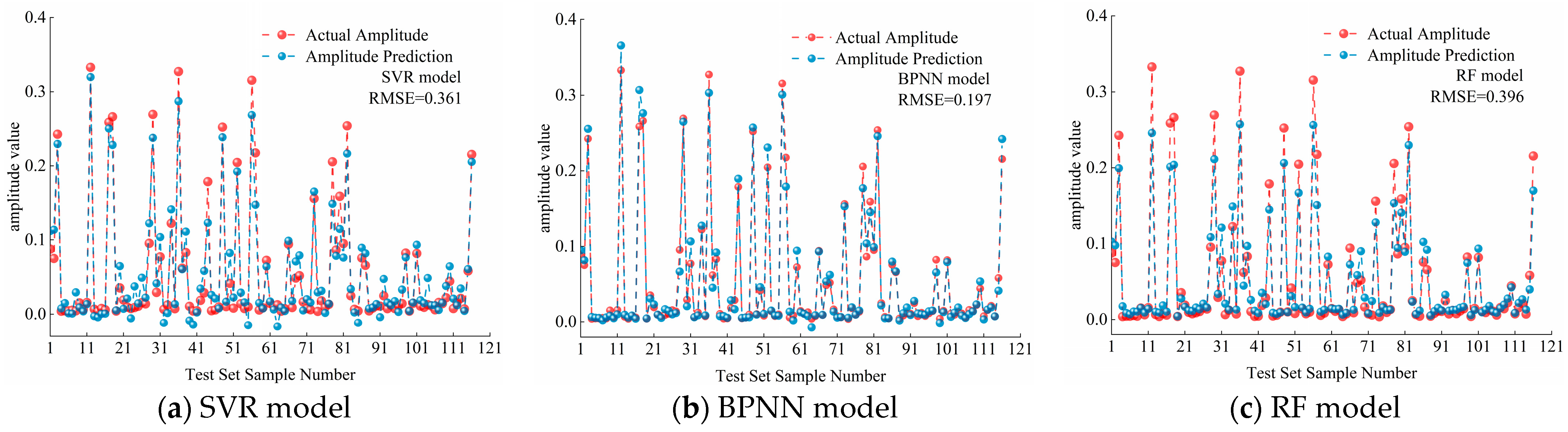
- The VIV data obtained from the numerical simulation are organized to establish the VIV-A and VIV-R datasets, and the prediction models are established by combining the three algorithms. Among them, the BPNN model predicts the amplitude best, and the SVR model predicts the VIV characteristic parameters with the best agreement.
- (4)
- The BPNN and SVR algorithms are improved and optimized by combining the GA and PSO algorithms, respectively, and the results show that the GA-BPNN model predicts the amplitude better than the BPNN model, and the PSO-SVR model predicts the VIV characteristic parameters better than the SVR model, which proves the validity of the improved algorithms. Compared with the wind tunnel test and numerical simulation, the proposed prediction model can significantly improve the computational efficiency while considering the computational accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VIV | Vortex-induced vibration |
| DDST | Double-deck steel truss |
| RMSE | Root mean square error |
| R2 | Coefficient of determination |
| UDF | User-defined function |
| SVR | Support Vector Regression |
| BPNN | Backpropagation Neural Network |
| RF | Random Forest |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
References
- Wang, B.; Li, W.; Zhao, C.; Zhang, Q.; Li, G.; Liu, X.; Yan, B.; Cai, X.; Zhang, J.; Zheng, S. L2-Norm Quasi 3-D Phase Unwrapping Assisted Multitemporal InSAR Deformation Dynamic Monitoring for the Cross-Sea Bridge. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 18926–18938. [Google Scholar] [CrossRef]
- Hong, C.; Lyu, Z.; Wang, F.; Zhao, Z.; Wang, L. Wave-Current Loads on a Super-Large-Diameter Pile in Deep Water: An Experimental Study. Appl. Sci. 2023, 13, 8859. [Google Scholar] [CrossRef]
- Gao, D.; Deng, Z.; Yang, W.; Chen, W. Review of the Excitation Mechanism and Aerodynamic Flow Control of Vortex-Induced Vibration of the Main Girder for Long-Span Bridges: A Vortex-Dynamics Approach. J. Fluids Struct. 2021, 105, 103348. [Google Scholar] [CrossRef]
- Hu, C.; Zhao, L.; Wang, X.; Ge, Y. Spatio-Temporal Distribution of Aerodynamic Forces and Their Associated Vortex Drift Patterns around a Closed-Box Girder during Torsional Vortex-Induced Vibration. Eng. Struct. 2024, 302, 117459. [Google Scholar] [CrossRef]
- Zhong, Y.; Li, M.; Ma, C. Aerodynamic Admittance of Truss Girder in Homogenous Turbulence. J. Wind Eng. Ind. Aerodyn. 2018, 172, 152–163. [Google Scholar] [CrossRef]
- Xin, D.; Zhan, J.; Zhang, H.; Ou, J. Control of Vortex-Induced Vibration of a Long-Span Bridge by Inclined Railings. J. Bridge Eng. 2021, 26, 04021093. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, Y.; Li, M.; Yang, X. Experimental and Numerical Studies on the Vortex-Induced Vibration of Two-Box Edge Girder for Cable-Stayed Bridges. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104336. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, X.; Li, J.; Xin, H.; Sun, Q.; Wang, J. Investigation of Vortex-Induced Vibration of a Cable-Stayed Bridge without Backstays Based on Wind Tunnel Tests. Eng. Struct. 2022, 250, 113436. [Google Scholar] [CrossRef]
- Wang, W.; Cao, S. Numerical Study of Aerodynamic Roles of Bridge Railings by Immersed Boundary Method. J. Wind Eng. Ind. Aerodyn. 2022, 228, 105111. [Google Scholar] [CrossRef]
- Duan, Q.; Ma, C.; Li, Q. Vortex-Induced Vibration Performance and Mechanism of Long-Span Railway Bridge Streamlined Box Girder. Adv. Struct. Eng. 2023, 26, 2506–2519. [Google Scholar] [CrossRef]
- Fang, C.; Hu, R.; Tang, H.; Li, Y.; Wang, Z. Experimental and Numerical Study on Vortex-Induced Vibration of a Truss Girder with Two Decks. Adv. Struct. Eng. 2020, 24, 136943322096902. [Google Scholar] [CrossRef]
- Tang, H.; Shum, K.M.; Tao, Q.; Jiang, J. Vortex-Induced Vibration of a Truss Girder with High Vertical Stabilizers. Adv. Struct. Eng. 2019, 22, 948–959. [Google Scholar] [CrossRef]
- Li, M.; Lin, Z.; Dai, R.; Wang, Y.; Li, M. Effects of Wind Barriers on the Aerodynamic Forces and Driving Safety of Vehicles on a Wide Bridge Girder at Various Angles of Attack. Phys. Fluids 2024, 36, 105109. [Google Scholar] [CrossRef]
- Bai, H.; Ji, N.; Xu, G.; Li, J. An Alternative Aerodynamic Mitigation Measure for Improving Bridge Flutter and Vortex Induced Vibration (VIV) Stability: Sealed Traffic Barrier. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104302. [Google Scholar] [CrossRef]
- Xu, F.; Ying, X.; Li, Y.; Zhang, M. Experimental Explorations of the Torsional Vortex-Induced Vibrations of a Bridge Deck. J. Bridge Eng. 2016, 21, 04016093. [Google Scholar] [CrossRef]
- Zhan, J.; Xin, D.; Ou, J.; Liu, Z. Experimental Study on Suppressing Vortex-Induced Vibration of a Long-Span Bridge by Installing the Wavy Railings. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104205. [Google Scholar] [CrossRef]
- Yang, Y.; Li, L.; Yao, G.; Wang, M.; Zhou, C.; Lei, T.; Tan, H. Study on the Influence of the Fully Enclosed Barrier on the Vortex-Induced Vibration Performance of a Long-Span Highway-Railway Double-Deck Truss Bridge. Phys. Fluids 2024, 36, 087132. [Google Scholar] [CrossRef]
- Pawar, S.; Rahman, S.M.; Vaddireddy, H.; San, O.; Rasheed, A.; Vedula, P. A Deep Learning Enabler for Nonintrusive Reduced Order Modeling of Fluid Flows. Phys. Fluids 2019, 31, 085101. [Google Scholar] [CrossRef]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep Learning for Universal Linear Embeddings of Nonlinear Dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef]
- Wei, S.; Jin, X.; Li, H. General Solutions for Nonlinear Differential Equations: A Rule-Based Self-Learning Approach Using Deep Reinforcement Learning. Comput. Mech. 2019, 64, 1361–1374. [Google Scholar] [CrossRef]
- Yan, Z.; Zheng, S.; Tai, X.; Yang, F.; Ding, Z. Machine Learning Models for Predicting VIV Amplitude of Streamlined Steel Box Girders. Structures 2024, 63, 106444. [Google Scholar] [CrossRef]
- Li, S.; Laima, S.; Li, H. Physics-Guided Deep Learning Framework for Predictive Modeling of Bridge Vortex-Induced Vibrations from Field Monitoring. Phys. Fluids 2021, 33, 037113. [Google Scholar] [CrossRef]
- Yan, W.-J.; Feng, Z.-Q.; Yang, W.; Yuen, K.-V. Bayesian Inference for the Dynamic Properties of Long-Span Bridges under Vortex-Induced Vibration with Scanlan’s Model and Dense Optical Flow Scheme. Mech. Syst. Signal Process. 2022, 174, 109078. [Google Scholar] [CrossRef]
- Fluent User’s Guide. Available online: https://ansyshelp.ansys.com/Views/Secured/corp/v221/en/flu_ug/flu_ug.html (accessed on 27 March 2025).
- Siedziako, B.; Øiseth, O. On the Importance of Cross-Sectional Details in the Wind Tunnel Testing of Bridge Deck Section Models. Procedia Eng. 2017, 199, 3145–3151. [Google Scholar] [CrossRef]
- Li, S.; Laima, S.; Li, H. Data-Driven Modeling of Vortex-Induced Vibration of a Long-Span Suspension Bridge Using Decision Tree Learning and Support Vector Regression. J. Wind Eng. Ind. Aerodyn. 2018, 172, 196–211. [Google Scholar] [CrossRef]
- Lu, Y.; Luo, Q.; Liao, Y.; Xu, W. Vortex-Induced Vibration Fatigue Damage Prediction Method for Flexible Cylinders Based on RBF Neural Network. Ocean Eng. 2022, 254, 111344. [Google Scholar] [CrossRef]
- Xu, W.; He, Z.; Zhai, L.; Wang, E. Vortex-Induced Vibration Prediction of an Inclined Flexible Cylinder Based on Machine Learning Methods. Ocean Eng. 2023, 282, 114956. [Google Scholar] [CrossRef]
- Hu, G.; Kwok, K.C.S. Predicting Wind Pressures around Circular Cylinders Using Machine Learning Techniques. J. Wind Eng. Ind. Aerodyn. 2020, 198, 104099. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, L.-D.; Tan, Z.-X.; Zhu, Q.; Meng, X.-L. Spanwise Layout Optimization of Aerodynamic Countermeasures for Multi-Mode Vortex-Induced Vibration Control on Long-Span Bridges. J. Wind Eng. Ind. Aerodyn. 2024, 244, 105616. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, L.; Li, K.; Xue, X.; Zhang, X.; Kim, B.; Li, C.Y. Machine-Learning Prediction of Aerodynamic Damping for Buildings and Structures Undergoing Flow-Induced Vibrations. J. Build. Eng. 2023, 63, 105374. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Zhang, Z. Machine Learning-Based Deep Data Mining and Prediction of Vortex-Induced Vibration of Circular Cylinders. Ocean Eng. 2023, 285, 115313. [Google Scholar] [CrossRef]
- Zhao, D.; Shao, Y.; Hu, H.; Hu, G.; Wang, Y. RBF-PSO-IS: An Innovative Metamodeling for Reliability Analysis of Bridge’s Vortex-Induced Vibration. Structures 2023, 55, 59–70. [Google Scholar] [CrossRef]
- Matlab. Available online: https://ww2.mathworks.cn/help/matlab/index.html?s_tid=hc_panel (accessed on 27 March 2025).
- Zhang, Y.-M.; Wang, H.; Bai, Y.; Mao, J.-X.; Chang, X.-Y.; Wang, L.-B. Switching Bayesian Dynamic Linear Model for Condition Assessment of Bridge Expansion Joints Using Structural Health Monitoring Data. Mech. Syst. Signal Process. 2021, 160, 107879. [Google Scholar] [CrossRef]




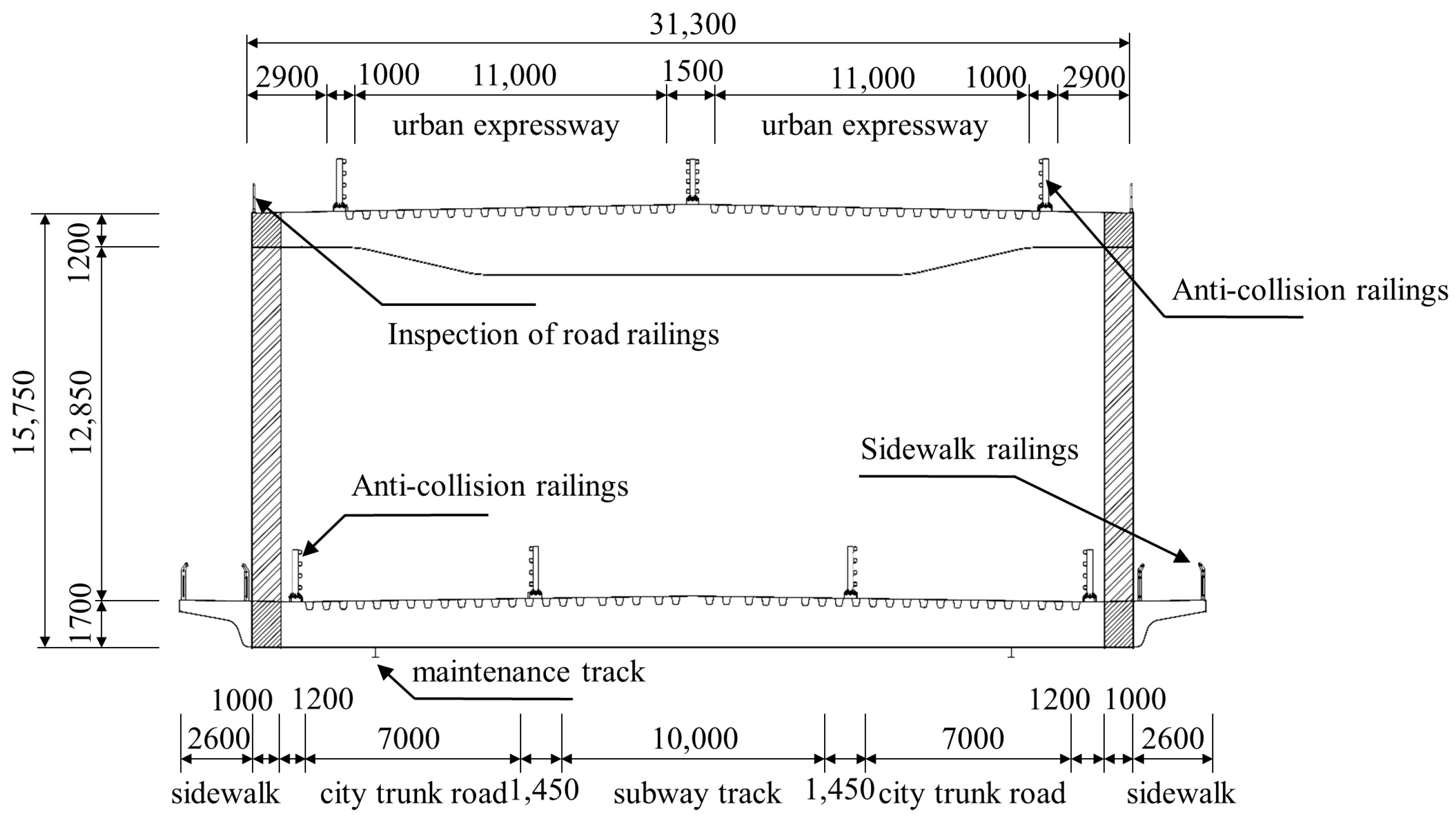

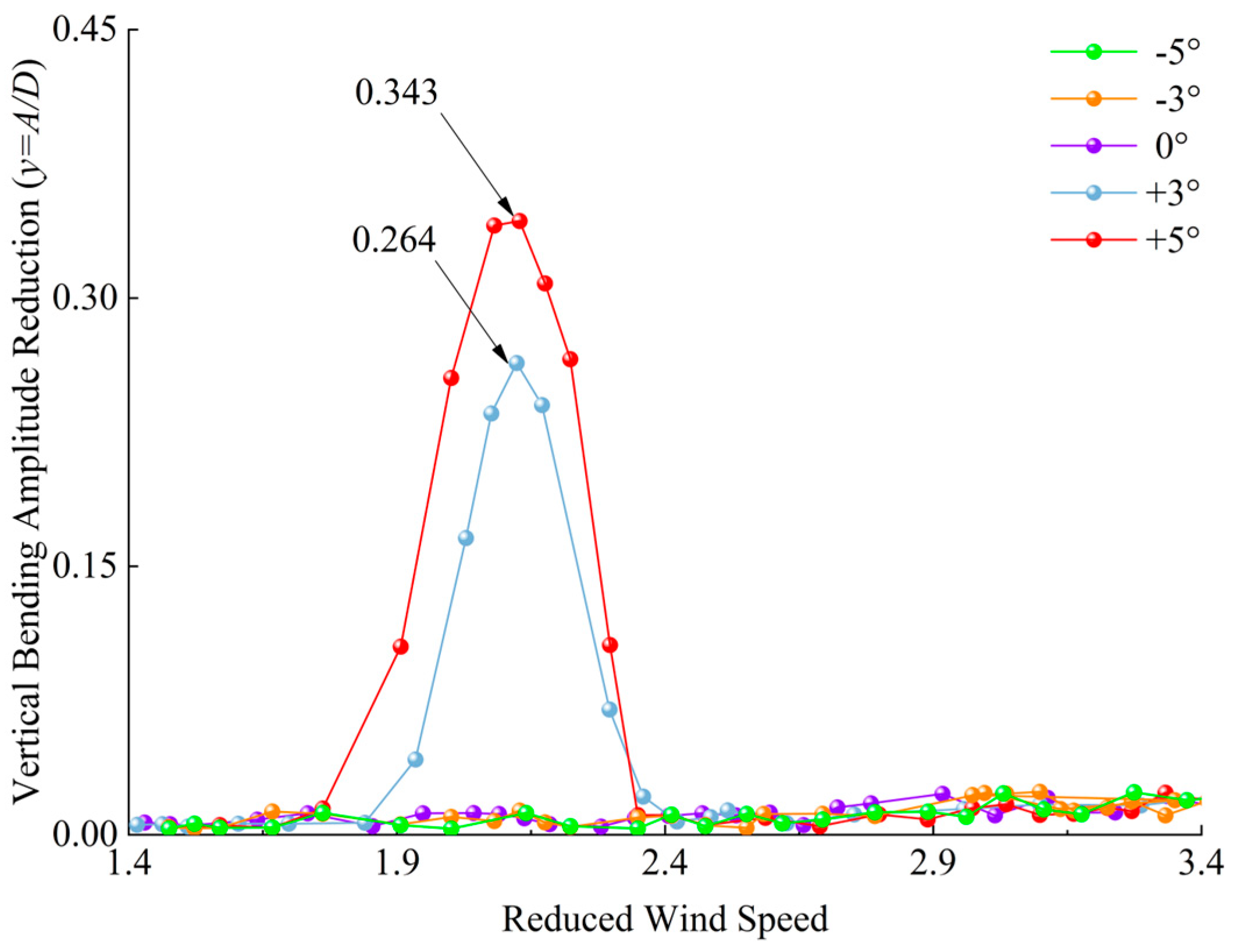








| Model | Frequency | Mass | Moment of Inertia | Vibration Pattern |
|---|---|---|---|---|
| 3 | 0.211 Hz | 6.845 × 104 kg/m | / | first-order symmetric vertical bending |
| 4 | 0.237 Hz | 7.008 × 104 kg/m | / | first-order antisymmetric vertical bending |
| 11 | 0.478 Hz | / | 1.309 × 107 kg·m2/m | first-order symmetric torsion |
| 25 | 0.706 Hz | / | 1.228 × 107 kg·m2/m | first-order antisymmetric torsion |
| Parameter | Unit | Real Bridge Value | Similarity Ratio | Test Model Value |
|---|---|---|---|---|
| height | m | 15.75 | 1:55 | 0.286 |
| width | m | 31.30 | 1:55 | 0.569 |
| mass | kg/m | 6.845 × 104 | 1:552 | 22.628 |
| moment of inertia | kg·m2/m | 1.309 × 107 | 1:554 | 1.431 |
| radius of gyration | m | 13.83 | 1:55 | 0.251 |
| vertical bending frequency | Hz | 0.211 | - | 2.218 |
| torsion frequency | Hz | 0.478 | - | 5.033 |
| vertical bending damping ratio | % | 0.50% | 1:1 | 0.38% |
| torsion damping ratio | % | 0.50% | 1:1 | 0.31% |
| Condition Number * | Wind Nozzle Angle | Wind Nozzle Tip Position | Wind Attack Angle | Condition Number | Wind Nozzle Angle | Wind Nozzle Tip Position | Wind Attack Angle |
|---|---|---|---|---|---|---|---|
| SW30-0.25-3 | 30° | 0.25 | +3° | SW30-0.25-5 | 30° | 0.25 | +5° |
| SW30-0.50-3 | 30° | 0.50 | +3° | SW30-0.50-5 | 30° | 0.50 | +5° |
| SW30-0.75-3 | 30° | 0.75 | +3° | SW30-0.75-5 | 30° | 0.75 | +5° |
| SW60-0.25-3 | 60° | 0.25 | +3° | SW60-0.25-5 | 60° | 0.25 | +5° |
| SW60-0.50-3 | 60° | 0.50 | +3° | SW60-0.50-5 | 60° | 0.50 | +5° |
| SW60-0.75-3 | 60° | 0.75 | +3° | SW60-0.75-5 | 60° | 0.75 | +5° |
| SW90-0.25-3 | 90° | 0.25 | +3° | SW90-0.25-5 | 90° | 0.25 | +5° |
| SW90-0.50-3 | 90° | 0.50 | +3° | SW90-0.50-5 | 90° | 0.50 | +5° |
| SW90-0.75-3 | 90° | 0.75 | +3° | SW90-0.75-5 | 90° | 0.75 | +5° |
| Condition Number * | Deflector Height Ratio | Wind Attack Angle | Condition Number | Deflector Height Ratio | Wind Attack Angle |
|---|---|---|---|---|---|
| SD1-1.3-3 | 1.3 | +3° | SD1-1.3-5 | 1.3 | +5° |
| SD1-1.5-3 | 1.5 | +3° | SD1-1.5-5 | 1.5 | +5° |
| SD1-2.0-3 | 2.0 | +3° | SD1-2.0-5 | 2.0 | +5° |
| SD1-3.0-3 | 3.0 | +3° | SD1-3.0-5 | 3.0 | +5° |
| SD1-4.0-3 | 4.0 | +3° | SD1-4.0-5 | 4.0 | +5° |
| SD2-1.3-3 | 1.3 | +3° | SD2-1.3-5 | 1.3 | +5° |
| SD2-1.5-3 | 1.5 | +3° | SD2-1.5-5 | 1.5 | +5° |
| SD2-2.0-3 | 2.0 | +3° | SD2-2.0-5 | 2.0 | +5° |
| SD2-3.0-3 | 3.0 | +3° | SD2-3.0-5 | 3.0 | +5° |
| SD2-4.0-3 | 4.0 | +3° | SD2-4.0-5 | 4.0 | +5° |
| SD3-1.3-3 | 1.3 | +3° | SD3-1.3-5 | 1.3 | +5° |
| SD3-1.5-3 | 1.5 | +3° | SD3-1.5-5 | 1.5 | +5° |
| SD3-2.0-3 | 2.0 | +3° | SD3-2.0-5 | 2.0 | +5° |
| SD3-3.0-3 | 3.0 | +3° | SD3-3.0-5 | 3.0 | +5° |
| SD3-4.0-3 | 4.0 | +3° | SD3-4.0-5 | 4.0 | +5° |
| Condition Number * | Wind Nozzle Angle | Wind Nozzle tip Position | Deflector Height Ratio | Stabilizer Plate Height | Wind Attack Angle |
|---|---|---|---|---|---|
| SC1-0-1-3 | 60° | 0.50 | / | 45.5 | +3° |
| SC0-1-1-3 | / | / | 2 | 45.5 | +3° |
| SC1-1-0-3 | 60° | 0.50 | 2 | / | +3° |
| SC1-1-1-3 | 60° | 0.50 | 2 | 45.5 | +3° |
| SC1-0-1-5 | 60° | 0.50 | / | 45.5 | +5° |
| SC0-1-1-5 | / | / | 2 | 45.5 | +5° |
| SC1-1-0-5 | 60° | 0.50 | 2 | / | +5° |
| SC1-1-1-5 | 60° | 0.50 | 2 | 45.5 | +5° |
| Model | Parameter | Search Space | Optimal Parameter | Optimal Cross-Fold |
|---|---|---|---|---|
| SVR | C | {0.1~10.0} | 10.0 | 10 |
| γ | {0.1~10.0} | 10.0 | ||
| BPNN | hidden layer | {1, 2, 3} | 2 | 10 |
| hidden layer node | {5~50} | [13,6] | ||
| RF | n | {50~200} | 120 | 10 |
| leaf | {1~20} | 1 |
| Model | RMSE | Variation Range | R2 | Variation Range |
|---|---|---|---|---|
| BPNN | 0.197 | / | 0.9723 | / |
| GA-BPNN | 0.150 | −23.9% | 0.9898 | 1.8% |
| PSO-BPNN | 0.164 | −16.8% | 0.9878 | 1.6% |
| Model | Parameter | RMSE | Variation Range | R2 | Variation Range |
|---|---|---|---|---|---|
| SVR | Onset wind speed | 0.026 | / | 0.9398 | / |
| Lock interval length | 0.024 | / | 0.8520 | / | |
| Maximum reduction Amplitude | 0.393 | / | 0.9299 | / | |
| GA-SVR | Onset wind speed | 0.019 | −26.9% | 0.9290 | −1.1% |
| Lock interval length | 0.022 | −8.3% | 0.8748 | 2.7% | |
| Maximum reduction Amplitude | 0.315 | −19.8% | 0.9475 | 1.9% | |
| PSO-SVR | Onset wind speed | 0.017 | −34.6% | 0.9421 | 0.2% |
| Lock interval length | 0.026 | −19.8% | 0.8875 | 4.2% | |
| Maximum reduction Amplitude | 0.295 | −24.9% | 0.9462 | 1.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Hou, H.; Yao, G.; Wu, B. Vortex-Induced Vibration Performance Prediction of Double-Deck Steel Truss Bridge Based on Improved Machine Learning Algorithm. J. Mar. Sci. Eng. 2025, 13, 767. https://doi.org/10.3390/jmse13040767
Yang Y, Hou H, Yao G, Wu B. Vortex-Induced Vibration Performance Prediction of Double-Deck Steel Truss Bridge Based on Improved Machine Learning Algorithm. Journal of Marine Science and Engineering. 2025; 13(4):767. https://doi.org/10.3390/jmse13040767
Chicago/Turabian StyleYang, Yang, Huiwen Hou, Gang Yao, and Bo Wu. 2025. "Vortex-Induced Vibration Performance Prediction of Double-Deck Steel Truss Bridge Based on Improved Machine Learning Algorithm" Journal of Marine Science and Engineering 13, no. 4: 767. https://doi.org/10.3390/jmse13040767
APA StyleYang, Y., Hou, H., Yao, G., & Wu, B. (2025). Vortex-Induced Vibration Performance Prediction of Double-Deck Steel Truss Bridge Based on Improved Machine Learning Algorithm. Journal of Marine Science and Engineering, 13(4), 767. https://doi.org/10.3390/jmse13040767









