A Method for Dynamic Response Analysis of Offshore Substation Platform Foundations Based on Modal Truncation
Abstract
1. Introduction
2. Materials and Methods
2.1. Nemark-β Method
2.2. Vibration Equation Decoupling and Modal Truncation
2.2.1. Decoupling of the Equation Governing Equation Governing Vibration
2.2.2. Modal-Truncation Method
2.2.3. Dynamic Response Calculation
3. Results
3.1. Six-DOF Mass-Damping-Spring Model
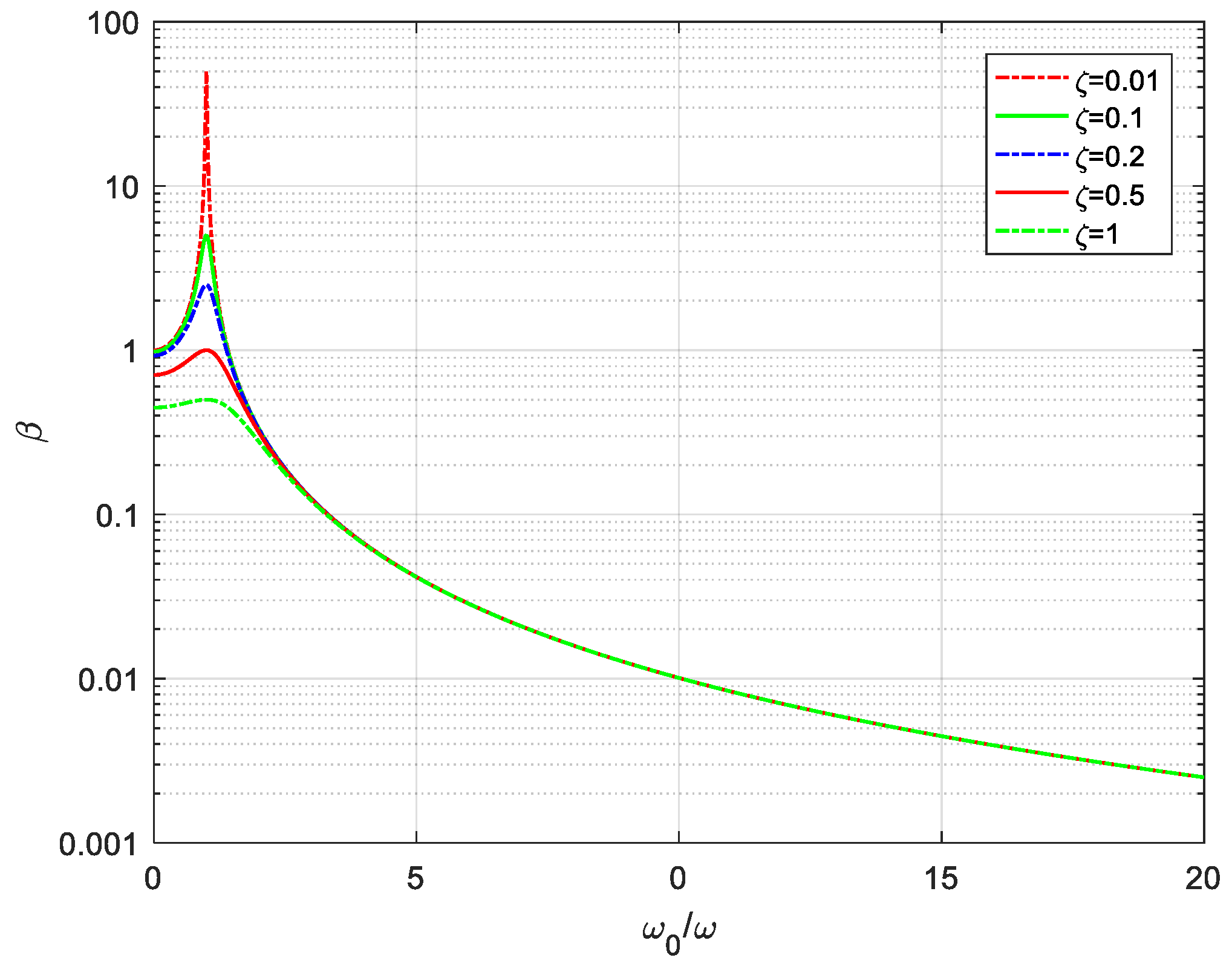
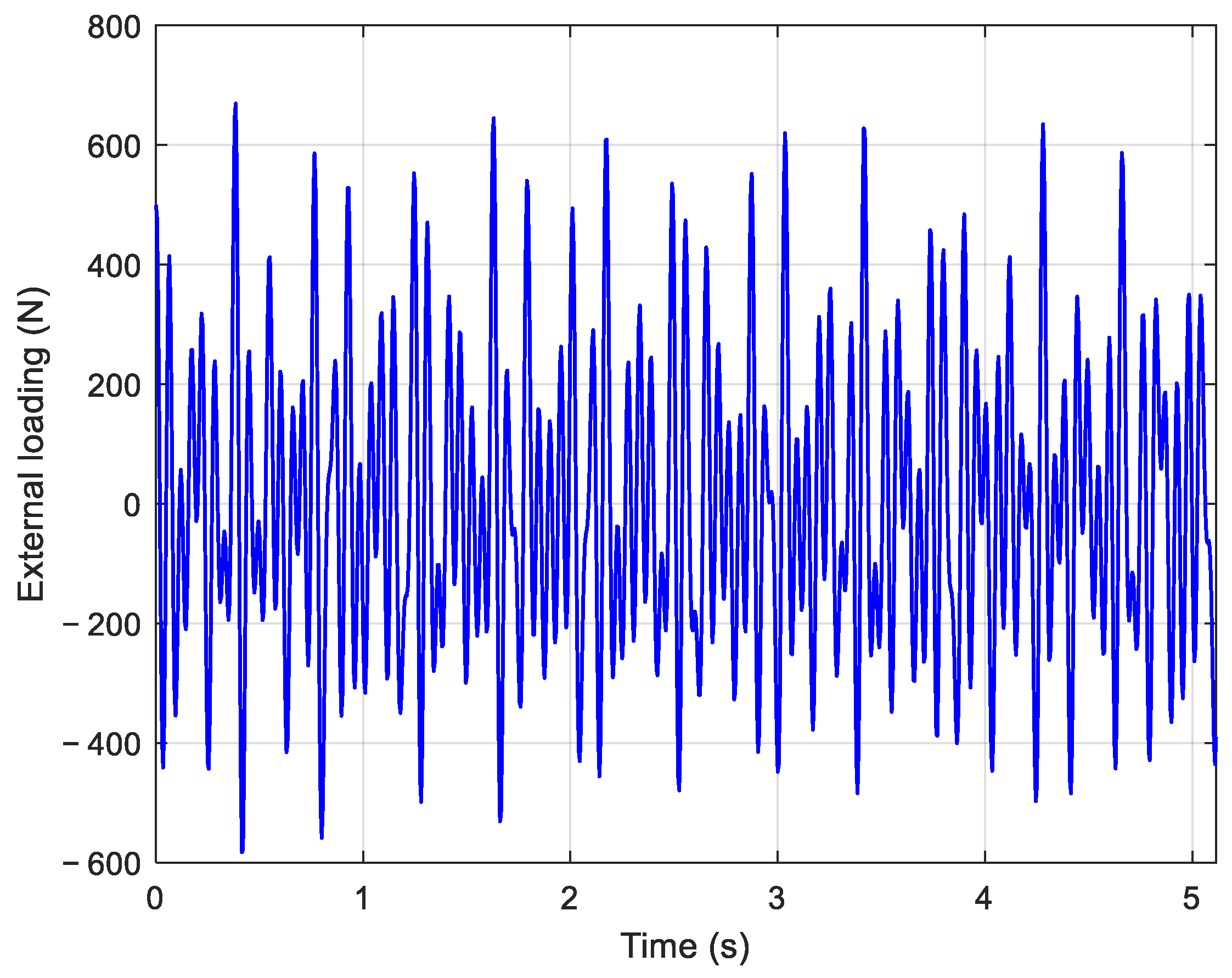
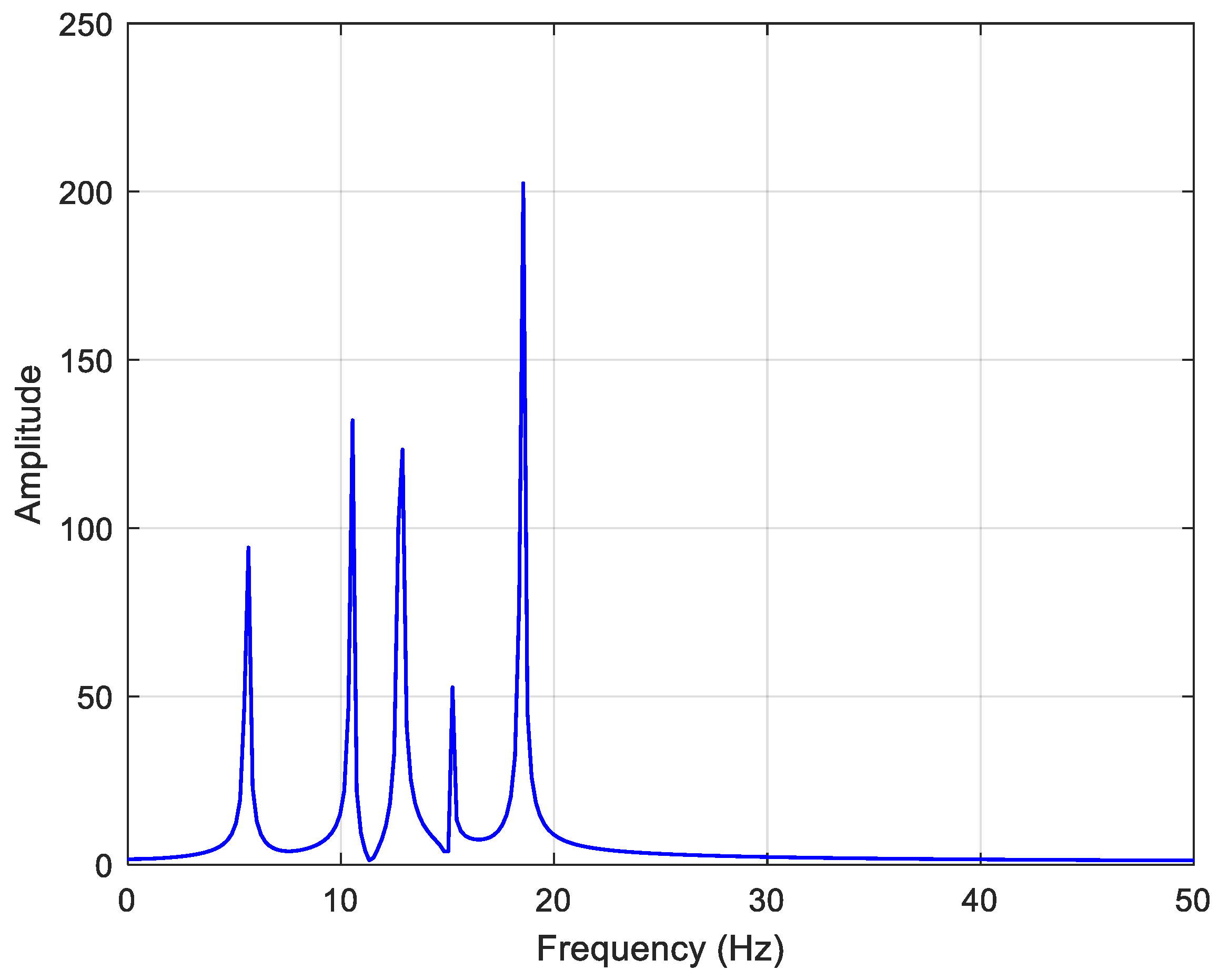
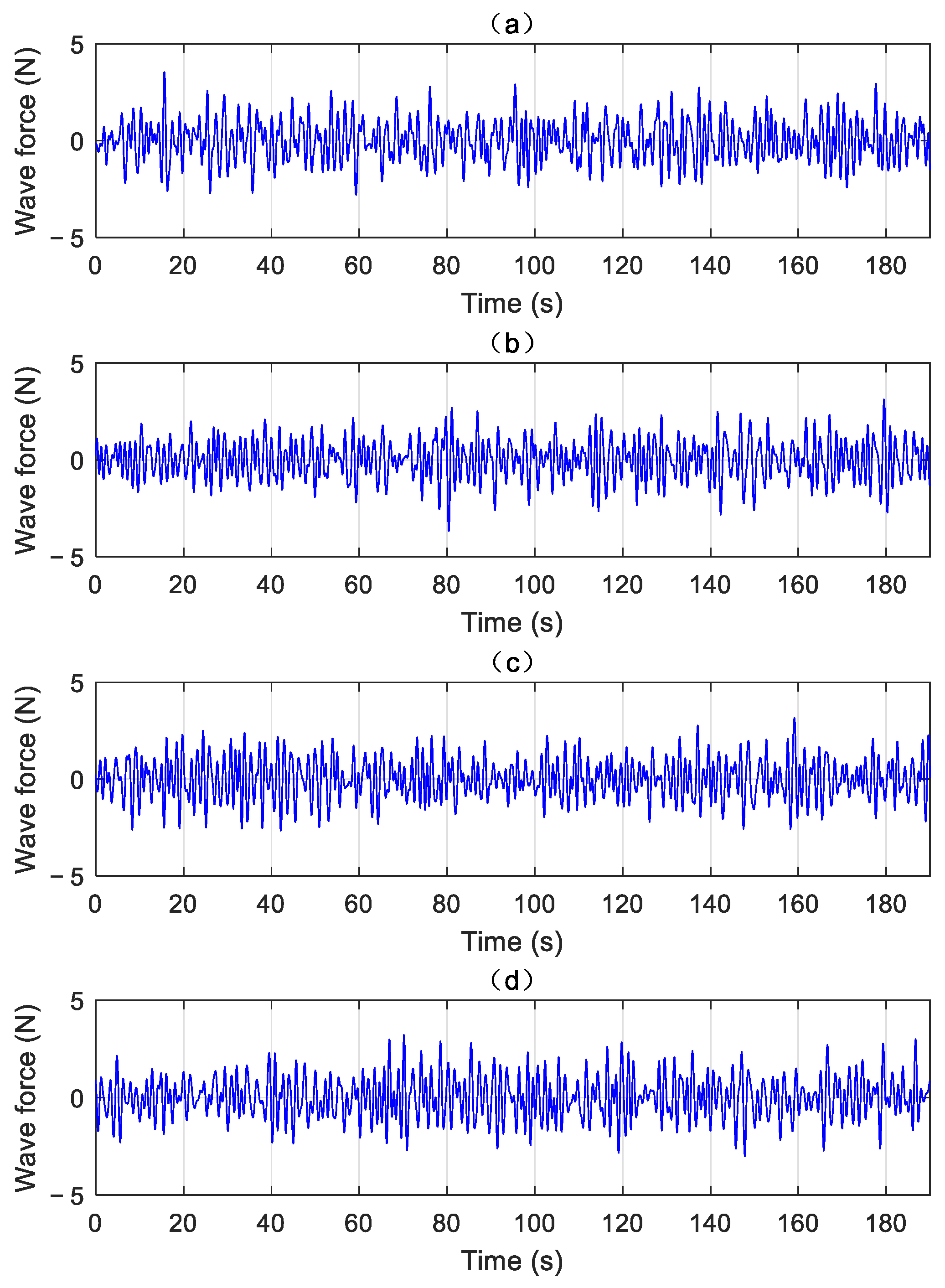
3.1.1. External Load Simulation
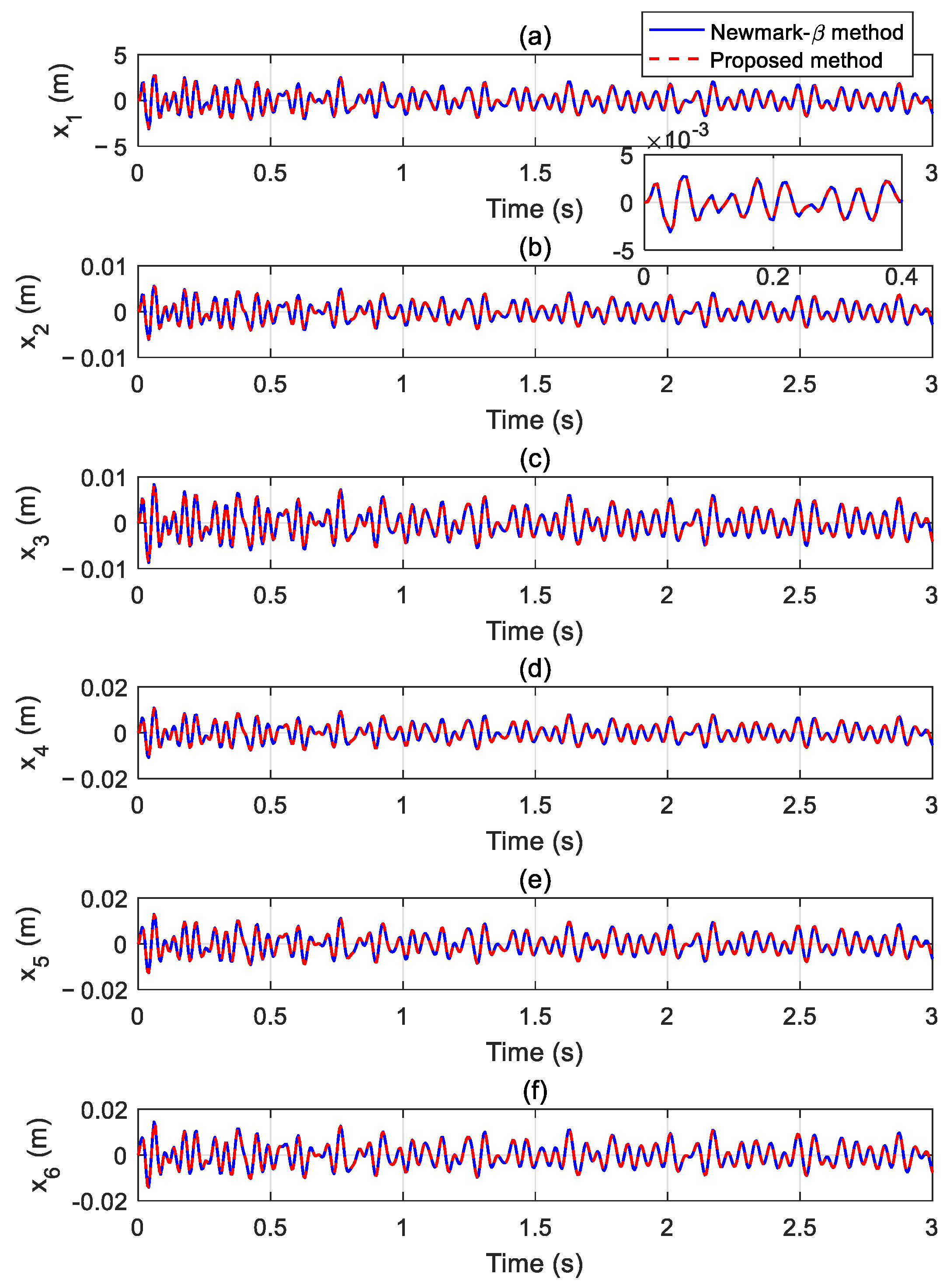
3.1.2. Dynamic Response Calculation of Six-DOF System
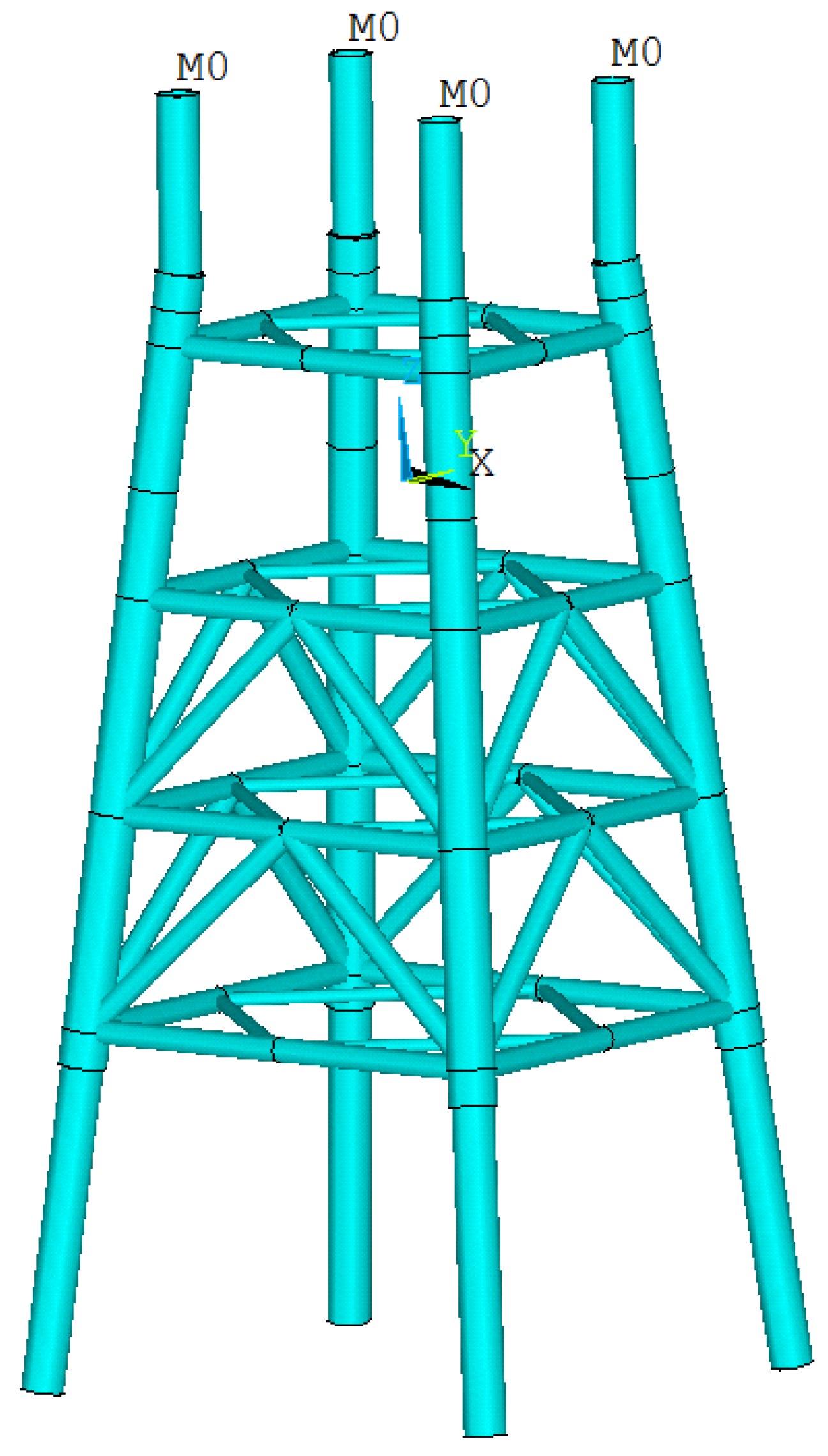
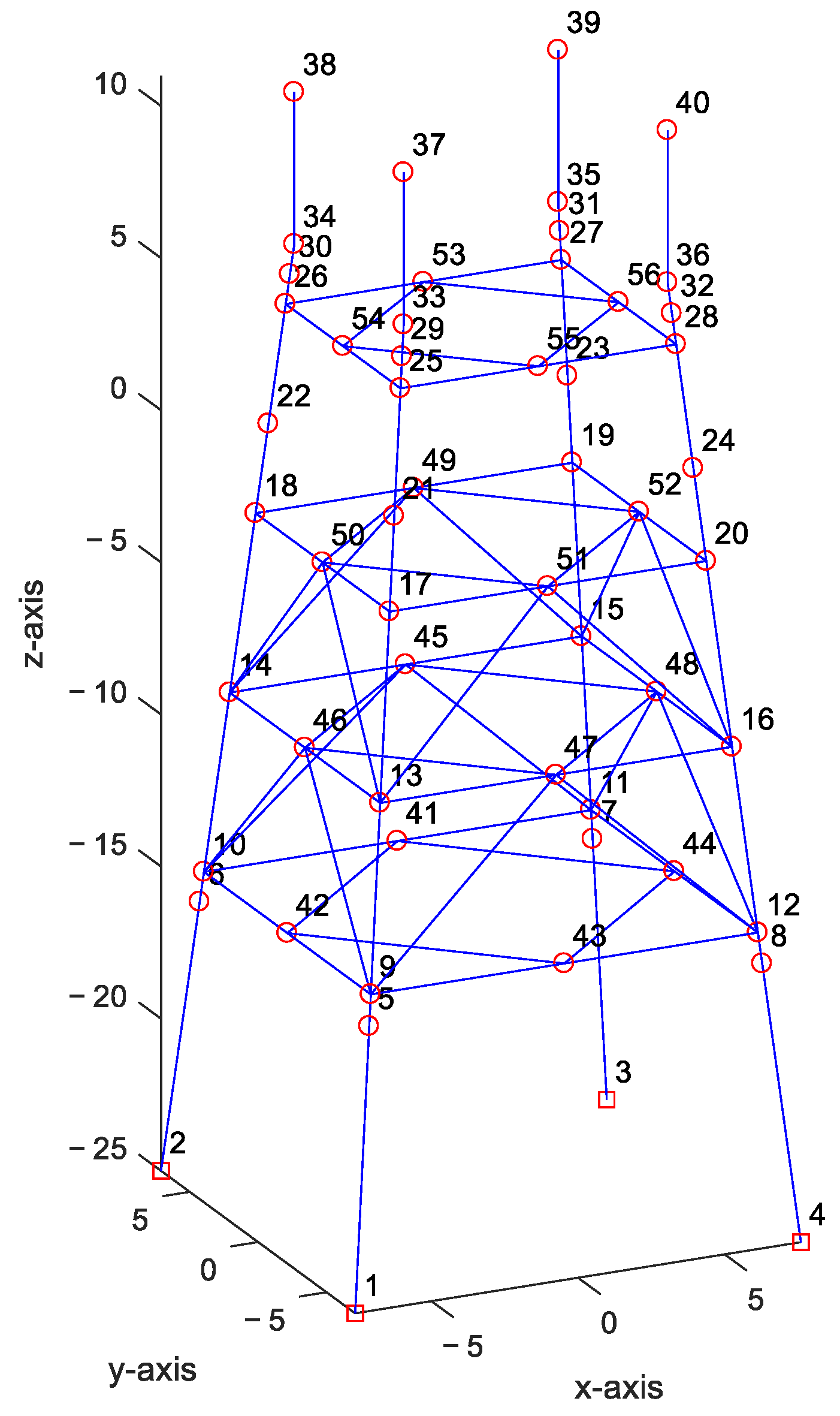
3.2. Jacket Foundation Structure
3.2.1. Element Modal Analysis
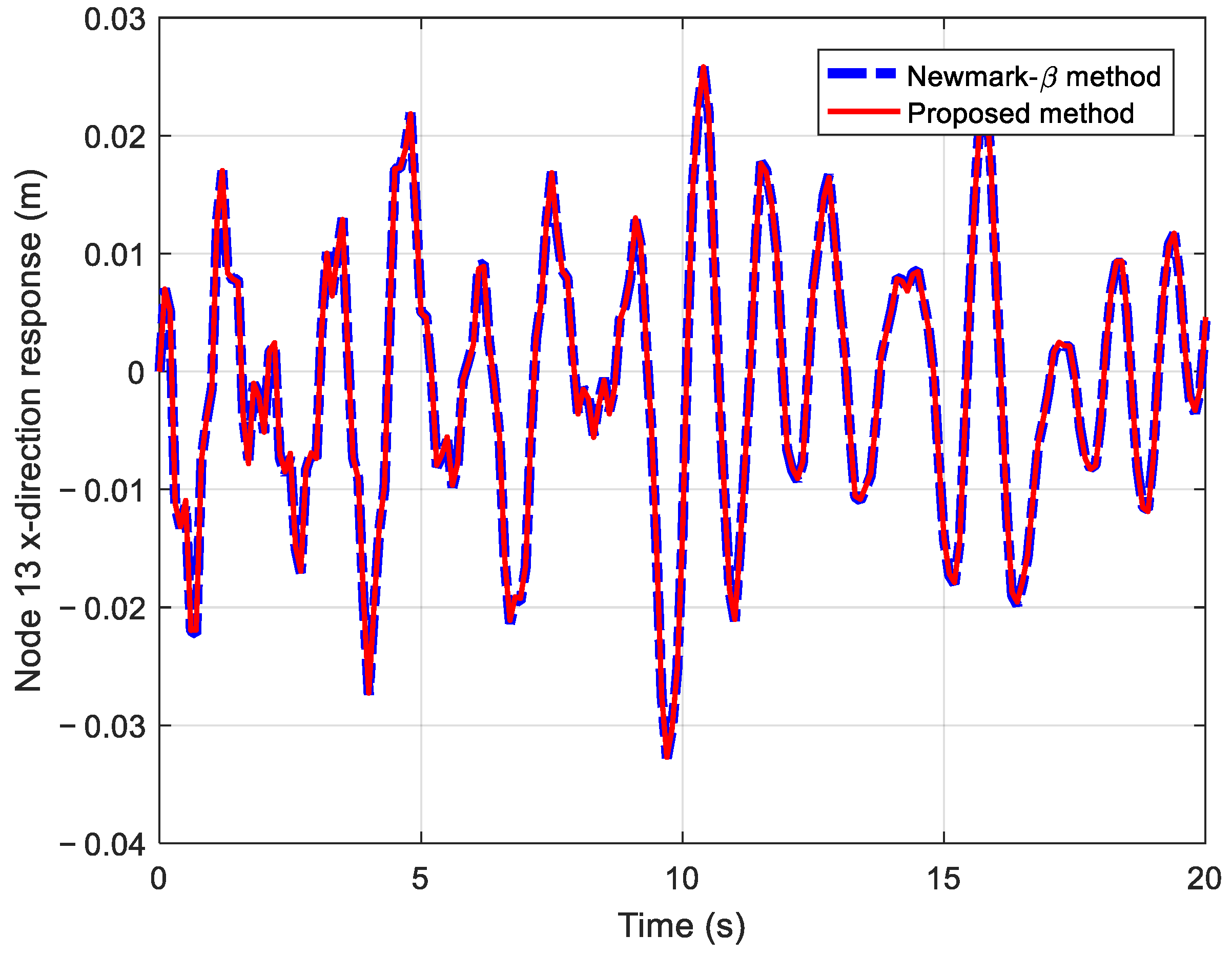
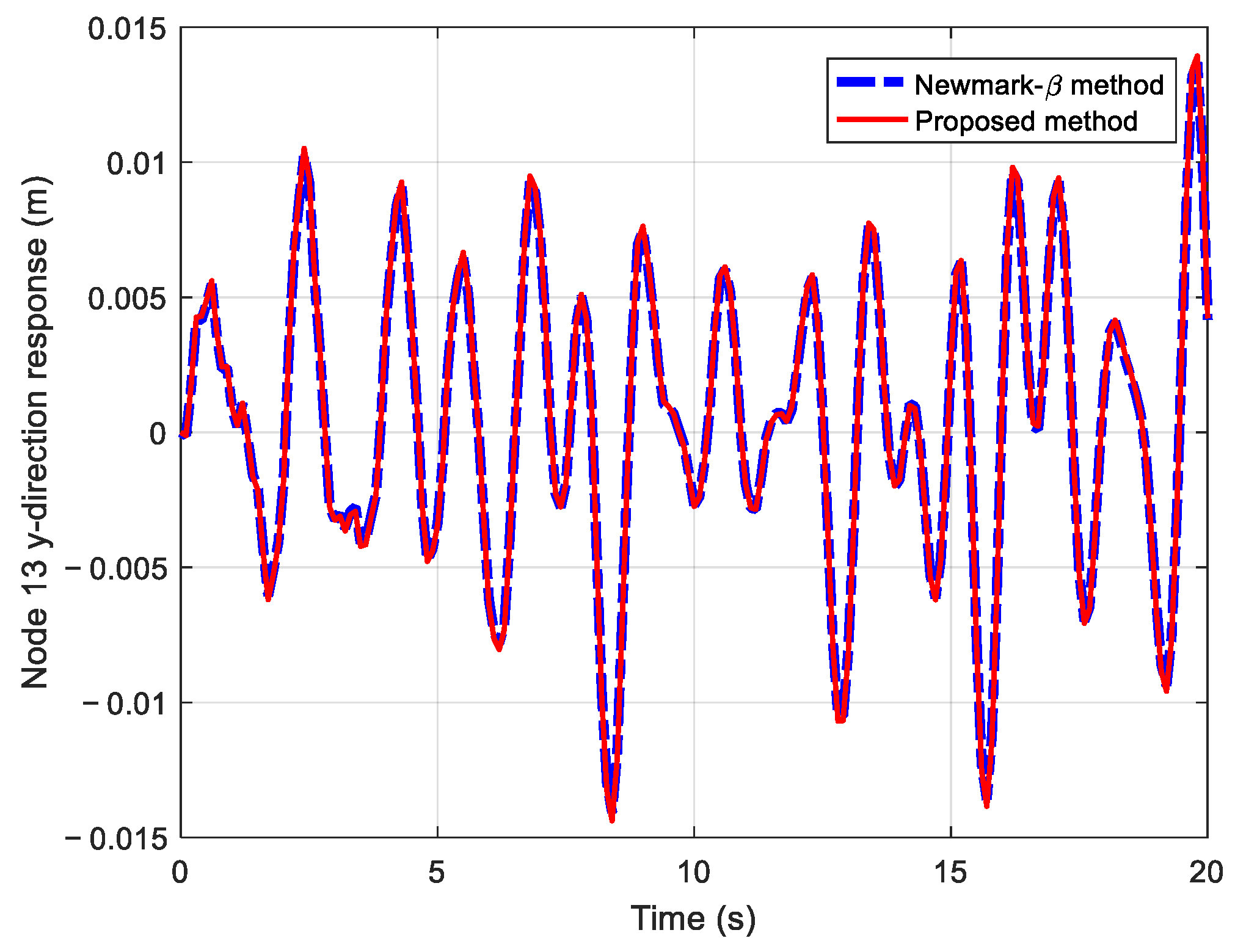
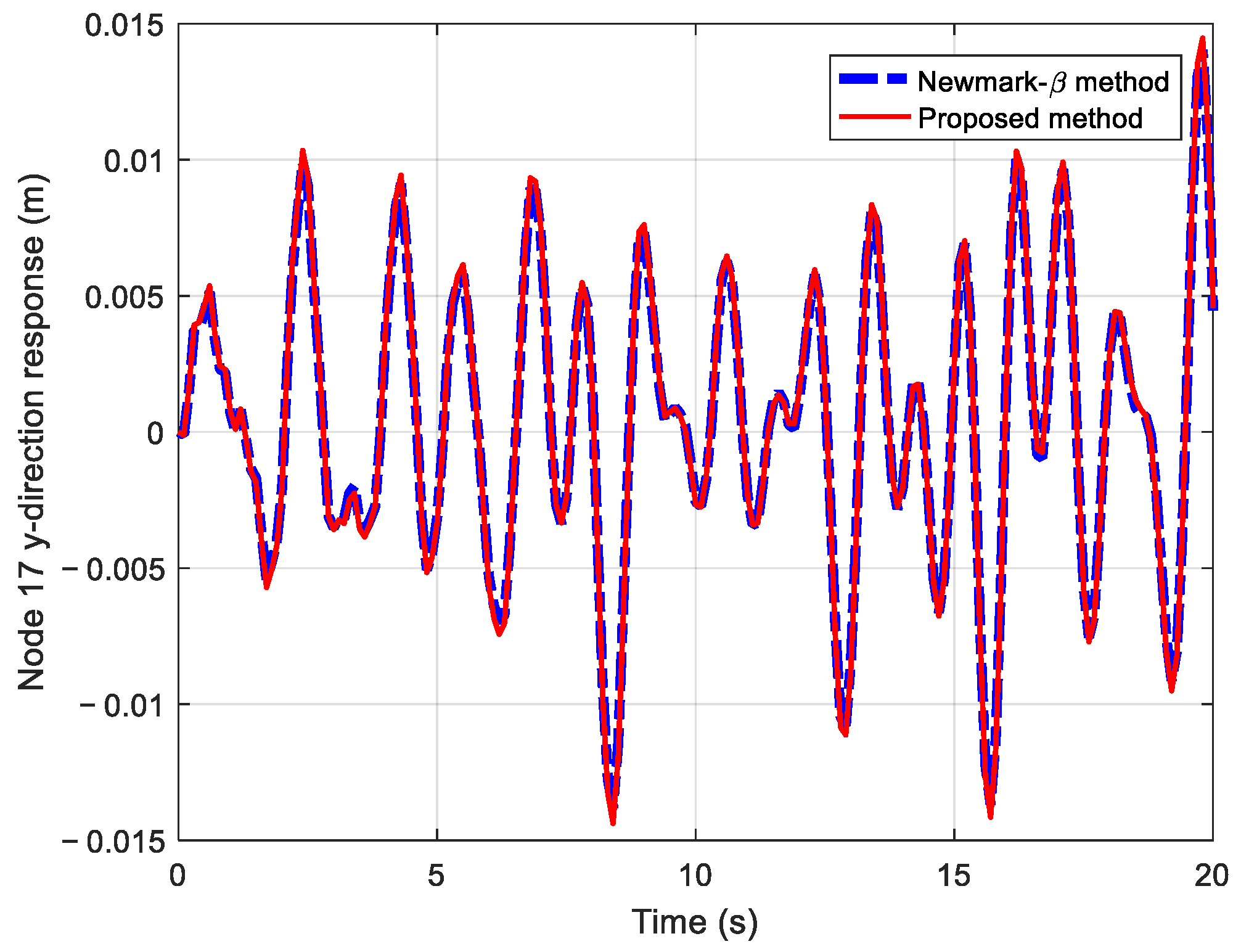
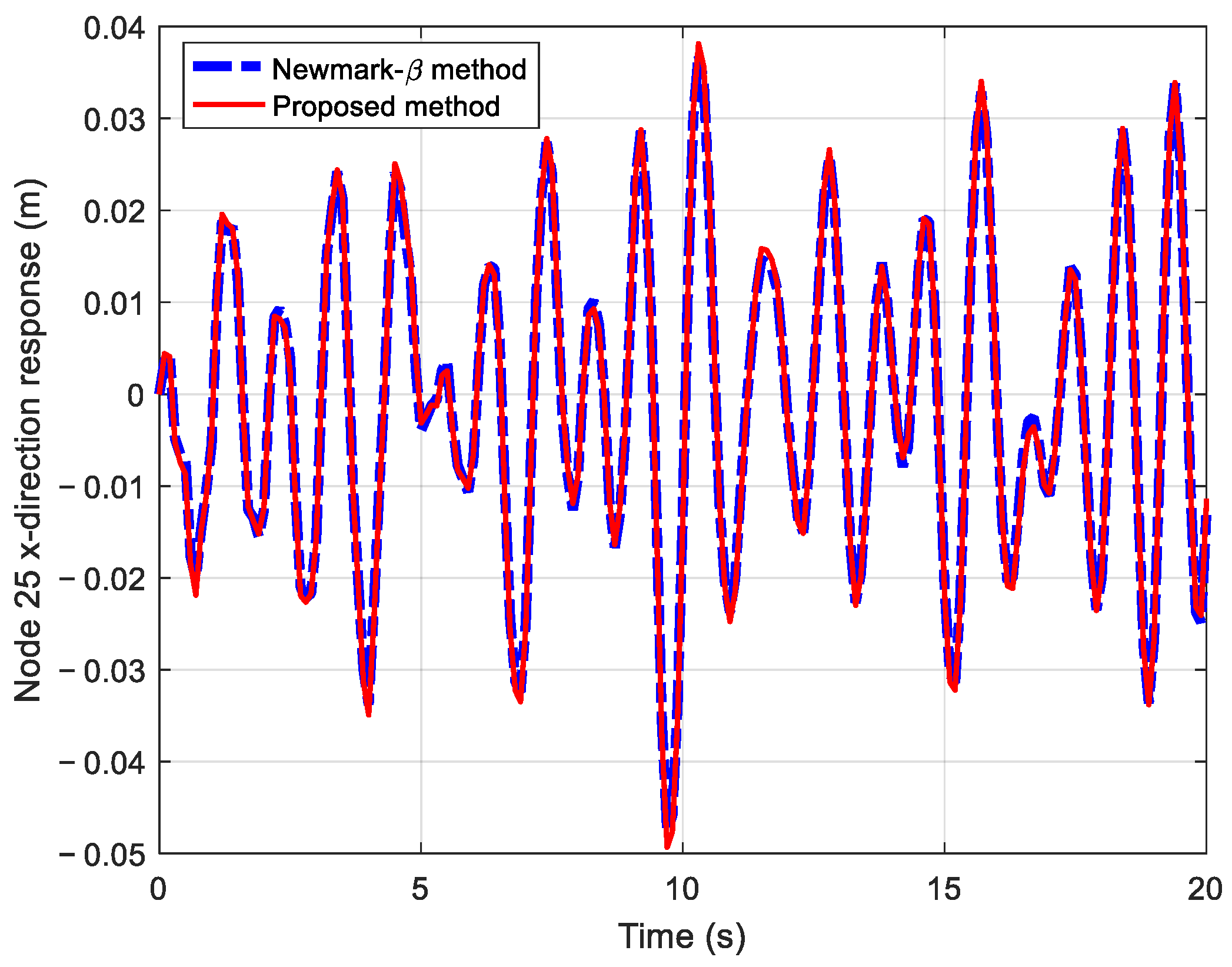
3.2.2. Dynamic Response Analysis
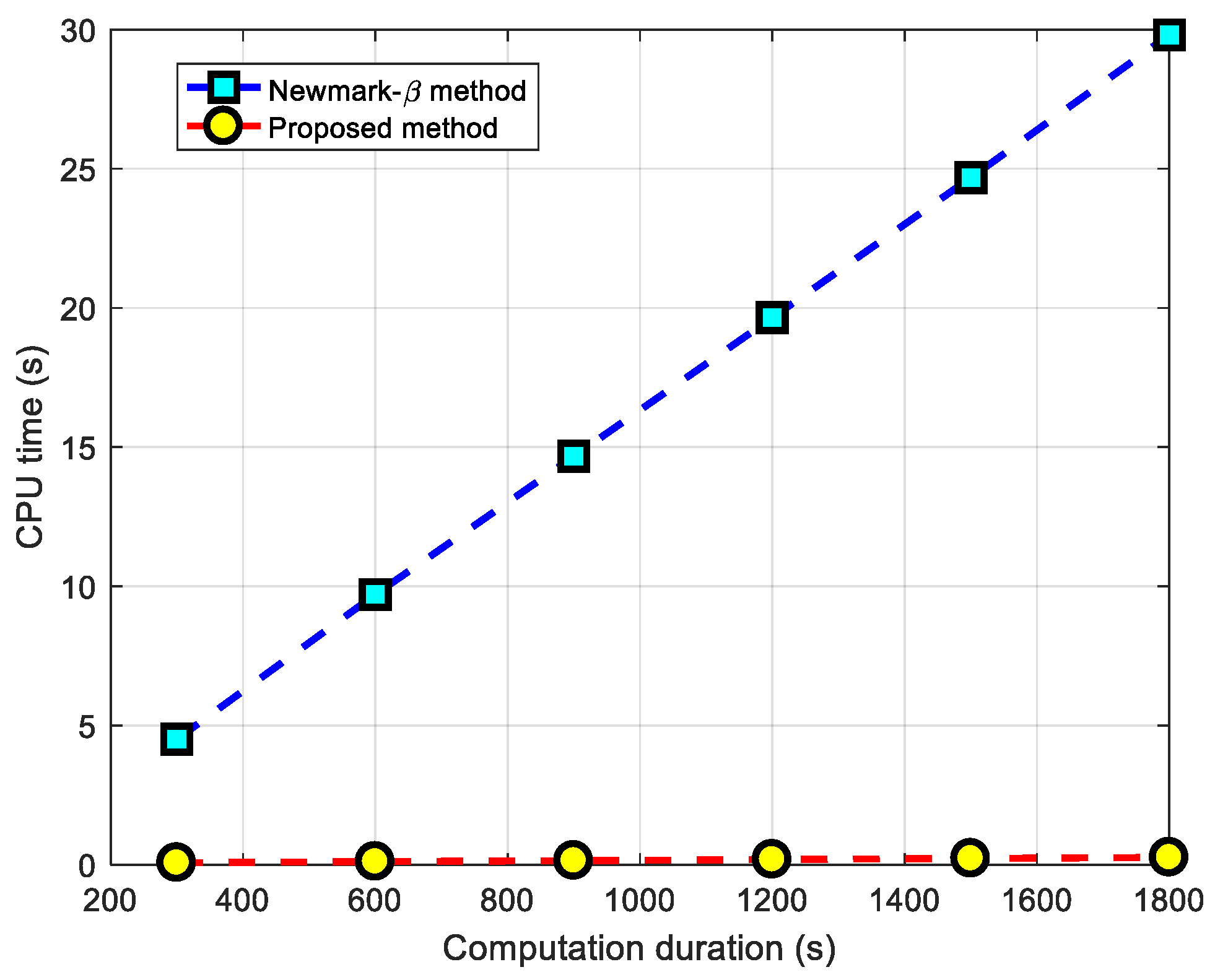
3.2.3. Analysis of Computational Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| , , | mass matrix, damping matrix, stiffness matrix |
| , , | displacement, velocity, acceleration |
| external force acting on the structure | |
| , , | discrete displacement, velocity, acceleration |
| discrete external force | |
| , | parameters of Newmark-β method |
| , | Rayleigh damping coefficients |
| modal shape matrix | |
| , , | displacement, velocity, acceleration in modal space coordinate |
| , , | modal mass, damping, stiffness |
| , and | diagonal elements of , and |
| , and | the elements of vectors , and |
| jth row and ith column element of | |
| degree of freedom | |
| imaginary unit | |
| and | Fourier transform of and |
| and | natural frequency and external load frequency |
| damping ratio | |
| and | lower and upper limits of the wave load spectrum |
| DOF | degree of freedom |
| RMS | root mean square error |
References
- Alassi, A.; Banales, S.; Ellabban, O.; Adam, G.; Maciver, C. HVDC Transmission: Technology Review, Market Trends and Future Outlook. Renew. Sust. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Wang, H.J.; Liu, C.; Guo, Y.H.; Zhao, Y.; Li, X.Y.; Lian, J.J. Experimental and numerical research on the wet-towing of wide-shallow bucket jacket foundation for offshore substation. Ocean Eng. 2023, 175, 114126. [Google Scholar] [CrossRef]
- Kelma, S.; Schmoor, K.A.; Goretzka, J.; Hansen, M. Safety aspects for support structures of offshore wind turbines. Bautechnik 2014, 91, 543–553. [Google Scholar] [CrossRef]
- Solland, G.; Johansen, A. Design recommendations for grouted pile sleeve connections. Mar. Struct. 2018, 60, 1–14. [Google Scholar] [CrossRef]
- Jalbi, S.; Bhattacharya, S. Concept design of jacket foundations for offshore wind turbines in 10 steps. Soil Dynam. Earthq. Eng. 2020, 139, 106357. [Google Scholar] [CrossRef]
- Macangus-Gerrard, G. Offshore Electrical Engineering Manual, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 343–344. [Google Scholar]
- Schoefs, F.; Oumouni, M.; Ahmadivala, M.; Luxcey, N.; Dupriez-Robin, F.; Guerin, P. Unified System Analysis for Time-Variant Reliability of a Floating Offshore Substation. J. Mar. Sci. Eng. 2023, 11, 1924. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, H.Y.; Tao, A.; Wang, K.; Su, K. Study on Structural Dynamic Response of Offshore Booster Station under Combined Wind, Wave and Current Loads. Water Power 2022, 48, 104640. [Google Scholar]
- Wang, Y.F.; Xu, C.H.; Yu, M.Z.; Huang, Z.C. Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters. Sustainability 2024, 16, 3385. [Google Scholar] [CrossRef]
- Klose, M.; Dalhoff, P.; Argyriadis, K. Integrated load and strength analysis for offshore wind turbines with jacket structures. In Proceedings of the 17th (2007) International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 2nd ed.; McGraw-Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
- Bishop, R.E.D.; Price, W.G. The generalized antisymmetric fluid forces applied to a ship in a seaway. Int. Shipbuild. Prog. 1977, 24, 3–14. [Google Scholar] [CrossRef]
- Jin, W.L.; Zhen, Z.S.; Zou, D.Q.; Li, H.B. Hybrid method for stochastic response analysis of offshore platform structures. Ocean Eng. 2001, 19, 14–19. [Google Scholar]
- Karadenia, H. Spectral analysis of offshore structures under combined wave and earthquake loadings. In Proceedings of the Ninth International Offshore and Polar Engineering Conference, Brest, France, 30 May–5 June 1999. [Google Scholar]
- Lu, H.C.; Fan, T.H.; Li, X.C.; Chen, C.H. A rapid time-continuous response analysis algorithm for offshore structures by combination of modal superposition and complex exponential decomposition. Ocean Eng. 2021, 234, 109272. [Google Scholar] [CrossRef]
- Craig, R.R.; Kurdila, A.J., Jr. Fundamentals of Structural Dynamics, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Veletsos, A.S.; Ventura, C.E. Efficient analysis of dynamic response of linear systems. Earthq. Eng. Struct. Dynam. 1984, 12, 521–536. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Ventura, C.E. Dynamic analysis of structures by the DFT method. J. Struct. Eng. 1985, 111, 2625–2642. [Google Scholar] [CrossRef]
- Mansur, W.J.; Carrer, J.A.M.; Ferreira, W.G.; Claret de Gouveia, A.M.; Venancio-Filho, F. Time-segmented frequency-domain analysis for non-linear multi-degree-of-freedom structural systems. J. Sound. Vib. 2000, 237, 457–475. [Google Scholar] [CrossRef][Green Version]
- Mansur, W.J.; Soares, D., Jr.; Ferro, M.A.C. Initial conditions in frequency-domain analysis: The FEM applied to the scalar wave equation. J. Sound. Vib. 2004, 270, 767–780. [Google Scholar] [CrossRef]
- Lee, U.; Kim, S.; Cho, J. Dynamic analysis of the linear discrete dynamic systems subjected to the initial conditions by using an FFT-based spectral analysis method. J. Sound. Vib. 2005, 288, 293–306. [Google Scholar] [CrossRef]
- Liu, F.S.; Li, H.J.; Wang, W.Y.; Liang, B.C. Initial-condition consideration by transferring and loading reconstruction for the dynamic analysis of linear structures in the frequency domain. J. Sound Vib. 2015, 336, 164–178. [Google Scholar] [CrossRef]
- Huang, W.P.; Bai, X.L. Structural Dynamic; Modern Education Press: Beijing, China, 2010. [Google Scholar]
- Rayleigh, L. Theory of Sound; Dover: New York, NY, USA, 1945; Volume 1. [Google Scholar]





| Component | ||||
|---|---|---|---|---|
| 1 | 150 | 0 | 10.5 | |
| 2 | 120 | 0.02 | 5.6 | |
| 3 | 200 | 0.05 | 12.8 | |
| 4 | 50 | 0.01 | 15.2 | |
| 5 | 230 | 0 | 18.5 |
| Order | |||
|---|---|---|---|
| 1 | 1 | 2.9058 | 2.9058 × 104 |
| 2 | 1 | 25.1489 | 2.5149 × 105 |
| 3 | 1 | 64.5395 | 6.4540 × 105 |
| 4 | 1 | 112.0537 | 1.1205 × 106 |
| 5 | 1 | 156.8065 | 1.5681 × 106 |
| 6 | 1 | 188.5156 | 1.8855 × 106 |
| Order | Frequency (Hz) | Order | Frequency (Hz) |
|---|---|---|---|
| 1 | 1.0288 | 11 | 5.1716 |
| 2 | 1.0404 | 12 | 10.9985 |
| 3 | 1.1415 | 13 | 11.4781 |
| 4 | 2.0243 | 14 | 11.5403 |
| 5 | 2.1595 | 15 | 12.4356 |
| 6 | 2.1815 | 16 | 13.3252 |
| 7 | 2.1852 | 17 | 15.4094 |
| 8 | 2.1914 | 18 | 15.5904 |
| 9 | 4.4029 | 19 | 18.2234 |
| 10 | 4.4352 | 20 | 18.5487 |
| DOF | RMSE |
|---|---|
| Node 13, x-direction | 0.00024265 |
| Node 13, y-direction | 0.00018149 |
| Node 17, x-direction | 0.00048893 |
| Node 17, y-direction | 0.00033327 |
| Node 25, x-direction | 0.00096182 |
| Node 25, y-direction | 0.00044151 |
| Computation Duration (s) | Computation Time with Proposed Method (s) | Computation Time with Newmark-β Method (s) |
|---|---|---|
| 300 | 0.06764 | 4.5073 |
| 600 | 0.1102 | 9.7071 |
| 900 | 0.1445 | 14.6700 |
| 1200 | 0.1853 | 19.6525 |
| 1500 | 0.2226 | 24.6802 |
| 1800 | 0.2615 | 29.8099 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Lu, H.; Zhao, E. A Method for Dynamic Response Analysis of Offshore Substation Platform Foundations Based on Modal Truncation. J. Mar. Sci. Eng. 2025, 13, 750. https://doi.org/10.3390/jmse13040750
Chen J, Lu H, Zhao E. A Method for Dynamic Response Analysis of Offshore Substation Platform Foundations Based on Modal Truncation. Journal of Marine Science and Engineering. 2025; 13(4):750. https://doi.org/10.3390/jmse13040750
Chicago/Turabian StyleChen, Jiefeng, Hongchao Lu, and Enjin Zhao. 2025. "A Method for Dynamic Response Analysis of Offshore Substation Platform Foundations Based on Modal Truncation" Journal of Marine Science and Engineering 13, no. 4: 750. https://doi.org/10.3390/jmse13040750
APA StyleChen, J., Lu, H., & Zhao, E. (2025). A Method for Dynamic Response Analysis of Offshore Substation Platform Foundations Based on Modal Truncation. Journal of Marine Science and Engineering, 13(4), 750. https://doi.org/10.3390/jmse13040750







