A New Energy Management Strategy Supported by Reinforcement Learning: A Case Study of a Multi-Energy Cruise Ship
Abstract
1. Introduction
1.1. Background
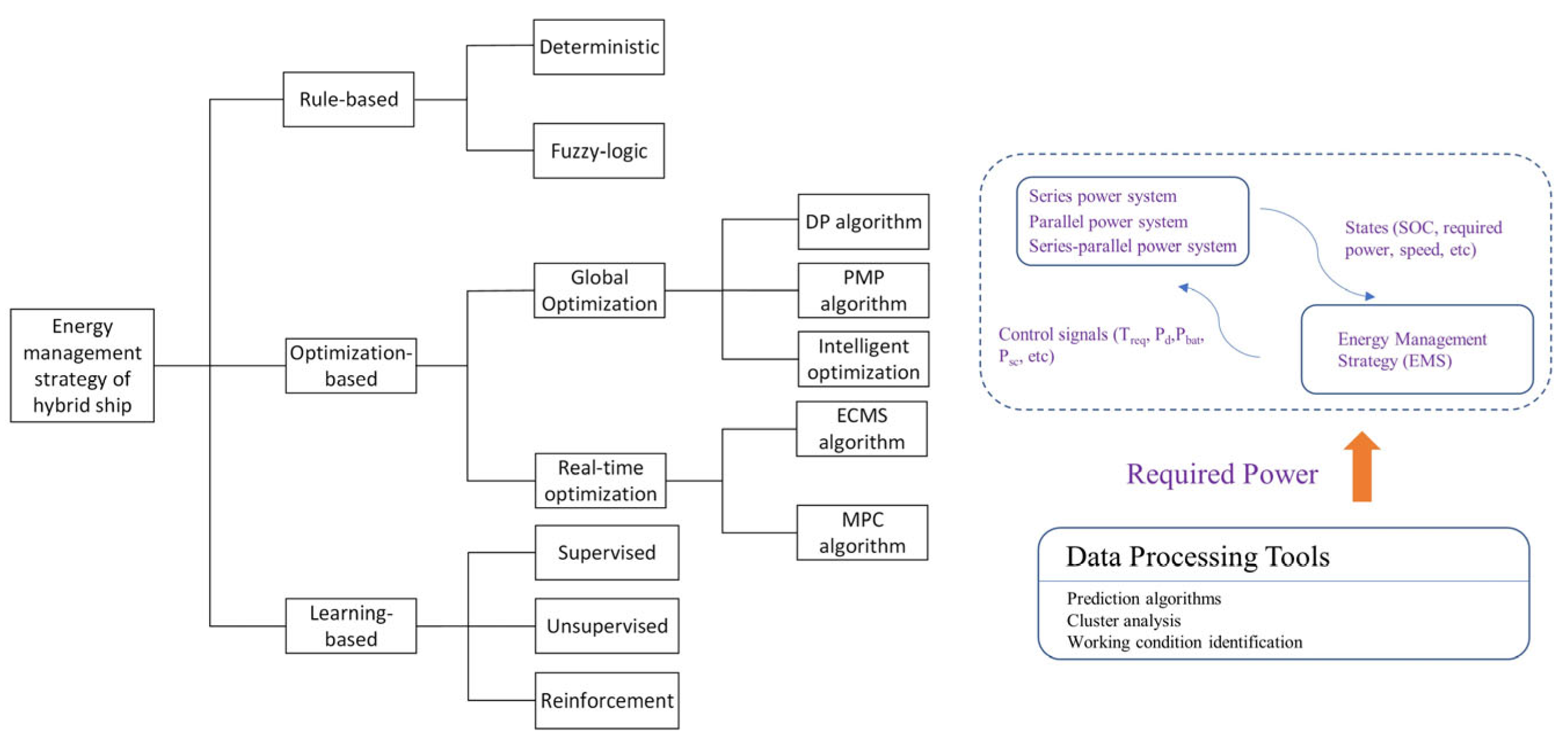
1.2. Literature Review
1.3. Motivation and Contributions
- (1)
- The action space of reinforcement learning algorithms is predominantly discrete, with action values that will inevitably result in discretization errors. One traditional solution is to enhance the precision of discretization. However, this improvement in precision may result in a significant increase in dimensional complexity, which could negatively impact the calculation speed. This limitation significantly constrains the applicability of reinforcement learning algorithms in the energy management of hybrid ships.
- (2)
- Existing energy management strategies are less likely to utilize the output power of multiple diesel generator sets as an action space, thereby preventing the coordinated operation of multiple generator sets and energy storage units to achieve the objective of optimal fuel efficiency.
- (3)
- The most prevalent approach to addressing intricate constraints during maritime navigation is the penalty function methodology. However, when there are multiple constraints, it is of the utmost importance to select the most appropriate penalty coefficients.
- (1)
- Combining the structure of deep learning and the idea of reinforcement learning and synthesizing the advantages of both, cutting-edge deep reinforcement learning algorithms are introduced in the energy management problem of hybrid ships. Energy management strategies such as DDPG based on the actor–critic framework are proposed for the control problem on continuous state–action space.
- (2)
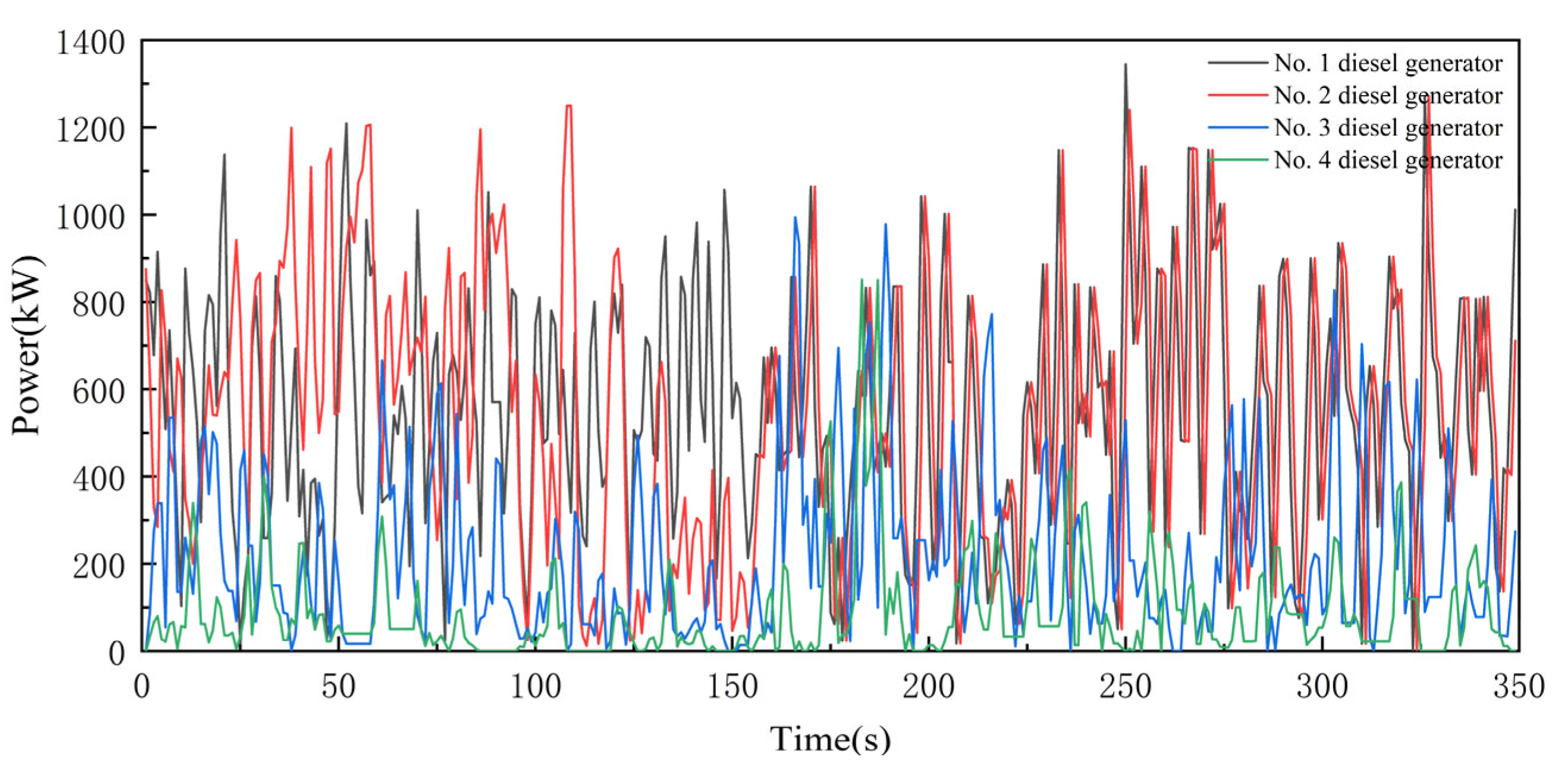
- Multiple energy sources increase the complexity of the system, and it is a key problem for hybrid ships to rationally distribute the power output of each energy unit and improve the fuel economy of the whole ship without jeopardizing the healthy life of the components. Therefore, the strategy proposed in this study considers the cooperative work of multiple diesel generator sets and supercapacitors.
- (3)
- Through comparative analysis, the superiority of the DDPG algorithm to other reinforcement learning algorithms and rule-based strategies, as well as real fuel consumption data of real ships, is concluded.
2. Mathematical Model of Hybrid Power System
2.1. Object Ship
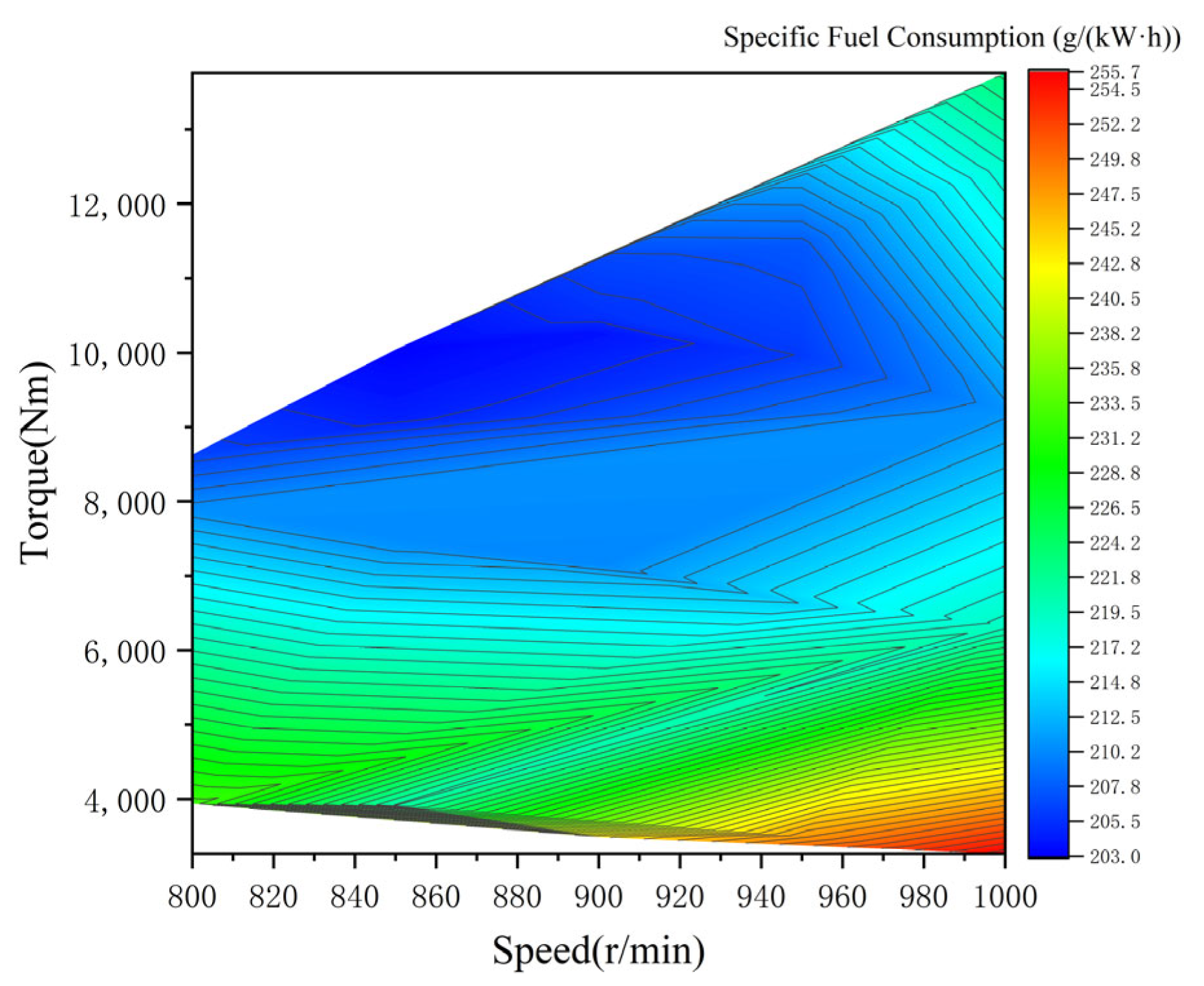
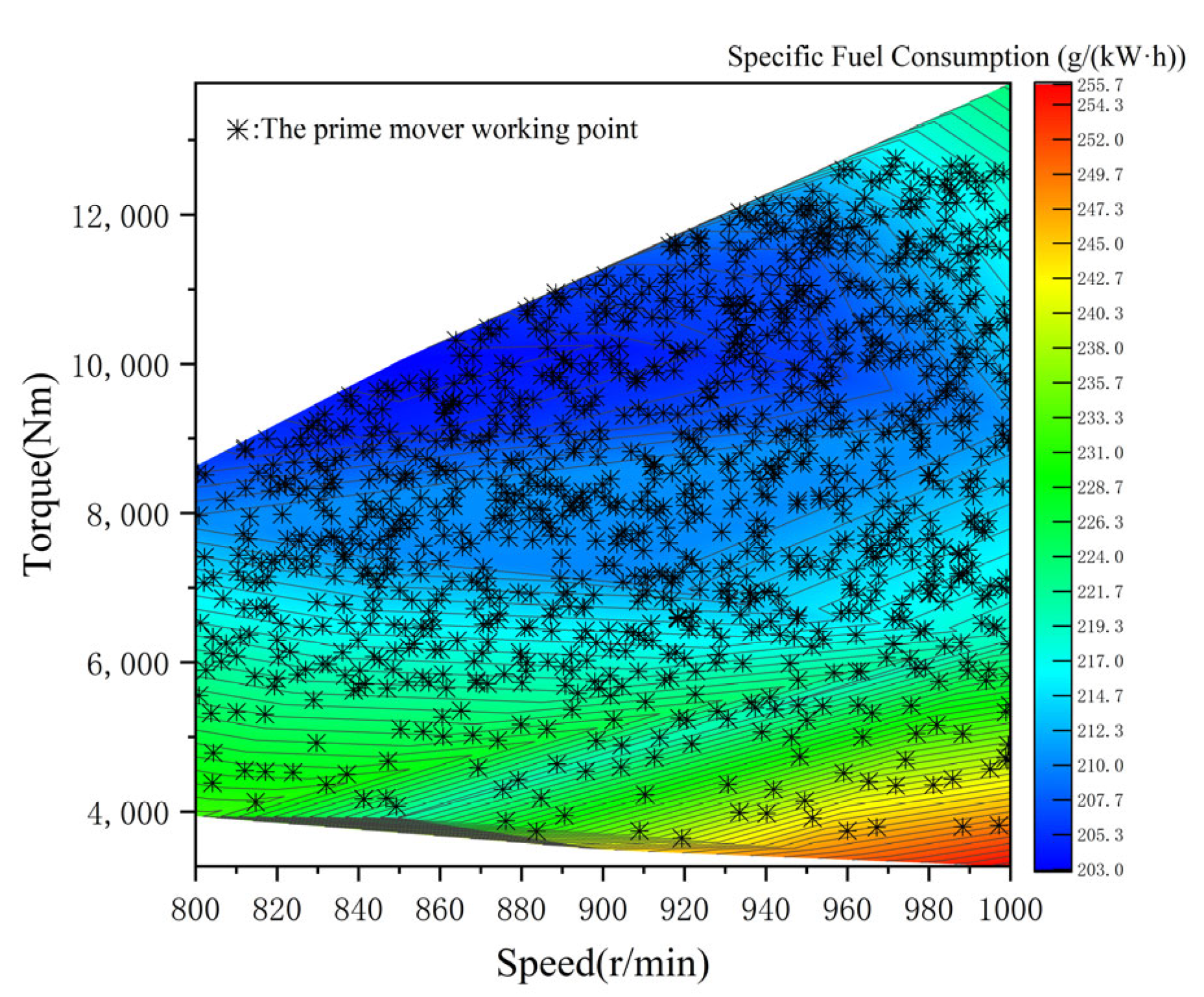
2.2. Modeling of Diesel Generator
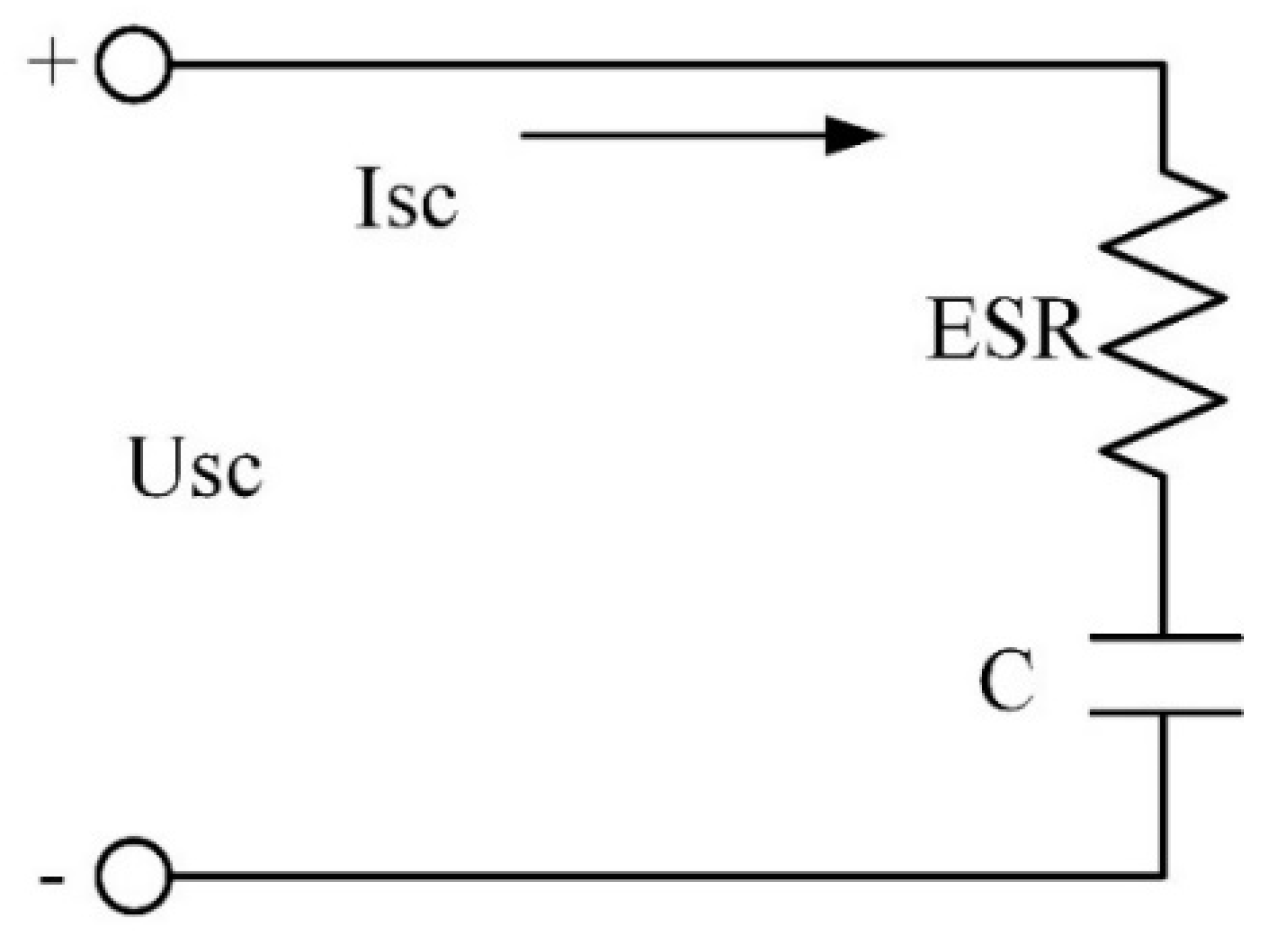
2.3. Modeling of Supercapacitor
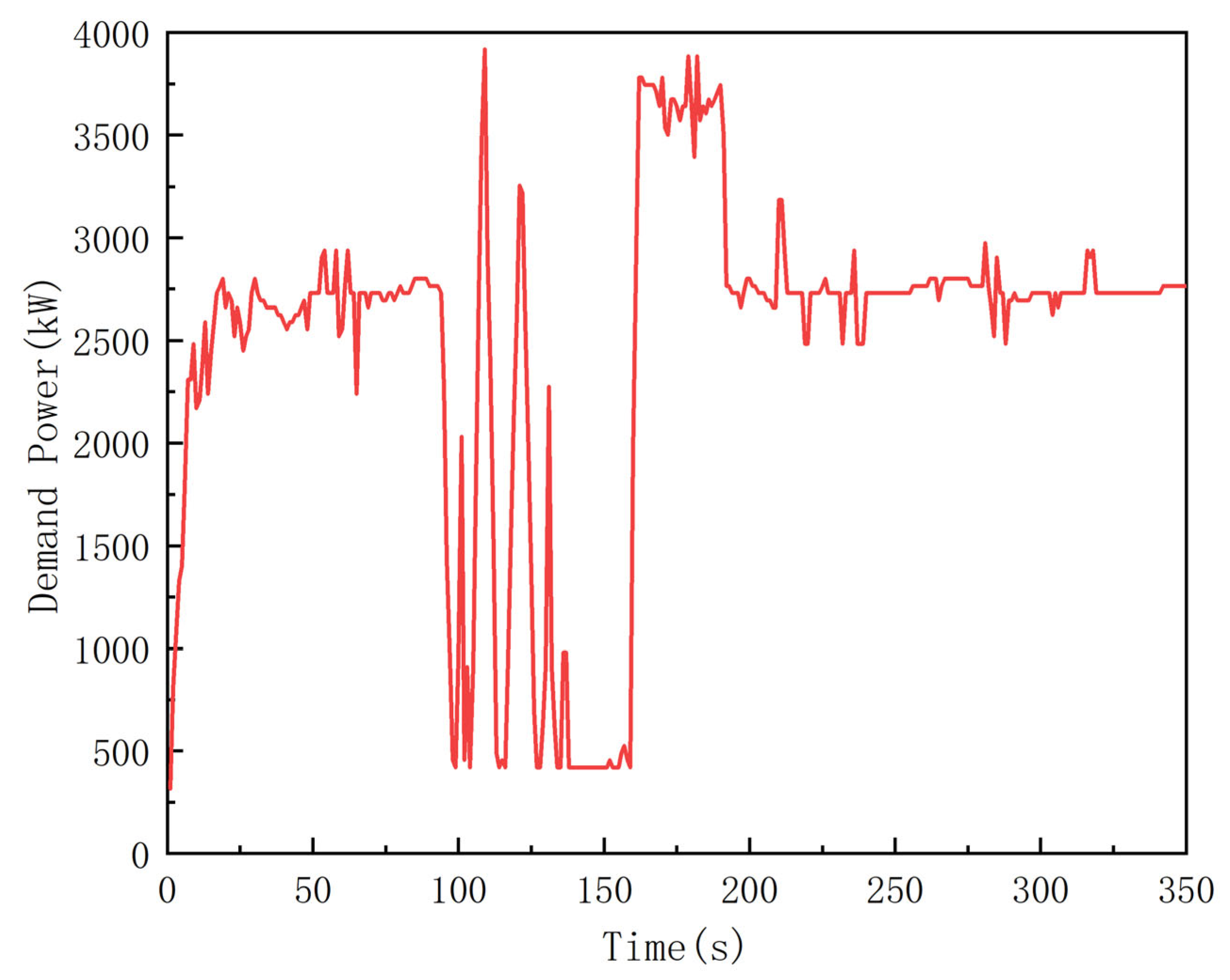
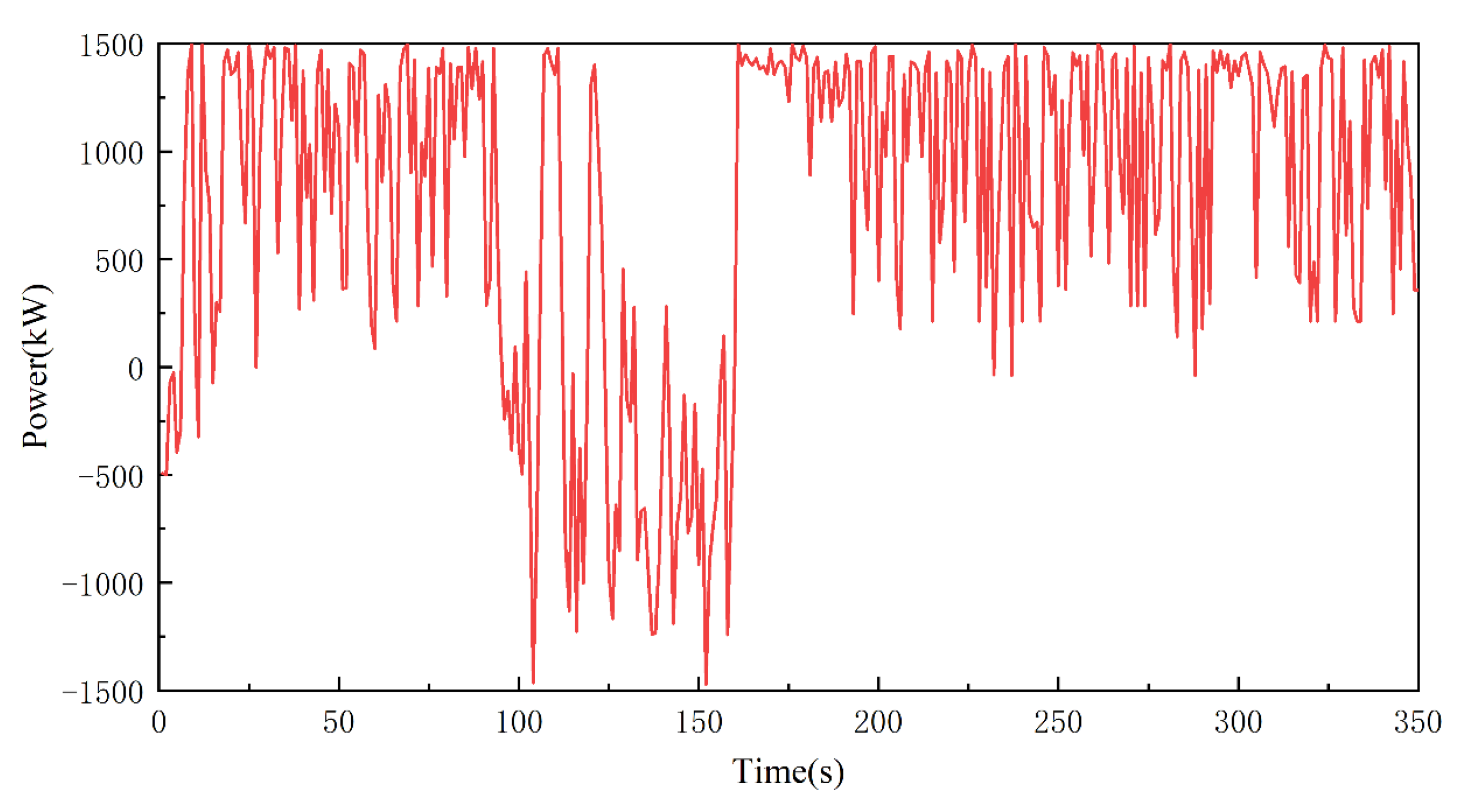
2.4. Modeling of Load
3. Proposed Energy Management Strategy
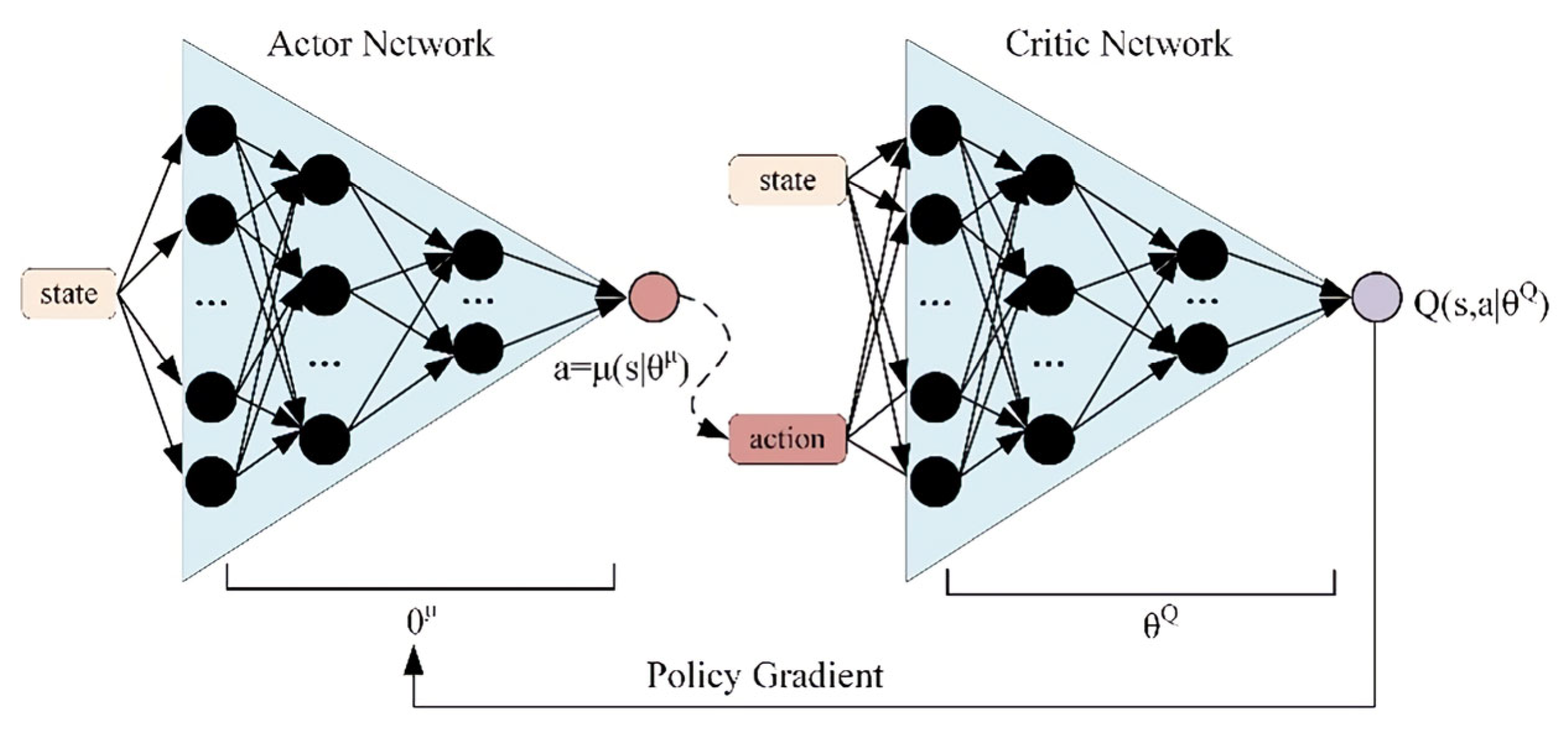
3.1. DDPG Algorithm
- (1)
- The loss function takes the partial derivative with respect to the network parameters ;
- (2)
- ;
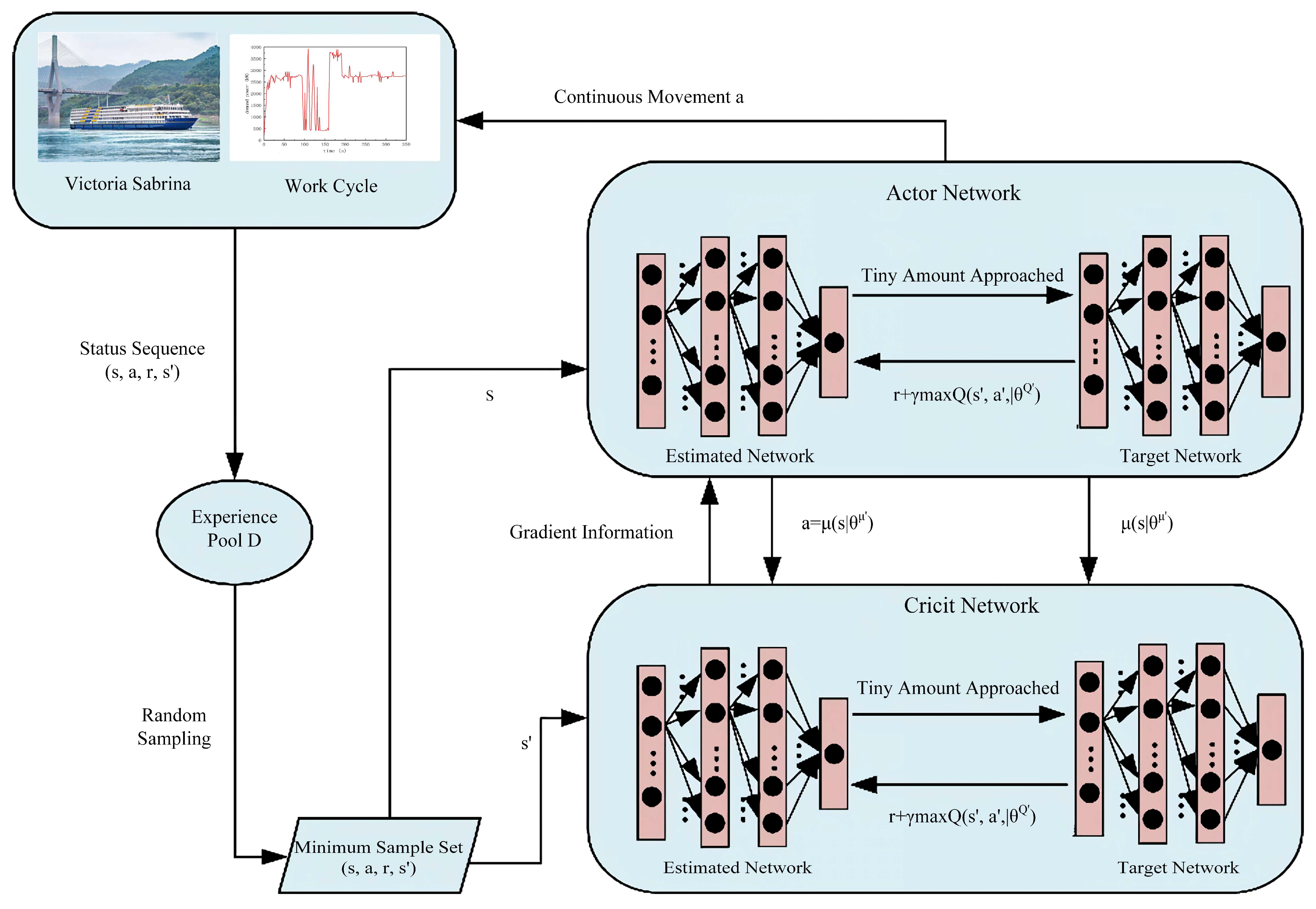
3.2. Energy Management Strategy Based on DDPG Algorithm
- (1)
- The state of the system at the next instance depends only on the state of the system at the current moment and on the action taken, which means that the system has Markovian property.
- (2)
- The optimization objective of the system is not the optimum at a specific moment in time. It is the cumulative target optimum of the entire process.
- (3)
- The system does not necessarily need a specific model in which the system controller only needs to be aware of the current system state and the reward for the action to be taken.
- (1)
- The power demand of the system at the next instance and the SOC of the supercapacitor are constantly changing. In addition, the system state at the next instance is only related to the system controller action at the current moment.
- (2)
- The optimization objective of the energy management problem is to minimize the fuel consumption of the ship during the entire journey rather than only at a certain time.
- (3)
- The controller cannot predict the power demand of the ship during its journey. The currently consumed fuel volume can be determined, and the system enters the next state after the current action has been executed.
- (1)
- State: The selection of the state space S directly affects the optimization effect of the reinforcement learning strategy and the computation speed of the reinforcement learning algorithm. In this study, the power demand , SOC of the supercapacitor, and running time t of the hybrid ship during the entire operation were considered the state variables of reinforcement learning. The SOC range is [0.3, 0.8] according to the data provided by the manufacturer.
- (2)
- Action: For the series-connected ship hybrid system investigated in this study, the system state SOC and power demand must be able to make a state transfer after an action. The hybrid system is rewarded according to this action. Therefore, the action space in the presented hybrid ship energy management strategy based on the DDPG algorithm is set to the output power ( of each of the four diesel generator prime movers:where
- (3)
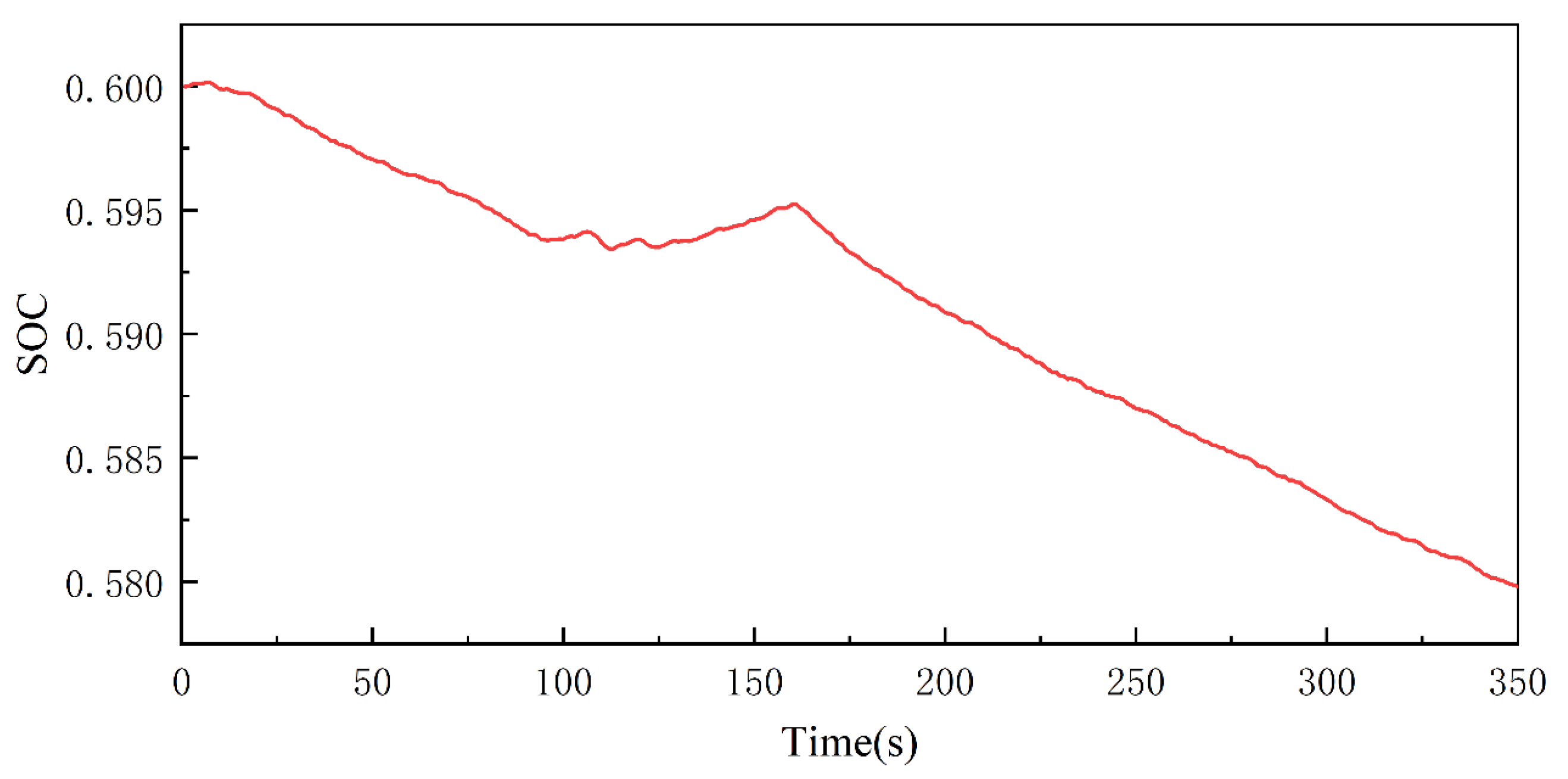
- Reward Function: The objective of the reinforcement learning algorithm is to determine the optimal set of strategies that maximize the cumulative discount reward. For the energy management strategy of the series ship hybrid system, the optimization goal is to minimize the fuel consumption of the entire ship. Therefore, the reward function is set to the quantity associated with the sum of the specific fuel consumption and power consumption of the supercapacitor at a given moment.where represents the weight of the power retention of the supercapacitor, which is similar to the weight factor of the equivalent fuel consumption. The is the capacity expected to be maintained by the supercapacitor (it was set to 0.6). The SOC reference level of 0.6 was chosen to optimally balance energy availability for abrupt load fluctuations, component lifespan preservation (avoiding overcharging > 0.8 or deep discharge < 0.3 per manufacturer guidelines), and system efficiency gain. In engineering practice, to reduce the fuel consumption of a ship during navigation, the previously presented sum is expected to be as small as possible. In addition, the supercapacitor is expected to work within its reasonable operating range. Because the aim of reinforcement learning is to obtain the highest possible reward, the tanh function was introduced to process the sum mathematically. The processed reward function is expressed as follows:The reward function expects the charge state of the supercapacitor to remain within the allowed operation interval . If the supercapacitor charge state exceeds this interval, the agent gains a negative reward. Otherwise, the reward is positive and related to the sum of the specific fuel consumption and supercapacitor charge consumption.
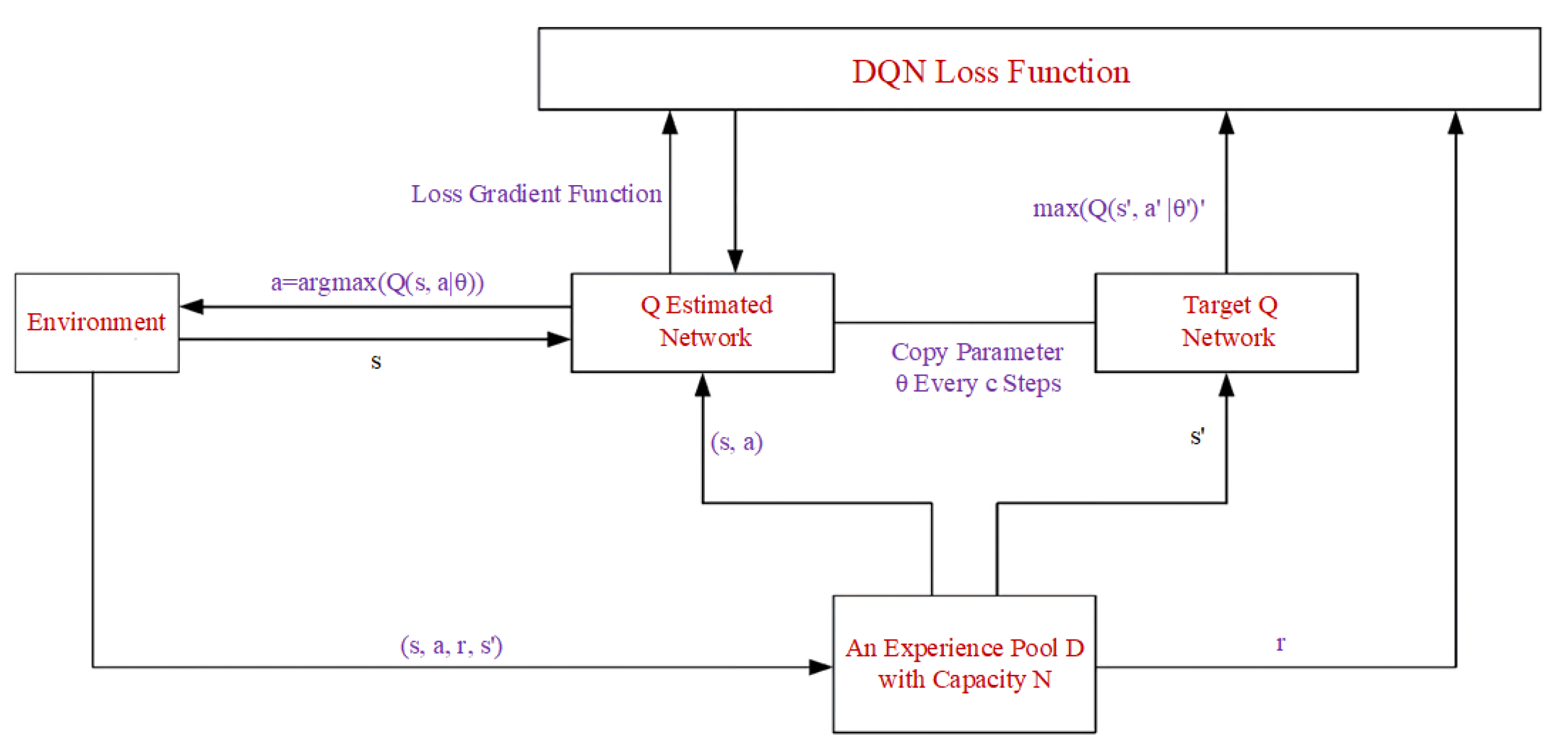
3.3. Comparative Energy Management Strategy
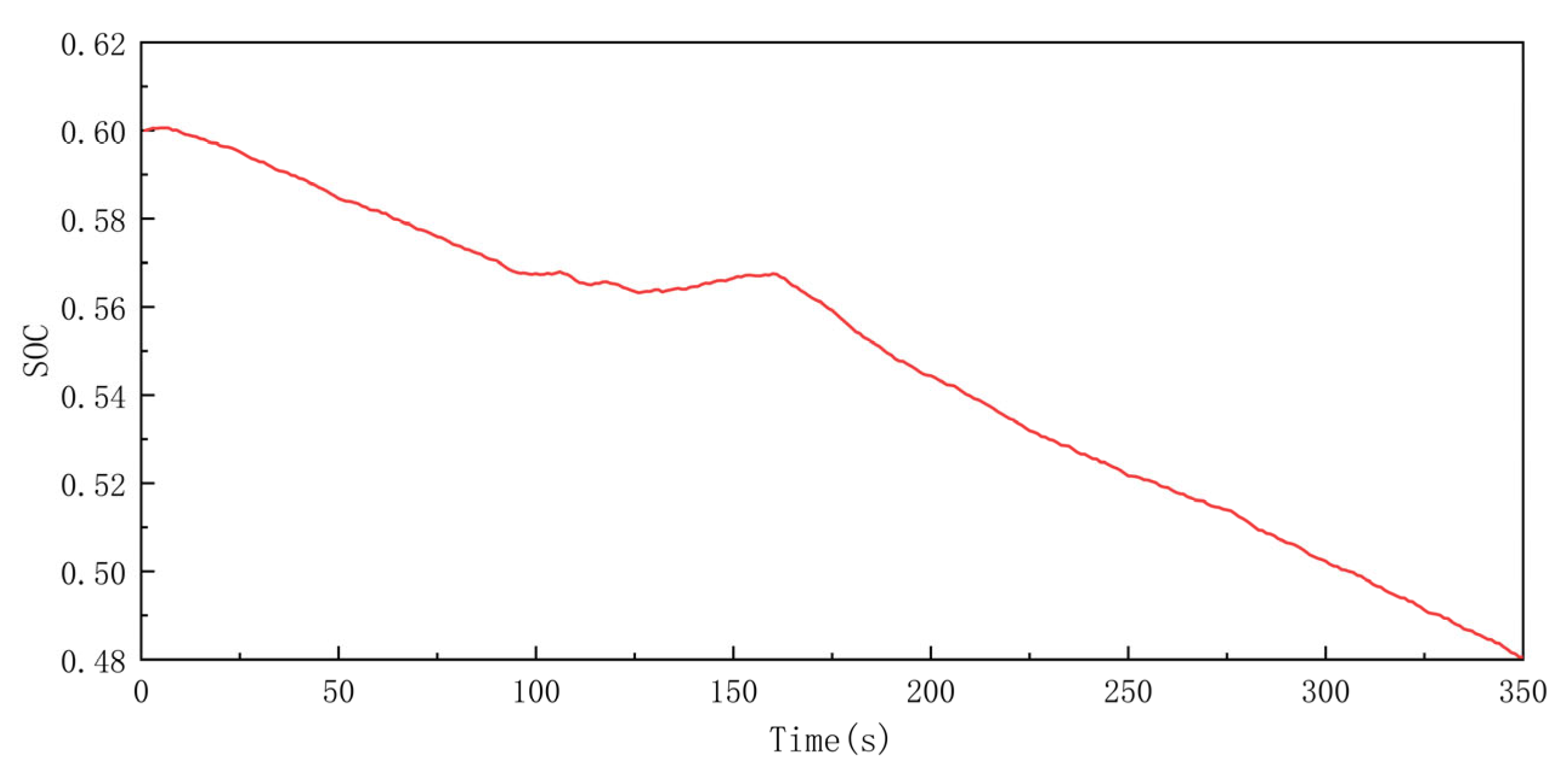
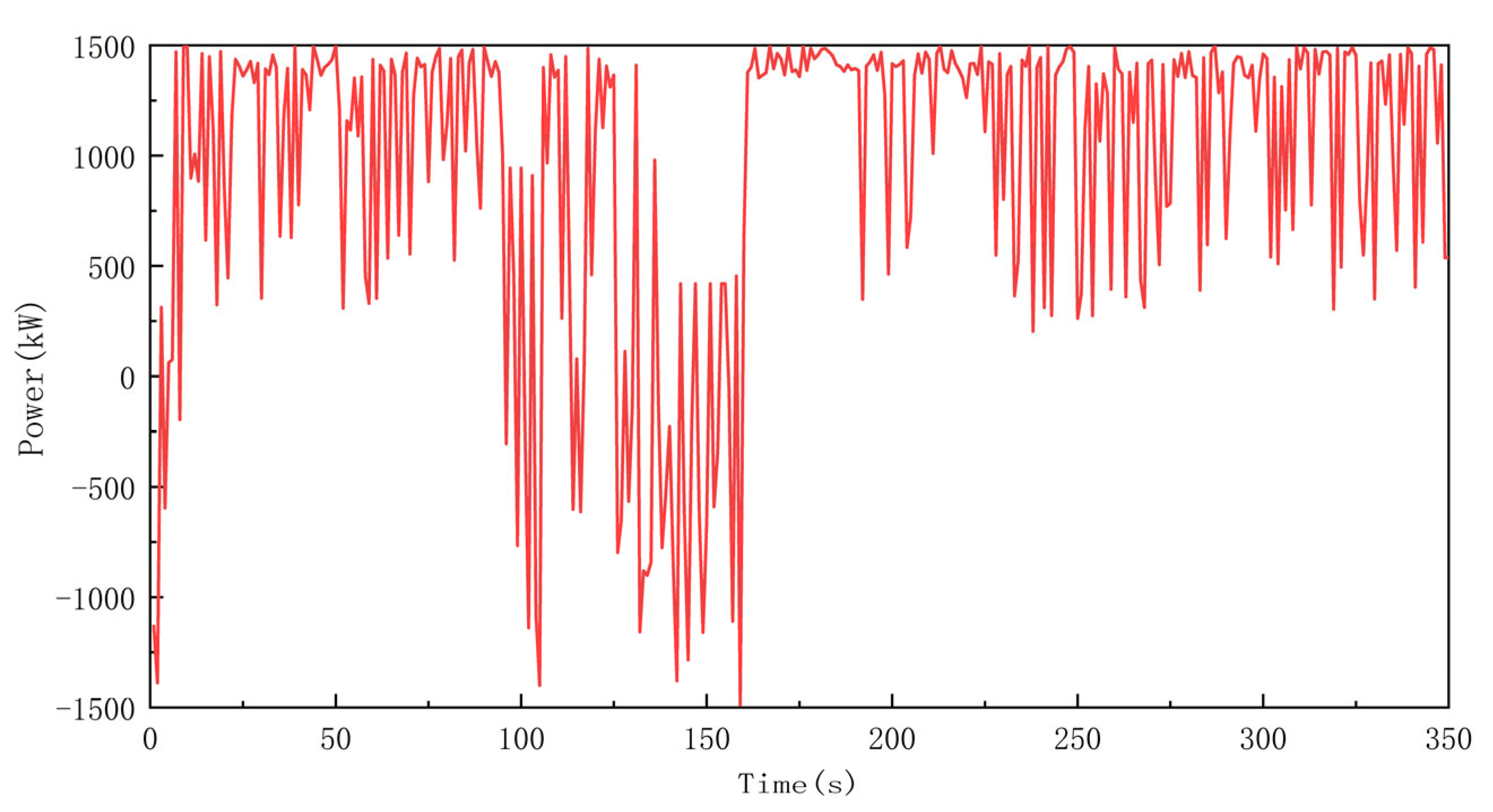
4. Simulation Results and Analysis
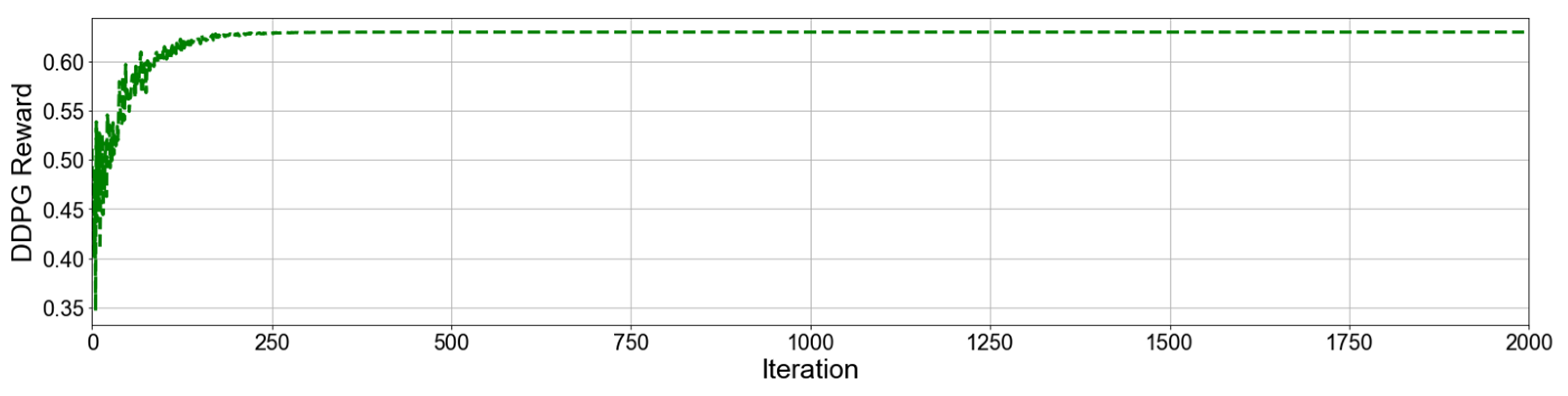
4.1. Analysis of DDPG Algorithm
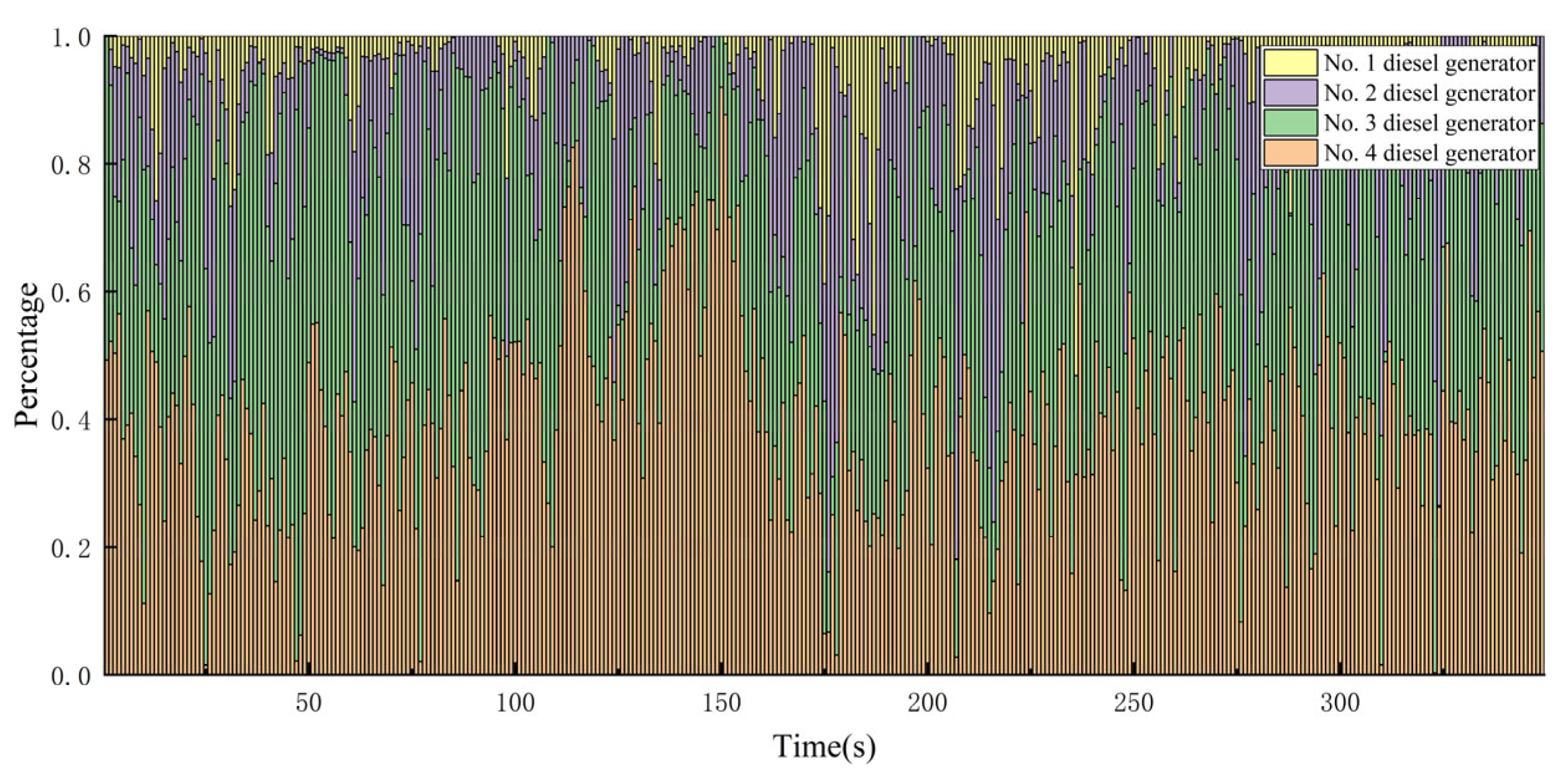
4.2. Comparative Analysis
5. Conclusions
- Both DDPG and DQN algorithms converge stably. Although the convergence speed of the DDPG algorithm is slightly lower than that of the DQN algorithm, the energy management strategy based on the DDPG algorithm obtains higher rewards. This indicates that the DDPG algorithm is more suitable for the control of continuous systems. The output power fluctuations of the diesel generator under the DQN algorithm are more pronounced.
- In terms of fuel economy, the rule-based energy management strategy performed worst. The average specific fuel consumption and total fuel consumption were the highest. However, the strategy was still more fuel-efficient than the real ship data, with a reduction in the total fuel consumption of approximately 5.5% compared to that of the real ship. The energy management strategy based on the DDPG algorithm had the lowest average specific fuel consumption and total fuel consumption, with a 15.8% reduction in the total fuel consumption compared to that of the real ship. This is followed by the energy management strategy based on the DQN algorithm, which reduced the total fuel consumption by 12.6% compared to that of the real ship. This result is consistent with the characteristics of the different energy management strategies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uyan, E.; Atlar, M.; Gürsoy, O. Energy Use and Carbon Footprint Assessment in Retrofitting a Novel Energy Saving Device to a Ship. J. Mar. Sci. Eng. 2024, 12, 1879. [Google Scholar] [CrossRef]
- Du, Z.; Chen, Q.; Guan, C.; Chen, H. Improvement and Optimization Configuration of Inland Ship Power and Propulsion System. J. Mar. Sci. Eng. 2023, 11, 135. [Google Scholar] [CrossRef]
- Tang, D.; Tang, H.; Yuan, C.; Dong, M.; Diaz-Londono, C.; Tinaiero, G.D.A.; Guerrero, J.M.; Zio, E. Economic and resilience-oriented operation of coupled hydrogen-electricity energy systems at ports. Appl. Energy 2025, 390C, 125825. [Google Scholar] [CrossRef]
- Guo, X.; Lang, X.; Yuan, Y.; Tong, L.; Shen, B.; Long, T.; Mao, W. Energy Management System for Hybrid Ship: Status and Perspectives. Ocean Eng. 2024, 310, 118638. [Google Scholar] [CrossRef]
- Gao, Y.; Tan, Y.; Jiang, D.; Sang, P.; Zhang, Y.; Zhang, J. An Adaptive Prediction Framework of Ship Fuel Consumption for Dynamic Maritime Energy Management. J. Mar. Sci. Eng. 2025, 13, 409. [Google Scholar] [CrossRef]
- Rindone, C. AIS Data for Building a Transport Maritime Network: A Pilot Study in the Strait of Messina (Italy). In Computational Science and Its Applications—ICCSA 2024 Workshops; Springer Nature: Cham, Switzerland, 2024; pp. 213–226. [Google Scholar] [CrossRef]
- Shen, D.; Lim, C.-C.; Shi, P. Fuzzy Model Based Control for Energy Management and Optimization in Fuel Cell Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 14674–14688. [Google Scholar] [CrossRef]
- Seng, U.K.; Malik, H.; García Márquez, F.P.; Alotaibi, M.A.; Afthanorhan, A. Fuzzy Logic-Based Intelligent Energy Management Framework for Hybrid PV-Wind-Battery System: A Case Study of Commercial Building in Malaysia. J. Energy Storage 2024, 102, 114109. [Google Scholar] [CrossRef]
- Nivolianiti, E.; Karnavas, Y.L.; Charpentier, J.-F. Energy Management of Shipboard Microgrids Integrating Energy Storage Systems: A Review. Renew. Sustain. Energy Rev. 2024, 189, 114012. [Google Scholar] [CrossRef]
- Li, L.; Yang, C.; Zhang, Y.; Zhang, L.; Song, J. Correctional DP-Based Energy Management Strategy of Plug-In Hybrid Electric Bus for City-Bus Route. IEEE Trans. Veh. Technol. 2015, 64, 2792–2803. [Google Scholar] [CrossRef]
- Upadhyaya, A.; Mahanta, C. Optimal Online Energy Management System for Battery-Supercapacitor Electric Vehicles Using Velocity Prediction and Pontryagin’s Minimum Principle. IEEE Trans. Veh. Technol. 2025, 74, 2652–2666. [Google Scholar] [CrossRef]
- Kanellos, F.D. Optimal Power Management With GHG Emissions Limitation in All-Electric Ship Power Systems Comprising Energy Storage Systems. IEEE Trans. Power Syst. 2014, 29, 330–339. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, Y.; Li, X.; Liu, X.; Yan, J. Power Management Optimization in Plug-in Hybrid Electric Vehicles Subject to Uncertain Driving Cycles. eTransportation 2020, 3, 100029. [Google Scholar] [CrossRef]
- Ou, K.; Yuan, W.-W.; Choi, M.; Yang, S.; Jung, S.; Kim, Y.-B. Optimized Power Management Based on Adaptive-PMP Algorithm for a Stationary PEM Fuel Cell/Battery Hybrid System. Int. J. Hydrogen Energy 2018, 43, 15433–15444. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Geertsma, R.D.; Boonen, E.J.; Visser, K.; Negenborn, R.R. Ship Energy Management for Hybrid Propulsion and Power Supply with Shore Charging. Control Eng. Pract. 2018, 76, 133–154. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Q.; Gao, D.; Shi, W.; Yu, W. Two-Level Model Predictive Control Energy Management Strategy for Hybrid Power Ships with Hybrid Energy Storage System. J. Energy Storage 2022, 52, 104763. [Google Scholar] [CrossRef]
- Kofler, S.; Du, Z.P.; Jakubek, S.; Hametner, C. Predictive Energy Management Strategy for Fuel Cell Vehicles Combining Long-Term and Short-Term Forecasts. IEEE Trans. Veh. Technol. 2024, 73, 16364–16374. [Google Scholar] [CrossRef]
- Song, T.; Fu, L.; Zhong, L.; Fan, Y.; Shang, Q. HP3O Algorithm-Based All Electric Ship Energy Management Strategy Integrating Demand-Side Adjustment. Energy 2024, 295, 130968. [Google Scholar] [CrossRef]
- Jung, W.; Chang, D. Deep Reinforcement Learning-Based Energy Management for Liquid Hydrogen-Fueled Hybrid Electric Ship Propulsion System. J. Mar. Sci. Eng. 2023, 11, 2007. [Google Scholar] [CrossRef]
- Huotari, J.; Ritari, A.; Ojala, R.; Vepsäläinen, J.; Tammi, K. Q-Learning Based Autonomous Control of the Auxiliary Power Network of a Ship. IEEE Access 2019, 7, 152879–152890. [Google Scholar] [CrossRef]
- Xiao, H.; Fu, L.; Shang, C.; Bao, X.; Xu, X.; Guo, W. Ship Energy Scheduling with DQN-CE Algorithm Combining Bi-Directional LSTM and Attention Mechanism. Appl. Energy 2023, 347, 121378. [Google Scholar] [CrossRef]
- Fu, J.; Sun, D.; Peyghami, S.; Blaabjerg, F. A Novel Reinforcement-Learning-Based Compensation Strategy for DMPC-Based Day-Ahead Energy Management of Shipboard Power Systems. IEEE Trans. Smart Grid 2024, 15, 4349–4363. [Google Scholar] [CrossRef]
- Chen, W.; Tai, K.; Lau, M.W.S.; Abdelhakim, A.; Chan, R.R.; Kåre Ådnanes, A.; Tjahjowidodo, T. Optimal Power and Energy Management Control for Hybrid Fuel Cell-Fed Shipboard DC Microgrid. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14133–14150. [Google Scholar] [CrossRef]
- Rudolf, T.; Schürmann, T.; Schwab, S.; Hohmann, S. Toward Holistic Energy Management Strategies for Fuel Cell Hybrid Electric Vehicles in Heavy-Duty Applications. Proc. IEEE 2021, 109, 1094–1114. [Google Scholar] [CrossRef]
- Hu, X.; Liu, T.; Qi, X.; Barth, M. Reinforcement Learning for Hybrid and Plug-In Hybrid Electric Vehicle Energy Management: Recent Advances and Prospects. IEEE Ind. Electron. Mag. 2019, 13, 16–25. [Google Scholar] [CrossRef]
- Li, Y.; Tang, D.; Yuan, C.; Diaz-Londono, C.; Agundis-Tinajero, G.D.; Guerrero, J.M. The Roles of Hydrogen Energy in Ports: Comparative Life-Cycle Analysis Based on Hydrogen Utilization Strategies. Int. J. Hydrogen Energy 2025, 106, 1356–1372. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, Y.; Tong, L. Research on Online Identification Method of Ship Condition Based on Improved DBN Algorithm. In Proceedings of the 2023 7th International Conference on Transportation Information and Safety (ICTIS), Xi’an, China, 4–6 August 2023; pp. 349–354. [Google Scholar] [CrossRef]
- Rekioua, D.; Mokrani, Z.; Kakouche, K.; Rekioua, T.; Oubelaid, A.; Logerais, P.O.; Ali, E.; Bajaj, M.; Berhanu, M.; Ghoneim, S.S.M. Optimization and Intelligent Power Management Control for an Autonomous Hybrid Wind Turbine Photovoltaic Diesel Generator with Batteries. Sci. Rep. 2023, 13, 21830. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Y.; Wang, L.; He, H. Obstacle Avoidance Strategy for an Autonomous Surface Vessel Based on Modified Deep Deterministic Policy Gradient. Ocean Eng. 2022, 243, 110166. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peng, J.; Zhang, H.; He, H. Deep Reinforcement Learning of Energy Management with Continuous Control Strategy and Traffic Information for a Series-Parallel Plug-in Hybrid Electric Bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Du, G.; Zou, Y.; Zhang, X.; Liu, T.; Wu, J.; He, D. Deep Reinforcement Learning Based Energy Management for a Hybrid Electric Vehicle. Energy 2020, 201, 117591. [Google Scholar] [CrossRef]

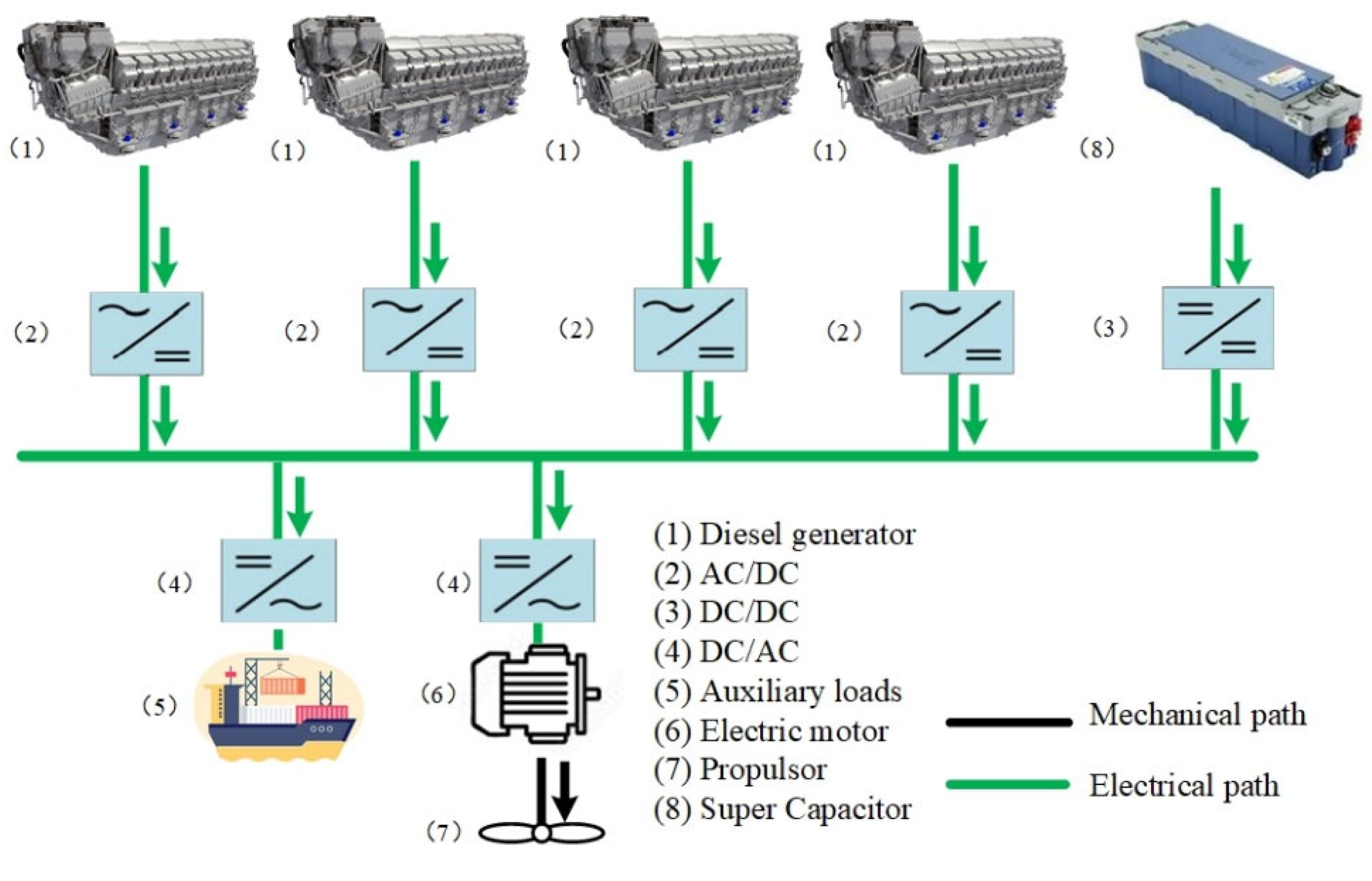

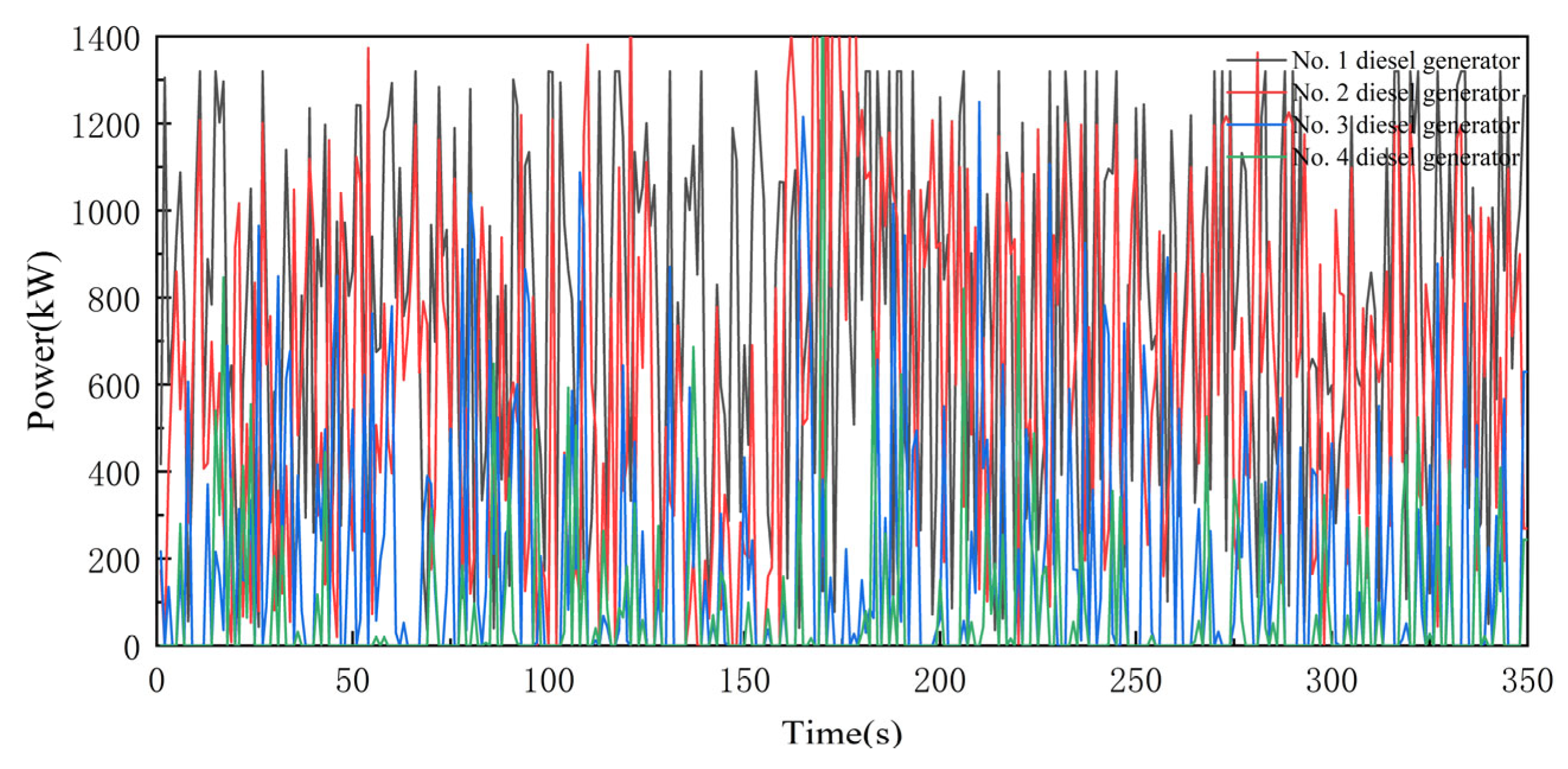
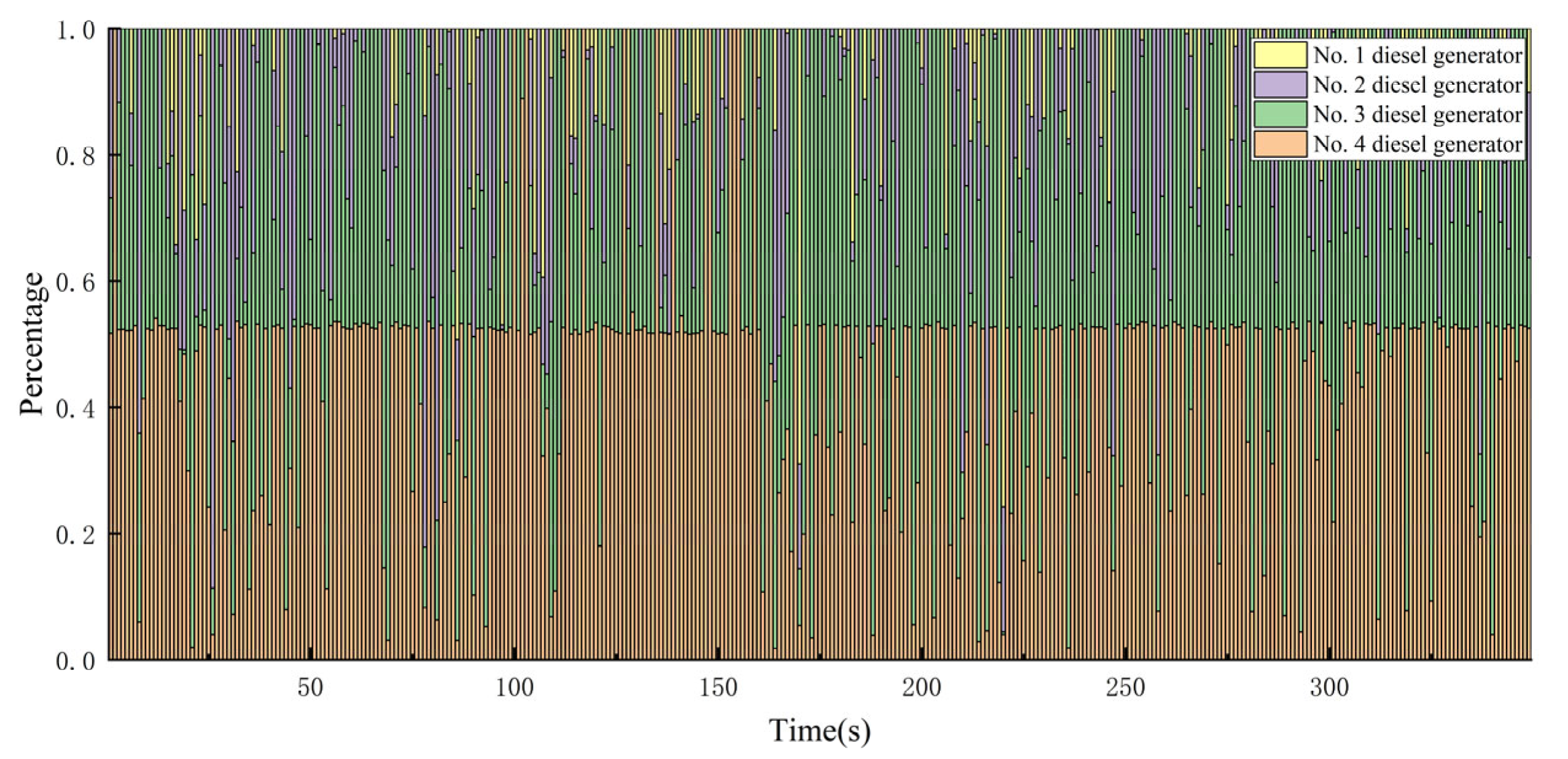

| Component | Parameter | Value |
|---|---|---|
| Prime motor | Maximum Power/kW | 1935 |
| Rated Power/kW | 1320 | |
| Rated Speed (r/min) | 1000 | |
| Quantity | 4 | |
| Generator | Rated Speed/kW | 1250 |
| Rated Torque/Nm | 11,937.5 | |
| Rated Speed (r/min) | 1000 | |
| Quantity | 4 | |
| Super capacitor | Capacity /F | 129 |
| Maximum/Minimum Voltage/V | 820/604 | |
| Rated Power/kW | 1000 | |
| Quantity | 2 | |
| Main propulsion | Rated Voltage/V | 690 |
| Rated Power/kW | 1680 | |
| Quantity | 2 | |
| Side propulsion | Rated Power/kW | 450 |
| Rated Voltage/V | 690 | |
| Rated Speed (r/min) | 1500 | |
| Quantity | 1 |
| Hyperparameter | Value |
|---|---|
| Episode | 2000 |
| Experience pool capacity | 500 |
| The number of samples of the minimum sample set | 32 |
| Episode of replication network parameters | 300 |
| Learning rate α | 0.01 |
| Discount rate γ | 0.9 |
| Weight factor β | 0.1 |
| ε in ε-greedy | 0.9 |
| The reduction of ε | 0.05 |
| Approximation coefficient τ | 0.01 |
| Data Strategy | Average Specific Fuel Consumption/g/(kW-h) | Total Fuel Consumption/kg | Relative Reduction/% |
|---|---|---|---|
| Real ship | 230.46 | 57.63 | 0 |
| Ruled-based | 227.48 | 54.44 | 5.5% |
| DQN-based | 219.37 | 50.35 | 12.6% |
| DDPG-based | 212.65 | 48.54 | 15.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Tang, D.; Yuan, Y.; Yuan, C.; Shen, B.; Guerrero, J.M. A New Energy Management Strategy Supported by Reinforcement Learning: A Case Study of a Multi-Energy Cruise Ship. J. Mar. Sci. Eng. 2025, 13, 720. https://doi.org/10.3390/jmse13040720
Guo X, Tang D, Yuan Y, Yuan C, Shen B, Guerrero JM. A New Energy Management Strategy Supported by Reinforcement Learning: A Case Study of a Multi-Energy Cruise Ship. Journal of Marine Science and Engineering. 2025; 13(4):720. https://doi.org/10.3390/jmse13040720
Chicago/Turabian StyleGuo, Xiaodong, Daogui Tang, Yupeng Yuan, Chengqing Yuan, Boyang Shen, and Josep M. Guerrero. 2025. "A New Energy Management Strategy Supported by Reinforcement Learning: A Case Study of a Multi-Energy Cruise Ship" Journal of Marine Science and Engineering 13, no. 4: 720. https://doi.org/10.3390/jmse13040720
APA StyleGuo, X., Tang, D., Yuan, Y., Yuan, C., Shen, B., & Guerrero, J. M. (2025). A New Energy Management Strategy Supported by Reinforcement Learning: A Case Study of a Multi-Energy Cruise Ship. Journal of Marine Science and Engineering, 13(4), 720. https://doi.org/10.3390/jmse13040720








