Assessment of Undrained Bearing Capacity of Foundations on Anisotropic Clay Slope Under Inclined Load
Abstract
:1. Introduction
2. Methodology
2.1. Lower Bound Limit Analysis (LBLA)
2.1.1. Numerical Model
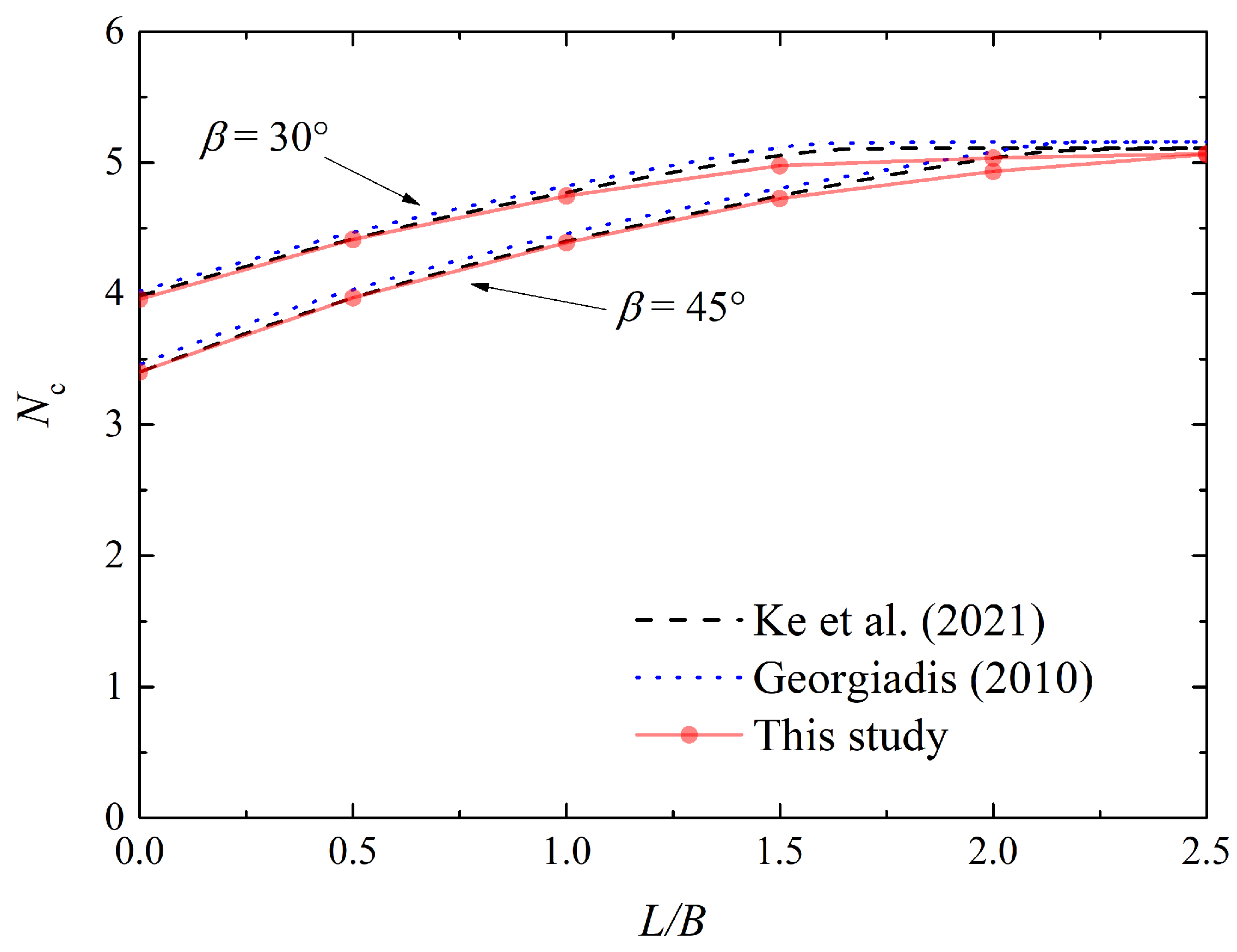
2.1.2. Validation
2.2. Multivariate Adaptive Regression Splines (MARS)
3. Results and Discussion
3.1. LBLA Results and Discussion
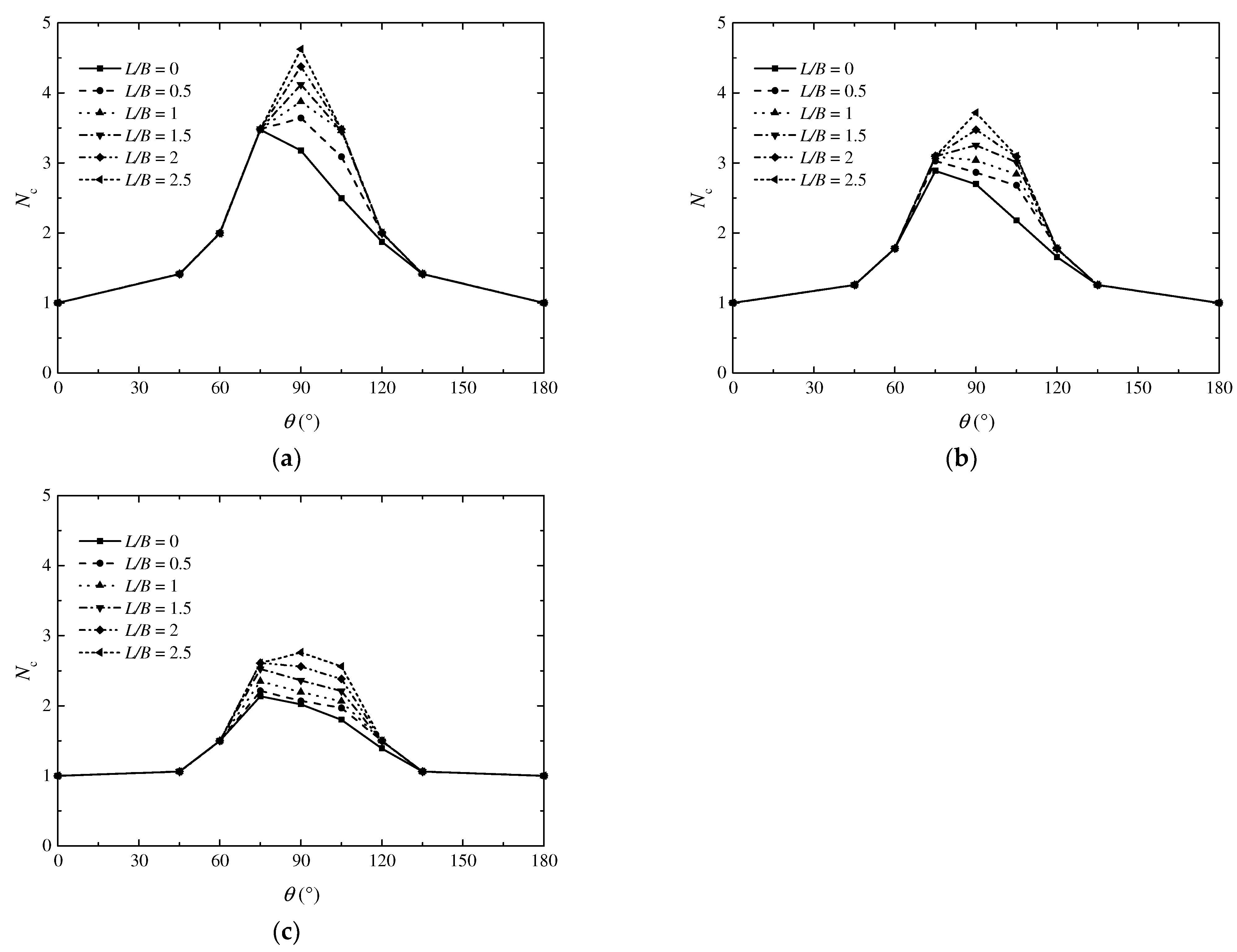
3.1.1. Bearing Capacity
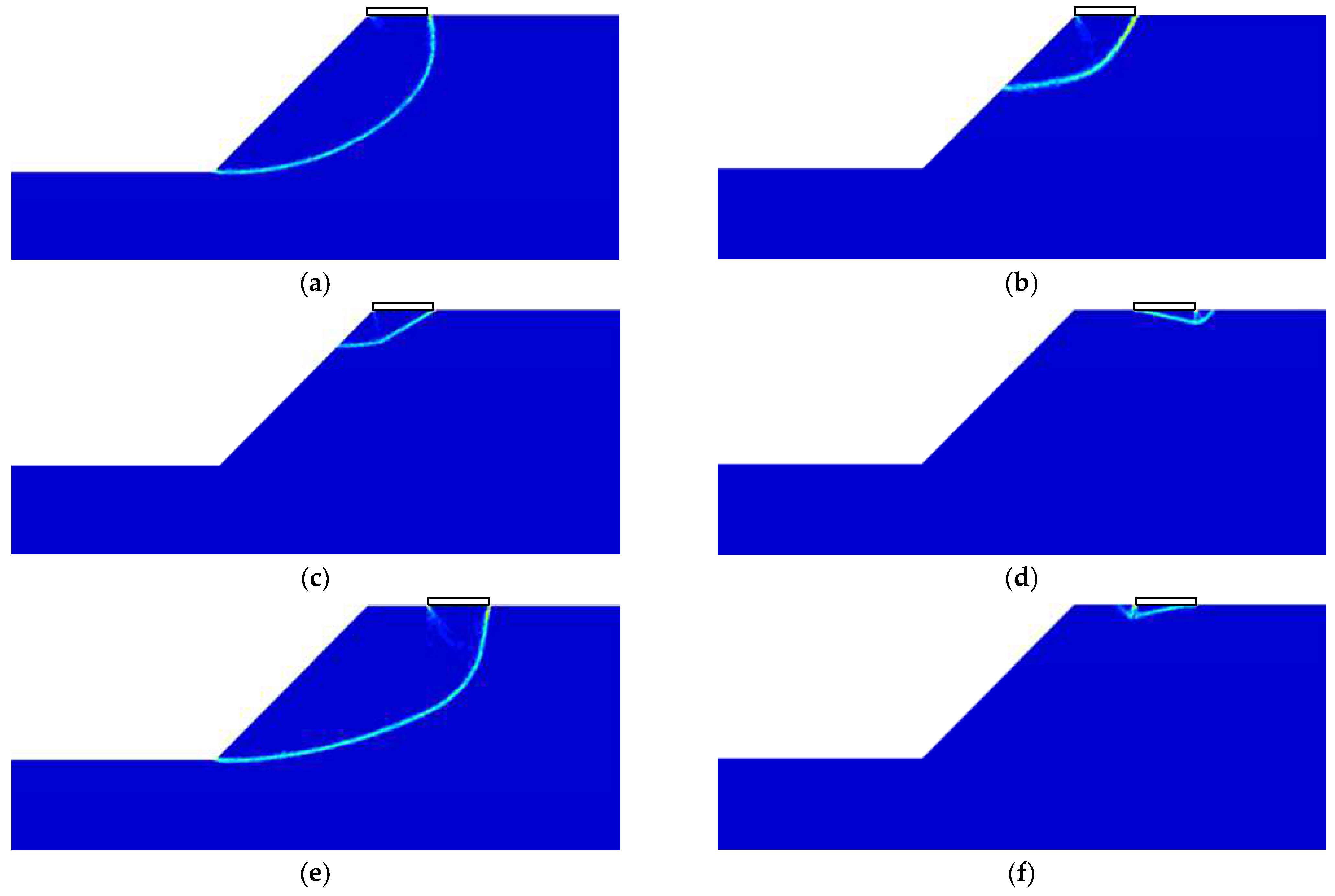
3.1.2. Failure Modes
3.2. MARS Results and Discussion
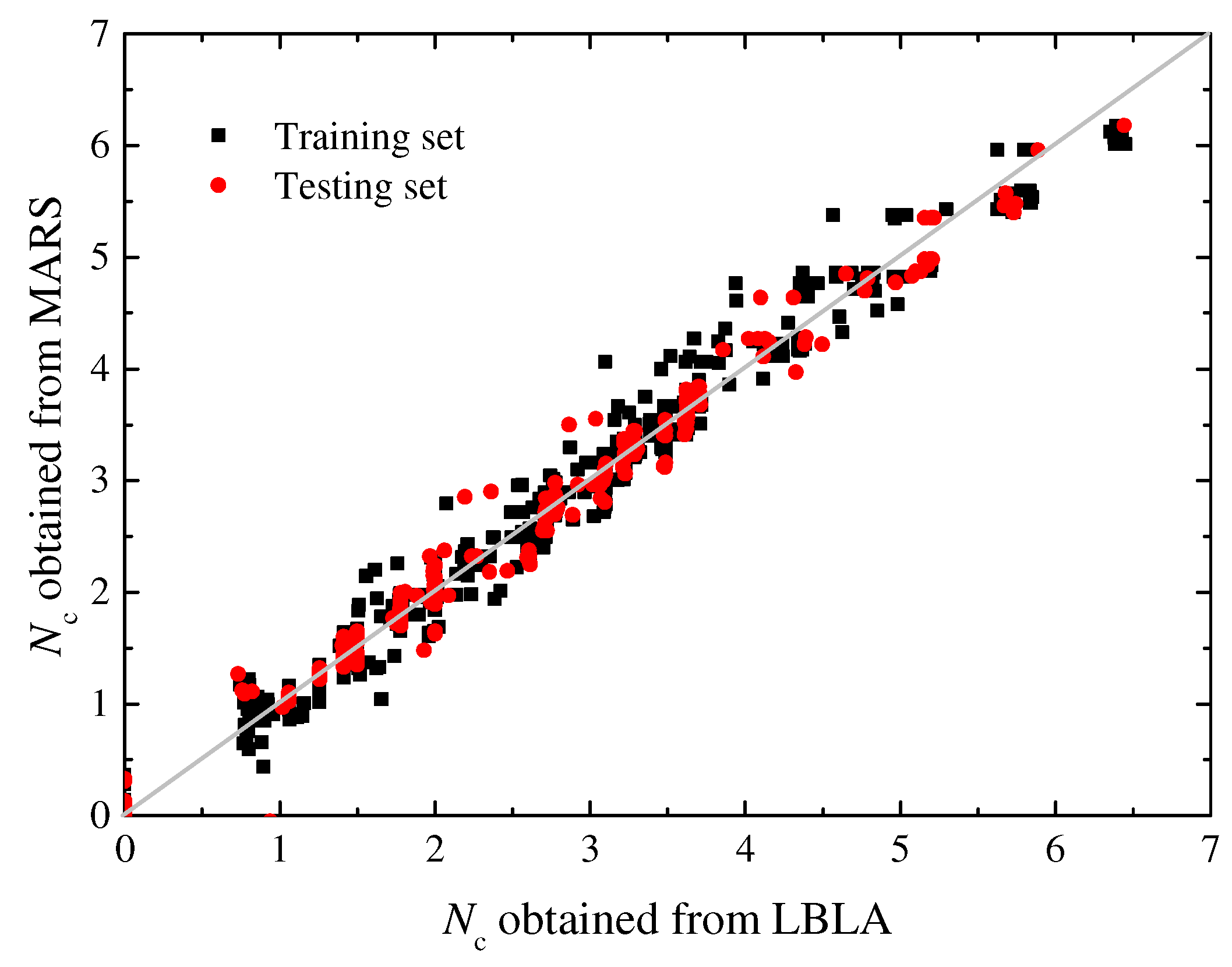
3.2.1. Model Performance
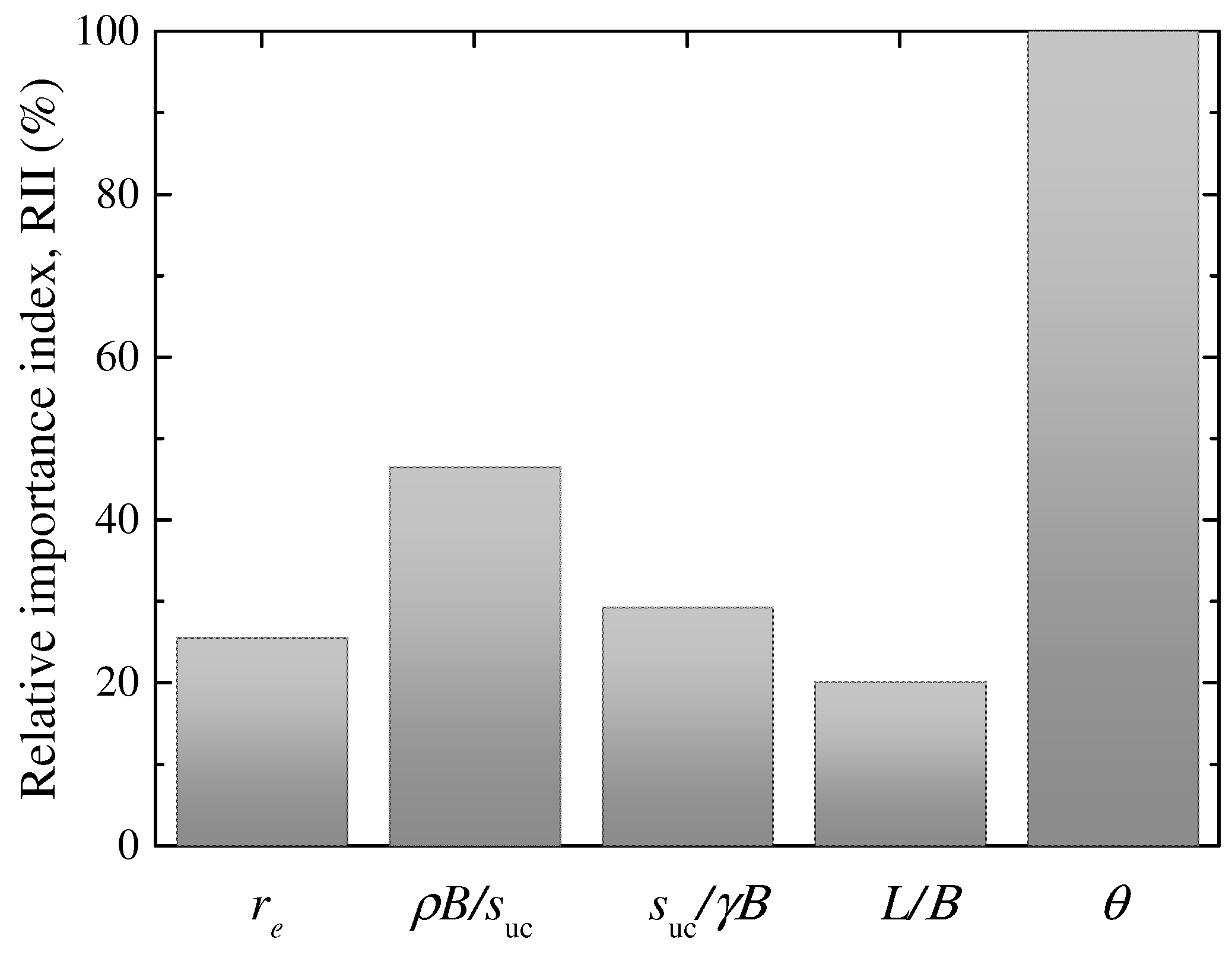
3.2.2. Feature Importance
4. Conclusions
- (1)
- Both normalized strength ratio ρB/suc and anisotropy ratio re exhibit positive correlations with bearing capacity factors, accompanied by failure mechanism transitions from deep-seated toe failure to shallow face failure patterns, evidenced by shear surface elevation.
- (2)
- The bearing capacity factor diminishes as the suc/γB decreases, which may potentially trigger failure mode transformation from localized bearing capacity failure to global slope instability. Both of these failure types include the toe failure mode, which can be distinguished based on the presence of distinct active and passive wedges.
- (3)
- As the foundation moves away from the slope, the influence of the slope on the foundation diminishes, resulting in an increase in bearing capacity. The failure mode gradually transitions from face failure to the Prandtl-type failure.
- (4)
- The foundation has the maximum bearing capacity when the load angle is between 75 and 90 degrees. As the angle increases or decreases further, the bearing capacity of the foundation decreases. Changes in the load angle significantly affect the failure mode of the foundation. It should be noted that the same load angle can cause significantly different failure modes under different soil conditions.
- (5)
- The MAE, RMSE, and R2 of the testing set obtained from the MARS are 0.112, 0.169, and 0.983, respectively, indicating that the empirical equation derived from MARS can reasonably predict the bearing capacity of foundations on anisotropic slopes. With the help of the RII (relative importance index), it is found that the load angle significantly affects the bearing capacity of the foundation, followed by ρB/suc, suc/γB, and re, while the influence of L/B is relatively lower. In practice, these variables are all very important and should not be overlooked.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Georgiadis, K. An upper-bound solution for the undrained bearing capacity of strip footings at the top of a slope. Géotechnique 2010, 60, 801–806. [Google Scholar] [CrossRef]
- Yang, S.; Leshchinsky, B.; Cui, K.; Zhang, F.; Gao, Y. Influence of failure mechanism on seismic bearing capacity factors for shallow foundations near slopes. Géotechnique 2021, 71, 594–607. [Google Scholar] [CrossRef]
- Lee, K.M.; Manjunath, V.R. Experimental and numerical studies of geosynthetic-reinforced sand slopes loaded with a footing. Can. Geotech. J. 2000, 37, 828–842. [Google Scholar] [CrossRef]
- Castelli, F.; Lentini, V. Evaluation of the bearing capacity of footings on slopes. Int. J. Phys. Model. Geotech. 2012, 12, 112–118. [Google Scholar] [CrossRef]
- Salih Keskin, M.; Laman, M. Model studies of bearing capacity of strip footing on sand slope. KSCE J. Civ. Eng. 2013, 17, 699–711. [Google Scholar] [CrossRef]
- Naeini, S.A.; Rabe, B.K.; Mahmoodi, E. Bearing capacity and settlement of strip footing on geosynthetic reinforced clayey slopes. J. Cent. South Univ. 2012, 19, 1116–1124. [Google Scholar] [CrossRef]
- Javdanian, H. On the behaviour of shallow foundations constructed on reinforced soil slope—A numerical analysis. Int. J. Geotech. Eng. 2017, 14, 188–195. [Google Scholar] [CrossRef]
- Satvati, S.; Alimohammadi, H.; Rowshanzamir, M.; Hejazi, S.M. Bearing Capacity of Shallow Footings Reinforced with Braid and Geogrid Adjacent to Soil Slope. Int. J. Geosynth. Ground Eng. 2020, 6, 41. [Google Scholar] [CrossRef]
- Farzaneh, O.; Askari, F.; Ganjian, N. Three-Dimensional Stability Analysis of Convex Slopes in Plan View. J. Geotech. Geoenviron. Eng. 2008, 134, 1192–1200. [Google Scholar] [CrossRef]
- Georgiadis, K. Undrained Bearing Capacity of Strip Footings on Slopes. J. Geotech. Geoenviron. Eng. 2010, 136, 677–685. [Google Scholar] [CrossRef]
- Shiau, J.S.; Merifield, R.S.; Lyamin, A.V.; Sloan, S.W. Undrained Stability of Footings on Slopes. Int. J. Geomech. 2011, 11, 381–390. [Google Scholar] [CrossRef]
- Hicks, M.A.; Nuttall, J.D.; Chen, J. Influence of heterogeneity on 3D slope reliability and failure consequence. Comput. Geotech. 2014, 61, 198–208. [Google Scholar] [CrossRef]
- Keshavarz, A.; Beygi, M.; Vali, R. Undrained seismic bearing capacity of strip footing placed on homogeneous and heterogeneous soil slopes by finite element limit analysis. Comput. Geotech. 2019, 113, 103094. [Google Scholar] [CrossRef]
- Jin, L.; Feng, Y.; Zhang, H.; Feng, Q. The use of improved radial movement optimization to calculate the ultimate bearing capacity of a nonhomogeneous clay foundation adjacent to slopes. Comput. Geotech. 2020, 118, 103338. [Google Scholar] [CrossRef]
- Bransby, M.F.; Randolph, M.F. Combined loading of skirted foundations. Géotechnique 1998, 48, 637–655. [Google Scholar] [CrossRef]
- Chen, H.; Shen, Z.; Wang, L.; Qi, C.; Tian, Y. Prediction of undrained failure envelopes of skirted circular foundations using gradient boosting machine algorithm. Ocean Eng. 2022, 258, 111767. [Google Scholar]
- Gao, Z.; Zhao, J.; Yao, Y. A generalized anisotropic failure criterion for geomaterials. Int. J. Solids Struct. 2010, 47, 3166–3185. [Google Scholar] [CrossRef]
- Tran, D.T.; Onjaipurn, T.; Kumar, D.R.; Chim-Oye, W.; Keawsawasvong, S.; Jamsawang, P. An eXtreme Gradient Boosting prediction of uplift capacity factors for 3D rectangular anchors in natural clays. Earth Sci. Inform. 2024, 17, 2027–2041. [Google Scholar] [CrossRef]
- Ladd, C.C. Stability Evaluation during Staged Construction. J. Geotech. Eng. 1991, 117, 540–693. [Google Scholar] [CrossRef]
- Won, J.Y. Anistropic strength ratio and plasiticty index of natural clays. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering 2013, Paris, France, 2–6 September 2013; pp. 445–448. [Google Scholar]
- Casagrande, A.; Carillo, N. Shear failure of anisotropic materials. J. Boston Soc. Civ. Eng. 1944, 31, 74–87. [Google Scholar]
- Davis, E.H.; Christian, J.T. Bearing capacity of anisotropic cohesive soil. J. Soil. Mech. Found. Div. 1971, 97, 753–769. [Google Scholar] [CrossRef]
- Prevost, J.H. Undrained shear tests on clay. J. Soil Mech. Found. Div. 1979, 105, 49–64. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Galindo-Torres, S.A.; Zhang, X.; Krabbenhøft, J. AUS: Anisotropic undrained shear strength model for clays. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2652–2666. [Google Scholar] [CrossRef]
- Lai, V.Q.; Chenari, R.J.; Banyong, R.; Keawsawasvong, S. Undrained Stability of Opening in Underground Walls in Anisotropic Clays. Int. J. Geomech. 2023, 23, 06022042. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, M. Prediction of Undrained Shear Strength Utilizing a Hybrid Stacking Model Enhanced by Bayesian Optimization Algorithm. Transp. Res. Rec. 2024. [Google Scholar] [CrossRef]
- Duong, N.T.; Shiau, J.; Keawsawasvong, S.; Lai, V.Q. Three-dimensional undrained stability analysis of circular tunnel heading in anisotropic and heterogeneous clay: FELA, ANN, MARS, and XGBoost. Model. Earth Syst. Environ. 2024, 10, 5503–5527. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Zhou, H.; Diao, Y.; Zheng, G.; Han, J.; Jia, R. Failure modes and bearing capacity of strip footings on soft ground reinforced by floating stone columns. Acta Geotech. 2017, 12, 1089–1103. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Goh, A.T.C. Multivariate adaptive regression splines for inverse analysis of soil and wall properties in braced excavation. Tunn. Undergr. Space Technol. 2017, 64, 24–33. [Google Scholar] [CrossRef]
- Lai, V.Q.; Shiau, J.; Keawsawasvong, S.; Tran, D.T. Bearing Capacity of Ring Foundations on Anisotropic and Heterogenous Clays: FEA, NGI-ADP, and MARS. Geotech. Geol. Eng. 2022, 40, 3913–3928. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.V. Generalised Tresca criterion for undrained total stress analysis. Geotech. Lett. 2015, 5, 313–317. [Google Scholar] [CrossRef]
- Kumar, D.R.; Samui, P.; Wipulanusat, W.; Keawsawasvong, S.; Sangjinda, K.; Jitchaijaroen, W. Soft-Computing Techniques for Predicting Seismic Bearing Capacity of Strip Footings in Slopes. Buildings 2023, 13, 1371. [Google Scholar] [CrossRef]
- Ke, L.; Gao, Y.; Zhao, Z.; Zhou, Y.; Ji, J. Undrained Bearing Capacity of Strip Footing near Slopes Considering the Orientation of Strength Increase. Int. J. Geomech. 2021, 21, 06021016. [Google Scholar] [CrossRef]
- Mukhopadhyay, T. A multivariate adaptive regression splines based damage identification methodology for web core composite bridges including the effect of noise. J. Sandw. Struct. Mater. 2017, 20, 885–903. [Google Scholar] [CrossRef]
- Zheng, G.; Zhang, W.; Zhou, H.; Yang, P. Multivariate adaptive regression splines model for prediction of the liquefaction-induced settlement of shallow foundations. Soil Dyn. Earthq. Eng. 2020, 132, 106097. [Google Scholar] [CrossRef]
- Zhou, H.; Zheng, G.; Yin, X.; Jia, R.; Yang, X. The bearing capacity and failure mechanism of a vertically loaded strip footing placed on the top of slopes. Comput. Geotech. 2018, 94, 12–21. [Google Scholar] [CrossRef]
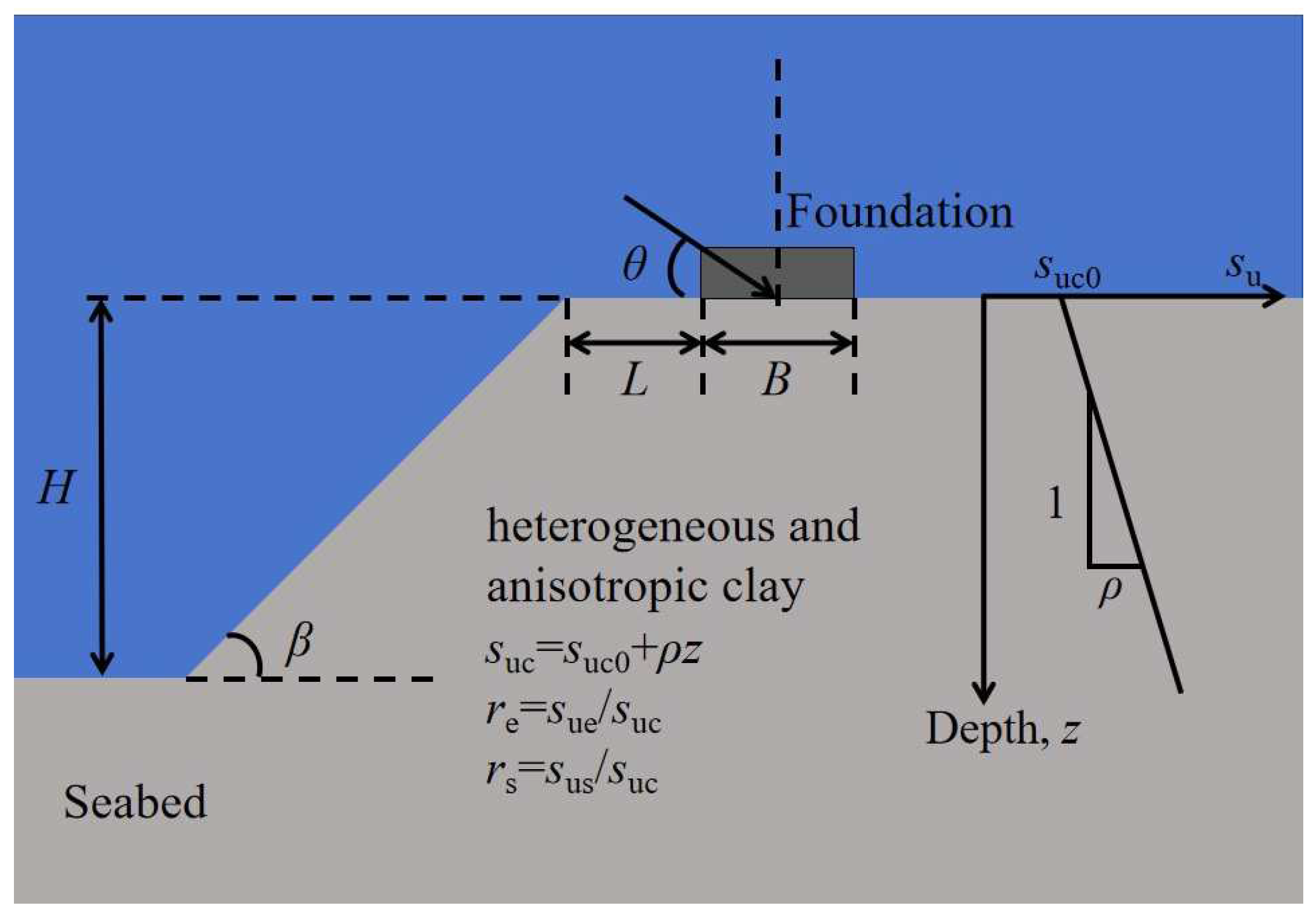


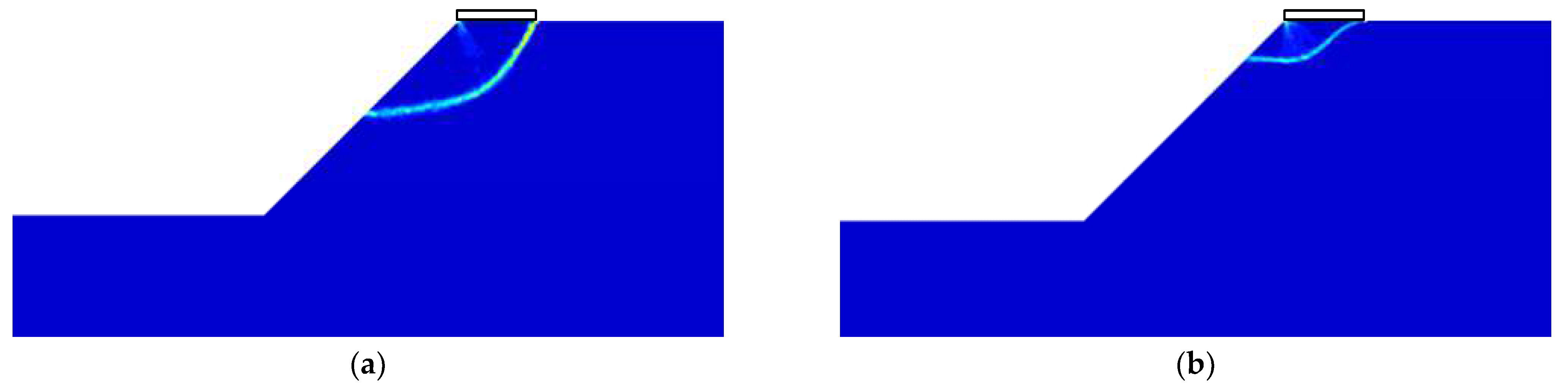
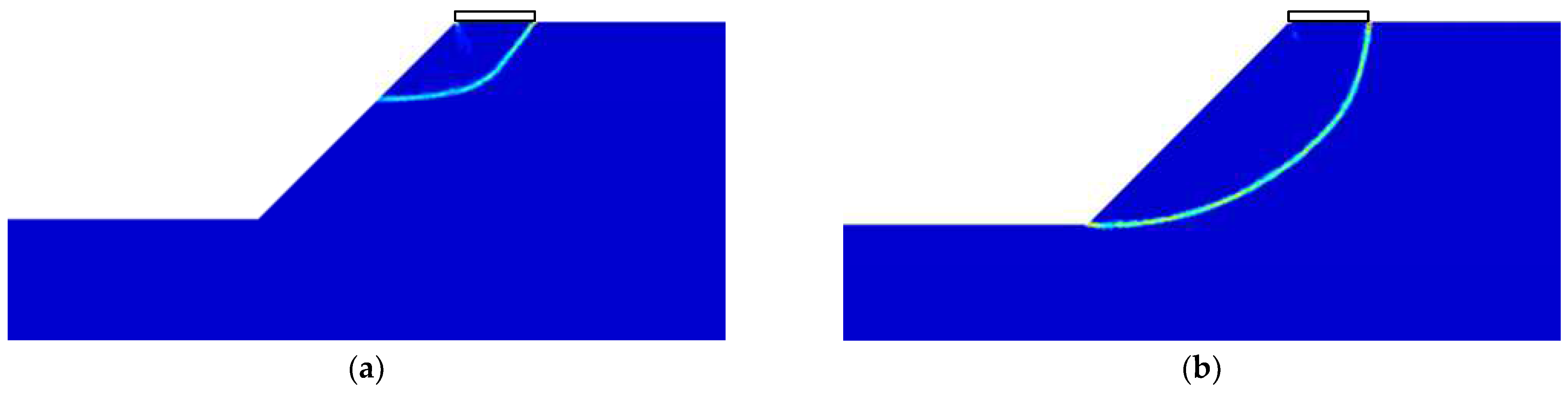


| Parameters | Input Values |
|---|---|
| Normalized foundation setback, L/B | 0, 0.5, 1, 1.5, 2, and 2.5 |
| Load angle, θ | 0°, 45°, 60°, 75°, 90°, 105°, 120°, 135° and 180° |
| Strength ratio, suc/γB | 0.5, 1, 1.5, and 2 |
| Heterogeneous index, ρB/suc | 0, 0.5, and 1 |
| Anisotropic ratio, re | 0.6, 0.8, and 1 |
| BF | Equation | BF | Equation |
|---|---|---|---|
| BF1 | max(0, θ − 90) | BF20 | BF8 × max(0, ρB/suc − 0.5) |
| BF2 | max(0, re − 0.8) | BF21 | BF8 × max(0, 0.5 − ρB/suc) |
| BF3 | max(0, 0.8 − re) | BF22 | max(0, 0.5 − L/B) × max(0, θ − 75) |
| BF4 | max(0, 0.5 − ρB/suc) | BF23 | max(0, 105 − θ) |
| BF5 | BF4 × max(0, 40 − suc/γB) | BF24 | max(0, θ − 105) × max(0, 0.8 − re) |
| BF6 | BF4 × max(0, θ − 105) | BF25 | max(0, 90 − θ) × max(0, re − 0.8) |
| BF7 | BF4 × max(0, 105 − θ) | BF26 | max(0, 90 − θ) × max(0, 0.8 − re) |
| BF8 | max(0, θ − 60) | BF27 | max(0, ρB/suc − 0.5) × max(0, θ − 75) |
| BF9 | max(0, 60 − θ) | BF28 | max(0, ρB/suc − 0.5) × max(0, 75 − θ) |
| BF10 | max(0, 90 − θ) × max(0, ρB/suc − 0.5) | BF29 | BF7 × max(0, suc/γB − 40) |
| BF11 | max(0, 90 − θ) × max(0, 0.5 − ρB/suc) | BF30 | BF7 × max(0, 40 − suc/γB) |
| BF12 | max(0, 120 − θ) | BF31 | BF12 × max(0, re − 0.8) |
| BF13 | BF5 × max(0, re − 0.8) | BF32 | BF12 × max(0, 0.8 − re) |
| BF14 | BF5 × max(0, 0.8 − re) | BF33 | BF12 × max(0, ρB/suc − 0.5) |
| BF15 | max(0, L/B − 0.5) | BF34 | BF12 × max(0, 0.5 − ρB/suc) |
| BF16 | max(0, 0.5 − L/B) × max(0, θ − 90) | BF35 | max(0, θ − 120) × max(0, L/B − 0.5) |
| BF17 | BF11 × max(0, suc/γB − 40) | BF36 | max(0, θ − 120) × max(0, 0.5 − L/B) |
| BF18 | BF11 × max(0, 40 − suc/γB) | BF37 | max(0, 90 − θ) × max(0, L/B − 1.5) |
| BF19 | BF6 × max(0, 40 − suc/γB) | BF38 | max(0, 90 − θ) × max(0, 1.5 − L/B) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, X.; Zhu, J.; Chen, H. Assessment of Undrained Bearing Capacity of Foundations on Anisotropic Clay Slope Under Inclined Load. J. Mar. Sci. Eng. 2025, 13, 681. https://doi.org/10.3390/jmse13040681
Chu X, Zhu J, Chen H. Assessment of Undrained Bearing Capacity of Foundations on Anisotropic Clay Slope Under Inclined Load. Journal of Marine Science and Engineering. 2025; 13(4):681. https://doi.org/10.3390/jmse13040681
Chicago/Turabian StyleChu, Xuanxuan, Jiang Zhu, and Hongzhen Chen. 2025. "Assessment of Undrained Bearing Capacity of Foundations on Anisotropic Clay Slope Under Inclined Load" Journal of Marine Science and Engineering 13, no. 4: 681. https://doi.org/10.3390/jmse13040681
APA StyleChu, X., Zhu, J., & Chen, H. (2025). Assessment of Undrained Bearing Capacity of Foundations on Anisotropic Clay Slope Under Inclined Load. Journal of Marine Science and Engineering, 13(4), 681. https://doi.org/10.3390/jmse13040681