Preliminary Development of a Novel Salvage Catamaran and Evaluation of Hydrodynamic Performance

Abstract

With the rapid advancement of the marine economy, conventional salvage equipment has become increasingly inadequate in meeting the operational demands of complex aquatic environments and deep-sea salvage operations. This study presents the preliminary design of a novel salvage catamaran and proposes a multi-level fuzzy comprehensive evaluation framework for hydrodynamic performance under multi-sea-state and multi-operational conditions. A hydrodynamic performance evaluation indicator system was established, integrating resistance and seakeeping criteria. Computational fluid dynamics (CFDs) simulations with overset grids were employed to calculate the resistance characteristics. Potential flow-theory-based analysis quantified motion responses under irregular waves. The framework effectively distinguishes performance variations across five sea states and two sets of loading conditions through composite scoring. Key findings demonstrate that wave-added resistance coefficients increase proportionally with a significant wave height (Hs) and spectral peak period (Tp), while payload variations predominantly influence heave amplitudes. A fuzzy mathematics-driven model assigned entropy–Analytic Hierarchy Process (AHP) hybrid weights, revealing operational trade-offs: Case1-Design achieved optimal seakeeping and resistance, whereas Case5-Light exhibited critical motion thresholds. Adaptive evaluation strategies were proposed, including dynamic weight adjustments for long/short-wave-dominated regions via sliding window entropy updates. This work advances the systematic evaluation of catamarans, offering a validated methodology for balancing hydrodynamic efficiency and operational safety in salvage operations.

1. Introduction

With the rapid advancement of marine economics and waterborne transportation industries, salvage operations have become increasingly prominent in emergency responses, environmental protection, and resource development. Conventional salvage vessels frequently encounter challenges such as inadequate stability and limited deck workspace under complex sea conditions [1]. During heavy-load salvage operations, these vessels are prone to excessive roll responses and structural stress concentrations, posing significant safety risks and meaning they struggle to meet operational demands in complex coastal zones and deep-sea environments [2]. Against this backdrop, the development of novel salvage vessels holds critical significance. Catamarans, leveraging their twin-hull configuration to deliver enhanced stability, expansive deck operational space, and superior load-bearing capacity, have emerged as a prioritized solution for specialized maritime engineering vessel design [3].

Despite the inherent advantages of catamaran configurations in structural stability and operational space, the nonlinear hydrodynamic characteristics arising from complex flow–field interactions remain a pivotal challenge in design optimization. Salvage operations impose stringent hydrodynamic requirements, necessitating a balance between precise low-speed maneuverability and high-speed transit efficiency. This dual demand underscores the criticality of optimizing key hydrodynamic performance metrics, including rapidity and seakeeping capabilities. The evaluation of vessels’ hydrodynamic performance constitutes a multifaceted process involving heterogeneous parameters [4]. The intrinsic diversity of the assessment criteria and the ambiguity in classifying multidimensional operational data introduce substantial complexity to comprehensive performance analysis.

The current methodologies for predicting the hydrodynamic performance of ships in waves primarily rely on three approaches [5,6,7,8,9]: experimental fluid dynamics (EFD), potential flow theory, and computational fluid dynamics (CFD). To address the challenges of rapidity and seakeeping in catamarans, scholars worldwide have conducted extensive research on resistance and navigational performance in both calm water and waves. Trimulyono et al. [10] employed a stepped hull design methodology and utilized CFD to analyze the effects of dual-step positioning on the performance of both monohull and catamaran planing hulls. The results demonstrated that variations in step location could significantly modify hull performance. Zou et al. [11] conducted a numerical investigation on the interactions between waterjet propulsion systems and catamarans. By implementing the Unsteady Reynolds-Averaged Navier–Stokes (URANS) approach for hull simulations, the findings revealed that the overall efficiency of the waterjet device positioned aft of the hull ranged from approximately 0.75 to 0.8 times that of the free-stream efficiency. Han et al. [12] developed a suspended catamaran and conducted a series of towing tank experiments to investigate the motion responses of the craft in regular waves. The experimental results indicated that under beam sea conditions, the average reduction rates of the cabin’s heave motion and roll motion reached 62% and −57%, respectively. Duman et al. [13] investigated the wave resistance of zero-carbon passenger ferries in shallow water, employing a catamaran-based approach to decompose residual resistance into viscous pressure and wave-making components via velocity-dependent form factors. Their work characterized wave resistance contributions into low-, medium-, and high-speed regimes. Ozturk et al. [14] demonstrated the full-scale resistance and seakeeping performance of the Double-M vessel, a 15 m next-generation emergency response and rescue vessel (ERRV). Under regular head waves (λ/L = 1–2.5) at Fr = 0.7, the Double-M exhibited a 10.34% reduction in relative added resistance compared to the Delft 372 catamaran, along with 72.5% and 35.5% reductions in heave and pitch motions, respectively. Nazemian et al. [15] developed a machine learning (ML)-based predictor for calm water resistance optimization. By integrating genetic algorithms (GAs) with regression models—including regression trees (RT), support vector machines (SVM), and artificial neural networks (ANN)—the study achieved hull form optimizations for diverse catamarans. Key parameters included resistance-driven dimensional coefficients, structural weight reduction, and battery performance enhancements.

Javanmard et al. [16] conducted numerical simulations on the motion responses of a 2.5 m scale model of the 112 m INCAT Tasmania high-speed catamaran under irregular wave conditions. By implementing Ride Control Systems (RCSs), they analyzed heave, pitch motions, and vertical accelerations in head seas under full-scale wave heights of 2.7 m and 4 m. Yang et al. [17] investigated the hydrodynamic performance of a partially air-cushion-supported catamaran (PACSCAT) navigating with flexible seals in waves. Through scaled model tests, the study characterized PACSCAT’s motion behaviors across varying wavelengths by monitoring critical parameters including heave, pitch, accelerations, and air cushion pressure boundaries. He et al. [18] evaluated uncertainty quantification (UQ) methods for resistance, motions, and slamming loads in variable regular waves representing specific sea states. The methodology was benchmarked against irregular wave tests and deterministic regular wave studies, with applications demonstrated on the high-speed Delft catamaran at Fr = 0.5 in sea state 6. Deng et al. [19] conducted a numerical investigation based on the Reynolds-Averaged Navier–Stokes (RANS) equations to examine the resistance characteristics in calm water, added resistance, and head wave motion responses of a high-speed vessel under varying wave amplitudes. A systematic analysis was performed to quantify the hull trim effects on calm water resistance, as well as the wave amplitude dependencies of both the added resistance and motion characteristics. Mai et al. [20] examined the wave characteristics of demi-hulls of a catamaran under regular and irregular waves with diverse wave directions and speeds. Comparative analyses against ambient wave parameters revealed discrepancies in wavelength, directional spectra, and energy distribution within the inter-hull region, highlighting the coupled effects of operational speed and sea state on wave field modulation. Gaidai et al. [21] utilized AQWA software (Release 15.0, ANSYS, Inc., Canonsburg, PA, USA) to assess the wave-induced hydrodynamic responses of a specialized maintenance vessel under realistic sea conditions. The study identified excessive motion amplitudes in specific sea states, posing significant risks to crew transfer operations.

By addressing the hydrodynamic performance evaluation problem, Liu et al. [22] proposed an accurate and efficient viscous flow-based wake learning method utilizing a Kriging model, which employs a Proper Orthogonal Decomposition (POD) method with qualitative and quantitative error analysis. This approach can guide the sensitivity analysis of design variables, selection of design variables and spatial domains, as well as novel flow field predictions, thereby achieving the comprehensive optimization of hull shape performance. By addressing the challenge of determining weights due to excessive evaluation metrics, Ji et al. [23] proposed a deep reinforcement learning (DRL)-based weight adjustment model. This model dynamically optimizes metric weights by incorporating experts’ subjective preferences through reward mechanisms. Guan et al. [24,25] introduced a SWATH (Small Waterplane Area Twin Hull)-oriented evaluation method incorporating composite weighting factors for resistance and seakeeping. Comparative analyses revealed that optimized hull forms derived from this method exhibited superior hydrodynamic performance compared to baseline configurations.

Extensive research has been conducted by global scholars on the hydrodynamic performance metrics of catamarans, particularly rapidity and seakeeping. However, existing studies predominantly focus on isolated performance indicators, with limited methodologies integrating both rapidity and seakeeping into a unified hydrodynamic assessment framework. To address this gap, this study presents the preliminary design of a novel salvage catamaran and proposes a novel multi-level fuzzy comprehensive evaluation model based on fuzzy mathematics theory, specifically tailored for salvage catamarans under multi-sea-state and multi-operational conditions. A hierarchical hydrodynamic performance evaluation index system is established, incorporating key parameters such as resistance characteristics under varying speeds and motion response amplitudes in irregular waves. Through the systematic quantification of hydrodynamic response amplitudes across diverse operational scenarios, the model enables holistic performance benchmarking. By leveraging fuzzy comprehensive evaluation theory, this work provides a paradigm-shifting approach to assess the coupled effects of rapidity–seakeeping interactions, offering critical insights for optimizing salvage catamaran designs in complex maritime environments.

2. Model Description

2.1. Structural Design of the Salvage Catamaran

Conventional monohull salvage vessels face the following limitations during operations: (1) restricted transverse stability, leading to excessive roll angles under beam sea conditions, which compromises crane operations and crew safety; (2) limited deck space, which is insufficient for deploying large-scale salvage systems and auxiliary equipment; and (3) side-mounted cranes that cause uneven weight distribution during heavy-load salvage, increasing capsizing risks. The proposed novel catamaran design addresses these issues: (1) enhanced transverse stability through a 9 m hull separation, significantly improving righting moment; (2) expansive moon pool workspace between hulls for the simultaneous deployment of heavy-duty salvage systems and monitoring equipment; and (3) centrally positioned cranes around the moon pool, ensuring a balanced load distribution and eliminating capsizing risks by maintaining heavy loads along the vessel’s central axis.

To address the operational requirements for the marine salvage of floating targets, a novel catamaran salvage vessel design has been preliminarily developed. Innovative structural improvements have been made to the conventional flat-deck catamaran configuration. The vessel consists of dual parallel hulls with the wheelhouse and operation cabin positioned on elevated platforms above the respective bow and stern sections of the hulls. A moon pool is formed between the wheelhouse and operation cabin, creating a stabilized microenvironment that offers superior protection for submersible equipment compared to the surrounding turbulent waters during deployment/retrieval operations. The salvage system is centrally installed within the moon pool, with the conceptual top-view design presented in a schematic in Figure 1. This design integrates the inherent advantages of catamarans—enhanced seakeeping performance, operational comfort, and spacious deck layout—with optimized arrangements for salvage equipment installation, thereby ensuring efficient salvage operations.

The hull elevation has been increased to enable the smooth transit of salvage targets through the bow platform into the inter-hull moon pool. Structural reinforcement is achieved through fore and aft bulkhead connections between the twin hulls. A flexible connected salvage mechanism between the upper hull and twin lower hulls enhances stability while mitigating the heave motion induced by wave impacts, thereby improving seakeeping performance. The salvage system incorporates winches, rigid frames, and flexible mesh systems to directly hoist targets above the water surface. Twin azimuth thrusters at the stern provide exceptional maneuverability with a reduced turning radius, significantly enhancing navigation precision in complex sea conditions. Pre-salvage positioning involves maneuvering the vessel to align the bow with the target for moon pool entry, as illustrated in Figure 2d, followed by the activation of the pre-installed salvage system. The comprehensive layout of the catamaran configuration is depicted in Figure 2.

The salvage system comprises four primary components: (1) the salvage device—polygonal salvage basket; (2) lifting apparatuses—quadruple hoisting winches; (3) retractable positioning platform; and (4) salvage control system. The large-aperture square rigid frame structure expands the operational coverage, facilitating vessel positioning adjustments to ensure that salvage targets are efficiently captured within the basket’s operational envelope. A rigid base ring integrated with flexible salvage netting at the lower section prevents the unintended displacement of secured targets through mechanical constraints. Polygonal steel guide rails enable automatic alignment correction and centering during hoisting operations, ensuring the stabilized positioning of targets within the netting system during vertical ascent, while maintaining structural integrity. The lifting mechanism consists of four hoisting winches (electric capstans) mounted on fore/aft compartment roofs at four corners of the moon pool. Steel cables connect the winches to four corners of the basket’s upper frame, enabling vertical motion control. Flexible couplings mitigate vibration transmission from wave-induced motions (including heave, pitch, and roll), thereby reducing superstructure oscillations and enhancing navigability. Retractable positioning platforms are installed near the moon pool’s central axis within fore/aft compartments. Hydraulic actuators on both platform sides control deployment/retraction cycles. During standby conditions, the platforms remain retracted parallel to the compartment bulkheads. Operational deployment occurs post target positioning to secure salvage objects. The aft platform is integrated with compartment access, enabling the transit of the crew to the secured target for operational interventions.

2.2. Case Condition

For analyzing the 6-degree-of-freedom (6-DoF) motion characteristics of the catamaran salvage vessel in hydrodynamic environments, a multi-body/multi-reference frame methodology was implemented by defining two reference coordinate systems. These consist of an earth-fixed inertial coordinate system and a hull-attached non-inertial coordinate system that follows the vessel motion. The hull coordinate system (as illustrated in Figure 3) originates at the stern waterline center, with a positive X-axis direction from port to starboard, positive Y-axis direction from bow to stern, and positive Z-axis direction vertically upward from keel to deck. The motion components are defined as follows: surge/sway/heave for translational displacements along the X/Y/Z axes, respectively, and roll/pitch/yaw for rotational motions on the X/Y/Z axes, respectively.

The catamaran configuration features extended inter-hull spacing, with computational modeling based on full-scale dimensions. The principal hull parameters are tabulated in

Table 1. Principal hull parameters of salvage catamaran.

Main Parameter	Symbol	Unit	Value
Length between perpendiculars	LPP	m	20
Waterline length	LWL	m	20
Molded breadth	Btotal	m	12
Breadth of demi-hull	b	m	1.5
Demi-hull spacing	s	m	9
Light-load draft	TL	m	1.1
Design-load draft	TD	m	1.5
Displacement	Δ	kg	19,144

.

Two operational loading conditions are defined: the light-load condition (pre-salvage) and design-load condition (post salvage). The operational window is confined to moderate sea conditions (sea state 2 to 3) per the World Meteorological Organization’s classifications. Five representative sea states were selected for comprehensive wave environment assessment, with the vessel responses calculated under both loading conditions in each sea state [26,27,28,29]. Irregular waves were simulated using the JONSWAP spectrum, with the spectral energy distribution illustrated in Figure 4. The environmental parameters for various sea states and loading conditions are systematically documented in

Table 2. Case condition.

Case Number	Significant Wave Height (Hs)	Spectral Peak Period (Tp)
1	0.5	5.16 s
2	0.63	6.23 s
3	0.76	7.02 s
4	0.88	7.52 s
5	1	8.3 s

.

The actual sea states are systematically designated as Cases 1 through 5 according to their tabulated sequence, with subsequent computational analyses adopting this case-based nomenclature.

3. Evaluation Indicator System and Assessment Model Formulation

3.1. Evaluation Indicator System

The assessment of ship hydrodynamic performance necessitates establishing a scientifically rigorous evaluation index system to ensure analytical accuracy [30]. A comprehensive evaluation framework must integrate three essential components: (1) systematically defined evaluation indices, (2) scientifically weighted parameters, and (3) validated assessment methodologies, developed in strict adherence to the principles of scientific rigor, parameter independence, system completeness, operational simplicity, and practical implementability.

Following these principles, ship hydrodynamic performance is hierarchically decomposed into two primary indices: resistance performance and seakeeping performance. The resistance performance index is quantified through two secondary parameters: the mean resistance coefficient in calm water and the wave-added resistance coefficient under irregular wave conditions. Resistance includes C_T and C_AW, which are critical for prolonged missions and can govern the towing capacity under waves. Seakeeping performance evaluation employs three motion components: heave, roll, and pitch responses in irregular seas. Resistance performance is benchmarked against calm water design speed and its corresponding mean resistance coefficient. Seakeeping criteria specify threshold limits: significant single-amplitude roll/pitch motions ≤ 5° and heave motion ≤ 4 m. These parameters directly impact operational safety, ensure crane stability during hoisting, and guarantee the safety of the equipment and people onboard.

The determination of index weights constitutes a critical step in comprehensive evaluation processes, directly influencing the accuracy of results. The scientific validity and rationality of weighting methodologies fundamentally affect evaluation conclusions, necessitating multifactorial considerations during weight calculation. This study employs dual weighting approaches: the subjective weighting method and objective weighting method. The subjective method relies on expert domain knowledge through the Analytic Hierarchy Process (AHP), incorporating decision makers’ professional judgments with inherent subjectivity. The entropy-based weighting method, as an objective approach utilizing entropy for uncertainty quantification, is widely adopted. This research synthesizes both methodologies for weight determination.

The Analytic Hierarchy Process (AHP) [31] demonstrates high efficiency in multi-level decision-making scenarios. The procedural implementation for weight determination comprises the following:

(1) Construction of the judgment matrix:

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

(1)

Elements must belong to the same hierarchical level, with parametric relationships as specified in Equations (2)–(4).

$$a_{ii}=1, i=1,2,\cdots n$$

(2)

$$a_{ij}=1/a_{ji}, i,j=1,2,\cdots n$$

(3)

$$a_{ij}=a_{ik}/a_{jk}, i,j,k=1,2,\cdots n$$

(4)

(2) Eigenvalue derivation: Calculate eigenvalues of the judgment matrix A.

(3) Consistency check: Validate the matrix coherence through maximum eigenvalue verification:

$$AW={\lambda }_{max}W$$

(5)

where W is the relative weight vector and λ_max denotes the principal eigenvalue corresponding to W.

The Consistency Index (C.I.) is defined as follows:

$$C.I.={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(6)

The Consistency Ratio (C.R.) is calculated as follows:

$$C.R.={\displaystyle \frac{C.I.}{R.I.}}$$

(7)

where the Random Index (R.I.) values are tabulated according to the matrix order n (see

Table 3. Random Index (R.I.) values for AHP consistency check.

Matrix order (n)	1	2	3	4	5	6	7	8	9	10	11
R.I.	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52

).

When the Consistency Ratio (C.R.) satisfies C.R. < 0.1, the judgment matrix is deemed acceptable, and the relative weight vector W is subsequently derived.

The entropy-based weighting method [32] is implemented through the following procedural steps:

(1) The quantification of the information entropy contributions:

$$E_j=-k{\displaystyle \sum _{i=1}^t{p}_{ij}\ln p_{ij}, j=1,2,\cdots ,m}$$

(8)

where k = 1/lnt, with p_ij representing the normalized weight value of each x_ij:

$$p_{ij}=x_{ij}/{\displaystyle \sum _{i=1}^t{x}_{ij}, i=1,2,\cdots ,t}$$

(9)

(2) Definition of the contribution consistency degree (D_j):

$$D_j=1-E_j, j=1,2,\cdots ,m$$

(10)

(3) Weight calculation for criterion attributes:

$$a_j=D_j/{\displaystyle \sum _{i=1}^m{D}_j}, j=1,2,\cdots ,m$$

(11)

The criterion weights obtained via the AHP and entropy methods are denoted as ${A^1}_i=\left({a^1}_1,{a^1}_2,\cdots ,{a^1}_m\right)$ and ${A^2}_i=\left({a^2}_1,{a^2}_2,\cdots ,{a^2}_m\right)$, respectively, where I indicates the i-th primary criterion with the m sub-criteria. The combined weight is calculated as follows:

$$A_i=\beta {A^1}_i+\left(1-\beta \right){A^2}_i$$

(12)

where β is the preference coefficient.

Decision makers determine β based on the preference orientation. β = 0: fully objective weighting (exclusion of expert judgment). β = 1: fully subjective weighting (exclusion of empirical data). This study adopts β = 0.5 to balance the methodological perspectives.

3.2. Fuzzy Comprehensive Evaluation Model Formulation

The fuzzy comprehensive evaluation method accounts for multifactorial uncertainties through membership degree theory, enabling the quantitative transformation of qualitative assessments [33]. This approach effectively mitigates subjective biases and demonstrates superior capability in handling ambiguous, non-quantifiable parameters.

Primary criterion set:

$$U=\left\{u_1,u_2,\cdots ,u_n\right\}$$

(13)

For each primary criterion u_i (i = 1, 2, …, n) containing the m sub-criteria, the secondary criterion set is defined as follows:

$$u_i=\left\{u_{i1},u_{i2},\cdots ,u_{im}\right\}$$

(14)

Primary weight vector:

$$A=\left\{a_1,a_2,\cdots ,a_n\right\}$$

(15)

Secondary weight vector for u_i:

$$A_i=\left\{a_{i1},a_{i2},\cdots ,a_{im}\right\}$$

(16)

Evaluation grade set:

$$V=\left\{v_1,v_2,\cdots ,v_p\right\}$$

(17)

A membership degree relationship exists between the fuzzy set elements and evaluation grade set elements. When the membership degree lies within the interval (0,1), it indicates the partial belonging of the individual element to the fuzzy set.

Hydrodynamic performance is hierarchically evaluated from the basic to advanced levels, where secondary-level evaluations determine the membership degrees for the primary-level criteria. The membership degree of the sub-criterion u_ij to the evaluation grade v_k is defined as follows:

$$r_{ijk}, i=1,2,\cdots ,n; j=1,2,\cdots ,m; k=1,2,\cdots ,p$$

(18)

Secondary-level membership matrix:

$$R_i=\left[\begin{array}{c}{R}_{i1}\\ R_{i2}\\ \cdots \\ R_{im}\end{array}\right]=\left[\begin{array}{cccc}{r}_{i11}& r_{i12}& \cdots & r_{i1p}\\ r_{i21}& r_{i22}& \cdots & r_{i2p}\\ \cdots & \cdots & \cdots & \cdots \\ r_{im1}& r_{im2}& \cdots & r_{imp}\end{array}\right], i=1,2,\cdots ,n$$

(19)

Primary-level membership vector:

$$B_i=A_i\circ R_i, i=1,2,\cdots ,n$$

(20)

where ◦ denotes the fuzzy composition operator and B_i constitutes the primary fuzzy evaluation result.

Integrated evaluation matrix:

$$R=\left[\begin{array}{cccc}{B}_1& B_2& \cdots & B_n\end{array}\right]$$

(21)

Final comprehensive evaluation set:

$$B=A\circ R$$

(22)

After selecting the appropriate membership functions (e.g., triangular, trapezoidal) and composition operators (e.g., max–min, max–product), the normalized final evaluation vector is obtained as follows:

$$N_{score}=B\times V$$

(23)

4. Hydrodynamic Performance Indicator Calculation

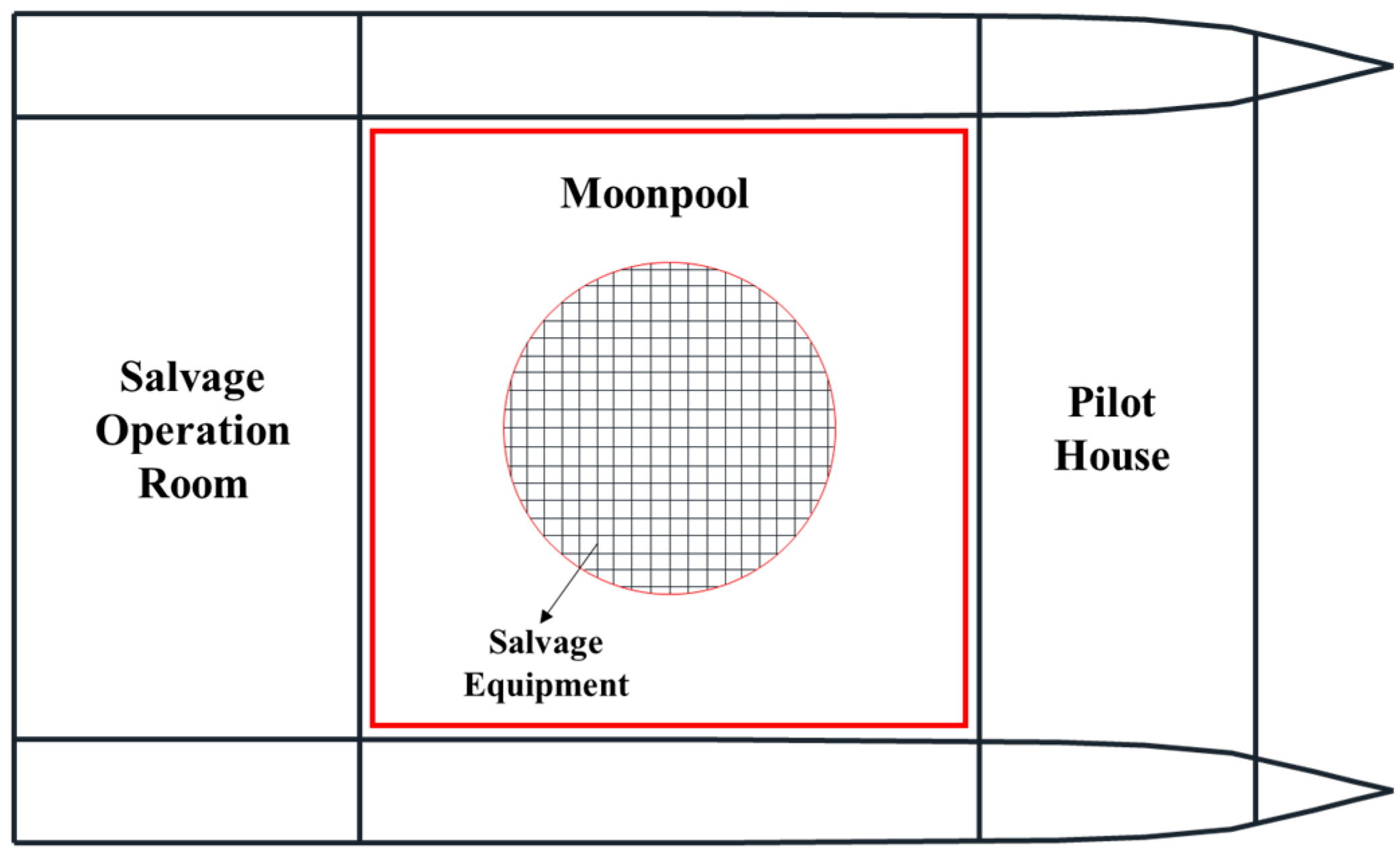
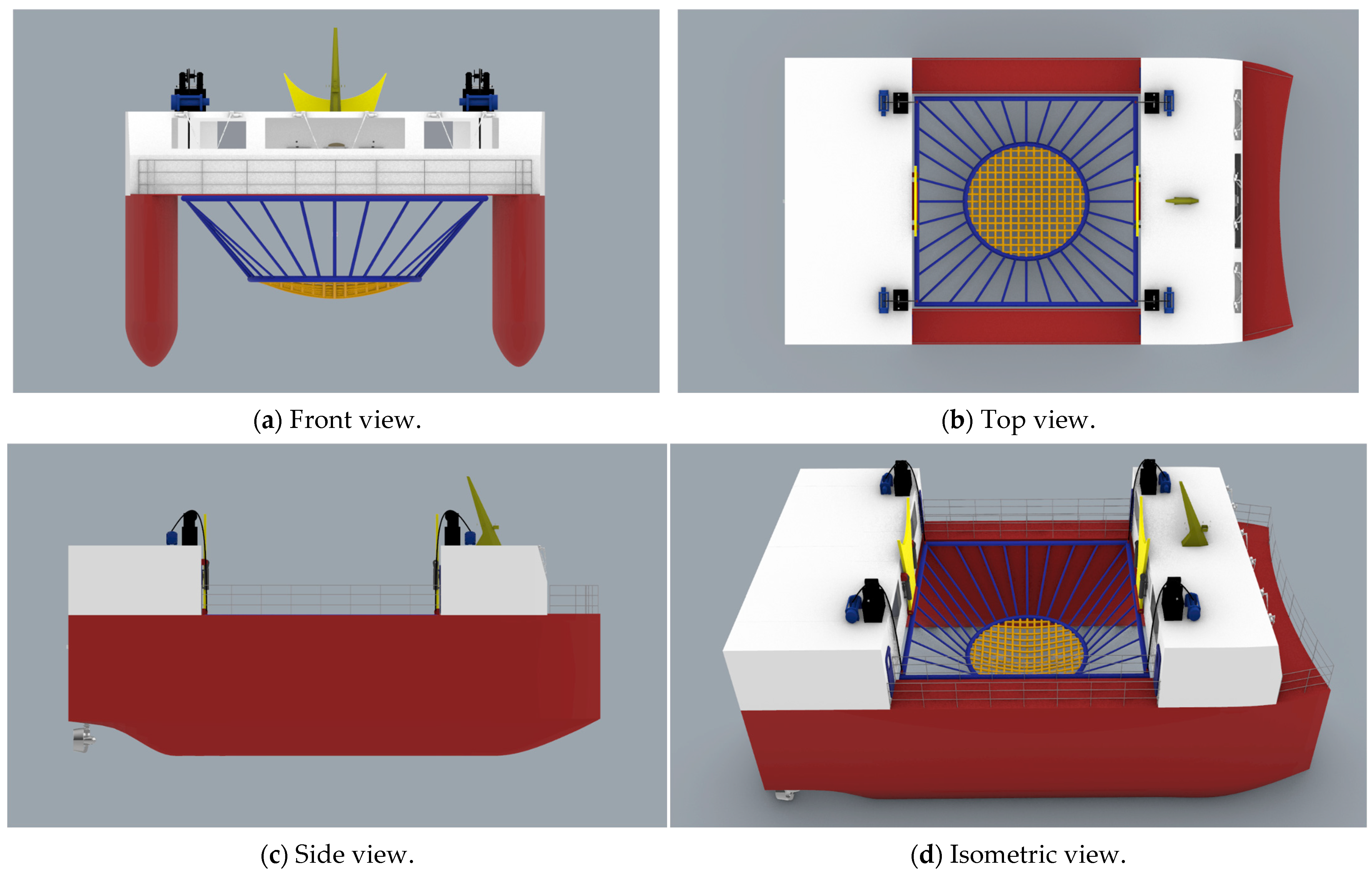
4.1. Resistance Performance

With the rapid advancement of computer technology, the efficiency of numerical computation has significantly improved. CFD technology has been extensively applied in naval architecture and marine engineering due to its superior characteristics of high efficiency, low costs, and strong operability. This study employs the CFD software STAR-CCM+ (Release 18.04.008-R8) for numerical simulations of ship propulsion performance indicators. The Navier–Stokes equations and continuity equation for incompressible fluids are adopted to resolve the turbulent flow problems, with the k-ε turbulence model implemented to close the N-S equations. Recognized as the most prevalent and widely used turbulence model, the k-ε model comprises two governing equations for the turbulent kinetic energy and dissipation rate [34]. To accurately track free surface deformation and complete resistance calculations for ships in both calm water and waves, the Volume of Fluid (VOF) method is employed to capture free surface variations.

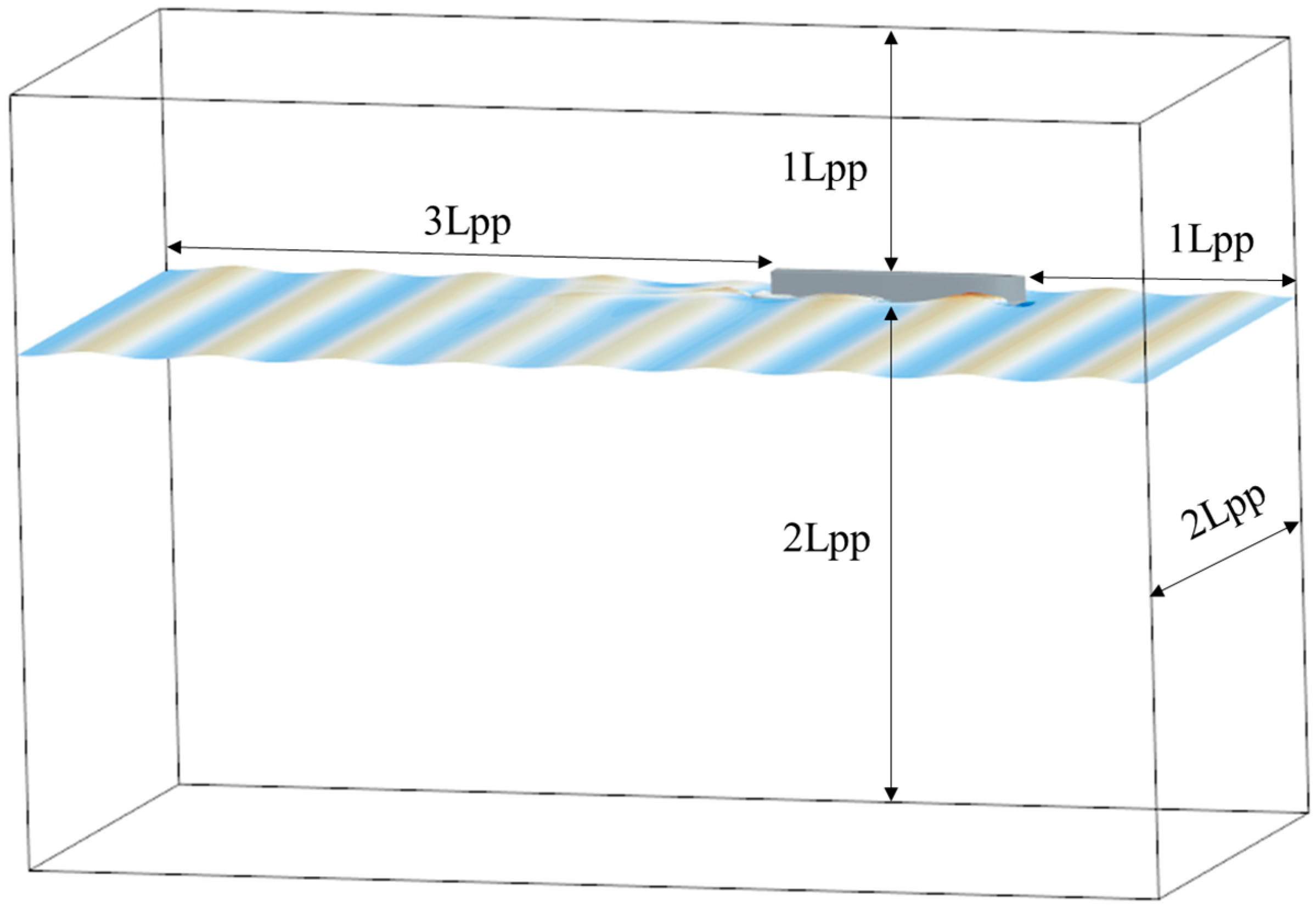
To ensure numerical simulation accuracy, eliminate boundary-induced reflected waves, and enhance computational efficiency, the appropriate configuration of the computational domain is essential. A rectangular computational domain (as illustrated in Figure 5) is established, with longitudinal dimensions of five times the ship length (Lpp), extending 2 Lpp upstream and 3 Lpp downstream from the stern origin. Vertically, the domain spans 2 Lpp below and 1 Lpp above the design waterline. The transverse dimension is set as 2 Lpp, with a 2.5 Lpp wave damping zone positioned at the domain outlet. The boundary conditions are specified as follows: no-slip wall for the hull surface, velocity inlet for the domain entrance and top, bottom, and far-side boundaries, pressure outlet for the domain exit, and symmetry plane for the near-side boundary. The computational domain and boundary configuration are illustrated in Figure 6.

For calm water resistance calculations, local grid refinement is implemented in the Kelvin wave region of the free surface to accurately capture wave patterns. A prism layer mesh with six layers is generated around the hull to resolve the near-wall flow characteristics, employing a growth rate of 1.3 between successive layers. The wall y+ value can be used to evaluate the quality of the near-wall mesh. It represents the dimensionless distance from the wall surface to the first node away from the wall surface. Generally speaking, different turbulence models have different requirements for the wall y+ value. For example, for the standard k-ε turbulence model, it is usually desired that the wall y+ value is within the range from 30 to 300. In this way, it is ensured that the turbulent boundary layer in the near-wall region can be well resolved, making the calculation results more accurate. The hull surface mesh configuration is presented in Figure 7. To achieve high simulation accuracy and computational efficiency, we have used the method of prism layers and near-wall refinement in the meshing of the hull surface. The meshing method can perform more precise discretization and description of the boundary layer. In addition, the mesh structure of the prism layer can make the mesh denser near the wall surface and gradually sparser in the region away from the wall surface. This gradient mesh distribution not only meets the requirements for mesh resolution in boundary layer simulation, but also avoids excessive mesh refinement throughout the entire computational domain, thus effectively controlling the number of meshes and computational costs. Compared with uniformly distributed meshes, this meshing method can significantly improve computational efficiency on the premise of ensuring computational accuracy.

Numerical simulations of catamarans in irregular waves employ the overset grid technique. The computational domain is divided into two distinct grid zones: overset grids and background grids. Separate meshes are generated for the background and overset domains, with an interface established between them to facilitate data exchange. Considering the VOF wave model implementation, two levels of volumetric grid refinement are created to capture Kelvin waves, hull wake flows, and free surface features. To ensure accurate data transfer between the overlapping regions and the realistic simulation of catamaran motions in regular waves, the grid sizes are strictly matched between the two domains. Sufficient grid resolution along both the wave height and propagation directions is maintained to mitigate numerical dissipation, with the mesh dimensions determined by the incident wavelength requirements: 60–100 cells per wavelength and 10–20 cells in the wave height direction. The grid refinement in overlapping regions and the free surface is illustrated in Figure 8.

Given the geometric symmetry and identical flow fields around the twin hulls of the catamaran, a half-model configuration is adopted to enhance computational efficiency. The RANS-based standard k-ε model is selected for turbulence closure. The implicit unsteady (second-order backward Euler) method is set as solution method, with the time step as 0.01 s. The governing equations are discretized using the finite volume method and solved through the SIMPLE algorithm. The ship motions in waves are simulated via the Dynamic Fluid Body Interaction (DFBI) approach, while free surface evolution is captured using the VOF method.

To verify the rationality of grid sizing in the numerical simulations of the salvage catamaran and quantify the uncertainties arising from spatial discretization, this study conducted a grid convergence analysis. Three grid sets with varying resolutions (designated as fine, medium, and coarse) were generated [35]. The grid convergence index (GCI) method was employed to assess the numerical uncertainties and convergence behavior induced by grid density. The complete methodological details of the GCI implementation can be found in [36].

This study primarily focuses on numerical investigations of resistance and seakeeping performance for the salvage catamaran, with rigorous quantification of the discretization uncertainties inherent in these simulations. Three distinct grid configurations were systematically implemented for each computational case: fine (N_F), medium (N_M), and coarse (N_C) mesh systems. φ1, φ2, and φ3 correspond to the solutions (calm water resistance coefficient and wave-added resistance coefficient) with the fine, medium, and coarse grids. The calm water resistance coefficient was calculated in Fr = 0.7 conditiond, and the wave-added resistance coefficient was calculated under Case4 wave conditions. The convergence ratio R, approximate relative error Ea,21, extrapolated relative error Eext,21, and fine-grid convergence index GCIfine,21, were calculated following the verification methodology. As demonstrated in

Table 4. Results of the mesh convergence study.

	NF	NM	NC	R	φ1	φ2	φ3	Ea,21	Eext,21	GCIfine,21
Calm water	4,178,100	2,943,657	2,074,712	0.733	4.503	4.525	4.555	0.489%	0.596%	1.68%
Irregular wave	5,386,814	3,117,000	1,800,256	0.7	3.33	3.355	3.391	0.739%	0.847%	2.11%

, all spatial convergence studies exhibited monotonic convergence (0 < R < 1). The discretization error for the fine-grid configuration was confirmed to be below 2.11%, validating the numerical reliability of the adopted mesh system. The medium grid was selected for subsequent simulations to balance the accuracy and computational cost.

To validate the reliability of the numerical methodology, experimental data from the internationally recognized Delft-372 benchmark hull are adopted for verification [37]. This hull form has accumulated extensive experimental datasets under various Froude number (Fr) conditions, including calm water resistance characteristics and motion responses in wave conditions, thereby providing a robust basis for validating numerical approaches. The experiments were conducted in the CNR-INSEAN No. 2 towing tank. Three CCD cameras were employed to measure the model motions, while the total wave-induced resistance was directly measured using load cells installed between the hulls.

Typical Fr values of 0.5, 0.55, 0.6, 0.65, 0.7, and 0.75 are selected for calm water resistance validation. For the hydrodynamic performance evaluation in head wave conditions, numerical simulations are conducted with multiple wave parameters at Fr = 0.7, and the computational results are compared against scaled model test data. To facilitate quantitative comparison, results are processed through non-dimensionalization. The dimensionless form of the mean calm water resistance is expressed as follows:

$$C_T={\displaystyle \frac{R_{calm}}{0.5\rho S{U}_{ship}^2}}$$

(24)

where R_calm represents the longitudinal mean resistance in calm water, S denotes the wetted surface area, and U_ship is the ship speed.

The wave-added resistance R_AW in regular waves is defined as the difference between the mean resistance in waves and calm water. The nondimensional form of R_AW is as follows:

$$C_{AW}={\displaystyle \frac{R_{AW}}{\rho g{\eta }^2{b}^2/L_{pp}}}$$

(25)

where b represents the ship breadth, η denotes the incident wave amplitude, and L_pp indicates the length between perpendiculars.

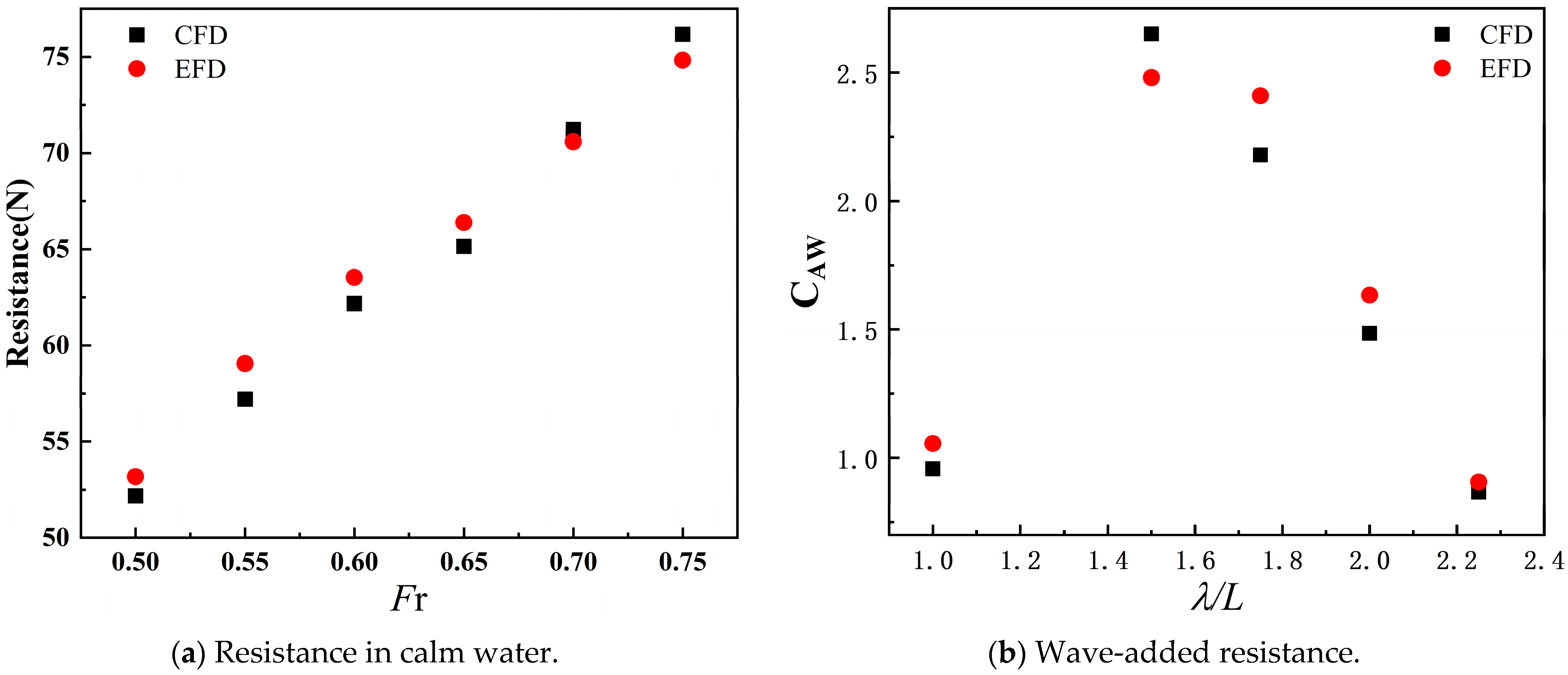
The numerical results and experimental measurements, as illustrated in Figure 9, demonstrate the validity of the numerical methodology employed in this study. For the calm water resistance, the percentage errors at Fr = 0.5–0.75 are 1.87%, 3.16%, 2.12%, 1.86%, 0.92%, and 1.81%, respectively. Regarding the wave-added resistance coefficient (1.0–2.25), the corresponding errors are 9.38%, 6.85%, 9.54%, 9.12%, and 4.3%, all below 10%. The crossover at λ/L = 1.5 maybe arises from the wave-breaking effects not fully captured by the RANS k-ε model. Viscous damping in experiments reduces the wave-added resistance, causing EFD overprediction, and overestimates turbulence dissipation in steep waves, causing CFD limitations. The close agreement between the computational results and experimental data demonstrates the reliability of the CFD solver employed in this study, confirming its capability to accurately predict ship resistance in both calm water and waves.

For the calm water resistance analysis of the novel catamaran salvage vessel, six operational conditions spanning from low to high speeds are investigated. A single demi-hull with symmetry boundary conditions is simulated, requiring the multiplication of the computed resistance by a factor of two to obtain the total resistance of the twin-hull configuration.

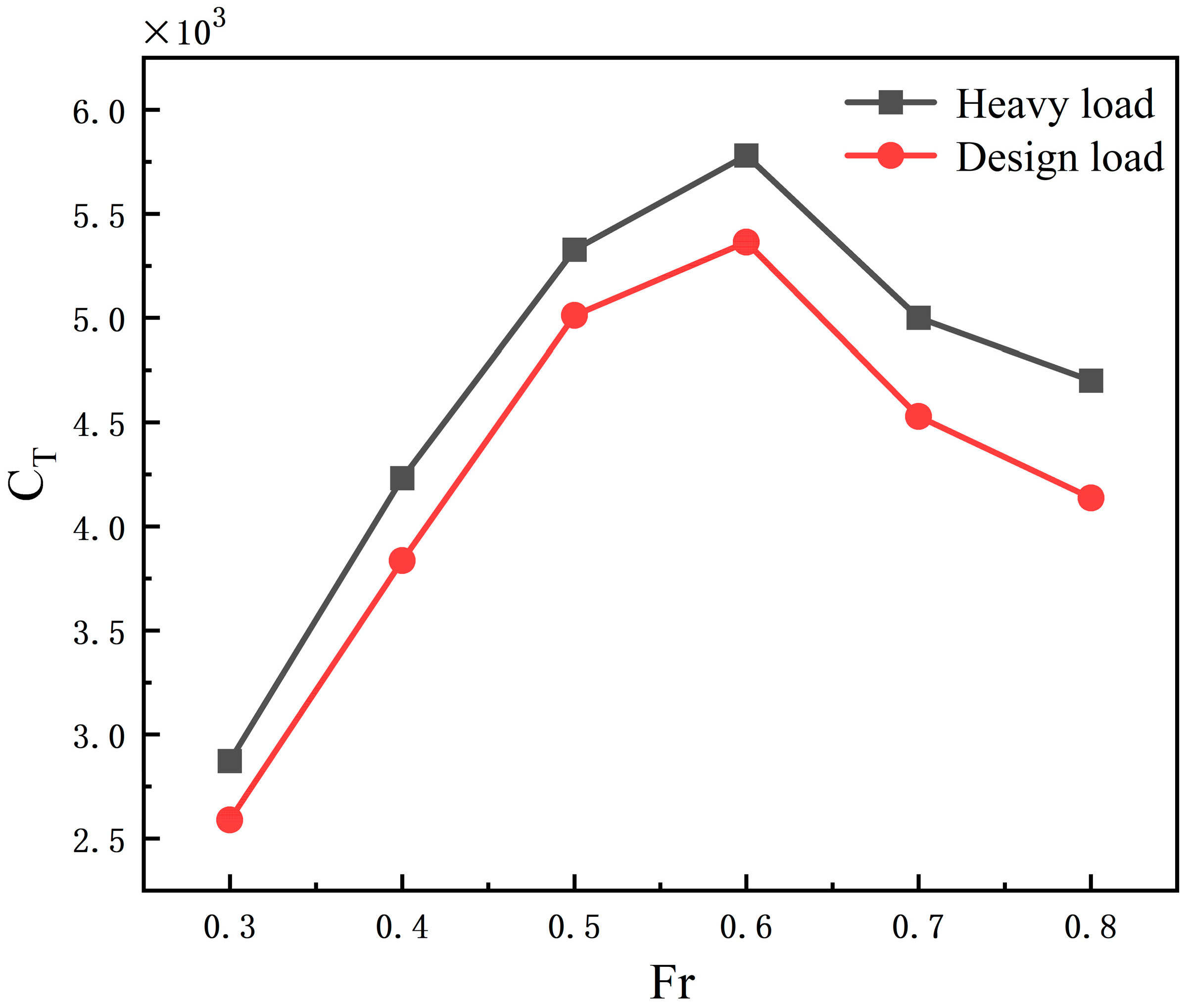
The design speed of the proposed catamaran salvage vessel is 15 knots (Fr ≈ 0.5), which serves as the baseline for propulsion performance evaluation. Calm water resistance coefficients under both light-load and design-load conditions are calculated across varying speeds, as shown in Figure 10. The results reveal that resistance increases progressively with speed under both loading conditions, peaking at Fr = 0.6 before declining. The design-load condition consistently exhibits higher resistance than the light-load condition across all speeds, with the discrepancy amplifying as speed increases.

Comparative wave pattern profiles at the design speed for both loading conditions in calm water are presented in Figure 11. The analysis indicates that wave crests and troughs in the design-load condition exceed those in the light-load condition. Under light-load conditions, the average liquid surface elevation measures approximately −0.01 m, closely aligning with the still water level. This indicates a shallower hull draft, exerting minimal influence on the elevation of the surrounding water level. In contrast, heavy-load conditions exhibit an average liquid surface elevation of approximately 0.43 m, significantly surpassing the light-load scenario. This demonstrates deeper hull immersion, resulting in a marked overall water level rise in the vicinity. The intensified hull–fluid interactions under heavy loading further amplify the hydrodynamic disturbances, with the hull exerting stronger fluid disturbance effects on the surrounding flow field.

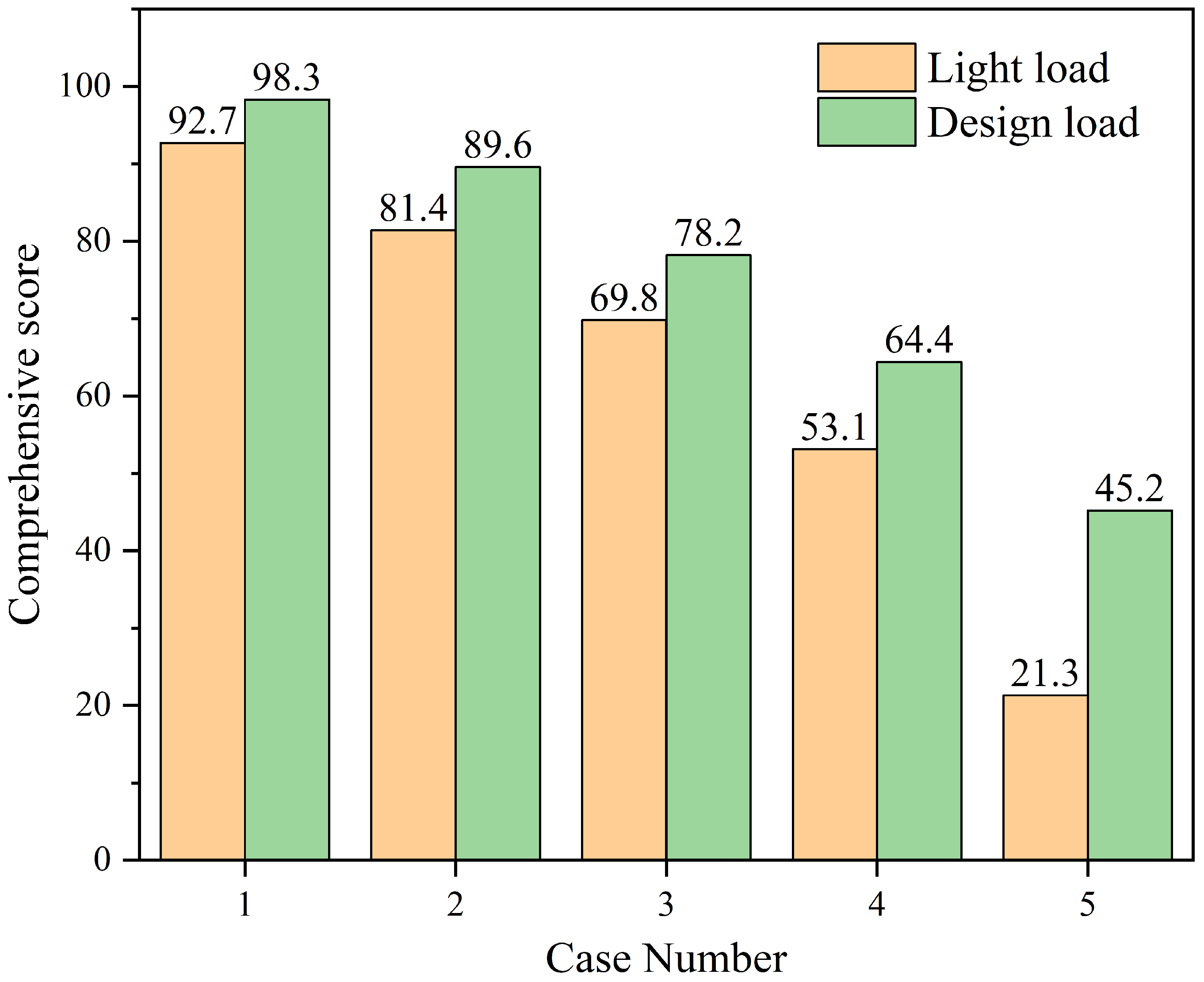
Based on the irregular wave conditions under different sea states described in Section 2.2, the wave-added resistance coefficients for Cases 1–5 are calculated using the JONSWAP wave spectrum. Numerical simulations are conducted at the design speed (15 knots) in head wave conditions, with the computational results of wave-added resistance coefficients across varying sea states presented in Figure 12. For sea states 1 to 5, the wave-added resistance coefficients under heavy-load conditions exhibit increments of 0.334, 0.476, 0.51, 0.62, and 0.641 compared to light-load conditions, with corresponding growth rates of 30.71%, 28.85%, 23.39%, 22.88%, and 21.82%, respectively. This demonstrates a monotonic decline in the growth rates from 30.71% (sea state 1) to 21.82% (sea state 5), indicating that the influence of heavy-load conditions on wave-added resistance marginally diminishes with increasing sea state severity. In lower sea states (1–2), where wave disturbances are relatively mild, the increased draft under heavy-load conditions induces significant flow field modifications, resulting in higher sensitivity in resistance amplification. In higher sea states (4–5), an elevated wave energy intensity dominates ship–wave interactions, where nonlinear hydrodynamic interactions govern hull motions. Consequently, the percentage contribution of heavy-load effects to resistance increments becomes less pronounced compared to the baseline resistance induced by intense wave actions. The results demonstrate that the wave-added resistance coefficients for both loading conditions exhibit a positive correlation with sea state severity, increasing proportionally with significant wave height (Hs) and spectral peak period (Tp). The comparative free surface profiles between the two loading conditions at the design speed under irregular wave conditions are illustrated in Figure 13. The analysis reveals that the wave crests and troughs of irregular waves are more pronounced in the design-load condition than in the light-load condition. Under light-load conditions, the wave amplitudes are smaller with gentler liquid surface fluctuations, while heavy-load conditions exhibit larger wave amplitudes and more pronounced liquid surface variations. This indicates that the ship hull exerts a greater influence on wave patterns during heavy-load operations, resulting in stronger hydrodynamic responses. Wave propagation appears more dispersed in light-load scenarios, allowing for relatively unrestricted wave transmission, whereas under heavy-load conditions, wave patterns become more concentrated with increased obstruction and disturbance near the hull region, leading to alterations in both the wave propagation direction and morphological characteristics.

4.2. Seakeeping Performance

To optimize computational efficiency, seakeeping analysis in this section is performed using the potential flow-theory-based AQWA software (Release 15.0, ANSYS, Inc.). Initially, hydrodynamic meshes are generated for the catamaran hulls. During the numerical setup, each wavelength must span at least seven maximum element sizes. Insufficient grid density may lead to non-convergent results, while excessive refinement would cause computational inefficiency. Therefore, the mesh size is determined based on the maximum frequency of interest during grid generation. The resulting mesh configuration is illustrated in Figure 14.

The hydrodynamic responses are analyzed through simulations of unit amplitude regular waves with varying frequencies and incident directions, providing preliminary insights into the vessel’s hydrodynamic performance [10]. Given the catamaran’s structural symmetry, the wave directions are limited to 0–180° with 45° increments: 0° (head waves), 90° (beam waves), and 180° (following waves). The wave frequency range is set from 0.01592 Hz to 1.04151 Hz according to the mesh resolution requirements. The detailed parameters are listed in

Table 5. Parameters of different wave directions and frequencies.

Parameter (Unit)	Value
Wave direction (°)	0, 45, 90, 135, 180
Wave frequency (Hz)	0.01592–1.04151
Frequency interval	0.025

.

Prior to analysis, the validation of the computational results is essential. The experimental data for validation are obtained from the Delft model tests [37], which have been extensively studied with comprehensive datasets including calm water resistance at various speeds and motion responses in waves. This internationally recognized benchmark is therefore selected to verify the rationality of the numerical methodology. Based on the experimental data, numerical simulations of multiple head wave conditions at Fr = 0.7 are conducted, and a comparative analysis with scaled model test results is performed. 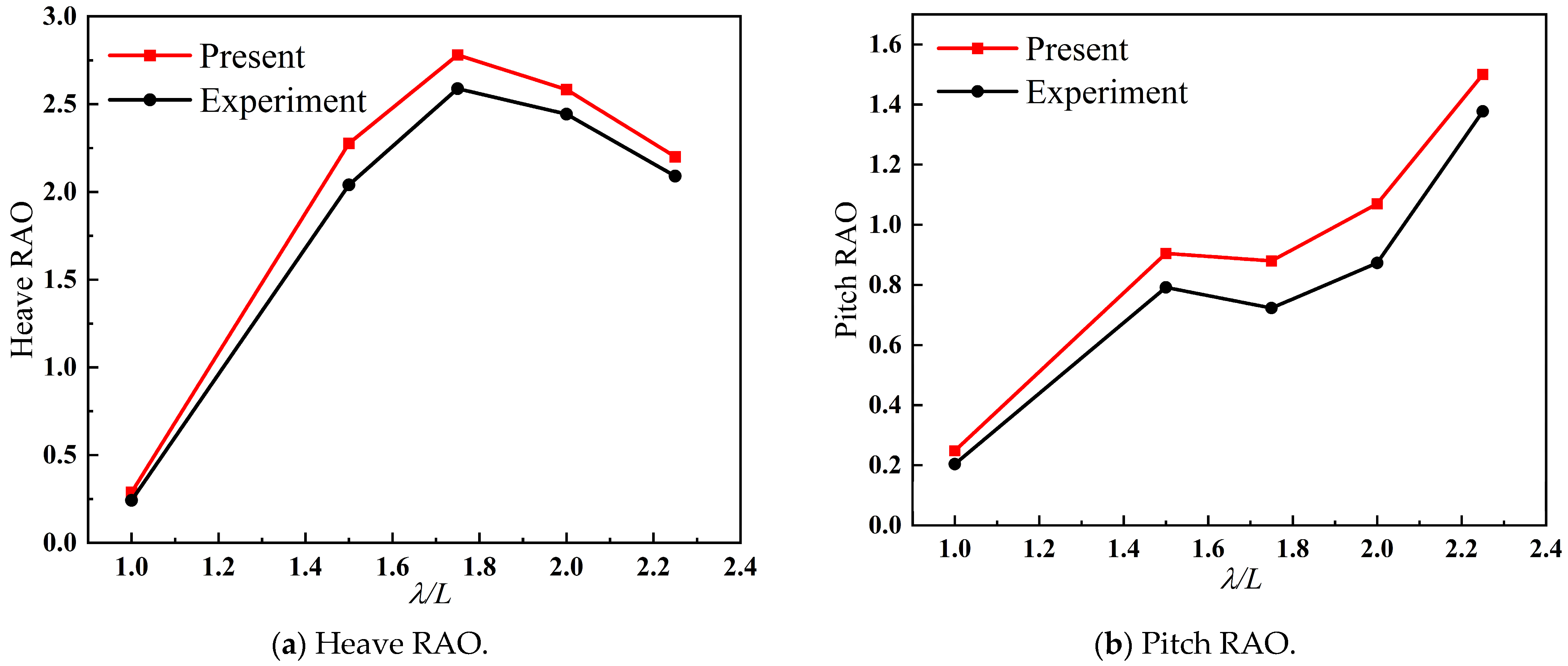The validation outcomes, as shown in Figure 15, confirm the effectiveness of the proposed numerical approach.

A close agreement in trend is observed between the computational and experimental results, though the former generally overestimates the latter due to the neglect of fluid viscosity in the potential flow theory. This discrepancy validates the reliability of the potential flow solver, demonstrating its applicability for predicting catamaran motions in waves.

Using the unit amplitude regular waves with varying frequencies and incident angles defined in the previous section, hydrodynamic responses are calculated for both the light-load and design-load conditions. The relationships between frequency, wave direction, and Response Amplitude Operators (RAOs) are comprehensively illustrated in Figure 16, Figure 17 and Figure 18. The results indicate that motion amplitudes generally decrease with increasing wave frequencies, with the design-load condition exhibiting larger RAO magnitudes than the light-load condition. Pronounced low-frequency characteristics are observed at reduced wave frequencies, while motion responses asymptotically approach zero at higher frequencies.

As shown in the heave RAO curves (Figure 16), the maximum heave motions occur under beam wave conditions (90°), while oblique waves show minimal influence. Similar heave variation patterns are observed across all wave directions except 90°. For the light-load condition, RAOs exhibit a steep waterfall-like decline in the low-frequency regions, reaching the first trough at 0.3 Hz. A moderate recovery occurs in the mid-frequency regions with limited amplitude growth. The twin-hull configuration induces dual RAO peaks at a 90° wave incidence, where the maximum peak corresponds to the global extremum. This suggests intense motion responses between 0.3 and 0.6 Hz under beam waves. Despite sharing similar RAO trends, the design-load condition produces larger motion magnitudes. Dual peaks are also observed in mid-frequency regions at 90° incidence, but the secondary peak is smaller than in the light-load condition, indicating stabilized motions around 0.5 Hz for the design-load case.

Wave direction significantly affects the rotational motion responses. The pitch RAO curves (Figure 17) reveal maximum pitch motions under head (0°) and following (180°) waves. Longitudinal wave forces show limited impact on pitch amplitude variations, with negligible changes observed at 90° incidence. For light-load conditions, RAOs demonstrate an initial rise followed by a decline in the low-frequency regions. Complex multi-peak phenomena emerge in the mid-frequency ranges, where oblique waves generate higher peak responses than head/following waves. In contrast, the design-load condition eliminates mid-frequency multi-peak behavior at 0° and 180° incidences, while maintaining other trend similarities.

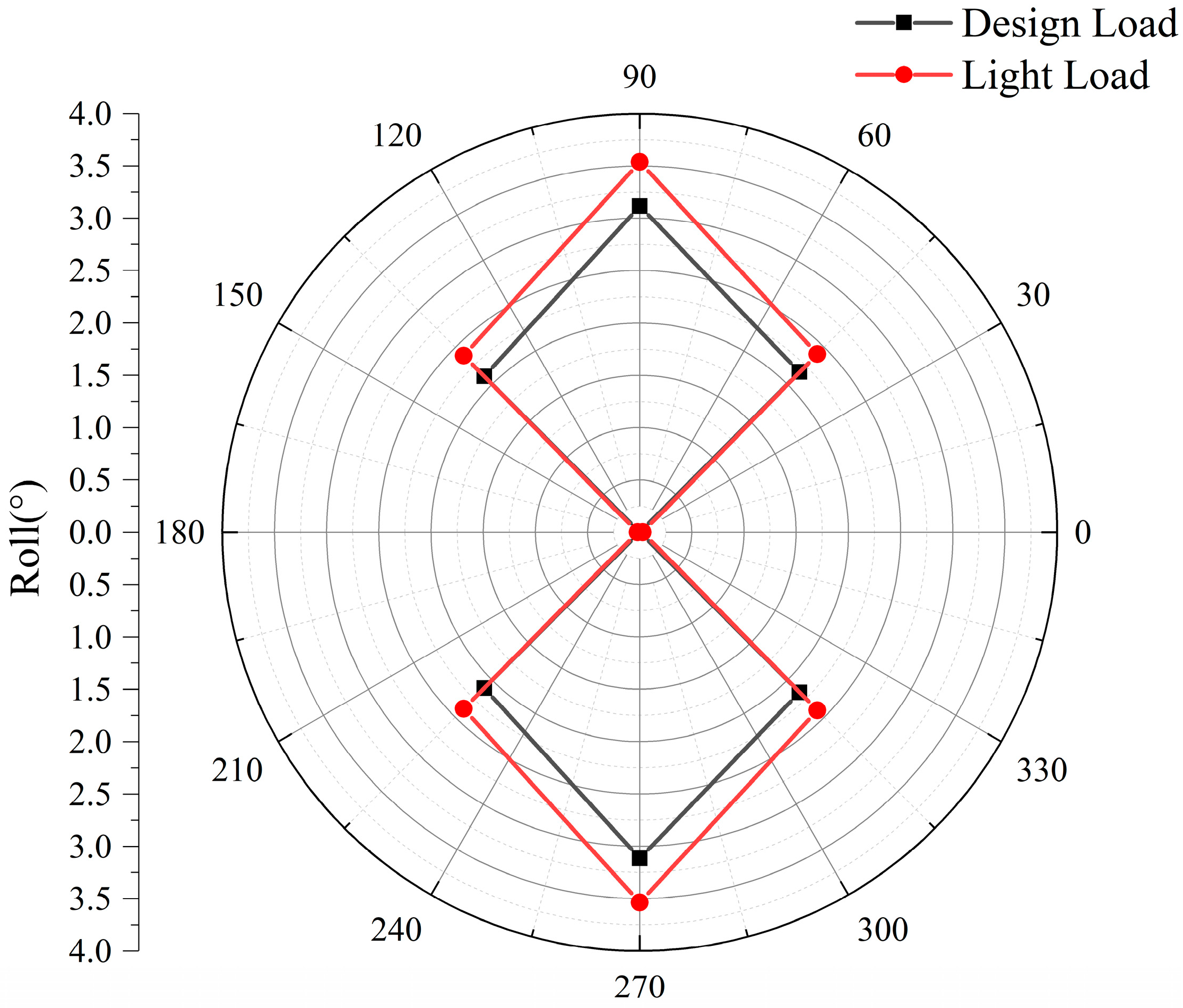
The roll RAO curves (Figure 18) show maximum roll motions under beam waves (90°), with significantly amplified peaks compared to other wave directions. Longitudinal wave forces minimally influence the roll amplitude variations, as evidenced by near-zero RAO values at 0° and 180° incidences. At a 90° wave incidence, the light-load condition exhibits dual RAO peaks, with the mid-frequency peak reaching the maximum magnitude. The design-load condition displays a single peak at 90° incidence, but develops dual peaks in the mid-frequency regions under oblique waves.

Based on the irregular wave conditions under varying sea states defined in Section 2.2, numerical simulations of Cases 1–5 are conducted using the JONSWAP spectrum. The simulations are carried out at the design speed with wave incidence angles ranging from 0° to 180° at 45° intervals, yielding five directional conditions. Head waves (0°) are selected as the evaluation basis for heave and pitch motions, while beam waves (90°) serve as the reference for roll motions. Figure 19, Figure 20 and Figure 21 present motion response envelope diagrams of heave, roll, and pitch under Case4 sea conditions, where the radial coordinates represent significant motion response values.

The response amplitudes of heave, pitch, and roll decrease with the increasing payload across all wave directions. For the heave motion, both loading conditions exhibit consistent response patterns with positive values, though the payload variation significantly affects the heave motion characteristics. The wave incidence angles show limited influence on the heave responses, with maximum amplitudes occurring under 90° beam waves, aligning with the findings from regular wave analyses. Pitch motion responses demonstrate consistent trends between loading conditions, with payload showing a negligible impact. Maximum pitch amplitudes occur at 0° (head waves), diminish to near-zero values at 90° (beam waves), and exhibit intermediate magnitudes at 45° (oblique waves). Roll motion patterns remain consistent across loading conditions, with payload exerting minimal influence. Roll amplitudes approach zero at 0° (head waves), peak at 90° (beam waves), and progressively increase at 45° (oblique waves), reaching magnitudes comparable to the beam wave conditions.

5. Comprehensive Hydrodynamic Performance Evaluation

Based on the fuzzy comprehensive evaluation methodology described in Section 3 and the hydrodynamic performance indicators calculated in Section 4, the summarized response amplitudes of the evaluation metrics are presented in

Table 6. Summarized response amplitudes of evaluation metrics.

Indicator	Sub-Indicator	Case1		Case2		Case3		Case4		Case5
		Light Load	Design Load	Light Load	Design Load	Light Load	Design Load	Light Load	Design Load	Light Load	Design Load
u1	u11	5.01	5.33	5.01	5.33	5.01	5.33	5.01	5.33	5.01	5.33
	u12	1.09	1.42	1.65	2.13	2.18	2.69	2.71	3.33	2.94	3.58
u2	u21	1.12	0.88	1.75	1.32	2.1	1.68	2.37	1.85	2.78	2.2
	u22	0.65	0.48	0.92	0.71	1.25	0.98	1.4	1.1	1.65	1.32
	u23	1.85	1.62	2.83	2.45	3.2	2.91	3.53	3.11	3.85	3.4

. Among these, the calm water resistance coefficient and wave-added resistance coefficient under the “propulsion performance” primary indicator are classified as cost-type criteria, where lower values indicate superior performance. Similarly, heave, pitch, and roll motions under the “seakeeping” primary indicator also belong to cost-type criteria.

The weight coefficients are determined through an integrated Analytic Hierarchy Process (AHP) and the entropy weight method with a preference coefficient of 0.5, as detailed in

Table 7. Weight coefficients.

Indicator (U)	Weight (A)	Sub-Indicator (ui)	Weight
			A1i	A2i	Ai
u1	0.333	u11	0.5	0.004	0.252
		u12	0.5	0.207	0.354
u2	0.667	u21	0.539	0.38	0.46
		u22	0.297	0.112	0.205
		u23	0.164	0.165	0.165

. As shown in the results, the C_T (calm water resistance) metric exhibits low variability across all samples (range: 5.01–5.33), leading to higher information entropy, reduced utility value, and consequently a lower entropy weight. In contrast, heave motion demonstrates greater data dispersion, resulting in an elevated entropy weight. The heave metric attains the highest weight (29.6%), aligning with the practical engineering prioritization of seakeeping performance. The relatively low roll weight (10.5%) reflects the inherent roll stability superiority of catamarans over monohulls. While most indicator values remain within acceptable ranges, outliers may adversely affect the evaluation outcomes. Metrics deviating significantly from the equilibrium values risk having their weights disproportionately amplified or attenuated. To mitigate data distortion, the evaluation metrics are converted into percentage-scaled values using semi-trapezoidal membership functions. The normalized percentage-scale data, tabulated in

Table 8. Normalized percentage-scale data.

Indicator	Sub-Indicator	Case1		Case2		Case3		Case4		Case5
		Light Load	Design Load	Light Load	Design Load	Light Load	Design Load	Light Load	Design Load	Light Load	Design Load
u1	u11	100	0	100	0	100	0	100	0	100	0
	u12	100	89.6	79.5	41.8	56.2	35.5	34.9	0	25.3	0
u2	u21	87.4	100	56.6	78.4	35.8	63.2	21.6	51.1	0	34.7
	u22	89.7	100	62.4	81.2	41	61.5	28.2	53.8	0	30.8
	u23	90.5	100	60.1	74	43.9	58.3	23.7	47.1	0	21.3

, will be utilized for subsequent fuzzy membership degree calculations.

Following the theoretical framework in Section 3, Gaussian functions are selected as membership functions to calculate second-level correlation matrices (Ri) for propulsion and seakeeping performance. The M (·, +) operator is employed to combine Ri with weight sets (Ai), generating membership degree matrices (Bi), which simultaneously serve as first-level fuzzy comprehensive evaluation matrices. Based on the hierarchical structure of the evaluation system, the matrices (Bi) are restructured to form the first-level correlation matrix R. The first-level fuzzy evaluation sets are aggregated and utilized as the evaluation matrix for second-level fuzzy comprehensive assessment, thereby deriving second-level membership degree matrices under different operational conditions. Following normalization and multiplication with alternative sets, the final evaluation scores are obtained. The comprehensive assessment results are summarized in

Table 9. Comprehensive assessment results.

Case Number	Condition	Scores
1	Light load	92.7
	Design load	98.3
2	Light load	81.4
	Design load	89.6
3	Light load	69.8
	Design load	78.2
4	Light load	53.1
	Design load	64.4
5	Light load	21.3
	Design load	45.2

.

Figure 22 presents the comprehensive scores of different cases under different load conditions. Analysis of the evaluation results indicates that under Case1 sea conditions, the catamaran achieves superior seakeeping and satisfactory propulsion performance in the design-load condition, ranking highest overall. In light-load conditions, it exhibits optimal wave-added resistance coefficients with balanced seakeeping metrics. Conversely, under Case5 sea states, both the heave and roll motions reach critical thresholds in light-load operations, necessitating operational caution. The design-load condition yields the lowest score due to severe motion responses, requiring avoidance in such sea states. The assessment identifies heave and roll motions as the dominant factors in seakeeping scores, indicating their optimization as critical for total score enhancement. For operations in long-period wave regions, increasing the heave weight coefficients is recommended. In short-period wave environments, elevating the pitch entropy weights improves system adaptability. A trade-off exists between propulsion and seakeeping performance, as demonstrated by Case5-Light achieving the maximum propulsion score, but catastrophic seakeeping failure, necessitating the avoidance of extreme light-load operations. Reducing the negative correlation between C_T (calm water resistance) and C_AW (wave-added resistance) is essential, as a C_T increase may reduce C_AW through speed reduction. Hull-form optimization strategies (e.g., block coefficient reduction) could synergistically decrease both parameters. Case2-Design under moderate sea conditions provides the optimal balance between energy efficiency and comfort.

6. Conclusions

This study focuses on a novel catamaran salvage vessel, establishing a hydrodynamic performance evaluation system that integrates both propulsion and seakeeping criteria. By quantifying the results through composite scores, the system effectively distinguishes hydrodynamic performance across varying sea states and operational conditions. The main conclusions are summarized as follows:

(1) This study presents the preliminary development of a novel salvage catamaran featuring an innovative moon pool configuration that enhances both operational safety and navigational maneuverability during salvage operations. Through CFD-based simulations, the hydrodynamic resistance characteristics were systematically investigated, encompassing calm water resistance and wave-added resistance under varying loading conditions. Wave-added resistance coefficients exhibit a proportional increase with a significant wave height (Hs) and spectral peak period (Tp). The design-load condition consistently generated higher calm water resistance compared to the light-load condition across all sea states, with this discrepancy amplifying progressively as the Hs and Tp increased.

(2) The seakeeping performance was analyzed using the potential flow theory to predict motion responses under various sea states and loading conditions. Short-term motion characteristics were evaluated across five wave directions in irregular wave environments. The results indicated that heave amplitudes exhibited a decreasing trend with increased payload, while the pitch and roll responses remained largely unaffected by the load variations. This differential sensitivity highlights the dominant influence of vertical mass distribution on heave motion compared to rotational degrees of freedom.

(3) This study develops a multi-level fuzzy evaluation framework that integrates entropy weight and the AHP hybrid weighting methodology to address the historical disconnect between seakeeping and rapidity assessments in hydrodynamic performance evaluation across diverse sea states. The proposed framework enables the multi-objective, hierarchical evaluation of hydrodynamic performance. For operations in long-period wave regions, heave weight coefficients should be increased. In short-period wave environments, pitch entropy weights require elevation. Adaptive assessment can be achieved by modifying the entropy method data windows (e.g., sliding window updates) for regions with variable wave period distributions.

While this study focuses on the evaluation of propulsion and seakeeping performance through numerical simulations, the current limitations include the absence of real-sea condition validations. Future work will prioritize prototype development followed by systematic tank tests and open-water trials. To further optimize hull configuration parameters—such as hull spacing, moon pool geometry, and load distribution—a comprehensive framework integrating AI-driven optimization algorithms will be implemented. Subsequent research directions should also investigate multi-objective design optimization balancing propulsion efficiency and seakeeping stability, thereby advancing the holistic development of next-generation salvage catamarans.