Multi-Channel Underwater Acoustic Signal Analysis Using Improved Multivariate Multiscale Sample Entropy
Abstract
1. Introduction
2. Methodology
2.1. Improved Multivariate Multiscale Sample Entropy
2.2. Algorithm Comparison
3. Simulation Analysis
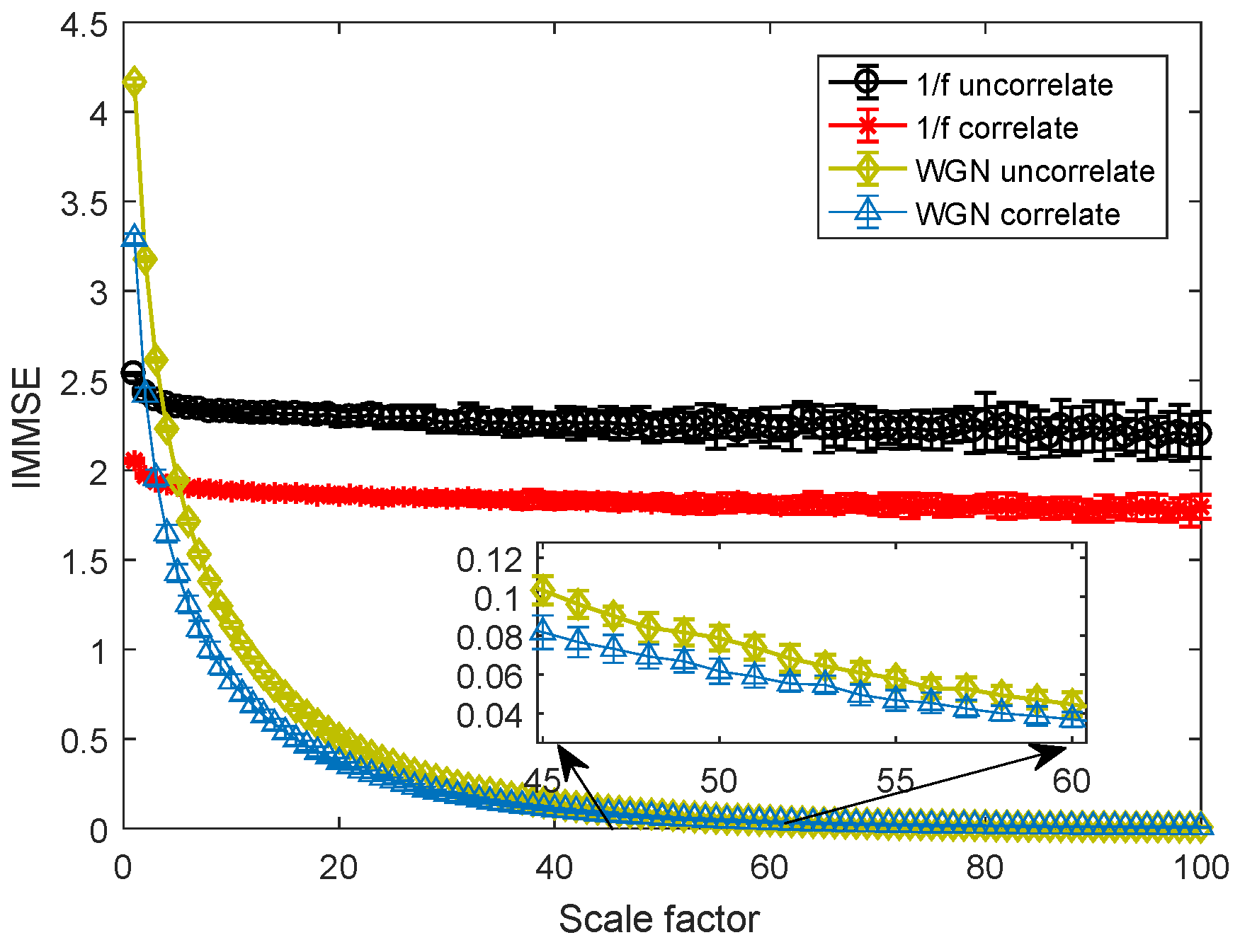
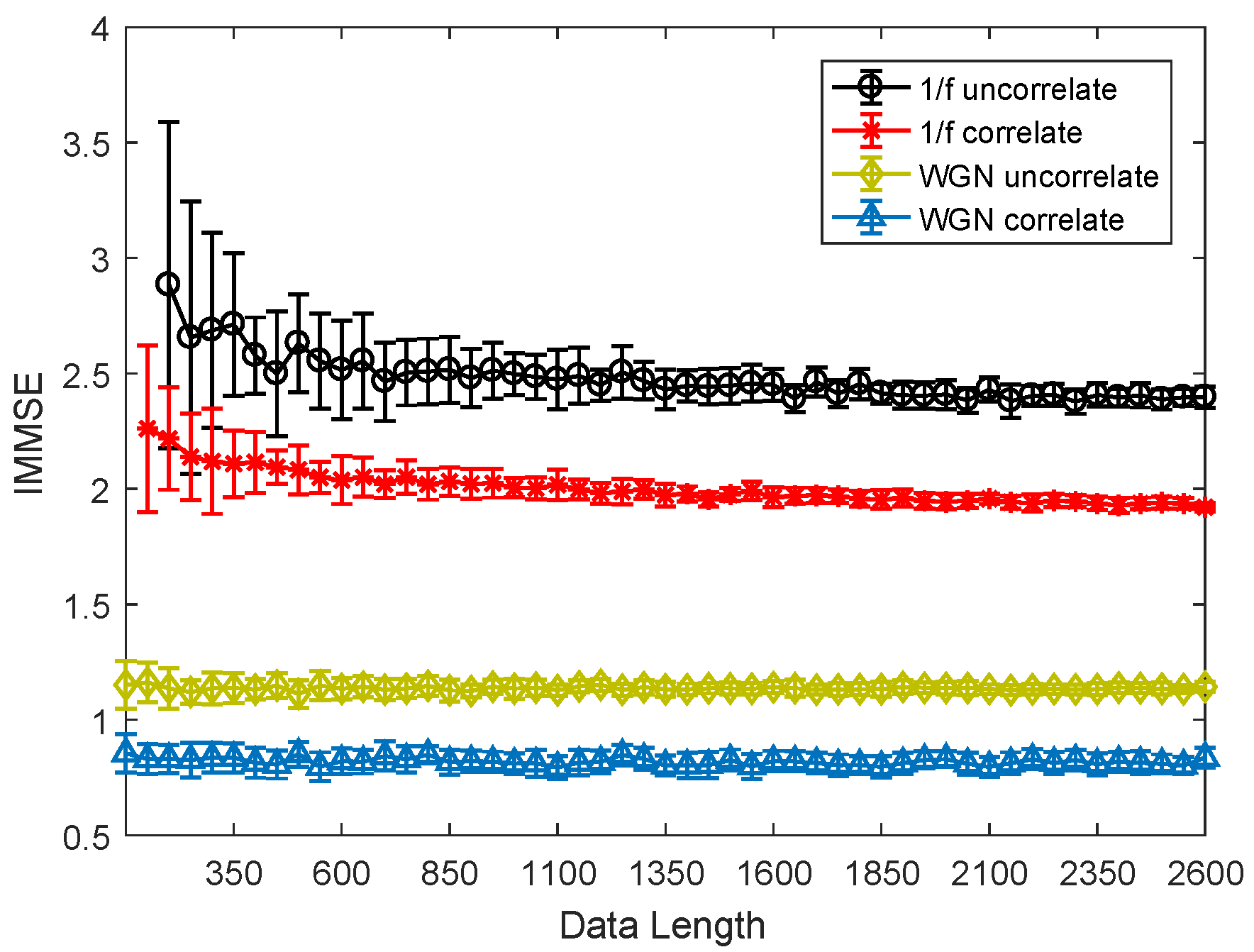
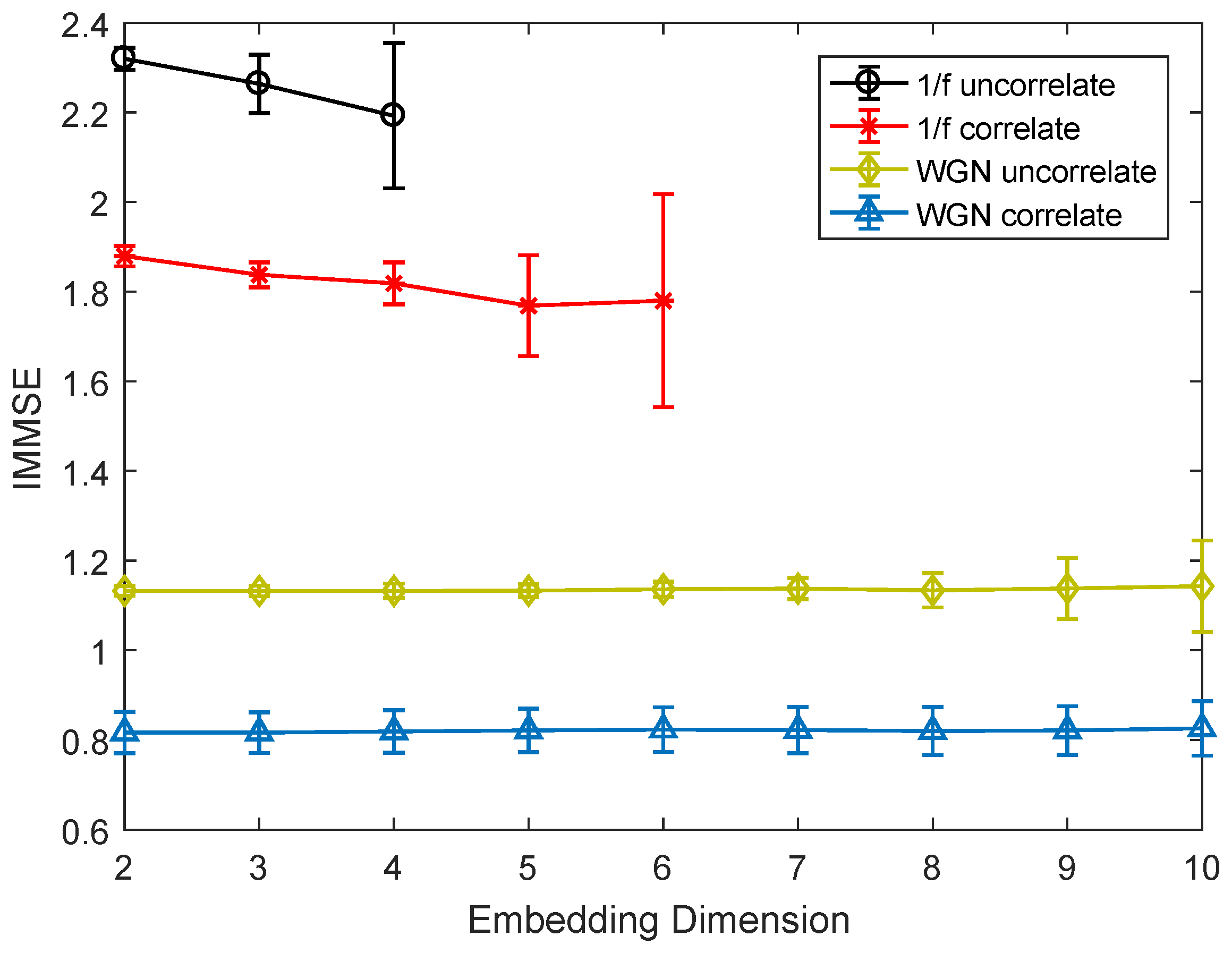
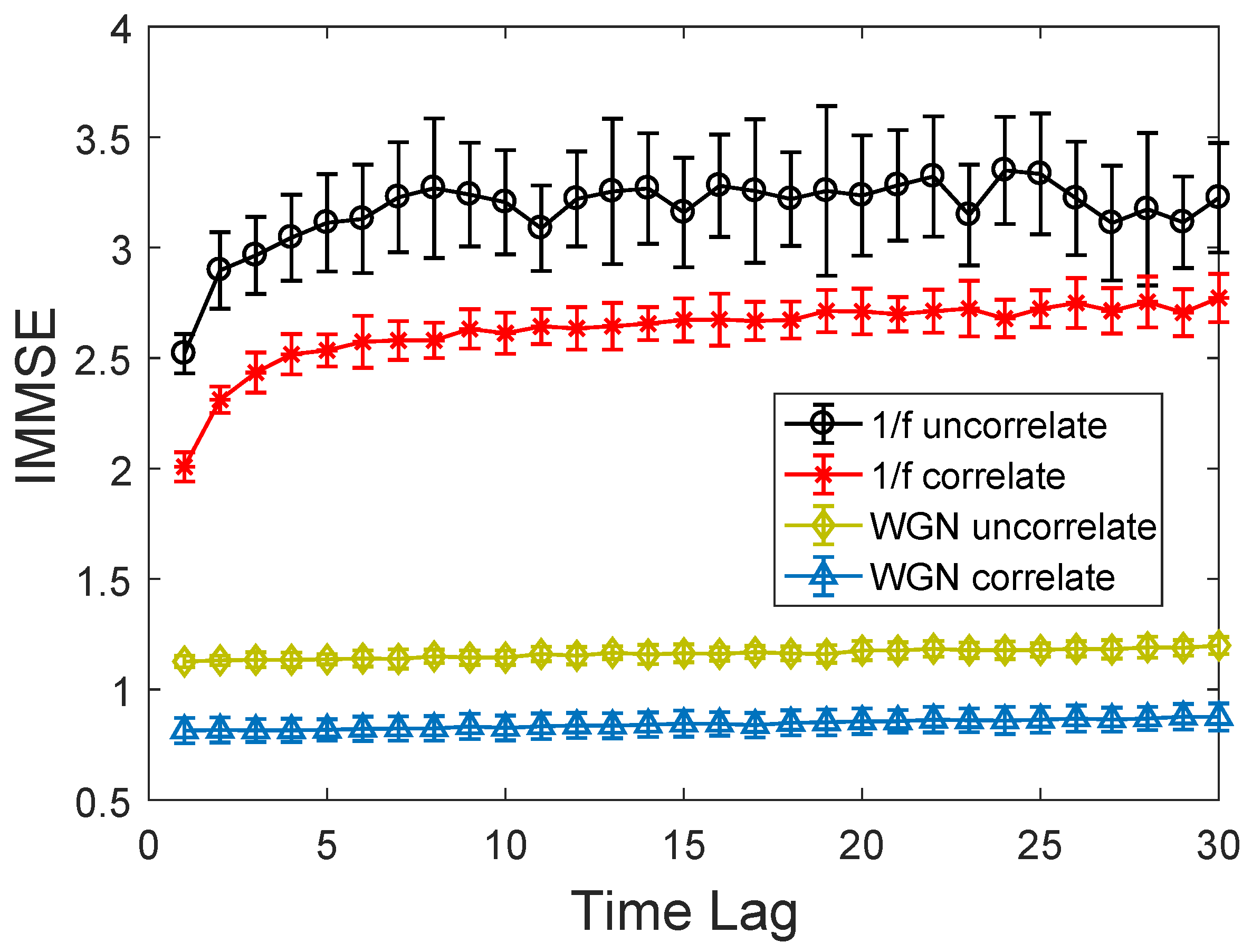
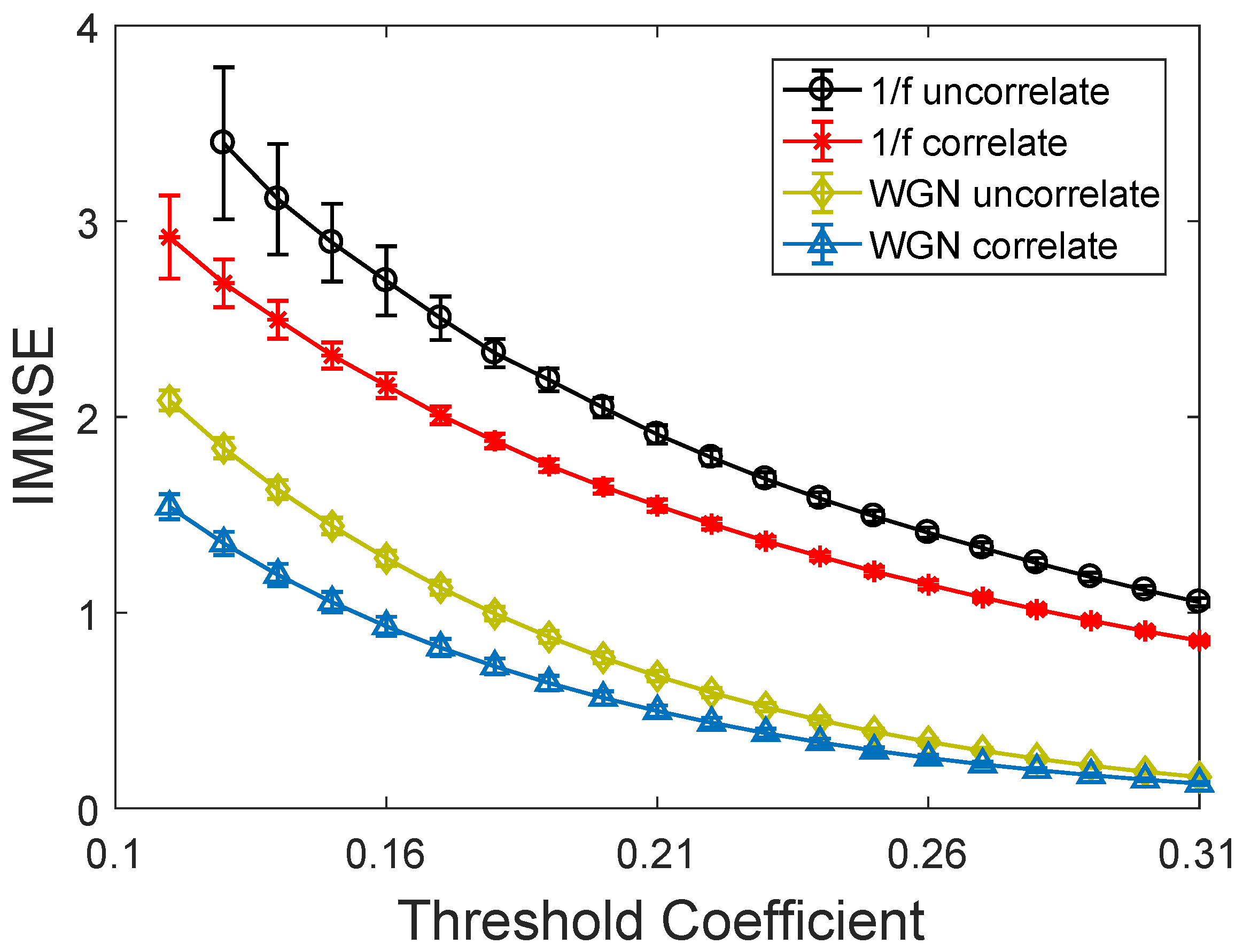
3.1. Parameter Selection
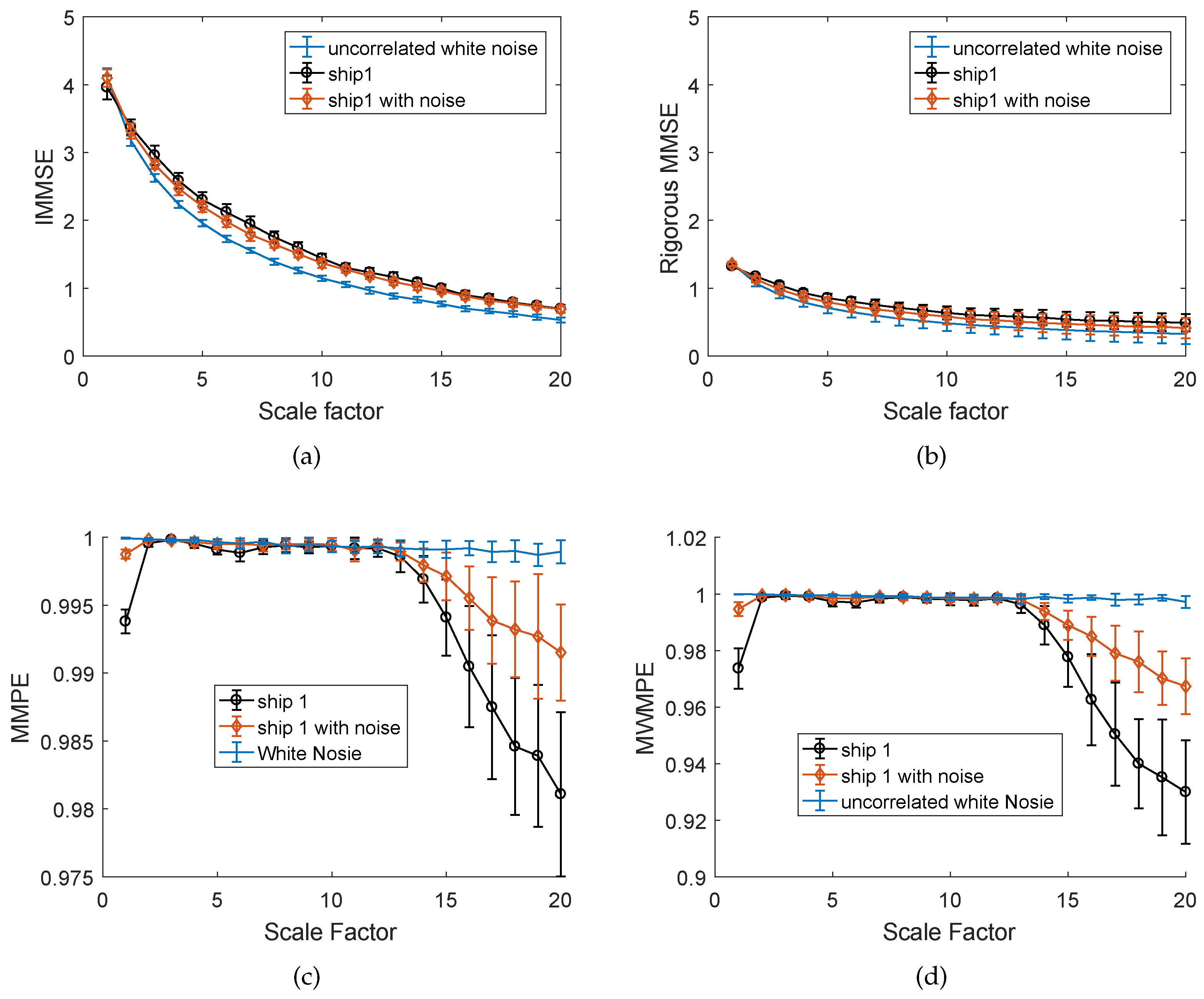
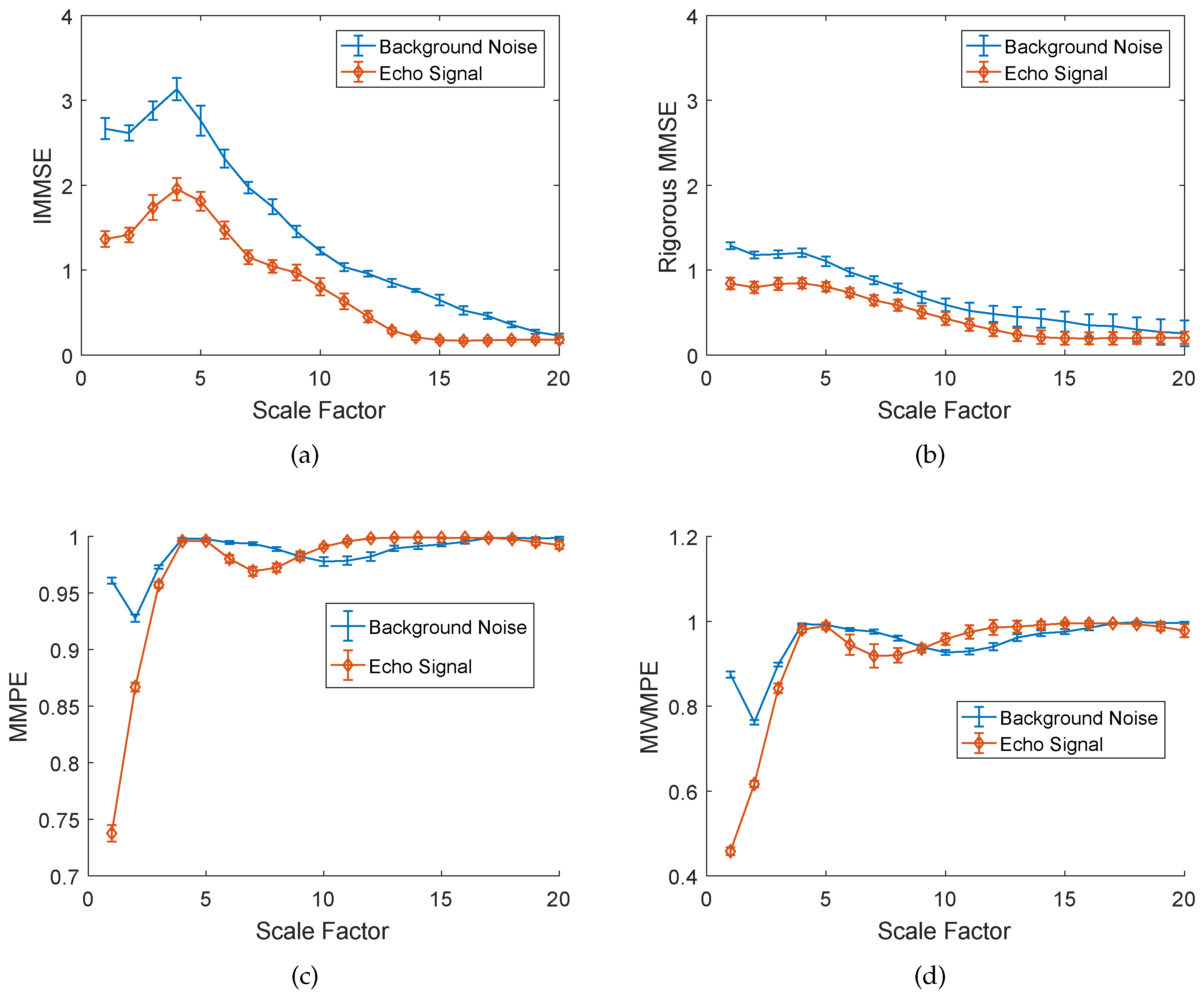
3.2. Noise Sensitivity Analysis
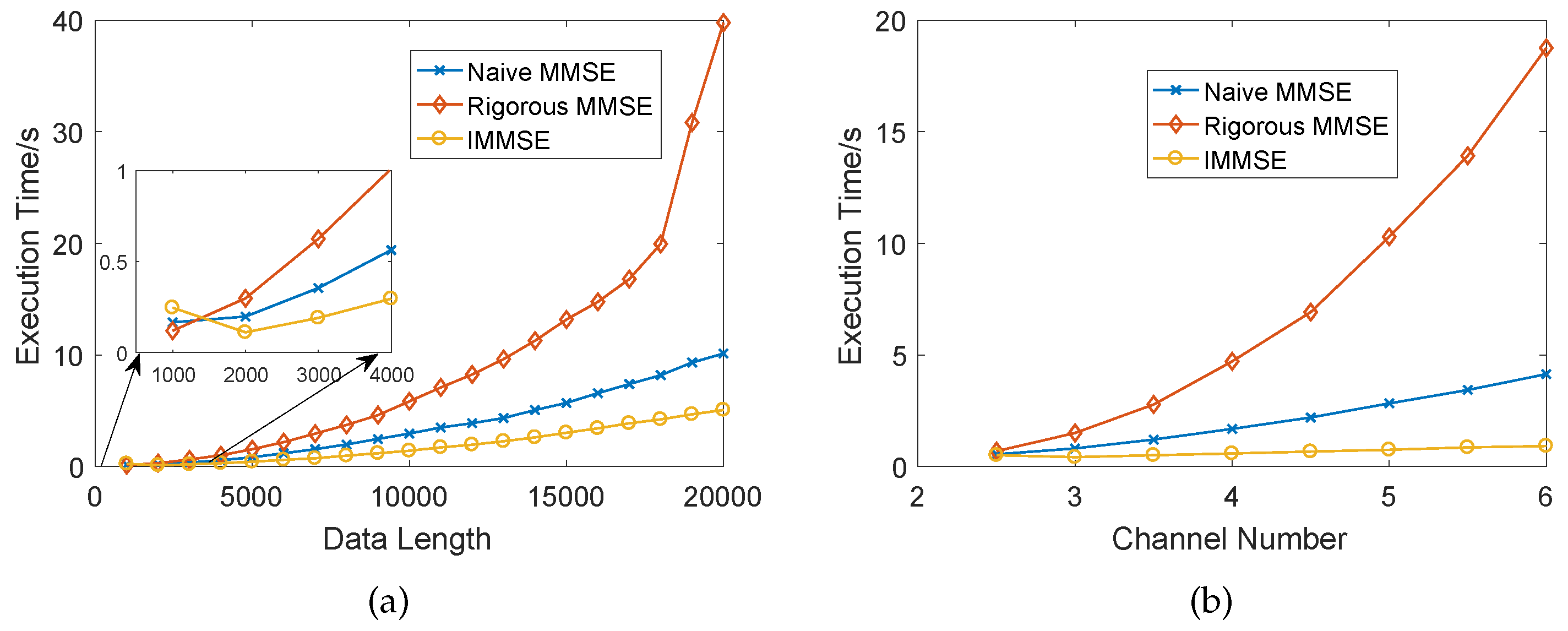
3.3. Computational Efficiency
4. Real-World Data Analysis
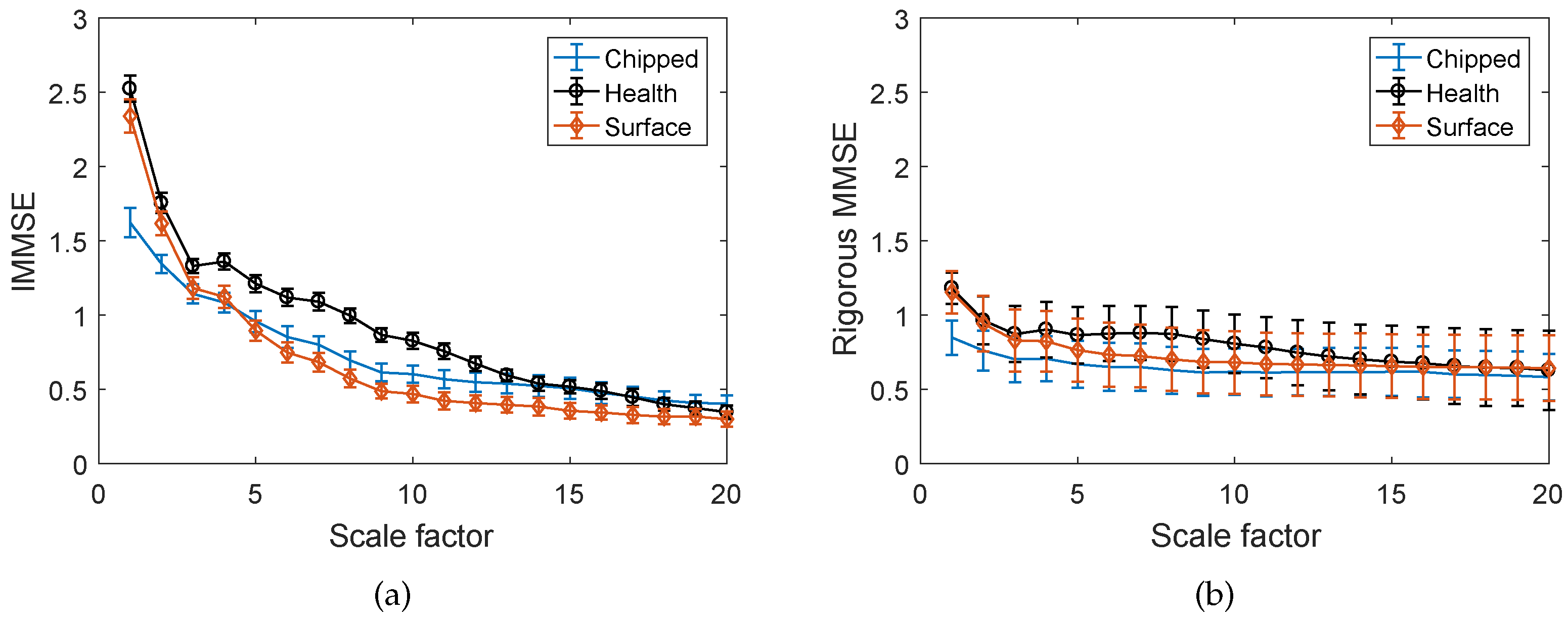
4.1. Case 1
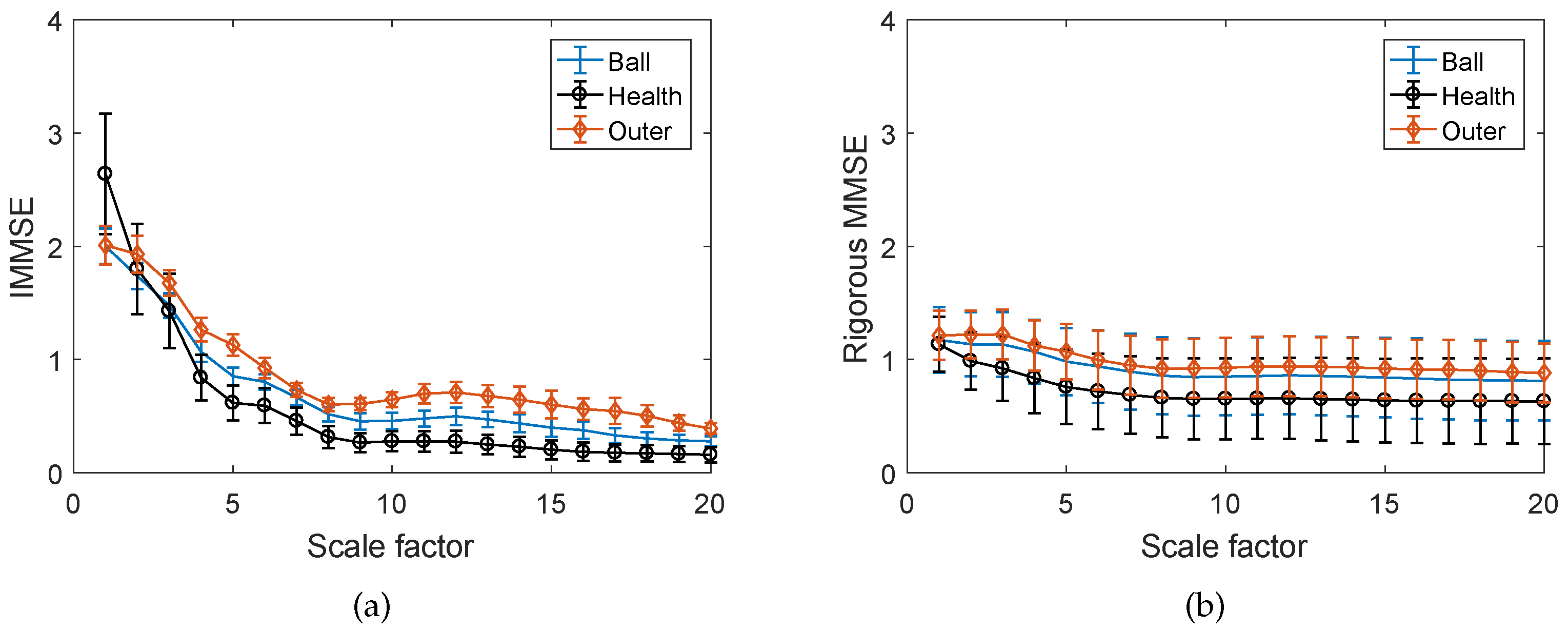
4.2. Case 2
4.3. Case 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Macek, W.M. Nonlinear dynamics and complexity in the generalized Lorenz system. Nonlinear Dyn. 2018, 94, 2957–2968. [Google Scholar] [CrossRef]
- Sharma, A.; Patidar, V.; Purohit, G.; Sud, K.K. Effects on the bifurcation and chaos in forced Duffing oscillator due to nonlinear damping. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2254–2269. [Google Scholar]
- Li, H.; Shen, Y.; Han, Y.; Dong, J.; Li, J. Determining Lyapunov exponents of fractional-order systems: A general method based on memory principle. Solitons Fractals 2023, 168, 113167. [Google Scholar]
- Siddagangaiah, S.; Chen, C.; Hu, W.; Farina, A. The dynamical complexity of seasonal soundscapes is governed by fish chorusing. Commun. Earth Environ. 2022, 3, 109. [Google Scholar] [CrossRef]
- Patel, P.; Raghunandan, R.; Annavarapu, R. EEG-based human emotion recognition using entropy as a feature extraction measure. Brain Inf. 2021, 8, 20. [Google Scholar]
- Wiercigroch, M.; Badiey, M.; Simmen, J.; Cheng, A.D. Non-linear dynamics of underwater acoustics. J. Sound Vib. 1999, 220, 771–786. [Google Scholar]
- Wiercigroch, M.; Cheng, A.H.D.; Simmen, J.; Badiey, M. Nonlinear behavior of acoustic rays in underwater sound channels. Chaos Solitons Fractals 1998, 9, 193–207. [Google Scholar]
- Li, Y.; Gao, P.; Tang, B.; Yi, Y.; Zhang, J. Double feature extraction method of ship-radiated noise signal based on slope entropy and permutation entropy. Entropy 2021, 24, 22. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Yi, Y. A novel complexity-based mode feature representation for feature extraction of ship-radiated noise using VMD and slope entropy. Appl. Acoust. 2022, 196, 108899. [Google Scholar]
- Li, W.; Shen, X.; Li, Y. A comparative study of multiscale sample entropy and hierarchical entropy and its application in feature extraction for ship-radiated noise. Entropy 2019, 21, 793. [Google Scholar] [CrossRef]
- He, Y.; Huang, J.; Zhang, B. Approximate entropy as a nonlinear feature parameter for fault diagnosis in rotating machinery. Meas. Sci. Technol. 2012, 23, 045603. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy analysis. IEEE Signal Process. Lett. 2012, 19, 91–94. [Google Scholar] [CrossRef]
- Cao, L.; Mees, A.; Judd, K. Dynamics from multivariate time series. Physical D 1998, 121, 75–88. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Multivariate multiscale sample entropy of traffic time series. Nonlinear Dyn. 2016, 86, 479–488. [Google Scholar] [CrossRef]
- Li, W.; Shen, X.; Li, Y.; Chen, Z. Improved multivariate multiscale sample entropy and its application in multi-channel data. Chaos 2023, 33, 6. [Google Scholar] [CrossRef]
- Lang, S.; Zhu, H.; Sun, G.; Jiang, Y.; Wei, C. A study on methods for determining phase space reconstruction parameters. J. Comput. Nonlinear Dyn. 2022, 17, 011006. [Google Scholar] [CrossRef]
- Ma, H.; Han, C. Selection of embedding dimension and delay time in phase space reconstruction. Front. Electr. Electron. Eng. China 2006, 1, 111–114. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbane, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403. [Google Scholar] [CrossRef]
- Matilla-García, M.; Morales, I.; Rodríguez, J.M.; Ruiz Marín, M. Selection of embedding dimension and delay time in phase space reconstruction via symbolic dynamics. Entropy 2021, 23, 221. [Google Scholar] [CrossRef] [PubMed]
- Morabito, F.C.; Labate, D.; Foresta, F.L.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Multivariate weighted multiscale permutation entropy for complex time series. Nonlinear Dyn. 2017, 88, 1707–1722. [Google Scholar]
- Zhang, X.; Zhang, S.; Dong, W.; Song, S.; Wang, K. Method for locating single-phase disconnection faults in a smart distribution system based on refined composite multiscale permutation q-complexity entropy and random forest. IEEE Sens. J. 2023, 23, 11925–11935. [Google Scholar]
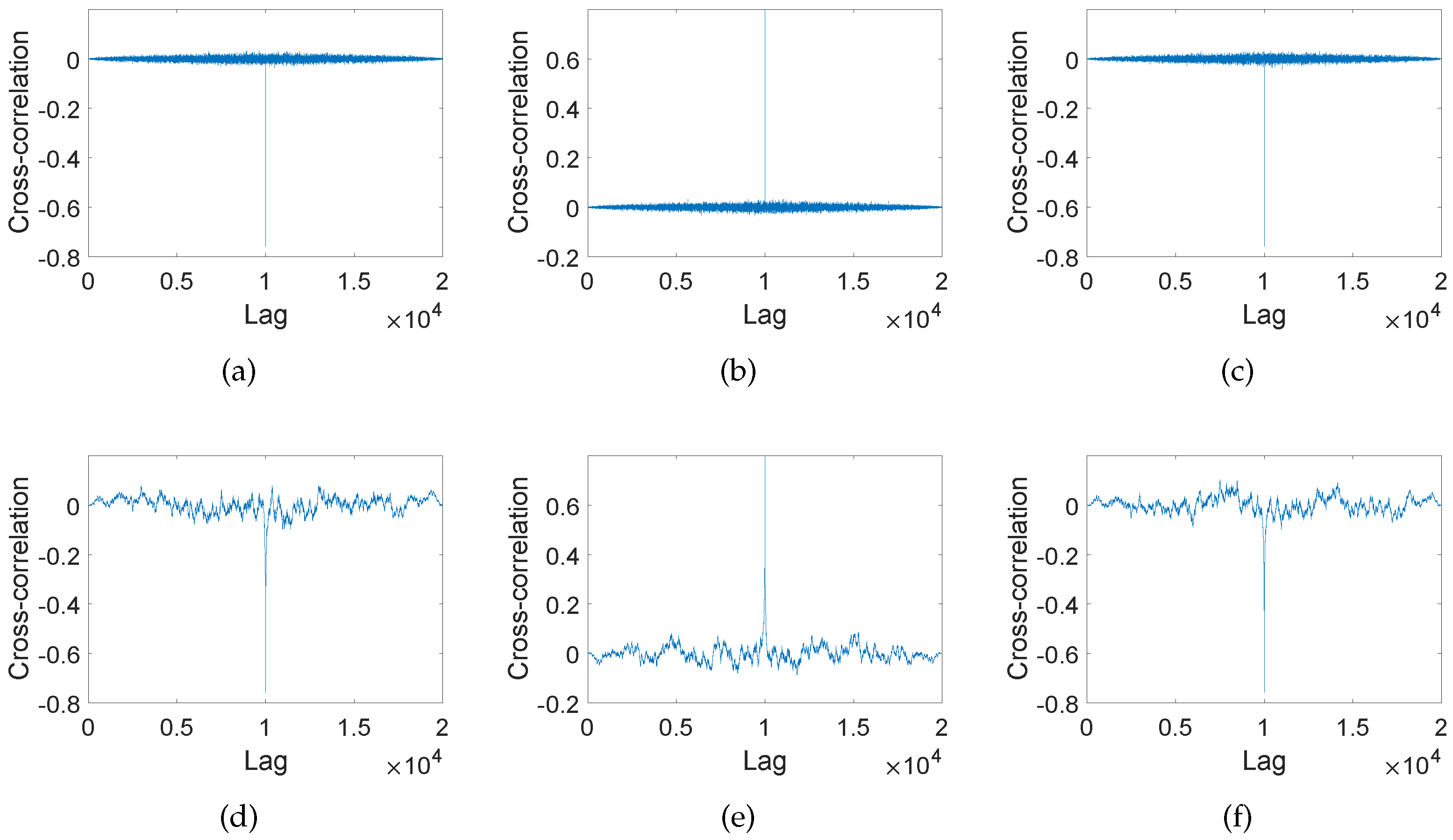

| Gaussian White Noise | Noise | |||||
|---|---|---|---|---|---|---|
| Ch.1 | Ch.2 | Ch.3 | Ch.1 | Ch.2 | Ch.3 | |
| Ch.1 | 1.0000 | −0.7589 | −0.7589 | 1.0000 | −0.7589 | −0.7589 |
| Ch.2 | −0.7589 | 1.0000 | 0.8000 | −0.7589 | 1.0000 | 0.8000 |
| Ch.3 | −0.7589 | 0.8000 | 1.0000 | −0.7589 | 0.8000 | 1.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Li, Y.; Wang, M. Multi-Channel Underwater Acoustic Signal Analysis Using Improved Multivariate Multiscale Sample Entropy. J. Mar. Sci. Eng. 2025, 13, 675. https://doi.org/10.3390/jmse13040675
Zhou J, Li Y, Wang M. Multi-Channel Underwater Acoustic Signal Analysis Using Improved Multivariate Multiscale Sample Entropy. Journal of Marine Science and Engineering. 2025; 13(4):675. https://doi.org/10.3390/jmse13040675
Chicago/Turabian StyleZhou, Jing, Yaan Li, and Mingzhou Wang. 2025. "Multi-Channel Underwater Acoustic Signal Analysis Using Improved Multivariate Multiscale Sample Entropy" Journal of Marine Science and Engineering 13, no. 4: 675. https://doi.org/10.3390/jmse13040675
APA StyleZhou, J., Li, Y., & Wang, M. (2025). Multi-Channel Underwater Acoustic Signal Analysis Using Improved Multivariate Multiscale Sample Entropy. Journal of Marine Science and Engineering, 13(4), 675. https://doi.org/10.3390/jmse13040675






