Free- and Forced-Vibration Characteristic Analysis of a Double-Layered Cylindrical Shell with General Boundary Conditions
Abstract
1. Introduction
2. Theoretical Model
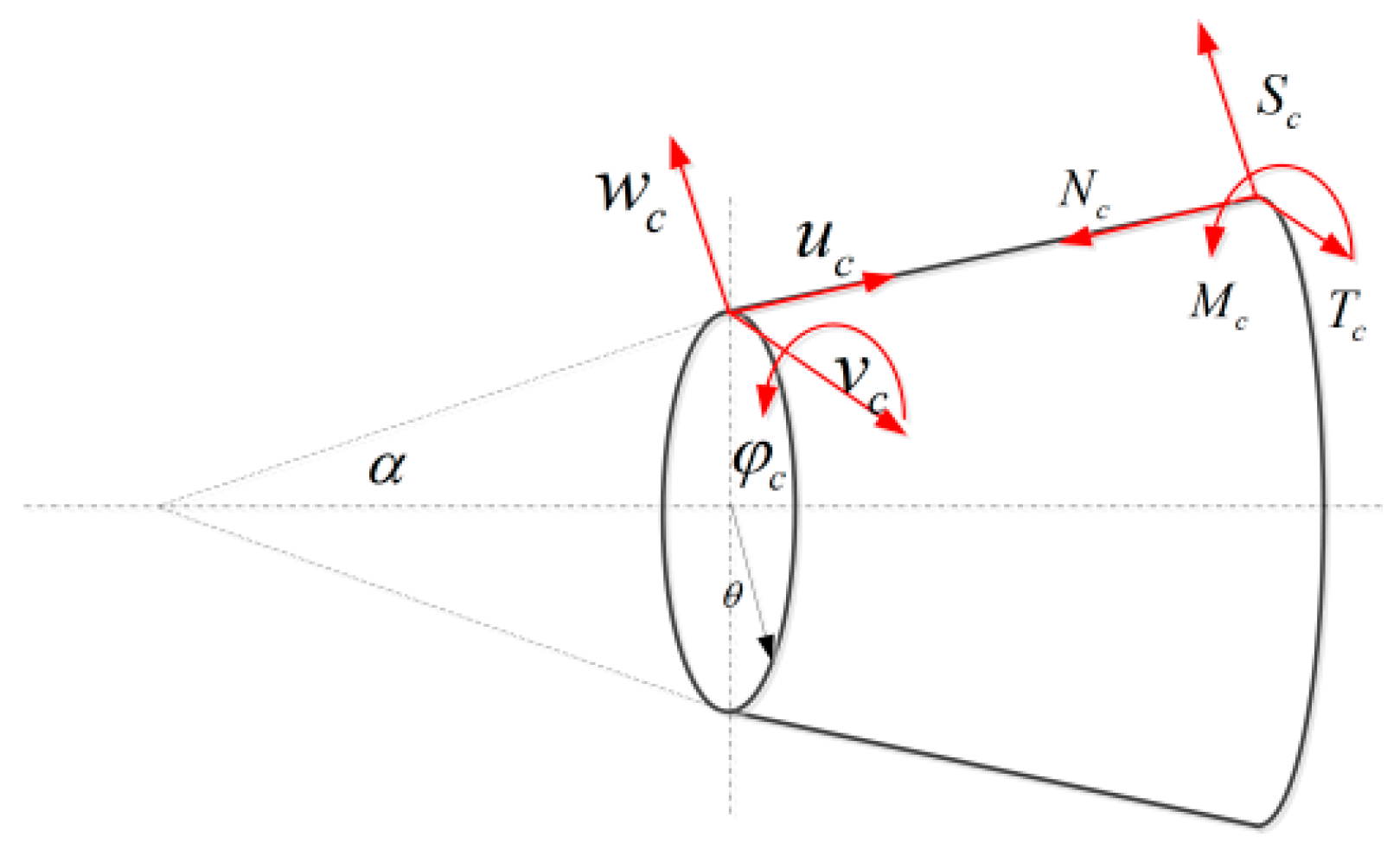
2.1. Vibration Equation of Conical Shell
2.2. Assembly of Two Conical Shells
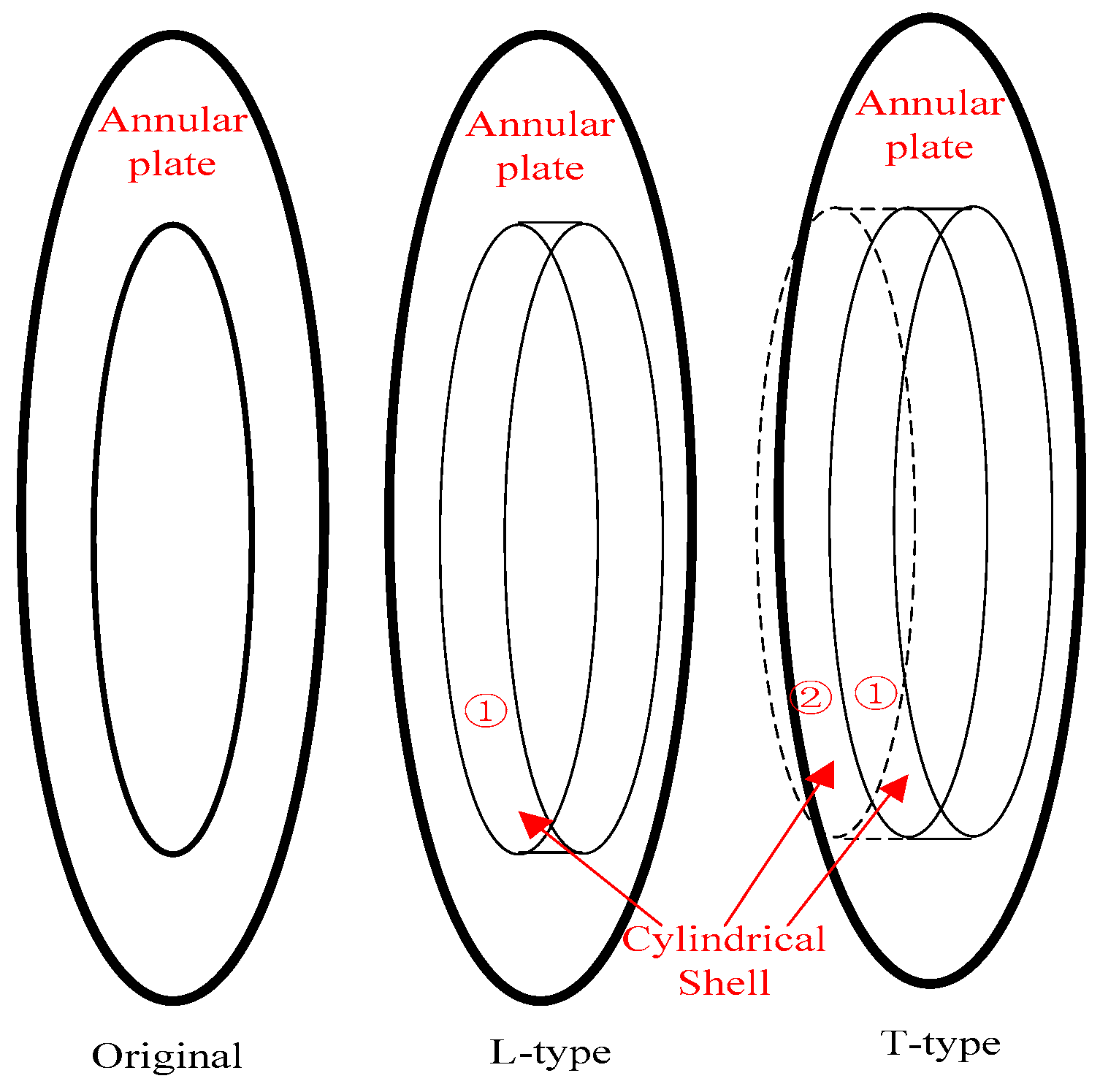
2.3. Ribbed Structural Form
2.4. Application of Boundary Conditions
2.5. Response Solving
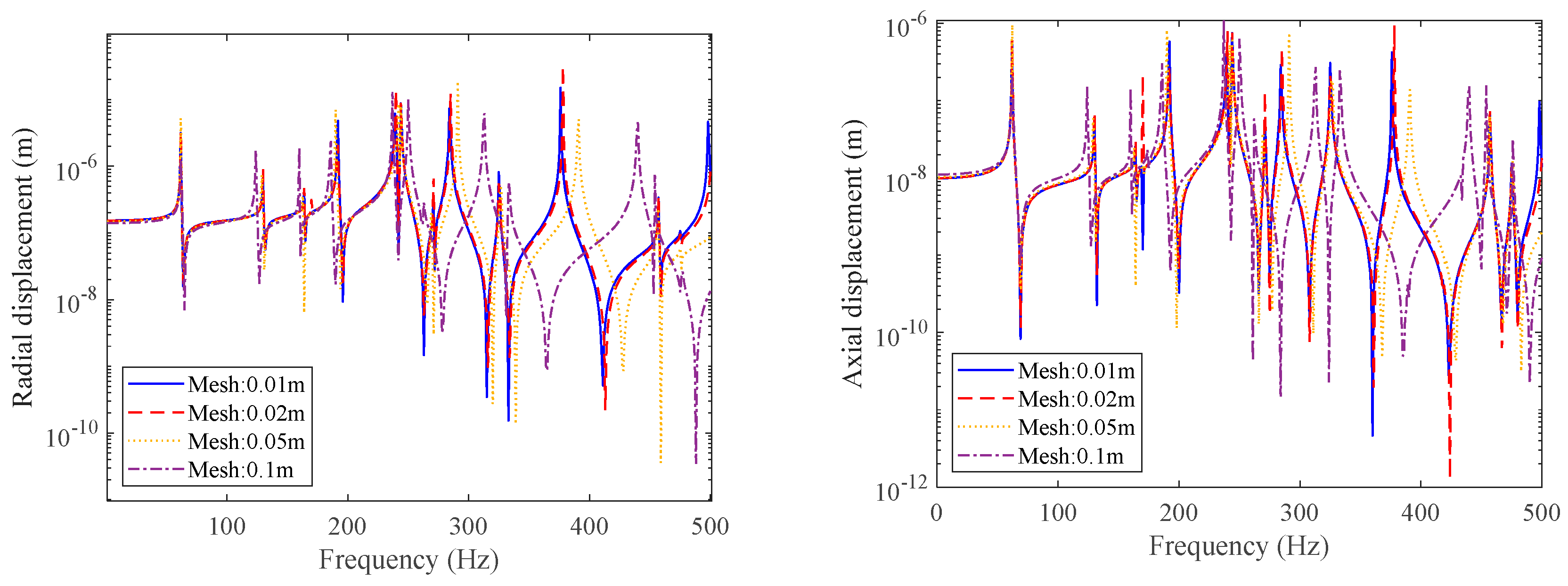
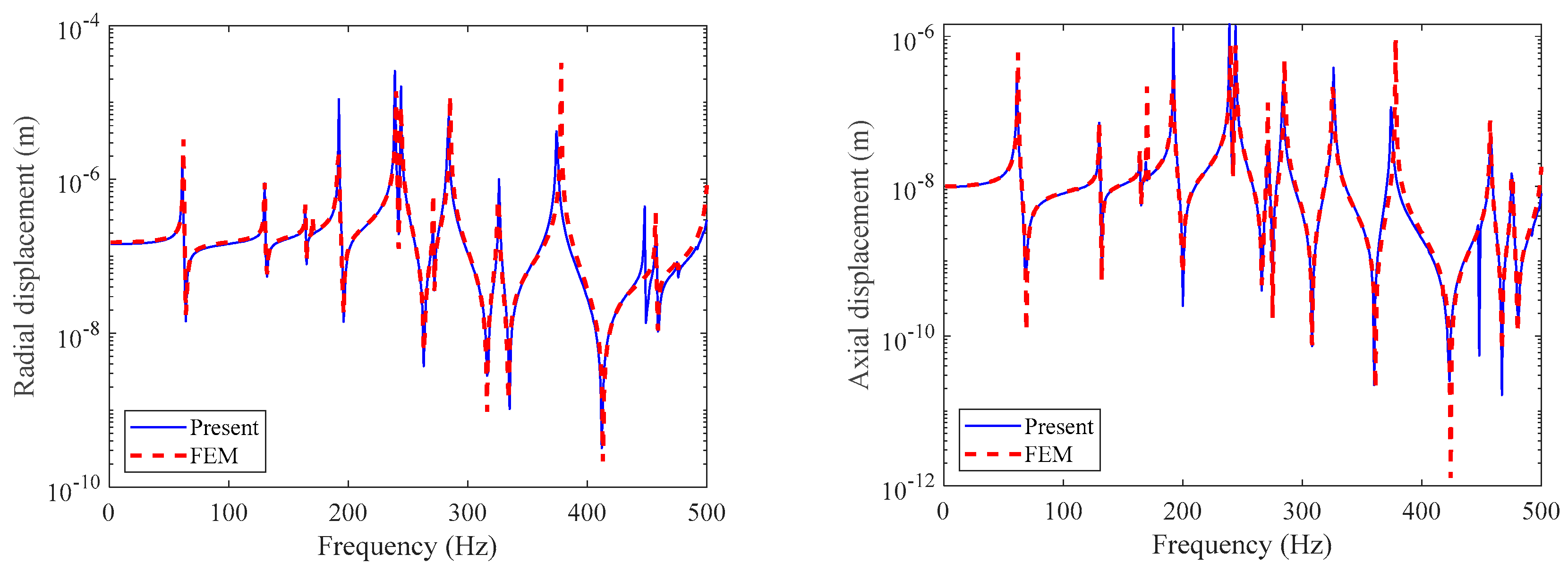
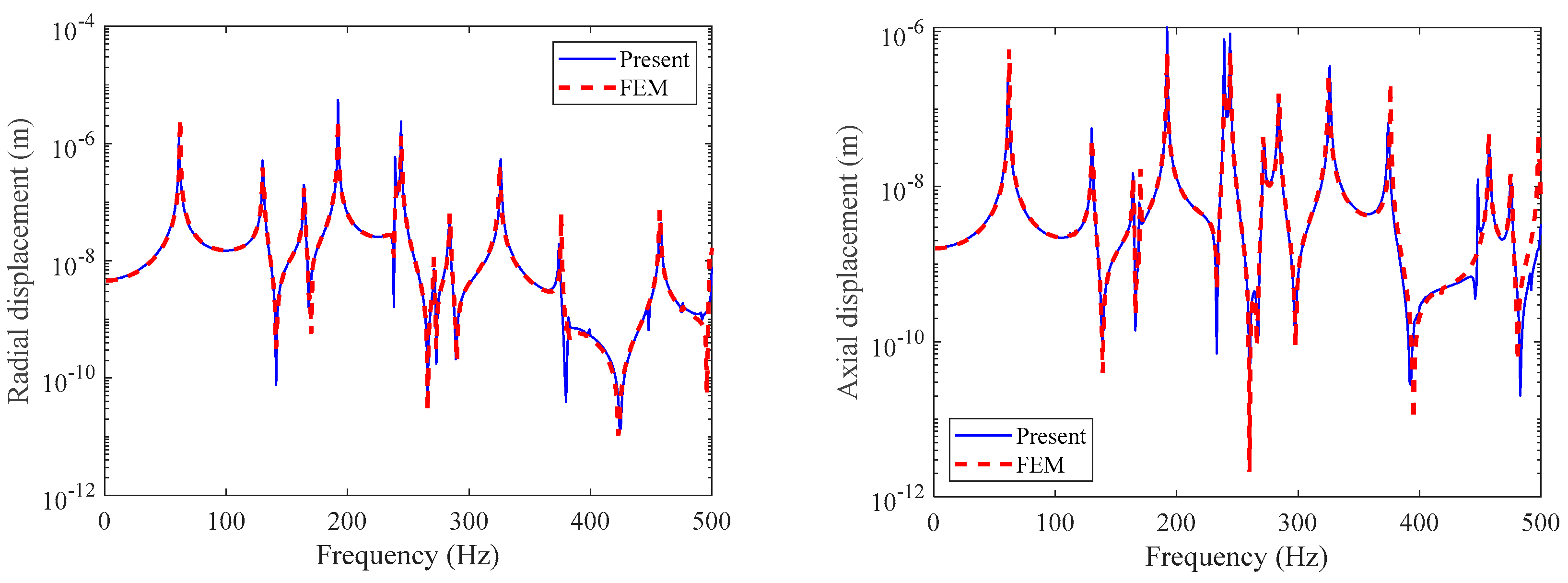
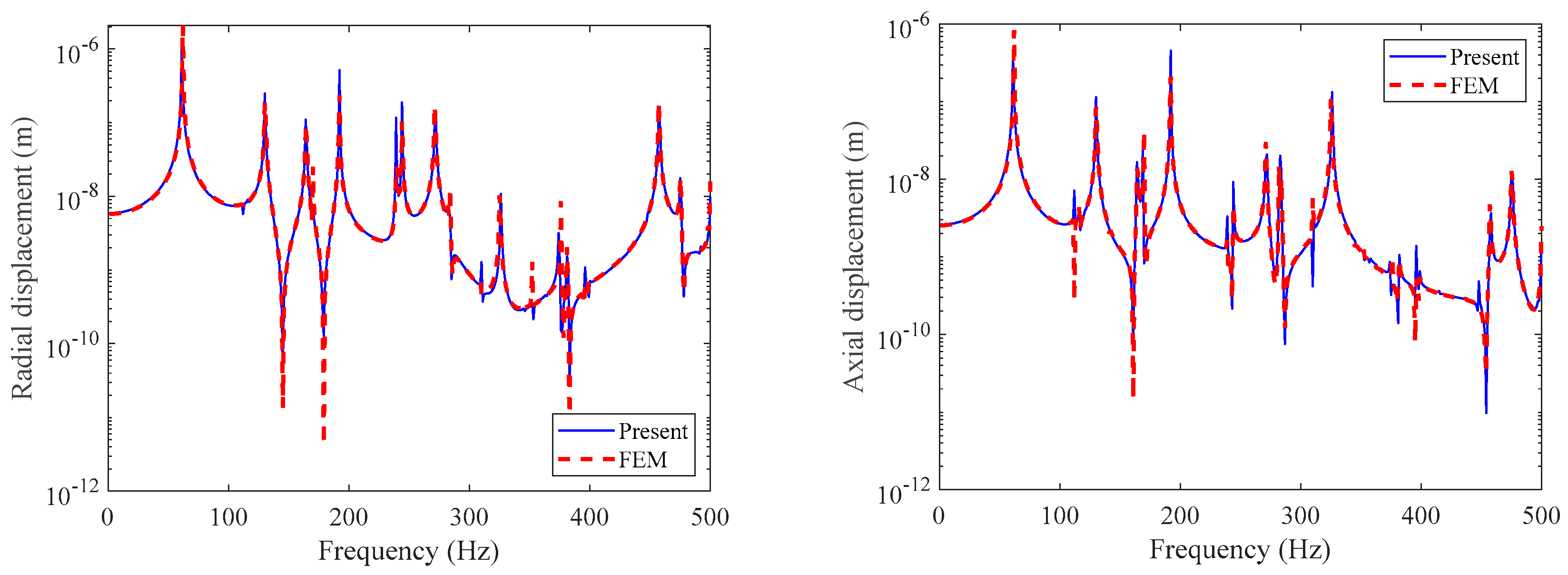
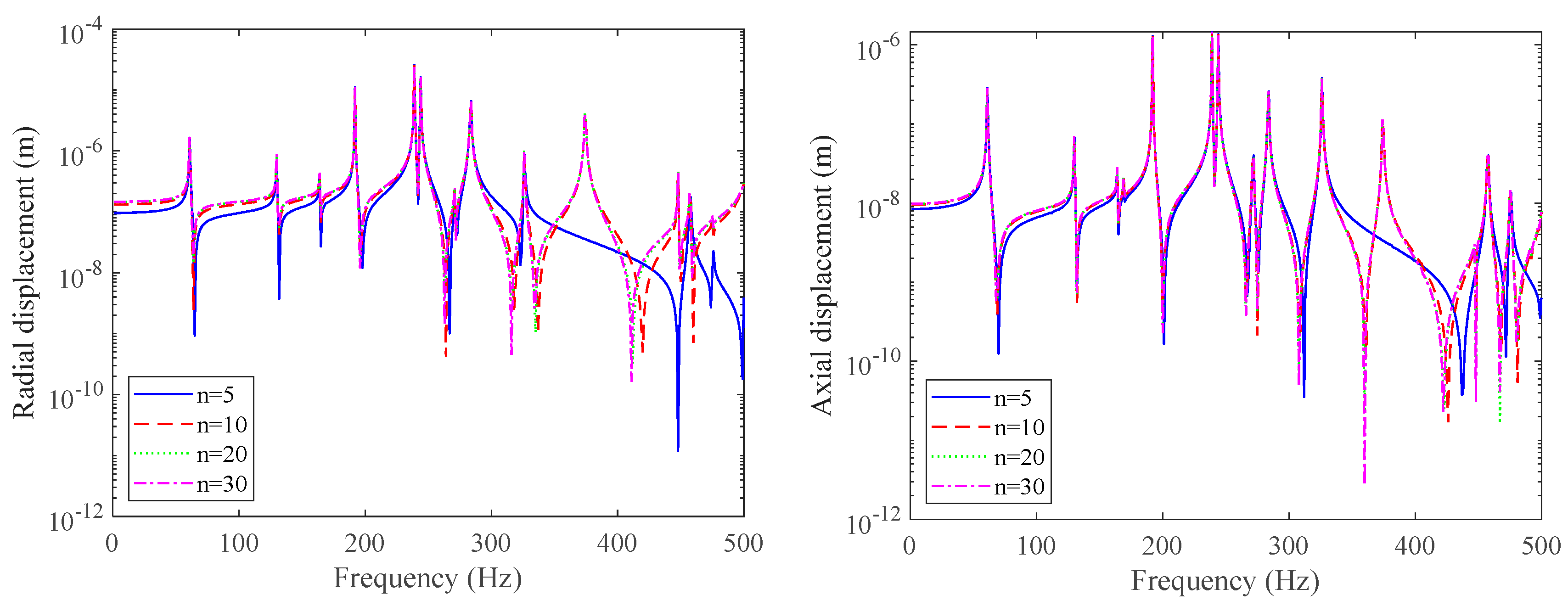
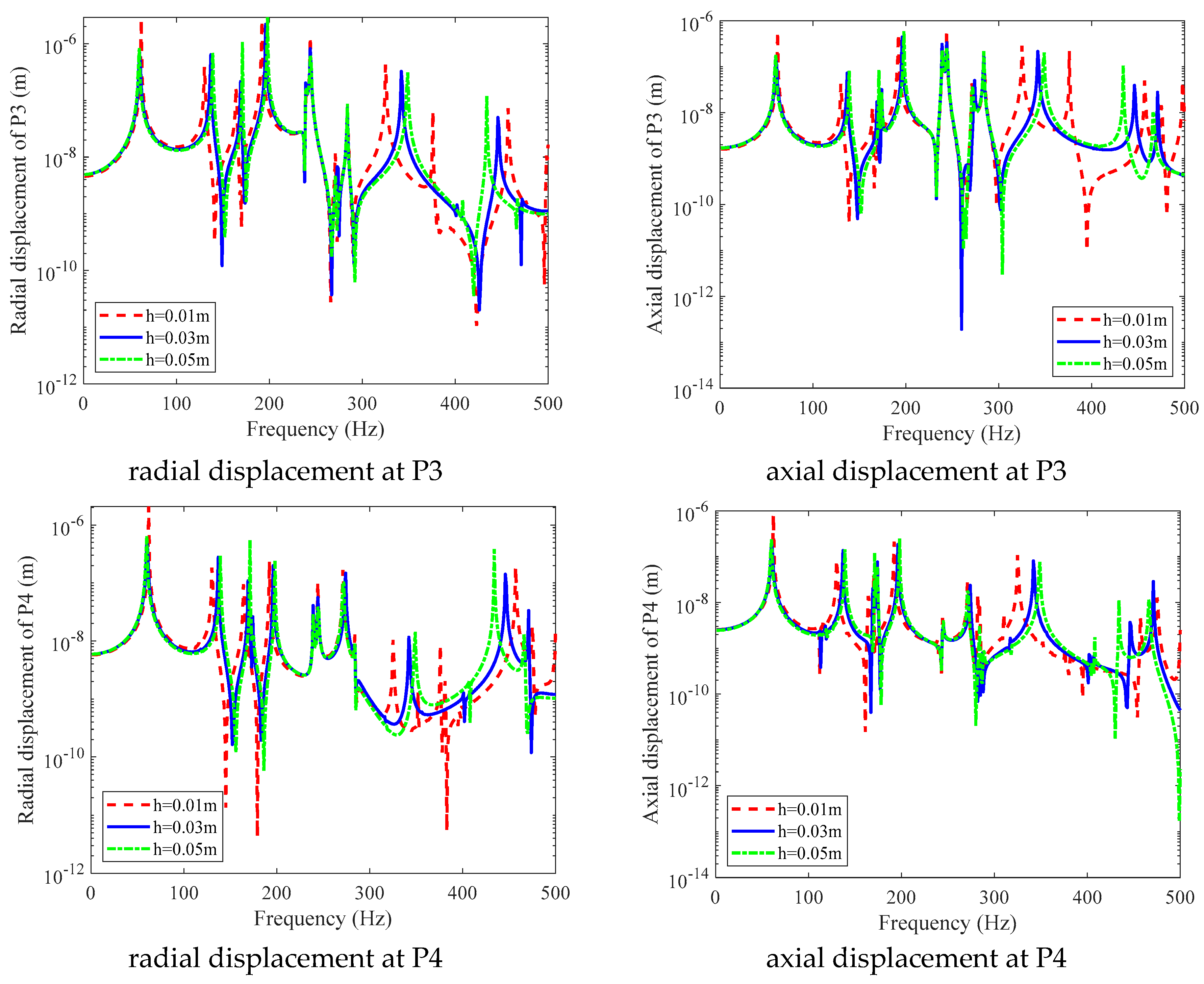
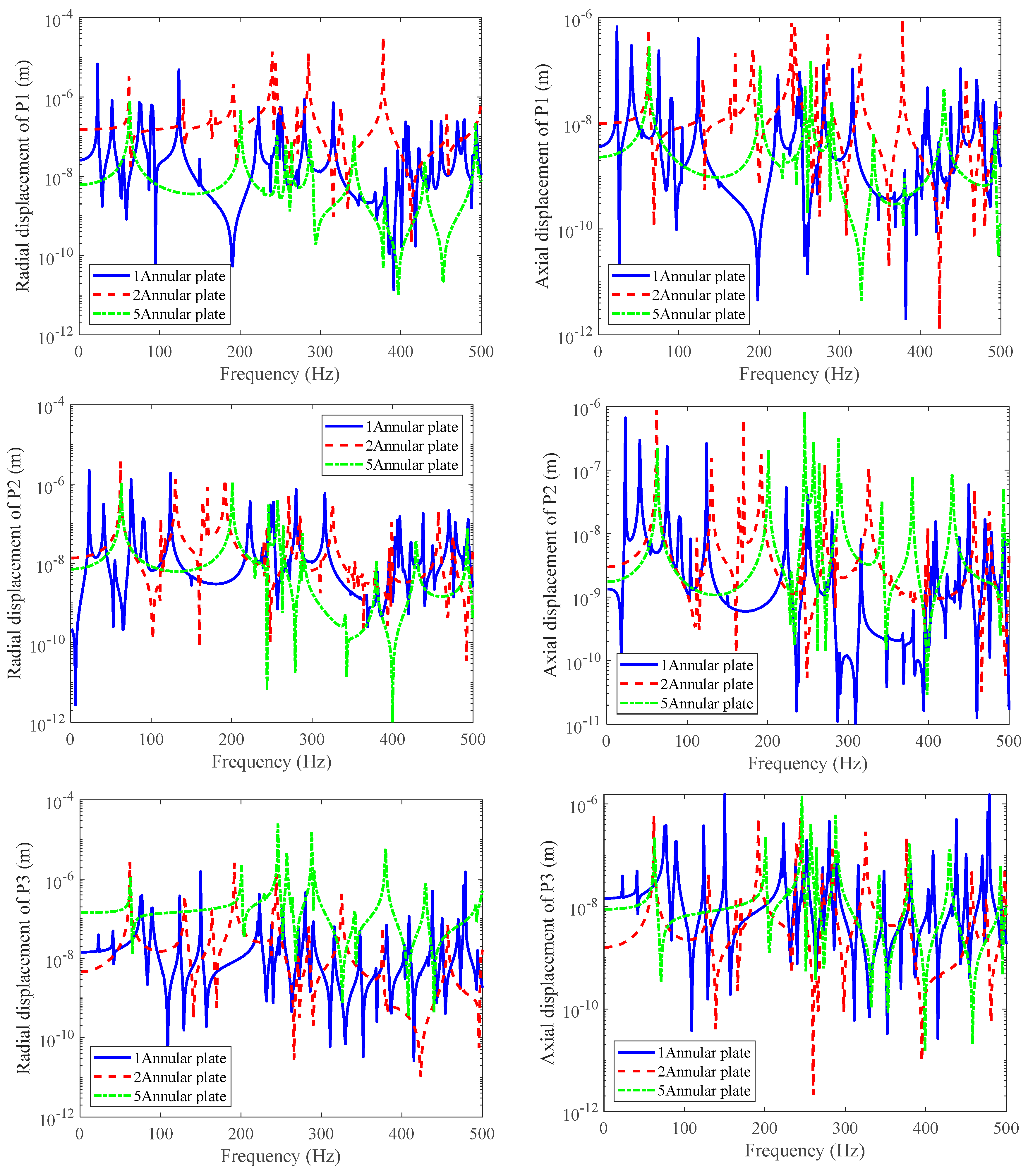
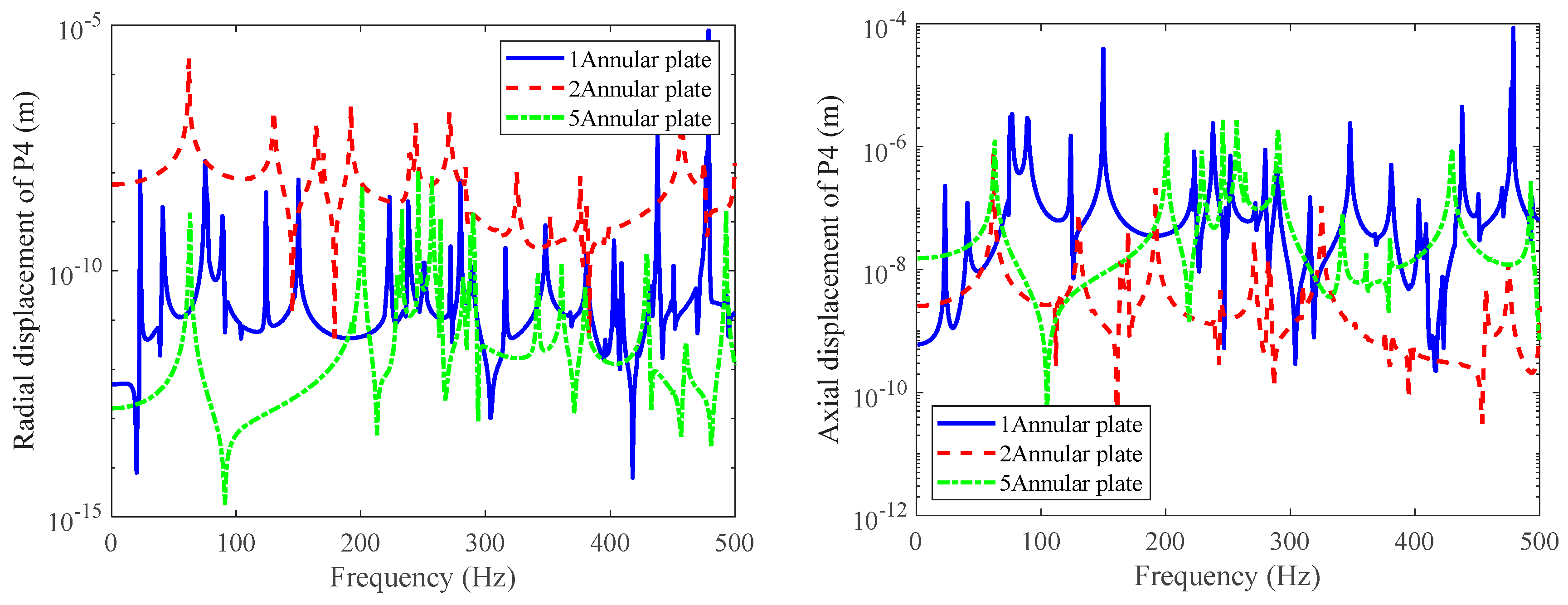
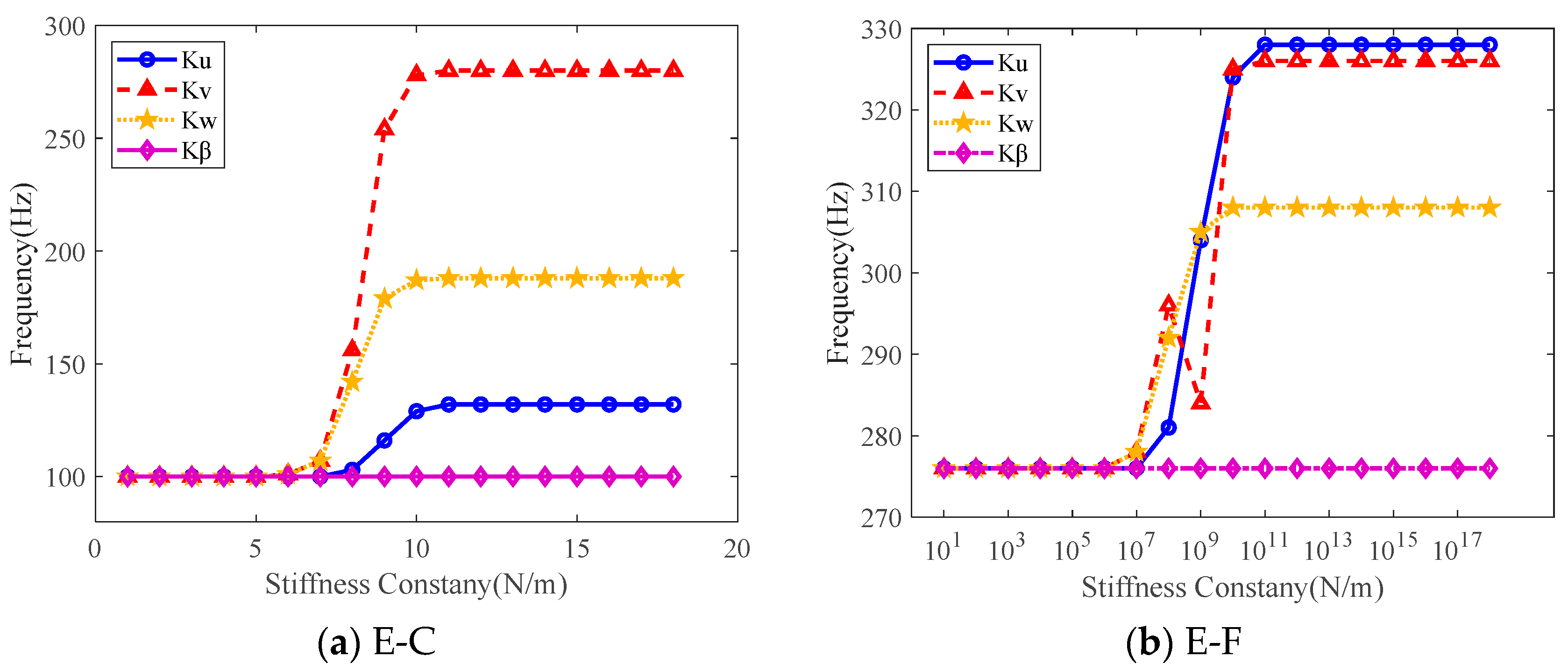
3. Numerical Discussion
3.1. Conical Shell Verification
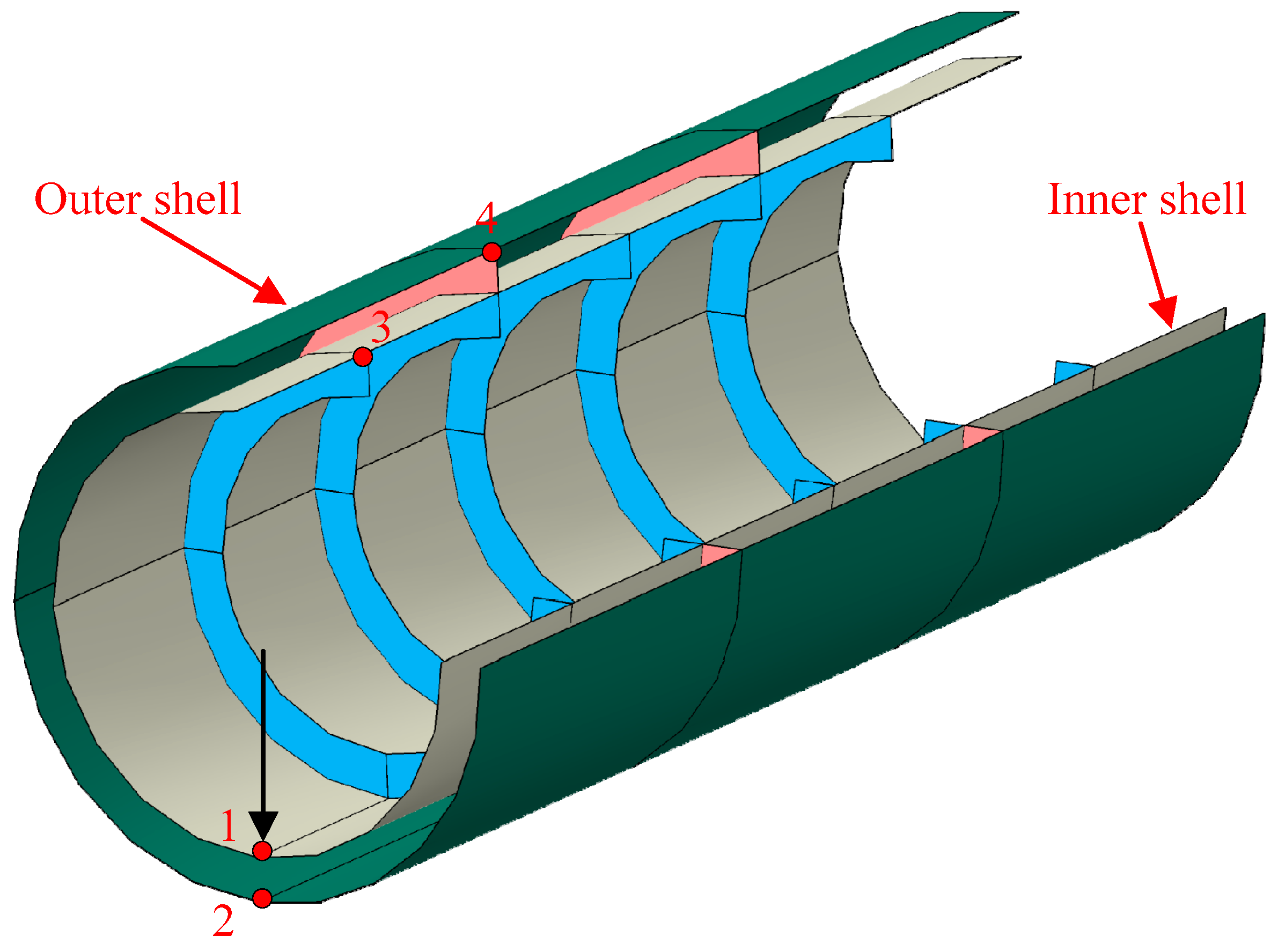
3.2. Double-Layered Cylindrical Shell Model
3.3. Influence of Elastic Boundaries
4. Conclusions
- (1)
- This method is based on analytical methods and does not require excessive mesh division for combined shell structures. For combined structures, without the need to derive cylindrical shells or even more complex structures such as double-layered cylindrical shells, starting from the dynamic stiffness matrix of a single conical shell, this method can be applied to various common combined shell structures. The calculation method in this article is correct and can effectively model the dynamics of combined shell structures such as conical shells and double-layered cylindrical shells. It has the advantages of a high computational efficiency and fast convergence;
- (2)
- The calculation method proposed in this article is applicable to any boundary condition and is not limited to the classical boundaries in the traditional literature. Through parametric analysis, we found that the arbitrary boundary stiffness of the combined shell is related to its own origin dynamic stiffness value. When the elastic stiffness in any direction at both ends of the combined shell is of the same magnitude as the dynamic stiffness in that direction, the influence of elastic boundary stiffness on the natural frequency of the double-layered cylindrical shell becomes more significant;
- (3)
- The parameters of the solid rib plate between the reinforced ribs and the double-layered cylindrical shell have an impact on the natural frequency of the combined shell. Different rib forms have little effect on the low-frequency response, and the T-shaped ribs have the highest stiffness and therefore the highest natural frequency value. The thickness of the middle solid rib plate has a relatively small impact on low frequencies, while the number of solid rib plates has a significant impact on the response throughout the entire frequency band.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahrami, S.; Shirmohammadi, F.; Saadatpour, M.M. Vibration analysis of thin shallow shells using spectral element method. Appl. Math. Model. 2017, 44, 470–480. [Google Scholar] [CrossRef]
- Thinh, T.I.; Nguyen, M.C. Dynamic stiffness method for free vibration of composite cylindrical shells containing fluid. Appl. Math. Model. 2016, 40, 9286–9301. [Google Scholar] [CrossRef]
- Qatu, M.S. Recent research advances in the dynamic behavior of shells: 1989–2000, Part 2: Homogeneous shells. Appl. Mech. Rev. 2002, 55, 415–434. [Google Scholar] [CrossRef]
- Qu, Y.; Chen, Y.; Long, X.; Hua, H.; Meng, G. A modified variational approach for vibration analysis of ring-stiffened conical–cylindrical shell combinations. Eur. J. Mech.-A/Solids 2013, 37, 200–215. [Google Scholar] [CrossRef]
- Jin, G.; Ye, T.; Jia, X.; Gao, S. A general Fourier solution for the vibration analysis of composite laminated structure elements of revolution with general elastic restraints. Compos. Struct. 2014, 109, 150–168. [Google Scholar] [CrossRef]
- Zou, M.S.; Liu, S.X.; Qi, L.B. An analytical formulation for the underwater acoustic radiation of a cylindrical shell with an internal flexural floor based on the reciprocity theorem. Appl. Acoust. 2019, 154, 18–27. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, J. A Study on the Vibration Analysis of Thick-Walled, Fluid-Conveying Pipelines with Internal Hydrostatic Pressure. J. Mar. Sci. Eng. 2023, 11, 2338. [Google Scholar] [CrossRef]
- Yin, C.; Lei, Z.; Jin, Z.; Shi, Z. Effects of Connecting Structures in Double-Hulled Water-Filled Cylindrical Shells on Shock Wave Propagation and the Structural Response to Underwater Explosion. J. Mar. Sci. Eng. 2024, 12, 1949. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibration of Shells; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washinton, DC, USA, 1973. [Google Scholar]
- Amabili, M.; Païdoussis, M.P. Review of studies on geometrically nonlinear vibrations and dynamics of circular cylindrical shells and panels, with and without fluid-structure interaction. Appl. Mech. Rev. 2003, 56, 349–381. [Google Scholar] [CrossRef]
- Khorasani, M.; Elahi, H.; Eugeni, M.; Lampani, L.; Civalek, O. Vibration of FG porous three-layered beams equipped by agglomerated nanocomposite patches resting on Vlasov’s foundation. Transp. Porous Media 2022, 142, 157–186. [Google Scholar] [CrossRef]
- Kolarević, N.; Nefovska-Danilović, M.; Petronijević, M. Dynamic stiffness method in the vibration analysis of circular cylindrical shell. Građevinski Materijali i Konstrukcije 2016, 59, 45–61. [Google Scholar] [CrossRef]
- Kolarević, N.; Nefovska-Danilović, M. Dynamic stiffness–based free vibration study of open circular cylindrical shells. J. Sound Vib. 2020, 486, 115600. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, J. Free vibration of partially fluid-filled or fluid-surrounded composite shells using the dynamic stiffness method. Acta Mech. 2020, 231, 3961–3978. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, G.; Wang, Z.; Sun, Y. Dynamic stiffness formulation and vibration analysis of coupled conical-ribbed cylindrical-conical shell structure with general boundary condition. Ocean. Eng. 2021, 234, 109294. [Google Scholar]
- Zhang, C.; Jin, G.; Ma, X.; Ye, T. Vibration analysis of circular cylindrical double-shell structures under general coupling and end boundary conditions. Appl. Acoust. 2016, 110, 176–193. [Google Scholar] [CrossRef]
- Li, Z.; Jin, G.; Ye, T.; Yang, T.J.; Zhong, S.; Tian, L. A unified vibration modeling of open cylindrical shell-rectangular plate coupling structures based on the dynamic stiffness method. J. Sound Vib. 2023, 563, 117870. [Google Scholar] [CrossRef]
- Li, Z.; Ye, T.; Jin, G.; Yang, T.J.; Tian, L.; Chen, Y. Dynamic stiffness formulation for vibration analysis of an open cylindrical shell and its coupling structures based on a generalized superposition method. J. Sound Vib. 2022, 538, 117237. [Google Scholar] [CrossRef]
- Chen, M.; Xie, K.; Jia, W.; Xu, K. Free and forced vibration of ring-stiffened conical–cylindrical shells with arbitrary boundary conditions. Ocean. Eng. 2015, 108, 241–256. [Google Scholar] [CrossRef]
- Xie, K.; Chen, M.; Li, Z. Free and forced vibration analysis of ring-stiffened conical–cylindrical–spherical shells through a semi-analytic method. J. Vib. Acoust. 2017, 139, 031001. [Google Scholar] [CrossRef]
- Tian, L.; Ye, T.; Jin, G. Vibration analysis of combined conical-cylindrical shells based on the dynamic stiffness method. Thin-Walled Struct. 2021, 159, 107260. [Google Scholar] [CrossRef]
- Tian, L.; Jin, G.; He, T.; Ye, T.; Liu, Z.; Khadimallah, M.A.; Li, Z. A hybrid analytic–numerical formulation for the vibration analysis of a cylindrical shell coupled with an internal flexural floor structure. Thin-Walled Struct. 2023, 183, 110382. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Y. An exact solution for vibration analysis of pipe coupled with conical-ring stiffened cylindrical shells with arbitrary boundary condition. Ocean. Eng. 2022, 266, 112861. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Y.; Duan, Y. Exact solutions for free and forced vibrations of cross-ply composite laminated combined conical–cylindrical shells with arbitrary boundary conditions. Ocean. Eng. 2023, 285, 115371. [Google Scholar] [CrossRef]
- Wang, X.; Xu, E.; Jiang, C.; Wu, W. Vibro-acoustic behavior of double-walled cylindrical shells with general boundary conditions. Ocean. Eng. 2019, 192, 106529. [Google Scholar] [CrossRef]
- Yu, A.; Zhao, Y.; Chen, Q.; Liu, J.; Zhou, Z.; Cao, X. Vibration transmission analyses of double-layer cylindrical shell with fully immersed elastic connections through experimental and analytical approaches. Thin-Walled Struct. 2024, 199, 111781. [Google Scholar] [CrossRef]
- Xie, K.; Jia, W.; Dong, W.; Chen, M. Vibro-acoustic analysis of double-walled cylindrical shells through a novel semi-analytic method. Eur. J. Mech.-A/Solids 2022, 94, 104559. [Google Scholar] [CrossRef]
- Xie, K.; Chen, M. Wave based method for vibration analysis of double-walled cylindrical shells. Appl. Acoust. 2018, 139, 293–306. [Google Scholar] [CrossRef]
- Xie, K.; Chen, M.; Li, Z. An analytic method for free and forced vibration analysis of stepped conical shells with arbitrary boundary conditions. Thin-Walled Struct. 2017, 111, 126–137. [Google Scholar] [CrossRef]
- Jia, W.; Chen, M.; Zhou, Z.; Xie, K. Vibration analysis of double-walled cylindrical shells interconnected with arbitrary connections using a unified semi-analytical method. Ocean. Eng. 2022, 251, 110879. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, D.; He, D. Vibration characteristics of a laminated composite double-cylindrical shell system coupled with a variable number of annular plates. Materials 2022, 15, 4246. [Google Scholar] [CrossRef]
- Yoshikawa, S.; Williams, E.G.; Washburn, K.B. Vibration of two concentric submerged cylindrical shells coupled by the entrained fluid. J. Acoust. Soc. Am. 1994, 95, 3273–3286. [Google Scholar] [CrossRef]
- Caresta, M.; Kessissoglou, N.J. Free vibrational characteristics of isotropic coupled cylindrical–conical shells. J. Sound Vib. 2010, 329, 733–751. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liu, G.R.; Lam, K.Y. Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach. Appl. Acoust. 2001, 62, 229–243. [Google Scholar] [CrossRef]
- Tong, L. Free vibration of composite laminated conical shells. Int. J. Mech. Sci. 1993, 35, 47–61. [Google Scholar] [CrossRef]
- Irie, T. Natural frequencies of truncated conical shells. J. Sound Vib. 1984, 92, 447. [Google Scholar] [CrossRef]






| n | α = 30° | α = 45° | α = 60° | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | |
| 0 | 0.1910 | 0.1910 | 0.1900 | 0.2854 | 0.2854 | 0.2850 | 0.3628 | 0.3628 | 0.3618 |
| 1 | 0.5923 | 0.5923 | 0.5921 | 0.5254 | 0.5255 | 0.5252 | 0.4753 | 0.4754 | 0.4745 |
| 2 | 0.7910 | 0.7910 | 0.7909 | 0.6878 | 0.6879 | 0.6876 | 0.5720 | 0.5722 | 0.5714 |
| 3 | 0.7284 | 0.7284 | 0.7285 | 0.6972 | 0.6973 | 0.6971 | 0.5998 | 0.6001 | 0.5994 |
| 4 | 0.6353 | 0.6352 | 0.6354 | 0.6662 | 0.6664 | 0.6662 | 0.6048 | 0.6054 | 0.6047 |
| 5 | 0.5531 | 0.5531 | 0.5534 | 0.6301 | 0.6304 | 0.6303 | 0.6069 | 0.6077 | 0.6071 |
| 6 | 0.4949 | 0.4949 | 0.4954 | 0.6028 | 0.6032 | 0.6032 | 0.6147 | 0.6159 | 0.6153 |
| 7 | 0.4653 | 0.4653 | 0.4660 | 0.5910 | 0.5918 | 0.5920 | 0.6329 | 0.6343 | 0.6338 |
| 8 | 0.4644 | 0.4645 | 0.4654 | 0.5983 | 0.5992 | 0.5995 | 0.6632 | 0.6650 | 0.6646 |
| 9 | 0.4892 | 0.4892 | 0.4903 | 0.6245 | 0.6257 | 0.6260 | 0.7060 | 0.7084 | 0.7080 |
| n | α = 30° | α = 45° | α = 60° | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | |
| 0 | 0.9889 | 0.9889 | 0.9888 | 0.8801 | 0.8801 | 0.8798 | 0.7853 | 0.7853 | 0.7844 |
| 1 | 0.9535 | 0.9535 | 0.9534 | 0.8673 | 0.8673 | 0.8670 | 0.7821 | 0.7821 | 0.7813 |
| 2 | 0.8643 | 0.8642 | 0.8642 | 0.8329 | 0.8329 | 0.8326 | 0.7738 | 0.7738 | 0.7730 |
| 3 | 0.7582 | 0.7580 | 0.7581 | 0.7876 | 0.7875 | 0.7872 | 0.7641 | 0.7640 | 0.7632 |
| 4 | 0.6629 | 0.6626 | 0.6628 | 0.7426 | 0.7424 | 0.7422 | 0.7570 | 0.7569 | 0.7562 |
| 5 | 0.5901 | 0.5896 | 0.5899 | 0.7069 | 0.7066 | 0.7065 | 0.7566 | 0.7565 | 0.7558 |
| 6 | 0.5426 | 0.5421 | 0.5425 | 0.6855 | 0.6852 | 0.6852 | 0.7655 | 0.7654 | 0.7648 |
| 7 | 0.5207 | 0.5201 | 0.5207 | 0.6809 | 0.6806 | 0.6806 | 0.7854 | 0.7853 | 0.7847 |
| 8 | 0.5232 | 0.5224 | 0.5232 | 0.6936 | 0.6932 | 0.6933 | 0.8186 | 0.8166 | 0.8161 |
| 9 | 0.5477 | 0.5468 | 0.5477 | 0.7229 | 0.7223 | 0.7226 | 0.8597 | 0.8594 | 0.8590 |
| m | n | EI-C | EII-C | EIII-C | EI-F | EII-F | EIII-F | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WBM | DSM | WBM | DSM | WBM | DSM | WBM | DSM | WBM | DSM | WBM | DSM | ||
| 1 | 1 | 99.5 | 99.5 | 86.7 | 86.8 | 86.5 | 86.6 | 32.2 | 32.2 | 39.9 | 39.9 | 30.4 | 30.4 |
| 2 | 63.4 | 63.5 | 61.2 | 61.2 | 59.2 | 59.3 | 23.9 | 24.0 | 28.6 | 28.6 | 23.9 | 24.0 | |
| 3 | 67.8 | 67.9 | 68.8 | 68.9 | 66.9 | 66.9 | 39.9 | 40.0 | 39.9 | 40.0 | 39.8 | 39.8 | |
| 4 | 82.3 | 82.3 | 83.1 | 83.1 | 81.9 | 81.9 | 39.6 | 39.7 | 39.6 | 39.7 | 39.6 | 39.7 | |
| 5 | 88.8 | 88.9 | 89.2 | 89.3 | 88.5 | 88.6 | 35.4 | 35.5 | 35.4 | 35.5 | 35.4 | 35.5 | |
| 6 | 89.2 | 89.3 | 88.5 | 88.5 | 87.7 | 87.8 | 32.2 | 32.3 | 32.2 | 32.3 | 32.2 | 32.3 | |
| 7 | 82.6 | 82.9 | 82.2 | 82.2 | 81.5 | 81.5 | 31.2 | 31.3 | 31.2 | 31.3 | 31.2 | 31.3 | |
| 8 | 76.5 | 76.5 | 76.3 | 76.3 | 75.9 | 76.0 | 33.4 | 33.5 | 33.4 | 33.5 | 33.4 | 33.5 | |
| 2 | 1 | 166.0 | 166.1 | 155.45 | 155.5 | 153.0 | 153.1 | 113.3 | 113.4 | 103.9 | 104.0 | 94.0 | 94.1 |
| 2 | 119.8 | 119.8 | 108.9 | 108.9 | 108.2 | 108.3 | 75.9 | 76.0 | 67.3 | 67.4 | 67.1 | 67.2 | |
| 3 | 100.1 | 100.2 | 94.4 | 94.4 | 94.3 | 94.3 | 60.4 | 60.4 | 60.4 | 60.5 | 60.3 | 60.3 | |
| 4 | 97.6 | 97.7 | 94.9 | 94.9 | 94.4 | 94.5 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | 46.0 | |
| 5 | 95.4 | 95.4 | 94.0 | 94.1 | 93.3 | 93.3 | 37.0 | 37.1 | 37.0 | 37.1 | 37.0 | 37.1 | |
| 6 | 90.4 | 90.5 | 89.4 | 89.4 | 89.1 | 89.2 | 34.3 | 34.4 | 34.3 | 34.4 | 34.3 | 34.4 | |
| 7 | 84.4 | 84.5 | 83.4 | 83.5 | 83.0 | 83.1 | 37.4 | 37.5 | 37.4 | 37.5 | 37.4 | 37.5 | |
| 8 | 79.3 | 79.3 | 79.1 | 79.2 | 78.2 | 78.3 | 43.9 | 44.0 | 43.9 | 44.0 | 43.9 | 44.0 | |
| 3 | 1 | 175.2 | 175.3 | 178.4 | 178.5 | 173.0 | 173.1 | 117.6 | 117.6 | 127.6 | 127.7 | 111.8 | 111.9 |
| 2 | 148.3 | 148.3 | 140.9 | 141.0 | 139.8 | 139.8 | 85.6 | 85.6 | 85.9 | 86.0 | 84.8 | 84.8 | |
| 3 | 123.0 | 123.1 | 117.6 | 117.7 | 117.5 | 117.5 | 68.0 | 68.0 | 68.4 | 68.5 | 66.5 | 66.6 | |
| 4 | 108.0 | 108.0 | 104.3 | 104.4 | 104.3 | 104.3 | 81.4 | 81.5 | 82.2 | 82.3 | 81.1 | 81.1 | |
| 5 | 98.0 | 98.1 | 95.7 | 95.7 | 95.2 | 95.3 | 88.4 | 88.5 | 88.9 | 88.9 | 88.2 | 88.3 | |
| 6 | 90.7 | 90.7 | 90.7 | 90.8 | 89.5 | 89.6 | 89.1 | 89.2 | 88.5 | 88.5 | 97.7 | 87.8 | |
| 7 | 84.5 | 86.4 | 84.3 | 84.4 | 84.1 | 84.2 | 82.9 | 82.9 | 82.2 | 82.2 | 81.5 | 81.5 | |
| 8 | 80.7 | 80.8 | 80.9 | 81.0 | 80.5 | 80.6 | 76.7 | 76.8 | 76.5 | 76.5 | 76.0 | 76.1 | |
| 4 | 1 | 181.9 | 191.0 | 180.4 | 180.5 | 176.4 | 176.4 | 152.5 | 152.6 | 158.8 | 158.9 | 151.0 | 151.0 |
| 2 | 160.1 | 160.2 | 152.3 | 152.3 | 151.2 | 151.3 | 136.7 | 136.7 | 126.4 | 126.4 | 125.9 | 125.9 | |
| 3 | 134.5 | 134.6 | 126.7 | 126.8 | 125.9 | 126.0 | 109.0 | 109.1 | 101.5 | 101.6 | 101.4 | 101.5 | |
| 4 | 115.6 | 115.7 | 110.0 | 110.0 | 109.7 | 109.8 | 100.1 | 100.2 | 96.4 | 96.4 | 95.9 | 95.9 | |
| 5 | 102.0 | 102.1 | 98.7 | 98.8 | 98.6 | 98.7 | 95.7 | 95.8 | 94.1 | 94.2 | 03.3 | 93.3 | |
| 6 | 91.6 | 91.7 | 90.9 | 92.2 | 90.7 | 90.8 | 90.2 | 90.3 | 89.2 | 89.3 | 89.1 | 89.2 | |
| 7 | 86.3 | 86.6 | 85.6 | 85.7 | 85.1 | 85.2 | 84.5 | 84.6 | 83.5 | 83.6 | 83.1 | 83.2 | |
| 8 | 82.2 | 82.3 | 82.5 | 82.6 | 81.7 | 81.7 | 79.8 | 79.8 | 79.7 | 79.8 | 78.7 | 78.8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhu, H.; Duan, Y. Free- and Forced-Vibration Characteristic Analysis of a Double-Layered Cylindrical Shell with General Boundary Conditions. J. Mar. Sci. Eng. 2025, 13, 641. https://doi.org/10.3390/jmse13040641
Wu J, Zhu H, Duan Y. Free- and Forced-Vibration Characteristic Analysis of a Double-Layered Cylindrical Shell with General Boundary Conditions. Journal of Marine Science and Engineering. 2025; 13(4):641. https://doi.org/10.3390/jmse13040641
Chicago/Turabian StyleWu, Jianghai, Hongzhen Zhu, and Yong Duan. 2025. "Free- and Forced-Vibration Characteristic Analysis of a Double-Layered Cylindrical Shell with General Boundary Conditions" Journal of Marine Science and Engineering 13, no. 4: 641. https://doi.org/10.3390/jmse13040641
APA StyleWu, J., Zhu, H., & Duan, Y. (2025). Free- and Forced-Vibration Characteristic Analysis of a Double-Layered Cylindrical Shell with General Boundary Conditions. Journal of Marine Science and Engineering, 13(4), 641. https://doi.org/10.3390/jmse13040641







