Fast and Stable Scanning Technology for a Rotating Dual Grating Based on Inertial Navigation Feedforward and Fuzzy PID Control for Shipborne Platforms
Abstract
1. Introduction
2. Related Works
3. Methodology
3.1. The Rotating Dual-Grating Two-Dimensional Scanning Model Based on Inertial Navigation Feedforward Technology
3.1.1. Model Derivation
3.1.2. Model Verification
3.2. Design and Simulation of the Fuzzy PID Control System for the Rotating Dual-Grating Two-Dimensional Scanning Model Based on Inertial Navigation Feedforward Technology
3.2.1. Analysis of the Impact of Sea-Surface Disturbance
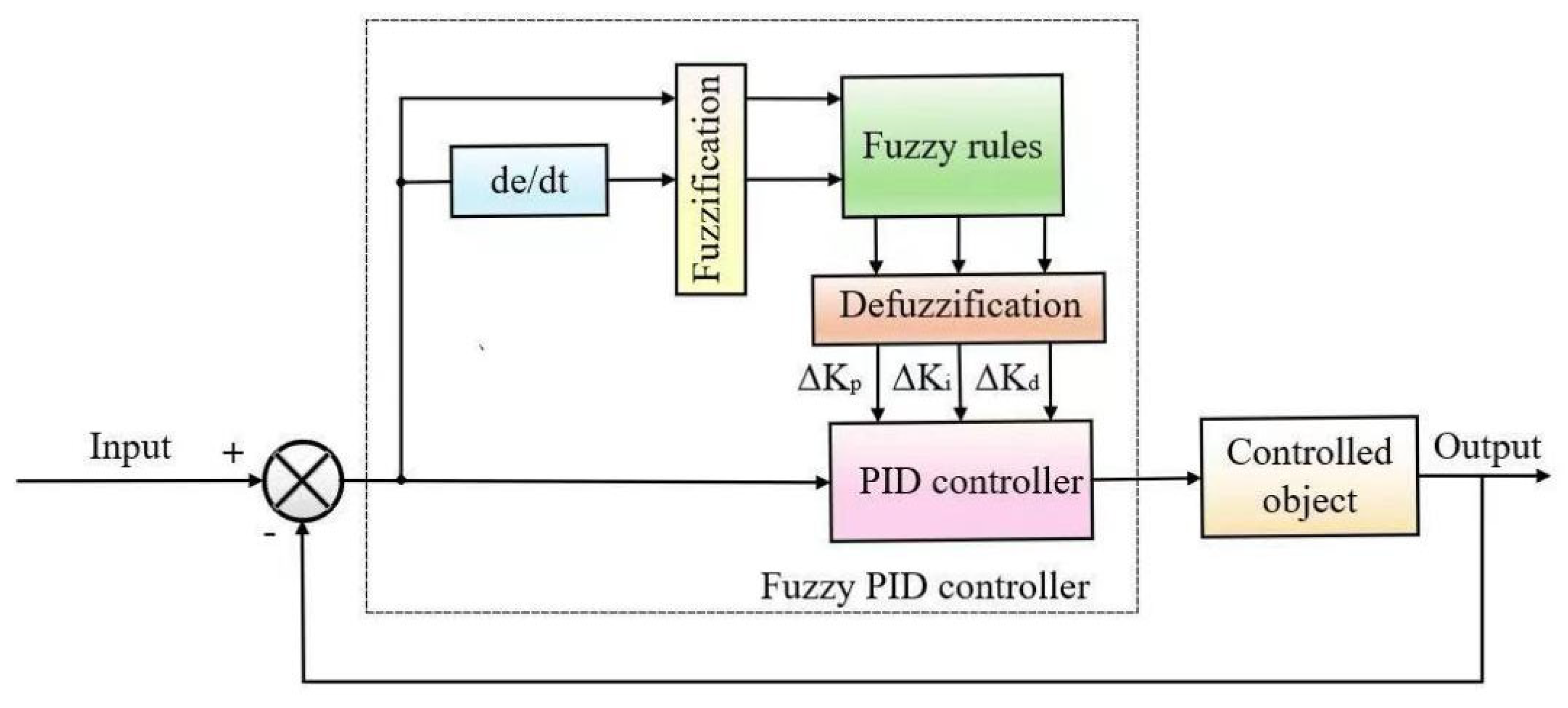
3.2.2. Design of the Fuzzy PID Control System for the Rotating Dual-Grating Two-Dimensional Scanning Model Based on Inertial Navigation Feedforward Technology
3.2.3. Simulation Verification
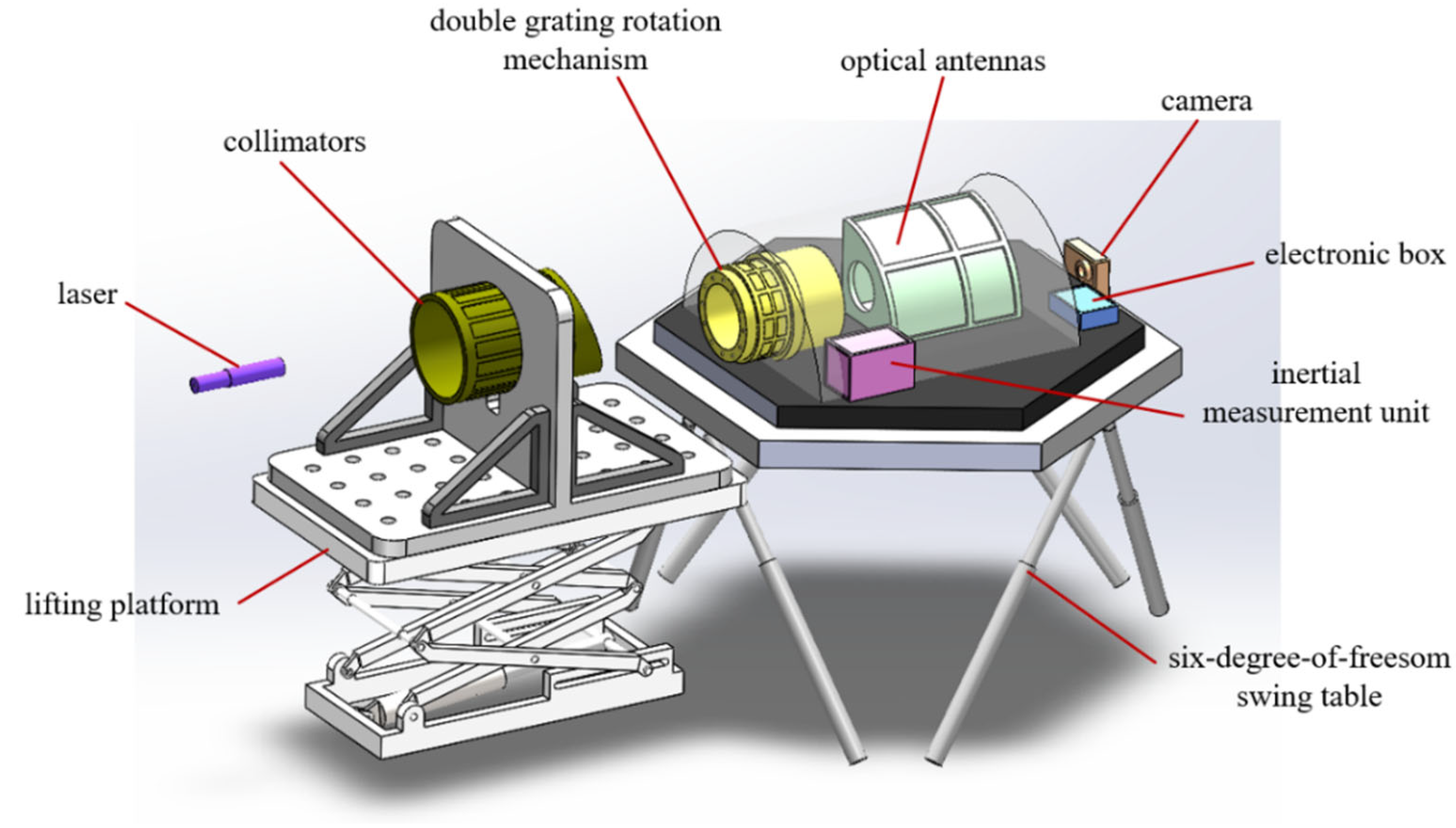
3.3. Experimental Design
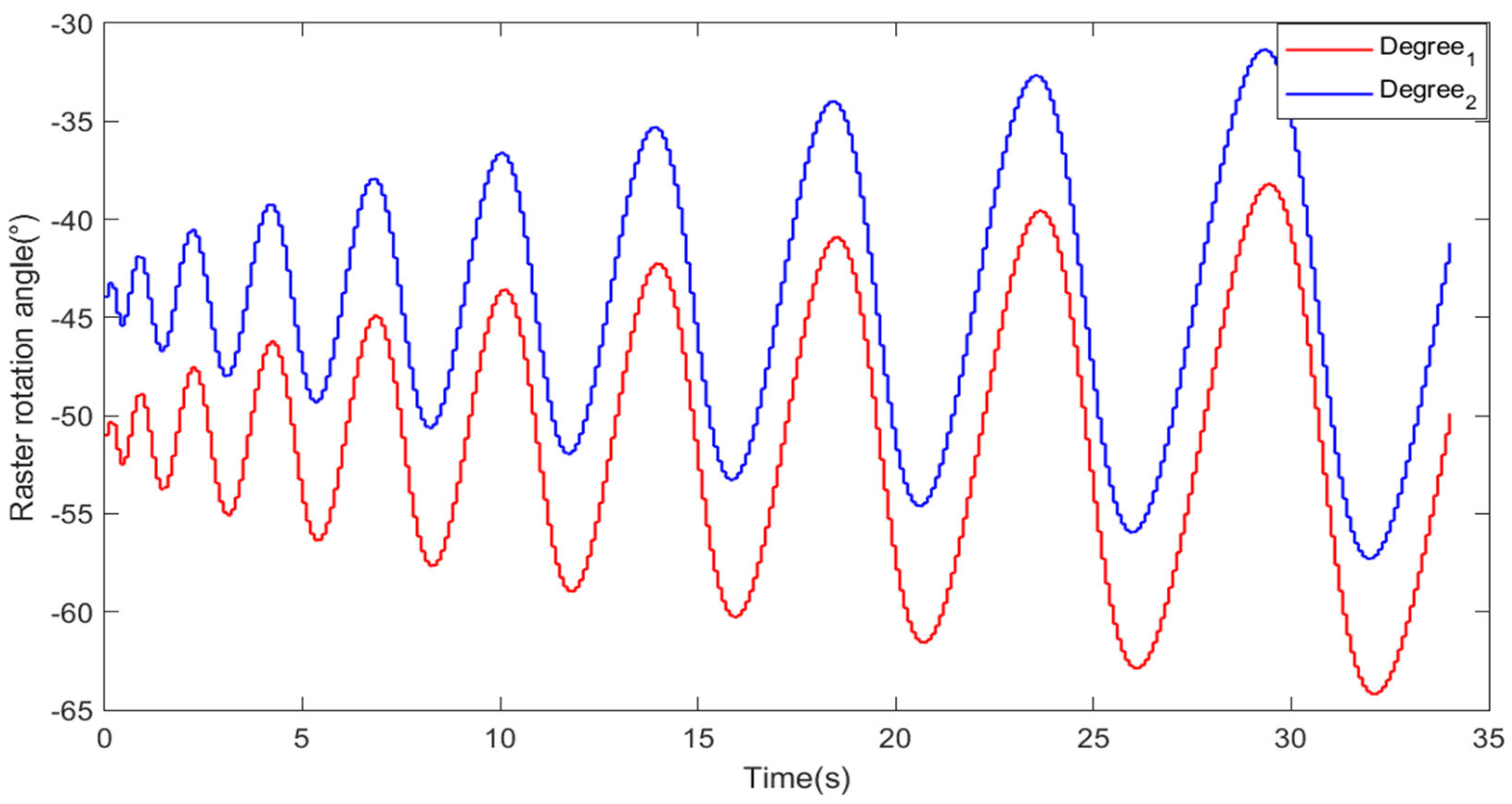
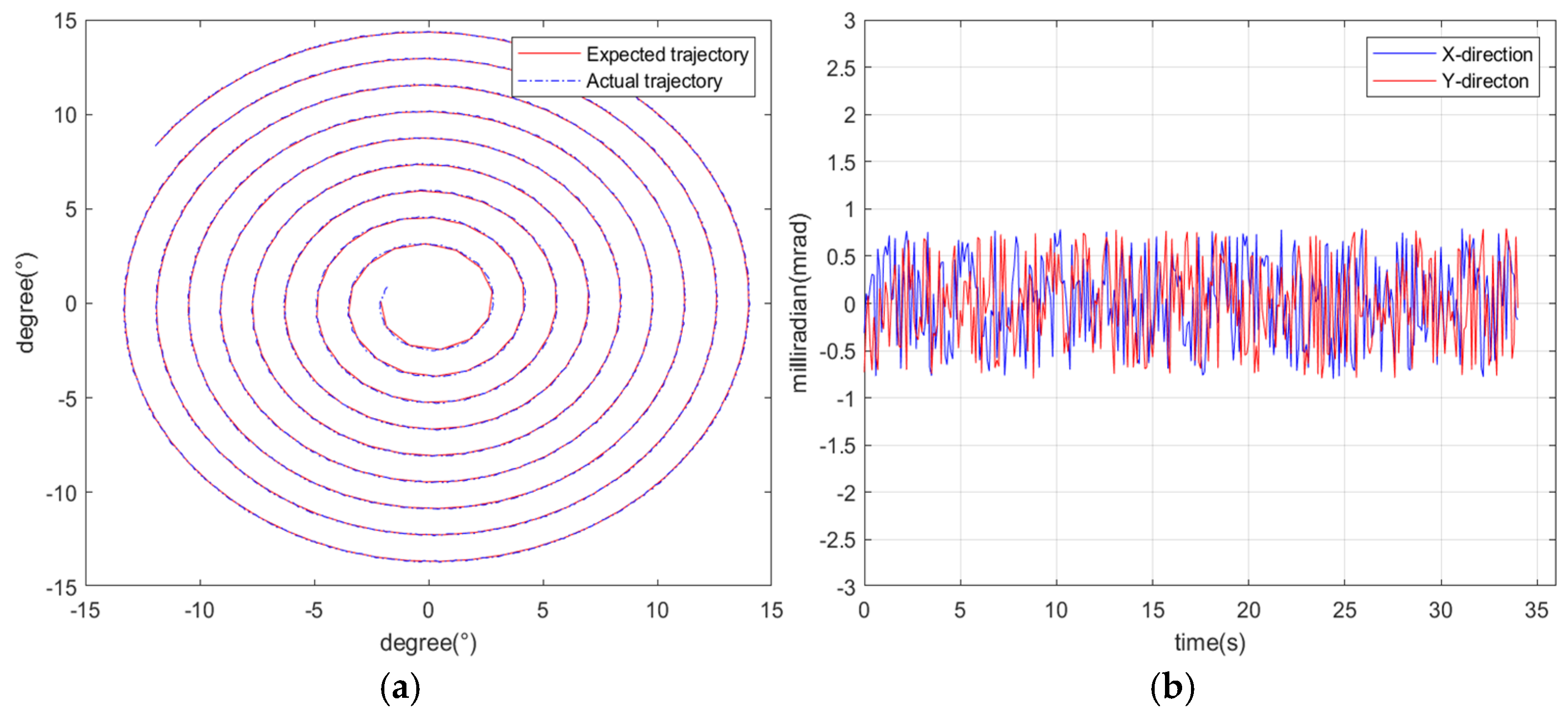
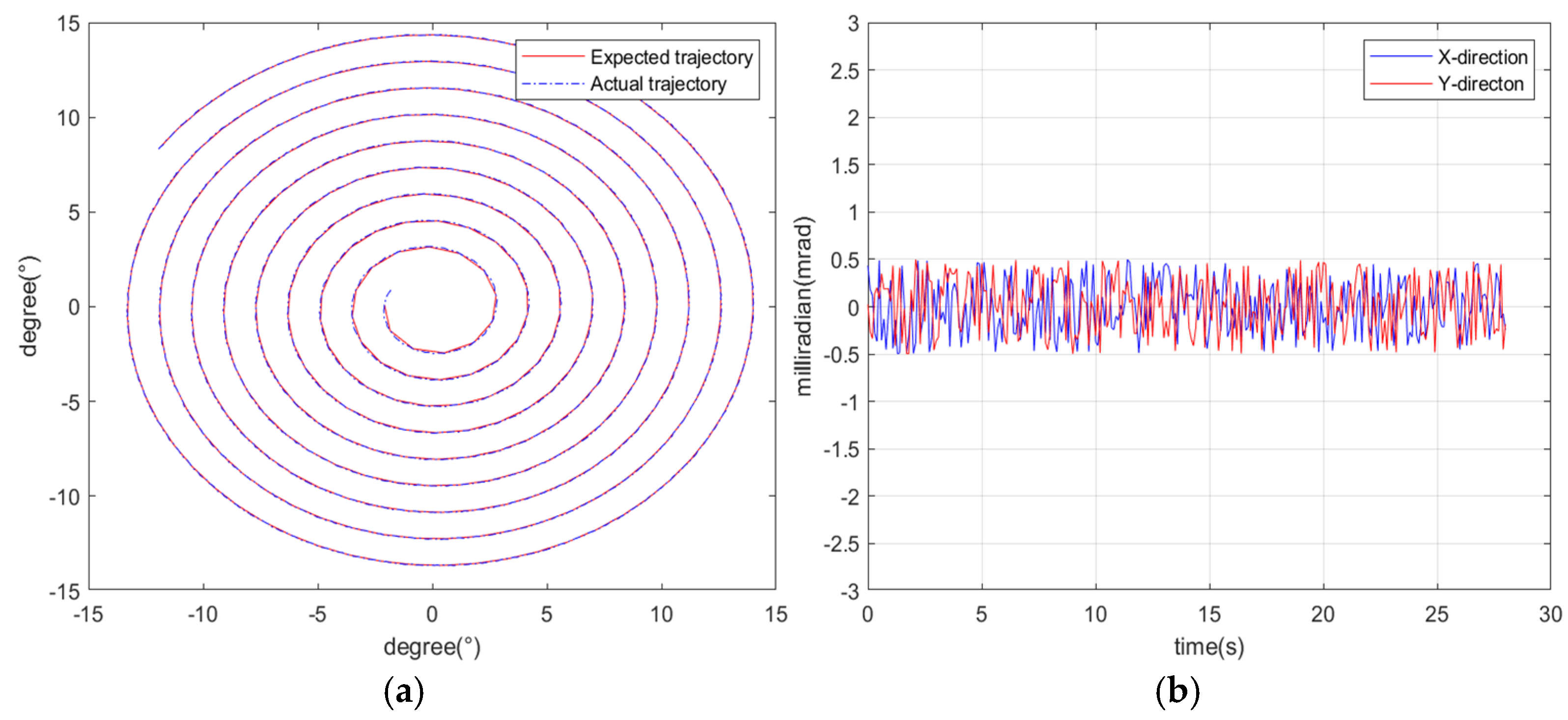
4. Results & Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F. Naval Electro-Optical System Technology and Its Evoluationary Trend. Opt. Optoelectron. Technol. 2021, 19, 1–6. [Google Scholar]
- Zhang, D. ADRC Based Study on Stable Tracking Control of Ship-Borne Photoelectric Platform. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2018. [Google Scholar]
- Yan, Z. Design and Analysis of Space-Borne Two-Dimens Onal Tracking Turntable Against the Environment of Space. Master’s Thesis, Graduate School of Chinese Academy of Sciences (Shanghai Institute of Technical Physics), Shanghai, China, 2014. [Google Scholar]
- Guo, Z.; Zeng, X. A Method for Improving the Stabilization of the Heavy Load Shipborne Electro-optical Platform. Opt.-Electron. Eng. 2011, 38, 28–33. [Google Scholar]
- Yi, X.; Liu, Y.; Teng, Y.; Liu, J.; Wang, J.; Zhang, J. Control Technology of Dual Liquid Crystal Polarization Gratings Based on Model Prediction Under Airborne Platform. Acta Opt. Sin. 2024, 44, 2006001. [Google Scholar]
- Oh, C.; Kim, J.; Muth, J.; Serati, S.; Escuti, M.J. High-Throughput Continuous Beam Steering Using Rotating Polarization Gratings. IEEE Photon. Technol. Lett. 2010, 22, 200–202. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Y.F.; Hei, M.; Xiong, F.R.; Li, K.; Fan, D.P. Analytic solution of optical beam steering based on rotational double prisms. Opt. Precis. Eng. 2013, 21, 1373–1379. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Y.F.; Hei, M.; Xiong, F.R.; Li, K.; Fan, D.P. Analytical inverse solution for rotational double prism beam steering. Opt. Precis. Eng. 2013, 21, 1693–1700. [Google Scholar] [CrossRef]
- Qin, C. Research on Fast Scanning Technology of Rotating Double Prism. Master’s Thesis, University of Chinese Academy of Sciences (Institute of Optoelectronic Technology), Chengdu, China, 2021. [Google Scholar]
- Zhang, J.; Song, Y.; Wang, J.; Liu, Y. Research on Technology of Airborne Optoelectronic Tracking Platform Based on Dual Liquid Crystal Polarization Grating. Acta Photonica Sin. 2024, 53, 0311002. [Google Scholar]
- Zhu, R.; He, Z.; Wang, T.; Chen, X. Design of DC motor control based on fuzzy adaptive PID algorithm. Mod. Electron. Tech. 2025, 48, 103–108. [Google Scholar]
- Ramasamy, M.; Somasundram, R.; Ramasamy, A. dSPACE real time implementation of fuzzy PID position controller for vertical rotating single link arm robot using four-quadrant BLDC drive. Acta Sci. Technol. 2017, 39, 301–311. [Google Scholar] [CrossRef]
- Luo, Q.; An, A.; Zhang, H.; Meng, F. Non-linear performance analysis and voltage control of MFC based on feedforward fuzzy logic PID strategy. J. Cent. South Univ. 2019, 26, 3359–3371. [Google Scholar] [CrossRef]
- Li, J.; Pan, S.; Lou, J.; Li, Y.; Xu, Y. Application of fuzzy PID variable structure adaptive algorithm in steering motor vector control of unmanned vehicles. Electr. Mach. Control 2024, 28, 152–159. [Google Scholar]
- Chen, L. Design of ATP coarse tracking system for shipborne laser communication. Electron. Des. Eng. 2020, 28, 113–116. [Google Scholar]
- Ma, J. Research on Position Servo System of Shipborne Turntable Based on Double Time-Varying Boundary Layer Sliding Mode Control. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2022. [Google Scholar]
- Lin, Y. Research of Electro-Optical Tracking System for Wireless Laser Communication. Ph.D. Thesis, Wuhan University, Wuhan, China, 2017. [Google Scholar]
- Li, J.; Chen, K.; Peng, Q.; Wang, Z.; An, T.; Ma, H.; Xiang, C. Wide-range, Fast and High Precision Scanning Technology Based on Rotational Double Prisms. Electro-Opt. Technol. Appl. 2020, 35, 44–48. [Google Scholar]
- Chang, J.; Huang, K. Study on Optimizing Technology for Feed Forward Compensation of Ship-swaying for Shipborne Servo in Satellite Communication. Syst. Control Theory Appl. 2017, 36, 16–19+37. [Google Scholar]
- Lv, S. Key Technologies for Shipboard Optoelectronic Tracking and Pointing Based on Feedforward Control. Master’s Thesis, Graduate School of Chinese Academy of Sciences, Chengdu, China, 2014. [Google Scholar]
- Wang, Y.; Liu, Z.; Zhou, B. Establishment of shipboard electro-optical tracking and pointing disturbance model and feedforward compensation. Electron. Meas. Technol. 2018, 41, 6–12. [Google Scholar]
- Zhou, Y.; Fan, D.; Fan, S.; Chen, Y.; Liu, G. Laser scanning by rotating polarization gratings. Appl. Opt. 2016, 55, 5149–5157. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Research on Tracking and Scanning Characteristics of Servo System Based on Dual liquid Crystal Polarization Gratings. Master’s Thesis, Changchun University of Science and Technology, Changchun, China, 2023. [Google Scholar]
- Sain, D.; Praharaj, M.; Mohan, B.; Yang, J. Interval type-2 fuzzy PID controllers with interval of confidence and various types of footprints of uncertainty. Inf. Sci. 2025, 699, 121795. [Google Scholar] [CrossRef]
- Kim, S. Moment of inertia and friction torque coefficient identification in a servo drive system. IEEE Trans. Ind. Electron. 2019, 66, 60–70. [Google Scholar] [CrossRef]
- Lv, H.; Zheng, R.; Yang, B.; Liu, B.; Yang, B. Application research of heading control algorithm for AUV. Ship Sci. Technol. 2020, 42, 108–114. [Google Scholar]
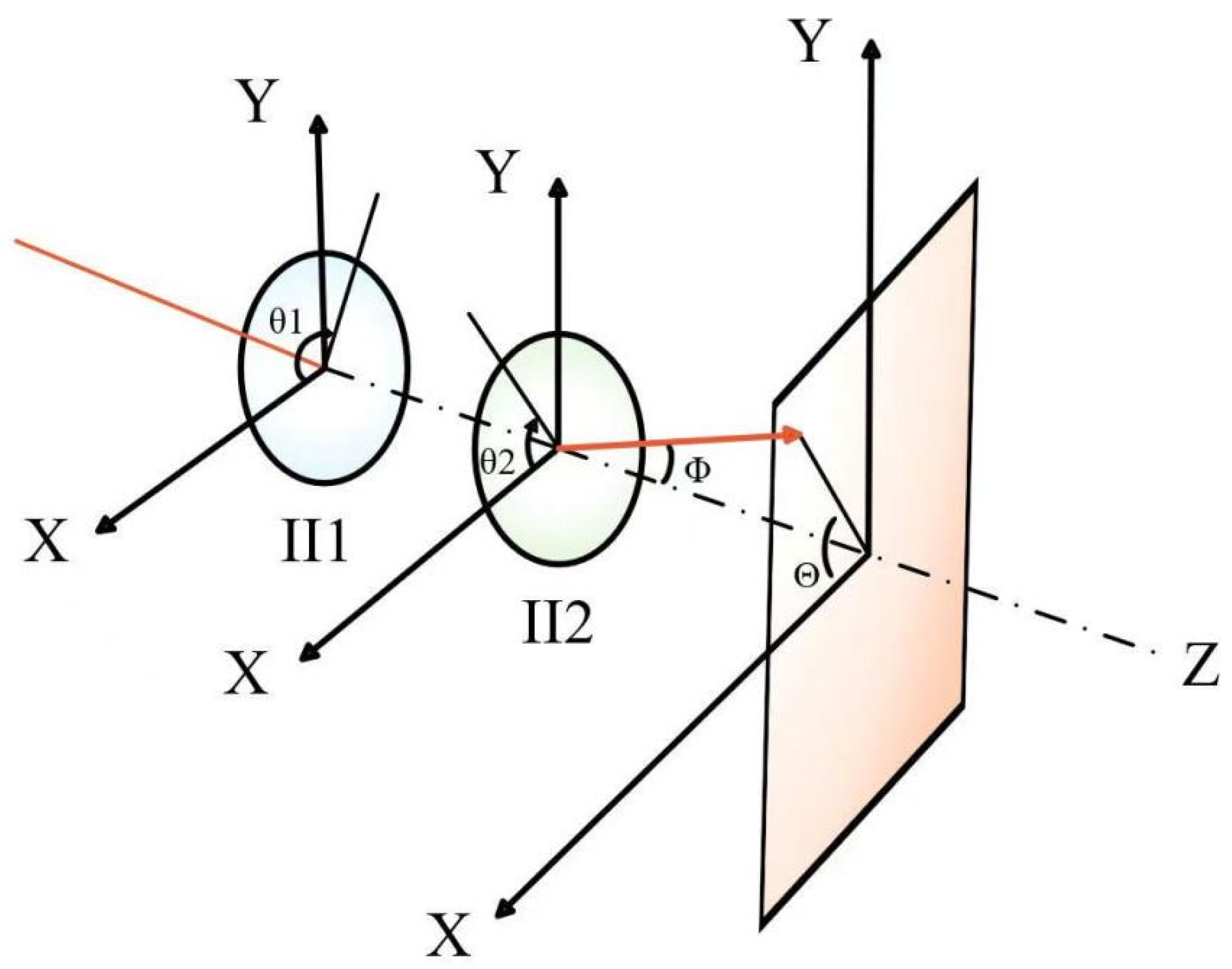
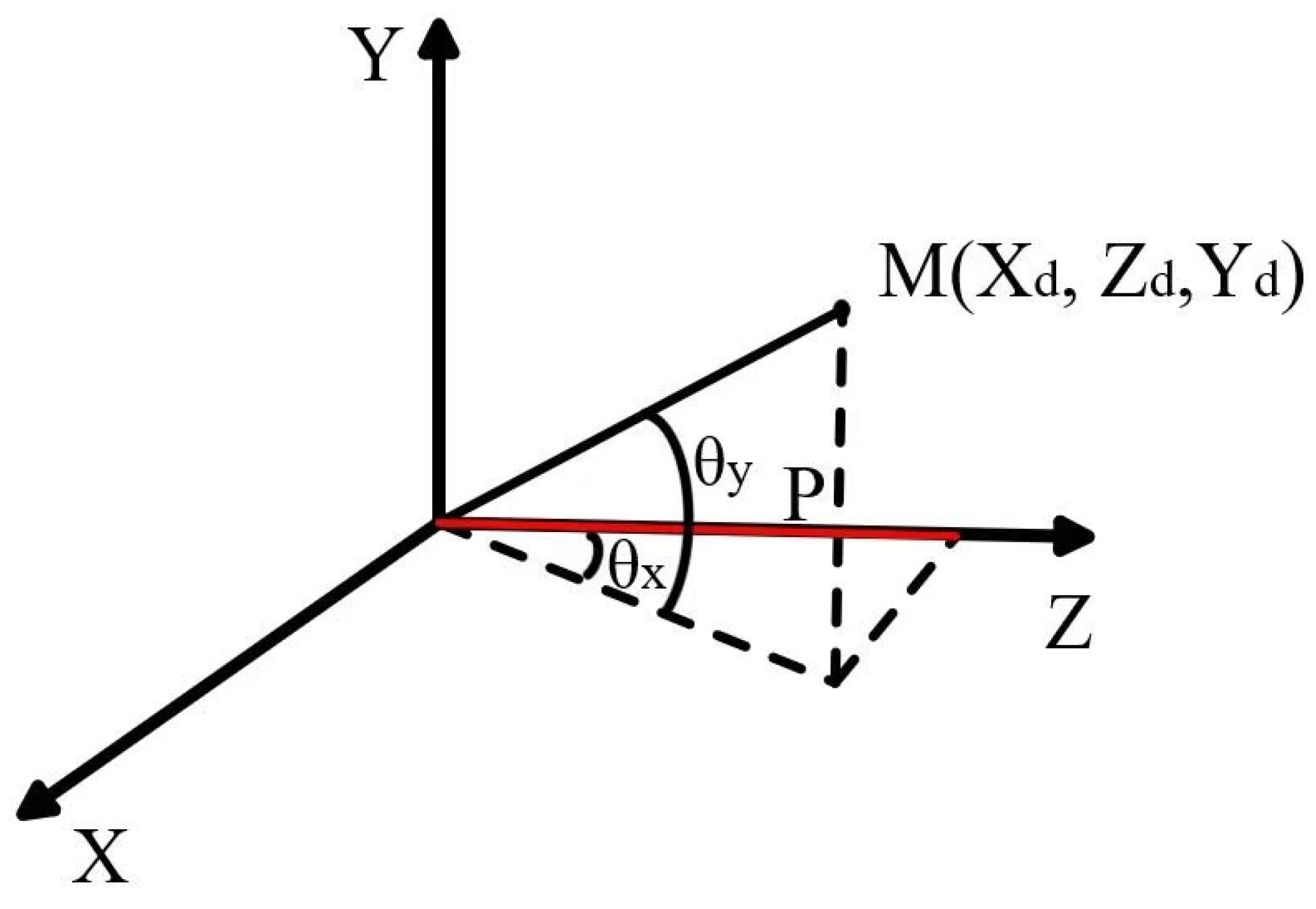

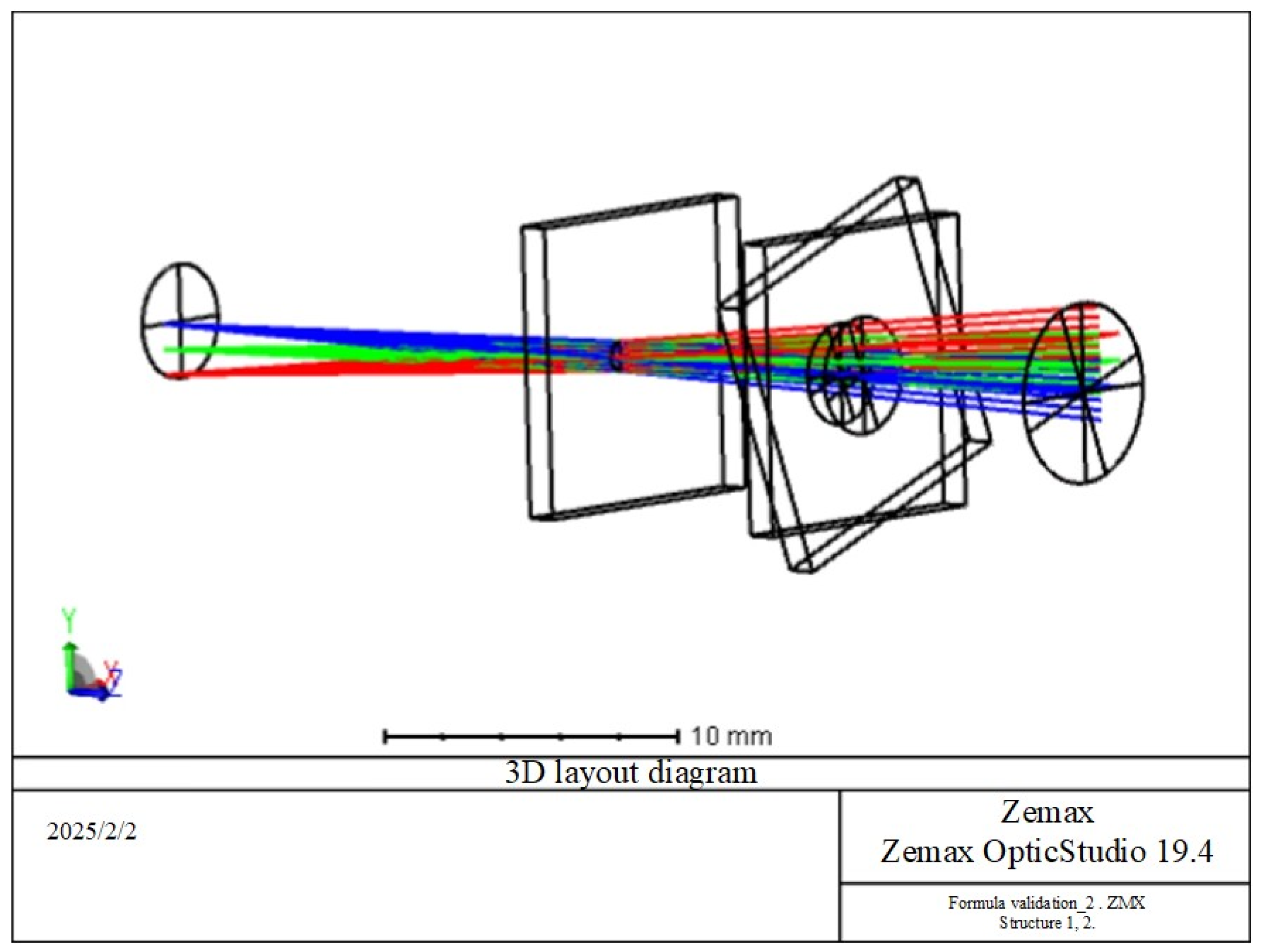




| Incident Azimuth Angle | Incident Pitch Angle | The X Coordinate from Which the Formula Emerges | The X Coordinate from Which the Zemax Emerges | The Y Coordinate from Which Zemax Emerges | The Y Coordinate from Which Zemax Emerges | The Difference Between the X Coordinate from the Formula and the X Coordinate from Zemax. | The Difference Between the Y Coordinate from the Formula and the Y Coordinate from Zemax. |
|---|---|---|---|---|---|---|---|
| 0.1° | 0° | 1.78143214 | 1.7453503 | 0.00800332 | 0.00164635 | −0.03608184 | −0.00635697 |
| 0.1° | 20° | 1.78143214 | 1.7453505 | −363.96229 | −363.97422 | −0.03608164 | −0.01193 |
| 0.1° | 40° | 1.78143214 | 1.7453517 | −839.09051 | −839.109 | −0.03608044 | −0.01849 |
| 0.1° | 60° | 1.78143214 | 1.7453527 | −1732.0375 | −1732.0699 | −0.03607944 | −0.0324 |
| 0.1° | 80° | 1.78143214 | 1.7453545 | −5671.2447 | −5671.345 | −0.03607764 | −0.1003 |
| 0.1° | 100° | 1.78143214 | 1.7453499 | 5671.24473 | 5671.345 | −0.03608224 | 0.10027 |
| 0.1° | 120° | 1.78143214 | 1.7453516 | 1732.03755 | 1732.070 | −0.03608054 | 0.03245 |
| 0.1° | 140° | 1.78143214 | 1.7453506 | 839.090514 | 839.10881 | −0.03608154 | 0.018296 |
| 0.1° | 160° | 1.78143214 | 1.7453502 | 363.962295 | 363.97422 | −0.03608194 | 0.011925 |
| 0.1° | 180° | 1.78143214 | 1.7453506 | −0.0080033 | −0.0016464 | −0.03608154 | 0.0063569 |
| ec | e | ||||
|---|---|---|---|---|---|
| NB | NS | ZO | PS | PB | |
| NB | PB | PB | PB | PS | ZO |
| NS | PB | PS | PS | ZO | NS |
| ZO | PB | PS | ZO | NS | NB |
| PS | PS | ZO | NS | NS | NB |
| PB | ZO | NS | NB | NB | NB |
| ec | e | ||||
|---|---|---|---|---|---|
| NB | NS | ZO | PS | PB | |
| NB | NB | NB | NB | NS | ZO |
| NS | NB | NS | NS | ZO | PS |
| ZO | NB | NS | ZO | PS | PB |
| PS | ZO | ZO | ZO | PS | PB |
| PB | ZO | PS | PS | PB | PB |
| ec | e | ||||
|---|---|---|---|---|---|
| NB | NS | ZO | PS | PB | |
| NB | PS | NB | NB | NB | PS |
| NS | ZO | NB | NB | NS | ZO |
| ZO | ZO | NS | NS | NS | ZO |
| PS | PB | ZO | ZO | ZO | PB |
| PB | PB | PS | PS | PS | PB |
| Motor Position | Shaft System 1 | Shaft System 2 |
|---|---|---|
| Model | YT450-10-A | YT434-10-A |
| Installation form | Segmented packaging | Segmented packaging |
| Motor type | Permanent Magnet DC Torque Motor | Permanent Magnet DC Torque Motor |
| Maximum no-load speed | 100 r/min | 110 r/min |
| Peak stall torque | 80 N·m | 70 N·m |
| Peak stall voltage | 27 V | 27 V |
| Peak stall current | 32 A | 30 A |
| Continuous stall torque | 40 N·m | 35 N·m |
| Continuous stall current | 16 A | 15 A |
| Continuous stall voltage | 13.5 V | 13.5 V |
| Weight | 0.12 kg | 0.51 kg |
| Name | PTN-1 Metal Grating Angle Encoder |
|---|---|
| Communication protocol | BiSS-C |
| Absolute bit count | 21 bit–28 bit |
| Supply voltage | 5 ± 0.5 V |
| Electrical rated speed | 300–2100 r/min |
| Working current | ≤350 mA |
| Working temperature | −40–75 °C |
| Storage temperature | −55–+80 °C |
| IP rating | IP64 |
| Impact | Under working conditions, ≤1000 m/s2, three-axis, 6 ms |
| Vibration | Under working conditions, 55–2000 HZ, ≤300 m/s2, three-axis |
| Relative humidity | ≤90%RH, non-condensing |
| Maximum outer diameter | 412 mm |
| Accuracy | 3″ |
| Angular resolution | 0.02″ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, W.; Liu, Y.; Teng, Y.; Wang, Q.; Wang, H.; Zhang, F.; Shi, F.; Yi, X. Fast and Stable Scanning Technology for a Rotating Dual Grating Based on Inertial Navigation Feedforward and Fuzzy PID Control for Shipborne Platforms. J. Mar. Sci. Eng. 2025, 13, 600. https://doi.org/10.3390/jmse13030600
Xi W, Liu Y, Teng Y, Wang Q, Wang H, Zhang F, Shi F, Yi X. Fast and Stable Scanning Technology for a Rotating Dual Grating Based on Inertial Navigation Feedforward and Fuzzy PID Control for Shipborne Platforms. Journal of Marine Science and Engineering. 2025; 13(3):600. https://doi.org/10.3390/jmse13030600
Chicago/Turabian StyleXi, Wang, Yang Liu, Yunjie Teng, Qiran Wang, Hengjie Wang, Fujing Zhang, Fengshou Shi, and Xinqing Yi. 2025. "Fast and Stable Scanning Technology for a Rotating Dual Grating Based on Inertial Navigation Feedforward and Fuzzy PID Control for Shipborne Platforms" Journal of Marine Science and Engineering 13, no. 3: 600. https://doi.org/10.3390/jmse13030600
APA StyleXi, W., Liu, Y., Teng, Y., Wang, Q., Wang, H., Zhang, F., Shi, F., & Yi, X. (2025). Fast and Stable Scanning Technology for a Rotating Dual Grating Based on Inertial Navigation Feedforward and Fuzzy PID Control for Shipborne Platforms. Journal of Marine Science and Engineering, 13(3), 600. https://doi.org/10.3390/jmse13030600





