Convex Optimization-Based Adaptive Neural Network Control for Unmanned Surface Vehicles Considering Moving Obstacles
Abstract
1. Introduction
2. Problem Description
Dynamic Model of Unmanned Surface Vehicles
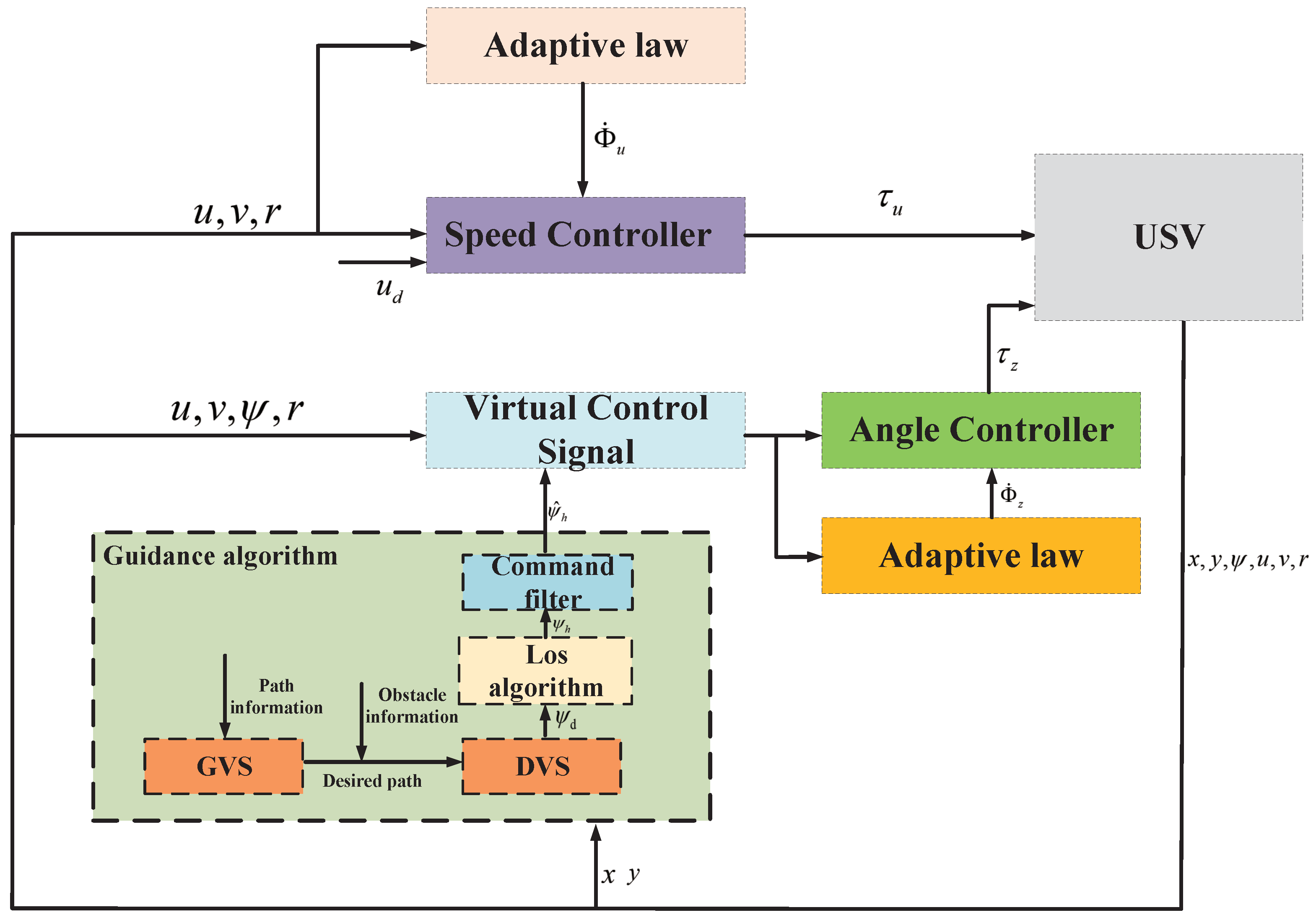
3. Design and Performance Analysis of Obstacle Avoidance Controller
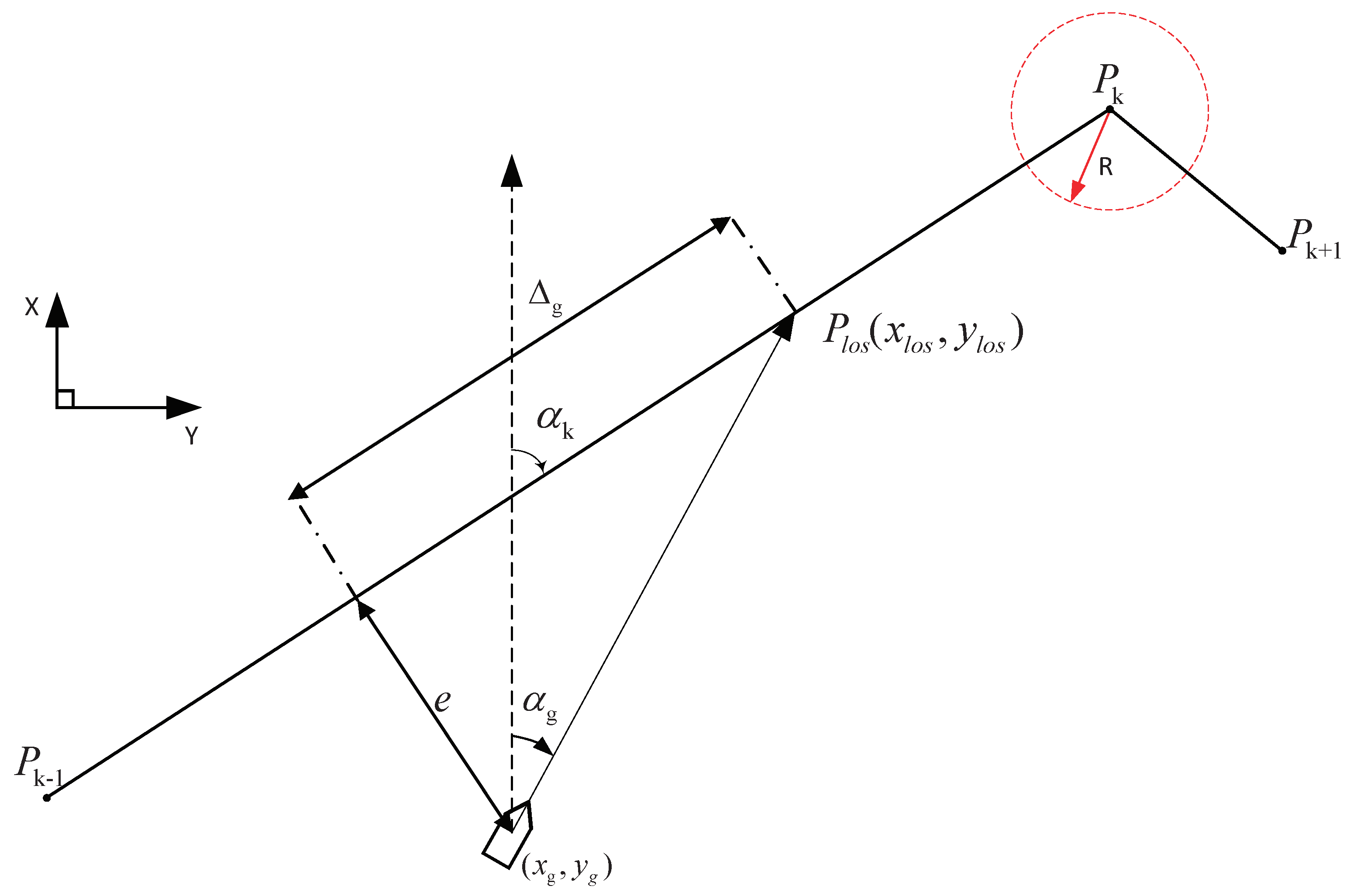
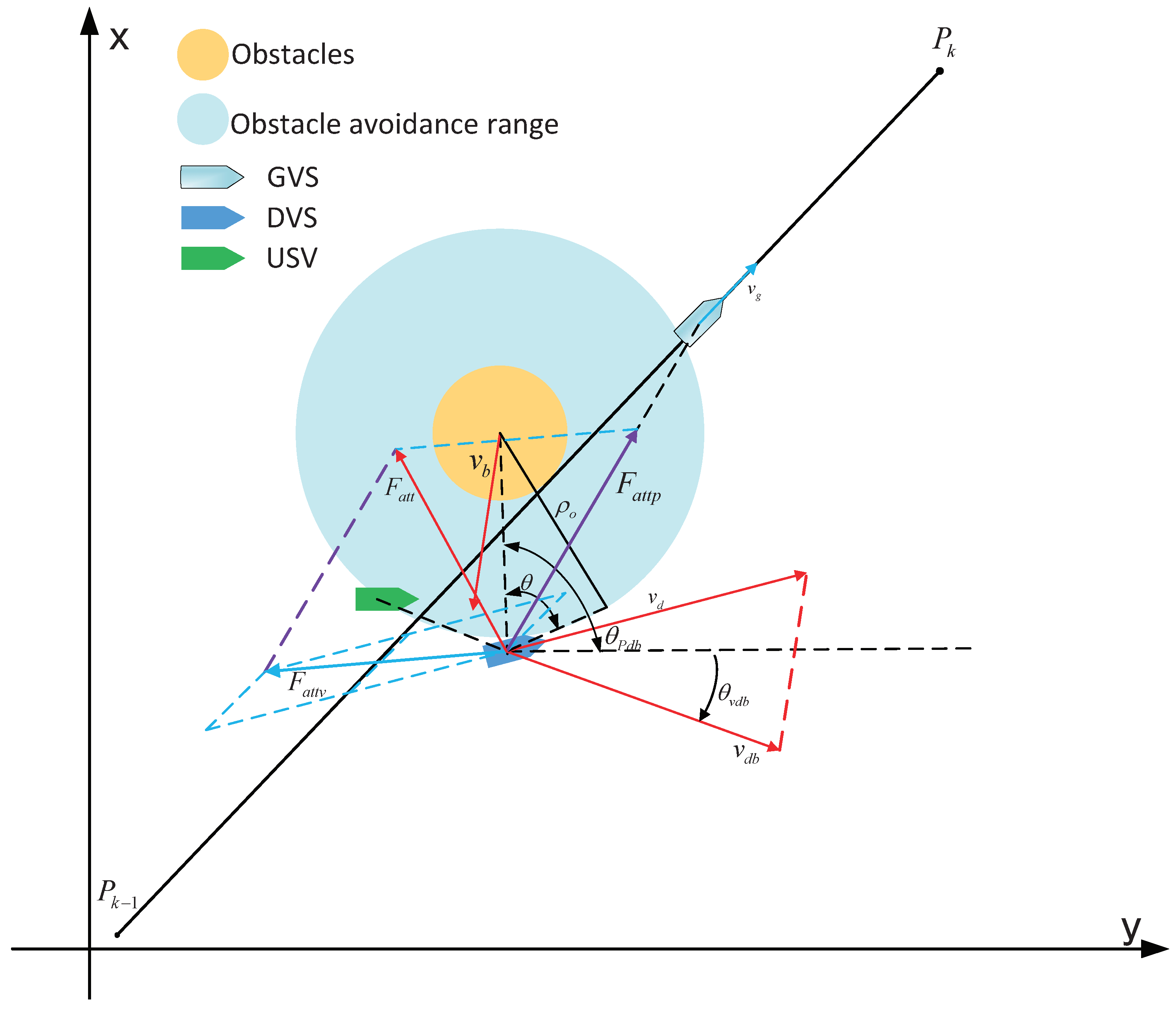
3.1. Real-Time Obstacle Avoidance Path Generation Algorithm
3.2. Adaptive Neural Control Strategy for Forward Speed Subsystem
3.3. Adaptive Neural Control Strategy for Heading Angle Subsystem
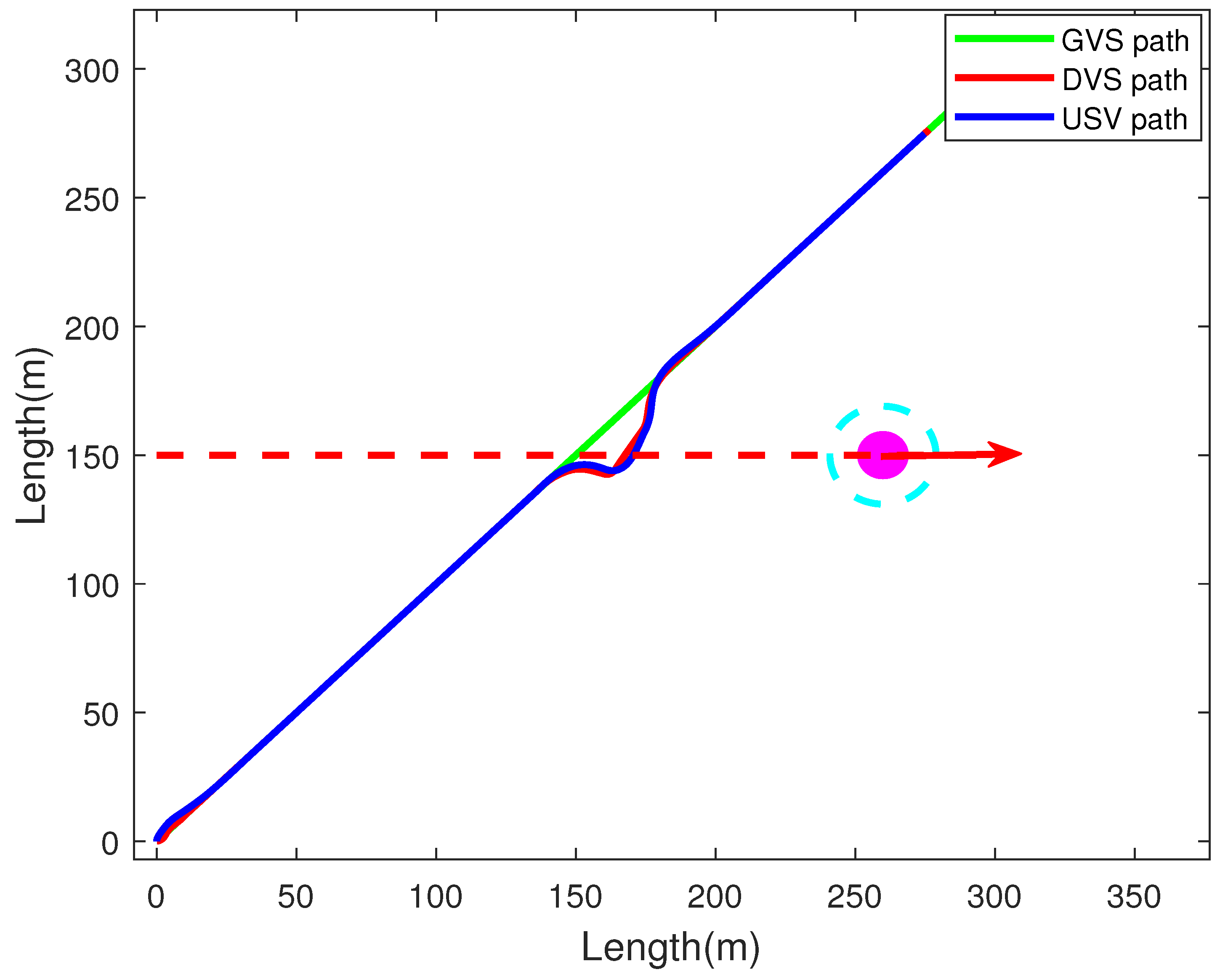
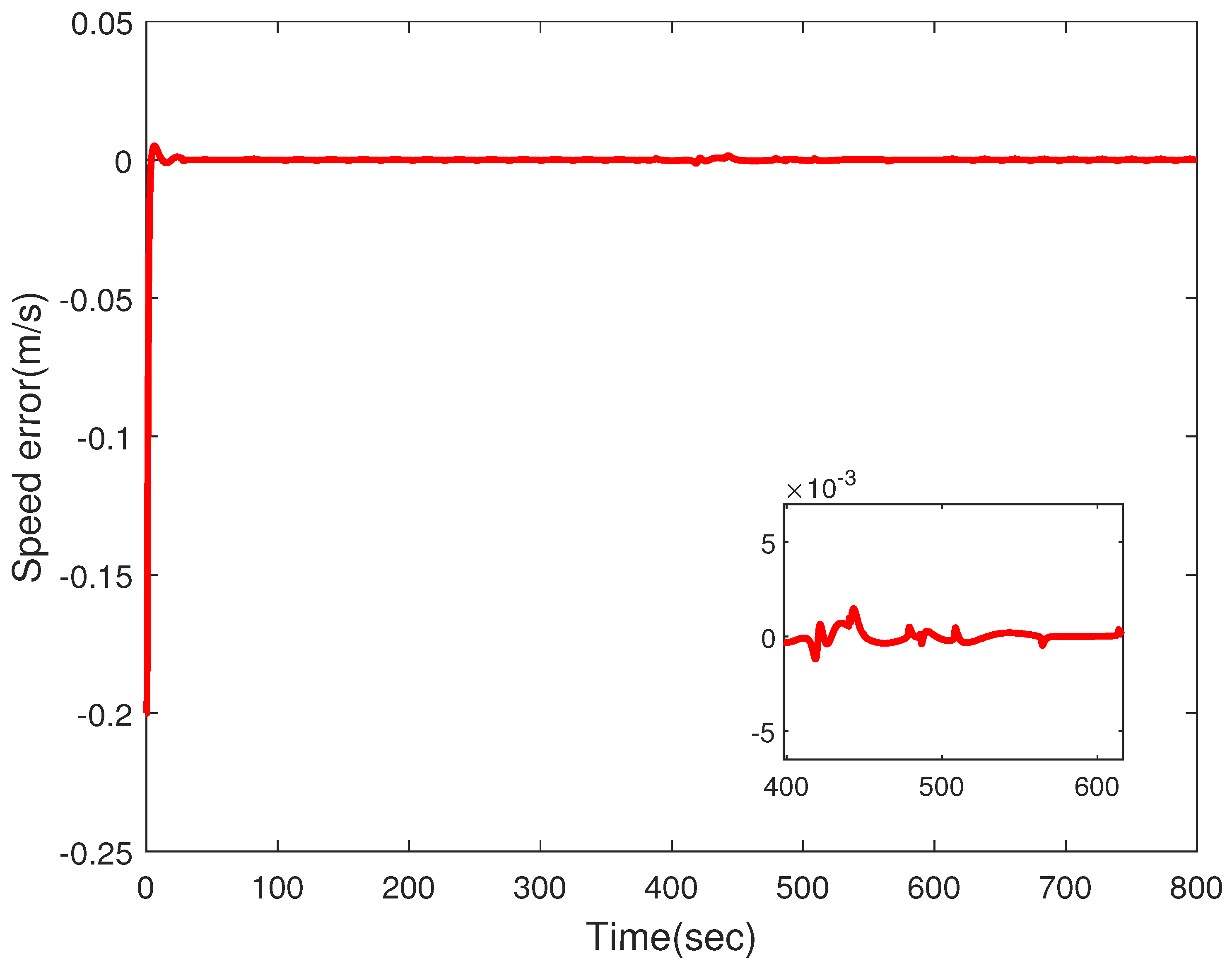
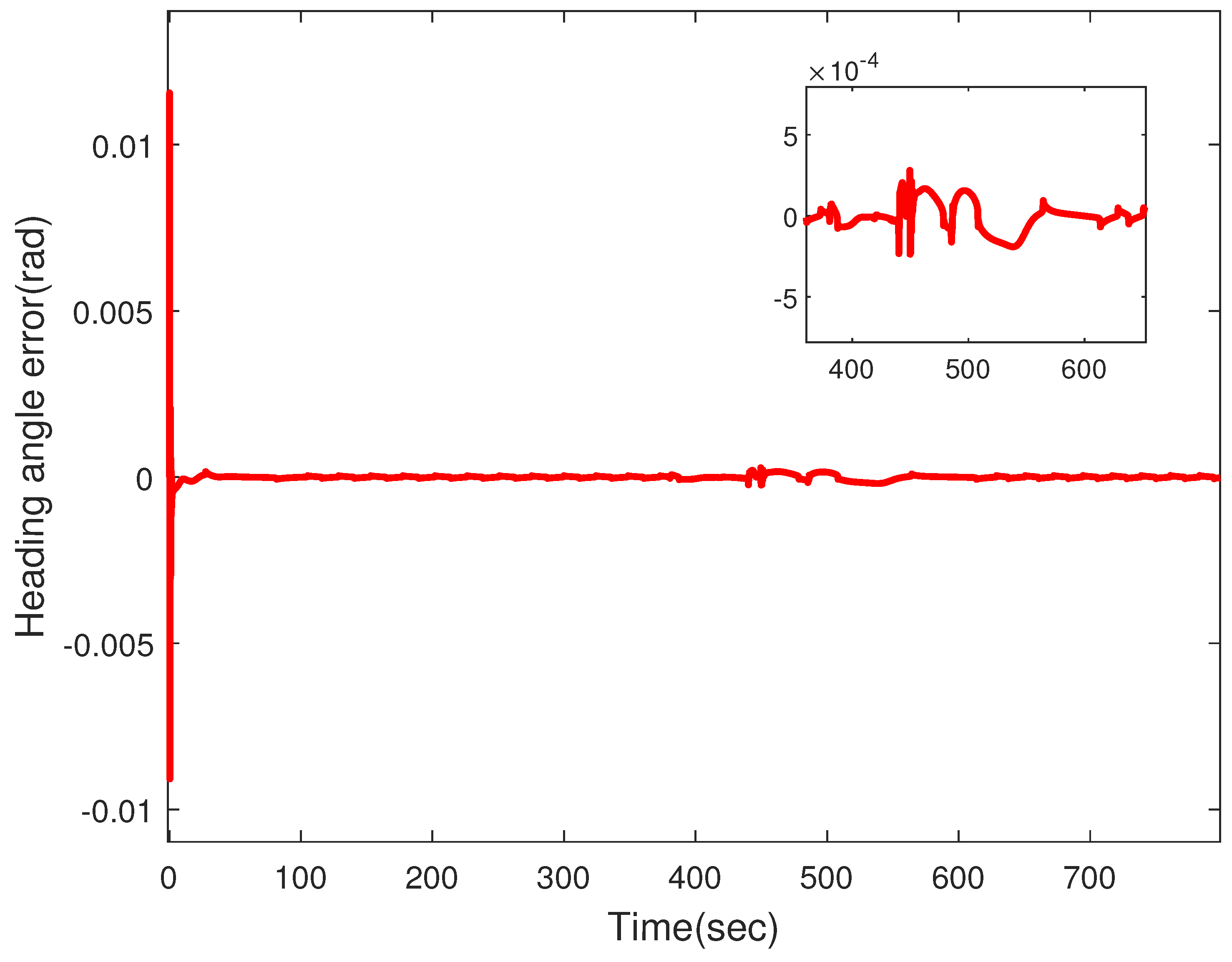
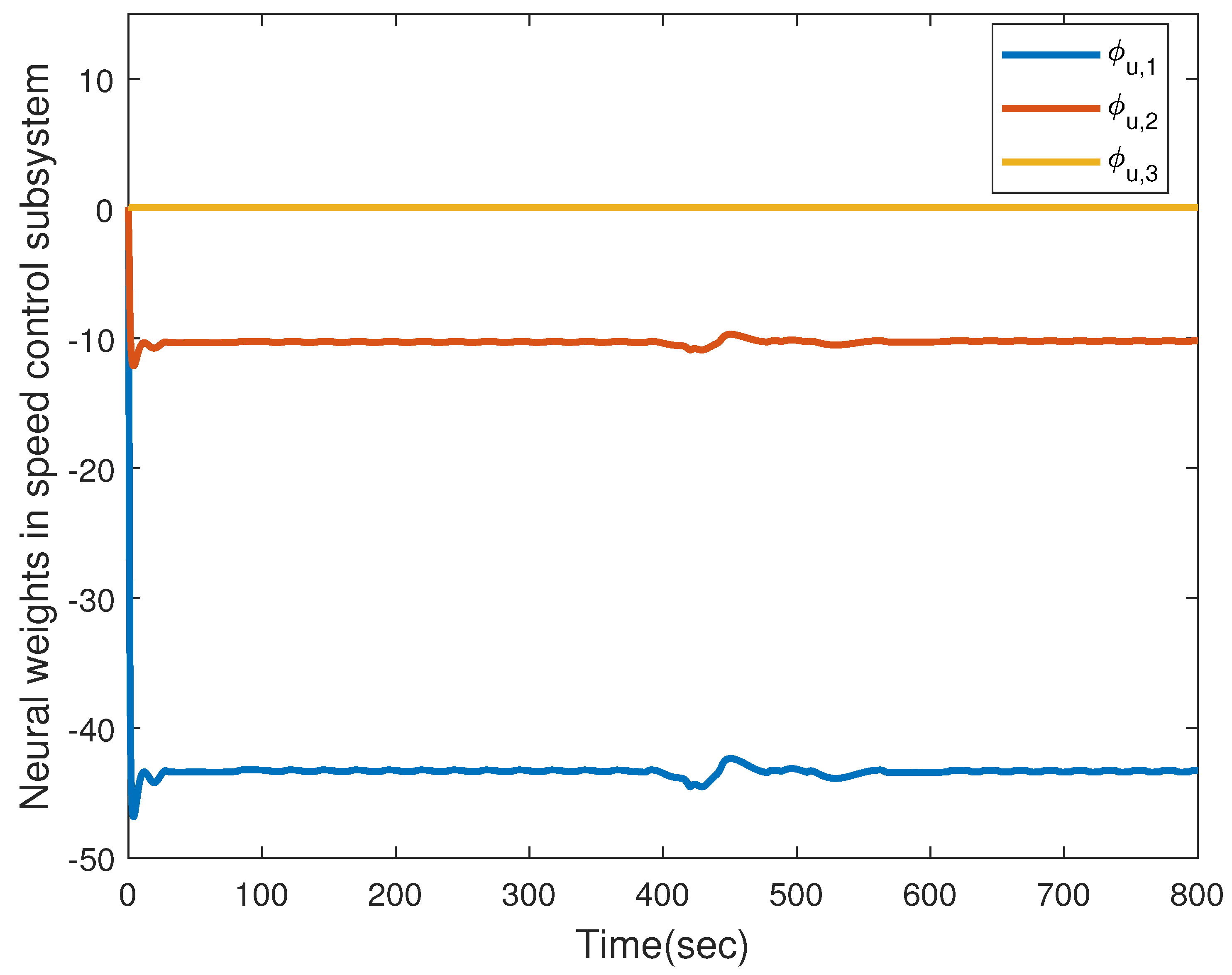
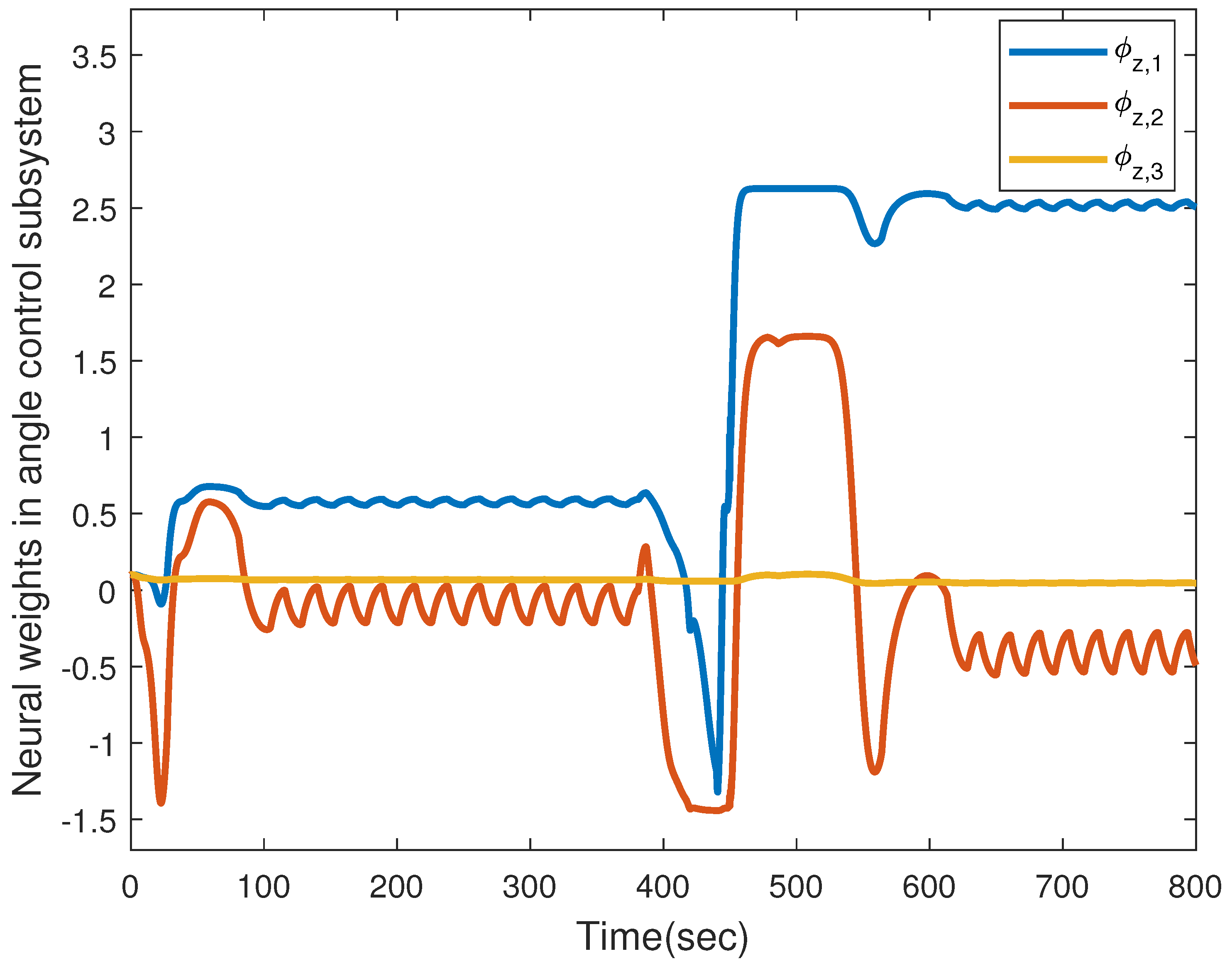
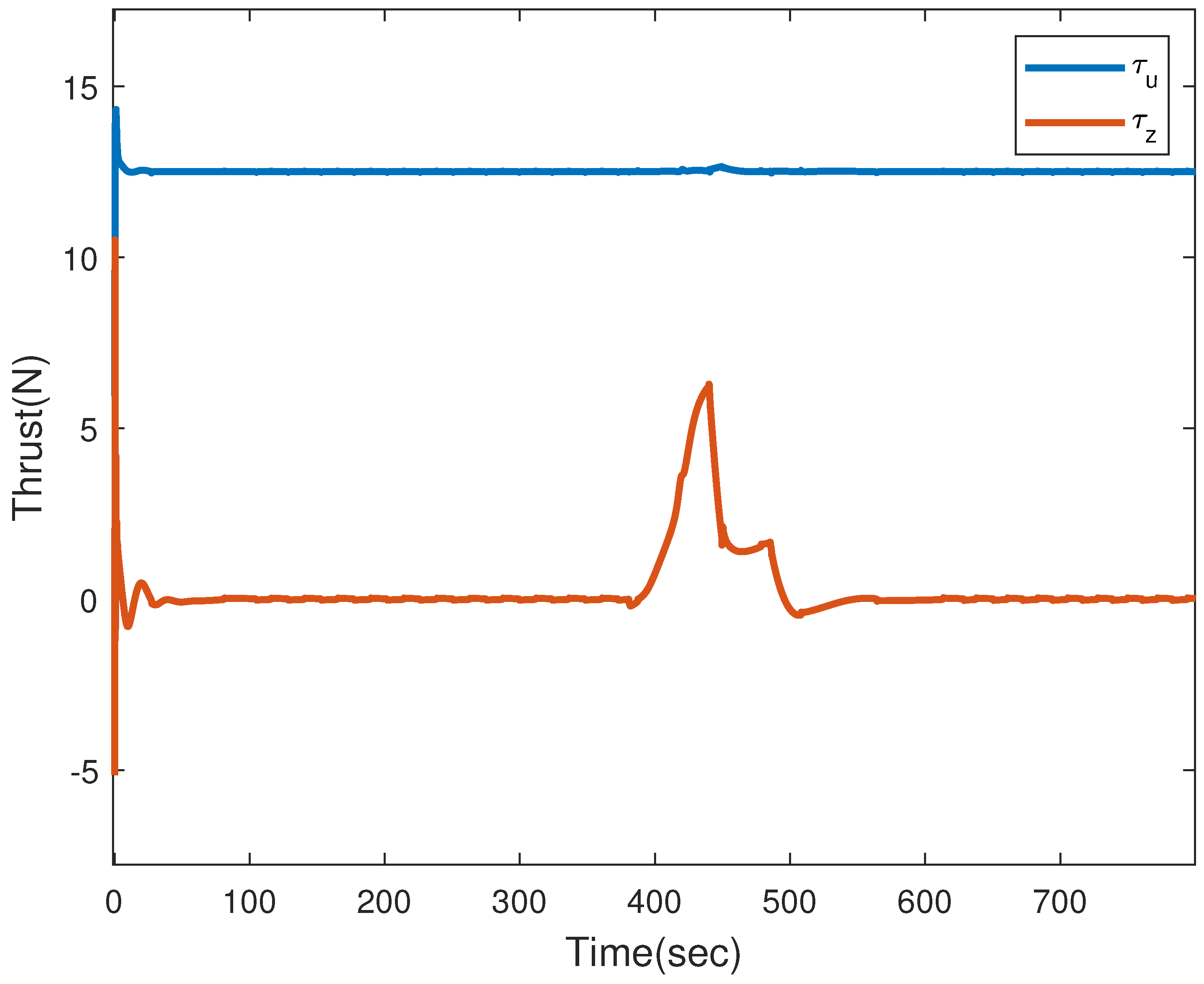
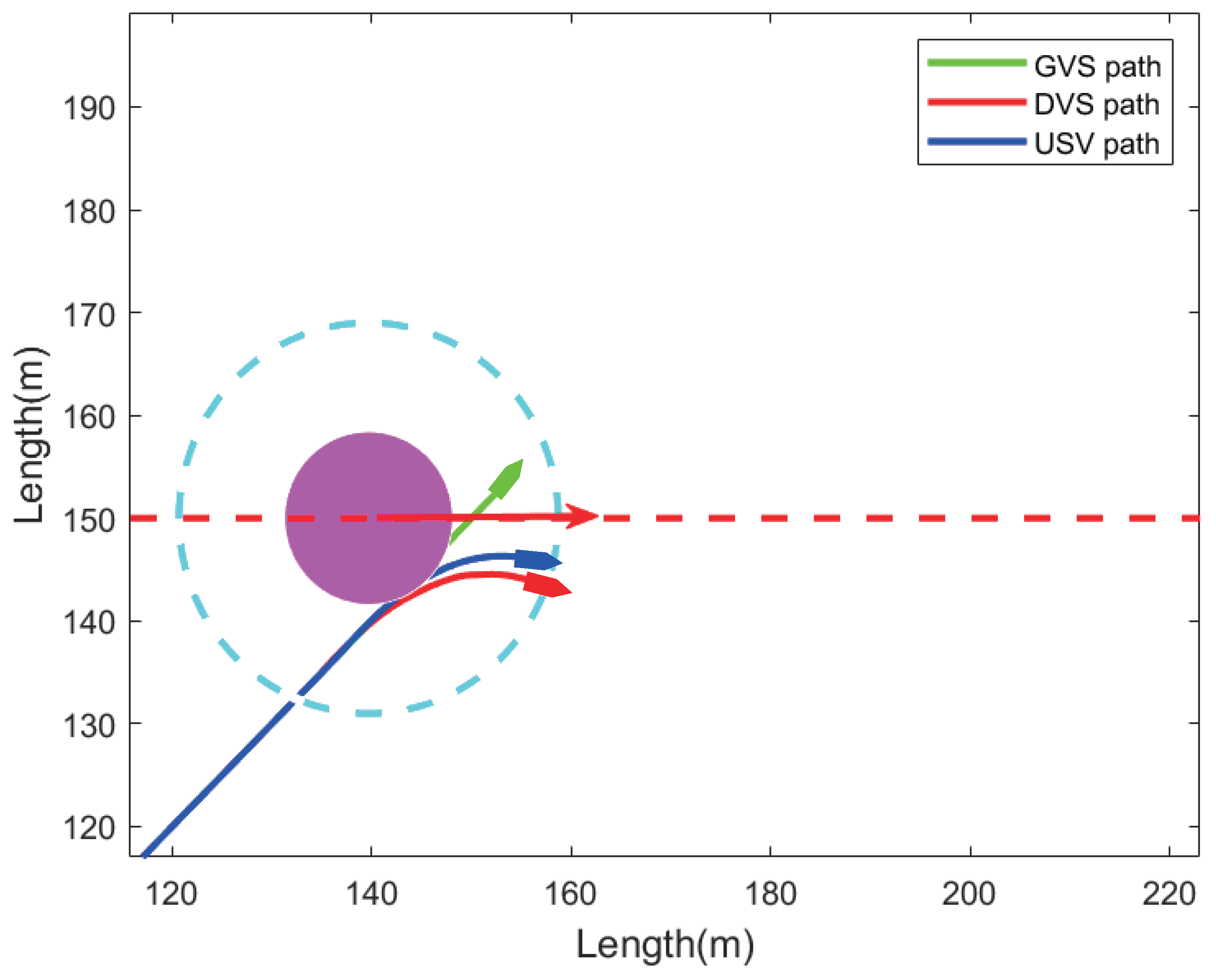
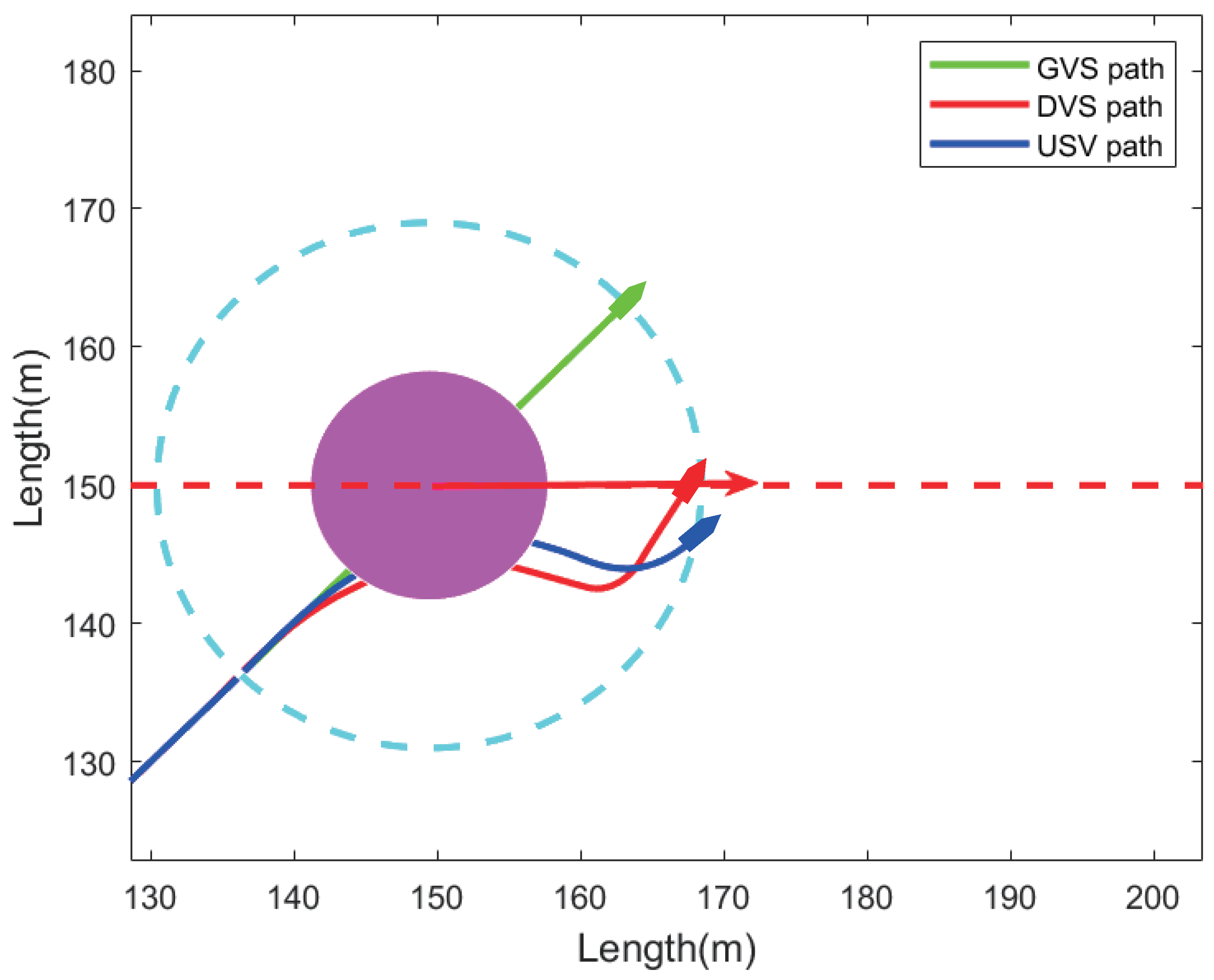
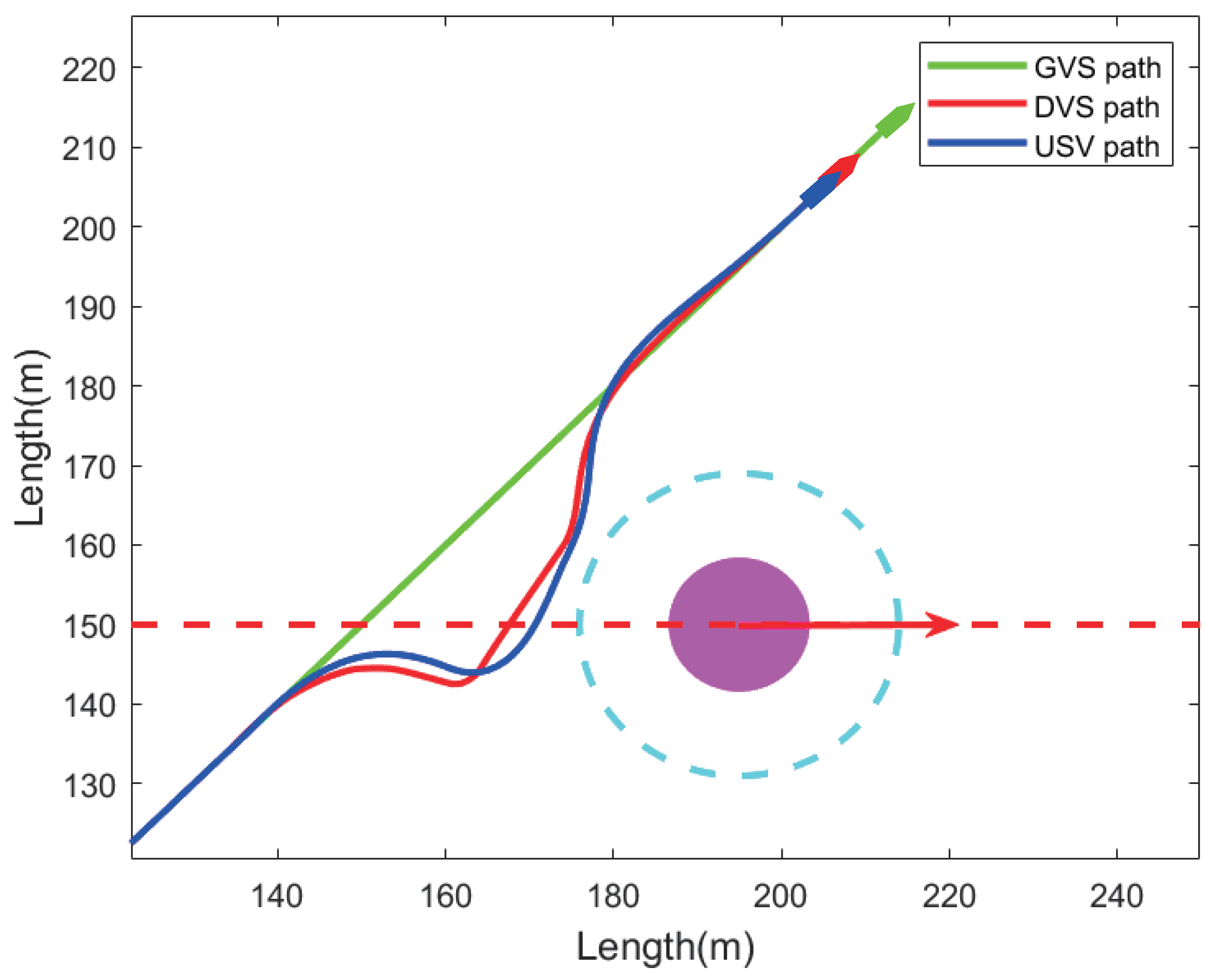
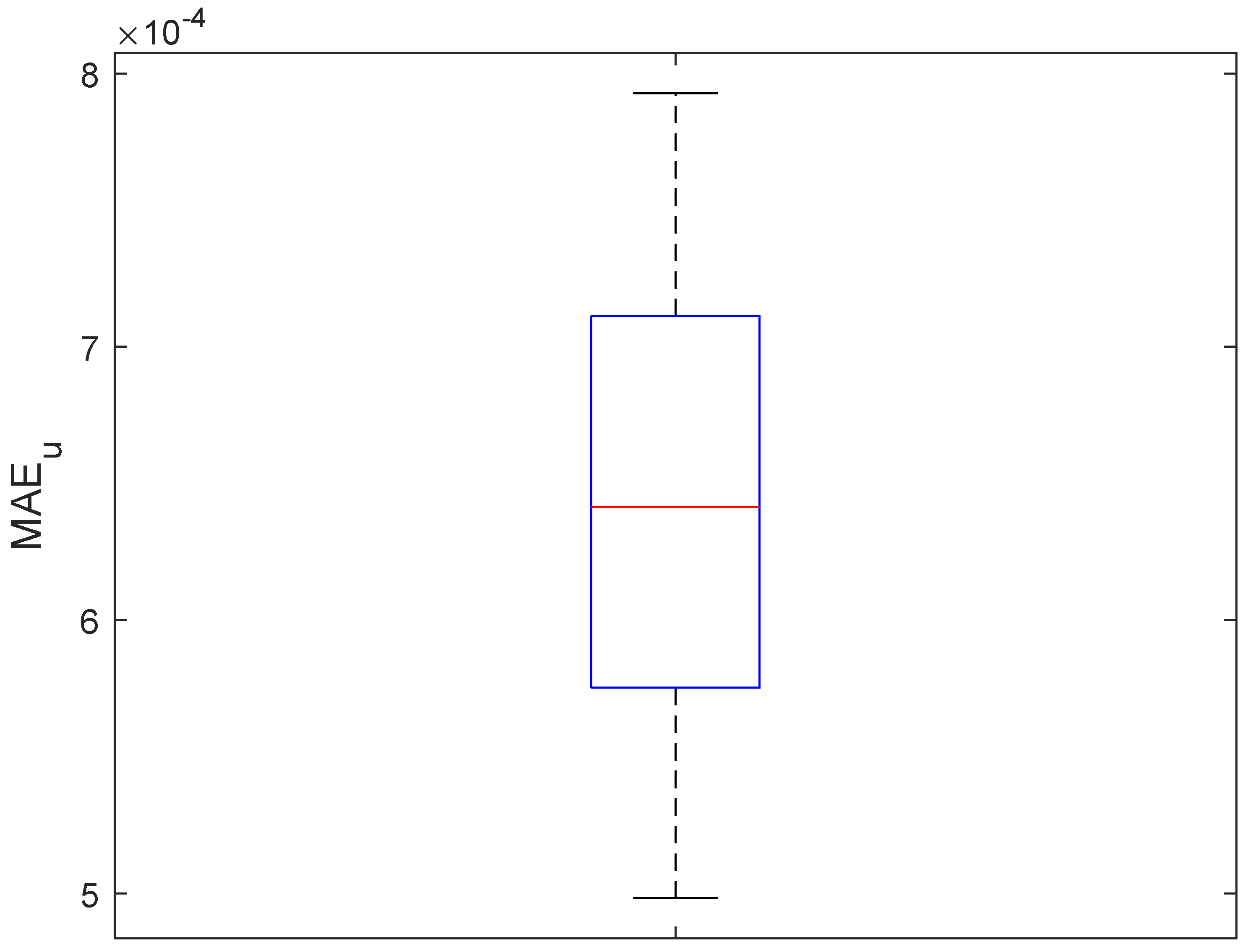
4. Simulation Results and Performance Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gonzalez-Garcia, A.; Collado-Gonzalez, I.; Cuan-Urquizo, R.; Sotelo, C.; Sotelo, D.; Castañeda, H. Path-following and lidar-based obstacle avoidance via nmpc for an autonomous surface vehicle. Ocean Eng. 2022, 266, 112900. [Google Scholar] [CrossRef]
- Guo, B.; Guo, N.; Cen, Z. Obstacle avoidance with dynamic avoidance risk region for mobile robots in dynamic environments. IEEE Robot. Automat. Lett. 2022, 7, 5850–5857. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, H.; Feng, Y. MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles. World Electr. Veh. J. 2022, 13, 221. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, J.; Li, H.; Xia, J.; Liu, Z. Guidance Method with Collision Avoidance Using Guiding Vector Field for Multiple Unmanned Surface Vehicles. Drones 2025, 9, 105. [Google Scholar] [CrossRef]
- Li, Y.; Hou, P.; Cheng, C.; Wang, B. Research on Collision Avoidance Methods for Unmanned Surface Vehicles Based on Boundary Potential Field. J. Mar. Sci. Eng. 2025, 13, 88. [Google Scholar] [CrossRef]
- Yuan, X.; Tong, C.; He, G.; Wang, H. Unmanned Vessel Collision Avoidance Algorithm by Dynamic Window Approach Based on COLREGs Considering the Effects of the Wind and Wave. J. Mar. Sci. Eng. 2023, 11, 1831. [Google Scholar] [CrossRef]
- Du, B.; Xie, W.; Zhang, W.; Chen, H. A target tracking guidance for unmanned surface vehicles in the presence of obstacles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4102–4115. [Google Scholar] [CrossRef]
- Ahiska, K.; Leblebicioglu, M.K. A hierarchical control scheme for trajectory tracking usvs in environments with disturbances and dynamic obstacles. IEEE Trans. Intell. Veh. 2024, 1–10. [Google Scholar] [CrossRef]
- Wen, G.; Lam, J.; Fu, J.; Wang, S. Distributed MPC-Based Robust Collision Avoidance Formation Navigation of Constrained Multiple USVs. IEEE Trans. Intell. Veh. 2024, 9, 1804–1816. [Google Scholar] [CrossRef]
- Kang, T.; Gu, N.; Wang, D.; Liu, L.; Hu, Q.; Peng, Z. Neurodynamics-based attack-defense guidance of autonomous surface vehicles against multiple attackers for domain protection. IEEE Trans. Ind. Electron. 2024, 71, 12655–12663. [Google Scholar] [CrossRef]
- Shin, J.; Kwak, D.J.; Lee, Y.-i. Adaptive path-following control for an unmanned surface vessel using an identified dynamic model. IEEE/ASME Trans. Mechatron. 2017, 22, 1143–1153. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yuan, C.; Luo, J. Adaptive path following control of unmanned surface vehicles considering environmental disturbances and system constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 339–353. [Google Scholar] [CrossRef]
- Chen, L.; Cui, R.; Yang, C.; Yan, W. Adaptive neural network control of underactuated surface vessels with guaranteed transient performance: Theory and experimental results. IEEE Trans. Ind. Electron. 2020, 67, 4024–4035. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.; Tong, S. Adaptive fuzzy control for heterogeneous vehicular platoon systems with collision avoidance and connectivity preservation. IEEE Trans. Fuzzy Syst. 2023, 31, 3934–3943. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Wang, Q.-G.; Yu, J. Adaptive command filtered backstepping tracking control for auvs considering model uncertainties and input saturation. IEEE Trans. Circuits Syst. II Exp. Briefs 2023, 70, 1475–1479. [Google Scholar] [CrossRef]
- Li, Y.; Wan, J.; Wang, X.; Sun, Z.; Li, H.; Yu, Z.; Kou, L.; Li, J.; Yang, Y. Path-following control based on alos guidance law for USV. Electronics 2025, 14, 749. [Google Scholar] [CrossRef]
- Wang, X.; Yi, H.; Xu, J.; Xu, C.; Song, L. PID Controller Based on Improved DDPG for Trajectory Tracking Control of USV. J. Mar. Sci. Eng. 2024, 12, 1771. [Google Scholar] [CrossRef]
- Qin, J.; Du, J.; Li, J. Adaptive finite-time trajectory tracking event-triggered control scheme for underactuated surface vessels subject to input saturation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8809–8819. [Google Scholar] [CrossRef]
- Li, F.; Li, H.; Wu, C. Gaussian process-based learning model predictive control with application to USV. IEEE Trans. Ind. Electron. 2024, 71, 16388–16397. [Google Scholar] [CrossRef]
- Park, B.S.; Kwon, J.-W.; Kim, H. Neural network-based output feedback control for reference tracking of underactuated surface vessels. Automatica 2017, 77, 353–359. [Google Scholar] [CrossRef]
- Xiang, X.; Yu, C.; Zhang, Q. Robust fuzzy 3d path following for autonomous underwater vehicle subject to uncertainties. Comput. Oper. Res. 2017, 84, 165–177. [Google Scholar] [CrossRef]
- Lv, M.; Gu, N.; Wang, D.; Han, B.; Peng, Z. Human-in-the-loop coordinated path following of marine vehicles based on continuous twisting control. IEEE Trans. Ind. Inform. 2025, 21, 465–474. [Google Scholar] [CrossRef]
- Liu, J.; Du, J. Composite learning tracking control for underactuated autonomous underwater vehicle with unknown dynamics and disturbances in three-dimension space. Appl. Ocean Res. 2021, 112, 102686. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Z.; Gong, M.; Ni, T. Event-triggered asymptotic tracking control of underactuated ships with prescribed performance. IEEE Trans. Intell. Transp. Syst. 2023, 24, 645–656. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castañeda, H. Guidance and control based on adaptive sliding mode strategy for a usv subject to uncertainties. IEEE J. Ocean. Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Sun, C.; Liu, J.; Yu, J. Improved adaptive fuzzy control for unmanned surface vehicles with uncertain dynamics using high-power functions. Ocean Eng. 2024, 312, 119168. [Google Scholar] [CrossRef]
- Zhang, G.; Deng, Y.; Zhang, W.; Huang, C. Novel dvs guidance and path-following control for underactuated ships in presence of multiple static and moving obstacles. Ocean Eng. 2018, 170, 100–110. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, X. A novel dvs guidance principle and robust adaptive path-following control for underactuated ships using low frequency gain-learning. ISA Trans. 2015, 56, 75–85. [Google Scholar] [CrossRef]
- Lekkas, A.M.; Fossen, T.I. Integral LOS path following for curved paths based on a monotone cubic hermite spline parametrization. IEEE Trans. Control Syst. Technol. 2014, 22, 2287–2301. [Google Scholar] [CrossRef]
- Oh, S.-R.; Sun, J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Eng. 2010, 37, 289–295. [Google Scholar] [CrossRef]
- Zhang, G.; Han, J.; Li, J.; Zhang, X. Apf-based intelligent navigation approach for usv in presence of mixed potential directions: Guidance and control design. Ocean Eng. 2022, 260, 111972. [Google Scholar] [CrossRef]
- Wrat, G.; Ranjan, P.; Mishra, S.K.; Jose, J.T.; Das, J. Neural network-enhanced internal leakage analysis for efficient fault detection in heavy machinery hydraulic actuator cylinders. Proc. IMechE Part C J. Mech. Control Eng. Sci. 2025, 239, 1021–1031. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, X. Command filter and universal approximator based backstepping control design for strict-feedback nonlinear systems with uncertainty. IEEE Trans. Autom. Control 2020, 65, 1310–1317. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.-G.; Yu, J. Convex optimization-based adaptive fuzzy control for uncertain nonlinear systems with input saturation using command filtered backstepping. IEEE Trans. Fuzzy Syst. 2023, 31, 2086–2091. [Google Scholar] [CrossRef]
- Boyd, S. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Khalil, H.K. Adaptive output feedback control of nonlinear systems represented by input-output models. IEEE Trans. Autom. Control 1996, 41, 177–188. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.-G.; Yu, J. Event-triggered adaptive neural network tracking control for uncertain systems with unknown input saturation based on command filters. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 8702–8707. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Tong, S. Fuzzy adaptive optimized leader-following formation control for second-order stochastic multiagent systems. IEEE Trans. Ind. Inform. 2022, 18, 6026–6037. [Google Scholar] [CrossRef]
- Sonnenburg, C.R.; Woolsey, C.A. Modeling, identification, and control of an unmanned surface vehicle. J. Field Robot. 2013, 30, 371–398. [Google Scholar] [CrossRef]
- Xu, W.; Liu, J.; Yu, J.; Han, Y. Low complexity adaptive neural network three-dimensional tracking control for autonomous underwater vehicles considering uncertain dynamics. Eng. Appl. Artif. Intell. 2025, 142, 109860. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yu, J. Simplified adaptive backstepping control for uncertain nonlinear systems with unknown input saturation and its application. Control Eng. Pract. 2023, 139, 105639. [Google Scholar] [CrossRef]


| 0.02 | ||
| −2.25 | ||
| −23.13 | ||
| −2.79 | ||
| −3.49 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 30 | 20 | ||
| 30 | 0.1 | ||
| 0.1 | 20 | ||
| 20 | 0.1 | ||
| 0.1 | 1500 | ||
| 5 | 0.1 | ||
| 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Liu, J.; Sun, C.; Dai, B. Convex Optimization-Based Adaptive Neural Network Control for Unmanned Surface Vehicles Considering Moving Obstacles. J. Mar. Sci. Eng. 2025, 13, 587. https://doi.org/10.3390/jmse13030587
Liu D, Liu J, Sun C, Dai B. Convex Optimization-Based Adaptive Neural Network Control for Unmanned Surface Vehicles Considering Moving Obstacles. Journal of Marine Science and Engineering. 2025; 13(3):587. https://doi.org/10.3390/jmse13030587
Chicago/Turabian StyleLiu, Dongxiao, Jiapeng Liu, Chongwei Sun, and Baobin Dai. 2025. "Convex Optimization-Based Adaptive Neural Network Control for Unmanned Surface Vehicles Considering Moving Obstacles" Journal of Marine Science and Engineering 13, no. 3: 587. https://doi.org/10.3390/jmse13030587
APA StyleLiu, D., Liu, J., Sun, C., & Dai, B. (2025). Convex Optimization-Based Adaptive Neural Network Control for Unmanned Surface Vehicles Considering Moving Obstacles. Journal of Marine Science and Engineering, 13(3), 587. https://doi.org/10.3390/jmse13030587






