Cooperative Patrol Control of Multiple Unmanned Surface Vehicles for Global Coverage
Abstract
1. Introduction
2. Related Work
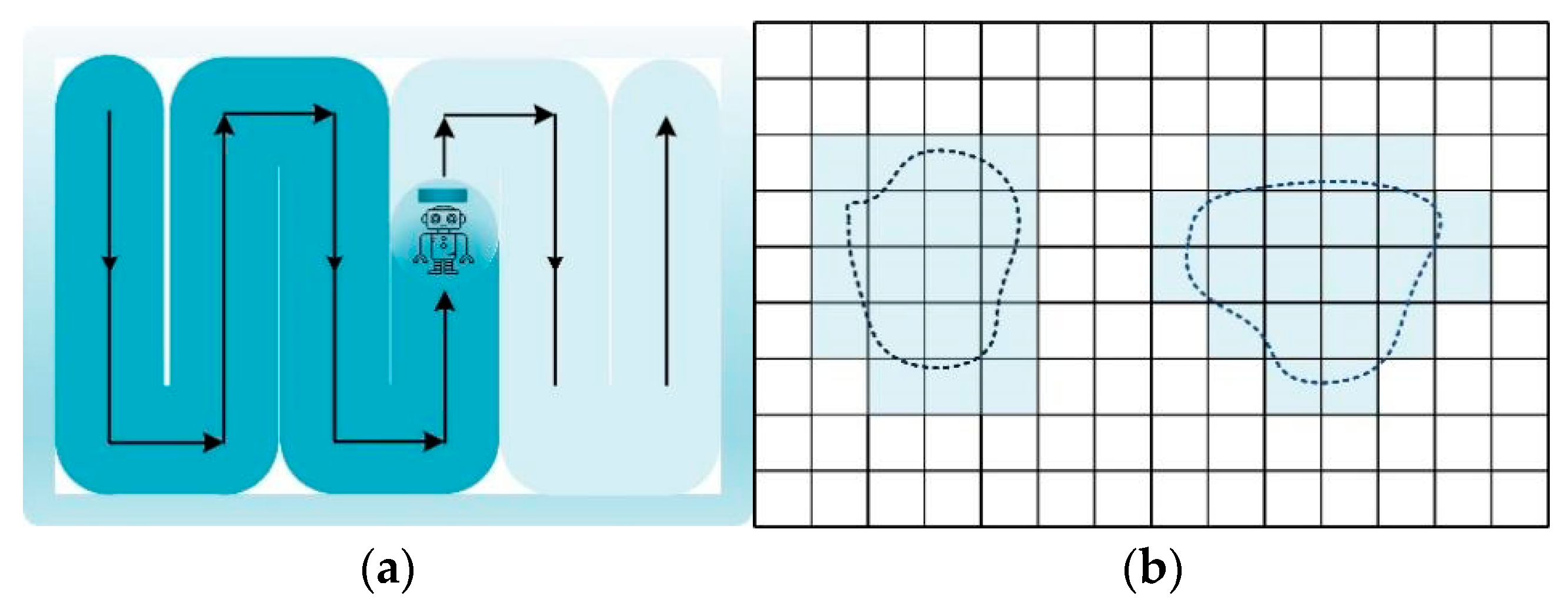
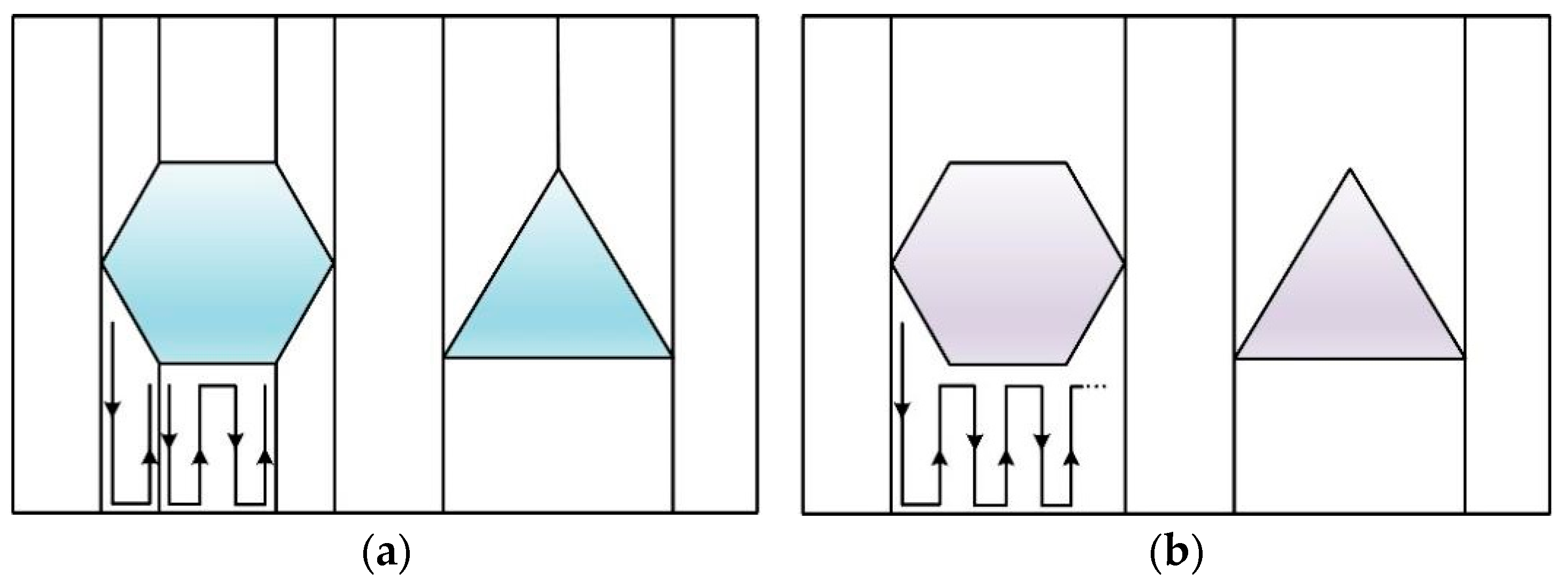
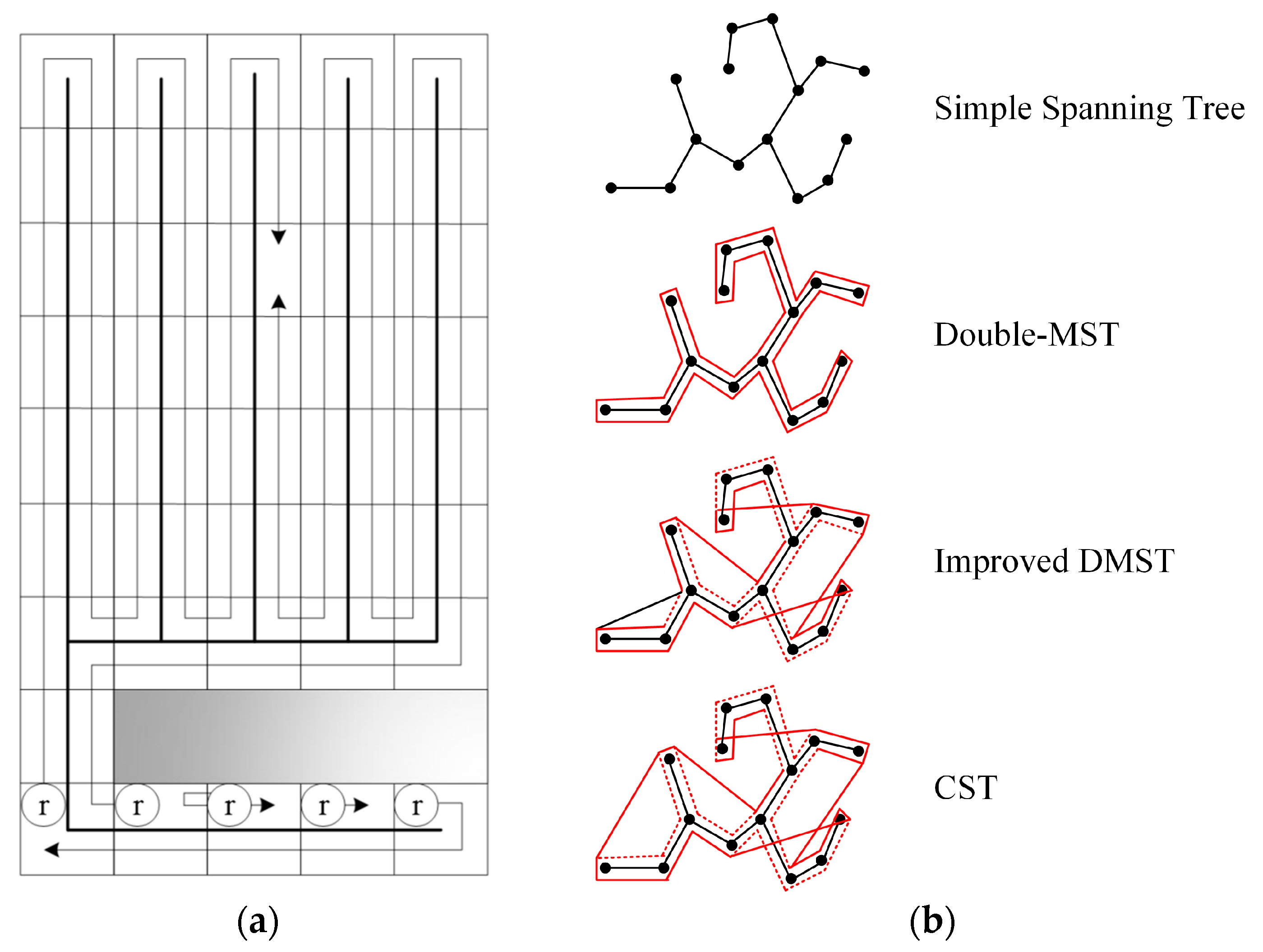
2.1. Exact-Approximate Cell Decomposition Method
2.2. Approximate Cell Decomposition Method
3. System Models
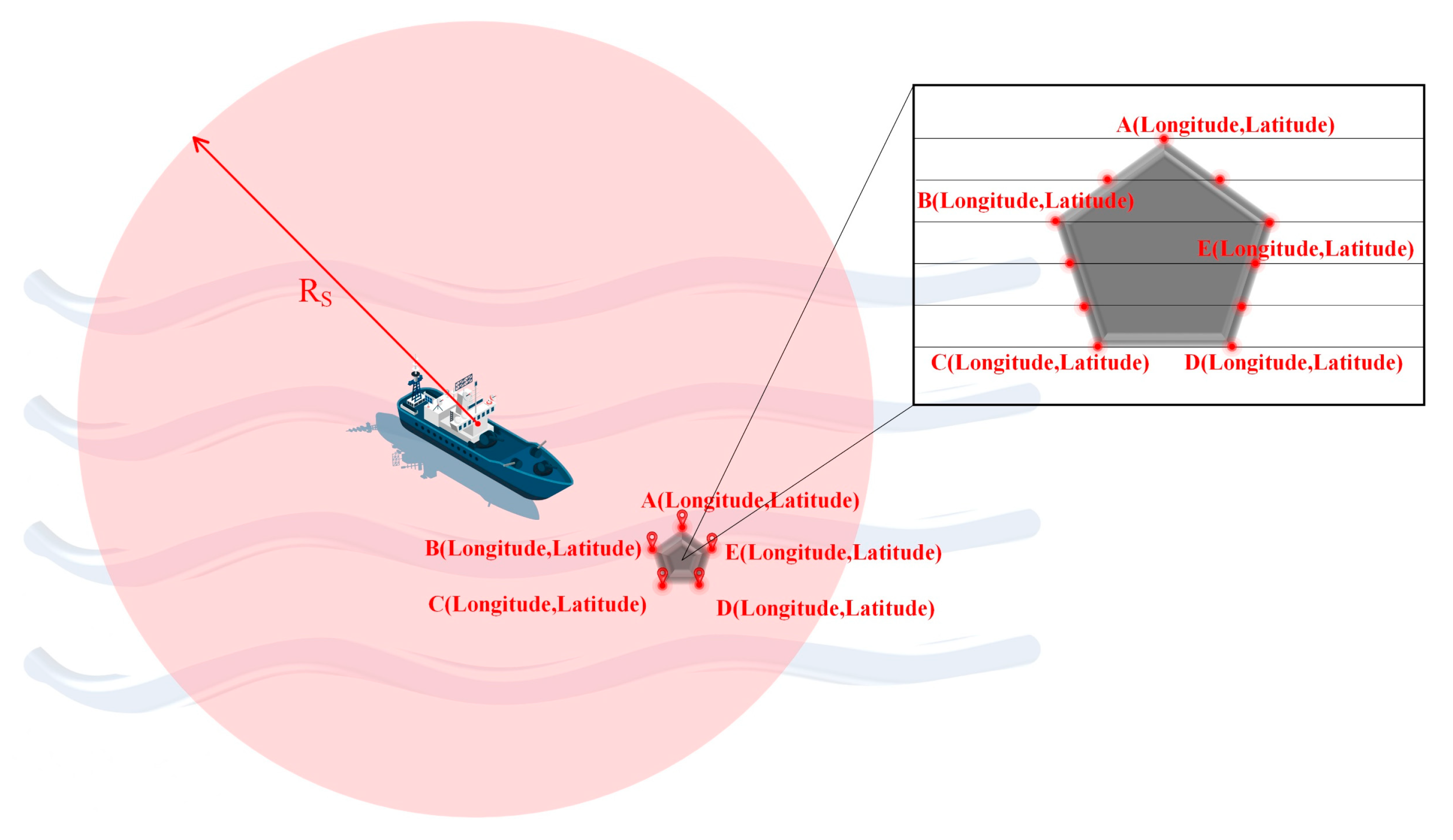
3.1. Patrol Information Graph
3.2. Cooperative Information Graph
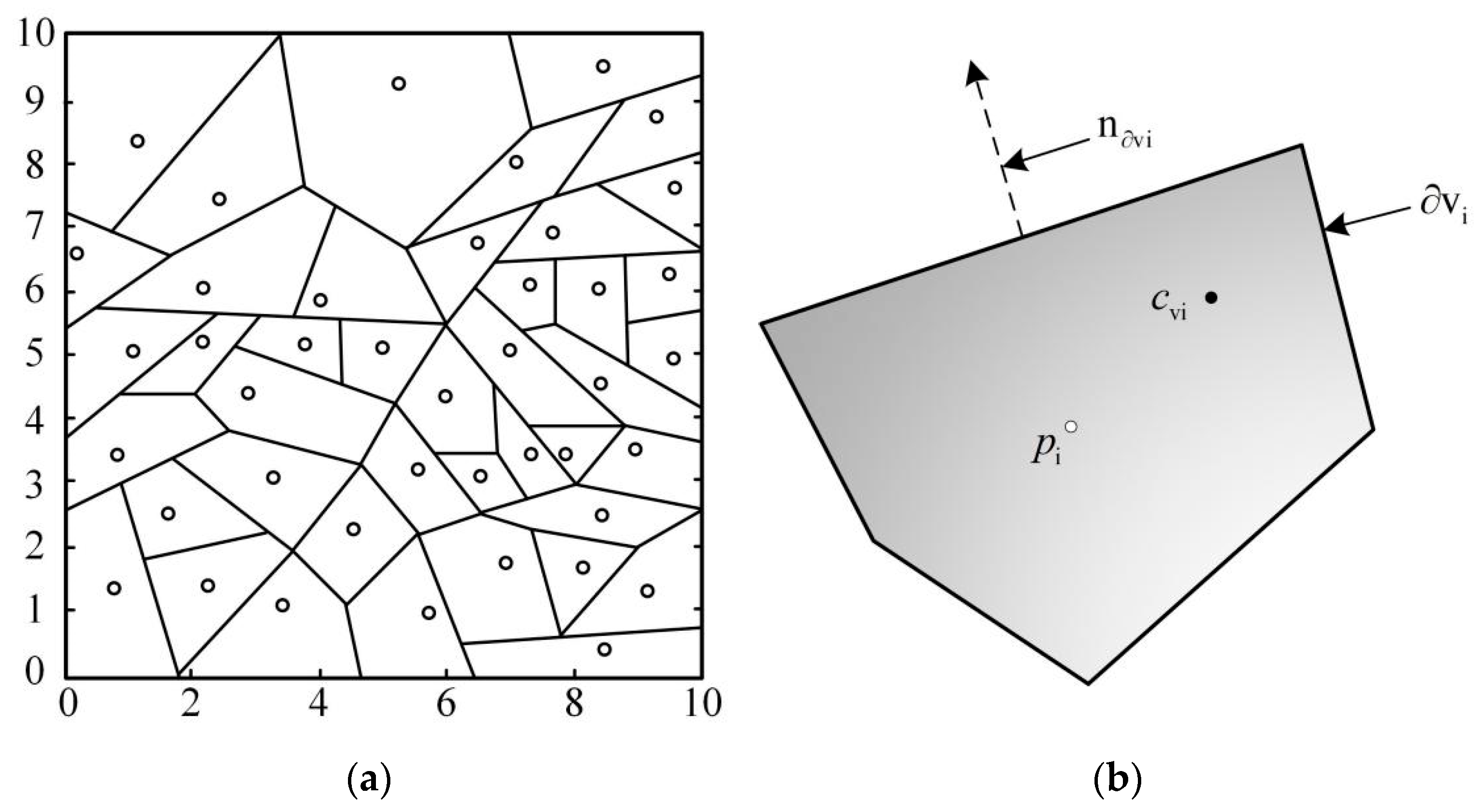
3.3. Obstacle Information Map
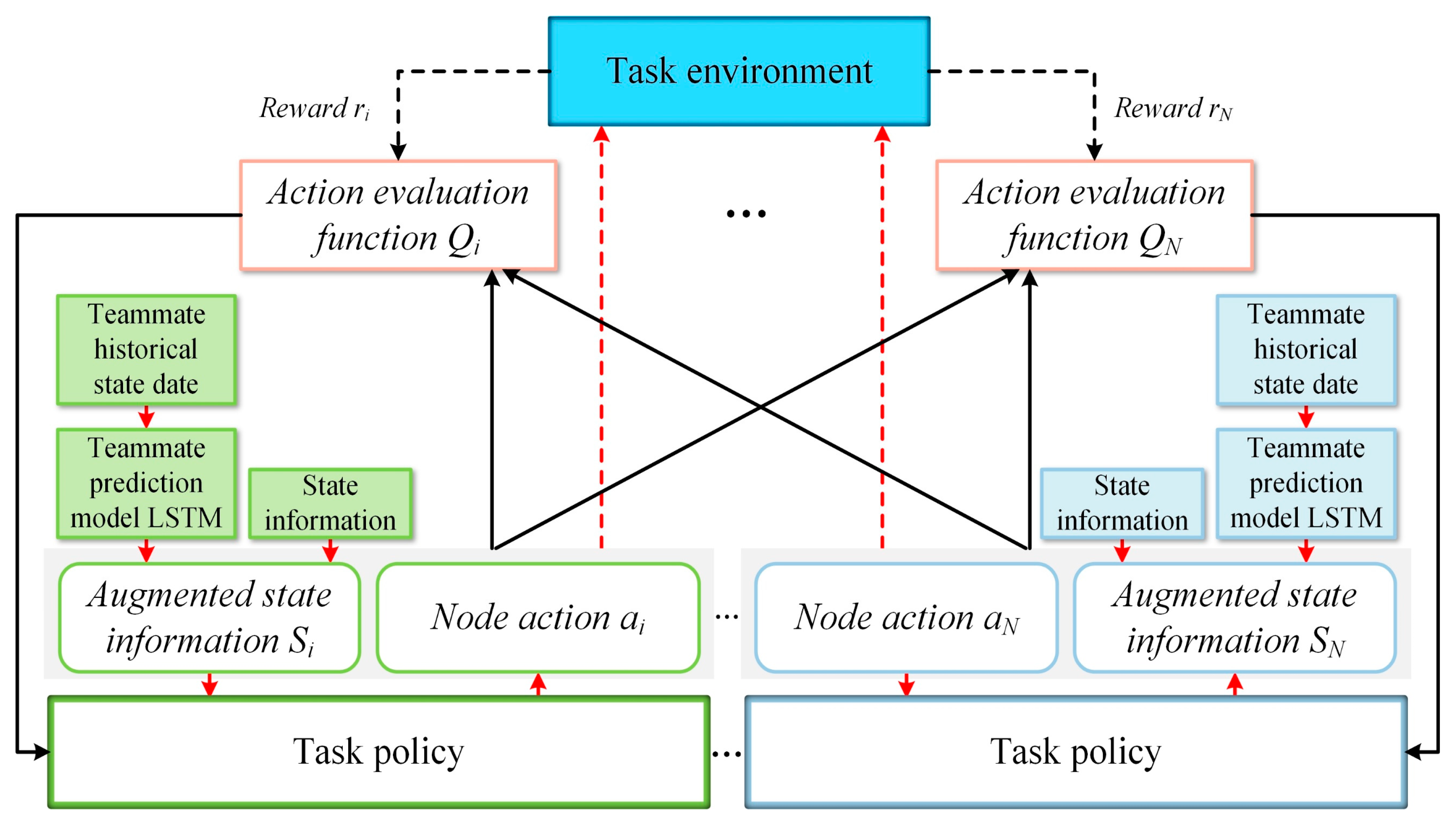
4. Proposed Strategy
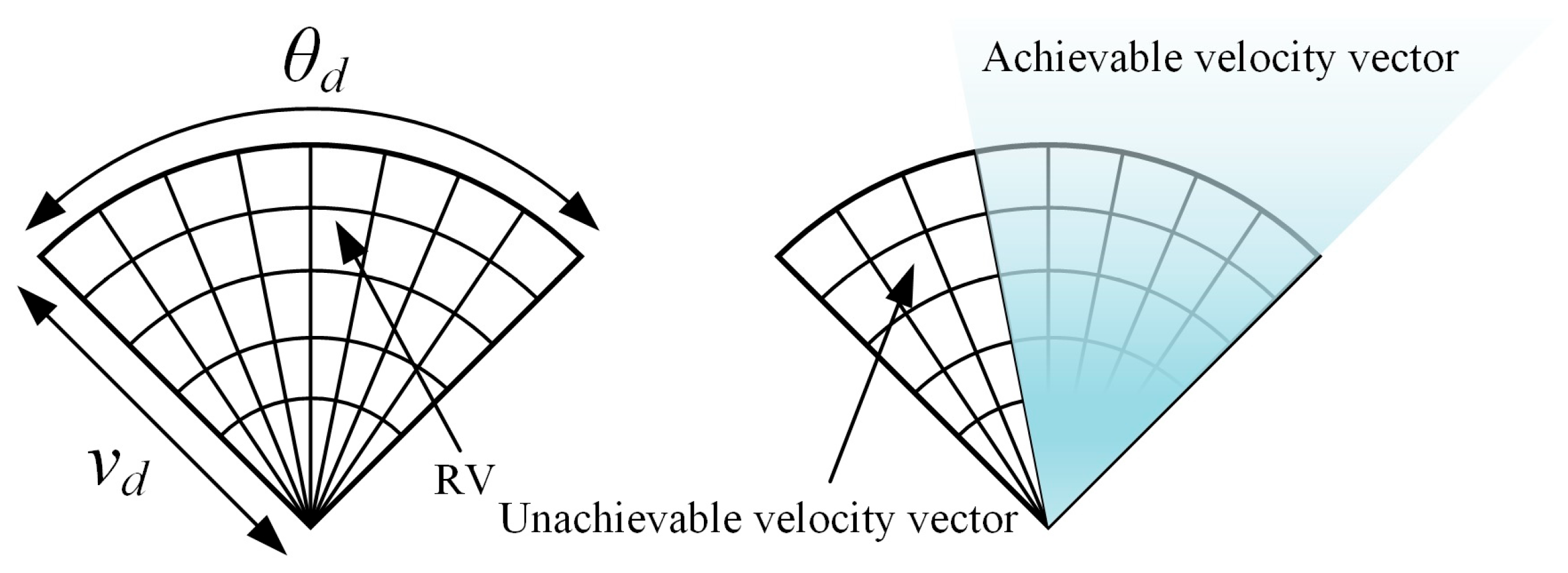
4.1. Action State Output of Unmanned Surface Vehicles Based on the Dynamic Window
4.2. Reward Function Design
- The system should be able to acquire patrol information of the entire task area.
- Under the condition of acquiring task data for the entire task area, patrol efficiency should be maximized and task costs minimized.
- Ensure the safety of all nodes during navigation, avoiding collisions between nodes and obstacles.
4.2.1. Patrol Reward
4.2.2. Cooperative Reward
4.2.3. Obstacle Avoidance Reward
4.2.4. Efficiency Reward
5. Strategy Training
5.1. Training Process
| Algorithm 1 Multi-USV cooperative Patrol Control algorithm |
| Require: Multi-agent , Policy network , Q Network parameters Replay buffer 1: Assign target network parameters 2: for do 3: , 4: end for 5: while not stop do 6: for do 7: Obtain the current environment state , and obtain based on . 8: is noise) 9: end for 10: Execute action to obtain reward and add new state values , and add them to 11: if is the terminal state, then 12: Reset the environment 13: break 14: end if 15: end for 16: Randomly sample from , and add it to . 17: for do 18: Calculate the Q-value, 19: Update the Q-value network parameters 20: 21: Update the policy network parameters 22: 23: for do 24: Update the target network parameters: 25: 26: 27: end for 28: end while |
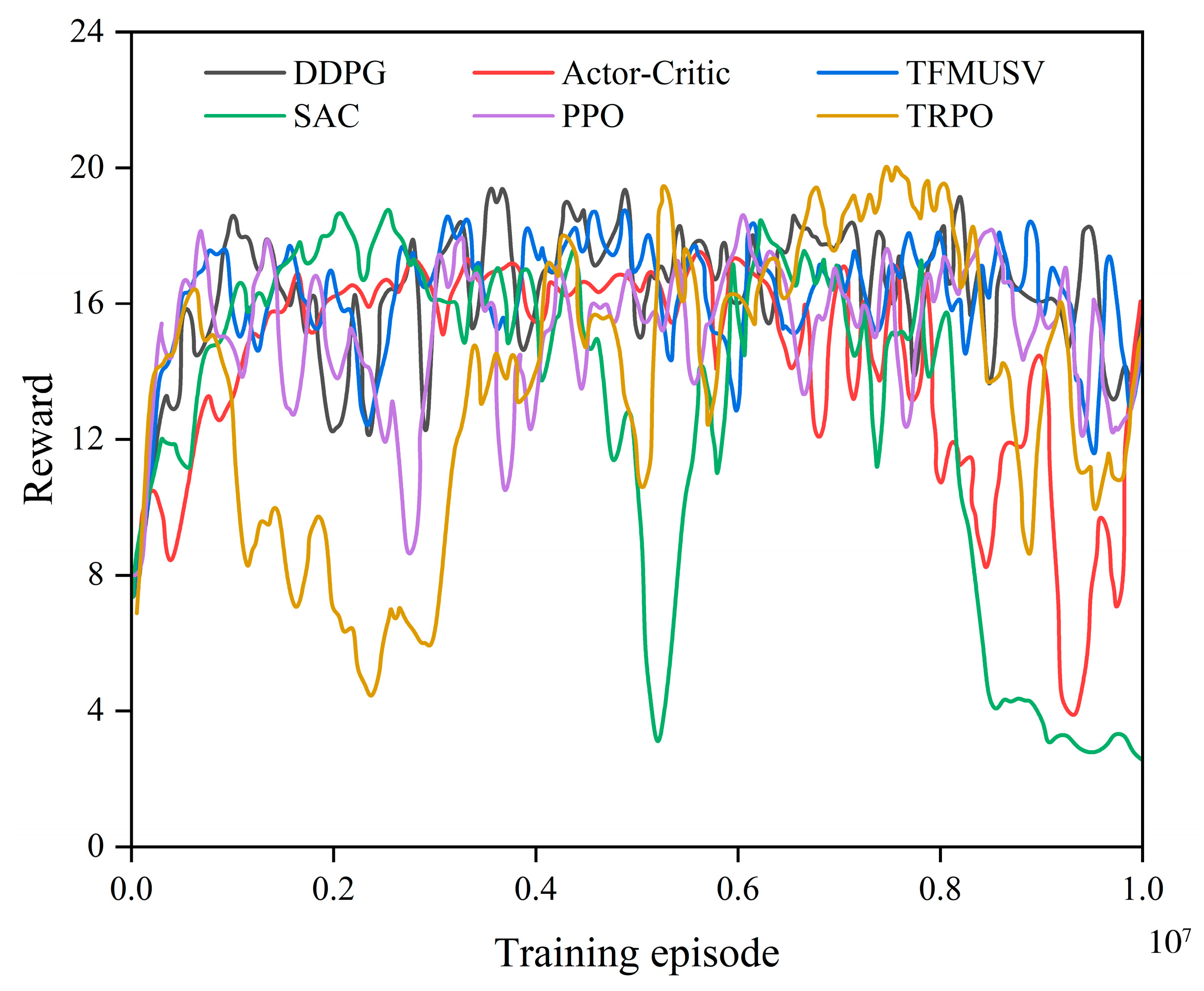
5.2. Training Result
6. Simulation Test
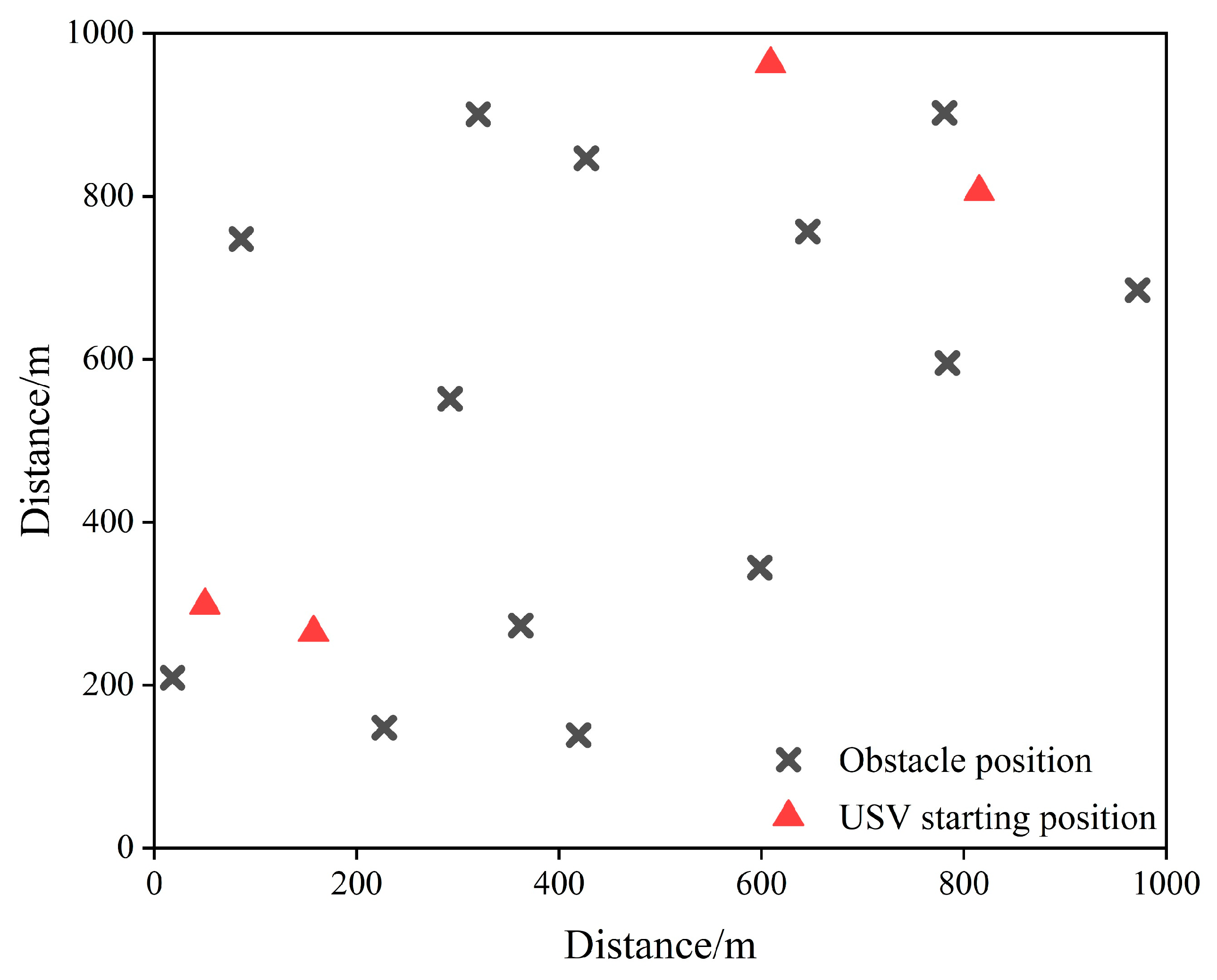
6.1. Test Evaluation Parameters
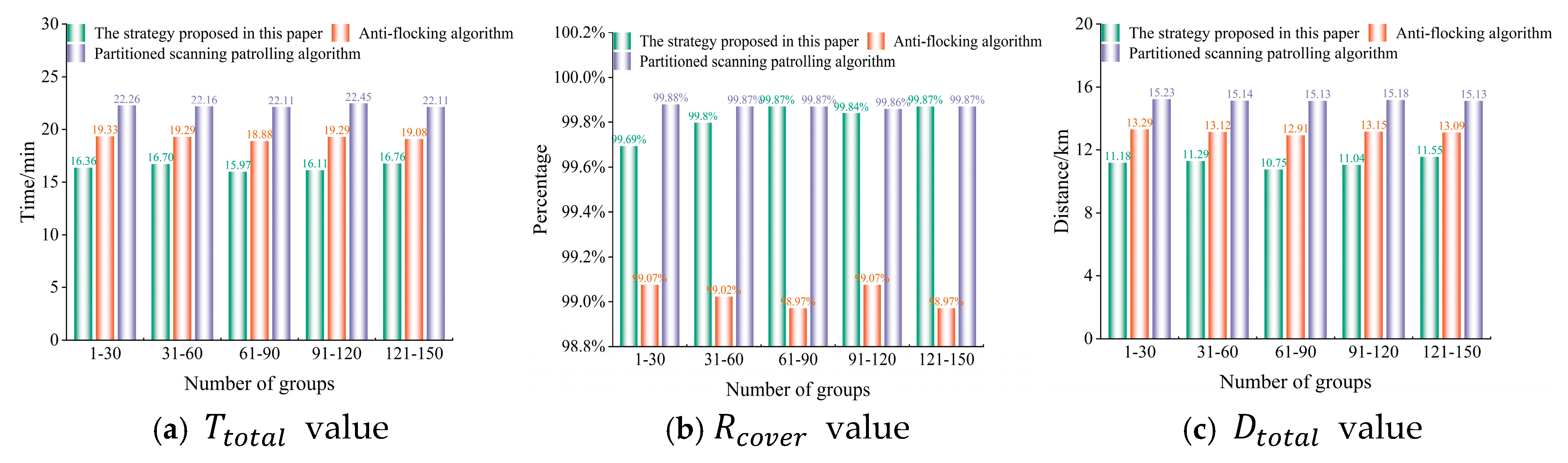
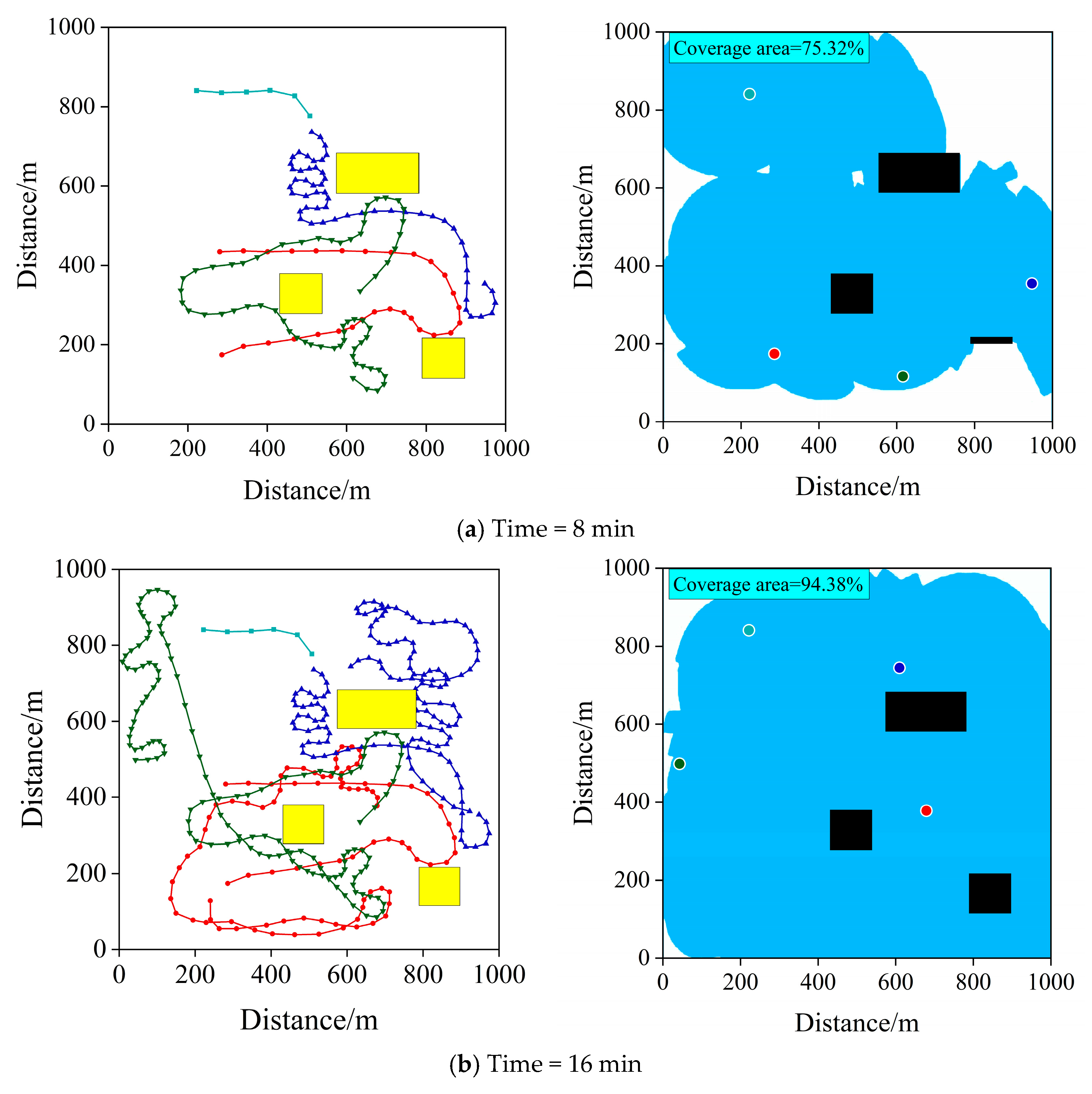
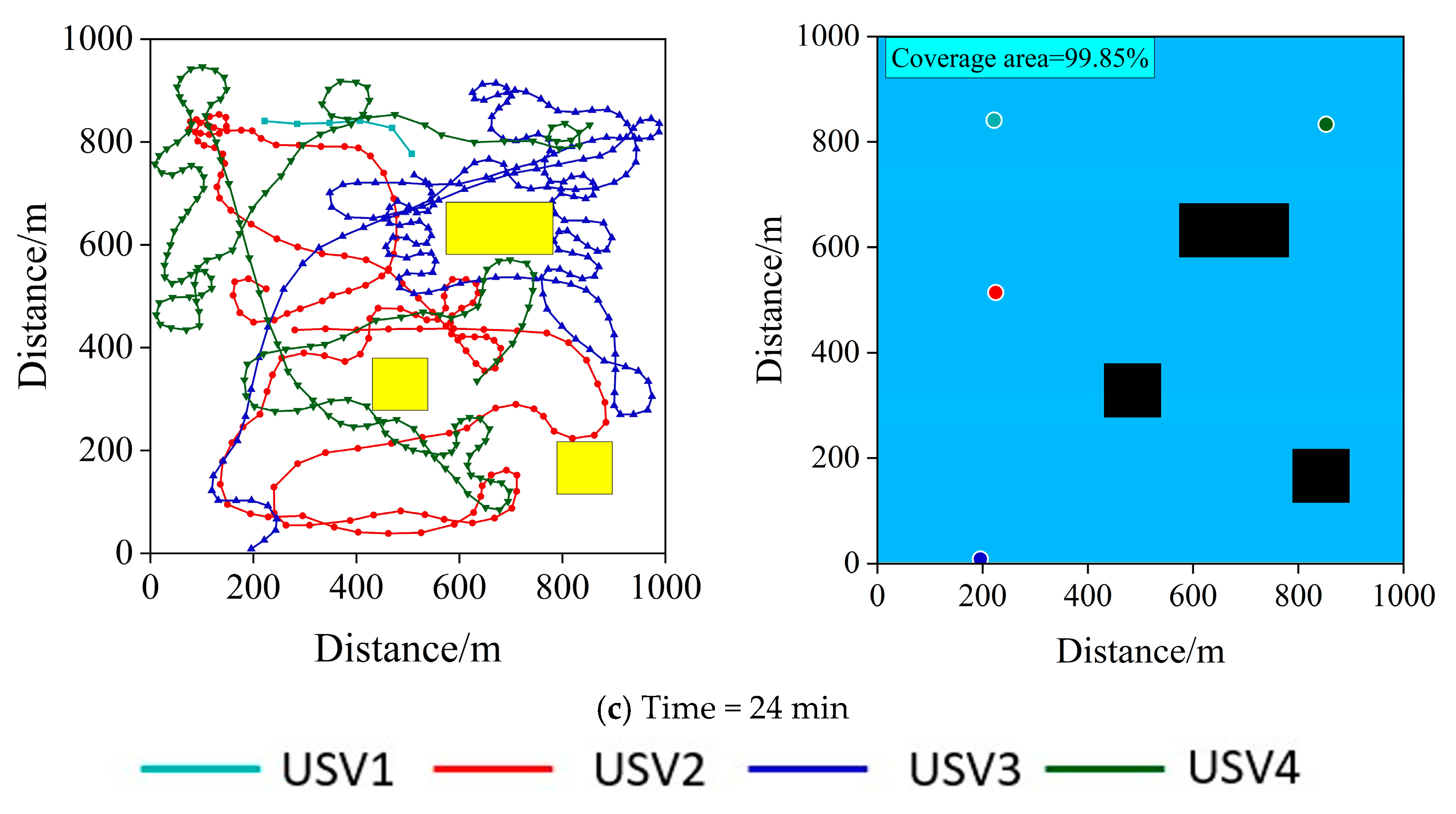
6.2. Patrolling Performance Test
6.2.1. Performance Comparison of Three Algorithms
6.2.2. Performance Analysis of the Proposed Algorithm
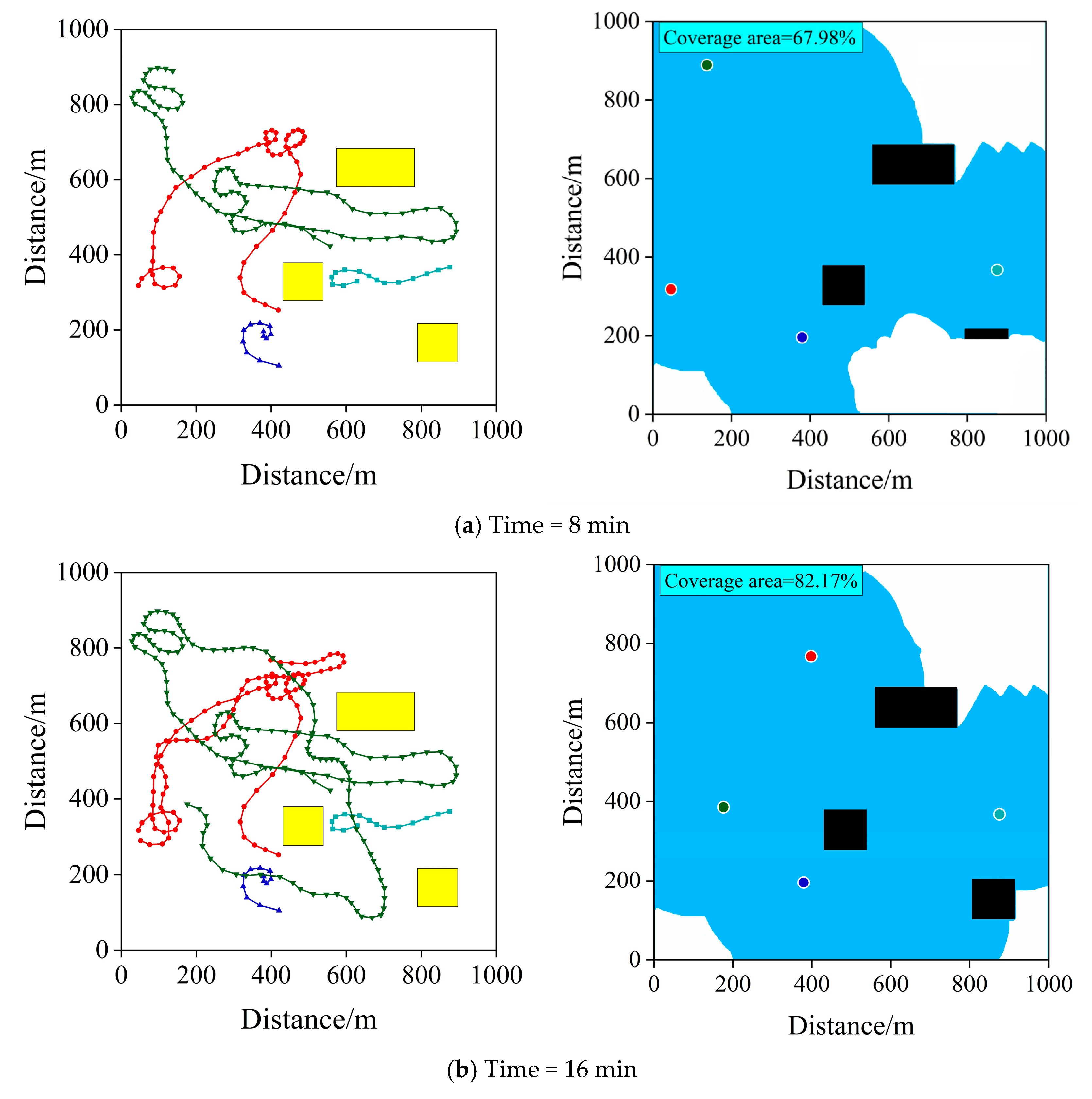
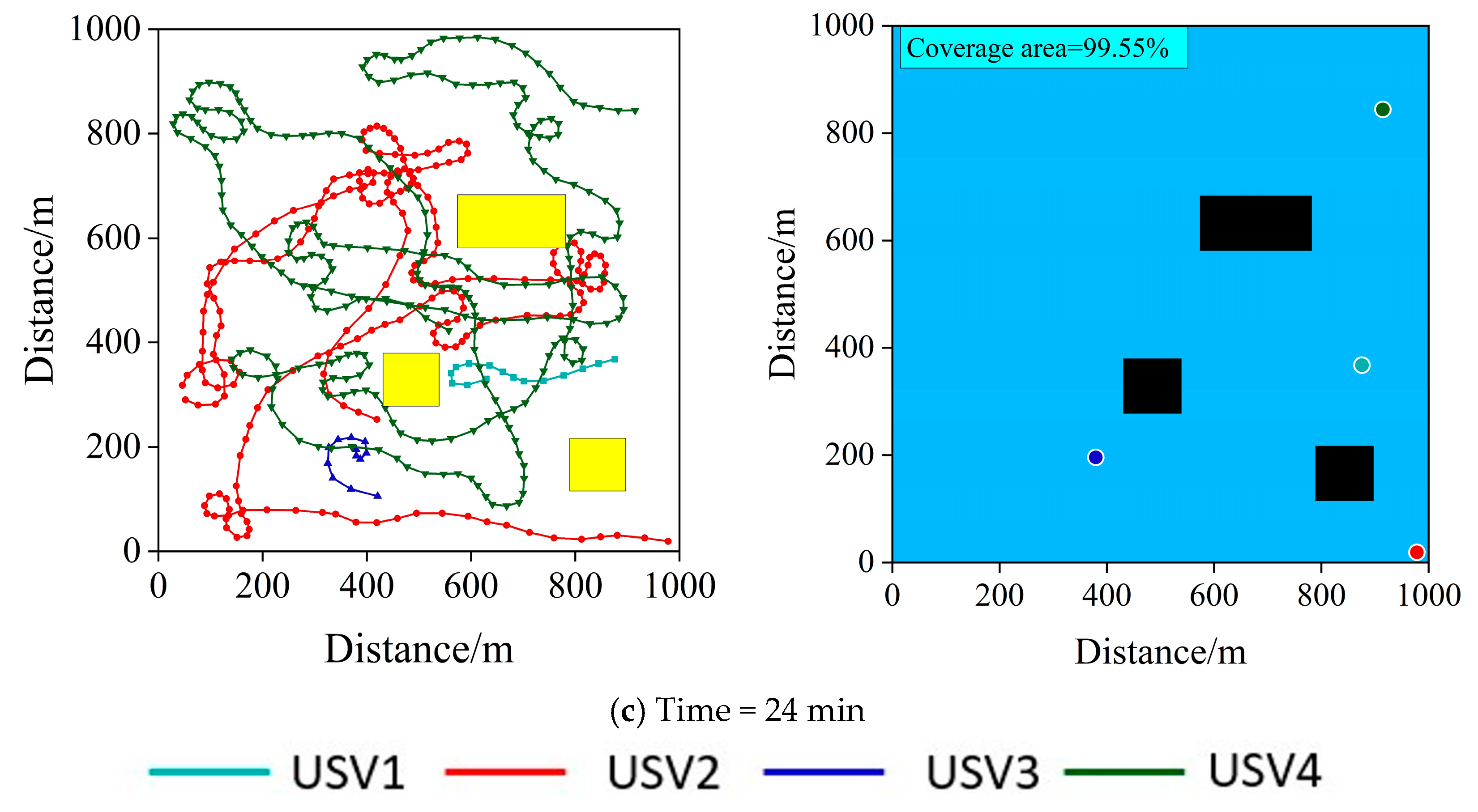
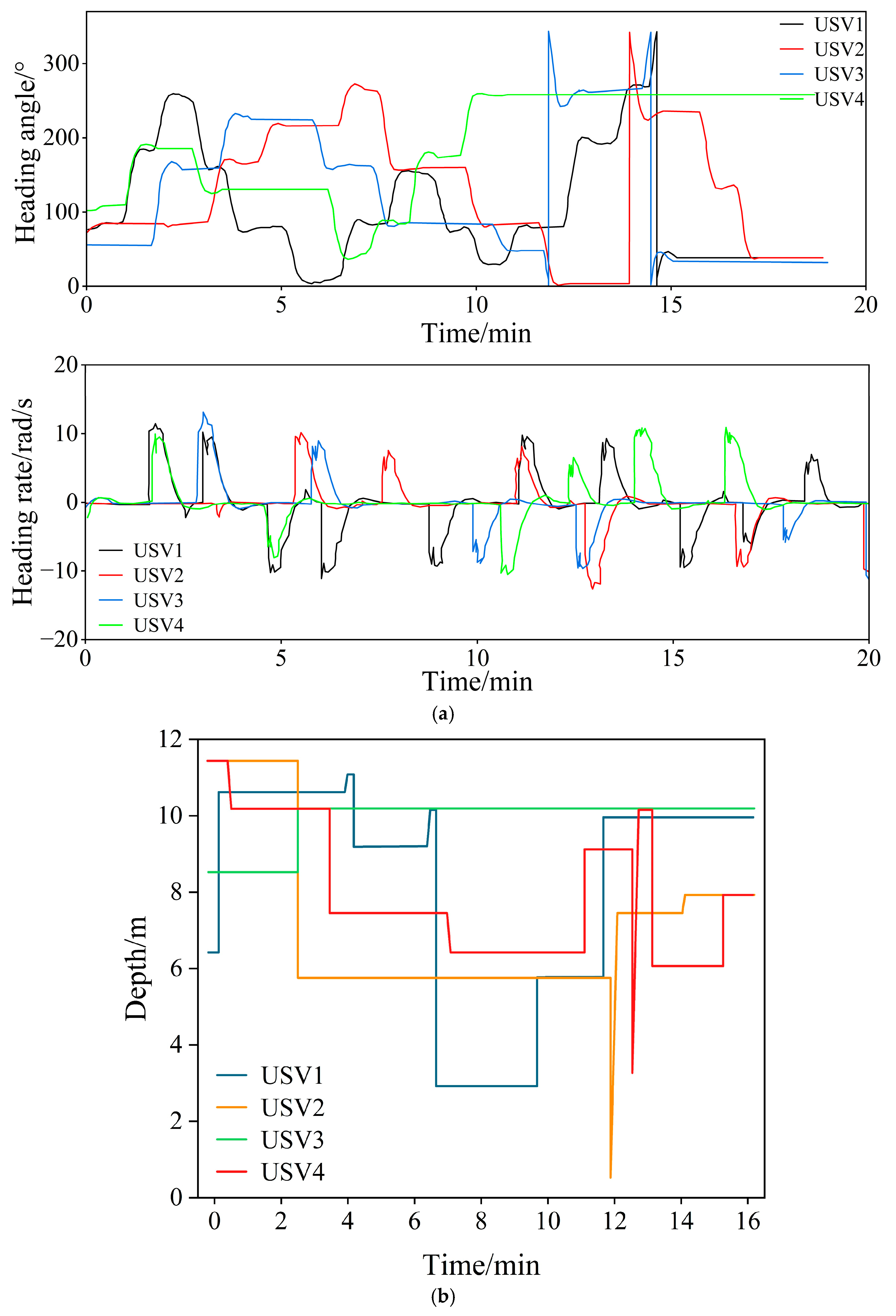
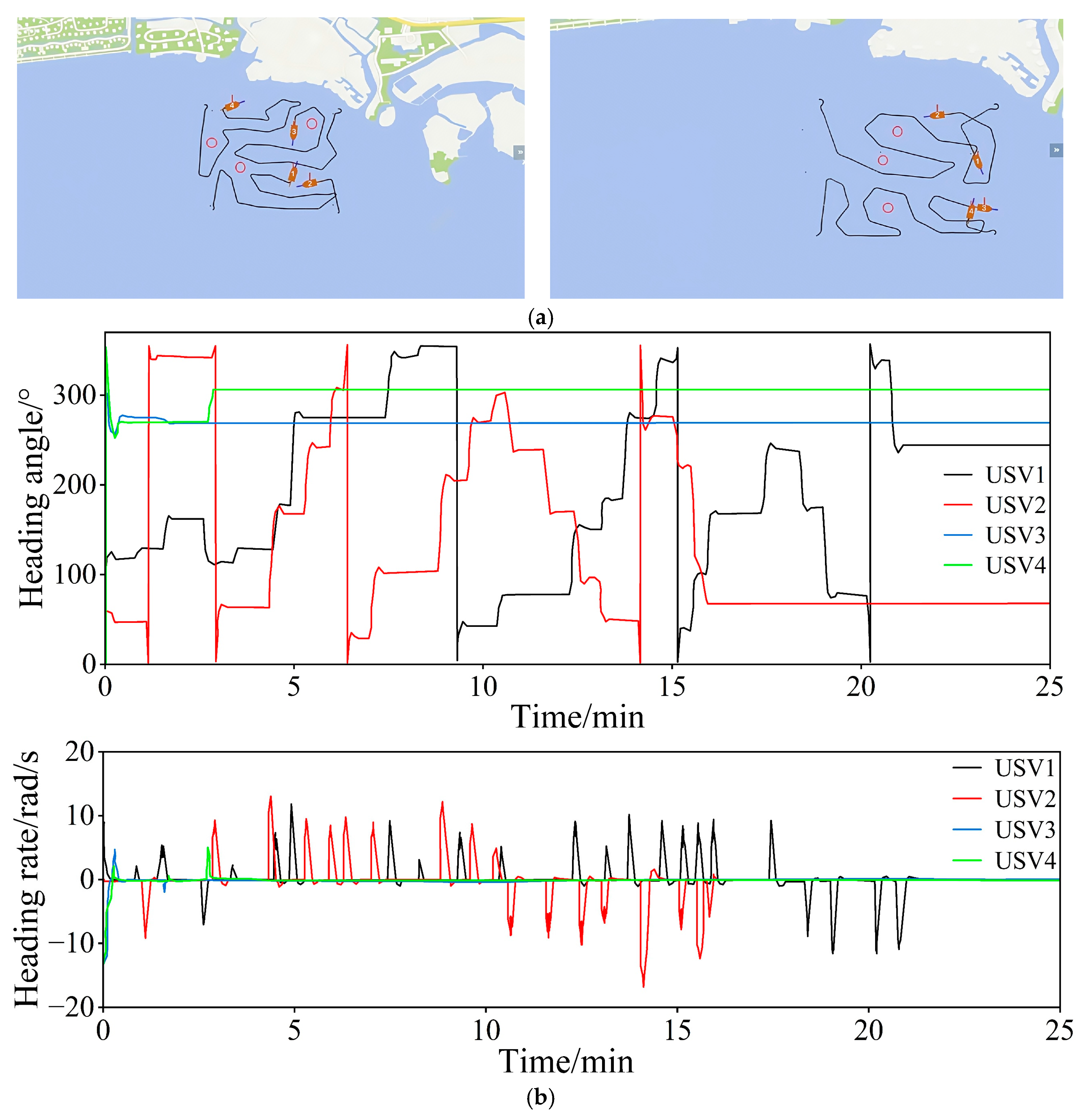
6.3. Robustness Performance Test
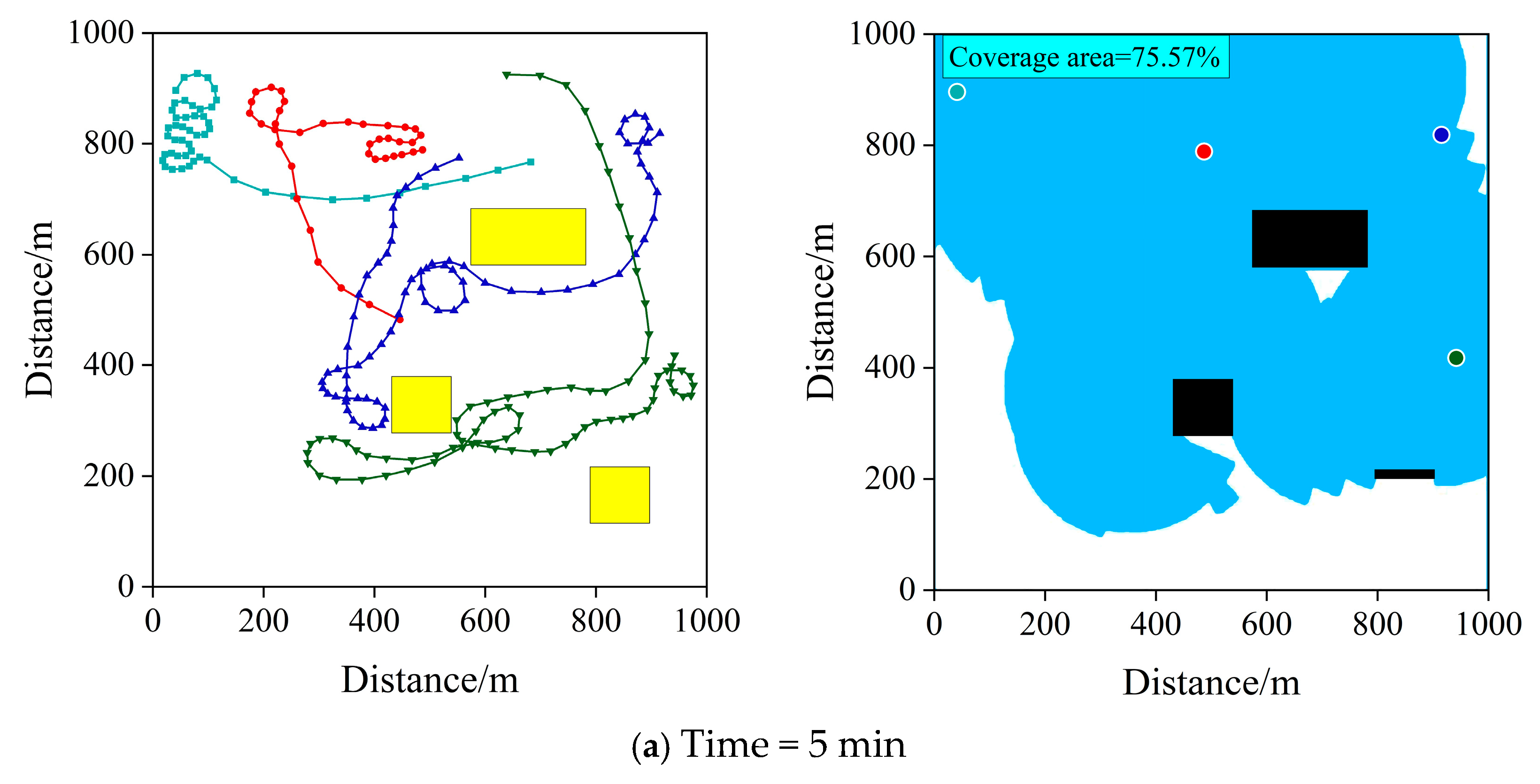
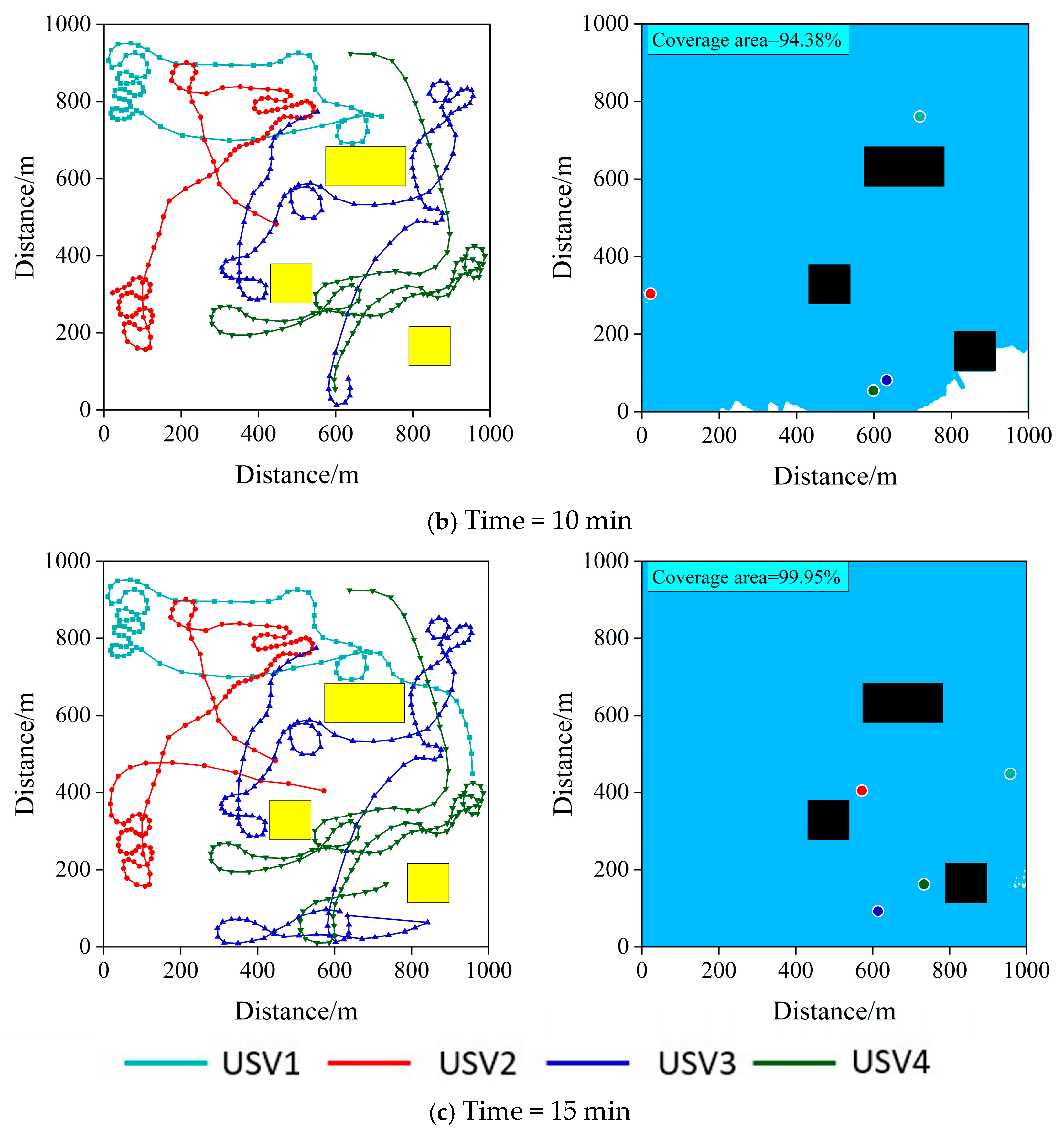
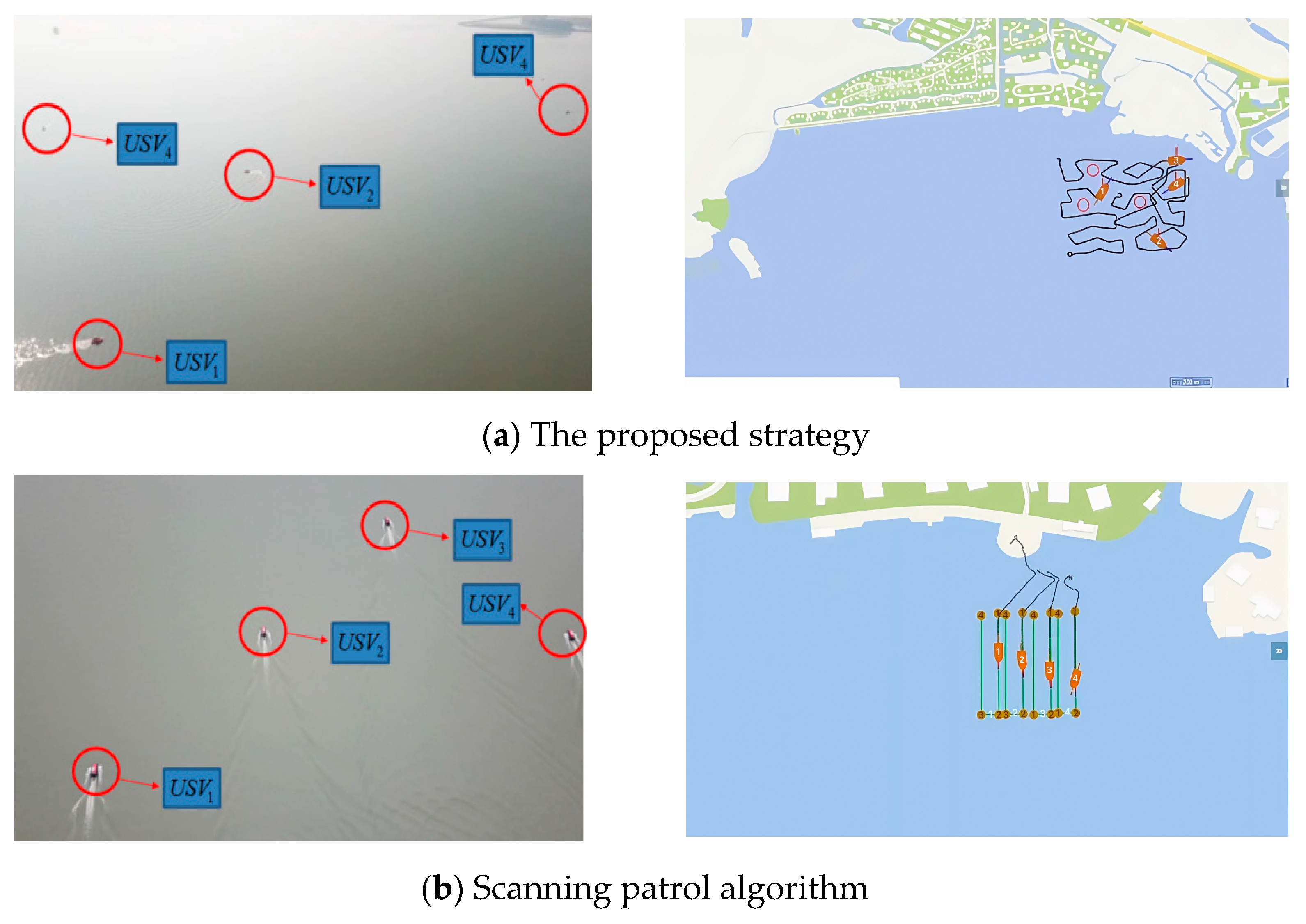
7. Practical Test
7.1. Experimental Scenario
7.2. Experimental Results and Analysis
8. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, D.; Pan, Y.J. Optimal Motion Planning for Heterogeneous Multi-USV Systems Using Hexagonal Grid-Based Neural Networks and Parallelogram Law Under Ocean Currents. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 43–50. [Google Scholar] [CrossRef]
- Chen, T.; Peng, H.; Chang, X.; Zhang, X.; Wang, D. Co-Design of USV Control System Based on Fuzzy Satisfactory Optimization for Automatic Target Arriving and Berthing. IEEE Access 2024, 12, 102449–102460. [Google Scholar] [CrossRef]
- Guo, X.; Narthsirinth, N.; Zhang, W.; Hu, Y. Unmanned Surface Vehicles (USVs) Scheduling Method by a Bi-Level Mission Planning and Path Control. Comput. Oper. Res. 2024, 162, 106472. [Google Scholar] [CrossRef]
- Xu, Y.; Li, K.; Li, Y. Distributed Optimal Control of Nonlinear Multi-Agent Systems Based on Integral Reinforcement Learning. Optim. Control Appl. Methods 2024, 172, 104321. [Google Scholar] [CrossRef]
- Marchukov, Y.; Montano, L. Occupation-aware planning method for robotic monitoring missions in dynamic environments. Robot. Auton. Syst. 2025, 185, 104892. [Google Scholar] [CrossRef]
- Gao, S.; Peng, Z.; Wang, H.; Liu, L.; Wang, D. Long Duration Coverage Control of Multiple Robotic Surface Vehicles Under Battery Energy Constraints. IEEE/CAA J. Autom. Sin. 2024, 11, 1695–1698. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y.; Paik, J.K. Optimal Coverage Path Planning for USV-Assisted Coastal Bathymetric Survey: Models, Solutions, and Lake Trials. Ocean Eng. 2024, 296, 116921. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y. Energy Efficient Coverage Path Planning for USV-Assisted Inland Bathymetry Under Current Effects: An Analysis on Sweep Direction. Ocean Eng. 2024, 305, 117910. [Google Scholar] [CrossRef]
- Zhao, L.; Bai, Y. Joint-Optimized Coverage Path Planning Framework for USV-Assisted Offshore Bathymetric Mapping: From Theory to Practice. Knowl.-Based Syst. 2024, 304, 112449. [Google Scholar] [CrossRef]
- Garg, A.; Jha, S.S. Learning Continuous Multi-UAV Controls with Directed Explorations for Flood Area Coverage. Robot. Auton. Syst. 2024, 180, 104774. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, D.; Zhou, C.; Sun, G. Improved Grey Wolf Algorithm Based on Dynamic Weight and Logistic Mapping for Safe Path Planning of UAV Low-Altitude Penetration. J. Supercomput. 2024, 80, 25818–25852. [Google Scholar] [CrossRef]
- Novak, D.; Tebbani, S.; Goricanec, J.; Orsag, M.; Le Brusquet, L. Battery Management Optimization for an Energy-Aware UAV Mapping Mission Path Planning. In Proceedings of the 2024 10th International Conference on Control, Decision and Information Technologies (CoDIT), Vallette, Malta, 1–4 July 2024; pp. 2645–2650. [Google Scholar]
- Vashisth, A.; Patel, D.; Conover, D.; Bera, A. Multi-Robot Informative Path Planning for Efficient Target Mapping Using Deep Reinforcement Learning. arXiv 2024, arXiv:2409.16967. [Google Scholar]
- Pérez-González, A.; Benítez-Montoya, N.; Jaramillo-Duque, Á.; Cano-Quintero, J.B. Coverage Path Planning with Semantic Segmentation for UAV in PV Plants. Appl. Sci. 2021, 11, 12093. [Google Scholar] [CrossRef]
- Wang, Y.; Xi, M.; Weng, Y. Intelligent Path Planning Algorithm of Autonomous Underwater Vehicle Based on Vision Under Ocean Current. Expert Syst. 2025, 42, e13399. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, A.; Kumar, V.; Singh, S.; Gautam, M. Autonomous Underwater Vehicle Path Planning Using Fitness-Based Differential Evolution Algorithm. J. Comput. Sci. 2025, 85, 102498. [Google Scholar] [CrossRef]
- Soleymani, F.; Miah, M.S.; Spinello, D. Optimal Non-Autonomous Area Coverage Control with Adaptive Reinforcement Learning. Eng. Appl. Artif. Intell. 2023, 122, 106068. [Google Scholar] [CrossRef]
- Papatheodorou, S.; Stergiopoulos, Y.; Tzes, A. Distributed Area Coverage Control with Imprecise Robot Localization. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 214–219. [Google Scholar]
- Yu, J.; Mi, R.; Han, J.; Yang, W. Voronoi-Based Adaptive Area Optimal Coverage Control for Multiple Manipulator Systems with Uncertain Kinematics and Dynamics. Commun. Nonlinear Sci. Numer. Simul. 2024, 138, 108235. [Google Scholar] [CrossRef]
- Magalhães, A.C.; Raffo, G.V.; Pimenta, L.C.A. Safe Voronoi-Based Coverage Control for Multi-Robot Systems with Constraints. In Proceedings of the 2023 Latin American Robotics Symposium (LARS), 2023 Brazilian Symposium on Robotics (SBR), and 2023 Workshop on Robotics in Education (WRE), Salvador, Brazil, 9–11 October 2023; pp. 188–193. [Google Scholar]
- Hazon, N.; Kaminka, G.A. Redundancy, Efficiency and Robustness in Multi-Robot Coverage. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 735–741. [Google Scholar]
- Ozkahraman, O.; Ogren, P. Combining Control Barrier Functions and Behavior Trees for Multi-Agent Underwater Coverage Missions. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Republic of Korea, 14–18 December 2020; pp. 5275–5282. [Google Scholar]
- Hyatt, P.; Brock, Z.; Killpack, M.D. A Versatile Multi-Robot Monte Carlo Tree Search Planner for On-Line Coverage Path Planning. arXiv 2020, arXiv:2002.04517. [Google Scholar]
- Dong, W.; Liu, S.; Ding, Y.; Sheng, X.; Zhu, X. An Artificially Weighted Spanning Tree Coverage Algorithm for Decentralized Flying Robots. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1689–1698. [Google Scholar] [CrossRef]
- Xu, R.; Yao, S.; Gouhe, W.; Zhao, Y.; Huang, S. A Spanning Tree Algorithm with Adaptive Pruning with Low Redundancy Coverage Rate. Comput. Ind. Eng. 2023, 186, 109745. [Google Scholar] [CrossRef]
- Kim, S.; Lin, R.; Coogan, S.; Egersted, M. Area Coverage Using Multiple Aerial Robots With Coverage Redundancy and Collision Avoidance. IEEE Control Syst. Lett. 2024, 8, 610–615. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Z.; Wang, S.; Li, J.; Kan, Z. Fast Temporal Logic Mission Planning of Multiple Robots: A Planning Decision Tree Approach. IEEE Robot. Autom. Lett. 2024, 9, 6146–6153. [Google Scholar] [CrossRef]
- Lu, W.; Xiong, H.; Zhang, Z.; Hu, Z.; Wang, T. Scalable Optimal Formation Path Planning for Multiple Interconnected Robots via Convex Polygon Trees. J. Intell. Robot. Syst. 2023, 109, 63. [Google Scholar] [CrossRef]
- Zhu, L.; Cheng, J.; Zhang, H.; Zhang, W.; Liu, Y. Multi-Robot Environmental Coverage With a Two-Stage Coordination Strategy via Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5022–5033. [Google Scholar] [CrossRef]
- Gosrich, W.; Mayya, S.; Li, R.; Paulos, J.; Yim, M.; Ribeiro, A.; Kumar, V. Coverage Control in Multi-Robot Systems via Graph Neural Networks. arXiv 2021, arXiv:2109.15278. [Google Scholar]
- Stolfi, D.H.; Brust, M.R.; Danoy, G.; Bouvry, P. A Cooperative Coevolutionary Approach to Maximise Surveillance Coverage of UAV Swarms. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 10–13 January 2020; pp. 1–6. [Google Scholar]
- Xin, B.; Wang, H.; Li, M. Multi-Robot Cooperative Multi-Area Coverage Based on Circular Coding Genetic Algorithm. J. Adv. Comput. Intell. Intell. Inform. 2023, 27, 1183–1191. [Google Scholar] [CrossRef]
- Nemer, I.A.; Sheltami, T.R.; Mahmoud, A.S. A Game Theoretic Approach of Deployment a Multiple UAVs for Optimal Coverage. Transp. Res. Part A Policy Pract. 2020, 140, 215–230. [Google Scholar] [CrossRef]





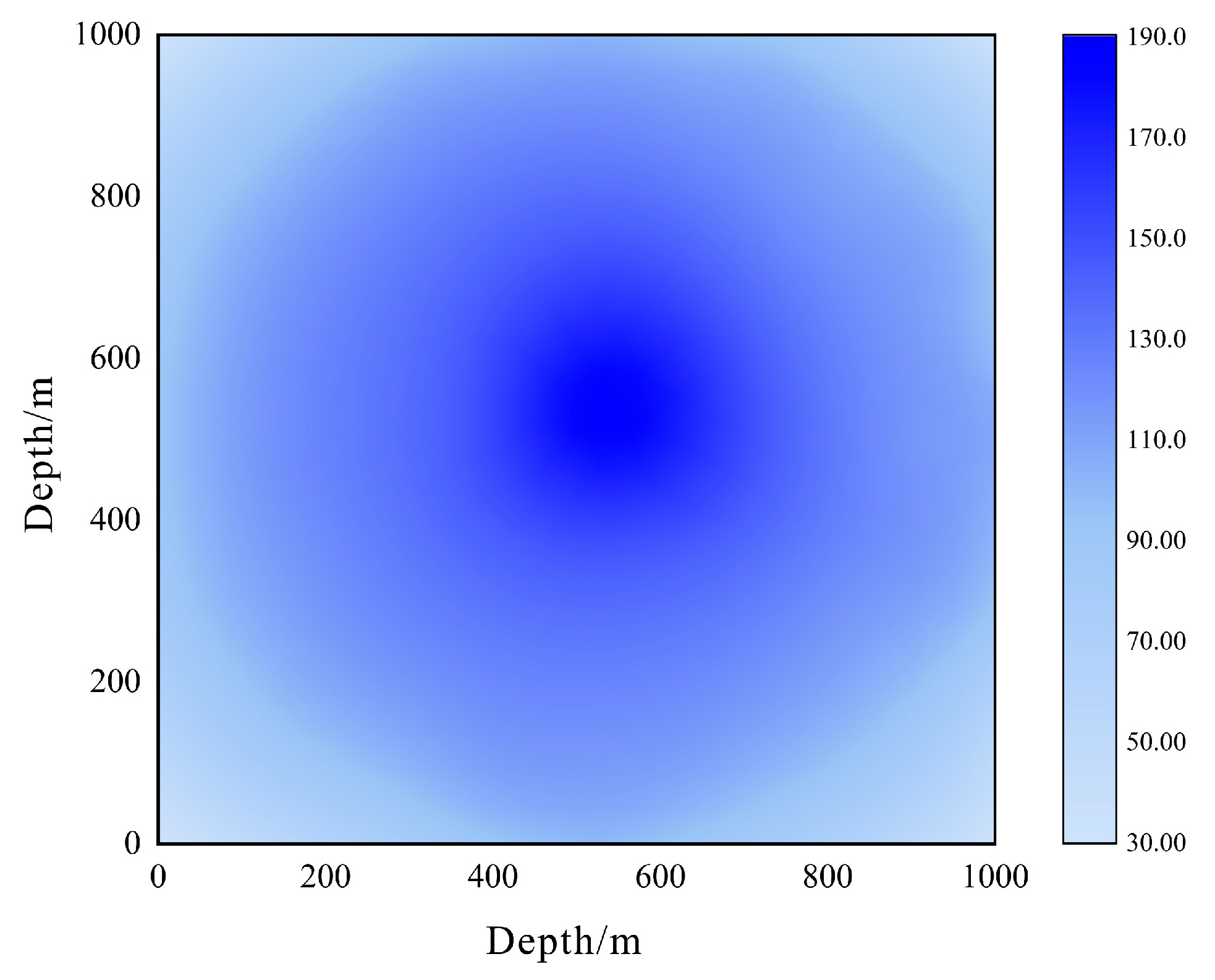

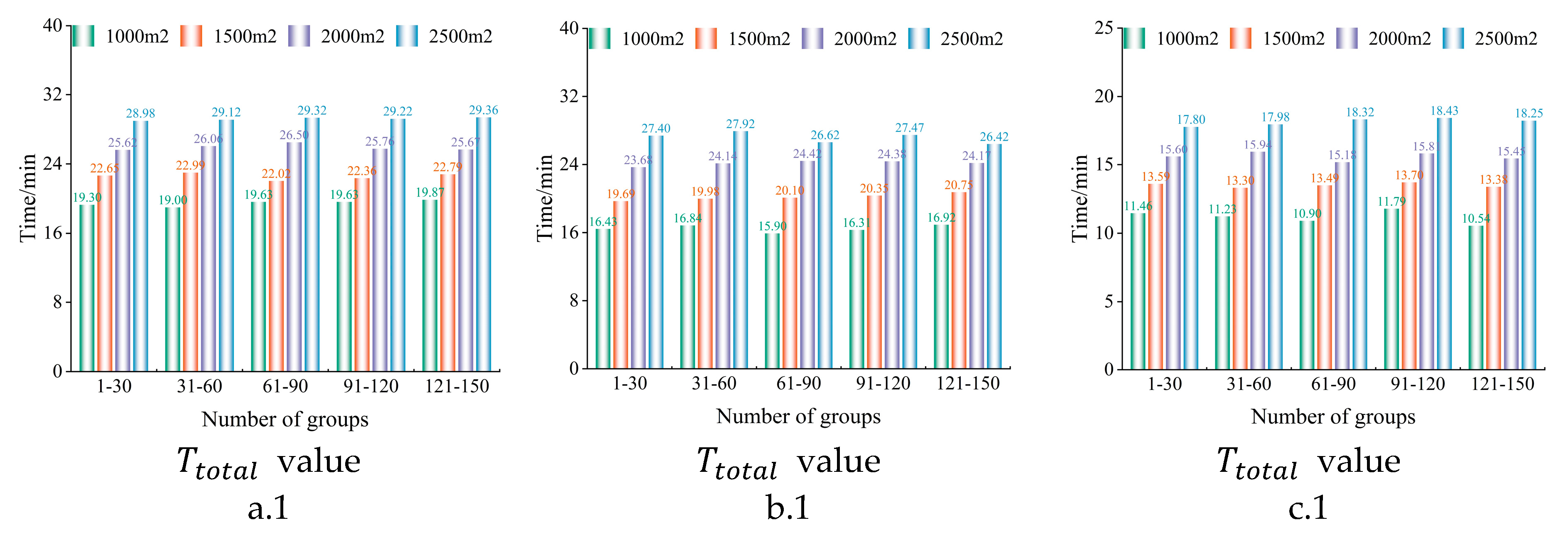

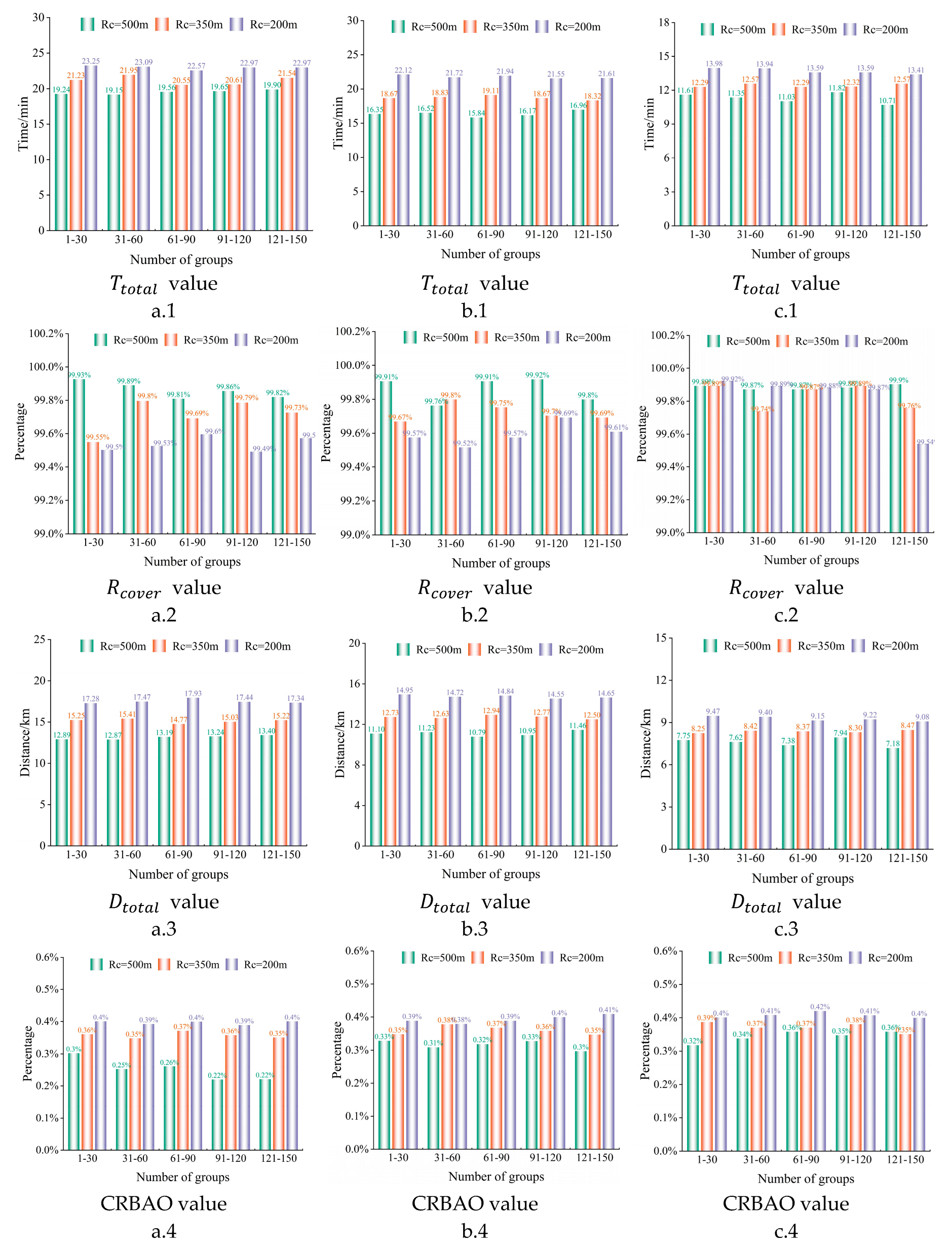
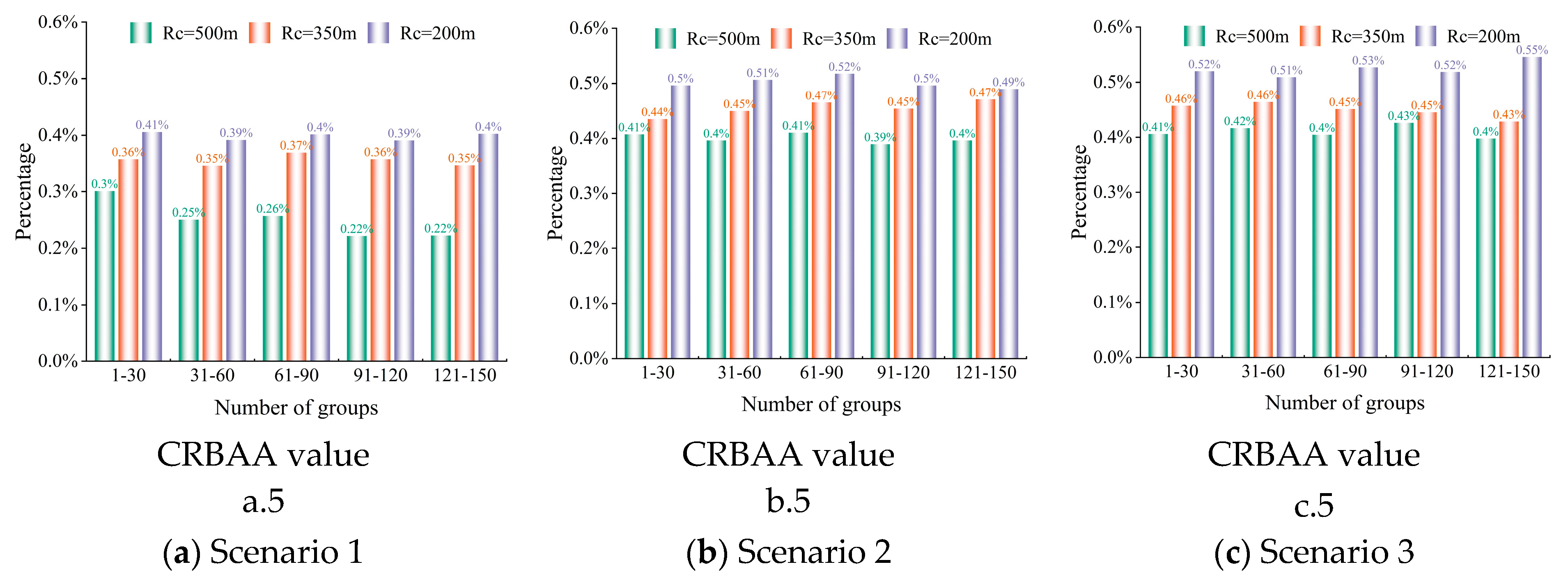
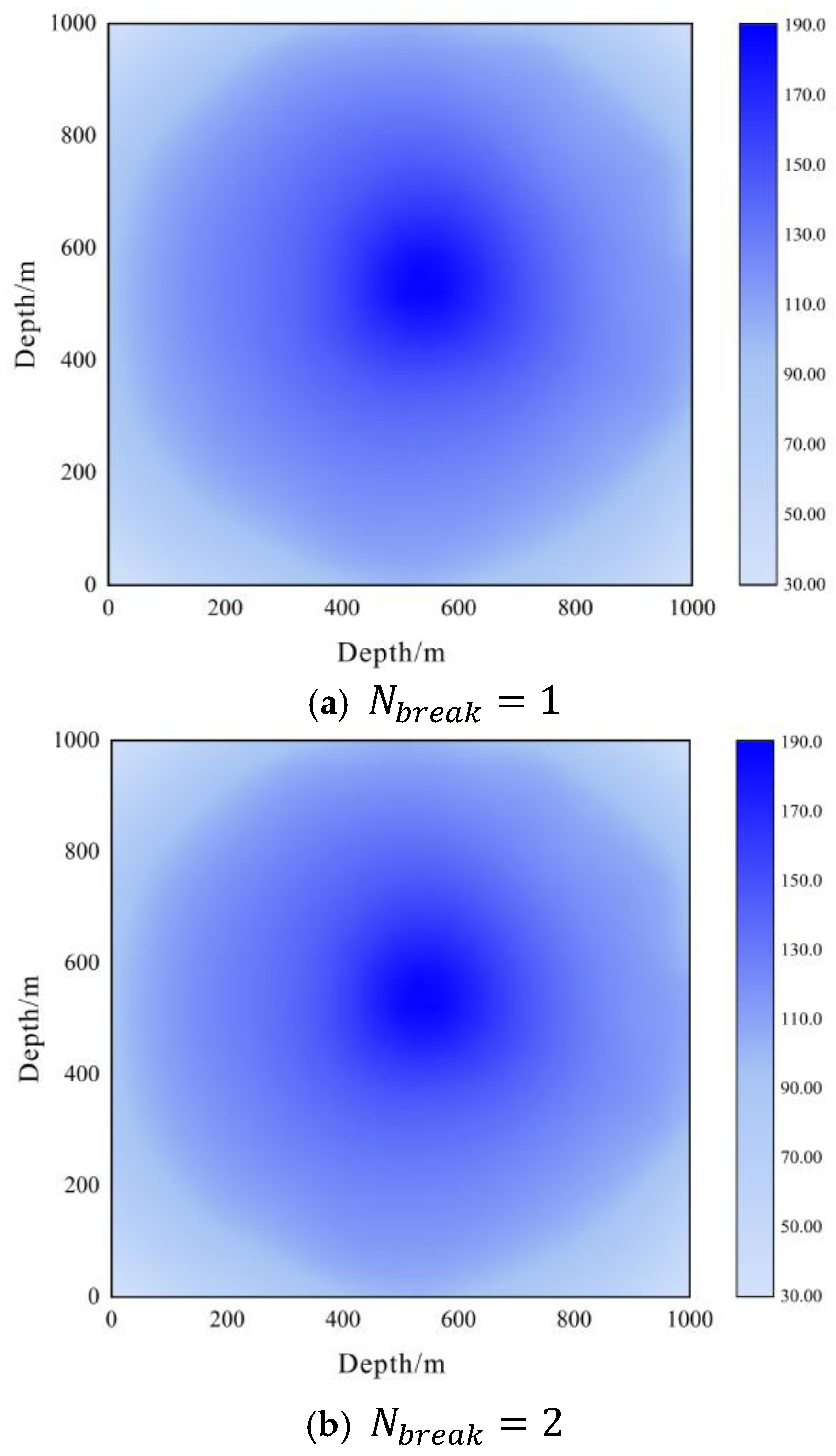
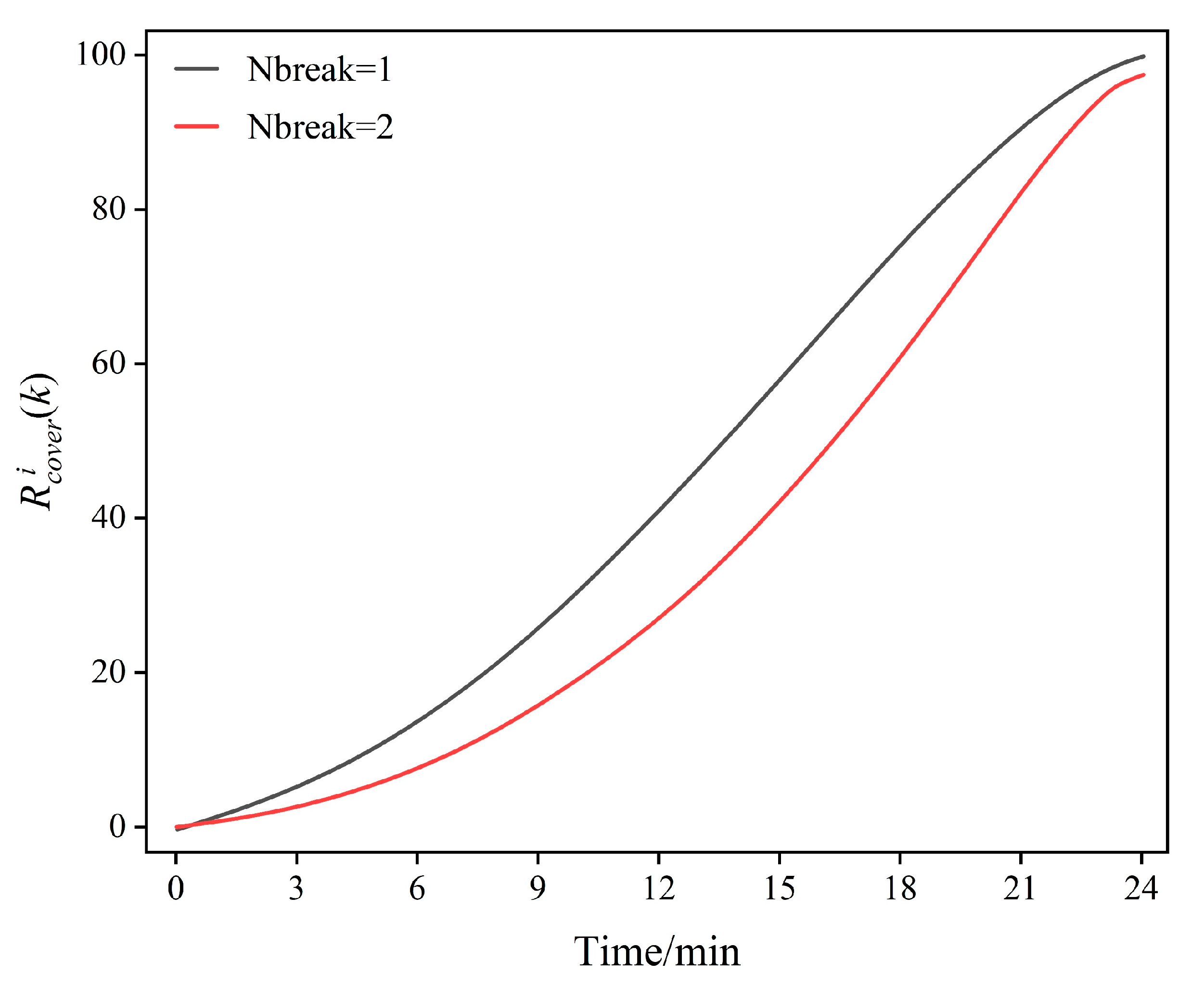
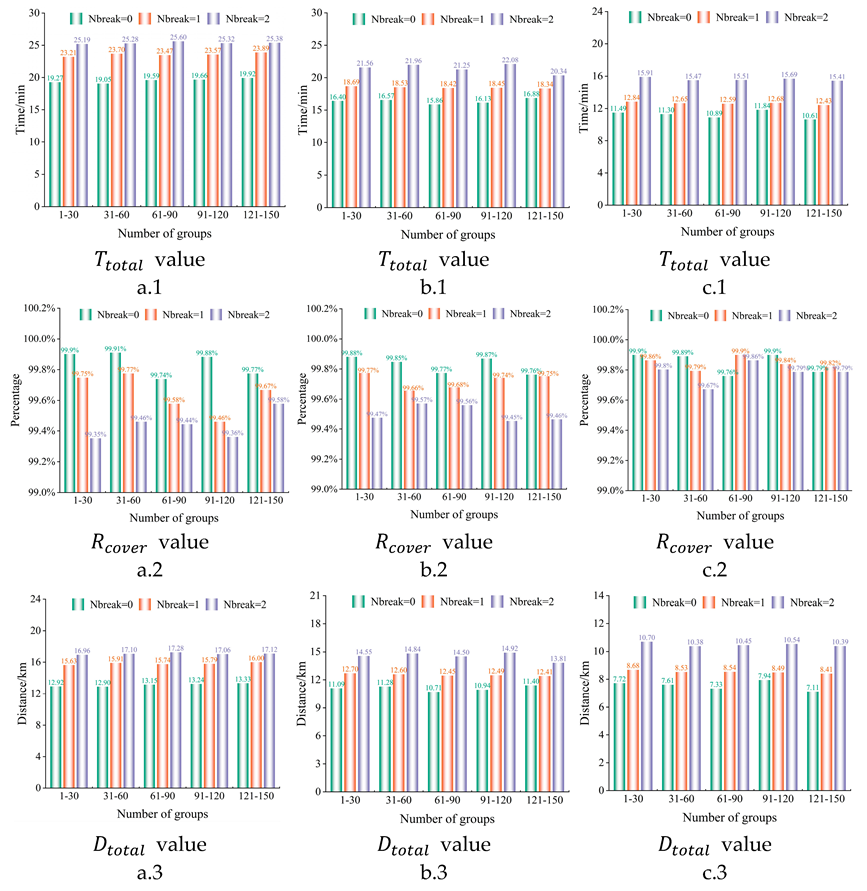
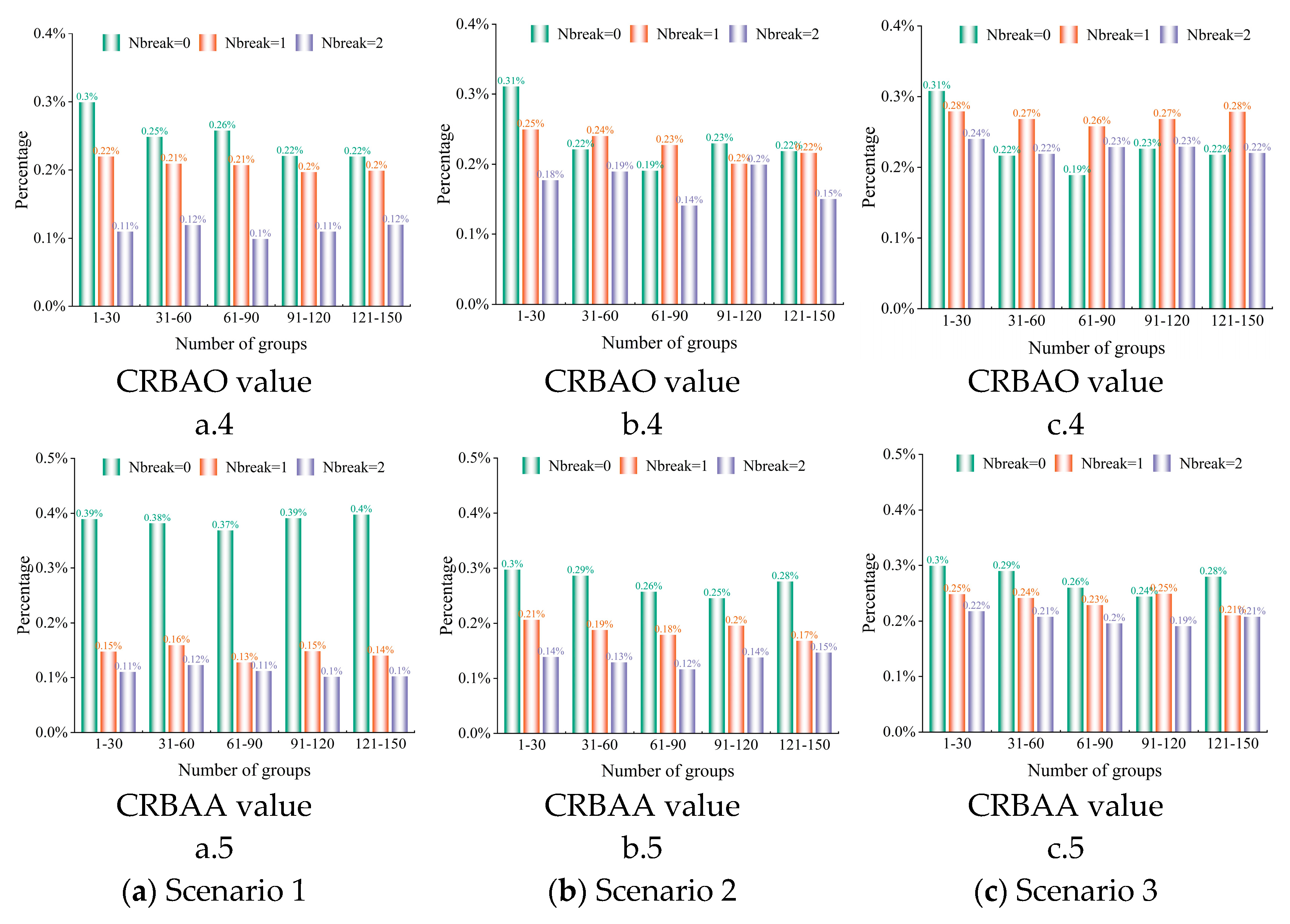
| Training Hyperparameters | Value |
|---|---|
| Batch | 1024 |
| Experience replay buffer | 106 |
| Discount factor | 0.95 |
| Learning rate | 0.01 |
| 100 m | |
| 500 m | |
| Max episode | 20,000 |
| Total episode | 1 × 107 |
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 0.35 | 0.35 | 0.43 | 0.46 | 0.48 | 0.25 | |
| 0.43 | 0.39 | 0.31 | 0.35 | 0.51 | 0.28 | |
| 0.39 | 0.43 | 0.45 | 0.51 | 0.44 | 0.51 | |
| 0.31 | 0.41 | 0.28 | 0.48 | 0.35 | 0.50 |
| Test Algorithm | CRBAA | CRBAO | |||
|---|---|---|---|---|---|
| The proposed strategy in this paper | 9.5 min | 1.7 km | 99.75% | 0.15% | 0.00% |
| Scanning patrol algorithm | 18.8 min | 3.3 km | 100% | 0.00 | 0.00% |
| The Number of Faulty Nodes | , CRBAA, CRBAO |
|---|---|
| 13.5 min, 8 km, 99.96%, 0.48%, 0.94%, 99.96% | |
| 14.9 min, 9 km, 99.94%, 0.44%, 0.41%, 99.69% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xu, X.; Li, G.; Lu, L.; Gu, Y.; Xiao, Y.; Sun, W. Cooperative Patrol Control of Multiple Unmanned Surface Vehicles for Global Coverage. J. Mar. Sci. Eng. 2025, 13, 584. https://doi.org/10.3390/jmse13030584
Liu Y, Xu X, Li G, Lu L, Gu Y, Xiao Y, Sun W. Cooperative Patrol Control of Multiple Unmanned Surface Vehicles for Global Coverage. Journal of Marine Science and Engineering. 2025; 13(3):584. https://doi.org/10.3390/jmse13030584
Chicago/Turabian StyleLiu, Yuan, Xirui Xu, Guoxing Li, Lingyun Lu, Yunfan Gu, Yuna Xiao, and Wenfang Sun. 2025. "Cooperative Patrol Control of Multiple Unmanned Surface Vehicles for Global Coverage" Journal of Marine Science and Engineering 13, no. 3: 584. https://doi.org/10.3390/jmse13030584
APA StyleLiu, Y., Xu, X., Li, G., Lu, L., Gu, Y., Xiao, Y., & Sun, W. (2025). Cooperative Patrol Control of Multiple Unmanned Surface Vehicles for Global Coverage. Journal of Marine Science and Engineering, 13(3), 584. https://doi.org/10.3390/jmse13030584





