Abstract
The growing demand for electricity in developing countries has called attention and interest to renewable energy sources to mitigate the adverse environmental effects caused by energy generation through fossil fuels. Among different renewable energy sources, such as photovoltaic, wind, and biomass, hydraulic energy represents an attractive solution to address the demand for electricity in rural areas of Colombia that are not connected to the electrical grid. In the current paper, the fluid–structure interaction (FSI) of a recently designed Vertical-Axis Hydrokinetic Turbine (VAHT) Straight-Bladed (SB) Darrieus-type, modified with symmetric winglets, was studied by implementing the sliding mesh method (SMM). By coupling with Computational Fluid Dynamics (CFD) numerical simulations, the FSI study demonstrated that the hydrodynamic loads obtained can cause potential fatigue damage in the blades of the Straight-Bladed (SB) Darrieus VAHT. Fatigue life was assessed using the stress–life (S-N) approach, and materials such as structural steel, short glass fiber reinforced composites (SGFRC), and high-performance polymers (HPP), such as PEEK, were studied as potential materials for the construction of the blades. FSI results showed that the biaxiality index (BI) provides a good understanding of the dominant stresses in the blades as the azimuth angle changes. It was also shown that structural steel and PEEK are good materials for the manufacturing of the blades, both from a fatigue resistance and modal perspective.
Keywords:
hydrokinetic Darrieus turbine; CFD; VAHT; winglets; FSI; material fatigue; sliding mesh method 1. Introduction
The transition from traditional fossil fuels, including coal, oil, and natural gas, to renewable energy sources such as solar, wind, biomass, geothermal, and hydroenergy has drawn significant attention because of the environmental harm caused by fossil fuels and the advantages of renewables [1,2]. However, renewable energy sources can only partially replace conventional energy generation methods, making it essential to continue developing alternative sources to supplement electrical energy production. Unlike the intermittent electrical energy generation provided by solar and wind energy, hydrokinetic turbines can harness clean, abundant, and steady energy from predictable ocean currents, waves, tides, and rivers [3,4]. For instance, installing hydrokinetic turbines in rivers is a promising solution for providing electricity to impoverished rural communities that utility companies deem economically unviable for grid extension [5]. Although hydrokinetic generation faces challenges related to the availability of running water due to cyclical weather variations, it offers a minimal ecological footprint, requires low operational costs, and eliminates the need for dams or reservoirs for water storage, making it attractive for rural electrification initiatives [6,7].
Hydrokinetic turbines are classified based on the rotor’s orientation relative to the flow direction into horizontal-axis turbines (HAHT) and vertical-axis turbines (VAHT). While in HAHT, the rotational axis is parallel to the flowing water direction, in VAHT, it is at a right angle to the free surface of the water [8]. HAHT are suitable for bottom-structure-mounted (BSM) or seafloor arrangements and possess some advantages associated with their high self-starting capabilities, which are related to the blades’ adequate taper and twist design to ensure that lift forces are evenly distributed along their length, with optimal performance at higher rotor speeds. These characteristics simplify generator matching and minimize gear coupling [9]. Although VAHT systems have a lower self-starting torque compared to HAHT, they are less sensitive to flow direction, eliminating the need for a yaw-control mechanism. Additionally, VAHT configurations require less water-sealed generator infrastructure due to their ease of installation above water in Floating and Near-surface Structure Mounted, FSM and NSM, arrangements, respectively [10]. Among the VAHT, the Savonius and the Darrieus constitute some of the most common designs. Different studies using CFD and experimental validation have proven that the Savonius displays its higher power coefficient () at a tip to speed ratio (TSR) or λ = 0.8 and offers some advantages over the Darrieus, such as its higher capacity to self-start, its more cost-effective simple construction, and stability or less sensitivity to changes in flow conditions [11,12,13]. However, the Darrieus turbine offers a higher power coefficient (), especially the straight-bladed or H-type Darrieus, which can generate electricity ranging from 300 W to 2 kW, making it suitable for use in remote areas [9,14,15]. Moreover, on a small scale, a standalone hydraulic H-type Darrieus turbine can be designed to generate electricity for household power. At the same time, in a hydro farm arrangement, it can be connected to the grid [16].
Improving the performance and reliability of VAHTs has received significant attention from the research community. Significant studies have focused on two prominent issues that increase drag and affect the hydrodynamic efficiency of VAHTs, namely, dynamic stall and tip vortex shedding [17,18,19,20]. In VAHTs, dynamic stall, generated when the angle of attack surpasses its critical value (also known as static stall angle), causes an abrupt and unsteady flow separation. At the same time, vortex shedding occurs due to adverse pressure gradients as water flows over the blade surface near the trailing edge, leading to its development [21]. The useful life of VAHTs can be increased by reducing the occurrence of stall and vortex shedding, which can improve the overall efficiency of VAHTs and diminish the occurrence of undesirable structural vibrations and noise [22]. Implementing passive flow control devices, such as winglets, is one way to reduce wingtip vortices. These devices prevent high-pressure water from migrating to low-pressure regions, thereby reducing rotational flow at the tip and ensuring smoother, more efficient water movement over the surface of the blade [23].
Several studies have been carried out with the implementation of winglets to improve the power coefficient of vertical-axis turbines. For instance, it was shown that implementing winglets increases the as a function of the tip speed ratio (λ) and the azimuthal angle (). It was claimed that increased in the upstream region within the range of 90° < < 180° at a maximum tip speed ratio TSR of λ = 2.29 [24]. Additionally, an enhancement in the aerodynamic performance of a baseline airfoil with a different winglet design was performed. It was concluded that a symmetrical winglet (BMAX) improved aerodynamic performance by 14%, compared to the 3.5% provided by the blended winglet [25]. Using numerical CFD simulations, the study in [26] carried out one of the earliest studies to identify the type of winglet that optimized the performance of a Darrieus-type hydrokinetic turbine. Two winglet designs were examined: an asymmetric winglet and a symmetric winglet. The symmetric winglet consists of two separate winglets: one extending along the extrados and the other along the intrados of the blade. The numerical results revealed that winglets enhanced turbine performance by reducing vortex size at the blade tips. Furthermore, the symmetric winglet configuration outperformed the asymmetric design, delivering the best results and increasing turbine power prediction by approximately 20% [26]. The effect of winglet height and pitch angle on the hydrodynamic performance of a HAHT was analyzed in [22]. The results indicated that the optimal configuration led to a 7% increase in the turbine’s power output, with the ideal conditions corresponding to a pitch angle of 33.2° and a winglet height equal to 2.04% of the turbine radius. Similarly, the performance of a straight-bladed Darrieus wind turbine with winglets was evaluated in [23]. The authors found that the winglets enhanced performance by 10–19% and reduced vortex formation at the blade tips. However, they also discovered that adding winglets did not improve performance at every azimuthal position of the turbine.
Considering that one of the main drawbacks of VAHTs is their low , certain geometrical parameters of the rotor might be modified to enhance their efficiency. Among these parameters, the solidity, the number of blades, the blade shape, the aspect ratio, and the helicity are the ones that are frequently modified to increase the . In this regard, some researchers have shown that the turbine’s optimal operating point occurs at lower solidity values at a higher TSR. Furthermore, while numerical studies predict significantly better performance at low solidity, experimental research shows only minimal differences in performance, as the losses not accounted for in the simulations due to simplifications come into play [27].
Another important aspect to consider in the design of VAHTs is the fluid–structure interaction (FSI), which refers to the significant interaction between the flow around a structure and the structure itself, where changes in the structure notably affect the flow and vice versa. FSI simulation solution strategies are primarily categorized into monolithic and partitioned methods. Partitioned methods are further classified into one-way and two-way coupling [28,29]. Whether one-way or two-way coupling methods are used, the solutions are based on a partitioned approach, where distinct computations are performed for different physical fields, such as fluid dynamics and structural dynamics. Information is exchanged between the fluid and structure solvers at the fluid–structure interface, which defines the boundary between the fluid and solid domains. The nature of this exchange depends on the coupling method: in one-way coupling, only the fluid pressure exerted on the structure is transmitted to the structure solver, whereas in two-way coupling, the displacement of the structure is also conveyed to the fluid solver [30,31]. By implementing FSI, the durability and the prevention of catastrophic failure can be evaluated by analyzing the interaction between water and the turbine structure, including its blades and other structural components [32]. Generally, two-way coupling solutions offer greater accuracy, particularly for large deflections where structural deformation significantly impacts the fluid field. While the one-way coupling method does not ensure energy conservation at the interface, two-way coupling does. However, one-way coupling simulations offer the advantage of significantly reducing computational time, eliminating the need to calculate fluid mesh deformation, and preserving consistent mesh quality [33]. For instance, the validity of one-way coupling was examined in the context of FSI for a horizontal-axis wind turbine. It was shown under different wind speed conditions that blade pressure distributions and deflections showed fairly reasonable results with the inviscid model, and the stresses over the structure were below the limits of the mechanical strength of the blade’s material [34]. Regarding CFD simulations, unsteady simulations are typically performed using partitioned methods. In the so-called Sliding Mesh Method (SMM), the domain is partitioned into multiple non-overlapping zones connected through either conformal or nonconformal interfaces, which can rotate or slide relative to one another [32,33]. The SMM exchanges data across the rotating/sliding interfaces to ensure continuity. It has been shown that, for large FSI simulations, the SMM requires significantly less memory while maintaining the same level of accuracy compared to other methods such as the overset (Chimera approach) [34,35]. Through FSI, different aspects of VAHTs, such as hydrodynamic damping, can be studied. Hydrodynamic damping is crucial in the dynamic stability of hydraulic turbine components and their structural vibration behavior [36]. This is particularly important under operating conditions such as part-load and full-load regimes, which can lead to other coupled phenomena such as resonance, blade flutter, and mechanical fatigue. Once hydrodynamic loads are transferred to the structure, one parameter that can be particularly useful in the interpretation of the dominant stresses in a given location (i.e., critical zones or where the structure is more prone to fail) is the biaxiality index (), which is defined as the ratio of the minimum over the maximum principal stresses. The helps determine whether a specific location is subjected to a particular stress state comparable to testing conditions. Under the complex interaction of the hydrodynamic forces with the structure of the turbine, analysis of the is useful to understand the regions of the winglets and the blade span where normal, torsional, and biaxial stresses where more dominant. For instance, if the location of interest has a value of = 0, −1, and 1, it indicates that it is primarily subjected to normal, shear, and biaxial stresses, respectively.
The objective of the current study is to perform a CFD-FSI analysis to evaluate the performance of a recently proposed enhanced design straight-bladed Darrieus VAHT with symmetric winglets [37]. The main contributions of the current work can be summarized as follows:
- Although numerous research papers focus on straight-blade vertical-axis Darrieus turbines, studies examining the hydrodynamic performance of these turbines modified with symmetric winglets are scarce [37]. Additionally, the study in [26] demonstrated that incorporation of symmetric winglets in these turbines overcomes the performance of asymmetric tip devices, which are more common in literature; therefore, further research in this direction is worth, with the present contribution representing a step forward.
- To the best of coauthors’ knowledge, studies on the fluid–structure interaction of blades with winglets are rare in the literature, and none specifically address symmetric winglets. Therefore, this study aims to fill this gap by incorporating a fatigue analysis of different materials (structural steel, short glass fiber reinforced composites and high-performance polymers) under a zero-based cyclic load, using the loads transferred from the CFD study.
- Moreover, present work incorporates the analysis of structural parameters such as the biaxiality index (BI), not often presented in FSI studies. This index is analyzed as a function of the azimuth angle, illustrating its correlation with lift and drag forces acting on the blade. This examination provides insights into the effect of hydrodynamic forces on the mechanical stresses and deformations of the winglets and along the blade span.
- Finally, a modal analysis was conducted to examine the differences in the turbine’s vibration modes and their correlation with the mechanical properties of the materials used for the blades.
The content of this study is organized into several sections: Section 2 introduces the investigated turbine configuration, covering geometric and operational parameters as well as the numerical setup. Section 3 describes the FSI methodology, while Section 4 presents the results of the FSI study, including deformations, stress distributions, the evolution of the biaxiality index along a turbine revolution, and the fatigue and modal analyses for the selected materials. Finally, Section 5 provides the study’s conclusions and suggestions for future work.
2. Turbine Configuration
2.1. Geometric Model
The base design, without winglets, was based on the turbine blades studied experimentally and numerically by Yagmur et al. [38]. The geometrical characteristics of such a turbine are provided in Table 1.

Table 1.
Geometrical parameters of the turbine studied in [38].
The study of López et al. [37] dealt with improving the hydrodynamic efficiency of a straight-bladed Darrieus hydrokinetic turbine by enhancing the geometry of the winglets added as tip devices. In such a study, symmetric winglets were added to the base blade. In the new model, the cant and sweep angles (as defined in Figure 1) were varied according to a design of experiments to identify the configuration that yields the highest power coefficient. After verifying and validating the simulations against the experimental and numerical results from [38], López et al. ended up with an improved hydrodynamic design for the winglet, featuring a cant angle of and a sweep angle of . The winglet height and chord length at the tip were fixed as 0.07 H and 0.25 respectively (Figure 1). In that case, the turbine power coefficient (or efficiency) was improved around 20% regarding the base case of Yagmur et al. without winglets at the optimal tip speed ratio = 1 [38].
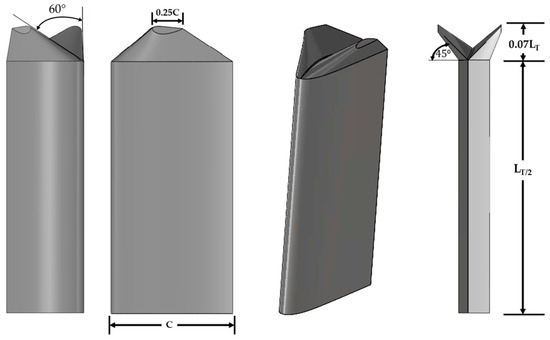
Figure 1.
Sketch of the improved blade with winglets obtained in. Only the upper half is shown in the figure.
2.2. Numerical Configuration
Three-dimensional unsteady simulations of the dynamic behavior of the turbine were carried out using the sliding mesh strategy. Therefore, the complete computational domain, consisting of a portion of the water channel including the VAHT with rectangular prism shape, was divided in two subdomains: one containing the turbine of cylindrical shape, which represents the rotating part of the model (rotational subdomain), and another non-moving domain that comprises the remainder of the full domain (steady subdomain). This arrangement is illustrated in Figure 2. Both subdomains are meshed separately and connected by a non-conformal interface. The dimensions of the computational domain are given in Table 2.
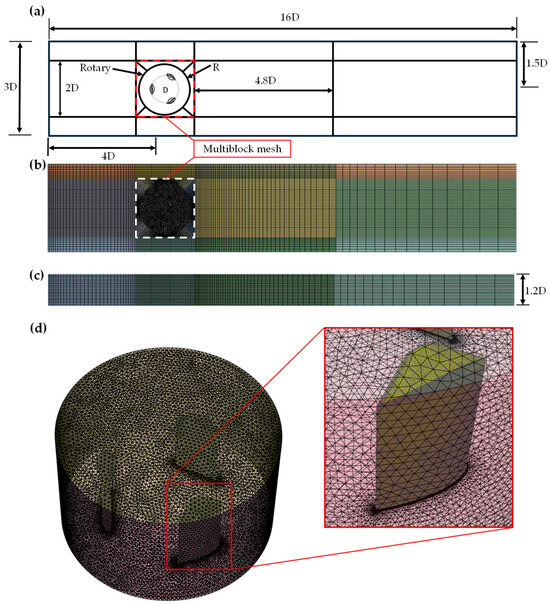
Figure 2.
(a) Dimensions of the mesh for the rotating and steady domains for the FSI analysis, (b) Top view of the final design of the structured mesh, (c) Front view of the mesh, (d) 3D view of the sliding mesh.

Table 2.
Dimensions of the computational domain, according to Figure 2, in terms of turbine diameter.
Moreover, due to the symmetry of the flow around the turbine, the geometry employed for the simulations only considers the upper half of the model to reduce the computational cost, resulting in a computational blade height of H/2 plus the winglet length. To further simplify the geometry, the CFD simulations excluded the turbine axis and support arms. The computational domain maintains the same dimensions and boundary conditions as those used in [38], ensuring that the blockage effects influencing the turbine’s performance in the simulation remain consistent with the experimental and numerical results reported by [38]. The selected domain for the numerical calculations consists of a 16D × 3D × 1.2D rectangular parallelepiped, where the rotating subdomain has a diameter of 1.8D. Rezaeiha et al. [39] investigated different diameters for the rotating region, specifically 1.25D, 1.5D and 2D. They found that the difference in the power coefficient between these cases was below 1%, indicating that the choice of diameter had no significant impact. Considering the number of elements, the grid quality around the blade and the blockage ratio, the rotating subdomain diameter was set to 1.8D. This rotating region moves around the turbine axis at a prescribed angular velocity, ω, in the counterclockwise direction. The left boundary of the stationary domain is defined as a velocity inlet with a freestream velocity , while the right boundary is set as a zero-gauge pressure outlet. The mid-span plane of the computational domain is designated as a symmetry boundary, and the remaining surfaces are set as no-slip walls. The rotor’s center is located at 4D from the inlet. Once the computational domain was defined, a structured mesh was generated to ensure proper flow alignment with the turbine. The proposed structured mesh topology allows for refinement in the regions containing the turbine’s near wake, as shown in Figure 2b,c. This refinement ensures that the element size in the background region remains comparable to that of the rotating region, facilitating accurate data transfer across the interface. Figure 2d shows the mesh in the rotating subdomain. A local mesh refinement is performed in the transition between the straight blade and the winglet, considering these regions’ small size and complexity. Such a refinement ensures accurate numerical results. Particularly, prism-like shape elements were used to estimate the flow within the boundary layer, with a growing rate of 20%. This mesh design assures a higher mesh density close to the turbine.
The mesh was generated using the commercial software ICEM-CFD 2022R1 and Ansys meshing modules, while CFD and FSI were carried out using Ansys fluent 2022R1 and mechanical workbench 2022R1, respectively. The fundamental governing equations of the model assume incompressible and isothermal flow, treating water as a Newtonian fluid and neglecting gravitational effects. The problem was solved in the transient state due to the turbine’s dynamic behavior, utilizing the Transition Shear Stress Transport (Transition SST) turbulence model [40,41]. This model was selected not only because the Reynolds number calculated for a blade was approximately Re = 30,000 but also because it performs better than other two-equation models in flows with a strong adverse pressure gradient, such as those occurring around a turbine. It is the preferred choice for describing turbulent flow in turbomachinery. Furthermore, physically, the Reynolds number of the blade changes over time, leading to multiple phenomena occurring in the boundary layer, such as the laminar boundary layer, transition to turbulence, laminar separation, flow reattachment, and turbulent separation, allowing for the transition between laminar and turbulent flow regimes within the turbine. A time step of 0.036 s, corresponding to 0.5° of turbine rotation, was defined, with a maximum of 75 iterations specified for each time step and a residual convergence criterion of 10−6. The reference values for calculating the hydrodynamic forces and moments acting on the turbine blades as they interact with the fluid are shown in Table 3, based on those presented in [38].

Table 3.
Computational parameters used in the simulations.
Verification and validation studies of the hydrodynamic CFD simulations for the Yagmur et al. turbine [38] were conducted in the previous work by the authors [37]; therefore, they will not be repeated here. As a result of that work, it was demonstrated that a mesh consisting of approximately 4 million elements was sufficient to obtain a grid-independent solution. Furthermore, the differences between the computed power coefficients in both studies were less than 5% for all the investigated turbine tip speed ratios, thereby confirming the validation of performed computations. Comprehensive details of the CFD simulation for both the base and enhanced turbines can be found in [37].
3. Fluid–Structure Interaction (FSI) Approach
Once the effective hydrodynamic forces and moments due to the flow around the turbine are obtained, the FSI can be performed. It should be emphasized that the sliding mesh method (SMM) allows the correct handling of the mapping of results between the CFD and structural analysis modules of the ANSYS software (Ansys 2022 R1). In this context, the rotational domain was designed as a cylinder with a diameter 1.8 times larger than the turbine’s diameter, with its faces aligned with the upper and lower walls of the stationary domain (Figure 2a). The final mesh design proposed in Figure 2 comprises the division of the stationary domain using multiblocking, which is essential for generating structured elements throughout the entire steady domain. It also shows the separation of the rotating domain through mesh interfaces, which was discretized using an unstructured mesh dominated by tetrahedra for simplicity and speed. Flow regions near the blades are meshed with prismatic elements to enable the proper resolution of the developing boundary layer. The domain discretization results in a hybrid mesh of hexahedral, tetrahedral, and prismatic elements, with a non-conformal interface between the rotating and stationary zones.
A cylindrical coordinate system was selected to analyze deformations and stresses in the radial (), circumferential (), and longitudinal () directions. The boundary conditions used in the FSI analysis were applied at 0.25 from the mid-span of each blade, setting zero displacement ( = = = 0) and torque ( = = = 0), in such a way that each blade acts as a cantilever beam. Normal stresses and deformations were analyzed to compare the structural behavior with the mechanical and fatigue strength of the proposed materials for the manufacturing of the blades. In addition, the biaxiality index was used to analyze the stress distribution along the blades span and the winglets. A modal analysis was added to obtain the natural frequencies and the first four vibrational modes.
Fatigue Analysis
The straight-bladed Darrieus VAHT fatigue analysis with symmetric winglets was performed using a stress-life (S-N) approach, using the modified Goodman line theory, under a zero-based loading scenario ( = / = 0), as shown in Equation (1). In this equation, and are the alternating and mean components of the hydrodynamic normal stresses transmitted to the blades of the turbine, and and represent the modified fatigue and ultimate tensile strength of the materials used in manufacturing the blades, respectively. Figure 3a–c, show a fully reversed loading ( = 0), zero-based loading ( = = /2), and a constant life - Goodman diagram, respectively. One of the key assumptions in the S-N approach for high cycling fatigue (HCF) is that the modified fatigue strength is estimated in a manner that cracks neither nucleate nor propagate under the loading cycles.
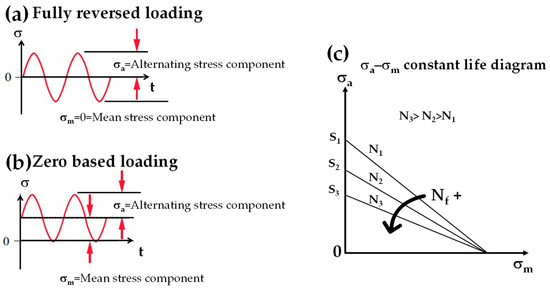
Figure 3.
(a) Fully reversed loading, (b) zero loading, and (c) constant - Goodman diagram.
Materials such as structural steel (SS), short glass-fiber-reinforced polyamide composites (SGFRC), and a thermoplastic high-performance polymer (HPP) such as polyether ether ketone (PEEK) were used for the structural simulation of the blades. Their fatigue and mechanical properties, which were obtained from different sources [42,43,44,45,46,47,48,49,50], are shown in Table 4. It should be clarified that the mechanical properties of SGFRC were taken at the ply angle of 0°, where the fibers, aligned with the length of the composites, offer maximum strength. To estimate the fatigue life of the materials mentioned above, the Basquin relationship was used. It has been demonstrated for many engineering materials that the S-N behavior can be modeled using the following power–law relationship:

Table 4.
Properties of the different materials for the structural analysis.
In Equation (2), is the fatigue strength under fully reversed loading ( = / = −1), is the number of cycles to fatigue failure, and and are constants that depend on intrinsic and extrinsic conditions associated with factors such as the material and the geometry (as well as testing conditions), respectively.
4. Results and Discussion
Figure 4 shows the azimuthal positioning of the blades regarding the incoming flow, where the turbine rotates counterclockwise. In the figure, Blade 1 is located perpendicularly to the flow velocity, which is aligned with the horizontal -axis, i.e., in the angular position .
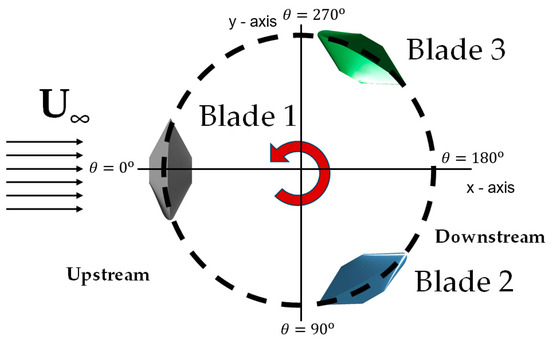
Figure 4.
Definition of the azimuth angle regarding the incoming flow. Turbine rotates counterclockwise.
The comprehensive CFD simulation of the enhanced blade with winglets was performed in [37]; therefore, those results will not be repeated here, and readers are referred to that study for full details. As an example, Figure 5 illustrates the pressure and skin friction coefficient distributions along the full blade in the case of at . Such coefficients are important because, as dimensionless variables, they are directly related to the pressure and friction forces exerted by the flow on the blade, which are the relevant quantities for the FSI analysis.
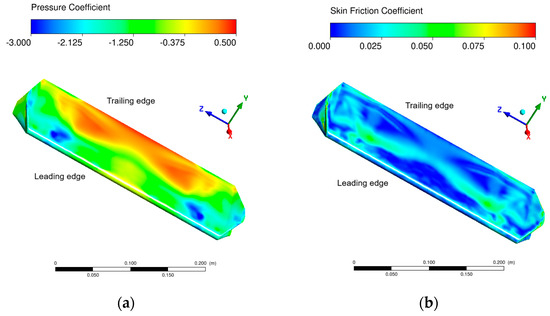
Figure 5.
(a) Pressure coefficient contour on the full blade and (b) skin friction coefficient contour maps on a full blade view for and azimuthal angle .
4.1. Fatigue Strength of the Materials
Fatigue strength as a function of the number of cycles to failure is shown in Figure 6. It can be observed that HPP, such as PEEK, shows higher fatigue strength compared to SGFRC using the S-N approach. These mechanical properties were used to simulate the FSI of the turbine under repeated loading conditions ( = 0), applying Goodman’s theory as outlined in the fatigue analysis section.
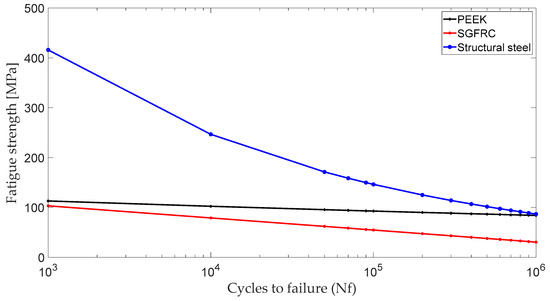
Figure 6.
Fatigue strength vs. cycles to failure for PEEK, SGFRC, and structural steel (SS).
4.2. FSI Analysis of the VAH Straight-Bladed Darrieus Turbine with Winglets
The FSI process begins with the fluid dynamic analysis of the turbine in ANSYS Fluent, where the flow around the turbine blades is simulated as the turbine rotates. During each time step, corresponding to one degree of turbine rotation, the forces and moments acting on each blade and the entire turbine are calculated. These force and moment calculations depend on the interaction of the flow with the blades at a given rotation position, meaning that each time step reflects a specific load for a given location on the blades. Throughout the fluid dynamics analysis, a detailed tracking of the turbine power coefficient, , was conducted, monitoring its behavior within each turbine rotation. As expected, the values fluctuated due to the rotation; however, no significant variations were observed after the seventh rotation, indicating a stabilization in its mean value. To ensure that no further significant variations occurred, additional turbine rotations were allowed, confirming that the trend remained stable. Consequently, the FSI analysis was performed at the end of the 20th turn, when the system’s behavior was sufficiently stabilized for the structural study.
For the FSI analysis, forces such as pressure and shear stresses are applied as loads in the Static Structural module of ANSYS Workbench, where the structural analysis is conducted. In this analysis, stresses, deformations, and potential fatigue failure are calculated based on the loads transferred at each time step, meaning that the structural results correspond to a specific moment in the turbine’s rotational cycle, i.e., a particular rotational angle. Therefore, each set of stresses and deformations obtained from the structural analysis is related to the exact position of the blades at that particular instant within the rotation cycle.
Structural and Fatigue Analysis
Directional deformation of the blades, made of structural steel, in the radial, circumferential, and longitudinal axes is shown in Figure 7a–c, for the azimuth angle , respectively. It should be noted that the maximum directional deformation occurs in the radial direction (), followed by the circumferential deformation (), and the maximum total deformation occurs in Blade 1, at the same location as the maximum radial deformation. This location corresponds to the point where the chord length of the winglet is minimal, and the blade resembles a cantilever beam (or an overhanging beam, considering the whole blade) in relation to the fixing structural supports, where the boundary conditions were applied. Normal stress in the radial (), circumferential (), and longitudinal () axes is shown in Figure 8, where it can be observed that the dominant stress is oriented along the radial direction due to the combination of the hydrodynamic loads and the inertial effects. The maximum principal stress () is well below the mechanical strength of the structural steel. It is located, along with the normal stress components, at the point where the blades are assembled to the structural supports (see Figure 8d). Based on the FSI computational results, the maximum deformation remains well within the elastic limits of the structural steel.
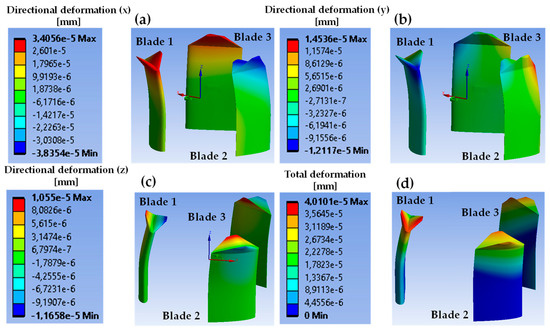
Figure 7.
(a) Directional deformation in the radial (), (b) circumferential (), and (c) longitudinal directions (), and (d) total deformation (mm) for structural steel. A comma denotes a decimal sign and e means a power of 10.
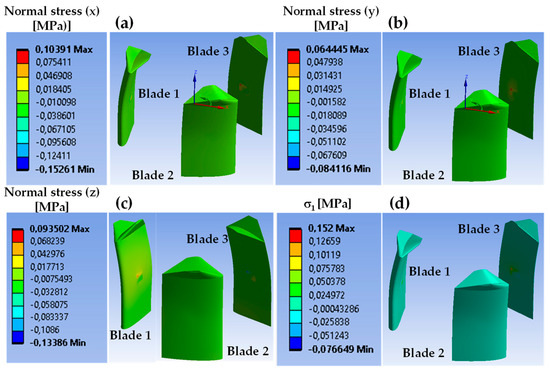
Figure 8.
(a) Normal stress (), (b) normal stress (), (c) normal stress (), and (d) maximum principal stress distribution of the blades for structural steel. A comma denotes a decimal sign.
Figure 9 shows the interpretation of the BI based on the Mohr circle, representing a two-dimensional different state of stress, such as uniaxial normal stress (Figure 9a), pure shear (Figure 9b), and biaxial stresses (Figure 9c). As depicted in Figure 10a–c, for the azimuth angle , the is distributed along the extrados (outer side) and intrados (inner side), displaying tension–compression stresses () due to bending, shear stresses (), and biaxial stresses (), which can be attributed to a combination of different hydrodynamic, structural, and inertial forces. As observed in the green-like regions where along different sections of the winglets, this can be associated with hydrodynamic lift forces that vary as a function of both the azimuth and the angle of attack. Since lift forces act perpendicular to the chord line, they cause bending moments and tension–compression stresses along the winglets and the blade span. Moreover, a similar analysis can be made for the drag forces acting along the blade length, which induce shear stresses, i.e., . Interestingly, for symmetrical winglets, the distribution of shear stresses varies along the extrados and the intrados. For instance, in Figure 10b,c, the extrados shows mainly shear stresses, while in the intrados, the most dominant stress is tension–compression caused by bending. It is believed that the shear stresses observed on the extrados in Figure 10c may be caused by vortical structures detached where flow reversals occur, generating oscillatory forces that contribute to shear and biaxial stresses, as well as to the variation of drag and lift forces, which in turn create torsional moments along both the blade span and the winglet chord line (see reference [37]). Additionally, in the intrados of Figure 10b, bending stresses () are mainly present. Biaxial stresses shown in Figure 10b,c with a are also associated with the combination of tensile and compressive bending stresses caused by lift and drag forces. Similar distribution was observed in the winglets when SGFRC and PEEK were used as fatigue-resistant materials to simulate the blades. Other factors influencing the variation of the include the centrifugal forces, which induce axial tensile stresses in both the winglets and the blade span as it rotates.
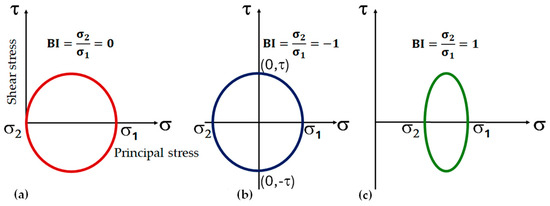
Figure 9.
Biaxiality index () represented in a two-dimensional state of stress: (a) uniaxial normal stress, (b) pure shear, and (c) biaxial stresses.
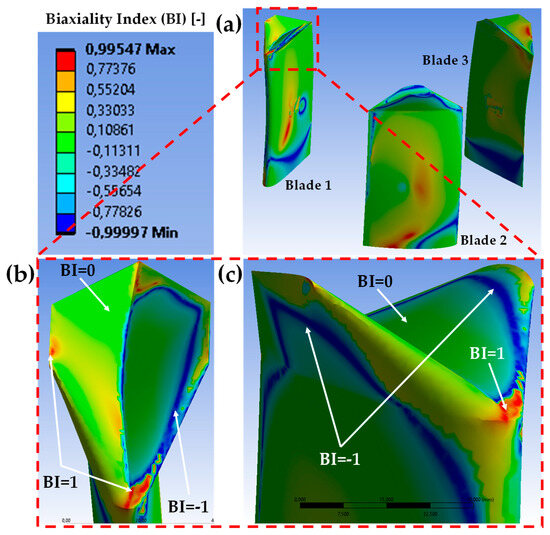
Figure 10.
Biaxiality index () of the blades for structural steel: (a) isometric view, (b) top view of Blade 1, and (c) left view of Blade 1. A comma denotes a decimal sign.
The directional deformation of the blades in the radial (), circumferential (), and longitudinal () directions using SGFRC is shown in Figure 11a–c, respectively. It can be observed that the total deformation of the blades (Figure 11d) is two orders of magnitude higher than that of structural steel, which may impose restrictions in terms of stiffness when contemplating this material for blade manufacturing. Figure 12a–c show the normal stress in the , , and directions, respectively. Given the stress concentration at locations where the aforementioned stresses are higher, it is likely that the blades are prone to fail in these areas according to the fatigue strength provided by SGFRC. Based on the results obtained for SGFRC, it can be seen that flexible materials can amplify bending and shear stresses due to deformations under the hydrodynamic loads transferred to the turbine’s structure. The stress concentrators are associated with the holes and notches required for assembling the structural supports to the blades, which coincide with the regions where bending stresses are higher. Regarding the structural behavior of PEEK, Figure 13 shows the directional deformation results of the blades. It can be observed that, in comparison, the deformation in the radial (), circumferential (), and longitudinal directions () is one order of magnitude higher than that of structural steel. This is advantageous, as a structure made entirely of PEEK will be lighter than one made of structural steel. The total deformation of the blades made with PEEK is one-third of that observed with SGFRC, and it occurs in the region where the chord length of the winglets is smaller, as expected. The distribution of the normal stresses along the blades using PEEK in the , , and directions is shown in Figure 14a–c, along with the principal stress (Figure 14d), respectively. The distribution of these stresses is mainly similar to those shown in Figure 8 for structural steel, even for the principal stress (comparing Figure 8d with Figure 14d), which presents potential as an alternative material for fabricating the blades of a Darrieus VAHT. Using the S-N approach for structural steel and PEEK, a combination of alternating and mean components of the equivalent von Mises stress results in a fatigue safety factor that guarantees an infinite fatigue life under the conditions of the current study.
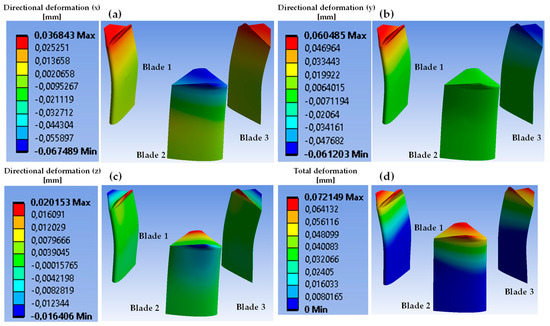
Figure 11.
(a) Directional deformation in the radial (), (b) circumferential (), and (c) longitudinal directions (), and (d) total deformation (mm) for SGFRC. A comma denotes a decimal sign.
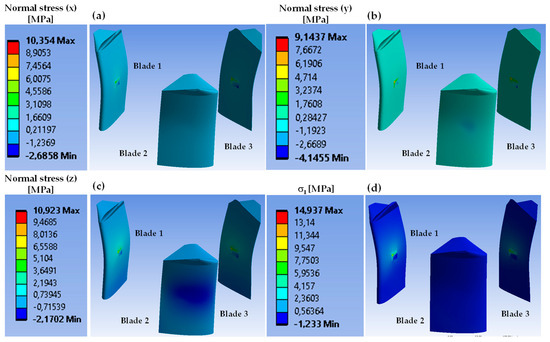
Figure 12.
(a) Normal stress (), (b) normal stress (), (c) normal stress (), and (d) maximum principal stress () distribution of the blades for SGFRC. A comma denotes a decimal sign.
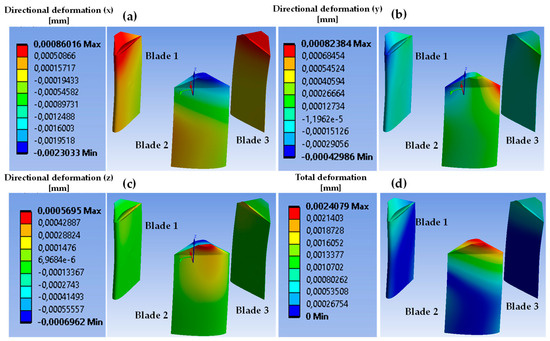
Figure 13.
(a) Directional deformation in the radial (), (b) circumferential (), and (c) longitudinal directions (), and (d) total deformation (mm) for PEEK. A comma denotes a decimal sign, and e means a power of 10.
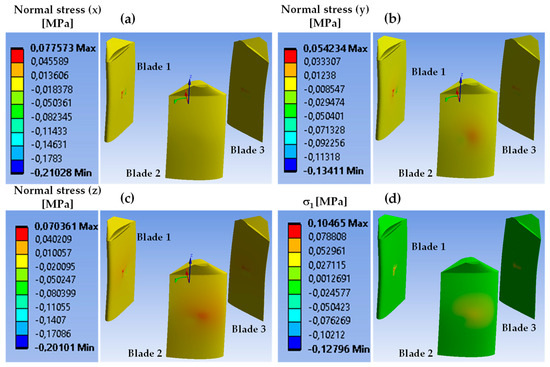
Figure 14.
(a) Normal stress (), (b) normal stress (), (c) normal stress (), and (d) maximum principal stress distribution of the blades for PEEK. A comma denotes a decimal sign.
Since structural steel and PEEK are the best-performing materials, the radial deformation and normal stress evolution in the () direction were measured as a function of the azimuthal rotation. Figure 15a–f and 15g–l show the directional deformation and the normal stress in the radial direction of structural steel from to azimuth angle in increments of 60°, respectively. It can be observed that radial deformations and stresses vary with the azimuth angle, with maximum values occurring at an azimuth position of . These maximum values are found at the location of the minimum chord line of the winglet and at the point where the boundary conditions are applied (i.e., where the blade structural supports are fixed). Radial deformations and normal stresses in the radial direction () change from compression to tension and vice versa in the winglet region due to bending stresses as the blade rotates. The variation of the with the azimuth angle is shown in Figure 15m–r, where it is visible that the region that corresponds to biaxial stresses (the red region with ) moves with the azimuth angle. As shown in [37], changes in the tangential () and normal force coefficients () with azimuth angle affect the lift and drag coefficients. As a result, biaxial stresses, caused by radial and circumferential stress components, will shift over the winglet as the blade rotates, as shown for each azimuth angle in Figure 15m–r. Unlike regions of biaxial stresses () that move constantly over the winglet with the rotation of the blade, the regions of tension–compression stresses due to bending (green region with ), are distributed over the blade span and most of the surface of the winglets. Similarly, regions of shear stresses (shown in blue for ) are highly localized and remain relatively constant between azimuth angles from 120° to 240°, corresponding to the angles where and exhibit lower values (as in [37]). Regarding the structural behavior of PEEK as a material for the blades, Figure 16 shows fairly similar results compared to structural steel in terms of normal stresses in the radial direction () and biaxiality index as a function of the azimuth angle. Except for the directional deformation of the blades simulated with PEEK in the radial direction, which is one order of magnitude higher compared to structural steel as the azimuth angle changes (due to the lower stiffness of PEEK), the manufacturing of the blades with PEEK appears feasible based on its structural performance.
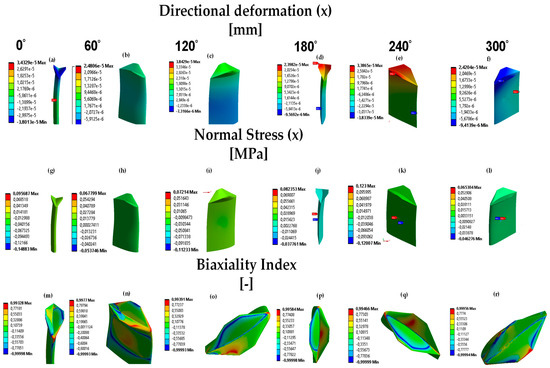
Figure 15.
(a–f) Directional deformation in the radial direction (), at 0°, 60°, 120°, 180°, 240°, and 300° azimuth angles. (g–l) Normal stress in the radial direction () at 0°, 60°, 120°, 240°, and 300° azimuth angles, respectively. (m–r) Biaxiality index at 0°, 60°, 120°, 240°, and 300° azimuth angles, respectively, for structural steel. A comma denotes a decimal sign, and e means a power of 10.
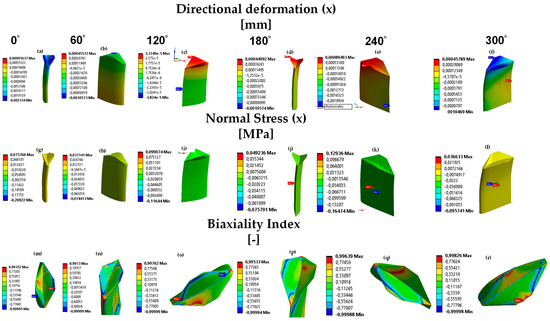
Figure 16.
(a–f) Directional deformation in the radial direction (), at 0°, 60°, 120°, 180°, 240°, and 300° azimuth angles. (g–l) Normal stress in the radial direction () at 0°, 60°, 120°, 240°, and 300° azimuth angles, respectively. (m–r) Biaxiality index at 0°, 60°, 120°, 240°, and 300° azimuth angles, respectively, for PEEK. A comma denotes a decimal sign, and e means a power of 10.
Figure 17a–l shows the variation of the equivalent alternating von Mises stress () with respect to the variation of the azimuth angle for structural steel and PEEK, respectively. It should be noted that the von Mises alternating stresses are lower than the normal radial stress (), which is maximum in the upstream region at . The von Mises alternating fatigue stress values obtained for structural steel and PEEK are very similar and are approximately half of those for the main principal stress (). Once the structural analysis of the blades as a function of the azimuth rotation is performed, it can be observed that the S-N method provides a simple approach to estimating the number of cycles required for failure under completely reversed loading. The S-N approach and the Goodman model are valuable tools for estimating the fatigue life under the presence of mean stress components from external hydrodynamic cyclic loading imposed under the conditions of the current study. Based on the present FSI analysis, the equivalent alternating von Mises stress shows that structural steel and PEEK constitute good materials for manufacturing the blades, and their stresses are much lower than the fatigue strength of these materials. Furthermore, considering the locations where the maximum stresses are present, the stiffness of the turbine blades can be reinforced in these zones using a higher cross-sectional area.
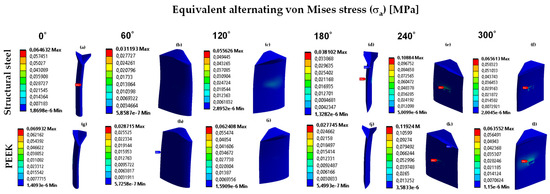
Figure 17.
(a–l) Equivalent alternating von Mises stress at 0°, 60°, 120°, 180°, 240°, and 300° azimuth angles for structural steel and PEEK, respectively. A comma denotes a decimal sign, and e means a power of 10.
4.3. Modal Analysis
Natural frequencies and vibration modes were determined for an undamped structural system. Figure 18a–d shows the turbine blades’ first four natural frequencies and vibration modes using structural steel. It can be seen that the first natural frequency (see Figure 18a) is very high, and its associated vibration mode is characterized by the bending of the blade in a direction parallel to the incoming flow. As observed in Figure 18b–d, the second vibration mode is characterized by torsional or twisting moments along the length of the blade. In addition, the third and fourth vibration modes have a second- or higher-order bending moment and coupled bending and torsional moments, respectively. It should be noted in Figure 18c that the third higher-order bending vibration mode results in a greater curvature along the length of the blade compared to Figure 18a. The dynamic behavior of the fourth complex vibration mode, which involves both bending and torsion, can be explained as a combination of the effects of the hydrodynamic forces exerted by the incoming fluid and the structural response to the torsional moments generated by the fluid. Although the vibration modes for structural steel have high frequencies, the mass of the water surrounding the turbine blades increases the inertia, which reduces the obtained natural frequencies of the turbine.
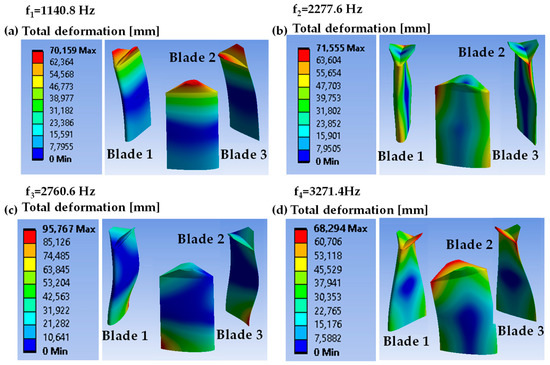
Figure 18.
(a–d) Total deformation and first (f1), second (f2), third (f3), and fourth (f4) natural frequencies and associated vibration modes for structural steel, respectively. A comma denotes a decimal sign.
Natural frequencies and vibration modes using PEEK are shown in Figure 19a–d. Lower natural frequencies were obtained when the blades were simulated with PEEK, compared to structural steel. Considering that the blades behave as beams, this can be attributed to the fact that the natural frequency of the blades (fi) is directly proportional to the ratio of the elastic modulus (E) to the density of the material (ρ), i.e., fi E/ρ, which is higher for steel compared to PEEK. Moreover, the difference in the density of both materials causes variation in mass distribution along the length of the blades, which modifies the shape of the vibration mode. For instance, by comparing Figure 19b with Figure 18b, it can be observed that the second vibration mode of PEEK closely resembles the first vibration mode (Figure 19a), which is primarily bending. In contrast, for structural steel, both bending and torsional moments are dominant, as shown in Figure 18a,b. Unlike structural steel, whose first and second natural frequencies are significantly separated (almost by a factor of two), the natural frequencies of PEEK are relatively close to each other. This explains why the second vibration mode looks similar to the first mode instead of resembling a fully torsional one. Based on the lower natural frequencies obtained for PEEK compared to structural steel, even in the scenario where the rotor becomes excited at the first natural frequency (approximately 1.8 × 104 rpm), it is possible that the damping offered by the water will limit the amplitude of the deformation of the blades during resonance, limiting its harmful dynamic effects. In this context, several studies have shown that the effect of added mass (the mass of the fluid surrounding the turbine) and the hydrodynamic damping provided by the flow significantly impact the structural behavior of the turbine near resonance. For instance, it has been shown that high-velocity fluids with significant inertia effectively reduce the structure’s vibration amplitudes at the onset of resonance, acting as a damper [51,52,53,54,55,56,57,58].
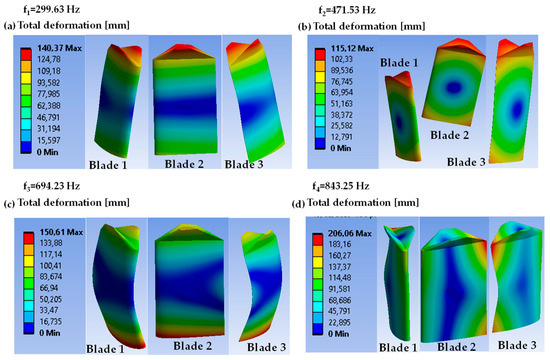
Figure 19.
(a–d) Total deformation and first (f1), second (f2), third (f3), and fourth (f4) natural frequencies and associated vibration modes for PEEK, respectively. A comma denotes a decimal sign.
5. Summary and Conclusions
A fluid–structure interaction (FSI) study was performed for a straight-blade Darrieus VAHT with winglets. The current analysis builds upon a previous study focused on a sensibility analysis study of the winglet design, which demonstrated that a symmetric winglet configuration with cant and sweep angles of 45° and 60°, respectively, yielded the highest average power coefficient at a tip speed ratio λ = 1. Using this geometric configuration and the same flow parameters from that study, the hydrodynamic forces were transferred to the structure using a one-way coupling approach, leading to the following conclusions:
- The sliding mesh method was successfully employed to transfer the hydrodynamic loads to the VAHT blades to perform the FSI study using a cyclic zero-based fatigue loading with the Goodman theory and the S-N method.
- Structural steel, SGFRC, and PEEK were used as materials to simulate the fatigue behavior of the VAHT blades. While SGFRC displayed poor structural behavior and fatigue resistance, structural steel and PEEK performed very well. Their equivalent alternating von Mises stresses remained well below their yield and fatigue strength during one azimuthal rotation, indicating an infinite fatigue life under the conditions of the current study. An equivalent alternating von Mises stress of half of the main principal stress was found during one azimuthal rotation, mainly related to the nature of the zero-based loading scenario ( = /2).
- The biaxiality index () was employed to understand the most dominant stresses in the winglet and the blade span regions during one azimuthal rotation. It was found that tension–compression bending stresses () were the predominant stresses along the blade, which operates as a cantilever beam under the current boundary conditions. However, shear stresses induced by the torsional moments and shedding vortex () were also observed in both regions (winglet and blade span), along with localized biaxial stresses. Unlike biaxial stresses (), which shift along the winglet’s surface with the blade’s azimuthal rotation, shear stresses only change between 120° and 240°. Variations in biaxial stresses are due to changes in the radial and tangential (or circumferential) normal stress components. In contrast, those of shear stresses are related to the variation of the lift and drag coefficients between 120° and 240°.
- The modal analysis of the blades in the first to fourth vibration modes of the best-performing materials (structural steel and PEEK) not only showed higher natural frequencies but also distinct bending, torsional, higher-order bending, and bending-torsional coupled modes for structural steel. Natural frequencies for PEEK were lower than those of structural steel, with the first and second modes having close values.
- Future experimental studies need to be performed to understand the effect of the added mass and the fluid damping on the dynamic response of the VAHT in the vicinity of resonance.
- Numerical simulations employing two-way coupling FSI are planned in the near future.
Future research will encompass the construction and experimental testing of a turbine prototype with the proposed winglets to validate the numerical findings presented in this study. On the other hand, additional experimental studies need to be performed to understand the effect of the added mass and the fluid damping on the dynamic response of the VAHT in the vicinity of resonance.
Author Contributions
Conceptualization, E.E.N., J.P.C.R., S.L. and O.D.L.; methodology, E.E.N., J.P.C.R., S.L. and O.D.L.; software, E.E.N. and D.G.G.; validation, E.E.N., D.G.G. and S.L.; formal analysis, E.E.N., D.G.G. and S.L.; investigation, E.E.N., D.G.G., S.L. and O.D.L.; resources, O.D.L. and S.L.; data curation, D.G.G. and S.L.; writing—original draft preparation, E.E.N.; writing—review and editing, S.L., E.E.N. and O.D.L.; visualization, D.G.G. and S.L.; supervision, E.E.N. and S.L.; project administration, E.E.N.; funding acquisition, E.E.N. and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
Vicerrectoría de Investigación, Innovación y Emprendimiento of Universidad Autónoma de Occidente through the research project 22INTER-411.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon reasonable request from the corresponding author.
Acknowledgments
The financial support of Vicerrectoría de Investigación, Innovación y Emprendimiento of Universidad Autónoma de Occidente is gratefully acknowledged. This work was also supported by Vicerrectoria de Investigaciones of Universidad de los Andes. M.A. Hidalgo is also sincerely acknowledged for his valuable discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kusakana, K.; Vermaak, H.J. Hydrokinetic power generation for rural electricity supply: Case of South Africa. Renew. Energy 2023, 55, 467–473. [Google Scholar] [CrossRef]
- Niebuhr, C.M.; van Dijk, M.; Neary, M.V.; Bhagwan, J.N. A review of hydrokinetic turbines and enhancement techniques for canal installations: Technology, applicability and potential. Renew. Sustain. Energy Rev. 2019, 113, 109240. [Google Scholar] [CrossRef]
- Pandey, B.; Karki, A. Hydroelectric Energy: Renewable Energy and the Environment; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Ridgill, M.; Neill, S.P.; Lewis, M.J.; Robins, P.E.; Patil, S.D. Global riverine theoretical hydrokinetic resource assessment. Renew. Energy 2021, 174, 654–665. [Google Scholar] [CrossRef]
- Zomers, A. The challenge of rural electrification. Energy Sustain. Dev. 2003, 7, 69–76. [Google Scholar] [CrossRef]
- Santos, L.F.S.D.; Camacho, R.G.R.; Tiago Filho, G.H.; Botan, A.C.B.; Vinent, B.A. Energy potential and economic analysis of hydrokinetic turbines implementation in rivers: An approach using numerical predictions (CFD) and experimental data. Renew. Energy 2019, 143, 648–662. [Google Scholar] [CrossRef]
- Henrique Da Costa Oliveira, C.; De Lourdes Cavalcanti Barros, M.; Alves Castelo Branco, D.; Soria, R.; Cesar Colonna Rosman, P. Evaluation of the hydraulic potential with hydrokinetic turbines for isolated systems in locations of the Amazon region. Sustain. Energy Technol. Assess. 2021, 45, 101079. [Google Scholar] [CrossRef]
- Lain, S.; Contreras, L.T.; López, O.D. A review on computational fluid dynamics modeling and simulation of horizontal axis hydrokinetic turbines. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 375. [Google Scholar] [CrossRef]
- Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Appl. Energy 2009, 86, 1823–1835. [Google Scholar] [CrossRef]
- Vermaak, H.J.; Kusakana, K.; Koko, S.P. Status of micro-hydrokinetic river technology in rural applications: A review of literature. Renew. Sustain. Energy Rev. 2014, 29, 625–633. [Google Scholar] [CrossRef]
- Dewan, A.; Tomar, S.S.; Bishnoi, A.K.; Singh, T.P. Computational fluid dynamics and turbulence modelling in various blades of Savonius turbines for wind and hydro energy: Progress and perspectives. Ocean Eng. 2023, 283, 115168. [Google Scholar] [CrossRef]
- Ferrari, G.; Federici, D.; Schito, P.; Inzoli, F.; Mereu, R. CFD study of Savonius wind turbine: 3D model validation and parametric analysis. Renew. Energy 2017, 105, 722–734. [Google Scholar] [CrossRef]
- Alizadeh, H.; Jahangir, M.H.; Ghasempour, R. CFD-based improvement of Savonius type hydrokinetic turbine using optimized barrier at the low-speed flows. Ocean Eng. 2020, 202, 107178. [Google Scholar] [CrossRef]
- Tantichukiad, K.; Yahya, A.; Mohd Mustafah, A.; Mohd Rafie, A.S.; Mat Su, A.S. Design evaluation reviews on the savonius, darrieus, and combined savonius-darrieus turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2023, 237, 1348–1366. [Google Scholar] [CrossRef]
- Kamal, M.M.; Saini, R.P. A numerical investigation on the influence of savonius blade helicity on the performance characteristics of hybrid cross-flow hydrokinetic turbine. Renew. Energy 2022, 190, 788–804. [Google Scholar] [CrossRef]
- Patel, V.; Eldho, T.I.; Prabhu, S.V. Experimental investigations on Darrieus straight blade turbine for tidal current application and parametric optimization for hydro farm arrangement. Int. J. Mar. Energy 2017, 17, 110–135. [Google Scholar] [CrossRef]
- Buchner, A.J.; Soria, J.; Honnery, D.; Smits, A.J. Dynamic stall in vertical axis wind turbines: Scaling and topological considerations. J. Fluid Mech. 2018, 841, 746–766. [Google Scholar] [CrossRef]
- López, O.D.; Mejía, O.E.; Escorcia, K.M.; Suárez, F.; Lain, S. Comparison of sliding and overset mesh techniques in the simulation of a vertical axis turbine for hydrokinetic applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
- Raciti Castelli, M.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Nobile, R.; Vahdati, M.; Barlow, J.F.; Mewburn-Crook, A. Unsteady flow simulation of a vertical axis augmented wind turbine: A two-dimensional study. J. Wind. Eng. Ind. Aerodyn. 2014, 125, 168–179. [Google Scholar] [CrossRef]
- Ramesh, K.; Gopalarathnam, A.; Granlund, K.; Ol, M.V.; Edwards, J.R. Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding. J. Fluid Mech. 2014, 751, 500–538. [Google Scholar] [CrossRef]
- Hoerner, S.; Abbaszadeh, S.; Maître, T.; Cleynen, O.; Thévenin, D. Characteristics of the fluid–structure interaction within Darrieus water turbines with highly flexible blades. J. Fluids Struct. 2019, 88, 13–30. [Google Scholar] [CrossRef]
- Ghiss, M.; Bahri, Y.; Souaissa, K.; Troudi, H.; Ting, D.S.K.; Tourki, Z. Enhancing Vertical Axis Wind Turbine Performance Using Winglets. In International Conference Design and Modeling of Mechanical Systems; Springer: Cham, Switzerland, 2021; pp. 323–334. [Google Scholar] [CrossRef]
- Xu, W.; Li, G.; Wang, F.; Li, Y. High-resolution numerical investigation into the effects of winglet on the aerodynamic performance for a three-dimensional vertical axis wind turbine. Energy Convers. Manag. 2020, 205, 112333. [Google Scholar] [CrossRef]
- Narayan, G.; John, B.B. Effect of winglets induced tip vortex structure on the performance of subsonic wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Lain, S.; Taborda, M.A.; López, O.D. Numerical Study of the Effect of Winglets on the Performance of a Straight Blade Darrieus Water Turbine. Energies 2018, 11, 297. [Google Scholar] [CrossRef]
- Guillaud, N.; Balarac, G.; Goncalvès, E.; Zanette, J. Large Eddy Simulations on Vertical Axis Hydrokinetic Turbines-Power coefficient analysis for various solidities. Renew. Energy 2020, 147, 473–486. [Google Scholar] [CrossRef]
- Ye, J.; Zhou, H.; He, K. A generalized framework of two-way coupled numerical model for fluid-structure-seabed interaction (FSSI): Explicit algorithm. Eng. Geol. 2024, 340, 107679. [Google Scholar] [CrossRef]
- Hoseini, S.S.; Najafi, G.; Ghobadian, B.; Akbarzadeh, A.H. Impeller shape-optimization of stirred-tank reactor: CFD and fluid structure interaction analyses. Chem. Eng. J. 2021, 413, 127497. [Google Scholar] [CrossRef]
- Benra, F.K.; Dohmen, H.J.; Pei, J.; Schuster, S.; Wan, B. A Comparison of One-Way and Two-Way Coupling Methods for Numerical Analysis of Fluid-Structure Interactions. J. Appl. Math. 2011, 2011, 853560. [Google Scholar] [CrossRef]
- Li, F.; Fu, J.; Chen, J.; Hu, D. Two-way coupling fluid–structure interaction analysis on dynamic response of offshore wind turbine. Mar. Georesources Geotechnol. 2024, 42, 1677–1686. [Google Scholar] [CrossRef]
- Dörfler, P.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Pozarlik, A.K.; Kok, J.B.W. Numerical investigation of one- and two-way fluid-structure interaction in combustion systems. In International Conference on Computational Methods for Coupled Problems in Science and Engineering–COUPLED PROBLEMS; CIMNE: Barcelona, Spain, 2007; pp. 610–614. [Google Scholar]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind. Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef]
- Kang, Y.S.; Sohn, D.; Kim, J.H.; Kim, H.G.; Im, S. A sliding mesh technique for the finite element simulation of fluid–solid interaction problems by using variable-node elements. Comput. Struct. 2014, 130, 91–104. [Google Scholar] [CrossRef]
- Trivedi, C. A review on fluid structure interaction in hydraulic turbines: A focus on hydrodynamic damping. Eng. Fail. Anal. 2017, 77, 1–22. [Google Scholar] [CrossRef]
- López, O.D.; Botero, N.; Nunez, E.E.; Lain, S. Performance Improvement of a Straight-Bladed Darrieus Hydrokinetic Turbine through Enhanced Winglet Designs. J. Mar. Sci. Technol. 2024, 12, 977. [Google Scholar] [CrossRef]
- Yagmur, S.; Kose, F.; Dogan, S. A study on performance and flow characteristics of single and double H-type Darrieus turbine for a hydro farm application. Energy Convers. Manag. 2021, 245, 114599. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. CFD simulation of a vertical axis wind turbine operating at a moderate tip speed ratio: Guidelines for minimum domain size and azimuthal increment. Renew. Energy 2017, 107, 373–385. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Badshah, M.; Badshah, S.; VanZwieten, J.; Jan, S.; Amir, M.; Malik, S.A. Coupled Fluid-Structure Interaction Modelling of Loads Variation and Fatigue Life of a Full-Scale Tidal Turbine under the Effect of Velocity Profile. Energies 2019, 12, 2217. [Google Scholar] [CrossRef]
- Biswas, R.; Sharma, N.; Singh, K.K. Numerical analysis of mechanical and fatigue behaviour of glass and carbon fibre reinforced polymer composite. Mater. Today Proc. 2023, 3, 479. [Google Scholar] [CrossRef]
- Shrestha, R.; Simsiriwong, J.; Shamsaei, N.; Moser, R.D. Cyclic deformation and fatigue behavior of polyether ether ketone (PEEK). Int. J. Fatigue 2016, 82, 411–427. [Google Scholar] [CrossRef]
- Rae, P.J.; Brown, E.N.; Orler, E.B. The mechanical properties of poly(ether-ether-ketone) (PEEK) with emphasis on the large compressive strain response. Polymer 2007, 48, 598–615. [Google Scholar] [CrossRef]
- Nunez, E.E.; Gheisari, R.; Polycarpou, A.A. Tribology review of blended bulk polymers and their coatings for high-load bearing applications. Tribol. Int. 2019, 129, 92–111. [Google Scholar] [CrossRef]
- Chen, F.; Gatea, S.; Ou, H.; Lu, B.; Long, H. Fracture characteristics of PEEK at various stress triaxialities. J. Mech. Behav. Biomed. Mater. 2016, 64, 173–186. [Google Scholar] [CrossRef]
- Abbasnezhad, N.; Khavandi, A.; Fitoussi, J.; Arabi, H.; Shirinbayan, M.; Tcharkhtchi, A. Influence of loading conditions on the overall mechanical behavior of polyether-ether-ketone (PEEK). Int. J. Fatigue 2018, 109, 83–92. [Google Scholar] [CrossRef]
- Zago, A.; Springer, G.S. Constant Amplitude Fatigue of Short Glass and Carbon Fiber Reinforced Thermoplastics. J. Reinf. Plast. Compos. 2001, 20, 564–595. [Google Scholar] [CrossRef]
- Mortazavian, S.; Fatemi, A. Fatigue behavior and modeling of short fiber reinforced polymer composites: A literature review. Int. J. Fatigue 2015, 70, 297–321. [Google Scholar] [CrossRef]
- Trivedi, C.; Cervantes, M.J. Fluid-structure interactions in Francis turbines: A perspective review. Renew. Sustain. Energy Rev. 2017, 68, 87–101. [Google Scholar] [CrossRef]
- Ali, S.; Park, H.; Lee, D. Structural Optimization of Vertical Axis Wind Turbine (VAWT): A Multi-Variable Study for Enhanced Deflection and Fatigue Performance. J. Mar. Sci. Eng. 2025, 13, 19. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Liu, X.; Presas, A.; Deng, L.; Zhao, W.; Xia, M.; Wang, Z. Numerical theory and method on the modal behavior of a pump-turbine rotor system considering gyro-effect and added mass effect. J. Energy Storage 2024, 85, 111064. [Google Scholar] [CrossRef]
- Luo, W.; Liu, W.; Chen, S.; Zou, Q.; Song, X. Development and Application of an FSI Model for Floating VAWT by Coupling CFD and FEA. J. Mar. Sci. Eng. 2024, 12, 4. [Google Scholar] [CrossRef]
- Urban, O.; Pochylý, F.; Habán, V. Estimation of added effects and their frequency dependence in various fluid–structure interaction problems. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 631. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, W.; Dong, Y.; Xue, D. Resonance mechanism of flapping wing based on fluid structure interaction simulation. Chin. J. Aeronaut. 2024, 37, 243–262. [Google Scholar] [CrossRef]
- Yusuf, A.O.; Hasan, M.A.; Khalil, E. Vibration mitigation of wind turbines with tuned liquid damper using fluid-structure coupling analysis. Int. J. Dynam. Control 2024, 12, 3517–3533. [Google Scholar] [CrossRef]
- Lain, S.; Garcia, M.J.; Quintero, B.; Orrego, S. CFD numerical simulations of Francis turbines. Rev. Fac. Ing. Univ. Antioquia 2010, 51, 31–40. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).