Next Article in Journal
The Mooring Optimization and Hydrodynamic Characteristics of the Combined Concept of a 15 MW FOWT with WECs
Previous Article in Journal
Vibroacoustic Response of a Disc-Type Underwater Glider During Its Entry into Water
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 13
Issue 3
10.3390/jmse13030546
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantitative Analysis of Bound Water Content in Marine Clay and Its Influencing Factors During the Freezing Process by Nuclear Magnetic Resonance

by
Xuehan Shan
1,†,
Huie Chen
1,†,
Chuqiao Meng
2,
Zuojun Lv
3,
Qingbo Yu
1,
Zhaoxi Wang
1 and
Qing Wang
1,*
1
College of Construction Engineering, Jilin University, Changchun 130026, China
2
School of Civil Engineering and Transportation, Northeast Forestry University, Harbin 150090, China
3
Power China Northwest Survey Design and Research Institute Co., Ltd., Xi’an 710065, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
J. Mar. Sci. Eng. 2025, 13(3), 546; https://doi.org/10.3390/jmse13030546
Submission received: 11 February 2025 / Revised: 3 March 2025 / Accepted: 6 March 2025 / Published: 12 March 2025
Browse Figures
Review Reports Versions Notes

Abstract

:
The change in bound water content with temperature is a core issue in studying temperature effects in clayey soils. This study used nuclear magnetic resonance (NMR) techniques to measure pore water in three types of marine clay, ranging from inland to coastal areas. The T2 cutoff values were proposed to distinguish between bulk water, capillary water, and bound water, and the curves of unfrozen water and bound water content with changing temperatures were obtained during the freezing process. Additionally, the impact of soil properties on bound water content was analyzed. The research findings indicated that the pore water in marine clay is dominated by bound water, and the change in bound water content with temperature in each soil layer can be divided into four stages: the trace phase change stage, the intense phase change stage, the transitional phase change stage, and the stabilizing stage. Further, the effect of soil properties such as organic matter content, soluble salt content, and cation exchange capacity on bound water content was illustrated, and clay content and bound water content were found not to be strictly positively correlated.

1. Introduction

Recently, with the rapidly growing economy and construction, world land resources have become scarce, and reclamation projects have become a new means of urbanization. Therefore, marine soft clay soil foundations are widely used in engineering [1,2]. Yet, engineering and geological problems have gradually emerged. Marine clay, characterized by a high content of clay particles, elevated water content, and numerous pores, exhibits significant compressibility and low bearing capacity. These properties contribute to pronounced creep behavior in clay, resulting in settlement deformations that can lead to severe safety incidents [3]. Pores of clay contain large amounts of bound water, which enables the soil to have complex physical and mechanical properties [4,5]. Furthermore, variations in both the composition and quantity of bound water influence the hydration behavior of clay particles, resulting in different properties of soil [6]. As mentioned above, marine clay raises many geological problems due to its properties and brings many challenges to marine clay engineering. Therefore, determining the boundary values of different kinds of pore water in soil not only helps to explore the hydration mechanism of clay but also plays a protective role in geotechnical engineering [7].
The water present in the soil pores can be categorized based on its state and properties into three types: bulk water, capillary water, and bound water. Water is attracted to the surface of soil particles by the electrostatic force called bound water [6,8]. According to the distance and the interaction forces between water and soil particles, bound water can further be classified into loosely bound water (LBW) and tightly bound water (TBW) [9]. The characteristics of bound water are quite different from those of those of bulk water [10]. Numerous previous studies have shown that bound water significantly affects the physical properties of soils, like specific heat capacity [11], dielectric constant [12,13,14], freezing point [15,16], as well as mechanical properties, e.g., deformation properties [17], permeability [18,19], and strength [20,21]. Research on the properties and occurrence states of bound water in marine clays is limited. Therefore, it is crucial to study and quantitatively analyze the characteristics of bound water in clay.
In previous studies, the methods to measure bound water content include the centrifugal setting method [22,23], X-ray diffraction (XRD) method [24,25], volumetric flask method [2], dilatometric method [26,27,28], and differential scanning calorimetry (DSC) method [29,30]. While these methods are widely used, they have some limitations. The principle of the DSC method is to measure the heat released by the soil sample as it cools and thereby calculate the unfrozen water content, offering fast measurement but interfering with the samples [31,32]. The volumetric flask method, centrifugal setting method, and dilatometric method are less accurate and are prone to artificial errors [22], while the XRD method is mainly used for qualitative measurements of bound water [6]. Until now, many new methods have been proposed to quantitatively classify the bound water content, such as the time domain reflectometry (TDR) method [28,33,34], isothermal adsorption experiments (IAEs) [6,35], the nuclear magnetic resonance (NMR) method [36,37,38] and thermogravimetric analysis (TGA) [35,39]. The TDR method determines the dielectric constant, and thereby calculates the unfrozen water content in soil, while the IAE method has been extensively used to characterize clay–water interaction. NMR method and TGA method are accurate and precise, and will not damage the samples. However, the TGA method lacks the unified classification standard of TBW and LBW [39].
In addition to experimental methods, there are numerous models available for calculating the unfrozen water content of soil, thus contributing to the quantitative analysis of bound water. A model to predict volumetric water content based on soil temperature was developed by Zhang et al. [40]. Anderson and Kozlowski [41,42] proposed some gravimetric models for calculating unfrozen water content by changing temperatures. An exponential function model about saturation and temperature has been obtained by McKenzie et al. [43]. Moreover, deriving the relationship between soil microstructure and pore water through thermodynamic models has become a hot issue in soil–water research recently. Xiao et al. [44] proposed a thermodynamic model for predicting unfrozen water content, established an empirical equation between unfrozen water content and pore radius, and illustrated the phase change mechanism of frozen soil from a thermodynamic point of view. Yang et al. [45] proposed a thermodynamic model based on solid mechanics that can be used to describe the mechanical characteristics and temperature effects of fine-grained gassy soils. Li et al. [46] developed a thermodynamic model of freeze nucleation in saline soils to quantify the supercooling and freeze crystallization properties of saline soils in cold regions. In summary, the thermodynamic model can relate the microstructure to the soil–water interactions, reveal the mechanism of soil–water interactions during the freezing process, and then quantitatively predict the amount of unfrozen water in the soil. However, the selection and determination of parameters in thermodynamic models is often a complex and difficult process. Due to the complexity and diversity of soils, the thermodynamic parameters of different soils may differ significantly. Therefore, in this paper, the NMR test is selected and combined with SEM images to quantitatively analyze the bound water content in marine clay and qualitatively analyze the effect of microstructure, so that it can reveal the change behavior of bound water during the freezing process of marine clay in a more comprehensive perspective.
To study the factors affecting bound water content in the soil, this paper selected three locations for sampling work from inland to the coastal direction in Chongming Island, Shanghai (Figure 1). The soil samples’ bound water content was measured by the NMR technique.

2. Materials and Methods

2.1. NMR Method

NMR is a physical phenomenon triggered by the spin motion of atomic nuclei in the presence of a magnetic field. The hydrogen nucleus (1H) exhibits exceptionally high sensitivity during NMR in a dual magnetic field, resulting in substantial and stable NMR signals. Consequently, hydrogen nuclei are the preferred choice for NMR testing.
Before the application of a magnetic field, the orientation of the spin axis of 1H is random, and when applied with a static magnetic field, the spin axis direction of 1H is the same as that of the static magnetic field. Once the static magnetic field is removed, collisions among hydrogen nuclei occur, resulting in energy release. Subsequently, the hydrogen nuclei return to a stable state where their magnetic moments cancel each other out [47]. In this process, the 1H population produces a gradually decaying oscillation signal, which is the FID signal. This signal oscillates with a sinusoidal law and decays with an exponential law, thus forming a curve known as the free induction decay (FID) curve. The time required for the macroscopic magnetization intensity to decrease to zero in the direction perpendicular to the static magnetic field during this process is known as the transverse relaxation time (T2). Therefore, the FID signal is closely related to T2, and the FID curve can be transformed by Fourier transformation to generate T2 distribution curves.
The signal intensity of the FID curves correlates with the amount of 1H, so it can reflect the pore water content in the soil. The T2 value of water molecules depends closely on the size of the pores where water molecules exist, and the relationship equation between the two is [48]:
1 T 2 ≈ ρ 2 S V
where ρ 2 is the transverse relaxation rate, a constant related to the sample properties; S is the area of water-saturated pores; and V is the volume of water-saturated pores. If the pore shape in the soil is considered as spherical, the equation can be expressed as:
1 T 2 ≈ ρ 2 3 R
where R is the pore radius. It can be found that T2 is proportional to R. When water molecules are situated in larger pores, the value of T2 increases. Therefore, T2 can be utilized to differentiate between bulk water, capillary water, and bound water within the soil.

2.2. Soil Samples

Soil from southeast Chongming Island, Shanghai, China, was sampled and used in the study. Chongming Island is a typical multi-phase reclamation area, with the reclamation project gradually expanding from west to east [49]. To better investigate the differences of samples in different locations, drilling sampling was conducted at three sampling sites (A, B, and C) located in different reclamation areas from west to east, as shown in Figure 1. Within each borehole, the mucky clay, clay, and silty clay were taken as the research objects, and the soil samples were named as shown in Table 1. All soil samples were taken from a depth of 0–55 m, wax-sealed, and then wrapped in cling film.
Part of the soil samples were air-dried, passed through a 2 mm sieve, and prepared for property testing, as shown in Table 2. As shown in Table 2, the water content of mucky clay and clay layers in the study area is relatively high, with 40.81–45.88% for silty clay, 39.22–46.63% for clay, while the water content of silty clay is relatively low, ranging from 29.18 to 37.93%. However, the density of silty clay is greater than that of mucky clay and clay, where the density of silty clay is 1.8–2.05 g/cm3, the density of silty clay is 1.75–1.83 g/cm3, and the density of clay is 1.78–1.83 g/cm3.

2.3. NMR Test

The original soil samples were made into cylinders 25 mm in diameter and 60 mm in height, and then put into the NMR system’s (Suzhou Niumag Analytical Instrument Corporation, Suzhou, China) sample chamber. The temperature of the sample is controlled by jointly utilizing high-temperature heating instruments and cooling devices to regulate the temperature of the liquid surrounding the sample chamber. The temperature of the sample is set: 5 °C, 2 °C, 0 °C, −0.5 °C, −1 °C, −1.5 °C, −2 °C, −3 °C, −5 °C, −7 °C, and −15 °C. At each temperature set point, data were collected after 1 h of stabilization and inverted to obtain T2 distribution curves.

3. Results and Discussion

3.1. Determination of T2 Cutoff Values for Different Types of Pore Water in Soils

In order to investigate the content and variations of different kinds of pore water in soil, it is important to determine cutoff points between the components. T2 can be used as an important indicator in NMR tests to differentiate between different types of pore water in the soil. Since the interactions between soil particles and pore water decrease as the distance between them increases, pore water relaxes faster in smaller pores. In other words, water present in larger pores corresponds to a higher T2 value, while water present in smaller pores corresponds to a lower T2 value [38]. Similarly, in water with weaker adsorption, such as bulk water and capillary water, the T2 value is relatively high; conversely, TBW and LBW exhibit lower T2 values due to their stronger adsorption characteristics.
Previous studies exist that use T2 cutoff values to differentiate the types of pore water. Dastidar [50] proposed that the T2 cutoff value is less than 1 ms for bound water, 1–10 ms for capillary water, and greater than 10 ms for bulk water. Bayer and Bird et al. [51,52] considered the T2 cutoff values for micropores to be less than 60 ms, for mesopores to be 60–300 ms, and for macropores to be greater than 300 ms. Jaeger et al. [53] stated that the T2 cutoff value for bound water in frozen soils is 0.9–1.1 ms in their latest study. Recent studies [54] proposed three T2 cutoff values to distinguish TBW, LBW, capillary, and bulk water. An et al. [55] used two T2 cutoff values for classifying various pore water types in the soil.
It is worth noting that the T2 cutoff value for pore water in different soils is different. Furthermore, it has been proposed [56] that when temperatures drop below −5 °C, all pore water in the soil is bound water. To better determine the bound water content in marine clays, T2 cutoff values for bound water were proposed for a wide range of freezing temperatures from 5 °C to −15 °C. For all the tests in this paper, we ensured that all samples were measured three times repeatedly, the results were averaged, and the standard deviations were all less than 1.
The T2 distribution curves for all soil samples during the freezing process are presented in Figure 2. The peak area of the curve represents the content of unfrozen water in the soil, which decreases gradually as the temperature decreases. When the temperature varies within a positive range, there is little change in peak area, indicating that water in the soil remains largely unfrozen. As the temperature decreases from 0 °C to −3 °C, the peak area decreases gradually, indicating that the bulk water starts to freeze. As the temperature continuously decreases from −3 °C to −7 °C, the peak area decreases slowly, at this stage, most bulk water has frozen into ice and LBW begins to freeze. When the temperature changes from −7 °C to −15 °C, the peak area almost remains stable, indicating that most of the LBW has finished freezing, and the remaining unfrozen water is almost TBW. However, the variation of the maximum T2 value and the peak area is different. When the temperature drops gradually from 5 °C, the maximum T2 value also decreases gradually until the temperature drops to about −3 °C, while the maximum T2 value is almost unchanged.
The surface of soil particles generally carries negative charges, and these negative charges create an electric field around the soil particles. Polar water molecules can be attracted and oriented by the charges on the surface of the soil particles. Therefore, when water molecules are close to the surface of the negatively charged soil particles, they are attracted by the electrostatic force of the electric field, and the closer the distance, the stronger the electrostatic force. The distance between the bound water and the soil particles is short, so the bound water is tightly adsorbed on the surface of the soil particles by the electrostatic force. This kind of force makes the molecular arrangement of the bound water orderly and with high thermodynamic potential energy. From the perspective of melting, bound water in micropores, with higher thermodynamic potential energy and a lower freezing point, melts before capillary water and bulk water. At this time, the maximum T2 value remains relatively unchanged, although the peak area increases gradually. When the maximum T2 value starts to increase, it indicates that capillary water begins to occur in the soil pores, and when the T2 maximum value increases dramatically, it indicates that bulk water begins to appear in the pores of the soil. Therefore, in this paper, the maximum T2 value, which is relatively stable at temperatures below −3 °C, is used as the cutoff point to distinguish bound water and capillary water. According to Figure 2, the T2 cutoff value for mucky clay is 2.81–3.01 ms; the T2 cutoff value for clay is 2.85–3.37 ms; and the T2 cutoff value for silty clay is 3.10–4.06 ms. It can be concluded that in the marine clay, the T2 cutoff value of bound and capillary water ranges between 2.81 and 4.06 ms. Notably, the mucky clay particles are arranged more densely, the pore volume is smaller, and so is the T2 cutoff value. Meanwhile, the silty clay particles are more loosely arranged, the pore volume is larger, and the T2 cutoff value is also larger.

3.2. Changing Behavior of Bound Water Content and Unfrozen Water Content

Based on the above analysis, we propose that when relaxation time is shorter than the T2 cutoff value, all pore water in the soil is bound water. Conversely, when relaxation time exceeds the T2 cutoff value, capillary water begins to occur in the soil pores. The entire area encircled by the curve and the axis represents all unfrozen water in the soil. Calculation of the bound water content ( θ b ) can be determined by the ratio of the area enclosed by the curve on the left side of the T2 cutoff value to the peak area, and the calculation of the unfrozen water content ( θ u ) requires first determining the total pore water content of the soil before freezing.
The initial magnetization (M0) indicates the current content of pore water, which is numerically equal to the peak area of the FID curve. Therefore, the unfrozen water content can be determined at a particular temperature by the ratio of the peak area of the FID curve under negative to positive temperature conditions. However, as the water molecule activity decreases with decreasing temperature, the M0 measured by the NMR test will be different even at positive temperatures, so a temperature correction for M0 is necessary based on Curie’s law [57,58]. The calibrated M0 (calculated) is the total pore water content of the soil before freezing. By selecting the peak area of NMR signals at various positive temperatures for fitting, a linear relationship between temperature and M0 was observed:
M 0 = α − β T
where α and β are fitting parameters. The fitting results are shown in Figure 3.
The M0 (calculated) at negative temperatures can be extrapolated from the fitting results, so the unfrozen water content at a particular temperature can be calculated by the following equation:
θ u = M 0 ( m e a s u r e d ) M 0 ( c a l c u l a t e d ) V ω
where θ u is the content of unfrozen water in the soil, and V ω is the initial volumetric content of pore water in the soil.
The changes in unfrozen water content as well as bound water content during the freezing process of all the original soil samples are given in Figure 4a–f. The changes in unfrozen and bound water contents for the same soil sample are similar. Consequently, all curves can be roughly divided into four stages.
In the first stage, the temperature is greater than −2 to −2.5 °C, and the curve shape remains mostly unchanged. The soil gradually cools from the initial temperature, and when it reaches the freezing point, due to the existence of the phenomenon of “supercooling” [59], most of the pore water in the soil remains in a metastable state that has not yet crystallized into nuclei, and only a small portion of the water freezes into ice. Therefore, this stage can be referred to as the trace phase change stage, where the unfrozen water content and the bound water content of the soil are both close to their respective initial water contents. When the temperature drops below the freezing point, the content of unfrozen water and bound water in the soil sharply decreases until the temperature reaches −5 °C, at which point the second stage ends. At this stage, the temperature reaches freezing point, nuclei are formed in the soil with soil particles as the crystallization centers, and most of the bulk water and LBW in the soil freezes into ice. This stage can also be referred to as the intense phase change stage. When the temperature continues to drop between −5 °C and −7 °C, the curve enters the third stage, also called the transitional phase change stage. The content of unfrozen water and bound water in the soil decreases slowly, and the remaining unfrozen water in the soil transitions from being dominated by weakly bound water to being dominated by strongly bound water. As temperatures fall below −7 °C, the unfrozen water in the soil is completely taken up by TBW. The film of TBW is extremely thin, making it difficult to freeze. At this stage, nearly all unfrozen water exists as bound water, with its content approaching zero. Thus, this stage can also be referred to as the stabilizing stage.
In addition, it can be found that the difference between unfrozen and bound water contents in soils with different initial water contents is significant at higher temperatures. As the temperature decreases, the impact of initial water content on the content of unfrozen water and bound water in the soil gradually decreases, and the curves tend to overlap. This indicates that while initial water content greatly affects the quantity of pore water within the soil, it does not significantly influence either the rate or trend of changes in pore water as temperature changes.

3.3. Influence of Clay Content on Bound Water Content

Clay particles usually have a negative charge on the surface due to selective adsorption, molecular dissociation on the surface, and isomorphous substitution. Negatively charged clay particles will attract polar water molecules, forming a layer of water film around them. The water film around the clay particles contains hydration ions (counterions) and water molecules serving as the main body, the counterions have the opposite charge to the clay particle surface. Therefore, this water film can be referred to as both the counterion layer and the bound water layer. Based on this charged capacity of the clay particles, the number of clay particles will significantly influence the content of bound water, which is confirmed by Zhang et al. [60].
The particle size distribution curves for different soil samples are given in Figure 2. Combined with the range of particle sizes and particle size distribution curves, the particles of the soil samples could be classified into three main categories [61]: clay (<5 μm), silt (5–75 μm), and sand (75–2000 μm). As can be seen in Figure 5, it can be seen that the clay content was highest in the mucky clay and lowest in the silty clay at each sampling site. The clay content of each soil sample is shown in Table 3.
At a temperature of 2 °C, the unfrozen water content of the soil was closest to the initial water content of the soil samples, so the bound water content in the soil at 2 °C was taken as the initial bound water content, and the ratio of the bound water to the total pore water in the soil, namely the bound water fraction (S), was calculated. It was found that the bound water fraction of each soil sample was greater than 80%, which indicates that the pore water in marine clay is dominated by bound water.
Variations in clay content and bound water fraction (S) of marine clays are plotted in Figure 6a,b. From Figure 6, it is evident that the mucky clay layer contains the highest clay content and the highest bound water fraction S (95.9–98.0%). The clay layer follows, with the bound water fraction S varying from 90.1% to 94.5%, while the silty clay layer has the lowest clay content and the lowest bound water fraction S (84.7–86.9%). This indicates that the bound water content increases with the increase in clay particles, which is due to the increase in clay particles leading to the enhancement of adsorption and cementation between particles. The above conclusion is in agreement with that of Mitchell [62] based on the Gouy–Chapman double-layer theory. However, for the same soil layers (specifically, the silty clay layer and clay layer), the trends of clay particle content and bound water fraction are not consistent, indicating that there is not a strict positive correlation between the content of bound water and clay particles. This phenomenon may be due to the differences in the microstructure of the soil.

3.4. Influence of Micro-Structure on Bound Water Content

The microstructure of clayey soils can greatly affect the adsorption of water by clay particles. Particle morphology, arrangement, pore size, and distribution all belong to the microstructure of the soil. To qualitatively analyze the microstructure of soil samples in each soil layer, SEM images of each soil sample at 2000× magnification were obtained, as illustrated in Figure 7a–i. In the images, the pores in the soil can be classified into four categories [63]: macropores (>4 μm), mesopores (0.4–4 μm), small pores (0.04–0.4 μm), and micropores (<0.04 μm).
From Figure 7a–c, it can be observed that for the mucky clay layer, mesopores dominate the pores of soil samples at point A, with a dispersed clay particle distribution and fewer aggregates, resulting in a greater specific surface area. Small pores dominate the pore distribution of the soil samples at point B, and clay particles mainly fill the voids among soil particles in the form of platy aggregates. In the pore spaces of the soil sample at point C, small pores and mesopores are prevalent, with through cracks, and the clay particles mainly exist in the form of blocky aggregates.
Figure 7d–f shows that the pore distribution of the clay layer is mainly dominated by small pores. In the soil sample at point A, there are fewer clay aggregates, which are mainly distributed on the surface of large particles and silt particles, with a greater contact area with the water molecules. At points B and C, the microstructure of soil samples tends to be an aggregate structure, with a larger number of clay particles aggregating together in the pore space.
From Figure 7g–i, in the silty clay layer, quartz and other large particles of primary minerals are relatively more prevalent, while mesopores and macropores are the most prevalent. The microstructure of the soil samples at points A and B is a framework–aggregate structure, while the soil samples at point C show a framework structure, and the structures are all relatively loose.
Since the bound water is influenced by the electrostatic attraction on the surface of soil particles, the distance between soil particles is positively correlated with the film thickness of bound water. When the distance between soil particles is beyond a certain threshold, not only does bound water exist between soil particles, but unbound water may also appear. Conversely, the smaller the distance between soil particles, the thinner the bound water film. Therefore, this paper suggests that the bound water content is also largely correlated with the pore distribution and size.
Meanwhile, Han et al. [61] considered that bound water film is also related to the specific surface area of the clay particles, the larger the specific surface area, the greater the area of the water film around the clay particles. Among different particle shapes, spherical particles have the smallest specific surface area, and flaky or platy particles have the largest specific surface area.
For the mucky clay layer, the bound water fraction tends to decrease consistently from inland to the coastal direction, although the clay particle content decreases first and then increases. The soil sample at point B contains a higher proportion of small pores and lower clay content, and the clay particles are mostly distributed in the pores as platy aggregates, while in the soil sample at point C, the blocky aggregates of the clay particles are more, with small specific surface area. Platy aggregates have a significantly larger specific surface area than blocky aggregates; therefore, the bound water fraction at point B is slightly higher than that at point C. The pores of the soil sample at point A are dominated by mesopores with a high content of clay particles. Clay particles at point A, however, are dispersed in the pores of soil and have a large specific surface area, resulting in the highest bound water fraction at point A, as shown in Figure 8.
For the clay layer, the clay content tends to increase from inland to coastal direction, but the bound water fraction decreases and then increases. As all the pores in the clay layer soil samples are dominated by small pores, the arrangement and clay particle content determine the bound water fraction in the clay layer. There are more blocky aggregates of clay particles in the soil samples at point B, which leads to a reduced contact area between clay particles and water molecules, so although the clay particles content of soil samples at point B is higher than that at point A, the bound water fraction is smaller. The clay particles in the soil sample at point C are also more aggregated, and the clay content is the highest, which holds the absolute advantage, so the soil sample at point C has the highest bound water fraction. This is shown in Figure 9.
For the silty clay layer, the trends of clay particle content and bound water fraction are consistent from inland to coastal directions. The soil structure of this layer is relatively loose, and the clay particles are mostly dispersed on the surface of large particles and in the pores, rarely forming aggregates. Therefore, the contact area between clay particles and water molecules is considerably large. The pores in the soil sample at point C are mostly macropores and the bound water film is thicker. Therefore, despite having the least clay particles and the smallest bound water fraction of the soil sample, the bound water fraction of the soil sample at point C is still close to that of the soil sample at point B, as shown in Figure 10.

3.5. Influence of Soil Properties on Bound Water Content

In addition to the strong attraction of clay particles to bound water, there is also a significant correlation between soil properties and the bound water content.

3.5.1. Effect of Organic Matter

The organic matter in marine clay is mainly composed of humic substances, including plant and animal residues, microorganisms, and their metabolites. Compared with clay particles, organic matter has strong surface activity and viscosity and is a hydrophilic substance. Its specific surface area and water absorption are much greater than kaolinite and illite, but lower than that of montmorillonite. Therefore, organic matter has obvious water absorption and water-holding capacities [64].
As can be seen from Figure 11a, the clay layer has the highest organic matter content, followed by the silty clay layer, and the mucky clay layer has the lowest organic matter content. Combined with Figure 11b, it can be known that the highest bound water fraction is found in the mucky clay layer and the lowest in the silty clay layer, indicating that organic matter is not the dominant factor affecting the content of bound water. However, for the same soil layer, the organic matter content of marine clay has a strong positive correlation with the bound water fraction, indicating that organic matter is highly hydrophilic. In other words, in the same soil layer, higher organic matter content results in a higher proportion of bound water content to total pore water content.

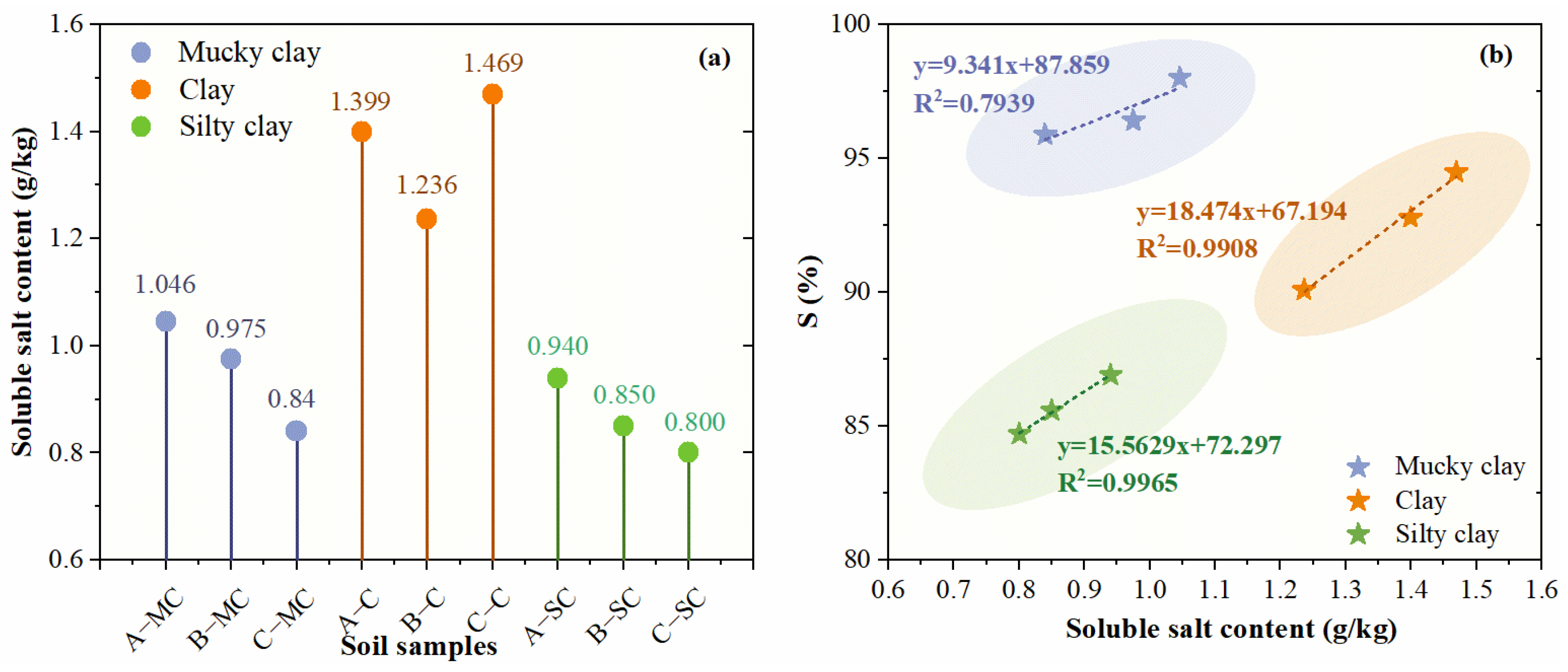
3.5.2. Effect of Soluble Salt Content

The amount of bound water adsorbed by soil particles is the result of the interactions between soil and water, so the bound water content depends not only on the clay content and microstructure but also on the properties of the aqueous solution in the pores. Clay particles with large specific surface energy can interact with the aqueous solution, thereby adsorbing positive charges on the surface of clay particles and forming a double electric layer. Therefore, the content of soluble salts in soil is also an important factor that can affect the content of bound water.
As shown in Figure 12a, the clay layer has the highest soluble salt content, followed by the silty clay layer, and the mucky clay layer has the least soluble salt content. Combined with the bound water fractions of each soil layer in Figure 12b, the highest bound water fraction is found in the mucky clay layer, followed by the clay layer, and the lowest bound water fraction is found in the silty clay layer. Figure 12a,b present inconsistent patterns, so it can be inferred that the content of soluble salt is not a key factor influencing the content of bound water in different types of soils. However, in the same soil layer, the bound water fraction of soil samples and the total amount of soluble salts show a strong linear relationship. It indicates that within a certain range, increased soluble salt content in the soil leads to more ions entering the diffusion layer. Therefore, the bound water film becomes thicker. Additionally, it can be found that the soluble salt content in the marine clay is relatively high, and the change in the phase transition of the pore water during the freezing process will also lead to a change in the salt ion concentration [65]. During the gradual decrease in temperature, the solubility of the salts decreases continuously, which in turn leads to the precipitation of salt crystals. The precipitated crystallized salt adheres to the soil particles or fills in the pores of the soil; thus, the amount of large pores decreases and the amount of small pores increases. In addition, more bound water exists in small pores. Therefore, the more salinity there is, the higher the bound water fraction, the slower the change in bound water content during the freezing process, and the slower the decrease in the maximum T2 value obtained in the NMR test.

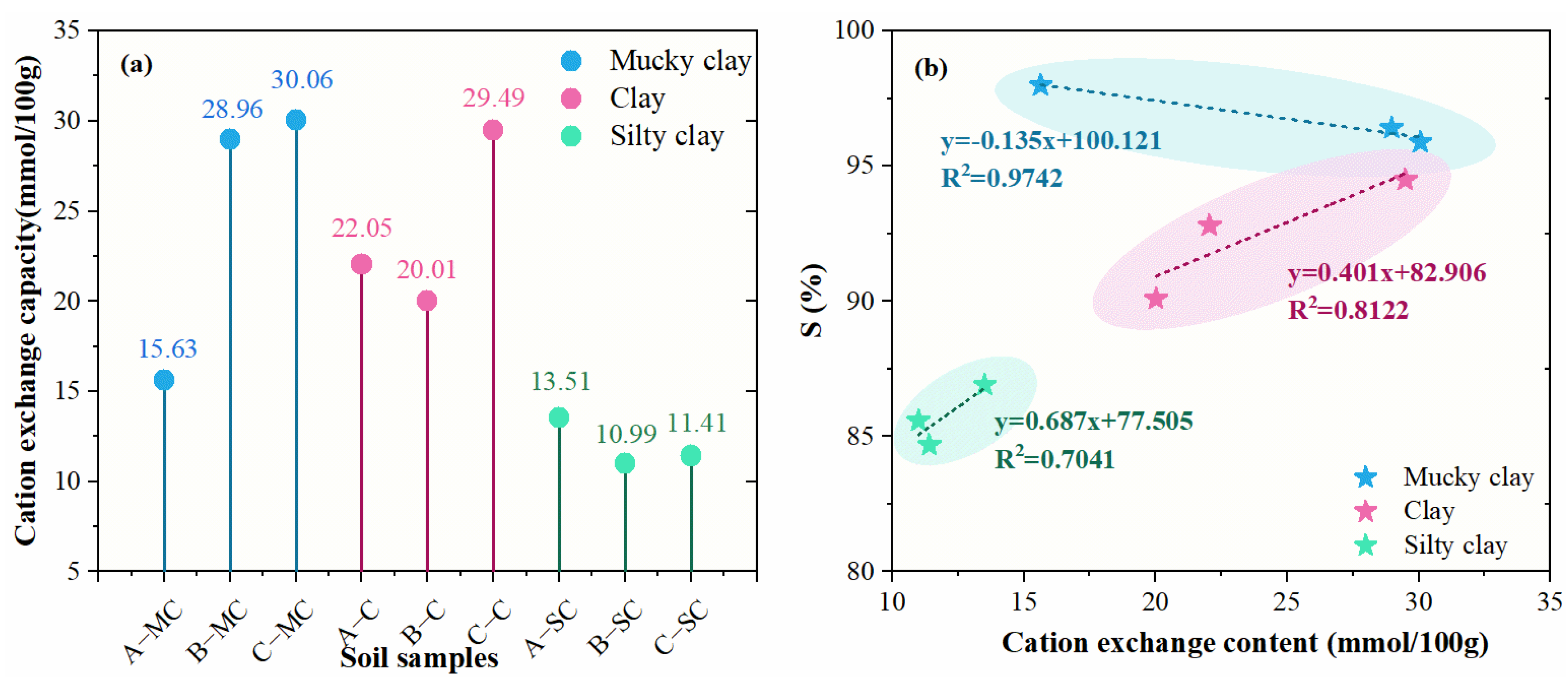
3.5.3. Effect of Cation Exchange Capacity

The more ions in the pore water, the stronger the ion exchange reaction and osmotic diffusion, thus affecting the bound water content adsorbed by soil particles. Therefore, there is a close relationship between cation exchange capacity and bound water content.
In addition, the type of clay directly affects the clay–water interaction because it determines the mineral composition, particle shape, specific surface area, and other physicochemical properties, such as cation exchange capacity. Different types of clay have different water absorption and water holding capacities. For example, kaolinite, montmorillonite, and illite are three common clay minerals with different water adsorption capacities. Montmorillonite has a layered structure, allowing it to easily absorb water and swell between layers. Therefore, its bound water content is high, and it has a large volume change after absorbing water, which generates a large pressure on the surrounding soil. Kaolin, on the other hand, is relatively more stable, with less water-absorbing and swelling. In summary, the type of clay has a significant impact on the stability of infrastructure by affecting the ability of the soil to adsorb water and its physicochemical properties. Therefore, the influence of clay type needs also to be fully considered during infrastructure construction and maintenance.
The relationship between cation exchange capacity and bound water content in different soil layers, as shown in Figure 13a,b, is consistent. Additionally, there is a strong correlation between cation exchange capacity and bound water fraction within the same soil layer. In clay and silty clay layers, the cation content is positively correlated with the bound water fraction because the exchangeable cations will adsorb water molecules around them to form a diffusion layer. Therefore, the greater the amount of exchangeable cations, the thicker the diffusion layer, and the higher the bound water content. In contrast, the bound water fraction and cation exchange capacity are negatively correlated, due to the complex composition of mucky clay. This may be due to the high concentration of cations in the silty clay, the ion concentration in the diffusion layer is saturated. When the ion concentration continues to increase, some of the ions enter the fixed layer from the diffusion layer, meaning the diffusion layer becomes thinner and the bound water content begins to decrease.

4. Conclusions

Based on the differences in the freezing point and content of bound water, capillary water, and bulk water with temperature, in this paper, the NMR technique was used to measure three kinds of marine clay soils from inland to coastal directions. The unfrozen water content of each soil sample at different temperatures was obtained, and the T2 cutoff values were proposed to differentiate between bound water and capillary water. Meanwhile, the freezing behavior of bound water was investigated, and the bound water content of soil samples was calculated. Additionally, factors influencing the bound water content during freezing were also investigated. The conclusions were as follows:
  • T2 thresholds were determined to differentiate between bound water and capillary water in marine clays. In particular, the T2 cutoff values for the mucky clay layer range from 2.81 to 3.01 ms; for the clay layer, they range from 2.85 to 3.37 ms; and for the silty clay layer, they range from 3.10 to 4.06 ms.
  • The content of unfrozen water and bound water at different temperatures during the freezing process was calculated, and the change curves of unfrozen water content and bound water content with temperature were divided into four stages: the trace phase change stage, the intense phase change stage, the transitional phase change stage, and the stabilizing stage. In the trace phase change stage, soil samples with different initial water contents have significant differences in unfrozen water and bound water. However, as the temperature decreases, this difference also gradually decreases until reaching the stabilizing stage, where the unfrozen water in the soil is dominated by the bound water, and the content tends to be close to zero.
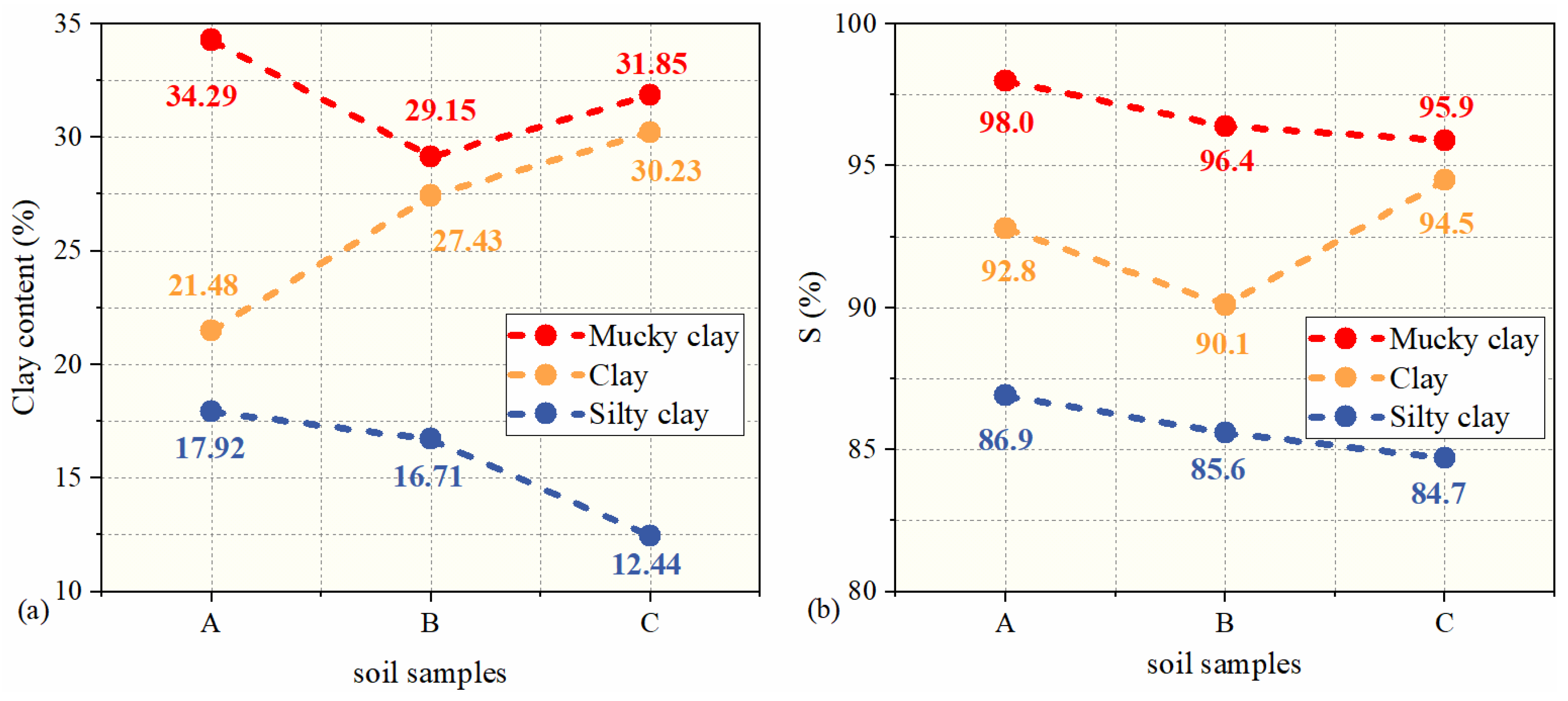
  • Quantitatively analyzed the bound water fraction (S) of the soil samples, and found that the bound water fraction of each soil sample was greater than 80%. This indicates that the pore water in marine clays is dominated by bound water.
  • The clay content and clay types greatly determine the content of bound water in the soil. Generally, the higher the clay content, the higher the bound water content. However, due to the differences in the microstructure of the soil, the clay content is not strictly positively correlated with the bound water content of the soil.
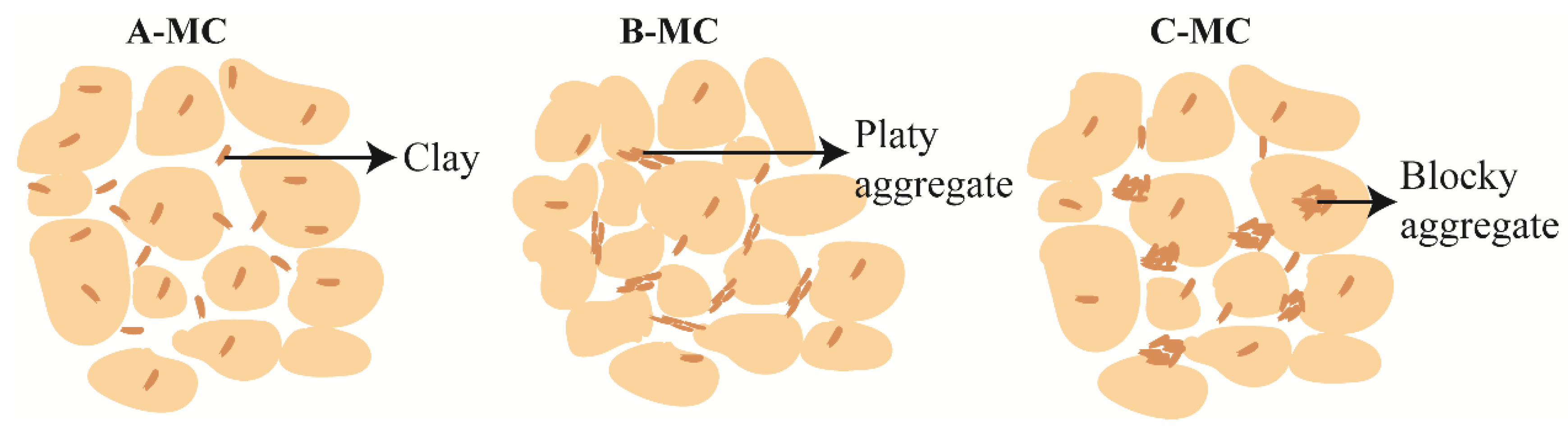
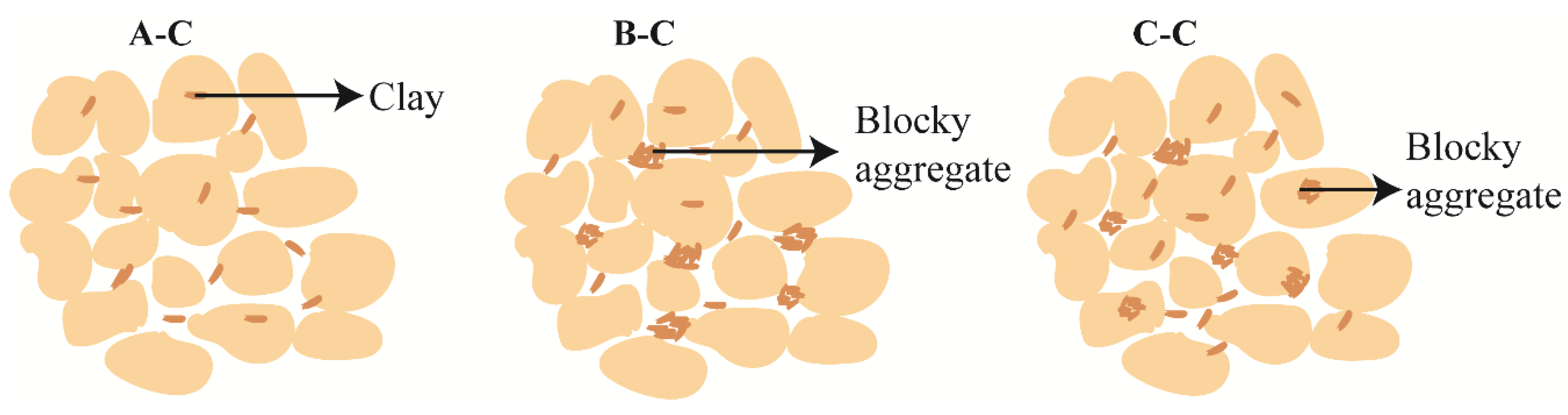
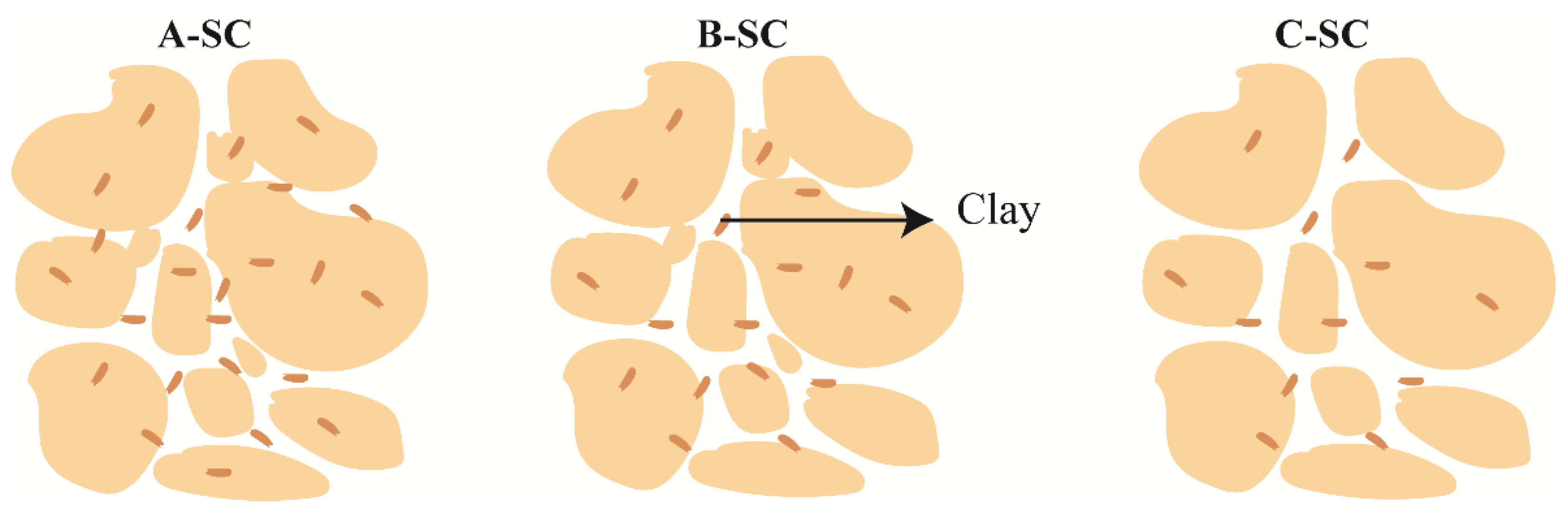
  • The microstructure of the soil also has a certain effect on the bound water content. Larger pores lead to thicker bound water films, while smaller pores result in thinner films. For the same layer of soil with similar material composition, the dispersed arrangement of clay particles can adsorb more bound water, while the formation of clay aggregates will reduce the bound water content. Platy aggregates tend to adsorb more bound water compared to blocky aggregates.
  • The properties of the soil also have a great influence on the bound water content. For the same layer of soil, the changing trends of organic matter content, soluble salt content, and cation exchange capacity are almost consistent with the changes in the bound water fraction. However, the cation exchange capacity and the bound water fraction in the mucky clay layer showed a negative correlation.
However, there are some limitations in this paper. In this study, the NMR method was used to quantitatively analyze the bound water content of marine clay and qualitatively analyze the microstructure of marine clay in conjunction with SEM images. In future research, more emphasis will be placed on quantitatively analyzing SEM images, extracting microstructural parameters, and applying the microstructural parameters to the thermodynamic model to reveal the relationships between the microstructural parameters and soil–water interaction.

Author Contributions

Conceptualization, X.S. and H.C.; methodology, X.S. and H.C.; software, X.S.; validation, X.S., H.C., C.M., Q.Y. and Q.W.; formal analysis, X.S.; investigation, Z.L.; resources, Z.L.; data curation, X.S., H.C., C.M., Q.Y. and Z.W.; writing—original draft preparation, X.S.; writing—review and editing, X.S.; visualization, X.S.; supervision, H.C. and Q.W.; project administration, H.C. and Q.W.; funding acquisition, Q.W. and Q.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 42330708) and the National Natural Science Foundation of China (Grant No. 42302329).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used and analyzed during the current study are available from the corresponding author on reasonable request.

Acknowledgments

We sincerely thank the editors and all anonymous reviewers for their constructive reviews which helped to improve the paper.

Conflicts of Interest

Author Zuojun Lv was employed by the company Power China Northwest Survey Design and Research Institute Co., Ltd., and declared that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Feng, W.-Q.; Zheng, X.-C.; Yin, J.-H.; Chen, W.-B.; Tan, D.-Y. Case study on long-term ground settlement of reclamation project on clay deposits in Nansha of China. Mar. Georesources Geotechnol. 2021, 39, 372–387. [Google Scholar] [CrossRef]
  2. Li, S.; Wang, C.; Guo, F.; Liu, X.; Han, S.; Gao, R. Effect of Bound Water Content on Secondary Compression of Three Marine Silty Clays. J. Mar. Sci. Eng. 2022, 10, 261. [Google Scholar] [CrossRef]
  3. Rao, S.N.; Panda, A.P. Non-linear analysis of undrained cyclic strength of soft marine clay. Ocean Eng. 1999, 26, 241–253. [Google Scholar]
  4. Rattan Lal, M.K.S. Principles of Soil Physics; CRC Press: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
  5. Marshall, T.J.; Holmes, J.W.; Rose, C.W. Soil Physics; Cambridge University Press: London, UK, 1996. [Google Scholar]
  6. Wang, H.; Qian, H.; Gao, Y.; Li, Y. Classification and physical characteristics of bound water in loess and its main clay minerals. Eng. Geol. 2020, 265, 105394. [Google Scholar] [CrossRef]
  7. Yang, E.-J.; Zeng, Z.-T.; Mo, H.-Y.; Hu, T.; Yang, C.-L.; Tang, S.-H. Analysis of Bound Water and Its Influence Factors in Mixed Clayey Soils. Water 2021, 13, 2991. [Google Scholar] [CrossRef]
  8. Li, S.; Wang, C.; Zhang, X.; Zou, L.; Dai, Z. Classification and characterization of bound water in marine mucky silty clay. J. Soils Sediments 2019, 19, 2509–2519. [Google Scholar] [CrossRef]
  9. Yan-long, L.; Tie-hang, W.; Li-jun, S. Determination of Bound Water Content of Loess Soils by Isothermal Adsorption and Thermogravimetric Analysis. Soil Sci. 2015, 180, 90–96. [Google Scholar] [CrossRef]
  10. Low, P.F. Nature and Properties of Water in Montmorillonite-Water Systems. Soil Sci. Soc. Am. J. 1979, 43, 651–658. [Google Scholar] [CrossRef]
  11. Etzler, F.M. A statistical thermodynamic model for water near solid interfaces. J. Colloid Interface Sci. 1983, 92, 43–56. [Google Scholar] [CrossRef]
  12. Yamaguchi, S. On the Sensitivity of Clay. Bull. Disaster Prev. Res. Inst. Kyoto Univ. 1959, 28, 1–30. [Google Scholar]
  13. Wagner, N.; Scheuermann, A. On the relationship between matric potential and dielectric properties of organic free soils: A sensitivity study. Rev. Can. Géotech. 2009, 46, 1202–1215. [Google Scholar] [CrossRef]
  14. Escorihuela, M.J.; de Rosnay, P.; Kerr, Y.H.; Calvet, J.-C. Influence of Bound-Water Relaxation Frequency on Soil Moisture Measurements. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4067–4076. [Google Scholar] [CrossRef]
  15. Zhang, S.; Pei, H. Determining the bound water content of montmorillonite from molecular simulations. Eng. Geol. 2021, 294, 106353. [Google Scholar] [CrossRef]
  16. Chai, M.; Zhang, J.; Zhang, H.; Mu, Y.; Sun, G.; Yin, Z. A method for calculating unfrozen water content of silty clay with consideration of freezing point. Appl. Clay Sci. 2018, 161, 474–481. [Google Scholar] [CrossRef]
  17. Wang, S.; Zhu, W.; Qian, X.; Xu, H.; Fan, X. Temperature effects on non-Darcy flow of compacted clay. Appl. Clay Sci. 2017, 135, 521–525. [Google Scholar] [CrossRef]
  18. Singh, P.N.; Wallender, W.W. Effects of adsorbed water layer in predicting saturated hydraulic conductivity for clays with Kozeny-Carman equation. J. Geotech. Geoenviron. Eng. 2008, 134, 829–836. [Google Scholar] [CrossRef]
  19. Ren, X.; Zhao, Y.; Deng, Q.; Kang, J.; Li, D.; Wang, D. A relation of hydraulic conductivity—Void ratio for soils based on Kozeny-Carman equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
  20. Zhu, W.; Zhang, C.L.; Chiu, A.C.F. Soil-water transfer mechanism for solidified dredged materials. J. Geotech. Geoenviron. Eng. 2007, 133, 588–598. [Google Scholar] [CrossRef]
  21. Ye, C.; Guo, Z.; Cai, C.; Wang, J.; Deng, J. Effect of water content, bulk density, and aggregate size on mechanical characteristics of Aquults soil blocks and aggregates from subtropical China. J. Soils Sediments 2016, 17, 210–219. [Google Scholar] [CrossRef]
  22. Yen, P.S.; Lee, D.J. Errors in bound water measurements using centrifugal settling method. Water Res. 2001, 35, 4004–4009. [Google Scholar] [CrossRef]
  23. Jin, B.; Wilen, B.M.; Lant, P. Impacts of morphological, physical and chemical properties of sludge flocs on dewaterability of activated sludge. Chem. Eng. J. 2004, 98, 115–126. [Google Scholar] [CrossRef]
  24. Liu, H.; Liu, P.; Hu, H.; Zhang, Q.; Wu, Z.; Yang, J.; Yao, H. Combined effects of Fenton peroxidation and CaO conditioning on sewage sludge thermal drying. Chemosphere 2014, 117, 559–566. [Google Scholar] [CrossRef] [PubMed]
  25. Logsdon, S.D.; Laird, D.A. Electrical conductivity spectra of smectites as influenced by saturating cation and humidity. Clays Clay Miner. 2004, 52, 411–420. [Google Scholar] [CrossRef]
  26. Lee, D.J. Interpretation of bound water data measured via dilatometric technique. Water Res. 1996, 30, 2230–2232. [Google Scholar] [CrossRef]
  27. Koopmans, R.W.R.; Miller, R.D. Soil Freezing and Soil Water Characteristic Curves. Soil Sci. Soc. Am. J. 1966, 30, 680–685. [Google Scholar] [CrossRef]
  28. Spaans, E.J.A.; Baker, J.M. Examining the use of time domain reflectometry for measuring liquid water content in frozen soil. Water Resour. Res. 1995, 31, 2917–2925. [Google Scholar] [CrossRef]
  29. Williams, P.J. Experimental Determination of Apparent Specific Heats of Frozen Soils. Geotechnique 1964, 14, 133–142. [Google Scholar] [CrossRef]
  30. He, D.-Q.; Zhang, Y.-J.; He, C.-S.; Yu, H.-Q. Changing profiles of bound water content and distribution in the activated sludge treatment by NaCl addition and pH modification. Chemosphere 2017, 186, 702–708. [Google Scholar] [CrossRef]
  31. Su, Z.; Tan, X.; Chen, W.; Jia, H.; Xu, F. A model of unfrozen water content in rock during freezing and thawing with experimental validation by nuclear magnetic resonance. J. Rock Mech. Geotech. Eng. 2022, 14, 1545–1555. [Google Scholar] [CrossRef]
  32. Kozlowski, T. A comprehensive method of determining the soil unfrozen water curves 2. Stages of the phase change process in frozen soil-water system. Cold Reg. Sci. Technol. 2003, 36, 81–92. [Google Scholar] [CrossRef]
  33. Zhou, X.; Zhou, J.; Kinzelbach, W.; Stauffer, F. Simultaneous measurement of unfrozen water content and ice content in frozen soil using gamma ray attenuation and TDR. Water Resour. Res. 2014, 50, 9630–9655. [Google Scholar] [CrossRef]
  34. Dirksen, C.; Dasberg, S. Improved Calibration of Time Domain Reflectometry Soil Water Content Measurements. Soil Sci. Soc. Am. J. 1993, 57, 660. [Google Scholar] [CrossRef]
  35. Osipov, V.I. Nanofilms of adsorbed water in clay: Mechanism of formation and properties. Water Resour. 2012, 39, 709–721. [Google Scholar] [CrossRef]
  36. Yuan, Y.; Rezaee, R.; Verrall, M.; Hu, S.-Y.; Zou, J.; Testmanti, N. Pore characterization and clay bound water assessment in shale with a combination of NMR and low-pressure nitrogen gas adsorption. Int. J. Coal Geol. 2018, 194, 11–21. [Google Scholar] [CrossRef]
  37. Kong, L.; Wang, Y.; Sun, W.; Qi, J. Influence of plasticity on unfrozen water content of frozen soils as determined by nuclear magnetic resonance. Cold Reg. Sci. Technol. 2020, 172, 102993. [Google Scholar] [CrossRef]
  38. Tian, H.; Wei, C.; Lai, Y.; Chen, P. Quantification of Water Content during Freeze–Thaw Cycles: A Nuclear Magnetic Resonance Based Method. Vadose Zone J. 2018, 17, 160124. [Google Scholar] [CrossRef]
  39. Wang, Y.; Lu, S.; Ren, T.; Li, B. Bound Water Content of Air-Dry Soils Measured by Thermal Analysis. Soil Sci. Soc. Am. J. 2011, 75, 481–487. [Google Scholar] [CrossRef]
  40. Zhang, M.; Pei, W.; Li, S.; Lu, J.; Jin, L. Experimental and numerical analyses of the thermo-mechanical stability of an embankment with shady and sunny slopes in a permafrost region. Appl. Therm. Eng. 2017, 127, 1478–1487. [Google Scholar] [CrossRef]
  41. Kozlowski, T. A semi-empirical model for phase composition of water in clay-water systems. Cold Reg. Sci. Technol. 2007, 49, 226–236. [Google Scholar] [CrossRef]
  42. Anderson, D.M.; Tice, A.R. Predicting unfrozen water contents in frozen soils from surface area measurements. Highw. Res. Rec. 1972, 393, 12–18. [Google Scholar]
  43. McKenzie, J.M.; Voss, C.I.; Siegel, D.I. Groundwater flow with energy transport and water-ice phase change: Numerical simulations, benchmarks, and application to freezing in peat bogs. Adv. Water Resour. 2007, 30, 966–983. [Google Scholar] [CrossRef]
  44. Xiao, Z.; Lai, Y.M.; Zhang, J. A thermodynamic model for calculating the unfrozen water content of frozen soil. Cold Reg. Sci. Technol. 2020, 172, 103011. [Google Scholar] [CrossRef]
  45. Yang, G.C.; Bai, B. A thermodynamic model to simulate the thermo-mechanical behavior of fine-grained gassy soil. Bull. Eng. Geol. Environ. 2020, 79, 2325–2339. [Google Scholar] [CrossRef]
  46. Li, K.Y.; Wang, C.; Wu, Y.M.; Lin, Z.K.; Ren, J.P.; Gao, J.; Li, S.Y. Study on the supercooling and crystallization mechanism of saline soil based on thermodynamic framework. J. Hydrol. 2024, 628, 130451. [Google Scholar] [CrossRef]
  47. Chen, Y.; Zhou, Z.; Wang, J.; Zhao, Y.; Dou, Z. Quantification and division of unfrozen water content during the freezing process and the influence of soil properties by low-field nuclear magnetic resonance. J. Hydrol. 2021, 602, 126719. [Google Scholar] [CrossRef]
  48. Cowan, B. Nuclear Magnetic Resonance and Relaxation; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
  49. Lv, Z. Study on the Characteristics of Bound Water and Secondary Consolidation of Cohesive Soil in the Southeast of Chongming Island. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
  50. Dastidar, R. Nuclear Magnetic Resonance (NMR) Study of Freezing and Thawing of Saturated Porous Media and Application to Shale and Pore Volume Compressibility Estimation. Ph.D. Thesis, The University of Oklahoma, Norman, OK, USA, 2007. [Google Scholar]
  51. Bayer, J.V.; Jaeger, F.; Schaumann, G.E. Proton Nuclear Magnetic Resonance (NMR) Relaxometry in Soil Science Applications. Open Magn. Reson. J. 2010, 3, 15–26. [Google Scholar] [CrossRef]
  52. Bird, N.R.A.; Preston, A.R.; Randall, E.W.; Whalley, W.R.; Whitmore, A.P. Measurement of the size distribution of water-filled pores at different matric potentials by stray field nuclear magnetic resonance. Eur. J. Soil Sci. 2005, 56, 135–143. [Google Scholar] [CrossRef]
  53. Jaeger, F.; Shchegolikhina, A.; As, H.V.; Schaumann, G.E. Proton NMR Relaxometry as a Useful Tool to Evaluate Swelling Processes in Peat Soils. Open Magn. Reson. J. 2010, 3, 27–45. [Google Scholar] [CrossRef]
  54. Zhou, J.; Zhou, H.D. Quantitative Analysis of Unfrozen Water Content of Muddy Clay Under Extremely Low Temperature Freezing Conditions. In Proceedings of the 20th International Conference on Cold Regions Engineering (ICCRE), Univ Alaska Anchorage, Coll Engn, Anchorage, AK, USA, 13–16 May 2024; pp. 79–93. [Google Scholar]
  55. An, R.; Gao, H.D.; Chen, C.; Zhang, X.W. Quantification and division of unfrozen water content of frozen soils during freezing and the influence of freeze-thaw cycles. Bull. Eng. Geol. Environ. 2024, 83, 440. [Google Scholar] [CrossRef]
  56. Jaeger, F.; Bowe, S.; Van As, H.; Schaumann, G.E. Evaluation of 1H NMR relaxometry for the assessment of pore-size distribution in soil samples. Eur. J. Soil Sci. 2009, 60, 1052–1064. [Google Scholar] [CrossRef]
  57. Pajzderska, A.; Gonzalez, M.A.; Mielcarek, J.; Wąsicki, J. Water Behavior in MCM-41 As a Function of Pore Filling and Temperature Studied by NMR and Molecular Dynamics Simulations. J. Phys. Chem. C 2014, 118, 23701–23710. [Google Scholar] [CrossRef]
  58. Kiwilsza, A.; Pajzderska, A.; Gonzalez, M.A.; Mielcarek, J.; Wąsicki, J. QENS and NMR Study of Water Dynamics in SBA-15 with a Low Water Content. J. Phys. Chem. C 2015, 119, 16578–16586. [Google Scholar] [CrossRef]
  59. Han, Y.; Wang, Q.; Kong, Y.; Cheng, S.; Wang, J.; Zhang, X.; Wang, N. Experiments on the initial freezing point of dispersive saline soil. CATENA 2018, 171, 681–690. [Google Scholar] [CrossRef]
  60. Zhang, S.Q.; Pei, H.F.; Ploetze, M.; Zhang, C.; Tan, D.Y. Investigation of Bound Water in Clay Based on Isothermal Adsorption Experiments and Metadynamics Studies from the Perspective of Water Potential. J. Geotech. Geoenviron. Eng. 2024, 150, 04024113. [Google Scholar] [CrossRef]
  61. Han, M.; Peng, W.; Ma, B.; Yu, Q.; Kasama, K.; Furukawa, Z.; Niu, C.; Wang, Q. Micro–composition evolution of the undisturbed saline soil undergoing different freeze–thaw cycles. Cold Reg. Sci. Technol. 2023, 210, 103825. [Google Scholar] [CrossRef]
  62. Mitchell, J.K. Fundamentals of soil behavior. Soil Sci. Soc. Am. J. 1976, 40, 827–866. [Google Scholar]
  63. Shen, J.; Wang, Q.; Chen, Y.; Han, Y.; Zhang, X.; Liu, Y. Evolution process of the microstructure of saline soil with different compaction degrees during freeze-thaw cycles. Eng. Geol. 2022, 304, 106699. [Google Scholar] [CrossRef]
  64. Keller, G.H. Organic matter and the geotechnical properties of submarine sediments. Geo-Mar. Lett. 1982, 2, 191–198. [Google Scholar] [CrossRef]
  65. Zhang, S.; Zhang, J.; Gui, Y.; Chen, W.; Dai, Z. Deformation properties of coarse-grained sulfate saline soil under the freeze-thaw-precipitation cycle. Cold Reg. Sci. Technol. 2020, 177, 103121. [Google Scholar] [CrossRef]
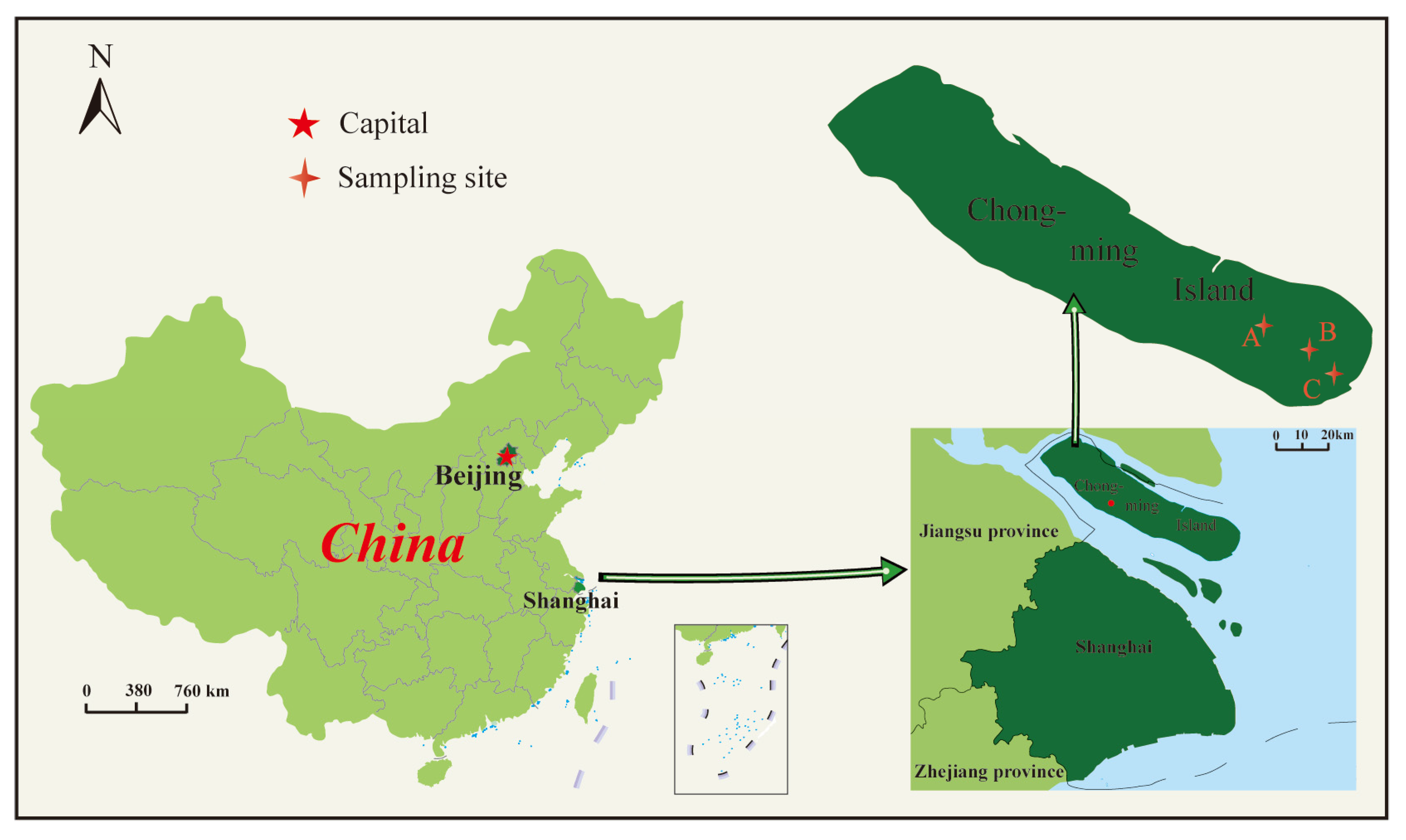
Jmse 13 00546 g001
Figure 1. Geographical location of the study area.
Figure 1. Geographical location of the study area.
Jmse 13 00546 g001
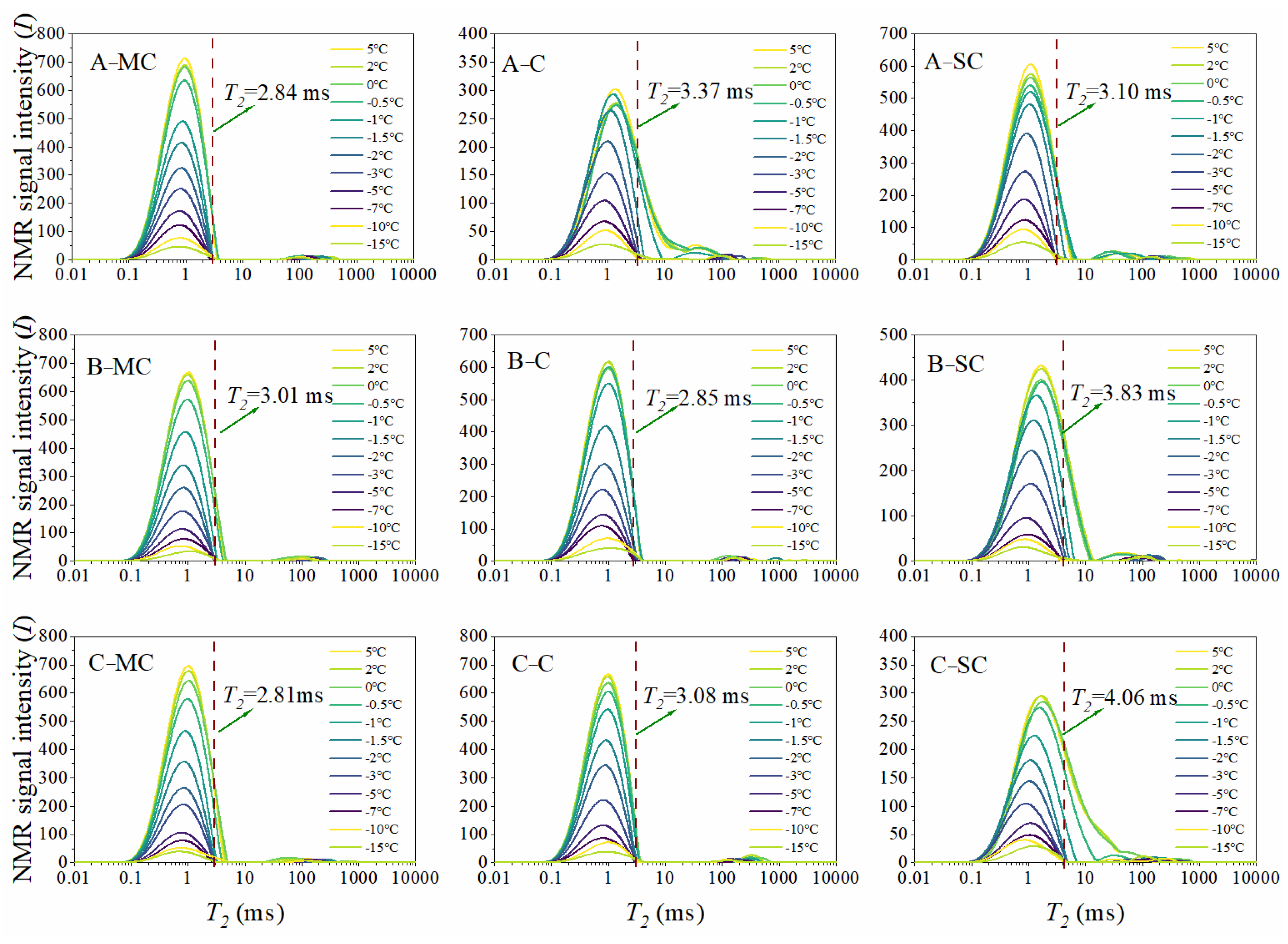
Jmse 13 00546 g002
Figure 2. T2 distribution curves during the freezing process.
Figure 2. T2 distribution curves during the freezing process.
Jmse 13 00546 g002
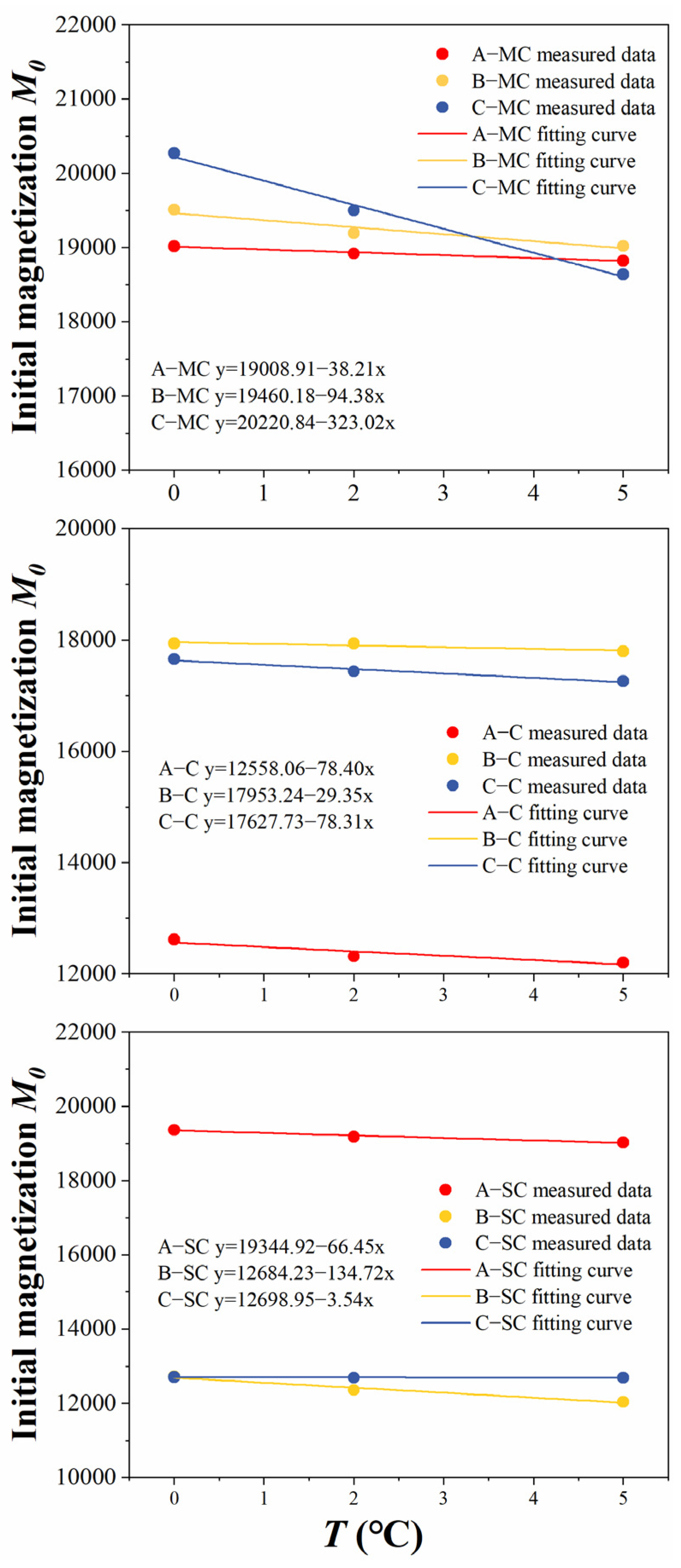
Jmse 13 00546 g003
Figure 3. Relationships between M0 and T.
Figure 3. Relationships between M0 and T.
Jmse 13 00546 g003
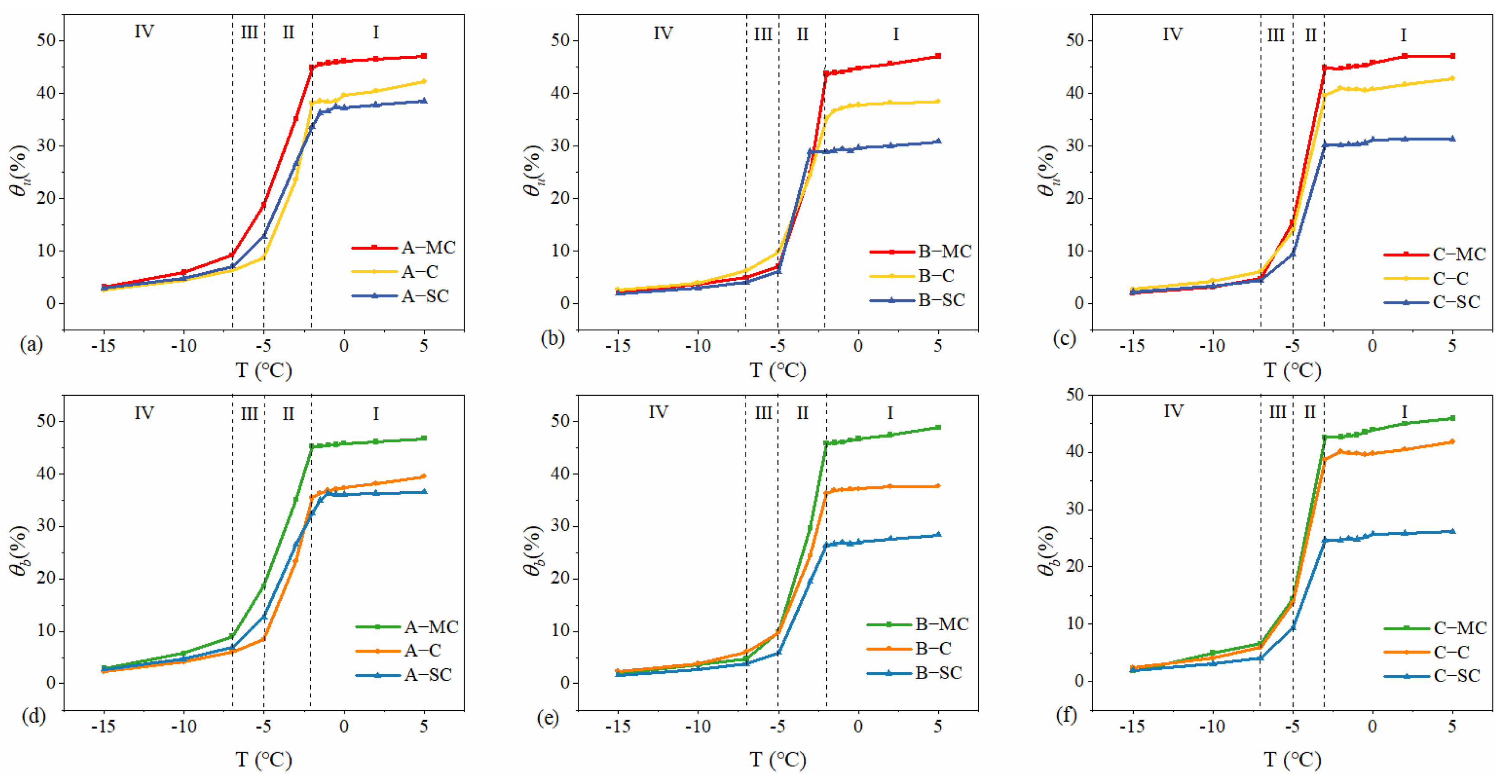
Jmse 13 00546 g004
Figure 4. (a–c) Relationships between θu and T. (d–f) Relationships between θb and T.
Figure 4. (a–c) Relationships between θu and T. (d–f) Relationships between θb and T.
Jmse 13 00546 g004
Jmse 13 00546 g005
Figure 5. Particle size distribution of soil samples at sampling sites (a) A, (b) B, and (c) C.
Figure 5. Particle size distribution of soil samples at sampling sites (a) A, (b) B, and (c) C.
Jmse 13 00546 g005
Jmse 13 00546 g006
Figure 6. (a) Clay content of all soil samples. (b) Bound water fraction (S) of all soil samples.
Figure 6. (a) Clay content of all soil samples. (b) Bound water fraction (S) of all soil samples.
Jmse 13 00546 g006
Jmse 13 00546 g007
Figure 7. SEM images of soil samples (a) A-MC, (b) B-MC, (c) C-MC, (d) A-C, (e) B-C, (f) C-C, (g) A-SC, (h) B-SC, (i) C-SC. (2000× magnification).
Figure 7. SEM images of soil samples (a) A-MC, (b) B-MC, (c) C-MC, (d) A-C, (e) B-C, (f) C-C, (g) A-SC, (h) B-SC, (i) C-SC. (2000× magnification).
Jmse 13 00546 g007
Jmse 13 00546 g008
Figure 8. Microstructure of mucky clay.
Figure 8. Microstructure of mucky clay.
Jmse 13 00546 g008
Jmse 13 00546 g009
Figure 9. Microstructure of clay.
Figure 9. Microstructure of clay.
Jmse 13 00546 g009
Jmse 13 00546 g010
Figure 10. Microstructure of silty clay.
Figure 10. Microstructure of silty clay.
Jmse 13 00546 g010
Jmse 13 00546 g011
Figure 11. (a) Organic matter content of each soil layer. (b) Relationship between bound water fraction and organic matter content.
Figure 11. (a) Organic matter content of each soil layer. (b) Relationship between bound water fraction and organic matter content.
Jmse 13 00546 g011
Jmse 13 00546 g012
Figure 12. (a) Soluble salt content of each soil layer. (b) Relationship between bound water fraction and soluble salt content.
Figure 12. (a) Soluble salt content of each soil layer. (b) Relationship between bound water fraction and soluble salt content.
Jmse 13 00546 g012
Jmse 13 00546 g013
Figure 13. (a) Cation exchange content of each soil layer. (b) Relationship between bound water fraction and cation exchange capacity.
Figure 13. (a) Cation exchange content of each soil layer. (b) Relationship between bound water fraction and cation exchange capacity.
Jmse 13 00546 g013
Table 1. Naming of each type of soil.
Table 1. Naming of each type of soil.
Soil TypeSampling Site ASampling Site BSampling Site C
Mucky clayA-MCB-MCC-MC
ClayA-CB-CC-C
Silty clayA-SCB-SCC-SC
Table 2. Properties of soil samples.
Table 2. Properties of soil samples.
Soil TypeWater Content ω (%)Density ρ (g/cm3)Liquid Limit ω L (%)Plasticity Limit ω P (%)Total Soluble Salts (g/kg)Cation Exchange Capacity (mmol/100 g)
A-MC40.811.8340210.95715.63
A-C46.631.7858301.46929.49
A-SC37.931.8244230.94013.51
B-MC45.881.7749321.04628.96
B-C39.221.8344241.39920.05
B-SC29.182.0531230.85010.99
C-MC43.281.7551290.84030.06
C-C41.781.8048251.23620.01
C-SC31.301.8026210.80011.14
Table 3. The clay content of each soil sample.
Table 3. The clay content of each soil sample.
Sampling Site ASampling Site BSampling Site C
A-MCA-CA-SCB-MCB-CB-SCC-MCC-CC-SC
Clay content (%)34.2921.4817.9229.1527.4316.7131.8530.2312.44
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Shan, X.; Chen, H.; Meng, C.; Lv, Z.; Yu, Q.; Wang, Z.; Wang, Q. Quantitative Analysis of Bound Water Content in Marine Clay and Its Influencing Factors During the Freezing Process by Nuclear Magnetic Resonance. J. Mar. Sci. Eng. 2025, 13, 546. https://doi.org/10.3390/jmse13030546

AMA Style

Shan X, Chen H, Meng C, Lv Z, Yu Q, Wang Z, Wang Q. Quantitative Analysis of Bound Water Content in Marine Clay and Its Influencing Factors During the Freezing Process by Nuclear Magnetic Resonance. Journal of Marine Science and Engineering. 2025; 13(3):546. https://doi.org/10.3390/jmse13030546

Chicago/Turabian Style

Shan, Xuehan, Huie Chen, Chuqiao Meng, Zuojun Lv, Qingbo Yu, Zhaoxi Wang, and Qing Wang. 2025. "Quantitative Analysis of Bound Water Content in Marine Clay and Its Influencing Factors During the Freezing Process by Nuclear Magnetic Resonance" Journal of Marine Science and Engineering 13, no. 3: 546. https://doi.org/10.3390/jmse13030546

APA Style

Shan, X., Chen, H., Meng, C., Lv, Z., Yu, Q., Wang, Z., & Wang, Q. (2025). Quantitative Analysis of Bound Water Content in Marine Clay and Its Influencing Factors During the Freezing Process by Nuclear Magnetic Resonance. Journal of Marine Science and Engineering, 13(3), 546. https://doi.org/10.3390/jmse13030546

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop